Performance Assessment of BDS-3 PPP-B2b/INS Loosely Coupled Integration

Abstract

The BeiDou global navigation satellite system (BDS-3) has been officially providing a real-time precise point positioning (PPP) augmentation service, known as the PPP-B2b service, since 2020. Decimeter-level positioning accuracy is expected to be achieved based on the PPP-B2b service. It shows great potential for global navigation satellite system (GNSS) real-time applications, including, for example, vehicle positioning on land. However, the application of the PPP-B2b service is still full of challenges in the urban environment because of GNSS signal blockage. The inertial navigation system (INS) is a popular technology which can provide continuous positions under GNSS challenging scenarios. In this study, we constructed a BDS-3 PPP-B2b/INS loosely coupled integration system for vehicle positioning and evaluated its performance through two automotive experiments. In the first experiment, four periods of 30 s GNSS outages were simulated to evaluate the performance of PPP-B2b/INS loosely coupled integration during GNSS outages. During the simulated GNSS outages, PPP-B2b positioning did not work. Nevertheless, PPP-B2b/INS loosely coupled integration provided continues solution through INS mechanization. The averaged positioning errors at the last epoch of outages were 300.6/498.0/41.0 cm for PPP-B2b/MEMS-IMU and 18.6/21.8/6.1 cm for PPP-B2b/Tactical-IMU loosely coupled integration, in the east, north and up directions, respectively. In the second experiment, we drove the land vehicle in a complex urban environment for 15 min. During this period, two GNSS signal interruptions occurred due to the occlusion of bridges, lasting 15 s and 5 s, respectively. The results show that the improvement of positioning accuracy in the east, north, and up components were 64.1%, 77.8%, and 73.8% respectively for PPP-B2b/MEMS-IMU loosely coupled integration, and 63.9%, 79.5%, and 74.4% respectively for PPP-B2b/Tactical-IMU loosely coupled integration, as compared to the positioning accuracy of PPP-B2b only.

1. Introduction

Real-time kinematic (RTK) and precise point positioning (PPP) are usually conducted to satisfy the high-precision positioning requirements of autonomous cars and unmanned aerial vehicles. RTK technology can archive centimeter-level positioning accuracy with short initialization time [1,2], but it needs regional corrections from a reference station or reference network. The concept of PPP technology was proposed in 1997 [3,4], and it could obtain decimeter- even to centimeter-level positioning accuracy using standalone global navigation satellite system (GNSS) equipment [5]. Over the decades, PPP has become a widely used high-precision GNSS positioning technology. Precise GNSS satellite products are indispensable for the implementation of PPP. Motivated by the requirements of GNSS real-time applications, the international GNSS service (IGS) has been providing real-time service (RTS) through Internet communication since 2013 [6,7]. The RTS corrections, including precise orbit correction, clock offset correction, and code biases, are sent to users based on the Networked Transport of RTCM via Internet Protocol (NTRIP) [8]. By applying these corrections, the users can compute precise satellite orbits and clocks, and then carry out real-time PPP. However, RTS may be interrupted when the Internet is unavailable [9].

The commissioning of the BeiDou global navigation satellite system (BDS-3) was announced on 31 July 2020 [10,11]. Several featured services are provided by BDS-3, including short message communication, international search and rescue, and the PPP-B2b service, in addition to global positioning, navigation and time (PNT) services [12]. The BDS-3 PPP-B2b service can support real-time PPP based on PPP-B2b corrections broadcast by 3 BDS-3 geostationary earth orbit (GEO) satellites [13,14]. The PPP-B2b corrections include satellite orbit correction, clock correction, and code bias correction. At present, the BDS-3 PPP-B2b service only provides corrections for BDS-3/GPS satellites. The BDS-3 PPP-B2b service can be obtained free of charge. In addition, unlike IGS-RTS, Internet communication is not required since the BDS-3 PPP-B2b service is a satellite-based service. Therefore, the PPP-B2b service has great potential for real-time GNSS applications. Recently, publications have presented the precision of PPP-B2b corrections and positioning performance based on the PPP-B2b service [15,16,17,18,19]. These results indicate that the signal-in-space accuracy of precise ephemeris calculated with PPP-B2b corrections is at the decimeter- even to centimeter-level. In term of positioning performance, centimeter-level accuracy in the static mode and decimeter-level in the kinematic mode could be achieved. However, positioning performance based on the BDS-3 PPP-B2b service would be significantly degraded in severe environments, due to GNSS signal blockages. To overcome this weakness, GNSS should be integrated with other sensors [20]. The inertial navigation system (INS) is an autonomous and spontaneous navigation system, which has potential to overcome degradation of GNSS positioning performance when GNSS signal outage occurs. Many valuable studies in PPP/INS integration have been published in the past decades, including loosely coupled (LC) model and tightly coupled (TC) integration [21,22,23,24,25]. In these publications, the precise ephemeris derived from IGS final precise products or from the IGS RTS service is adopted for PPP/INS integration processing. However, there is a considerable delay obtaining IGS final precise products. As for the IGS RTS service, the PPP/INS integration is restricted when there is a lack of Internet communication. It is worth mentioned that the above disadvantages can be overcome when the BDS-3 PPP-B2b service has implemented PPP/INS integration.

To our knowledge, there has until now been no published research on BDS-3 PPP-B2b/INS integration. In this paper, we focus on performance assessment of BDS-3 PPP-B2b/INS loosely coupled integration. Two vehicle kinematic experiments were carried out to assess the performance of PPP-B2b/INS loosely coupled integration. The rest of the paper is organized as follows. In Section 2, the methodology is introduced, including PPP positioning based on PPP-B2b corrections, the INS model, and their loosely coupled integration. In Section 3, the experimental set-ups and data processing strategies are presented in detail. Section 4 presents the performance of PPP-B2b/INS loosely coupled integration in urban environments. Finally, conclusions and perspectives are illustrated in Section 5.

2. Methodology

BDS-3 PPP-B2b/INS loosely coupled integration can be divided into three parts, including PPP positioning based on the PPP-B2b service, the INS model, and the integration of BDS-3 PPP-B2b and INS. In this section, these three parts are described in detail.

2.1. PPP Positioning Based on PPP-B2b Service

As is known, precise satellite orbit and clock products play a key role in PPP processing. For PPP-B2b service, the satellite orbit corrections and clock offset corrections are broadcast by BDS-3 GEO satellites. Up to now, the PPP-B2b service has provided corrections only for BDS-3/GPS satellites. According to the PPP-B2b Interface Control Document (ICD) from China Satellite Navigation Office (CSNO) [26], the PPP-B2b orbit corrections are given in the radial $\left(\delta O_{radial}\right)$, along-track $\left(\delta O_{along}\right)$, and cross-track $\left(\delta O_{cross}\right)$ directions. Hence, the orbit correction vector $\delta {\mathit{O}}_{B2b}={\left[\begin{array}{ccc}\delta O_{radial}& \delta O_{along}& \delta O_{cross}\end{array}\right]}^T$ should first be transformed to the Earth-Center Earth-Fixed (ECEF) frame. This is because the satellite positions derived from CNAV1/LNAV broadcast ephemeris are based on the ECEF frame. This transformation can be described as follows:

$$\delta {\mathit{X}}^{sat}=\left[\begin{array}{ccc}{\mathit{e}}_{radial}& {\mathit{e}}_{along}& {\mathit{e}}_{cross}\end{array}\right]·\delta {\mathit{O}}_{B2b}$$

(1)

with

$$\{\begin{array}{c}{\mathit{e}}_{radial}=\frac{\mathit{r}}{\left|\mathit{r}\right|}\\ {\mathit{e}}_{cross}=\frac{\mathit{r}\times \dot{\mathit{r}}}{\left|\mathit{r}\times \dot{\mathit{r}}\right|}\\ {\mathit{e}}_{along}={\mathit{e}}_{cross}\times {\mathit{e}}_{radial}\end{array}$$

(2)

where $\delta {\mathit{X}}^{sat}={\left[\begin{array}{ccc}\delta O_x& \delta O_y& \delta O_z\end{array}\right]}^T$ represents the PPP-B2b orbit correction vector in the ECEF frame. $\mathit{r}$ and $\dot{\mathit{r}}$ are the satellite position and velocity vectors derived from broadcast ephemeris. Then, the precise satellite position vector ${\mathit{X}}_{prec}$ can be computed by

$${\mathit{X}}_{prec}={\mathit{X}}_{brdc}-\delta {\mathit{X}}^{sat}$$

(3)

where ${\mathit{X}}_{brdc}$ is the satellite position vector derived from broadcast ephemeris. As described in ICD document, the PPP-B2b clock correction parameter is defined as offset to the broadcast ephemeris clock in meters. The precise satellite clock offset is given by

$$d{t}_{prec}^{sat}=d{t}_{brdc}^{sat}-\frac{C_0}{c}$$

(4)

where $C_0$ represents the PPP-B2b clock correction parameter; $d{t}_{brdc}^{sat}$ is the satellite clock offset derived from broadcast ephemeris; $d{t}_{prec}^{sat}$ denotes the precise PPP-B2b clock offset; $c$ is the velocity of light in a vacuum.

The GNSS raw code and carrier-phase measurements can read as [27,28]

$$\{\begin{array}{c}{P}_i=\rho +c·\left(d{t}_r-d{t}^s\right)+T+\frac{f_1^2}{f_i^2}·I_1+B_{r,i}-B_i^s+{\epsilon }_{P_i}\\ L_i=\rho +c·\left(d{t}_r-d{t}^s\right)+T-\frac{f_1^2}{f_i^2}·I_1+{\lambda }_i\left(N_i+b_{r,i}-b_i^s\right)+{\epsilon }_{L_i}\end{array}$$

(5)

where $i$ represents the frequency number; $P_i$ and $L_i$ are raw code and phase measurements; $\rho$ denotes the geometric distance from satellite to receiver; $d{t}_r$ and $d{t}^s$ are the clock offsets at the receiver and satellite, respectively; $f_i$ is the frequency value, $T$ is the tropospheric delay, and $I_1$ denotes the ionospheric delay for $L_1$; $B_{r,i}$ and $B_i^s$ represent the code bias at the receiver/satellite end; $b_{r,i}$ and $b_i^s$ denote the phase bias at the receiver/satellite end; ${\epsilon }_{P_i}$ and ${\epsilon }_{L_i}$ are the unmodelled errors of code/phase measurements. The relativistic effect, Sagnac effect, Shapiro time delay [29], site displacements [30], and phase windup [31] should be corrected according to the corresponding models.

The ionosphere-free code and phase combinations are usually adopted by PPP to eliminate the first-order ionospheric delay. The ionospheric-free code and phase combinations read as [32]:

$$\{\begin{array}{c}{P}_{IF}=\alpha ·P_i+\left(1-\alpha \right)·P_j=\rho +c·d{\overline{t}}_r-c·d{t}^s-B_{IF}^s+T+{\epsilon }_{P_{IF}}\\ L_{IF}=\alpha ·L_i+\left(1-\alpha \right)·L_j=\rho +c·d{\overline{t}}_r-c·d{t}^s+T+{\lambda }_{IF}·{\overline{N}}_{IF}+{\epsilon }_{L_{IF}}\end{array}$$

(6)

where $\alpha =f_i^2/\left(f_i^2-f_j^2\right)$ and ${\lambda }_{IF}·{\overline{N}}_{IF}={\lambda }_{IF}{N}_{IF}-b_{IF}^s+b_{r,IF}-B_{r,IF}$, $b_{IF}^s$ and $b_{r,IF}$ are phase bias of ionospheric-free phase combination at the satellite/receiver end, $B_{IF}^s$ and $B_{r,IF}$ represent code bias of ionospheric-free code combination at the satellite/receiver end, ${\lambda }_{IF}$ and $N_{IF}$ are the ionospheric-free wavelength and the ionospheric-free ambiguity, respectively; $d{\overline{t}}_r$ is the recombined receiver clock offset, which absorbs the receiver code bias of ionospheric-free code combination; ${\epsilon }_{P_{IF}}$ and ${\epsilon }_{L_{IF}}$ denote the unmodelled errors of ionospheric-free code and phase combinations. It is noted that the ionospheric-free code bias at the satellite end should be corrected by applying PPP-B2b differential code bias corrections [15].

When the recovered PPP-B2b precise satellite orbits and clock offsets have been applied, the satellite orbit and clock errors are considered eliminated. The tropospheric delay can be divided into the dry and wet parts. The Saastamoinen model is usually used to correct the dry part, and the wet part must be estimated as unknown. Then the ionospheric-free code and phase combinations can be linearized as

$$\{\begin{array}{c}{p}_{IF}=-\mathit{e}·\mathit{x}+c·d{\overline{t}}_r+M_W·zwd+{\epsilon }_{P_{IF}}\\ l_{IF}=-\mathit{e}·\mathit{x}+c·d{\overline{t}}_r+M_W·zwd+{\lambda }_{IF}·{\overline{N}}_{IF}+{\epsilon }_{L_{IF}}\end{array}$$

(7)

where $\mathit{e}$, $\mathit{x}$ represent the unit vector from receiver to satellite, and the vector of position increment, respectively; $zwd$ denotes the zenith wet delay and $M_W$ is the corresponding mapping function. In this equation, the remaining unknown parameters include only the receiver position increment vector $\mathit{x}$, the receiver clock offset $d{\overline{t}}_r$, the zenith wet delay $zwd$ and the ionosphere-free ambiguity ${\lambda }_{IF}{\overline{N}}_{IF}$. By adopting a Kalman filter, the unknown parameters can be exactly estimated. It should be noted that in this paper the ionospheric-free Doppler combination is used to derive the velocity [23].

2.2. INS Model

The mechanization of INS in the navigation frame ($n$-frame) can be expressed as an integral process for the following equation [33,34]:

$$\left[\begin{array}{c}{\dot{\mathit{p}}}_{INS}^n\\ {\dot{\mathit{v}}}_{INS}^n\\ {\dot{\mathit{C}}}_b^n\end{array}\right]=\left[\begin{array}{c}{\mathit{D}}^{-1}{\mathit{v}}_{INS}^n\\ {\mathit{C}}_b^n{\mathit{f}}^b-\left(2{\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n\right)\times {\mathit{v}}_{INS}^n+{\mathit{g}}^n\\ {\mathit{C}}_b^n\left({\mathsf{\omega }}_{ib}^b\times \right)-\left({\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n\right)\times {\mathit{C}}_b^n\end{array}\right]$$

(8)

where ${\mathit{D}}^{-1}$ is the diagonal matrix to transform the rectangular coordinates into geodetic coordinates; ${\mathit{p}}_{INS}^n$ and ${\mathit{v}}_{INS}^n$ denote the INS position vector and INS velocity vector in $n$-frame; ${\mathit{C}}_b^n$ represents the transformation matrix from body-frame ($b$-frame) to $n$-frame; ${\mathit{f}}^b$ is the inertial measurement unit (IMU) specific force measurement projected in $b$-frame; ${\mathsf{\omega }}_{ib}^b$ denotes the IMU angular rate measurement expressed in $b$-frame; ${\mathsf{\omega }}_{ie}^n$ is the vector of earth rotation rate expressed in $n$-frame; ${\mathit{g}}^n$ is the gravity vector presented in $n$-frame; ${\mathsf{\omega }}_{en}^n$ represents the rotation rate of ECEF frame relative to that of $n$-frame expressed in $n$-frame; The symbol “$\times$” represents the cross-product operator. Obviously, the INS update of position, velocity, and attitude can be implement based on Equation (8).

The perturbation of position, velocity and attitude must be considered in the INS data processing. In this paper, the error model of attitude, velocity, and position is defined as the psi-angle error model, which reads as

$$\left[\begin{array}{c}\delta {\dot{\mathit{p}}}_{INS}^n\\ \delta {\dot{\mathit{v}}}_{INS}^n\\ \dot{\mathsf{\varphi }}\end{array}\right]=\left[\begin{array}{c}-{\mathsf{\omega }}_{en}^n\times \delta {\mathit{p}}_{INS}^n+\delta {\mathit{v}}_{INS}^n\\ -\left(2{\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n\right)\times \delta {\mathit{v}}_{INS}^n+{\mathit{C}}_b^n{\mathit{f}}^b\times \mathsf{\varphi }+\delta {\mathit{g}}^n+{\mathit{C}}_b^n\delta {\mathit{f}}^b\\ -\left({\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n\right)\times \mathsf{\varphi }-{\mathit{C}}_b^n\delta {\mathsf{\omega }}_{ib}^b\end{array}\right]$$

(9)

where $\delta {\mathit{p}}_{INS}^n$ and $\delta {\mathit{v}}_{INS}^n$ are the error vector of INS position and velocity, respectively; $\mathsf{\varphi }$ indicates the vector of misalignment angles; $\delta {\mathit{g}}^n$ is the gravity error; $\delta {\mathit{f}}^b$ is error vector of specific force measurement; $\delta {\mathsf{\omega }}_{ib}^b$ denotes error vector of the IMU angular rate. Generally, the error vectors of specific force and angular rate measurement include scale factor errors, bias errors, and white noise [35]. Here, only bias errors are considered and the bias errors of IMU sensors are described as the first Gauss-Markov procedure [34]:

$$\left[\begin{array}{c}\delta {\dot{\mathit{B}}}_a\\ \delta {\dot{\mathit{B}}}_g\end{array}\right]=-\frac{1}{\tau }\left[\begin{array}{c}\delta {\mathit{B}}_a\\ \delta {\mathit{B}}_g\end{array}\right]+\left[\begin{array}{c}{\mathit{w}}_a\\ {\mathit{w}}_g\end{array}\right]$$

(10)

where $\delta {\mathit{B}}_g$ and $\delta {\mathit{B}}_a$ represent the error vector of gyro biases and accelerometer biases, respectively; $\tau$ is the correction time; and ${\mathit{w}}_a$, ${\mathit{w}}_g$ represents the driving noise for accelerometer and gyro, respectively.

2.3. PPP-B2b/INS Loosely Coupled Integration Model

A typical state vector of 15 states is used in PPP-B2b/INS loosely coupled integration, which can be expressed as

$${\mathit{X}}_k={\left[\begin{array}{ccccc}\delta {\mathit{p}}_{INS}^n& \delta {\mathit{v}}_{INS}^n& \mathsf{\varphi }& \delta {\mathit{B}}_a& \delta {\mathit{B}}_g\end{array}\right]}^T$$

(11)

The system model of PPP-B2b/INS loosely coupled integration in the discrete form can be simplified as

$${\mathit{X}}_k=\left(\mathit{I}+\mathit{F}·\Delta t\right){\mathit{X}}_{k-1}+{\mathsf{\Gamma }}_{k-1}{\mathit{w}}_{k-1},{\mathit{w}}_{k-1}~N\left(0,{\mathit{Q}}_{k-1}\right)$$

(12)

where ${\mathit{X}}_{k-1}$ and ${\mathit{X}}_k$ are the vector of state parameter at epoch $k-1$ and $k$, respectively; $\mathit{I}$ is the identify matrix; $\Delta t$ denotes the time interval between two adjacent epochs; ${\mathit{w}}_{k-1}$ represents the vector of the process noise at epoch $k-1$, and ${\mathsf{\Gamma }}_{k-1}$ denotes the matrix of the noise distribution; ${\mathit{Q}}_{k-1}$ represents the covariance matrix of process noise; $\mathit{F}$ is the dynamic matrix, which can be derived from the INS error model as follows:

$$\mathit{F}=\left[\begin{array}{ccccc}{\mathit{F}}_{rr}& {\mathit{F}}_{rv}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathit{F}}_{vr}& {\mathit{F}}_{vv}& \left({\mathit{f}}^b\times \right)& {\mathit{C}}_b^n& \mathbf{0}\\ {\mathit{F}}_{\varphi r}& {\mathit{F}}_{\varphi v}& -\left({\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n\times \right)& \mathbf{0}& -{\mathit{C}}_b^n\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& -\frac{1}{\tau }\mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& -\frac{1}{\tau }\mathit{I}\end{array}\right]$$

(13)

where 0 denotes the zero matrix; ${\mathit{F}}_{rr}$, ${\mathit{F}}_{rv}$, ${\mathit{F}}_{vr}$, ${\mathit{F}}_{vv}$, ${\mathit{F}}_{\varphi r}$, and ${\mathit{F}}_{\varphi v}$ are sub-matrices of dynamic matrix, which can be derived from Equation (9). Then the Kalman time update can be expressed as [36]

$$\{\begin{array}{c}{\mathit{X}}_k^{-}={\mathsf{\Phi }}_{k,k-1}{\mathit{X}}_{k-1}^{+}\\ {\mathit{P}}_k^{-}={\mathsf{\Phi }}_{k,k-1}{\mathit{P}}_{k-1}^{+}{\mathsf{\Phi }}_{k,k-1}^T+{\mathit{Q}}_{k-1}\end{array}$$

(14)

where the superscript “$+$” and “$-$” denote the estimated and predicted information; ${\mathsf{\Phi }}_{k,k-1}=\left(\mathit{I}+\mathit{F}·\Delta t\right)$ represents the state transition matrix; ${\mathit{P}}_k$ represents the covariance matrix of the states.

When the PPP-B2b positioning solution and INS predicted solution are available at the same epoch, the Kalman filter measurement update can be operated. However, the positions and velocities from INS are referred to the IMU center, while those from PPP-B2b positioning are typically based on the GNSS antenna phase center. Therefore, the corresponding lever-arm offsets must be compensated. Here, the accurate lever-arm offsets are measured and directly applied to the position and velocity from INS. Then, the observation model for PPP-B2b/INS loosely coupled integration can be expressed as

$${\mathit{Z}}_k={\mathit{H}}_k{\mathit{X}}_k+\left[\begin{array}{c}{\mathsf{\epsilon }}_p\\ {\mathsf{\epsilon }}_v\end{array}\right],\left[\begin{array}{c}{\mathsf{\epsilon }}_p\\ {\mathsf{\epsilon }}_v\end{array}\right]~N\left(0,{\mathit{R}}_k\right)$$

(15)

with

$${\mathit{Z}}_k=\left[\begin{array}{c}{\mathit{p}}_{GNSS}^n\\ {\mathit{v}}_{GNSS}^n\end{array}\right]-\left[\begin{array}{c}{\mathit{p}}_{INS}^n\\ {\mathit{v}}_{INS}^n\end{array}\right]$$

(16)

$${\mathit{H}}_k=\left[\begin{array}{ccccc}{\mathit{I}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& \left({\mathit{C}}_b^n{\mathit{l}}^b\times \right)& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathit{I}}_{3\times 3}& {\mathit{H}}_{\varphi }& {\mathbf{0}}_{3\times 3}& -{\mathit{C}}_b^n\left({\mathit{l}}^b\times \right)\end{array}\right]$$

(17)

where ${\mathit{H}}_{\varphi }=\left[\left({\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n\right)\times {\mathit{C}}_b^n\left({\mathit{l}}^b\times \right)+{\mathit{C}}_b^n\left({\mathit{l}}^b\times {\mathsf{\omega }}_{ib}^b\right)\times \right]$; ${\mathit{p}}_{GNSS}^n$, ${\mathit{v}}_{GNSS}^n$ denote the vector of position and velocity obtained from PPP-B2b positioning; ${\left[\begin{array}{cc}{\mathsf{\epsilon }}_p& {\mathsf{\epsilon }}_v\end{array}\right]}^T$ denotes the vector of measurement noise of position and velocity and ${\mathit{R}}_k$ represents its related covariance matrix; ${\mathit{l}}^b$ represents the vector of lever-arm offsets; ${\mathit{H}}_k$ is the design matrix; ${\mathit{Z}}_k$ is defined as the innovation vector, which consists of the difference of positions and velocities between PPP-B2b positioning solution and INS predicted solution. Finally, the Kalman measurement update can be given as

$$\{\begin{array}{c}{\mathit{K}}_k={\mathit{P}}_k^{-}{\mathit{H}}_k^T{\left({\mathit{H}}_k{\mathit{P}}_k^{-}{\mathit{H}}_k^T+{\mathit{R}}_k\right)}^{-1}\\ {\mathit{X}}_k^{+}={\mathit{X}}_k^{-}+{\mathit{K}}_k\left({\mathit{Z}}_k-{\mathit{H}}_k{\mathit{X}}_k^{-}\right)\\ {\mathit{P}}_k^{+}=\left(\mathit{I}-{\mathit{K}}_k{\mathit{H}}_k\right){\mathit{P}}_k^{-}\end{array}$$

(18)

where ${\mathit{K}}_k$ is the Kalman gain.

3. Description of Experiments

In order to assess the performance of BDS-3 PPP-B2b/INS loosely coupled integration, two land vehicle experiments in open-sky scenery and urban canyon scenery (hereinafter referred to as Experiment A and Experiment B, respectively) were carried out in Qingdao, China. In these two experiments, a tactical-grade IMU (ISA100C) [37] and a MEMS-grade IMU (ADIS-16505) [38] were equipped to evaluate the impact of IMU grade on BDS-3 PPP-B2b/INS loosely coupled integration. Two GNSS antennas were mounted on the roof of the land vehicle, and connected to a NovAtel PwrPak7 receiver [39] and a FRII-PLUS PPP-B2b receiver (http://www.femtomes.com, accessed on 20 October 2021). The FRII-PLUS receiver was only used to collected PPP-B2b messages, while all GNSS observations used in the evaluation were collected by the PwrPak7 receiver. The sampling rate of GNSS observations was 1 Hz. Figure 1 shows the installation of experimental equipment. Relevant specific information for the IMU sensors is listed in

Table 1. Parameters of the IMU sensors used in the experiments.

IMU Sensor	Grade	Sampling Rate	Bias		Random Walk
			Gyro. (°/h)	Acc. (mGal)	Angular (°/$\sqrt{\mathit{h}}$)	Velocity $(\mathbf{m}/\mathbf{s}/\sqrt{\mathit{h}})$
IAS100C	Tactical	200 Hz	0.75	1000	0.03	0.1
ADIS-16505	MEMS	100 Hz	10	1500	0.34	0.18

.

During these two experiments, a GNSS base station was established on the roof of Engineering-C building in the China University of Petroleum (East China). It should be noted that the distance between the base and rover stations was less than 5 km. Using GNSS observations collected by PwrPak7, and IMU data from ISA100C, together with GNSS measurements at the base station, the smoothed RTK/INS tightly coupled solution was obtained by commercial Inertial Explorer software (IE 8.90) from the NovAtel company, and this solution was used as reference.

In PPP-B2b positioning, the B1C and B2a signals of BDS-3, L1 and L2 signals of GPS were selected to form the ionospheric-free combination, and the cut-off elevation angle was set to 7 degrees. The remaining processing strategies are shown in detail in

Table 2. Strategies of PPP-B2b positioning.

Item	Model/Strategy
Satellite orbit and clock	Applying the PPP-B2b precise products
Weight method	Elevation-dependent weight [40]
Phase windup	Corrected [31]
Sagnac effect	Corrected [29]
Special relativistic effect	Corrected [29]
Shapiro time delay	Corrected [29]
Tidal effects	Corrected according to IERS Conventions 2010 [30]
Troposphere	Saastamoinen model [41] is adopted to correct hydrostatic delay, the zenith wet delay is estimated for each epoch as a random walk noise, and Global Mapping Function [42] is used.
Phase ambiguity	Estimated as a constant for each ambiguity arc
Estimator	Kalman filter

.

4. Result and Discussion

In this section, the performance of BDS-3 PPP-B2b/INS loosely coupled integration was investigated in both open-sky and complex urban environments.

4.1. Experiment A

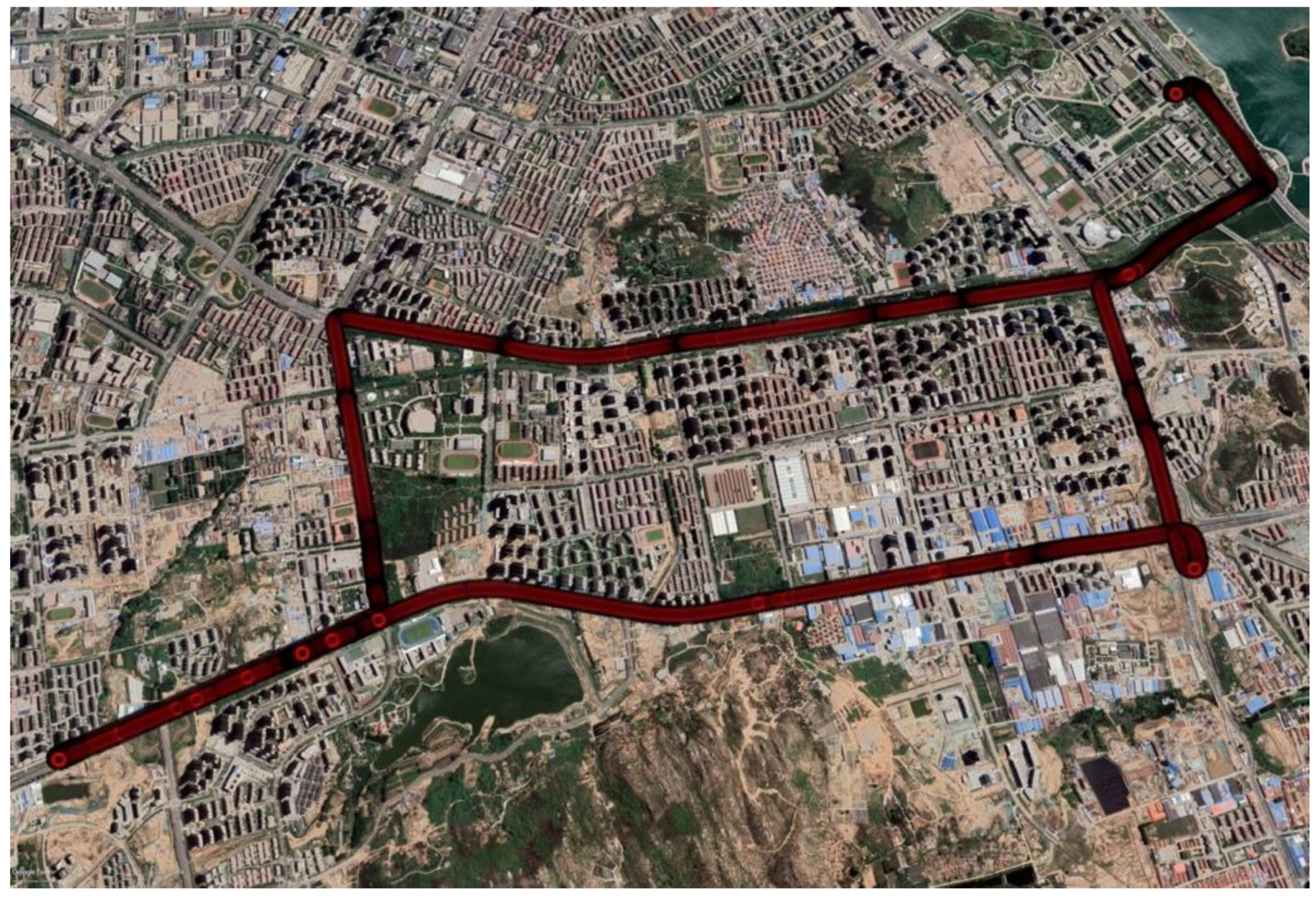
Experiment A was conducted from 16:30:40 to 16:59:59 on 3 December 2021 in GPS time. The trajectory of the land vehicle is shown in Figure 2.

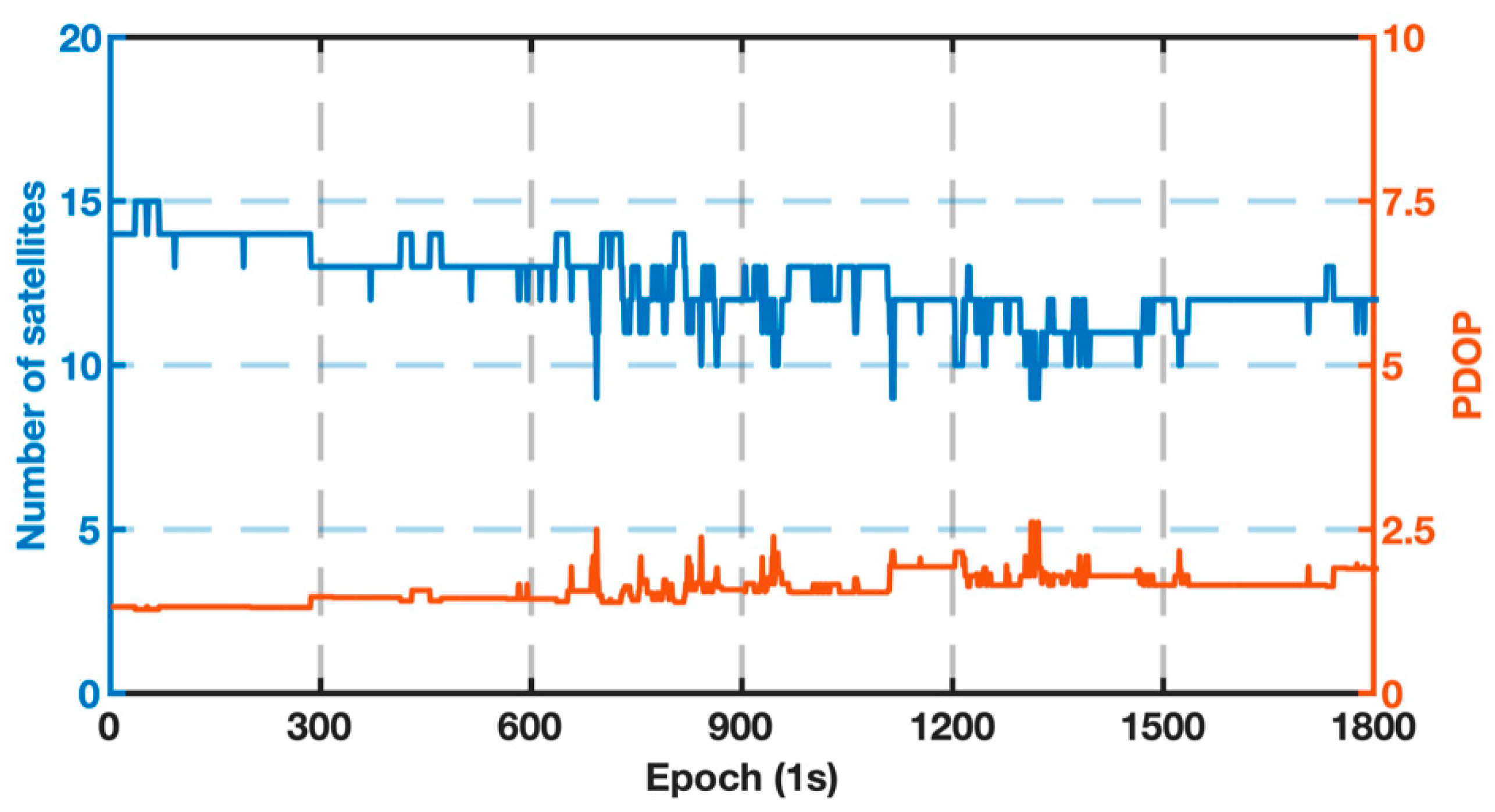
During Experiment A, the velocities of the land vehicle were within $\pm$20 m/s in the east and north directions and within $\pm$1 m/s in the vertical direction. The number of visible BDS-3/GPS satellites and the position dilution of precision (PDOP) values are shown in Figure 3. The number of visible satellites ranged from 9 to 15 with an average value of 12.5, and the PDOP varied from 1.28 to 2.70 with an average value of 1.59.

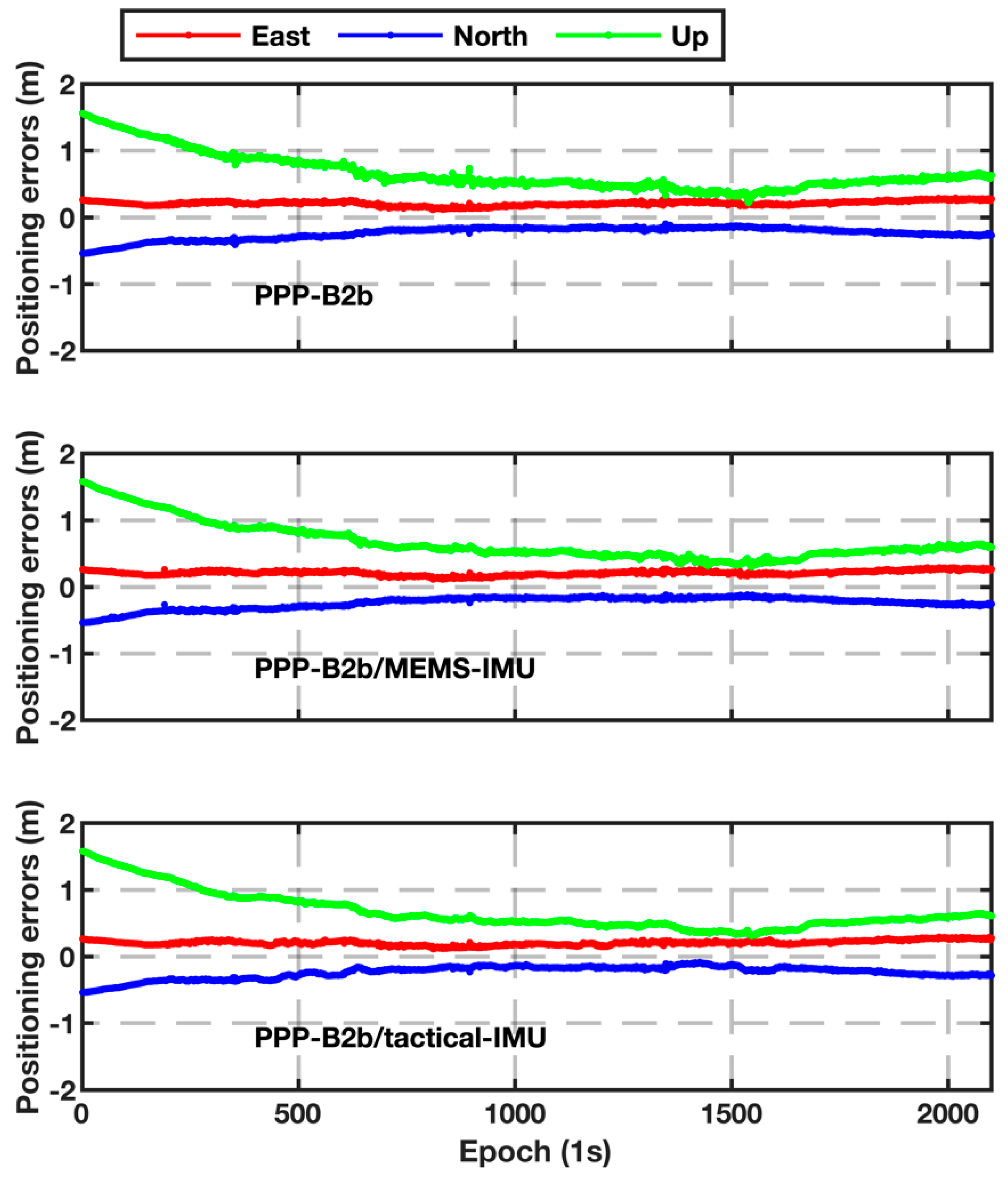
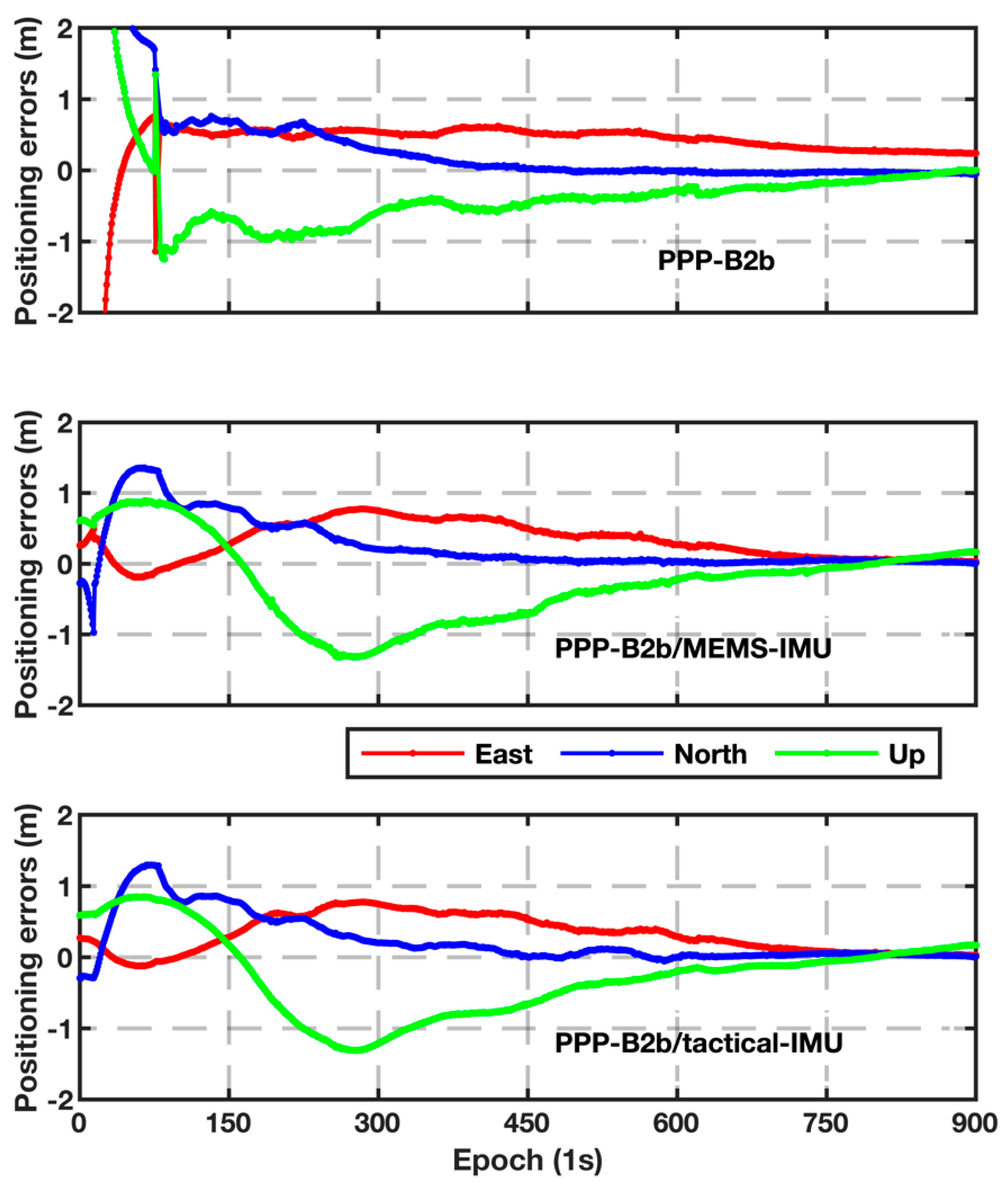
Figure 4 shows the positioning errors of PPP-B2b only, PPP-B2b/MEMS-IMU loosely coupled integration, and PPP-B2b/tactical-IMU loosely coupled integration, respectively. As with traditional PPP processing, a convergence period is indispensable in PPP-B2b positioning and PPP-B2b/INS loosely coupled integration. In this study, the convergence time was defined for horizontal/vertical positioning accuracy better than 30 cm/60 cm, with such a positioning accuracy for at least 60 continuous epochs. The statistics of the positioning results are summarized in

Table 3. Statistics of the positioning errors (unit: cm).

Schemes	Bias			RMS
	East	North	Up	East	North	Up
PPP-B2b	6.7	23.7	26.5	8.1	24.2	27.5
PPP-B2b/MEMS-IMU	6.6	23.3	26.0	7.9	24.0	27.0
PPP-B2b/tactical-IMU	6.2	23.5	25.8	7.1	23.8	26.5

. It should be noted that positioning results before full convergence were excluded when calculating positioning accuracy. The biases in the east, north and up directions were 6.7/23.7/26.5 cm for PPP-B2b only, and the corresponding values for PPP-B2b/tactical-IMU and PPP-B2b/MEMS-IMU loosely coupled integration schemes were 6.6/23.3/26.0 cm and 6.2/23.5/25.8 cm, respectively. In terms of the root mean square (RMS) value of positioning errors, the improvement of PPP-B2b/INS loosely coupled integration was not significant compared to PPP-B2b only. This is because Experiment A was carried out within an open-sky environment and thus PPP-B2b on its own was already able to obtain high-precision positioning accuracy.

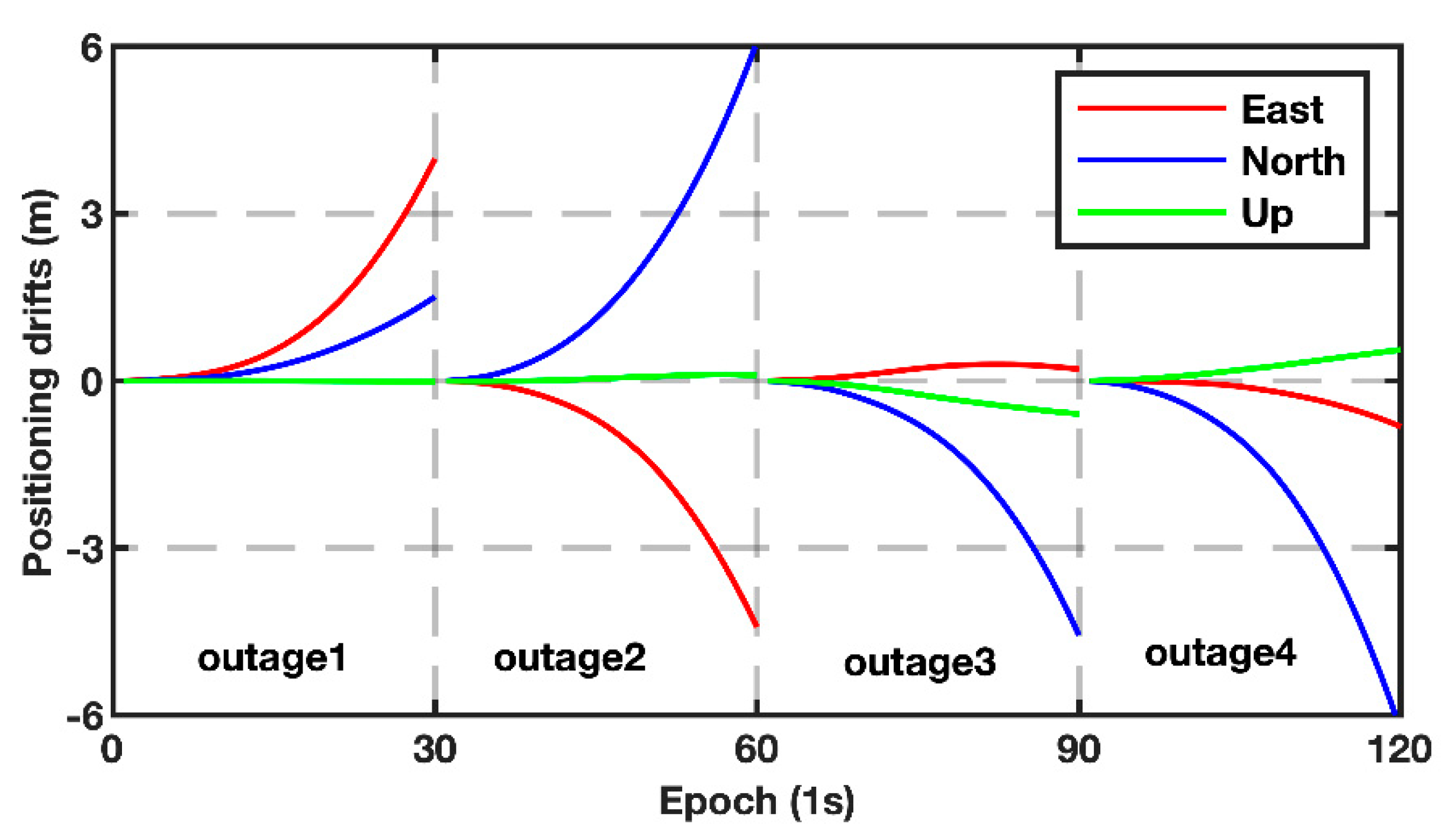
It is recognized that PPP-B2b only is unable to obtain a high-precision solution during GNSS signal outages, while PPP-B2b/INS loosely coupled integration continues to work by INS mechanization. Four periods of GNSS signal outage were simulated to present the superiority of PPP-B2b/INS loosely coupled integration. The periods of GNSS outage were simulated from the 600th/900th/1200th/1500th epoch, and each period lasted 30 s. The corresponding positioning errors of PPP-B2b/MEMS-IMU and PPP-B2b/tactical-IMU loosely coupled integration are plotted in Figure 5 and Figure 6, respectively. Clearly, the positioning accuracy become progressively worse with increased time of GNSS outages in both PPP-B2b/MEMS-IMU and PPP-B2b/tactical-IMU loosely coupled integration schemes. When the GNSS signal outage time increased to 30 s, the positioning errors in the east, north, and up directions decreased to 300.0 cm, 498.0 cm, and 41.0 cm, respectively, for PPP-B2b/MEMS-IMU loosely coupled integration. The results for the PPP-B2b/tactical-IMU loosely coupled integration scheme dropped to 18.6 cm, 21.8 cm, and 6.1 cm in the east, north, and up components, respectively.

Table 4. Statistics of positioning errors for PPP-B2b/INS loosely coupled integration during GNSS outages (unit: cm).

Schemes	Direction	5 s	10 s	15 s	20 s	25 s	30 s
PPP-B2b/tactical-IMU	East	0.5	1.8	3.9	7.7	12.7	18.6
	North	0.8	2.5	5.3	9.3	14.6	21.8
	Up	0.4	1.3	2.5	3.7	5.0	6.1
PPP-B2b/MEMS-IMU	East	3.8	17.4	45.7	97.4	180.5	300.6
	North	8.0	35.2	87.3	174.6	308.9	498.0
	Up	1.8	7.2	15.7	24.7	33.4	41.0

lists the statistics results, showing that the positioning performance of PPP-B2b/tactical-IMU loosely coupled integration is significantly better than that of PPP-B2b/MEMS-IMU loosely coupled integration.

4.2. Experiment B

To fully demonstrate the performance of BDS-3 PPP-B2b/INS loosely coupled integration in an urban scenario, we conducted Experiment B in a complex urban environment. Experiment B was carried out from 09:00:00 to 09:49:59 on 5 December 2021 in GPS time. The trajectory of the land vehicle is shown in Figure 7.

Figure 8 presents the number of visible BDS-3/GPS satellites and the values of PDOP. The number of available BDS-3/GPS satellites dropped frequently, and at the same time the PDOP value significantly increased as several typical city features such as tall buildings, trees, and over-bridges appeared along the vehicle route.

During the first 35 min, there were enough satellites for the implementation of PPP-B2b positioning. The positioning errors of PPP-B2b only, PPP-B2b/MEMS-IMU loosely coupled integration and PPP-B2b/tactical-IMU loosely coupled integration are plotted in Figure 9. It can be found that all three schemes provided similar positioning accuracy in this 35-min period. The RMS values of positioning errors were 20.7 cm, 17.3 cm, and 47.6 cm in the east, north, and up directions for PPP-B2b only. For PPP-B2b/INS loosely coupled integration, the corresponding RMS values were 20.8 cm, 17.4 cm, and 47.5 cm for the PPP-B2b/MEMS-IMU scheme, and 20.3 cm, 17.4 cm, and 47.5 cm for the PPP-B2b/tactical-IMU scheme. It should be noted that a convergence period of 15 min was removed when we computed the positioning accuracy. Clearly, the equipped IMU sensors could not improve the performance of the PPP-B2b service when there was no GNSS signal blockage.

From 09:35:00 to the end of Experiment B, the land vehicle crossed two over-bridges, as shown in Figure 10. Two GNSS signal outages appeared when the land vehicle crossed the bridges, lasting 15 s and 5 s, respectively. During these two GNSS signal outages, PPP-B2b positioning could be implemented, because the number of visible satellites was less than four. Therefore, the PPP-B2b positioning was re-converged after crossing the bridges. Figure 11 shows the positioning errors of PPP-B2b only, PPP-B2b/MEMS-IMU loosely coupled integration, and PPP-B2b/tactical-IMU loosely coupled integration. It can be seen that the positioning accuracy of PPP-B2b/INS loosely coupled integration exhibited better performance than PPP-B2b positioning during the re-convergence phase. The overall positioning accuracies for the three schemes were calculated from 09:35:00 to 09:49:59 and are presented in

Table 5. The positioning accuracy during the period from 09:35:00 to 09:49:59 (unit: cm).

Schemes	Bias			RMS
	East	North	Up	East	North	Up
PPP-B2b	14.9	48.1	12.9	114.2	200.0	244.3
PPP-B2b/MEMS-IMU	31.7	25.1	25.2	41.0	44.5	64.0
PPP-B2b/tactical-IMU	32.1	24.2	25.1	41.2	41.0	62.5

. The RMS values of positioning errors for the east, north, and up components were 114.2 cm, 200.0 cm, and 244.3 cm for PPP-B2b only. These figures improved to 41.0 cm, 44.5 cm, and 64.0 cm for PPP-B2b/MEMS-IMU loosely coupled integration, and to 41.2 cm, 41.0 cm, and 62.5 cm for PPP-B2b/tactical-IMU loosely coupled integration. Obviously, the performance of PPP-B2b/INS loosely coupled integration was significantly improved compared to PPP-B2b only in the last 15-min period of Experiment B. The positioning accuracy of PPP-B2b/tactical-IMU loosely coupled integration was slightly better than that of PPP-B2b/MEMS-IMU loosely coupled integration.

5. Conclusions

Since July 2020, PPP-B2b has served as a featured service of BDS-3 to support real-time PPP. Compared to the IGS RTS service, PPP-B2b is a satellite-based service, which is not limited by Internet communication. Its high-precision positioning performance shows great potential in real-time GNSS applications. However, the BDS-3 PPP-B2b service continues to encounter challenges in urban environments due to GNSS signal outages. In order to overcome the drawbacks of the BDS-3 PPP-B2b service in urban environments, we set up a BDS-3 PPP-B2b/INS loosely coupled integration system and evaluated its performance in different urban scenarios.

The experimental results indicate that PPP-B2b/INS loosely coupled integration cannot improve the positioning performance in open-sky environments where there are enough GPS/BDS-3 satellites for PPP-B2b positioning. However, PPP-B2b/INS loosely coupled integration can show its superiority when GNSS signal outage occurs. During GNSS signal outages, the INS mechanization can provide continuous positioning. Therefore, the performance of PPP-B2b positioning can be improved by adopting PPP-B2b/INS loosely coupled integration in GNSS blockage environments. In the first experiment, we simulated four 30-s periods of GNSS signal outages. At the last epoch of the simulated outages, the averaged positioning errors in the east, north, and up directions were 300.0 cm, 498.0 cm, and 41.0 cm, respectively, for PPP-B2b/MEMS-IMU loosely coupled integration, and 18.6 cm, 21.8 cm, and 6.1 cm, respectively, for PPP-B2b/tactical-IMU loosely coupled integration. In addition, we also evaluated the performance of PPP-B2b/INS loosely coupled integration in a real complex urban environment. When the land vehicle crossed bridges, two GNSS signal interruptions appeared that lasted 15 s and 5 s, respectively. Compared to PPP-B2b only, the respective improvement of positioning accuracy in the east, north, and up components was 64.1%, 77.8%, and 73.8% for PPP-B2b/MEMS-IMU loosely coupled integration, and 63.9%, 79.5%, and 74.4% for PPP-B2b/Tactical-IMU loosely coupled integration.

It can be concluded that when there are sufficient valid satellites for PPP-B2b positioning, the positioning accuracy of PPP-B2b/INS loosely coupled integration depends mainly on the accuracy of PPP-B2b. In urban environments, positioning performance can be significantly improved compared to PPP–B2b alone, by adopting PPP-B2b/INS loosely coupled integration especially in GNSS signal blockage environments.