An Advanced Framework for Multi-Scale Forest Structural Parameter Estimations Based on UAS-LiDAR and Sentinel-2 Satellite Imagery in Forest Plantations of Northern China
Abstract
:1. Introduction
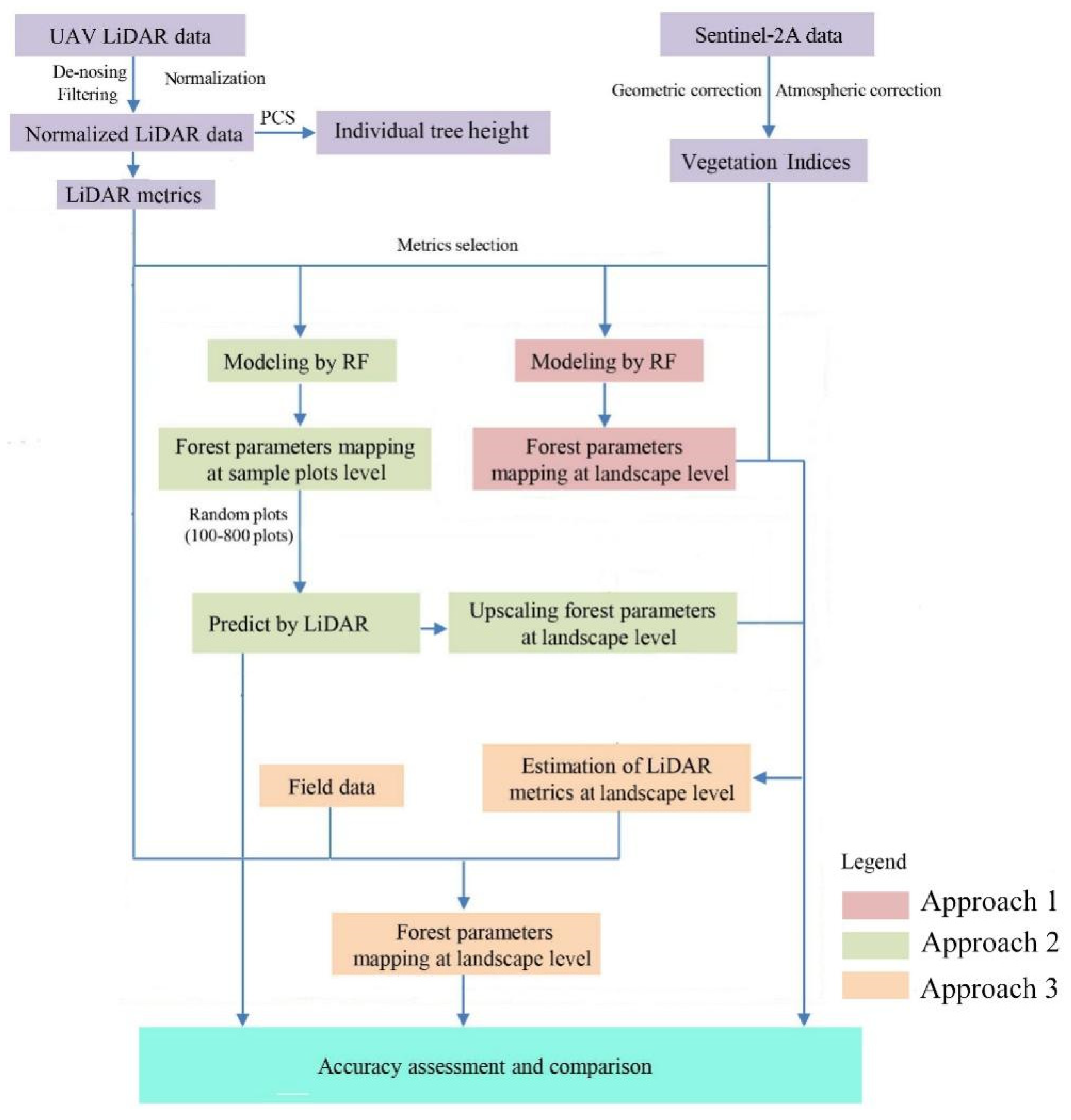
2. Materials and Methods
2.1. Study Area
2.2. Field Data
2.3. UAS-LiDAR Data Acquisition and Pre-Processing
2.4. The Metrics Derived from UAS-LiDAR Data
2.5. Sentinel-2 Data Acquisition and Pre-Processing
2.6. Vegetation Indices Derived from Sentinel-2 Data
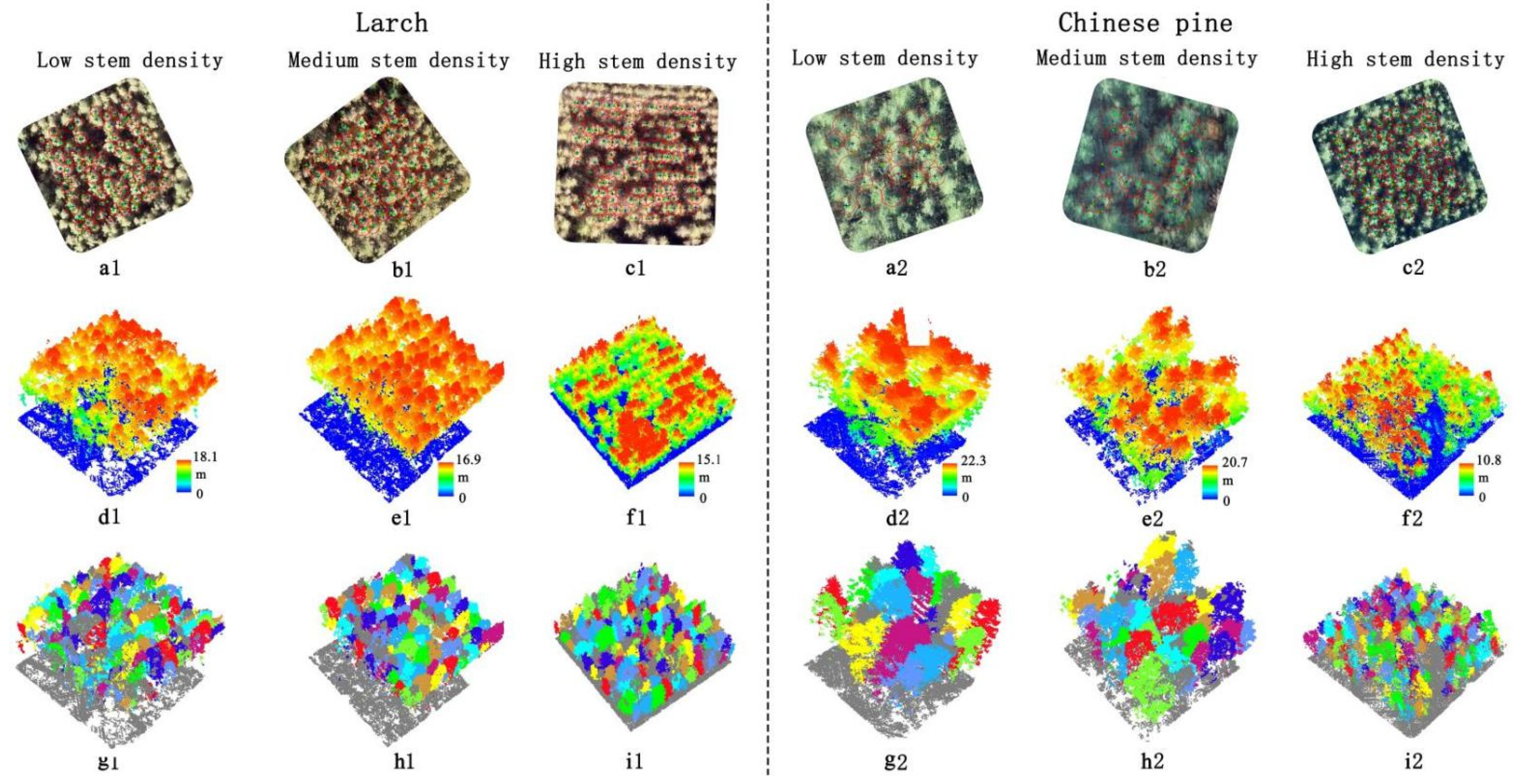
2.7. Individual Tree Crown Segmentation and Tree Height Extracted
2.8. Estimation of Forest Structural Parameters by Random Forest
2.9. Forest Structural Parameters Upscaling Estimation Approaches
2.10. Model Accuracy Evaluation
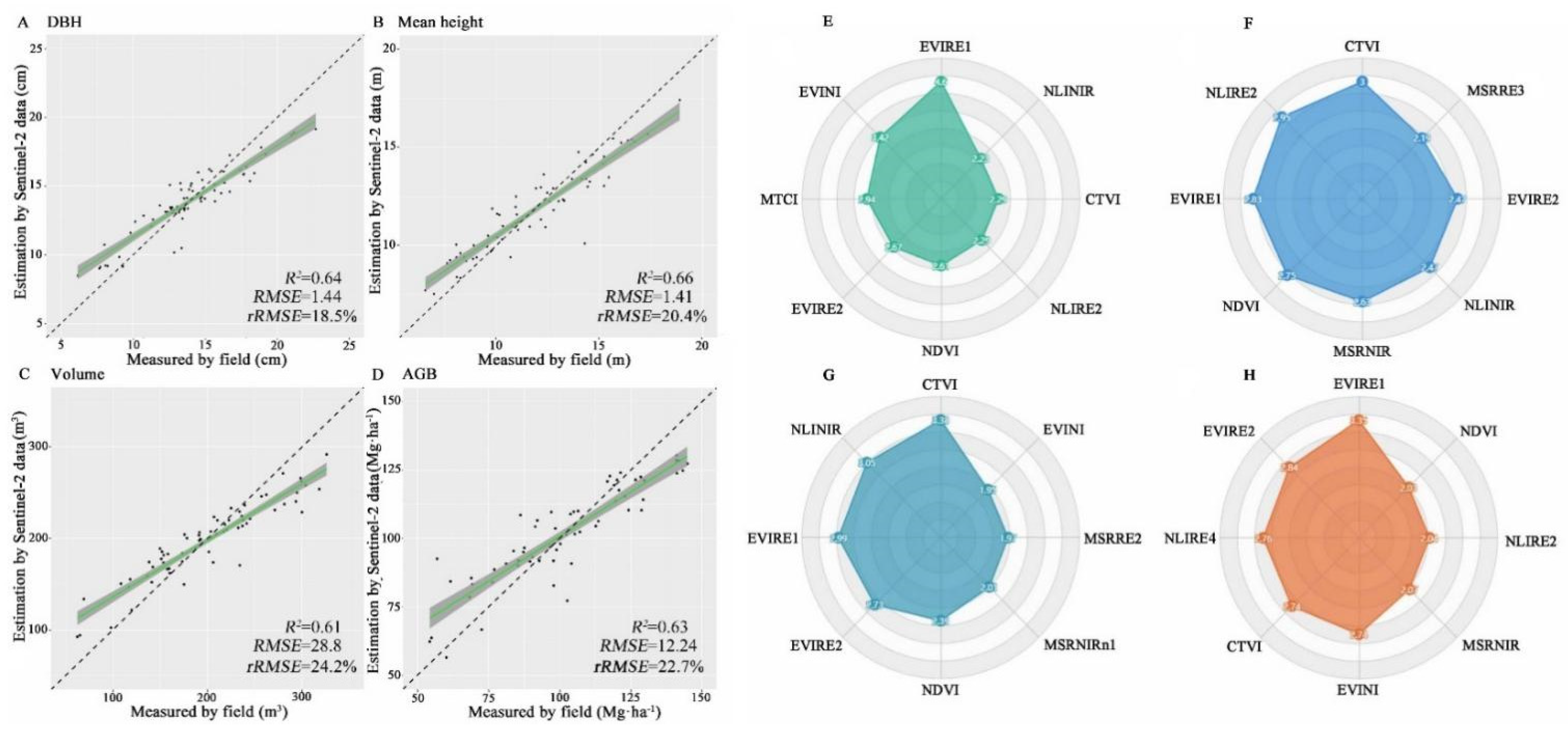
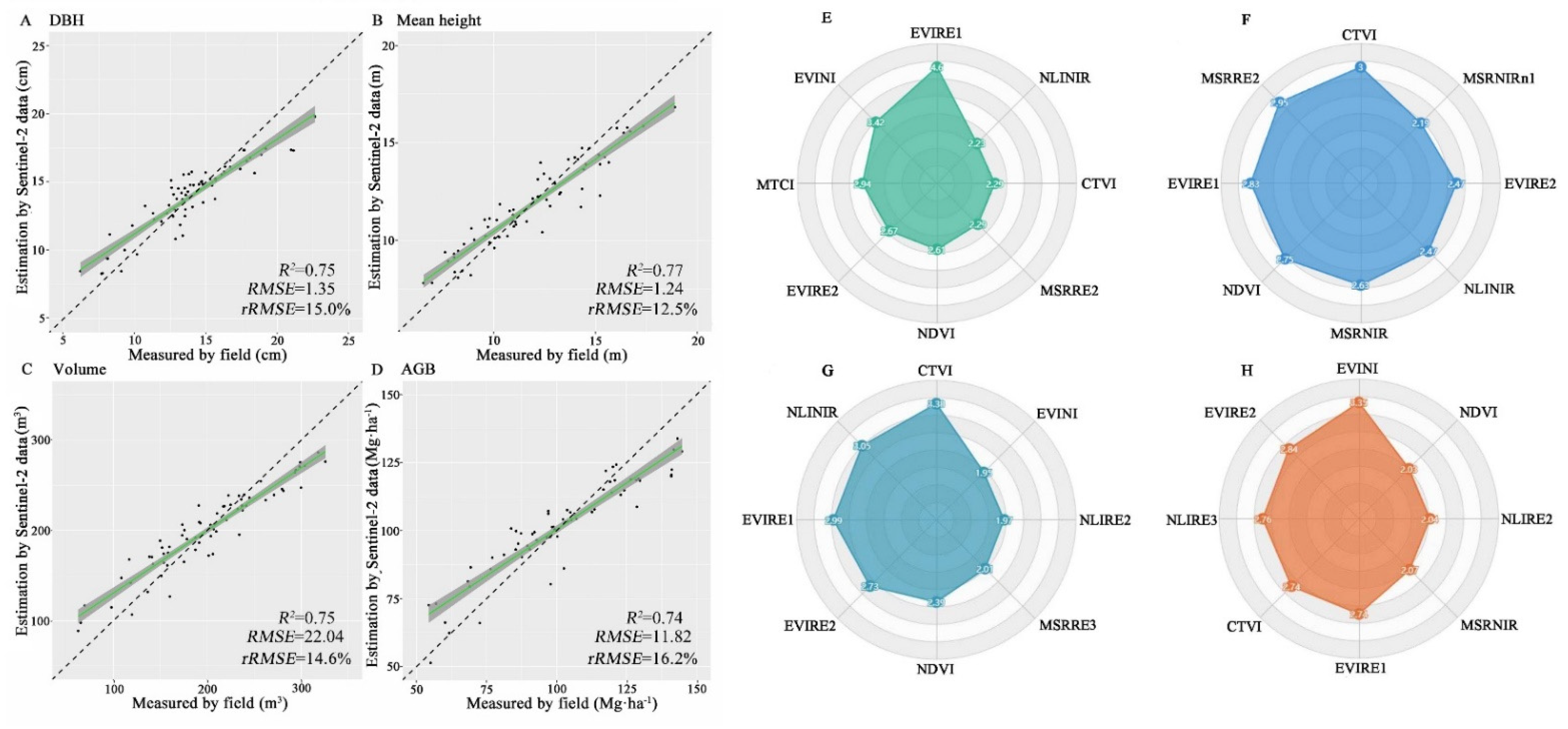
3. Results
4. Discussion
4.1. Estimation of Forest Structural Parameters by UAS-LiDAR
4.2. Estimation of Forest Structural Parameters by UAS-LiDAR Combined with Multi-Spectral Imageries
4.3. Sample Amplification Using UAS-LiDAR Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Jackson, R.B. The Structure, Distribution, and Biomass of the World’ s Forests. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 593–622. [Google Scholar] [CrossRef] [Green Version]
- Volkov, I.; Banavar, J.R.; Maritan, A.; Hubbell, S.P.; Clark, J.S.; Mclachlan, J.S. The stability of forest. Nature 2004, 427, 696. [Google Scholar] [CrossRef] [PubMed]
- Mountain, R.; Collins, F.; Collins, F.; Square, N.; Southwest, P.; Hole, W.; Sciences, E.; Region, N.; Biology, E. A synthesis of current knowledge on forests and carbon storage in the United States. ISSUES Ecol. 2011, 21, 1902–1924. [Google Scholar]
- Carnus, J.-M.; Parrotta, J.A.; Brockerhoff, E.G.; Arbez, M.; Jactel, H.; Kremer, A.; Lamb, D.; O’Hara, K.; Walters, B. Planted forests and biodiversity. J. For. 2006, 104, 65–77. [Google Scholar] [CrossRef]
- Rodríguez-suárez, J.A.; Soto, B.; Perez, R.; Diaz-fierros, F. Influence of Eucalyptus globulus plantation growth on water table levels and low flows in a small catchment. J. Hydrol. 2011, 396, 321–326. [Google Scholar] [CrossRef]
- Fagan, M.E.; Morton, D.C.; Cook, B.D.; Masek, J.; Zhao, F.; Nelson, R.F.; Huang, C. Mapping pine plantations in the southeastern U.S. using structural, spectral, and temporal remote sensing data. Remote Sens. Environ. 2018, 216, 415–426. [Google Scholar] [CrossRef]
- Li, H.; Bo, H.; Wang, J.; Shao, H.; Huang, S. Separation of supercoiled from open circular forms of plasmid DNA, and biological activity detection. Cytotechnology 2011, 63, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Avtar, R.; Suzuki, R.; Sawada, H. Natural forest biomass estimation based on plantation information using PALSAR data. PLoS ONE 2014, 9, e86121. [Google Scholar] [CrossRef]
- Dabi, H.; Bordoloi, R.; Das, B.; Paul, A.; Tripathi, O.P.; Mishra, B.P. Biomass, carbon stock and soil physicochemical properties in plantation of East Siang district, Arunachal Pradesh, India. Environ. Chall. 2021, 4, 100191. [Google Scholar] [CrossRef]
- Wulder, M.A.; Skakun, R.S.; Kurz, W.A.; White, J.C. Estimating time since forest harvest using segmented Landsat ETM+ imagery. Remote Sens. Environ. 2004, 93, 179–187. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Lefsky, M.; Cohen, W.; Parker, G.; Harding, D. Lidar Remote Sensing for Ecosystem Studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef] [Green Version]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Guo, Q.; Tao, S.; Kelly, M.; Xu, G. Lidar with multi-temporal MODIS provide a means to upscale predictions of forest biomass. ISPRS J. Photogramm. Remote Sens. 2015, 102, 198–208. [Google Scholar] [CrossRef]
- Gleason, C.; Im, J. A review of remote sensing of forest biomass and biofuel: Options for small-area applications. GIScience Remote Sens. 2011, 48, 141–170. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return lidar: An example from low density, fire prone ponderosa pine forests. For. Ecol. Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
- Andersen, H.; Mcgaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. Remote Sensing of Vegetation Structure Using Computer Vision. Remote Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef] [Green Version]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-D mapping of a multi-layered Mediterranean forest using ALS data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef] [Green Version]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef] [Green Version]
- Nagai, M.; Witayangkurn, A.; Shrestha, A.; Chinnachodteeranun, R.; Honda, K.; Shibasaki, R. UAV-based sesor web moitorig system. Int. J. Navig. Obs. 2009, 2, 785–789. [Google Scholar]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.; Li, Z.; Fu, L.; Hu, K. Review on the Applications of UAV-Based LiDAR and Photogrammetry in Forestry. Sci. Silvae Sin. 2017, 53, 134–148. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Tao, S.; Guo, Q.; Li, L.; Xue, B.; Kelly, M.; Li, W.; Xu, G.; Su, Y. Airborne Lidar-derived volume metrics for aboveground biomass estimation: A comparative assessment for conifer stands. Agric. For. Meteorol. 2014, 198–199, 24–32. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Assessment of individual tree detection and canopy cover estimation using unmanned aerial vehicle based light detection and ranging (UAV-LiDAR) data in planted forests. Remote Sens. 2019, 11, 908. [Google Scholar] [CrossRef] [Green Version]
- Wallace, L.; Musk, R.; Lucieer, A. An assessment of the repeatability of automatic forest inventory metrics derived from UAV-borne laser scanning data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7160–7169. [Google Scholar] [CrossRef]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. ISPRS Journal of Photogrammetry and Remote Sensing Estimating forest structural attributes using UAV-LiDAR data in Ginkgo plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Dempewolf, J.; Nagol, J.; Hein, S.; Thiel, C.; Zimmermann, R. Measurement of within-season tree height growth in a mixed forest stand using UAV imagery. Forests 2017, 8, 231. [Google Scholar] [CrossRef] [Green Version]
- Goldbergs, G.; Maier, S.W.; Levick, S.R.; Edwards, A. Efficiency of individual tree detection approaches based on light-weight and low-cost UAS imagery in Australian Savannas. Remote Sens. 2018, 10, 161. [Google Scholar] [CrossRef] [Green Version]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Kennedy, R. ISPRS Journal of Photogrammetry and Remote Sensing Characterization of aboveground biomass in an unmanaged boreal forest using Landsat temporal segmentation metrics. ISPRS J. Photogramm. Remote Sens. 2014, 92, 137–146. [Google Scholar] [CrossRef]
- Zald, H.S.J.; Wulder, M.A.; White, J.C.; Hilker, T.; Hermosilla, T.; Hobart, G.W.; Coops, N.C. Remote Sensing of Environment Integrating Landsat pixel composites and change metrics with lidar plots to predictively map forest structure and aboveground biomass in. Remote Sens. Environ. 2016, 176, 188–201. [Google Scholar] [CrossRef] [Green Version]
- Chi, H.; Sun, G.; Huang, J.; Li, R.; Ren, X.; Ni, W. Estimation of Forest Aboveground Biomass in Changbai Mountain Region Using ICESat/GLAS and Landsat/TM Data. Remote Sens. 2017, 9, 707. [Google Scholar] [CrossRef] [Green Version]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Shen, W.; Li, M.; Huang, C.; Tao, X.; Wei, A. Agricultural and Forest Meteorology Annual forest aboveground biomass changes mapped using ICESat/GLAS measurements, historical inventory data, and time-series optical and radar imagery for Guangdong province, China. Agric. For. Meteorol. 2018, 259, 23–38. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Lin, H.; Long, J.; Li, X. Study on volume estimation model of Wangyedian forest farm based on GF-2. J. Cent. South Univ. For. Technol. 2020, 3, 79–84,118. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef] [Green Version]
- Véga, C.; Durrieu, S.; Morel, J.; Allouis, T. A sequential iterative dual-filter for Lidar terrain modeling optimized for complex forested environments. Comput. Geosci. 2012, 44, 31–41. [Google Scholar] [CrossRef]
- Meng, X.; Wang, L.; Silván-Cárdenas, J.L.; Currit, N. A multi-directional ground filtering algorithm for airborne LIDAR. ISPRS J. Photogramm. Remote Sens. 2009, 64, 117–124. [Google Scholar] [CrossRef] [Green Version]
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Valderrama-Landeros, L.; Flores-de-Santiago, F.; Kovacs, J.M.; Flores-Verdugo, F. An assessment of commonly employed satellite-based remote sensors for mapping mangrove species in Mexico using an NDVI-based classification scheme. Environ. Monit. Assess. 2018, 190, 23. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Wang, X.; Xie, S.; Zhang, X.; Chen, C.; Guo, H.; Du, J.; Duan, Z. A robust Multi-Band Water Index (MBWI) for automated extraction of surface water from Landsat 8 OLI imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 73–91. [Google Scholar] [CrossRef]
- Naito, H.; Ogawa, S.; Valencia, M.O.; Mohri, H.; Urano, Y.; Hosoi, F.; Shimizu, Y.; Chavez, A.L.; Ishitani, M.; Selvaraj, M.G.; et al. Estimating rice yield related traits and quantitative trait loci analysis under different nitrogen treatments using a simple tower-based field phenotyping system with modified single-lens reflex cameras. ISPRS J. Photogramm. Remote Sens. 2017, 125, 50–62. [Google Scholar] [CrossRef]
- Reyes-Trujillo, A.; Daza-Torres, M.C.; Galindez-Jamioy, C.A.; Rosero-García, E.E.; Muñoz-Arboleda, F.; Solarte-Rodriguez, E. Estimating canopy nitrogen concentration of sugarcane crop using in situ spectroscopy. Heliyon 2021, 7, E06566. [Google Scholar] [CrossRef] [PubMed]
- Dang, A.T.N.; Nandy, S.; Srinet, R.; Luong, N.V.; Ghosh, S.; Senthil Kumar, A. Forest aboveground biomass estimation using machine learning regression algorithm in Yok Don National Park, Vietnam. Ecol. Inform. 2019, 50, 24–32. [Google Scholar] [CrossRef]
- Kowalski, K.; Senf, C.; Hostert, P.; Pflugmacher, D. Characterizing spring phenology of temperate broadleaf forests using Landsat and Sentinel-2 time series. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102172. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Hornero, A.; Hernández-Clemente, R.; North, P.R.J.; Beck, P.S.A.; Boscia, D.; Navas-Cortes, J.A.; Zarco-Tejada, P.J. Monitoring the incidence of Xylella fastidiosa infection in olive orchards using ground-based evaluations, airborne imaging spectroscopy and Sentinel-2 time series through 3-D radiative transfer modelling. Remote Sens. Environ. 2020, 236, 111480. [Google Scholar] [CrossRef]
- Fernández-Manso, A.; Fernández-Manso, O.; Quintano, C. SENTINEL-2A red-edge spectral indices suitability for discriminating burn severity. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 170–175. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Qian, B.; He, L.; Liu, J.; Wang, R.; Jing, Q.; Champagne, C.; McNairn, H.; Powers, J.; et al. Estimating crop biomass using leaf area index derived from Landsat 8 and Sentinel-2 data. ISPRS J. Photogramm. Remote Sens. 2020, 168, 236–250. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Tsakiri, M.; Patias, P. Evaluation of single-date and multi-seasonal spatial and spectral information of Sentinel-2 imagery to assess growing stock volume of a Mediterranean forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 1–14. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and sentinel-2 imagery in a mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 2005, 3408, 345–359. [Google Scholar] [CrossRef]
- de Oliveira, M.F.; dos Santos, A.F.; Kazama, E.H.; de Souza Rolim, G.; da Silva, R.P. Determination of application volume for coffee plantations using artificial neural networks and remote sensing. Comput. Electron. Agric. 2021, 184, 106096. [Google Scholar] [CrossRef]
- Gibson, R.; Danaher, T.; Hehir, W.; Collins, L. A remote sensing approach to mapping fire severity in south-eastern Australia using sentinel 2 and random forest. Remote Sens. Environ. 2020, 240, 111702. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Remote Sensing of Environment Continuous change detection and classi fi cation of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.; Su, Y.; Guo, Q. Comparison of Canopy Cover Estimations From. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4225–4236. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Melo, J.B.; Vasconcelos, M.J. Estimating the Above-Ground Biomass in Miombo Savanna Woodlands (Mozambique, East Africa) Using L-Band Synthetic Aperture Radar Data. Remote Sens. 2013, 5, 1524–1548. [Google Scholar] [CrossRef] [Green Version]
- Draper, C.; Reichle, R.; de Jeu, R.; Naeimi, V.; Parinussa, R.; Wagner, W. Estimating root mean square errors in remotely sensed soil moisture over continental scale domains. Remote Sens. Environ. 2013, 137, 288–298. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Lei, X.D.; Dong, L.H. How large is the difference in large-scale forest biomass estimations based on new climate-modified stand biomass models? Ecol. Indic. 2021, 126, 107569. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Pajares, G. Overview and Current Status of Remote Sensing Applications Based on Unmanned Aerial Vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. Int. J. For. Res. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Nichol, J.E.; Sarker, M.L.R. Improved biomass estimation using the texture parameters of two high-resolution optical sensors. IEEE Trans. Geosci. Remote Sens. 2011, 49, 930–948. [Google Scholar] [CrossRef] [Green Version]
- Goodbody, T.R.H.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest inventory purposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef] [Green Version]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Wallace, L.O.; Lucieer, A.; Watson, C.S. Assessing the Feasibility of Uav-Based Lidar for High Resolution Forest Change Detection. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XXXIX-B7, 2012 XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 499–504. [Google Scholar] [CrossRef] [Green Version]
- Corte, A.P.D.; Souza, D.V.; Rex, F.E.; Sanquetta, C.R.; Mohan, M.; Silva, C.A.; Zambrano, A.M.A.; Prata, G.; Alves de Almeida, D.R.; Trautenmüller, J.W.; et al. Forest inventory with high-density UAV-Lidar: Machine learning approaches for predicting individual tree attributes. Comput. Electron. Agric. 2020, 179, 105815. [Google Scholar] [CrossRef]
- Wang, D.; Song, Q.; Liao, X.; Ye, H.; Shao, Q.; Fan, J.; Cong, N.; Xin, X.; Yue, H.; Zhang, H. Integrating satellite and unmanned aircraft system (UAS) imagery to model livestock population dynamics in the Longbao Wetland National Nature Reserve, China. Sci. Total Environ. 2020, 746, 140327. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E.; Yang, Z. Using Landsat-derived disturbance and recovery history and lidar to map forest biomass dynamics. Remote Sens. Environ. 2014, 151, 124–137. [Google Scholar] [CrossRef]
- Bolton, D.K.; White, J.C.; Wulder, M.A.; Coops, N.C. Updating stand-level forest inventories using airborne laser scanning and Landsat time series data. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 174–183. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Adamczyk, J.; Osberger, A. Red-edge vegetation indices for detecting and assessing disturbances in Norway spruce dominated mountain forests. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 90–99. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating aboveground biomass of the mangrove forests on northeast Hainan Island in China using an upscaling method from field plots, UAV-LiDAR data and Sentinel-2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Stevens, D.L. Variable density grid-based sampling designs for continuous spatial populations. Environmetrics 1997, 8, 167–195. [Google Scholar] [CrossRef]
- Teich, M.; Bebi, P. Evaluating the benefit of avalanche protection forest with GIS-based risk analyses—A case study in Switzerland. For. Ecol. Manag. 2009, 257, 1910–1919. [Google Scholar] [CrossRef]
- Theobald, D.M.; Stevens, D.L.; White, D.; Urquhart, N.S.; Olsen, A.R.; Norman, J.B. Using GIS to generate spatially balanced random survey designs for natural resource applications. Environ. Manag. 2007, 40, 134–146. [Google Scholar] [CrossRef]
- Pearse, G.D.; Morgenroth, J.; Watt, M.S.; Dash, J.P. Optimising prediction of forest leaf area index from discrete airborne lidar. Remote Sens. Environ. 2017, 200, 220–239. [Google Scholar] [CrossRef]
- Lin, Y.; Hyyppä, J.; Jaakkola, A. Mini-UAV-borne LIDAR for fine-scale mapping. IEEE Geosci. Remote Sens. Lett. 2011, 8, 426–430. [Google Scholar] [CrossRef]
- Andersen, H.; Strunk, J.; Temesgen, H. Sampling Tool for Estimating Forest Biomass Interior Alaska. West. J. Appl. For. 2011, 26, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Ståhl, G.; Holm, S.; Gregoire, T.G.; Gobakken, T.; Næsset, E.; Nelson, R. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark county, Norway. Can. J. For. Res. 2011, 41, 96–107. [Google Scholar] [CrossRef] [Green Version]
- Andersen, H.E.; Strunk, J.; Temesgen, H.; Atwood, D.; Winterberger, K. Using multilevel remote sensing and ground data to estimate forest biomass resources in remote regions: A case study in the boreal forests of interior Alaska. Can. J. Remote Sens. 2012, 37, 596–611. [Google Scholar] [CrossRef]
- Xie, B.; Cao, C.; Xu, M.; Bashir, B.; Singh, R.P.; Huang, Z.; Lin, X. Regional forest volume estimation by expanding LiDAR samples using multi-sensor satellite data. Remote Sens. 2020, 12, 360. [Google Scholar] [CrossRef] [Green Version]



| Tree Species | Tree Height (m) | DBH (cm) | Volume (m3·ha−1) | AGB (Mg·ha−1) |
|---|---|---|---|---|
| Larch | 5.9–20.3 | 6.2–29.2 | 62.5–375.0 | 28.8–157.1 |
| Chinese pine | 7.8–19.6 | 9.8–31.2 | 108.6–372.4 | 77.0–169.8 |
| Parameters | Value |
|---|---|
| Weight (kg) | 15.5 |
| Flight height (m) | 60 |
| Maximum flight speed (m/s) | 10 |
| Cruising radius (km) | 2 |
| LiDAR type | Rigel VUX-1 |
| Scanning angle (°) | ±60° |
| Point density (pts/m3) | ≥25 |
| Wavelength (nm) | 1055 |
| Scanning frequency (Hz) | 10–200 |
| Measurement range (m) | 3–920 |
| The resolution of scanning angle (°) | 0.001 |
| Metrics | Description |
|---|---|
| h25, h50, h75, h95 | The percentiles of the canopy height distributions by first echo (25th, 50th, 75th, and 95th) |
| hmean | The mean height of all points after normalization |
| hcv | The coefficient of variation of height of all points after normalized (the ratio of the standard deviation to the mean) |
| hskewness, hkurtosis | The skewness and kurtosis of the heights of all points by first echo |
| d1, d3, d5, d7, d9 | The proportion of points above the quantiles (10th, 30th, 50th, 70th, and 90th) to total number of points |
| Vegetation Indices | Formula | Reference |
|---|---|---|
| Normalized Difference Vegetation Index (NDVI) | (B7 − B4)/(B7 + B4) | [47] |
| MERIS Terrestrial Chlorophyll Index (MTCI) | (B6 − B5)/(B5 − B4) | [48] |
| Water Index (WI) | B8a/B9 | [49] |
| Corrected Transformed Vegetation Index (CTVI) | [50] | |
| Enhanced Vegetation Index Red Edge 1(B5) (EVIRE1) | 2.5 × (B5 − B4)/(1 + B5 + 6 × B4 − 7.5 × B2) | [51] |
| Enhanced Vegetation Index Red Edge 2(B6) (EVIRE2) | 2.5 × (B6 − B4)/(1 + B6 + 6 × B4 − 7.5 × B2) | [52] |
| Nir infrared Enhanced Vegetation Index (EVINI) | 2.5 × (B8 − B4)/(1 + B8 + 6 × B4 − 7.5 × B2) | [53] |
| Modified Simple Ratio Nir infrared (MSRNIR) | [54] | |
| Modified Simple Ratio Red Edge 3(B7) (MSRRE3) | [55] | |
| Modified Simple Ratio Red Edge 4 (B8a) (MSRRE4) | [56] | |
| Nonlinear Index Red Edge 1(B5) (NLIRE1) | (B52 − B4)/(B52 + B4) | [57] |
| Nonlinear Index Red Edge 2(B6) (NLIRE2) | (B62 − B4)/(B62 + B4) | [58] |
| Nonlinear Index Near infrared (NLINIR) | (B82 − B4)/(B82 + B4) | [59] |
| Nonlinear Index Red Edge 4(B8a) (NLIRE4) | (B8a2 − B4)/(B8a2 + B4) | [60] |
| Sample Plots | The Number of Individual Tree | Accurate Segmentation | Over Segmentation | Omission Segmentation | r | p | f |
|---|---|---|---|---|---|---|---|
| P1 | 30 | 29 | 2 | 1 | 0.97 | 0.94 | 0.95 |
| P2 | 88 | 79 | 6 | 9 | 0.90 | 0.93 | 0.91 |
| P3 | 90 | 80 | 6 | 10 | 0.89 | 0.93 | 0.91 |
| P4 | 95 | 78 | 9 | 17 | 0.82 | 0.90 | 0.86 |
| P5 | 130 | 102 | 12 | 28 | 0.78 | 0.89 | 0.84 |
| P6 | 135 | 104 | 13 | 31 | 0.77 | 0.89 | 0.83 |
| P7 | 140 | 107 | 17 | 33 | 0.76 | 0.86 | 0.81 |
| P8 | 158 | 125 | 23 | 33 | 0.79 | 0.84 | 0.82 |
| P9 | 178 | 133 | 34 | 45 | 0.74 | 0.80 | 0.77 |
| P10 | 20 | 19 | 0 | 1 | 0.95 | 1.00 | 0.97 |
| P11 | 29 | 27 | 2 | 2 | 0.93 | 0.93 | 0.93 |
| P12 | 86 | 80 | 5 | 6 | 0.93 | 0.94 | 0.94 |
| P13 | 94 | 84 | 8 | 10 | 0.89 | 0.91 | 0.90 |
| P14 | 97 | 85 | 8 | 12 | 0.88 | 0.91 | 0.89 |
| P15 | 108 | 93 | 11 | 15 | 0.86 | 0.89 | 0.88 |
| P16 | 109 | 94 | 8 | 15 | 0.83 | 0.90 | 0.86 |
| P17 | 140 | 125 | 14 | 15 | 0.82 | 0.88 | 0.85 |
| P18 | 146 | 129 | 15 | 17 | 0.84 | 0.88 | 0.86 |
| P19 | 151 | 131 | 14 | 20 | 0.81 | 0.88 | 0.84 |
| Plot Number | Accuracy | Tree Height (m) | DBH (cm) | Volume (m3·ha−1) | AGB (Mg·ha−1) |
|---|---|---|---|---|---|
| 100 | R2 | 0.76 | 0.73 | 0.72 | 0.71 |
| rRMSE | 12.5% | 15.6% | 17.2% | 17.9% | |
| 200 | R2 | 0.75 | 0.74 | 0.72 | 0.71 |
| rRMSE | 12.3% | 15.1% | 16.6% | 18.0% | |
| 300 | R2 | 0.77 | 0.76 | 0.73 | 0.73 |
| rRMSE | 12.7% | 14.8% | 16.5% | 16.2% | |
| 400 | R2 | 0.78 | 0.77 | 0.74 | 0.72 |
| rRMSE | 11.9% | 14.1% | 15.8% | 16.4% | |
| 500 | R2 | 0.80 | 0.77 | 0.75 | 0.74 |
| rRMSE | 11.5% | 13.6% | 15.1% | 15.2% | |
| 600 | R2 | 0.80 | 0.78 | 0.75 | 0.76 |
| rRMSE | 11.3% | 12.7% | 15.2% | 14.9% | |
| 700 | R2 | 0.81 | 0.78 | 0.75 | 0.77 |
| rRMSE | 11.2% | 13.1% | 15.1% | 15.1% | |
| 800 | R2 | 0.81 | 0.79 | 0.76 | 0.76 |
| rRMSE | 11.0% | 12.5% | 15.2% | 15.2% |
| Approaches | Accuracy Indicator | Tree Height (m) | DBH (cm) | Volume (m3·ha−1) | AGB (Mg·ha−1) |
|---|---|---|---|---|---|
| Approach 1 | R2 | 0.64 | 0.61 | 0.60 | 0.62 |
| rRMSE | 24.1% | 22.9% | 27.3% | 25.9% | |
| Approach 2 | R2 | 0.78 | 0.75 | 0.73 | 0.73 |
| rRMSE | 14.5% | 16.1% | 18.8% | 19.6% | |
| Approach 3 | R2 | 0.77 | 0.73 | 0.72 | 0.70 |
| rRMSE | 17.2% | 18.5% | 17.1% | 20.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Shen, X.; Zhang, Z.; Cao, F.; She, G.; Cao, L. An Advanced Framework for Multi-Scale Forest Structural Parameter Estimations Based on UAS-LiDAR and Sentinel-2 Satellite Imagery in Forest Plantations of Northern China. Remote Sens. 2022, 14, 3023. https://doi.org/10.3390/rs14133023
Wu X, Shen X, Zhang Z, Cao F, She G, Cao L. An Advanced Framework for Multi-Scale Forest Structural Parameter Estimations Based on UAS-LiDAR and Sentinel-2 Satellite Imagery in Forest Plantations of Northern China. Remote Sensing. 2022; 14(13):3023. https://doi.org/10.3390/rs14133023
Chicago/Turabian StyleWu, Xiangqian, Xin Shen, Zhengnan Zhang, Fuliang Cao, Guanghui She, and Lin Cao. 2022. "An Advanced Framework for Multi-Scale Forest Structural Parameter Estimations Based on UAS-LiDAR and Sentinel-2 Satellite Imagery in Forest Plantations of Northern China" Remote Sensing 14, no. 13: 3023. https://doi.org/10.3390/rs14133023
APA StyleWu, X., Shen, X., Zhang, Z., Cao, F., She, G., & Cao, L. (2022). An Advanced Framework for Multi-Scale Forest Structural Parameter Estimations Based on UAS-LiDAR and Sentinel-2 Satellite Imagery in Forest Plantations of Northern China. Remote Sensing, 14(13), 3023. https://doi.org/10.3390/rs14133023








