Curvilinear Flight Synthetic Aperture Radar (CF-SAR): Principles, Methods, Applications, Challenges and Trends
Abstract
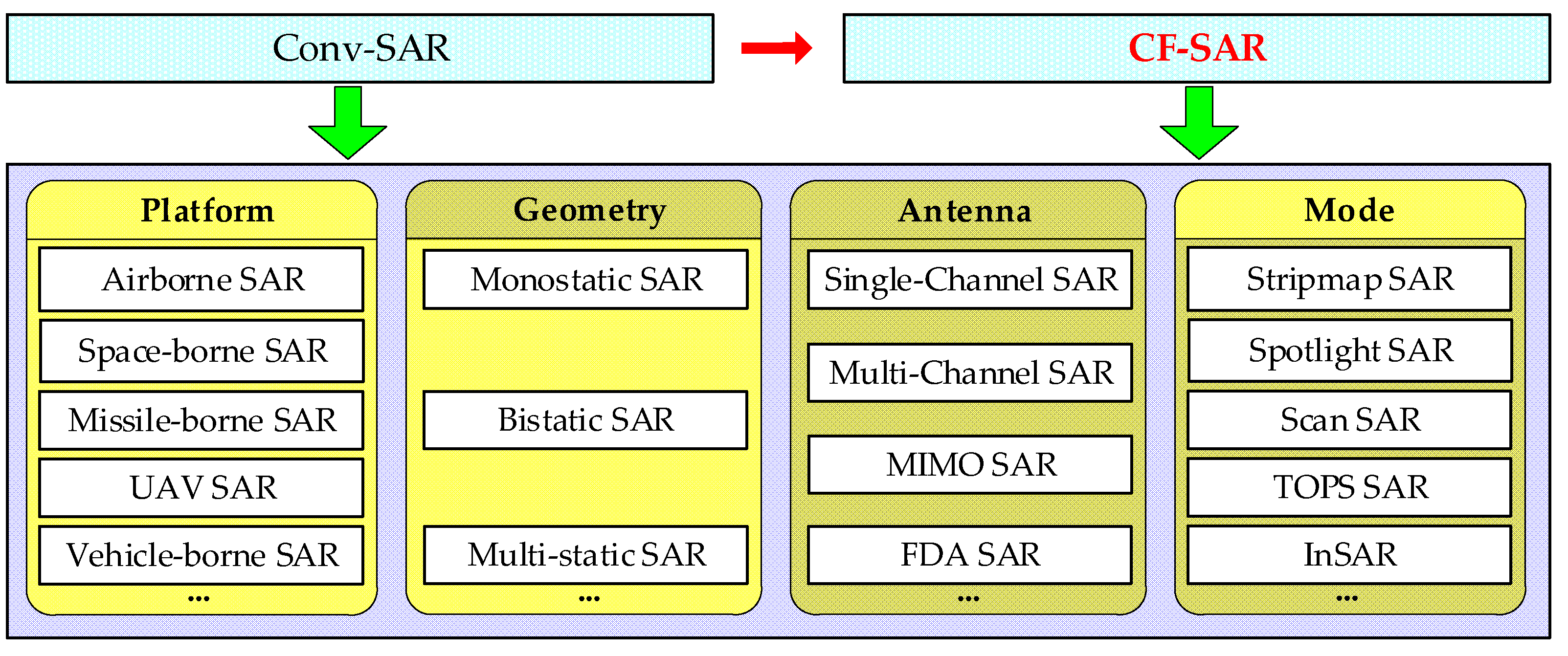
:1. Introduction
- ➢
- Highly adaptable to detection geometries. Taking complex application scenarios, such as mountain or urban surveying, as an example, Conv-SAR has to abandon imaging quality in exchange for a safe working environment. This is because the imaging geometry of Conv-SAR no longer meets the imaging requirements when performing terrain avoidance to obtain a safe path. However, the emergence of CF-SAR forces the detection geometry boundary of Conv-SAR to no longer be restricted to the condition of uniform linear virtual synthetic aperture. In other words, by effectively dealing with the nonlinear or non-uniform sampling data introduced by the curve trajectory, CF-SAR ensures the imaging performance and output rate under different detection geometries.
- ➢
- In-depth utilization of detection capabilities. Taking the selection of imaging area as an example, Conv-SAR has a forward-looking blind zone [5]. However, CF-SAR can solve the problem of forward-looking imaging through the autonomous adjustment of radar trajectory and arbitrary control of beam steering, which maximize the technical advantages of SAR. In other words, the nonlinear motion of the SAR platform can provide more degrees of freedom to explore the detection capabilities of SAR. As a special case of CF-SAR, the 3D imaging of the circular SAR [6] also demonstrates that CF-SAR can deeply utilize the detection ability of SAR. Similarly, a timely and rapid revisit of CF-SAR also provides a prerequisite for the SAR moving target indication capability.
2. Principle of CF-SAR
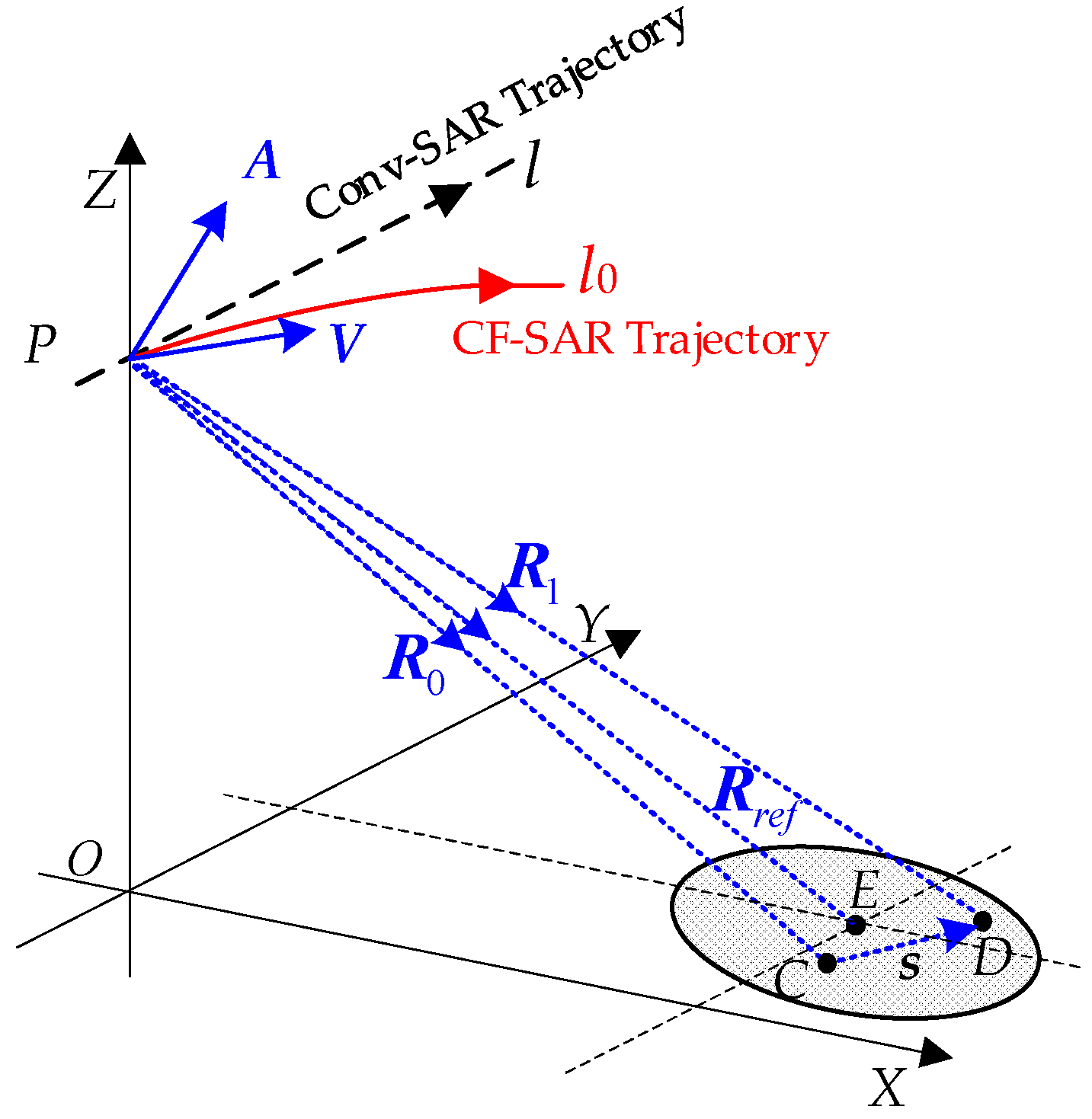
2.1. Basic Concept
2.2. Unified Model
2.3. General Characteristics
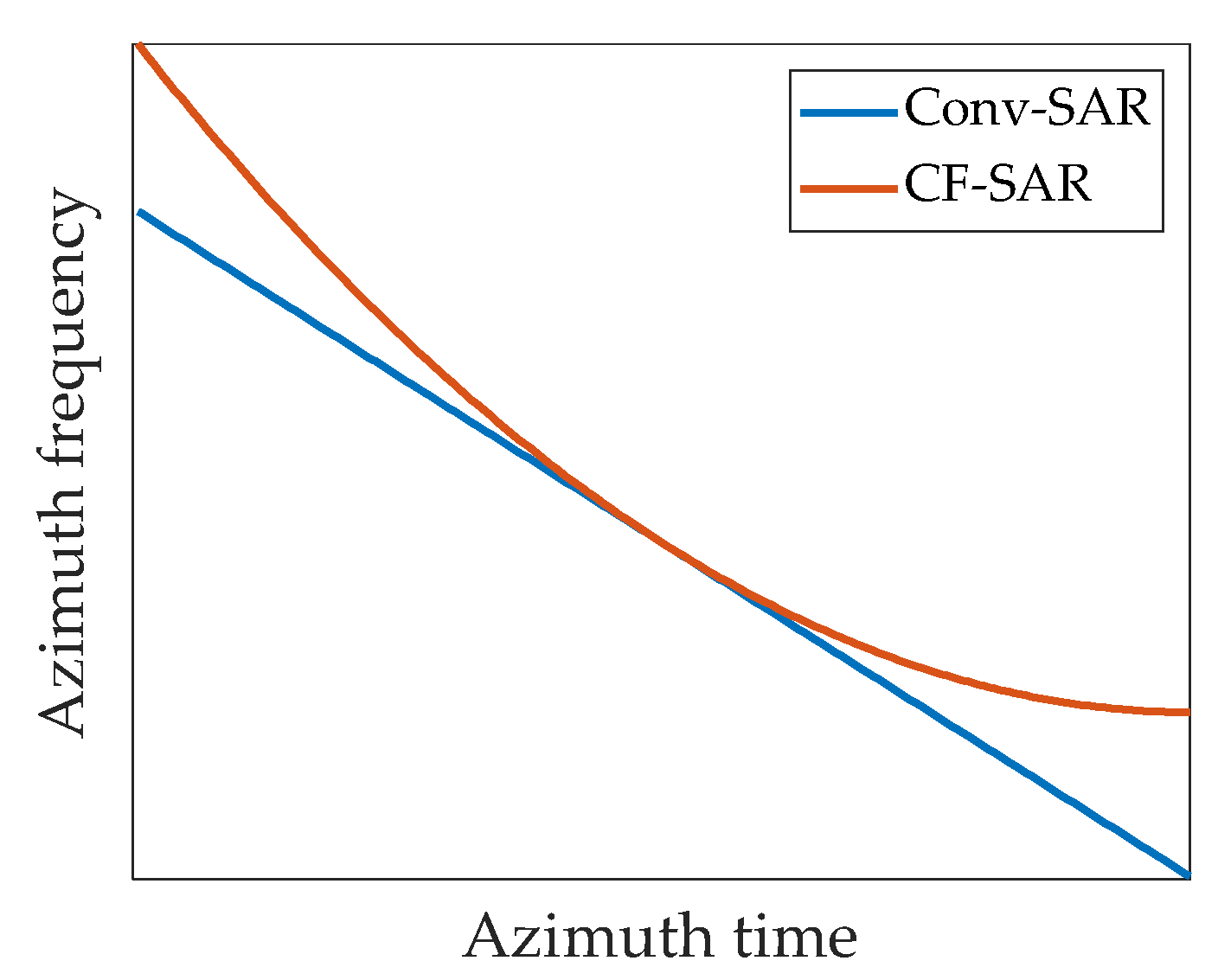
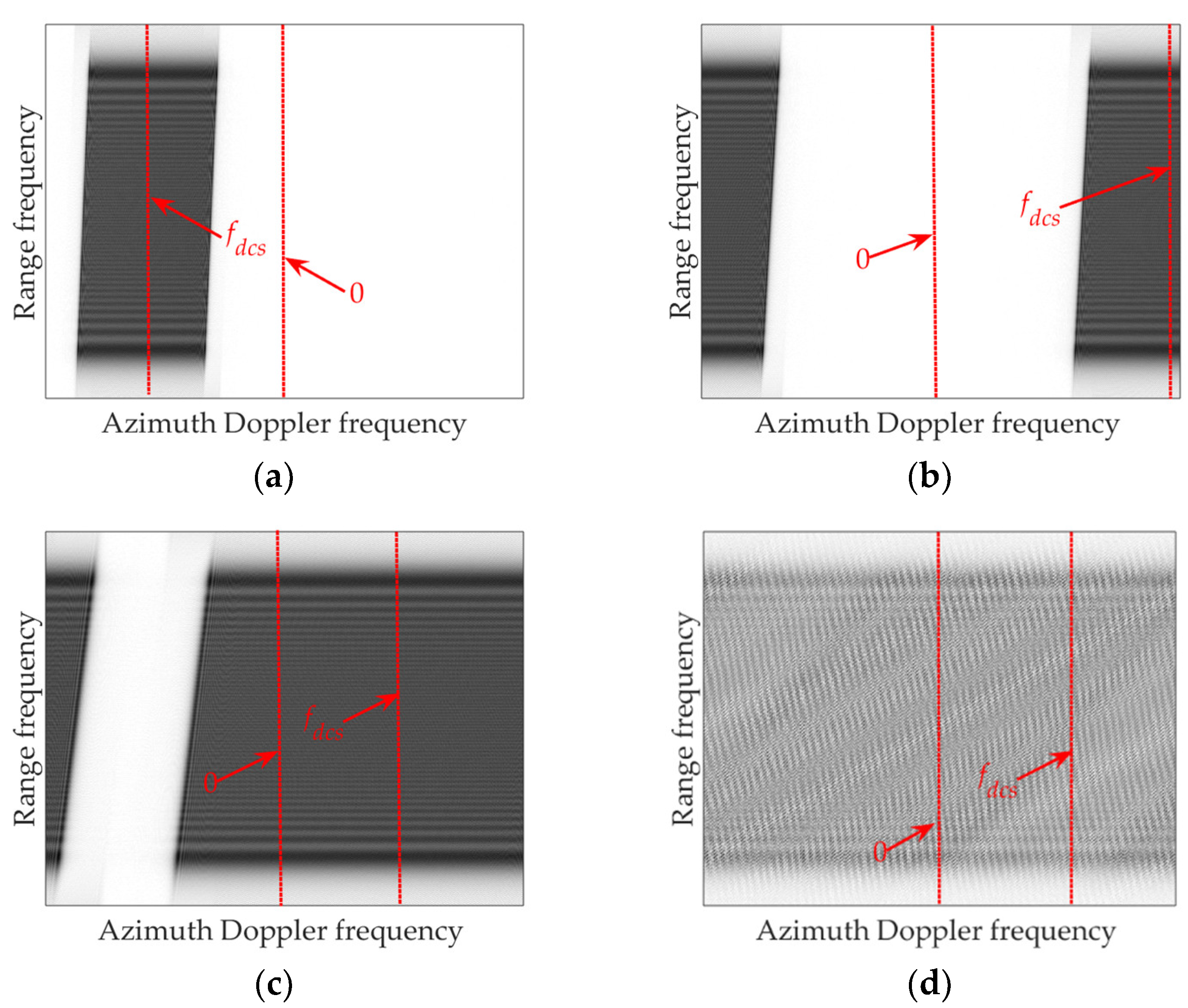
2.3.1. Coupling
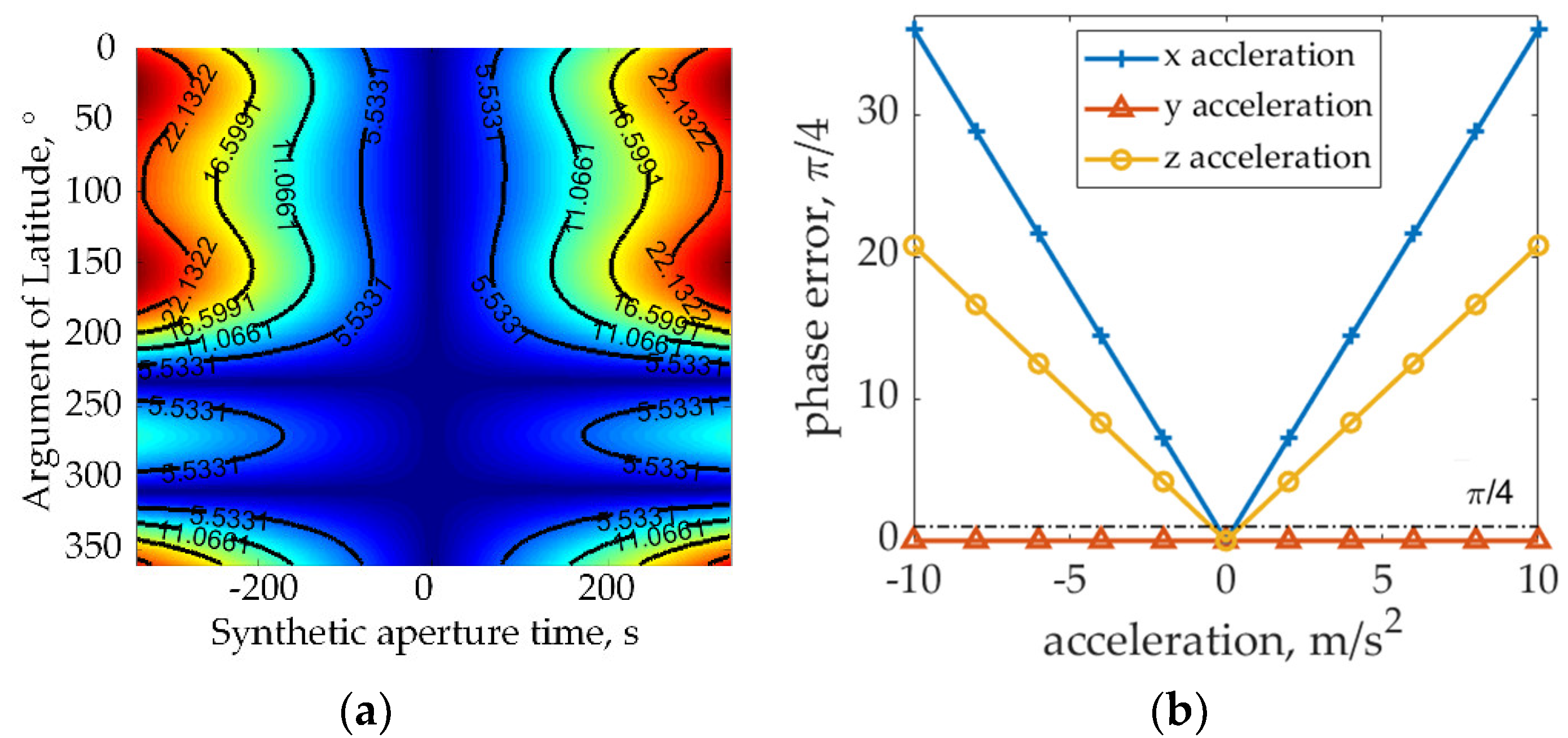
2.3.2. Spatial Variation
2.3.3. Bandwidth
2.3.4. Resolution
- ➢
- Range Resolution:
- ➢
- Azimuth Resolution:
2.3.5. Beam Steering
- ➢
- Instantaneous Azimuth Angle:
- ➢
- Instantaneous Elevation Angle:
2.3.6. Integration Time
3. Current Methodologies Review
3.1. Imaging Model Establishment
3.1.1. Range History Approximation
3.1.2. Imaging Coordinate System Transformation
3.2. Imaging Algorithm Design
3.2.1. Time Domain Algorithm
3.2.2. Hybrid Domain Algorithm
3.2.3. Frequency Domain Algorithm
4. Application Discussions
4.1. Typical Platforms
4.1.1. Airborne CF-SAR
4.1.2. UAV-Borne CF-SAR
4.1.3. Spaceborne CF-SAR
4.2. New Configurations
4.2.1. Multi-Channel CF-SAR
4.2.2. Bi-/Multi-Static CF-SAR
4.3. Advanced Technologies
4.3.1. Ground Moving Target Indication
4.3.2. Interference Suppression
5. Challenges and Trends
5.1. Challenges
- ➢
- Design of imaging algorithm with low computational complexity and unified multi-modality. There have been many theoretical studies on the design of CF-SAR imaging algorithms, but the core of performing real-time processing in practical applications is reducing the computational complexity of the algorithm. In addition, based on advanced beam-steering technology, CF-SAR usually has a variety of imaging modes to satisfy different missions. How we can promote the existing Conv-SAR unified imaging algorithm [133] or develop a new unified imaging algorithm for CF-SAR is worth considering.
- ➢
- Allocation of imaging resources with multiple configuration. Several new configurations of CF-SAR, such as multi-channel and bi-/multi-static, have the potential to make full use of spatial, angular, and frequency resources of radar. However, how we should allocate these resources reasonably to maximize the efficiency of resource utilization has not yet been resolved, such as breaking through the limits of physical resolution, obtaining multi-dimensional and multi-angle imaging capabilities, having a continuous video imaging function, and exact image inversion under the case of complex terrain or lack of echo [13].
- ➢
- Visualization of imaging results with geometric correction and prior information. The imaging planes of CF-SAR are mostly not in the ground plane, and the slant plane description of Conv-SAR does not apply. Therefore, the geometric correction processing of the focused image is unavoidable; otherwise, the final interpretation of the image will be affected. In addition, applying some existing prior information, e.g., polarization, optics, etc., to the visualization of imaging results would also be very helpful for CF-SAR image correction and interpretation, which further improves the practical value of CF-SAR.
5.2. Trends
- ➢
- Multifunctional integration. A set of systems to complete multiple functions can greatly improve the work efficiency of CF-SAR. Therefore, multifunctional integrations, such as simultaneous SAR and GMTI [134], imaging recognition integration [135], and even imaging communication integration [136], are potential development fields.
- ➢
- Strong robust radar system. The rapid development of CF-SAR technology requires the support of actual system equipment. There is currently no dedicated CF-SAR system, especially spaceborne CF-SAR in medium and geosynchronous orbits. Although some demonstration systems have been developed, whether they are robust in practical complex working environments is still a difficulty to consider.
- ➢
- Cognitive detection. The core task of radar is still detection. CF-SAR provides radar with high-resolution detection capabilities, but whether radar parameters, working modes, and detection functions can be cognitively adjusted according to detection missions and scenarios will greatly affect future intelligent detection.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Reigber, A.; Scheiber, R.; Jager, M.; Prats-Iraola, P.; Hajnsek, I.; Jagdhuber, T.; Papathanassiou, K.P.; Nannini, M.; Aguilera, E.; Baumgartner, S.; et al. Very-High-Resolution Airborne Synthetic Aperture Radar Imaging: Signal Processing and Applications. Proc. IEEE 2013, 101, 759–783. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G.-C. Motion Compensation/Autofocus in Airborne Synthetic Aperture Radar: A Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 185–206. [Google Scholar] [CrossRef]
- Li, Y.; Huo, T.; Yang, C.; Wang, T.; Wang, J.; Li, B. An Efficient Ground Moving Target Imaging Method for Airborne Circular Stripmap SAR. Remote Sens. 2022, 14, 210. [Google Scholar] [CrossRef]
- Hu, R.; Rao, B.S.M.R.; Murtada, A.; Alaee-Kerahroodi, M.; Ottersten, B. Automotive Squint-Forward-Looking SAR: High Resolution and Early Warning. IEEE J. Sel. Top. Signal Process. 2021, 15, 904–912. [Google Scholar] [CrossRef]
- Hong, W.; Wang, Y.; Lin, Y.; Tan, W.; Wu, Y. Research progress on three-dimensional SAR imaging techniques. J. Radars 2018, 7, 633–654. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Zhang, L.; Wei, H.; Lin, C.; Liu, N.; Wan, J. General range model for multi-channel SAR/GMTI with curvilinear flight trajectory. Electron. Lett. 2019, 55, 111–112. [Google Scholar] [CrossRef]
- Ren, Y.; Tang, S.; Guo, P.; Zhang, L.; So, H.C. 2-D Spatially Variant Motion Error Compensation for High-Resolution Airborne SAR Based on Range-Doppler Expansion Approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5201413. [Google Scholar] [CrossRef]
- Hu, C.; Long, T.; Zeng, T.; Liu, F.; Liu, Z. The Accurate Focusing and Resolution Analysis Method in Geosynchronous SAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3548–3563. [Google Scholar] [CrossRef]
- Sun, G.-C.; Liu, Y.; Xiang, J.; Liu, W.; Xing, M.; Chen, J. Spaceborne Synthetic Aperture Radar Imaging Algorithms: An overview. IEEE Geosci. Remote Sens. Mag. 2022, 10, 161–184. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Li, K.-X.; Liu, Y.-Y.; Zhou, Y.-G.; Li, X.-P. Study of the influence of time-varying plasma sheath on radar echo signal. IEEE Trans. Plasma Sci. 2017, 45, 3166–3176. [Google Scholar] [CrossRef]
- Song, L.; Li, X.; Liu, Y. Effect of Time-Varying Plasma Sheath on Hypersonic Vehicle-Borne Radar Target Detection. IEEE Sens. J. 2021, 21, 16880–16893. [Google Scholar] [CrossRef]
- Chen, Z.; Zeng, Z.; Huang, Y.; Wan, J.; Tan, X. SAR Raw Data Simulation for Fluctuant Terrain: A New Shadow Judgment Method and Simulation Result Evaluation Framework. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5215018. [Google Scholar] [CrossRef]
- Chen, J.; Sun, G.-C.; Wang, Y.; Guo, L.; Xing, M.; Gao, Y. An Analytical Resolution Evaluation Approach for Bistatic GEOSAR Based on Local Feature of Ambiguity Function. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2159–2169. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, H.; Fang, T.; Deng, Y.; Yu, W.; Zhang, L.; Fan, H. Processing of Very High Resolution GF-3 SAR Spotlight Data with Non-Start–Stop Model and Correction of Curved Orbit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2112–2122. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Zhang, Y.; Li, Q.; Gu, Y.; Lin, C. Processing of Monostatic SAR Data with General Configurations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6529–6546. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Zhang, L.; Lin, C.; Huang, Y.; Tang, S. Ground Moving Target Imaging and Analysis for Near-Space Hypersonic Vehicle-Borne Synthetic Aperture Radar System with Squint Angle. Remote Sens. 2018, 10, 1966. [Google Scholar] [CrossRef] [Green Version]
- Jun, S.; Zhang, X.; Yang, J. Principle and Methods on Bistatic SAR Signal Processing via Time Correlation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3163–3178. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Tang, S.; Zhang, L.; Guo, P.; Zhao, Y. An Omega-K Algorithm for Highly Squinted Missile-Borne SAR with Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1569–1573. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An Improved Range Model and Omega-K-Based Imaging Algorithm for High-Squint SAR with Curved Trajectory and Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Gao, Y.; Chen, J. Equivalent hyperbolic range model for synthetic aperture radar with curved track. Electron. Lett. 2016, 52, 1252–1253. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Sun, G.-C.; Gao, Y.; Liu, W.; Guo, L.; Lan, Y. Focusing of Medium-Earth-Orbit SAR Using an ASE-Velocity Model Based on MOCO Principle. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3963–3975. [Google Scholar] [CrossRef]
- Eldhuset, K. A new fourth-order processing algorithm for spaceborne SAR. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 824–835. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Qi, X.; Song, H.; Wang, R.; Mo, Y.; Zheng, S. An Accurate Range Model Based on the Fourth-Order Doppler Parameters for Geosynchronous SAR. IEEE Geosci. Remote Sens. Lett. 2014, 11, 205–209. [Google Scholar] [CrossRef]
- Li, D.; Wu, M.; Sun, Z.; He, F.; Dong, Z. Modeling and Processing of Two-Dimensional Spatial-Variant Geosynchronous SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3999–4009. [Google Scholar] [CrossRef]
- Deng, B.; Qin, Y.; Li, Y.; Wang, H.; Li, X. A Novel Approach to Range Doppler SAR Processing Based on Legendre Orthogonal Polynomials. IEEE Geosci. Remote Sens. Lett. 2009, 6, 13–17. [Google Scholar] [CrossRef]
- Bie, B.; Quan, Y.; Sun, G.-C.; Liu, W.; Xing, M. A Modified Range Model and Doppler Resampling Based Imaging Algorithm for High Squint SAR on Maneuvering Platforms. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1923–1927. [Google Scholar] [CrossRef]
- Zhu, D.; Zhu, Z. Range Resampling in the Polar Format Algorithm for Spotlight SAR Image Formation Using the Chirp Z-Transform. IEEE Trans. Signal Process. 2007, 55, 1011–1023. [Google Scholar] [CrossRef]
- Mao, X.; Zhu, D.; Zhu, Z. Polar Format Algorithm Wavefront Curvature Compensation Under Arbitrary Radar Flight Path. IEEE Geosci. Remote Sens. Lett. 2012, 9, 526–530. [Google Scholar] [CrossRef]
- Sun, G.-C.; Xing, M.; Xia, X.-G.; Wu, Y.; Bao, Z. Beam Steering SAR Data Processing by a Generalized PFA. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4366–4377. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, L.; Cao, Y.; Yeo, T.-S.; Wang, G. A Novel Algorithm for Hypersonic SAR Imaging with Large Squint Angle and Dive Trajectory. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4016105. [Google Scholar] [CrossRef]
- Liu, W.; Sun, G.-C.; Xing, M.; Li, H.; Bao, Z. Focusing of MEO SAR Data Based on Principle of Optimal Imaging Coordinate System. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5477–5489. [Google Scholar] [CrossRef]
- Tang, S.; Guo, P.; Zhang, L.; So, H.C. Focusing Hypersonic Vehicle-Borne SAR Data Using Radius/Angle Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 281–293. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, W.; Sun, G.-C.; Chen, X.; Han, L.; Xing, M. A Fast Cartesian Back-Projection Algorithm Based on Ground Surface Grid for GEO SAR Focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5217114. [Google Scholar] [CrossRef]
- Frey, O.; Magnard, C.; Ruegg, M.; Meier, E. Focusing of Airborne Synthetic Aperture Radar Data from Highly Nonlinear Flight Tracks. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1844–1858. [Google Scholar] [CrossRef] [Green Version]
- Jun, S.; Long, M.; Xiaoling, Z. Streaming BP for Non-Linear Motion Compensation SAR Imaging Based on GPU. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2035–2050. [Google Scholar] [CrossRef]
- Ponce, O.; Prats-Iraola, P.; Pinheiro, M.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully Polarimetric High-Resolution 3-D Imaging with Circular SAR at L-Band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]
- Ulander, L.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Zhao, L.; Zhou, S.; Bi, G.; Yang, H. Spectrum-Oriented FFBP Algorithm in Quasi-Polar Grid for SAR Imaging on Maneuvering Platform. IEEE Geosci. Remote Sens. Lett. 2017, 14, 724–728. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, G.-C.; Yang, Z.; Guo, L.; Xing, M. Cartesian Factorized Backprojection Algorithm for High-Resolution Spotlight SAR Imaging. IEEE Sens. J. 2018, 18, 1160–1168. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.-C.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5812–5827. [Google Scholar] [CrossRef]
- Lin, C.; Tang, S.; Zhang, L.; Guo, P. Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle. Remote Sens. 2018, 10, 1275. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhou, S.; Yang, L. A new fast factorized back-projection algorithm with reduced topography sensibility for mis-sile-borne SAR focusing with diving movement. Remote Sens. 2020, 12, 2616. [Google Scholar] [CrossRef]
- Hu, C.; Tian, Y.; Zeng, T.; Long, T.; Dong, X. Adaptive Secondary Range Compression Algorithm in Geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1397–1413. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, B.; Han, X.; Wang, R.; Song, H.; Deng, Y. A Novel High-Order Range Model and Imaging Approach for High-Resolution LEO SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3473–3485. [Google Scholar] [CrossRef]
- Hu, C.; Liu, Z.; Long, T. An Improved CS Algorithm Based on the Curved Trajectory in Geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 795–808. [Google Scholar] [CrossRef]
- Chen, J.; Sun, G.-C.; Wang, Y.; Xing, M.; Li, Z.; Zhang, Q.; Liu, L.; Dai, C. A TSVD-NCS Algorithm in Range-Doppler Domain for Geosynchronous Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1631–1635. [Google Scholar] [CrossRef]
- He, F.; Chen, Q.; Dong, Z.; Sun, Z. Processing of Ultrahigh-Resolution Spaceborne Sliding Spotlight SAR Data on Curved Orbit. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 819–839. [Google Scholar] [CrossRef]
- Zeng, T.; Li, Y.; Ding, Z.; Long, T.; Yao, D.; Sun, Y. Subaperture Approach Based on Azimuth-Dependent Range Cell Migration Correction and Azimuth Focusing Parameter Equalization for Maneuvering High-Squint-Mode SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6718–6734. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.-C.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms with Nonlinear Trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Zhang, T.; Ding, Z.; Tian, W.; Zeng, T.; Yin, W. A 2-D Nonlinear Chirp Scaling Algorithm for High Squint GEO SAR Imaging Based on Optimal Azimuth Polynomial Compensation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5724–5735. [Google Scholar] [CrossRef]
- Bie, B.; Quan, Y.; Xu, K.; Ren, A.; Xiao, G.; Sun, G.-C.; Xing, M. High-Speed Maneuvering Platform SAR Imaging with Optimal Beam Steering Control. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5216012. [Google Scholar] [CrossRef]
- Zhu, D.; Xiang, T.; Wei, W.; Ren, Z.; Yang, M.; Zhang, Y.; Zhu, Z. An Extended Two Step Approach to High-Resolution Airborne and Spaceborne SAR Full-Aperture Processing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8382–8397. [Google Scholar] [CrossRef]
- D’Aria, D.; Monti-Guarnieri, A.V. High-Resolution Spaceborne SAR Focusing by SVD-Stolt. IEEE Geosci. Remote Sens. Lett. 2007, 4, 639–643. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Zhang, L.; So, H.C. Focusing High-Resolution Highly-Squinted Airborne SAR Data with Maneuvers. Remote Sens. 2018, 10, 862. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.; Jiang, Y.; Zhang, S.; Zhang, Y.; Yeo, T.S. Generalized Omega-K Algorithm for Geosynchronous SAR Image Formation. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2286–2290. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.-C. Acceleration Model Analyses and Imaging Algorithm for Highly Squinted Airborne Spotlight-Mode SAR with Maneuvers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1120–1131. [Google Scholar] [CrossRef]
- Liu, W.; Sun, G.-C.; Xia, X.-G.; You, D.; Xing, M.; Bao, Z. Highly Squinted MEO SAR Focusing Based on Extended Omega-K Algorithm and Modified Joint Time and Doppler Resampling. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9188–9200. [Google Scholar] [CrossRef]
- Zhao, S.; Deng, Y.; Wang, R. Imaging for High-Resolution Wide-Swath Spaceborne SAR Using Cubic Filtering and NUFFT Based on Circular Orbit Approximation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 787–800. [Google Scholar] [CrossRef]
- Tang, S.; Lin, C.; Zhou, Y.; So, H.C.; Zhang, L.; Liu, Z. Processing of Long Integration Time Spaceborne SAR Data with Curved Orbit. IEEE Trans. Geosci. Remote Sens. 2018, 56, 888–904. [Google Scholar] [CrossRef]
- Chen, J.; Sun, G.-C.; Xing, M.; Liang, B.; Gao, Y. Focusing Improvement of Curved Trajectory Spaceborne SAR Based on Optimal LRWC Preprocessing and 2-D Singular Value Decomposition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4246–4258. [Google Scholar] [CrossRef]
- Dang, Y.; Liang, Y.; Bie, B.; Ding, J.; Zhang, Y. A Range Perturbation Approach for Correcting Spatially Variant Range Envelope in Diving Highly Squinted SAR with Nonlinear Trajectory. IEEE Geosci. Remote Sens. Lett. 2018, 15, 858–862. [Google Scholar] [CrossRef]
- Page, D.; Owirka, G.; Nichols, H.; Scarborough, S.; Minardi, M.; Gorham, L. Detection and tracking of moving vehicles with Gotcha radar systems. IEEE Aerosp. Electron. Syst. Mag. 2014, 29, 50–60. [Google Scholar] [CrossRef]
- Scarborough, S.M.; Casteel, J.C.H.; Gorham, L.; Minardi, M.J.; Majumder, U.K.; Judge, M.G.; Zelnio, E.; Bryant, M.; Nichols, H.; Page, D. A challenge problem for SAR-based GMTI in urban environments. In Proceedings of the SPIE Defense, Security, and Sensing, Orlando, FL, USA, 13–17 April 2009. [Google Scholar] [CrossRef]
- Guo, B.; Vu, D.; Xu, L.; Xue, M.; Li, J. Ground Moving Target Indication via Multichannel Airborne SAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3753–3764. [Google Scholar] [CrossRef]
- Perna, S. Airborne Synthetic Aperture Radar: Models, Focusing and Experiments. Ph.D. Dissertation, Dipartimento Ingegneria Elettronica delle Telecomunicazioni, Università degli Studi di Napoli “Federico II”, Naples, Italy, 2004. [Google Scholar]
- Zhang, Y.; Zhu, D.; Mao, X.; Yu, X.; Zhang, J.; Li, Y. Multirotors Video Synthetic Aperture Radar: System Development and Signal Processing. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 32–43. [Google Scholar] [CrossRef]
- Tsunoda, S.; Pace, F.; Stence, J.; Woodring, M.; Hensley, W.; Doerry, A.; Walker, B. Lynx: A high-resolution synthetic aperture radar. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 25–25 March 2000; pp. 51–58. [Google Scholar] [CrossRef] [Green Version]
- Sandia National Laboratories. Complex SAR Data. 2015. Available online: https://www.sandia.gov/radar/pathfinder-radar-isr-and-synthetic-aperture-radar-sar-systems/complex-data/ (accessed on 13 May 2022).
- Seguin, G.; Srivastava, S.; Auger, D. Evolution of the RADARSAT Program. IEEE Geosci. Remote Sens. Mag. 2014, 2, 56–58. [Google Scholar] [CrossRef]
- Buckreuss, S.; Werninghaus, R.; Pitz, W. The German satellite mission TerraSAR-X. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 4–9. [Google Scholar] [CrossRef]
- Shimada, M. JAXA Earth Observation Programs Digest. IEEE Geosci. Remote Sens. Mag. 2014, 2, 47–52. [Google Scholar] [CrossRef]
- Snoeij, P.; Attema, E.; Davidson, M.; Duesmann, B.; Floury, N.; Levrini, G.; Rommen, B.; Rosich, B. Sentinel-1 radar mission: Status and performance. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 32–39. [Google Scholar] [CrossRef]
- Mathieu, P.-P.; Borgeaud, M.; Desnos, Y.-L.; Rast, M.; Brockmann, C.; See, L.; Kapur, R.; Mahecha, M.; Benz, U.; Fritz, S. The ESA’s Earth Observation Open Science Program [Space Agencies]. IEEE Geosci. Remote Sens. Mag. 2017, 5, 86–96. [Google Scholar] [CrossRef]
- Sun, J.; Yu, W.; Deng, Y. The SAR Payload Design and Performance for the GF-3 Mission. Sensors 2017, 17, 2419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, L.; Zhang, Q.; Li, Y.; Qi, Y.; Yuan, X.; Liu, J.; Li, H. China’s Gaofen-3 Satellite System and Its Application and Prospect. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11019–11028. [Google Scholar] [CrossRef]
- Shang, M.; Han, B.; Ding, C.; Sun, J.; Zhang, T.; Huang, L.; Meng, D. A High-Resolution SAR Focusing Experiment Based on GF-3 Staring Data. Sensors 2018, 18, 943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR data focusing based on a two-step processing approach. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1993–2004. [Google Scholar] [CrossRef]
- Curlander, J.; McDonough, R. Synthetic Aperture Radar–Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Gebert, N.; Krieger, G.; Moreira, A. Digital Beamforming on Receive: Techniques and Optimization Strategies for High-Resolution Wide-Swath SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Zhang, L.; Xie, P.; Meng, Z.; Cao, Y. High-Resolution Imaging of Multi-Channel Forward-Looking Synthetic Aperture Radar Under Curve Trajectory. IEEE Access 2019, 7, 51211–51221. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, L.; Quan, Y.; Meng, Z.; Cao, Y. Parametric Azimuth-Variant Motion Compensation for Forward-Looking Multichannel SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8521–8537. [Google Scholar] [CrossRef]
- Liu, B.; He, Y. Improved DBF Algorithm for Multichannel High-Resolution Wide-Swath SAR. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1209–1225. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, R.; Deng, Y.; Yu, W.; Fan, H.; Liang, D.; Zhao, Q. A Novel Approach to Doppler Centroid and Channel Errors Estimation in Azimuth Multi-Channel SAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8430–8444. [Google Scholar] [CrossRef]
- Krieger, G. MIMO-SAR: Opportunities and Pitfalls. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2628–2645. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Xu, J.; Liao, G.; Xu, X.; Zhang, Y. A Range Ambiguity Resolution Approach for High-Resolution and Wide-Swath SAR Imaging Using Frequency Diverse Array. IEEE J. Sel. Top. Signal Process. 2017, 11, 336–346. [Google Scholar] [CrossRef]
- Nan, L.; Linrang, Z. Intrapulse Azimuth Frequency Scanning-Based 2-D Scanning SAR for HRWS Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9382–9396. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Zhou, Y.; Zhao, Q.; Wang, W. Elevated Frequency Diversity Array: A Novel Approach to High Resolution and Wide Swath Imaging for Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2020, 19, 4001505. [Google Scholar] [CrossRef]
- Zhang, M.; Liao, G.; Xu, J.; Lan, L.; Zhu, S.; Xing, M.; He, X. High-Resolution and Wide-Swath Imaging Based on Multifrequency Pulse Diversity and DPCA Technique. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4502505. [Google Scholar] [CrossRef]
- Aldharrab, A.; Davies, M.E. Staggered Coprime Pulse Repetition Frequencies Synthetic Aperture Radar (SCopSAR). IEEE Trans. Geosci. Remote Sens. 2022, 60, 5208711. [Google Scholar] [CrossRef]
- Sun, G.-C.; Xing, M.; Xia, X.-G.; Wu, Y.; Huang, P.; Wu, Y.; Bao, Z. Multichannel Full-Aperture Azimuth Processing for Beam Steering SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4761–4778. [Google Scholar] [CrossRef]
- He, F.; Dong, Z.; Zhang, Y.; Jin, G.; Yu, A. Processing of Spaceborne Squinted Sliding Spotlight and HRWS TOPS Mode Data Using 2-D Baseband Azimuth Scaling. IEEE Trans. Geosci. Remote Sens. 2020, 58, 938–955. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, L.; Zhang, Z.; Yu, W.; Deng, Y. On the Processing of Gaofen-3 Spaceborne Dual-Channel Sliding Spotlight SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5202912. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, L.; Zhou, Y.; Lin, C.; Tang, S.; Wan, J. Non-adaptive space-time clutter canceller for multi-channel synthetic aperture radar. IET Signal Process. 2019, 13, 472–479. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Liu, Z.; Yang, H.; Wu, J.; Yang, J. Bistatic Forward-Looking SAR MP-DPCA Method for Space–Time Extension Clutter Suppression. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6565–6579. [Google Scholar] [CrossRef]
- Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and useful relations for bistatic SAR processing. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2031–2038. [Google Scholar] [CrossRef]
- Comblet, F.; Khenchaf, A.; Baussard, A.; Pellen, F. Bistatic Synthetic Aperture Radar Imaging: Theory, Simulations, and Validations. IEEE Trans. Antennas Propag. 2006, 54, 3529–3540. [Google Scholar] [CrossRef]
- Zeng, T. Bistatic SAR: State of the Art and Development Trend. J. Radars 2012, 1, 329–341. [Google Scholar] [CrossRef]
- Yang, J. Bistatic synthetic aperture radar technology. J. Univ. Electron. Sci. Technol. China 2016, 45, 482–501. [Google Scholar]
- Rodriguez-Cassola, M.; Prats-Iraola, P.; Schulze, D.; Tous-Ramon, N.; Steinbrecher, U.; Marotti, L.; Nannini, M.; Younis, M.; Dekker, P.L.; Zink, M.; et al. First Bistatic Spaceborne SAR Experiments with TanDEM-X. IEEE Geosci. Remote Sens. Lett. 2012, 9, 33–37. [Google Scholar] [CrossRef] [Green Version]
- Walterscheid, I.; Espeter, T.; Brenner, A.R.; Klare, J.; Ender, J.H.G.; Nies, H.; Wang, R.; Loffeld, O. Bistatic SAR Experiments with PAMIR and TerraSAR-X—Setup, Processing, and Image Results. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3268–3279. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.D.; Neo, Y.L.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J.H.G. Focusing Bistatic SAR Data in Airborne/Stationary Configuration. IEEE Trans. Geosci. Remote Sens. 2010, 48, 452–465. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Deng, Y.; Wang, R.; Liu, K.; Liu, D.; Jin, G.; Zhang, Y. Focusing the L-Band Spaceborne Bistatic SAR Mission Data Using a Modified RD Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 294–306. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Pei, J.; Li, Z.; Huang, Y.; Yang, J. Inclined Geosynchronous Spaceborne–Airborne Bistatic SAR: Performance Analysis and Mission Design. IEEE Trans. Geosci. Remote Sens. 2016, 54, 343–357. [Google Scholar] [CrossRef]
- Tang, S.; Guo, P.; Zhang, L.; Lin, C. Modeling and Precise Processing for Spaceborne Transmitter/Missile-Borne Receiver SAR Signals. Remote Sens. 2019, 11, 346. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Liu, M.; Ai, G.; Wang, P.; Lv, K. Focusing of Bistatic SAR with Curved Trajectory Based on Extended Azimuth Nonlinear Chirp Scaling. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4160–4179. [Google Scholar] [CrossRef]
- Xiong, Y.; Liang, B.; Yu, H.; Chen, J.; Jin, Y.; Xing, M. Processing of Bistatic SAR Data with Nonlinear Trajectory Using a Controlled-SVD Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5750–5759. [Google Scholar] [CrossRef]
- Miao, Y.; Wu, J.; Sun, Z.; Li, Z.; Yang, J. Focusing Bistatic SAR Data Under Complicated Motion Through Differential Phase Filtering in Variable Doppler Bands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9196–9209. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Z.; Wang, Y.; Xiao, F. Joint Master–Slave Yaw Steering for Bistatic Spaceborne SAR with an Arbitrary Configuration. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1426–1430. [Google Scholar] [CrossRef]
- Deng, H.; Li, Y.; Liu, M.; Mei, H.; Quan, Y. A Space-Variant Phase Filtering Imaging Algorithm for Missile-Borne BiSAR with Arbitrary Configuration and Curved Track. IEEE Sens. J. 2018, 18, 3311–3326. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Qu, J.; Li, Z.; Huang, Y.; Yang, J. Echo Model without Stop-and-Go Approximation for Bistatic SAR with Maneuvers. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1056–1060. [Google Scholar] [CrossRef]
- Mao, X.; Shi, T.; Zhan, R.; Zhang, Y.-D.; Zhu, D. Structure-Aided 2-D Autofocus for Airborne Bistatic Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7500–7516. [Google Scholar] [CrossRef]
- Mei, H.; Meng, Z.; Liu, M.; Li, Y.; Quan, Y.; Zhu, S.; Xing, M. Thorough Understanding Property of Bistatic Forward-Looking High-Speed Maneuvering Platform SAR. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1826–1845. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Song, Y.; Yang, J.; Li, Z.; Huang, Y. Bistatic-Range-Doppler-Aperture Wavenumber Algorithm for Forward-Looking Spotlight SAR with Stationary Transmitter and Maneuvering Receiver. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2080–2094. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Huang, X. An Extended Fast Factorized Back Projection Algorithm for Missile-Borne Bistatic Forward-Looking SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2724–2734. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, Y.; Zhang, S.; Zhao, H.; Chen, Y. A New Imaging Algorithm for Forward-Looking Missile-Borne Bistatic SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1543–1552. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Li, Z.; Miao, Y.; Huang, Y.; Yang, J. PFA for Bistatic Forward-Looking SAR Mounted on High-Speed Maneuvering Platforms. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6018–6036. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Ou, N.; Liu, K.; Liang, D.; Deng, Y.; Wang, R. First Demonstration of Multipath Effects on Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2590–2604. [Google Scholar] [CrossRef]
- Xiao, P.; Guo, W.; Liu, M.; Liu, B. A Three-Step Imaging Algorithm for the Constellation of Geostationary and Low Earth Orbit SAR (ConGaLSAR). IEEE Trans. Geosci. Remote Sens. 2022, 60, 5203814. [Google Scholar] [CrossRef]
- Kraus, T.; Krieger, G.; Bachmann, M.; Moreira, A. Spaceborne Demonstration of Distributed SAR Imaging with TerraSAR-X and TanDEM-X. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1731–1735. [Google Scholar] [CrossRef]
- Budillon, A.; Gierull, C.H.; Pascazio, V.; Schirinzi, G. Along-Track Interferometric SAR Systems for Ground-Moving Target Indication: Achievements, Potentials, and Outlook. IEEE Geosci. Remote Sens. Mag. 2020, 8, 46–63. [Google Scholar] [CrossRef]
- Han, J.; Cao, Y.; Wu, W.; Wang, Y.; Yeo, T.-S.; Liu, S.; Wang, F. Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode. Remote Sens. 2021, 13, 4431. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, S.; Wang, X.; Huang, Y.; Wan, J.; Li, D.; Tan, X. Single Range Data-Based Clutter Suppression Method for Multichannel SAR. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4012905. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, B.; Tao, M.; Bai, X.; Chen, B.; Sun, G. A Large Scene Deceptive Jamming Method for Space-Borne SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4486–4495. [Google Scholar] [CrossRef]
- Tao, M.; Su, J.; Huang, Y.; Wang, L. Mitigation of Radio Frequency Interference in Synthetic Aperture Radar Data: Current Status and Future Trends. Remote Sens. 2019, 11, 2438. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhao, B.; Tao, M.; Chen, Z.; Hong, W. Review of synthetic aperture radar interference suppression. J. Radars 2020, 9, 86–106. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Yang, X.; Chen, Z.; Liu, J.; Li, J.; Hong, W. An Efficient Graph-Based Algorithm for Time-Varying Narrowband Interference Suppression on SAR System. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8418–8432. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Li, J.; Hong, W.; Nehorai, A. A Novel Tensor Technique for Simultaneous Narrowband and Wideband Interference Suppression on Single-Channel SAR System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9575–9588. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Li, J.; Chen, Z.; Yang, X. Reweighted Tensor Factorization Method for SAR Narrowband and Wideband Interference Mitigation Using Smoothing Multiview Tensor Model. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3298–3313. [Google Scholar] [CrossRef]
- Yang, H.; Tao, M.; Chen, S.; Xi, F.; Liu, Z. On the Mutual Interference Between Spaceborne SARs: Modeling, Characterization, and Mitigation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8470–8485. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, C.; Chen, Z.; Chen, J.; Liu, Y.; Li, J.; Hong, W. HRWS SAR Narrowband Interference Mitigation Using Low-Rank Recovery and Image-Domain Sparse Regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5217914. [Google Scholar] [CrossRef]
- Sun, G.-C.; Liu, Y.; Xing, M.; Wang, S.; Yang, J.; Bao, Z.; Bao, M. A Real-Time Unified Focusing Algorithm (RT-UFA) for Multi-Mode SAR via Azimuth Sub-Aperture Complex-Valued Image Combining and Scaling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5212117. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. Simultaneous High-Resolution Wide-Swath SAR Imaging and Ground Moving Target Indication: Processing Approaches and System Concepts. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5015–5029. [Google Scholar] [CrossRef]
- Hersey, R.K.; Culpepper, E. Radar processing architecture for simultaneous SAR, GMTI, ATR, and tracking. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, J.; Liang, X.-D.; Chen, L.-Y.; Wang, L.-N.; Li, K. First Demonstration of Joint Wireless Communication and High-Resolution SAR Imaging Using Airborne MIMO Radar System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6619–6632. [Google Scholar] [CrossRef]

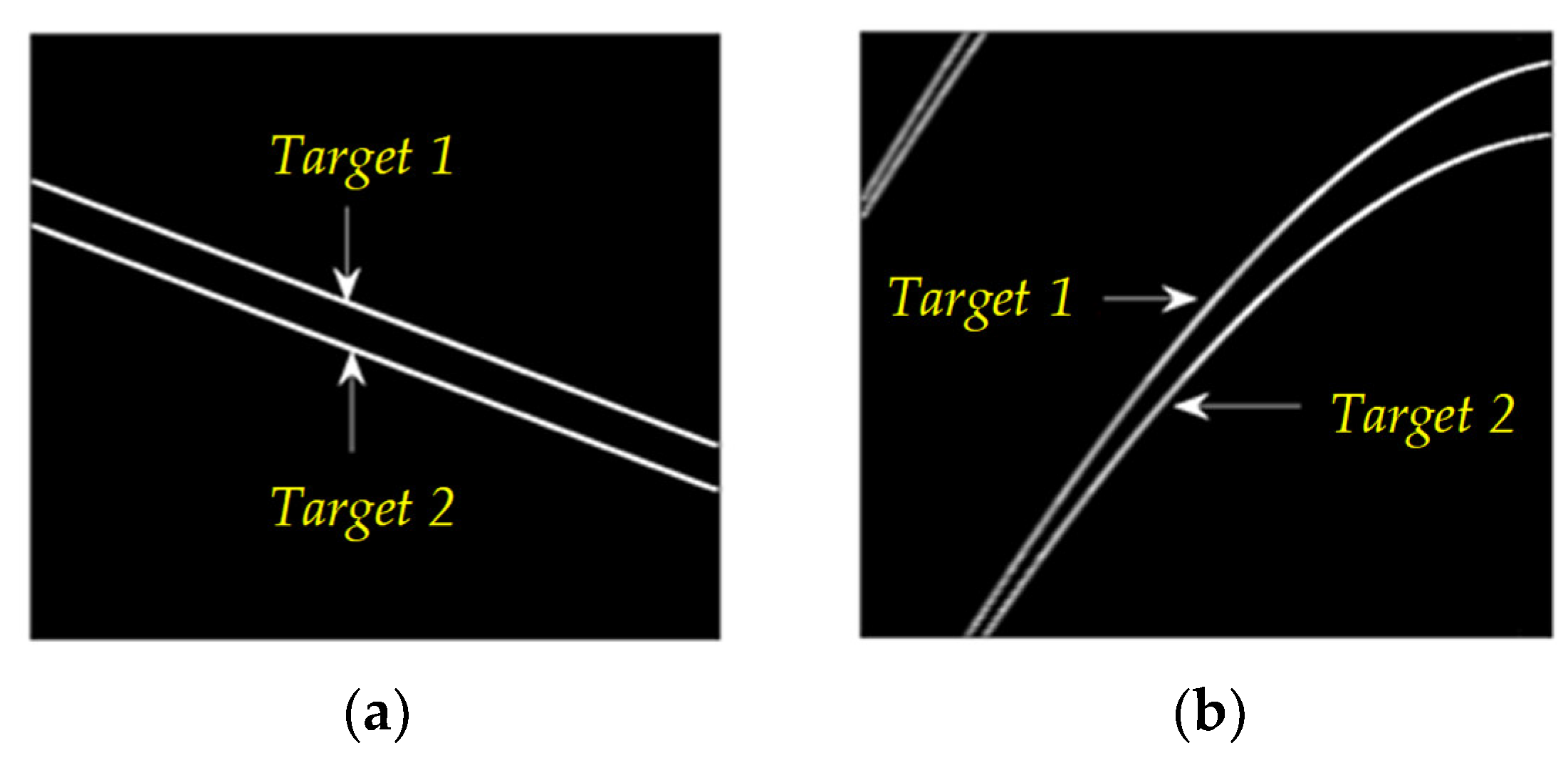
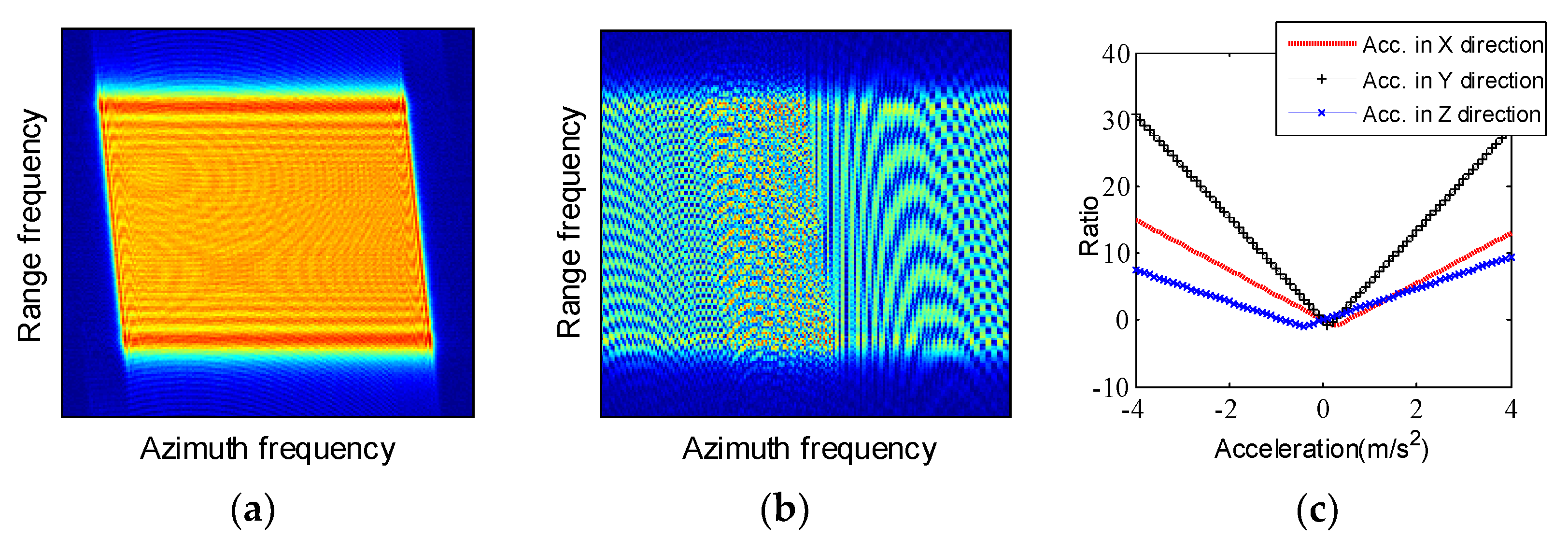
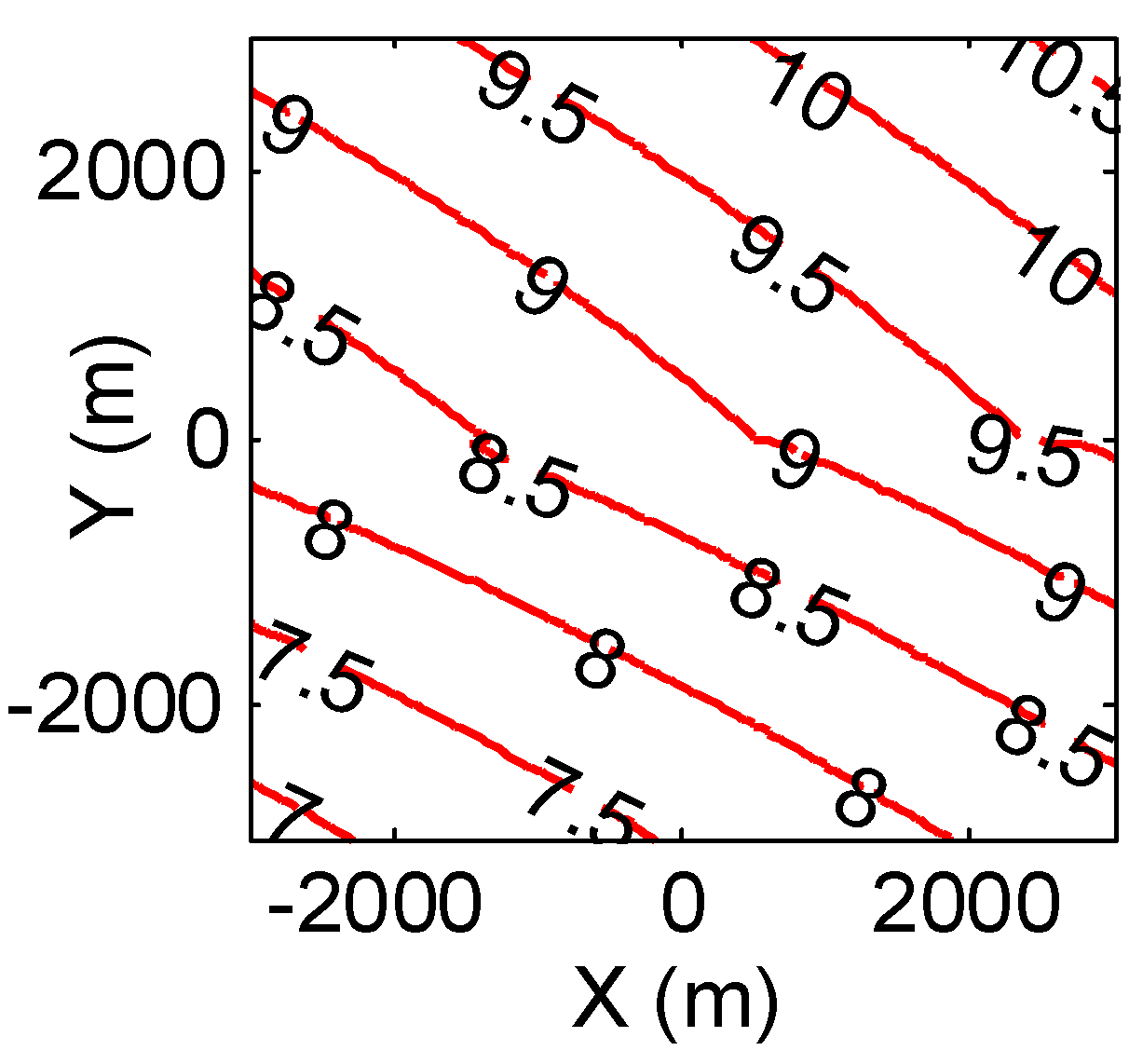

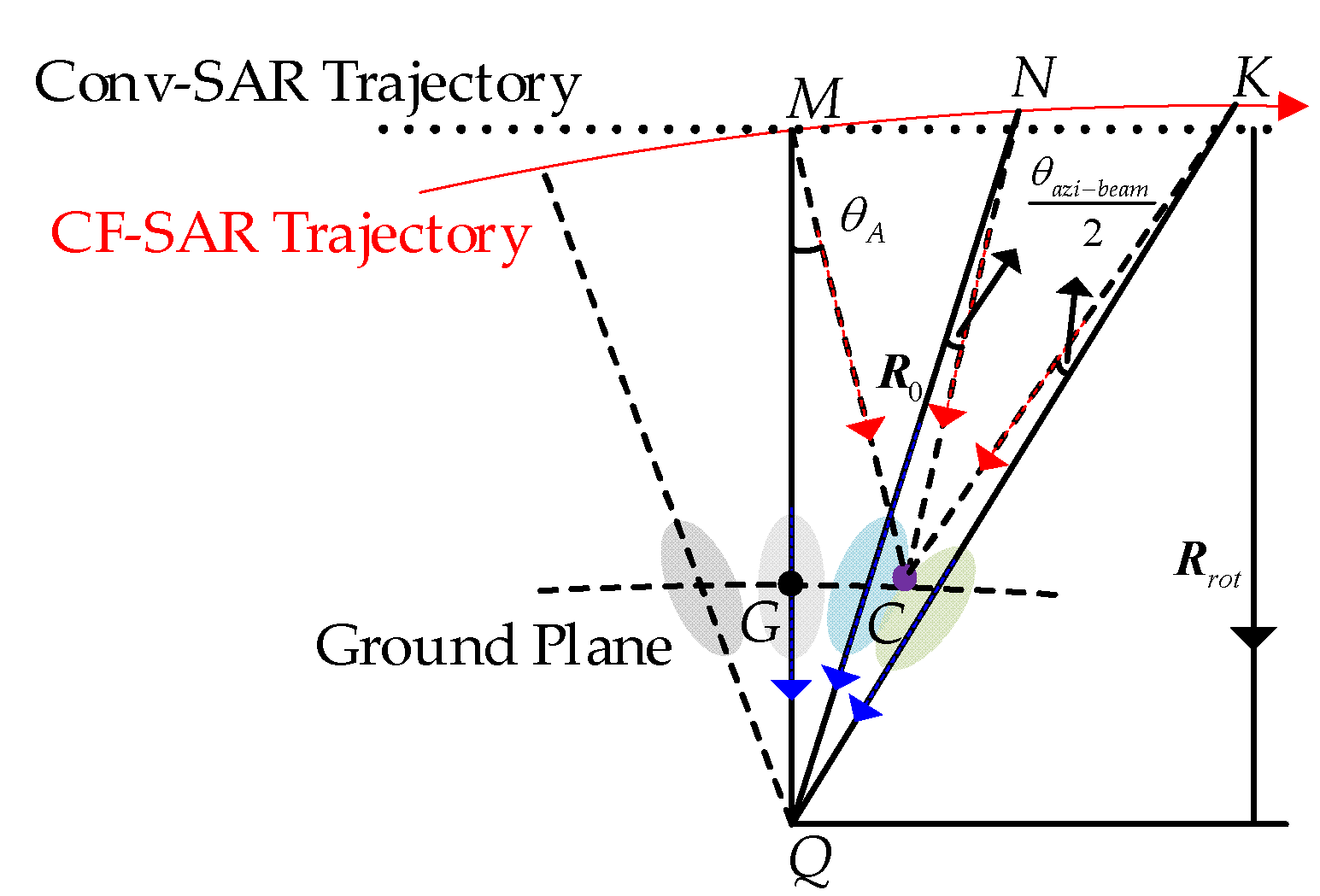




| Value | Physical Meaning | |
|---|---|---|
| Initial slant range | ||
| Relative radial velocity | ||
| Relative radial acceleration | ||
| Relative radial jerk | ||
| Very complicated | Relative radial high-order acceleration |
| Value | Physical Meaning | |
|---|---|---|
| Normalized initial slant range vector | ||
| Angular velocity vector | ||
| Angular acceleration vector | ||
| Angular jerk vector | ||
| Very complicated | Angular high-order acceleration vector |
| Working Mode | Value |
|---|---|
| Stripmap | |
| Spotlight | |
| Sliding spotlight | |
| TOPS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Tang, S.; Ren, Y.; Guo, P.; Zhou, Y.; Huang, Y.; Wan, J.; Zhang, L. Curvilinear Flight Synthetic Aperture Radar (CF-SAR): Principles, Methods, Applications, Challenges and Trends. Remote Sens. 2022, 14, 2983. https://doi.org/10.3390/rs14132983
Chen Z, Tang S, Ren Y, Guo P, Zhou Y, Huang Y, Wan J, Zhang L. Curvilinear Flight Synthetic Aperture Radar (CF-SAR): Principles, Methods, Applications, Challenges and Trends. Remote Sensing. 2022; 14(13):2983. https://doi.org/10.3390/rs14132983
Chicago/Turabian StyleChen, Zhanye, Shiyang Tang, Yi Ren, Ping Guo, Yu Zhou, Yan Huang, Jun Wan, and Linrang Zhang. 2022. "Curvilinear Flight Synthetic Aperture Radar (CF-SAR): Principles, Methods, Applications, Challenges and Trends" Remote Sensing 14, no. 13: 2983. https://doi.org/10.3390/rs14132983
APA StyleChen, Z., Tang, S., Ren, Y., Guo, P., Zhou, Y., Huang, Y., Wan, J., & Zhang, L. (2022). Curvilinear Flight Synthetic Aperture Radar (CF-SAR): Principles, Methods, Applications, Challenges and Trends. Remote Sensing, 14(13), 2983. https://doi.org/10.3390/rs14132983







