Abstract
The frequency of forest fires is increasing under global climate change, and forest fires can cause devastating disturbances to forest systems and varying degrees of recovery of forest ecosystems after a disaster. Due to the different intensity of forest fires and forest systems, and in particular the fact that forest ecological recovery is influenced by many topographical and climatic factors, the process of postfire vegetation recovery is unclear and must be studied in depth. In this study, the Greater Hinggan Mountain Range was taken as the study area. Based on the Moderate Resolution Imaging Spectroradiometer (MODIS) and Landsat time-series images acquired from 2000 to 2018, this study used the spatiotemporal data fusion method to construct reflectance images of vegetation with a relatively consistent growth period to study the vegetation restoration after forest fires. The vegetation restoration was characterized by disturbance index (DI) values, which eliminated phenological influence. Six types of topography and climatic factors (elevation, aspect, slope; temperature, precipitation, and wind speed) were coupled with DI. Through single-factor analysis of variance and multiple comparison statistical methods, it was found that there was a significant relationship between the six factors and DI, which indicated those factors had a significant impact on the restoration of forest vegetation in burned areas. The results will be useful as a reference for future monitoring and management of forest resources.
Keywords:
wildfires; vegetation restoration; vegetation index; disturbance index; MODIS; time series 1. Introduction
As the largest terrestrial ecosystem on the earth, forests are an important part of the earth’s biosphere, and play a vital role in maintaining the ecological balance of the entire earth [1,2,3]. The carbon storage of global forests accounts for about two-thirds of the total carbon of the entire terrestrial ecosystem, and the carbon absorption capacity of forest ecosystems accounts for more than 60% of the total NPP of terrestrial ecosystems [4]. However, the world has an average of more than 200,000 forest fires every year, and the area of burned forest accounts for more than 1% of the world’s total forest area. China has an average of more than 10,000 forest fires every year [5], burning hundreds of thousands to millions of hectares of forest accounting for about 5% to 8% of the country’s forest area. Fires will bring serious consequences to the forest. The most intuitive hazard is to burn a large area of vegetation and reduce the forest coverage of the entire area [6]. At the same time, the destruction of organic matter in the soil can easily cause land desertification and soil erosion [7,8,9]. A large number of animals, plants, and microorganisms are burned to death, and their living environment is also destroyed, breaking the ecological balance of the entire forest [10,11,12]. Forest fires often release most of the biological carbon into the atmosphere, thereby accelerating global warming [13,14]; In addition, the forest fire changes the stand structure, species composition, and community appearance of the community, and affects and maintains the normal operation of forest ecosystem [15,16,17]. Although some forest fires have a positive effect on the ecology of the forest, wildfires caused by human mistakes in forest areas where fires do not often occur are undoubtedly a devastating disaster for the regional forest system. The fires studied in this paper were human-caused.
Due to their extremely destructive nature, forest fires have received widespread attention from researchers and public. The main research focuses are the extraction of fire sites [18,19,20] and postfire vegetation restoration [21,22,23]. Remote sensing has been widely used for monitoring the ground surface, and it is considered to be one of the most efficient methods for exploring large-scale ecological changes. The changes in surface vegetation after a wildfire can be accurately identified from remote-sensing images [24,25,26,27]. Landsat series data have been widely used in the study of surface changes due to their own excellent characteristics [28]. Because the impact on vegetation restoration after a wildfire often requires a longer period of monitoring of the area, long-term series of data are often concerned, and this type of data also has unparalleled advantages in monitoring [29,30,31,32,33]. In addition, in order to achieve the accurate detection of vegetation, the impact of phenology must be minimized. Pastor-Guzman found that different vegetation indices had different responses to phenological factors, and mangroves were more sensitive to temperature and salinity [34]. Long-term monitoring of forest fires can be achieved by combining remote-sensing data in different wavebands, and efficient monitoring of forest ecological restoration can be achieved by applying different types of data in different forest restoration periods [28,35]. DI has a greater advantage over NDVI in characterizing forest ecosystem disturbance due to the inclusion of the midinfrared band, which can reveal information about the forest canopy. In general, when forest disturbance is enhanced, the DI is greater than 1; conversely, it is less than 1.
Much research has been performed on different aspects of forest restoration after fires. There have been many studies on the influence of terrain or climate factors on vegetation restoration after fire; for example, research found that vegetation restoration had a strong correlation with precipitation and temperature [36,37,38]; Topography had an impact on surface evapotranspiration after fire, which affected vegetation restoration [39]; Some researchers found that different slope directions had a great impact on the ecological evolution of vegetation, and there were differences in the succession rate of forests in different spatial patterns [40]. The total undergrowth coverage of the south-facing slope and flat position was higher than that of the north-facing slope, and the vegetation restoration degree of the flat and south-facing slope was better than that of the north-facing slope [41]. Regional climate change can interfere with the forest ecosystem [42,43], especially the interaction with fire, which can cause serious damage to the forest [44]. In the process of studying vegetation recovery after wildfires, climate change, seasonal change, and topographic factors may affect the postfire response [45,46,47]; there was a positive correlation between NDVI and precipitation during the postfire recovery period [48]. Drought may reduce ecosystem resilience; i.e., the ability to recover the predisturbance state [49]. However, some relevant studies only focused on the analysis of a single time phase, while the analysis of a long time series basically failed to consider the influence of phenological factors within the year [45,48,50]. Therefore, this study first constructed the interannual Landsat time series of the best growth period of vegetation in the region from 2000 to 2018 through a spatiotemporal fusion algorithm in order to eliminate the impact of the annual phenological factors on the Landsat image [51]. Then, we further analyzed the correlations between topographic factors (elevation, aspect and slop), climate factors (temperature, precipitation and wind speed), and DI over the years. It is of great significance to explore the influence of these factors on the ecological recovery of postfire vegetation to support the management of postfire forest monitoring.
By analyzing the relationship between six topographic and climatic factors and the DI in the Greater Hinggan Mountain Range, the effects of different factors on vegetation restoration were studied.
2. Materials and Methods
2.1. Study Area
The Greater Hinggan Mountain Range is located in the northern part of Heilongjiang Province and the Inner Mongolia Autonomous Region. It is the watershed of the west side of the inner Mongolia Plateau and the east side of the flat Songliao Plain (Figure 1). The region has a total length of over 1200 km, is 200–300 km wide, and has an average altitude of 1200–1300 m. The Greater Hinggan Mountain Range has a typical cold temperate continental monsoon climate, with warm summers and cold winters. The annual average temperature of the area is −2.8 °C; the lowest temperature is −52.3 °C [52,53]. The Greater Hinggan Mountain Range is the largest modern state-owned forest area, with a total area of 8.46 × 104 square kilometers and forest coverage of 6.46 × 104 square kilometers. Therefore, the forest coverage rate is about 76.4%, and the total storage capacity is about 5.01 × 108 m3, accounting for 7.8% of the national total. At the same time, this forest area previously experienced one of the most severe forest fires in China. On 6 May 1987, a severe forest fire occurred on the northern part of the Greater Hinggan Mountain Range. The burned area was 1.133 × 107 km2, and the area of overfired forest land was 1.114 × 107 km2, of which the affected area was 8.17 × 105 km2. About 266 people were wounded and 211 died, with 50,000 left homeless [54]. The fire seriously affected the social, economic, and ecological benefits of the forest area, causing unprecedented heavy losses to the country. After the catastrophic forest fires in the Greater Hinggan Mountain Range occurred in 1987, it became one of the areas for research on fire prevention and postfire forest management [55,56].
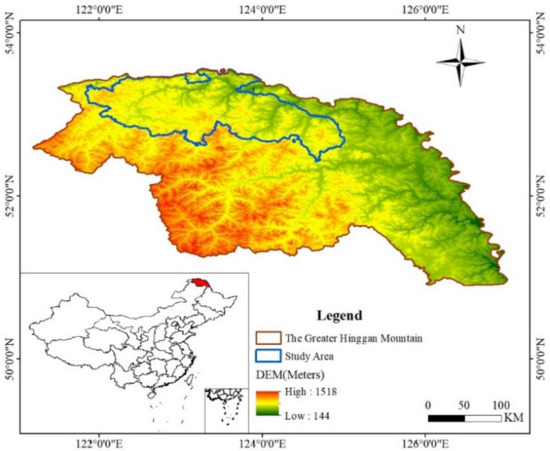
Figure 1.
Location of the Greater Hinggan Mountain Range and study area. The map was generated by the authors using QGIS version 3.10 (https://www.qgis.org/en/site/forusers/download.html) (accessed on 1 October 2020).
2.2. Data Used and Preprocessing
The entire burned forest area spanned two Landsat scenes (path 121/122, row 23), but it was difficult to acquire the two adjacent images in each year. Considering that around 90% of the burned forest area was within the scene of path 122 row 23, we extracted a sample area (Figure 1) from Landsat path 122 row 23 as the study area for the recovery monitoring. A total of 16 Landsat surface reflectance data from path 122, row 23 with and below 10% cloud cover during the vegetation growth period from 2000 to 2018 was considered. The data were downloaded from the United States Geological Survey (USGS, https://earthexplorer.usgs.gov, (accessed on 1 October 2020)); details of the data are given in Table 1. The Landsat surface reflectance data was corrected at the subpixel-level by topographic and atmospheric corrections. The FMASK algorithm was used to detect cloud cover/cloud shadow and to generate masks [57].

Table 1.
Landsat data acquisition date, sensor type, and cloud volume.
The MODIS 16 d synthetic vegetation index product MOD13Q1 for the periods 2000–2018 was downloaded from the National Aeronautics and Space Administration (NASA) and preprocessed. The zenith BRDF-adjusted reflectance product MCD43A4V006 with a spatial resolution of 500 m was obtained from NASA; this was the daily reflectance data for spatial and temporal fusion with Landsat data to generate the surface reflectance on the target date. The above MODIS data was converted from Sinusoidal projection to UTM projection with WGS84-51N coordinates.
After all the detailed processing, the river, road, and building areas in each image were masked based on the 10 m global resolution land cover data of Tsinghua University, supplemented by visual interpretation, and the boundary of the study area was extracted. The topography data was DEM elevation data with a spatial resolution of SRTM 30 m, and was derived from the United States Geological Survey (http://gdex.cr.usgs.gov/gdex, (accessed on 1 October 2020)); aspect and slope data were calculated by DEM; and the Atmospheric Administration (http://www.cdc.noaa.gov, (accessed on 1 October 2020)) obtained temperature, precipitation, and wind speed climatic data in the study area. Topographic and climate data were resampled to the same spatial resolution as Landsat data.
2.3. Synthesis of Target Image Based on STARFM Fusion Algorithm
The date of vegetation growth was not easy to determine due to complex reasons. In order to solve this problem, we choose the midpoint of the vegetation growth period as the time point of the study. The data at the midpoint of the growth period obtained by fusion could effectively eliminate the influence of phenology and made the research results more reliable. The spatial and temporal adaptive reflection fusion model (STARFM) [51], which mixes Landsat and MODIS data, was used to predict the daily surface reflectivity at the Landsat spatial resolution and MODIS time frequency. This method was tested in a conifer-dominated region in central British Columbia, Canada, and proved to generate daily surface reflectance with the same spatial resolution as Landsat data. The generated reflectance data was in good agreement with the actual Landsat reflectance data.
STARFM is a spatiotemporal data fusion model based on a moving window that not only considers the influence of spatial distance on the predicted pixels, but also considers the spectral difference and time difference between pixels. The homogeneous pixels in MODIS data show the relationship with the corresponding Landsat pixels as:
where represents the spatial position of the homogeneous pixel; represents the image acquisition time; represents the reflectivity of Landsat pixels; represents the reflectivity of the MODIS pixel; and indicates the difference in reflectance between different data. At , the following is the relationship between the MODIS reflectance and the Landsat reflectance of the same pixel:
When the ground cover type and the system error between the two types of data remain unchanged, , the above equation can be expressed as:
The MODIS pixels were mostly nonhomogeneous pixels, and the solar bidirectional reflection and the surface coverage type changed with time, which made the above ideal conditions challenging to meet. Therefore, the key point of the method was to find similar pixels from neighboring pixels of the target pixel and replace the homogeneous pixels with similar pixels.
2.4. Composite Images for Each Year
According to the vegetation index to obtain the required vegetation growth period midpoint, we combined Landsat and MODIS data to calculate the relatively consistent vegetation reflectance data from 2000 to 2018. The date of data acquisition and calculation results are shown in Table 2. In order to solve the discontinuity of the MCD43A4V006 data, the latest MCD43A4V006 data was used for fusion. The adjusted data date is marked in parentheses with the original date.

Table 2.
Dates of image acquisition in each year, midpoint of vegetation growth period, and the number of days between the two.
2.5. Remote-Sensing Index and Six Topographic and Climatic Factors
Since the launch of the first artificial Earth resource satellite in 1972, scientists have attempted to study and establish an approximate relationship between spectral response and vegetation coverage. The research results showed that the use of different combinations of red light and infrared bands of orbiting satellites for vegetation research works well. These bands are common on meteorological satellites and Earth observation satellites, and contain more than 90% of the vegetation information [58]. The different combinations of these bands are collectively called the vegetation index. Because the vegetation index discards some important information, researchers have developed a method of data compression. Principal component analysis provides a solution to reduce the amount of data and retain most of the information, but there are significant problems in the physical interpretation of derived features. Kauth and Thomas developed the KT transform to solve this problem, and achieved good results [59,60]. Healey calculated the disturbance index (DI) on the basis of KT transformation, and found that it could explain vegetation restoration well [61]. DI proved to be a useful technique for determining the spatial extent of changes in forested land cover types [29].
The calculation of the DI is based on the tasseled-cap transformation, which is a spectral transformation that converts the original high covariant data into three uncorrelated indices known as brightness (B), greenness (G), and wetness (W), effectively capturing the three major axes of spectral variation across the solar reflective spectrum [62]. The calculation of DI is based on the observation that disturbed forests usually have higher brightness values and lower green and humidity values compared to undisturbed forest areas. At a basic level, the DI records the normalized spectral distance of any given pixel from a nominal “mature forest” class to a “bare soil” class. At the same time, the spectral normalization step is conducted, and the intraimage statistics are used to normalize the radiation variations as:
where , , and represent the average tasseled-cap transformation brightness, greenness, and wetness of the “forest in a particular scene”; , , and are the corresponding standard deviations, so , , and represent normalized brightness, greenness, and wetness, respectively. After normalization, the three components are linearly combined to obtain DI as follows:
The disturbed forest area usually has a high positive value and low negative values of and , thus returning a high DI value; in contrast, the undisturbed forest area shows a low DI value.
Topography affects the growth of vegetation [41]. Different elevations often have different soil conditions, precipitation levels, and temperatures, which affect the growth of vegetation. The slope direction will cause a difference in illumination, and then affect the photosynthesis of vegetation; where the slope is large, the soil loss is often serious, and the nutrient content required for vegetation growth is relatively low. The three topographic factors of elevation, aspect, and slope and the three climatic factors of temperature, precipitation, and wind speed were selected to establish a coupling relationship with the DI [39,45,46]. Considering that the synthetic data for phenology elimination was from July, and July was also the month with the best vegetation growth in the study area, the climatic factor was calculated using the average data of July over the years. Based on the characteristics of terrain factors and climate factors, they were graded according to the following:
- The elevation interval of the study area was 247~1037 m. Due to the small difference in elevation, the elevation was divided into four levels at equal intervals of 200 m.
- The aspect of the study area was divided into 8 categories: north, northeast, east, southeast, south, southwest, west, and northwest.
- The slope range of the study area was 0°–55°. According to the standards of the International Geographic Association and the characteristics of the study area, it was divided into four categories: 0°~5°, 5°~15°, 15°~25°, and 25°~55° (the International Geographical Association standard divides the slope into six categories: 0°~5°, 5°~15°, 15°~25°, 25°~35°, 35~55°, and more than 55°; parts greater than 25° were combined into one category).
- The average temperature range in the study area in July over the years was 15.5~19.3 °C, divided into four grades: 15.5~16.5 °C, 16.5~17.5 °C, 17.5~18.5 °C, and 18.5~19.3 °C.
- In the study area, the precipitation interval in July of the year was 104~135 mm, which was divided into four grades: 104~112 mm, 112~120 mm, 120~128 mm, and 128~135 mm.
- The average wind speed in the study area in July over the years was 1.4~2 m/s, which was divided into four grades: 1.4~1.55 m/s, 1.55~1.7 m/s, 1.7~1.85 m/s, and 1.85~2 m/s.
2.6. Analysis of Variance and Multiple Comparisons
Analysis of variance (ANOVA), also known as the F-test, is a statistical method proposed by British statistician R.A. Fisher in 1923 that is used in a significance test among multiple groups of means. The basic idea of ANOVA is to decompose the sum of squared deviations of all data about the total mean into several parts. Each part represents the effect of the horizontal effects of a certain factor. The mean square of each part is compared with the error mean square to confirm or deny the importance of certain factors or interactions. ANOVA is calculated using the following equations:
where , α is the number of levels of the factor, and r is the number of experiments repeated; for a given test significance level α, the probability of F ≥ Fα is equal to α. When a small probability event of F ≥ Fα occurs in an experiment, it is reasonable to reject the null hypothesis and consider the effect of the factor to be significant.
The analysis of variance obtained by the F-test is the overall conclusion, which shows that the difference between the average of different levels of impact factors and at least one pair of averages has reached a significant level. As to which level is not answered, and the conclusion should be drawn through multiple comparisons. The least significant difference (LSD) method proposed by R.A. Fisher in 1935 is used for multiple comparisons. Due to the high sensitivity of this method, there may be small differences in the mean of each level. The LSD is calculated using the following equations:
where and are the number of samples, and are the sample values, is the error, and α is the significance level.
3. Results
3.1. Characteristics of DI Changes Prior to and after Phenological-Influence Elimination
As shown in Figure 2, DI eliminated the influence of phenology. By comparing the DI values of prior to and after eliminating phenological influence, we clearly found that the data curve was more stable after the phenology was eliminated. When there was no elimination of phenology, there was a clear upward trend in 2002, 2010, 2014, 2016, and 2018.
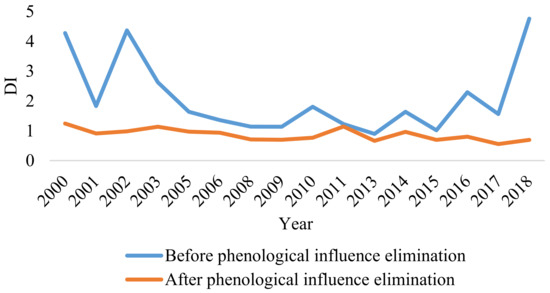
Figure 2.
Trend of DI prior to and after phenological-influence elimination in each year.
3.2. Analysis of the Impact of Six Topographic and Climatic Factors on DI
The mean values of DI under different grade factors were calculated, and the results are shown in Figure 3. Through the analysis, it was found that six topographic and meteorological factors affected DI, but the results were different. Among them, as the elevation increased, the DI showed a downward trend; the slope went from south to north and east to west. During the process, the DI showed a downward trend, indicating that the vegetation recovery became better; as the slope increased, the DI showed a downward trend and then an upward trend, indicating that the vegetation recovery was the best on a certain slope, and being above or below this slope would adversely affect the vegetation-restoration impact. As the temperature rose, the DI showed an upward trend; as the precipitation increased, the DI showed a downward trend; and as the wind speed increased, the DI showed a downward trend.
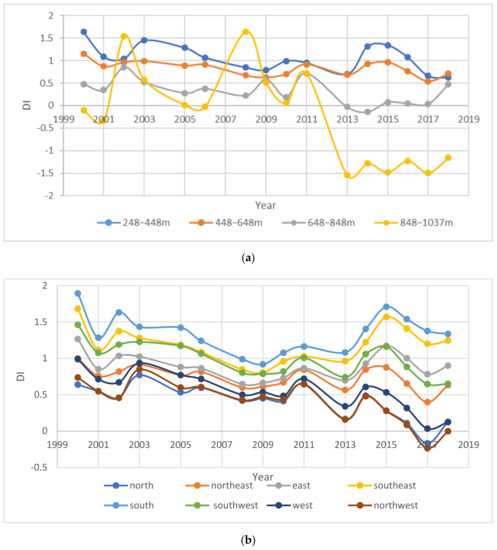
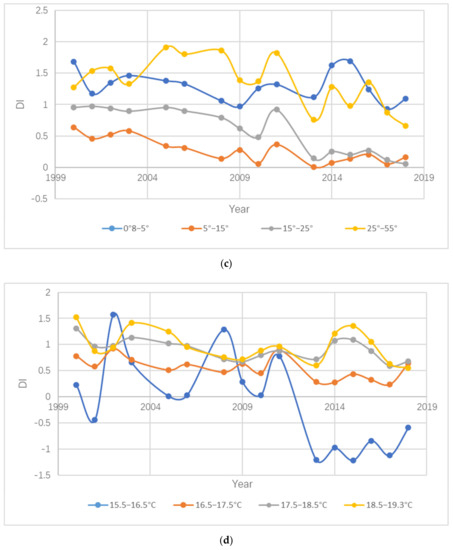
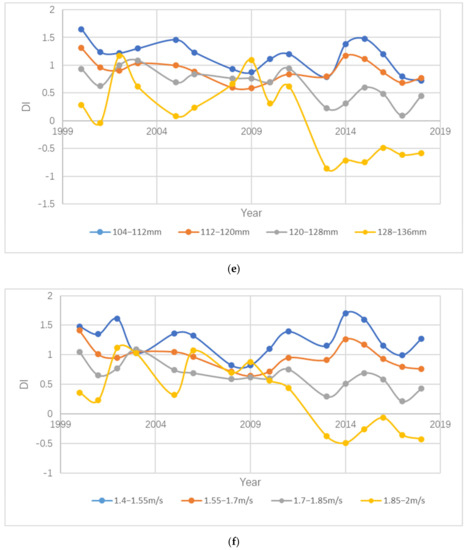
Figure 3.
The mean value of DI under six different topographic and climatic factors: (a) elevation; (b) aspect; (c) slope; (d) temperature; (e) precipitation; (f) wind speed.
3.3. One-Way Analysis of Variance and Multiple Comparisons
In analyzing the single-factor test results, we checked whether the factors had a significant effect on the test results. In order to accurately reflect the response of the DI to the six topographic and climatic factors, the relationships between the six topographic and climatic factors and the DI were further analyzed. A single-factor analysis of variance was used to analyze the differences in the DI under six topographic and climatic factors from the perspective of mathematical statistics. The results are shown in Table 3. Through the analysis, it was found that the p-value was less than 0.01 under different levels of six topographic and climatic factors, and the relationship was extremely significant. That is, under different levels of six topographic and climatic factors, the difference in the DI was extremely significant.

Table 3.
One-way ANOVA of six topographic and climatic factors DI.
The prerequisite for dealing with multiple comparisons is knowing that there are differences between treatments. According to the results in Table 3, all six topographic and climatic factors met the conditions, so the six factors were analyzed. The results of multiple comparative analyses are shown in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. According to Table 4, it was found that there were no significant differences between grade 1 and grade 2 among different elevation levels. The altitude difference between grade 1 and grade 2 was relatively low, and the elevation difference was relatively small. The similarity of the forest growth environment was relatively high. According to Table 6, it was found that there were no significant differences between types 1, 7, and 8 in the different slope directions. All types 1, 7, and 8 were on the side facing the sunlight, which affected the growth of vegetation and led to poor forest growth, which in turn led to a small DI difference and reduced the intergrade significance. According to Table 6, it was found that there were no significant differences between grade 1 and grade 4 among the different slope grades. In Figure 3c, it is clear that the DI decreased first and then increased as the slope increased, and the DI values of grade 1 and grade 4 were close to each other, which corresponded well to there being no significant differences between grade 1 and grade 4. Table 8 shows that there were significant differences between different temperature grades. According to Table 8, it was found that there were no significant differences between grade 1 and grade 2 among the different precipitation levels. In Figure 3e, it can be seen that there was a small difference in the DI value between grade 1 and grade 2, which was caused by the insensitivity of forest to the difference between precipitation levels. According to Table 9, it was found that there were significant differences among different wind speed grades.

Table 4.
Multiple comparisons of elevation factor and DI.

Table 5.
Multiple comparisons of aspect factor and DI.

Table 6.
Multiple comparisons of slope factor and DI.

Table 7.
Multiple comparisons of temperature factor and DI.

Table 8.
Multiple comparisons of precipitation factor and DI.

Table 9.
Multiple comparisons of wind speed factor and DI.
4. Discussion
As mentioned above, six topographic and climatic factors were found to have significant impacts on postfire forest ecological recovery. Although some researchers have considered topographic factors to be extremely important in the recovery of vegetation after wildfires [39], there has been no in-depth analysis. Adam M. Wilson concluded that elevation, slope, and NDVI were negatively correlated [37]; the decrease in the DI shown in Figure 3a–c was consistent with this conclusion. The impact of the elevation and slope on the DI was also quantitatively analyzed; in Adam M. Wilson’s model, the vegetation had a higher recovery rate when the temperature was higher, and it was also pointed out that this difference would decrease as the temperature rose. We found that the DI curve increased with increasing temperature class, as shown in Figure 3d; the difference between the 15.5~16.5 °C and 16.5~17.5 °C categories was large, while the difference between the third and fourth categories was small. This was consistent with Adam M. Wilson’s model. The study also found that vegetation restoration was positively correlated with summer precipitation, but in our experimental results, the DI and precipitation were negatively correlated, as shown in Figure 3d. This was because the relevant literature research came from a multiyear time series that analyzed the relationship between vegetation restoration and precipitation, while we studied the relationship between the DI in different regions and the precipitation at the spatial location in terms of spatial distribution. At the same time, while considering the relationship between elevation and DI shown in Figure 3a, we found elevation and precipitation factors had apparently opposite effects. It was thought that the negative correlation between precipitation and DI was due to an increase in elevation that then led to an increase in precipitation, so that the impact on vegetation restoration elevation in the mountains was far greater than that of precipitation [63]. A review of the literature revealed that most researchers focused on the study of ecosystem models, rather than on the quantitative study of the factors involved [64,65]. Although some researchers established a spatiotemporal dynamic prediction model [66], little attention has been paid to the importance of slope direction and wind speed.
In this paper, we found that there was a decreasing trend in the DI from south to north, due to the fact that the study area was located in the Northern Hemisphere at mid to high latitudes, where light conditions on northern slopes are significantly weaker than on southern slopes. In addition, the DI decreased significantly with an increasing wind speed, as the study area was at a high altitude and thus had a high wind speed, which led to a decrease in the DI. Of course, there were some shortcomings in the study. Although one-way ANOVA could explain the relationship between the variables and DI well, the interaction between factors was worthy of attention due to the inability to strip confounding factors well. Due to the subjectivity of factor grading and the effects of data processing, the results of a one-way ANOVA may be “distorted”, and impact factors with a similar impact capacity may be ranked differently. However, the factors that dominated the DI influence were less affected by the above factors. At the same time, the current results may have been due to the special geographical location of the experimental area, and studies of other areas may result in different conclusions. However, using only DI indicators cannot fully characterize forest ecological restoration. Therefore, more forest parameters should be introduced for optimization and analysis in the future.
5. Conclusions
This study analyzed and discussed the coupling relationship between the DI factor removing phenological interference and six topographic and climatic factors after the 1987 fire in the Greater Hinggan Mountain Range from 2000 to 2018, and realized an ecological dynamic monitoring by remote sensing. It was found that although the DI value increased and ecological recovery was disturbed in 2003, 2006, 2011, 2014, and 2018 after the wildfire, the local forest ecology showed a positive trend year by year on the whole. Through statistical analysis, although DI was found to be correlated with all six topographic and climatic factors, it was found that the influence of the elevation factor in the study was far greater than that of the other factors. The slope direction factor was very important to the ecological recovery, and the vegetation recovery on the sunny side was obviously better than that on the shady side. The research area had a high altitude in the south and a low altitude in the north. The decrease in the height led to a decrease in the slope and the difference in slope direction, which directly led to the forest restoration in the north being obviously better than that in the south. The above results can well explain the heterogeneity of regional forest recovery and the trend of forest ecological recovery, and then provide data support and technical guidance for forest growth monitoring and recovery management in burned areas. This study analyzed the impact of multiple factors on vegetation restoration after a fire. Compared with the deficiency in previous single-factor analyses, it realized the coupling analysis of multiple factors, which has certain reference significance for the future research of postfire forest ecosystems.
Author Contributions
Conceptualization, W.C. and X.C.; methodology, W.C.; software, X.C.; validation, X.C., W.C. and M.X.; formal analysis, X.C.; investigation, W.C.; resources, W.C.; data curation, X.C.; writing—original draft preparation, X.C.; writing—review and editing, X.C.; visualization, X.C.; supervision, M.X.; project administration, W.C.; funding acquisition, W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Open Fund of the State Key Laboratory of Remote Sensing Science (Grant No. OFSLRSS202105) and the National Natural Science Foundation of China (Grant No. 41601368). We thank the Haihe Laboratory of Sustainable Chemical Transformations for financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lucas, N.S.; Curran, P.J.; Plummer, S.E.; Danson, F.M. Estimating the stem carbon production of a coniferous forest using ecosystem simulation models driven by the remotely sensed red edge. Int. J. Remote Sens. 2000, 21, 619–631. [Google Scholar] [CrossRef]
- Flynn, K.M.; Traver, R.G. Green infrastructure life cycle assessment, A bio-infiltration case study. Ecol. Eng. 2013, 55, 9–22. [Google Scholar] [CrossRef]
- Wood, T.E.; Cavaleri, M.A.; Reed, S.C. Tropical forest carbon balance in a warmer world: A critical review spanning microbial- to ecosystem-scale processes. Biol. Rev. Camb. Philos. Soc. 2012, 87, 912–927. [Google Scholar] [CrossRef]
- Melillo, J.M.; McGuire, A.D.; Kicklighter, D.W.; Moore, B.; Vorosmarty, C.J.; Schloss, A.L. Global climate change and terrestrial net primary production. Nature 1993, 363, 234–240. [Google Scholar] [CrossRef]
- Qian, D.; Zhang, H.; He, L. Vegetation changes in conflagration area: Case study of Da Hingggan Mountains and Yellowstone National Park burned aera. J. Tianjin Norm. Univ. (Nat. Sci. Ed.) 2019, 39, 60–68. [Google Scholar]
- Guo, F.; Su, Z.; Tigabu, M.; Yang, X.; Lin, F.; Liang, H.; Wang, G. Spatial Modelling of Fire Drivers in Urban-Forest Ecosystems in China. Forests 2017, 8, 180. [Google Scholar] [CrossRef] [Green Version]
- Forkel, M.; Thonicke, K.; Beer, C.; Cramer, W.; Bartalev, S.; Schmullius, C. Extreme fire events are related to previous-year moisture conditions in permafrost-underlain larch forests of Siberia. Environ. Res. Lett. 2012, 7, 44021. [Google Scholar] [CrossRef]
- McKenzie, D.; Shankar, U.; Keane, R.E.; Stavros, E.N.; Heilman, W.E.; Fox, D.G.; Riebau, A.C. Smoke consequences of new wildfire regimes driven by climate change. Earth Future 2014, 2, 35–59. [Google Scholar] [CrossRef]
- Hu, T.X.; Sun, L.; Hu, H.Q.; Weise, D.R.; Guo, F.T. Soil Respiration of the Dahurian Larch (Larix gmelinii) Forest and the Response to Fire Disturbance in Da Xing’an Mountains, China. Sci. Rep. UK 2017, 7, 2967. [Google Scholar] [CrossRef] [Green Version]
- Huesca, M.; Litago, J.; Palacios-Orueta, A.; Montes, F.; Sebastián-López, A.; Escribano, P. Assessment of forest fire seasonality using MODIS fire potential: A time series approach. Agric. For. Meteorol. 2009, 149, 1946–1955. [Google Scholar] [CrossRef]
- Pastro, L.C.; Dickman, C.R.; Letnic, M. Burning for biodiversity or burning biodiversity? Prescribed burn vs. wildfire impacts on plants, lizards, and mammals. Ecol. Appl. 2011, 21, 3238–3253. [Google Scholar] [CrossRef]
- Thom, D.; Seidl, R. Natural disturbance impacts on ecosystem services and biodiversity in temperate and boreal forests. Biol. Rev. Camb. Philos. Soc. 2016, 91, 760–781. [Google Scholar] [CrossRef] [PubMed]
- Barnes, B.V.; Zak, D.R.; Denton, S.R.; Spurr, S.H. Regeneration Ecology Forest Ecology, 4th ed.; John Wiley: New York, NY, USA, 1998; pp. 94–121. [Google Scholar]
- Kennedy, R.E.; Ohmann, J.; Gregory, M.; Roberts, H.; Yang, Z.; Bell, D.M.; Kane, V.; Hughes, M.J.; Cohen, W.B.; Powell, S.; et al. An Empirical, Integrated Forest Biomass Monitoring System. Environ. Res. Lett. 2018, 13, 25004. [Google Scholar] [CrossRef]
- Fang, L.; Yang, J.; Zu, J.; Li, G.; Zhang, J. Quantifying influences and relative importance of fire weather, topography, and vegetation on fire size and fire severity in a Chinese boreal forest landscape. For. Ecol. Manag. 2015, 356, 2–12. [Google Scholar] [CrossRef]
- Ueyama, M.; Iwata, H.; Nagano, H.; Tahara, N.; Harazono, Y. Carbon dioxide balance in early-successional forests after forest fires in interior alaska. Agric. For. Meteorol. 2019, 275, 196–207. [Google Scholar] [CrossRef]
- Volkova, L.; Aparicio, A.G.W.; Westona, C.J. Fire intensity effects on post-fire fuel recovery in eucalyptus open forests of south-eastern australia. Sci. Total Environ. 2019, 670, 328–336. [Google Scholar] [CrossRef] [PubMed]
- Emilio, C.; María, P.M. Cartografía de grandes incendios forestales en la Península Ibérica a partir de imágenes NOAA-AVHRR. Ser. Geogr. 1998, 7, 109–128. [Google Scholar]
- García, M.J.; Caselles, V. Mapping burns and natural reforestation using thematic Mapper data. Geocarto Int. 1991, 6, 31–37. [Google Scholar] [CrossRef]
- Tian, X.R.; Shu, L.F.; Wang, M.Y. Direct emissions from Chinese forest fires 1991–2000. Fire Saf. J. 2003, 12, 6–10. [Google Scholar]
- Riaño, D.; Chuvieco, E.; Ustin, S.; Zomer, R.; Dennison, P.; Roberts, D.; Salas, J. Assessment of vegetation regeneration after fire through multitemporal analysis of AVIRIS images in the Santa Monica Mountains. Remote Sens. Environ. 2002, 79, 60–71. [Google Scholar] [CrossRef]
- Gouveia, C.; Dacamara, C.C.; Trigo, R.M. Post-fire vegetation recovery in Portugal based on spot/vegetation data. Nat. Hazard Earth Syst. Sci. 2010, 10, 4559–4601. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.M.; Sun, Z.Y.; Zhao, P.W. Temporal and spatial analysis A1:A53 FVC of burning sites in Genhe city based on remote sensing data. J. Northeast For. Univ. 2015, 43, 62–69. [Google Scholar]
- Cohen, W.B.; Goward, S.N. Landsat’s Role in Ecological Applications of Remote Sensing. BioScience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Casady, G.M.; Neary, D.G.; Bautista, S.; Alloza, J.A.; Carmel, Y.; Wittenberg, L.; Malkinson, D.; Orr, B.J. Monitoring post-wildfire vegetation response with remotely sensed time-series data in Spain, USA and Israel. Int. J. Wildland Fire 2010, 19, 75–93. [Google Scholar] [CrossRef]
- Hendrik, S.; Hiroshi, T.; Takashi, H. Detection of fire impact and vegetation recovery over tropical peat swamp forest by satellite data and ground-based NDVI instrument. Int. J. Remote Sens. 2010, 31, 5297–5314. [Google Scholar]
- Masek, J.G.; Goward, S.N.; Kennedy, R.E.; Cohen, W.B.; Moisen, G.G.; Schleeweis, K.; Huang, C. United States forest disturbance trends observed using Landsat time series. Ecosystems 2013, 16, 1087–1104. [Google Scholar] [CrossRef] [Green Version]
- Fang, L.; Yang, J.; Zhang, W.; Zhang, W.D.; Yan, Q. Estimating Tree Biomass Combining Allometry and Landsat-derived Disturbance History in Subtropical Planted Forests. Remote Sens. Environ. 2019, 235, 111423. [Google Scholar] [CrossRef]
- Masek, J.G.; Huang, C.; Wolfe, R.; Cohen, W.; Hall, F.; Kutler, J.; Nelson, P. North American forest disturbance mapped from a decadal Landsat record. Remote Sens. Environ. 2008, 112, 2914–2926. [Google Scholar] [CrossRef]
- Townshend, J.R.; Masek, J.G.; Huang, C.; Vermote, E.F.; Gao, F.; Channan, S.; Sexton, J.O.; Feng, M.; Narasimhan, R.; Kim, D.; et al. Global characterization and monitoring of forest cover using landsat data: Opportunities and challenges. Int. J. Digit. Earth 2012, 5, 373–397. [Google Scholar] [CrossRef] [Green Version]
- Todd, A.S.; Michael, A.W.; Healey, S.P.; Moisen, G.G. Detecting post-fire salvage logging from landsat change maps and national fire survey data. Remote Sens. Environ. 2012, 122, 166–174. [Google Scholar]
- Meng, R.; Wu, J.; Zhao, F.; Cook, B.D.; Hanavan, R.P.; Serbin, S.P. Measuring short-term post-fire forest recovery across a burn severity gradient in a mixed pine-oak forest using multi-sensor remote sensing techniques. Remote Sens. Environ. 2018, 210, 282–296. [Google Scholar] [CrossRef]
- Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C. Prevalence of Multiple Forest Disturbances and Impact on Vegetation Regrowth From Interannual Landsat Time Series (1985–2015). Remote Sens. Environ. 2019, 233, 111403. [Google Scholar] [CrossRef]
- Pastor-Guzman, J.; Dash, J.; Atkinson, P.M. Remote sensing of mangrove forest phenology and its environmental drivers. Remote Sens. Environ. 2018, 205, 71–84. [Google Scholar] [CrossRef] [Green Version]
- Morresi, D.; Vitali, A.; Urbinati, C.; Garbarino, M. Forest spectral recovery and regeneration dynamics in stand-replacing wildfires of central apennines derived from Landsat time series. Remote Sens. 2019, 11, 308. [Google Scholar] [CrossRef] [Green Version]
- Hope, A.; Albers, N.; Bart, R. Characterizing post-fire recovery of fynbos vegetation in the western cape region of South Africa using MODIS data. Int. J. Remote Sens. 2012, 33, 979–999. [Google Scholar] [CrossRef]
- Wilson, A.M.; Latimer, A.M.; Silander, J.A. Climatic controls on ecosystem resilience: Postfire regeneration in the Cape Floristic Region of South Africa. Proc. Natl. Acad. Sci. USA 2015, 112, 9058–9063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Z.; He, H.S.; Keane, R.E.; Zhu, Z.; Wang, Y.; Shan, Y. Current and future patterns of forest fire occurrence in China. Int. J. Wildland Fire 2020, 29, 104–119. [Google Scholar] [CrossRef]
- Nolan, R.H.; Lane, P.N.J.; Benyon, R.G.; Bradstock, R.A.; Mitchell, P.J. Changes in evapotranspiration following wildfire in resprouting eucalypt forests. Ecohydrology 2014, 7, 1363–1377. [Google Scholar] [CrossRef]
- Donnegan, J.A.; Rebertus, A.J. Rates and Mechanisms of Subalpine Forest Succession along an Environmental Gradient. Ecology 1999, 80, 1370–1384. [Google Scholar] [CrossRef]
- Liu, B.; Biswas, S.R.; Yang, J.; Liu, Z.; Han, S. Strong influences of stand age and topography on post-fire understory recovery in a Chinese boreal forest. For. Ecol. Manag. 2020, 473, 118307. [Google Scholar] [CrossRef]
- Röder, A.; Hill, J.; Duguy, B.; Alloza, J.A.; Vallejo, R. Using long time series of Landsat data to monitor fire events and post-fire dynamics and identify driving factors. A case study in the Ayora region (eastern Spain). Remote Sens. Environ. 2008, 112, 259–273. [Google Scholar] [CrossRef]
- Chambers, J.C.; Bradley, B.A.; Brown, C.S.; D’Antonio, C.; Germino, M.J.; Grace, J.B.; Hardegree, S.P.; Miller, R.F.; Pyke, D.A. Resilience to Stress and Disturbance, and Resistance to Bromus tectorum L. Invasion in Cold Desert Shrublands of Western North America. Ecosystems 2014, 17, 360–375. [Google Scholar] [CrossRef]
- Seidl, R.; Schelhaas, M.J.; Lexer, M.J. Unraveling the drivers of intensifying forest disturbance regimes in Europe. Glob. Change Biol. 2011, 17, 2842–2852. [Google Scholar] [CrossRef]
- Díaz-delgado, A.R.; Lloret, F.; Pons, X.; Terradas, J. Satellite Evidence of Decreasing Resilience in Mediterranean Plant Communities after Recurrent Wildfires. Ecol. Soc. Am. 2002, 83, 2293–2303. [Google Scholar]
- Schroeder, T.A.; Cohen, W.B.; Yang, Z. Patterns of forest regrowth following clearcutting in western Oregon as determined from a Landsat time-series. For. Ecol. Manag. 2007, 243, 259–273. [Google Scholar] [CrossRef]
- Singh, B.; Jeganathan, C.; Rathore, V.S. Improved NDVI based proxy leaf-fall indicator to assess rainfall sensitivity of deciduousness in the central Indian forests through remote sensing. Sci. Rep. 2020, 10, 17638. [Google Scholar] [CrossRef]
- Li, J.; Shi, J.; Luo, Y.Q.; Kari, H. The effect of fire intensity on the natural rehabilitation of forest vegetation. Ecol. Sci. 2010, 29, 193–199. [Google Scholar]
- Van Leeuwen, W.J.D. Monitoring the effects of forest restoration treatments on post-fire vegetation recovery with MODIS multitemporal data. Sensors 2008, 8, 2017–2042. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Jin, S.; Dahal, D.; Chen, X.; Young, C.; Liu, H.; Liu, S. Reconstructing satellite images to quantify spatially explicit land surface change caused by fires and succession: A demonstration in the Yukon River Basin of interior Alaska. ISPRS J. Photogramm. 2013, 79, 94–105. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.G.; Schwaller, M.R.; Hall, F.F. On the Blending of the Landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. Remote 2006, 44, 2207–2218. [Google Scholar]
- Yi, K.; Tani, H.; Zhang, J.; Guo, M.; Wang, X.; Zhong, G. Long-term satellite detection of post-fire vegetation trends in boreal forests of China. Remote Sens. 2013, 5, 6938–6957. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Moriya, K.; Sakai, T.; Koyama, L.; Cao, C. Monitoring of post-fire forest recovery under different restoration modes based on time series Landsat data. Eur. J. Remote Sens. 2014, 47, 153–168. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; McRae, D.J.; Jin, J.; Shu, L.; Zhao, F.; Wang, M. Changes of Forest Fire Danger and the Evaluation of the FWI System Application in the Daxing’ anling Region. Sci. Silv. Sin. 2010, 46, 127–132. [Google Scholar]
- Tan, K.; Piao, S.; Peng, C.; Fang, J. Satellite-based estimation of biomass carbon stocks for northeast China’s forests between 1982 and 1999. For. Ecol. Manag. 2007, 240, 114–121. [Google Scholar] [CrossRef]
- Fang, J.Y. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Huang, Z.; Cao, C.; Chen, W.; Xu, M.; Dang, Y.; Singh, R.P.; Bashir, B.; Xie, B.; Lin, X. Remote Sensing Monitoring of Vegetation Dynamic Changes after Fire in the Greater Hinggan Mountain Area: The Algorithm and Application for Eliminating Phenological Impacts. Remote Sens. 2020, 12, 156. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Delgado, A.R.; Pons, X. Spatial patterns of forest fires in Catalonia (NE of Spain) along the period 1975–1995. For. Ecol. Manag. 2001, 147, 67–74. [Google Scholar] [CrossRef]
- Kauth, R.J.; Thomas, G.S. The tasseled cap-A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, 29 June–1 July 1976; pp. 4B-41–4B-50. [Google Scholar]
- Crist, E.P.; Cicone, R.C. A Physically-Based Transformation of Thematic Mapper Data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote 1984, 22, 256–263. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.Q.; Krankina, O.N. Comparison of tasseled cap-based Landsat data structures for use in forest disturbance detection. Remote Sens. Environ. 2005, 97, 301–310. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Yan, M.; Li, Z.-Y.; Chen, E.-X.; Tian, X.; Gu, C.-Y.; Li, C.-M.; Fan, W.-W. Change of vegetation coverage in Genhe forest reserve, Daxing’an Mountains, Inner Mongolia. J. Ecol. 2016, 35, 508–515. [Google Scholar]
- Beck, P.; Atzberger, C.; Hogda, K.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Batt, R.D.; Carpenter, S.R.; Cole, J.J.; Pace, M.L.; Johnson, R.A. Changes in ecosystem resilience detected in automated measures of ecosystem metabolism during a wholelake manipulation. Proc. Natl. Acad. Sci. USA 2013, 110, 17398–17403. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).