PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry
Abstract
:1. Introduction
- (1)
- The generalized spatial smoothing-based tensor models are established. The core of the proposed algorithm is to solve the rank-deficiency issue via spatial smoothing. To utilize the multi-dimensional structure of the array measurement, the array data after smoothing is rearranged into a third-order PARAFAC tensor. Unlike the state-of-the-art PARAFAC estimator in [32], the improved PARAFAC approaches are robust to coherent targets owing to the spatial smoothing. In addition, since the third-order PARAFAC decomposition can be quickly accomplished via the existing COMFAC algorithm, the proposed frameworks are more effective than the existing fourth-order PARAFAC algorithms [12].
- (2)
- The ESPRIT-like strategies are developed for joint 2D-DOD, 2D-DOA, 2D-TPA and 2D-RPA estimation. After PARAFAC decomposition, the factor matrices that form the tensor are achieved. The 2D-DOD and 2D-DOA are estimated via the normalized vector cross-product technique. Thereafter, 2D-TPA and 2D-RPA are achieved via the least squares (LS) with the previously estimated 2D-DOD and 2D-DOA. All the estimated parameters are in closed-form and paired automatically. Since the multi-dimensional structure has been explored, they outperform the matrix-based smoothing methods in [37]. Furthermore, as the 2D-DOD and 2D-DOA estimation rely on the normalized vector cross-product technique instead of the uniformity of the sensor array, the proposed approaches are suitable for arbitrary geometries and sensor position errors, while the PARAFAC estimator in [32] is only effective for the ULA configuration.
- (3)
- The advantages of the proposed approaches are verified via theoretically analysis and simulations. The proposed approaches are analyzed with respect to computational complexity, identifiability, as well as the Cramer–Rao Bound (CRB). Computer simulations are designed to show its effectiveness.
2. Tensor and Problem Formulation
2.1. Tensor and PARAFAC Decomposition
2.2. Signal Model
3. The Proposed PARAFAC Estimators
3.1. Review of the Generalized Spatial Smoothing Approaches
3.2. PARAFAC Models and PARAFAC Decomposition
3.3. 2D-DOD and 2D-DOA Estimation
3.4. 2D-TPA and 2D-RPA Estimation
| Algorithm 1: Algorithmic steps of the T-TS approach | |
 | |
| Algorithm 2: Algorithmic steps of the T-RS approach | |
 | |
| Algorithm 3: Algorithmic steps of the T-TRS approach | |
 | |
4. Algorithm Analysis
4.1. Complexity Analysis
4.2. Identifiability Analysis
4.3. CRB
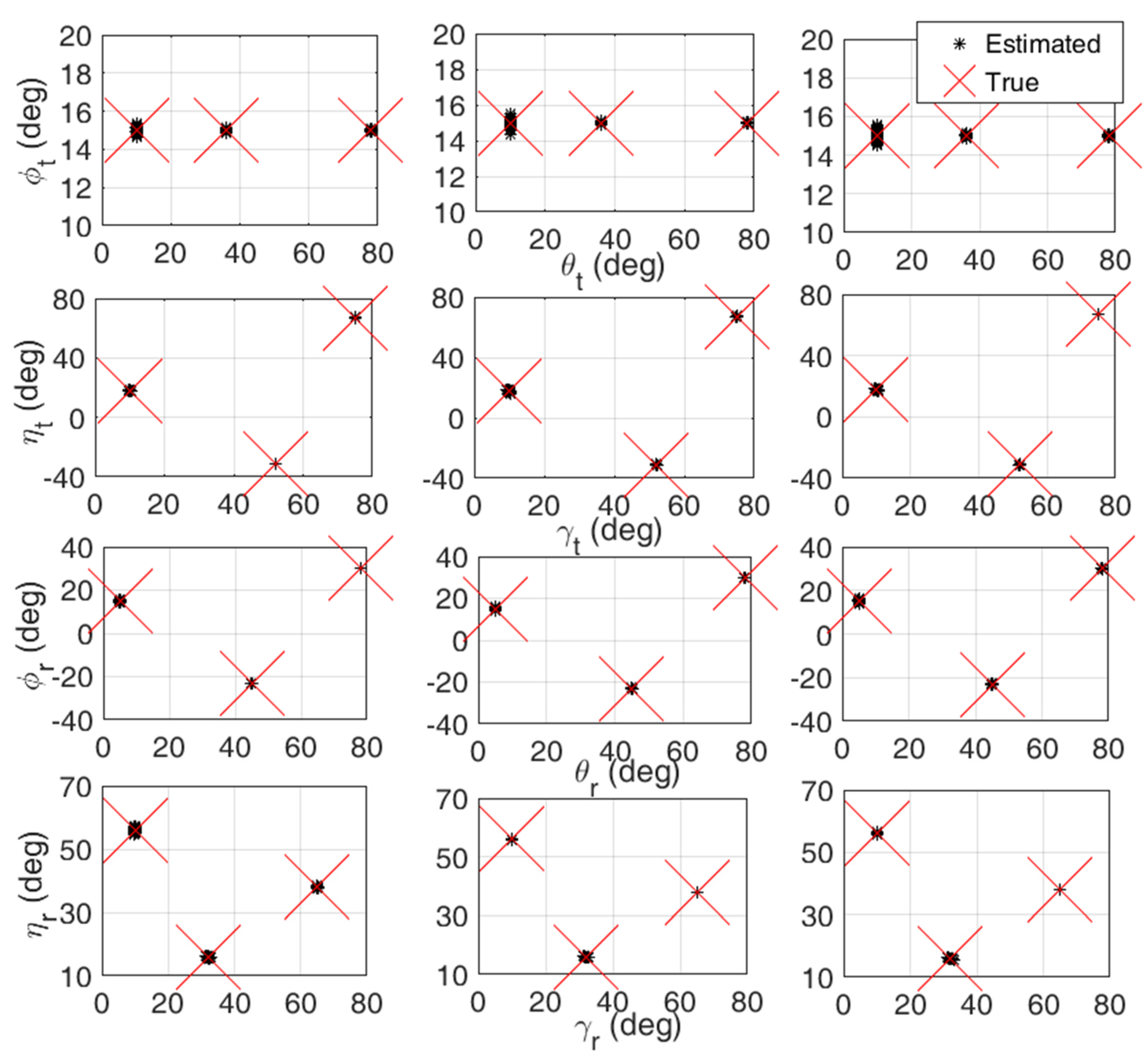
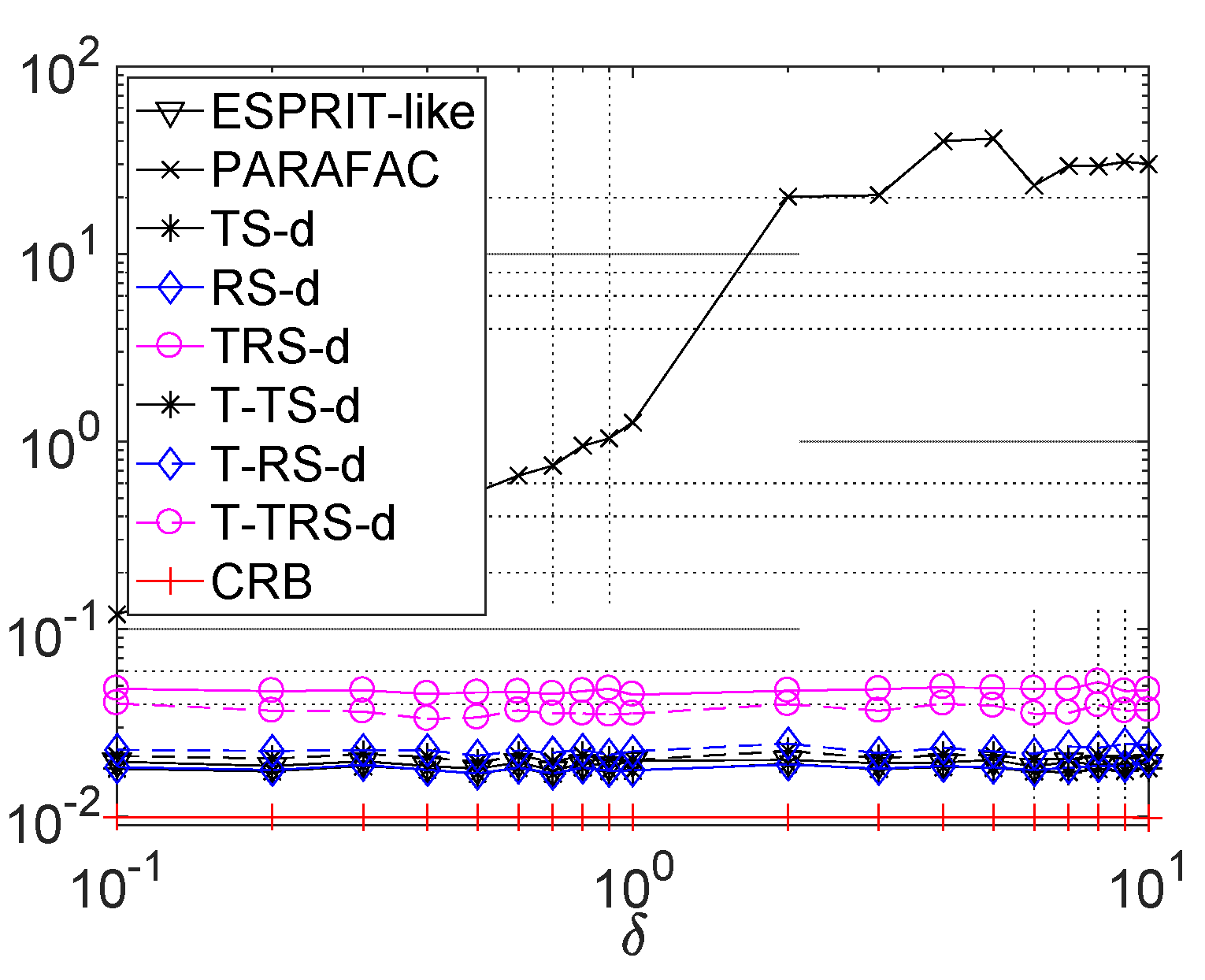
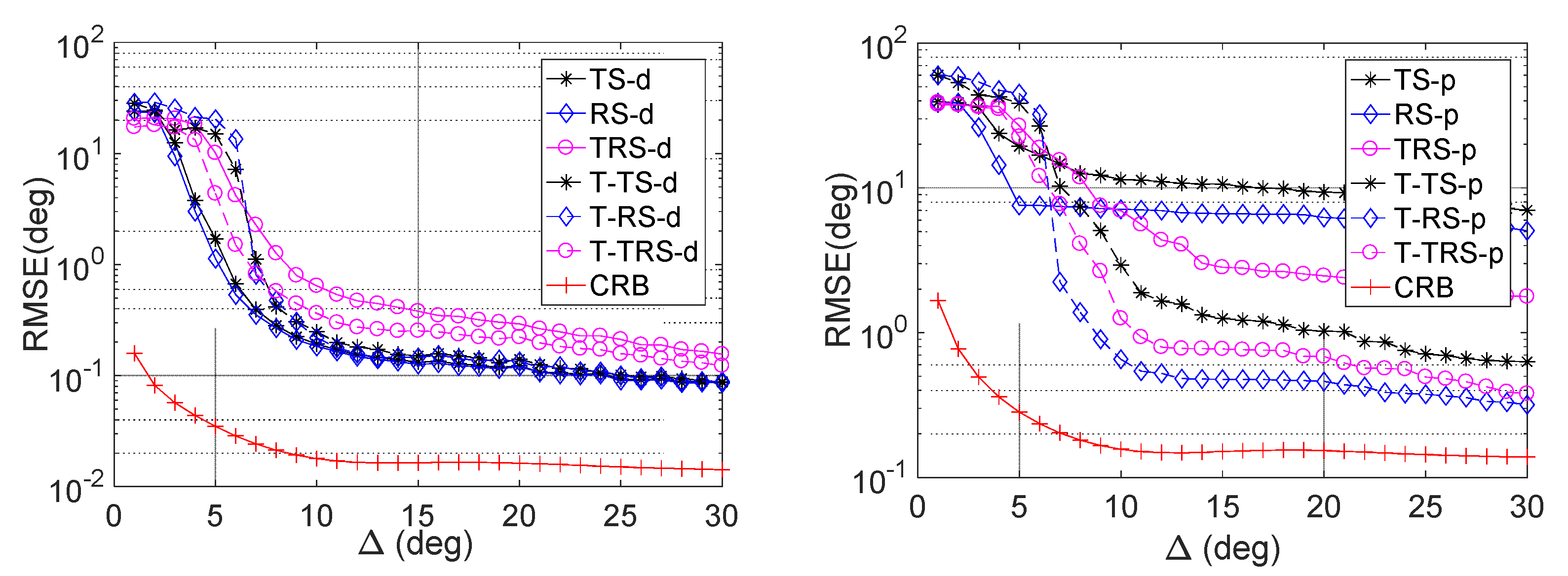
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fisher, E.; Haimovich, A.; Blum, R.; Ciminio, L.; Chizhik, D. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference (IEEE Cat. No. 04CH37509), Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Zhang, L.; Wen, F. A novel MIMO radar orthogonal waveform design algorithm based on intelligent ions motion. Remote Sens. 2021, 13, 1968. [Google Scholar] [CrossRef]
- Shi, J.; Yang, Z.; Liu, Y. On parameter identifiability of diversity-smoothing-based MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1660–1675. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO radar with colocated antennas. IEEE Signal Process Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Chen, D.; Chen, B.; Qin, G. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 770–771. [Google Scholar]
- Chen, J.; Gu, H.; Su, W. Angle estimation using ESPRIT without pairing in MIMO radar. Electron. Lett. 2008, 44, 1422–1423. [Google Scholar]
- Yan, H.; Li, J.; Liao, G. Multitarget identification and localization using bistatic MIMO radar systems. EURASIP J. Adv. Signal Process. 2008, 48, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xu, L.; Lei, X.; Xu, D. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, X.; Huang, Y.; Chen, C.; Li, J. Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple-input multiple-output radar. IET Radar Sonar Nav. 2012, 6, 796–801. [Google Scholar]
- Zhang, X.; Xu, Z.; Xu, L.; Xu, D. Trilinear decomposition-based transmit angle and receive angle estimation for multiple-input multiple-output radar. IET Radar Sonar Nav. 2011, 5, 626–631. [Google Scholar] [CrossRef]
- Cheng, Y.; Yu, R.; Gu, H.; Su, W. Multi-SVD based subspace estimation to improve angle estimation accuracy in bistatic MIMO radar. Signal Process. 2013, 93, 2003–2009. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, C.; Wen, F.; Huang, D. A quadrilinear decomposition method for direction estimation in bistatic MIMO radar. IEEE ACCESS 2018, 6, 18451–18458. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Lan, X.; Su, T. Traffic target location estimation based on tensor decomposition in intelligent transportation system. IEEE Trans. Intell. Transp. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Hao, P.; Gao, Y.; Wang, G.; Wang, Y. Multichannel signal detection in interference and noise when signal mismatch happens. Signal Process. 2020, 166, 107268. [Google Scholar] [CrossRef]
- Wu, J.; Wen, F.; Shi, J. Direction finding in bistatic MIMO radar with direction-dependent mutual coupling. IEEE Commun. Lett. 2021, 25, 2231–2234. [Google Scholar] [CrossRef]
- Wu, J.; Wen, F.; Shi, J. Fast angle estimation in MIMO system with direction-dependent mutual coupling. IEEE Commun. Lett. 2021, 25, 2913–2917. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Hao, P.; Gao, Y.; Wang, Y. Multichannel adaptive signal detection: Basic theory and literature review. Sci. China Inform. Sci. 2022, 65, 121301. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, P.; Li, X. Channel parameter estimation of mmWave MIMO system in urban traffic scene: A training channel based method. IEEE Trans. Intell. Transp. Syst. 2022, 1–9. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Tang, L.; Zhang, X.; Wu, Q. Self-Position awareness based on cascade direct localization over multiple source data. IEEE Trans. Intell. Transp. Syst. 2022, 1–9. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X. A low-complexity joint 2D-DOD and 2D-DOA estimation algorithm for MIMO radar with arbitrary arrays. Int. J. Electron. 2013, 100, 1455–1469. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Closed-form blind 2D-DOD and 2D-DOA estimation for MIMO radar with arbitrary arrays. Wirel. Per. Commun. 2013, 69, 175–186. [Google Scholar] [CrossRef]
- Xia, T. Joint diagonalization based 2D-DOD and 2D-DOA estimation for bistatic MIMO radar. Signal Process. 2015, 116, 7–12. [Google Scholar] [CrossRef]
- Serio, A.D.; Hugler, P.; Roos, F.; Waldschmidt, C. 2D-MIMO radar: A method for array performance assessment and design of a planar antenna array. IEEE Trans. Antenn. Propag. 2020, 68, 4604–4616. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Wang, X.; Wang, L. Angle estimation for MIMO radar in the presence of gain-phase errors with one instrumental Tx/Rx sensor: A theoretical and numerical study. Remote Sens. 2021, 13, 2964. [Google Scholar] [CrossRef]
- He, J.; Shu, T.; Li, L.; Truong, T.K. Mixed near-field and far-field localization and array calibration with partly calibrated arrays. IEEE Trans. Signal Process. 2022, 70, 2105–2118. [Google Scholar] [CrossRef]
- Wong, K.T.; Yuan, X. “Vector cross-product direction-finding” with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops. IEEE Trans. Signal Process. 2011, 59, 160–171. [Google Scholar] [CrossRef]
- Tanveer, A.; Zhang, X.; Zheng, W. DOA estimation for coprime EMVS arrays via minimum distance criterion based on PARAFAC analysis. IET Radar Sonar Nav. 2019, 13, 65–73. [Google Scholar]
- Zheng, G.; Song, Y.; Chen, C. Height measurement with meter wave polarimetric MIMO radar: Signal model and MUSIC-like algorithm. Signal Process. 2022, 190, 108344. [Google Scholar] [CrossRef]
- Shu, T.; He, J.; Dakulagi, V. 3-D near-field source localization using a spatially spread acoustic vector sensor. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 180–188. [Google Scholar] [CrossRef]
- Chintagunta, S.; Palanisamy, P. 2D-DOD and 2D-DOA estimation using the electromagnetic vector sensors. Signal Process. 2018, 147, 163–172. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J. Fast direction finding for bistatic EMVS-MIMO radar without pairing. Signal Process. 2020, 173, 107512. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Zhang, Z. Joint 2D-DOD, 2D-DOA, and polarization angles estimation for bistatic EMVS-MIMO radar via PARAFAC analysis. IEEE Trans. Veh. Technol. 2020, 69, 1626–1638. [Google Scholar] [CrossRef]
- Wang, X.; Huang, M.; Wan, L. Joint 2D-DOD and 2D-DOA estimation for coprime EMVS-MIMO radar. Circ. Syst. Signal Process. 2021, 40, 2950–2966. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Zhang, Z. Closed-form estimation algorithm for EMVS-MIMO radar with arbitrary sensor geometry. Signal Process. 2021, 186, 108117. [Google Scholar] [CrossRef]
- Ponnusamy, P.; Subramaniam, K.; Chintagunta, S. Computationally efficient method for joint DOD and DOA estimation of coherent targets in MIMO radar. Signal Process. 2019, 165, 262–267. [Google Scholar] [CrossRef]
- Chintagunta, S.; Ponnusamy, P.; Subramaniam, K. Polarization difference smoothing in bistatic MIMO radar. Prog. Electromagn. Res. Lett. 2020, 88, 67–74. [Google Scholar]
- Wen, F.; Shi, J.; Zhang, Z. Generalized spatial smoothing in bistatic EMVS-MIMO radar. Signal Process. 2022, 193, 108406. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Rao, W.; Li, D.; Zhang, J.Q. A Tensor-Based Approach to L-Shaped Arrays Processing with Enhanced Degrees of Freedom. IEEE Signal. Process. Lett. 2018, 25, 234–238. [Google Scholar] [CrossRef]
- Chen, Y.H. On spatial smoothing for two-dimensional direction-of-arrival estimation of coherent signals. IEEE Trans. Signal Process. 1997, 45, 1689–1696. [Google Scholar] [CrossRef] [Green Version]
- Bro, R.; Sidiropoulos, N.; Giannakis, G. A Fast Least Squares Algorithm for Separating Trilinear Mixtures. In Proceedings of the International Workshop ICA and BSS, Aussois, France, 11–15 January 1999; pp. 289–294. [Google Scholar]





| Algorithm | Computing Complexity | Identifiability |
|---|---|---|
| TS | ||
| RS | ||
| TRS | 36 | |
| T-TS | ||
| T-RS | ||
| T-TRS | 23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, H.; Wen, F.-Q.; Shi, J.-P. PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry. Remote Sens. 2022, 14, 2905. https://doi.org/10.3390/rs14122905
Zhang L, Wang H, Wen F-Q, Shi J-P. PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry. Remote Sensing. 2022; 14(12):2905. https://doi.org/10.3390/rs14122905
Chicago/Turabian StyleZhang, Lei, Han Wang, Fang-Qing Wen, and Jun-Peng Shi. 2022. "PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry" Remote Sensing 14, no. 12: 2905. https://doi.org/10.3390/rs14122905
APA StyleZhang, L., Wang, H., Wen, F.-Q., & Shi, J.-P. (2022). PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry. Remote Sensing, 14(12), 2905. https://doi.org/10.3390/rs14122905








