Quantitative Monitoring of Leaf Area Index in Rice Based on Hyperspectral Feature Bands and Ridge Regression Algorithm
Abstract
:1. Introduction
2. Materials and Methods
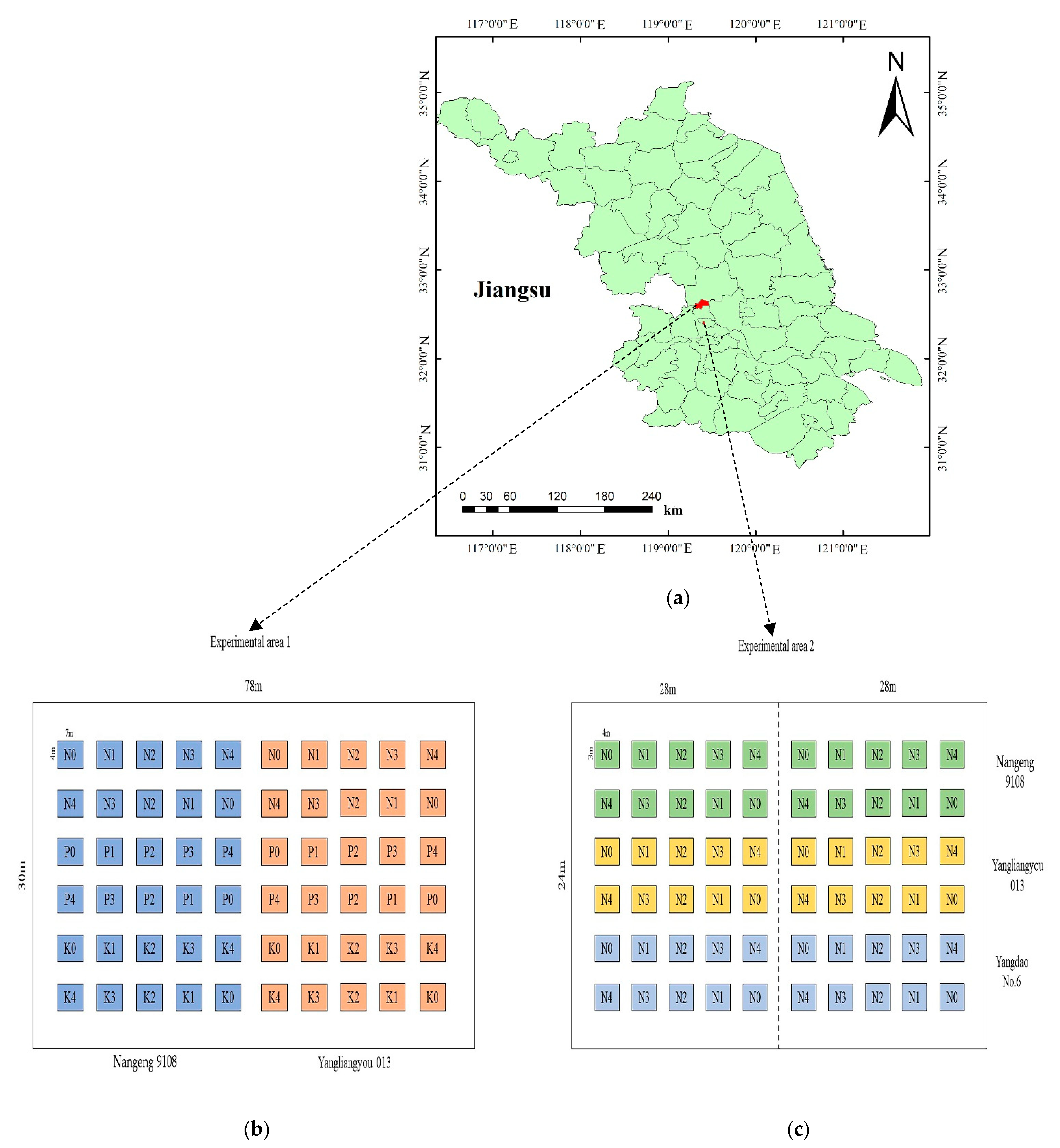
2.1. Experimental Design
2.2. Data Collection
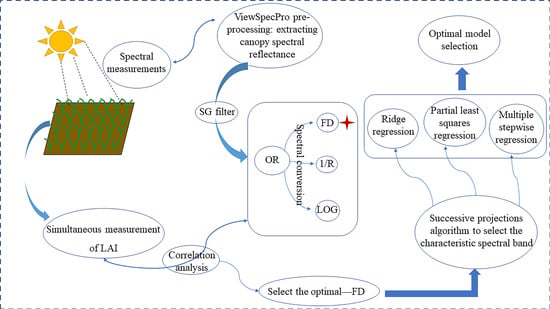
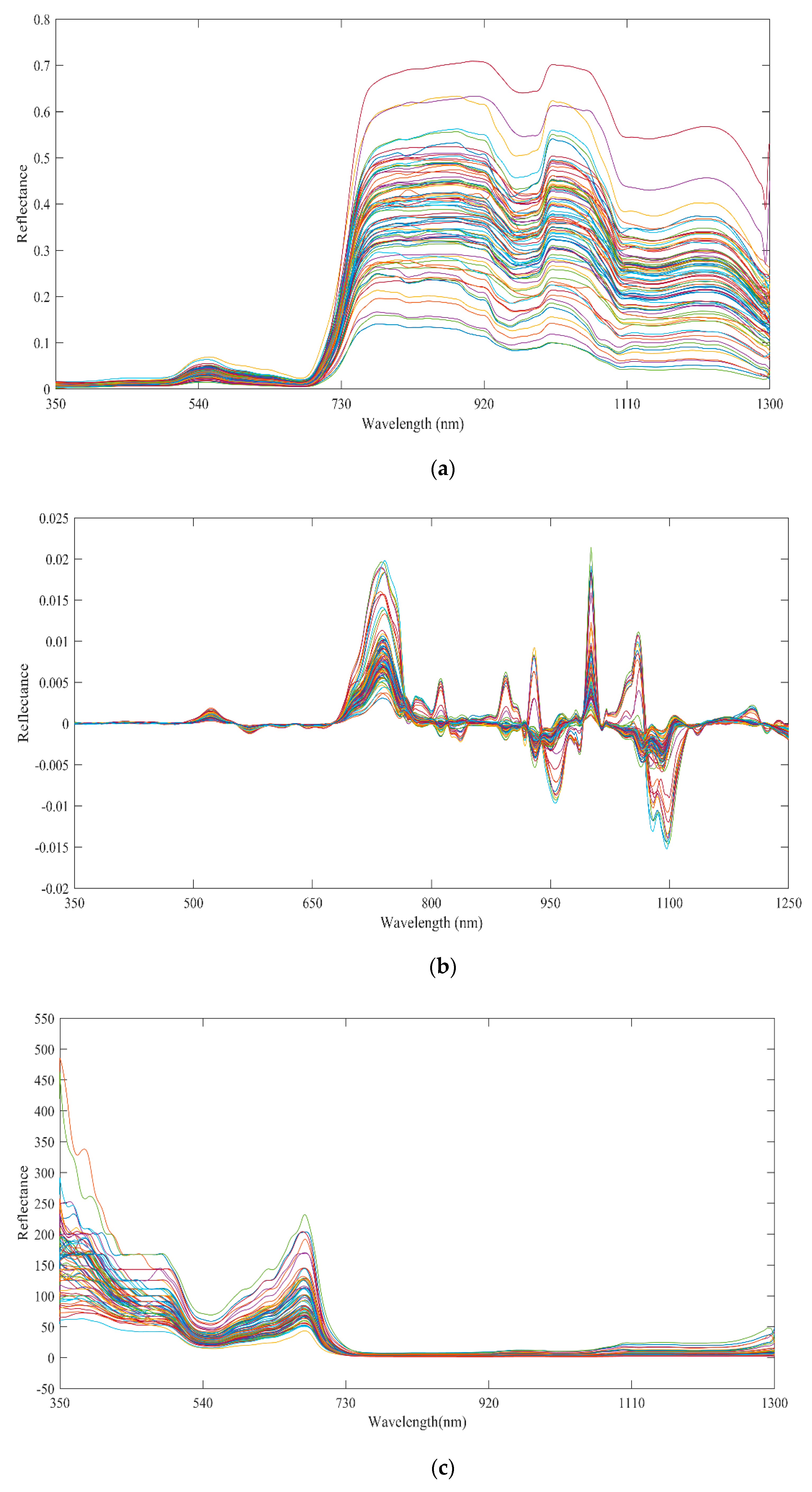
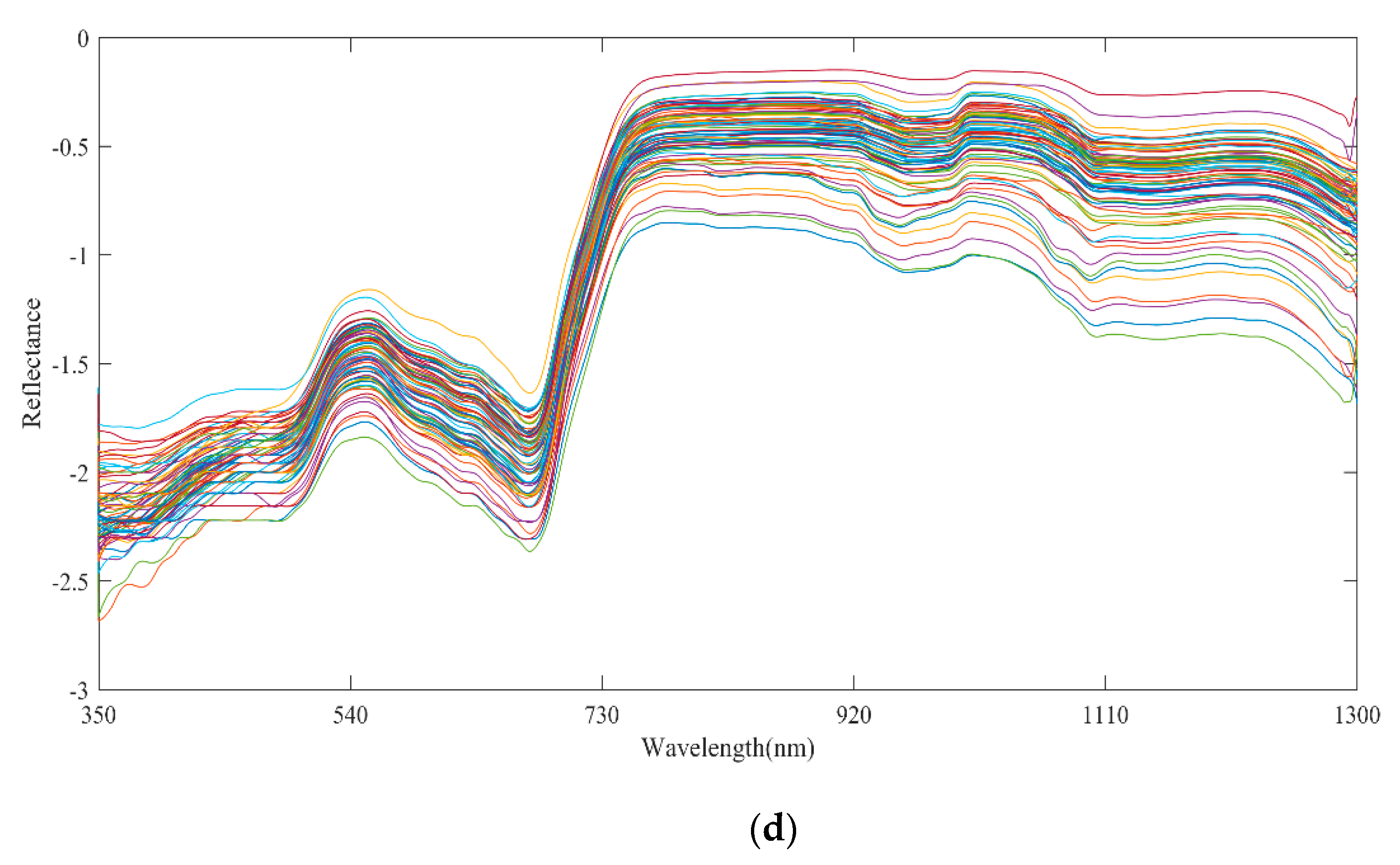
2.3. Hyperspectral Data Preprocessing
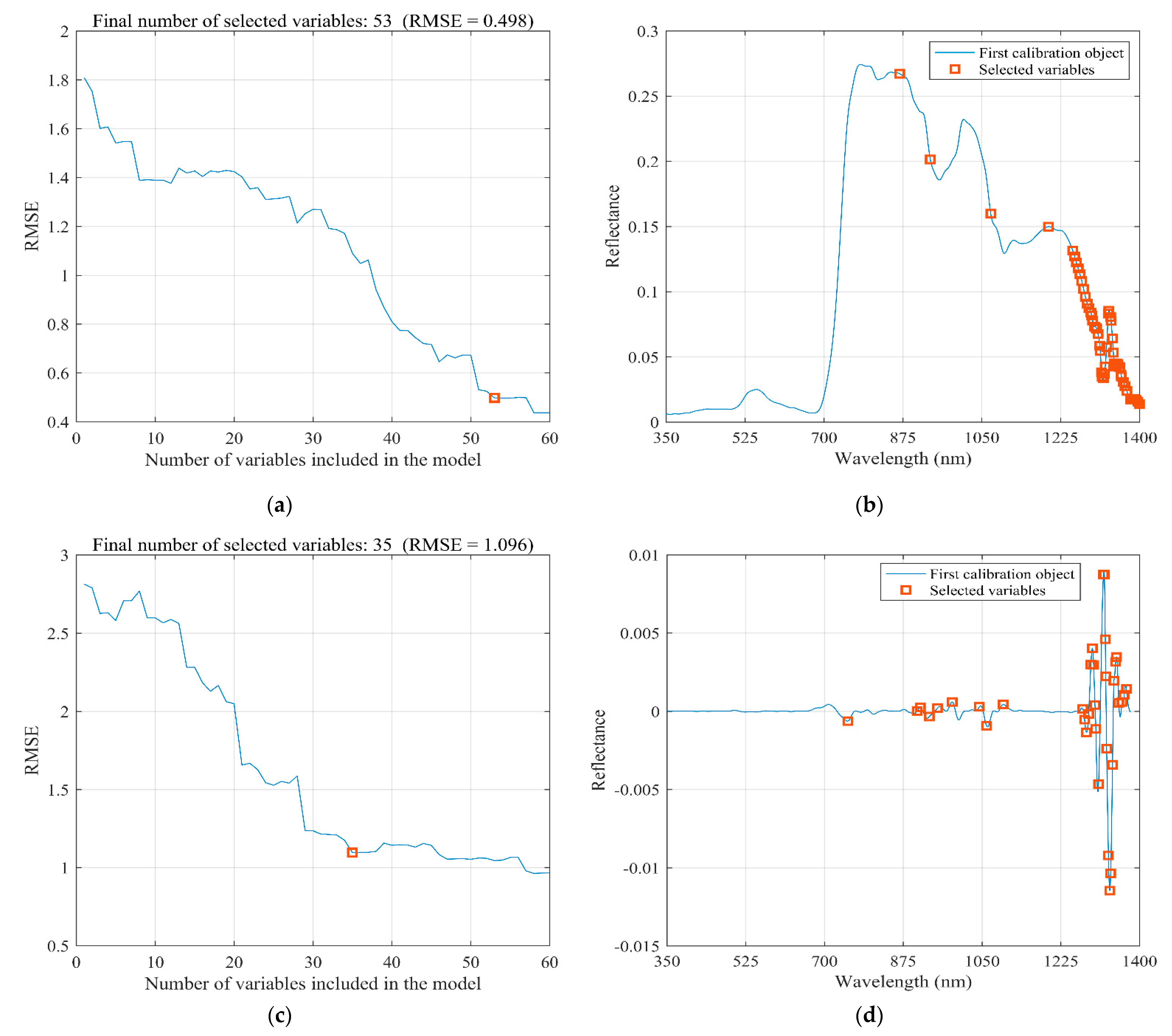
2.4. Method for Characteristic Bands Selection
| Algorithm 1: SPA | |
| Input: | . |
| Step 1: | ; |
| Step 2: | , Determine the unselected band variable. |
| Step 3: | Calculate the projection mapping of the unselected and initialized bands: |
| Step 4: | Determine the maximum projection: |
| Step 5: | |
| Step 6: | , return to step 2; |
| Step 7: | |
| Output: | Selected band. |
2.5. Method for Vegetation Indices Selection
2.6. Model Development
2.6.1. Multicollinearity Diagnosis
2.6.2. Modeling Methods
2.7. Model Evaluation
3. Results
3.1. Spectral Preprocessing
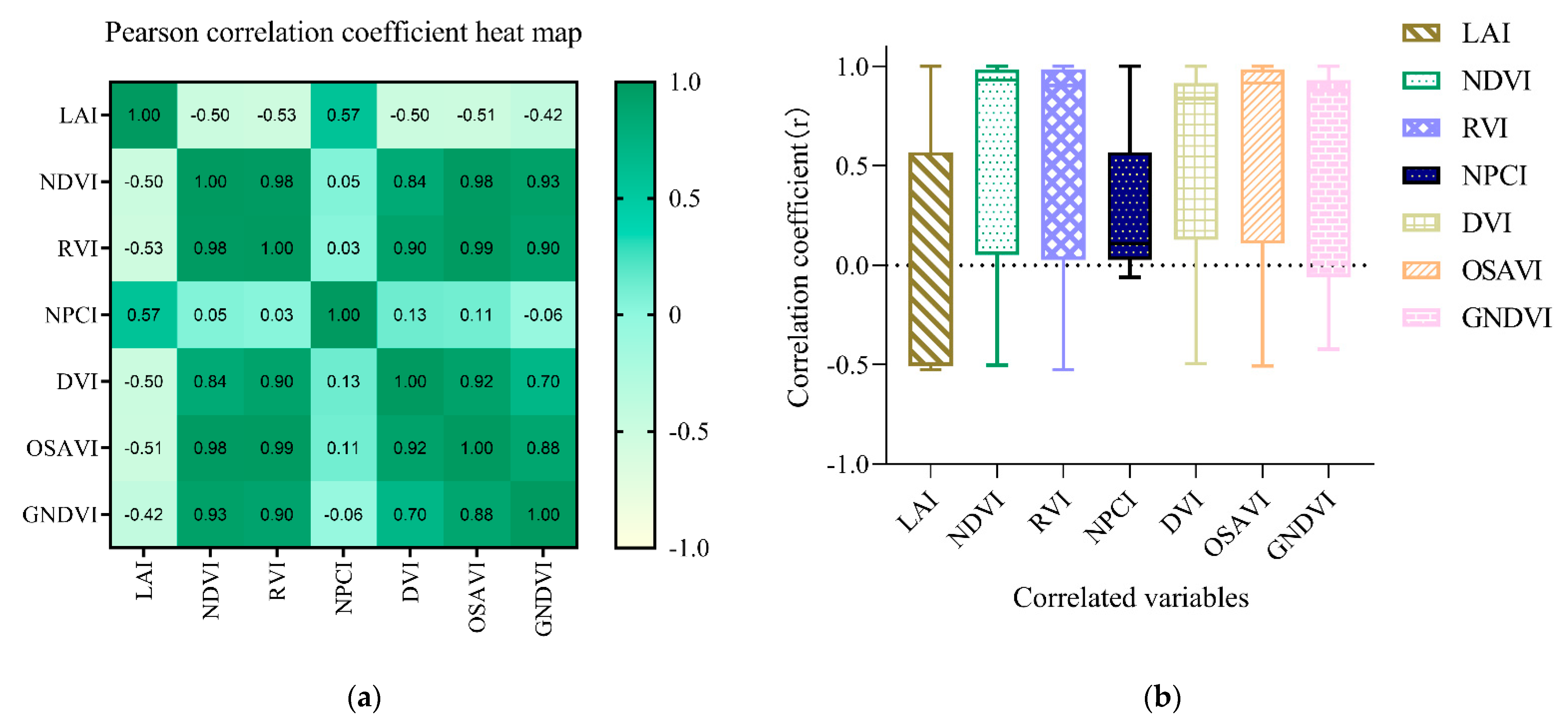
3.2. Correlations between Rice Canopy Spectral Transformations and LAI
3.3. Screening of Characteristic Bands
3.4. Determination of Multicollinearity
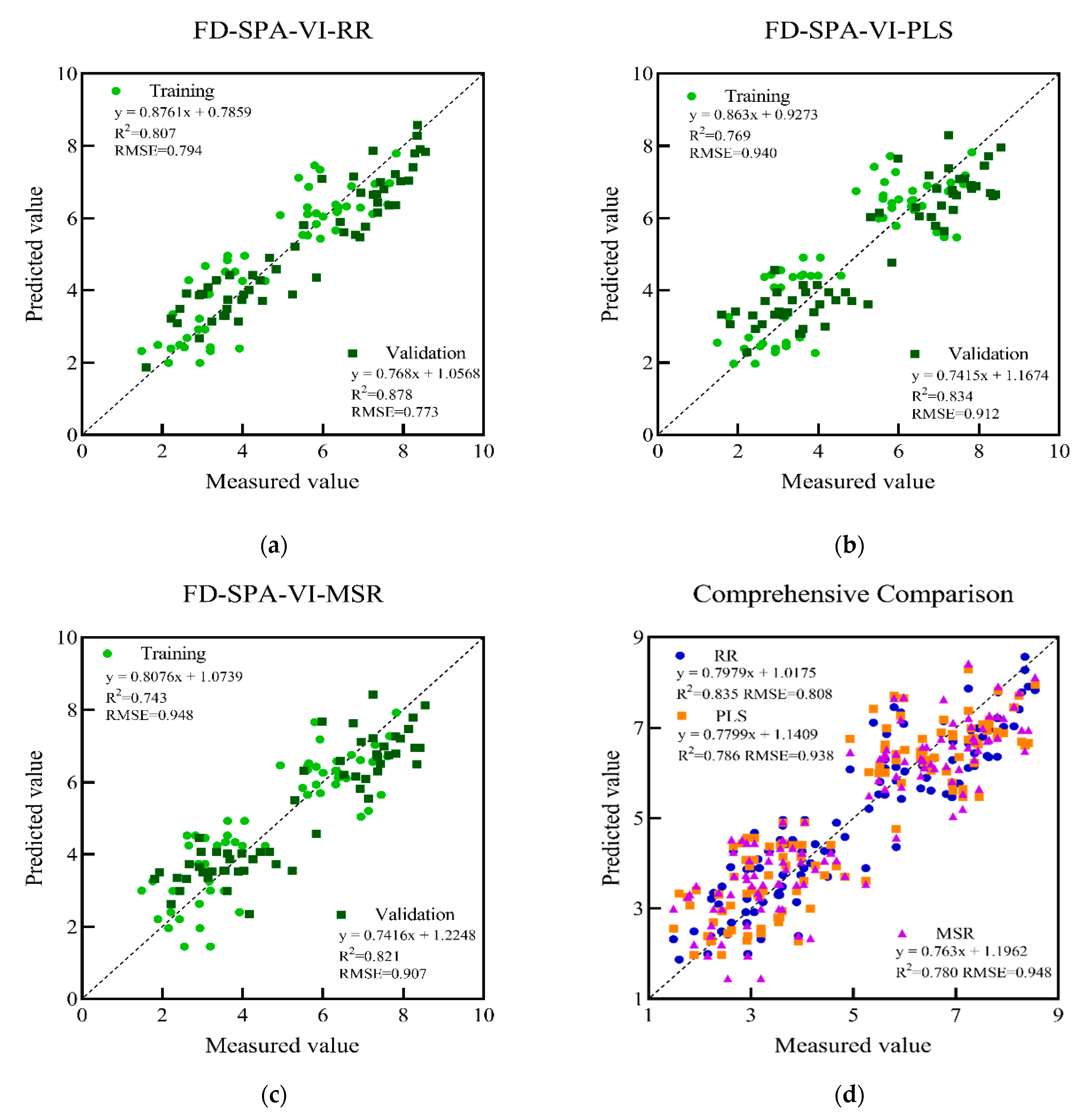
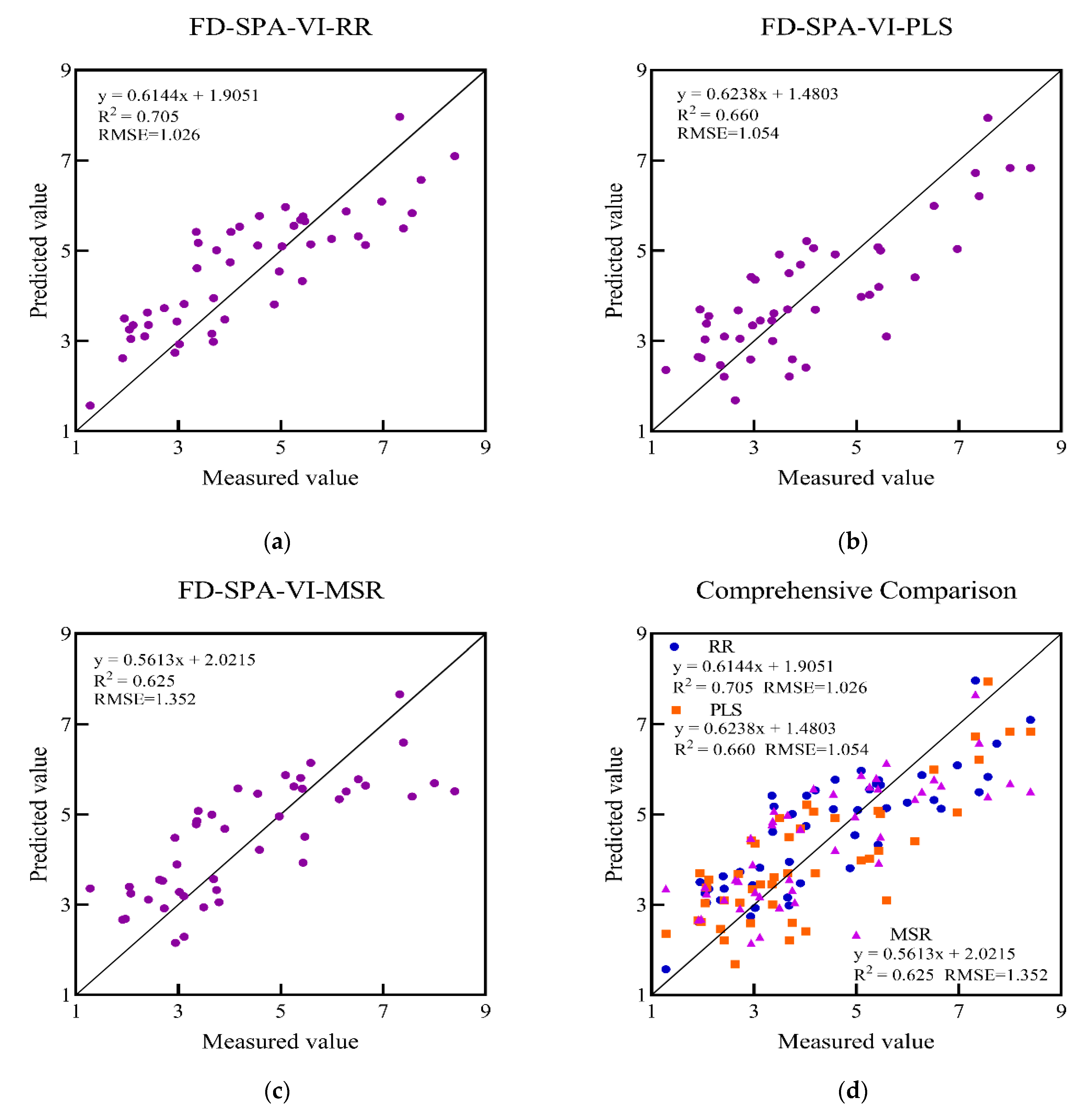
3.5. Establishment and Evaluation of LAI Estimation Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, K.; Gong, Y.; Fang, S.; Duan, B.; Yuan, N.; Peng, Y.; Wu, X.; Zhu, R. Combining spectral and texture features of UAV images for the remote estimation of rice LAI throughout the entire growing season. Remote Sens. 2021, 13, 3001. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining color indices and textures of UAV-based digital imagery for rice LAI estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liu, Q.; Liu, Q.; Li, X. LAI retrieval and uncertainty evaluations for typical row-planted crops at different growth stages. Remote Sens. Environ. 2008, 112, 94–106. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, G.; Song, X.; He, Q. Dynamic characteristics of canopy and vegetation water content during an entire maize growing season in relation to spectral-based indices. Remote Sens. 2022, 14, 584. [Google Scholar] [CrossRef]
- Olson, M.B.; Crawford, M.M.; Vyn, T.J. Hyperspectral indices for predicting nitrogen use efficiency in maize hybrids. Remote Sens. 2022, 14, 1721. [Google Scholar] [CrossRef]
- Prasad, N.; Semwal, M.; Kalra, A. Hyperspectral vegetation indices offer insights for determining economically optimal time of harvest in Mentha arvensis. Ind. Crops Prod. 2022, 180, 114753. [Google Scholar] [CrossRef]
- Yang, R.; Tian, H.; Kan, J. Classification of sugar beets based on hyperspectral and extreme learning machine methods. Appl. Eng. Agric. 2018, 34, 891–897. [Google Scholar] [CrossRef]
- El-Hendawy, S.; Al-Suhaibani, N.; Mubushar, M.; Tahir, M.U.; Marey, S.; Refay, Y.; Tola, E. Combining hyperspectral reflectance and multivariate regression models to estimate plant biomass of advanced spring wheat lines in diverse phenological stages under salinity conditions. Appl. Sci. 2022, 12, 1983. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Zhang, J.; Fan, Y.; Cheng, Y.; Wang, B.; Wu, X.; Tan, X.; Tan, T.; Li, S.; et al. Predicting grain yield and protein content using canopy reflectance in maize grown under different water and nitrogen levels. Field Crops Res. 2021, 260, 107988. [Google Scholar] [CrossRef]
- Gu, X.; Wang, L.; Song, X.; Xu, X. Estimating Leaf Nitrogen Accumulation in Maize Based on Canopy Hyperspectrum Data. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII, Edinburgh, UK, 26–29 September 2016. [Google Scholar]
- Gao, J.; Ni, J.; Wang, D.; Deng, L.; Li, J.; Han, Z. Pixel-level aflatoxin detecting in maize based on feature selection and hyperspectral imaging. Spectrochim. Acta A 2020, 234, 118269. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Gu, B.; Mu, J.; Ruan, P.; Li, D. Wheat hardness prediction research based on NIR hyperspectral analysis combined with ant colony optimization algorithm. Procedia Eng. 2017, 174, 648–656. [Google Scholar] [CrossRef]
- Liu, T.; Xu, T.y.; Yu, F.h.; Yuan, Q.y.; Guo, Z.h.; Xu, B. Chlorophyll content estimation of northeast japonica rice based on improved feature band selection and hybrid integrated modeling. Spectrosc. Spect. Anal. 2021, 41, 2556–2564. [Google Scholar]
- Wang, J.; Sun, L.; Feng, G.; Bai, H.; Yang, J.; Gai, Z.; Zhao, Z.; Zhang, G. Intelligent detection of hard seeds of snap bean based on hyperspectral imaging. Spectrochim. Acta A 2022, 275, 121169. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhou, Q.; Shang, J.; Liu, C.; Zhuang, T.; Ding, J.; Xian, Y.; Zhao, L.; Wang, W.; Zhou, G.; et al. UAV- and machine learning-based retrieval of wheat SPAD values at the overwintering stage for variety screening. Remote Sens. 2021, 13, 5166. [Google Scholar] [CrossRef]
- Wang, T.; Gao, M.; Cao, C.; You, J.; Zhang, X.; Shen, L. Winter wheat chlorophyll content retrieval based on machine learning using in situ hyperspectral data. Comput. Electron. Agric. 2022, 193, 106728. [Google Scholar] [CrossRef]
- Shi, X.; Yao, L.; Pan, T. Visible and near-infrared spectroscopy with multi-parameters optimization of Savitzky-Golay smoothing applied to rapid analysis of soil cr content of pearl river delta. J. Geogr. Environ. Protect. 2021, 9, 75–83. [Google Scholar] [CrossRef]
- Chen, S.; Hu, T.; Luo, L.; He, Q.; Zhang, S.; Li, M.; Cui, X.; Li, H. Rapid estimation of leaf nitrogen content in apple-trees based on canopy hyperspectral reflectance using multivariate methods. Infrared Phys. Technol. 2020, 111, 103542. [Google Scholar] [CrossRef]
- Sun, J.; Yang, W.; Zhang, M.; Feng, M.; Xiao, L.; Ding, G. Estimation of water content in corn leaves using hyperspectral data based on fractional order Savitzky-Golay derivation coupled with wavelength selection. Comput. Electron. Agric. 2021, 182, 105989. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Q.; Yi, X.; Ma, L.; Zhang, L.; Huang, C.; Zhang, Z.; Lv, X. Estimation of cotton leaf area index (LAI) based on spectral transformation and vegetation index. Remote Sens. 2022, 14, 136. [Google Scholar] [CrossRef]
- Feng, Z.-H.; Wang, L.-Y.; Yang, Z.-Q.; Zhang, Y.-Y.; Li, X.; Song, L.; He, L.; Duan, J.-Z.; Feng, W. Hyperspectral monitoring of powdery mildew diease severity in wheat based on machine learning. Front. Plant Sci. 2022, 13, 828454. [Google Scholar] [CrossRef] [PubMed]
- Cui, S.; Zhou, K.; Ding, R.; Cheng, Y.; Jiang, G. Estimation of soil copper content based on fractional-order derivative spectroscopy and spectral characteristic band selection. Spectrochim. Acta A 2022, 275, 121190. [Google Scholar] [CrossRef] [PubMed]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemometr. Intell. Lab. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Pearson, K. On the generalised equations of elasticity, and their application to the wave theory of light. Lond. Math. Soc. 1888, s1-20, 297–349. [Google Scholar] [CrossRef]
- Wang, F.; Huang, J.; Tang, Y.; Wang, X. New vegetation index and its application in estimating leaf area index of rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Harrell, D.L.; Tubaña, B.S.; Walker, T.W.; Phillips, S.B. Estimating rice grain yield potential using normalized difference vegetation index. Agron. J. 2011, 103, 1717–1723. [Google Scholar] [CrossRef]
- Adams, M.L.; Philpot, W.D.; Norvell, W.A. Yellowness index: An application of spectral second derivatives to estimate chlorosis of leaves in stressed vegetation. Int. J. Remote Sens. 1999, 20, 3663–3675. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature analysis of leaf reflectance spectra: Algorithm development for remote sensing of chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Serrano, L.; Peñuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in Mediterranean vegetation from AVIRIS data. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Etaga, H.O.; Ndubisi, R.C.; Oluebube, N.L. Effect of multicollinearity on variable selection in multiple regression. Sci. J. Appl. Math. Stat. 2021, 9, 141–153. [Google Scholar]
- Abeysiriwardana, H.D.; Gomes, P.I. Integrating vegetation indices and geo-environmental factors in GIS-based landslide-susceptibility mapping: Using logistic regression. J. Mt. Sci-Engl. 2022, 19, 477–492. [Google Scholar] [CrossRef]
- Midi, H.; Sarkar, S.K.; Rana, S. Collinearity diagnostics of binary logistic regression model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar] [CrossRef]
- Ivanda, A.; Šerić, L.; Bugarić, M.; Braović, M. Mapping chlorophyll-a concentrations in the Kaštela Bay and Brač Channel using ridge regression and Sentinel-2 satellite images. Electronics 2021, 10, 3004. [Google Scholar] [CrossRef]
- Hssaini, L.; Razouk, R.; Bouslihim, Y. Rapid prediction of fig phenolic acids and flavonoids using mid-infrared spectroscopy combined with partial least square regression. Front. Plant Sci. 2022, 13, 782159. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Xu, H.; Zhong, X. Prediction of soil heavy metal concentrations in copper tailings area using hyperspectral reflectance. Environ. Earth Sci. 2022, 81, 183. [Google Scholar] [CrossRef]
- Schmitz, P.K.; Kandel, H.J. Using canopy measurements to predict soybean seed yield. Remote Sens. 2021, 13, 3260. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, J.; Du, Y.; Zhai, T.; Fang, Y.; Li, Z. Exploring the potential of canopy reflectance spectra for estimating organic carbon content of aboveground vegetation in coastal wetlands. Int. J. Remote Sens. 2021, 42, 3850–3872. [Google Scholar] [CrossRef]
- Sapes, G.; Lapadat, C.; Schweiger, A.K.; Juzwik, J.; Montgomery, R.; Gholizadeh, H.; Townsend, P.A.; Gamon, J.A.; Cavender-Bares, J. Canopy spectral reflectance detects oak wilt at the landscape scale using phylogenetic discrimination. Remote Sens. Environ. 2022, 273, 112961. [Google Scholar] [CrossRef]
- Panigrahi, N.; Das, B.S. Evaluation of regression algorithms for estimating leaf area index and canopy water content from water stressed rice canopy reflectance. Inf. Process. Agric. 2021, 8, 284–298. [Google Scholar] [CrossRef]
- Duan, B.; Liu, Y.; Gong, Y.; Peng, Y.; Wu, X.; Zhu, R.; Fang, S. Remote estimation of rice LAI based on Fourier spectrum texture from UAV image. Plant Methods 2019, 15, 124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Y.; Gao, Y.; Wang, Y.; Luo, D.; Chen, S.; Ding, Z.; Fan, K. Using unmanned aerial vehicle-based multispectral image data to monitor the growth of intercropping crops in tea plantation. Front. Plant Sci. 2022, 13, 820585. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Ma, C.; Ding, F.; Li, Y.; Chen, W.; Li, J.; Xiao, Z. Hyperspectral estimation of winter wheat leaf area index based on continuous wavelet transform and fractional order differentiation. Sensors 2021, 21, 8497. [Google Scholar] [CrossRef]
- Xing, N.; Huang, W.; Dong, Y.; Ye, H.; Pignatti, S.; Laneve, G.; Casa, R. Estimation of winter wheat leaf area index at different growth stages using optimized red-edge hyperspectral vegetation indices. IOP Conf. Ser. Earth Environ. Sci. 2020, 509, 012027. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, K.; Xiao, C.; Wei, D.; Zhao, X.; Lan, J.; Wei, X.; Yao, Y.; Wang, B.; Sun, Y.; et al. Leaf area index estimation algorithm for GF-5 hyperspectral data based on different feature selection and machine learning methods. Remote Sens. 2020, 12, 2110. [Google Scholar] [CrossRef]
- Zhang, G.; Hao, H.; Wang, Y.; Jiang, Y.; Shi, J.; Yu, J.; Cui, X.; Li, J.; Zhou, S.; Yu, B. Optimized adaptive Savitzky-Golay filtering algorithm based on deep learning network for absorption spectroscopy. Spectrochim. Acta A 2021, 263, 120187. [Google Scholar] [CrossRef]
- Liu, T.; Xu, T.; Yu, F.; Yuan, Q.; Guo, Z.; Xu, B. A method combining ELM and PLSR (ELM-P) for estimating chlorophyll content in rice with feature bands extracted by an improved ant colony optimization algorithm. Comput. Electron. Agr. 2021, 186, 106177. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, J.; Xiong, S.; Zhang, Z.; Wei, Q.; Zhang, W.; Feng, W.; Ma, X. Hyperspectral assessment of leaf nitrogen accumulation for winter wheat using different regression modeling. Precis. Agric. 2021, 22, 1634–1658. [Google Scholar] [CrossRef]
- Xie, S.; Ding, F.; Chen, S.; Wang, X.; Li, Y.; Ma, K. Prediction of soil organic matter content based on characteristic band selection method. Spectrochim. Acta A 2022, 273, 120949. [Google Scholar] [CrossRef] [PubMed]
- Kleshchenko, A.D.; Savitskaya, O.V. Estimation of winter wheat yield using the principal component analysis based on the integration of satellite and ground information. Russ. Meteorol. Hydrol. 2021, 46, 881–887. [Google Scholar] [CrossRef]
- Peron-Danaher, R.; Russell, B.; Cotrozzi, L.; Mohammadi, M.; Couture, J.J. Incorporating multi-scale, spectrally detected nitrogen concentrations into assessing nitrogen use efficiency for winter wheat breeding populations. Remote Sens. 2021, 13, 3991. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Sharma, E.; Jui, S.J.; Deo, R.C.; Nguyen-Huy, T.; Ali, M. Kernel ridge regression hybrid method for wheat yield prediction with satellite-derived predictors. Remote Sens. 2022, 14, 1136. [Google Scholar] [CrossRef]


| Vegetation Index | Full Name | Calculation Formula | Citation |
|---|---|---|---|
| NDVI | Normalized Differential Vegetation Index | Adams et al. [28] | |
| GNDVI | Green Normalized Differential Vegetation Index | Gitelson et al. [29] | |
| OSAVI | Optimized Soil Adjusted Vegetation Index | Rondeaux et al. [30] | |
| DVI | Differential Vegetation Index | Richardson et al. [31] | |
| RVI | Ratio Vegetation Index | Serrano et al. [32] | |
| NPCI | Normalized Pigment Chlorophyll Index | Peñuelas et al. [33] |
| Selection Method | Main Bands | Optimum Band |
|---|---|---|
| SPA | 1347, 1349, 1322, 1301, 1298, 1331, 1327, 1320, 1340, 1343, 1336, 1292, 1354, 1334, 1309, 933, 1366, 1325, 1278, 1361, 913, 1282, 1295, 1287, 1324, 1097, 1371, 906, 752, 951, 1303, 1060, 1274, 984, 1044 | 752 nm, 913 nm, 984 nm, 1044 nm, 1097 nm, 1278 nm, 1295 nm, 1303 nm, 1347 nm, 1371 nm |
| Pearson | 554, 822, 823, 555, 824, 825, 826, 827, 828, 553, 675, 673, 674 | 554 nm, 555 nm, 675 nm, 822 nm, 824 nm, 825 nm, 826 nm, 827 nm, 828 nm, 553 nm |
| SPA Bands | VIF | Pearson Bands | VIF | VI | VIF |
|---|---|---|---|---|---|
| 752 nm | 44.154 | 553 nm | 52.292 | NDVI | 185.781 |
| 913 nm | 11.197 | 554 nm | 282.518 | DVI | 31.498 |
| 984 nm | 236.299 | 555 nm | 127.756 | NPCI | 1.373 |
| 1044 nm | 279.809 | 675 nm | 3.972 | RVI | 119.491 |
| 1097 nm | 54.865 | 822 nm | 79.731 | GNDVI | 9.783 |
| 1278 nm | 9.033 | 824 nm | 2098.171 | OSAVI | 130.941 |
| 1295 nm | 4.666 | 826 nm | 4414.197 | ||
| 1303 nm | 3.497 | 828 nm | 1553.898 | ||
| 1347 nm | 2.040 | 825 nm | 25,813.464 | ||
| 1371 nm | 4.557 | 827 nm | 27,061.104 |
| Variable Selection | Number of Variables | Modeling Method | R2 | RMSE |
|---|---|---|---|---|
| FD-SPA | 11 | RR | 0.718 | 1.071 |
| 11 | PLS | 0.703 | 1.138 | |
| 5 | MSR | 0.666 | 1.187 | |
| FD-Pearson | 11 | RR | 0.706 | 1.067 |
| 11 | PLS | 0.664 | 1.147 | |
| 3 | MSR | 0.653 | 1.167 | |
| FD-SPA-VI | 12 | RR | 0.807 | 0.794 |
| 12 | PLS | 0.769 | 0.940 | |
| 5 | MSR | 0.743 | 0.948 | |
| FD-Pearson-VI | 12 | RR | 0.722 | 1.001 |
| 12 | PLS | 0.694 | 1.065 | |
| 4 | MSR | 0.658 | 1.136 |
| Variable Selection | Modeling Set | Validation Set | ||
|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |
| FD-SPA-RR | 0.718 | 1.071 | 0.815 | 1.046 |
| FD-SPA-PLS | 0.703 | 1.138 | 0.786 | 1.118 |
| FD-SPA-MSR | 0.666 | 1.187 | 0.757 | 1.162 |
| FD-SPA-VI-RR | 0.807 | 0.794 | 0.878 | 0.773 |
| FD-SPA-VI-PLS | 0.769 | 0.940 | 0.834 | 0.912 |
| FD-SPA-VI-MSR | 0.743 | 0.948 | 0.821 | 0.907 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, S.; Gu, C.; Xi, X.; Zhang, Z.; Hong, Q.; Huo, Z.; Zhao, H.; Zhang, R.; Li, B.; Tan, C. Quantitative Monitoring of Leaf Area Index in Rice Based on Hyperspectral Feature Bands and Ridge Regression Algorithm. Remote Sens. 2022, 14, 2777. https://doi.org/10.3390/rs14122777
Ji S, Gu C, Xi X, Zhang Z, Hong Q, Huo Z, Zhao H, Zhang R, Li B, Tan C. Quantitative Monitoring of Leaf Area Index in Rice Based on Hyperspectral Feature Bands and Ridge Regression Algorithm. Remote Sensing. 2022; 14(12):2777. https://doi.org/10.3390/rs14122777
Chicago/Turabian StyleJi, Shu, Chen Gu, Xiaobo Xi, Zhenghua Zhang, Qingqing Hong, Zhongyang Huo, Haitao Zhao, Ruihong Zhang, Bin Li, and Changwei Tan. 2022. "Quantitative Monitoring of Leaf Area Index in Rice Based on Hyperspectral Feature Bands and Ridge Regression Algorithm" Remote Sensing 14, no. 12: 2777. https://doi.org/10.3390/rs14122777
APA StyleJi, S., Gu, C., Xi, X., Zhang, Z., Hong, Q., Huo, Z., Zhao, H., Zhang, R., Li, B., & Tan, C. (2022). Quantitative Monitoring of Leaf Area Index in Rice Based on Hyperspectral Feature Bands and Ridge Regression Algorithm. Remote Sensing, 14(12), 2777. https://doi.org/10.3390/rs14122777