Estimation of Downwelling Surface Longwave Radiation with the Combination of Parameterization and Artificial Neural Network from Remotely Sensed Data for Cloudy Sky Conditions
Abstract
:1. Introduction
2. Data
2.1. MODIS Satellite Data
2.2. Reanalysis Data
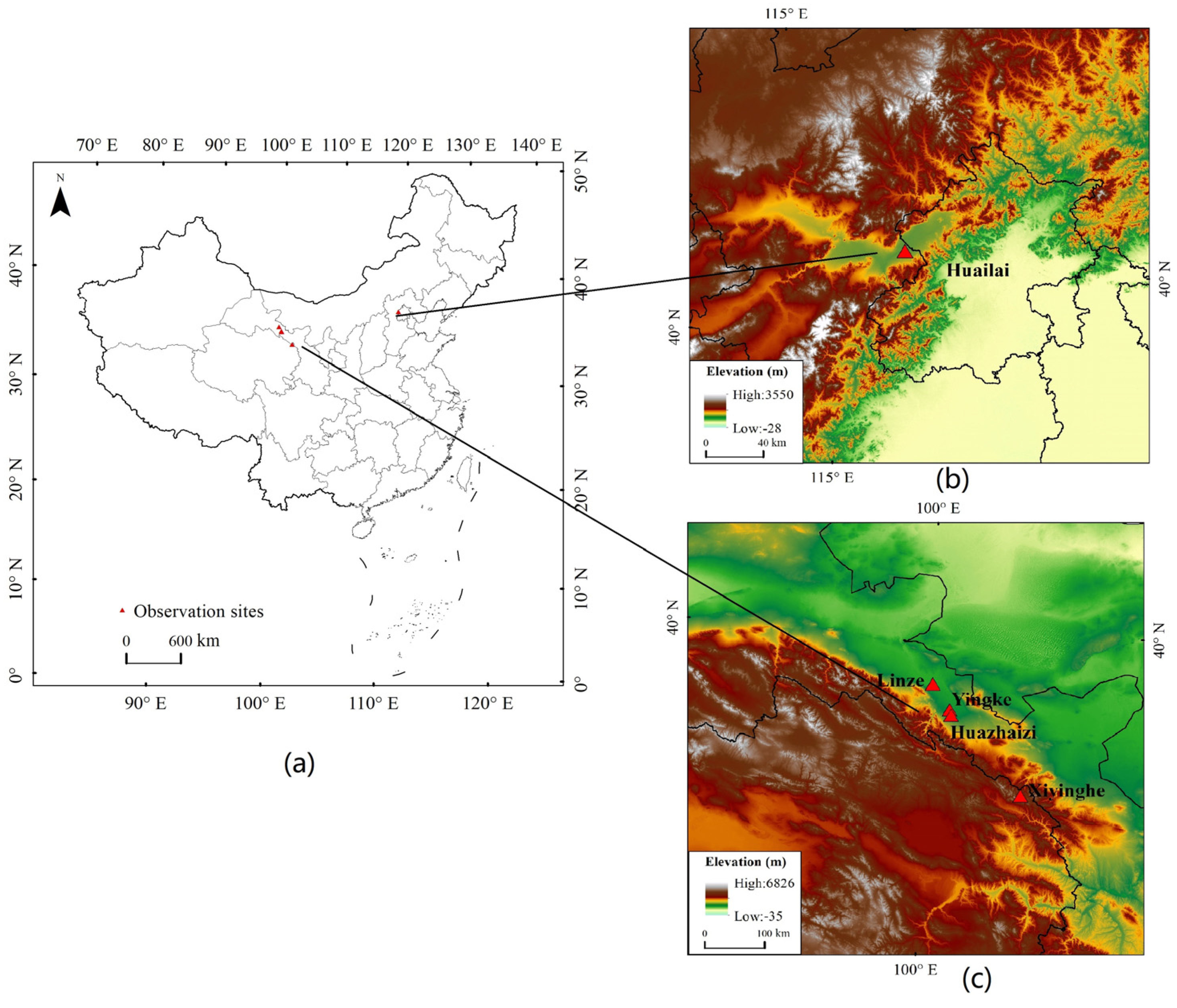
2.3. Site Observations
2.4. Simulated Data
3. Methodology
3.1. Estimating DSLR under Cloudy-Sky Conditions
3.1.1. Estimating DSLR under Clear-Sky Conditions
3.1.2. Estimating DSLR under Fully Cloudy-Sky Conditions
4. Results
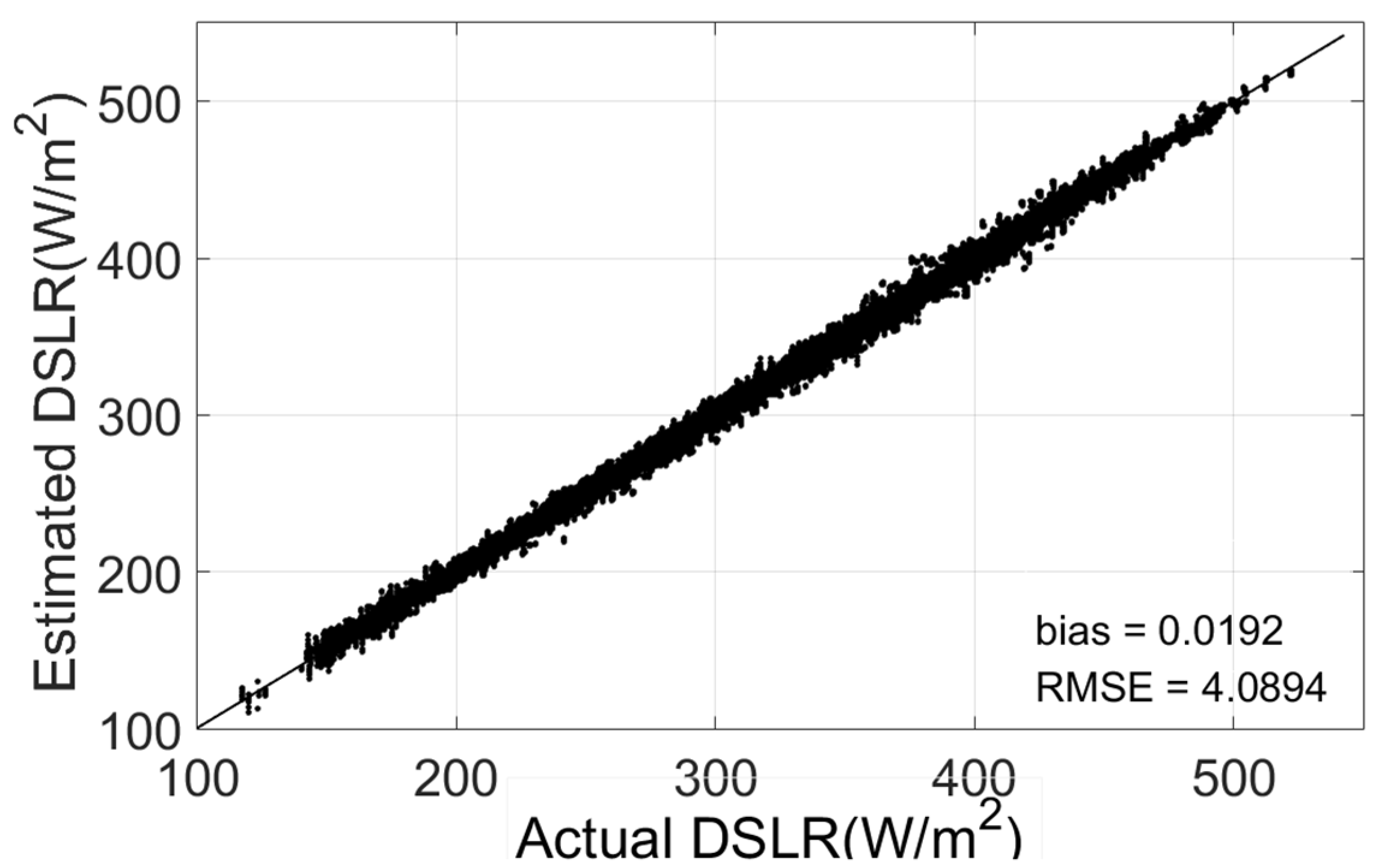
4.1. The Performance of GA-ANN Algorithm
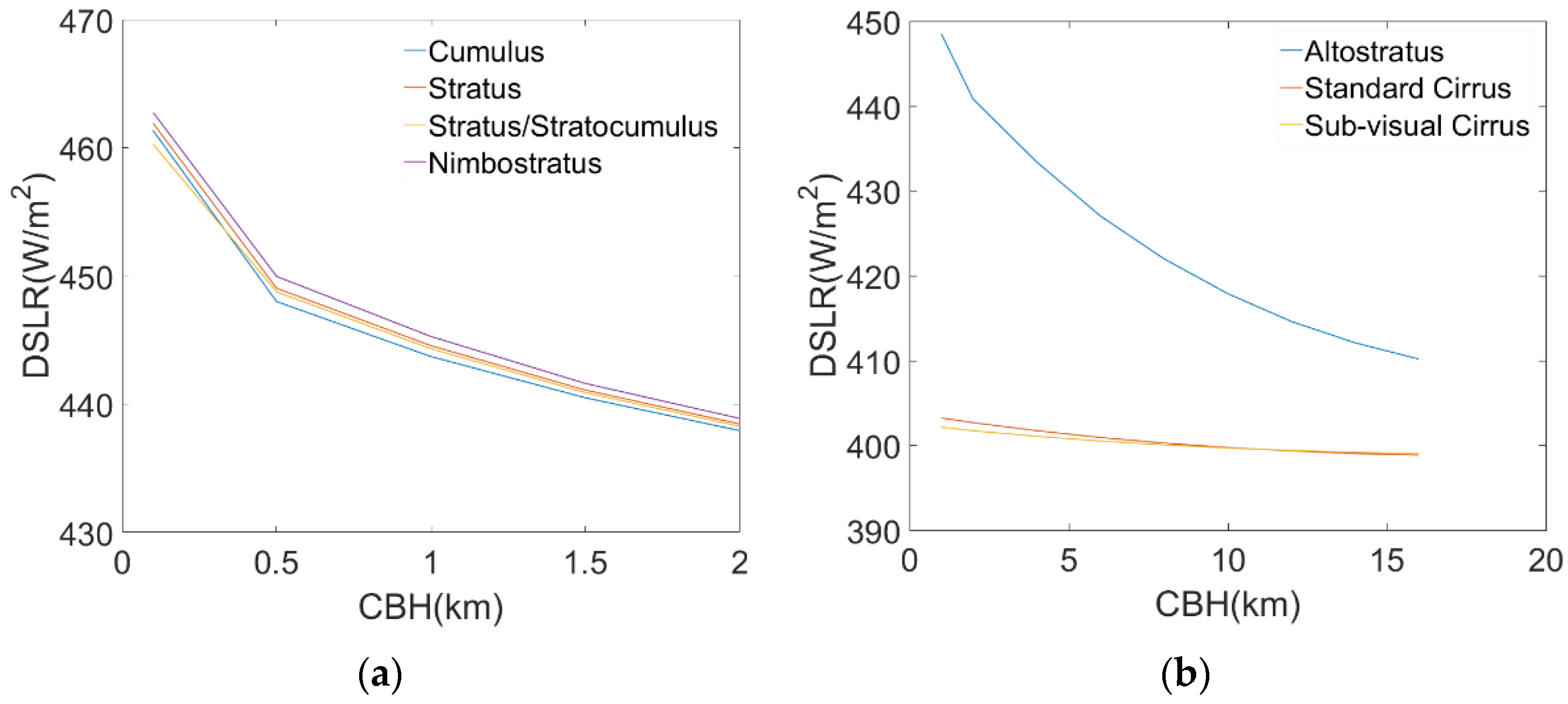
4.2. Sensitivity Analysis
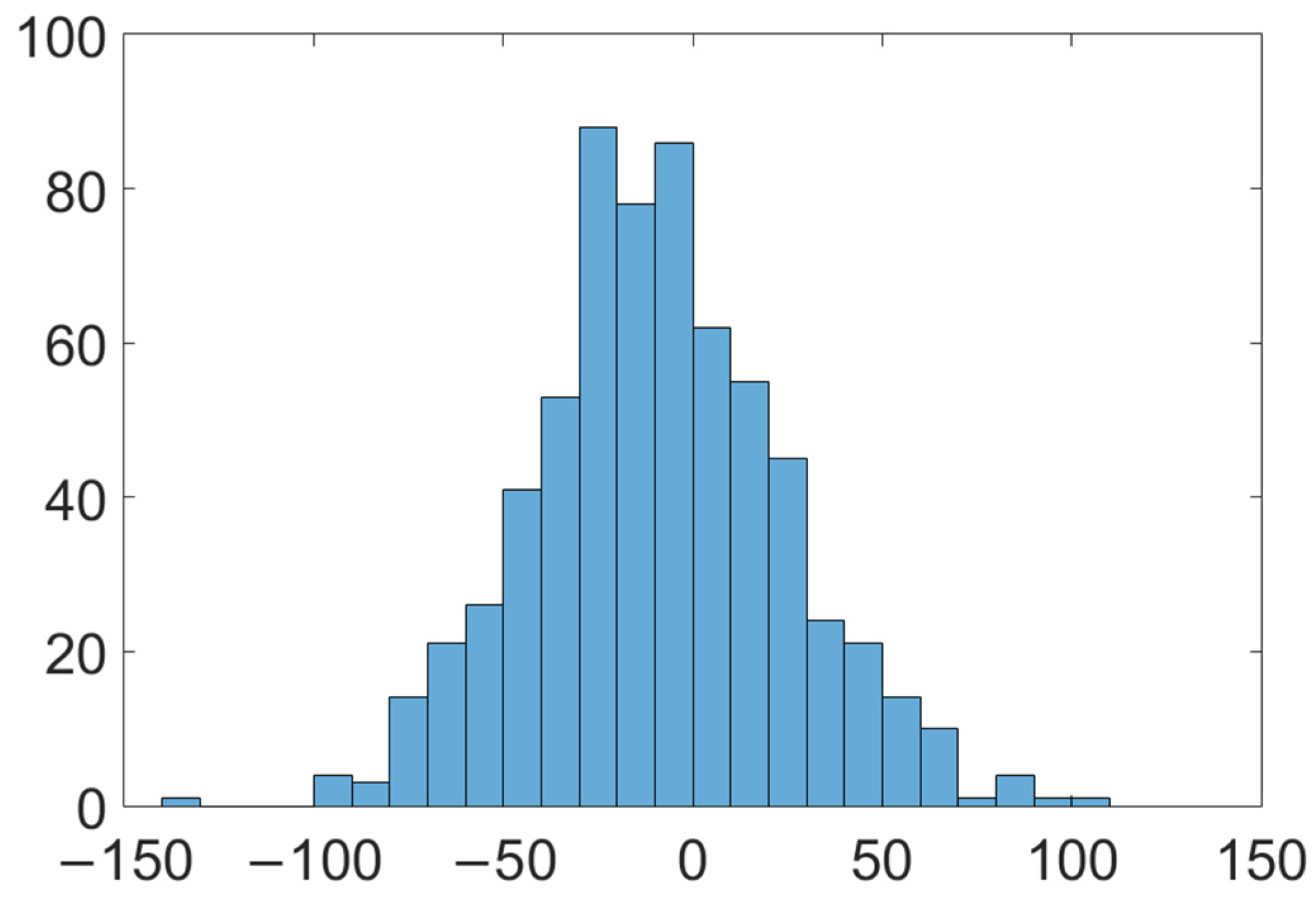
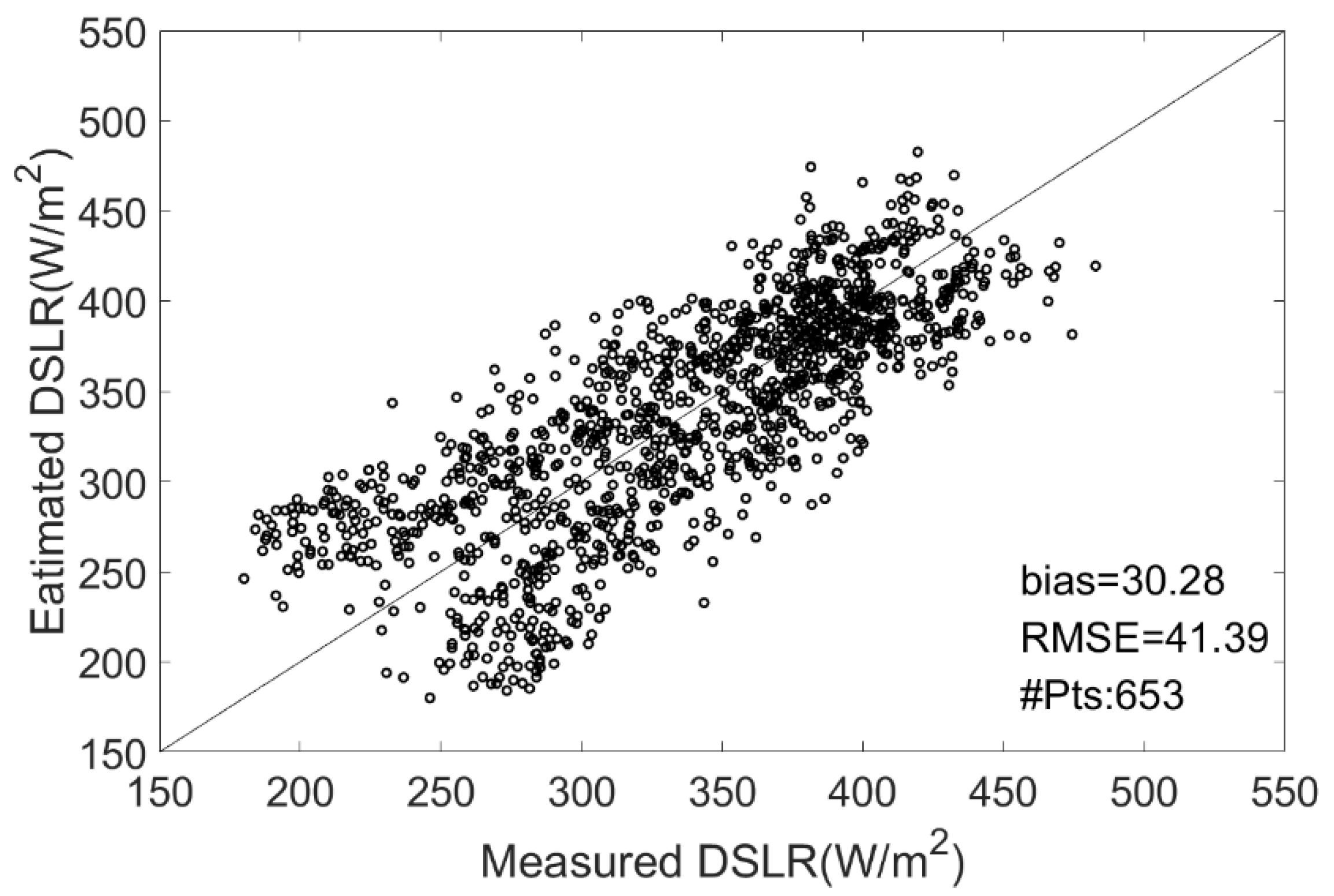
5. Validation
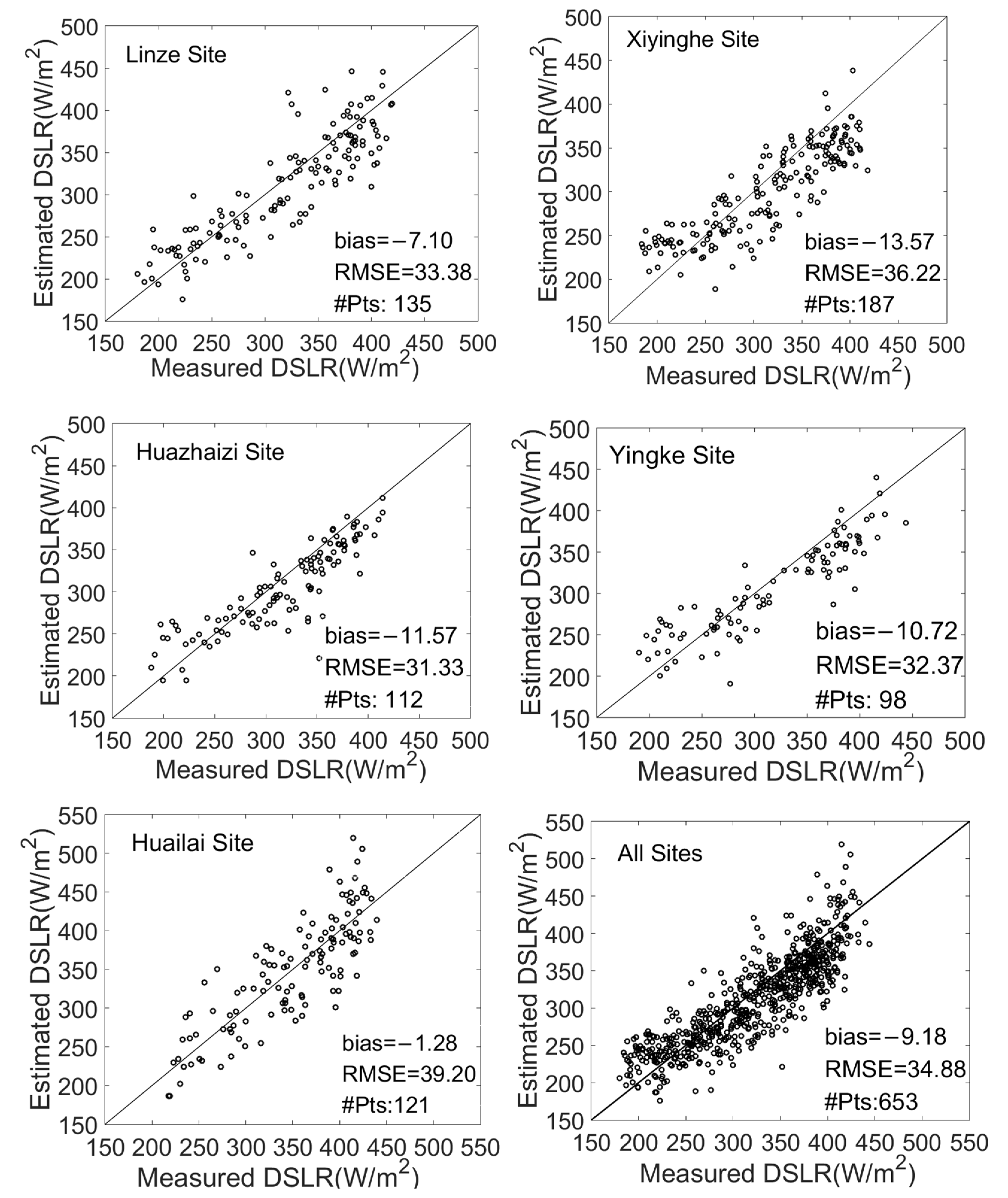
5.1. Validation Using in Situ Measurements
5.2. Comparison with Existing Methods
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deardoff, J.W. Efficient prediction of ground surface temperature and moisture, with inclusion of a layer of vegetation. J. Geophys. Res. Atmos. 1987, 96, 541–550. [Google Scholar]
- Aladosarboledas, I.; Vida, J.; Olmo, F.J. The estimation of thermal atmospheric radiation under cloudy conditions. Int. J. Climatol. 1995, 15, 589. [Google Scholar]
- Crawford, T.M.; Duchon, C.E. An improved parameterization for estimating effective atmospheric emissivity for use in calculating daytime downwelling longwave radiation. J. Appl. Meteorol. 1999, 38, 474–480. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Vacher, J.J.; Rocheteau, A. Estimating downward long-wave radiation on the Andean Altiplano. Agric. For. Meteorol. 2007, 145, 139–148. [Google Scholar] [CrossRef]
- Rooney, G.G. Modelling of downwelling long-wave radiation using cloud fraction obtained from laser cloud-base measurements. Atmos. Sci. Lett. 2005, 6, 160–163. [Google Scholar] [CrossRef]
- Zhong, L.; Zou, M.; Ma, Y.; Huang, Z.; Xu, K.; Wang, X.; Ge, N.; Cheng, M. Estimation of Downwelling Shortwave and Longwave Radiation in the Tibetan Plateau Under All-Sky Conditions. J. Geophys. Res. Atmos. 2019, 124, 11086–11102. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, F.; Guo, Y. A Comparative Study of Bulk Parameterization Schemes for Estimating Cloudy-Sky Surface Downward Longwave Radiation. Remote Sens. 2019, 11, 528. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Zheng, X.; Zhang, J.; Xia, X. A revisiting of the parametrization of downward longwave radiation in summer over the Tibetan Plateau based on high-temporal-resolution measurements. Atmos. Chem. Phys. 2020, 20, 4415–4426. [Google Scholar] [CrossRef] [Green Version]
- Dilley, A.C.; O’Brien, D.M. Estimating downward clear sky long-wave irradiance at the surface from screen temperature and precipitable water. Q. J. R. Meteorol. Soc. 1998, 124, 1391–1401. [Google Scholar] [CrossRef]
- Jacobs, J.D. Radiation Climate of Broughton Island. In Energy Budget Studies in Relation to Fast-Ice Breakup Processes in Davis Strait; Barry, R.G., Jacobs, J.D., Eds.; Occasional Paper No. 26; Institute of Arctic and Alp Research, University of Colorado: Boulder, CO, USA, 1978; pp. 105–120. [Google Scholar]
- Wang, T.; Shi, J.; Yu, Y.; Husi, L.; Gao, B.; Zhou, W.; Ji, D.; Zhao, T.; Xiong, C.; Chen, L. Cloudy-sky land surface longwave downward radiation (LWDR) estimation by integrating MODIS and AIRS/AMSU measurements. Remote Sens. Environ. 2018, 205, 100–111. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J. A framework for estimating cloudy sky surface downward longwave radiation from the derived active and passive cloud property parameters. Remote Sens. Environ. 2020, 248, 111972. [Google Scholar] [CrossRef]
- Ahn, S.-H.; Lee, K.-T.; Rim, S.-H.; Zo, I.-S.; Kim, B.-Y. Surface Downward Longwave Radiation Retrieval Algorithm for GEO-KOMPSAT-2A/AMI. Asia-Pac. J. Atmos. Sci. 2018, 54, 237–251. [Google Scholar] [CrossRef]
- Gupta, S.K.; Darnell, W.L.; Wilber, A.C. A Parameterization for Longwave Surface Radiation from Satellite Data—Recent Improvements. J. Appl. Meteorol. 1992, 31, 1361–1367. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Shi, J.; Ma, Y.; Letu, H.; Li, X. All-sky longwave downward radiation from satellite measurements: General parameterizations based on LST, column water vapor and cloud top temperature. ISPRS J. Photogramm. Remote Sens. 2020, 161, 52–60. [Google Scholar] [CrossRef]
- Savtchenko, A.; Ouzounov, D.; Ahmad, S.; Acker, J.; Leptoukh, G.; Koziana, J.; Nickless, D. Terra and aqua MODIS products available from NASA GES DAAC. Adv. Space Res. 2004, 34, 710–714. [Google Scholar] [CrossRef]
- Wolfe, R.E.; Nishihama, M.; Fleig, A.J.; Kuyper, J.A.; Roy, D.P.; Storey, J.C.; Patt, F.S. Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sens. Environ. 2002, 83, 31–49. [Google Scholar] [CrossRef]
- Xu, T.R.; Liu, S.M.; Xu, L.; Chen, Y.J.; Jia, Z.Z.; Xu, Z.W.; Nielson, J. Temporal Upscaling and Reconstruction of Thermal Remotely Sensed Instantaneous Evapotranspiration. Remote Sens. 2015, 7, 3400–3425. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G. Watershed Allied Telemetry Experimental Research. J. Geophys. Res. Atmos. 2012, 114, 2191–2196. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q.; Ma, M.G.; Liu, Q.H.; Jin, R.; Guo, J.W.; Wang, L.X.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.M.; Xu, Z.W.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Guo, A.L.; Liu, S.M.; Zhu, Z.L.; Xu, Z.W.; Xiao, Q.; Ju, Q.; Zhang, Y.; Yang, X.F. Impact of Lake/Reservoir Expansion and Shrinkage on Energy and Water Vapor Fluxes in the Surrounding Area. J. Geophys. Res. Atmos. 2020, 125, e2020JD032833. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.-L. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ. 2008, 112, 3482–3492. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S. Estimation of high-spatial resolution clear-sky longwave downward and net radiation over land surfaces from MODIS data. Remote Sens. Environ. 2009, 113, 745–754. [Google Scholar] [CrossRef]
- Yan, G.J.; Wang, T.X.; Jiao, Z.H.; Mu, X.H.; Zhao, J.; Chen, L. Topographic radiation modeling and spatial scaling of clear-sky land surface longwave radiation over rugged terrain. Remote Sens. Environ. 2016, 172, 15–27. [Google Scholar] [CrossRef]
- Wang, J.; Tang, B.-H.; Zhang, X.-Y.; Wu, H.; Li, Z.-L. Estimation of Surface Longwave Radiation over the Tibetan Plateau Region Using MODIS Data for Cloud-Free Skies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3695–3703. [Google Scholar] [CrossRef]
- Wang, C.; Tang, B.-H.; Wu, H.; Tang, R.; Li, Z.-L. Estimation of Downwelling Surface Longwave Radiation under Heavy Dust Aerosol Sky. Remote Sens. 2017, 9, 207. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K. Artificial Neural Networks—Methodological Advances and Biomedical Applications; IntechOpen: London, UK, 2011. [Google Scholar]
- Peng, Z.; Letu, H.S.; Wang, T.X.; Shi, C.; Zhao, C.F.; Tana, G.G.; Zhao, N.Z.; Dai, T.; Tang, R.L.; Shang, H.Z.; et al. Estimation of shortwave solar radiation using the artificial neural network from Himawari-8 satellite imagery over China. J. Quant. Spectrosc. Radiat. Transf. 2020, 240, 106672. [Google Scholar] [CrossRef]
- Si, M.L.; Tang, B.H.; Li, Z.L.; Nerry, F.; Zhang, X.; Shang, G.F. An Artificial Neuron Network With Parameterization Scheme for Estimating Net Surface Shortwave Radiation From Satellite Data Under Clear Sky—Application to Simulated GF-5 Data Set. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4262–4272. [Google Scholar] [CrossRef]
- Stephens, G.L.; Wild, M.; Stackhouse, P.W.; L’Ecuyer, T.; Kato, S.; Henderson, D.S. The Global Character of the Flux of Downward Longwave Radiation. J. Clim. 2012, 25, 2329–2340. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.C.; Dickinson, R.E. Global atmospheric downward longwave radiation at the surface from ground-based observations, satellite retrievals, and reanalyses. Rev. Geophys. 2013, 51, 150–185. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Yu, S.; Xin, X.; Liu, Q. Estimation of clear-sky longwave downward radiation from HJ-1B thermal data. Sci. China Earth Sci. 2012, 56, 829–842. [Google Scholar] [CrossRef]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. R. Meteorol. Soc. 1996, 122, 1127–1151. [Google Scholar] [CrossRef]
- Yu, S.; Xin, X.; Liu, Q.; Zhang, H.; Li, L. Comparison of Cloudy-Sky Downward Longwave Radiation Algorithms Using Synthetic Data, Ground-Based Data, and Satellite Data. J. Geophys. Res. Atmos. 2018, 123, 5397–5415. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Josey, S.A.; Pascal, R.W.; Taylor, P.K.; Yelland, M.J. A new formula for determining the atmospheric longwave flux at the ocean surface at mid-high latitudes. J. Geophys. Res. Ocean. 2003, 108, C4. [Google Scholar] [CrossRef]
- Trigo, I.F.; Barroso, C.; Viterbo, P.; Freitas, S.C.; Monteiro, I.T. Estimation of downward long-wave radiation at the surface combining remotely sensed data and NWP data. J. Geophys. Res. Atmos. 2010, 115, D24. [Google Scholar] [CrossRef]
- Schmetz, P.; Schmetz, J.; Raschke, E. Estimation of Daytime Downward Longwave Radiation at The Surface From Satellite And Grid Point Data. Theor. Appl. Climatol. 1986, 37, 136–149. [Google Scholar] [CrossRef]
- Gupta, S.K.; Kratz, D.P.; Stackhouse, P.W.; Wilber, A.C.; Zhang, T.P.; Sothcott, V.E. Improvement of Surface Longwave Flux Algorithms Used in CERES Processing. J. Appl. Meteorol. Climatol. 2010, 49, 1579–1589. [Google Scholar] [CrossRef]
- Diak, G.R.; Bland, W.L.; Mecikalski, J.R.; Anderson, M.C. Satellite-based estimates of longwave radiation for agricultural applications. Agric. For. Meteorol. 2000, 103, 349–355. [Google Scholar] [CrossRef]
- Gao, B.-C.; Kaufman, Y.J. Water vapor retrievals using Moderate Resolution Imaging Spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. Atmos. 2003, 108, 4389. [Google Scholar] [CrossRef]
- Swinbank, W.C. Long-wave Radiation From Clear Skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D. Thermal Radiation From Atmosphere. J. Geophys. Res. 1969, 74, 5397–5403. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s Global Energy Budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Viudez-Mora, A.; Costa-Suros, M.; Calbo, J.; Gonzalez, J.A. Modeling atmospheric longwave radiation at the surface during overcast skies: The role of cloud base height. J. Geophys. Res. Atmos. 2015, 120, 199–214. [Google Scholar] [CrossRef] [Green Version]


| Data Sources | Product | Resolution | Parameters |
|---|---|---|---|
| MODIS | MOD021KM | 1 km | Radiance of bands 28, 29, 31, 33, 34, 36 |
| MOD03 | 1 km | Latitude, Longitude | |
| MOD05 | 1 km | WVC | |
| MOD35 | 1 km | Cloud mask | |
| ERA5 | 0.25° × 0.25° | Cloud base height | |
| 0.25° × 0.25° | Total cloud cover | ||
| 0.25° × 0.25° | 2 m air temperature | ||
| 0.25° × 0.25° | 2 m dew point temperature | ||
| 0.25° × 0.25° | Cloud base temperature |
| Site Name | Lat and Lon (Deg) | Land Cover | Elevation (m) | Temporal Period |
|---|---|---|---|---|
| Yingke | 38.85, 100.4167 | Cropland | 1519 | 2010.01.01–2010.12.31 |
| Huazhaizi | 38.7667, 100.45 | Desert | 1731 | 2010.01.01–2010.12.31 |
| Linze | 39.238, 100.062 | Cropland | 1402 | 2018.01.01–2018.12.31 |
| Xiyinghe | 37.561, 101.855 | Alpine grassland | 3616 | 2018.01.01–2018.12.31 |
| Huailai | 40.3574, 115.7928 | Cropland | 480 | 2017.01.01–2017.12.31 |
| Inputs of GA-ANN | Output of GA-ANN | |
|---|---|---|
| Clear sky | DSLR | |
| Cloudy sky | , CBH | DSLR |
| DSLR Affected by CBH | DSLR Affected by | |||||
|---|---|---|---|---|---|---|
| Max (W/m2) | Min (W/m2) | Difference (W/m2) | Max (W/m2) | Min (W/m2) | Difference (W/m2) | |
| Cumulus | 461.348 | 437.934 | 23.414 | 456.952 | 433.198 | 23.754 |
| Altostratus | 448.52 | 410.177 | 38.343 | 470.913 | 431.144 | 39.769 |
| Stratus | 461.914 | 438.454 | 23.460 | 459.25 | 433.133 | 26.117 |
| Stra-tus/Stratocumulus | 460.272 | 438.273 | 21.999 | 458.555 | 433.44 | 25.115 |
| Nimbostratus | 462.762 | 438.882 | 23.880 | 460.568 | 433.106 | 27.462 |
| Standard cirrus | 403.231 | 398.846 | 4.385 | 400.486 | 400.089 | 0.397 |
| Subvisual cirrus | 402.139 | 399.032 | 3.107 | 400.426 | 399.771 | 0.655 |
| Sites | Bias (W/m2) | RMSE (W/m2) | No. of Points |
|---|---|---|---|
| Huailai | 20.27 | 36.04 | 121 |
| Yingke | 36.82 | 45.62 | 98 |
| Huaizhazi | 30.82 | 40.30 | 112 |
| Linze | 42.64 | 47.33 | 135 |
| Xiyinghe | 24.08 | 38.23 | 187 |
| Algorithms | Model | Bias (W/m2) | RMSE (W/m2) |
|---|---|---|---|
| This study | GA-ANN | −9.18 | 34.88 |
| Yu et al. [38] | Empirical Algorithms Based on Cloud Fraction (Crawford and Duchon [3]) | 35.8 | 52.6 |
| Empirical Algorithms Based on Cloud Fraction (Iziomon et al. [39]) | 6.4 | 40.4 | |
| Empirical Algorithms Based on Cloud Fraction (Josey et al. [40]) | −34.4 | 48.4 | |
| Empirical Algorithms Based on Cloud Fraction (Trigo et al. [41]) | 3.3 | 32.3 | |
| Single-Layer Cloud Model (Schmetz et al. [42]) | 21.7 | 42.5 | |
| Single-Layer Cloud Model (Gupta et al. [43]) | 15.9 | 33.3 | |
| Single-Layer Cloud Model (Diak et al. [44]) | 24.3 | 41.8 | |
| Wang et al. [11] | Single-Layer Cloud Model | −7.7 | 32.8 |
| Yang and Cheng [12] | Single-Layer Cloud Model | 5.42 | 30.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Tang, B.-H.; Zhao, Y. Estimation of Downwelling Surface Longwave Radiation with the Combination of Parameterization and Artificial Neural Network from Remotely Sensed Data for Cloudy Sky Conditions. Remote Sens. 2022, 14, 2716. https://doi.org/10.3390/rs14112716
Jiang Y, Tang B-H, Zhao Y. Estimation of Downwelling Surface Longwave Radiation with the Combination of Parameterization and Artificial Neural Network from Remotely Sensed Data for Cloudy Sky Conditions. Remote Sensing. 2022; 14(11):2716. https://doi.org/10.3390/rs14112716
Chicago/Turabian StyleJiang, Yun, Bo-Hui Tang, and Yanhong Zhao. 2022. "Estimation of Downwelling Surface Longwave Radiation with the Combination of Parameterization and Artificial Neural Network from Remotely Sensed Data for Cloudy Sky Conditions" Remote Sensing 14, no. 11: 2716. https://doi.org/10.3390/rs14112716
APA StyleJiang, Y., Tang, B.-H., & Zhao, Y. (2022). Estimation of Downwelling Surface Longwave Radiation with the Combination of Parameterization and Artificial Neural Network from Remotely Sensed Data for Cloudy Sky Conditions. Remote Sensing, 14(11), 2716. https://doi.org/10.3390/rs14112716







