Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation
Abstract
:1. Introduction
2. Methodology
2.1. Observations and Reanalysis
2.2. Models
2.3. Evaluation Metrics
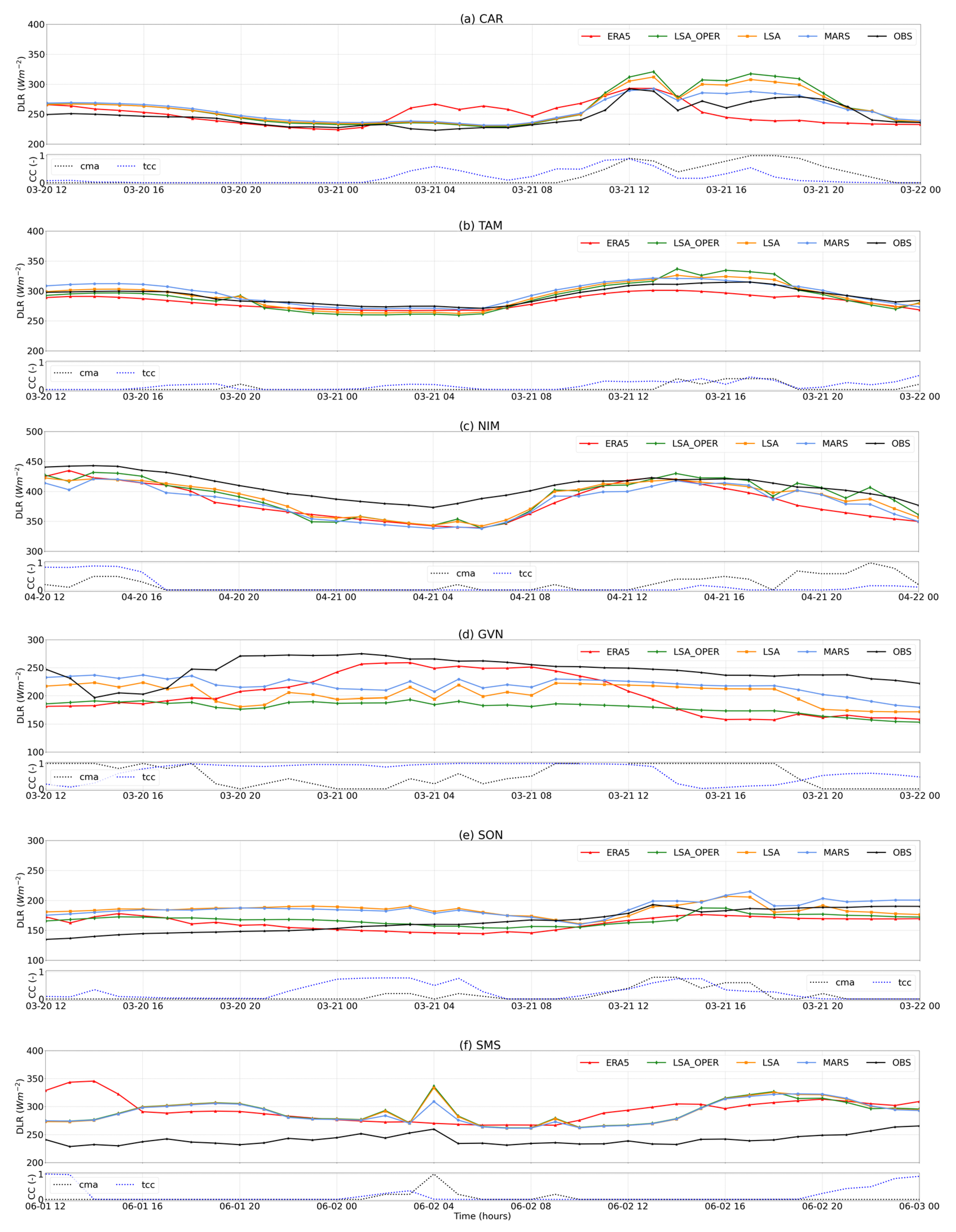
3. Results
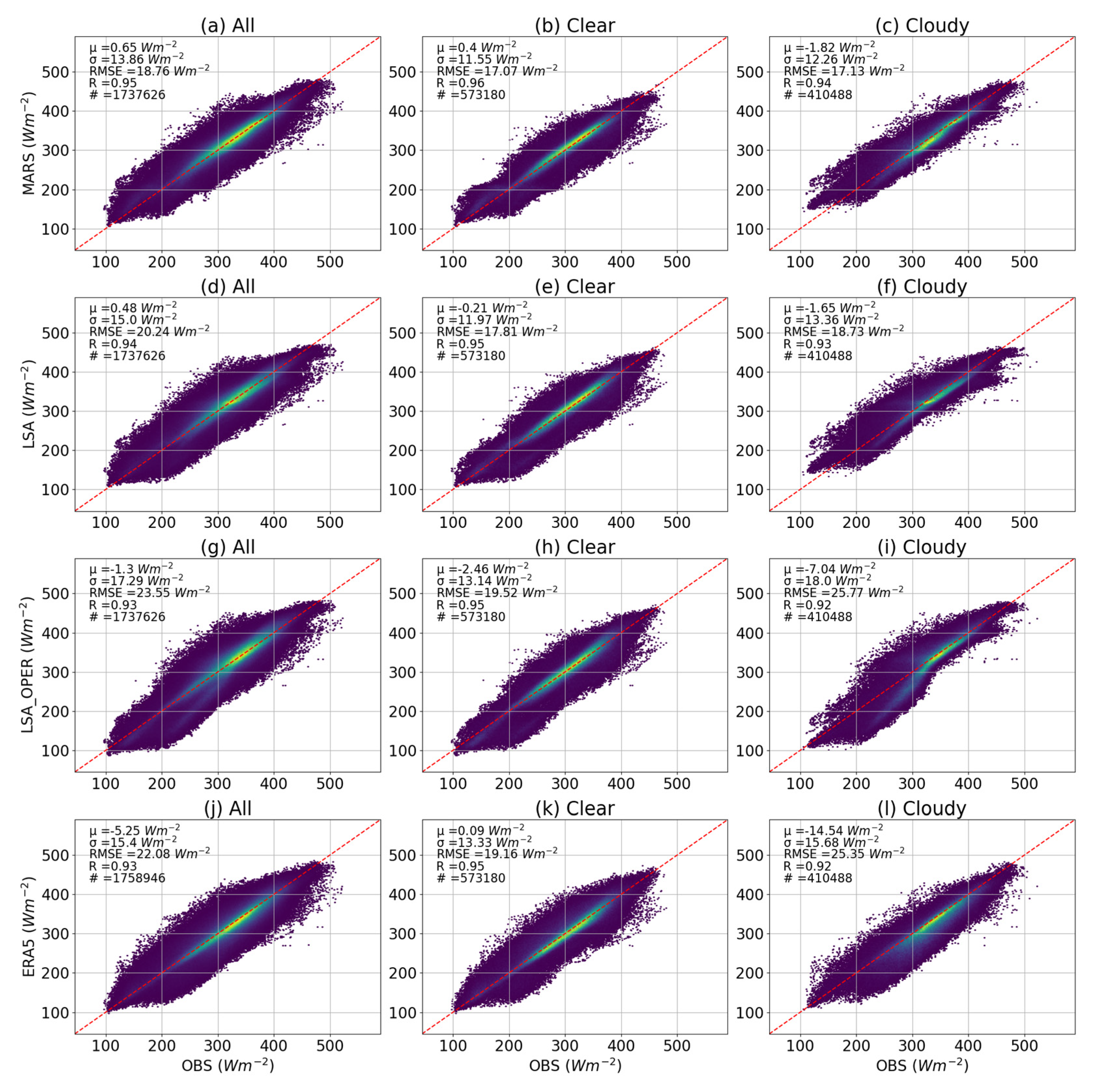
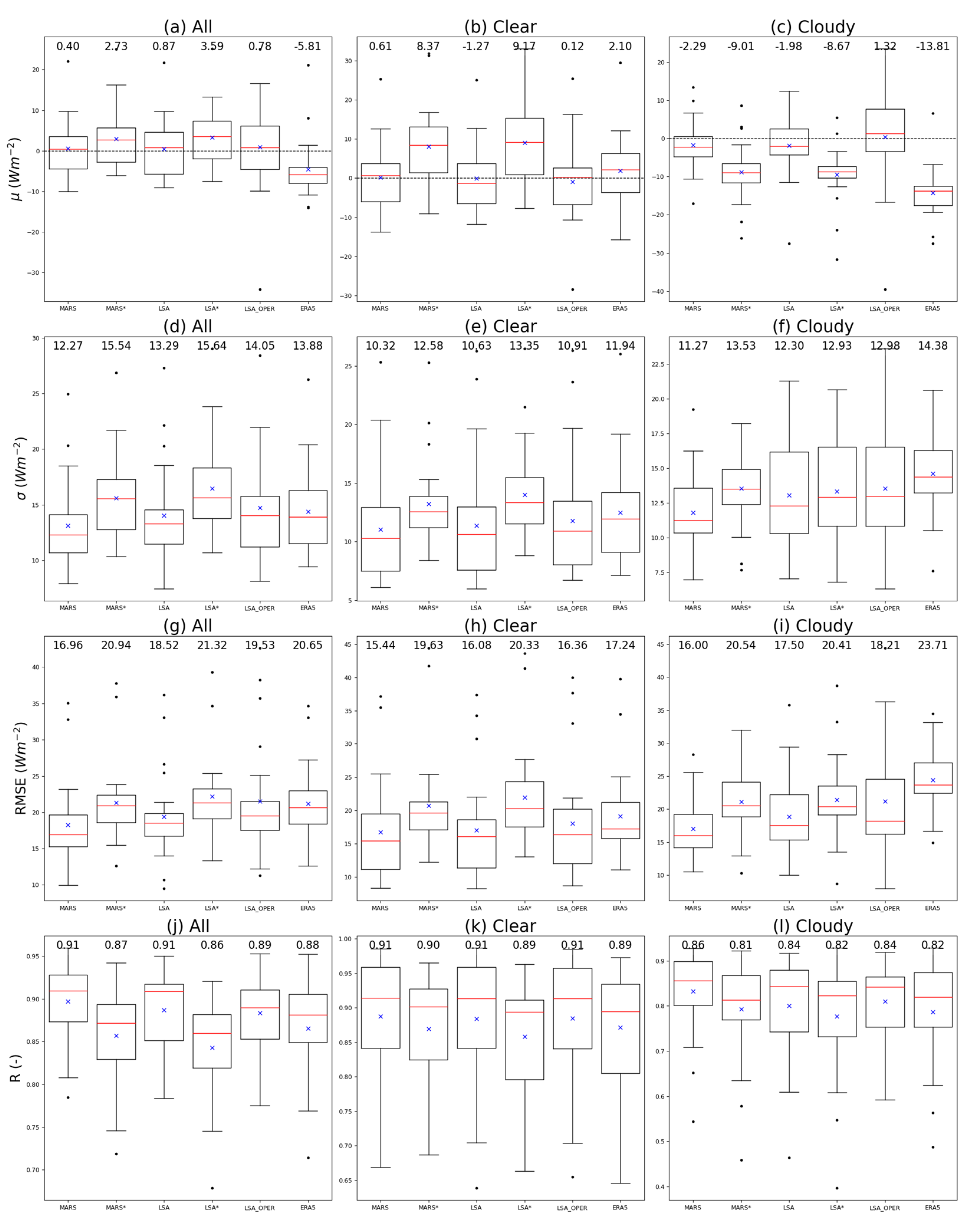
3.1. Model Evaluation
3.2. Impact of Satellite Information
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. LSA-SAF Algorithm
| Clear-Sky | Cloudy-Sky | |||||||
|---|---|---|---|---|---|---|---|---|
| Profiles | α | β | γ | δ | α | β | γ | δ |
| Dry Cold | 0.653 | 4.796 | 1.253 | −0.739 | 0.968 | 2.257 | −0.236 | −0.877 |
| Dry Warm | 0.704 | 3.720 | 1.655 | −0.151 | 3.446 | 0.369 | 0.278 | −0.443 |
| Moist | 0.587 | 3.344 | 1.686 | −0.203 | 3.446 | 0.369 | 0.278 | −0.443 |
| Clear-Sky | Cloudy-Sky | |||||||
|---|---|---|---|---|---|---|---|---|
| Profiles | α | β | γ | δ | α | β | γ | δ |
| Dry Cold | 2.289 | 4.992 | −2.368 | −1.129 | 1.804 | 3.026 | 0.436 | −0.991 |
| Dry Warm | 0.865 | 3.701 | 0.532 | −0.135 | 3.229 | 0.324 | 0.737 | −0.562 |
| Moist | 1.466 | 3.051 | 0.5709 | −0.187 | 3.229 | 0.324 | 0.737 | −0.562 |
Appendix B. Models Training
| Training (#31820) | Verification (#541360) | |||
|---|---|---|---|---|
| Models | Bias | RMSE | Bias | RMSE |
| LSA | 0.24 | 20.41 | −0.27 | 18.99 |
| MARS | −0.00 | 19.71 | 0.12 | 18.00 |
| Training (#19566) | Verification (#390922) | |||
|---|---|---|---|---|
| Models | Bias | RMSE | Bias | RMSE |
| LSA | 1.20 | 21.71 | −1.06 | 19.95 |
| MARS | −0.00 | 19.36 | −1.55 | 18.19 |
Appendix C. Evaluation Detailed Results
| µ | RMSE | R | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 |
| BRB | 5.72 | 5.77 | 10.33 | 1.46 | 9.36 | 10.10 | 10.84 | 11.22 | 13.26 | 14.03 | 17.09 | 14.99 | 0.92 | 0.91 | 0.91 | 0.88 |
| BUD | 0.40 | 1.14 | 6.66 | −1.80 | 7.93 | 7.44 | 8.13 | 9.42 | 9.98 | 9.49 | 12.22 | 12.61 | 0.91 | 0.92 | 0.91 | 0.86 |
| CAB | −0.41 | −0.39 | 0.00 | −7.09 | 11.84 | 13.29 | 13.65 | 13.96 | 15.60 | 17.33 | 17.99 | 20.65 | 0.93 | 0.91 | 0.91 | 0.89 |
| CAM | 0.44 | 0.87 | 2.79 | −4.58 | 15.38 | 16.61 | 15.88 | 16.96 | 19.87 | 21.39 | 21.03 | 23.33 | 0.87 | 0.85 | 0.85 | 0.82 |
| CAR | 3.60 | 4.09 | 5.86 | −8.04 | 9.74 | 10.60 | 11.09 | 11.38 | 13.57 | 14.89 | 15.98 | 17.89 | 0.96 | 0.95 | 0.95 | 0.94 |
| CNR | 0.34 | 3.96 | 4.75 | −0.11 | 12.84 | 13.43 | 14.22 | 15.83 | 16.88 | 18.52 | 20.01 | 21.07 | 0.91 | 0.90 | 0.89 | 0.86 |
| DAA | 5.71 | 5.45 | 6.38 | −4.24 | 11.62 | 12.69 | 12.77 | 10.46 | 16.27 | 17.44 | 18.07 | 16.28 | 0.94 | 0.93 | 0.93 | 0.93 |
| ENA | −8.78 | −7.89 | −3.89 | −6.24 | 14.35 | 14.34 | 13.96 | 16.78 | 20.12 | 20.15 | 19.07 | 22.69 | 0.84 | 0.84 | 0.83 | 0.77 |
| FLO | −6.96 | −7.09 | −1.79 | −7.28 | 10.80 | 10.95 | 11.00 | 12.43 | 15.73 | 15.92 | 14.73 | 18.14 | 0.91 | 0.91 | 0.91 | 0.88 |
| GAN | 3.52 | 5.90 | 14.38 | −9.07 | 15.18 | 18.55 | 18.99 | 13.87 | 21.77 | 25.44 | 29.06 | 22.53 | 0.90 | 0.87 | 0.86 | 0.91 |
| GOB | −7.61 | −6.99 | −6.68 | −8.86 | 11.35 | 12.17 | 12.72 | 11.62 | 18.72 | 19.07 | 19.53 | 19.54 | 0.88 | 0.88 | 0.88 | 0.88 |
| GVN | −1.70 | −7.07 | −34.06 | −10.88 | 18.49 | 20.28 | 21.99 | 18.75 | 23.23 | 26.68 | 42.63 | 27.26 | 0.88 | 0.85 | 0.85 | 0.86 |
| NIM | −9.96 | −9.00 | −4.59 | −13.84 | 11.88 | 12.01 | 14.58 | 14.63 | 18.48 | 18.04 | 18.72 | 23.71 | 0.93 | 0.94 | 0.94 | 0.92 |
| LIN | 3.59 | 2.38 | 0.78 | −3.88 | 12.76 | 14.03 | 15.68 | 13.88 | 16.96 | 18.14 | 20.34 | 20.05 | 0.93 | 0.91 | 0.90 | 0.90 |
| PAL | 0.69 | 0.14 | 0.77 | −4.62 | 12.27 | 13.43 | 14.05 | 14.20 | 16.19 | 17.49 | 18.60 | 20.87 | 0.92 | 0.91 | 0.90 | 0.88 |
| PAR | −1.20 | −3.02 | 4.90 | −4.58 | 9.09 | 8.34 | 8.28 | 10.38 | 11.29 | 10.72 | 11.30 | 13.45 | 0.78 | 0.82 | 0.83 | 0.71 |
| PAY | 0.60 | 5.22 | 2.72 | −6.25 | 13.02 | 13.18 | 15.58 | 17.01 | 17.24 | 18.67 | 22.06 | 23.97 | 0.92 | 0.91 | 0.89 | 0.85 |
| PTR | 7.89 | 9.75 | 16.61 | 8.06 | 9.79 | 10.17 | 10.15 | 12.87 | 14.87 | 16.21 | 21.04 | 18.69 | 0.86 | 0.85 | 0.86 | 0.77 |
| SBO | −6.85 | −4.39 | −4.37 | −5.81 | 13.82 | 14.13 | 14.90 | 13.71 | 19.44 | 19.66 | 20.70 | 19.52 | 0.88 | 0.87 | 0.85 | 0.88 |
| SMS | 22.07 | 21.70 | 25.10 | 21.12 | 20.34 | 22.17 | 21.93 | 20.40 | 35.04 | 36.19 | 38.23 | 34.65 | 0.85 | 0.83 | 0.83 | 0.85 |
| SON | 9.73 | 1.81 | −9.88 | −5.08 | 24.98 | 27.29 | 28.44 | 26.26 | 32.76 | 33.03 | 35.67 | 33.05 | 0.81 | 0.78 | 0.78 | 0.79 |
| TAM | −6.15 | −8.79 | −6.82 | −14.05 | 10.55 | 12.64 | 11.33 | 10.41 | 14.95 | 18.62 | 16.14 | 20.36 | 0.96 | 0.94 | 0.95 | 0.95 |
| TOR | −2.67 | −2.30 | −8.38 | −7.80 | 13.91 | 14.73 | 18.50 | 14.38 | 18.39 | 19.35 | 25.14 | 21.86 | 0.93 | 0.92 | 0.90 | 0.91 |
| µ | RMSE | R | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 |
| BRB | 4.29 | 5.41 | 5.03 | 5.36 | 6.81 | 7.45 | 8.49 | 8.05 | 9.84 | 11.00 | 11.91 | 12.22 | 0.91 | 0.91 | 0.90 | 0.89 |
| BUD | −4.58 | −2.89 | 0.89 | −1.71 | 6.12 | 6.46 | 6.89 | 7.79 | 8.92 | 8.48 | 8.71 | 11.06 | 0.94 | 0.94 | 0.94 | 0.89 |
| CAB | −1.45 | −1.53 | −2.19 | 2.10 | 6.47 | 6.54 | 6.85 | 12.02 | 9.52 | 9.77 | 10.15 | 16.40 | 0.97 | 0.97 | 0.97 | 0.92 |
| CAM | 3.44 | 2.32 | 1.88 | 8.64 | 12.99 | 13.11 | 13.20 | 14.97 | 19.02 | 19.03 | 18.99 | 22.86 | 0.84 | 0.83 | 0.83 | 0.80 |
| CAR | 2.27 | 2.68 | 2.23 | −3.58 | 6.19 | 5.99 | 6.73 | 7.99 | 8.31 | 8.24 | 8.96 | 11.61 | 0.99 | 0.99 | 0.98 | 0.97 |
| CNR | 1.58 | 1.96 | 1.27 | 10.87 | 8.55 | 8.62 | 8.97 | 11.63 | 12.49 | 12.71 | 12.98 | 18.88 | 0.96 | 0.96 | 0.96 | 0.93 |
| DAA | 6.10 | 5.01 | 3.14 | −2.00 | 10.80 | 11.11 | 11.18 | 7.69 | 15.44 | 15.34 | 14.97 | 12.55 | 0.93 | 0.93 | 0.93 | 0.94 |
| ENA | −9.59 | −10.46 | −8.86 | 2.51 | 15.21 | 15.40 | 15.02 | 15.77 | 21.49 | 22.05 | 21.12 | 21.00 | 0.83 | 0.83 | 0.83 | 0.79 |
| FLO | −7.48 | −7.56 | −5.23 | −0.83 | 10.82 | 10.80 | 11.22 | 12.89 | 16.74 | 16.82 | 16.36 | 16.93 | 0.91 | 0.91 | 0.91 | 0.89 |
| GAN | −9.00 | −6.89 | −5.11 | −7.03 | 13.76 | 14.28 | 15.30 | 14.54 | 21.73 | 21.45 | 21.87 | 21.50 | 0.86 | 0.86 | 0.86 | 0.86 |
| GOB | −7.55 | −6.56 | −7.70 | −7.22 | 10.32 | 11.16 | 11.90 | 10.15 | 17.87 | 18.20 | 19.14 | 17.24 | 0.88 | 0.87 | 0.87 | 0.89 |
| GVN | −2.98 | −11.82 | −28.34 | −6.23 | 20.37 | 23.89 | 23.62 | 17.12 | 25.50 | 30.77 | 40.02 | 25.13 | 0.73 | 0.64 | 0.65 | 0.75 |
| NIM | −13.80 | −10.86 | −10.66 | −15.68 | 10.83 | 10.99 | 13.70 | 12.90 | 19.94 | 18.11 | 20.50 | 23.45 | 0.94 | 0.95 | 0.95 | 0.93 |
| LIN | 4.05 | 4.10 | 2.93 | 6.48 | 6.86 | 7.01 | 6.95 | 10.75 | 10.68 | 10.92 | 10.46 | 16.54 | 0.98 | 0.98 | 0.98 | 0.95 |
| PAL | 0.61 | 0.36 | −0.22 | 3.02 | 7.72 | 7.91 | 8.05 | 11.94 | 11.50 | 11.74 | 11.94 | 17.16 | 0.96 | 0.96 | 0.96 | 0.92 |
| PAR | 1.53 | −1.27 | 6.95 | 4.78 | 8.12 | 6.94 | 7.22 | 8.07 | 10.92 | 9.86 | 12.16 | 11.60 | 0.67 | 0.70 | 0.70 | 0.65 |
| PAY | 2.96 | 3.34 | 2.17 | 6.17 | 7.98 | 7.87 | 8.05 | 13.92 | 13.10 | 13.11 | 13.03 | 19.67 | 0.96 | 0.96 | 0.96 | 0.91 |
| PTR | 8.74 | 12.74 | 16.27 | 12.14 | 7.34 | 7.70 | 8.48 | 11.04 | 13.41 | 16.68 | 19.92 | 18.84 | 0.85 | 0.85 | 0.85 | 0.78 |
| SBO | −7.54 | −6.36 | −7.90 | −3.65 | 12.86 | 12.83 | 13.26 | 11.92 | 18.61 | 18.30 | 19.20 | 17.19 | 0.90 | 0.90 | 0.89 | 0.91 |
| SMS | 25.26 | 24.99 | 25.40 | 29.40 | 19.07 | 19.65 | 19.67 | 19.20 | 37.13 | 37.40 | 37.64 | 39.75 | 0.79 | 0.78 | 0.79 | 0.81 |
| SON | 12.64 | 8.16 | 0.12 | 9.71 | 25.32 | 26.27 | 26.30 | 26.00 | 35.46 | 34.25 | 33.05 | 34.50 | 0.71 | 0.71 | 0.72 | 0.74 |
| TAM | −2.67 | −4.41 | −7.61 | −11.25 | 8.53 | 8.93 | 9.33 | 7.14 | 11.43 | 12.17 | 14.15 | 15.20 | 0.96 | 0.96 | 0.96 | 0.97 |
| TOR | −2.22 | −2.36 | −5.75 | 1.69 | 10.64 | 10.63 | 10.91 | 13.48 | 16.22 | 16.08 | 17.27 | 19.24 | 0.95 | 0.95 | 0.96 | 0.94 |
| µ | RMSE | R | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 | MARS | LSA | LSA_OPER | ERA5 |
| BRB | 3.30 | 1.59 | 9.20 | −9.94 | 8.37 | 9.04 | 9.33 | 11.73 | 11.44 | 12.08 | 15.33 | 17.96 | 0.71 | 0.64 | 0.62 | 0.62 |
| BUD | 5.35 | 4.01 | 11.75 | −6.80 | 7.96 | 7.30 | 7.03 | 10.53 | 11.33 | 10.00 | 14.66 | 14.86 | 0.83 | 0.83 | 0.84 | 0.63 |
| CAB | −2.74 | −2.99 | −3.17 | −15.53 | 10.19 | 11.57 | 12.34 | 13.88 | 14.12 | 15.97 | 17.61 | 23.71 | 0.90 | 0.88 | 0.87 | 0.87 |
| CAM | −0.65 | 0.19 | 2.94 | −13.56 | 12.36 | 13.67 | 12.98 | 15.42 | 17.20 | 18.85 | 18.17 | 24.27 | 0.84 | 0.83 | 0.83 | 0.83 |
| CAR | 1.09 | 0.67 | 4.45 | −17.54 | 11.11 | 12.78 | 12.65 | 14.36 | 15.38 | 17.50 | 18.16 | 25.45 | 0.90 | 0.87 | 0.86 | 0.87 |
| CNR | −2.92 | 3.69 | 4.49 | −12.52 | 11.33 | 12.5 | 13.70 | 15.38 | 15.80 | 17.54 | 20.34 | 23.32 | 0.86 | 0.83 | 0.81 | 0.83 |
| DAA | −0.10 | 0.08 | 8.82 | −17.90 | 13.54 | 17.71 | 16.71 | 15.34 | 18.20 | 23.23 | 23.57 | 26.65 | 0.90 | 0.85 | 0.86 | 0.89 |
| ENA | −10.56 | −7.51 | −0.98 | −17.58 | 10.98 | 9.55 | 9.61 | 14.11 | 17.84 | 15.21 | 13.36 | 25.28 | 0.81 | 0.84 | 0.84 | 0.75 |
| FLO | −7.35 | −8.22 | −1.46 | −13.58 | 8.25 | 7.53 | 7.49 | 10.73 | 12.82 | 12.78 | 9.86 | 19.42 | 0.86 | 0.88 | 0.88 | 0.81 |
| GAN | 6.77 | 12.47 | 23.50 | −12.51 | 14.42 | 20.12 | 19.22 | 13.12 | 21.07 | 28.25 | 33.82 | 22.67 | 0.93 | 0.92 | 0.92 | 0.93 |
| GOB | −9.19 | −11.47 | −1.60 | −25.76 | 13.65 | 12.30 | 12.05 | 16.55 | 19.73 | 21.17 | 17.07 | 33.16 | 0.84 | 0.83 | 0.84 | 0.82 |
| GVN | −2.29 | −4.06 | −39.48 | −17.53 | 14.04 | 14.65 | 16.32 | 20.61 | 18.76 | 19.76 | 44.43 | 31.10 | 0.86 | 0.85 | 0.85 | 0.77 |
| NIM | −0.76 | −4.19 | 6.61 | −11.05 | 11.78 | 14.27 | 12.31 | 16.87 | 16.00 | 19.23 | 17.45 | 24.68 | 0.79 | 0.67 | 0.73 | 0.70 |
| LIN | −0.27 | −1.98 | −6.62 | −12.94 | 11.15 | 11.91 | 14.79 | 13.53 | 15.18 | 16.54 | 21.41 | 22.27 | 0.90 | 0.89 | 0.87 | 0.88 |
| PAL | −2.19 | −3.03 | −3.53 | −13.81 | 10.50 | 11.09 | 12.60 | 14.38 | 14.26 | 15.52 | 18.21 | 23.39 | 0.90 | 0.88 | 0.86 | 0.86 |
| PAR | −5.96 | −5.65 | 1.32 | −13.61 | 6.99 | 7.05 | 6.34 | 7.60 | 10.48 | 10.38 | 7.93 | 16.66 | 0.54 | 0.46 | 0.59 | 0.49 |
| PAY | −4.00 | 3.42 | −2.22 | −16.68 | 11.07 | 11.75 | 16.22 | 16.95 | 16.13 | 16.88 | 23.52 | 27.53 | 0.89 | 0.88 | 0.85 | 0.83 |
| PTR | −3.92 | −3.20 | 6.48 | −7.99 | 8.84 | 8.19 | 7.77 | 12.73 | 12.04 | 11.14 | 12.06 | 18.07 | 0.65 | 0.61 | 0.66 | 0.56 |
| SBO | −4.71 | 4.08 | 11.83 | −19.26 | 15.42 | 18.68 | 18.15 | 16.46 | 20.48 | 24.02 | 25.58 | 28.74 | 0.83 | 0.75 | 0.77 | 0.80 |
| SMS | 13.41 | 10.98 | 16.51 | 6.54 | 16.26 | 17.80 | 18.12 | 16.11 | 25.61 | 26.29 | 29.20 | 23.01 | 0.78 | 0.73 | 0.73 | 0.81 |
| SON | 9.83 | −0.99 | −16.69 | −15.14 | 19.23 | 21.27 | 23.62 | 20.31 | 28.30 | 29.40 | 36.30 | 31.49 | 0.77 | 0.70 | 0.73 | 0.76 |
| TAM | −17.03 | −27.47 | −9.71 | −27.56 | 13.16 | 17.99 | 15.31 | 15.86 | 23.98 | 35.80 | 22.34 | 34.43 | 0.93 | 0.88 | 0.91 | 0.89 |
| TOR | −4.93 | −4.37 | −13.86 | −14.48 | 11.27 | 11.7 | 16.83 | 13.37 | 15.89 | 16.67 | 26.48 | 23.21 | 0.92 | 0.90 | 0.89 | 0.89 |
Appendix D. FLUXNET2015 Validation
| Station | Acronym | Location | Latitude and Longitude (°) | Elev. (m) | Avail. (Years) | Annual DLR (W·m−2) |
|---|---|---|---|---|---|---|
| Neustift | AT-Neu | Austria | 47.12°N; 11.32°E | 970 | 6.96 | 288.86 |
| Brasschaat | BE-Bra | Belgium | 51.31°N; 4.52°E | 16 | 7.33 | 322.16 |
| Lonzee | BE-Lon | Belgium | 50.55°N; 4.75°E | 167 | 7.38 | 320.71 |
| Chamau | CH-Cha | Switzerland | 47.21°N; 8.41°E | 393 | 9.29 | 321.45 |
| Davos | CH-Dav | Switzerland | 46.82°N; 9.86°E | 1639 | 7.70 | 273.69 |
| Früebüel | CH-Fru | Switzerland | 47.12°N; 8.54°E | 982 | 8.80 | 306.25 |
| Laegern | CH-Lae | Switzerland | 47.48°N; 8.36°E | 689 | 9.25 | 304.40 |
| Oensingen grassland | CH-Oe1 | Switzerland | 47.29°N; 7.73°E | 450 | 4.87 | 326.28 |
| Oensingen crop | CH-Oe2 | Switzerland | 47.29°N; 7.73°E | 452 | 10.66 | 326.24 |
| Bily Kriz forest | CZ-BK1 | Czech Republic | 49.50°N; 18.54°E | 875 | 7.23 | 313.66 |
| Bily Kriz grassland | CZ-BK2 | Czech Republic | 49.49°N; 18.54°E | 855 | 5.32 | 313.12 |
| Trebon | CZ-wet | Czech Republic | 49.03°N; 14.77°E | 426 | 7.82 | 322.84 |
| Anklam | DE-Akm | Germany | 53.87°N; 13.68°E | −1 | 4.52 | 320.87 |
| Gebesee | DE-Geb | Germany | 51.10°N; 10.92°E | 162 | 11.00 | 307.30 |
| Grillenburg | DE-Gri | Germany | 50.95°N; 13.51°E | 385 | 8.07 | 311.01 |
| Hainich | DE-Hai | Germany | 51.08°N; 10.45°E | 430 | 8.84 | 310.49 |
| Klingenberg | DE-Kli | Germany | 50.89°N; 13.52°E | 478 | 10.58 | 303.74 |
| Lackenberg | DE-Lkb | Germany | 49.10°N; 13.31°E | 1308 | 3.60 | 296.89 |
| Leinefelde | DE-Lnf | Germany | 51.33°N; 10.37°E | 451 | 5.96 | 306.42 |
| Oberbärenburg | DE-Obe | Germany | 50.79°N; 13.72°E | 734 | 6.90 | 301.53 |
| Rollesbroich | DE-RuR | Germany | 50.62°N; 6.30°E | 515 | 3.48 | 318.72 |
| Selhausen Juelich | DE-RuS | Germany | 50.87°N; 6.45°E | 103 | 2.65 | 330.62 |
| Schechenfilz Nord | DE-SfN | Germany | 47.81°N; 11.33°E | 590 | 2.44 | 323.40 |
| Spreewald | DE-Spw | Germany | 51.89°N; 14.03°E | 61 | 4.33 | 322.56 |
| Tharandt | DE-Tha | Germany | 50.96°N; 13.57°E | 385 | 10.74 | 311.30 |
| Zarnekow | DE-Zrk | Germany | 53.88°N; 12.89°E | 0 | 1.61 | 328.96 |
| Soroe | DK-Sor | Denmark | 55.49°N; 11.65°E | 40 | 6.81 | 314.17 |
| Hyytiala | FI-Hyy | Finland | 61.85°N; 24.30°E | 181 | 4.25 | 306.04 |
| Lompolojankka | FI-Lom | Finland | 67.99°N; 24.21°E | 274 | 2.93 | 282.32 |
| Grignon | FR-Gri | France | 48.84°N; 1.95°E | 125 | 10.80 | 328.80 |
| Le Bray | FR-LBr | France | 44.72°N; 0.77°W | 61 | 5.01 | 333.98 |
| Puechabon | FR-Pue | France | 43.74°N; 3.60°E | 270 | 9.11 | 318.07 |
| Guyaflux | GF-Guy | French Guiana | 5.28°N; 52.93°W | 48 | 2.00 | 411.47 |
| Ankasa | GH-Ank | Gana | 5.27°N; 2.69°W | 124 | 2.00 | 405.94 |
| Borgo Cioffi | IT-BCi | Italy | 40.52°N; 14.96°E | 20 | 4.12 | 331.83 |
| Castel d’Asso1 | IT-CA1 | Italy | 42.38°N; 12.03°E | 200 | 3.35 | 341.22 |
| Castel d’Asso2 | IT-CA2 | Italy | 42.38°N; 12.03°E | 200 | 2.59 | 345.66 |
| Castel d’Asso3 | IT-CA3 | Italy | 42.38°N; 12.02°E | 197 | 2.90 | 339.64 |
| Collelongo | IT-Col | Italy | 41.85°N; 13.59°E | 1560 | 7.35 | 280.26 |
| Ispra ABC-IS | IT-Isp | Italy | 45.81°N; 8.63°E | 210 | 2.00 | 335.75 |
| Lavarone | IT-Lav | Italy | 45.96°N; 11.28°E | 1353 | 10.43 | 289.81 |
| Monte Bondone | IT-MBo | Italy | 46.02°N; 11.05°E | 1550 | 8.97 | 282.15 |
| Arca di Noe | IT-Noe | Italy | 40.61°N; 8.15°E | 25 | 9.50 | 349.74 |
| Renon | IT-Ren | Italy | 46.59°N; 11.43°E | 1730 | 8.84 | 280.63 |
| Roccarespampani 1 | IT-Ro1 | Italy | 42.49°N; 11.93°E | 235 | 1.00 | 310.57 |
| Roccarespampani 2 | IT-Ro2 | Italy | 42.39°N; 11.92°E | 160 | 1.51 | 332.02 |
| Torgnon | IT-Tor | Italy | 45.84°N; 7.58°E | 2160 | 5.81 | 274.69 |
| Horstermeer | NL-Hor | Netherlands | 52.24°N; 5.07°E | 2 | 7.00 | 326.18 |
| Loobos | NL-Loo | Netherlands | 52.17°N; 5.74°E | 25 | 10.95 | 343.79 |
| Fyodorovskoye | RU-Fyo | Russia | 56.46°N; 32.92°E | 265 | 2.76 | 293.74 |
| Stordalen grassland | SE-St1 | Sweden | 68.35°N; 19.05°E | 351 | 1.99 | 297.90 |
| Mongu | ZM-Mon | Zambia | 15.44°S; 23.25°E | 1053 | 1.85 | 358.19 |
| MARS | LSA | |||||||
| Condition | µ | σ | RMSE | R | µ | σ | RMSE | R |
| ALL | 0.05 | 18.49 | 24.14 | 0.88 | 0.86 | 19.01 | 24.66 | 0.87 |
| UL | −16.91 | 15.53 | 26.45 | 0.41 | −16.79 | 14.99 | 25.82 | 0.42 |
| ML | 0.06 | 18.32 | 23.90 | 0.85 | 0.77 | 18.76 | 24.35 | 0.84 |
| LL | 20.51 | 16.75 | 30.81 | 0.39 | 26.68 | 16.07 | 34.78 | 0.41 |
| MED | 0.42 | 16.40 | 22.52 | 0.87 | 1.16 | 16.85 | 22.77 | 0.86 |
| LSA_OPER | ERA5 | |||||||
| Condition | µ | σ | RMSE | R | µ | σ | RMSE | R |
| ALL | −1.60 | 20.90 | 27.24 | 0.86 | −8.71 | 18.93 | 26.71 | 0.87 |
| UL | −9.94 | 15.94 | 23.07 | 0.41 | −20.90 | 17.74 | 30.77 | 0.37 |
| ML | −1.63 | 21.05 | 27.40 | 0.82 | −8.92 | 18.76 | 26.55 | 0.84 |
| LL | 9.95 | 16.37 | 24.82 | 0.46 | 15.32 | 18.24 | 28.79 | 0.38 |
| MED | −2.02 | 18.83 | 25.88 | 0.85 | −8.08 | 16.29 | 23.82 | 0.86 |
References
- Cheng, J.; Liang, S.; Wang, W. Surface Downward Longwave Radiation. Compr. Remote Sens. 2018, 5, 196–216. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Downward Atmospheric Longwave Irradiance Under Clear and Cloudy Skies: Measurement and Parameterization. Atmos. Sol. Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Schär, C.; Loeb, N.; Dutton, E.G.; König-Langlo, G. The Global Energy Balance from a Surface Perspective. Clim. Dyn. 2013, 40, 3107–3134. [Google Scholar] [CrossRef] [Green Version]
- Held, I.M.; Soden, B.J. Water Vapor Feedback and Global Warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef] [Green Version]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2001: The Scientific Basis; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: New York, NY, USA, 2001. Available online: https://www.ipcc.ch/site/assets/uploads/2018/07/WG1_TAR_FM.pdf (accessed on 14 January 2022).
- Bertoldi, G.; Rigon, R.; Tappeiner, U. Modelling Evapotranspiration and the Surface Energy Budget in Alpine Catchments. In Evapotranspiration—Remote Sensing and Modelling; IntechOpen: London, UK, 2012; Chapter 17. [Google Scholar] [CrossRef] [Green Version]
- Naud, C.M.; Miller, J.R.; Landry, C. Using Satellites to Investigate the Sensitivity of Longwave Downward Radiation to Water Vapour at High Elevations. Geophys. Res. Atmos. 2012, 117, D05101. [Google Scholar] [CrossRef]
- Chang, K.; Zhang, Q. Modeling of Downward Longwave Radiation and Radiative Cooling Potential in China. Renew. Sustain. Energy 2019, 11, 066501. [Google Scholar] [CrossRef]
- Dilley, A.C.; O’Brien, D.M. Estimating Downward Clear Sky Long-wave Irradiance at the Surface from Screen Temperature and Precipitable Water. R. Meteorol. Soc. 1998, 124, 1391–1401. [Google Scholar] [CrossRef]
- Prata, A.J. A New Long-Wave Formula for Estimating Downward Clear-Sky Radiation at the Surface. R. Meteorol. Soc. 1996, 122, 1121–1151. [Google Scholar] [CrossRef]
- Berdahl, P.; Fromberg, R. The Thermal Radiance of Clear Skies. Sol. Energy 1982, 29, 299–314. [Google Scholar] [CrossRef]
- Brutsaert, W. On a Derivable Formula for Long-wave Radiation from Clear Skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]
- Tuzet, A. A simple method for Estimating Downward Longwave Radiation from Surface and Satellite Data by Clear Sky. Remote Sens. 1990, 11, 125–131. [Google Scholar] [CrossRef]
- Trigo, I.F.; Barroso, C.; Viterbo, P.; Freitas, S.C.; Monteiro, I.T. Estimation of Downward Long-wave Radiation at the Surface Combining Remotely Sensed Data and NWP Data. Geophys. Res. Atmos. 2010, 115, D24118. [Google Scholar] [CrossRef]
- Bilbao, J.; De Miguel, A.H. Estimation of Daylight Downward Longwave Atmospheric Irradiance under Clear-Sky and All-Sky Conditions. Appl. Meteorol. Climatol. 2007, 46, 878–889. [Google Scholar] [CrossRef]
- Josey, S.A.; Pascal, R.W.; Taylor, P.K.; Yelland, M.J. A New Formula for Determining the Atmospheric Longwave Flux at Ocean Surface at Mid-High Latitudes. Geophys. Res. Oceans 2003, 108, 3108. [Google Scholar] [CrossRef]
- Diak, G.R.; Bland, W.L.; Mecikalski, J.R.; Anderson, M.C. Satellite-based Estimates of Longwave Radiation for Agricultural Applications. Agric. For. Meteorol. 2000, 103, 349–355. [Google Scholar] [CrossRef]
- Crawford, T.M.; Duchon, C.E. An Improved Parameterization for Estimating Effective Atmospheric Emissivity for Use in Calculating Daytime Downwelling Longwave Radiation. Appl. Meteorol. Climatol. 1999, 38, 474–480. [Google Scholar] [CrossRef]
- Formetta, G.; Bancheri, M.; David, O.; Rigon, R. Performances of Site Specific Parameterizations of Longwave Radiation. Hydrol. Earth Syst. Sci. 2016, 20, 4641–4654. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.-H.; Nnadi, F. Predicting Downward Longwave Radiation for Various Land Use in All-Sky Condition: Northeast Florida. Adv. Meteorol. 2014, 2014, 525148. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, X.; Wei, Y.; Zhang, W.; Hou, N.; Xu, J.; Jia, K.; Yao, Y.; Xie, X.; Jiang, B.; et al. Estimating Surface Downward Longwave Radiation using Machine Learning Methods. Atmosphere 2020, 11, 1147. [Google Scholar] [CrossRef]
- Obot, N.I.; Humphrey, I.; Chendo, M.A.C.; Udo, S.O. Deep Learning and Regression Modelling of Cloudless Downward Longwave Radiation. Beni-Suef Univ. J. Basic Appl. Sci. 2019, 8, 23. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Wang, T.; Shi, J.; Peng, B.; Zhao, R.; Yu, Y. Remote Sensed Clear-Sky Surface Longwave Downward Radiation by Using Multivariate Adaptive Regression Splines Method. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Cao, Y.; Li, M.; Zhang, Y. Estimating the Clear-Sky Longwave Downward Radiation in the Artic from FengYun-3D MERSI-2 Data. Remote Sens. 2022, 14, 606. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Ma, Y.; Letu, H.; Li., X. All-Sky Longwave Downward Radiation from Satellite Measurements: General Parameterizations Based on LST, Column Water Vapor and Cloud Top Temperature. Photogramm. Remote Sens. 2020, 161, 52–60. [Google Scholar] [CrossRef]
- Yu, S.; Xin, X.; Liu, Q.; Zhang, H.; Li, L. An Improved Parameterization for Retrieving Clear-Sky Downward Longwave Radiation from Satellite Thermal Infrared Data. Remote Sens. 2019, 11, 425. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Shi, J.C.; Wang, T.X.; Peng, B.; Husi, L.; Yu, Y.C.; Zhao, R. New Methods for Deriving Clear-Sky Surface Longwave Downward Radiation Based on Remotely Sensed Data and Ground Measurements. Earth Space Sci. 2019, 6, 2071–2086. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Shi, J.C.; Wang, T.X.; Peng, B.; Zhao, R.; Yu, Y.C. Clear-Sky Longwave Downward Radiation Estimation by Integrating MODIS Data and Ground-Based Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 450–459. [Google Scholar] [CrossRef]
- Zhou, Q.; Flores, A.; Glenn, N.F.; Walters, R.; Han, B. A Machine Learning Approach to Estimation of Downward Solar Radiation from Satellite-Derived Data Products: An Application over a Semi-Arid Ecosystem in the U.S. PLoS ONE 2017, 12, e0180239. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; yan, G.; Chen, L. Consistent Retrieval Methods to Estimate Land Surface Shortwave and Longwave Radiative Flux Components under Clear-Sky Conditions. Remote Sens. Environ. 2012, 124, 61–71. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM Ensemble of Global Land-Atmosphere Energy FLUXES. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef] [Green Version]
- Nisbet, R.; Miner, G.; Yale, K. Advanced Algorithms for Data Mining. In Handbook of Statistical Analysis and Data Mining Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2018; Chapter 8; pp. 149–167. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. Global Atmospheric Downward Longwave Radiation at the Surface from Ground-based Observations, Satellite Retrievals, and Reanalysis. Rev. Geophys. 2013, 51, 150–185. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S. Estimation of High-spatial Resolution Clear-sky Longwave Downward and Net Radiation Over Land Surfaces from MODIS Data. Remote Sens. Environ. 2009, 113, 745–754. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Gilgen, H.; Morcrette, J.-J.; Slingo, A. Evaluation of Downward Longwave Radiation in General Circulation Models. Am. Meteorol. Soc. 2001, 14, 3227–3239. [Google Scholar] [CrossRef]
- European Space Agency. Meteosat Second Generation: The Satellite Development; ESA Publishing Division: Noordwijk, The Netherlands, 1999; ISBN 92-9092-634-1.
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Hoke, M.L.; Chetwynd, J.H.; Bernstein, L.S.; Shettle, E.P.; Matthew, M.W.; Adler-Golden, S.M. MOD-TRAN4 Version 2 User’s Manual Air Force Res. Lab; Space Vehicles Directorate, Air Force Material Command: Hanscom Air Force Base, MA, USA, 2000; Available online: https://home.cis.rit.edu/~cnspci/references/berk2003.pdf (accessed on 14 January 2022).
- Chevallier, F.; Chédin, A.; Chéruy, F.; Morcrette, J.-J. TIGR-like Atmospheric-Profile Databases for Accurate Radiative-Flux Computation. R. Meteorol. Soc. 2000, 126, 777–785. [Google Scholar] [CrossRef]
- LSA-SAF. EUMETSAT Network of Satellite Application Facility on Land Surface Analysis: Down-Welling Longwave Flux (DSLF); Product User Manual, Issue 3.4, SAF/LAND/IPMA/PUM_DSLF/3.4; EUMETSAT Network of Satellite Application Facilities: Darmstadt, Germany, 2015. [Google Scholar]
- Friedman, J.H. Multivariate Adaptative Regression Splines. Ann. Stat. 1991, 19, 1–141. Available online: https://projecteuclid.org/journals/annals-of-statistics/volume-19/issue-1/Multivariate-Adaptive-Regression-Splines/10.1214/aos/1176347963.full (accessed on 14 January 2022).
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): Structure and data description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef] [Green Version]
- Mlawer, E.J.; Turner, D.D. Spectral Radiation Measurements and Analysis in the ARM Program. Meteorol. Monogr. 2016, 57, 14.1–14.17. [Google Scholar] [CrossRef]
- Emetere, M.E.; Akinyemi, M.L. Documentation of Atmospheric Constants Over Niamey, Niger: A Theoretical Aid for Measuring Instruments. R. Meteorol. Soc. Meteorol. Appl. Sci. Technol. Weather Clim. 2017, 24, 260–267. [Google Scholar] [CrossRef]
- Sengupta, M. Atmospheric Radiation Measurement (ARM) User Facility: Sky Radiometers on Stand for Downwelling Radiation (SKYRAD60S); 2005-11-26 to 2007-01-07, ARM Mobile Facility (NIM) Niamey, Niger (M1); ARM Data Center: Oak Ridge, TN, USA, 2005. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 Dataset and the ONEFlux Processing Pipeline for Eddy Covariance Data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the Separation of Net Ecosystem Exchange into Assimilation and Ecosystem Respiration: Review and Improved Algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Morcrette, J.-J.; Barker, H.W.; Cole, J.N.S.; Iacono, M.J.; Pincus, R. Impact of a New Radiation Package, McRad, in the ECMWF Integrated Forecasting System. Am. Meteorol. Soc. 2008, 136, 4773–4798. [Google Scholar] [CrossRef]
- Dutra, E.; Muñoz-Sabater, J.; Boussetta, S.; Komori, T.; Hirahara, S.; Balsamo, G. Environmental Lapse Rate for High-Resolution Land Surface Downscaling: An Application to ERA5. Earth Space Sci. 2020, 7, e2019EA000984. [Google Scholar] [CrossRef] [Green Version]
- Derrien, M.; Le Gléau, H. MSG/SEVIRI Cloud Mask and Type from SAFNWC. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- Derrien, M.; Le Gléau, H. Improvement of Cloud Detection Near Sunrise and Sunset by Temporal-Differencing and Region-Growing Techniques with Real-Time SEVERI. Remote Sens. 1010, 31, 1765–1780. [Google Scholar] [CrossRef]
- Friedman, J.H.; Roosen, C.B. An introduction to Multivariate Adaptative Regression Splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Marcot, B.G.; Hanea, A.M. What is an Optimal Value of K in K-fold Cross-validation in Discrete Bayesian Network Analysis. Comput. Stat. 2020, 36, 2009–2031. [Google Scholar] [CrossRef]
- Wu, C.Z.; Goh, A.T.C.; Zhang, W.G. Study on Optimization of Mars Model for Prediction of Pile Drivability Based on Cross-validation. In Proceedings of the 7th International Symposium on Geotechnical Safety and Risk (ISGSR), Taipei, Taiwan, 11–13 December 2019; pp. 572–577, ISBN 978-981-11-27285-0. [Google Scholar]
- Zhao, Y.; Hasan, Y.A. Machine Learning Algorithms for Predicting Roadside Fine Particulate Matter Concentration Level in Hong Kong Central. Comput. Ecol. Softw. 2013, 3, 61–73. [Google Scholar]
- Palharini, R.S.A.; Vila, D.A. Climatological Behaviour of Precipitating Clouds in the Northeast Region of Brazil. Adv. Meteorol. 2017, 2017, 5916150. [Google Scholar] [CrossRef]
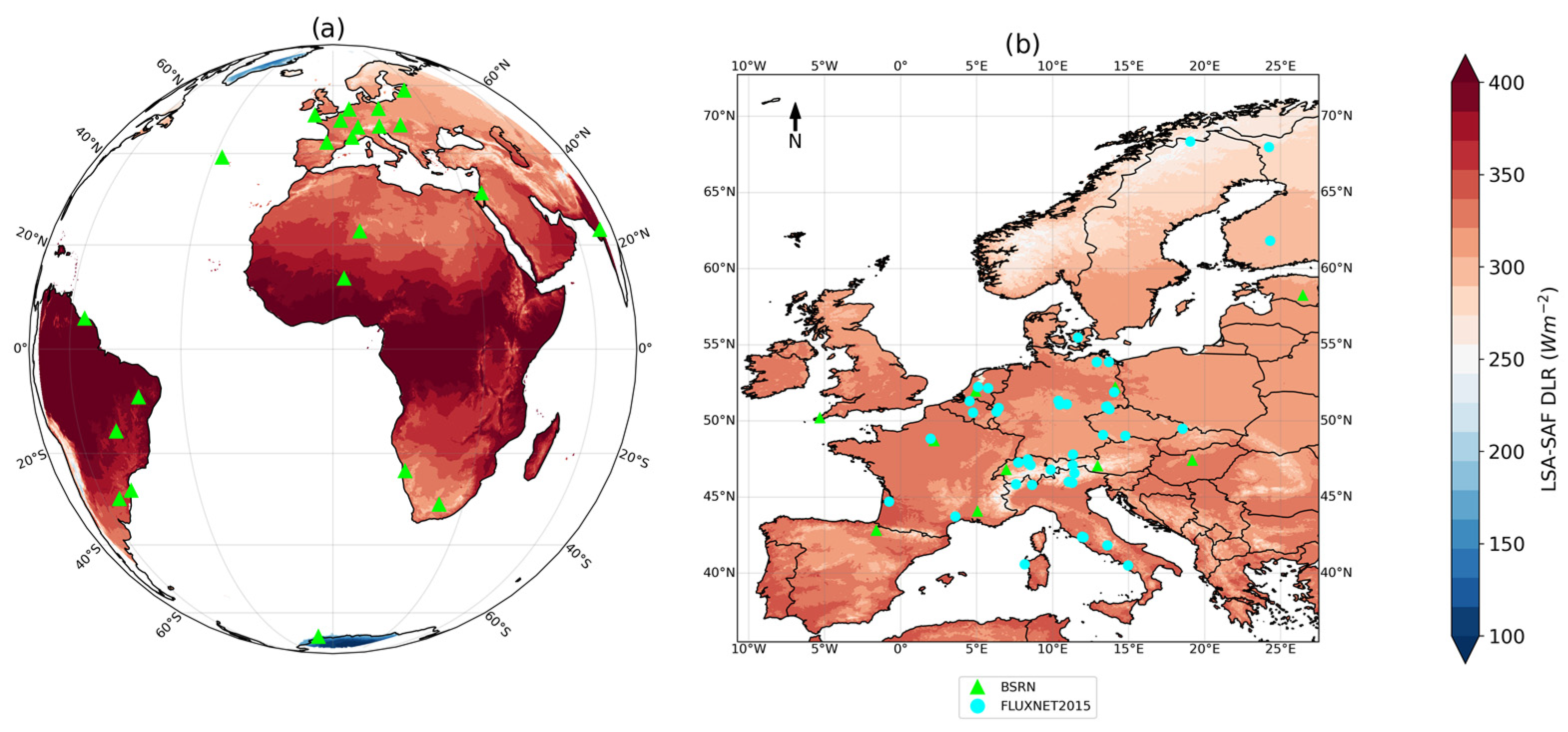
| Station | Acronym | Network | Location | Latitude and Longitude (°) | Elev. (m) | Avail. (Years) | Annual DLR (W·m−2) |
|---|---|---|---|---|---|---|---|
| Brasília | BRB | BSRN | Brazil | 15.60°S; 47.71°W | 1023 | 7.12 | 364.45 |
| Budapest | BUD | BSRN | Hungary | 47.43°N; 19.18°E | 139 | 0.08 | 373.82 |
| Cabauw | CAB | BSRN | Netherlands | 51.97°N; 4.93°E | 0 | 14.69 | 323.69 |
| Camborne | CAM | BSRN | U.K. | 50.22°N; 5.32°W | 88 | 11.64 | 324.57 |
| Carpentras | CAR | BSRN | France | 44.08°N; 5.06°E | 100 | 14.15 | 321.74 |
| Cener | CNR | BSRN | Spain | 42.82°N; 1.60°W | 471 | 10.28 | 321.71 |
| De Aar | DAA | BSRN | South Africa | 30.67°S; 23.99°E | 1287 | 6.25 | 303.88 |
| Eastern North Atlantic | ENA | BSRN | Azores | 39.09°N; 28.03°W | 15.2 | 1.00 | 359.34 |
| Florianopolis | FLO | BSRN | Brazil | 27.61°S; 48.52°W | 11 | 5.70 | 386.40 |
| Gandhinagar | GAN | BSRN | India | 23.11°N; 72.63°E | 65 | 1.58 | 401.45 |
| Gobabeb | GOB | BSRN | Namibia | 23.56°S; 15.04°E | 407 | 7.54 | 338.67 |
| Neumayer | GVN | BSRN | Antarctica | 70.65°S; 8.25°W | 42 | 14.89 | 216.87 |
| Niamey | NIM | ARM | Africa | 13.48°N; 2.18°E | 223 | 1.02 | 392.11 |
| Lindenberg | LIN | BSRN | Germany | 52.21°N; 14.12°E | 125 | 13.99 | 315.06 |
| Palaiseau | PAL | BSRN | France | 48.71°N; 2.21°E | 156 | 15.63 | 322.61 |
| Paramaribo | PAR | BSRN | Suriname | 5.81°N; 55.22°W | 4 | 0.58 | 421.16 |
| Payerne | PAY | BSRN | Switzerland | 46.82°N; 6.94°E | 491 | 15.70 | 315.05 |
| Petrolina | PTR | BSRN | Brazil | 9.07°S; 40.32°W | 387 | 7.56 | 386.86 |
| Sede Boqer | SBO | BSRN | Israel | 30.86°N; 34.78°E | 500 | 7.49 | 332.86 |
| São Martinho da Serra | SMS | BSRN | Brazil | 29.44°S; 53.82°W | 489 | 6.04 | 327.19 |
| Sonnblick | SON | BSRN | Austria | 47.05°N; 12.96°E | 3109 | 6.28 | 249.07 |
| Tamanrasset | TAM | BSRN | Algeria | 22.79°N; 5.53°E | 1385 | 15.88 | 330.70 |
| Toravere | TOR | BSRN | Estonia | 58.25°N; 26.46°E | 70 | 15.70 | 308.71 |
| Training | Evaluation | |||||
|---|---|---|---|---|---|---|
| Model | Predictors | Cloud Info. | Predictand | Period | Predictors | Cloud Info. |
| MARS | tcwv, t2m, d2m (ERA5) | cf (MSG) | DLR (BSRN, ARM) | 2004–2019 1 | tcwv, t2m, d2m (ERA5) | cf (MSG) |
| LSA | ||||||
| MARS* | tcwv, t2m, d2m (ERA5) | tcc (ERA5) | ||||
| LSA* | ||||||
| LSA_OPER | tcwv, t2m, d2m (ERA-40) | tcc(ERA-40) | DLR (MODTRAN-4) | 1992–1993 | tcwv, t2m, d2m (ECMWF operational NWP) | cf (MSG) |
| ERA5 | - | - | - | - | - | - |
| MARS | LSA | |||||||
| Condition | µ | RMSE | R | µ | RMSE | R | ||
| ALL | 0.65 | 13.86 | 18.76 | 0.95 | 0.48 | 15.00 | 20.24 | 0.94 |
| UL | −9.13 | 12.02 | 18.54 | 0.61 | −11.65 | 13.74 | 21.51 | 0.54 |
| ML | 0.51 | 13.53 | 18.35 | 0.92 | 0.77 | 14.78 | 19.96 | 0.91 |
| LL | 18.82 | 14.52 | 26.97 | 0.69 | 12.21 | 15.70 | 24.47 | 0.70 |
| MED | 0.40 | 12.27 | 16.96 | 0.91 | 0.87 | 13.29 | 18.52 | 0.91 |
| LSA_OPER | ERA5 | |||||||
| Condition | µ | RMSE | R | µ | RMSE | R | ||
| ALL | −1.30 | 17.29 | 23.55 | 0.93 | −5.25 | 15.40 | 22.08 | 0.93 |
| UL | −2.47 | 13.37 | 17.76 | 0.57 | −11.91 | 14.34 | 22.49 | 0.52 |
| ML | −0.86 | 17.53 | 23.91 | 0.90 | −5.31 | 15.37 | 22.07 | 0.90 |
| LL | −9.87 | 14.50 | 22.56 | 0.73 | 6.44 | 15.51 | 21.73 | 0.70 |
| MED | 0.78 | 14.05 | 19.53 | 0.89 | −5.81 | 13.88 | 20.65 | 0.88 |
| MARS* | LSA* | |||||||
|---|---|---|---|---|---|---|---|---|
| Condition | µ | RMSE | R | µ | RMSE | R | ||
| ALL | 3.07 | 16.68 | 22.05 | 0.93 | 3.21 | 17.79 | 23.16 | 0.92 |
| UL | −9.39 | 13.87 | 20.59 | 0.53 | −11.26 | 14.55 | 22.14 | 0.51 |
| ML | 3.07 | 16.44 | 21.73 | 0.89 | 3.58 | 17.73 | 23.02 | 0.88 |
| LL | 22.01 | 15.92 | 30.25 | 0.70 | 16.48 | 16.85 | 27.61 | 0.71 |
| MED | 2.73 | 15.54 | 20.94 | 0.87 | 3.59 | 15.64 | 21.32 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, F.M.; Dutra, E.; Trigo, I.F. Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation. Remote Sens. 2022, 14, 1704. https://doi.org/10.3390/rs14071704
Lopes FM, Dutra E, Trigo IF. Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation. Remote Sensing. 2022; 14(7):1704. https://doi.org/10.3390/rs14071704
Chicago/Turabian StyleLopes, Francis M., Emanuel Dutra, and Isabel F. Trigo. 2022. "Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation" Remote Sensing 14, no. 7: 1704. https://doi.org/10.3390/rs14071704
APA StyleLopes, F. M., Dutra, E., & Trigo, I. F. (2022). Integrating Reanalysis and Satellite Cloud Information to Estimate Surface Downward Long-Wave Radiation. Remote Sensing, 14(7), 1704. https://doi.org/10.3390/rs14071704








