Abstract
The excessive extraction and recharge of groundwater lead to long-time seasonal land subsidence in Los Angeles, USA, and especially in the Santa Ana basin. The rate of land subsidence in the Santa Ana basin has been rising, which could pose a danger to infrastructure and human lives. However, the most recent research on land surface deformation in the area was conducted using the traditional parameter estimation method, resulting in little understanding of the regional spatiotemporal characteristics. The parametric method consists of a least square linear inversion, using the pre-defined mathematical geometric or geophysical theoretical models to describe groundwater deformation, and it requires precise external environmental variables and accurate geophysical parameters, which are more difficult to implement. In this study, multitemporal InSAR-derived deformation time series are analyzed by using 69 descending C-band Sentinel-1A SAR scenes acquired from 2015 to 2018. A method based on independent component analysis (ICA) is applied to characterize the spatial pattern and temporal evolution of land subsidence in the Santa Ana basin. The results reveal two different spatial and temporal deformation patterns in the basin. First, a widespread seasonal deformation is identified by the first component, related to annual seasonal groundwater level changes, and the overall deformation shows a concentrated spatial pattern. The second component captures a long-term signal with a large-scale spatial pattern. For quantitative assessment, the obtained deformation time series are compared with the GNSS data, validating an accuracy of millimeters. We further calculate the cross-correlation coefficient and the elastic skeletal storage coefficient from the ICA-derived seasonal deformation and groundwater level, which reveals that the deformation responds quickly (i.e., a lag of 8 days) to the change in groundwater and the Santa Ana aquifer retains almost the same elasticity for at least 15 years. Quantifying the spatiotemporal characteristics of the deformation in the Santa Ana basin can provide a reference for the monitoring and managing of groundwater.
1. Introduction
The large-area regional decline funnels formed by groundwater overexploitation change the groundwater pressure, the stress state in the aquifer, and the upper and lower stagnant layers of the aquifer [1,2]. The resulting consolidation of aquitards ultimately leads to land subsidence [3,4,5]. As a possible environmental geological disaster, subsidence caused by the overexploitation of groundwater affects many areas, including Shanghai, Tianjin and Xi’an in China, and Los Angeles, Santa Clara Valley and Houston in the USA [6,7,8,9,10,11]. Land subsidence can pose huge hazards to surrounding buildings or underground facilities. In coastal areas, it can also lead to adverse consequences such as backflow of seawater and failure of harbor facilities. In karst areas, the excessive exploitation of groundwater can cause surface collapse. In addition, land subsidence may cause a surface response of the aquifer system to permanent compaction, resulting in a significant reduction in the storage capacity of the aquifer and groundwater reserves [12].
Los Angeles has experienced great subsidence in the past few decades, mainly due to urban construction and the overexploitation of groundwater [13]. Since only a small amount of rainfall can seep into the groundwater, the overexploitation of groundwater eventually leads to an imbalance in the groundwater cycle. The aquifer system is associated with the deformation signal, and the extraction and recharge of groundwater cause the Los Angeles basin to expand and contract [14,15,16,17,18]. By analyzing InSAR time series, complex surface deformation was monitored in the Santa Ana basin due to groundwater extraction and aquifer compaction [10]. The amplitude of vertical deformation has previously been established by using long-span data composed of 26 SAR images and continuous GNSS measurements, which confirmed that the wider deformation mode in the Santa Ana basin was due to a vertical movement related to the annual variation in groundwater level [19]. Scientists from the US Geological Survey have recorded large-scale land subsidence and have found that most of the subsidence was caused by the overexploitation of groundwater, even exceeding the historical maximum of 30 cm/year [13]. Long-term subsidence also leads to ground fissures in the basin, which can cause huge losses to infrastructures such as houses, bridges, roads, and underground pipelines.
Interferometric Synthetic Aperture Radar (InSAR) is one of the most promising technologies to study land deformation caused by aquifer compaction. The rapid development of this technology over the past few decades has contributed to significant progress in monitoring drainage-related surface movements in many countries [20,21]. Combining groundwater flow models with InSAR observations facilitates the understanding of aquifer compaction phenomena associated with groundwater extraction. In addition, the use of InSAR-derived surface displacements in the predictive models can more effectively determine the structural boundaries of the aquifer system, and its hydrogeological heterogeneity, as well as the values of storage coefficients and hydraulic conductivity [22,23,24,25,26].
Extracting and isolating the spatiotemporal deformation information driven by different geophysical processes from the observed InSAR time series is an important and difficult task in current InSAR time series analysis. In order to increase the understanding of geophysical processes, people need to extract useful information from massive InSAR observations. However, the deformation time series provided by InSAR are affected by many factors, including various error sources and geophysical signals that are difficult to quantify. Principal component analysis (PCA) and independent component analysis (ICA), as blind source separation (BSS) technologies, have been introduced into the field of InSAR to separate geophysical signals of interest. PCA uses the second-order statistical information of the mixed signal to extract uncorrelated principal components (PCs), which have been applied to filter InSAR time series [27], invert geodetic time series [28], and identify ground motion with various characteristics [29,30]. The ICA algorithm, which is an extension of PCA, uses high-order statistical information to measure the independence of the source signals. The independent components (ICs) are not correlated and are independent of each other. Specifically, ICA has also been applied to InSAR data processing, including atmospheric delay extraction [31], DEM error estimation [32], and spatiotemporal analysis of InSAR time series [9,33,34,35].
In this paper, we employ the ICA method to investigate the spatiotemporal patterns of the observed InSAR time series in the Santa Ana basin, Los Angeles, which has the potential to provide reliable measurements of the ground displacements for the mechanism interpretation of surface deformation associated with groundwater exploitation. We first investigate and analyze the land deformation in the Santa Ana basin by using the multitemporal InSAR as applied to the process descending C-band Sentinel-1A SAR data acquired from 2015 to 2018. The ICA algorithm is then applied to extract the spatiotemporal characteristics over the Santa Ana basin based on the InSAR time series. We identify the seasonal variations, which are captured by the first component. Through spatiotemporal analysis, we also reveal several deformation modes. Generally, the seasonal subsidence/uplift is usually controlled by the groundwater level, and we confirm this conclusion by estimating the cross-correlation coefficient between the isolated seasonal ground deformation and the groundwater level. Furthermore, the elastic skeletal storage coefficient is calculated from the ICA-derived seasonal deformation, and our results suggest that the land deformation in the Santa Ana Basin undergoes elastic seasonal deformation. Therefore, when InSAR observations contain deformation that is difficult to quantify and is insufficient to describe a single deforming phenomenon, this paper can inspire related research.
2. Methods
2.1. Time Series Inversion
Let us assume that SAR images covering the same area are acquired, and interferograms are formed by selecting an appropriate spatiotemporal baseline threshold. The selected interferometric pairs are processed by differential interferometry and phase unwrapping relative to the reference point to obtain the final unwrapped interferograms [36]. The sensitivity of parameter estimation to the interferogram network can be reduced by transforming short-baseline interferograms into sequential interferograms [37]. We take the unwrapped interferometric phase with a short baseline as the observation value, and consider the sequential interferometric phase as the unknown parameter; then, the functional equation between the two can be expressed in the following form:
where represents the known vector of the unwrapped phase values of differential interferograms, is denoted as the sequential interferograms in time series, and is the coefficient matrix. If the obtained interferograms belong to a single subset, then matrix is a full rank matrix, and the unknown parameters can be solved by the least square (LS) method:
However, it is not common for all interferograms to belong to a single subset, resulting in the matrix being a singular matrix, which will produce infinite sets of solutions. In this case, singular value decomposition (SVD) [38] and iterative reweighted least squares (IWLS) [39] can be used to obtain the pseudo inverse of matrix , so as to obtain the minimum normal solution of the equations. However, large discontinuities may be introduced into the obtained phases of the time series, resulting in physically meaningless results, especially when atmospheric delay exists in the interferometric phase [40]. In order to improve the time sampling rate of the phase and obtain a meaningful sequential phase, the above function model can be established in each subset and solved by LS [32].
2.2. ICA Decomposition
ICA is a statistical method for transforming an observed multidimensional random vector into components that are statistically as independent from each other as possible [41]. The ICA algorithm can change the data and produce “clearer” source signals, which are independent of each other and belong to a non-Gaussian signal [42]. With ICA, a unique solution is obtained by maximizing the mutual independence of the estimated sources, especially the non-Gaussian of the source. This assumption is based on the central limit theorem (CLT), which shows that the sum of independent random variables with a non-Gaussian distribution tends to a Gaussian distribution [43,44].
To strictly define ICA, we can use a statistical model, which assumes that the observed value is a linear combination of independent source signals. The relationship between the observed signal and the independent source signal can be described as:
In this model, we assume that the mixed observer and source signal are random variables, and is the linear combination coefficient. Let us assume that is an InSAR phase time series with acquisitions, points at each acquisition, and independent components mixed in the InSAR phase time series. Before performing the ICA separation, we need to remove from the unwrapped interferogram the possible planar component (related to orbital errors, APS, etc.) and a stratigraphic component of the APS, as it can be temporally correlated that will affect the result of the ICA separation. Then, the above mixing model can be written as:
where the subscripts indicate the size of the corresponding variable, , , and . In Equation (4), represents the observation matrix, and each column in represents the phase time series of each pixel. includes independent components, and each row in represents an independent component signal at points. is a coefficient matrix, each row represents the linear combination coefficient of independent components, and each column represents the time characteristics of the independent components. It should be noted that and are both unknown. There are various solving algorithms that operate under different assumptions, such as the FastICA algorithm [45], infomax algorithm [46], and maximum likelihood estimation algorithm [47]. Among them, FastICA is the most commonly used, with the advantage of computational efficiency. In this study, we employ the FastICA algorithm to decompose the InSAR time series.
Firstly, the mixed InSAR phase time series are preprocessed by centering and whitening. The purpose of centering is to cause the average value of each row in the mixed signal matrix to be 0, and the centered matrix is calculated by:
The purpose of whitening is to make the mixed observations obtained at each acquisition of InSAR phase time series uncorrelated. The whitened matrix is described by:
where and are the eigenvector matrix and eigenvalue matrix based on the PCA algorithm, respectively. After the whitening matrix is obtained by preprocessing, the second step is to solve the rotation matrix . The FastICA algorithm uses a fixed-point iteration to derive the matrix , and the iterative formula is described by:
where is nonlinear function. The mixing matrix and source matrix can be expressed as:
where represents the inverse matrix of the mixed matrix . Through the above iterative process, the source signals can be estimated one by one. Figure 1 illustrates the data processing flow in this study.
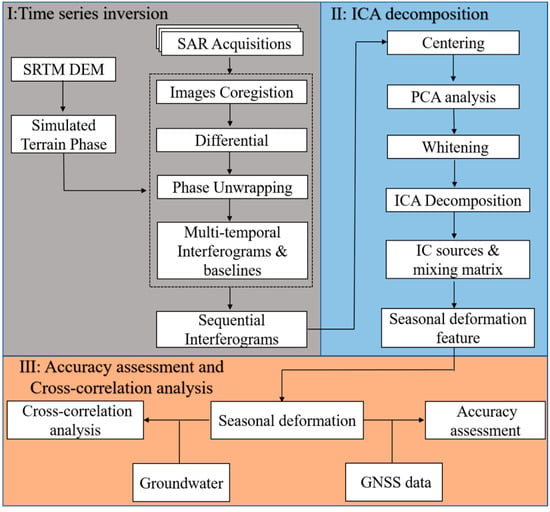
Figure 1.
Flowchart of the data processing procedure.
3. Study Area and Datasets Used
3.1. Santa Ana Basin
The Santa Ana basin lies within Orange County, southeast of the Los Angeles area, USA [10]. It is characterized by the abrupt rise of prominent mountains from relatively flat inland valleys and coastal plains (Figure 2). Characterized by a Mediterranean climate, the Santa Ana basin is hot and dry in the summer, and cool and humid in the winter. The average annual precipitation varies from 25 to 61 cm in inland valleys and coastal plains, and 60 to 120 cm in the San Gabriel and San Bernardino Mountains. Due to the semi-arid climate and the huge water demand of the local population, the hydrological cycle of the Santa Ana basin is dominated by precipitation, artificial recharge, groundwater pumping, and the discharge of treated wastewater. Bounded by relatively impermeable mountains and hills, the hydrous sediments in this area are located in valleys and coastal plains filled with alluvium. Rivers and streams in the San Jacinto, San Gabriel, and San Bernardino mountains are diverted to groundwater recharge facilities. Therefore, the pumped groundwater is the main source of water supply in the basin, satisfying approximately 2/3 of the total water demand, and artificial recharge accounts for approximately 3/4 of the groundwater extracted from the coastal aquifer systems [48]. The excessive exploitation and recharge of groundwater lead to long-term seasonal deformation in the Santa Ana basin, so that studying and judging the spatiotemporal deformation characteristics can thus provide a reference for the management of the groundwater.
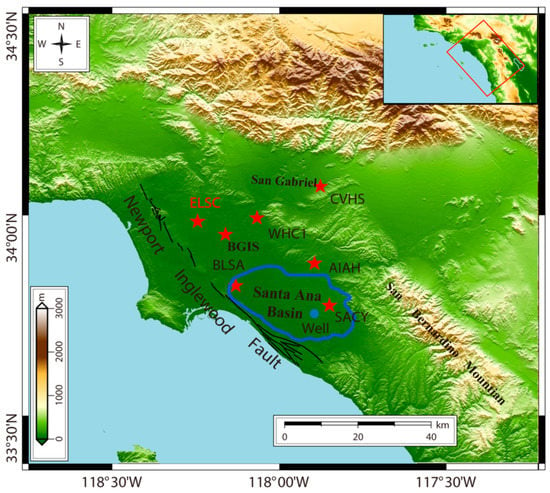
Figure 2.
Topographic map of the study area generated from SRTM DEM data with 30 m resolution. Red rectangle shows the coverage of the descending Sentinel-1 SAR images used here. Blue solid line outlines the investigated Santa Ana basin. Red stars show the locations of the 6 SCIGN GNSS sites for accuracy validation, and the ELSC GNSS station is selected as the reference point. Blue dot indicates the location of a groundwater well.
The basin is mainly composed of three main aquifer systems, known as the Shallow, Principal, and Deep, which are hydraulically connected, and the Newport–Inglewood fault forms the southwest boundary of all aquifers except shallow aquifer. The total thickness of sedimentary rocks in the basin exceeds 20,000 feet, with fresh water only in the upper 2000 to 4000 feet, and the thickness of freshwater sediments is less than 1000 feet at the edge of the basin [49]. Since the Oligocene period, structural folding and faulting have occurred along the basin margins, as well as down warping and deposition within the basin. From a hydrogeological point of view, the Newport–Inglewood fault zone is the most important tectonic feature of the basin, and the fold and fault along it create natural limitations on the intrusion of seawater into the groundwater basin [50]. In the coastal and central part of the basin, a series of complex interconnected sand and gravel deposits are widely separated by clay and silt deposits or aquitards with lower permeability, and the clay and silt deposits become thinner and more discontinuous, which make it easier for large amounts of groundwater to flow between shallow and deeper aquifers.
3.2. Datasets Used
In this study, a dataset of the C-band Sentinel-1A SAR images acquired from the descending orbit (Path 71, Frame 480) was used to analyze the surface deformation of the Santa Ana basin. The acquisition period was from May 2015 to April 2018, and 69 Sentinel-1A SAR scenes were acquired. The reason for acquisitions before 2015 not being used is that some images are separated by more than 24 days, and a loss of correlation in that case is not conducive to reliable data processing. The detailed parameters of the used SAR dataset are listed in Table 1. Meanwhile, the external STRM DEM with 30 m resolution was used to remove the influence of the topographic phase [51]. For the Los Angeles area, we downloaded groundwater level data from the USGS groundwater information website. GPS data downloaded from SCIGN website (http://geodesy.unr.edu/ accessed on 2 April 2022) were used to verify the InSAR measurements.

Table 1.
Parameters of the SAR datasets used in the study.
4. Experiments and Results
4.1. Results of the InSAR Processing
For the descending Sentinel-1A data, the maximum perpendicular baseline is 250 m, and the temporal baseline changes from 6 days to 96 days. We create a short-baseline interferometric network, where 135 interferograms are initially generated (Figure 3). The resolution of each ground pixel in the interferogram is about 50 m × 50 m, generated by performing multi-looking with a factor of 20 looks in the range and 4 looks in the azimuth, respectively. An improved Goldstein filter method is then applied to remove the noise in the interferograms, and we use the minimum cost flow algorithm to unwrap each interferogram. In order to reduce the unwrapping error, we only choose interferograms with coherence greater than the average threshold of 0.6, and the GNSS site ELSC is selected as the reference point of unwrapping. We convert the interferometric phase with short baselines into sequential interferometric phase by the LS method, and the phase is multiplied by the constant −λ/4π to obtain the deformation time series. Before ICA separation, temporal high-pass filtering is used to remove part of the high-frequency turbulent atmosphere.
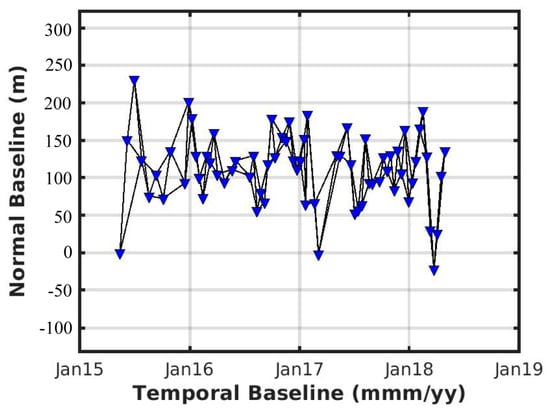
Figure 3.
Spatiotemporal baselines of the interferometric pairs.
Figure 4 shows the deformation rate map in the line-of-sight (LOS) direction for the study area. There is a main subsidence zone in the Santa Ana basin, and the deformation rates are mainly between 10 mm/year and 20 mm/year, which agrees well with the results obtained in [52]. There is a large uplift trend in the southern end of the Santa Ana basin, which is expected to be related to groundwater. In addition, we draw a section line A–B and obtain the deformation rate of the observation points along the section line. We observe that the rate changes exponentially within the basin and linearly away from the basin.
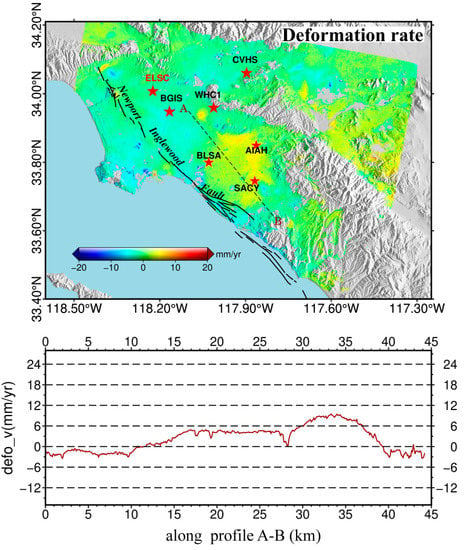
Figure 4.
(Top) Mean LOS rate map over the Santa Ana basin from 2015 to 2018. A–B is the selected section line transecting obvious surface deformation. Red Pentagrams show the locations of the SCIGN GNSS sites for accuracy validation. (Bottom) Deformation rate of the observation points along the profile A–B.
Additionally, in order to develop a better understanding of the deformation characteristic, we calculate the LOS displacement velocity fields for different years. Figure 5a–c illustrates the deformation patterns during the periods 2015–2016, 2016–2017, and 2017–2018, respectively. An inconsistent spatial deformation pattern occurred from 2015 to 2018, and the deformation rates varied with time. During the first and third years, the basin showed a trend of uplift and the maximum deformation rate reached 30 mm/year, while the second year showed a trend of subsidence. The uplift was relatively small from 2015 to 2016, which is related to mountain runoff and abnormal winter rainfall. The surface uplift accelerated and was rather large from 2017 to 2018. The spatial characteristics of the deformation rate in 2017–2018 are the most obvious, with a maximum uplift range, and the rates are mainly between 20 mm/year and 30 mm/year. As the overall surface uplift is greater than subsidence, it still shows the trend of uplift. Again, the section line A–B is selected at the same location. It can be observed that the fluctuations in the first two years are relatively flat and in the third year are considerably greater. Combined with the existing research results for this area, without considering the impact of tectonic movements, it is speculated that the groundwater recharge of this aquifer is greater than extraction during these three years. Therefore, the possibility of the irrecoverable inelastic compression of this aquifer cannot be ruled out.
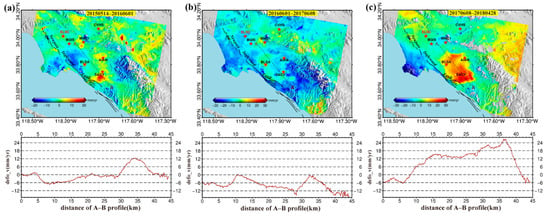
Figure 5.
Mean LOS velocity maps over the Santa Ana basin for different years: (a) 20150514–20160601, (b) 20160601–20170608, and (c) 20170608–20180428. A–B is the selected section line transecting obvious surface deformation. Red Pentagrams show the locations of the SCIGN GNSS sites for accuracy validation.
4.2. ICA Decomposition of InSAR Time Series
ICA can separate spatiotemporal deformation patterns embedded in the InSAR time series without any prior information about potential signal sources. In addition, ICA does not need to establish the functional relationship between the observed value and the unknown source, which avoids the error caused by an inaccurate model. The input observation of ICA can only be a two-dimensional matrix, so the first step is to form a two-dimensional matrix of InSAR time series. There are 69 acquisitions of InSAR time series, with 1662774 points at each acquisition, which constitute the matrix (i.e., X in Equation (4) with a size of 69 × 1,662,774).
We need to determine the number of independent components before the ICA separation. Too many independent components will cause the interested components to be divided into several fake independent components, and too few independent components will cause other components to be divided into the components of interest, leading to the introduction of errors, which is undesirable for deformation analysis. Principal component analysis of InSAR time series can determine the number of independent components and reduce the data dimension. Based on the PCA, the first four principal components account for a total of 89.4% of the data variance, at 68.03%, 13.63%, 5.08% and 2.66%, respectively, whereas the fifth component accounts for only 1.83% (Figure 6). Given a threshold, when the percentage of variance is lower than this threshold, we remove it as an error, and the principal components above this threshold are retained. For the real descending InSAR time series, 2% is selected as the threshold. The percentage of variance of the fifth principal component is lower than 2%, and the first four principal components are retained for the following ICA decomposition. The number of independent components is equal to the number of principal components, that is, four independent components are thus finally determined.
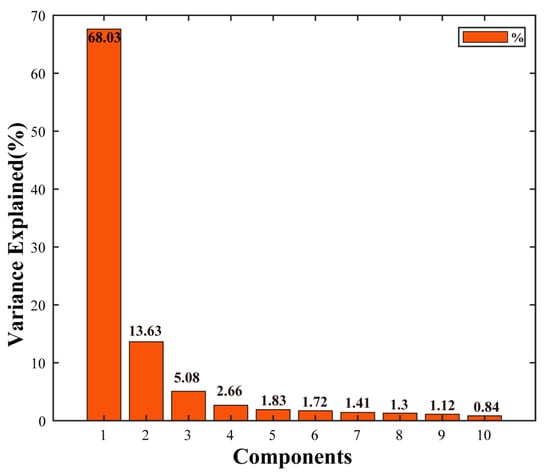
Figure 6.
Percentage of variance explained in the first 10 components of the PCA used to choose the number of components for ICA.
We apply the FastICA algorithm to the InSAR time series [41], and Figure 7 shows the temporal and spatial characteristics of the independent components (ICs) obtained from the InSAR time series. In order to visually compare each component, the spatial component is usually standardized, that is, the spatial value range is scaled to [–1,1]. Figure 7a–d show the score value of the spatial pattern of the four independent components, respectively, and the score value represents the spatial contribution of the corresponding component of the point. Figure 7e shows the temporal eigenvectors of each independent component. For the first independent component of ICA (IC1), the temporal eigenvector shows obvious seasonality, and the subsidence trend in the summer is opposite to that in winter. The score value map is mainly concentrated in the Santa Ana basin, with a positive value, and the shape is similar to a subsidence area. According to the temporal and spatial characteristics of the IC1, we can conclude that the Santa Ana basin has a seasonal deformation with a period of about one year. IC2 describes a linear deformation process with an obvious high time correlation. The score map basically covers the whole study area, but the score value is about zero in the basin, indicating that there is a small linear motion there. We speculate that IC2 may be related to tectonic movements along nearby faults. The IC3 and IC4 score maps describe randomly distributed signals (Figure 7c,d, respectively), and the temporal eigenvectors of IC3 and IC4 are random and swing up and down at zero. We assume that these two components are related to error signals. It can be seen from the above analysis that IC1 is the component we are most interested in and can adequately describe the spatiotemporal characteristics of the Santa Ana basin.
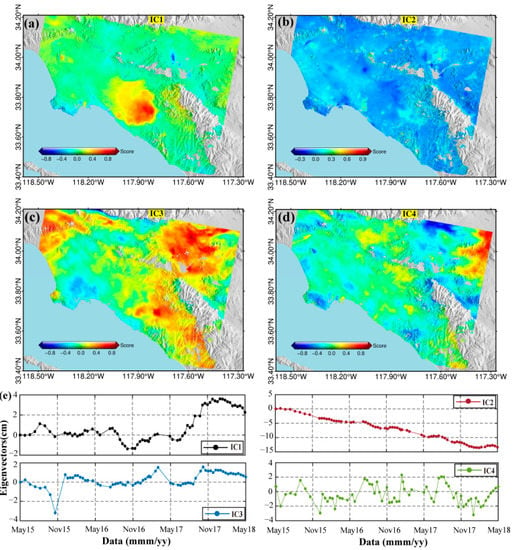
Figure 7.
ICA decomposition results for the descending InSAR time series. Four independent components are isolated. (a–d) Score values of the spatial patterns of the four independent components, respectively; (e) temporal eigenvectors of each independent component.
By multiplying the temporal eigenvector of IC1 by the corresponding score value, we reconstruct a new InSAR deformation time series, which only contains the seasonal deformation in the basin (Figure 8). We further calculate the deformations associated with the IC1 derived deformations by multiplying the temporal evolution of the IC1 with the scores. To verify the accuracy of the IC1-derived deformation time series, a comparison is conducted between IC1-derived and GNSS displacement time series. We select six typical GNSS stations in the study area and mark them as pentagons in Figure 1. The GPS derived 3-D displacement time series are projected into the LOS directions of the descending orbit. Figure 9 shows the comparison, and it is clear that both the IC1 and GNSS results show seasonal oscillations. IC1-derived deformation time series are in agreement with the GNSS displacement time series. We calculate the RMSE between InSAR and GNSS data by averaging the GNSS data on a temporal window equal to the satellite revisit time and evaluating the GNSS data in correspondence of the satellite acquisition date. At these points, the mean RMSE are 3.8 mm. The minimum and maximum RMSEs are 2.3 mm at site CVHS, and 5.1 mm at site SACY, respectively.
Figure 8.
Deformation time series reconstructed from the independent spatial components and temporal eigenvectors for IC1.
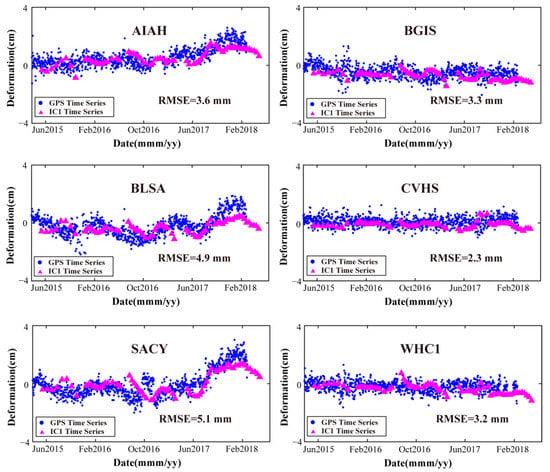
Figure 9.
Comparison between the GNSS- and ICA-derived LOS displacements at GNSS stations AIAH, BGIS, BLSA, CVHS, SACY and WHC1. Blue dots and magenta triangles represent GNSS- and IC1-derived deformations, respectively. The RMSEs between them are marked in the sub-plots.
5. Discussion
5.1. Cross-Correlation Analysis between IC1-Derived Deformation and Groundwater
The temporal eigenvector of IC1 shows seasonal characteristics, which is inferred to be related to the change in the groundwater level in the basin. The groundwater well data are obtained from the USGS and consist of daily water levels, and the well location is marked in Figure 1. We conduct cross-correlation analysis between the time series of the IC1 eigenvectors and the groundwater well data. For reconstructing the InSAR seasonal time series, the point closest to the well location is selected, with a score value of 3.4. The seasonal time series deformation of that point is obtained by multiplying its score by the corresponding time series of the IC1 eigenvector. Figure 10a shows the comparison between the seasonal time series of this point and the water level in the well. As can be seen from the figure, their changes with time show good agreement, and the positive correlation between deformation time series and groundwater levels shows that the subsidence in the Santa Ana basin is controlled by the fluctuations in the process of groundwater exploitation.
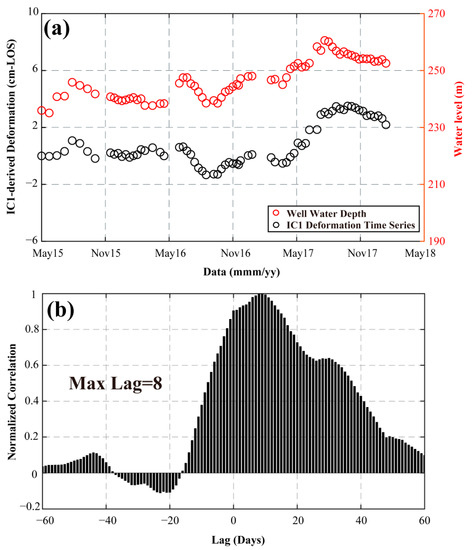
Figure 10.
(a) Comparison between the IC1-derived deformation time series and groundwater levels. The red dots represent the water level and the black dots represent the IC1-derived deformation time series. (b) Cross-correlation coefficient between the IC1-derived deformation and groundwater level.
We further explain the relationship between water level and IC1-derived deformation time series through a cross-correlation analysis, which can quantify the seasonal effects on surface deformation. The cross-correlation coefficient is a standard parameter for estimating the degree of correlation between two series and provides a good explanation for the correlation between IC1-derived deformation time series and groundwater level with different time scales in the basin. Figure 10b shows the cross-correlation coefficient, and the maximum delay represents the number of days of delay when the cross-correlation coefficient reaches a maximum. The IC1-derived deformation time series and groundwater level are positively correlated with a lag of only 8 days, indicating that the surface deformation responds quickly to the changes in water level. Therefore, by using the cross-correlation coefficient, we can determine that the seasonal deformation of the basin is mainly caused by the groundwater factor.
In aquifer systems, the elastic skeletal storage coefficient is the key hydraulic parameter reflecting the stable flow of groundwater, which is very important for the evaluation of groundwater resources. In the Santa Ana basin, ICA separates the accurate seasonal displacement component (IC1), which is very helpful to the estimation of basin model parameters. We then assessed whether the land subsidence observed in the Santa Ana basin was recoverable (elastic) or unrecoverable (inelastic). Taking into account the seasonal component IC1, we calculate a change in the displacement component of 0.98 cm during the observation period, and the change in groundwater level elevation is 16.6 m. The acquisitions of both deformation and groundwater data provide us a chance to calculate elastic skeletal storage coefficient for the aquifer [53]. The elastic skeletal storage coefficient estimated in this study is , which is accordant with previous results derived from the combination of InSAR and GNSS observations acquired during the period 2003–2007 [16]. This indicates that the elasticity of the aquifer in the Santa Ana Basin did not weaken from 2003 to 2018.
5.2. Comparison of PCA and ICA
As the preprocessing step of ICA, PCA decomposes the covariance matrix of mixed signals into a linear combination of multiple principal components (PCs) by calculating the eigenvector and eigenvalue. PCA not only reduces the dimension of the data, but also removes noise and preserves as many source signal features as possible. To compare the performance of ICA and PCA, we also apply PCA to the InSAR time series. The first step is to form a two-dimensional matrix of InSAR time series with a size of 69 × 1,662,774. Figure 11 shows the results of PCA, and four principal components are obtained. Figure 11a–d show the score values of the spatial patterns of the four principal components, respectively, and the spatial component is standardized. Figure 11e shows the temporal eigenvectors of each principal component.
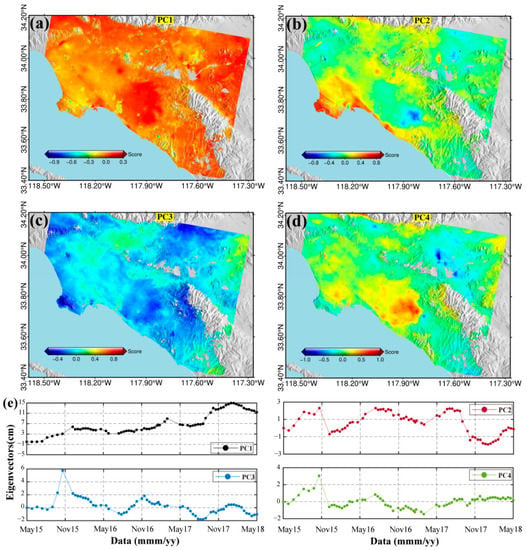
Figure 11.
PCA results for the descending InSAR time series. Four independent components are isolated. (a–d) show the score values of the spatial patterns of the principal components, respectively, and (e) shows the temporal eigenvectors of each principal component.
These four principal components account for the main features of the mixed InSAR signal, including long-term deformation, seasonal fluctuation, and noise. However, the four principal components are only uncorrelated and not independent of each other. The seasonal motion can be observed for the eigenvector time series (Figure 11d). In contrast, ICA can completely separate the seasonal motion as an independent component. Therefore, in the presence of high levels of noise, ICA can still be used to extract the deformation signal of interest.
5.3. Newport–Inglewood Fault Structure from IC1 Score Map
The Newport–Inglewood fault (NIF) has been identified as an active fault zone, which is located on the western edge of the Santa Ana basin and can produce damaging earthquakes [14]. The score value ranges from −0.6 to −0.2 along the west side of the NIF, while the score ranges from 0.2 to 1 along the east side, as shown in Figure 12. The comparison of IC1 score values on both sides of NIF is very obvious, and the fault is the active boundary of seasonal displacement. Outside the basin, the score decreases rapidly, especially at the western margin of the basin bounded by the NIF. The fault can prevent the movement of groundwater, resulting in long-term uplift. It should be noted that the seasonal deformation in the Santa Ana basin is more complex due to the contribution of anthropogenic and tectonic signals. By using the multitemporal InSAR method and ICA, it is determined that most of the deformation near NIF is related to groundwater pumping rather than tectonic fault movements.
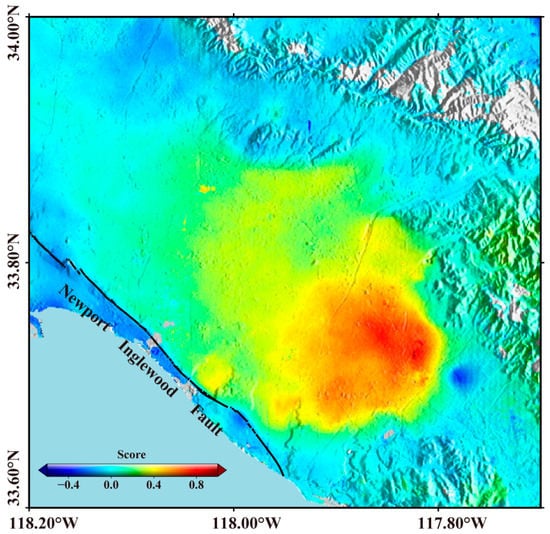
Figure 12.
Local map of IC1 score values around the NIF.
6. Conclusions
As a blind source signal separation method, ICA can separate the temporal and spatial characteristics of signals, therefore being suitable for InSAR time series analysis. In this paper, we verify the feasibility of ICA to extract the spatiotemporal information from InSAR observations. The experimental results from the analysis of the Sentienal-1A data show that the ICA method can successfully derive the temporal and spatial characteristics of deformation sources from InSAR time series, even if there are error signals.
We investigated and analyzed the land deformation of the Santa Ana basin in Los Angeles by using the multitemporal InSAR technique and descending C-band Sentinel-1 SAR data acquired from 2015 to 2018. There is a main subsidence zone in the Santa Ana basin, and the deformation rates are mainly between 10 mm/year and 20 mm/year. The uplift was relatively small from 2015 to 2016, while the surface uplift accelerated and the uplift amplitude was large from 2017 to 2018. The spatial characteristics of the deformation rate in 2017–2018 were the most obvious, with the rates being mainly between 20 mm/year and 30 mm/year. The subsidence is related to the height of the groundwater level in the aquifer, indicating that the extraction and recharge of artificial groundwater are the main influencing factors. ICA is used to separate the spatiotemporal characteristics of four independent components, including two deformation components and two noise components. The temporal eigenvector of IC1 is seasonal with a period of about one year, and the score value map shows deformation concentrated in the Santa Ana basin. IC1 is the component we are interested in that can fully describe the spatiotemporal characteristics of the Santa Ana basin. We reconstruct the seasonal deformation time series by multiplying the temporal eigenvector of IC1 by the corresponding score value. The IC1-derived deformation time series are in agreement with the GNSS-derived ones, which verifies the accuracy of the ICA decomposition. The study also demonstrated that there is a positive correlation between IC1-derived deformation time series and groundwater levels, with a lag of only 8 days.
The seasonal deformation can be further used to estimate the properties of the aquifer system in the Santa Ana basin, such as groundwater storage loss and skeletal storativity; a process which can be carried out in the future. Quantifying the characteristics of the aquifer system through InSAR is still a frontier topic, and it is believed that the combination of ICA and InSAR measurements will better guide water resources management and help evaluate the health status of aquifer systems.
Author Contributions
Conceptualization, K.Z., Q.S. and J.H.; methodology, K.Z. and X.Z.; software, J.H.; validation, K.Z., Q.S. and J.H.; formal analysis, K.Z. and Q.S.; investigation, H.W.; resources, K.Z. and Q.S.; writing—original draft preparation, K.Z., Q.S. and J.H.; writing—review and editing, all authors.; supervision, J.H.; funding acquisition, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the National Natural Science Foundation of China (42030112), the Nature Science Foundation of Hunan Province (2020JJ2043), the Project of Innovation-driven Plan of Central South University (2019CX007), and the Postgraduate Independent Exploration and Innovation Project of Central South University (512191040).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The Sentinel-1 data are made freely available by the European Space Agency and distributed and archived by the Alaska Satellite Facility (https://www.asf.alaska.edu/sentinel/ accessed on 20 March 2022), the GPS data used in this study can be downloaded from the Nevada Geodetic Laboratory (http://geodesy.unr.edu/ accessed on 2 April 2022), groundwater level data were obtained from the USGS (https://waterdata.usgs.gov/nwis accessed on 10 April 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Terzaghi, K. Principles of soil mechanics, IV—Settlement and consolidation of clay. Eng. News Rec. 1925, 95, 874–878. [Google Scholar]
- Peng, M.M.; Lu, Z.; Zhao, C.Y.; Motagh, M.; Bai, L.; Conway, B.D.; Chen, H.Y. Mapping land subsidence and aquifer system properties of the Willcox Basin, Arizona, from InSAR observations and independent component analysis. Remote Sens. Environ. 2022, 271, 112894. [Google Scholar] [CrossRef]
- Thu, T.M.; Fredlund, D.G. Modelling subsidence in the Hanoi city area, Vietnam. Can. Geotech. J. 2000, 37, 621–637. [Google Scholar] [CrossRef]
- Phien-wej, N.; Giao, P.H.; Nutalaya, P. Land subsidence in Bangkok, Thailand. Eng. Geol. 2006, 82, 187–201. [Google Scholar] [CrossRef]
- Ortiz-Zamora, D.; Ortega-Guerrero, A. Evolution of long-term land subsidence near Mexico City: Review, field investigations, and predictive simulations. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Shen, S.L.; Ma, L.; Xu, Y.S.; Yin, Z.Y. Interpretation of increased deformation rate in aquifer IV due to groundwater pumping in Shanghai. Can. Geotech. J. 2013, 50, 1129–1142. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Lyu, H.-M.; Han, J.; Shen, S.-L. Dewatering-induced building settlement around a deep excavation in soft deposit in Tianjin, China. J. Geotech. Geoenviron. Eng. 2019, 145, 05019003. [Google Scholar] [CrossRef]
- Peng, M.; Zhao, C.; Zhang, Q.; Lu, Z.; Li, Z. Research on Spatiotemporal Land Deformation (2012–2018) over Xi’an, China, with Multi-Sensor SAR Datasets. Remote Sens. 2019, 11, 664. [Google Scholar] [CrossRef] [Green Version]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.J.; Baker, B. Remote Sensing of Ground Deformation for Monitoring Groundwater Management Practices: Application to the Santa Clara Valley During the 2012–2015 California Drought. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Riel, B.; Simons, M.; Ponti, D.; Agram, P.; Jolivet, R. Quantifying Ground Deformation in the Los Angeles and Santa Ana Coastal Basins Due to Groundwater Withdrawal. Water Resour. Res. 2018, 54, 3557–3582. [Google Scholar] [CrossRef] [Green Version]
- Qu, F.; Lu, Z.; Zhang, Q.; Bawden, G.W.; Kim, J.-W.; Zhao, C.; Qu, W. Mapping ground deformation over Houston–Galveston, Texas using multi-temporal InSAR. Remote Sens. Environ. 2015, 169, 290–306. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology; Waveland Press: Long Grove, IL, USA, 2018. [Google Scholar]
- Hu, B.; Chen, X.L.; Zhang, X.F. Using Multisensor SAR Datasets to Monitor Land Subsidence in Los Angeles from 2003 to 2017. J. Sens. 2019, 2019, 9389820. [Google Scholar] [CrossRef] [Green Version]
- Watson, K.M.; Bock, Y.; Sandwell, D.T. Satellite interferometric observations of displacements associated with seasonal groundwater in the Los Angeles basin. J. Geophys. Res. Solid Earth 2002, 107. [Google Scholar] [CrossRef]
- Wisely, B.A.; Schmidt, D. Deciphering vertical deformation and poroelastic parameters in a tectonically active fault-bound aquifer using InSAR and well level data, San Bernardino basin, California. Geophys. J. Int. 2010, 181, 1185–1200. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Ding, X.L.; Li, Z.W.; Zhang, L.; Zhu, J.J.; Sun, Q.; Gao, G.J. Vertical and horizontal displacements of Los Angeles from InSAR and GPS time series analysis: Resolving tectonic and anthropogenic motions. J. Geodyn. 2016, 99, 27–38. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.-W.; Massoud, E.; Farr, T.G.; Lundgren, P.; Famiglietti, J.S. Monitoring groundwater change in California’s Central Valley using Sentinel-1 and GRACE observations. Geosciences 2019, 9, 436. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Danskin, W.R. InSAR analysis of natural recharge to define structure of a ground-water basin, San Bernardino, California. Geophys. Res. Lett. 2001, 28, 2661–2664. [Google Scholar] [CrossRef] [Green Version]
- Bawden, G.W.; Thatcher, W.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature 2001, 412, 812–815. [Google Scholar] [CrossRef]
- Gambolati, G.; Teatini, P. Geomechanics of subsurface water withdrawal and injection. Water Resour. Res. 2015, 51, 3922–3955. [Google Scholar] [CrossRef]
- Bejar-Pizarro, M.; Ezquerro, P.; Herrera, G.; Tomas, R.; Guardiola-Albert, C.; Hernandez, J.M.R.; Merodo, J.A.F.; Marchamalo, M.; Martinez, R. Mapping groundwater level and aquifer storage variations from InSAR measurements in the Madrid aquifer, Central Spain. J. Hydrol. 2017, 547, 678–689. [Google Scholar] [CrossRef] [Green Version]
- Chaussard, E.; Bürgmann, R.; Shirzaei, M.; Fielding, E.J.; Baker, B. Predictability of hydraulic head changes and characterization of aquifer-system and fault properties from InSAR-derived ground deformation. J. Geophys. Res. Solid Earth 2014, 119, 6572–6590. [Google Scholar] [CrossRef]
- Miller, M.M.; Shirzaei, M. Spatiotemporal characterization of land subsidence and uplift in Phoenix using InSAR time series and wavelet transforms. J. Geophys. Res. Solid Earth 2015, 120, 5822–5842. [Google Scholar] [CrossRef] [Green Version]
- Miller, M.M.; Shirzaei, M.; Argus, D. Aquifer Mechanical Properties and Decelerated Compaction in Tucson, Arizona. J. Geophys. Res. Solid Earth 2017, 122, 8402–8416. [Google Scholar] [CrossRef]
- Jiang, L.; Bai, L.; Zhao, Y.; Cao, G.; Wang, H.; Sun, Q. Combining InSAR and Hydraulic Head Measurements to Estimate Aquifer Parameters and Storage Variations of Confined Aquifer system in Cangzhou North China Plain. Water Resour. Res. 2018, 54, 8234–8252. [Google Scholar] [CrossRef]
- Gualandi, A.; Liu, Z. Variational Bayesian Independent Component Analysis for InSAR Displacement Time—Series With Application to Central California, USA. J. Geophys. Res. Solid Earth 2021, 126. [Google Scholar] [CrossRef]
- Chen, T.; Yan, Z.; Zhang, L.; Li, S. Monitoring Land Surface Displacement over Xuzhou (China) in 2015–2018 through PCA-Based Correction Applied to SAR Interferometry. Remote Sens. 2019, 11, 1494. [Google Scholar] [CrossRef] [Green Version]
- Kositsky, A.; Avouac, J.P. Inverting geodetic time series with a principal component analysis-based inversion method. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Boni, R.; Pilla, G.; Meisina, C. Methodology for Detection and Interpretation of Ground Motion Areas with the A-DInSAR Time Series Analysis. Remote Sens. 2016, 8, 686. [Google Scholar] [CrossRef] [Green Version]
- Vajedian, S.; Motagh, M. Extracting sinkhole features from time-series of TerraSAR-X/TanDEM-X data. Isprs. J. Photogramm. 2019, 150, 274–284. [Google Scholar] [CrossRef]
- Maubant, L.; Pathier, E.; Daout, S.; Radiguet, M.; Doin, M.P.; Kazachkina, E.; Kostoglodov, V.; Cotte, N.; Walpersdorf, A. Independent Component Analysis and Parametric Approach for Source Separation in InSAR Time Series at Regional Scale: Application to the 2017–2018 Slow Slip Event in Guerrero (Mexico). J. Geophys. Res. Solid Earth 2020, 125. [Google Scholar] [CrossRef]
- Liang, H.Y.; Zhang, L.; Lu, Z.; Li, X. Nonparametric Estimation of DEM Error in Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10004–10014. [Google Scholar] [CrossRef]
- Ebmeier, S.K. Application of independent component analysis to multitemporal InSAR data with volcanic case studies. J. Geophys. Res. Solid Earth 2016, 121, 8970–8986. [Google Scholar] [CrossRef]
- Cohen-Waeber, J.; Bürgmann, R.; Chaussard, E.; Giannico, C.; Ferretti, A. Spatiotemporal Patterns of Precipitation-Modulated Landslide Deformation From Independent Component Analysis of InSAR Time Series. Geophys. Res. Lett. 2018, 45, 1878–1887. [Google Scholar] [CrossRef]
- Chaussard, E.; Farr, T.G. A New Method for Isolating Elastic From Inelastic Deformation in Aquifer Systems: Application to the San Joaquin Valley, CA. Geophys. Res. Lett. 2019, 46, 10800–10809. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE T. Geosci. Remote. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Hu, J.; Ge, Q.Q.; Liu, J.H.; Yang, W.Y.; Du, Z.G.; He, L.H. Constructing Adaptive Deformation Models for Estimating DEM Error in SBAS-InSAR Based on Hypothesis Testing. Remote Sens. 2021, 13, 2006. [Google Scholar] [CrossRef]
- Ren, H.R.; Feng, X.M. Calculating vertical deformation using a single InSAR pair based on singular value decomposition in mining areas. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102115. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Burgmann, R.; Li, Z.W.; Sun, Q.; Ma, Z.F. A Strain-Model Based InSAR Time Series Method and Its Application to The Geysers Geothermal Field, California. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021939. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, L.; Feng, G.; Lu, Z.; Sun, Q. On the Accuracy of Topographic Residuals Retrieved by MTInSAR. IEEE Trans. Geosci. Remote 2017, 55, 1053–1065. [Google Scholar] [CrossRef]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [Green Version]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Hyvarinen, A.; Cristescu, R.; Oja, E. A fast algorithm for estimating overcomplete ICA bases for image windows. In Proceedings of the Ijcnn’99 International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999. [Google Scholar]
- Oja, E.; Yuan, Z. The fastICA algorithm revisited: Convergence analysis. IEEE Trans. Neural Netw. 2006, 17, 1370–1381. [Google Scholar] [CrossRef] [PubMed]
- Langlois, D.; Chartier, S.; Gosselin, D. An Introduction to Independent Component Analysis: InfoMax and FastICA algorithms. Tutor. Quant. Methods Psychol. 2010, 6, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Bakir, T.; Peter, A.; Riley, R.; Hackett, J. Non-Negative Maximum Likelihood ICA for Blind Source Separation of Images and Signals with Application to Hyperspectral Image Subpixel Demixing. In Proceedings of the IEEE International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006. [Google Scholar]
- Belitz, K.; Hamlin, S.N.; Burton, C.A.; Kent, R.; Fay, R.G.; Johnson, T. Water Quality in the Santa Ana Basin, California, 1999–2001; USGS Publications Warehouse: Reston, VA, USA, 2004. [Google Scholar]
- Herndon, R.; Bonsangue. Hydrogeology of the Orange County Groundwater Basin–An Updated.Overview. In Geology of the Orange County Region, Southern California, South Coast Geological Society Field Trip Guide Book; South Coast Geological Society: Santa Ana, CA, USA, 2006; pp. 157–179. [Google Scholar]
- Woodside, G.; Westropp, M. Orange County water district groundwater management plan 2015 update. In Orange County Water District; Orange County Water District: Fountain Valley, CA, USA, 2015. [Google Scholar]
- Wu, W.; Cui, H.; Hu, J.; Yao, L. Detection and 3D visualization of deformations for high-rise buildings in Shenzhen, China from high-resolution TerraSAR-X datasets. Appl. Sci. 2019, 9, 3818. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Lu, Z.; Ding, X.L.; Jung, H.S.; Feng, G.C.; Lee, C.W. Mapping ground surface deformation using temporarily coherent point SAR interferometry: Application to Los Angeles Basin. Remote Sens. Environ. 2012, 117, 429–439. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hudnut, K.W.; Ingebritsen, S.; Phillips, S.P.; Peltzer, G.; Rogez, F.; Rosen, P. Detection of aquifer system compaction and land subsidence using interferometric synthetic aperture radar, Antelope Valley, Mojave Desert, California. Water Resour. Res. 1998, 34, 2573–2585. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).