Regional “Bare-Earth” Digital Terrain Model for Costa Rica Based on NASADEM Corrected for Vegetation Bias
Abstract
:1. Introduction
2. Materials and Methods
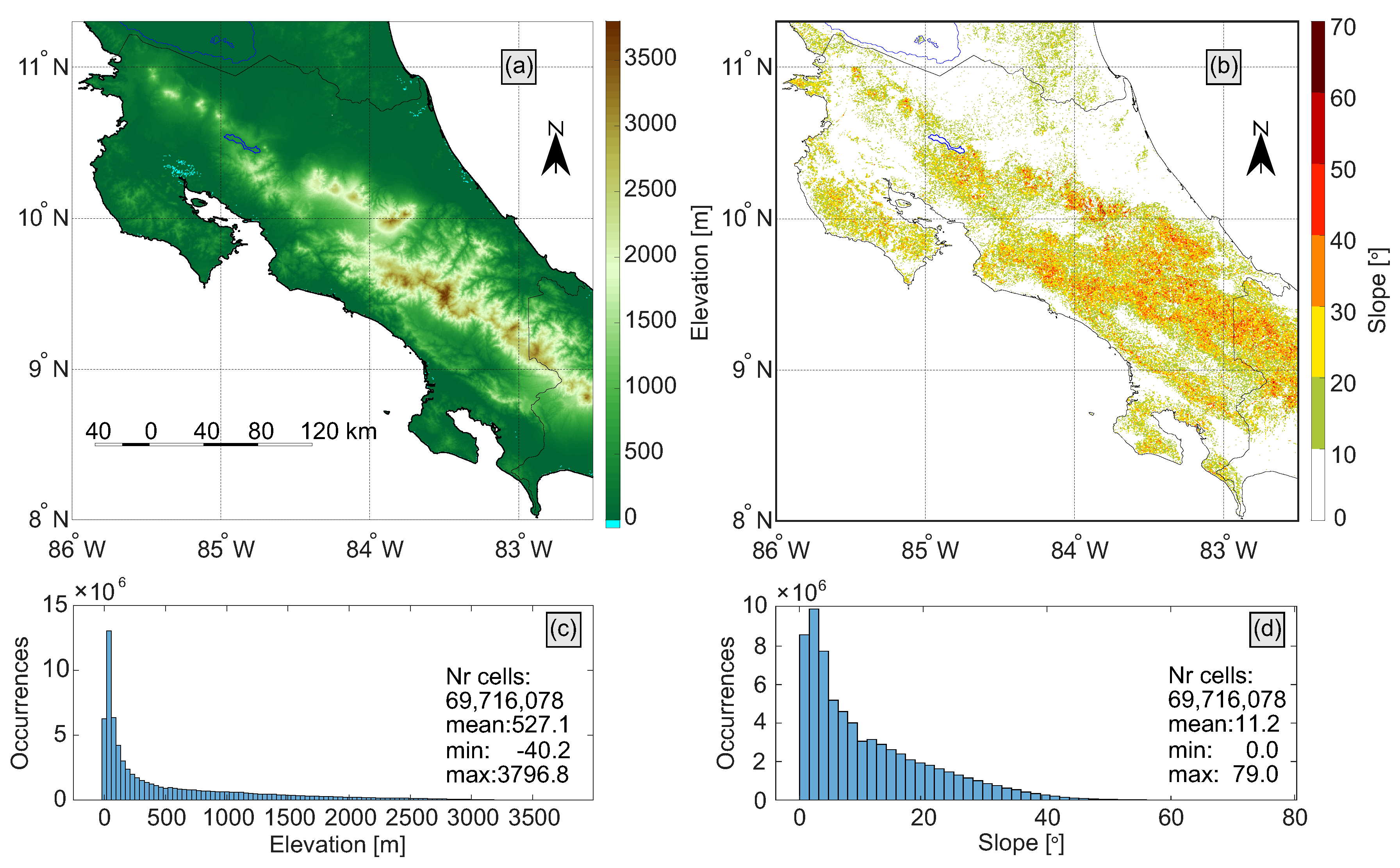
2.1. Study Area
2.2. Data
2.2.1. Digital Elevation Models
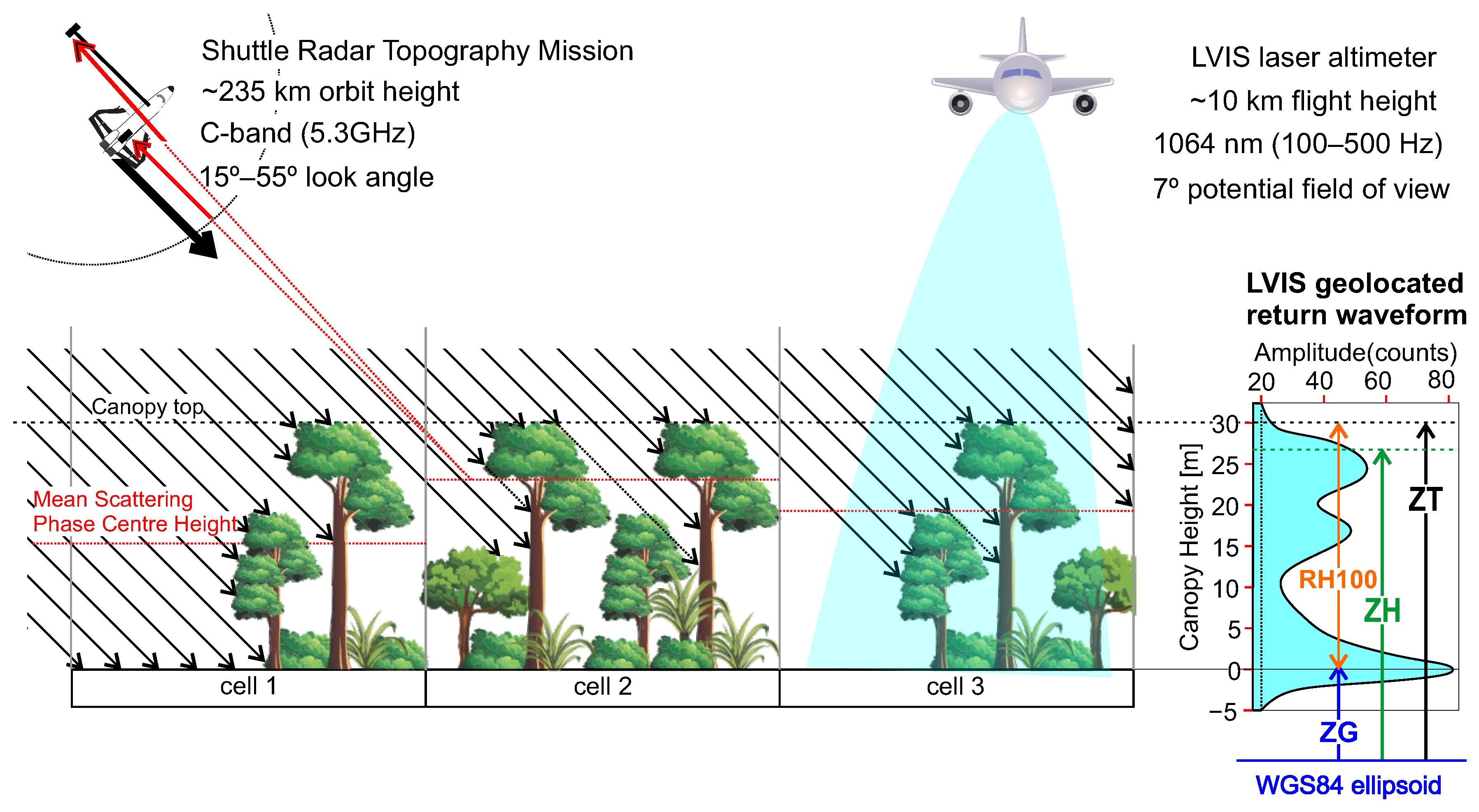
2.2.2. LVIS
2.2.3. Levelling Dataset
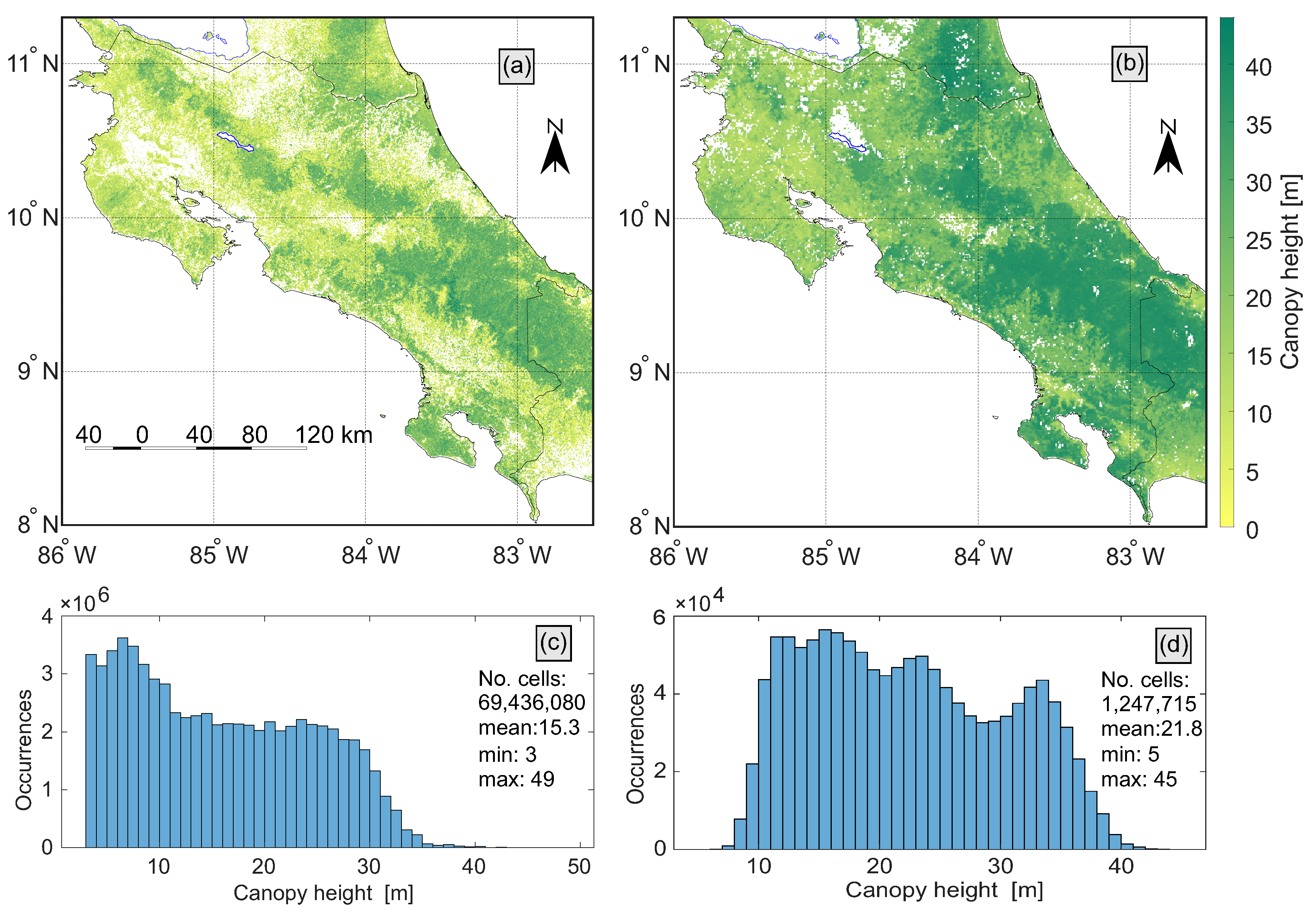
2.2.4. Global Forest Canopy Height 2019
2.2.5. Forest Canopy Height Map
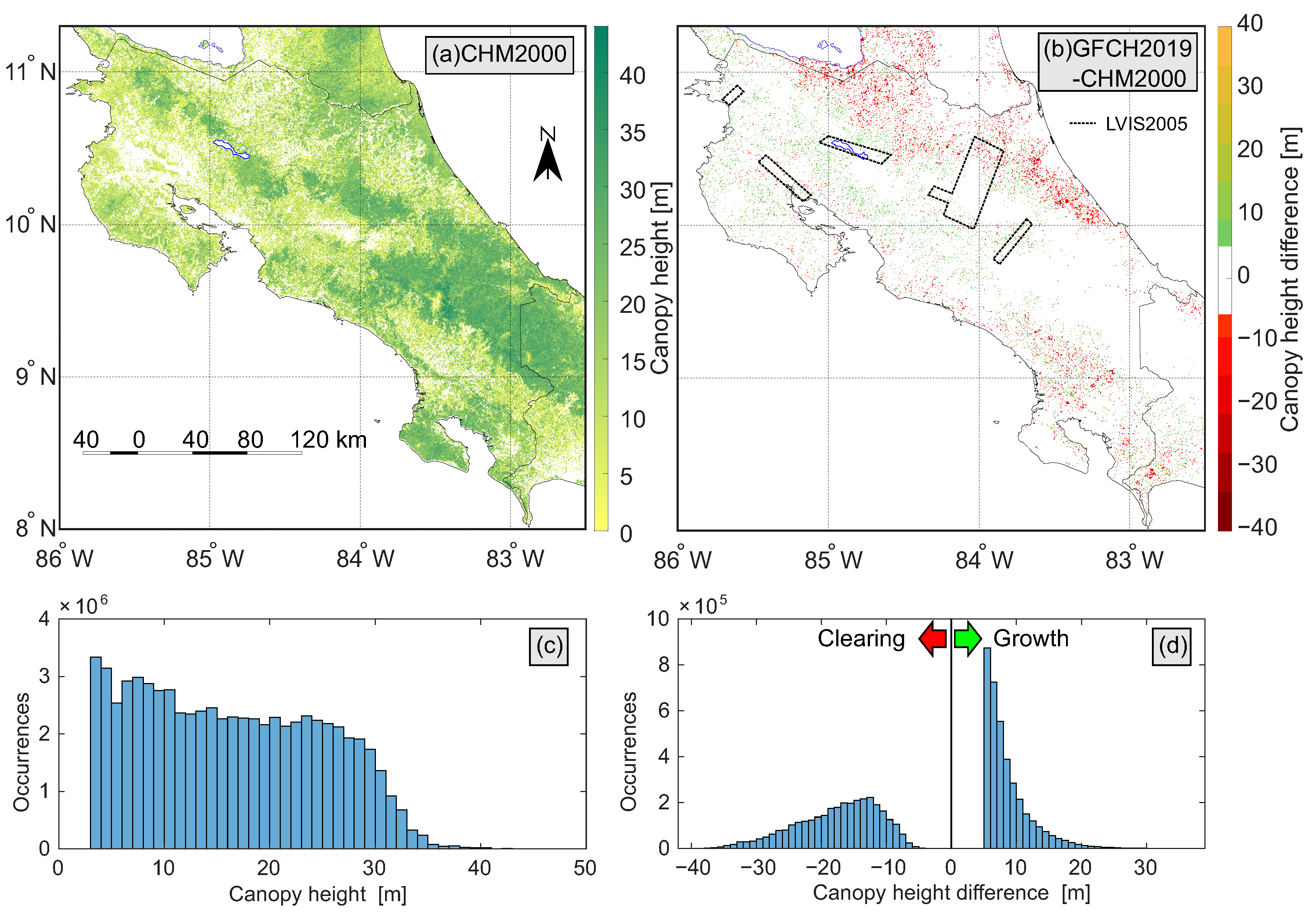
2.2.6. Global Forest Change Model 2000 to 2019
2.3. Methods
2.3.1. Evaluation of Global DEMs for Costa Rica
2.3.2. Model of Canopy for Year 2000
- Clearing: Cells with zero canopy height in 2019 and densities above 50% in 2000. CHM2000 for these cells was computed as canopy height interpolated with the nearest neighbour method from FCHM2005 and multiplied by the canopy density value. The choice of the threshold for density was made using different test areas and comparisons to Landsat images. If no threshold was set or FCHM2005 was taken without scaling by density, the resulting model tended to add rather high vegetation to agricultural areas given that FCHM2005 is a low-resolution model that overestimates canopy heights. Furthermore, for this reason, the expected accuracy of CHM2000 for the clearing case is lower than for others. It was observed that the areas of volcano craters and their surroundings that are not covered by any vegetation had positive canopy densities in 2000. These areas were manually enclosed in polygons and excluded from clearing cases.
- Growth: In this case, canopy heights in 2019 were above 5 , but the density was zero in 2000. The value for canopy height in CHM2000 was then set to zero. The reason for the 5 threshold is that GFCH2019 defines canopy height for vegetation above 3 , while the canopy density model uses a 5 value. In this way, all cells with heights below 5 are the same in CHM2000 and GFCH2019.
- No change: In all other cases, CHM2000 was equal to GFCH2019 assuming no natural change in canopy height. In Dubayah et al., 2010 [38], the estimation of tree height change specifically in a tropical forest of Costa Rica was provided. They quantified changes in forest canopy height and other related parameters using data from LVIS 1998 and LVIS2005. Pairwise comparisons of nearly coincident LiDAR footprints between these years showed that secondary forests had a net gain of in height, while old-growth forests had diminished, with a height net loss of . Therefore, in similar forest types in Costa Rica, a 19-year linear prediction would give growth in secondary forests of and height loss in primary forests of . As our study did not distinguish either land use nor forest types, as well as such a linear trend is not reasonable for long-term prediction, no such estimation was applied. Nevertheless, we are aware that using canopy heights determined for 2019 for the correction of a DEM that corresponds to the year 2000 could result in errors of several metres magnitude just due to the natural canopy height change.
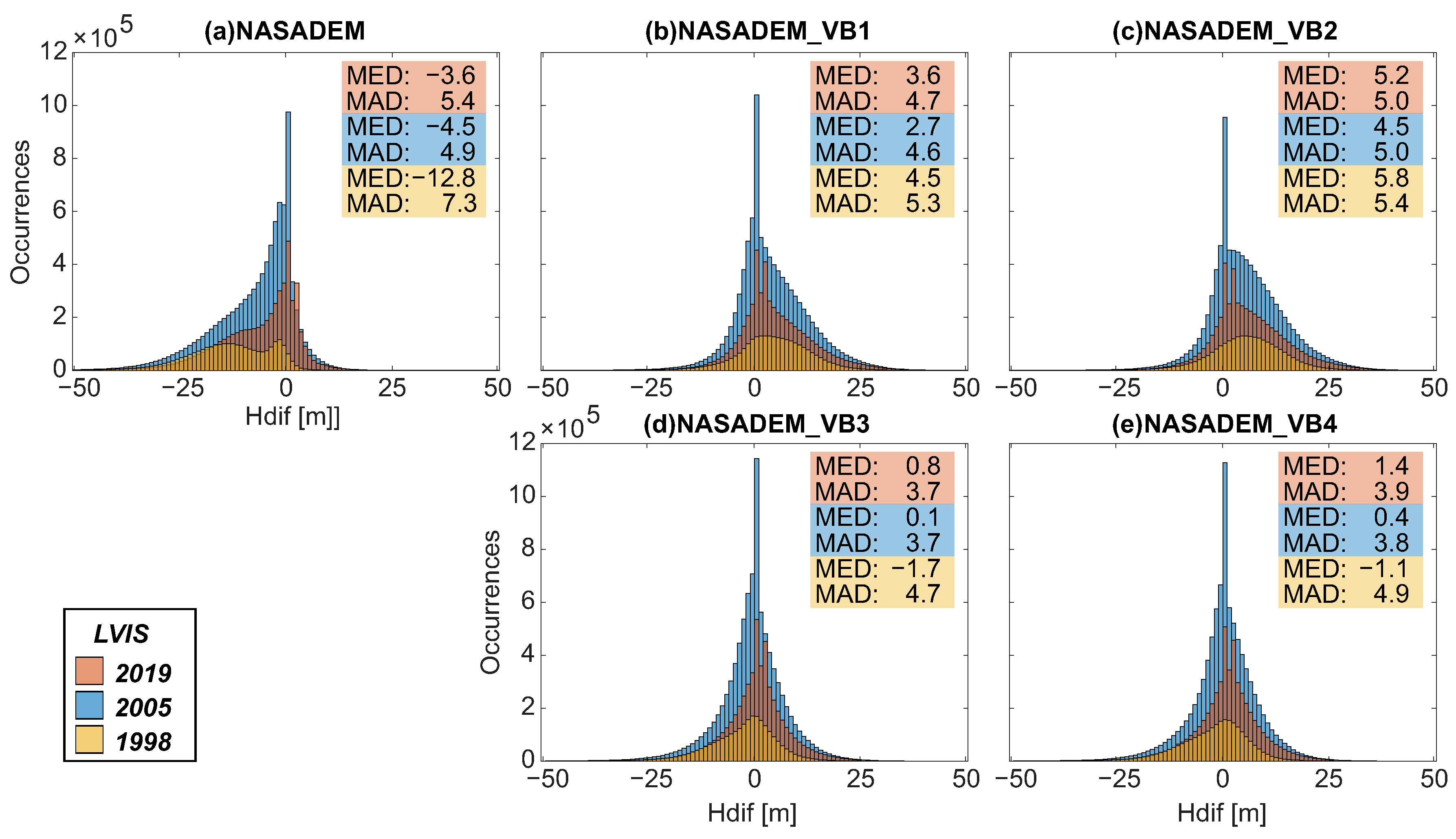
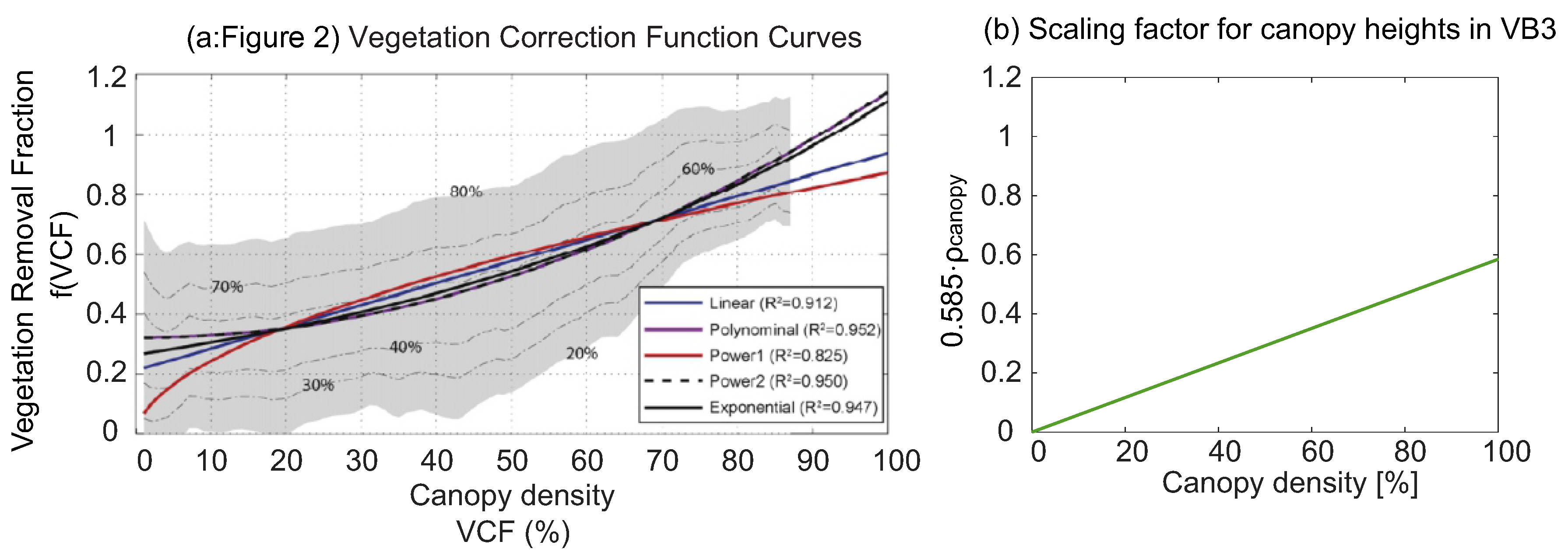
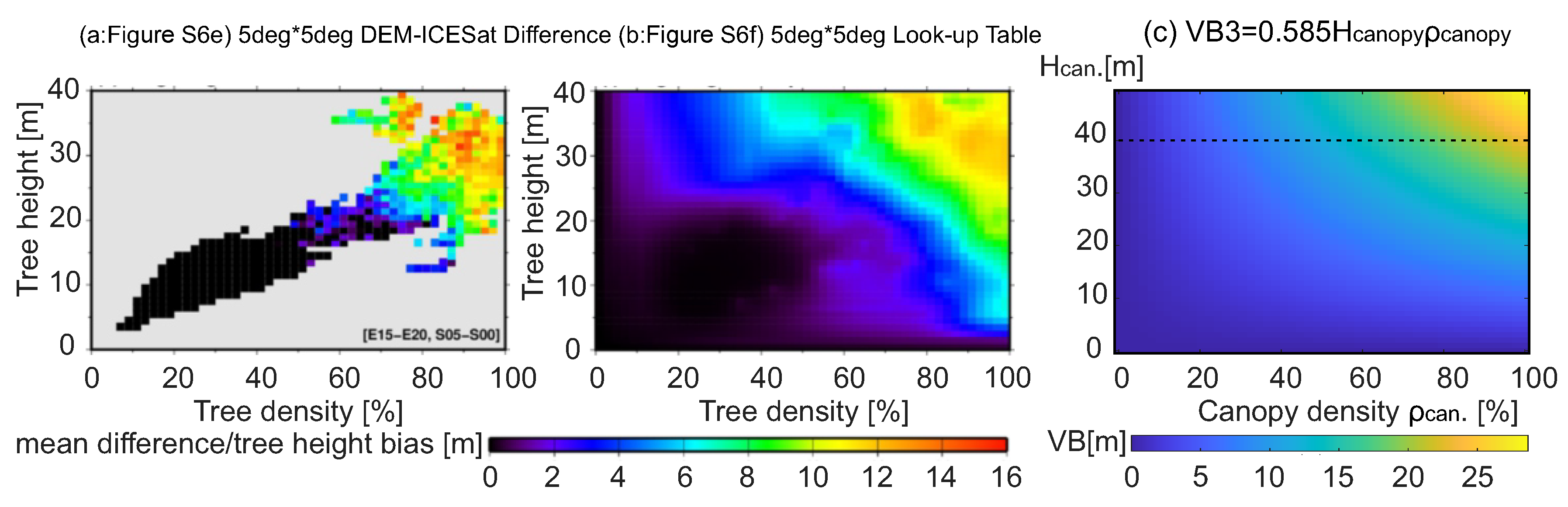
2.3.3. NASADEM Correction for Vegetation Bias
- ;
- ;
- ;
- .
2.3.4. CRDTM2020 and CRDTM2020plus
3. Results
3.1. Canopy Height Model 2000
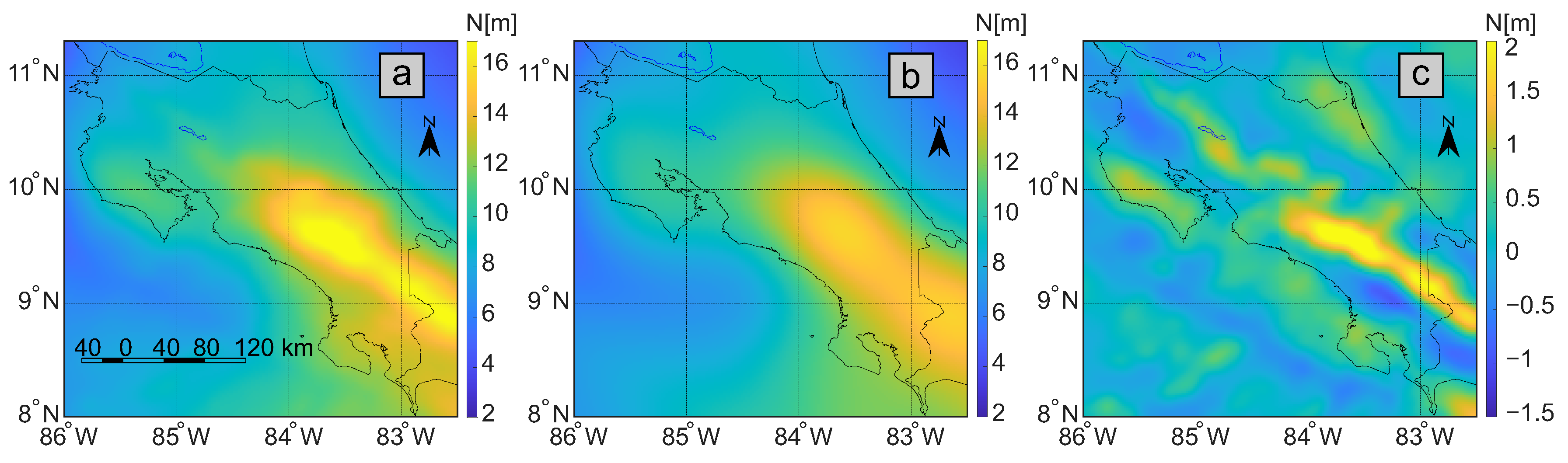
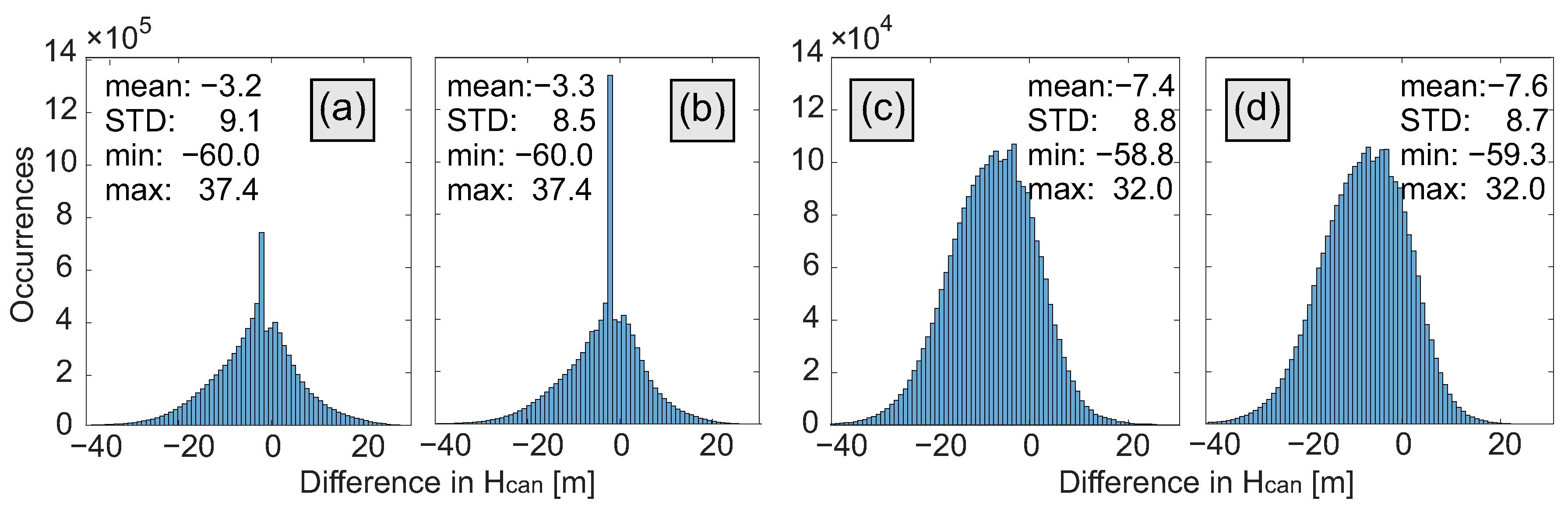
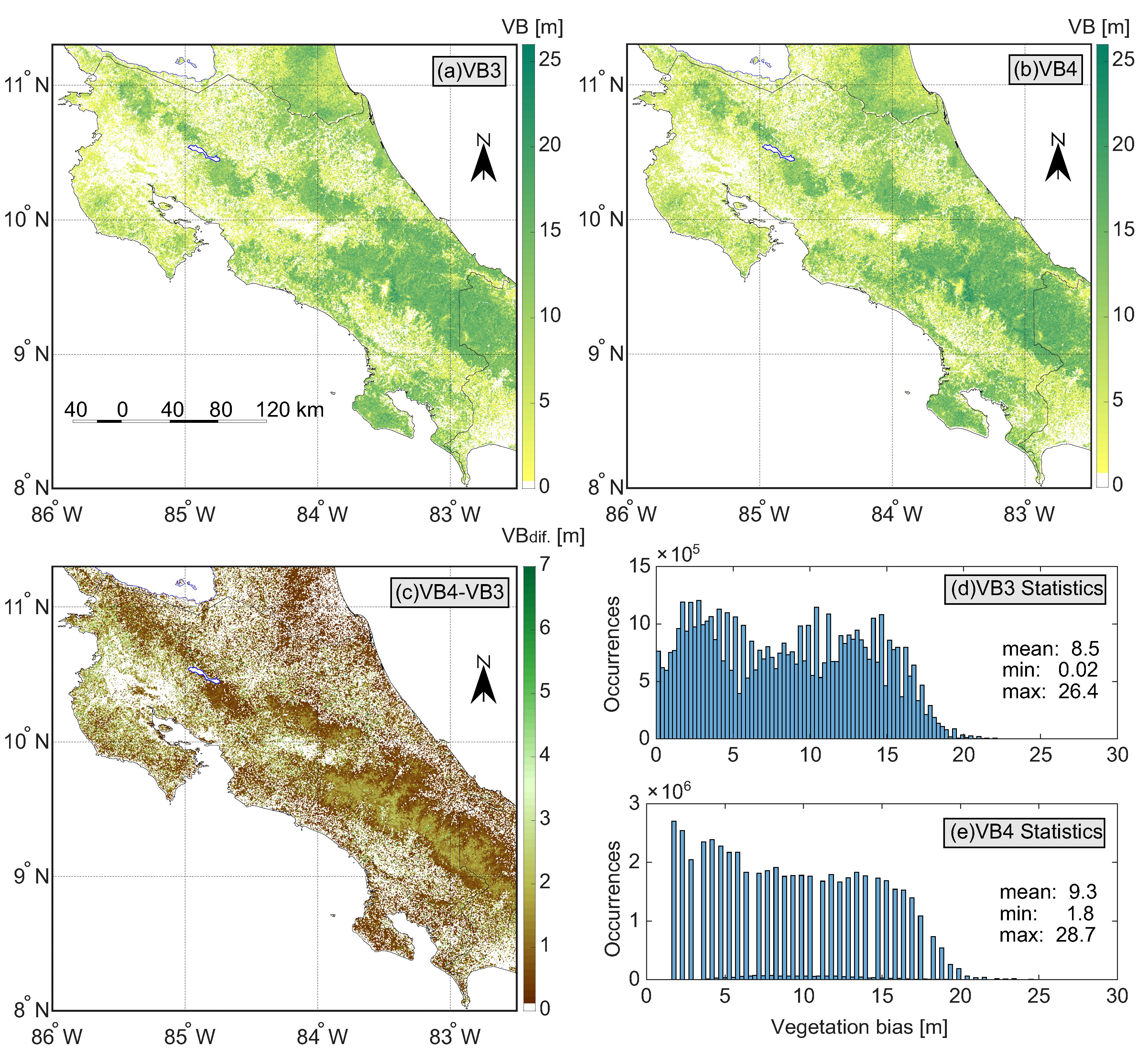
3.2. Vegetation Bias
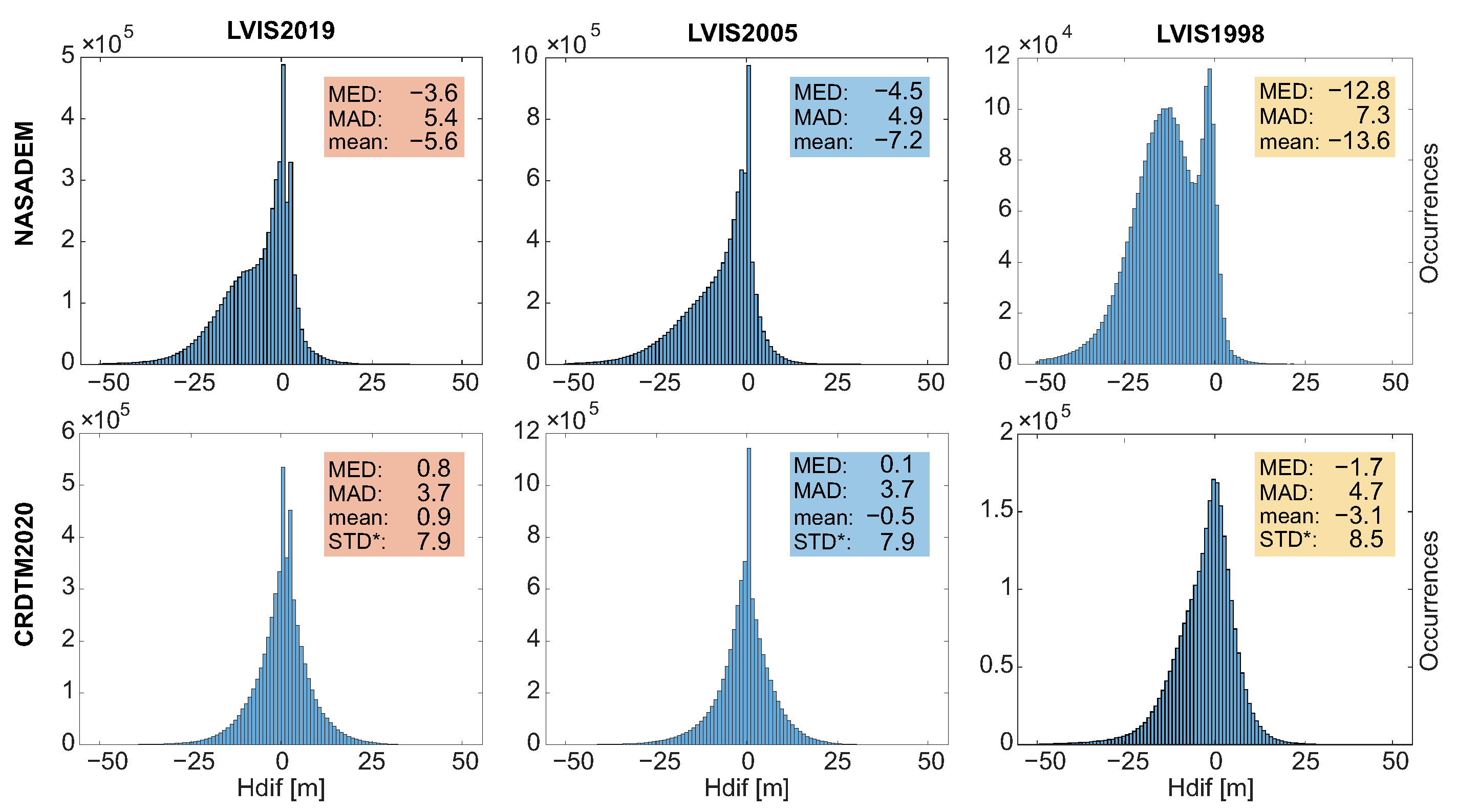
3.3. CRDTM2020 and Validation
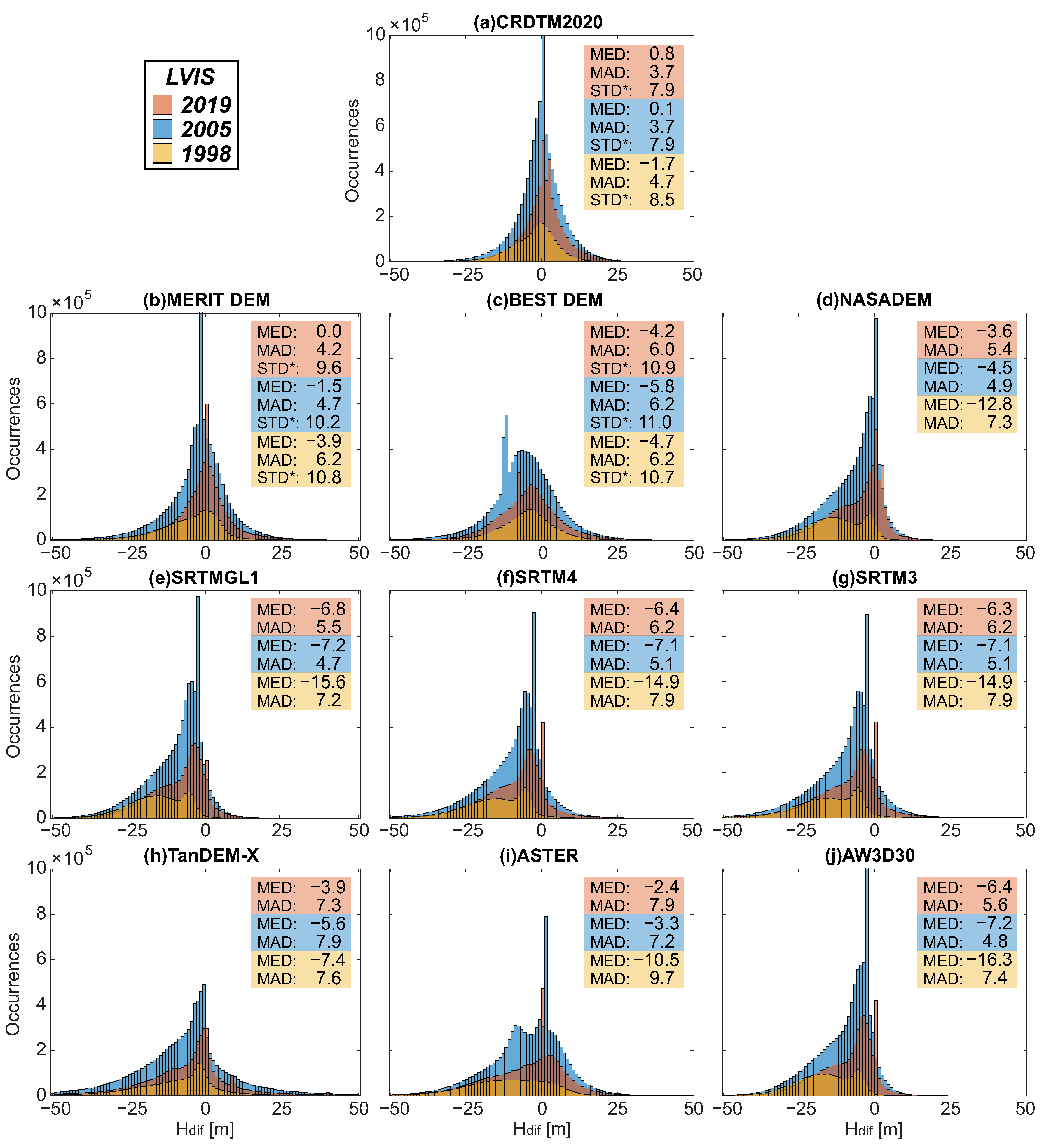
3.4. DEMs Evaluation
4. Discussion
4.1. Vegetation Bias
4.2. CRDTM2020
4.3. DEMs Evaluation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ripple, W.J.; Wolf, C.; Newsome, T.M.; Barnard, P.; Moomaw, W.R. World Scientists’ Warning of a Climate Emergency. BioScience 2020, 70, 8–12. [Google Scholar] [CrossRef]
- O’Loughlin, F.E.; Paiva, R.C.D.; Durand, M.; Alsdorf, D.E.; Bates, P.D. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Hirt, C.; Rexer, M.; Pail, R.; Yamazaki, D. The tree-canopy effect in gravity forward modelling. Geophys. J. Int. 2019, 219, 271–289. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef] [Green Version]
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m global map of elevation with forests and buildings removed. J. Phys. Energy 2022, preprint. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne LiDAR. J. Geophys. Res. Biogeosci. 2011, 116, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G.; Carroll, M.; Dimiceli, C.; Sohlberg, R.A. Global Percent Tree Cover at a Spatial Resolution of 500 Meters: First Results of the MODIS Vegetation Continuous Fields Algorithm. Earth Interact. 2003, 7, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Baugh, C.A.; Bates, P.D.; Schumann, G.; Trigg, M.A. SRTM vegetation removal and hydrodynamic modeling accuracy. Water Resour. Res. 2013, 49, 5276–5289. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Guo, Q.; Ma, Q.; Li, W. SRTM DEM Correction in Vegetated Mountain Areas through the Integration of Spaceborne LiDAR, Airborne LiDAR, and Optical Imagery. Remote Sens. 2015, 7, 11202–11225. [Google Scholar] [CrossRef] [Green Version]
- Magruder, L.; Neuenschwander, A.; Klotz, B. Digital terrain model elevation corrections using space-based imagery and ICESat-2 laser altimetry. Remote Sens. Environ. 2021, 264, 112621. [Google Scholar] [CrossRef]
- Wilson, M.D.; Bates, P.; Alsdorf, D.; Forsberg, B.; Horritt, M.; Melack, J.; Frappart, F.; Famiglietti, J. Modeling large-scale inundation of Amazonian seasonally flooded wetlands. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Carabajal, C.C.; Harding, D.J. SRTM C-band and ICESat laser altimetry elevation comparisons as a function of tree cover and relief. Photogramm. Eng. Remote Sens. 2006, 72, 287–298. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Landa, A.; Algeet-Abarquero, N.; Fernández-Moya, J.; Guillén-Climent, M.L.; Pedroni, L.; García, F.; Espejo, A.; Villegas, J.F.; Marchamalo, M.; Bonatti, J.; et al. An Operational Framework for Land Cover Classification in the Context of REDD+ Mechanisms. A Case Study from Costa Rica. Remote Sens. 2016, 8, 593. [Google Scholar] [CrossRef] [Green Version]
- Moran, M.D.; Monroe, A.; Stallcup, L. A proposal for practical and effective biological corridors to connect protected areas in northwest Costa Rica. Nat. Conserv. 2019, 36, 113–137. [Google Scholar] [CrossRef] [Green Version]
- Beita Morera, C.; Sandoval Murillo, L.F.; Alvarado Alfaro, L.D. Ecological corridors in Costa Rica: An evaluation applying landscape structure, fragmentation-connectivity process, and climate adaptation. Conserv. Sci. Pract. 2021, 3, e475. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- NASA JPL. NASA Shuttle Radar Topography Mission Global 1 arc Second [Data Set]. NASA EOSDIS Land Processes DAAC. 2013. Available online: https://lpdaac.usgs.gov/products/srtmgl1v003/ (accessed on 24 September 2020).
- NASA JPL. NASADEM Merged DEM Global 1 arc Second V001 [Data Set]. NASA EOSDIS Land Processes DAAC. 2020. Available online: https://lpdaac.usgs.gov/products/nasadem_hgtv001/ (accessed on 8 September 2020).
- Buckley, S.M.; Agram, P.S.; Belz, J.E.; Crippen, R.E.; Gurrola, E.M.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.M.; Neumann, M.; et al. NASADEM: User Guide; Technical Report; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2020. [Google Scholar]
- Crippen, R.; Buckley, S.; Agram, P.; Belz, E.; Gurrola, E.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.; Neumann, M.; et al. Nasadem Global Elevation Model: Methods and Progress. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 125–128. [Google Scholar] [CrossRef] [Green Version]
- Japan Aerospace Exploration Agency. ALOS Global Digital Surface Model (DSM) “ALOS World 3D-30 m” (AW3D30) Ver.3.2/3.1 Product Description; Technical Report; Japan Aerospace Exploration Agency: Tokyo, Japan, 2021. [Google Scholar]
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Generation of the 30 m-Mesh Global Digital Surface Model by ALOS Prism. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2016, XLI-B4, 157–162. [Google Scholar] [CrossRef] [Green Version]
- NASA/METI/AIST/Japan Spacesystems and U.S./Japan ASTER Science Team. ASTER Global Digital Elevation Model V003 [Data Set]. NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/astgtmv003/ (accessed on 18 November 2020).
- NASA JPL. NASA Shuttle Radar Topography Mission Global 3 arc Second [Data Set]. NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/srtmgl3v003/ (accessed on 18 September 2020).
- Jarvis, A.; Reuter, H.; Nelson, A.; Guevara, E. Hole-filled SRTM for the Globe Version 4 [Data Set]. Available from the CGIAR-CSI SRTM 90 m Database. 2008. Available online: http://srtm.csi.cgair.org (accessed on 4 April 2020).
- Paiva, R.; O’Loughlin, F. Bare-Earth SRTM [Data Set]. 2015. Available online: https://data.bris.ac.uk/data/dataset/10tv0p32gizt01nh9edcjzd6wa (accessed on 18 November 2020).
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Borla Tridon, D.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Blair, J.B.; Rabine, D.L.; Hofton, M.A. The Laser Vegetation Imaging Sensor: A medium-altitude, digitisation-only, airborne laser altimeter for mapping vegetation and topography. ISPRS J. Photogramm. Remote Sens. 1999, 54, 115–122. [Google Scholar] [CrossRef]
- Kenyi, L.W.; Dubayah, R.; Hofton, M.; Schardt, M. Comparative analysis of SRTM-NED vegetation canopy height to LIDAR-derived vegetation canopy metrics. Int. J. Remote Sens. 2009, 30, 2797–2811. [Google Scholar] [CrossRef]
- Hofton, M.A.; Rocchio, L.E.; Blair, J.B.; Dubayah, R. Validation of Vegetation Canopy Lidar sub-canopy topography measurements for a dense tropical forest. J. Geodyn. 2002, 34, 491–502. [Google Scholar] [CrossRef]
- Blair, J.; Hofton, M.; Rabine, D. Processing of NASA LVIS Elevation and Canopy (LGE, LCE and LGW) Data Products. 2018. Available online: http://lvis.gsfc.nasa.gov (accessed on 12 November 2020).
- Blair, J.B.; Hofton, M. LVIS Classic L2 Geolocated Surface Elevation and Canopy Height Product, Version 1. [8°N, 86°W; 11.3°N, 82.5°W]. 2020. Available online: https://nsidc.org/data/LVISC2/versions/1 (accessed on 30 September 2020).
- Potapov, P.; Hansen, M.C.; Kommareddy, I.; Kommareddy, A.; Turubanova, S.; Pickens, A.; Adusei, B.; Tyukavina, A.; Ying, Q. Landsat analysis ready data for global land cover and land cover change mapping. Remote Sens. 2020, 12, 426. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.A. There is No Such Thing as “The” EGM96 Geoid: Subtle Points on the Use of a Global Geopotential Model; IGeS Bulletin, International Geoid Service: Milan, Italy, 1998; pp. 17–28. [Google Scholar]
- Geospatial Sciences Division/NGA/PRGB. WW15MGH.DAC [Data Set]. Available online: http://earth-info.nga.mil/GandG/wgs84/gravitymod/egm96/binary/binarygeoid.html (accessed on 15 September 2018).
- Carrera-Hernández, J.J. Not all DEMs are equal: An evaluation of six globally available 30 m resolution DEMs with geodetic benchmarks and LiDAR in Mexico. Remote Sens. Environ. 2021, 261, 112474. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using LiDAR remote sensing at la Selva, Costa Rica. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height estimation from Shuttle Radar Topography Mission and National Elevation Datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef] [Green Version]
- Uuemaa, E.; Ahi, S.; Montibeller, B.; Muru, M.; Kmoch, A. Vertical Accuracy of Freely Available Global Digital Elevation Models (ASTER, AW3D30, MERIT, TanDEM-X, SRTM, and NASADEM). Remote Sens. 2020, 12, 3482. [Google Scholar] [CrossRef]
- Chen, W.; Yao, T.; Zhang, G.; Li, F.; Zheng, G.; Zhou, Y.; Xu, F. Towards ice-thickness inversion: An evaluation of global digital elevation models (DEMs) in the glacierized Tibetan Plateau. Cryosphere 2022, 16, 197–218. [Google Scholar] [CrossRef]
- Bettiol, G.M.; Ferreira, M.E.; Motta, L.P.; Cremon, É.H.; Sano, E.E. Conformity of the NASADEM_HGT and ALOS AW3D30 dem with the altitude from the brazilian geodetic reference stations: A case study from Brazilian Cerrado. Sensors 2021, 21, 2935. [Google Scholar] [CrossRef]
- Gesch, D.B. Best Practices for Elevation-Based Assessments of Sea-Level Rise and Coastal Flooding Exposure. Front. Earth Sci. 2018, 6. [Google Scholar] [CrossRef] [Green Version]




| DEM | Mesh Size | Mission | DTM/DSM | Provider | Reference |
|---|---|---|---|---|---|
| MERIT DEM | 3″ ≈ 90 | SRTM | DTM | Univ. of Tokyo [4] | WGS84/EGM96 geoid |
| BEST DEM | 3″ ≈ 90 | SRTM | DTM | bris.ac.uk [27] | WGS84/EGM96 geoid |
| NASADEM | 1″ ≈ 30 | SRTM | DSM | LP DAAC/USGS [19] | WGS84/EGM96 geoid |
| SRTMGL1 v003 | 1″ ≈ 30 | SRTM | DSM | LP DAAC/USGS [18] | WGS84/EGM96 geoid |
| SRTM v4.1 | 3″ ≈ 90 | SRTM | DSM | CGIAR-CSI [26] | WGS84/EGM96 geoid |
| SRTM3 v2.1 | 3″ ≈ 90 | SRTM | DSM | USGS [25] | WGS84/EGM96 geoid |
| TanDEM-X | 3″ ≈ 90 | TDX | DSM | DLR [28] | WGS84/WGS84 ellipsoid |
| ASTER GDEM v3 | 1″ ≈ 30 | Terra | DSM | NASA/METI [24] | WGS84/EGM96 geoid |
| AW3D30 v3.1 | 1″ ≈ 30 | ALOS | DSM | JAXA [22,23] | WGS84/EGM96 geoid |
| Parameter | Description | Units |
|---|---|---|
| SHOTNUMBER | LVIS shot number for the unique identification of laser shots | N/A |
| GLON | Longitude of the lowest detected mode within the waveform | |
| GLAT | Latitude of the lowest detected mode within the waveform | |
| ZG | Mean elevation of the lowest detected mode within the waveform | m |
| ZH * | Mean elevation of the highest detected mode within the waveform | m |
| ZT | Elevation of the highest detected signal | m |
| RH85 * | Height (relative to ZG) at which 85% of the waveform energy occurs | m |
| RH90 * | Height (relative to ZG) at which 90% of the waveform energy occurs | m |
| RH95 * | Height (relative to ZG) at which 95% of the waveform energy occurs | m |
| RH100 | Height (relative to ZG) at which 100% of the waveform energy occurs | m |
| Mean | STD* | MAD | Q1 | Q2(MED) | Q3 | Points with Absolute Difference (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | (m) | (m) | ≤5 m | ≤10 m | ≤15 m | ≤20 m | |
| LVIS2019: 5,195,224 points | ||||||||||
| NASADEM | −5.6 | 9.3 | 5.4 | −11.7 | −3.6 | 0.7 | 50% | 69% | 82% | 91% |
| NASADEM_VB1 | 5.6 | 8.9 | 4.7 | 0.1 | 3.6 | 10.0 | 48% | 72% | 86% | 93% |
| NASADEM_VB2 | 6.9 | 9.1 | 5.0 | 0.7 | 5.2 | 11.7 | 42% | 67% | 83% | 92% |
| NASADEM_VB3 | 0.9 | 7.9 | 3.7 | −3.2 | 0.8 | 4.3 | 59% | 83% | 93% | 97% |
| NASADEM_VB4 | 1.7 | 8.0 | 3.9 | −2.6 | 1.4 | 5.3 | 57% | 82% | 92% | 97% |
| LVIS2005: 9,280,657 points | ||||||||||
| NASADEM | −7.2 | 9.5 | 4.9 | −12.4 | −4.5 | −0.3 | 49% | 68% | 80% | 89% |
| NASADEM_VB1 | 4.2 | 8.7 | 4.6 | −0.8 | 2.7 | 9.1 | 51% | 74% | 88% | 94% |
| NASADEM_VB2 | 5.7 | 8.9 | 5.0 | 0.2 | 4.5 | 10.8 | 45% | 70% | 85% | 93% |
| NASADEM_VB3 | −0.5 | 7.9 | 3.7 | −4.0 | 0.1 | 3.4 | 60% | 84% | 93% | 97% |
| NASADEM_VB4 | 0.3 | 8.0 | 3.8 | −3.2 | 0.4 | 4.5 | 59% | 83% | 93% | 97% |
| LVIS1998: 2,570,730 points | ||||||||||
| NASADEM | −13.6 | 9.9 | 7.3 | −19.7 | −12.8 | −5.2 | 24% | 39% | 58% | 76% |
| NASADEM_VB1 | 4.4 | 9.0 | 5.3 | −0.5 | 4.5 | 10.1 | 41% | 69% | 87% | 95% |
| NASADEM_VB2 | 5.4 | 9.1 | 5.4 | 0.4 | 5.8 | 11.2 | 36% | 65% | 85% | 94% |
| NASADEM_VB3 | −3.1 | 8.5 | 4.7 | −7.4 | −1.7 | 2.3 | 53% | 79% | 91% | 96% |
| NASADEM_VB4 | −2.5 | 8.7 | 4.9 | −7.0 | −1.1 | 3.2 | 51% | 79% | 91% | 96% |
| Levelling dataset: 2233 points | ||||||||||
| NASADEM | −3.5 | 10.0 | 3.7 | −6.6 | −2.7 | 0.8 | 57% | 78% | 85% | 90% |
| NASADEM_VB1 | 0.3 | 10.4 | 4.1 | −4.4 | −0.9 | 4.0 | 56% | 77% | 85% | 90% |
| NASADEM_VB2 | 2.0 | 10.7 | 4.7 | −3.4 | 0.7 | 6.3 | 53% | 75% | 84% | 89% |
| NASADEM_VB3 | −1.3 | 10.1 | 3.8 | −5.0 | −1.5 | 2.5 | 59% | 79% | 86% | 91% |
| NASADEM_VB4 | −0.3 | 10.0 | 3.9 | −4.2 | −0.7 | 3.7 | 59% | 79% | 86% | 91% |
| Mean | STD* | min/max | MAD | Q1 | Q2(MED) | Q3 | Points with Absolute Difference (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | (m) | (m) | (m) | ≤5 m | ≤10 m | ≤15 m | ≤20 m | |
| LVIS2019: 5,195,224 points | |||||||||||
| CRDTM2020 | 0.9 | 7.9 | −248/250 | 3.7 | −3.2 | 0.8 | 4.3 | 59% | 83% | 93% | 97% |
| MERIT | −0.7 | 9.6 | −199/259 | 4.2 | −5.1 | 0.0 | 3.4 | 56% | 78% | 88% | 93% |
| BEST | −3.9 | 10.9 | −196/260 | 6.0 | −10.4 | −4.2 | 1.7 | 36% | 63% | 79% | 87% |
| NASADEM | −5.6 | 9.3 | −257/250 | 5.4 | −11.7 | −3.6 | 0.7 | 50% | 69% | 82% | 91% |
| SRTMGL1 | −8.6 | 9.4 | −190/263 | 5.5 | −14.9 | −6.8 | −2.5 | 37% | 58% | 72% | 83% |
| SRTM4 | −8.3 | 10.7 | −208/250 | 6.2 | −14.9 | −6.4 | −1.7 | 38% | 59% | 74% | 84% |
| SRTM3 | −8.3 | 10.7 | −208/250 | 6.2 | −14.9 | −6.3 | −1.7 | 38% | 59% | 74% | 84% |
| TanDEM-X | −6.0 | 14.5 | −249/338 | 7.3 | −14.1 | −3.9 | 1.0 | 36% | 55% | 68% | 77% |
| ASTER | −4.8 | 13.5 | −181/260 | 7.9 | −13.6 | −2.4 | 3.7 | 36% | 59% | 73% | 83% |
| AW3D30 | −8.6 | 9.5 | −213/247 | 5.6 | −15.0 | −6.4 | −2.3 | 40% | 61% | 74% | 85% |
| LVIS2005: 9,280,657 points | |||||||||||
| CRDTM2020 | −0.5 | 7.9 | −186/276 | 3.7 | −4.0 | 0.1 | 3.4 | 60% | 84% | 93% | 97% |
| MERIT | −2.6 | 10.2 | −220/282 | 4.7 | −6.8 | −1.5 | 2.7 | 52% | 75% | 86% | 92% |
| BEST | −5.8 | 11.0 | −222/286 | 6.2 | −11.9 | −5.8 | 0.7 | 32% | 59% | 81% | 89% |
| NASADEM | −7.2 | 9.5 | −199/266 | 4.9 | −12.4 | −4.5 | −0.3 | 49% | 68% | 80% | 89% |
| SRTMGL1 | −9.8 | 9.3 | −205/264 | 4.7 | −14.9 | −7.2 | −3.1 | 35% | 60% | 74% | 85% |
| SRTM4 | −9.7 | 10.7 | −231/272 | 5.1 | −15.2 | −7.1 | −2.8 | 34% | 59% | 74% | 83% |
| SRTM3 | −9.7 | 10.7 | −211/272 | 5.1 | −15.2 | −7.1 | −2.8 | 34% | 59% | 74% | 83% |
| TanDEM-X | −7.6 | 15.3 | −237/205 | 7.9 | −16.1 | −5.6 | 0.2 | 32% | 51% | 65% | 75% |
| ASTER | −5.0 | 12.4 | −203/273 | 7.2 | −11.7 | −3.3 | 2.9 | 36% | 62% | 77% | 86% |
| AW3D30 | −10.0 | 9.5 | −204/280 | 4.8 | −15.4 | −7.2 | −2.9 | 36% | 60% | 74% | 84% |
| LVIS1998: 2,570,730 points | |||||||||||
| CRDTM2020 | −3.1 | 8.5 | −258/380 | 4.7 | −7.4 | −1.7 | 2.3 | 53% | 79% | 91% | 96% |
| MERIT | −6.1 | 10.8 | −229/384 | 6.2 | −11.5 | −3.9 | 1.5 | 44% | 68% | 81% | 89% |
| BEST | −6.0 | 10.7 | −229/388 | 5.7 | −10.9 | −4.7 | 0.6 | 36% | 63% | 79% | 87% |
| NASADEM | −13.6 | 9.9 | −258/369 | 7.3 | −19.7 | −12.8 | −5.2 | 24% | 39% | 58% | 76% |
| SRTMGL1 | −16.6 | 9.7 | −230/370 | 7.2 | −22.7 | −15.6 | −8.4 | 11% | 30% | 47% | 66% |
| SRTM4 | −16.6 | 10.9 | −238/374 | 7.9 | −23.1 | −14.9 | −7.2 | 13% | 34% | 50% | 66% |
| SRTM3 | −16.5 | 10.9 | −238/374 | 7.9 | −23.1 | −14.9 | −7.2 | 13% | 34% | 50% | 66% |
| TanDEM-X | −10.4 | 14.0 | −300/345 | 7.6 | −18.4 | −7.4 | −1.1 | 33% | 51% | 64% | 74% |
| ASTER | −11.4 | 13.5 | −181/372 | 9.7 | −20.3 | −10.5 | −0.9 | 24% | 44% | 60% | 73% |
| AW3D30 | −17.0 | 9.9 | −241/361 | 7.4 | −23.5 | −16.3 | −8.7 | 11% | 29% | 45% | 63% |
| Levelling dataset: 2,233 points | |||||||||||
| CRDTM2020 | −1.2 | 10.0 | −162/183 | 3.8 | −4.9 | −1.5 | 2.6 | 59% | 79% | 86% | 91% |
| MERIT | −0.9 | 10.6 | −161/187 | 4.2 | −5.5 | −1.4 | 3.1 | 54% | 78% | 86% | 89% |
| BEST | −7.7 | 11.4 | −165/181 | 6.0 | −14.3 | −8.3 | −2.2 | 25% | 51% | 73% | 86% |
| NASADEM | −3.5 | 10.0 | −169/183 | 3.7 | −6.6 | −2.7 | 0.8 | 57% | 78% | 85% | 90% |
| SRTMGL1 | −4.7 | 10.2 | −205/187 | 3.8 | −8.2 | −4.1 | −0.7 | 48% | 74% | 84% | 89% |
| SRTM4 | −4.5 | 10.6 | −171/186 | 3.8 | −8.2 | −4.1 | −0.5 | 47% | 75% | 84% | 89% |
| SRTM3 | −4.6 | 10.6 | −165/186 | 3.8 | −8.1 | −4.1 | −0.5 | 47% | 75% | 84% | 89% |
| TanDEM-X | −3.3 | 12.1 | −162/187 | 4.3 | −7.2 | −2.1 | 1.5 | 53% | 71% | 80% | 86% |
| ASTER | −0.7 | 12.3 | −166/182 | 6.0 | −6.7 | −0.6 | 5.3 | 43% | 68% | 80% | 87% |
| AW3D30 | −4.7 | 10.3 | −162/188 | 3.7 | −8.0 | −4.0 | −0.5 | 49% | 75% | 84% | 89% |
| Points above Bare-Earth | Points above Vegetation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | STD* | min/max | MAD | Q1 | MED | Q3 | mean | STD* | MAD | Q1 | MED | Q3 | |
| (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | |
| LVIS2019: 5,195,224 points, 31.6% bare-earth, 68.4% vegetated | |||||||||||||
| CRDTM2020 | 2.3 | 6.0 | −181/217 | 2.1 | −0.1 | 1.7 | 4.2 | 0.3 | 8.5 | 4.5 | −4.7 | 0.0 | 4.3 |
| MERIT | 1.6 | 6.4 | −198/235 | 2.2 | −1.0 | 0.7 | 3.5 | −1.8 | 10.6 | 5.2 | −7.4 | −1.4 | 3.3 |
| BEST | −3.1 | 8.9 | −196/235 | 4.2 | −7.9 | −3.7 | 1.0 | −4.2 | 11.6 | 6.9 | −11.9 | −4.5 | 2.0 |
| NASADEM | −0.4 | 5.4 | −194/206 | 2.1 | −2.0 | 0.6 | 2.6 | −8.1 | 9.5 | 6.4 | −14.6 | −7.5 | −1.5 |
| SRTMGL1 | −3.4 | 5.9 | −129/207 | 2.8 | −5.5 | −2.7 | 0.1 | −10.8 | 9.5 | 6.3 | −17.5 | −10.2 | −4.4 |
| SRTM4 | −3.0 | 6.8 | −208/226 | 2.9 | −5.6 | −2.2 | 0.6 | −10.8 | 11.1 | 6.8 | −18.1 | −10.0 | −4.0 |
| SRTM3 | −3.0 | 6.8 | −208/226 | 2.9 | −5.6 | −2.2 | 0.6 | −10.8 | 11.1 | 6.8 | −18.1 | −10.0 | −4.0 |
| TanDEM-X | −1.5 | 12.0 | −207/307 | 4.3 | −6.3 | −0.6 | 2.3 | −7.9 | 15.2 | 8.2 | −17.1 | −6.5 | 0.2 |
| ASTER | 0.6 | 10.3 | −146/229 | 4.7 | −3.0 | 0.8 | 5.9 | −7.3 | 14.0 | 9.4 | −17.1 | −6.3 | 2.2 |
| AW3D30 | −3.1 | 5.7 | −188/212 | 2.9 | −5.2 | −2.4 | 0.6 | −11.2 | 9.6 | 6.6 | −18.2 | −10.4 | −4.4 |
| LVIS2005: 9,280,657 points, 16.4% bare-earth, 83.6% vegetated | |||||||||||||
| CRDTM2020 | 0.5 | 3.6 | −116/92 | 0.9 | −0.7 | 0.3 | 1.0 | −0.7 | 8.5 | 4.4 | −4.9 | −0.4 | 4.0 |
| MERIT | −0.7 | 3.9 | −143/95 | 0.9 | −2.2 | −1.3 | −0.4 | −3.0 | 11.0 | 5.7 | −8.3 | −1.9 | 3.3 |
| BEST | −7.9 | 6.2 | −150/86 | 2.3 | −12.0 | −9.9 | −4.6 | −5.4 | 11.6 | 6.7 | −11.7 | −5.0 | 1.6 |
| NASADEM | −0.4 | 3.0 | −116/92 | 0.8 | −1.3 | 0.2 | 0.5 | −8.5 | 9.8 | 5.8 | −14.2 | −6.4 | −1.5 |
| SRTMGL1 | −3.5 | 3.0 | −121/80 | 0.7 | −4.5 | −2.8 | −2.5 | −11.0 | 9.6 | 5.6 | −16.6 | −8.9 | −4.3 |
| SRTM4 | −3.5 | 3.5 | −167/94 | 0.9 | −4.6 | −2.8 | −2.5 | −11.0 | 11.3 | 6.2 | −17.2 | −8.9 | −3.9 |
| SRTM3 | −3.5 | 3.5 | −149/94 | 1.0 | −4.6 | −2.8 | −2.5 | −11.0 | 11.3 | 6.2 | −17.2 | −8.9 | −3.9 |
| TanDEM-X | −2.3 | 13.0 | −201/115 | 4.2 | −6.0 | −1.0 | 2.2 | −8.6 | 15.5 | 8.4 | −17.7 | −7.1 | −0.3 |
| ASTER | 0.1 | 6.9 | −131/106 | 2.5 | −3.7 | 1.2 | 2.0 | −6.0 | 13.0 | 8.2 | −13.6 | −4.8 | 3.0 |
| AW3D30 | −3.3 | 3.1 | −112/89 | 0.7 | −4.1 | −2.8 | −2.5 | −11.3 | 9.8 | 5.9 | −17.2 | −9.2 | −4.3 |
| LVIS1998: 2,570,730 points, 0.3% bare-earth, 99.7% vegetated | |||||||||||||
| CRDTM2020 | 1.5 | 3.5 | −46/25 | 1.7 | −0.5 | 1.0 | 2.9 | −3.1 | 8.6 | 4.7 | −7.4 | −1.7 | 2.3 |
| MERIT | 1.3 | 3.7 | −67/31 | 2.2 | −1.1 | 0.7 | 3.5 | −6.1 | 10.8 | 6.2 | −11.6 | −3.9 | 1.5 |
| BEST | −2.3 | 4.6 | −67/28 | 2.3 | −4.7 | −2.6 | −0.2 | −6.0 | 10.7 | 5.7 | −10.9 | −4.7 | 0.6 |
| NASADEM | −0.5 | 2.4 | −66/16 | 1.3 | −1.8 | −0.4 | 0.8 | −13.6 | 9.9 | 7.2 | −19.8 | −12.9 | −5.2 |
| SRTMGL1 | −4.3 | 2.5 | −73/11 | 1.3 | −5.6 | −4.3 | −3.0 | −16.7 | 9.7 | 7.1 | −22.7 | −15.7 | −8.4 |
| SRTM4 | −4.5 | 2.8 | −77/20 | 1.3 | −5.7 | −4.5 | −3.2 | −16.6 | 10.9 | 7.9 | −23.1 | −14.9 | −7.3 |
| SRTM3 | −4.5 | 2.8 | −77/20 | 1.3 | −5.8 | −4.5 | −3.2 | −16.6 | 10.9 | 7.9 | −23.1 | −14.9 | −7.3 |
| TanDEM-X | −1.7 | 4.6 | −86/40 | 1.4 | −2.7 | −1.2 | 0.1 | −10.5 | 14.1 | 7.7 | −18.4 | −7.4 | −1.1 |
| ASTER | 3.4 | 5.7 | −56/30 | 3.3 | 0.3 | 3.9 | 7.0 | −11.4 | 13.5 | 9.7 | −20.3 | −10.5 | −1.0 |
| AW3D30 | −4.8 | 3.4 | −43/41 | 1.3 | −5.9 | −4.6 | −3.4 | −17.1 | 9.9 | 7.4 | −23.6 | −16.4 | −8.8 |
| Levelling dataset: 2233 points, 54.4% bare-earth, 45.6% vegetated | |||||||||||||
| CRDTM2020 | −2.6 | 7.2 | −162/183 | 2.6 | −4.5 | −2.0 | 0.8 | −0.1 | 11.8 | 5.1 | −5.8 | −0.7 | 4.5 |
| MERIT | −2.3 | 8.1 | −161/187 | 3.3 | −5.5 | −2.3 | 1.2 | 0.8 | 13.0 | 5.7 | −5.6 | 0.3 | 5.9 |
| BEST | −9.9 | 9.2 | −165/178 | 5.0 | −14.9 | −10.1 | −4.9 | −5.8 | 12.8 | 6.8 | −13.4 | −6.4 | 0.1 |
| NASADEM | −2.6 | 7.3 | −162/183 | 2.7 | −4.6 | −2.0 | 0.8 | −4.5 | 12.4 | 5.1 | −9.6 | −4.1 | 0.7 |
| SRTMGL1 | −4.1 | 7.5 | −161/187 | 2.9 | −6.5 | −3.7 | −0.7 | −5.5 | 12.6 | 5.2 | −10.9 | −5.0 | −0.6 |
| SRTM4 | −3.8 | 8.0 | −161/186 | 2.9 | −6.3 | −3.6 | −0.6 | −5.5 | 13.0 | 5.3 | −10.9 | −5.0 | −0.2 |
| SRTM3 | −3.8 | 8.0 | −161/186 | 2.9 | −6.3 | −3.6 | −0.5 | −5.5 | 13.0 | 5.3 | −10.9 | −5.1 | −0.3 |
| TanDEM-X | −2.7 | 9.7 | −162/187 | 3.1 | −4.8 | −1.3 | 1.4 | −4.1 | 14.4 | 6.0 | −10.8 | −3.6 | 1.6 |
| ASTER | 0.7 | 10.2 | −153/180 | 4.9 | −4.3 | 0.8 | 5.6 | −2.5 | 14.3 | 7.5 | −10.3 | −3.0 | 4.8 |
| AW3D30 | −3.9 | 7.7 | −162/188 | 2.8 | −6.0 | −3.7 | −0.5 | −5.7 | 12.6 | 5.2 | −11.4 | −4.7 | −0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimenova, O.; Roberts, C.; Rizos, C. Regional “Bare-Earth” Digital Terrain Model for Costa Rica Based on NASADEM Corrected for Vegetation Bias. Remote Sens. 2022, 14, 2421. https://doi.org/10.3390/rs14102421
Pimenova O, Roberts C, Rizos C. Regional “Bare-Earth” Digital Terrain Model for Costa Rica Based on NASADEM Corrected for Vegetation Bias. Remote Sensing. 2022; 14(10):2421. https://doi.org/10.3390/rs14102421
Chicago/Turabian StylePimenova, Olga, Craig Roberts, and Chris Rizos. 2022. "Regional “Bare-Earth” Digital Terrain Model for Costa Rica Based on NASADEM Corrected for Vegetation Bias" Remote Sensing 14, no. 10: 2421. https://doi.org/10.3390/rs14102421
APA StylePimenova, O., Roberts, C., & Rizos, C. (2022). Regional “Bare-Earth” Digital Terrain Model for Costa Rica Based on NASADEM Corrected for Vegetation Bias. Remote Sensing, 14(10), 2421. https://doi.org/10.3390/rs14102421







