Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event
Abstract
:1. Introduction
1.1. Landsat 8 and 9 Characteristics
1.2. Cross-Calibration Based on Underfly Events
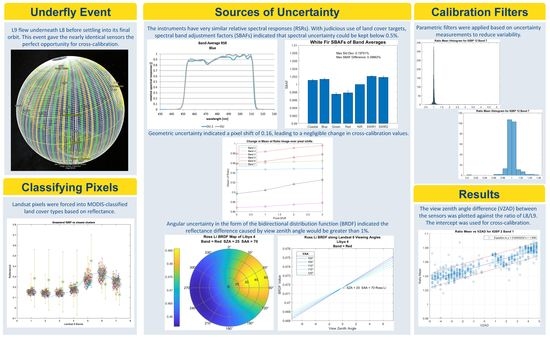
2. Sources of Uncertainty
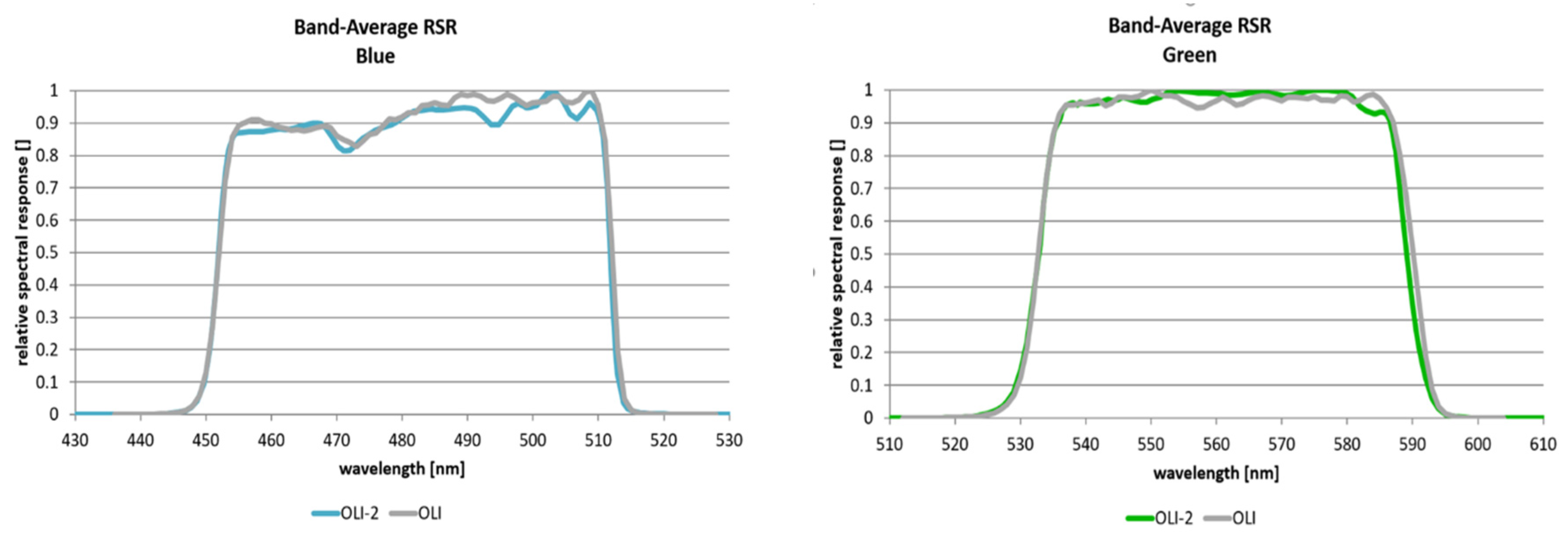
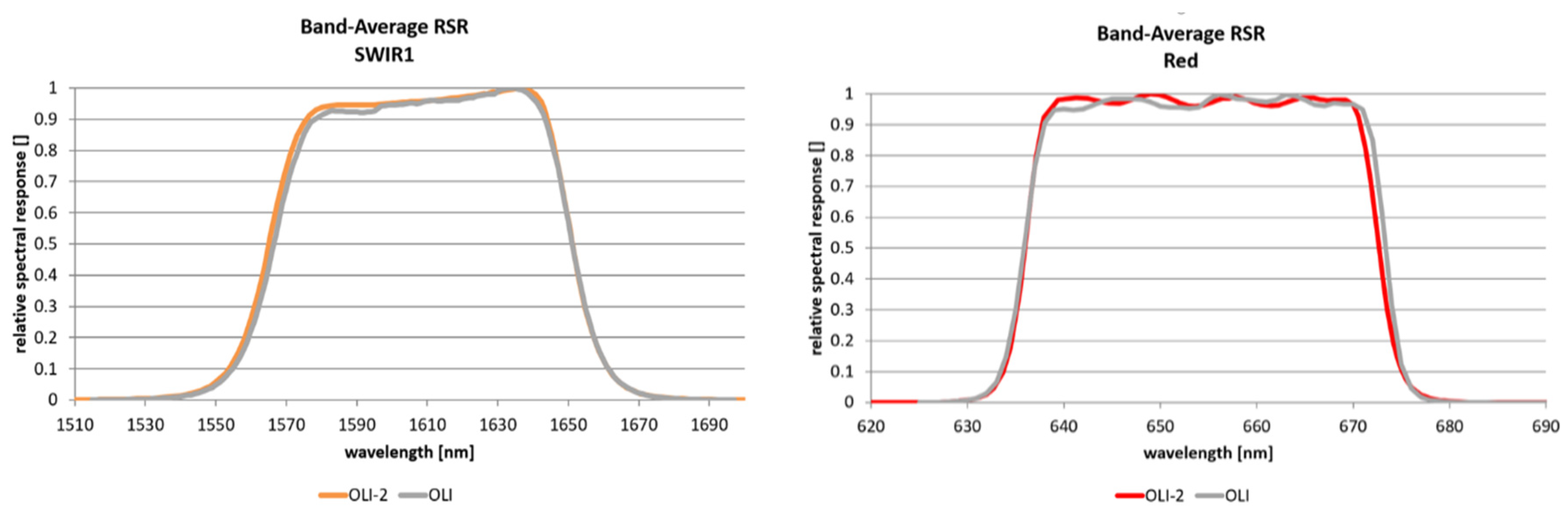
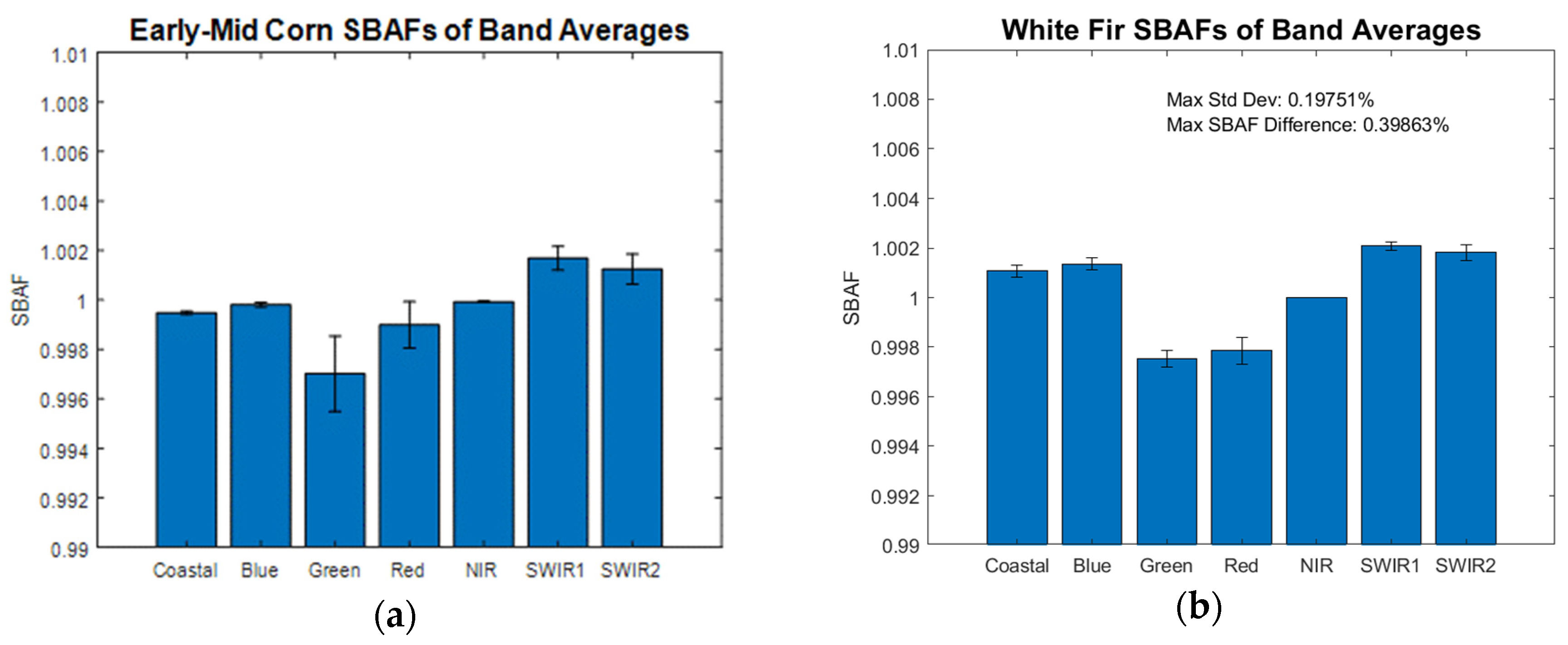
2.1. Spectral Uncertainty
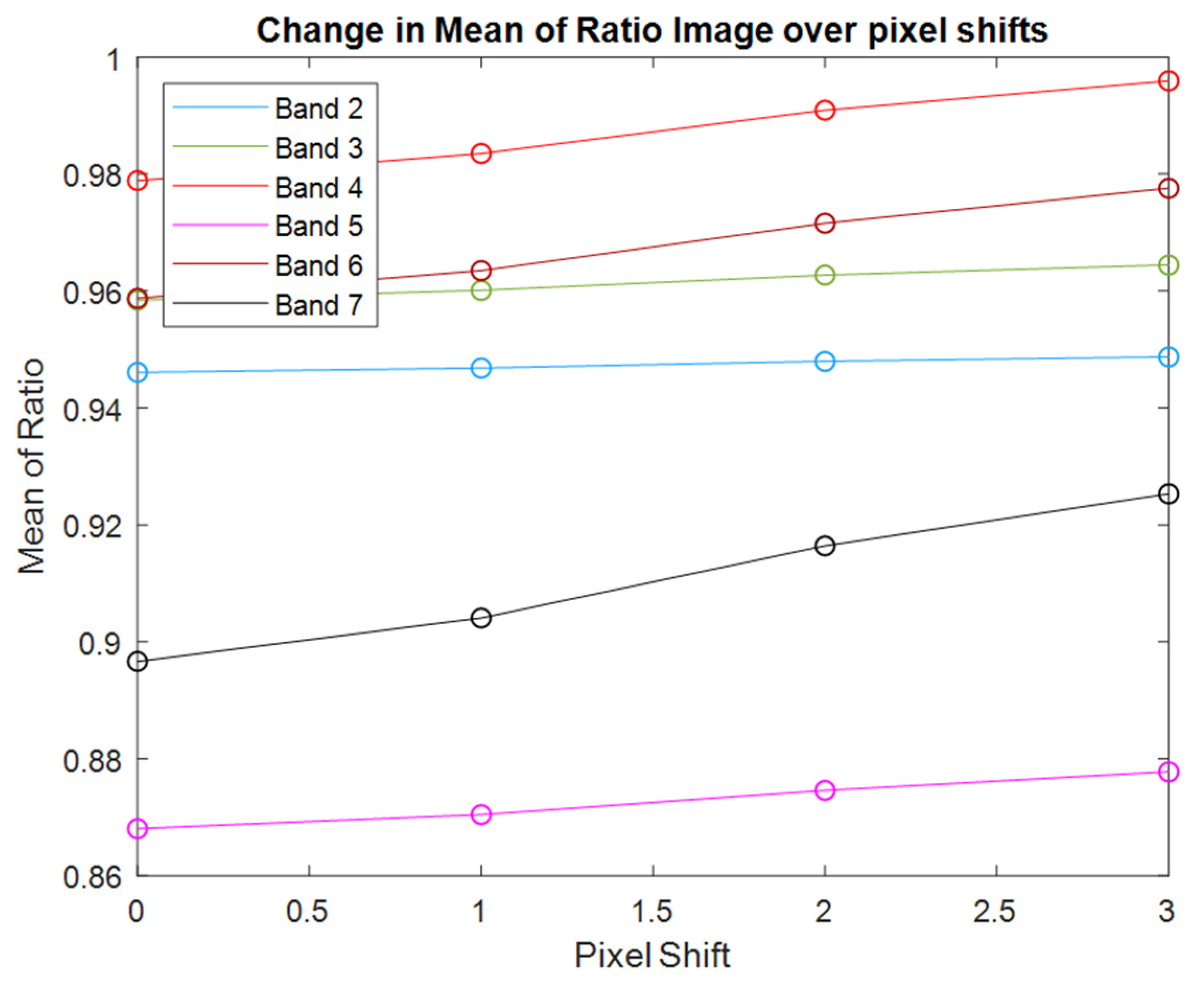
2.2. Geometric Uncertainty
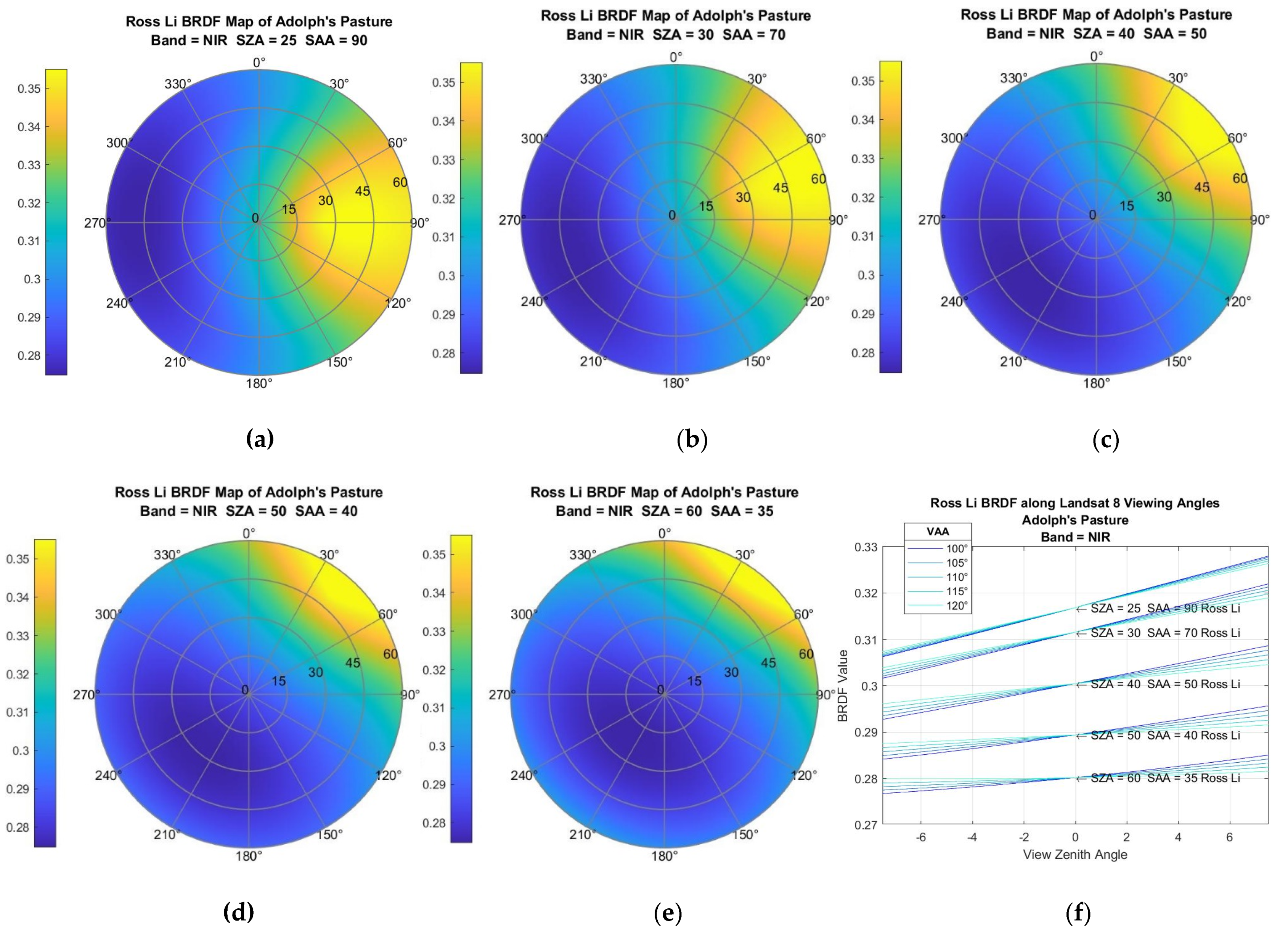
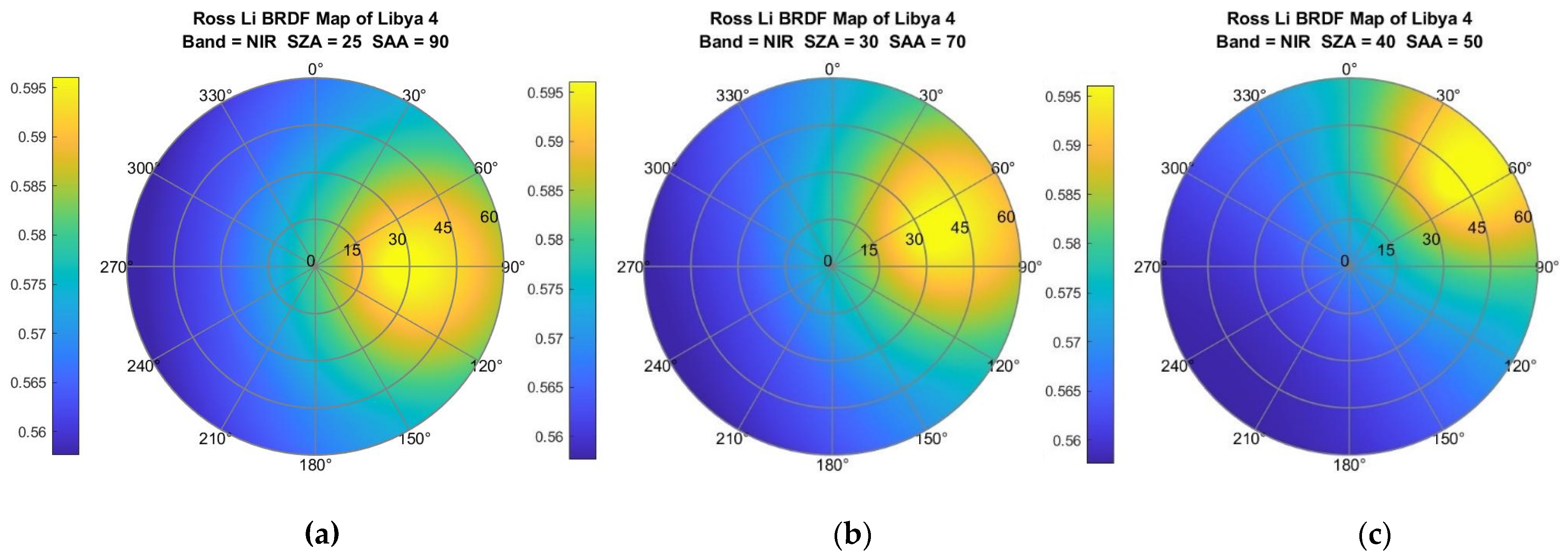
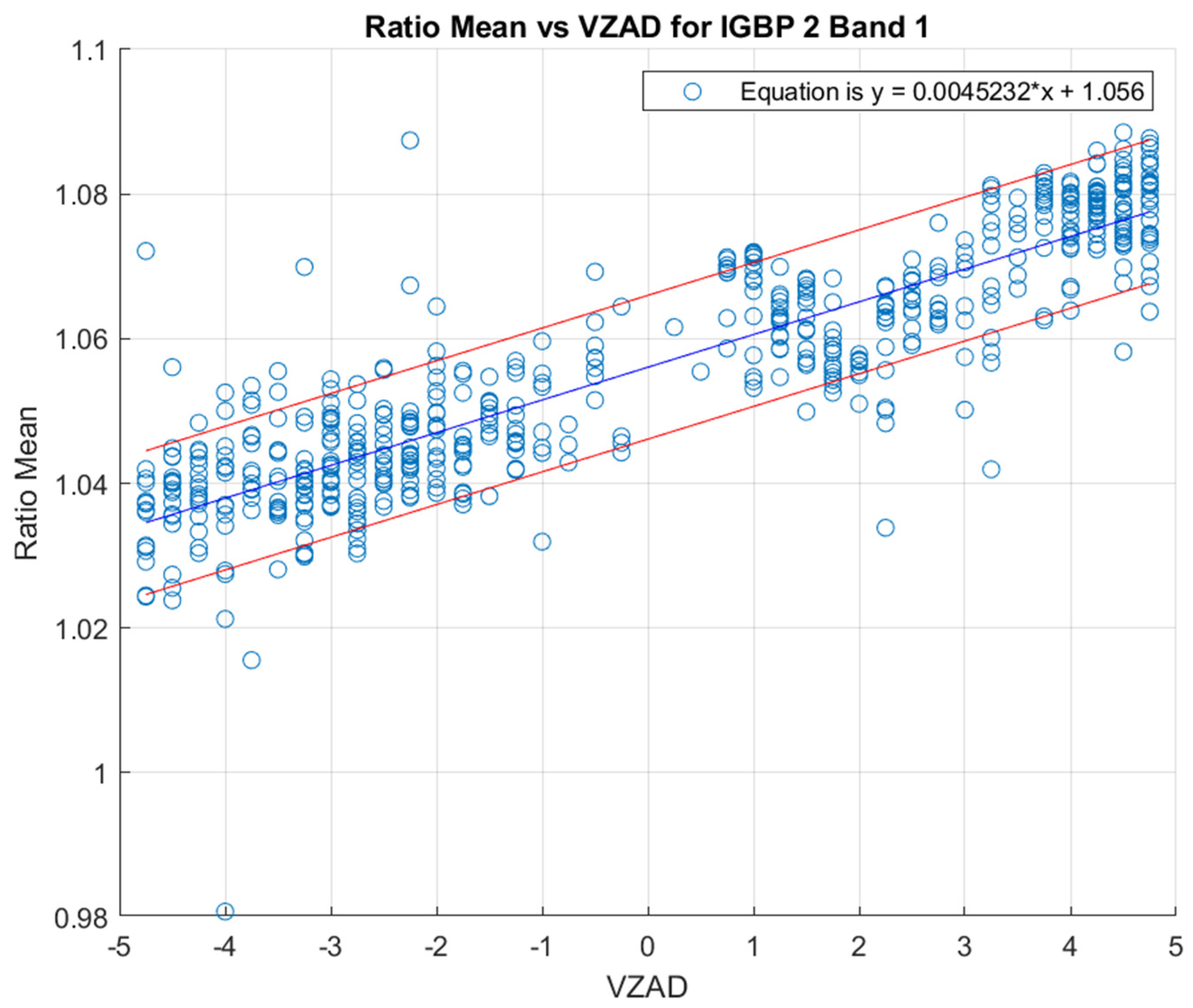
2.3. Angular Uncertainty
3. Data-Acquisition Methodology
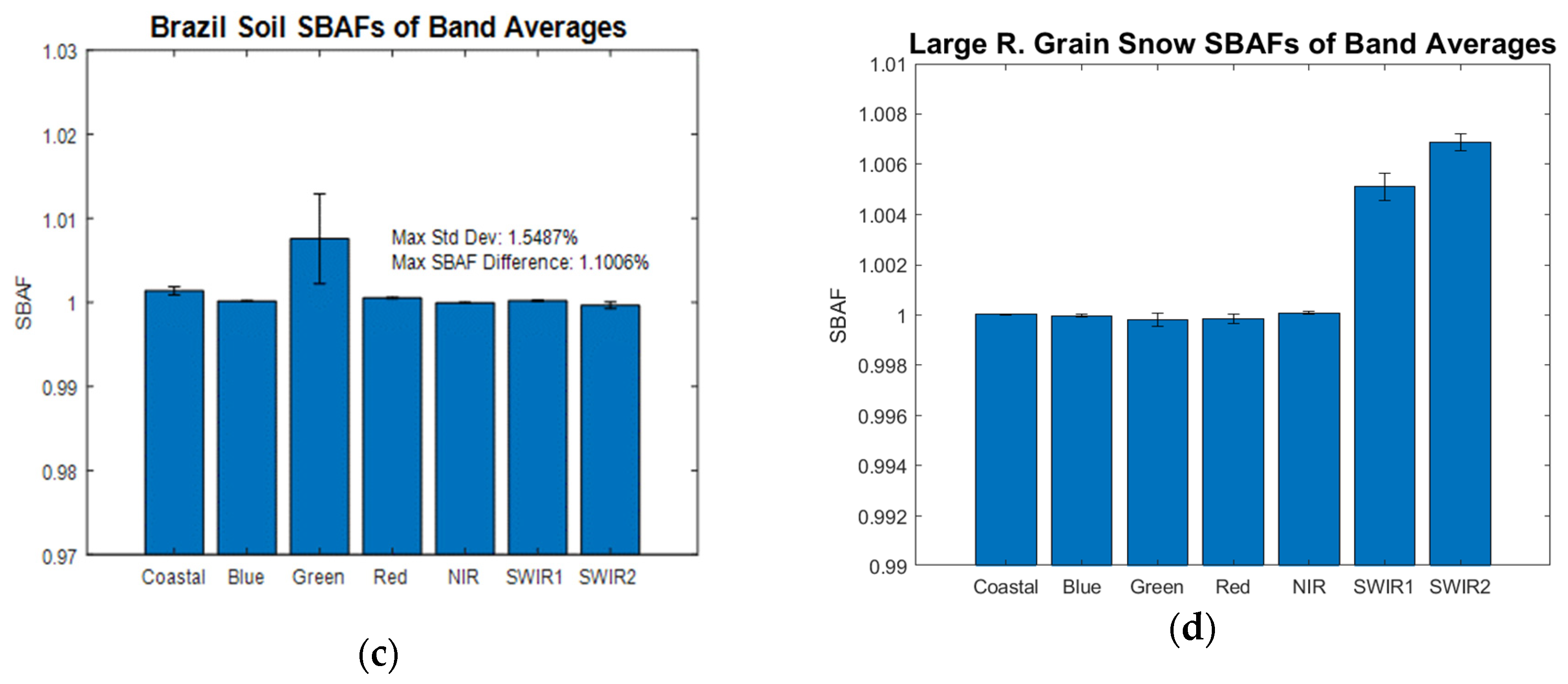
3.1. Spectral Characterization of Land Cover Types
3.2. IGBP Cover-Type Spectra Matching
3.3. Global Classification of Pixels during Underfly
3.3.1. SDSU EPICS—November Analysis
3.3.2. Global Classification of Pixels Procedure
- Overlap regions were identified in the scene pairs.
- To ensure only homogeneous regions were processed, edges in the imagery were detected with the Canny edge detector [21].
- To further ensure that edges were avoided, each edge detected in the previous step was dilated by one pixel on either side.
- Each pixel within homogeneous regions was then classified as described previously into an IGBP class. Three IGBP class types had no matching clusters: evergreen needleleaf trees, deciduous broadleaf trees, and closed shrublands.
- There were 150 clusters out of the 500 that did not meet the NDVI or BSI thresholds (vegetation and soil). Out of these clusters, snow pixels were classified using the BQA band, and water pixels were used in the TIRS bands. Any pixels not falling into these categories were rejected.
- For each pixel pair, the cross-calibration ratio (L8/L9) was calculated.
- For each scene pair, data were aggregated according to IGBP land cover type and spectral band. The following scene-based statistics were gathered: cross-calibration ratio min, mean, max and standard deviation values; min, mean, max and standard deviation for Landsat 8 and 9 reflectance levels; VAAD min, mean, and max values; VZAD (rounded into 0.25° bins); as well as WRS-2 path/row values.
3.4. Analysis of Bands 8–11
4. Results
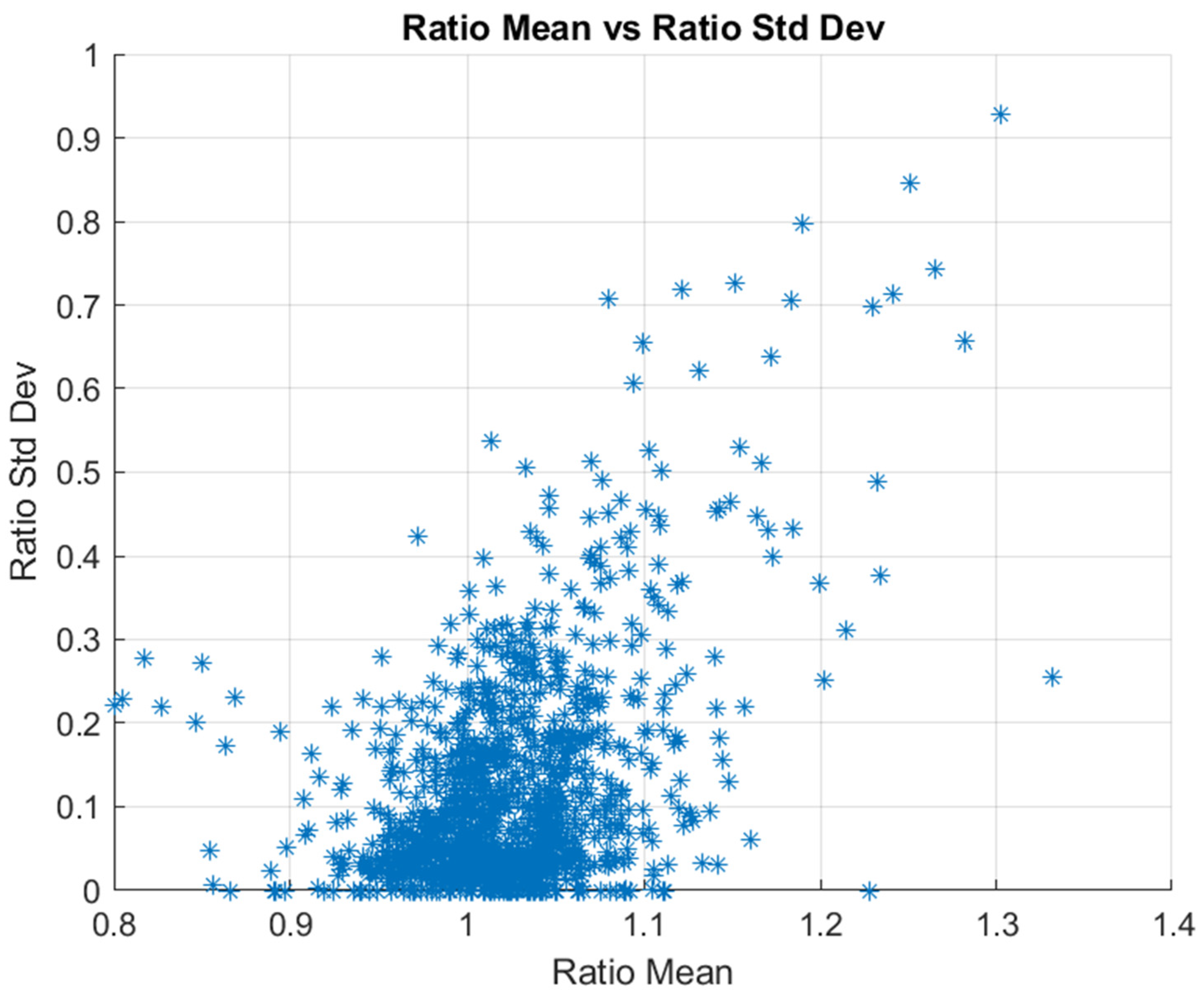
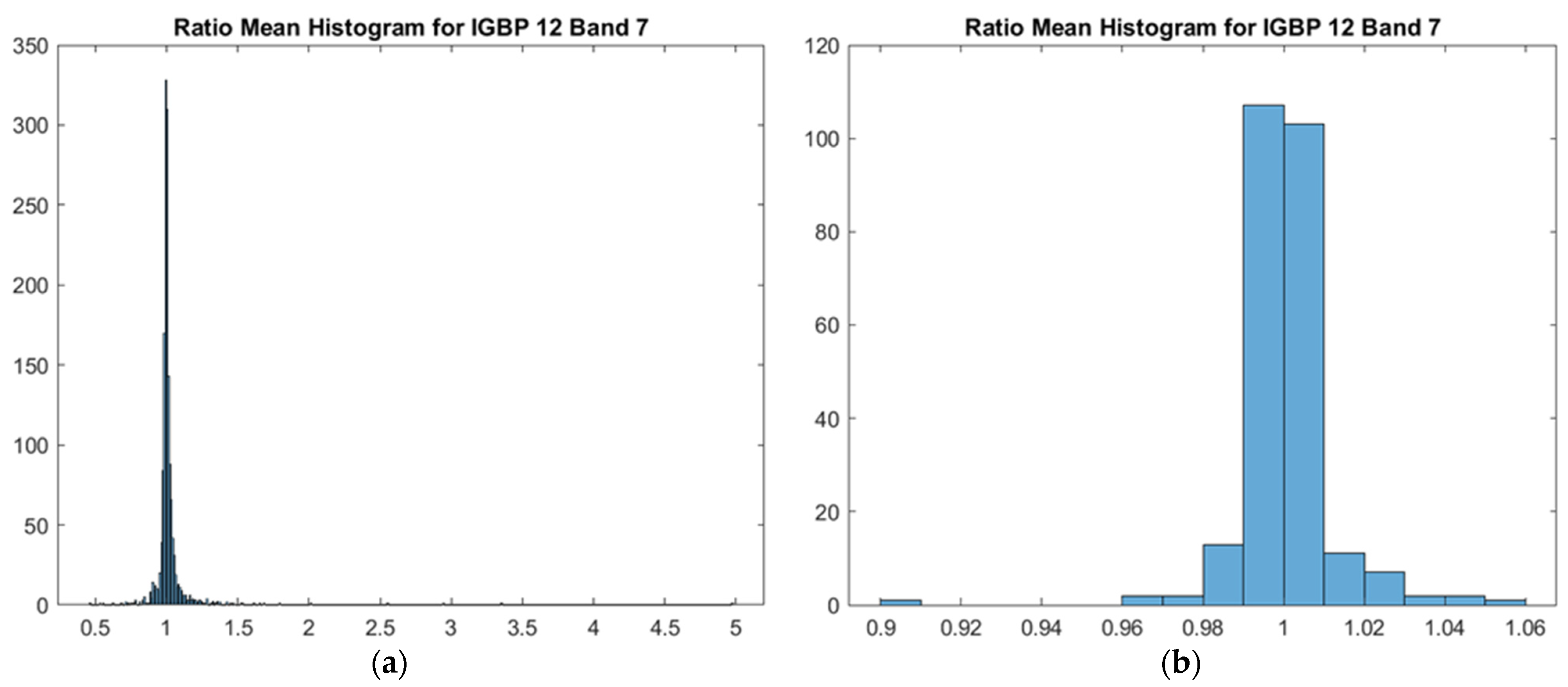
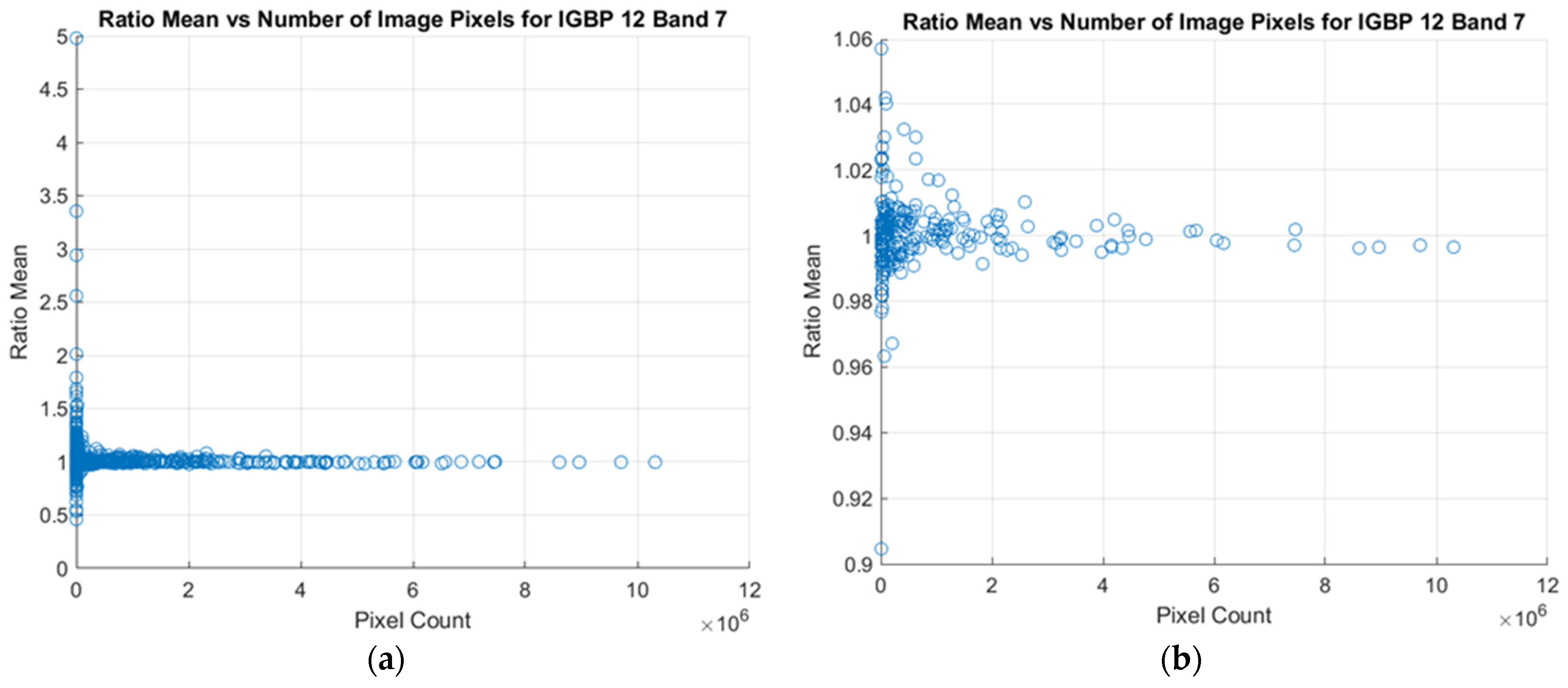
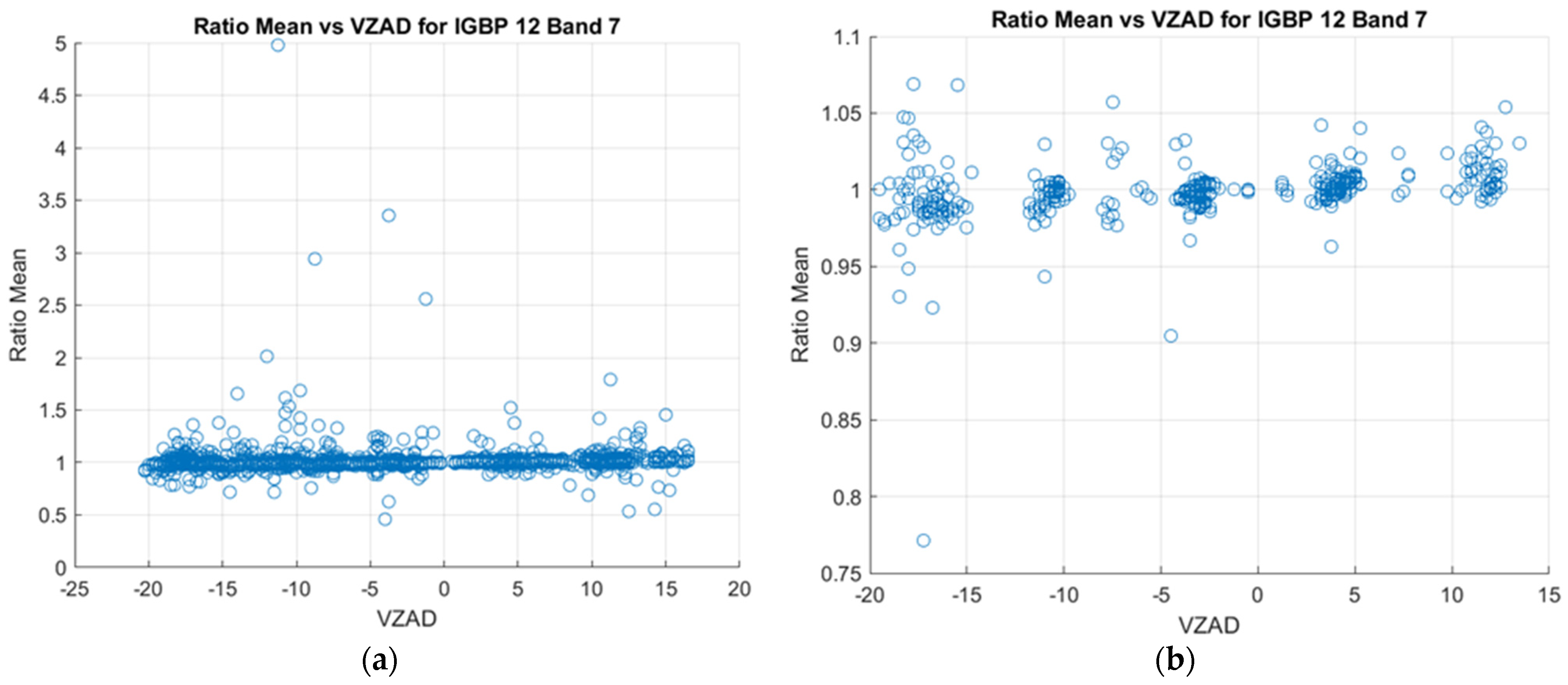
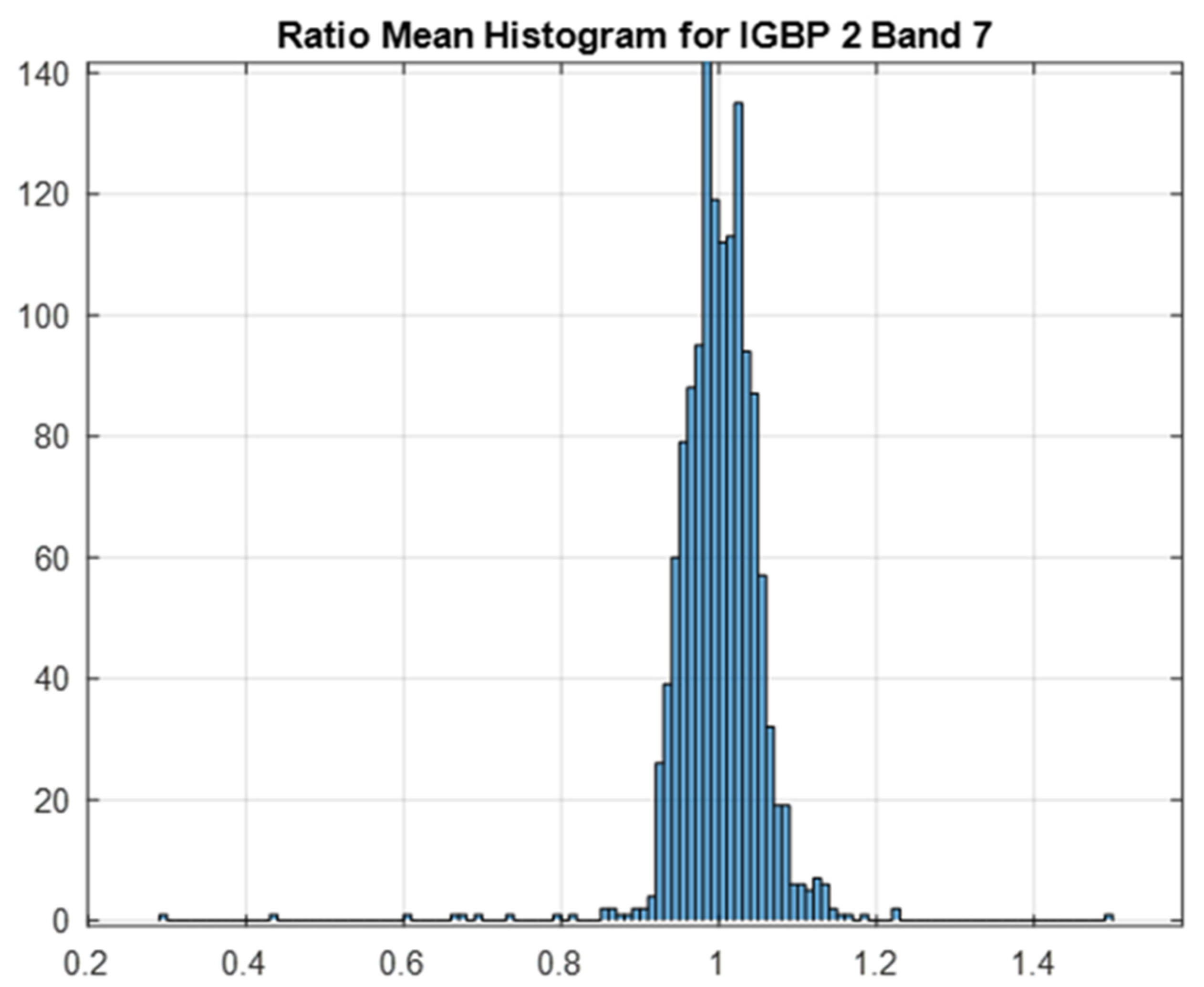
4.1. Outlier Reduction
4.2. Cross-Calibration Ratio Estimators
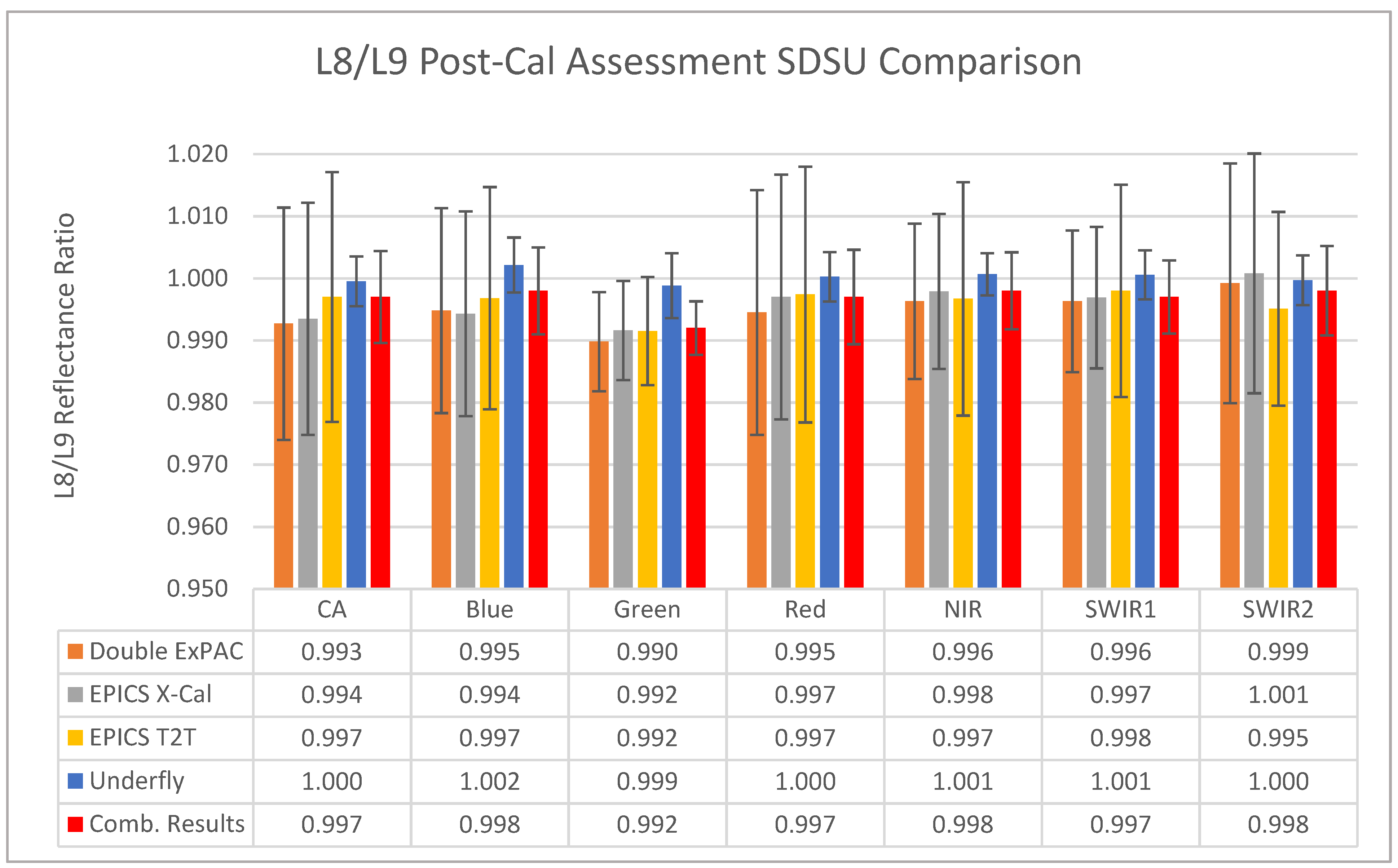
4.3. Initial Calibration Estimates
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Deciduous Needleleaf | Mixed Forests | Open Shrublands | Woody Savannas | Savannas | Grasslands | Cropland | Natural Vegetation | Evergreen Broadleaf |
|---|---|---|---|---|---|---|---|---|---|
| Min VZAD | −10 | −10 | −10 | −10 | −10 | −10 | −10 | −10 | −10 |
| Max VZAD | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Min VAAD L8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Min VAAD L9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Min # of Pixels | 10,000 | 1000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 5000 | 5000 |
| Min Reflectance L8 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| Max Reflectance L8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Min Reflectance L9 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| Max Reflectance L9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Min Std Dev L8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Max Std Dev L8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Min Std Dev L9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Max Std Dev L9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Min Std Dev of Ratio | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 |
| Max Std Dev of Ratio | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Parameters | Dark Soil | Light Soil | Sand |
|---|---|---|---|
| Min VZAD | −10 | −10 | −10 |
| Max VZAD | 10 | 10 | 10 |
| Min VAAD L8 | 0 | 0 | 0 |
| Min VAAD L9 | 0 | 0 | 0 |
| Min # of Pixels | 10,000 | 10,000 | 1000 |
| Min Reflectance L8 | 0.01 | 0.01 | 0.01 |
| Max Reflectance L8 | 1 | 1 | 1 |
| Min Reflectance L9 | 0.01 | 0.01 | 0.01 |
| Max Reflectance L9 | 1 | 1 | 1 |
| Min Std Dev L8 | 0 | 0 | 0 |
| Max Std Dev L8 | 1 | 1 | 1 |
| Min Std Dev L9 | 0 | 0 | 0 |
| Max Std Dev L9 | 1 | 1 | 1 |
| Min Std Dev of Ratio | −1 | −1 | −1 |
| Max Std Dev of Ratio | 0.2 | 0.2 | 0.2 |
References
- Masek, J.G.; Wulder, M.A.; Markham, B.; McCorkel, J.; Crawford, C.J.; Storey, J.; Jenstrom, D.T. Landsat 9: Empowering open science and applications through continuity. Remote Sens. Environ. 2020, 248, 111968. [Google Scholar] [CrossRef]
- MarkhamM, B.; McCorkel, J.; Montanaro, M.; Morland, E.; Pearlman, A.; Pedelty, J.; Wenny, B.; Barsi, J.; Donley, E.; Efremova, B.; et al. Landsat 9: Mission Status and Prelaunch Instrument Performance Characterization and Calibration. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5788–5791. [Google Scholar] [CrossRef]
- Metzler, M.D.; Malila, W.A. Characterization and comparison of Landsat-4 and Landsat-5 Thematic Mapper data. Photogramm. Eng. Remote Sens. 1985, 51, 1315–1330. [Google Scholar]
- Teillet, P.M.; Markham, B.L.; Barker, J.L.; Storey, J.C.; Irish, R.R.; Seiferth, J.C. Landsat sensor cross-calibration using nearly coincidental matching scenes. In Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI; SPIE: Bellingham, WA, USA, 2000; Volume 4049. [Google Scholar]
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric Cross Calibration of Landsat 8 Operational Land Imager (OLI) and Landsat 7 Enhanced Thematic Mapper Plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef] [Green Version]
- Teillet, P.M.; Fedosejevs, G.; Thome, K.J.; Barker, J.L. Impacts of spectral band difference effects on radiometric cross-calibration between satellite sensors in the solar-reflective spectral domain. Remote Sens. Environ. 2007, 110, 393–409. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.; Choi, T.; Angal, A.; Xiong, X. Use of EO-1 Hyperion data to calculate spectral band adjustment factors (SBAF) between the L7 ETM+ and Terra MODIS sensors. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Thenkabail, P.; Aneece, I. Global Hyperspectral Imaging Spectral-Library of Agricultural Crops for Conterminous United States V001 [Data Set]. NASA EOSDIS Land Processes DAAC, 2019. Available online: https://lpdaac.usgs.gov/products/ghisaconusv001 (accessed on 20 March 2021).
- Meerdink, S.K.; Hook, S.J.; Roberts, D.A.; Abbott, E.A. The ECOSTRESS spectral library version 1.0. Remote Sens. Environ. 2019, 230, 111196. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER Spectral Library Version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- World Agroforestry (ICRAF); International Soil Reference and Information Centre (ISRIC). ICRAF-ISRIC Soil VNIR Spectral Library. In World Agroforestry—Research Data Repository, V1; World Agroforestry (ICRAF): Nairobi, Kenya, 2021. [Google Scholar] [CrossRef]
- Salvatori, R.; Salzano, R.; Franco, S.D.; Fontinovo, G.; Plini, P. SISpec 2.0 Snow-Ice Spectral Library; National Research Council of Italy, Institute of Polar Sciences: Rome, Italy, 2020.
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Wanner, W.; Strahler, A.H.; Hu, B.; Lewis, P.; Muller, J.-P.; Li, X.; Schaaf, C.L.B.; Barnsley, M.J. Global retrieval of bidirectional reflectance and albedo over land from EOS MODIS and MISR data: Theory and algorithm. J. Geophys. Res. Atmos. 1997, 102, 17143–17161. [Google Scholar] [CrossRef] [Green Version]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef] [Green Version]
- Leigh, L.; Shrestha, M.; Hasan, N.; Kaewmanee, M. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Site for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. In Proceedings of the CALCON 2019, Utah State University, Logan, UT, USA, 19–21 September 2019. [Google Scholar]
- Shrestha, M.; Leigh, L.; Helder, D. Classification of North Africa for use as an extended pseudo invariant calibration site (EPICS) for radiometric calibration and stability monitoring of optical satellite sensors. Remote Sens. 2019, 11, 875. [Google Scholar] [CrossRef] [Green Version]
- Rueda, J.F.; Leigh, L.; Pinto, C.T.; Kaewmanee, M.; Helder, D. Classification and Evaluation of Extended PICS (EPICS) on a Global Scale for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2021, 13, 3350. [Google Scholar] [CrossRef]
- Remote Sensing Phenology. NDVI, the Foundation for Remote Sensing Phenology. USGS, 2018. Available online: https://www.usgs.gov/special-topics/remote-sensing-phenology/science/ndvi-foundation-remote-sensing-phenology (accessed on 25 October 2021).
- Diek, S.; Fornallaz, F.; Schaepman, M.E.; De Jong, R. Barest Pixel Composite for Agricultural Areas Using Landsat Time Series. Remote Sens. 2017, 9, 1245. [Google Scholar] [CrossRef] [Green Version]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Hartung, J.; Knapp, G.; Singa, B.K. Statistical Meta-Analysis with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 44–46. [Google Scholar]
- Khakurel, P.; Leigh, L.; Kaewmanee, M.; Pinto, C.T. Extended Pseudo Invariant Calibration Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2021, 13, 1545. [Google Scholar] [CrossRef]
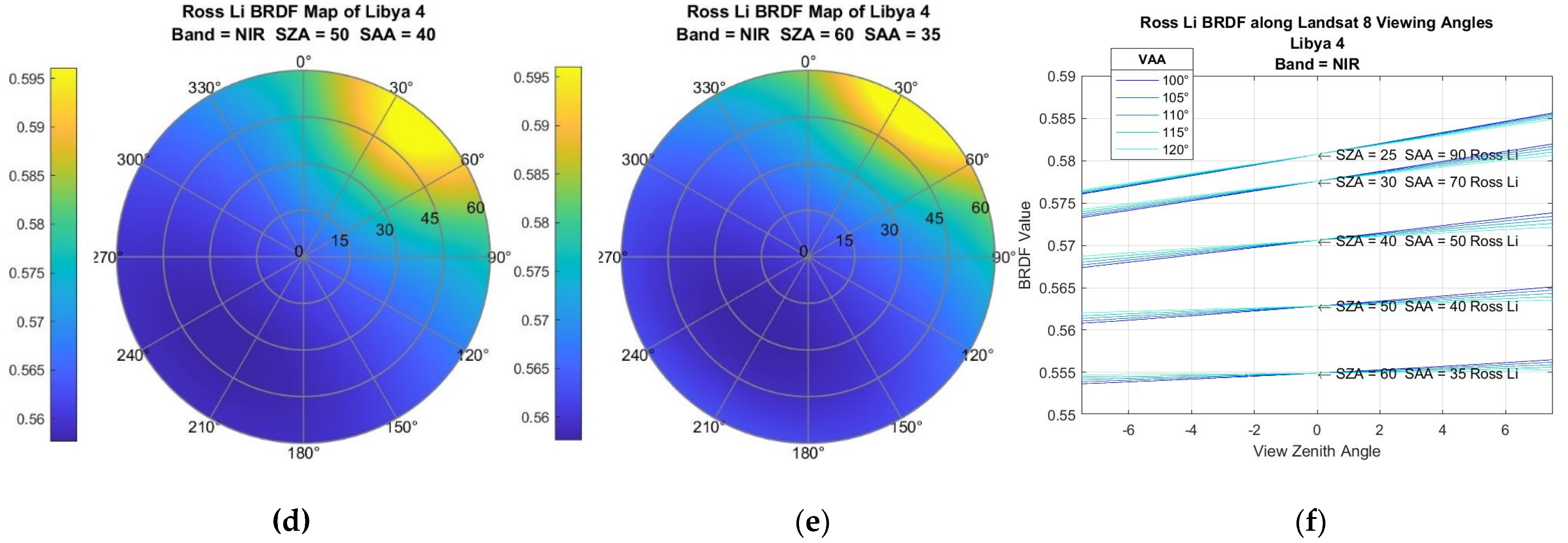
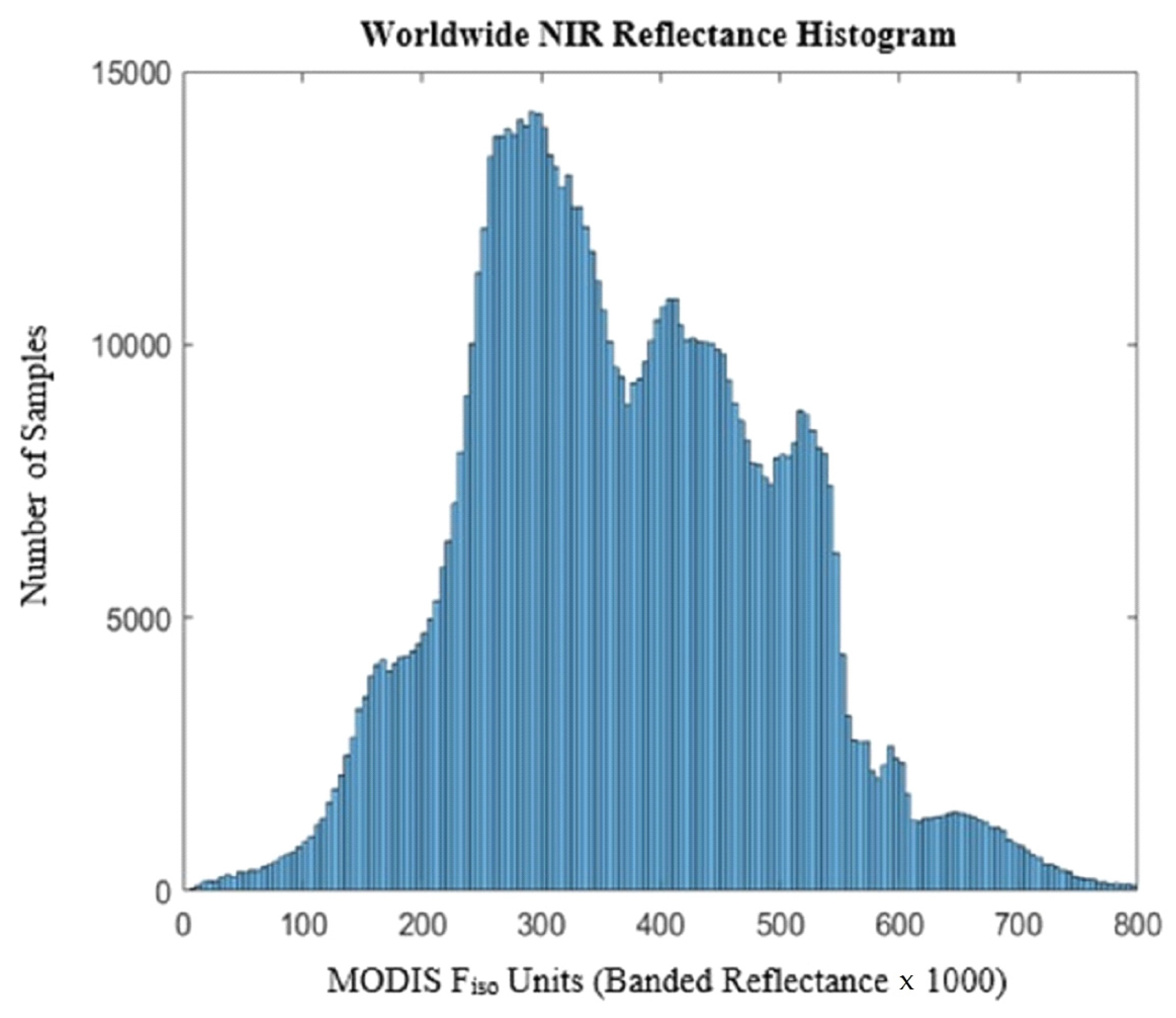
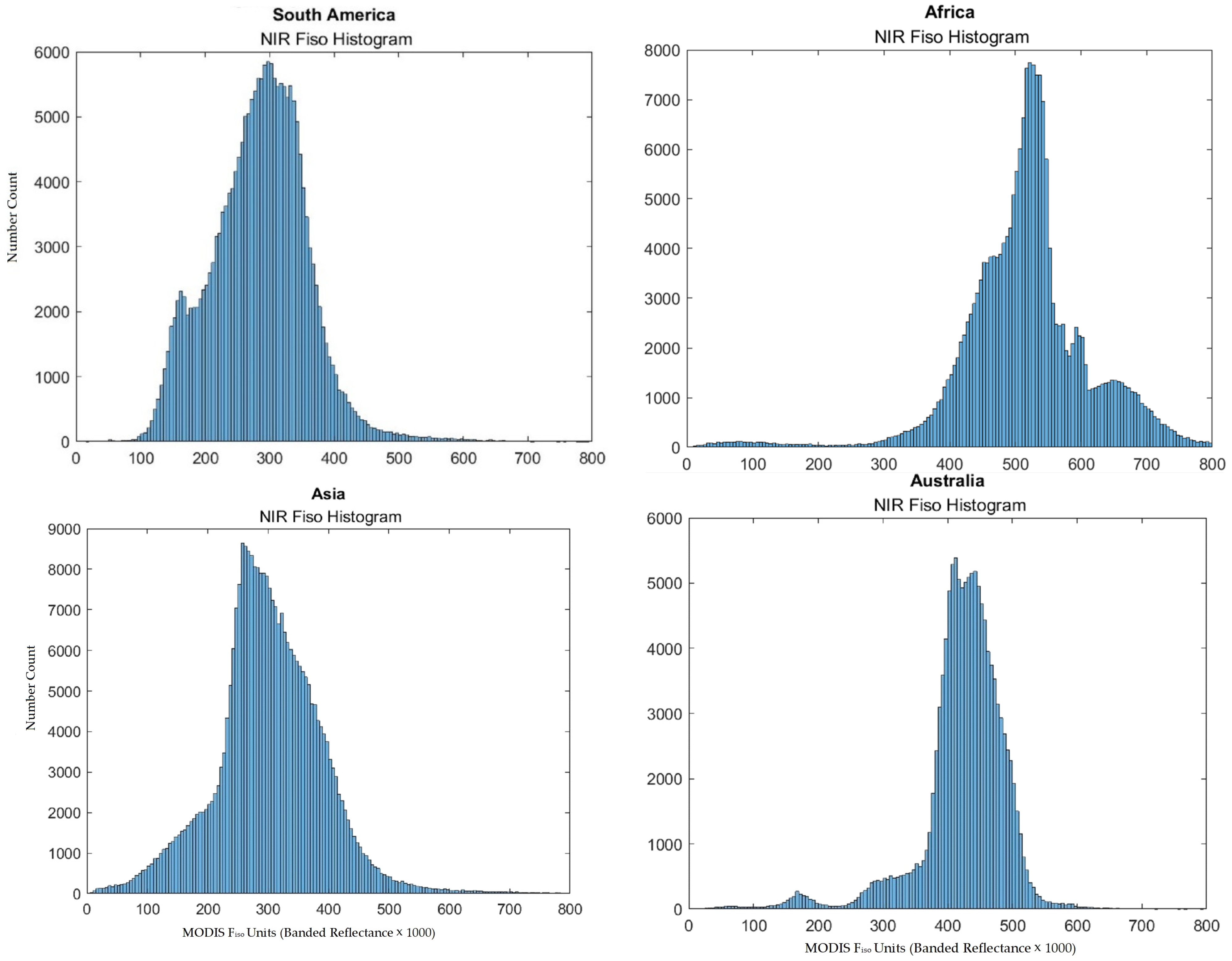
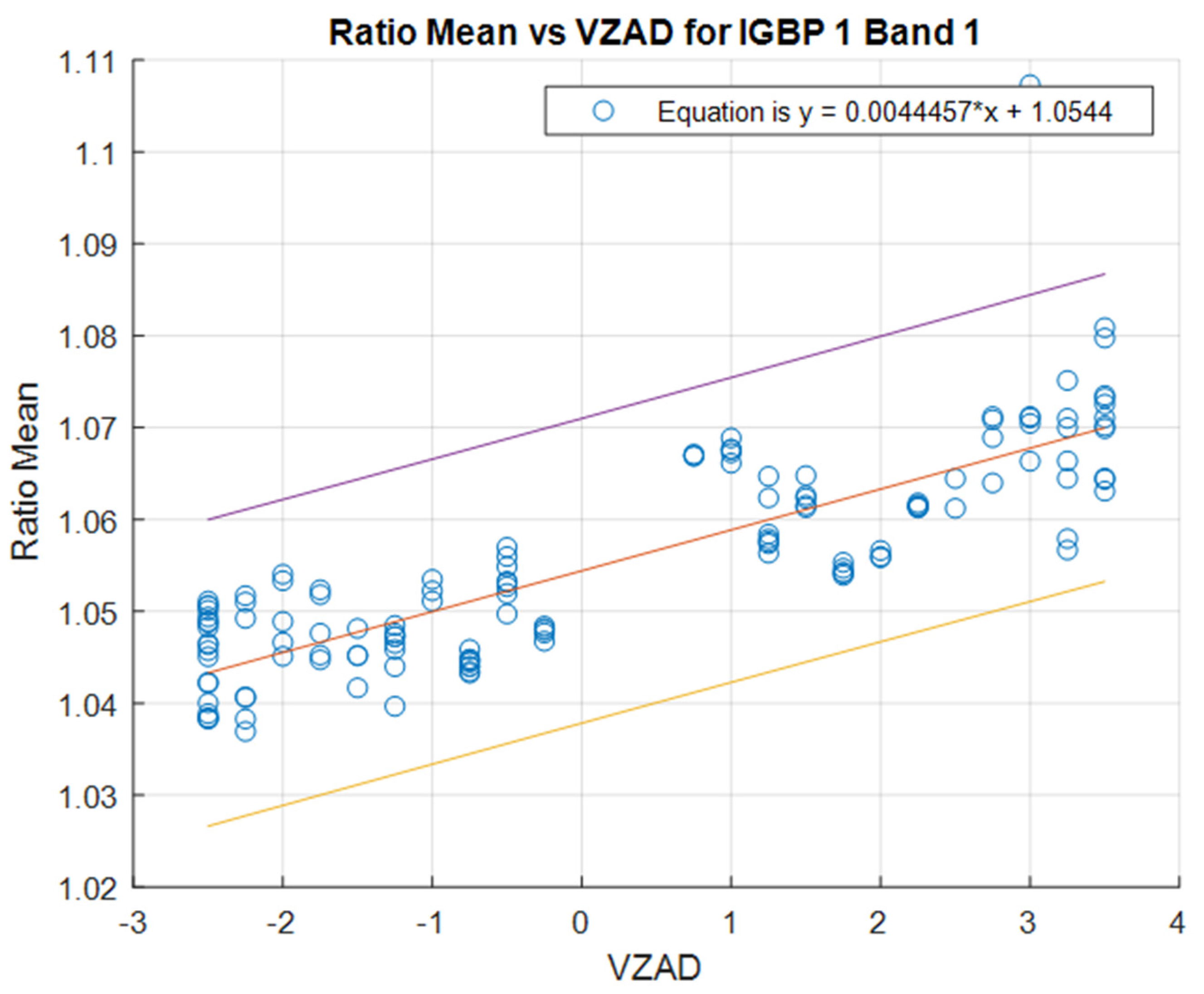
| Name | Value | Description |
|---|---|---|
| Evergreen Needleleaf Forests | 1 | Dominated by evergreen conifer trees (canopy > 2 m). Tree cover >60%. |
| Evergreen Broadleaf Forests | 2 | Dominated by evergreen broadleaf and palmate trees (canopy > 2 m). Tree cover >60%. |
| Deciduous Needleleaf Forests | 3 | Dominated by deciduous needleleaf (larch) trees (canopy > 2 m). Tree cover >60%. |
| Deciduous Broadleaf Forests | 4 | Dominated by deciduous broadleaf trees (canopy > 2 m). Tree cover >60%. |
| Mixed Forests | 5 | Dominated by neither deciduous nor evergreen (40–60% of each) tree type (canopy > 2 m). Tree cover >60%. |
| Closed Shrublands | 6 | Dominated by woody perennials (1–2 m height) >60% cover. |
| Open Shrublands | 7 | Dominated by woody perennials (1–2 m height) 10–60% cover. |
| Woody Savannas | 8 | Tree cover 30–60% (canopy > 2 m). |
| Savannas | 9 | Tree cover 10–30% (canopy > 2 m). |
| Grasslands | 10 | Dominated by herbaceous annuals (<2 m). |
| Permanent Wetlands | 11 | Permanently inundated lands with 30–60% water cover and >10% vegetated cover. |
| Croplands | 12 | At least 60% of area is cultivated cropland. |
| Urban and Built-up Lands | 13 | At least 30% impervious surface area including building materials, asphalt, and vehicles. |
| Cropland/Natural Vegetation Mosaics | 14 | Mosaics of small-scale cultivation 40–60% with natural tree, shrub, or herbaceous vegetation. |
| Permanent Snow and Ice | 15 | At least 60% of area is covered by snow and ice for at least 10 months of the year. |
| Barren | 16 | At least 60% of area is non-vegetated barren (sand, rock, soil) areas with less than 10% vegetation. |
| Water Bodies | 17 | At least 60% of area is covered by permanent water bodies. Has not received a map label because of missing inputs. |
| IGBP # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | 0.026 | 0.020 | 0.086 | 0.030 | 0.025 | 0.055 | 0.084 | 0.038 | 0.045 | 0.087 | 0.078 | 0.042 | 0.540 | 0.143 |
| Green | 0.048 | 0.048 | 0.102 | 0.062 | 0.054 | 0.092 | 0.131 | 0.070 | 0.082 | 0.133 | 0.121 | 0.079 | 0.578 | 0.221 |
| Red | 0.045 | 0.034 | 0.108 | 0.052 | 0.043 | 0.146 | 0.193 | 0.061 | 0.084 | 0.162 | 0.151 | 0.082 | 0.586 | 0.308 |
| NIR | 0.256 | 0.335 | 0.219 | 0.314 | 0.309 | 0.276 | 0.306 | 0.321 | 0.316 | 0.318 | 0.313 | 0.327 | 0.519 | 0.369 |
| SWIR1 | 0.183 | 0.191 | 0.144 | 0.235 | 0.207 | 0.409 | 0.416 | 0.233 | 0.277 | 0.355 | 0.355 | 0.270 | 0.125 | 0.468 |
| SWIR2 | 0.094 | 0.079 | 0.095 | 0.108 | 0.091 | 0.319 | 0.343 | 0.113 | 0.164 | 0.250 | 0.246 | 0.159 | 0.093 | 0.428 |
| IGBP | Dark | Light | Sand |
|---|---|---|---|
| Blue | 0.126 | 0.131 | 0.147 |
| Green | 0.176 | 0.242 | 0.281 |
| Red | 0.248 | 0.354 | 0.441 |
| NIR | 0.291 | 0.437 | 0.529 |
| SWIR1 | 0.385 | 0.614 | 0.711 |
| SWIR2 | 0.371 | 0.506 | 0.664 |
| Dark Soil | Light Soil | Sand | ||||
|---|---|---|---|---|---|---|
| Mean | ±σ | Mean | ±σ | Mean | ±σ | |
| Band 1 | 1.056 | 0.015 | 1.055 | 0.014 | 1.056 | 0.014 |
| Band 2 | 1.050 | 0.016 | 1.050 | 0.013 | 1.050 | 0.007 |
| Band 3 | 1.039 | 0.017 | 1.040 | 0.014 | 1.041 | 0.007 |
| Band 4 | 1.032 | 0.014 | 1.031 | 0.014 | 1.032 | 0.008 |
| Band 5 | 1.021 | 0.015 | 1.021 | 0.013 | 1.021 | 0.008 |
| Band 6 | 0.994 | 0.015 | 0.993 | 0.013 | 0.994 | 0.011 |
| Band 7 | 1.001 | 0.016 | 1.000 | 0.012 | 1.000 | 0.012 |
| Band 8 | 1.025 | 0.008 | 1.025 | 0.012 | 1.027 | 0.008 |
| Deciduous Needleleaf | Mixed Forests | Open Shrublands | Woody Savannas | Savannas | ||||||
| Mean | ±σ | Mean | ±σ | Mean | ±σ | Mean | ±σ | Mean | ±σ | |
| Band 1 | 1.056 | 0.011 | 1.056 | 0.011 | 1.054 | 0.009 | 1.056 | 0.010 | 1.056 | 0.010 |
| Band 2 | 1.051 | 0.012 | 1.050 | 0.012 | 1.050 | 0.009 | 1.051 | 0.012 | 1.051 | 0.011 |
| Band 3 | 1.035 | 0.014 | 1.032 | 0.014 | 1.038 | 0.009 | 1.034 | 0.014 | 1.036 | 0.014 |
| Band 4 | 1.033 | 0.016 | 1.032 | 0.017 | 1.031 | 0.008 | 1.033 | 0.017 | 1.033 | 0.015 |
| Band 5 | 1.025 | 0.014 | 1.023 | 0.013 | 1.021 | 0.007 | 1.024 | 0.014 | 1.023 | 0.014 |
| Band 6 | 0.997 | 0.018 | 0.996 | 0.017 | 0.993 | 0.007 | 0.997 | 0.018 | 0.996 | 0.014 |
| Band 7 | 1.007 | 0.016 | 1.005 | 0.019 | 0.999 | 0.007 | 1.005 | 0.019 | 1.003 | 0.014 |
| Band 8 | 1.016 | 0.018 | 1.018 | 0.018 | 1.025 | 0.009 | 1.020 | 0.016 | 1.020 | 0.012 |
| Grasslands | Cropland | Natural Vegetation | Evergreen Broadleaf | |||||||
| Mean | ±σ | Mean | ±σ | Mean | ±σ | Mean | ±σ | |||
| Band 1 | 1.055 | 0.014 | 1.055 | 0.011 | 1.057 | 0.010 | 1.056 | 0.011 | ||
| Band 2 | 1.051 | 0.014 | 1.051 | 0.012 | 1.052 | 0.010 | 1.050 | 0.012 | ||
| Band 3 | 1.038 | 0.016 | 1.037 | 0.014 | 1.037 | 0.012 | 1.031 | 0.014 | ||
| Band 4 | 1.033 | 0.015 | 1.032 | 0.014 | 1.036 | 0.015 | 1.031 | 0.018 | ||
| Band 5 | 1.033 | 0.015 | 1.022 | 0.013 | 1.026 | 0.012 | 1.024 | 0.015 | ||
| Band 6 | 0.995 | 0.013 | 0.995 | 0.013 | 0.998 | 0.013 | 0.994 | 0.017 | ||
| Band 7 | 1.001 | 0.013 | 1.001 | 0.012 | 1.005 | 0.012 | 1.005 | 0.019 | ||
| Band 8 | 1.023 | 0.010 | 1.022 | 0.012 | 1.021 | 0.013 | 1.016 | 0.017 | ||
| Mean | Std. Dev. | |
|---|---|---|
| Band 1 | 1.056 | 0.003 |
| Band 2 | 1.051 | 0.003 |
| Band 3 | 1.037 | 0.003 |
| Band 4 | 1.032 | 0.004 |
| Band 5 | 1.021 | 0.001 |
| Band 6 | 0.995 | 0.004 |
| Band 7 | 1.002 | 0.004 |
| Band 8 | 1.023 | 0.003 |
| Mean | Std. Dev. | |
|---|---|---|
| Band 1 | 1.020 | 0.005 |
| Band 2 | 1.000 | 0.005 |
| Band 3 | 0.987 | 0.006 |
| Band 4 | 1.003 | 0.007 |
| Band 5 | 1.027 | 0.007 |
| Band 6 | 0.998 | 0.010 |
| Band 7 | 1.004 | 0.011 |
| Band 8 | 1.006 | 0.003 |
| Band 10 | 0.932 | 0.009 |
| Band 11 | 0.954 | 0.008 |
| Underfly Reprocessed Radiance Ratios | Underfly Reprocessed Reflectance Ratios | |||
|---|---|---|---|---|
| Mean | Std. Dev. | Mean | Std. Dev. | |
| Band 1 | 1.000 | 0.003 | 1.000 | 0.004 |
| Band 2 | 1.000 | 0.005 | 1.002 | 0.004 |
| Band 3 | 0.999 | 0.003 | 0.999 | 0.005 |
| Band 4 | 0.997 | 0.003 | 1.000 | 0.004 |
| Band 5 | 0.999 | 0.006 | 1.001 | 0.003 |
| Band 6 | 0.997 | 0.005 | 1.001 | 0.004 |
| Band 7 | 0.996 | 0.005 | 1.000 | 0.004 |
| Band 8 | 1.001 | 0.005 | 1.004 | 0.003 |
| Band 10 | 0.997 | 0.009 | ||
| Band 11 | 1.008 | 0.008 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gross, G.; Helder, D.; Begeman, C.; Leigh, L.; Kaewmanee, M.; Shah, R. Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event. Remote Sens. 2022, 14, 2418. https://doi.org/10.3390/rs14102418
Gross G, Helder D, Begeman C, Leigh L, Kaewmanee M, Shah R. Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event. Remote Sensing. 2022; 14(10):2418. https://doi.org/10.3390/rs14102418
Chicago/Turabian StyleGross, Garrison, Dennis Helder, Christopher Begeman, Larry Leigh, Morakot Kaewmanee, and Ramita Shah. 2022. "Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event" Remote Sensing 14, no. 10: 2418. https://doi.org/10.3390/rs14102418
APA StyleGross, G., Helder, D., Begeman, C., Leigh, L., Kaewmanee, M., & Shah, R. (2022). Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event. Remote Sensing, 14(10), 2418. https://doi.org/10.3390/rs14102418