Performance and Uncertainty of Satellite-Derived Bathymetry Empirical Approaches in an Energetic Coastal Environment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Ground Reference Bathymetry Data
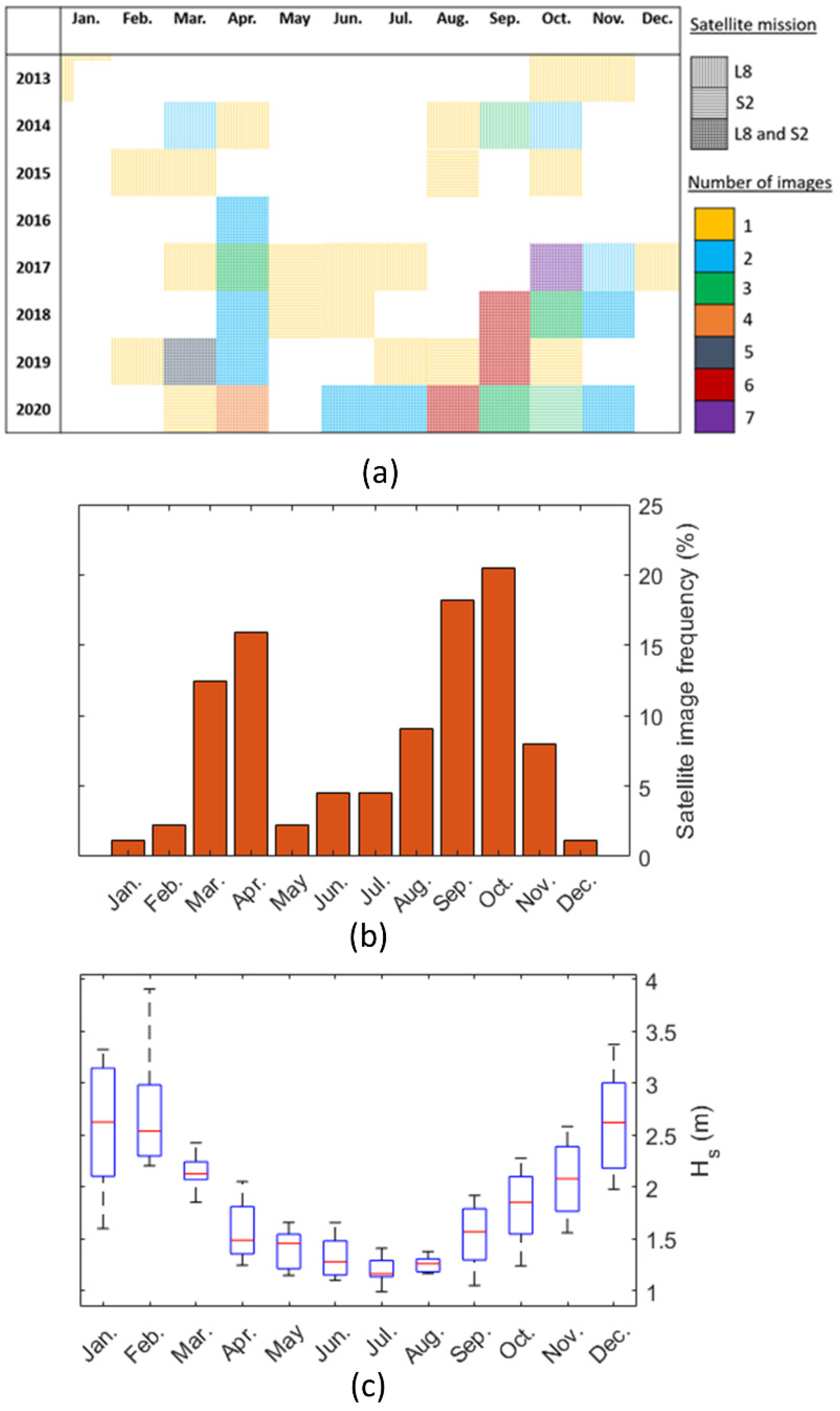
2.3. Selection and Processing of Landsat-8 and Sentinel-2 Images
2.4. Inter-Comparison of SDB Empirical Model Performance
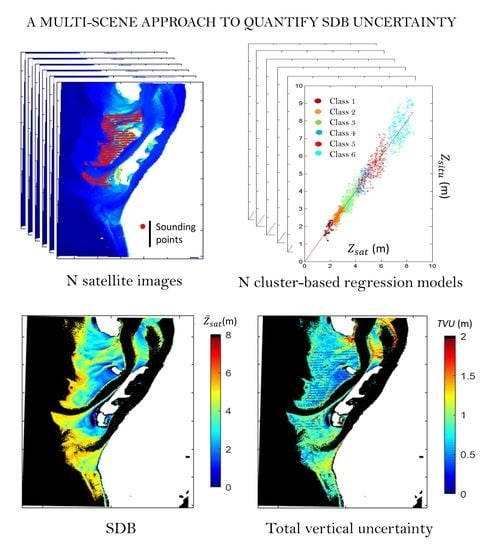
2.5. Assessment of SDB Uncertainty Using a Multi-Scene Approach
3. Results
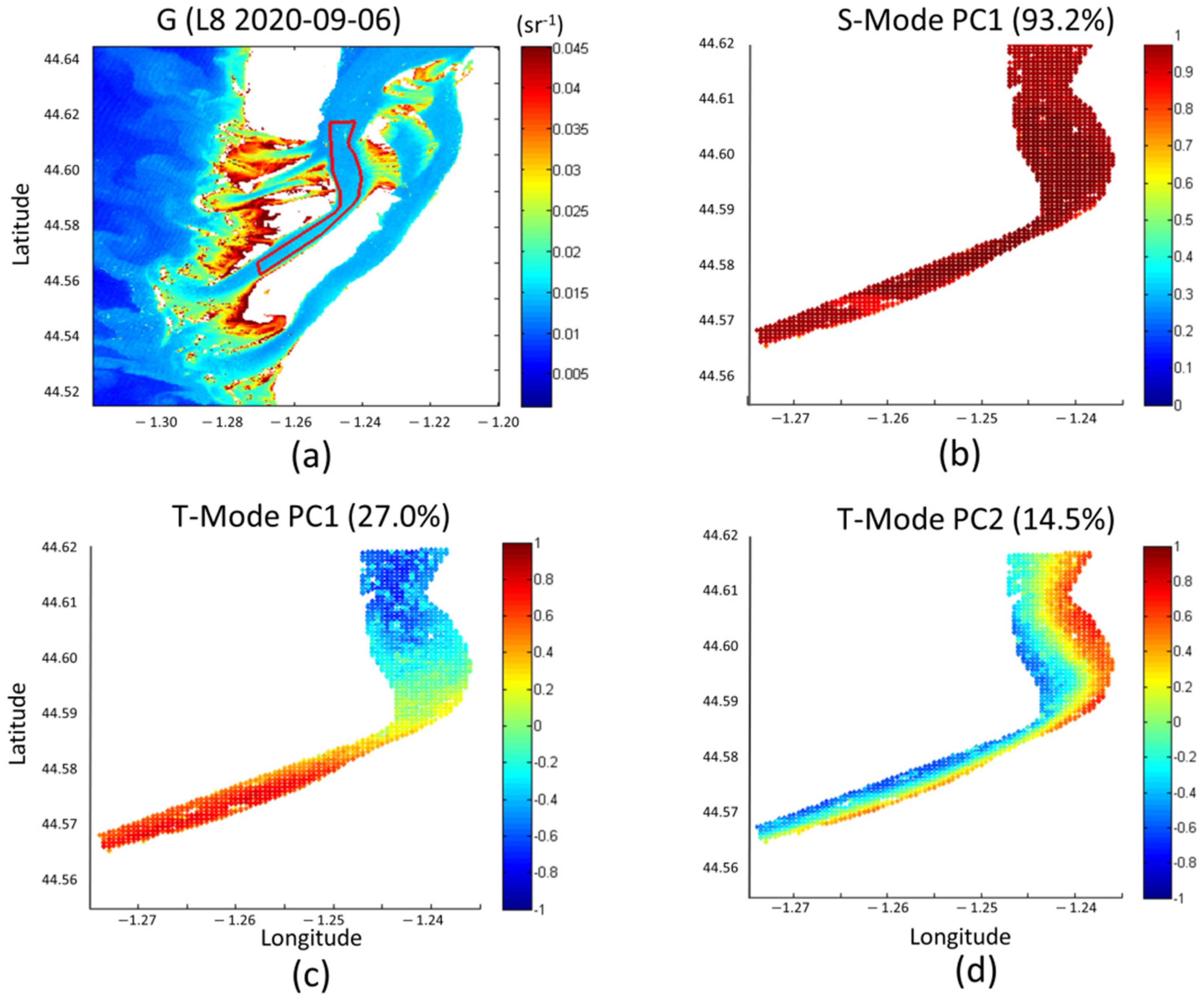
3.1. Hydrological Conditions and Spatio-Temporal Variability of Rrs
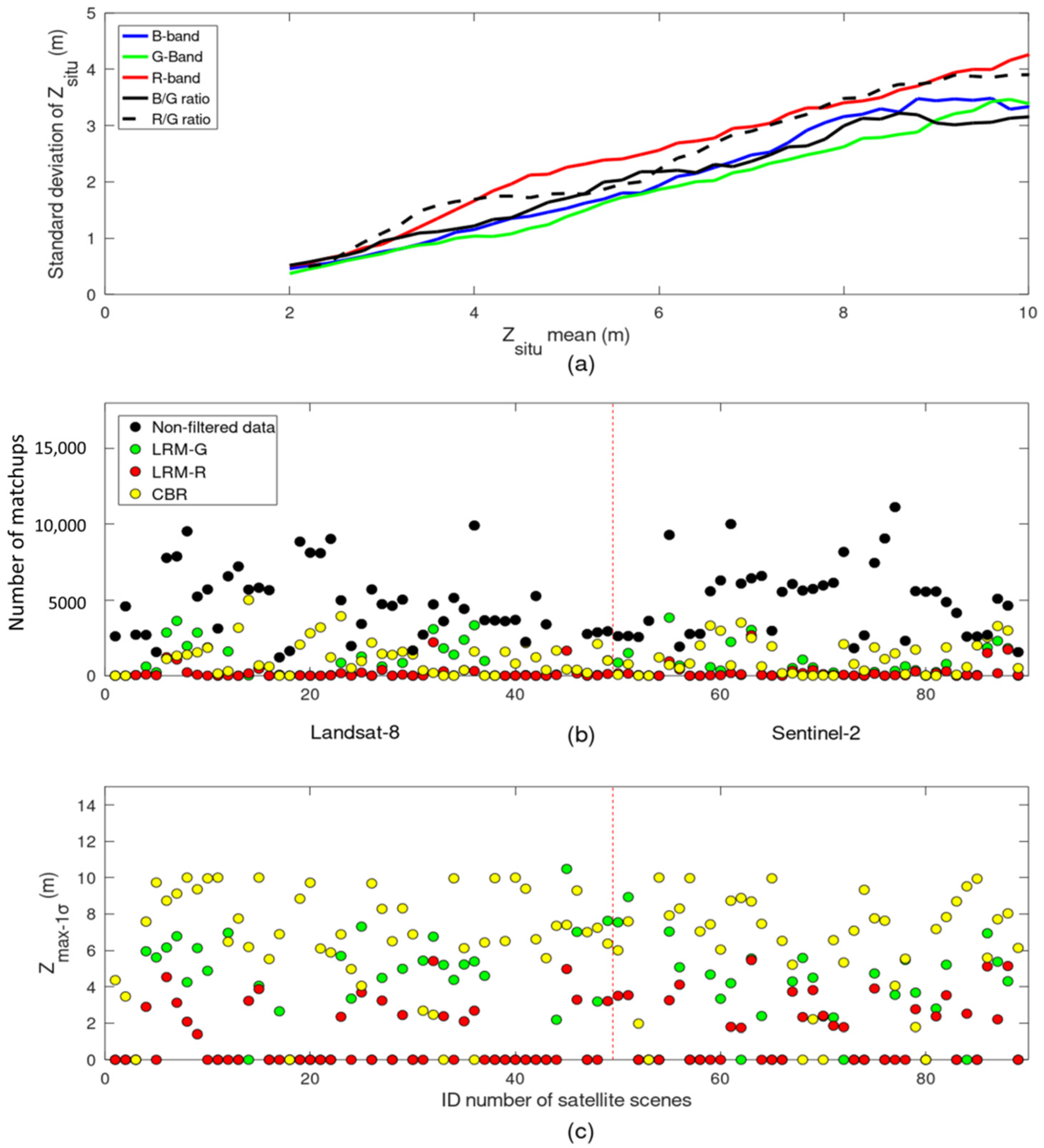
3.2. Sensitivity of Linear Regression Models to Bathymetry Changes
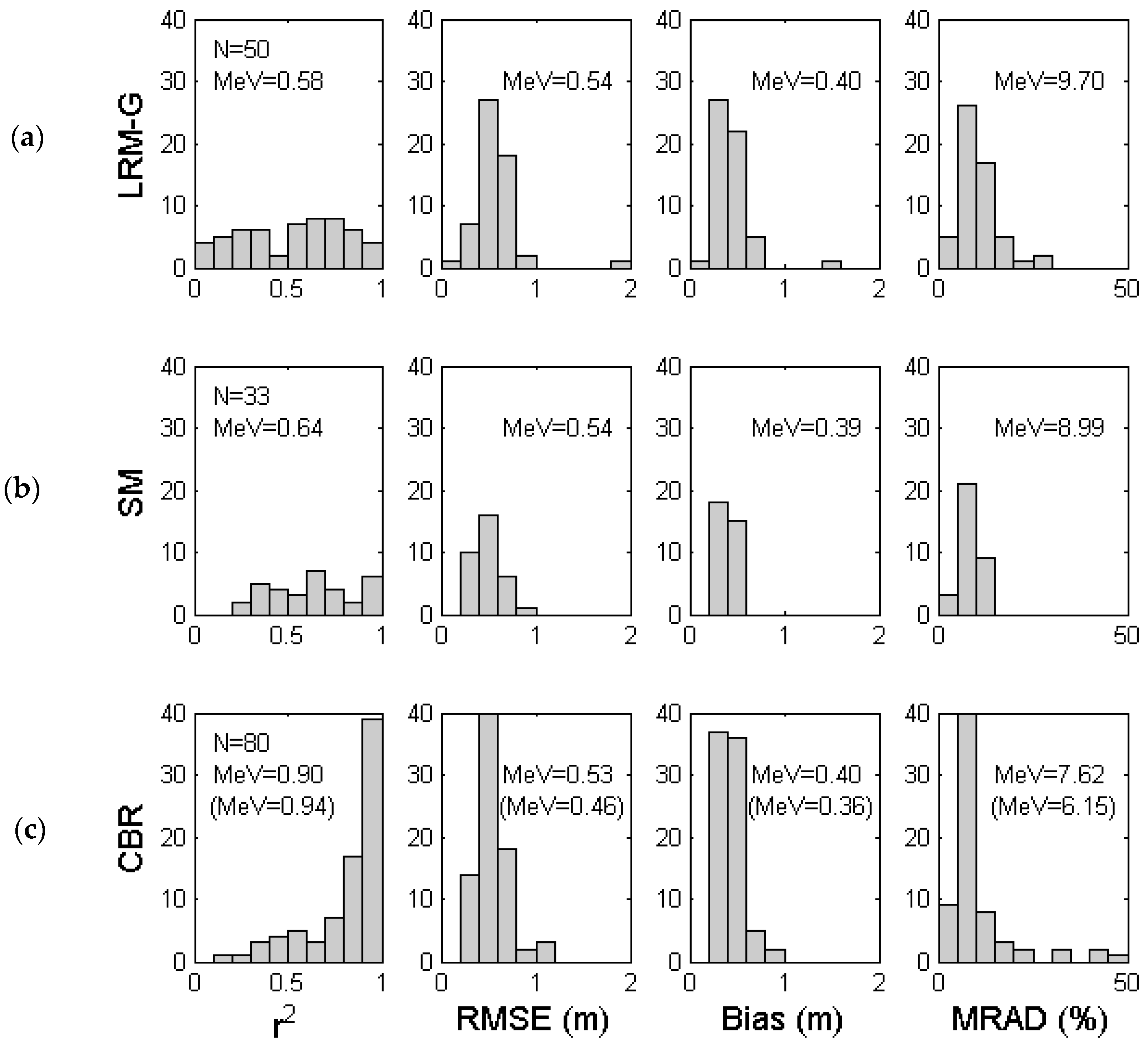
3.3. Inter-Comparison of the Performance of Empirical SDB Approaches
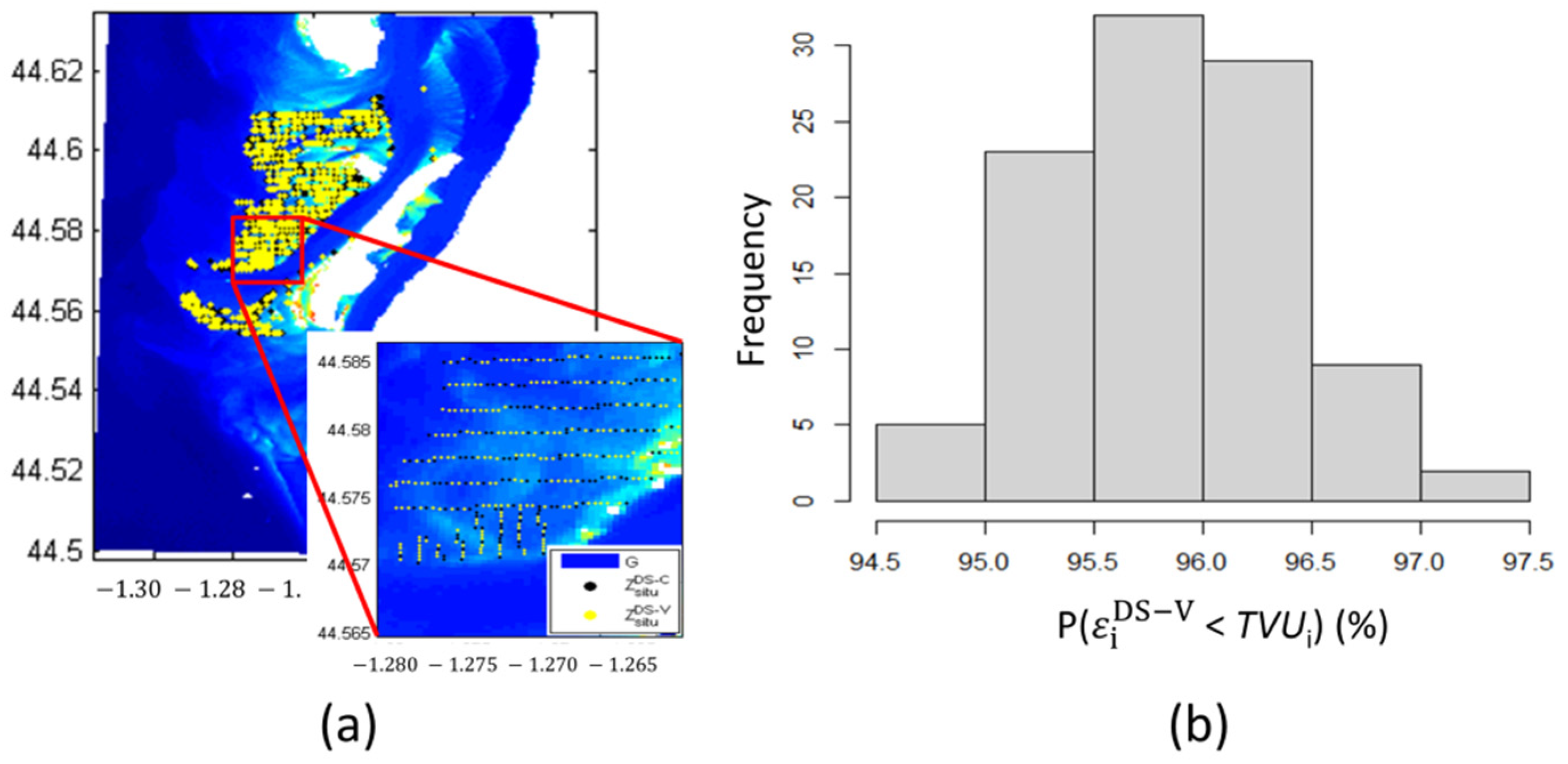
3.4. Validation of the SDB Uncertainty Model
4. Discussion
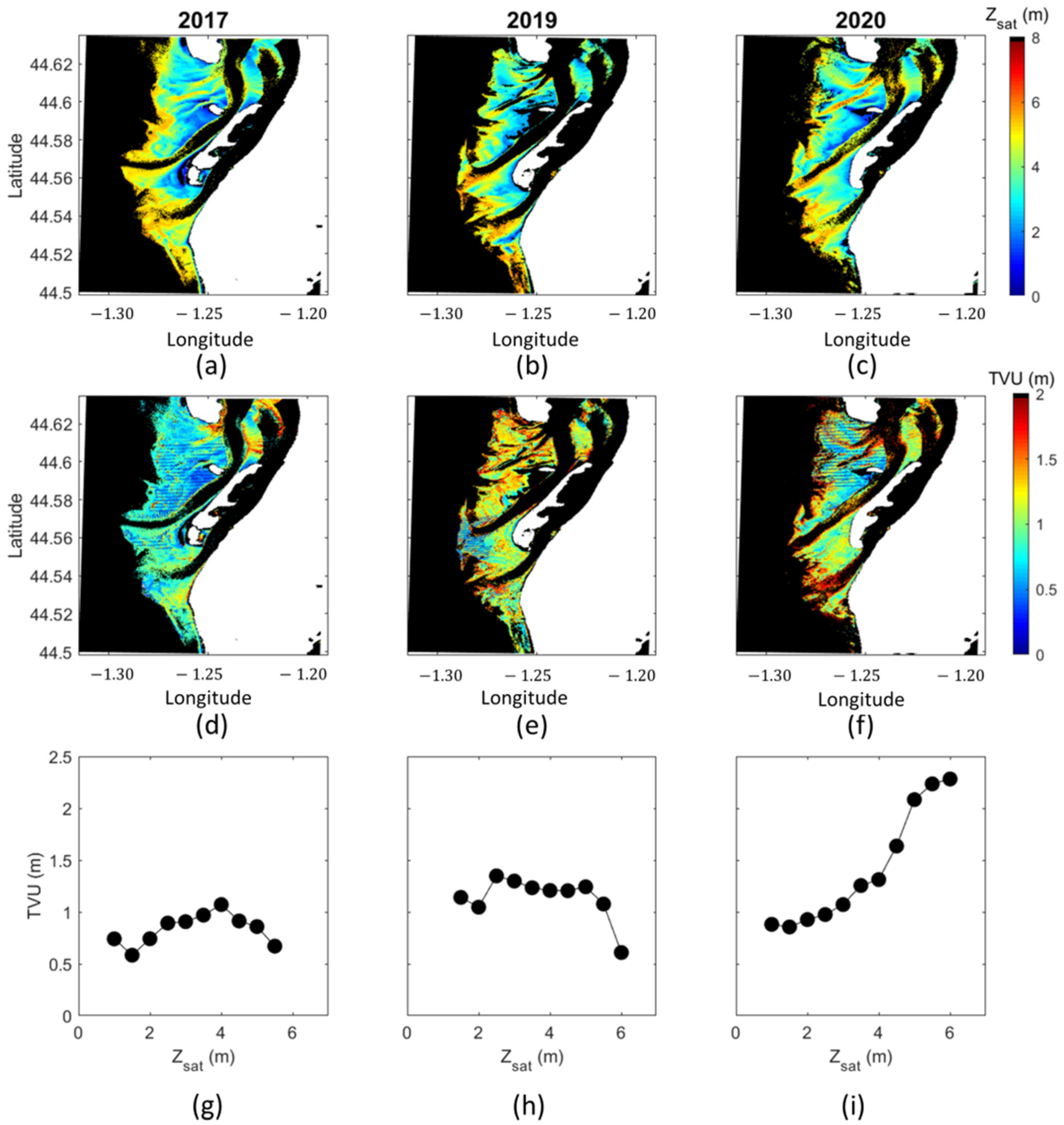
4.1. Impact of the Multi-Scene Approach on Uncertainty
4.2. Impact of the Spatial Distribution of Sounding Point on Uncertainty
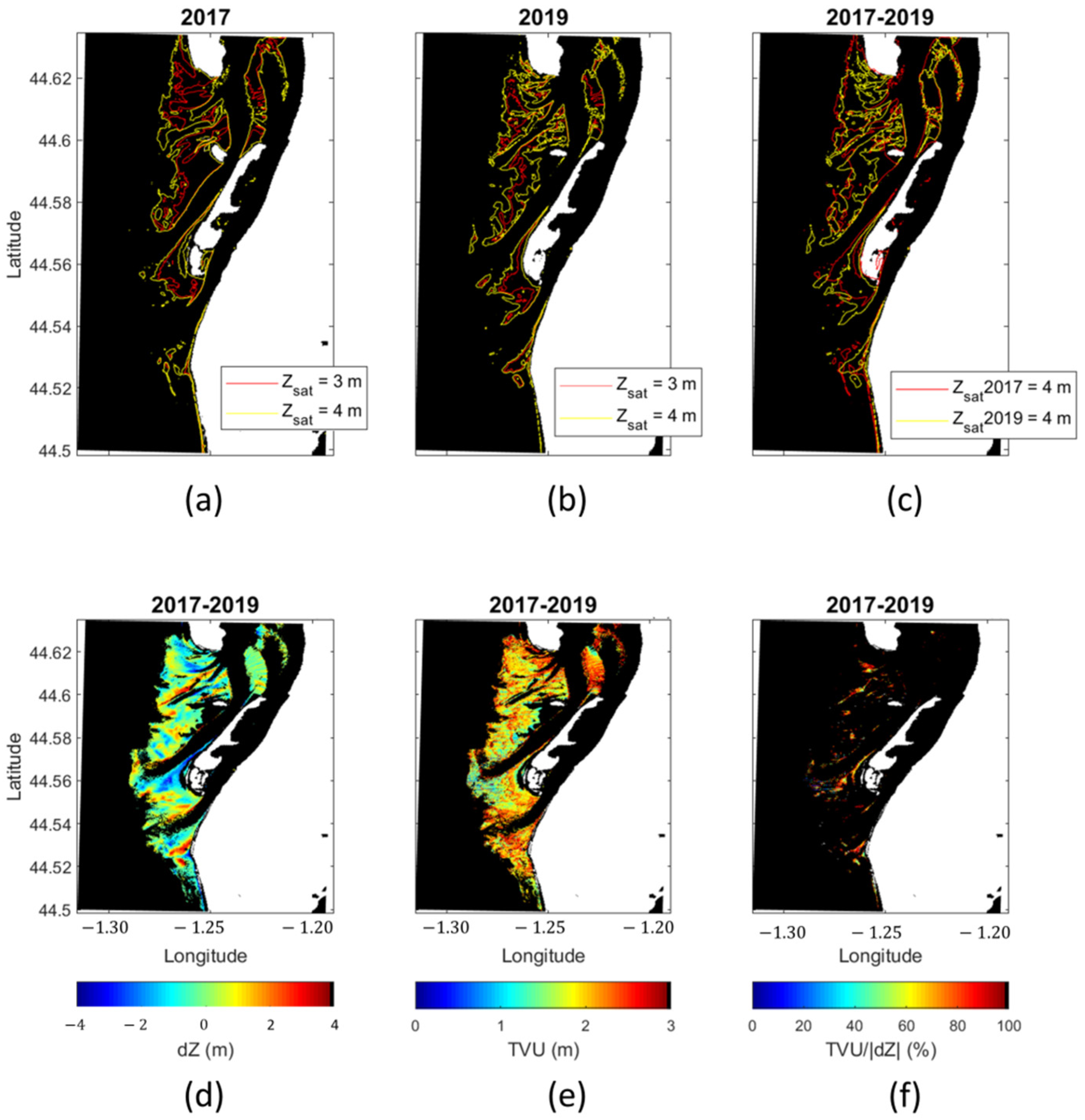
4.3. Morphodynamics Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Newton, A.; Weichselgartner, J. Hotspots of coastal vulnerability: A DPSIR analysis to find societal pathways and responses. Estuar. Coast. Shelf Sci. 2014, 140, 123–133. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Wong, P.P.; Burkett, V.R.; Woodroffe, C.D.; Hay, J.E. Climate change and coastal vulnerability assessment: Scenarios for integrated assessment. Sustain. Sci. 2008, 3, 89–102. [Google Scholar] [CrossRef]
- Ranasinghe, R. Assessing climate change impacts on open sandy coasts: A review. Earth-Sci. Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef] [Green Version]
- Benveniste, J.; Cazenave, A.; Vignudelli, S.; Fenoglio-Marc, L.; Shah, R.; Almar, R.; Andersen, O.; Birol, F.; Bonnefond, P.; Bouffard, J.; et al. Requirements for a Coastal Hazards Observing System. Front. Mar. Sci. 2019, 6, 348:1–348:24. [Google Scholar] [CrossRef] [Green Version]
- Lebbe, T.B.; Rey-Valette, H.; Chaumillon, E.; Camus, G.; Almar, R.; Cazenave, A.; Claudet, J.; Rocle, N.; Meur-Férec, C.; Viard, F.; et al. Designing coastal adaptation strategies to tackle sea level rise. Front. Mar. Sci. 2021, 8, 740602:1–740602:13. [Google Scholar] [CrossRef]
- International Hydrographic Organization. International Hydrographic Publication C-55 Status of Hydrographic Surveying and Charting Worldwide. 2022. Available online: https://iho.int/uploads/user/pubs/cb/c-55/c55.pdf (accessed on 11 March 2022).
- Jacob, B.; Stanev, E.V. Understanding the impact of bathymetric changes in the German bight on coastal hydrodynamics: One step toward realistic morphodynamic model. Front. Mar. Sci. 2021, 8, 640214:1–640214:18. [Google Scholar] [CrossRef]
- Honegger, D.A.; Haller, M.C.; Holman, R.A. High-resolution bathymetry estimates via X-band marine radar: 1. beaches. Coastal Eng. 2019, 149, 39–48. [Google Scholar] [CrossRef]
- Cesbron, G.; Melet, A.; Almar, R.; Lifermann, A.; Tullot, D.; Crosnier, L. Pan-european sateliite-derived coastal bathymetry—Review, user needs and future services. Front. Mar. Sci. 2021, 8, 740830:1–740830:15. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. cBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Capo, S.; Lubac, B.; Marieu, V.; Robinet, A.; Bru, D.; Bonneton, P. Assessment of the decadal morphodynamic evolution of a mixed energy inlet using ocean color remote sensing. Ocean Dyn. 2014, 64, 1517–1530. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.F. Hyperspectral remote sensing for shallow waters: II deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Honegger, D.A.; Haller, M.C.; Holman, R.A. High-resolution bathymetry estimates via X-band marine radar: 2. Effects of currents at tidal inlets. Coastal Eng. 2020, 156, 103626–103643. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Wei, C.; Zhao, Q.; Lu, Y.; Fu, D. Assessment of empirical algorithms for shallow water bathymetry using multi-spectral imagery of Pearl River delta coast, china. Remote Sens. 2021, 13, 3123. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in australian and caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Wand, M.; Lee, Z.; Briceno, H.O.; Yu, X.; Jiang, L.; Garcia, R.; Wang, J.; Luis, K. Shallow water bathymetry with multi-spectral satellite ocean color sensors: Leveraging temporal variation in image data. Remote Sens. Environ. 2020, 250, 112035–112050. [Google Scholar] [CrossRef]
- Botha, E.; Brando, V.; Dekker, A.; Botha, E.J.; Brando, V.E.; Dekker, A.G. Effects of per-pixel variability on uncertainties in bathymetric retrievals from high-resolution satellite images. Remote Sens. 2016, 8, 459. [Google Scholar] [CrossRef] [Green Version]
- Caballero, I.; Stumpf, R. Towards routine mapping of shallow bathymetry in environments with variable turbidity: Contribution of Sentinel-2A/B satellites mission. Remote Sens. 2020, 12, 451. [Google Scholar] [CrossRef] [Green Version]
- Geyman, E.C.; Maloof, A.C. A simple method for extracting water depth from multispectral satellite imagery in regions of variable bottom type. Earth Space Sci. 2019, 6, 527–537. [Google Scholar] [CrossRef]
- International Hydrographic Organization. International Hydrographic Publication C-44 Standards for Hydrographic Surveys Edition 6.0.0. 2020. Available online: https://iho.int/uploads/user/pubs/standards/s-44/S-44_Edition_6.0.0_EN.pdf (accessed on 30 September 2020).
- IOCCG. Uncertainties in Ocean Colour Remote Sensing; Mélin, F., Ed.; IOCCG Report series, No. 18; International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2019; ISBN 978-1-896246-68-0. [Google Scholar]
- Hayes, M.O. Barrier island morphology as a function of tidal and wave regime. In Barrier Island; Leatherman, S.P., Ed.; Academic Press: New York, NY, USA, 1979; pp. 1–28. ISBN 0-12-440260-7. [Google Scholar]
- Senechal, N.; Sottolichio, A.; Bertrand, F.; Goeldner-Gianella, L.; Garlan, T. Observations of waves’ impact on currents in a mixed-energy tidal inlet: Arcachon on the southern French Atlantic coast. J. Coast. Res. 2013, 65, 2053–2058. [Google Scholar] [CrossRef]
- Castelle, B.; Bujan, S.; Ferreira, S.; Dodet, G. Foredune morphological changes and beach recovery from the extreme 2013/2014 winter at a high-energy sandy coast. Mar. Geol. 2017, 385, 41–55. [Google Scholar] [CrossRef]
- Nicolae Lerma, A.; Bulteau, T.; Lecacheux, S.; Idier, D. Spatial variability of extreme wave height along the Atlantic and channel French coast. Ocean Eng. 2015, 97, 175–185. [Google Scholar] [CrossRef]
- Cayocca, F. Long-term morphological modeling of a tidal inlet: The Arcachon Basin, France. Coast. Eng. 2001, 42, 115–142. [Google Scholar] [CrossRef]
- Nahon, A.; Idier, D.; Sénéchal, N.; Mallet, C.; Mugica, J. Imprints of wave climate and mean sea level variations in the dynamics of a coastal spit over the last 250 years: Cap Ferret, SW France. Earth Surf. Process. Landf. 2019, 44, 2112–2125. [Google Scholar] [CrossRef]
- Liénart, C.; Savoye, N.; Bozec, Y.; Breton, E.; Conan, P.; David, V.; Feunteun, E.; Grangeré, K.; Kerhervé, P.; Lebreton, B.; et al. Dynamics of particulate organic matter composition in coastal systems: A spatio-temporal study at multi-systems scale. Prog. Oceanogr. 2017, 156, 221–239. [Google Scholar] [CrossRef] [Green Version]
- Glé, C.; Del Amo, Y.; Sautour, B.; Laborde, P.; Chardy, P. Variability of nutrients and phytoplankton primary production in a shallow macrotidal coastal ecosystem (Arcachon Bay, France). Estuar. Coast. Shelf Sci. 2008, 76, 642–656. [Google Scholar] [CrossRef]
- Pedreros, R.; Howa, H.L.; Michel, D. Application of grain size trend analysis for the determination of sediment transport pathways in intertidal areas. Mar. Geol. 1996, 135, 35–49. [Google Scholar] [CrossRef] [Green Version]
- Pahlevan, N.; Lee, Z.; Hu, C.; Schott, J.R. Diurnal remote sensing of coastal/oceanic waters: A radiometric analysis for geostationary coastal and air pollution events. Appl. Opt. 2014, 53, 648–665. [Google Scholar] [CrossRef]
- Drusch, M.; del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isoal, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Pahlevan, N.; Scott, J.R.; Franz, B.A.; Zibordi, G.; Markham, B.; Bailey, S.; Schaaf, C.B.; Ondrusek, M.; Greb, S.; Strait, C.M. Landsat 8 remote sensing reflectance (Rrs) products: Evaluations, intercomparisons, and enhancements. Remote Sens. Environ. 2017, 190, 289–301. [Google Scholar] [CrossRef]
- Pahlevan, N.; Chittimalli, S.K.; Balasubramaniam, S.V.; Velluci, V. Sentinel-2/Landsat-8 product consistency and implications for monitoring aquatic systems. Remote Sens. Environ. 2019, 220, 19–29. [Google Scholar] [CrossRef]
- Li, J.; Chen, B. Global revisit interval analysis of Landsat-8-9 and Sentinel-2A -2B data for terrestrial monitoring. Sensors 2020, 20, 6631. [Google Scholar] [CrossRef]
- Bru, D.; Lubac, B.; Normandin, C.; Robinet, A.; Leconte, M.; Hagolle, O.; Martiny, N.; Jamet, C. Atmospheric correction of multi-spectral littoral images using a PHOTONS/AERONET-based regional aerosol model. Remote Sens. 2017, 9, 814. [Google Scholar] [CrossRef] [Green Version]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of metre-scale optical satellite data for inland and coastal water applications. Remote Sens. Environ. 2018, 216, 586–597. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Sensitivity analysis of the dark spectrum fitting atmospheric correction for metre- and decametre-scale satellite imagery using autonomous hyperspectral radiometry. Opt. Express 2020, 28, 29948–29965. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Retrieval of nearshore bathymetry from Sentinel-2A and 2B satellites in South Florida coastal waters. Estuar. Coast. Shelf Sci. 2019, 12, 451–474. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of Sentinel-3/OLCI data for mapping of suspended particulate matter and chlorophyll-a concentration in Belgian turbid coastal waters. Remote Sens. Environ. 2021, 256, 112284. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Lubac, B.; Loisel, H. Variability and classification of remote sensing reflectance spectra in the eastern English Channel and southern North Sea. Remote Sens. Environ. 2007, 110, 45–58. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Loisel, H.; Dessailly, D.; Mériaux, X. Optical classification of contrasted coastal waters. Remote Sens. Environ. 2012, 123, 306–323. [Google Scholar] [CrossRef]
- Knutti, R.; Hadorn, G.H.; Baumberger, D. Uncertainty Quantification Using Multiple Models—Prospects and Challenges. In Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives; Beisbart, C., Saam, N.J., Eds.; Springer: Cham, Switzerland, 2019; pp. 835–855. [Google Scholar] [CrossRef]
- Normandin, C.; Lubac, B.; Sottolichio, A.; Frappart, F.; Ygorra, B.; Marieu, V. Analysis of suspended sediment variability in a large highly turbid estuary using a 5-year-long remotely sensed data archive at high resolution. J. Geophys. Res. Oceans 2019, 124, 7661–7682. [Google Scholar] [CrossRef] [Green Version]
- Novoa, S.; Doxaran, D.; Ody, A.; Vanhellemont, Q.; Lafon, V.; Lubac, B.; Gernez, P. Atmospheric corrections and multiconditional algorithm for multi-sensor remote sensing of suspended particulate matter in low-to-high turbidity levels coastal waters. Remote Sens. 2017, 9, 61. [Google Scholar] [CrossRef] [Green Version]
- Moore, T.S.; Campbell, J.W.; Feng, H. A fuzzy logic classification scheme for selecting and blending satellite ocean color algorithms. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1764–1776. [Google Scholar] [CrossRef]
- Jackson, T.; Sathyendranath, S.; Mélin, F. An improved optical classification scheme for the Ocean Colour Essential Climate Variable and its applications. Remote Sens. Environ. 2017, 203, 152–161. [Google Scholar] [CrossRef]
- Burvingt, O.; Nicolae Lerma, A.; Lubac, B.; Mallet, C.; Senechal, N. Geomorphological control of sandy beaches and dunes alongside a mixed-energy tidal inlet. Mar. Geol. 2022; accepted. [Google Scholar]





| Date | Location | Number of Points | Zmin (m) | Zmax (m) | Zmedian (m) |
|---|---|---|---|---|---|
| 15 October 2013 | CH | 2231 | 1.1 | 17.5 | 5.6 |
| 27 November 2013 | ED; CH | 5716 | 0.0 | 18.1 | 5.0 |
| 18 March 2014 | ED; CH | 155,077 | 0.0 | 19.7 | 5.4 |
| 16 April 2014 | FD; CH; CO | 40,620 | 0.0 | 25.5 | 6.4 |
| 28 May 2014 | SP; CH | 4727 | 0.0 | 21.1 | 4.0 |
| 23 September 2014 | ED | 3750 | 0.0 | 16.4 | 5.9 |
| 19 March 2015 | ED | 5266 | 0.0 | 17.3 | 5.5 |
| 15 April 2015 | FD; SP; CO | 102,422 | 0.2 | 24.4 | 8.1 |
| 25 September 2015 | ED; CO | 11,552 | 0.0 | 18.4 | 5.1 |
| 13 October 2015 | ED | 9406 | 0.0 | 20.3 | 3.7 |
| 22 March 2016 | ED; CH | 5960 | 0.0 | 19.0 | 6.1 |
| 15 May 2016 | SP | 2986 | 0.0 | 25.5 | 5.1 |
| 11 April 2017 | ED; CH | 3856 | 0.0 | 17.0 | 5.9 |
| 23 June 2017 | FD; CH; CO | 8804 | 0.0 | 22.0 | 6.6 |
| 20 September 2017 | ED; SP | 7283 | 0.0 | 18.3 | 4.5 |
| 15 November 2017 | SP | 8348 | 0.0 | 18.8 | 3.1 |
| 25 April 2018 | ED | 4446 | 0.0 | 16.3 | 5.6 |
| 29 May 2018 | FD; CO | 9276 | 0.0 | 25.2 | 7.9 |
| 08 October 2018 | ED; CH; CO | 7300 | 0.0 | 24.3 | 5.5 |
| 26 November 2018 | SP | 1988 | 0.0 | 18.0 | 4.6 |
| 20 March 2019 | CO | 2484 | 0.0 | 21.6 | 11.2 |
| 19 April 2019 | ED; SP | 8579 | 0.0 | 16.1 | 4.5 |
| 14 May 2019 | FD; CH | 4874 | 0.0 | 25.4 | 5.1 |
| 17 June 2019 | FD; CH | 3236 | 0.0 | 21.3 | 4.8 |
| 16 September 2019 | ED; CH | 6835 | 0.0 | 16.1 | 4.8 |
| 23 March 2020 | ED | 6669 | 0.0 | 16.1 | 5.0 |
| 01 July 2020 | FD; CH; CO | 4833 | 0.1 | 26.1 | 13.1 |
| 01 September 2020 | SP | 6817 | 0.0 | 17.4 | 2.5 |
| 19 October 2020 | SP; CO | 5496 | 0.0 | 25.9 | 5.1 |
| Season | TS | TR (m) | TL (m) | Hs (m) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Sp | 20 | HT | 15 | Mean | 3.10 | Mean | 2.16 | Mean | 1.14 |
| Su | 24 | LT | 19 | Sd | 0.84 | Sd | 0.92 | Sd | 0.50 |
| Fa | 32 | F | 29 | Min | 1.50 | Min | 0.03 | Min | 0.25 |
| Wi | 13 | E | 26 | Max | 4.80 | Max | 3.60 | Max | 2.50 |
| S-Mode | T-Mode | |||||
|---|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC1 | PC2 | PC3 | |
| Season | *** | 0.20 | 0.92 | * | * | 0.50 |
| TS | 0.34 | * | 0.12 | ** | * | *** |
| TL | 0.78 | ** | 0.48 | ** | 0.78 | * |
| TR | 0.58 | * | 0.33 | * | 0.27 | 0.82 |
| Hs | 0.56 | * | 0.33 | 0.13 | 0.61 | 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubac, B.; Burvingt, O.; Nicolae Lerma, A.; Sénéchal, N. Performance and Uncertainty of Satellite-Derived Bathymetry Empirical Approaches in an Energetic Coastal Environment. Remote Sens. 2022, 14, 2350. https://doi.org/10.3390/rs14102350
Lubac B, Burvingt O, Nicolae Lerma A, Sénéchal N. Performance and Uncertainty of Satellite-Derived Bathymetry Empirical Approaches in an Energetic Coastal Environment. Remote Sensing. 2022; 14(10):2350. https://doi.org/10.3390/rs14102350
Chicago/Turabian StyleLubac, Bertrand, Olivier Burvingt, Alexandre Nicolae Lerma, and Nadia Sénéchal. 2022. "Performance and Uncertainty of Satellite-Derived Bathymetry Empirical Approaches in an Energetic Coastal Environment" Remote Sensing 14, no. 10: 2350. https://doi.org/10.3390/rs14102350
APA StyleLubac, B., Burvingt, O., Nicolae Lerma, A., & Sénéchal, N. (2022). Performance and Uncertainty of Satellite-Derived Bathymetry Empirical Approaches in an Energetic Coastal Environment. Remote Sensing, 14(10), 2350. https://doi.org/10.3390/rs14102350