Application of the Doppler Spectrum of the Backscattering Microwave Signal for Monitoring of Ice Cover: A Theoretical View
Abstract
1. Introduction
2. Method
2.1. Initial Assumptions
2.2. Semi-Empirical Model of the Doppler Spectrum for Ice Cover
2.3. Semi-Empirical Model of the Doppler Spectrum for Sea Waves
2.4. Basic Parameters of Doppler Spectrum
2.5. Comparison of Analytical and Semi-Empirical Models of Doppler Spectrum
3. Results
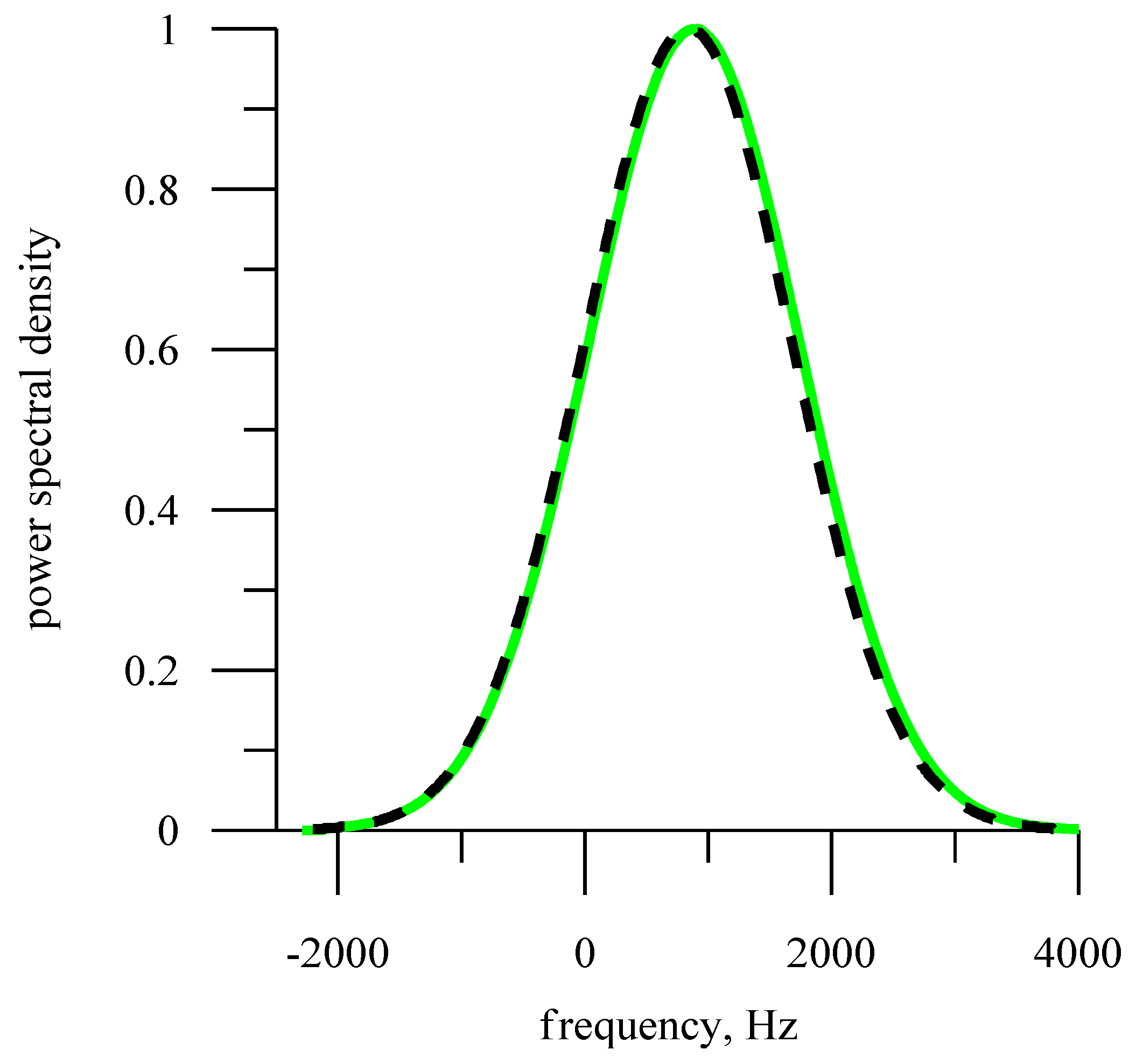
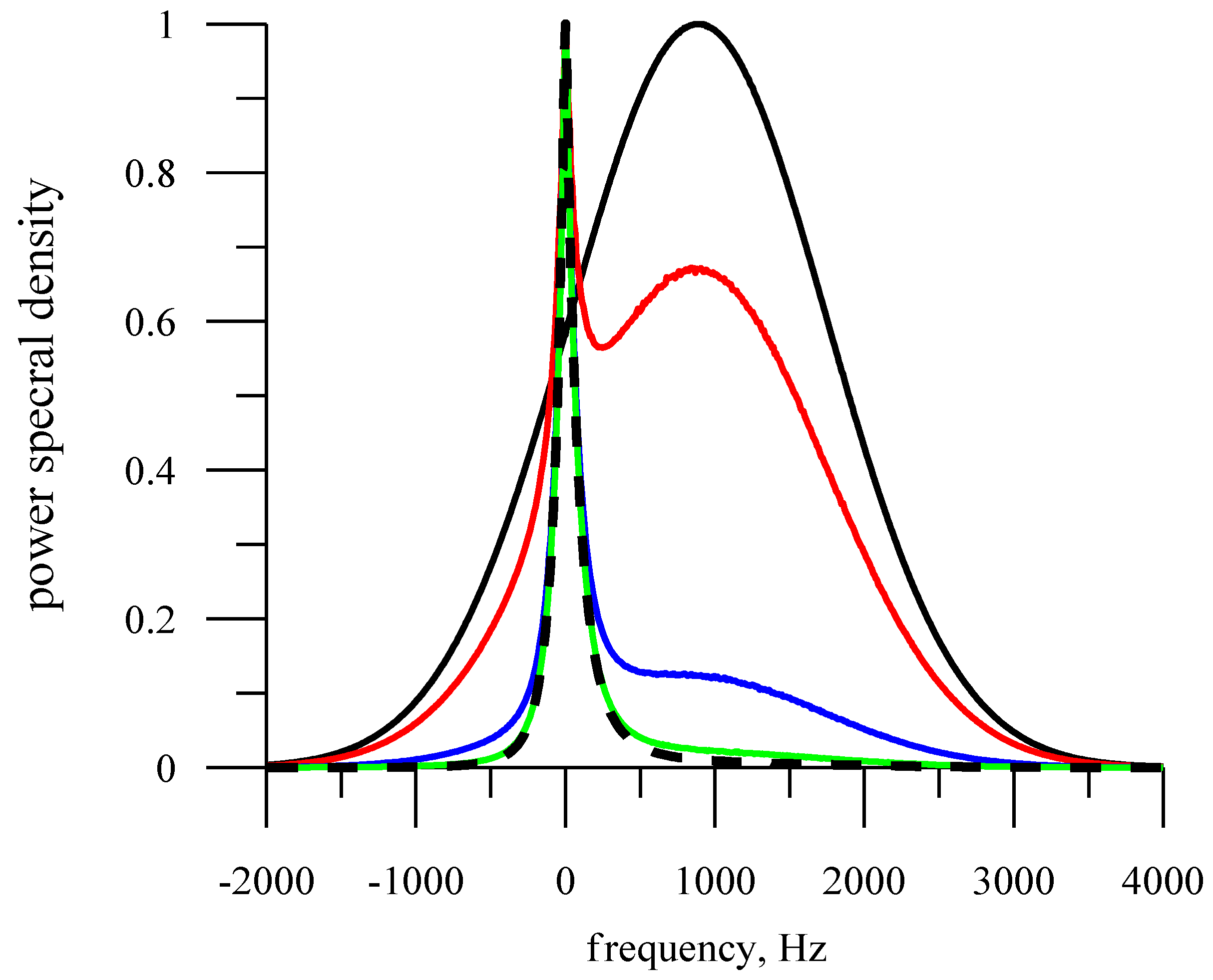
3.1. Comparison of Doppler Spectra
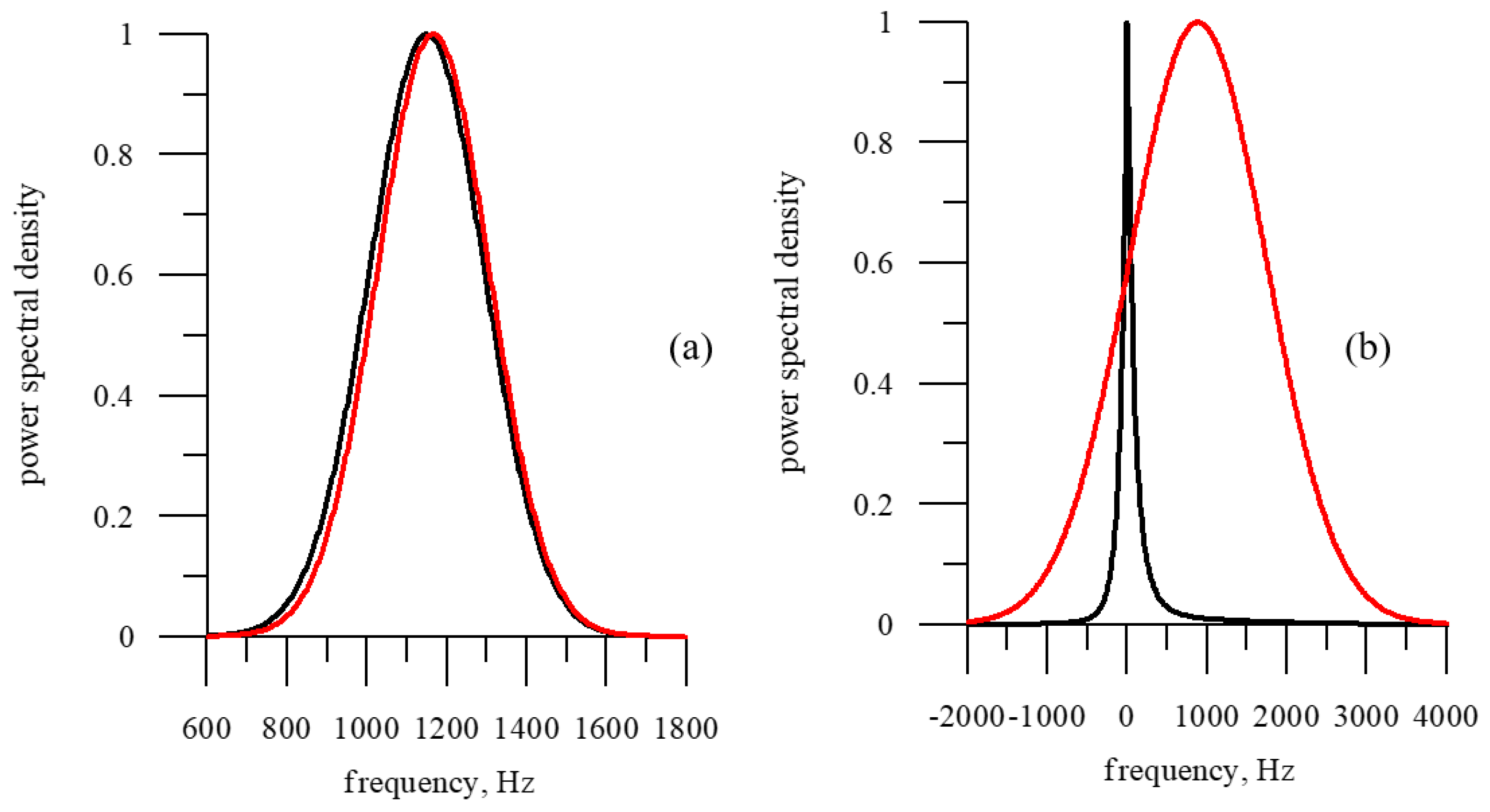
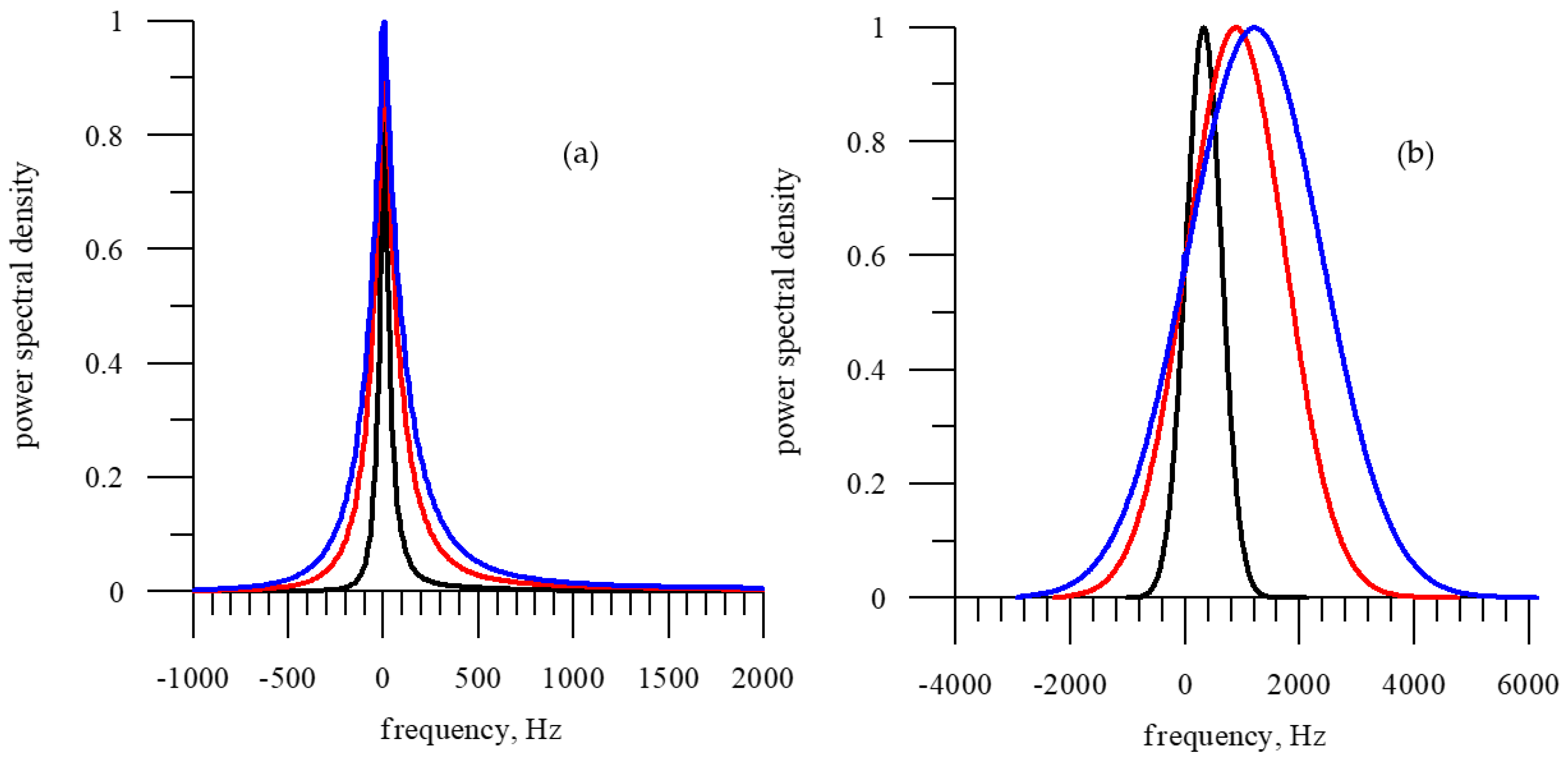
3.2. Influence of Sea Ice Concentration on the Doppler Spectrum
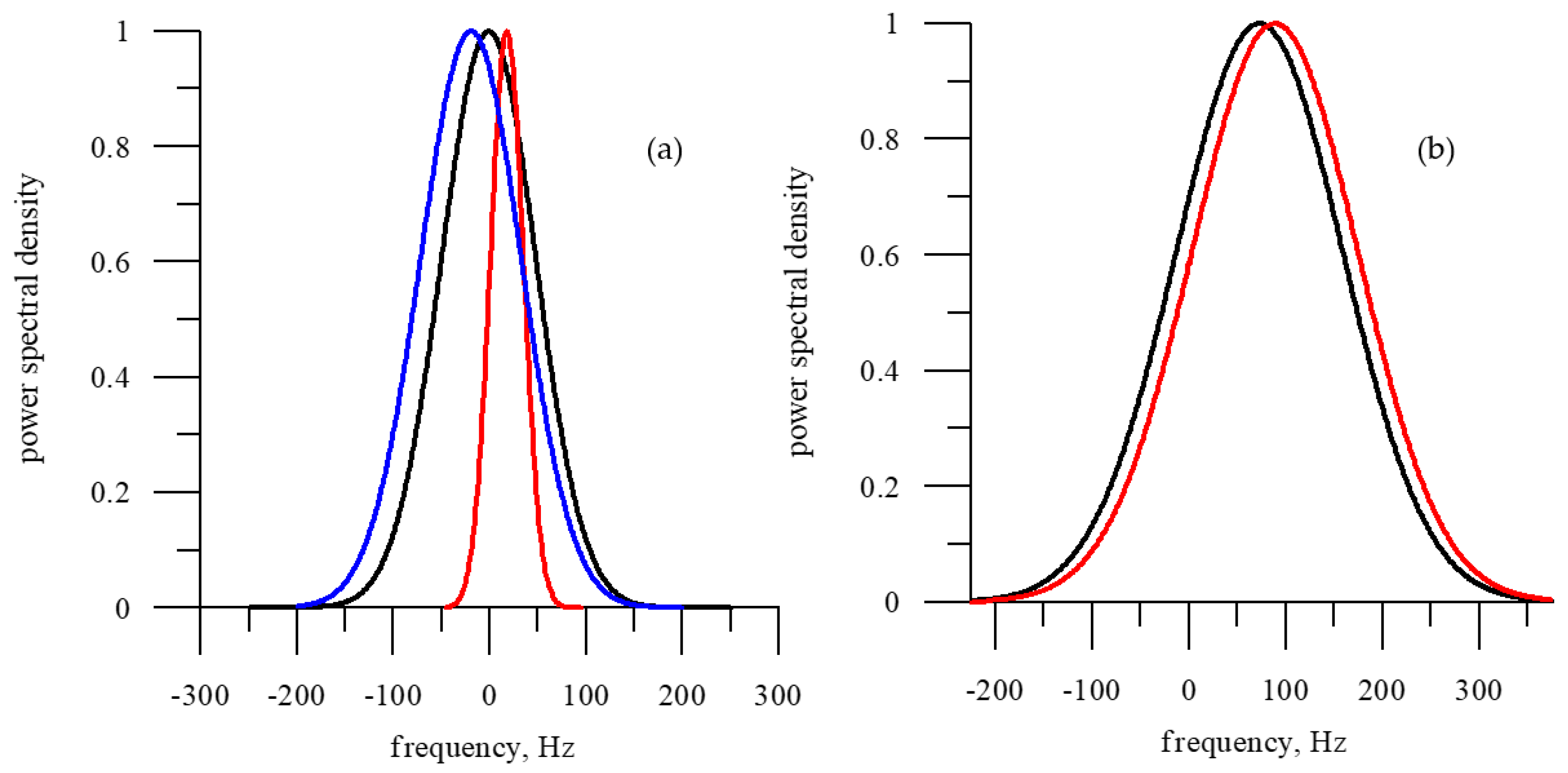
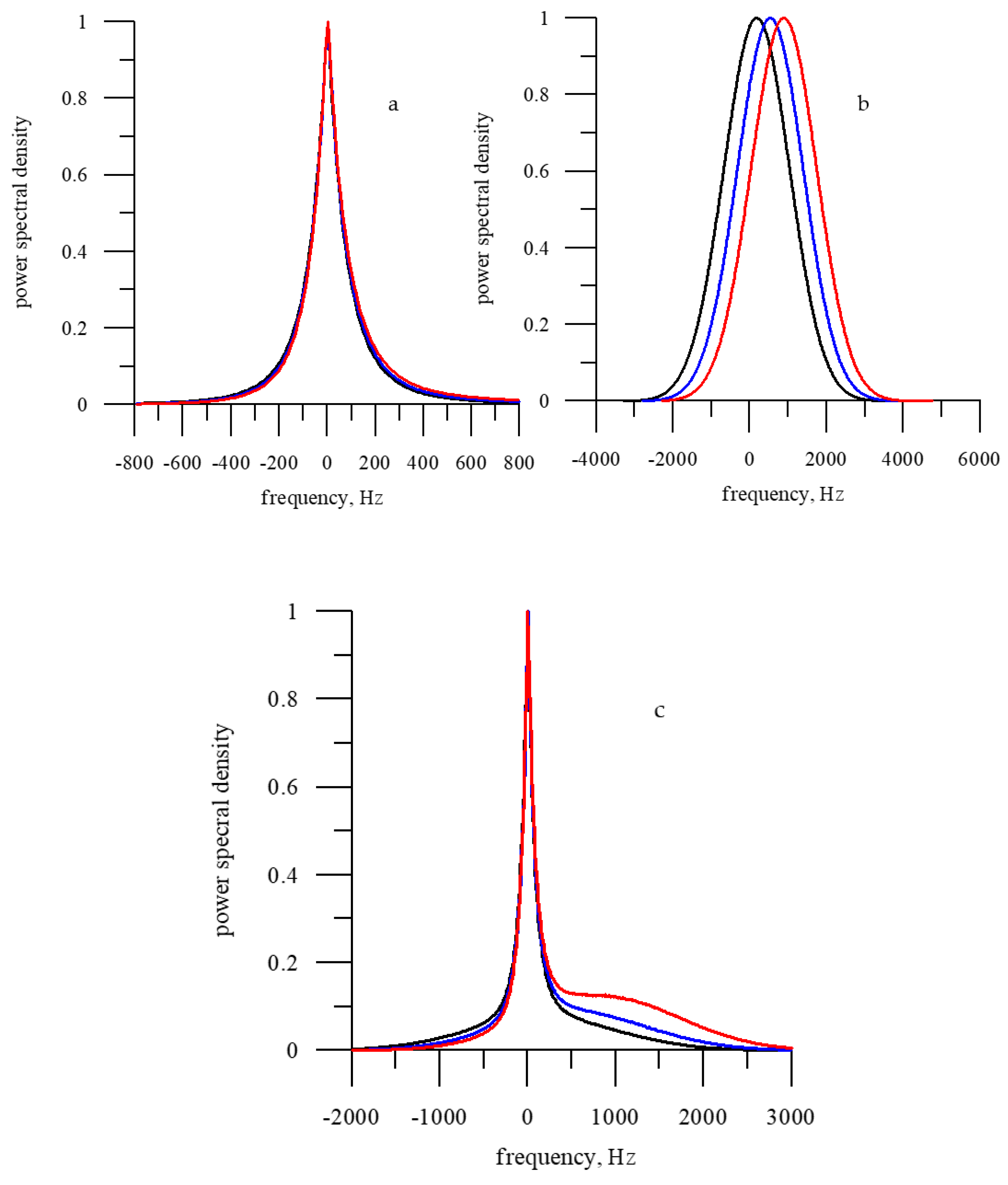
3.3. Impact of Width of Antenna Beam
3.4. Azimuthal Dependence
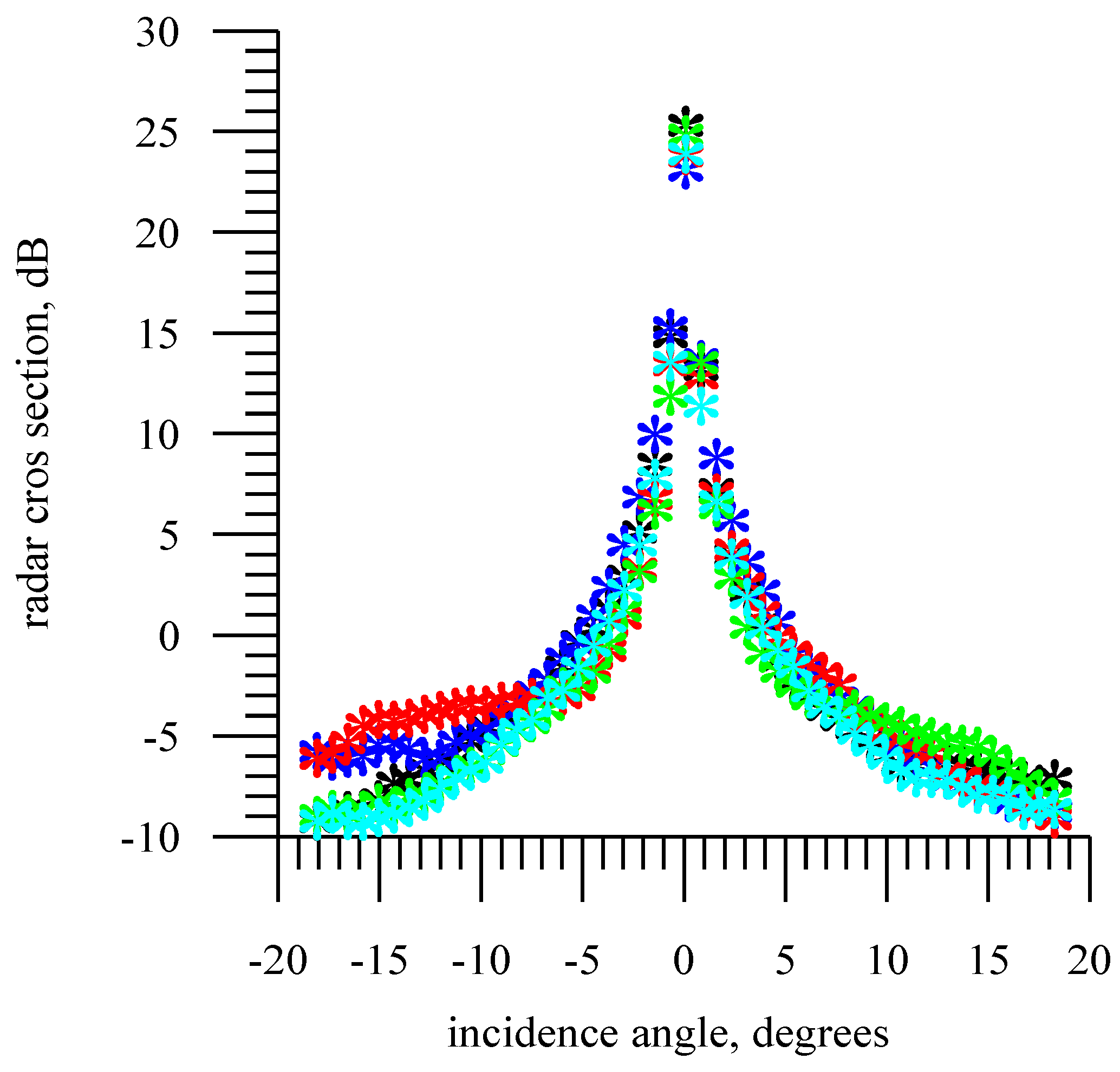
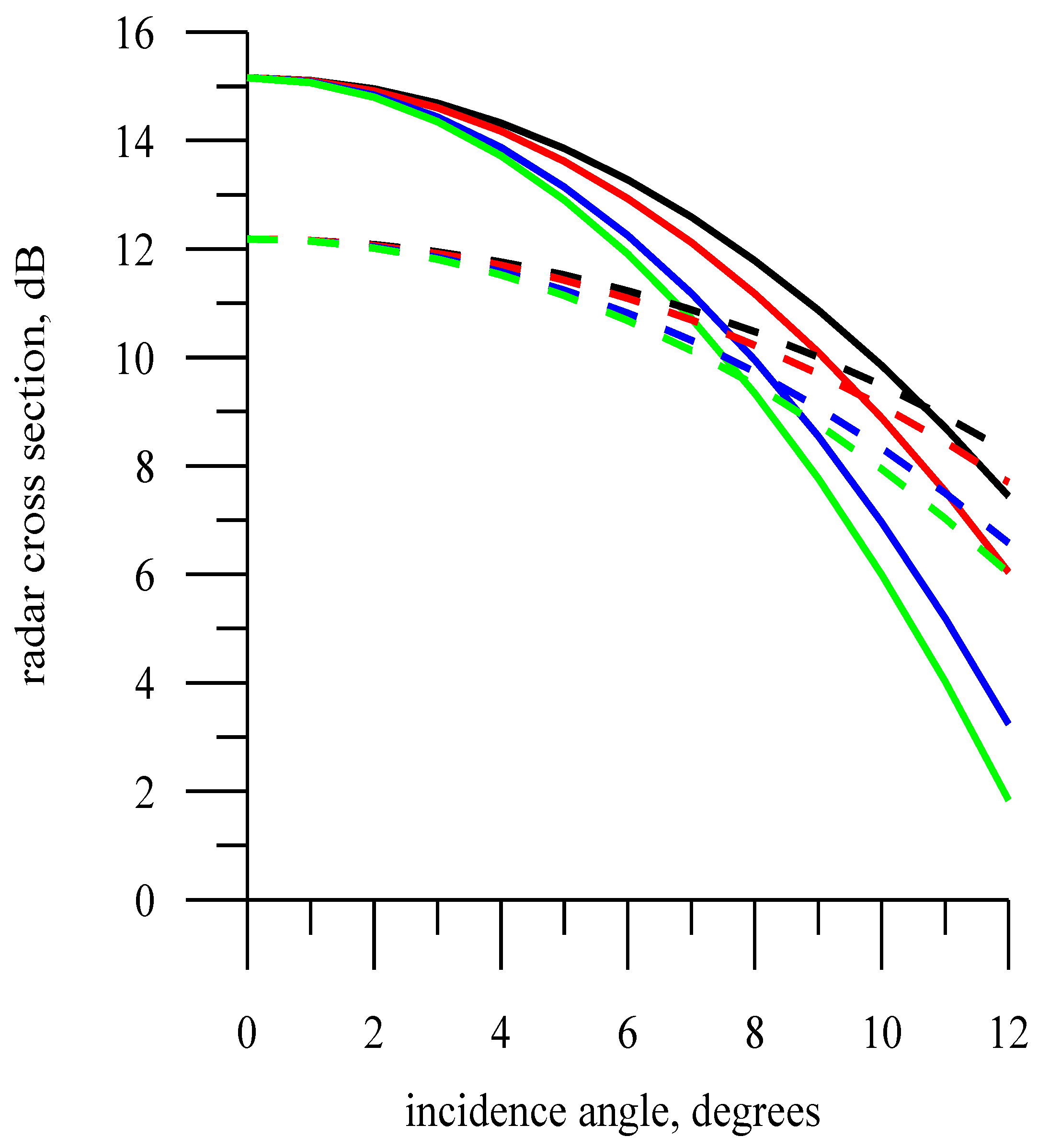
3.5. Dependence from Incidence Angle
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Available online: https://science2017.globalchange.gov/ (accessed on 21 February 2022).
- Available online: http://www.meteorf.ru/product/climat/ (accessed on 21 February 2022).
- Available online: https://svs.gsfc.nasa.gov/4750 (accessed on 1 February 2022).
- Carsey, F.D. Microwave Remote Sensing of Sea Ice; Geophysical Monograph 68; American Geophysical Union: Washington, DC, USA, 1992; p. 446. [Google Scholar]
- Haykin, S.; Lewis, E.O.; Raney, R.K.; Rossiter, J.R. Remote Sensing of Sea Ice and Icebergs; John Wiley & Sons: Hoboken, NJ, USA, 1994; Volume 13, p. 686. [Google Scholar]
- Anderson, H.S.; Long, D.G. Sea ice mapping method for Seawinds. IEEE Trans. Geosci. Remote Sens. 2005, 43, 647–657. [Google Scholar]
- Lebedev, S.A.; Kostianoy, A.G.; Popov, S.K. Satellite Altimetry of Sea Level and Ice Cover in the Barents Sea. Ecol. Montenegrina 2019, 25, 26–35. [Google Scholar] [CrossRef]
- Mitnik, L.M.; Viktorov, S.V. Radar of the Earth’s Surface from Space; Gidrometeoizdat: Leningrad, Russia, 1990; p. 200. (In Russian) [Google Scholar]
- Kacimi, S.; Kwok, R. The Antarctic sea ice cover from ICESat-2 and CryoSat-2: Freeboard, snow depth, and ice thickness. Cryosphere 2020, 14, 4453–4474. [Google Scholar] [CrossRef]
- Nekrasov, A.; Khachaturian, A.; Abramov, E.; Kurdel, P.; Gamcová, M.; Gamec, J.; Bogachev, M. On sea ice/water discrimination by airborne weather radar. IEEE Access 2020, 8, 120916–120922. [Google Scholar] [CrossRef]
- Comiso, J.C.; Nishio, F. Trends in the sea ice cover using enhanced and compatible AMSR-E, SSM/I, and SMMR data. J. Geophys. Res. 2008, 113, C02S07. [Google Scholar] [CrossRef]
- Brevik, L.-A.; Eastwood, S.; Lavergne, T. Use of C-Band Scatterometer for Sea Ice Edge Identification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2669–2677. [Google Scholar] [CrossRef]
- Murtazin, A.; Efgrafova, K.; Kudryavtsev, V. Application of ASCAT scatterometer data to study the ice cover in the Arctic. Uchenye Zap. Ross. Gos. Gidrol. Univ. 2015, 40, 160–173. (In Russian) [Google Scholar]
- Lipa, B.; Crissman, R.; Barrick, D. HF radar observations of Arctic pack-ice breakup. IEEE J. Ocean. Eng. 1986, 11, 270–275. [Google Scholar] [CrossRef]
- Walsh, J.; Dawe, D.; Srivastava, S. Remote sensing of icebergs by ground-wave Doppler radar. IEEE J. Ocean. Eng. 1986, 11, 276–284. [Google Scholar] [CrossRef]
- Chan, H. Iceberg Detection and Tracking Using High Frequency Surface Wave Rada; Report No 1310; Defence Research Establishment Ottawa: Ottawa, ON, Canada, 1997; p. 78. [Google Scholar]
- Shirasawa, K.; Ebuchi, N.; Leppäranta, M.; Takatsuka, T. Ice-edge detection from Japanese C-band radar and high-frequency radar coastal stations. Ann. Glaciol. 2013, 54, 59–64. [Google Scholar] [CrossRef]
- Fujiyoshi, Y.; Osumi, K.; Ohi, M.; Yamada, Y. Sea ice identification and derivation of its velocity field by X-band Doppler radar. J. Atmos. Ocean. Technol. 2013, 30, 1240–1249. [Google Scholar] [CrossRef][Green Version]
- Bass, F.G.; Fuks, I.M. Scattering of Waves by Statistically Rough Surfaces; Pergamon Press: Oxford, UK, 1979; p. 528. [Google Scholar]
- Isakovich, M.A. Scattering of waves from a statistically rough surface. J. Theor. Exp. Phys. 1952, 23, 305–314. (In Russian) [Google Scholar]
- Barrick, D.E. Rough surface scattering based on the specular point theory. IEEE Trans. AP-16 1968, 16, 449–554. [Google Scholar] [CrossRef]
- Valenzuela, G. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound. Layer Meteorol. 1978, 13, 61–86. [Google Scholar] [CrossRef]
- Karaev, V.; Kanevsky, M.; Balandina, G.; Challenor, P.; Gommenginger, C.; Srokosz, M. The Concept of a Microwave Radar with an Asymmetric Knifelike Beam for the Remote Sensing of Ocean Waves. J. Atmos. Ocean. Technol. 2005, 22, 1809–1820. [Google Scholar] [CrossRef]
- Karaev, V.; Kanevsky, M.; Meshkov, E. The effect of sea surface slicks on the doppler spectrum width of a backscattered microwave signal. Sensors 2008, 8, 3780–3801. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross-section of the sea surface: 1. Background model. J. Geophys. Res. 2003, 108, 8054. [Google Scholar] [CrossRef]
- Yurovskaya, M.V.; Dulov, V.A.; Chapron, B.; Kudryavtsev, V.N. Directional short wind wave spectra derived from the sea surface photography. J. Geophys. Res. Ocean. 2013, 118, 1–15. [Google Scholar] [CrossRef]
- Ryabkova, M.; Karaev, V.; Guo, J.; Titchenko, Y. A review of wave spectrum models as applied to the problem of radar probing of the sea surface. J. Geophys. Res. Ocean. 2019, 124, 7104–7134. [Google Scholar] [CrossRef]
- Hwang, P.A.; Fois, F. Surface roughness and breaking wave properties retrieved from polarimetric microwave radar backscattering. J. Geophys. Res. Ocean. 2015, 120, 3640–3657. [Google Scholar] [CrossRef]
- Kanevsky, M.B.; Karaev, V.Y. Spectral characteristics of superhigh frequency (SHF) radar signal backscattered by the sea surface at small incidence angles. Radiophys. Quantum Electron. 1996, 39, 347–352. [Google Scholar] [CrossRef]
- Meshkov, E.; Karaev, V. Determination of the parameters of sea surface roughness using the Doppler spectrum of a microwave radar signal reflected from a water surface. Radiophys. Quantum Electron. 2004, 47, 205–217. [Google Scholar] [CrossRef]
- Boisot, O.; Amarouche, L.; Lalaurie, J.-C.; Guérin, C.-A. Dynamical Properties of Sea Surface Microwave Backscatter at Low-Incidence: Correlation Time and Doppler Shift. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7385–7395. [Google Scholar] [CrossRef]
- Nouguier, F.; Guérin, C.-A.; Soriano, G. Analytical Techniques for the Doppler Signature of Sea Surfaces in the Microwave Regime—II: Nonlinear Surfaces. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4920–4927. [Google Scholar] [CrossRef]
- Nouguier, F.; Guerin, C.-A.; Soriano, G. Analytical techniques for the Doppler signature of sea surface in microwave regime—I: Linear surfaces. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4856–4864. [Google Scholar] [CrossRef]
- Fois, F.; Hoogeboom, P.; Chevalier, F.; Stoffelen, A. An analytical model for the description of the full-polarimetric sea surface Doppler signature. J. Geophys. Res. Ocean. 2015, 120, 988–1015. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gotwols, B.L.; Keller, W.C. A Comparison of Ku-Band Doppler Measurements at 20 Incidence with Predictions from a Time-Dependent Scattering Model. J. Geophys. Res. 1991, 96, 4947–4955. [Google Scholar] [CrossRef]
- Toporkov, J.; Brown, G. Numerical Simulations of Scattering from Time-Varying, Randomly Rough Surfaces. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1616–1625. [Google Scholar] [CrossRef]
- Toporkov, J.; Brown, G. Numerical Study of the Extended Kirchhoff Approach and the Lowest Order Small Slope Approximation for Scattering from Ocean-Like Surfaces: Doppler Analysis. IEEE Trans. Geosci. Remote Sens. 2002, 50, 417–425. [Google Scholar] [CrossRef]
- Toporkov, J.; Ouellette, J. Numerical simulation and analysis of beam resolved in plane bistatic scattering in a wavetank setup. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2022; pp. 7315–7318. [Google Scholar]
- Wang, J.; Xu, X. Doppler simulation and analysis for 2-D Sea surfaces up to Ku-band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 466–478. [Google Scholar] [CrossRef]
- Li, X.; Xu, X. Scattering and Doppler spectral analysis for two-dimensional linear and nonlinear sea surfaces. IEEE Trans. Geosci. Remote Sens. 2011, 49, 603–611. [Google Scholar] [CrossRef]
- TRMM Data Users Handbook; NASDA: Arlington, VA, USA, 2001; p. 226.
- GPM Data Utilization Handbook, 1st ed.; JAXA: Tokyo, Japan, 2014; p. 92.
- Karaev, V.; Panfilova, M.; Mitnik, L.; Ryabkova, M.; Titchenko Yu Meshkov, E.; Andreeva, Z.; Volgutov, R. Features of radar probing of ice cover at small incidence angles by the example of the Okhotsk Sea. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Iz Kosm. 2020, 17, 187–202. (In Russian) [Google Scholar] [CrossRef]
- Karaev, V.; Panfilova, M.; Ryabkova, M.; Titchenko, Y.; Meshkov, E. Remote sensing of the sea ice at small incidence angles: Verification of the theoretical models. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021; pp. 5629–5632. [Google Scholar] [CrossRef]
- Peureux, C.; Longepe, N.; Mouche, A.; Tison, C.; Tourain, C.; Lachiver, J.-M.; Hauser, D. Sea-ice detection from near-nadir Ku-band echoes from CFOSAT/SWIM scatterometer. Earth Space Sci. 2022. [Google Scholar] [CrossRef]
- Panfilova, M.; Shikov, S.; Karaev, V. Sea ice detection using Ku-band onboard GPM satellite. In Proceedings of the URSI GASS 2020, Rome, Italy, 29 August–5 September 2020. [Google Scholar]
- Karaev, V.; Ryabkova, M.; Panfilova, M.; Titchenko, Y.; Meshkov, E.; Zuikova, E. Microwave Doppler radar experiment on a river. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021; pp. 7350–7353. [Google Scholar]
- Ryabkova, M.; Karaev, V.; Panfilova, M.; Titchenko Yu Meshkov, E.; Zuikova, E. Doppler spectrum of backscattered microwave signal: Experiment at the river. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Iz Kosm. 2020, 17, 213–217. [Google Scholar] [CrossRef]
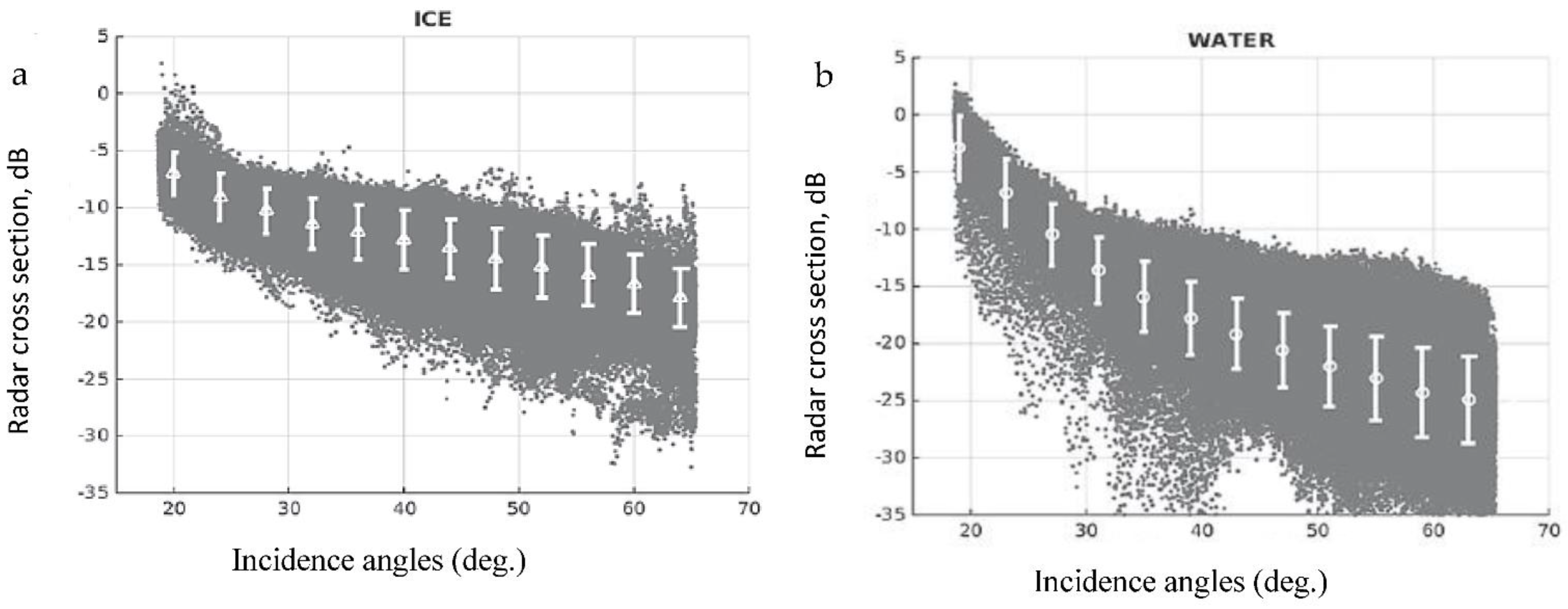
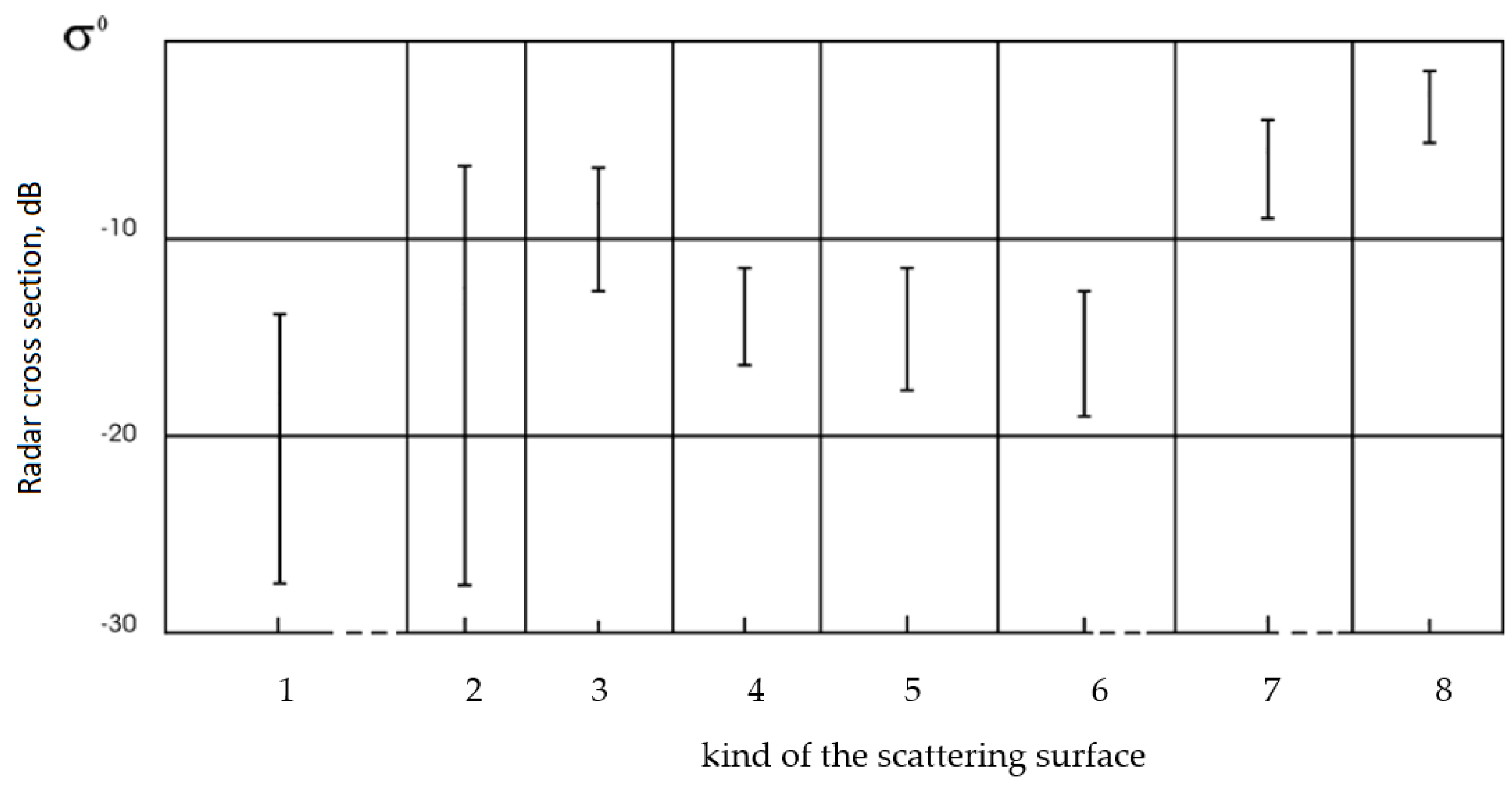
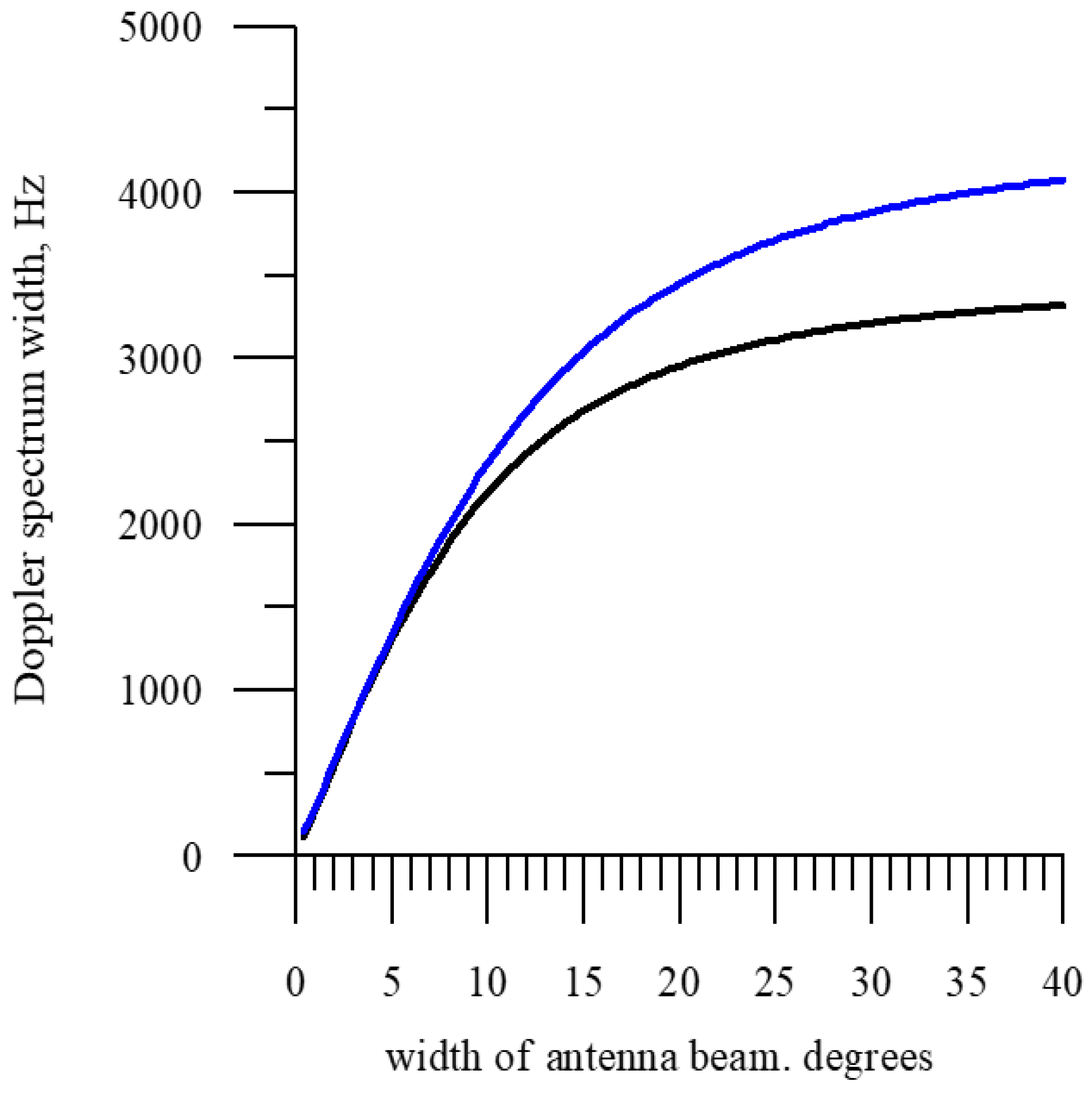
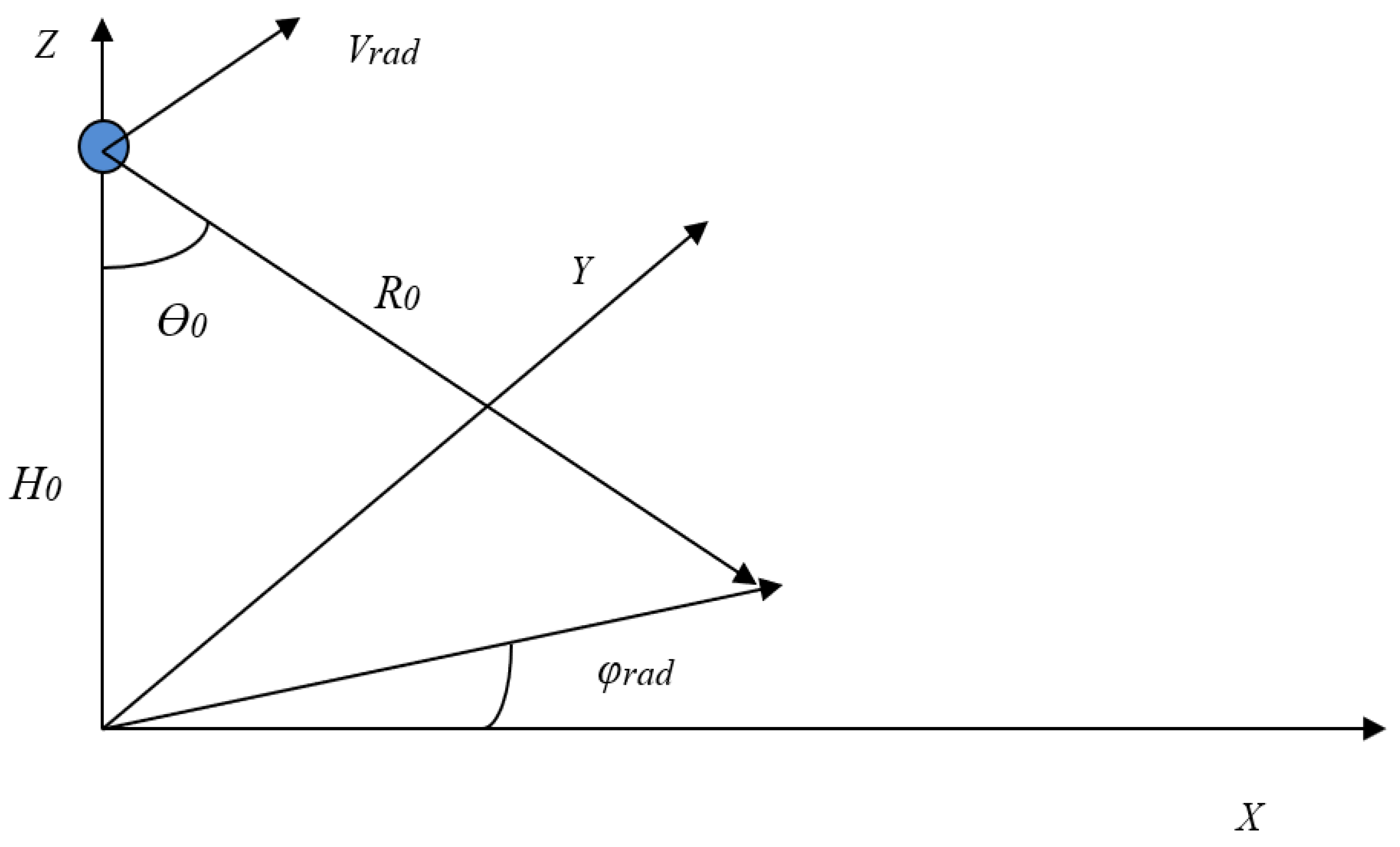





| N | |||||||
|---|---|---|---|---|---|---|---|
| sea | 2° | 2° | 1166 | 282 | 244 | 0.0 | 0.0 |
| ice | 2° | 2° | 1149 | 290 | 251 | −0.01 | 0.01 |
| sea | 14° | 2° | 887 | 1712 | 1474 | 0.01 | −0.04 |
| ice | 14° | 2° | 100 | 749 | 1733 | 3.5 | 18.4 |
| SIC | |||||
|---|---|---|---|---|---|
| 0 | 887 | 1712 | 1474 | 0.01 | −0.04 |
| 0.1 | 825 | 1710 | 1447 | 0.14 | −0.13 |
| 0.5 | 546 | 1584 | 1456 | 0.82 | 0.38 |
| 0.9 | 200 | 1066 | 1684 | 2.36 | 6.99 |
| 1 | 101 | 749 | 1734 | 3.5 | 18.4 |
| SIC | |||||
|---|---|---|---|---|---|
| 0 | 443 | 856 | 737 | 0.01 | −0.04 |
| 0.5 | 273 | 792 | 728 | 0.82 | 0.38 |
| 1 | 50 | 375 | 867 | 3.5 | 18.4 |
| N | |||||||
|---|---|---|---|---|---|---|---|
| sea | 2° | 2° | 1166 | 282 | 244 | 0.0 | 0.0 |
| ice | 2° | 2° | 1149 | 290 | 251 | −0.01 | 0.01 |
| sea | 6° | 2° | 1107 | 822 | 711 | 0.0 | −0.03 |
| ice | 6° | 2° | 529 | 1048 | 861 | 0.78 | −0.3 |
| sea | 10° | 2° | 1006 | 1305 | 1130 | −0.01 | −0.0 |
| ice | 10° | 2° | 164 | 793 | 1408 | 2.8 | 9.6 |
| sea | 14° | 2° | 887 | 1712 | 1474 | 0.01 | −0.03 |
| ice | 14° | 2° | 100 | 749 | 1733 | 3.5 | 18.4 |
| N | ||||||
|---|---|---|---|---|---|---|
| sea | 0° | 0 | 37 | 50 | 0.0 | 4.4 |
| ice | 0° | 0 | 12 | 47 | 0.0 | 63.2 |
| sea | 15° | 325 | 628 | 542 | 0.01 | 0.02 |
| ice | 15° | 37 | 29 | 50 | 0.0 | 9.0 |
| sea | 30° | 627 | 1211 | 1043 | 0.01 | −0.03 |
| ice | 30° | 71 | 530 | 1226 | 3.5 | 18.4 |
| sea | 45° | 887 | 1712 | 1474 | 0.01 | −0.04 |
| ice | 45° | 100 | 749 | 1733 | 3.5 | 18.4 |
| sea | 60° | 1086 | 2097 | 1805 | 0.01 | −0.04 |
| ice | 60° | 123 | 918 | 2123 | 3.5 | 18.4 |
| sea | 75° | 1211 | 2338 | 2013 | 0.0 | −0.04 |
| ice | 75° | 137 | 1024 | 2367 | 3.5 | 18.4 |
| sea | 90° | 1254 | 2421 | 2084 | 0.0 | −0.04 |
| ice | 90° | 142 | 1060 | 2451 | 3.5 | 18.4 |
| N | ||||||
|---|---|---|---|---|---|---|
| Ice | 0° | 0 | 496 | 1166 | 0.0 | 19.1 |
| Ice | 1° | 14 | 504 | 1198 | 1.1 | 19.5 |
| Ice | 2° | 30 | 531 | 1289 | 2.1 | 20.6 |
| Ice | 3° | 49 | 577 | 1421 | 2.9 | 21.3 |
| Ice | 4° | 71 | 648 | 1576 | 3.4 | 20.6 |
| Ice | 5° | 100 | 749 | 1733 | 3.5 | 18.4 |
| Sea | 0° | 0 | 1716 | 1479 | 0.0 | 0.0 |
| Sea | 1° | 179 | 1715 | 1478 | 0.0 | −0.03 |
| Sea | 2° | 356 | 1714 | 1477 | 0.0 | −0.03 |
| Sea | 3° | 533 | 1713 | 1476 | 0.0 | −0.03 |
| Sea | 4° | 710 | 1713 | 1475 | 0.0 | −0.03 |
| Sea | 5° | 887 | 1712 | 1474 | 0.0 | −0.03 |
| Sic50 | 0° | 0 | 1204 | 1453 | 0.0 | 2.8 |
| Sic50 | 1° | 89 | 1222 | 1454 | 0.4 | 2.7 |
| Sic50 | 2° | 182 | 1275 | 1458 | 0.7 | 2.2 |
| Sic50 | 3° | 286 | 1357 | 1463 | 0.9 | 1.6 |
| Sic50 | 4° | 406 | 1464 | 1462 | 0.9 | 1.0 |
| Sic50 | 5° | 546 | 1584 | 1456 | 0.8 | 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaev, V.; Titchenko, Y.; Panfilova, M.; Ryabkova, M.; Meshkov, E.; Ponur, K. Application of the Doppler Spectrum of the Backscattering Microwave Signal for Monitoring of Ice Cover: A Theoretical View. Remote Sens. 2022, 14, 2331. https://doi.org/10.3390/rs14102331
Karaev V, Titchenko Y, Panfilova M, Ryabkova M, Meshkov E, Ponur K. Application of the Doppler Spectrum of the Backscattering Microwave Signal for Monitoring of Ice Cover: A Theoretical View. Remote Sensing. 2022; 14(10):2331. https://doi.org/10.3390/rs14102331
Chicago/Turabian StyleKaraev, Vladimir, Yury Titchenko, Maria Panfilova, Maria Ryabkova, Eugeny Meshkov, and Kirill Ponur. 2022. "Application of the Doppler Spectrum of the Backscattering Microwave Signal for Monitoring of Ice Cover: A Theoretical View" Remote Sensing 14, no. 10: 2331. https://doi.org/10.3390/rs14102331
APA StyleKaraev, V., Titchenko, Y., Panfilova, M., Ryabkova, M., Meshkov, E., & Ponur, K. (2022). Application of the Doppler Spectrum of the Backscattering Microwave Signal for Monitoring of Ice Cover: A Theoretical View. Remote Sensing, 14(10), 2331. https://doi.org/10.3390/rs14102331








