1. Introduction
Prelaunch laboratory measurements are critical to the success of all satellite-based imaging spectroscopy missions. A key component is an absolute, SI-traceable radiometric calibration achieved by the sensor, using viewing sources for which the output is known through a well-defined traceability path to an SI standard such as the electric watt. Fusion of data from multiple sensors calibrated to SI is much simpler, and allows for comprehensive sets of long-term, consistent data and products. Reducing the absolute uncertainty in the radiometric calibration to <0.3% (k = 2) in the reflected solar part of the spectrum leads to climate quality data sets [
1].
Laboratory-based, absolute radiometric calibrations in the reflected solar portion of the spectrum (350 to 2500 nm) typically rely on sources of spectral radiance based on melting-point blackbodies, lamp-illuminated spherical integrating sources, or lamp-illuminated diffuser plaques [
2,
3,
4]. The state-of-the-art uncertainties for spectral radiance products that rely on calibrated source transfer standards are at best 3.2% (k = 2) for laboratory-based instrumentation [
5] and 5.0% (k = 2) for on-orbit sensors [
6]. Reductions in absolute uncertainty are achieved by producing reflectance-based products rather than spectral radiance, and state-of-the-art uncertainties have been shown to be <3.6% (k = 2) [
6,
7].
Clearly, significant improvements are needed to achieve <0.3% reflectance uncertainties for climate-quality data. One approach developed for the Climate Absolute Radiance and Refractivity Observatory (CLARREO) is that of the ratio radiometer. Reflectance is retrieved by taking the ratio of earth scene measurements to those of the incident solar irradiance. This approach is similar to that implemented for the on-orbit solar diffuser monitors for the Moderate Resolution Imaging Spectroradiometer [
8,
9] and the Visible Infrared Imaging Radiometer Suite [
10]. The ratio radiometer approach is being demonstrated by the Hyperspectral Imager for Climate Science (HySICS) as part of the CLARREO Pathfinder (CPF) mission to the International Space Station (ISS). The absolute uncertainty requirement for CPF HySICS is 0.6% (k = 2) due to limitations of the frequency at which the sensor can perform solar views because of ISS operations.
The CPF requirement of 0.6% uncertainty is still a factor of five more stringent than the state of the art. Demonstrating that this requirement is met for an on-orbit sensor cannot be accomplished through typical methods, such as intercomparisons with other sensors. Thus, an additional calibration method, which follows the traditional path of absolute prelaunch calibration with a transfer to orbit, is being undertaken as part of CPF’s independent calibration. The independent calibration achieves a significant improvement in uncertainties by making use of detector-based calibration of HySICS [
11]. A detector-based calibration is one in which a well-understood and stable detector package is calibrated in a standards laboratory to SI-traceable standards. The detector package is transported to the facility calibrating the sensor of interest and the package then provides the calibration of the source being used in the radiometric calibration. The approach is different from the source-based method described above, in which the source is calibrated and transported. The detector-based method for CPF Independent calibration relies on the Goddard Laser for Absolute Measurement of Radiance (GLAMR) system [
12]. The SI-traceability of GLAMR is through the electric watt as part of the absolute radiometric calibration of the detectors at the National Institute of Standards and Technology (NIST) using the Primary Optical Watt Radiometer (POWR). The transfer radiometers are absolutely calibrated with reference to an irradiance source with an uncertainty <0.3% (k = 2) in the VNIR and 0.3–3% in other spectral regions. The transfer radiometers’ calibration, along with their use with an extended radiance source, are the dominant uncertainties in the absolute radiometric calibration of HySICS. The overall uncertainty for the HySICS GLAMR calibration that makes use of the GLAMR sphere source is <1.2% (k = 2) in radiance [
12].
One challenge for the CPF independent calibration is ensuring that the GLAMR calibration process, coupled with an imaging spectrometer, provides the expected uncertainties, and that the sampling and processing methods do not lead to unexpected systematic errors. The independent calibration has made use of GLAMR data collected as part of the evaluation of the Solar, Lunar Absolute Reflectance Imaging Spectroradiometer (SOLARIS) that was developed as a calibration demonstration system for the original CLARREO mission [
13,
14]. The data were collected to understand the spectral sampling strategies and expected test time needed to ensure an accurate HySICS calibration while minimizing impact on the project’s critical path.
The current work presents the results of a sensitivity study undertaken to evaluate the appropriate GLAMR wavelength sampling strategy and radiance levels needed to ensure that the radiometric calibration uncertainty is dominated by the GLAMR source absolute uncertainty. The study relies on modeled GLAMR spectral radiance coupled with modeled absolute spectral response (ASR) for a simulated imaging spectrometer. The next section gives an overview of a GLAMR calibration approach, and a description of the GLAMR and SOLARIS data collections that are part of the modeling efforts.
Section 3 provides a description of how the GLAMR and SOLARIS data are converted to the spectral “supersets” needed for the sensitivity study. The advantage of using real data is that they include both realistic instrumental features and effects from the GLAMR source as part of the evaluation.
Section 3 also includes a discussion of the methods used to ensure that spurious SOLARIS and GLAMR data are not included in the modeled system. In
Section 4, results are given from the sensitivity study; these results are related to GLAMR spectral sampling and signal to noise ratio (SNR) effects in the sensor being tested due to GLAMR radiance levels, sensor integration time, and frame averaging of the imaging spectrometer data. This is followed by discussions of the results and the impact on planned testing for HySICS specifically, as well as for more general imaging spectrometer testing. The key result from the effort is that a 1 nm spectral sampling is needed with a radiance level that provides an in-band peak SNR >200 to ensure that the CPF requirements are met.
2. Detector-Based Calibration
The GLAMR detector-based calibration that is the basis for the current work relies on a tunable near-monochromatic laser light source coupled with a spherical integrating source (SIS). The narrower linewidth of the laser source compared to grating-based monochromators, and the large spectral range that can be covered by the tunable laser, lead to a higher fidelity calibration. The use of detector standards as part of the process allows both a relative and absolute spectral response measurement. The use of the SIS allows for a full focal plane evaluation of the imaging spectrometer if the exit port of the SIS overfills both the entrance pupil of the sensor and the full field. Current error budget estimates for a GLAMR-based radiometric calibration show that the uncertainties are dominated by the accuracy of the detector standards and the SIS uniformity [
12].
This basic approach used by GLAMR is similar to that of NIST for the Spectral Irradiance and Radiance Responsivity Calibrations using Uniform Sources (SIRCUS) facility, which is designed to lower the radiance and irradiance responsivity calibrations uncertainty down to a 0.1% level [
15]. The radiance and irradiance calibrations made by SIRCUS are traceable to POWR that is the US standard for optical power. The current GLAMR systems are based on a portable version of SIRCUS that was loaned to the Goddard Space Flight Center as part of its early CLARREO efforts.
The GLAMR light source and detectors can cover wavelengths in the spectral range from 340 to 2500 nm, which is a range suitable for calibrating instruments operating in the reflected solar portion of the spectrum. The main part of the light source consists of two tunable optical parametric oscillators (OPOs). Both OPOs use lithium triborate (LBO) nonlinear crystals pumped with a green light (532 nm) from frequency doubling of a neodymium doped yttrium vanadate laser at a 80 MHz repetition rate. The fundamental signal for these OPOs covers 680–1000 nm and 1100–1500. The use of an idler extends the achievable wavelengths upwards to 2500 nm and the second harmonic signal covers the UV and visible region of 340–680 nm.
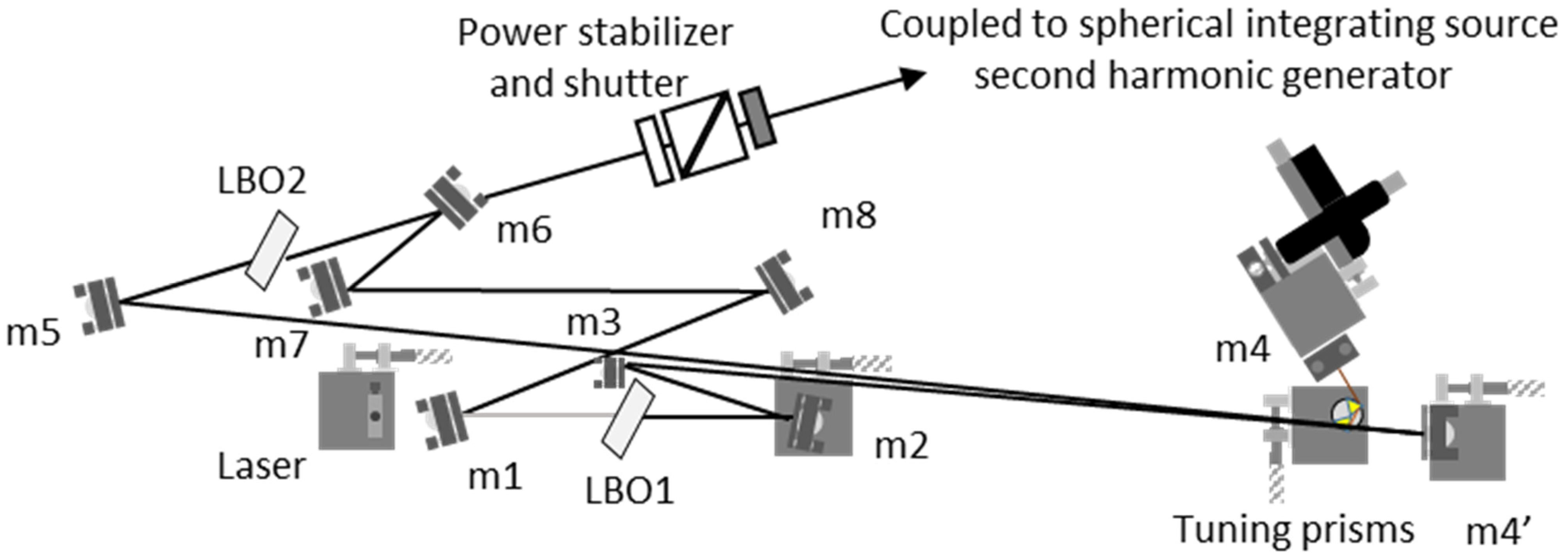
Figure 1 shows a simplified schematic of the optical path used to achieve the 550 to 700 nm spectral range. The removal of the LBO2 crystal shown in
Figure 1 provides the 1050 to 1400 nm spectral range. Redirection of the optical beam to a second harmonic generator, or including the idler mentioned above after mirror m2, provides the other spectral regions needed to obtain full spectral coverage.
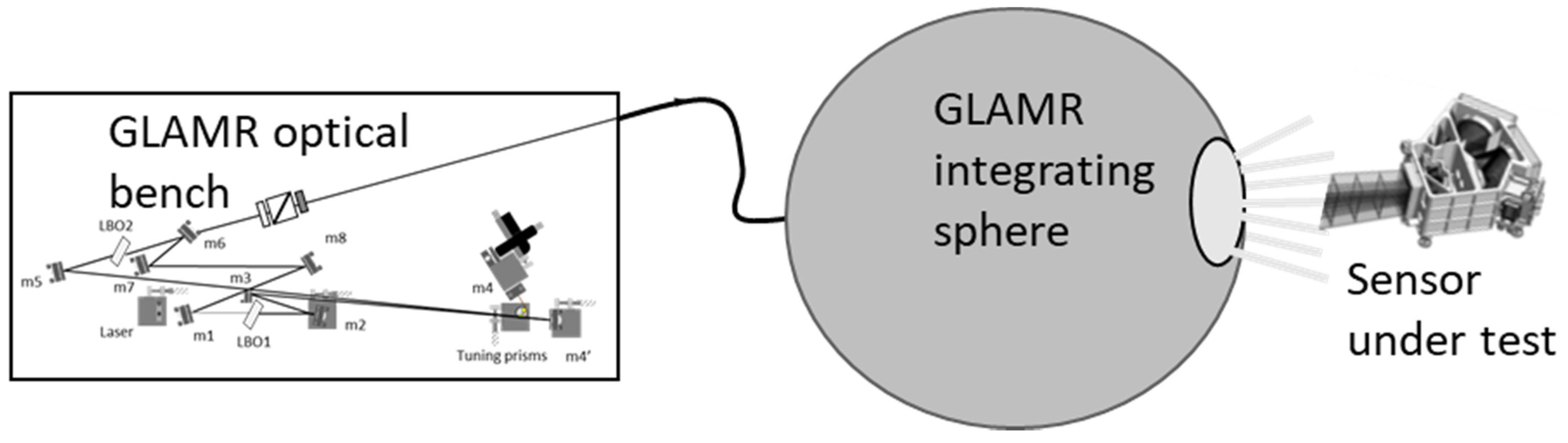
The monochromatic, broadband, and high-intensity output from the parametric conversion in the source laser is coupled with a multi-mode fiber that is directed to the GLAMR integrating sphere as illustrated in
Figure 2. The illuminated integrating sphere has a large exit port which can fill the full aperture and field of view of most sensors. A set of radiometers are used to measure the absolute radiance during the GLAMR calibration. The radiometers include a silicon-based trap detector radiometer, a single-detector indium gallium arsenide (InGaAs) radiometer, and an extended InGaAs detector coupled with an integrating sphere collector; these combine to cover the 340–2500 nm range generated by the GLAMR source. The radiometers are permanently attached to the integrating sphere and are regularly calibrated using transfer radiometers that are in turn calibrated using POWR. The absolute uncertainty level for the transfer radiometers is 0.09% when calibrated in irradiance mode [
15]. Work undertaken to evaluate the effects on the sphere uniformity and angular effects leads to the final GLAMR uncertainty of 0.6% (k = 2) for the radiance calibration of a test sensor for which both the field of view and entrance pupil are overfilled [
12].
A GLAMR-based radiometric calibration consists of tuning the GLAMR source across the spectral range of interest for the sensor under examination. The wavelength tuning is fully automated within each of the spectral ranges through computer control of the LBO temperature and the tuning prism stages that are shown in
Figure 1. The tuning process takes approximately 30 s per wavelength, allowing the GLAMR teams to measure several hundred calibration points in a single day, and the entire spectral range of the OPO can be scanned over several days.
Sensor calibration is accomplished by aligning the sensor being tested with the SIS to ensure full illumination of the instrument’s field and entrance aperture. The collection sequence begins with the shutter shown in
Figure 1 in the closed position while the GLAMR source is tuned to a desired wavelength. The shutter is opened to illuminate the sensor. The tuning process takes approximately 30 s and the system is held at a given wavelength for at least 30 s to allow the source to stabilize. As mentioned above, radiometers monitor the sphere output, and the radiometer outputs are coupled with a pair of crossed polarizers as part of the power stabilizer shown in
Figure 1. The shutter remains open until a sufficient number of samples is obtained by the sensor under examination. The shutter is closed, and the process is repeated until the spectral range is covered.
GLAMR telemetry includes wavelength, SIS radiance output, shutter state, and collection time. The sensor under examination typically collects during the entire tuning process in the multispectral sensor case, or the shutter state is used to trigger the collection of a sufficient number of frames/images in the imaging spectrometer case. Signal levels, shutter state telemetry, and time of collections are all used to pair the appropriate SIS absolute radiance with the sensor data. One of the improvements that has been made since the original GLAMR configurations is the inclusion of a time synchronization package that allows the data acquisition of the system being tested to be synchronized with the clocks of the sensor’s acquisition software and GLAMR’s control software. The synchronization simplifies matching of stabilized source signals with the sensor measurements.
Processing of the detector-based calibration consists of three basic steps: (1) pre-processing of the GLAMR and test sensor data; (2) conversion of sensor data to absolute spectral response (ASR); and (3) calculation of band-averaged calibration parameters.
Pre-processing includes the conversion of raw GLAMR telemetry to time-stamped absolute radiances for the sphere monitors. Also included in this step are the dark subtraction of illuminated test data using shutter data and the normalization of sensor data based on integration time and gain settings. ASR for each detector in the test sensor is calculated from
where
λn is the tuned GLAMR wavelength,
specify the detector number,
the absolute spectral response at
for detector (
i,
j),
DN(
λn,
i,
j) is the dark corrected sensor output for that detector, and
L(
λn) is the radiance from the GLAMR SIS at the tuned wavelength. Band-averaged spectral response for detector (
i,
j),
R(
i,
j), can be calculated from numerical integration of the
ASR over all
N GLAMR tuned wavelengths [
16].
The band-averaged center wavelength for detector (
i,
j),
λc(
i,
j) is calculated from
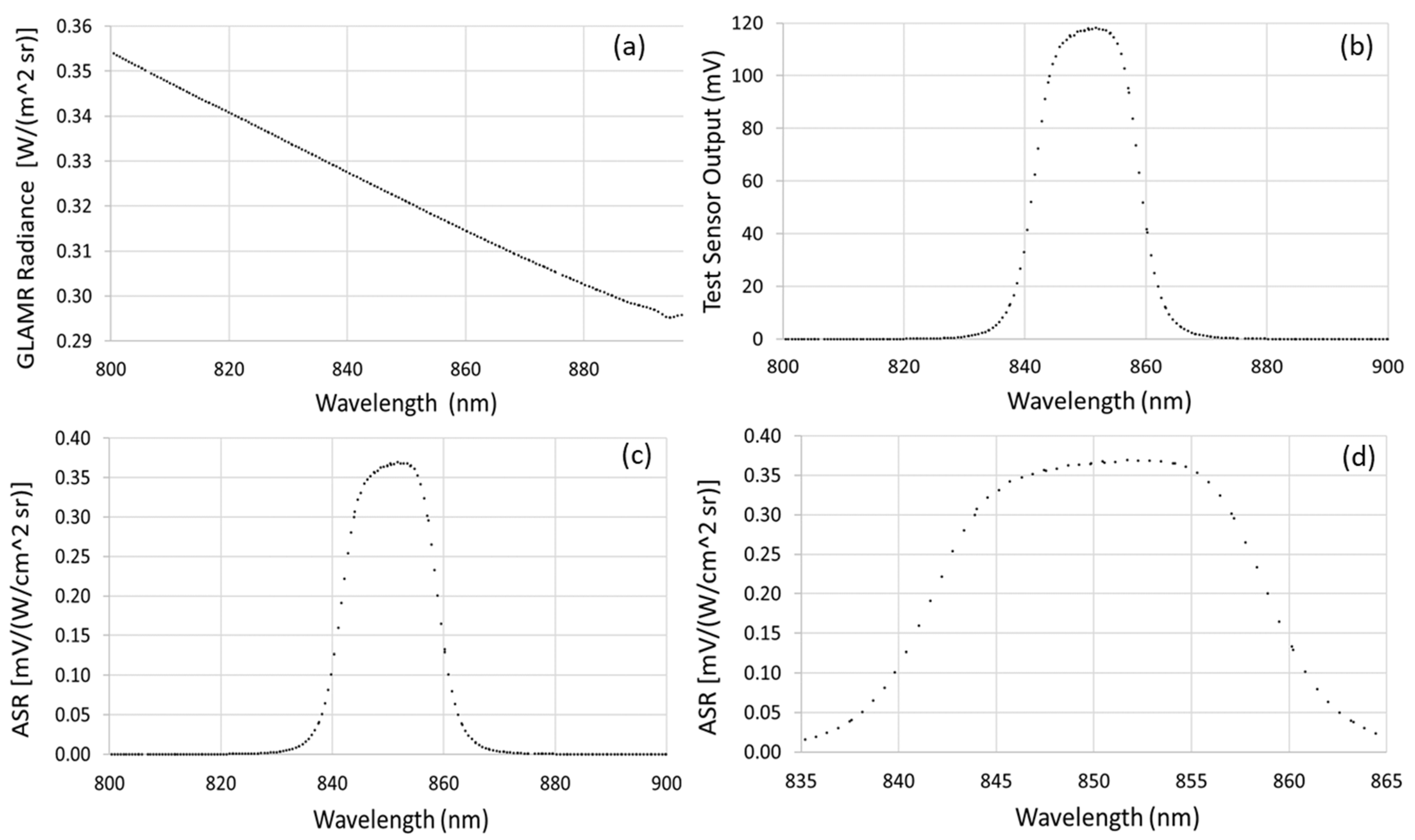
Figure 3 shows sample results from a single spectral band of a GLAMR-based calibration of a multispectral, filter-based, non-imaging radiometer [
5]. The results shown include the GLAMR source radiance output as a function of wavelength as determined from the monitoring radiometer of the GLAMR sphere source (
Figure 3a). Of note in the radiance curve is the sharp change in the spectral shape at 895 nm, which is due to a change in the laser configuration of the GLAMR system at that wavelength. Such a change in the spectral output of the source is not an issue for the sensor calibration since the radiance is well known from the monitoring radiometers in the sphere source.
The second graph (
Figure 3b) gives the sensor output for the GLAMR source radiance and wavelengths shown. The sensor output and source radiance are used to determine the ASR as a function of wavelength according to Equation (1); these are shown in the lower graphs (
Figure 3c,d). The two ASR graphs show the same data, but
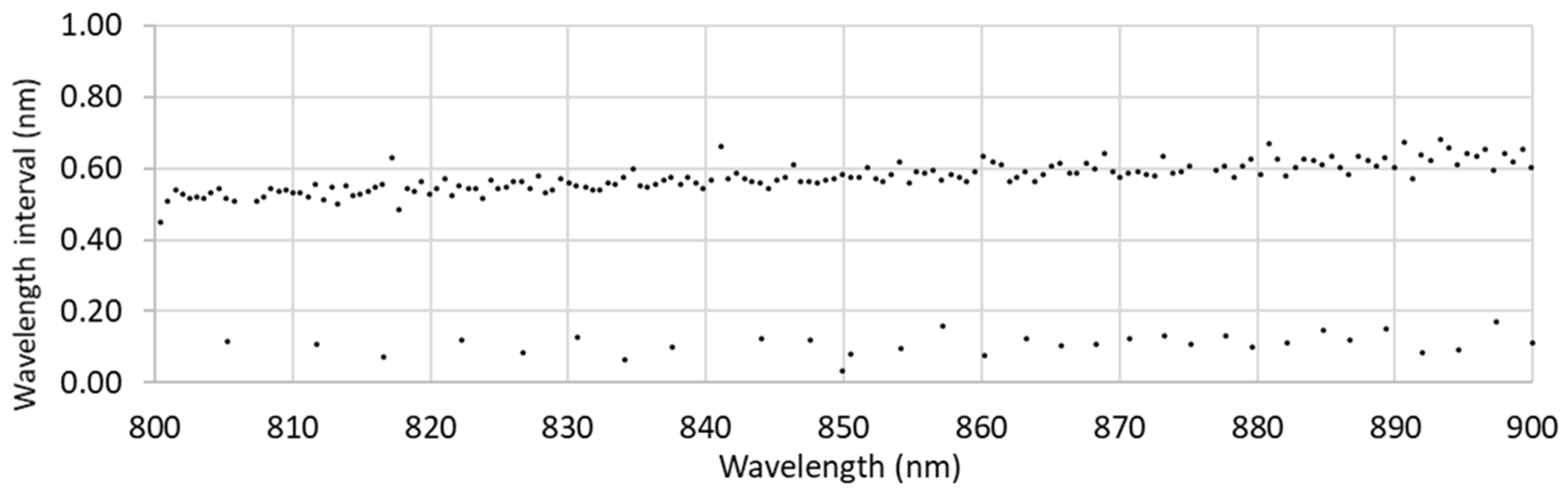
Figure 3a shows the full spectral range, and 3d shows a subset of that range to highlight individual GLAMR wavelength samples. One feature of the automated tuning system developed for GLAMR is that the wavelength interval is not constant over the collection. The impact, for the most part, is not noticeable in the full spectral range but can be seen in the subset spectral range. The spectral sampling effect is further shown in
Figure 4, which gives the GLAMR tuned wavelength interval for collection shown in
Figure 3.
The band-averaged spectral response of the sensor is calculated through numerical integration of the ASR data shown in
Figure 3 using Equation (2); this process is sensitive to spectral sampling. The impact of the tuning methodology is that multiple calibrations will lead to different results simply because the wavelengths sampled from one calibration to another will change, thus sampling different portions of the ASR curve leads to variations in the resulting band-averaged response. The effect is small for well-behaved ASRs, but the calibration requirements for CPF are stringent enough that the variability in retrieved band-averaged response needs to be <<0.1% for this effect to ensure that the impact is negligible on the overall HySICS calibration uncertainty.
Using actual GLAMR calibration data sets to understand the impacts of spectral sampling effects is non-trivial because real measurements will include noise from the test sensor. The approach chosen in the current work is to develop a set of modeled GLAMR outputs at a high spectral resolution much finer than would be needed for a calibration collection. A sensor spectral response model is developed at the same high spectral resolution as the GLAMR source model. The combination of the two allows for simulations of realistic GLAMR calibration outputs, such as those shown in
Figure 3, which can be used to evaluate the impact of data-set-to-data-set variability as well as impacts from the sampling interval. The GLAMR calibration model data set is described in the next section and the sensitivity studies conducted with it are presented in
Section 4.
3. Spectral Superset Models
The most accurate GLAMR-based calibration would ideally be one that spectrally samples the test sensor spectral response with both very high spectral resolution and very small sampling intervals. GLAMR has the capability to accomplish both, but scanning the full spectral range of a test sensor coupled with the limits that are typically placed on sensor testing schedules makes it impractical to conduct arbitrarily fine sampling. Spectral sampling effects are further complicated by the uncertainties in individual ASR values caused by noise in the test sensor. Determining a spectral sampling resolution that reduces uncertainties while optimizing test time is one of the motivating factors for the current work. The sensitivity study shown here is an approach that helps develop a GLAMR calibration test plan for an imaging spectrometer that reduces systematic uncertainties originating from the GLAMR sampling. The resulting test plan will provide parameters such as wavelength sampling, GLAMR source radiance levels, GLAMR source stability, test sensor integration time and gain, and number of test sensor samples. An additional benefit is that a set of metrics can be developed that provide quality checks on the calibration data set as the data are being collected.
A straightforward method to assess spectral sampling effects is to collect a GLAMR calibration at a very high spectral resolution and then subsample that test data set randomly and multiple times with varying spectral sampling. A spectral resolution of 0.05 nm would provide 20 times the number of samples for the current 1 nm GLAMR sampling strategy employed for imaging spectrometers. The challenge is that collecting such a data set over the spectral range of HySICS would take more than one year of daily calibration work, and such a data set would still suffer the effects of noise from the sensor under examination.
Thus, a model-based GLAMR calibration data set is the most suitable approach to understand the impacts of spectral sampling effects on the band-averaged spectral response as computed in Equation (2). The modeling approach allows the current work to concentrate on the impacts of spectral sampling while avoiding effects from sensor variability and avoiding the schedule impacts on the GLAMR Team to collect a high-spectral-sampling data set. The term “superset” is used to denote the high spectral resolution sampling of the modeled source and ASR at 0.05 nm spectral intervals. While the emphasis of the current work is to assess the uncertainties expected for the GLAMR-based radiometric calibration of CPF HySICS, the model-based approach here has applicability to a wider range of sensors, as long as there is a reasonable understanding of the general shape of the test sensor’s relative spectral response and the SNR expected for typical GLAMR radiance levels.
The modeled supersets described here are based on a set of GLAMR calibration data collected over several months as part of studies for the SOLARIS instrument. The two key elements from those collections are the GLAMR source radiance levels for the data sets, and the SOLARIS instrument ASRs derived from the measurements at the GLAMR source wavelengths. The spectral sampling of the multiple GLAMR calibrations was 1 nm or larger from 400 to 1100 nm at the 0.05 nm sampling interval, with 20–30 SOLARIS image frames collected for each shutter open state. The advantage to using real data from SOLARIS is that the sensitivity studies will include realistic instrumental features.
3.1. GLAMR Source Superset Model
The key element of the modeled data set is an assumed truth data set for the GLAMR source radiance at 0.05 nm spectral intervals. The GLAMR source superset model has been developed at 0.05 nm spectral sampling from 400–1100 nm. Each sample consists of 20 radiance samples at each wavelength to allow the radiance variability of the GLAMR source to be included as part of the superset model. The source variability, while small, affects the retrieved sensor ASR and will be present at approximately the same levels regardless of the spectral sampling and resolution chosen.
The first step in the GLAMR source superset generation was to determine the average source radiance and variability for each wavelength of the SOLARIS GLAMR calibration data sets. GLAMR radiance levels for all wavelengths of the superset are generated based on interpolation of the average radiance at surrounding wavelengths. Twenty radiance levels were determined for each of the modeled superset spectral samples based on the standard deviation of the SOLARIS GLAMR calibration source values from the nearest wavelength to the superset wavelength. The 20 superset radiance levels were generated based on random sampling of a gaussian distribution. The mean of the gaussian distribution at a modeled superset wavelength was determined by linear interpolation of the mean radiance measured at the two nearest wavelengths from the SOLARIS GLAMR calibration dataset. The variance of the gaussian distribution is the standard deviation of the measured radiance values from the SOLARIS GLAMR wavelength nearest to the modeled superset wavelength.
Figure 5a shows the GLAMR source superset for the full spectral range of the model. Both the original and modeled data are shown, though the two are not discernible at the scale of the full range.
Figure 5b shows the same data except over a limited spectral range to highlight the individual data points at each sample, as well as the original and modeled data. The data in the figure clearly demonstrate the spectral variability of the GLAMR source. Note that the data from 800 to 900 nm follow a similar shape as that shown in
Figure 3b. Numerous sharp changes in the spectral shape are due to changes in the laser configuration of the GLAMR system by the operator. These changes will vary from collection to collection based on the operator, power output, and configurations of the tuning optics. The spectral changes in the source radiance should not be a dominant uncertainty source since the source output is assumed known from the radiance levels reported by the monitoring radiometers in the sphere source.
Figure 5b shows the modeled GLAMR source superset data for 11 wavelengths between 668.2 and 668.7 nm. Also shown are the original GLAMR calibration source data between 668.2 and 668.7 nm. The change in radiance over the 20 samples is evident in the figure and can be seen to be <0.1% peak to peak from the measurements. The figure shows the 20 modeled data points. The gaussian assumption for the variation of the modeled source radiances overestimates the model peak-to-peak variability on average relative to the measured values. The larger variability is not viewed as an issue for the sensitivity study since the overestimation is the more conservative situation.
3.2. Imaging Spectrometer Superset Model
As mentioned, the imaging spectrometer superset is based on the SOLARIS imaging spectrometer that was developed as part of the original CLARREO project. The sensor is an Offner-Chrisp spectrometer that currently operates with a commercially-available 2160 × 2560 pixel, silicon-based sCMOS detector array. SOLARIS is a key element of the CPF independent calibration enabling evaluation of the GLAMR approaches planned for HySICS without affecting the program’s critical path. Work with SOLARIS has included performance characterization such as component level tests of optics, detector, and grating. Characterization has included determining the relative spectral response, noise, and temperature sensitivity while performing both laboratory measurements and field measurements [
17,
18,
19]. The same instrument characteristics that make it a suitable surrogate for independent calibration activities also makes it a suitable instrument for developing a spectrometer superset model to evaluate GLAMR calibration uncertainties.
The imaging spectrometer superset consists of modeled ASR values at the same 0.05 nm spacing as the GLAMR source superset described in the previous section. The superset ASRs are created for each SOLARIS instrument center wavelength at the center of the instrument’s field of view. The modeled ASRs are based on the ASR values from the multiple SOLARIS GLAMR calibration data sets. The use of the measured values provides a model with more realistic instrument line shapes. The challenge in developing the model is maintaining the realistic nature of the spectral sensitivity simulations while excluding SOLARIS noise artifacts from the GLAMR calibrations that would affect the conclusions derived from the sensitivity study.
A screening process was developed to remove anomalous data points from the measured ASR results using a median absolute deviation (MAD) approach. The process was applied to the SOLARIS output from each tuned GLAMR source wavelength for all the SOLARIS calibration data sets. Each SOLARIS frame at a GLAMR wavelength consists of a dark-corrected output for each spectral detector (SOLARIS band) and spatial detector (field of view angle). The peak signal is determined for each frame and used to normalize the signal for each detector. The average normalized signal, the standard deviation of that average, and the relative error (defined as the ratio of the standard deviation to the normalized average) are determined and reported for the 20 samples for each detector. The relative error is essentially an inverse SNR for each detector for each GLAMR tuned wavelength.
Outlier filtering is performed on 100 spectral detector groupings at a time centered on the peak average signal detector ±50 spectral detectors. The median absolute deviation for the relative error is found at each field of view (spatial detector row) using
where
represents the relative error of the pixel, and
is a distribution-dependent constant which is equal to
b = 1.4826 for a relative error with a normal distribution. Data points considered to be outliers are those with relative error >3
MAD from the median value and these are removed from ASR determination. An entire 20-sample data set is removed if the number of outlier pixels is >1% in this spectral region subset. Detectors that regularly fail the MAD filtering are marked and removed from all ASR calculations.
The end result is a set of SOLARIS data for which poor SNR data points within 50 spectral samples of a SOLARIS band center are removed. A smoothing spline is applied to the derived ASR values from the outlier-removed data set, and the spline fit is used to determine the ASR for each wavelength of the superset. The result is a set of modeled ASRs at 0.05 nm sampling for each of the 1300 SOLARIS spectral bands; these become the reference used for all comparisons in the sensitivity study. The modeled ASR is the imaging spectrometer superset. A set of reference band-averaged spectral response values are computed using Equation (2) and based on the full imaging spectrometer superset.
4. Sensitivity Studies
The motivating factor for a sensitivity study of spectral sampling of the GLAMR-based calibration is the stringent absolute uncertainties of CPF. The 0.3% (k = 1) absolute uncertainty requirement means that effects from typically ignored aspects of the radiometric calibration process can now play an important role. An additional factor is that radiometric testing for remote sensing flight projects is time constrained due to budget and overall project schedules. Such constraints are even more important for smaller-budget missions such as CPF.
The goal of the CPF independent calibration team is to characterize as large a spectral range of HySICS as possible, while still achieving an absolute radiometric uncertainty for the GLAMR calibration that is dominated by the SI-traceability of the GLAMR system. The outcome is that effects such as numerical integration techniques must cause minimal uncertainties while spectral sampling is as coarse as possible to limit schedule impacts. The supersets are used here to evaluate the impacts of GLAMR spectral sampling, source variability, and sensor noise on the accuracy of absolute radiometric calibration. The sensitivity results here need to have <0.1% (k = 1) effects to ensure that the absolute uncertainty of the GLAMR source that is traceable to SI is the dominant term in the error budget.
The result of a given sensitivity analysis is an uncertainty based on the standard deviation of a set of calibration simulations. A single calibration simulation is defined as a simulated ASR retrieval for a full range of GLAMR wavelengths. The simulation relies on spectral sampling simulating the GLAMR wavelength variability seen in
Figure 3 and
Figure 4 based on a starting wavelength and sampling interval, Δλ. Subsequent wavelengths in the list are generated by incrementing from the initial wavelength by Δλ ± ε, where ε is a randomly generated value based on a uniform distribution with values ±0.1 nm. The wavelength list is refined to the nearest GLAMR source superset value.
The GLAMR source radiance for the calibration simulation is determined for each wavelength by randomly selecting from the 20 GLAMR source superset radiance values at each wavelength. The source radiance for the calibration simulation is combined with the imaging spectrometer superset ASR for each simulated detector to create an imaging spectrometer frame image for all detectors in the simulation. Noise can be added to the frame values at this point as needed. Repeating the process for multiple frames and then further repeating for each simulated wavelength creates a set of simulated imaging spectrometer frames corresponding to a simulated full calibration collection by the imaging spectrometer using the GLAMR system. Processing these data as described in
Section 2 provides a retrieved set of ASRs, center wavelengths, and band-averaged spectral responses.
4.1. Spectral Sampling
The sensitivity of band-averaged response to spectral sampling increment was assessed using the above approach to create the GLAMR calibration simulations based on the superset data. Impacts from the wavelength sampling increment and the uneven spectral sampling are important features to understand the impact on uncertainties, due to the trade between spectral increments and test time for a GLAMR-based radiometric calibration. The issue is complicated by the fact that there is not a one-to-one relationship between the sample interval and the length of time to collect, due to the automated tuning approach that is used for GLAMR. For instance, increasing the sampling from 1.0 nm to 0.5 nm intervals triples the amount of time taken to collect the data, due to the need for manual inputs by the operator when tuning to small increments. Sensor noise in this case is assumed to be zero to isolate the impact of spectral sampling only.
The gain derived from the highest spectral resolution (Δλ = 0.05 nm) of the superset is considered the ‘true’ ASR for the instrument. This baseline gain of each band can be calculated as described in
Section 2. Band-averaged spectral response values were computed for several sampling intervals for multiple cases at each interval. The changes in response for the multiple cases at a given spectral interval were found to be negligible for Δλ < 2.5 nm, which is expected since the modeled ASR curves are reasonably smooth, and the bandwidths are approximately 5 nm.
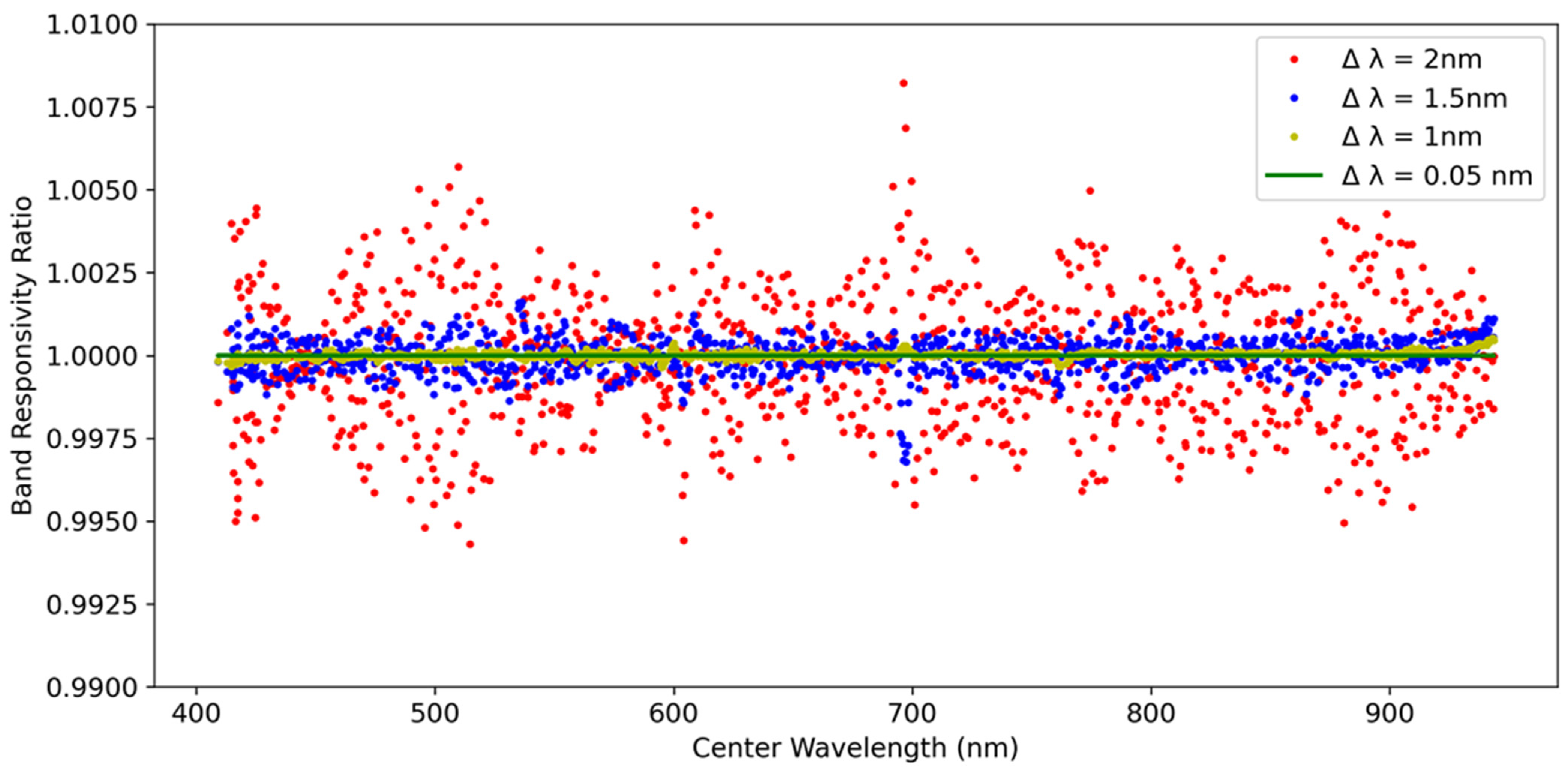
Figure 6 shows the band responsivity ratios derived for a single calibration simulation for values of Δλ = 1.0, 1.5, and 2.0 nm. The data for Δλ = 0.05 nm is also provided as the reference. Larger spectral sampling intervals show greater variability in responsivity ratio across all bands as expected. The ratio of the band responsivity for the case of Δλ = 2.0 nm shows that the error from integration is >0.3% for a large number of bands but is <1% in all cases. The total uncertainty limit for the CPF independent calibration is 0.3% for a GLAMR-based calibration, thus the 2 nm case would lead to unacceptable uncertainties. Lowering the wavelength increment to Δλ = 1.5 nm results in errors less than 0.2% for nearly all bands. A spectral sampling of Δλ = 1.0 nm results in errors much less than 0.1% for all bands, which is sufficient to ensure that the spectral sampling would not be a major error source in the CPF independent calibration 0.3% absolute uncertainty.
It is apparent in
Figure 6 that the uncertainty changes in a non-linear fashion with changing spectral sampling. The variability in the responsivity ratio is more than halved when going from 2 nm sampling to 1.5 nm, and likewise going from 1.5 nm to 1 nm. There is minimal change in uncertainty when going from 1 to 0.05 nm. The effect is the interplay between the spectral sampling of the GLAMR-based calibration and the spectral bandwidth of the imaging spectrometer being tested. Larger spectral sampling intervals lead to an inadequate retrieval of the instrument line shape that goes into the numerical integration in Equation (2), leading to large uncertainties. The reduction in uncertainties becomes limited once the line shape is adequately sampled.
Work related to other projects in addition to CPF has started to evaluate this effect in a more quantitative manner with additional sensitivity runs with varying bandwidths, band shapes, and spectral intervals. The results of that work are not critical to the current work since, as mentioned above, the goal here is to determine the coarsest level of sampling that would provide the accuracy needed for the HySICS calibration. There is also the added factor that using sampling intervals that are the same as those used in past GLAMR calibrations simplifies the test procedure development for HySICS testing. The spectral intervals shown in
Figure 6 all correspond to intervals already used in previous GLAMR calibrations for various projects. The fact that the 1 nm sampling case matches previously used testing procedures, provides satisfactory levels of uncertainties, and will fit within the HySICS testing schedule, meant that it was not necessary to explore fully the entire spectral sampling trade space.
4.2. Sensor Noise
The sensitivity to sensor noise of retrieved band-averaged spectral response was investigated using two noise models. The first uses the standard deviation of the imaging spectrometer signal multiplied by a random number in the range of −1 to 1 following a uniform probability distribution:
where
N1(
i,
j,
λn) is the noise from model 1 for imaging spectrometer detector (
i,
j) at wavelength
λn;
DNIS is the calibration simulation signal from the superset modeling; and
σIS is the standard deviation from the imaging spectrometer superset for that detector and wavelength. The second model,
N2, is generated from a term proportional to the inverse of the maximum signal to noise ratio (SNR) for each ASR curve and a second term related to the noise floor of the modeled sensor. Both terms are also modified by a uniform random number:
where
Nfloor is the noise floor term set here to a value of 10
−6;
SNR(
i,
j,
λn)
max is the maximum SNR at a given wavelength and detector that is set to 200 for the work here; and
DNIS(
i,
j,
λmax) is the imaging spectrometer superset model signal for the wavelength that has the maximum SNR. The choices for the limits on the random number generators in Equation (6) are to allow variability of the signal to noise about the average signal, while ensuring that signals remain above zero for cases where the noise floor dominates.
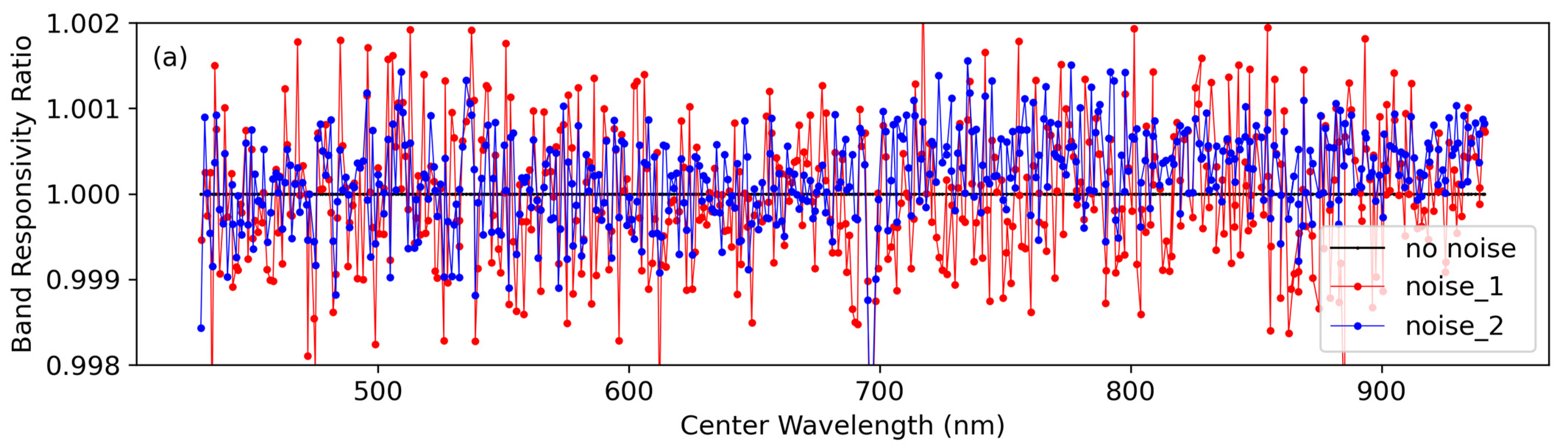
The noise models were applied to the calibration simulations and the retrieved band-averaged spectral responses were compared with those from the no-noise case. Spectral sampling intervals of 1.0 and 1.5 nm were examined. The scenario included 30 imaging spectrometer frames at each source wavelength for the calibration simulation.
Figure 7 shows the results for both cases and noise models. The key feature to note in the graphs is that the inclusion of the two sensor noise models does not significantly impact the retrieved response for the case where SNR > 200 for the spectral detectors most closely matching the tuned GLAMR wavelength. The combination of 1 nm sampling coupled with the 30 frames of data collected for each tuned wavelength minimizes errors to the point that the noise floor for the second noise model dominates. That effect is larger for larger radiance levels and this is the cause of the increase in the ratio at 700 nm.
4.3. Sensor Sampling
The last consideration discussed here is the impact that the number of sensor samples or frames has on retrieval accuracy. Increasing the number of imaging spectrometer data frames while viewing the GLAMR source is similar to increasing detector integration time but with the advantage of providing additional information on measurement repeatability. The end result of multiple frames will be an improvement in SNR for systems with random signal noise. The trade is once again collection time, but an additional consideration for imaging spectrometer applications is the volume of data that will be collected for larger numbers of frames. Ultimately, it becomes an optimization problem balancing between the data collection burden and the required quality of the uncertainty.
Multiple spectral sampling cases related to frame averaging as well as both noise models were examined. The results for the 1 nm sampling case are as expected, in that the overall uncertainty for all scenarios of noise models and sensor sampling led to uncertainties well below the threshold needed for the HySICS testing. Likewise, the results at larger spectral sampling intervals led to unacceptably high uncertainties even in the case where 50 frames of data were simulated.
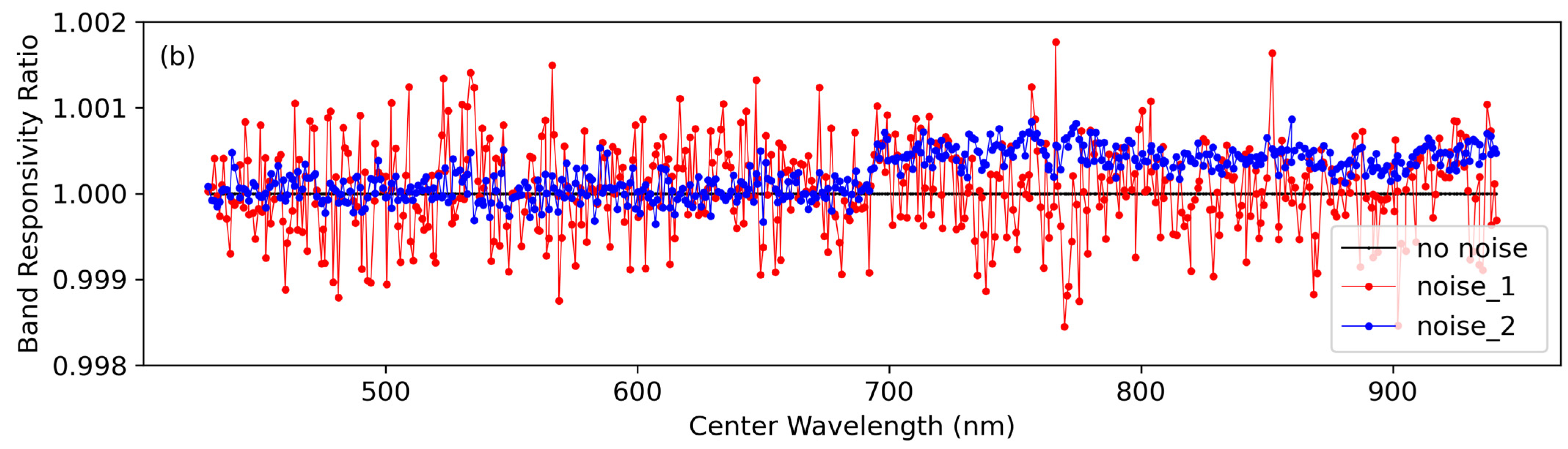
Figure 8 shows the results of the sensor sampling study for the 1.5 nm spectral sampling case for the N
2 noise model. The choice of noise model is made to avoid overly weighting the effects due to noise in the out-of-band region. The 1.5 nm spectral sampling case is the same as that shown in
Figure 7 above and helps to highlight how including multiple frames can help to reduce uncertainties below the 0.1% uncertainty for GLAMR sampling as part of the CPF independent calibration. Three frame-averaging cases, 1, 10, and 50 frames, are shown in
Figure 8. The unsurprising result for N = 1 shows that collecting a single frame of data will exceed 0.5% errors for a large number of bands. The N = 1 case corresponds to the similar 1.5 nm sampling case shown in
Figure 6, except that now there is a noise factor in the data set that leads to even larger uncertainties. Reasonable uncertainties generally less than 0.3% occur for N = 10, while uncertainties are <0.2% for N = 50 with a large fraction of the uncertainties being <0.1%.
5. Discussion
The primary motivation for the sensitivity studies shown here has been prompted by the absolute uncertainty needed for the GLAMR-based calibration of the HySICS sensor as part of the CPF independent calibration. Sensitivity tests using the spectral supersets described in
Section 3 demonstrate that selection of the GLAMR spectral sampling increment is a critical factor in band responsivity uncertainty. The sensor SNR also plays an important role, due to sensor noise, numbers of frames of data, or GLAMR source radiance level. A spectral sampling of 1 nm is shown to be necessary for cases where the SNR = 200 for the spectral detectors matching the tuned wavelength of the GLAMR source. Such an SNR value ensures that there is sufficient signal to evaluate the shoulders of the ASR of the sensor while also providing reasonable signal levels for the out-of-band region. A sampling interval of 1.5 nm is also shown to be suitable but is more sensitive to noise because of the poor sampling of the ASR shape coupled with the variability of the sensor output.
The expected behavior of the HySICS instrument is similar to that modeled in the imaging spectrometer superset, and the results shown here led to a test plan relying on a spectral interval of 1.0 nm and a collection of 30 frames at each GLAMR wavelength. Radiance levels will be set to ensure the highest SNR in each band without saturation for the standard operating 15 Hz frame rate of the sensor. The importance of the results shown here is that a 1.5 nm sampling would be sufficient to achieve the required accuracy given HySICS’s 6 nm nominal bandpass. Fortunately, the allotted test time can tolerate the 1.0 nm sampling. The result will be both improved accuracy for the HySICS calibration, and an improved understanding of the detector-to-detector relative calibration and isolation of the dominant noise sources.
The results can be extended to more general cases as well. The 1 nm sampling that was found to be suitable for the imaging spectrometer superset here is partially driven by the bandwidth of the imaging spectrometer bands. Sensors with larger bandwidths than the 5 nm case used here for the imaging spectrometer superset can tolerate larger sampling intervals, so long as there are >4 spectral samples with sufficient SNR covering the spectral range of the full width at half maximum of the ASR shape. A smaller spectral sampling interval would not only provide better absolute uncertainty but would also provide better band-to-band calibration, commonly referred to as flat-fielding. Additionally, the necessary parameters for sensors with narrower bandpasses and sharply peaked ASRs can be modeled. The imaging spectrometer superset for such a case would allow for the determination of sampling strategies to mitigate the non-uniform wavelength grid on the instrument profile retrieval. Likewise, optimized sampling strategies can be developed that would use varying wavelength intervals to sample the spectral shape at a denser sampling in sections that have sharper instrument features or are tailored to portions of the spectrum for which the instrument profiles might have different bandwidths.
6. Conclusions
Instrument modeling for imaging spectrometry as shown here is not unique [
20], but the importance of such models increases as uncertainty requirements continue to become more stringent. A key lesson learned from the CLARREO and subsequent CLARREO Pathfinder projects has been that climate quality accuracies lead to the need to understand the impacts of the prelaunch radiometric calibration test equipment on sensor calibration, including effects from the processing approaches applied to the test data. It is well known that radiometric calibration of a flight sensor takes place later in the test program, and, as such, is often subject to changing schedule constraints. The use of the approach shown here allows the test team to assess the accuracy impacts of possible shifts in schedule and reduced testing.
The use of a detector-based calibration approach coupled with a large aperture SIS offers numerous advantages for the radiometric calibration of imaging spectrometers. The detector-based calibration using the GLAMR system is reasonably efficient when coupled with an imaging spectrometer, since all spatial and spectral detectors can be calibrated with one scan through the spectrum. The work shown here gives confidence that limiting features of the GLAMR system related to spectral sampling and source radiance variations with wavelength can be overcome. The results obtained with the current spectral superset model show that CPF independent calibration uncertainties can be achieved if the in-band sensor SNR exceeds 200 through appropriate use of GLAMR source radiance levels, frame averaging, and sensor integration time or frame rate. Sampling the sensor ASR at 1 nm spectral intervals will ensure that the dominant uncertainty is the uncertainty of the SI-traceable radiance exiting the GLAMR SIS.
Future work will include extending the spectral superset model to the shortwave infrared portion of the spectrum. Modeling the GLAMR source is straightforward in this case, since data from past calibrations of multispectral sensors can be used. Plans are also underway to include additional imaging spectrometer supersets based on other sensor designs to look for unexpected effects in the GLAMR calibration approach. Sensitivity studies with the current model will continue to refine the test plan for CPF independent calibration of HySICS, and will include updated information on the HySICS sensor based on the prelaunch characterization data. The results are expected to confirm that a 0.3% absolute uncertainty is feasible, and give greater confidence that climate-quality, top-of-atmosphere reflectance will be achieved by the CPF mission.