Building Plane Segmentation Based on Point Clouds

Abstract

Planes are essential features to describe the shapes of buildings. The segmentation of a plane is significant when reconstructing a building in three dimensions. However, there is a concern about the accuracy in segmenting plane from point cloud data. The objective of this paper was to develop an effective segmentation algorithm for building planes that combines the region growing algorithm with the distance algorithm based on boundary points. The method was tested on point cloud data from a cottage and pantry as scanned using a Faro Focus 3D laser range scanner and Matterport Camera, respectively. A coarse extraction of the building plane was obtained from the region growing algorithm. The coplanar points where two planes intersect were obtained from the distance algorithm. The building plane’s optimal segmentation was then obtained by combining the coarse extraction plane points and the corresponding coplanar points. The results show that the proposed method successfully segmented the plane points of the cottage and pantry. The optimal distance thresholds using the proposed method from the uncoarse extraction plane points to each plane boundary point of cottage and pantry were 0.025 m and 0.030 m, respectively. The highest correct rate and the highest error rate of the cottage’s (pantry’s) plane segmentations using the proposed method under the optimal distance threshold were 99.93% and 2.30% (98.55% and 2.44%), respectively. The F1 score value of the cottage’s and pantry’s plane segmentations using the proposed method under the optimal distance threshold reached 97.56% and 95.75%, respectively. This method can segment different objects on the same plane, while the random sample consensus (RANSAC) algorithm causes the plane to become over-segmented. The proposed method can also extract the coplanar points at the intersection of two planes, which cannot be separated using the region growing algorithm. Although the RANSAC-RG method combining the RANSAC algorithm and the region growing algorithm can optimize the segmentation results of the RANSAC (region growing) algorithm and has little difference in segmentation effect (especially for cottage data) with the proposed method, the method still loses coplanar points at some intersection of the two planes.

1. Introduction

Buildings play a vital role in urban planning and management, urban development [1,2,3,4], and so on. The extraction of building planar features has essential applications in urban construction [5,6,7,8,9]. The building planar includes both rooftops and facades. Building planar data are obtained primarily using three methods: aerial photogrammetry, depth cameras, and light detection and ranging (LiDAR) scanners. These methods can provide dense point clouds of the rooftops and facades of the building. Aerial photogrammetry obtains detailed textural patterns of building planar features [10,11,12,13,14,15], and depth cameras acquire the distances from objects to the camera [16,17,18,19]. The LiDAR scanner provides high-density and high-precision geometric structure information of objects from different positions and provides high-quality point cloud data to reconstruct three-dimensional building models [20,21,22].

The planar features of buildings can be extracted using the neighborhood information of points [23]. The Hough Transform and RANSAC algorithms are generally used to segment planes in buildings [24,25]. The Hough Transform is used primarily to detect geometric shapes with given characteristics (such as lines, planes, and circles). Borrmann et al. [26] proposed a novel design where the accumulator has the same patch size in each accumulator ball space cell. The method detects planar features, such as the underlying structures of the environment. Hulik et al. [27] presented an optimization method of the Hough Transform to detect building planes, which has the same detection effect as the RANSAC algorithm when producing a more stable output result at the same speed. However, the size of the parameter space cannot be dynamically adjusted at runtime.

The RANSAC algorithm can detect planes or cylinders based on estimating the mathematical model parameters. Awwad et al. [28] extracted plane points through the RANSAC algorithm and solved the pseudo plane problem combining the normal vector of points. Firstly, the normal vector of each point was calculated, and then the initial plane was formed by point cloud clustering according to the angle threshold of the normal vector. Finally, the plane is optimized by the RANSAC algorithm. This algorithm can achieve a better segmentation effect. Xu et al. [29] segmented a building roof plane using the weighted RANSAC algorithm. They designed the weight function based on differences in the error distributions between the correct and incorrect plane hypotheses. However, the weighting definition requires reliable estimation of the normal vector for the surface where the point is located, which is less effective for small buildings or low point densities relative to the roof size. Li et al. [30] proposed an improved RANSAC method to solve the spurious plane problems for plane segmentation in buildings based on the normal distribution transformation cells for building plane segmentation. Compared with the traditional RANSAC method, the improved approach better identifies planes. However, the algorithm requires experience to select the optimal cell size under different conditions.

Other methods have been proposed to extract building planes. Sampath and Shan [31] extracted the plane of a building roof from unstructured airborne LiDAR point clouds using the fuzzy k-means approach based on the normal surface. The coplanar segments were separated based on density clustering and connectivity. The solution framework of this method can reach the overall within-cluster precision of 2.5°. Awrangjeb et al. [32] extracted roof feature points of buildings by combining LiDAR data with multi-spectral orthophoto imagery. However, the algorithm’s precision, especially for flat planes, decreased with the registration error. Zhou et al. [33] extracted planar features using gradients to calculate plane parameters effectively. However, this method may be affected by the number of iterations, the maximum number of clusters, and the minimum number of cluster pixels. Arnaud et al. [34] proposed a dynamic plane segmentation algorithm by creating point clusters with the same assumed plane parameters. Using this algorithm to estimate a room’s maximum size gave an average error of less than 10%.

Beyond the above methods, the region growing algorithm is also a classical approach to detect planes, circles, and other parameterized shapes [35]. The algorithm’s basic idea is to gather adjacent points from regions with similar properties. Jochem et al. [36] used the region growing algorithm to segment roof planes from buildings by combining raster data with airborne LiDAR point clouds. Compared with other methods, this method has higher completeness (94.4%) and correctness (88.4%) in 3D plane detection. However, this method also has some problems concerning the effective transmission of large datasets to different computing nodes. Kwak et al. [37] extracted the planar points using the region growing algorithm. Firstly, the seed points are randomly selected to determine the initial growth surface by fitting the neighborhood around the seed points, and then the distance between the point and the best fitting plane is taken as the regional growth condition to segment the plane.

The region growing algorithm alone can segment building planes. However, it may not be effective to segment the coplanar points of several joint planes. Thus, most research combined the region growing algorithm with other approaches to detect building planes. Deschaud and Goulette [38] proposed a feature extraction algorithm based on the combination of region growing algorithm and Hough Transform, which used normal vector and voxel growth to detect planes in unorganized point clouds. This method is a robust normal estimation based on noisy data points, and the optimal local seed plane is determined by calculating the local plane fraction of each point. Dong et al. [39] segmented building rooftops from airborne LiDAR point clouds by introducing the region growing algorithm and an adaptive RANSAC algorithm. This method extracted relatively small rooftop patches in the presence of outliers. However, the algorithm’s efficiency is relatively low when more buildings are segmented simultaneously with more outliers. Vo et al. [40] proposed the region growing algorithm based on octrees to realize building point clouds’ plane segmentation. The voxel models simplified the initial data to calculate the local surface properties, avoiding expensive searches for adjacent points. In addition, the algorithm still needs to set the voxel size based on the dataset and the desired feature detection level.

Aiming at the problem that coplanar points where two planes intersect that cannot be separated by region growing algorithm, this paper proposes an effective segmentation method for building planes that combines the region growing algorithm with the distance algorithm based on boundary points to improve the segmentation precision of building planes. This method improves the region growing algorithm when extracting building coplanar points to obtain the optimal building plane segmentation.

2. Methods

This section introduces the proposed method for building plane segmentation in detail. Firstly, the building plane is segmented coarsely using the region growing algorithm. The uncoarse extraction plane points are obtained after removing the coarse extraction plane points from the original building points. The coarse extraction plane’s boundary points are then extracted using the maximum value of the angle between the vectors formed between a point and its adjacent points on the tangent plane. Finally, the coplanar points where two planes intersect were obtained from the distance threshold from the uncoarse extraction plane points to the coarse extraction plane’s boundary points. The optimal plane segmentation is obtained by combining the coarse extraction plane points with the corresponding coplanar points. The workflow of the building plane point segmentation is shown in Figure 1.

2.1. Coarse Extraction of Plane Points

Region growing is a segmentation algorithm based on spatial proximity and homogeneity regarding a defined criterion. The building plane is extracted coarsely using the region growing algorithm in this paper. The algorithm’s idea is that points with a minimum curvature are selected as an initial seed point. The seed point’s adjacent points meet the angle value between the normal vector of the points and the normal vector of the current seed point. Furthermore, their curvature value is less than the set curvature value. These are regarded as new seed points to continue region growing until the seed point sequence is empty. The adjacent points are considered to belong to the same plane [41,42].

The normal vector and curvature are the surface’s basic characteristics and are an essential basis for surface feature recognition. The sampling point’s normal vector and curvature need to be estimated to obtain plane segmentation using the region-growing algorithm.

The normal vector of the point is estimated based on neighborhood range, which is usually calculated by the neighborhood radius or adjacent points. In this paper, the normal vector and curvature of a point were estimated using a curved surface composed of adjacent points. The normal vector of a point was calculated using principal component analysis or the eigenvectors and eigenvalues of the covariance matrix created from the adjacent points. The corresponding covariance matrix $\mathrm{C}$ for point $p_i$ is [43,44]:

$$\mathrm{C}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left(p_i-p_s\right){\left(p_i-p_s\right)}^T, p_s=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{p}_i$$

(1)

where $n$ is the number of adjacent points of $p_i$, and$p_s$ represents the center of the adjacent points. In this paper, the parameter $n$ of cottage and pantry is set to 50 and 60, respectively.

The normal vector of the point $p_i$ is [45]:

$$\mathrm{C}·{\overrightarrow{v}}_j={\lambda }_j·{\overrightarrow{v}}_j, j\in \left\{0, 1, 2\right\}$$

(2)

where ${\lambda }_j$represents the j-th eigenvalue of the covariance matrix, and ${\overrightarrow{v}}_j$ represents the j-th eigenvector. The normal vector is the eigenvector corresponding to the minimum eigenvalue. Its direction can be determined using the normal vector of a point and the vector formed by the point and the set viewpoint since the direction of the point’s normal vector is ambiguous.

As the eigenvalue ${\lambda }_0<{\lambda }_1<{\lambda }_2$represents the degree of change of a point along with the three main directions, the curvature $\mathsf{\sigma }$of point $p_i$ can be approximated as [44,46]:

$$\mathsf{\sigma }=\frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1+{\lambda }_2}$$

(3)

where ${\lambda }_0$,${\lambda }_1$, and ${\lambda }_2$ are the eigenvalues of the covariance matrix, and $\mathsf{\sigma }$ is the curvature of the point.

The angle value of the cottage and pantry between the normal vector of the current seed point and the normal vector of its adjacent points is set to$2.0°$ after obtaining the normal vectors and curvatures for all points. The reason for setting the angle value to $2.0°$ is because the points obtained are not strictly in the same plane. When the angle value between the normal vector of the current seed point and the normal vector of its adjacent points is within the threshold, it can be regarded as coplanar, which can make the surface as smooth as possible. Additionally, suppose each point is smoothly bent (i.e., the threshold of the angle between the normal vector of the current seed point and its adjacent point normal vector is very small). In that case, however, the offset of the surface will increase with an increased number of points. The curvature value of cottage and pantry is set to 0.5 in this paper to control the angle between the current seed point and average normal vectors since curvature measures the rate of change of surface normals. In this paper, the number of points of the smallest point clusters of cottage and pantry is set to 850 and 1000, respectively.

The operational steps are as follows:

• Calculate all points’ curvatures and add the minimum curvature point to the seed point set.
• Calculate the normal vector of the current seed point and its adjacent points. If the current seed point’s adjacent points not only meet the angle value between the normal vector of the points and the normal vector of the current seed point but also their curvature value is less than the set curvature value, the adjacent points to the seed point sequence.
• Delete the current seed point, and the adjacent points are regarded as new seed points to continue the region growing.
• This process will continue until the seed point sequence is empty.

2.2. Optimal Extraction of Plane Points

A coarse extraction of the building plane was obtained using the region growing algorithm. The uncoarse extraction plane points were obtained after removing the coarse extraction plane points from the original building points. However, the extracted plane lacked coplanar points from the two planes’ intersections since the algorithm is less effective in segmenting the coplanar points. The coplanar points are obtained by calculating the distance threshold from the uncoarse extraction plane points to the coarse extraction planes. In this paper, the coplanar points where the two planes intersect were obtained using the distance threshold from the uncoarse extraction plane points to the coarse extraction plane’s boundary points.

2.2.1. Boundary Points

Boundary points are essential geometric features. They play a vital role in reconstructing surface models. The coarse extraction plane’s boundary points were extracted based on the maximum value of the angle between the vectors formed between a point and its adjacent points on the micro-tangent plane.

After obtaining the normal vectors for all points, the angle criterion based on the maximum angle between vectors formed between a point and its adjacent points on the micro-tangent plane was used to determine whether it is located on a plane’s boundary.

The idea of boundary feature extraction based on the maximum value of the angle is to project the local point set onto the micro-tangent plane. Then, the angle is calculated between the vectors formed between a point and its adjacent points on the micro-tangent plane, and the maximum value of the angle is taken as the measurement criterion. For uniformly distributed internal point clouds, the angle value between the vectors formed between a point and its adjacent points is small. If the distribution of adjacent points is biased to one side, the angle value will be larger. According to this principle, if the maximum angle value between the vectors formed between a point and its adjacent points on the micro-tangent plane greater than the set threshold value, the point is regarded as a boundary point, otherwise it is an internal point.

In addition, an appropriate number of boundary points need to be extracted to calculate the distance from the uncoarse extraction plane points to the coarse extraction plane’s boundary points. If the angle threshold is too small, many inside points will be regarded as boundary points. If the angle threshold is too large, some boundary points may be missing. Thus, the angle threshold of the cottage and pantry was set to $\frac{\pi }{2}$in this paper.

The boundary point extraction process for the coarse extraction plane is as follows:

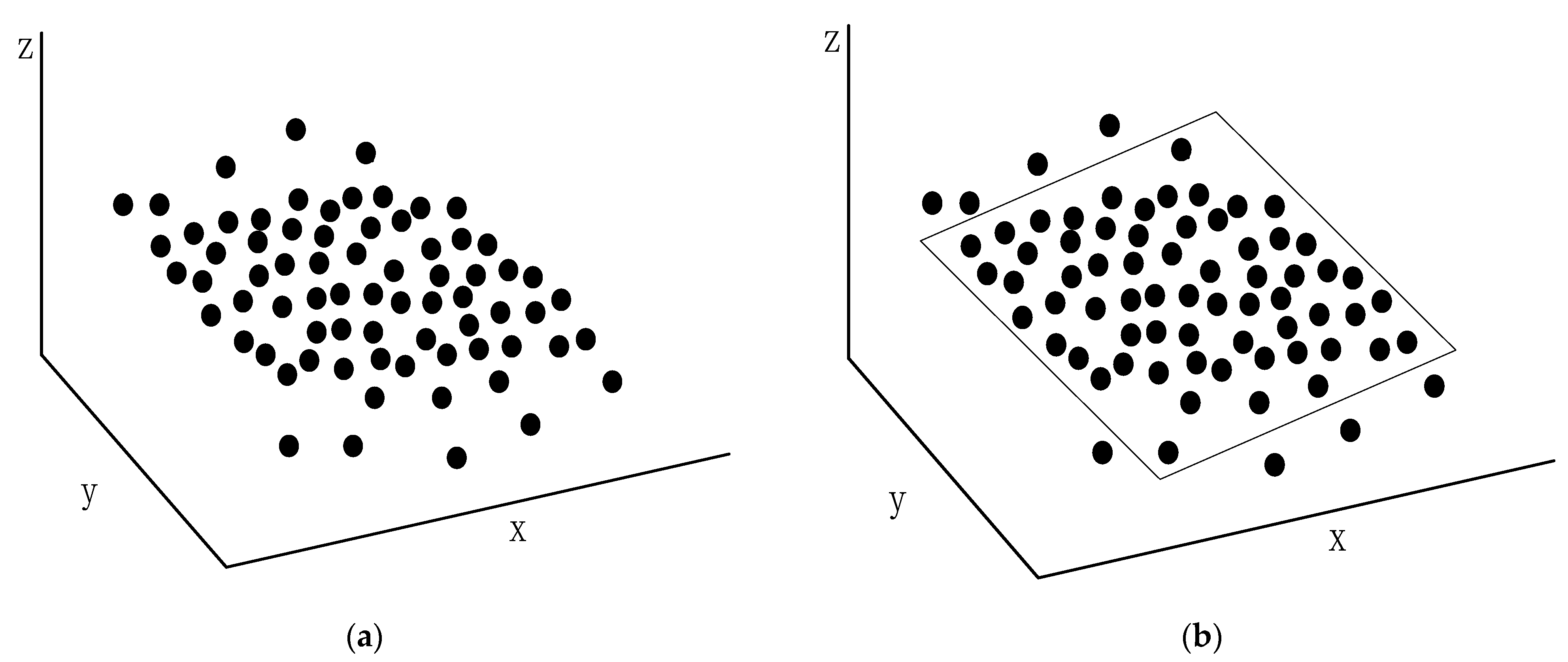
• Calculate the normal vector of the surface formed by a point and its neighboring points. The micro-tangent plane is calculated from the normal vector.
• Project these points to the micro-tangent plane.
• Calculate the angle between the vectors formed between a point and its adjacent points on the micro-tangent plane.
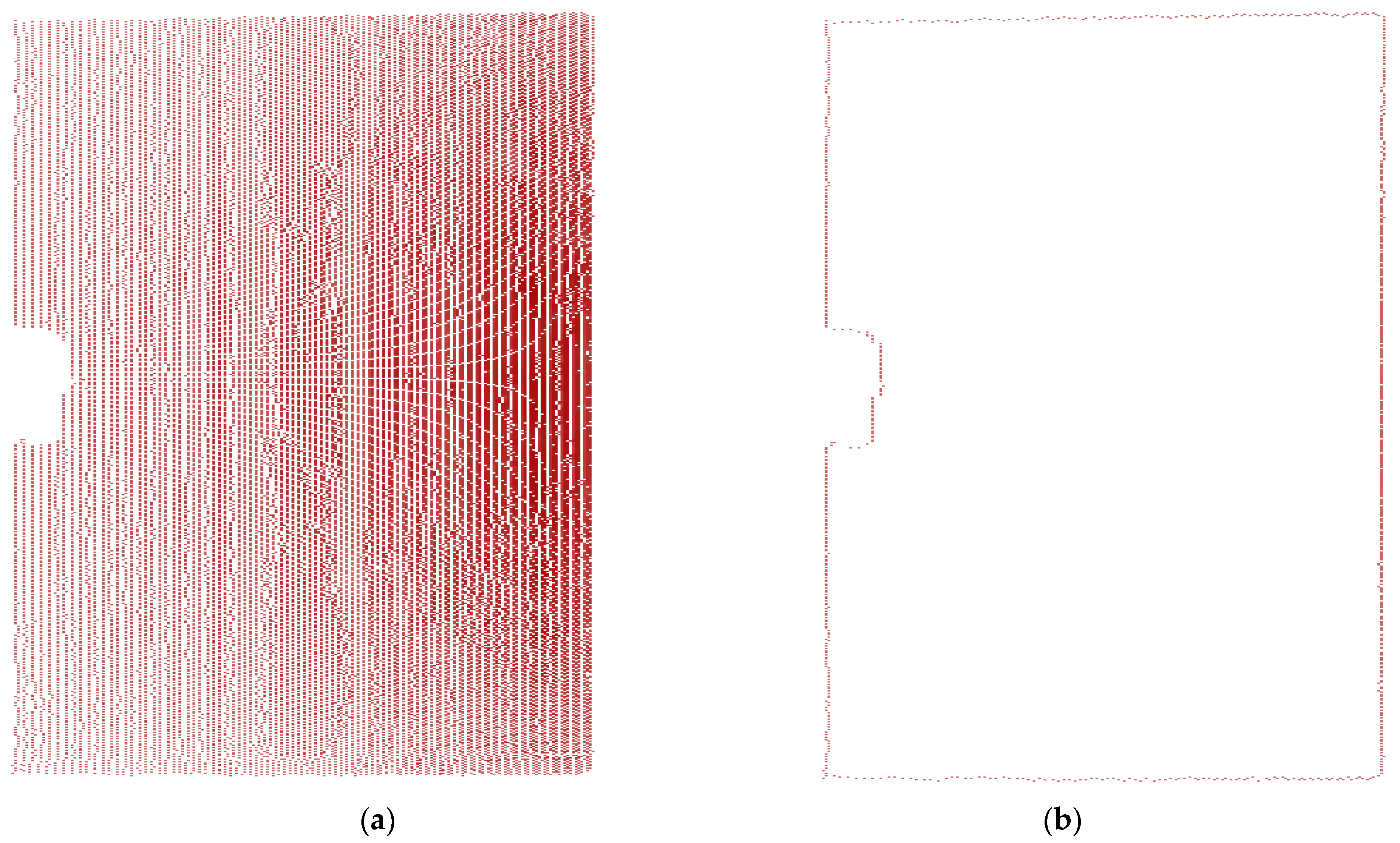
• If the maximum angle between adjacent vectors is greater than the set threshold value, it is regarded as a boundary point; otherwise, it is considered an interior point (Figure 2).

The boundary points extraction results are shown in Figure 3.

2.2.2. Coplanar points Extraction

After the boundary points were obtained, the coplanar points at which two planes intersect were then extracted using the distance threshold from the uncoarse extraction plane points to the boundary points of the coarse extraction plane. The uncoarse extraction plane points were obtained after removing the coarse extraction plane points from the original points of the building. Points among the uncoarse extraction plane points are represented as $\mathrm{P}\left(\mathrm{x}, \mathrm{y}, \mathrm{z}\right)$. A boundary point of the coarse extraction plane is represented as $\mathrm{Q}\left(\mathrm{l}, \mathrm{m}, \mathrm{n}\right)$. The distance$\mathrm{d}\left(\mathrm{P}, \mathrm{Q}\right)$ from the uncoarse extraction plane point to the boundary point is [47]:

$$\mathrm{d}\left(\mathrm{P}, \mathrm{Q}\right)=\sqrt{{\left(x-l\right)}^2+{\left(y-m\right)}^2+{\left(z-n\right)}^2}$$

(4)

The coarse extraction of the cottage plane and pantry plane was obtained using the region growing algorithm with 22 planes and 30 planes, respectively. The distances were calculated from the uncoarse extraction plane points to the coarse extraction plane’s boundary points. If the distance from a point of the uncoarse extraction plane to the plane boundary point is within the threshold, the point is assigned to the plane. The cottage’s data density obtained from the instrument is roughly uniform, and the distance between points is about 0.010 m. The pantry’s data density obtained by the depth camera is not uniform, with the distance between some points being 0.010 m, while the distance between some points is 0.040 m. The plane segmentation result will be different because of the various distance threshold from the uncoarse extraction plane points to the boundary points of the coarse extraction plane. The plane segmentation results of 0.020 m and 0.025 m from a distance between the uncoarse extraction plane points and each plane boundary point of the cottage were calculated, respectively. When the distance between the uncoarse extraction plane points and each plane boundary point of the cottage is 0.025 m, the plane segmentation result is optimal (Figure 4).

Finally, the coplanar points where two planes intersect were obtained using the distance threshold from the uncoarse extraction plane points to the coarse extraction plane’s boundary points. The optimal plane segmentation can be obtained by combining the coarse extraction plane points using region growing algorithm with the corresponding coplanar points based on the distance algorithm.

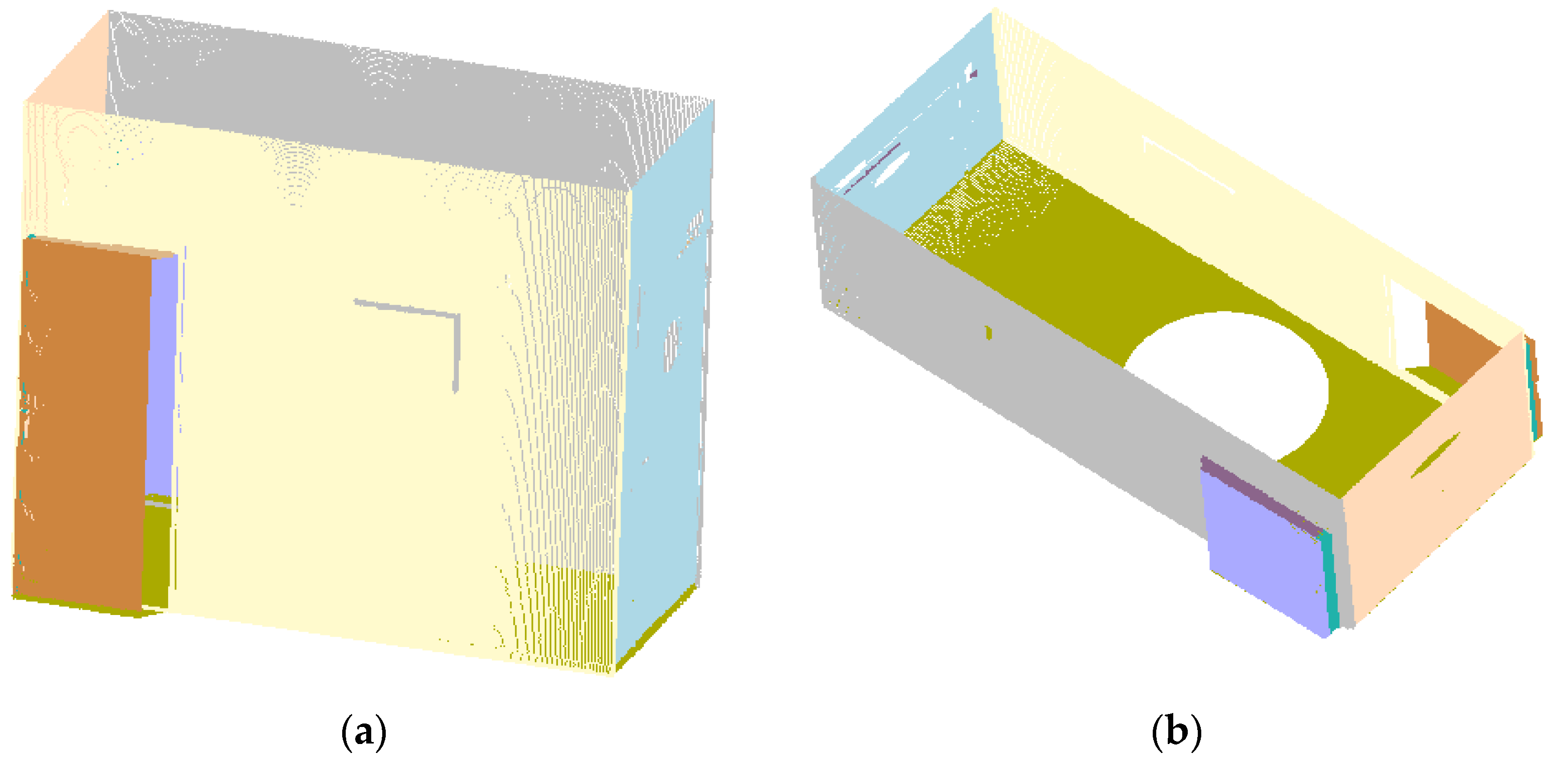
3. Results

The density of the cottage’s data obtained is roughly uniform, with a distance of about 0.010 m from point to point. The pantry’s data density obtained by the depth camera is uneven, and the distance is between 0.010 m and 0.040 m from some points. We evaluated the plane segmentation results using the proposed method when the distance thresholds from the uncoarse extraction plane points to each plane boundary point is set to 0.015 m, 0.020 m, 0.025 m, 0.030 m, and 0.035 m, respectively. The proposed method under different distance thresholds was tested on two datasets of indoor scenes that are cottage and pantry (Figure 5 and Figure 6). Furthermore, the RANSAC algorithm, the region growing algorithm, and the RANSAC-RG method were used to test point cloud data from cottage and pantry to verify the effectiveness of the proposed method.

The cottage and pantry were obtained based on the room detection datasets (Full-3D) [48] and the Stanford Large-Scale 3D Indoor Spaces Dataset by Matterport Camera [49], respectively. The cottage data were scanned by using the Faro Focus 3D laser range scanner. The scanner has a full 360° × 305° field of view and a high density of 91,352 points/m². We removed its roof points and delete some discrete points because of missing some of the roof points of the cottage.

The RANSAC algorithm randomly selects some points from a dataset to fit the plane and calculates the distance from other points to the fitting plane by continuous iterative method. If the distance from the point to the fitting plane is within the set distance threshold, the point is regarded as the interior. Otherwise, it is regarded as the exterior, and the model with the most interior points is the optimal plane model [50,51]. The RANSAC algorithm fitting plane points is shown in Figure 7. The region growing algorithm can also detect plane points. However, it will not determine the intersection points of two planes (Figure 8b). The proposed method can segment the building plane by combining the region growing algorithm with the distance algorithm based on the boundary points (Figure 8c).

In addition, the RANSAC-RG method combining the RANSAC algorithm with region growing algorithm was to evaluate the plane segmentation results since the RANSAC algorithm can cause the plane to become over-segmented. This is especially true when two objects on the same plane cannot be separated from each other in the algorithm. The region growing algorithm can separated different objects from the same plane. The RANSAC-RG method first uses the RANSAC algorithm to segment the building plane. Then, the subplane obtained by the RANSAC algorithm is optimally segmented by the region growing algorithm. However, the angle value between the normal vector of the current seed point and the normal vector of its adjacent points is too small to identify different objects when segmenting different objects from the same plane by region growing algorithm. The edge points of the plane will be lost when identifying successfully different objects from the same plane. Therefore, the distance algorithm based on boundary points is used to optimize the segmentation results. Finally, different planes are merged if they have the same normal vector, and their shortest distance is within 0.010 m (0.025 m) for the cottage (pantry) data.

The RANSAC (region growing, RANSAC-RG) algorithm was used to perform plane segmentation of a cottage and pantry, as shown in Figure 9 and Figure 10 (Figure 11, Figure 12, Figure 13 and Figure 14). Finally, the proposed method under the optimal distance threshold combing the region growing algorithm with the distance algorithm based on boundary points was used to perform the cottage’s and pantry’s plane segmentation (Figure 15 and Figure 16). The planes were labeled with different colors.

The segmentation accuracy was evaluated by comparing the number of points manually identified as a plane with the proposed method. The performance of these algorithms can be evaluated based on the classification precision. This paper evaluates the segmentation accuracy of several large planes of cottage and pantry using the proposed method under different distance thresholds from the uncoarse extraction plane points to each plane boundary point. In addition, the plane segmentation accuracy of the RANSAC (region growing and RANSAC-RG) algorithm was evaluated to verify the effectiveness of the proposed method under the optimal distance threshold. Correct refers to the ratio of the number of correct classification points assigned to a plane by an algorithm to the number of ground truth data of a plane (manually identified). Error refers to the ratio of the number of error classification points assigned to a plane by an algorithm to the number of the ground truth data of a plane (manually identified).

In addition, the measures of precision, recall, and F1 score are effective means for evaluating object classification. The average values of precision, recall, and F1 scores of several large planes are used to evaluate the segmentation results of cottage and pantry. Precision represents the ratio of the number of correctly predicted positive samples to the total number of predicted positive samples. Recall represents the ratio of the number of correctly predicted positive samples to the number of all samples in the actual class. The F1 score is the weighted average of the precision and recall. The three measurements are calculated using the equations as follows [33]:

$$\mathrm{precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}$$

(5)

$$\mathrm{recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$$

(6)

$$\mathrm{F}1=2·\frac{\mathrm{precision}·\mathrm{recall}}{\mathrm{precision}+\mathrm{recall}}$$

(7)

where TP denotes the number of points correctly assigned to a plane that is a part of that plane in the reference, and FP denotes the number of points incorrectly unassigned to a plane that is a part of that plane in the reference. FN denotes the number of points wrongly assigned to a plane that is not a part of that plane in the reference.

4. Discussion

The segmentation accuracy of several large planes of cottage and pantry were evaluated using the proposed method under different distance thresholds from the uncoarse extraction plane points to each plane boundary point. With the increase in the distance threshold, the correct rate of the plane segmentation was improved on the whole, while the error rate increased (

Table 1. Accuracy assessment of cottage’s plane segmentation using the proposed method under different distance thresholds.

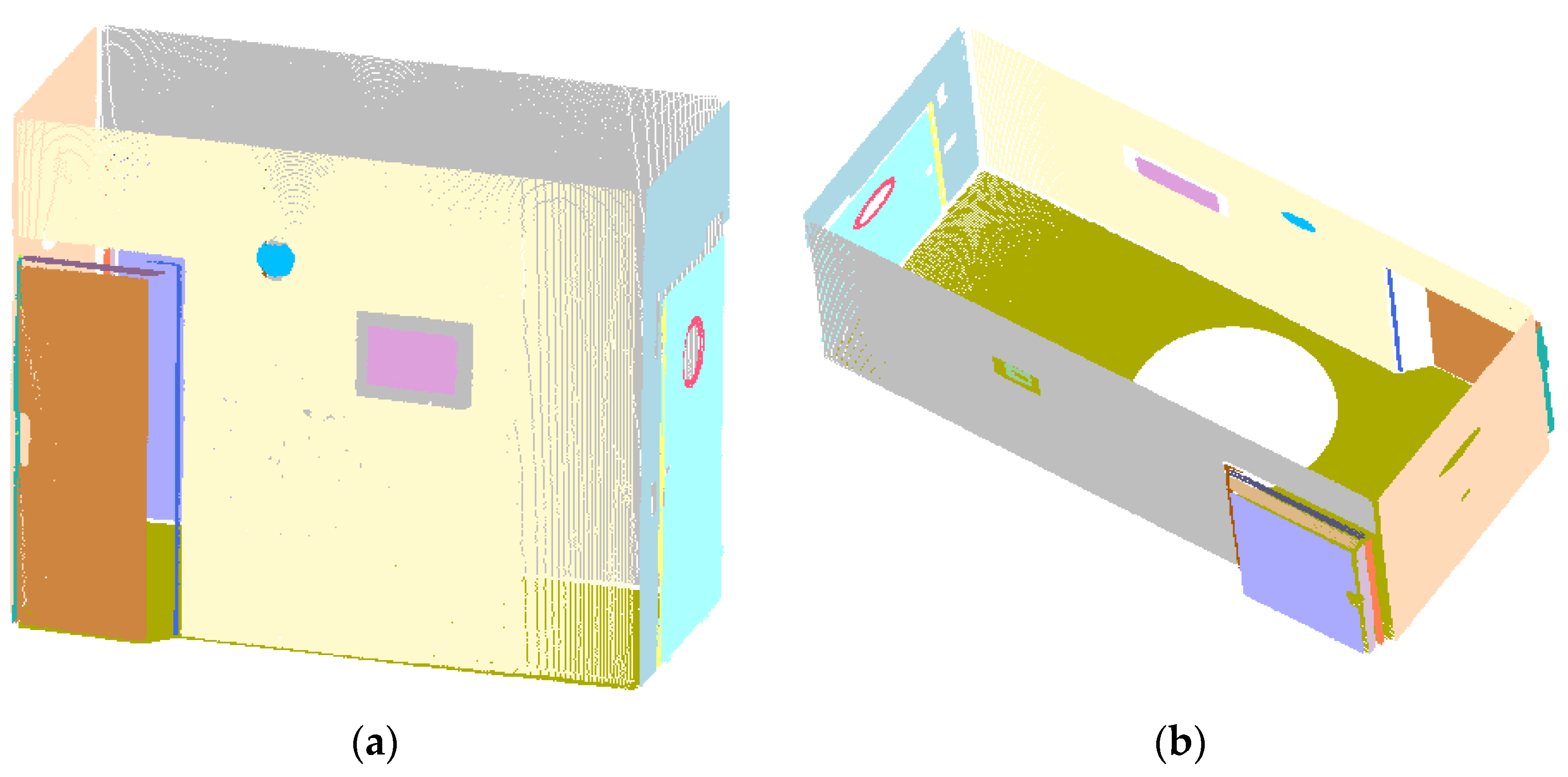
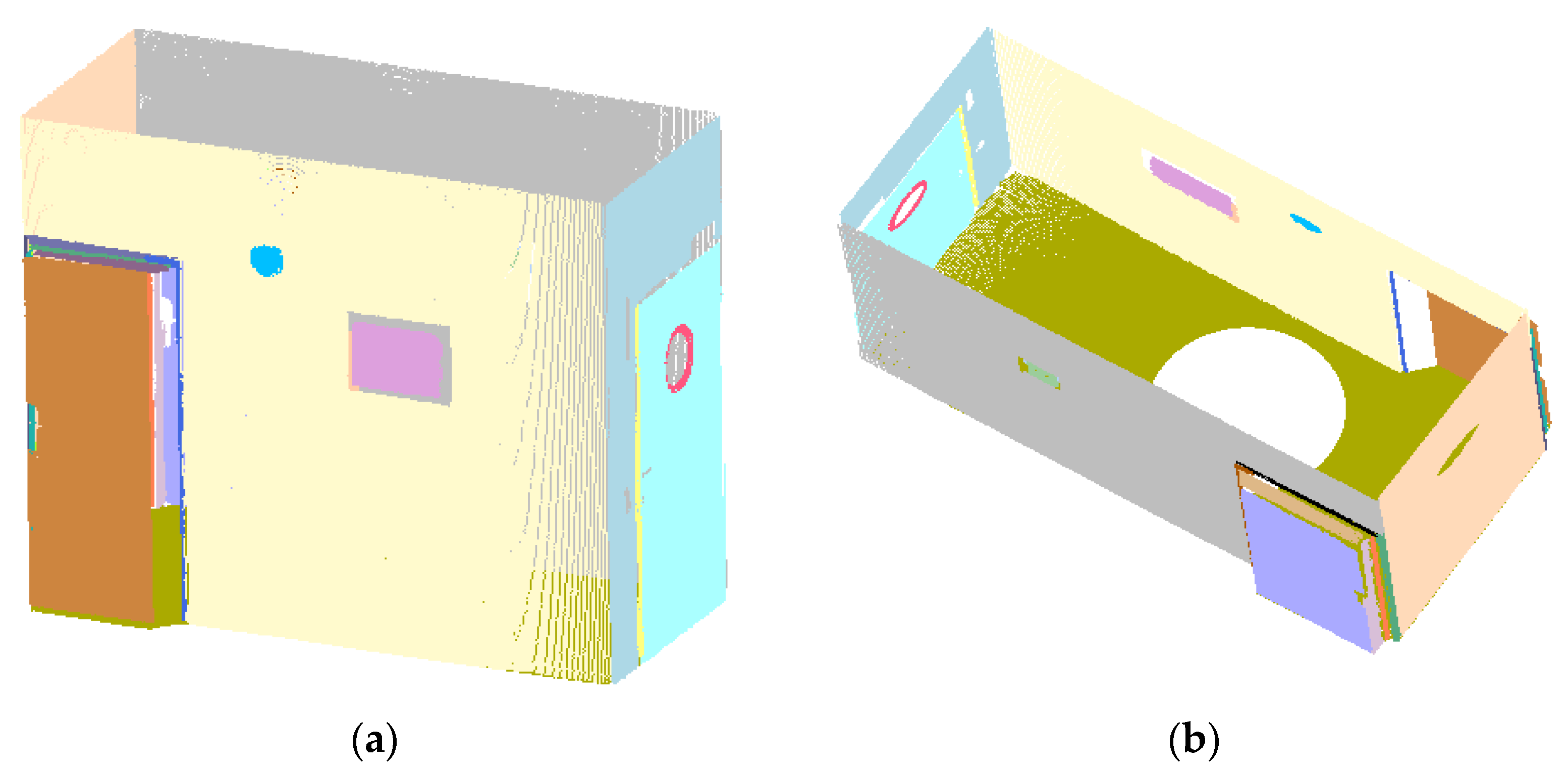
Plane	Accuracy	0.015 m	0.020 m	0.025 m	0.030 m	0.035 m
Plane 1	Correct	84.05%	84.62%	85.10%	85.49%	85.85%
	Error	0.34%	0.65%	0.98%	1.23%	1.49%
Plane 2	Correct	95.79%	96.03%	96.13%	96.17%	96.20%
	Error	0.09%	0.30%	0.54%	0.73%	1.05%
Plane 3	Correct	96.31%	96.20%	96.27%	96.46%	96.56%
	Error	0.17%	0.20%	0.34%	0.40%	0.44%
Plane 4	Correct	98.98%	99.55%	99.93%	99.81%	99.61%
	Error	1.89%	2.18%	2.30%	2.50%	2.99%
Plane 5	Correct	98.68%	98.89%	99.05%	99.14%	99.17%
	Error	0.57%	0.94%	1.27%	1.75%	2.46%
Plane 6	Correct	96.92%	97.72%	97.70%	98.34%	98.55%
	Error	0.00%	0.09%	0.41%	0.90%	1.52%
Plane 7	Correct	96.61%	97.20%	97.60%	98.57%	98.70%
	Error	0.00%	0.06%	0.33%	1.19%	1.38%
Plane 8	Correct	97.37%	98.23%	98.48%	98.42%	98.08%
	Error	0.88%	1.50%	1.85%	2.36%	2.73%

and

Table 2. Accuracy assessment of pantry’s plane segmentation using the proposed method under different distance thresholds.

Plane	Accuracy	0.015 m	0.020 m	0.025 m	0.030 m	0.035 m
Plane 01	Correct	96.32%	96.83%	97.32%	97.80%	98.18%
	Error	0.21%	0.32%	0.45%	0.74%	1.27%
Plane 02	Correct	95.95%	96.69%	97.35%	97.85%	98.05%
	Error	0.09%	0.21%	0.43%	0.61%	0.83%
Plane 03	Correct	89.52%	92.33%	94.48%	95.43%	95.49%
	Error	0.87%	1.48%	2.09%	2.33%	2.09%
Plane 04	Correct	90.96%	92.21%	93.37%	94.07%	93.35%
	Error	0.08%	0.18%	0.37%	0.57%	0.84%
Plane 05	Correct	88.19%	89.54%	90.85%	91.70%	92.11%
	Error	0.28%	0.60%	1.10%	1.96%	3.09%
Plane 06	Correct	94.01%	96.03%	97.66%	98.20%	97.28%
	Error	0.04%	0.22%	0.69%	0.91%	0.98%
Plane 07	Correct	94.16%	95.71%	97.04%	98.35%	99.34%
	Error	0.89%	1.24%	1.81%	2.44%	3.65%
Plane 08	Correct	97.24%	97.69%	98.14%	98.55%	99.03%
	Error	0.45%	0.60%	0.80%	1.04%	1.48%
Plane 09	Correct	66.62%	68.02%	69.02%	69.25%	68.44%
	Error	0.33%	0.59%	0.85%	0.92%	1.06%

). However, the correct rate of the plane segmentation does not always increase with the increase in the distance threshold. The correct rate of the cottage and pantry were the highest when the distance thresholds were set to 0.025 m (planes 4 and 8) (Table 1) and 0.030 m (plane 04, plane 06, and plane 09) (Table 2). The possible reason for this is that some points that do not belong to the plane are assigned to the plane because the distance threshold is set too large from the uncoarse extraction plane point to the boundary point. As the distance threshold increased, the precision of the cottage and pantry increased, while the recall rate decreased (

Table 3. Assessment of segmentation results for data using the proposed method under different distance thresholds.

	Cottage			Pantry
	precision	recall	F1 score	precision	recall	F1 score
0.015 m	95.59%	99.38%	97.39%	90.33%	99.60%	94.49%
0.020 m	96.06%	99.07%	97.40%	91.67%	99.33%	95.11%
0.025 m	96.28%	98.98%	97.56%	92.80%	98.98%	95.56%
0.030 m	96.55%	98.60%	97.51%	93.47%	98.65%	95.75%
0.035 m	96.59%	98.23%	97.35%	93.47%	98.23%	95.53%

). The maximum value of the F1 score was achieved using the proposed method for the cottage and pantry at a distance threshold of 0.025 m and 0.030 m, respectively (Table 3). Since the F1 score is the weighted average of the precision and recall, the distance threshold corresponding to the maximum of the F1 score value was optimal in this paper. Therefore, the optimal distance thresholds from the uncoarse extraction plane points to each plane boundary point of the cottage and pantry were 0.025 m and 0.030 m, respectively.

In addition, we compared the RANSAC (region growing and RANSAC-RG) algorithm with the proposed method under the optimal distance threshold based on the segmentation accuracy of several large planes of the cottage and pantry. Although the RANSAC algorithm can segment the building plane, it may over-segment and mistakenly divide the plane. This is especially true when two objects on the same plane cannot be separated from each other in the algorithm, such as the cottage’s door (plane 5) and cottage’s wall (plane 8) (

Table 4. Accuracy assessment of cottage’s plane segmentation.

Plane	Accuracy	RANSAC	Region Growing	RANSAC-RG	The Proposed Method
Plane 1	Correct	100.00%	82.10%	85.10%	85.10%
	Error	9.63%	0.07%	0.96%	0.98%
Plane 2	Correct	100.00%	94.99%	96.07%	96.13%
	Error	6.22%	0.00%	0.52%	0.54%
Plane 3	Correct	94.83%	94.39%	96.25%	96.27%
	Error	0.84%	0.00%	0.29%	0.34%
Plane 4	Correct	97.40%	97.73%	97.39%	99.93%
	Error	1.19%	1.01%	1.01%	2.30%
Plane 5	Correct	98.28%	95.48%	98.81%	99.05%
	Error	64.17%	0.06%	1.06%	1.27%
Plane 6	Correct	99.73%	95.16%	98.14%	97.70%
	Error	5.00%	0.00%	0.37%	0.41%
Plane 7	Correct	99.01%	94.87%	97.12%	97.60%
	Error	4.90%	0.00%	0.31%	0.33%
Plane 8	Correct	89.75%	92.69%	96.48%	98.48%
	Error	164.97%	0.00%	1.70%	1.85%

) (Figure 9b). The RANSAC algorithm divides several planes into the same on (plane 03 and plane 07 should be two different planes) (

Table 5. Accuracy assessment of pantry’s plane segmentation.

Plane	Accuracy	RANSAC	Region Growing	RANSAC-RG	The Proposed Method
Plane 01	Correct	96.38%	95.43%	97.10%	97.80%
	Error	1.76%	0.10%	0.70%	0.74%
Plane 02	Correct	99.91%	94.58%	97.98%	97.85%
	Error	6.21%	0.02%	0.87%	0.61%
Plane 03	Correct	97.89%	83.99%	81.06%	95.43%
	Error	252.84%	0.36%	2.58%	2.33%
Plane 04	Correct	80.18%	88.60%	90.74%	94.07%
	Error	28.76%	0.00%	0.08%	0.57%
Plane 05	Correct	100.00%	85.54%	92.09%	91.70%
	Error	30.61%	0.02%	2.21%	1.96%
Plane 06	Correct	84.78%	90.61%	95.23%	98.20%
	Error	93.32%	0.00%	0.82%	0.91%
Plane 07	Correct	94.76%	91.63%	98.36%	98.35%
	Error	76.37%	0.39%	2.65%	2.44%
Plane 08	Correct	95.23%	96.47%	98.41%	98.55%
	Error	2.02%	0.22%	0.84%	1.04%
Plane 09	Correct	84.95%	63.85%	66.53%	69.25%
	Error	17.48%	0.12%	0.30%	0.92%

) (Figure 13b). Although the correct rate of the cottage’s plane segmentation was 100.00% (plane 1 and plane 2) (Table 4) using the RANSAC algorithm, the error rate of the plane segmentation reached 64.17% (plane 5) and 164.97% (plane 8) (Table 4). The error rate of the pantry’s plane segmentation using the RANSAC algorithm reached 252.84% (plane 03) and 93.32% (plane 06) (Table 5), respectively.

The region growing algorithm uses the normal vector and curvature information to segment plane points, and the highest correct rate of the cottage’s and pantry’s plane segmentation was 97.73% (plane 4) (Table 4) and 96.47% (plane 08) (Table 5), respectively. However, this algorithm cannot effectively segment the building plane’s point cloud, especially the intersection point of two planes (Figure 10 and Figure 14). When the error rate of plane segmentation is 0.00%, the correct rate of the cottage’s and pantry’s plane segmentation is 95.16% (plane 6) (Table 4) and 90.61% (plane 06) (Table 5), respectively, which is the result of lacking the intersection point of the two planes.

The RANSAC-RG method combining the RANSAC algorithm and region growing algorithm can separate different objects on the same plane, such as the cottage’s door (plane 5) and cottage’s wall (plane 8) (Table 4) (Figure 11b). In addition, the error rate of cottage’s plane segmentation by the method was only 1.70% (plane 8) (Table 4), while the result of the RANSAC algorithm reached 164.97% (plane 8) (Table 4). The RANSAC algorithm segmented several planes that belong to different planes into the same plane, and then some smaller clusters connecting the two planes segmented using the region algorithm was lost, making one plane incomplete (plane 03) (Table 5). The correct rate of the plane segmentation of the method is generally higher than that of the region growing algorithm.

Compared with the RANSAC (region growing, and RANSAC-RG) algorithm, the cottage’s and pantry’s plane segmentation’s highest correct rate reached 99.93% (plane 4) (Table 4) and 98.55% (plane 08) (Table 5), respectively, using the proposed method. The proposed method can segment the plane points of buildings and significantly improve the segmentation effect, especially for coplanar points at the intersection of two planes (Figure 12 and Figure 16).

In the coarse extraction process, some non-smooth points in the plane will be removed. The segmentation accuracy of some planes is not high if there are too many non-smooth points inside a plane when using the region growing algorithm (the RANSAC-RG method and the proposed method) (plane 1) (Table 4). However, the RANSAC algorithm’s segmentation accuracy may not be affected (Figure 9). In addition, if there is no point connection in the middle part of a plane, the plane will be judged as two planes based on the region growing criterion by the region growing algorithm (the RANSAC-RG method and the proposed method) (plane 09) (Table 5) (Figure 14, Figure 15 and Figure 16b). Some points in the point cloud data of the pantry obtained from the depth camera cannot be roughly assigned on the same plane due to the limitations of the matching image accuracy. Thus, the segmentation of some planes is not ideal when using the region growing algorithm (RANSAC-RG method and the proposed method); however, the RANSAC algorithm can still segment certain planes (plane 05) (Table 5) (Figure 12b).

Although the RANSAC-RG method can optimize the segmentation results of the RANSAC (region growing) algorithm and has little difference in segmentation effect (especially for cottage data) with the proposed method, the algorithm still loses coplanar points at some intersection of the two planes (especially for pantry data) (Figure 15b). This is because more edge points of the subplane segmented optimally by the region growing algorithm can be lost due to the uneven distribution of the edge points, and there will also be some edge points lost even if a distance algorithm is used to optimize plane segmentation.

The proposed method, like the RANSAC algorithm, the region growing algorithm, and the RANSAC-RG method, still has misjudgments in recognizing coplanar points. The highest error rate of the cottage’s and pantry’s plane segmentation was 2.30% and 2.44%, respectively, using the proposed method.

From the overall analysis of several large planes, compared with the region growing algorithms, the RANSAC-RG method, and the proposed method, the precision value of cottage’s plane segmentation using the RANSAC algorithm reached 97.38% (

Table 6. Assessment of segmentation results for data.

	RANSAC			Region Growing			RANSAC-RG			The Proposed Method
	precision	recall	F1 score	precision	recall	F1 score	precision	recall	F1 score	precision	recall	F1 score
cottage	97.38%	83.69%	88.43%	93.43%	99.85%	96.47%	95.67%	99.20%	97.64%	96.28%	98.98%	97.56%
pantry	92.68%	72.69%	79.17%	87.86%	99.85%	93.18%	90.83%	98.68%	94.27%	93.47%	98.65%	95.75%

). This may be because the RANSAC algorithm can cause excessive segmentation, and it can contain more correctly classified numbers of plane points at the same time. The recall values of cottage’s (pantry’s) plane segmentation using the proposed method, the RANSAC-RG method and the region growing algorithms have a higher segmentation accuracy than the RANSAC algorithm. It can be seen that the proposed method, the RANSAC-RG method, and the region growing algorithm can segment planes more effectively compared with the RANSAC algorithm. The F1 score values of the cottage’s and pantry’s plane segmentation using the proposed method reached 97.56% and 95.75%, respectively (Table 6).

From the above analysis, the region growing algorithm cannot separate the coplanar points of two planes, and the RANSAC algorithm causes the plane to become over-segmented. Most research combined the region growing algorithm with other approaches to detect building planes. Our idea is how to accurately extract the coplanar points of two planes that cannot be separated by region growing algorithm. The traditional way to get the coplanar points of two planes is to calculate the distance from the uncoarse extraction plane points to the coarse extraction planes. Because the boundary information can express the object’s shape feature, our idea is that the coplanar points where two planes intersect were obtained from the distance threshold from the uncoarse extraction plane points to the coarse extraction plane’s boundary points. Our method is to optimize the region growing algorithm in extracting the coplanar points at the intersection of two planes. The algorithm can accurately segment the intersection planes formed from different angles because the region growing algorithm uses normal vector and curvature to segment the coarse extracted plane points, and the distance algorithm can obtain the coplanar points of the intersection of two planes.

5. Conclusions

We proposed an effective building plane segmentation algorithm, where the region growing algorithm coarsely segments the building plane. The coplanar points where two planes intersect were determined from the distance threshold from the uncoarse extraction plane points to the coarse extraction plane’s boundary points. The building plane’s optimal segmentation could be obtained by combining the coarse extraction plane points with the corresponding coplanar points. The results show that the proposed method can segment the plane points of a cottage and pantry. The optimal distance thresholds using the proposed method from the uncoarse extraction plane points to each plane boundary point of the cottage and pantry were 0.025 m and 0.030 m, respectively. The highest correct rate and the highest error rates of the cottage’s and pantry’s plane segmentations using the proposed method under the optimal distance threshold were 99.93% and 2.30% (98.55% and 2.44%), respectively. The F1 score values of the cottage’s and pantry’s plane segmentations using the proposed method under the optimal distance threshold reached 97.56% and 95.75%, respectively. Compared with the RANSAC algorithm, the proposed method can segment different objects on the same plane without causing excessive segmentation. The method can also extract coplanar points where two planes intersect that cannot be separated using the region growing algorithm. Although the RANSAC-RG method combining the RANSAC algorithm and region growing algorithm can optimize the segmentation results of the RANSAC (region growing) algorithm and has little difference in segmentation effect (especially for cottage data) with the proposed method, the method still loses coplanar points at some intersection of the two planes. Future tests of this approach will be conducted on buildings with large and complex scenes.