Next Article in Journal
Monitoring Cropland Phenology on Google Earth Engine Using Gaussian Process Regression
Next Article in Special Issue
Attributing the Evapotranspiration Trend in the Upper and Middle Reaches of Yellow River Basin Using Global Evapotranspiration Products
Previous Article in Journal
High-Precision Digital Surface Model Extraction from Satellite Stereo Images Fused with ICESat-2 Data
Previous Article in Special Issue
Impact of Climate Change on the Hydrological Regime of the Yarkant River Basin, China: An Assessment Using Three SSP Scenarios of CMIP6 GCMs
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 1
10.3390/rs14010145
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

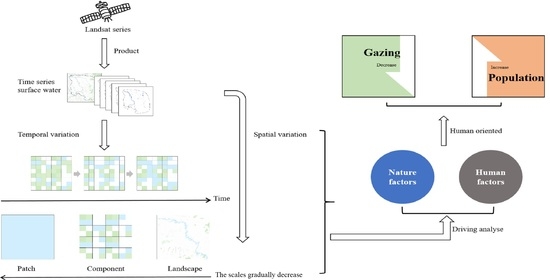
Modelling Dynamic Hydrological Connectivity in the Zoigê Area (China) Based on Multi-Temporal Surface Water Observation

by
Chao Gao
1,2,
Chang Huang
1,3,4,*,
Jianbang Wang
5 and
Zhi Li
2
1
Shaanxi Key Laboratory of Earth Surface System and Environmental Carrying Capacity, Northwest University, Xi’an 710127, China
2
College of Natural Resources and Environment, Northwest A&F University, Xianyang 712100, China
3
Institute of Earth Surface System and Hazards, Northwest University, Xi’an 710127, China
4
College of Urban and Environmental Sciences, Northwest University, Xi’an 710127, China
5
College of Earth and Environmental Sciences, Lanzhou University, Lanzhou 730000, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(1), 145; https://doi.org/10.3390/rs14010145
Submission received: 19 November 2021 / Revised: 21 December 2021 / Accepted: 27 December 2021 / Published: 29 December 2021
(This article belongs to the Special Issue Remote Sensing for Climate Extremes and Water Resources)
Browse Figures
Versions Notes

Abstract

:
The sustainability of wetlands is threatened by the past and present land use practices. Hydrological connectivity is one of the most important aspects to consider for wetland rehabilitation planning purposes. Circuit theory and connectivity indices can be used to model and assess hydrological connectivity. The aim of this study was to assess spatiotemporal variation in the hydrological connectivity of the Zoigê area from 2000–2019 using both methods. The study area contains a Ramsar wetland of international importance, namely the Sichuan Ruoergai Wetland National Nature Reserve. We used a global surface water observation product as the major input for both methods, and then analyzed the temporal and spatial characteristics, in terms of important components and patches. We found that the overall connectivity has increased slightly in the last 20 years, while the probability of connection between patches of surface water has increased significantly. Important components and patches represent steppingstone habitat for the dispersal of organisms in the landscape. The main determinants of hydrological connectivity are mostly human oriented, predominantly a decrease in large livestock population size and population increase.

Graphical Abstract

1. Introduction

The hydrological connectivity of a river basin is the interconnected network of pathways in a river landscape where water is exchanged in longitudinal, lateral, vertical, and temporal dimensions [1]. It is a key factor for water-mediated transfer of matter, energy, and/or organisms within or between elements of the hydrological cycle [2]. It plays an important role in promoting the formation, development, succession, and stability of lotic and lentic ecosystems [1,2,3,4]. Hydrological connectivity can be affected by climate change and human activities. Habitat patches could be reduced or fragmented, and thereby interfere with the original river network, solute and sediment transmission, microorganisms, and ecological processes, which would ultimately lead to degradation and loss of associated ecoservices [4]. Consequently, in order to maintain these ecoservices, or enhance them, the hydrological connectivity needs to be maintained, or improved, as much as possible [5,6].
Hydrological connectivity, or called river continuum, was first described in the 1980s [7]. Since then, different scholars working in the fields of landscape ecology [8,9], aquatic ecology [10], watershed ecology [11], and hydrology [12,13] have investigated the importance of hydrological connectivity to ecological processes. It is generally agreed that hydrological connectivity mediates the ecological processes within and between different landscape units and is a systematic index that integrates processes taking place in the physical and biological environments. GIS, field monitoring, and modelling using software applications can all be used to understand these processes. With the development of “3S” technology, graph theory, and ready availability of remotely sensed time series data, the modelling of connectivity in spatiotemporally dynamic environments has become increasingly popular [14]. Circuit theory and connectivity indices are both based on graph theory. They can be used to identify the relationship between habitat elements and ecological processes and have become the main means to evaluate connectivity [15]. Both approaches have inherent strengths and weaknesses. For example, circuit theory is good for measuring spatio-temporal changes in connectivity and expressing the potential spatially connected functionality [16,17], but it is not suitable for portraying connectivity at patch and component levels [18]. Connectivity indices are more useful for measuring dynamics of connectivity at component and patch scales and evaluating the temporal changes in connectivity at landscape scale. It cannot be used to identify potential functional connectivity and quantify the physical connections within hydrological networks [4,18]. Therefore, we used both circuit theory and connectivity indices to obtain a comprehensive understanding of hydrological connectivity.
The Zoigê area is located in the eastern part of the Qinghai–Tibetan Plateau. It is an important component for maintaining the plateau ecosystem and global climate and plays an important role in water conservation and ecological balance [19,20]. Human activities and global climate change have had an impact on the hydrology of this fragile ecological environment [21]. In the last few decades, the Zoigê area has experienced a remarkable reduction in surface water, transforming many swamps into terrestrial grasslands [20,22].
Altered hydrological conditions impact local livelihoods, especially livestock farming, and may lead to further degradation of the ecological environment [21]. Therefore, ecological issues in the Zoigê area have aroused wide attention in recent years, for example wetland information extraction [23], wetland degradation [24], and vegetation change [25]. This has potentially major consequences for inter alia, the health of a Ramsar wetland of international importance located in the region (i.e., Sichuan Ruoergai Wetland National Nature Reserve), and for habitats of the Near Threatened Black-necked Crane (Grus nigricollis). The transformation of wetlands to terrestrial grassland also has potentially significant implications for the desiccation of peatlands, release of methane (a major greenhouse gas), and loss of soil carbon. Most studies in the area have been carried out at a landscape level, with sub-landscape scale research relatively rare [25].
This study aimed to evaluate the hydrological connectivity of the Zoigê area using a combination of circuit theory and connectivity indices, both of which are based on graph theory, at a variety of spatial and temporal scales. Through this study, we tried to answer the following scientific questions: (1) How has the hydrological connectivity of the Zoigê area changed in the last 20 years? (2) What are the main determinants of hydrological connectivity in this region?

2. Materials and Methods

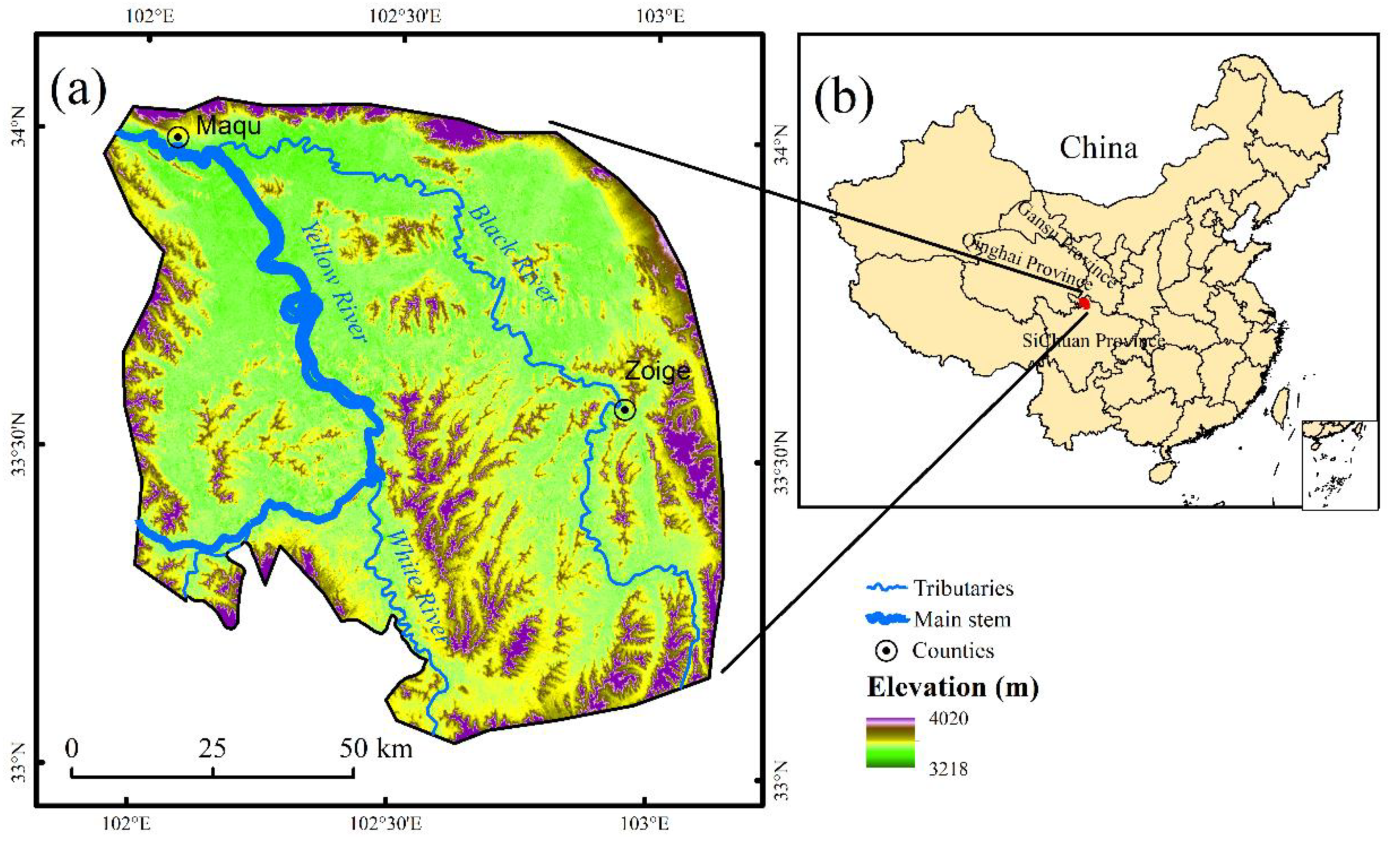
2.1. Study Area

The Zoigê area is located between the latitudes of 33°02N–34°03N and longitudes of 101°55E–103°09E (Figure 1). It is located in northern Sichuan, at the eastern end of the Qinghai–Tibet Plateau. Administrative regions include Zoigê County and Hongyuan County in Sichuan Province, and Maqu County and Luqu County in Gansu Province. The region has an alpine and monsoon climate, with a mean annual temperature of 0.9°–2.5°, and a mean annual precipitation of 500–800 mm (Table A1). The three largest rivers in the study area are the Yellow River, Black (Heihe) River, and White (Baihe) River. The Black River and White River are tributaries of the Yellow River. This region is rich in biodiversity, with the vegetation dominated by subalpine meadows and swamp vegetation [22]. Alpine bog, alpine peat, and alpine meadow soils have developed extensively in the area, mainly along the middle and lower gully reaches of the Black River Basin and Lake depressions, with perennial, seasonal, and temporary water logging [20]. Most (83%) local people in the Zoigê are Tibetan pastoralists who have depended on the grasslands for livestock grazing (e.g., yaks, sheep, and horses) [26].

2.2. Data Sources

In this study, five types of data were used. They were obtained from the following sources:
  • Surface water data were obtained from the global surface water dataset (GSWD) (resolution: 30 m) of the Joint Research Centre using Google Earth Engine (https://code.earthengine.google.com, accessed on 18 November 2021) (dataset: JRC/GSW1_3/YearlyHistory) [27].
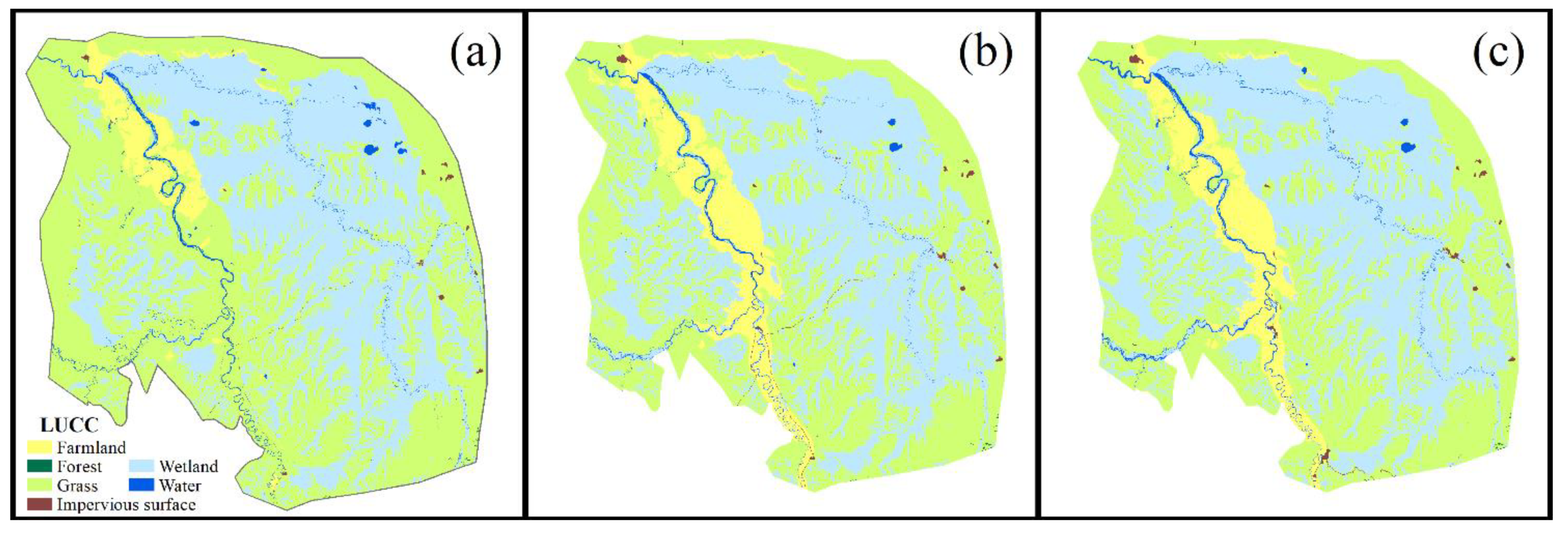
  • Land cover (LUCC) data (Figure A5) were obtained from the Global 30 dataset which has a spatial resolution of 30 m (http://www.globallandcover.com/, accessed on 18 November 2021).
  • Digital elevation model (DEM) (resolution: 30 m) data were obtained from the Geospatial Data Cloud (http://www.gscloud.cn/, accessed on 18 November 2021).
  • For the dynamic hydrological connectivity driver analysis, surface meteorological data were obtained from the China Meteorological Administration (http://data.cma.cn/, accessed on 18 November 2021).
  • Socioeconomic data were obtained from the local Sichuan provincial Bureau of Statistics.

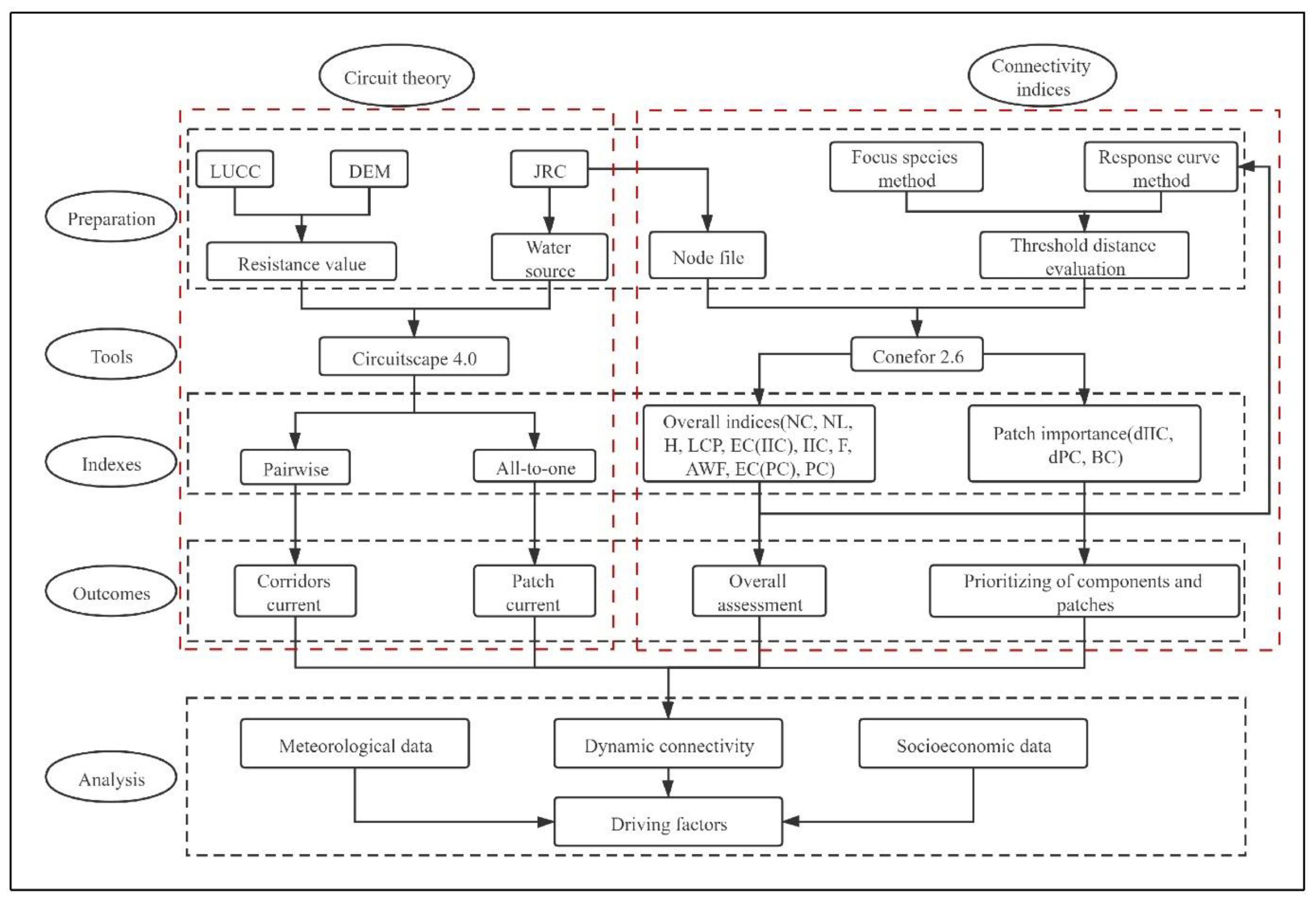
2.3. Data Analysis

Circuit theory was used to reveal landscape scale hydrological connectivity, while connectivity indices were used to quantify hydrological connectivity at a patch scale. Water bodies larger than 10 ha in the JRC data were used as the source data for circuit theory-based analysis. The LUCC and DEM data were used in conjunction with each other to determine a resistance value. The pairwise and all-to-one modes in Circuitscape 4.0 were then used to obtain current maps for the corridors and patches, respectively. For the calculation of the connectivity indices, the node file used the same JRC data, with the threshold distance determined according to the focus species and response curve methods. All connectivity indices were calculated in Conefor 2.6 [28]. The overall assessment was determined by calculating selected indices, namely the Number of Components (NC), the Number of Links (NL), the Harary index (H), the Landscape Coincidence Probability (LCP), the Integral Index of Connectivity (IIC), the Flux (F), the Area Weighted Flux (AWF), the Probability of Connectivity index (PC), the EC (IIC), and the EC (PC). The EC (IIC) and EC (PC) were computed as the square root of the numerator of the IIC and PC, respectively. Overall indices were also used to fit a response curve. The prioritization of components and patches were determined according to indices of patches, including dIIC, dPC, and Betweenness Centrality (BC). The dIIC and dPC were determined by removing individual patches from the landscape and quantifying the corresponding decrease in connectivity. The calculation of these indices can be referred to Appendix D. Finally, we evaluated the driving factors of dynamic connectivity according to meteorological data and socioeconomic data. The specific method was shown in Figure 2.

2.3.1. Circuit Theory

McRae et al. (2006) were the first to apply Circuit Theory (developed in physics) to the field of ecology [29], with the Random Walk Theory used to simulate the relocation diffusion process of individual species or gene flow in the landscape. In 2008, McRae published papers in Ecology introducing circuit theory, application, model operation, etc. in detail [16], and then developed Circuitscape software with Viral Shah for circuit simulation. A detailed description of circuit theory and more application results can be found at https://circuitscape.org/, (accessed on 18 November 2021). In circuit theory, the current passes through the circuit from the source to the ground destination through the electric resistance range. Therefore, input files for circuit simulation include ecological source files and landscape resistance surface files.
Ecological sources are defined as habitats that support species survival and outward dispersal (i.e., sources vs sinks) [17]. We referred to the research carried out by Bishop-Taylor et al., who investigated landscape connectivity for aquatic habitats in the Murray-Darling Basin [14,30]. The ecological source in their study was “water source”, with the area of surface water patches used for water source identification. By taking into consideration the patch area and spatial distribution pattern of surface water in the Zoigê area, the minimum area of a water source patch was set as 10 ha. Setting the minimum habitat patch size can improve the computational efficiency and facilitate the simulation of hydrological connectivity at a large-scale [17,31]. In order to eliminate the influence of geometric shape and the spatial position of patches of surface water on the current value simulation, we extracted the central point position of water source patches for use as the input for current to point data for simulation.
Landscape resistance (resistance value) refers to the difficulty of species migration between different landscape units, which is usually inversely proportional to habitat suitability. According to the user guide of Circuitscape, the resistance value should have a minimum value of 1. It acts as a multiplier; thus, high resistance values reduce movement proportionally. In this study, landscape resistance refers to the difficulty of surface water diffusion between different land use types and different terrains. In reference to existing related research on the determination of resistance value [17,32,33,34], considering the actual situation in the Zoite area, the final resistance value (R) in this study was determined as being affected by land use types and topography (Equation (1)):
R = Ri × (1 + α × Si)
where Ri is the resistance value set by grid i according to the land use type (Table 1), Si is the percentage slope of grid i, which was extracted according to the DEM of each year, and α was the coefficient of resistance value for controlling slope, which was taken as 1 in this study.

2.3.2. Hydrological Connectivity Indices

Hydrological connectivity indices, including landscape scale overall connectivity indices and patch scale connectivity indices were calculated using the Conefor software. Overall connectivity indices are a measure of the connectivity of all patch pairs according to a specified connectivity index (e.g., IIC). Patch scale connectivity indices calculate the relative decline in value (%) of the indices after removal of a patch. The patch, as a contribution to maintaining connectivity between other habitat areas, was expressed as dIIC. The input files for calculating landscape connectivity indices are generated using the Conefor plugin for ArcGIS 10.2, including node files and connection files. In order to maintain consistency with the circuit model, the node file used the same surface water patch data as the circuit model, and the connection file calculated the edge-to-edge distance of patches of surface water, which can be automatically calculated using Conefor plug-in. Conefor software also required a distance threshold.
Diffusion distance is influenced by different study areas, different research objects, and other factors, so the threshold distance should be determined considering the diffusion ability of species in the study area. The Zoigê area has a good ecological environment and abundant species. Although many research results have been discussed for different species in different regions [32,35,36,37], the diffusion behavior of a large number of species is still unclear, and the research results in different regions cannot be directly used for reference. Studies have shown that more generic analysis of connectivity, using a range of different dispersal distances, should be used to balance the competing requirements of species-specific information in connectivity analysis and generality in the analysis [38,39]. Cui (2020) and Qi et al. (2017) used the NC and NL indices to determine the maximum threshold, and then used “Distance-Landscape Connectivity Metrics” curves based on the variables “alternative distances” and “connectivity indices” to find the critical threshold distances [18,40].
Connectivity indices included binary indices [NC, NL, H, LCP, EC (IIC), and IIC] and probability indices [F, AWF, EC (PC), and PC]. Binary indices were based on a binary connection model and hence were suitable for analyzing the network topology of habitat. The probability indices were based on a probability connection model and hence were suitable for analyzing the actual movement of species [40]. Considering the application evaluation of these indices and the importance of intermediary centrality indices (BC) in the evaluation of hydrological connectivity [35,41], we finally chose the indices IIC, PC, and BC to quantify hydrological connectivity. It is worth noting that the connectivity indices for patch scale are used to quantify the relative importance of patches, so we only need the relative index values of these patches, that is, the relative degree of decline (%) for the IIC and PC values after the loss of the patches, which are expressed by dIIC and dPC, respectively. The BC value was used to evaluate the frequency of the shortest path of a specific patch, which is a supplement to dIIC and dPC.
This study adopted the method used by Cui et al. (2020) [40] and Qi et al. (2017) [18], and selected 36 diffusion distances (30–20,000 m) to calculate the values for selected indices [NC, NL, H, LCP, EC (IIC), IIC, F, AWF, EC (PC), and PC]. The values for NC and NL were used to determine the maximum distance, using “Distance—Hydrological connectivity Metrics” curves. These curves were used the variables “alternative distances” and “connectivity indices” to find the critical threshold distances using the cubic polynomial. The distance values corresponding to the inflection point on each curve were averaged to obtain the final optimal distance threshold. We then calculated the IIC and PC indices from 2000–2019 at the optimal threshold distance to evaluate the interannual changes in hydrological connectivity over 20 years. Finally, we calculated the dIIC, dPC, and BC indices in 2000, 2010, and 2019 to identify important components and patches.

3. Results

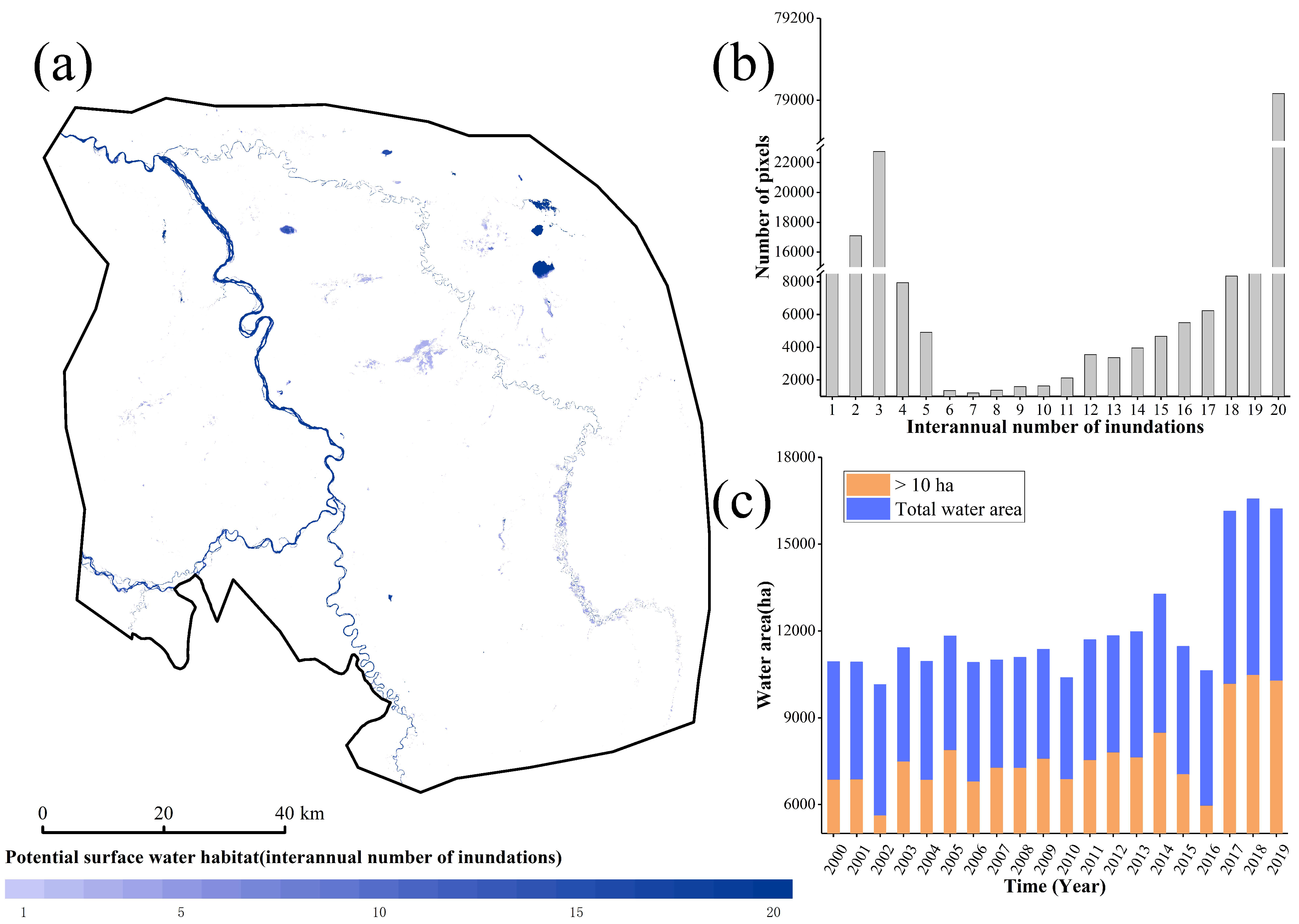
3.1. Surface Water Dynamics

There were a large number of patches of surface water, but most of these were small (<10 ha). In order to improve the calculation efficiency, we excluded patches with a surface area <10 ha. Only water bodies larger than 10 ha were selected for modelling the dynamic hydrological connectivity between water bodies. Further analysis revealed that the patches below the area threshold were usually distributed adjacent to a patch above the area threshold, so the spatial distribution characterization of the patches above the area threshold could be used to represent the spatial distribution characteristics of all patches (Figure 3a). Statistics for their inundation times found that the inundation frequency of most pixels was between 1–5 and 15–20 (Figure 3b). Counting the area ratios of patches above the threshold in the last 20 years, we found that the proportion of patches above the threshold was about 60%, while the minimum ratio and the maximum ratio were 55.23% and 66.66%, respectively. This could be used to characterize the interannual variation characteristics of the surface water (Figure 3c).

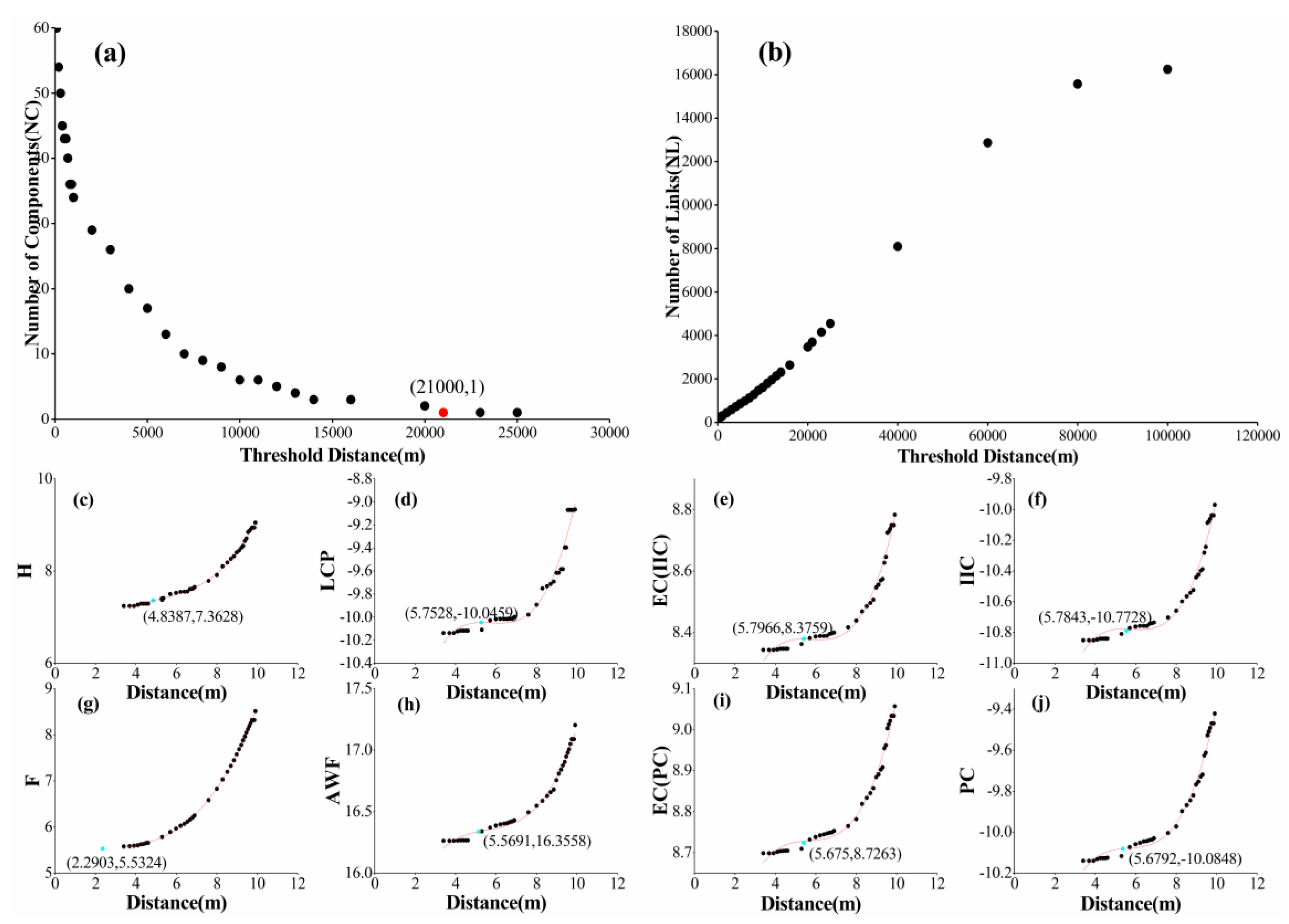
3.2. Optimal Threshold Distance

By choosing a threshold distance well-suited to our research objective, we could increase the accuracy of evaluation results. To find the optimal threshold distance, we calculated the connectivity indices of NC and NL at 43 distance values (from 30–2000 m). This step-wise approach was used to eliminate the value without ecological significance. When the NC and NL indices reached an extreme value with the increase of diffusion distance, an index value was no longer ecologically significant. The corresponding distance was regarded as the maximum diffusion distance for research purposes [18,40]. The NC valued decreased with an increase in the threshold distance. When the threshold distance reached 21,000 m, the NC value declined to 1, which indicated that all patches of surface water were connected directly or indirectly as a single component. The opposite was true for the NL value. When the distance was 120,000 m, the NL did not reach a maximum, but it tended to converge (Figure 4a,b). When the NL value reached the maximum, it indicated that a connection could exist between any two patches [18,40]. Therefore, the maximum distance with ecological significance was about 21,000 m.
Finally, 36 discrete distances within the range 30–20,000 m and the corresponding connectivity indices of H, LCP, EC (IIC), IIC, F, AWF, EC (PC), and PC were used to build the response curves, which marked the point of inflection on the curves. As the distance values were large and the values for the indices were small, we processed all the values logarithmically in order to get a good fit for the curves for the eight indices (Figure 4c–j). The fitting equations for the eight curves were given in Table 2. The R2 values for all curves were higher than 0.96 at the 95% level of significance. Of the distance values corresponding to the inflection points of the eight curves, the H and F indices values were abnormal, so the average value of the other six distance values were used to determine the optimal distance threshold for this study area, namely 300 m. Consequently, all connectivity indices in this study were calculated using 300 m as the optimal threshold distance.

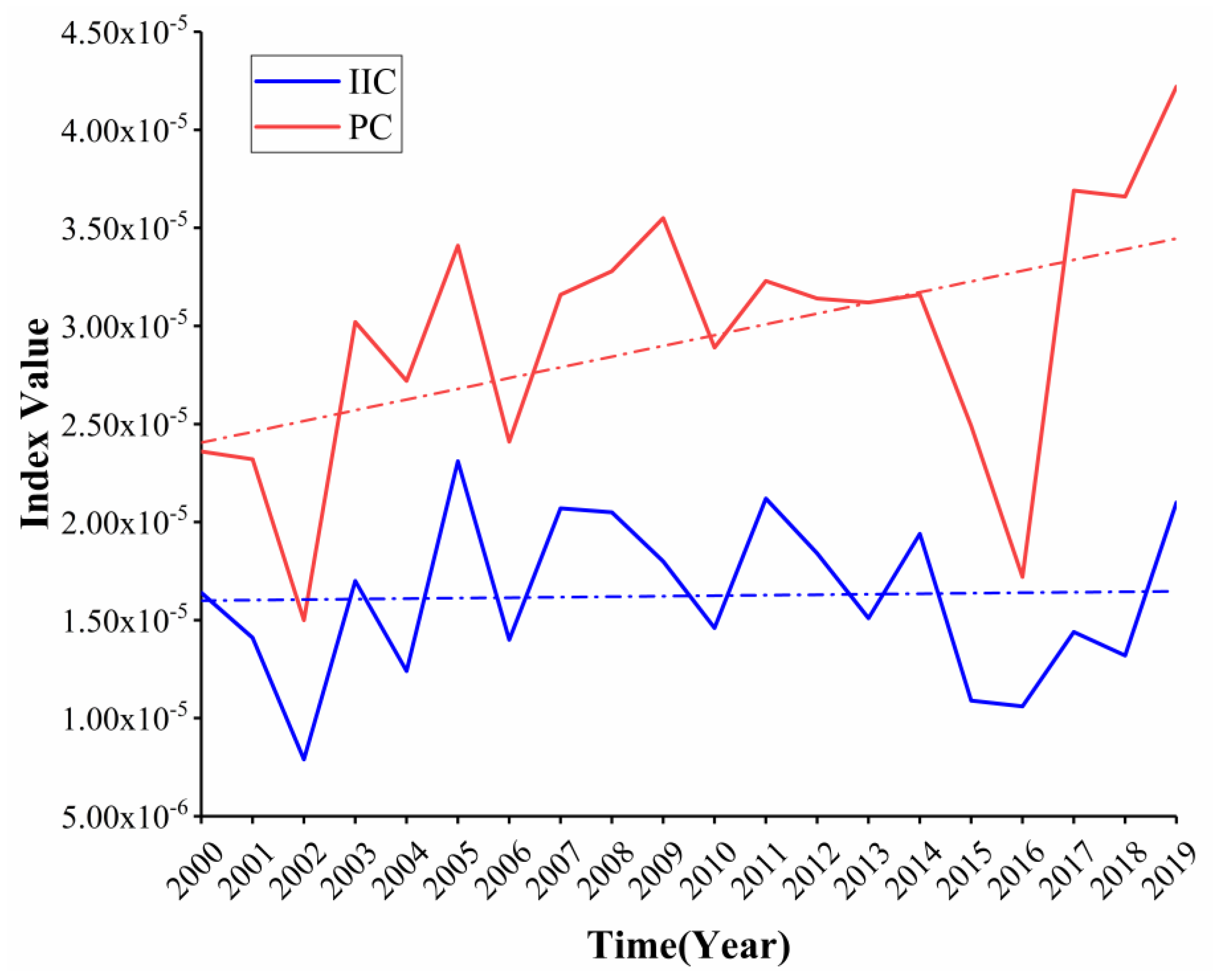
3.3. Annual Pattern of Hydrological Connectivity

We used both IIC and PC to evaluate the annual change of hydrological connectivity in the Zoigê area (Figure 5). The IIC values ranged from 5 × 10−6 to 2.5 × 10−5, trended slightly upward, with minimum and maximum values of 7.9 × 10−6 (2002) and 2.31 × 10−5 (2005), respectively. The PC values ranged from 1.5 × 10−6 to 4.5 × 10−5, trended significantly upward, with minimum and maximum values of 1.09 × 10−5 (2016) and 4.22 × 10−5 (2019), respectively. The IIC and PC values displayed very similar trends for the last 20 years, with the only notable differences for the periods 2008–2009 and 2015–2016. There was a trade-off relationship between the IIC and PC in 2008–2009, with both the IIC and PC decreasing in 2015–2016, although the PC decreased more than the IIC. Both the IIC and PC showed a local minimum in 2002. We compared the temporal variation of the IIC and PC indices (Figure 5) with the temporal variation in the area of surface water. We found that the patterns of variability for the three factors were similar over the last 20 years. We propose that the local minimum values for the IIC and PC indices in 2002 may be related to the reduction in surface water coverage in 2002. From 2008 to 2009 the IIC decreased, as the area of surface water and the PC increased. This indicated that as the surface water area increased, the overall connectivity of the study area decreased, although the probability of connectivity between patches increased. This may have been caused by the reclaiming of farmland on both sides of the Yellow River. IIC and PC exhibit a synergistic effect, similar to the relationship between actual evapotranspiration and potential evapotranspiration, which is why they have a significant correlation. In addition, from the definitions of IIC and PC (Appendix D), the biggest difference between IIC and PC is nlij and p ij * . When local patches are fragmented, nlij does not increase significantly, while the increasing rate of p ij *   is much greater than that of nlij. This is the explanation obtained from the formula regarding the significant correlation between IIC and PC. In general, landscape fragmentation was associated with increased hydrological connectivity. Furthermore, to increase farmland output, human activities had caused greater interference on farmland. In addition, the newly added farmland was originally grassland and located on both sides of the bank. This increased the potential connectivity between farmland but reduced the overall hydrological connectivity in the area.

3.4. Spatial Pattern of Hydrological Connectivity

3.4.1. Hydrological Connectivity at Landscape Scale

We used Circuitscape software to simulate the landscape scale current maps for the Zoigê area in 2000, 2010, and 2019. The higher the current value, the higher the importance of the grid for maintaining hydrological connectivity in the circuit (Figure 6). We used the all-to-one pattern to analyze the importance of patches in the study area and used the pairwise pattern to analyze the importance of corridors in the study area. From the result of the all-to-one pattern, the patches that affected hydrological connectivity were spatially heterogenous, with most distributed in the west and northeast of the study area. Of these patches, the most important in the west were the Yellow and White rivers, while in the northeast the most important were the isolated patches on both sides of the Black River. From the temporal series, the current value at the confluence of the Yellow River and the White River was significantly reduced, which was consistent with the scale of newly added farmland, indicating that as the area of farmland increased, the hydrological connectivity decreased in the study area. The new high current value region appeared in the middle of the study area, which indicated the importance of this region had greatly increased. The maximum current values in the three years were 438.60, 403.62, and 733.51, respectively, reflecting the change in the importance of the patches with high current values to the hydrological connectivity of the study area. We compared the current maps of the patches with the IIC of the same period in Figure 5 and found that the two have the same pattern of temporal variation, indicating the importance of the patches for the characterization of overall connectivity in the study area.
From the results of the pairwise pattern analysis, the important hydrological corridors in the study area could be classified as river course or non-river course corridors. Owing to the inherent characteristics of waterbodies, river courses were inevitably the primary connections between waterbodies. Therefore, river courses were the most important hydrological corridors connecting patches in the study area and should have high current values, except for the main stem of the Black River. Non-river course corridors were mainly located in the western part of the Yellow River floodplain and the northeastern part of the study area, with patch density being relatively low. In terms of the time series data analyzed, the corridors at the confluence of the Yellow River and the White River had decreased, as had their importance. The current value of the corridors in the northwest and middle of the study area had increased significantly, indicating that the hydrological connectivity in this region was probably increasing. We compared the corridors current map with the PC value of the same period in Figure 5 and found that the two display similar patterns of temporal variation. A comparison of the results for the between the patches current maps and IIC indices above indicated that the circuit model and the connectivity indices model had a good fit and hence could be used in combination.

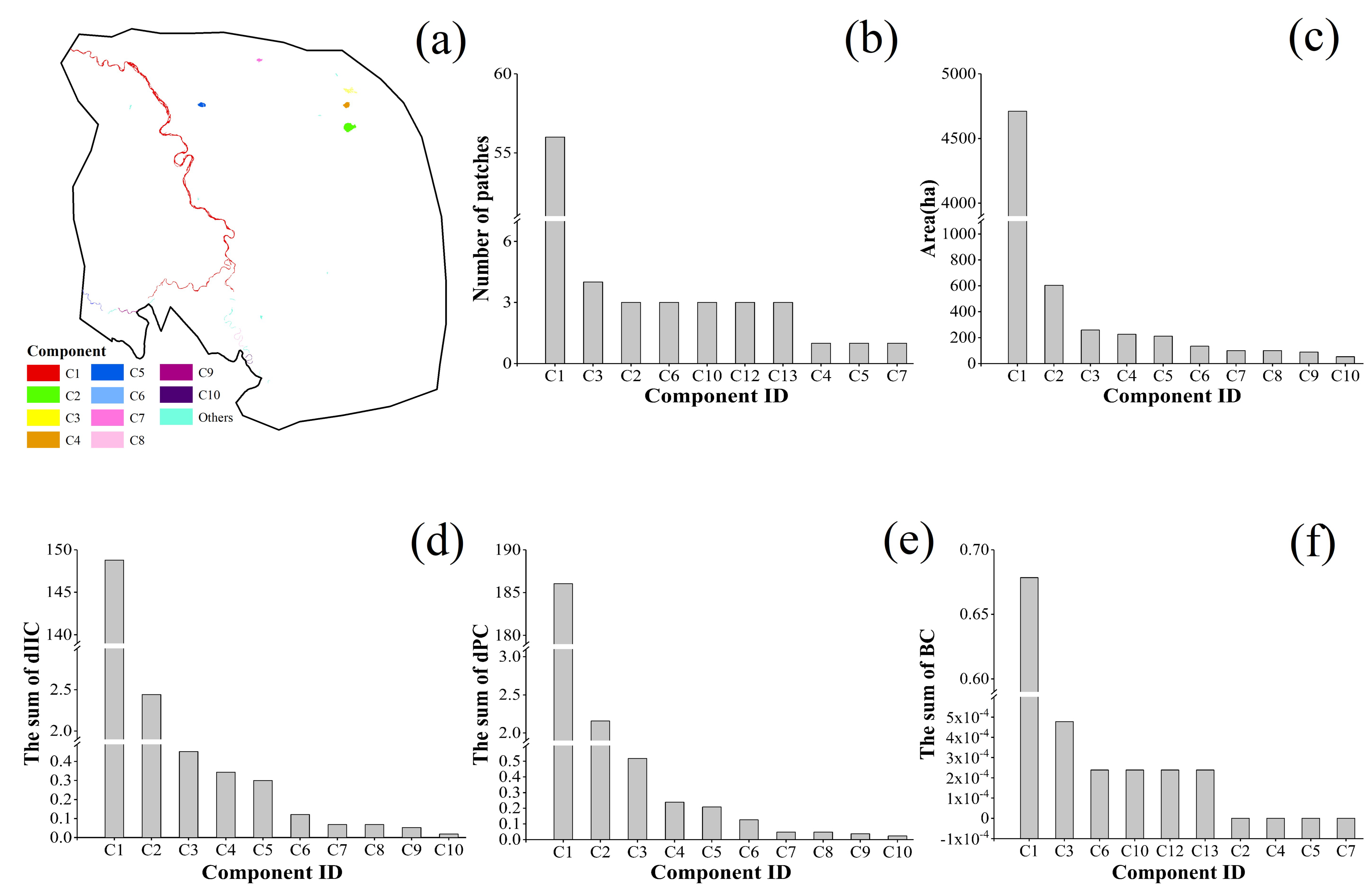
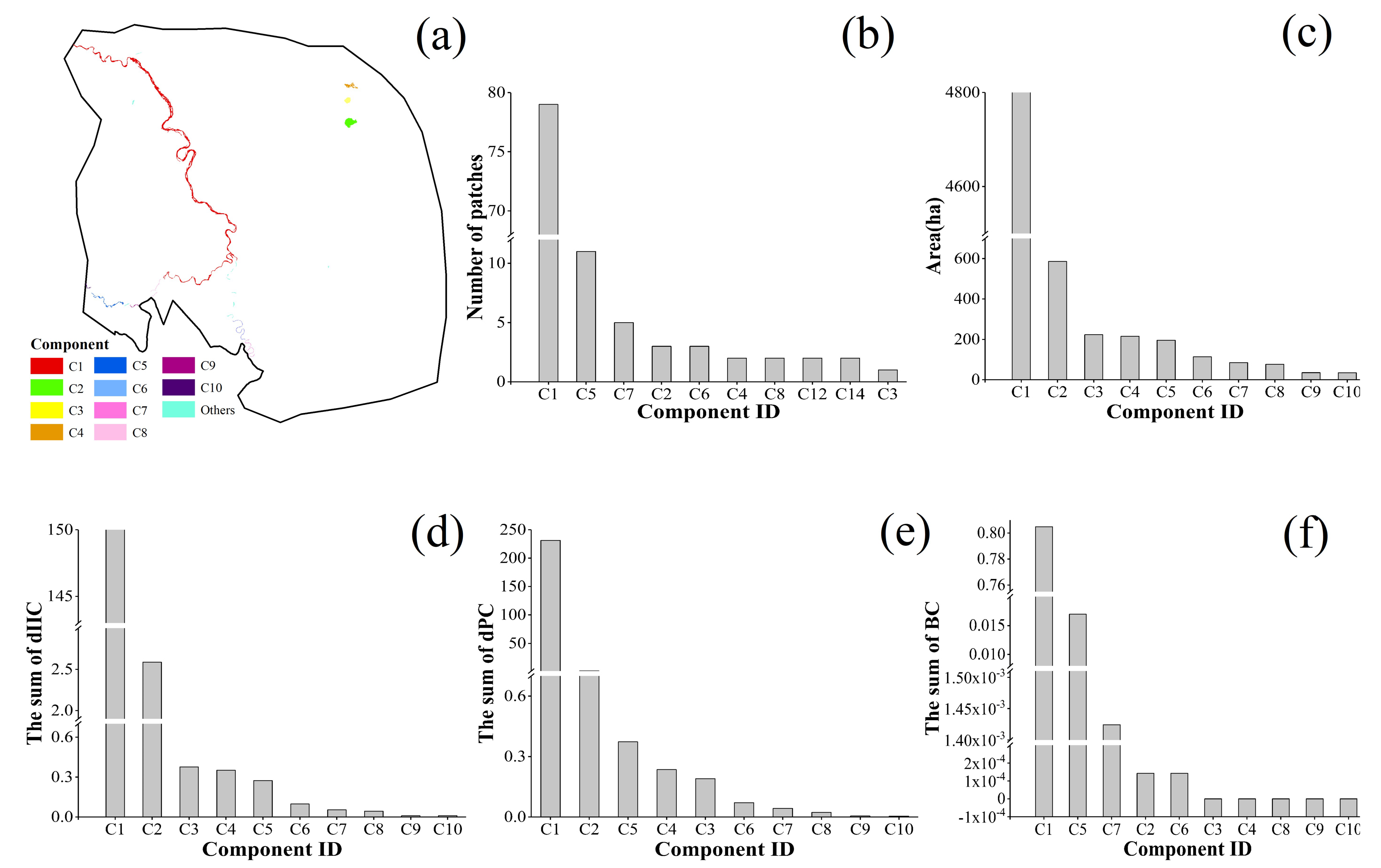
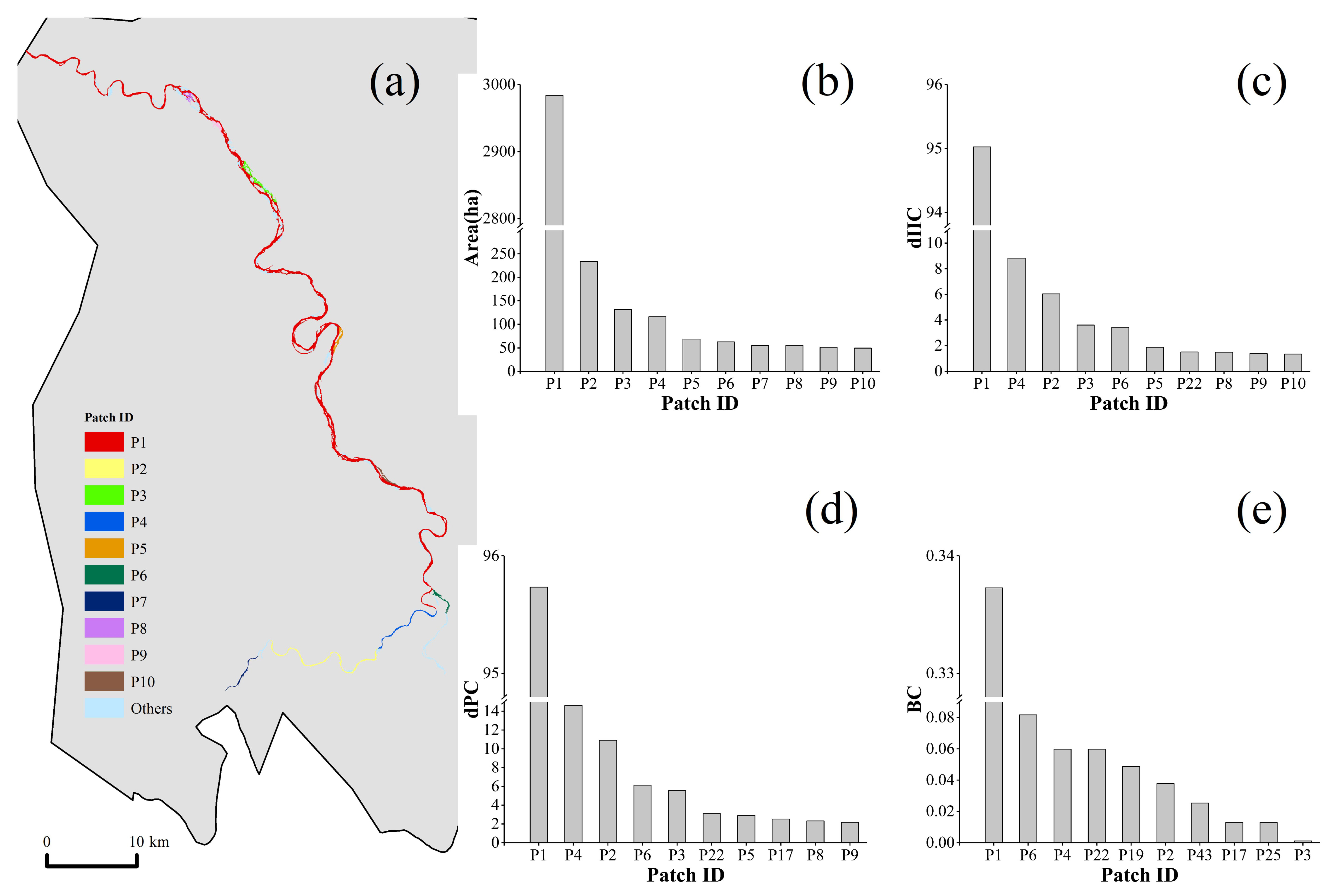
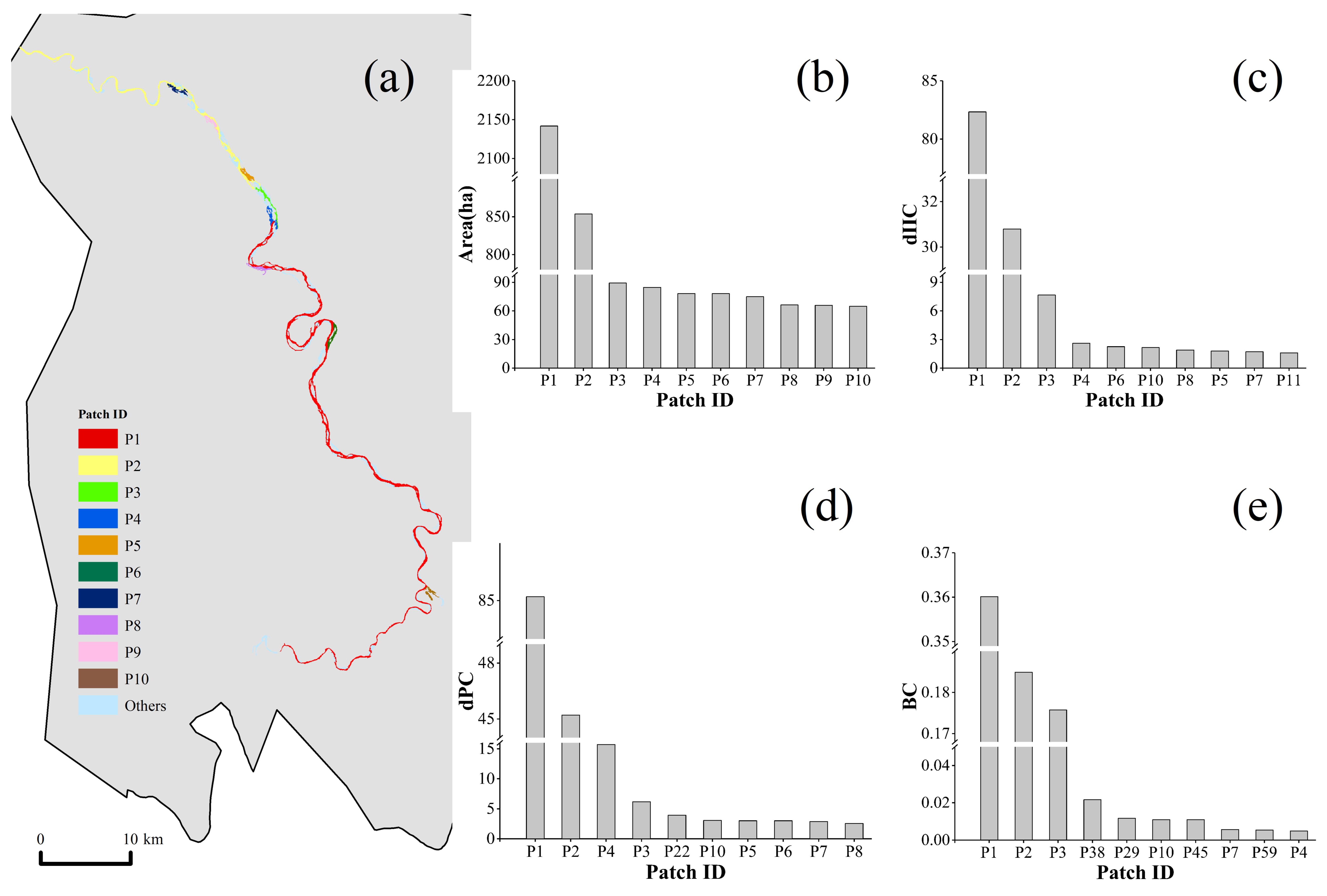
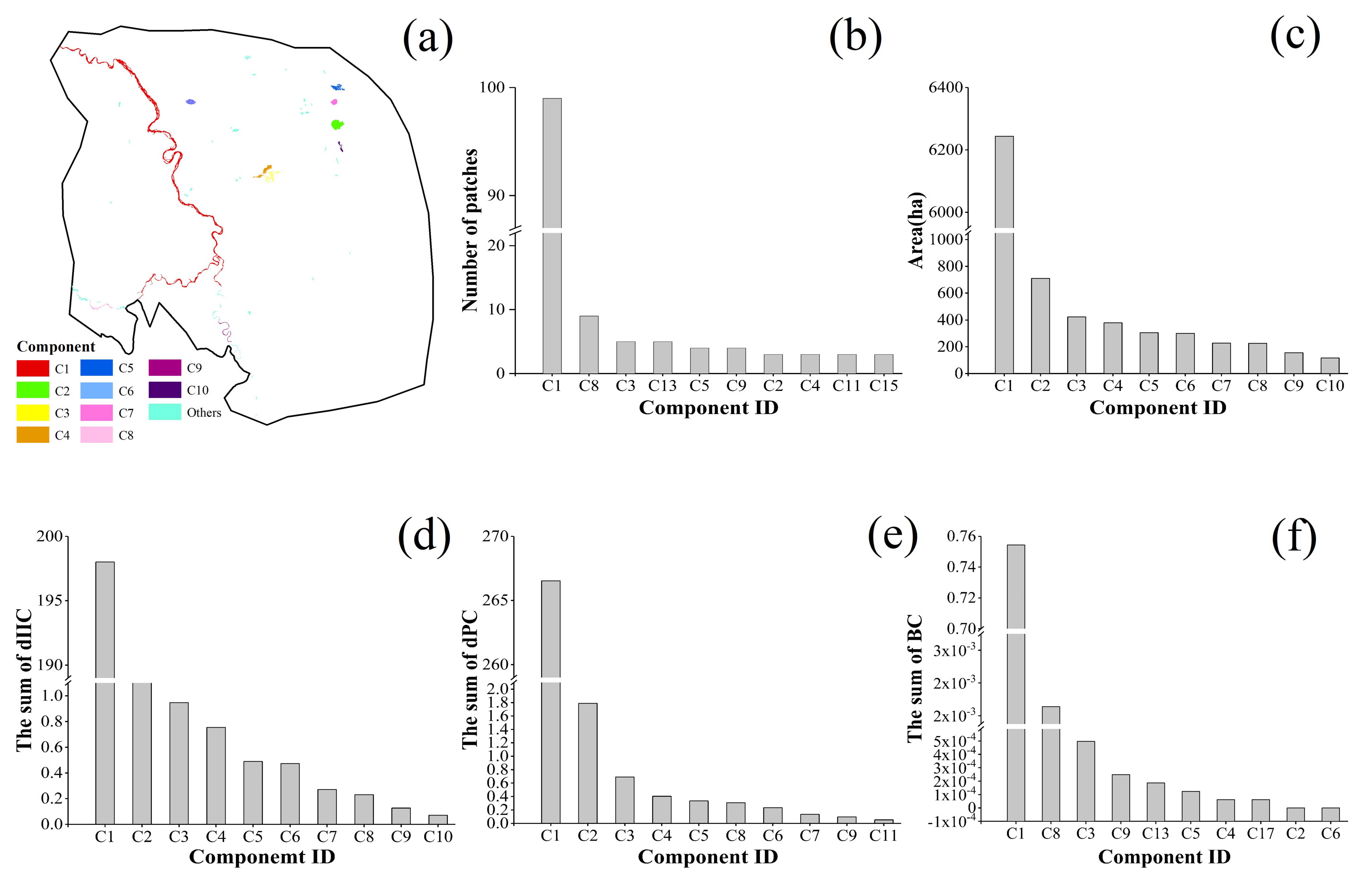
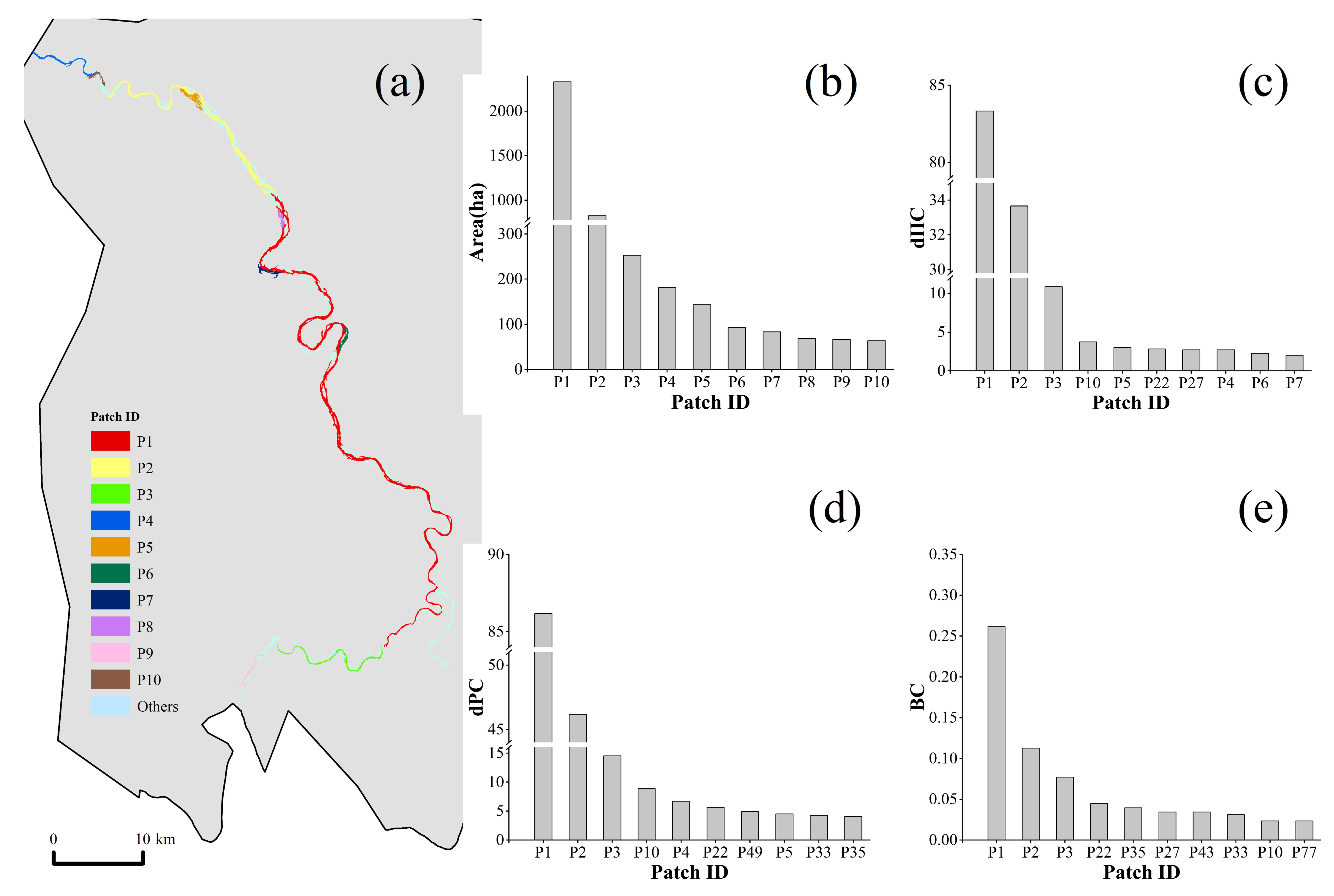
3.4.2. Important Components and Patches

Concentrations of patches are of great significance for maintaining and improving regional hydrological connectivity. We used Conefor software to divide all patches into several components, forming several big habitat patches at a large-scale [38]. Patch related indices that were calculated included the total number of patches per component (n), the total area of patches per component (ha), sum of dIIC, dPC, and BC. We sorted them in descending order in accordance with their surface area (viz. C1, C2, C3, etc.).

Important Components and Patches

The priority analysis of components could be used to determine the optimal components to use for further analyses (Appendix A Figure A1 and Figure A2 and Figure 7). The components, which were groups of patches connected together as a unit, are similar to big habitat patches at a large-scale [38,40]. The patches of surface water in 2019 could be divided into 50 components representing 50 big patches at a large-scale (Figure 7a). The number was significantly higher than in 2000 (25, Figure A1a) and 2010 (20, Figure A2a). C1 consisted of 99 patches with a combined area of 6244.02 ha, while the summation values for dIIC, dPC, and BC were 198.00, 266.53, and 0.75, respectively (Figure 7b–f). The values for four of the indices increased (BC was the exception), indicating that the importance of C1 was also increasing. In 2019, the total surface water area, the total water bodies larger than 10 ha, the IIC, and the PC increased, while the number of components with a BC value larger than zero increased to eight, which meant that those components acting as “steppingstone habitat” were increasing. This indicated that hydrological connectivity in the total study area had been improved significantly relative to conditions in 2000 (Figure A1b–f) and 2010 (Figure A2b–f).
We found that although some patches were relatively concentrated in space, they could be divided into different components. This indicated that these components may be isolated from each other in the landscape (taking the river course of the Yellow River in 2019, it could be divided into six components viz. C1, C8, C11, C13, C15, and C16), but the connectivity between them should have increased. In the northeastern and central part of the study area, the distribution of patches of surface water were relatively scattered, so it seemed easier to understand why they would be divided into different components. The main function of these smaller components in the study area was to provide steppingstone habitat, rather than to convey ecological flows, or form hydrological pathways. In the three years, the BC values of many components were > 0 (such as C3 in 2019), which indicated that several components were connected through this component. These components may not only be located near C3 but may also come from a greater distance. The loss of this type of habitat may affect the surrounding components connected to it. However, some components had a BC value of zero, indicating that no component was connected through this component, and that this component was completely isolated. This completely isolated component became the only habitat in the surrounding zone. The loss of this type of habitat may have a more serious impact on the small zone nearby, because there was no other habitat nearby that can provide service.

Important Patches

As C1 in each year was considered the most important component for the total hydrological connectivity, we used the same indices to identify the importance of the patches in the C1 component and arrange them in descending order in accordance with the size of the area (viz. P1, P2, P3, etc.). The C1 component was composed of 56, 79, and 99 patches of surface water (Figure A3a, Figure A4a and Figure 8a). Of these patches, the most important patch in each year was P1, which had the largest values for area, dIIC, dPC, and BC (Figure A3b–e, Figure A4b–e and Figure 8b–e). In terms of temporal variation, the area dIIC and dPC of P1 first decreased and then increased, indicating that the contribution of P1 to maintaining and improving regional connectivity first decreased and then increased, with the steppingstone function of P1 first increasing and then decreasing. C1 was the most important component in the study area. We further evaluated the important patches of surface water in C1. When the various indices for the patches were within 10% of this year, these patches were considered the most important patches. Therefore, the most important patches in 2000 were P1, P2, P4, and P6. In 2010 the most important patches were P1, P2, and P3. Lastly, the most important patches in 2019 were P1, P2, P3, and P10.

3.5. Determinants of Dynamic Connectivity

To analyze the determinants of hydrological connectivity, we calculated the grey degree of correlation between hydrological connectivity and major climate factors and human activities, respectively. Grey relational analysis is a quantitative method for measuring the degree of correlation between different factors and is suitable for quantitative analysis of a dynamic development process [22,24]. Taking into account the availability of data and the actual situation in the study area, we selected six impact factors for evaluation (Appendix B). Table 3 shows the grey degree of correlation between hydrological connectivity and these factors. The results indicated that the size of the population of large livestock and size of the human population had the greatest impact on hydrological connectivity in the Zoigê area, followed by annual precipitation, area of farmland, and mean annual temperature.
We found that the area of farmland first decreased and then increased, the large livestock population increased first and then decreased, while the other factors trended upward. The six factors, with the exception of annual precipitation, had a negative impact on hydrological connectivity. Therefore, an increase in annual precipitation and a decrease in large livestock population size were associated with an increase in hydrological connectivity, while climate warming and human activities all had an adverse effect on hydrological connectivity.
Most of the increase in farmland could be attributed to cultivation on the floodplain of the Yellow River (Appendix C). Most of the artificial surfaces and wetlands were located in the Black River Basin. Therefore, the increase in farmland area mainly affected the hydrological connectivity on both banks of the Yellow River, while other human activity factors mainly affected the hydrological connectivity in the Black River Basin.
Finally, we compared the nature of the changes in surface water and hydrological connectivity (Figure 3 and Figure 5) and found that the interannual variation of surface water and PC were similar, indicating that an increase in surface water was also one of the important factors leading to an increase in hydrological connectivity. Studies have shown that a large number of artificial ditches have been constructed in the Zoigê area to convert marshes into grasslands. This drainage network has caused wetland degradation and a continuous reduction in groundwater levels. This may have affected the hydrological connectivity in this region [21,24,42]. Artificial ditches can increase the hydrological connectivity in the short term but reduce the quality and area of wetlands and lower the adjacent water table. In the long run, this approach will damage human well-being and is not in line with the concept of sustainable development.

4. Discussion

Hydrological connectivity is an important component of aquatic ecosystems and hence provision of associated ecosystem services. It should therefore also be an important component of water management planning and conservation planning for freshwater habitats. Similarly, methods used to assess hydrological connectivity could be used to prioritize wetland rehabilitation interventions. In this study, we have used the research results of the two models [14,18,40], and integrated the models to evaluate dynamic hydrological connectivity in the Zoigê area. Grey relational analysis revealed the driving factors for the dynamic hydrological connectivity. We mainly use the connectivity indices to quantitatively evaluate hydrological connectivity, because it can accurately describe connectivity at the sub-landscape scale, in forms of either a component or a patch. For qualitative analysis, we adopted the simulation results of the circuit model, due to its good expression of potential spatial connection at the landscape scale.
While we have demonstrated the significant advantages provided by the methods used in this study to evaluate dynamic hydrological connectivity, the sources of the remote sensing data can have their own sources of error and bias with important implications for the analysis of hydrological connectivity. It would not have been possible to detect ephemeral (short-duration) waterbodies that were only present between dates for which JRC data was available. The spatial resolution of Landsat data would also have defined the lower limit for the detection of small waterbodies (<900 m2). In addition, optical remote sensing is limited by cloud cover and topography, particularly in mountainous areas with high relief. Although we used spatial data that had been subjected to a statistically rigorous validation process, the presence of cloud cover may not have been completely eliminated [27,43]. As the vegetation cover in the Zoigê area is relatively high, and waterbodies with a vegetation cover were easily classified as vegetation, it could have affected the results of the connectivity evaluation.
The data processing limit of the circuit model was 6 million pixels [33]. The computation time cost of the connectivity indices increases exponentially as the number of “source” increases. In order to improve the computational efficiency, we discarded water bodies smaller than 10 ha. Although we demonstrated that the errors associated with the temporal and spatial distribution characteristics of all patches, represented by patch size above the threshold, were within the acceptable range, potential errors may not have been eliminated by this treatment of the data. We also possibly ignored the influence of temporal changes in the resistance of the intervening landscape matrix between habitats as there is no reliable method to study how changes in landscape resistance to movement affect connectivity at present [14]. Finally, we may have ignored the impact of smaller water bodies (<10 ha) on the spread of certain specific species, even though the types or numbers of these species are likely to be relatively small.
Our study only considered surface water and ignored the recharge of groundwater to surface water. There are a large number of artificial ditches in the northeastern part of the Zoigê area, which facilitate the drainage of groundwater. However, the role of connected artificial ditches in draining water from peatland mainly occurs during the dry season of the year in the Zoigê area, which means that we may not be able to monitor some flooding events [43].
This study proves the applicability of both models for watershed scale hydrological connectivity modelling, but they cannot be directly applied to very large scales due to the computational limitation. The rise of remote sensing cloud-computing platforms (e.g., GEE) has greatly improved computing efficiency, and has revolutionized the application scope and spatio-temporal scale of remote sensing big-data. Therefore, GEE-based circuit model and connectivity indices modeling may be one of the effective methods to solve the above limitations.

5. Conclusions

Based on a GSWD product available through the GEE, changes to hydrological connectivity in the Zoigê area for the period 2000–2019 were evaluated using circuit theory and connectivity indices. Our results allowed us to conclude the following:
(1) The combination of circuit theory and connectivity indices can be used to effectively model dynamic hydrological connectivity, which provides useful tools for the evaluation of hydrological connectivity.
(2) The optimal threshold distance for hydrological connectivity in the Zoigê area was 300 m. When the threshold distance was 300 m, the overall connectivity in the study area at the landscape scale increases slightly, while the probability of connection between patches of surface water increases significantly. On the component scale and patch scale, we have identified the most important components and patches, which mainly play the role of steppingstone habitat for the dispersal of organisms in the landscape.
(3) Climate change and human activities have jointly led to changes in the hydrological connectivity pattern of the Zoigê area, but the impact of human activities has been the most significant. Of these factors, the increase in annual precipitation and the decrease in large livestock population had a positive impact on hydrological connectivity, while the other factors had a negative impact.

Author Contributions

Conceptualization, C.H. and C.G.; methodology, C.G.; software, C.G.; validation, C.G.; formal analysis, C.G. and J.W.; investigation, C.G. and C.H.; resources, C.G. and Z.L.; data curation, C.G.; writing—original draft preparation, C.G.; writing—review and editing, C.H. and Z.L.; visualization, C.G. and J.W.; supervision, C.H.; project administration, C.H. and C.G.; funding acquisition, C.H. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the Shaanxi Natural Science Foundation (2021JM-314), and the National Key R&D Program of China (2017YFC0404302).

Acknowledgments

We are very grateful to the anonymous editor of Mogo for touching up the manuscript and providing valuable suggestions. We would also like to thank the anonymous reviewers for their valuable comments that helped us improve the manuscript greatly.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Remotesensing 14 00145 g0a1 550
Figure A1. Statistics of different indices for the top 10 components in terms of connectivity for 2000. (a) Distribution of components, (b) Number of patches (n), (c) Area of components (ha), (d) The sum of dIIC, (e) The sum of dPC, and (f) The sum of BC. C1 = Yellow River floodplain, C2 = Haqiucuogan, C3 = Cuonidajian, C4 = Cuorewajian, C5 = Xingcuo, C6 = Yellow River floodplain @ Cairimaxiang (west), C7 = Mucuogan, C8 = White River floodplain (north), C9 = Yellow River floodplain @ Cairimaxiang (east), C10 = White River floodplain (south).
Figure A1. Statistics of different indices for the top 10 components in terms of connectivity for 2000. (a) Distribution of components, (b) Number of patches (n), (c) Area of components (ha), (d) The sum of dIIC, (e) The sum of dPC, and (f) The sum of BC. C1 = Yellow River floodplain, C2 = Haqiucuogan, C3 = Cuonidajian, C4 = Cuorewajian, C5 = Xingcuo, C6 = Yellow River floodplain @ Cairimaxiang (west), C7 = Mucuogan, C8 = White River floodplain (north), C9 = Yellow River floodplain @ Cairimaxiang (east), C10 = White River floodplain (south).
Remotesensing 14 00145 g0a1
Remotesensing 14 00145 g0a2 550
Figure A2. Statistics of different indices for the top 10 components in terms of connectivity for 2010. (a) Distribution of components, (b) Number of patches (n), (c) Area of components (ha), (d) The sum of dIIC, (e) The sum of dPC, and (f) The sum of BC. C1 = Yellow River floodplain, C2 = Haqiucuogan, C3 = Cuorewajian, C4 = Cuonidajian, C5 = Yellow River floodplain @ Cairimaxiang (west), C6 = White River floodplain (north), C7 = White River floodplain (south), C8 = Yellow River floodplain @ Cairimaxiang (east), C9 = Yellow River floodplain @ Cairimaxiang (middle), C10 = Yellow River floodplain @ Cairimaxiang (west).
Figure A2. Statistics of different indices for the top 10 components in terms of connectivity for 2010. (a) Distribution of components, (b) Number of patches (n), (c) Area of components (ha), (d) The sum of dIIC, (e) The sum of dPC, and (f) The sum of BC. C1 = Yellow River floodplain, C2 = Haqiucuogan, C3 = Cuorewajian, C4 = Cuonidajian, C5 = Yellow River floodplain @ Cairimaxiang (west), C6 = White River floodplain (north), C7 = White River floodplain (south), C8 = Yellow River floodplain @ Cairimaxiang (east), C9 = Yellow River floodplain @ Cairimaxiang (middle), C10 = Yellow River floodplain @ Cairimaxiang (west).
Remotesensing 14 00145 g0a2
Remotesensing 14 00145 g0a3 550
Figure A3. Statistics of different indices for the top 10 patches obtained from the results of connectivity modelling for 2000. (a) Distribution of patches (n), (b) Area of patches (ha), (c) dIIC, (d) dPC, and (e) BC.
Figure A3. Statistics of different indices for the top 10 patches obtained from the results of connectivity modelling for 2000. (a) Distribution of patches (n), (b) Area of patches (ha), (c) dIIC, (d) dPC, and (e) BC.
Remotesensing 14 00145 g0a3
Remotesensing 14 00145 g0a4 550
Figure A4. Statistics of different indices for the top 10 patches obtained from the results of connectivity modelling for 2010. (a) Distribution of patches, (b) Area of patches (n), (c) dIIC, (d) dPC, and (e) BC.
Figure A4. Statistics of different indices for the top 10 patches obtained from the results of connectivity modelling for 2010. (a) Distribution of patches, (b) Area of patches (n), (c) dIIC, (d) dPC, and (e) BC.
Remotesensing 14 00145 g0a4

Appendix B

Table
Table A1. Statistical data of Zoige County in 2000–2019.
Table A1. Statistical data of Zoige County in 2000–2019.
YearAnnual Precipitation
(mm)		Annual Average Temperature (°C)GDP
(104 yuan)		Farmland Area (ha)Number of
Livestock (Count)		Population
(Count)
2000596.41.23 21,7794725458,94564,075
2001597.11.68 22,8324743449,31565,444
2002548.21.50 24,9433664435,72365,923
2003764.72.27 26,8992775511,19966,551
2004655.61.51 36,5212934517,22466,504
2005666.42.01 41,9193075526,37969,882
2006529.42.54 47,0923086537,55370,283
2007613.72.02 55,8993089544,18971,850
2008468.71.64 59,6743714521,04173,353
2009571.32.53 73,0624006501,99774,602
20108522.72 85,1274162459,47875,791
20117052.28 99,9424162455,55776,477
2012749.62.53 116,0624243446,25970,000
2013770.52.77 130,4604121408,66177,900
2014720.62.73 139,1284202364,07278,400
2015541.42.65 153,6874172304,76478,100
2016601.32.86 164,2804171306,78677,400
2017705.12.88 175,9124171358,87578,741
2018790.82.83 187,5454170393,72478,000
2019718.52.79 259,0444170430,22977,000
Note: Missing data were shown in red, which were supplemented by a data fitting method.

Appendix C

Remotesensing 14 00145 g0a5 550
Figure A5. LUCC of Zoige region. (a) 2000, (b) 2010, and (c) 2019.
Figure A5. LUCC of Zoige region. (a) 2000, (b) 2010, and (c) 2019.
Remotesensing 14 00145 g0a5

Appendix D

Here lists definitions of the selected indices used in this study, which were obtained from Conefor’s User manual.
(1) Number of components (NC): A component (or connected region) is a set of nodes in which a path exists between every pair of nodes. Thus, there is no functional relation between nodes belonging to different components. An isolated node (patch) makes up a component itself. As a landscape gets more connected, it will present fewer components.
(2) Number of links (NL): As a landscape is more connected, it will present a larger total number of links (connections between habitat nodes in the landscape).
(3) Harary index:
H = 1 2 ∑ i = 1 n ∑ j = 1 ,   i ≠ j n 1 nl ij
where n is the total number of nodes in the landscape, and nlij is the number of links in the shortest path between patches i and j (shortest path in terms of topological distance, i.e., number of links). For patches that are not connected (belong to different components) nlij = ∞. Note that the case i = j is not included in the sum for H. As a landscape is more connected, it will present a higher H value.
(4) Landscape coincidence probability (LCP): LCP ranges from 0 to 1, increases with improved connectivity, and is computed as:
LCP = ∑ i = 1 NC ( c i A L ) 2
where NC is the number of components in the landscape, ci is the total component attribute (sum of the attributes of all the nodes belonging to that component), and AL is the attribute value that would correspond to a patch covering all the landscape with the best possible habitat (Here the AL equals total landscape area, namely area of the analyzed region, comprising both habitat and non-habitat patches). Therefore, LCP = 1 when all the landscape is occupied by water.
(5) Integral index of connectivity (IIC): IIC ranges from 0 to 1 and increases with improved connectivity. It is given by:
IIC = ∑ i = 1 n ∑ j = 1 n a i · a j 1 + nl ij A L 2
where n is the total number of nodes in the landscape, ai and aj are the attributes of nodes i and j, nlij is the number of links in the shortest path (topological distance) between patches i and j, and AL is the maximum landscape attribute. For nodes that not connected (belong to different components) the numerator in the equation for IIC equals zero (nlij = ∞). When i = j then nlij = 0 (no links are needed to reach a certain node from itself); this relates to the habitat availability concept that applies for IIC, in which a patch itself is considered as a space where connectivity exists. Here the IIC = 1 when all the landscape is occupied by water.
(6) Flux (F):
F = ∑ i = 1 n ∑ j = 1 , i ≠ j n P ij
where n is the total number of nodes in the landscape and pij is the probability of direct dispersal between nodes i and j. Note that the case i = j is not included in the sum for the F index.
p ij =   e − k · d ij
where dij is the distance between nodes i and j (as specified in the “Distances” connection file), pij is the probability of direct dispersal between nodes i and j (i.e., the probability that an organism is able to disperse a distance equal or larger than the distance between those nodes), and k is a constant set to make the function match to the probability-distance values specified by the user.
(7) Area-weighted flux (AWF):   AWF = ∑ i = 1 n ∑ j = 1 , i ≠ j n P ij · a i · a j .
(8) Probability of connectivity (PC): PC ranges from 0 to 1 and increases with improved connectivity. It is given by:
PC = ∑ i = 1 n ∑ j = 1 n a i · a j · p ij * A L 2
where p ij *   is defined as the maximum product probability of all possible paths between patches i and j (including single-step paths). If nodes i and j are close enough, the maximum probability path will simply be the step (direct movement) between nodes i and j ( p ij *   = pij). If nodes i and j are more distant, the “best” (maximum probability) path will probably comprise several steps through intermediate stepping stone nodes, yielding p ij *   > pij.
(9) Equivalent connectivity (EC(IIC) and EC(PC)):
EC ( IIC ) = ∑ i = 1 n ∑ j = 1 n a i · a j 1 + nl ij
EC ( PC ) = ∑ i = 1 n ∑ j = 1 n a i · a j · p ij *
where EC(IIC) and EC(PC) are just computed as the square root of the numerator of the IIC and PC, respectively.
(10) dI value (dIIC and dPC): The importance of an existing node for maintaining landscape connectivity (dI) according to a certain index (I) is calculated as a percentage as:
dIIC = 100 × IIC − IIC remove IIC
dPC = 100 × PC − PC remove PC
where I is the overall index value when all the initially existing nodes are present in the landscape and Iremove is the overall index value after the removal of that single node from the landscape (e.g., after a certain habitat patch loss).
(11) Betweenness centrality (dIIC and dPC):
BC = ∑ i = 1 n ∑ j = 1 , i ≠ j n p ( i , k , j ) ( i , j )   ( i ≠ j ≠ k )
BC quantifies the quantity of a patch stands in between other patches in a network. It calculates the sum of all shortest paths between all pairs that go through the patch k divided by the sum of all shortest paths between all pairs of patches.

References

  1. Ward, J.V. The Four-Dimensional Nature of Lotic Ecosystems. N. Am. Benthol. Soc. 1989, 8, 2–8. [Google Scholar] [CrossRef]
  2. Pringle, C.M. Hydrologic Connectivity and the Management of Biological Reserves: A Global Perspective. Ecol. Soc. Am. 2001, 11, 981–998. [Google Scholar] [CrossRef]
  3. Cai, Y.J.; Liang, J.S.; Zhang, P.Y.; Wang, Q.Y.; Wu, Y.; Ding, Y.R.; Wang, H.J.; Fu, C.; Sun, J.J. Review on strategies of close-to-natural wetland restoration and a brief case plan for a typical wetland in northern China. Chemosphere 2021, 285, 131534. [Google Scholar] [CrossRef]
  4. Gao, C.J.; Gao, X.C.; Peng, J. Summary Comments on Hydrologic Connectivity. Chin. J. Appl. Environ. Biol. 2017, 23, 0586–0594. [Google Scholar] [CrossRef]
  5. Lindenmayer, D.B.; Fischer, J. Tackling the Habitat Fragmentation Panchreston. Trends Ecol. Evol. 2007, 22, 127–132. [Google Scholar] [CrossRef] [PubMed]
  6. Candelaria, E.; Renata, P.; Pedro Luis, B.D.R. Forest Loss and the Biodiversity Threshold: An Evaluation Considering Species Habitat Requirements and the Use of Matrix Habitats. PLoS ONE 2013, 8, e82369. [Google Scholar] [CrossRef]
  7. Vannote, R.L.; Minshall, G.W.; Cummins, K.W.; Sedell, J.R.; Cushing, C.E. The River Continuum Concept. Can. J. Fish. Aquat. Sci. 1980, 37, 130–137. [Google Scholar] [CrossRef]
  8. Tischendorf, L.; Fahrig, L. On the Usage and Measurement of Landscape Connectivity. OIKOS 2000, 90, 7–19. [Google Scholar] [CrossRef] [Green Version]
  9. Malard, F.; Tockner, K.; Dole-Olivier, M.J.; Ward, J.V. A Landscape Perspective of Surface–Subsurface Hydrological Exchanges in River Corridors. Freshw. Biol. 2002, 47, 621–640. [Google Scholar] [CrossRef]
  10. Pringle, C. What is Hydrologic Connectivity and Why is it Ecologically Important? Hydrol. Processes 2003, 17, 2685–2689. [Google Scholar] [CrossRef]
  11. Turnbull, L.; Wainwright, J.; Brazier, R.E. A Conceptual Framework for Understanding Semi-Arid Land Degradation: Ecohydrological Interactions across Multiple-Space and Time Scales. Ecohydrology 2008, 1, 23–34. [Google Scholar] [CrossRef] [Green Version]
  12. Western, A.W.; Blöschl, G.; Grayson, R.B. Toward Capturing Hydrologically Significant Connectivity in Spatial Patterns. Water Resour. Res. 2001, 37, 83–97. [Google Scholar] [CrossRef]
  13. Freeman, M.C.; Pringle, C.M.; Jackson, C.R. Hydrologic Connectivity and the Contribution of Stream Headwaters to Ecological Integrity at Regional Scales1. J. Am. Water Resour. Assoc. 2007, 43, 5–14. [Google Scholar] [CrossRef]
  14. Bishop-Taylor, R.; Tulbure, M.G.; Broich, M. Evaluating Static and Dynamic Landscape Connectivity Modelling Using a 25-Year Remote Sensing Time Series. Landsc. Ecol. 2018, 33, 625–640. [Google Scholar] [CrossRef]
  15. Grafius, D.R.; Corstanje, R.; Siriwardena, G.M.; Plummer, K.E.; Harris, J.A. A bird’s eye view: Using circuit theory to study urban landscape connectivity for birds. Landsc. Ecol. 2017, 32, 1771–1787. [Google Scholar] [CrossRef] [PubMed]
  16. Mcrae, B.H.; Dickson, B.G.; Keitt, T.H.; Shah, V.B. Using Circuit Theory to Model Connectivity in Ecology, Evolution, and Conservation. Ecology 2008, 89, 2712–2724. [Google Scholar] [CrossRef]
  17. Liu, X.J.; Liu, D.F.; Zhao, H.Z.; He, J.H.; Liu, Y.L. Exploring the Spatio-Temporal Impacts of Farmland Reforestation on Ecological Connectivity Using Circuit Theory: A Case Study in the Agro-Pastoral Ecotone of North China. J. Geogr. Sci. 2020, 30, 1419–1435. [Google Scholar] [CrossRef]
  18. Qi, K.; Fan, Z.Q.; Ng, C.N.; Wang, X.R.; Xie, Y.J. Functional Analysis of Landscape Connectivity at the Landscape, Component, and Patch Levels: A Case Study of Minqing County, Fuzhou City, China. Appl. Geogr. 2017, 80, 64–77. [Google Scholar] [CrossRef]
  19. Bai, J.H.; Lu, Q.Q.; Wang, J.J.; Zhao, Q.Q.; Ouyang, H.; Deng, W.; Li, A.N. Landscape Pattern Evolution Processes of Alpine Wetlands and Their Driving Factors in the Zoige Plateau of China. J. Mt. Sci. 2013, 10, 54–67. [Google Scholar] [CrossRef]
  20. Huo, L.L.; Chen, Z.K.; Zou, Y.C.; Lu, X.G.; Guo, J.W.; Tang, X.G. Effect of Zoige Alpine Wetland Degradation on the Density and Fractions of Soil Organic Carbon. Ecol. Eng. 2013, 51, 287–295. [Google Scholar] [CrossRef]
  21. Li, Z.W.; Wang, Z.Y.; Gary, B.; Tami, N.; Pan, B.Z.; Li, Y.F. Shrinkage of the Ruoergai Swamp and Changes to Landscape Connectivity, Qinghai-Tibet Plateau. Catena 2015, 126, 155–163. [Google Scholar] [CrossRef]
  22. Li, W.L.; Xue, P.F.; Liu, C.L.; Yan, H.P.; Zhu, G.F.; Cao, Y.P. Monitoring and Landscape Dynamic Analysis of Alpine Wetland Area Based on Multiple Algorithms: A Case Study of Zoige Plateau. Sensors 2020, 20, 7315. [Google Scholar] [CrossRef] [PubMed]
  23. Wu, C.Y.; Chen, W.; Cao, C.X.; Tian, H.; Liu, D.; Bao, D.M. Diagnosis of Wetland Ecosystem Health in the Zoige Wetland, Sichuan of China. Wetlands 2018, 38, 469–484. [Google Scholar] [CrossRef]
  24. Shen, G.; Yang, Y.C.; Jin, Y.X.; Xu, B.; Zhou, Q.B. Remote Sensing and Evaluation of the Wetland Ecological Degradation Process of the Zoige Plateau Wetland in China. Ecol. Indic. 2019, 104, 48–58. [Google Scholar] [CrossRef]
  25. Bian, J.H.; Li, A.N.; Zhang, Z.J.; Zhao, W.; Lei, G.B.; Xia, H.M.; Tan, J.B. Grassland Fractional Vegetation Cover Monitoring Using the Composited Hj-1a/B Time Series Images and Unmanned Aerial Vehicles: A Case Study in Zoige Wetland China. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7192–7195. [Google Scholar] [CrossRef]
  26. Yan, Z.L.; Wu, N. Rangeland Privatization and Its Impacts on the Zoige Wetlands on the Eastern Tibetan Plateau. J. Mt. Sci. 2005, 2, 105–115. [Google Scholar] [CrossRef] [Green Version]
  27. Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-Resolution Mapping of Global Surface Water and Its Long-Term Changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
  28. Saura, S.; Josep, T. Conefor Sensinode 2.2: A Software Package for Quantifying the Importance of Habitat Patches for Landscape Connectivity. Environ. Model. Softw. 2009, 24, 135–139. [Google Scholar] [CrossRef]
  29. Mcrae, B.H. Isolation by Resistance. Evolution 2016, 60, 1551–1561. [Google Scholar] [CrossRef]
  30. Bishop-Taylo, R.; Tulbure, M.R.; Roich, M. Surface- Water Dynamics and Land Use Influence Landscape Connectivity across a Major Dryland Region. Ecol. Appl. 2017, 27, 1124–1137. [Google Scholar] [CrossRef] [PubMed]
  31. Anantharaman, R.; Hall, K.; Shah, V.B.; Edelman, A. Circuitscape in Julia: High Performance Connectivity Modelling to Support Conservation Decisions. Proc. JuliaCon. 2019, 1, 1–6. [Google Scholar]
  32. Xu, C.S.; Cheng, L.; Su, J.; Yin, H.W.; Guo, Y.Q. Developing Regional Econogical Networks along the Grand Canal based on an Integrated Analysis Framework. J. Resour. Ecol. 2021, 12, 801–813. [Google Scholar] [CrossRef]
  33. Liu, J. Structure Optimization of Green Infrastructure Based on Circuit Theory in Nanjing, China; NanJing University: NanJing, China, 2018. [Google Scholar]
  34. Yoon, E.J.; Kim, E.Y.; Kim, J.Y.; Lee, D.K. Connectivity Assessment Based on Circuit Theory for Suggestion of Ecological Corridor. J. Environ. Impact Assess. 2019, 28, 275–286. [Google Scholar] [CrossRef]
  35. Baranyi, G.; Saura, S.; Podani, J.; Jordan, F. Contribution of Habitat Patches to Network Connectivity: Redundancy and Uniqueness of Topological Indices. Ecol. Indic. 2011, 11, 1301–1310. [Google Scholar] [CrossRef]
  36. Saura, S.; Estreguil, C.; Mouton, C.; Rodríguez-Freire, M. Network Analysis to Assess Landscape Connectivity Trends: Application to European Forests (1990–2000). Ecol. Indic. 2011, 11, 407–416. [Google Scholar] [CrossRef]
  37. Saura, S.; Pascual-Hortal, L. A New Habitat Availability Index to Integrate Connectivity in Landscape Conservation Planning: Comparison with Existing Indices and Application to a Case Study. Landsc. Urban Plan. 2007, 83, 91–103. [Google Scholar] [CrossRef]
  38. Hernández, A.; Miranda, M.; Arellano, E.C.; Saura, S.; Ovalle, C. Landscape Dynamics and Their Effect on the Functional Connectivity of a Mediterranean Landscape in Chile. Ecol. Indic. 2015, 48, 198–206. [Google Scholar] [CrossRef]
  39. Saura, S.; Rubio, L. A Common Currency for the Different Ways in Which Patches and Links Can Contribute to Habitat Availability and Connectivity in the Landscape. Ecography 2010, 33, 523–537. [Google Scholar] [CrossRef]
  40. Cui, Y.; Xiao, R.; Zhang, M.X.; Wang, C.; Ma, Z.W.; Xiu, Y.J.; Wang, Q.; Guo, Y.T. Hydrological Connectivity Dynamics and Conservation Priorities for Surface-Water Patches in the Yellow River Delta National Nature Reserve, China. Ecohydrol. Hydrobiol. 2020, 20, 525–536. [Google Scholar] [CrossRef]
  41. Bodin, O.; Saura, S. Ranking Individual Habitat Patches as Connectivity Providers: Integrating Network Analysis and Patch Removal Experiments. Ecol. Model. 2010, 221, 2393–2405. [Google Scholar] [CrossRef]
  42. Li, Z.W.; Gao, P.; You, Y.C. Characterizing Hydrological Connectivity of Artificial Ditches in Zoige Peatlands of Qinghai-Tibet Plateau. Water 2018, 10, 1364. [Google Scholar] [CrossRef] [Green Version]
  43. Tulbure, M.G.; Broich, M.; Stehman, S.V.; Kommareddy, A. Surface Water Extent Dynamics from Three Decades of Seasonally Continuous Landsat Time Series at Subcontinental Scale in a Semi-Arid Region. Remote Sens. Environ. 2016, 178, 142–157. [Google Scholar] [CrossRef]
Remotesensing 14 00145 g001 550
Figure 1. Location and physiography of the study area. (a) Physiography, (b) Location.
Figure 1. Location and physiography of the study area. (a) Physiography, (b) Location.
Remotesensing 14 00145 g001
Remotesensing 14 00145 g002 550
Figure 2. Diagrammatic representation of the approach used in the study.
Figure 2. Diagrammatic representation of the approach used in the study.
Remotesensing 14 00145 g002
Remotesensing 14 00145 g003 550
Figure 3. Distribution of surface water in the Zoigê area. (a) Spatial pattern of potential surface water habitats, (b) Interannual pixel count for surface water, (c) Area statistics for surface water.
Figure 3. Distribution of surface water in the Zoigê area. (a) Spatial pattern of potential surface water habitats, (b) Interannual pixel count for surface water, (c) Area statistics for surface water.
Remotesensing 14 00145 g003
Remotesensing 14 00145 g004 550
Figure 4. The results for NC (a) and NL (b), fitting curves and inflection points for eight indices (c–j).
Figure 4. The results for NC (a) and NL (b), fitting curves and inflection points for eight indices (c–j).
Remotesensing 14 00145 g004
Remotesensing 14 00145 g005 550
Figure 5. Changes in hydrological connectivity (IIC and PC) of Zoigê area at a distance of 300 m, from 2000–2019.
Figure 5. Changes in hydrological connectivity (IIC and PC) of Zoigê area at a distance of 300 m, from 2000–2019.
Remotesensing 14 00145 g005
Remotesensing 14 00145 g006 550
Figure 6. Current distribution maps for the Zoigê area from 2000 to 2019. (a) Current of corridors in 2000, (b) Current of corridors in 2010, (c) Current of corridors in 2019, (d) Current of patches for 2000, (e) Current of patches for 2010, and (f) Current for patches in 2019.
Figure 6. Current distribution maps for the Zoigê area from 2000 to 2019. (a) Current of corridors in 2000, (b) Current of corridors in 2010, (c) Current of corridors in 2019, (d) Current of patches for 2000, (e) Current of patches for 2010, and (f) Current for patches in 2019.
Remotesensing 14 00145 g006
Remotesensing 14 00145 g007 550
Figure 7. Statistics of different indices for the top 10 components in terms of connectivity for 2019. (a) Distribution of components, (b) Number of patches per component (n), (c) Cumulative area of patches per component (ha), (d) The sum of dIIC, (e) The sum of dPC, and (f) The sum of BC. C1 = Yellow River floodplain, C2 = Haqiucuogan, C3 = Yellow River–Black River corridor (south), C4 = Yellow River–Black River (north), C5 = Cuonidajian, C6 = Xingcuo, C7 = Cuorewajian, C8 = Yellow River floodplain @ Cairimaxiang, C9 = White River floodplain, C10 = Cuodawa.
Figure 7. Statistics of different indices for the top 10 components in terms of connectivity for 2019. (a) Distribution of components, (b) Number of patches per component (n), (c) Cumulative area of patches per component (ha), (d) The sum of dIIC, (e) The sum of dPC, and (f) The sum of BC. C1 = Yellow River floodplain, C2 = Haqiucuogan, C3 = Yellow River–Black River corridor (south), C4 = Yellow River–Black River (north), C5 = Cuonidajian, C6 = Xingcuo, C7 = Cuorewajian, C8 = Yellow River floodplain @ Cairimaxiang, C9 = White River floodplain, C10 = Cuodawa.
Remotesensing 14 00145 g007
Remotesensing 14 00145 g008 550
Figure 8. Statistics of different indices for the top 10 patches obtained from the results of connectivity modelling for 2019. (a) Distribution of patches, (b) Area of patches, (c) dIIC, (d) dPC, and (e) BC.
Figure 8. Statistics of different indices for the top 10 patches obtained from the results of connectivity modelling for 2019. (a) Distribution of patches, (b) Area of patches, (c) dIIC, (d) dPC, and (e) BC.
Remotesensing 14 00145 g008
Table
Table 1. Resistance value of different land use types.
Table 1. Resistance value of different land use types.
Land Use TypeType CodeClassificationResistance
entry 1datadata
Forest20-20
Shrubland40-25
Grassland30-30
Cropland10-100
Wetland50>25 ha7
1–25 ha9
≤1 ha11
Waterbody60>25 ha1
1–25 ha3
≤1 ha5
Artificial surface80-1000
Table
Table 2. Curve fitting equations and inflection points.
Table 2. Curve fitting equations and inflection points.
Index TypeCurve Fitting EquationsR2Inflection Points (x)Corresponding
Distance (m)
Hy = 0.0093x3 − 0.135x2 + 0.7539x + 5.82210.99734.8387126.3050
LCPy = 0.0151x3 − 0.2606x2 + 1.4914x − 12.8760.96635.7528315.0716
EC(IIC)y = 0.0059x3 − 0.1026x2 + 0.5901x + 7.25360.98045.7966329.1784
IICy = 0.0119x3 − 0.2065x2 + 1.19x − 13.050.98035.7843325.1544
Fy = 0.0062x3 − 0.0426x2 + 0.1219x + 5.40220.99952.29039.877901
AWFy = 0.0082x3 − 0.137x2 + 0.7943x + 14.7650.99255.5691262.1980
EC (PC)y = 0.004x3 − 0.0681x2 + 0.3887x + 7.98260.98905.6750291.4883
PCy = 0.008x3 − 0.1363x2 + 0.7781x − 11.5730.98905.6792292.7152
Table
Table 3. Degree of correlation between hydrological connectivity and possible driving forces.
Table 3. Degree of correlation between hydrological connectivity and possible driving forces.
Influencing
Factor		Large Livestock PopulationPopulationAnnual
Precipitation		Farmland AreaMean Annual TemperatureGDP
Degree of Correlation0.8290.7740.770.7530.7430.578
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gao, C.; Huang, C.; Wang, J.; Li, Z. Modelling Dynamic Hydrological Connectivity in the Zoigê Area (China) Based on Multi-Temporal Surface Water Observation. Remote Sens. 2022, 14, 145. https://doi.org/10.3390/rs14010145

AMA Style

Gao C, Huang C, Wang J, Li Z. Modelling Dynamic Hydrological Connectivity in the Zoigê Area (China) Based on Multi-Temporal Surface Water Observation. Remote Sensing. 2022; 14(1):145. https://doi.org/10.3390/rs14010145

Chicago/Turabian Style

Gao, Chao, Chang Huang, Jianbang Wang, and Zhi Li. 2022. "Modelling Dynamic Hydrological Connectivity in the Zoigê Area (China) Based on Multi-Temporal Surface Water Observation" Remote Sensing 14, no. 1: 145. https://doi.org/10.3390/rs14010145

APA Style

Gao, C., Huang, C., Wang, J., & Li, Z. (2022). Modelling Dynamic Hydrological Connectivity in the Zoigê Area (China) Based on Multi-Temporal Surface Water Observation. Remote Sensing, 14(1), 145. https://doi.org/10.3390/rs14010145

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop