Abstract
The lack of ground control points (GCPs) affects the elevation accuracy of digital surface models (DSMs) generated by optical satellite stereo images and limits the application of high-resolution DSMs. It is a feasible idea to use ICESat-2 (Ice, Cloud, and land Elevation Satellite-2) laser altimetry data to improve the elevation accuracy of optical stereo images, but it is necessary to accurately match the two types of data. This paper proposes a DSM registration strategy based on terrain similarity (BOTS), which integrates ICESat-2 laser altimetry data without GCPs and improves the DSM elevation accuracy generation from optical satellite stereo pairs. Under different terrain conditions, Worldview-2, SV-1, GF-7, and ZY-3 stereo pairs were used to verify the effectiveness of this method. The experimental results show that the BOTS method proposed in this paper is more robust when there are a large number of abnormal points in the ICESat-2 data or there is a large elevation gap between DSMs. After fusion of ICESat-2 data, the DSM elevation accuracy extracted from the satellite stereo pair is improved by 73~92%, and the root mean square error (RMSE) of Worldview-2 DSM reaches 0.71 m.
1. Introduction
With the continuous development of satellite remote sensing technology, high-resolution stereo images have become the main way to obtain a digital elevation model (DEM) and digital surface model (DSM) in a large range. At the same time, the demand for high-precision DSMs has further increased in scientific research fields [1] such as earth sciences and natural disaster monitoring [2,3,4,5]. Linear array push-broom imaging is widely used in optical surveying satellites. The main factors affecting the accuracy of image positioning include satellite orbit accuracy, satellite attitude accuracy, sensor imaging accuracy, and the time synchronization accuracy of each system [6]. Accurate sensor geometric calibration [7,8,9] and regional network adjustment technology can improve image positioning accuracy [10]. The former needs to analyze the system error characteristics of imaging sensors and star sensors to ensure the consistency of the positioning accuracy of remote sensing images on a global scale. The latter needs to use the ground-measured control points or other methods with higher precision to correct the residual error in the image geometric model [11,12]. The lack of ground control points (GCPs) limits the use of regional network adjustment technology, and the vertical accuracy of satellite image positioning is often lower than the horizontal accuracy. For example, research work to optimize the positioning accuracy of Worldview-2 images shows that the horizontal positioning accuracy of the Worldview-2 rational function model can reach 3.8 m (root mean squared error, RMSE) without control points, while the vertical accuracy is only 5 m [13]. Using ICESat-2 (Ice, Cloud, and land Elevation Satellite-2) satellite laser altimeter data to improve the elevation accuracy of optical stereo images is a feasible idea.
The National Aeronautics and Space Administration (NASA) launched the second ICESat satellite on 15 September 2018, and it quantifies the impact of melting glaciers on the sea-level rise by providing global elevation data [14]. The satellite is equipped with an advanced topographic laser altimeter system (ATLAS) and uses micropulse photon-counting LiDAR (light detection and ranging) technology. The ranging accuracy reaches 10 cm. Since the release of ICESat-2 data, it has played an important role in coastal water depth measurement [15,16], glacier ablation and height change [17,18,19], forest fire area detection [20,21], forest biomass estimation [22,23], forest canopy height measurement [24,25], and DEM optimization [26]. The precision pointing determination (PPD) technology of ICESat-2 makes the planar positioning accuracy of the ICESat-2 laser point better than 6.5 m [27,28,29]. The original data were processed by ATL08 products, and the accuracy of the laser altimeter was 0.2 m in the plain area and 2.0 m in the mountainous area [30]. Carabajal et al. and Wang et al. [31,32] discussed the strategy of extracting geodetic control points from ATL08 data. Experiments show that selecting appropriate parameters for screening can obtain high-precision control points from ATL08.
The elevation accuracy of DSMs extracted from satellite stereo pairs is limited; while the accuracy of ICESat-2 laser altimeter data is high, the laser points are sparse and cannot directly establish a DSM. The DSM can be constructed by discrete point clouds combined with spatial interpolation [33]. The modeling results are susceptible to the spatial distribution of discrete point clouds. If the advantages of these two are combined, using ICESat-2 data to improve the accuracy of the DEM will undoubtedly have very good practical value. However, since the ICESat-2 laser altimetry data do not record the image of the laser point footprint, they cannot be directly used for satellite image regional network adjustment.
In this paper, multiple ICESat-2 footprints are combined into a DSM with sparse points but high elevation accuracy, and this DSM is used for accurate registration with the DSM obtained from satellite images. Currently, the more widely used DSM registration methods include the iterative closest point (ICP) algorithm [34] and the least Z-difference (LZD) algorithm [35]. Zhang et al. [36] compares the performance of ICP and LZD algorithms from algorithm theory, pull-in range, convergence speed, and computational efficiency. The ICP and LZD algorithms are both based on the least-squares principle, which is a locally optimal solution. Two DSMs must be roughly aligned by an initial transformation before registration. If the registered DSM has outliers and does not undergo initial changes, these methods will often fail, resulting in registration errors. To solve these problems, a DSM registration method based on terrain similarity (BOTS) was proposed in this paper. From a statistical point of view, this method establishes the objective function with the minimum standard deviation of view and a global solution to avoid the lack of a locally optimal solution. When there are many outliers in the ATL03 data or when the ATL03 data deviate greatly from the initial DSM, the use of the ICP method may cause registration failure. [37]. However, the BOTS algorithm is more robust and still effective. Compared with the current algorithm, the BOTS method has higher registration accuracy and can resist the influence of DSM gross errors on registration.
The rest of the paper is organized as follows. In Section 2, the study region and materials are provided. In Section 3, the data processing flow is provided, and the ATL03 data preprocessing and the BOTS method are explained in detail. Section 4 describes the experimental results, and Section 5 demonstrates the effects of the BOTS and ICP method on the accuracy of DSM after fusion ATL03 data. In Section 6, the conclusions are summarized.
2. Research Area and Materials
In order to test the effect of fusing ATL03 data on the accuracy of DSM, this study selected 5 stereo image pairs with different resolutions, topography, and landforms for experiments. In summary, the experimental data were selected as follows.
Study area A is located in the range of 36.02~36.33° north latitude and 95.07~96.05° east longitude, and the altitude is between 2700–4300 m. It belongs to the plateau desert mountain area with a complex topography and steep mountains. Study area B is located on the Qinghai–Tibet Plateau within the range of 32.75~33.35° north latitude and 91.67~92.35° east longitude, and the altitude is between 4700–6100 m. The vegetation in the area is mainly plateau grassland. Study area C is located in the middle and lower reaches of the Yangtze River within the range of 27.15~27.33° north latitude and 75.77~75.95° east longitude. The altitude is between 0 m and 1400 m, and the area is covered with tall vegetation and steep mountains. Study area D is located in the North China Plain within the range of 39.12~39.67° north latitude and 115.32~116.02° east longitude. The altitude is between 0 m and 1400 m, the vegetation in the area is dominated by crops, and the terrain is dominated by plains. Study area E is located in India within the range of 27.17~27.33° north latitude and 75.77~75.93° east longitude. The altitude is between 380~750 m, the vegetation in the area is dominated by crops, and the terrain is gentle. Table 1 describes the main parameters of the image in the study area. Figure 1 shows the spatial location of each study area and the distribution of satellite laser footprints.

Table 1.
The main parameters of the image in the study area.
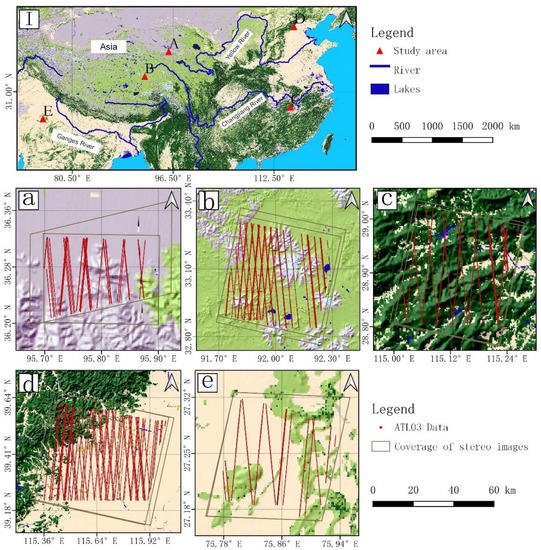
Figure 1.
Location of study area and the distribution of satellite laser footprints: (I) location of 5 study areas, (a–e) is the distribution of ATL03 footprints in study area A to study area E, as described in Table 1.
ATLAS data products are divided into 5 levels, and data sets can be obtained at the National Snow and Ice Data Center (NSIDC). ATL03 data were selected as reference data, which are L2-level data [38]. The distance between adjacent laser points along the track is 0.7 m, and the diameter of the laser footprint is approximately 17~20 m [38]. The recorded information includes each photon’s elevation, latitude, longitude, and photon propagation time in the WGS-84 coordinate system. In the ATL03 data, each photon is divided into signal photons and background photons. Signal photons are identified as land ice, sea ice, ocean, land, inland waters, and the corresponding confidence parameter values are provided [39]. ATL03 has a high spatial resolution along the trajectory direction and can express the terrain undulations in detail, which is more suitable for the registration method proposed in this paper. The experimental ATL03 data in this paper were obtained through the ICESat-2 laser altimetry data rapid analysis and visualization tool OpenAltimetry [40], covering the period from 2018 to 2021.
3. Method
3.1. Algorithm Flow
The horizontal positioning accuracy of ATLAS is better than 6.5 m, and the elevation accuracy is 0.2 m in plain areas and 2.0 m in mountainous areas, which is better than the vertical accuracy of satellite stereo pair. Therefore, the idea of DSM registration was used to optimize the geometric accuracy of the DSM. To obtain the best registration result, the ATL03 elevation laser points needed to be screened first. When using stereo pairs to extract DSM, semi-global matching (SGM) [41] was used as a dense matching method to minimize DSM elevation abnormal values. In this paper, the DSM extracted from the satellite stereo image pair was used as the reference data, and the DSM obtained by the ATL03 laser height measurement was used as the data to be registered. After the registration parameters were obtained, the registration parameters were inversely transformed on the satellite DSM to improve the elevation accuracy.
The DSM geometric accuracy optimization strategy was divided into the following 4 steps (as shown in Figure 2):
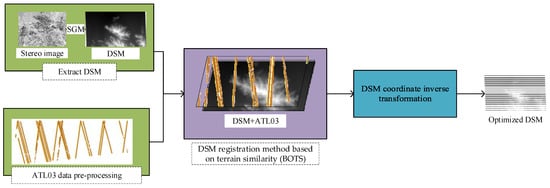
Figure 2.
DSM geometric accuracy optimization process based on terrain similarity.
- Step 1. Extract DSMCreate DSM with stereo images. The image geometry model adopts the rational function model (RFM). The output resolution is twice the image resolution. The DSM storage format is a regular grid, which is convenient for processing and calculation.
- Step 2. Data pre-processingExtract high-quality ATL03 photons and unify the spatial reference system among multisource data.
- Step 3. DSM registration based on terrain similarity (BOTS)Use DSM as the reference data and ATL03 as the source data to calculate the coordinate transformation parameters.
- Step 4. DSM coordinate inverse transformationTaking the DSM as the source data, use the calculated coordinate transformation parameters to inversely transform the coordinates of the DSM to improve the geometric accuracy of the DSM.
3.2. ATL03 Data Preprocessing
The ICESat-2 laser altimetry data are affected by factors such as terrain, collection time, clouds, and aerosols. The vertical accuracy of the laser point is not stable, and there are data points with large errors. Therefore, it is necessary to preprocess ATL03 before registration starts to eliminate incorrect data. The ATL03 data preprocessing process is shown in Figure 3, which specifically includes the following steps.
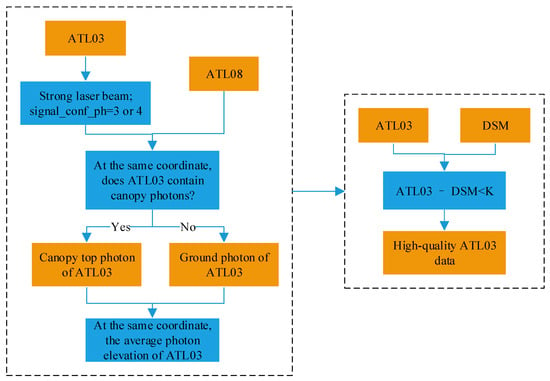
Figure 3.
ATL03 data preprocessing process.
3.2.1. Photon Screening
The h_te_uncertainty parameter in the ATL08 data indicates the total uncertainty of the fitting elevation in the 100 m interval. The smaller the value is, the higher the quality of the laser spot [31]. In the ATL03 data set, all photons are divided into signal photons and background photons, and the confidence of each signal photon on land, ocean, sea ice, land ice, and inland water is given through the signal_conf_ph parameter (Figure 4a). When the value of signal_conf_ph is −2, −1, 0, and 1, it means that the photon belongs to the transmitter echo pulse (TEP) photon, photon independent of surface type, noise photon, and buffer photon. When the value of signal_conf_ph is 2, 3, and 4, it indicates that the photon belongs to low-confidence, medium-confidence, and high-confidence photons, respectively.
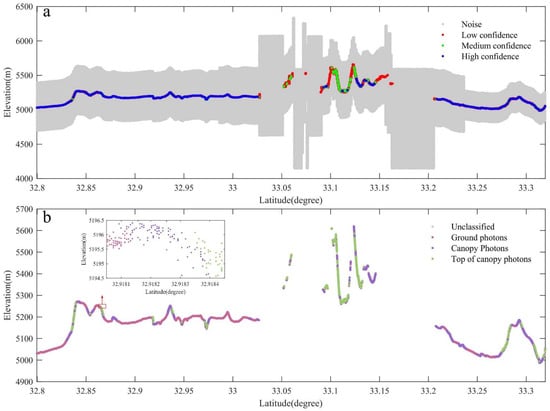
Figure 4.
ATL03 photon section view: (a) shows the ATL03 data classified by the signal_conf_ph parameter, (b) shows the result of the joint classification of ATL03 and ATL08 data with medium and high confidence.
To sum up, first, the weak energy photons were removed from the ATL03 data, and then select the photons whose surface coverage type is ‘land’ from the remaining photons. Finally, the ATL03 photons with medium- and high-confidence are sorted as experimental data.
3.2.2. Photon Classification
As shown in Figure 4b, combined with the ATL08 data [42], the filtered ATL03 photons could be classified into noise, terrain photons, vegetation canopy photons, and canopy top photons [43]. Since there were multiple types of photons at the same horizontal coordinate and the same type of photons was not unique, it was necessary to screen the classified photons so that only one type of photon remained at each horizontal coordinate. At this time, it was divided into two cases for processing. If the remaining photons included canopy top photons, the terrain and vegetation canopy photons were eliminated; if the remaining photons did not contain vegetation canopy photons and canopy top photons, the original terrain photons were retained. Finally, the average elevation value of the remaining photons was taken as the only elevation here.
3.2.3. Photon Resampling
Affected by factors such as data collection, data processing, and topography, the elevation of ATL03 data unavoidably had gross errors. Therefore, it was necessary to eliminate photons with abnormal elevations before performing the spatial transformation. The calculation idea was to remove the photons that exceeded the threshold as abnormal data from the original data by setting the elevation difference threshold between the photon and the DSM. This study used 3 times the average of the ATL03 photon and DSM elevation difference in a relatively flat terrain area as the threshold. Then, the photons were resampled, so that the spatial resolution of the photons along the track was consistent with the DSM spatial resolution.
3.3. DSM Registration Method Based on Terrain Similarity
When different satellite sensors collect data, there are errors in satellite attitude and orbit location measurement and the accuracy of these sensors are different. These factors result in a phenomenon of noncoincidence between DSM data sets in the same area (Figure 5). Conversion from one coordinate system into another results in area, shape, or angle distortion. Therefore, the misalignment between the two surfaces should be eliminated before applying data fusion [44]. Equation (1) was used to calculate the coordinate axis translation and rotation from one DSM data set to the other data set.
where T is the translation matrix; R is the rotation matrix; α, β, and γ are the rotation angles of the coordinate axis; and ∆x, ∆y, and ∆z are the translational amounts of the coordinate axis.
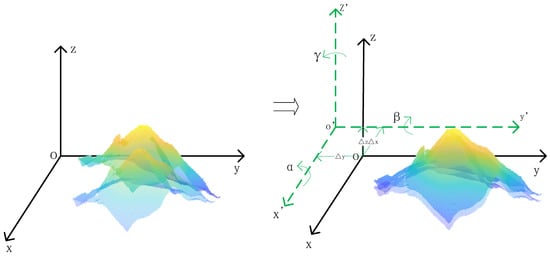
Figure 5.
Schematic diagram of DSM registration based on spatial coordinate transformation.
Within the same range of the surface, the topographical fluctuations expressed by the two DSM data sets should be similar. When the two are aligned in the horizontal direction, the elevation difference of homonymous points should be equal, which also means that the homonymous points’ standard deviation of elevation difference is the smallest.
Therefore, this algorithm uses the elevation difference standard deviation as the objective function to calculate the coordinate transformation parameters in four steps. The specific process is shown in Figure 6, and the detailed description is as follows.
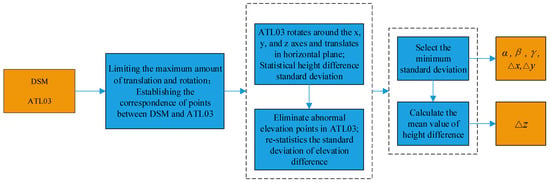
Figure 6.
Algorithm flow of DSM registration based on terrain similarity (BOTS).
- (1)
- Set the maximum translation and rotation amount. The purpose is to determine the range of horizontal movement, reduce unnecessary calculations, and improve registration efficiency. Determine the maximum horizontal moving distance by the remote sensing image accuracy and the horizontal accuracy of ICESat-2, which differs according to the image type.
- (2)
- Establish the corresponding point relationship. Use the coordinates of the ATL03 data to obtain the elevation values of these points on the DSM to form homonymous points. The height difference of homonymous points expresses the relationship between the two data sets.
- (3)
- Using ATL03 as the source data set and satellite DSM as the reference data set, perform spatial rotation transformation around the x, y, and z axes, and perform the translation in the x-y plane. Calculate the transformed coordinate values according to Equation (1) and use Equations (2) and (3) to calculate the elevation difference standard deviation of all homonymous points.where HATL03 (i,j) and HDSM (i,j) are the elevations of the homonymous points formed by ATL03 and DSM, ∆h (i,j) is the elevation difference of homonymous points after each transformation, ∆H is the elevation difference set of homonymous points, i is the number of homonymous points, and j is the number of transformation times.where ∆hsd (j) is the elevation difference standard deviation of all homonymous points under the j-th spatial transformation of ATL03, and is the elevation difference standard deviation set of the homonymous points.
- (4)
- According to Equation (4), sequentially eliminate the abnormal elevation value data in the ATL03 data, calculate the standard deviation of the elevation difference of homonymous points again using Equations (5) and (6), and select the rotation when the standard deviation of the elevation difference is the smallest. Take the amount of translation as the optimal parameter value of α, β, γ, ∆x, ∆y. At this time, the mean value of the height difference when the standard deviation of the elevation difference is the smallest is calculated as the translation parameter ∆z in the z-axis direction.
In the equation, Hu_ATL03 (i,j) is the ATL03 data with the elevation abnormal points eliminated under the j-th transformation, and Hut_ICESAT2 is the ATL03 data set after the elevation abnormal points are eliminated;
where ∆Hu is the recalculated elevation difference set, and ∆hu (i,j) is the recalculated elevation difference set under the j-th transformation;
∆husd (j) is the recalculated elevation difference standard deviation under the same transformation state and ∆husd_min is the smallest elevation difference standard deviation.
4. Results
As shown in Figure 7, the SGM matching method was used to extract five DSMs from the satellite stereo pairs in the study area. Figure 7a is WV2_DSM, the spatial resolution is 1.0 m; Figure 7b is ZY3_DSM, the spatial resolution is 5.0 m; Figure 7c is GF7_DSM, the spatial resolution is 1.5 m; Figure 7d is ZY3_DSM, the spatial resolution is 5.0 m; and Figure 7d is SV_DSM, the spatial resolution is 1.5 m. All DSM elevationare based on WGS84 ellipsoid, which is consistent with the spatial coordinate system of the ATL03 data. The BOTS registration results were compared with the ICP method in the horizontal and vertical.
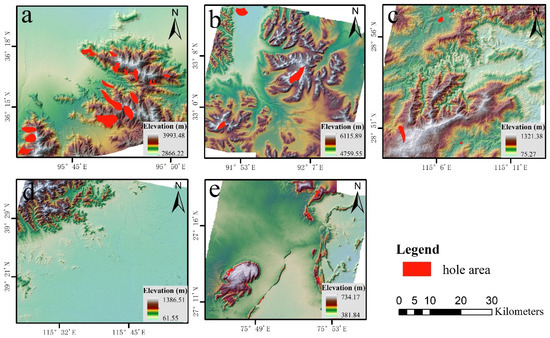
Figure 7.
SGM algorithm to extract DSM: (a)-WV2_DSM, (b)-ZY3_DSM, (c)-GF7_DSM, (d)-ZY3_DSM, (e)-SV_DSM.
To improve computational efficiency and reduce the memory consumption of the SGM algorithm, parallel computing technology was used to extract the DSM using the strategy of image block matching. In the image matching process, the SGM algorithm parameter configuration was as follows: the size of the tile was 1024 × 1024 pixels, the cost function used the census transform [45,46], and the matching window used 7 × 7 pixels. Figure 7 shows that the high-resolution DSM generated by the SGM algorithm had a relatively complete performance of the terrain. On the whole, it could accurately reconstruct the three-dimensional terrain of the mountainous area and had rich surface texture details, and there was no obvious modeling error in the plain area. However, in areas with the weak texture of the image, such as areas with snow cover and no obvious vegetation changes, areas with severe shadows on steep mountain slopes, and areas with severe image distortion, matching failures occurred. This caused the DSM to form holes, as indicated by the red area in Figure 7.
The ICESat-2 laser points in the study area were used as checkpoints to calculate the accuracy of the DSM’s elevation accuracy. Checkpoints should be distributed as evenly as possible across the entire DSM. According to the coordinates of these checkpoints, the elevation at the same position was obtained in the DSM and used Equation (7) to calculate the vertical RMSE.
where ai is the elevation value of the i-th ATL03 checkpoint data, zi is the elevation value of the corresponding point of the DSM data set to be evaluated, and N is the number of checkpoints.
The calculation results are shown in Table 2. It can be seen from Table 2 that the minimum elevation error of the original DSM extracted from the satellite stereo image was 2.6 m (WV2_DSM) and the highest was 19.2 m (ZY3_DSM_N32E91). After fusing ICESat-2 data, the elevation accuracy of the DSM was greatly improved. The highest elevation accuracy was WV2_DSM, with a median error of 0.7 m; the lowest was ZY3_DSM_N39E115, with a median error of 1.8 m. The elevation accuracy of the DSM was generally increased by 1 to 3 times, and the highest was even increased by 11 times (ZY3_DSM_N32E91).

Table 2.
DSM accuracy after fusion of ICESat-2 data.
5. Discussion
5.1. Accuracy Analysis of BOTS Method
By comparing and analyzing the movement vector of the DSM center in the horizontal direction when the ICP algorithm and the BOTS algorithm were registered, the effect of the algorithm based on terrain similarity (BOTS) was evaluated. Table 3 counts the translation of these two methods of the DSM center in the east and north directions and counts the translations of the difference. For WV2_DSM, SV_DSM, and GF7_DSM, it can be seen that, after being optimized by the two algorithms, the translational difference between the east and north directions of the DSM center reached the submeter level, which was less than the DSM’s spatial resolution. For the two ZY3_DSM data sets, the difference between the translational amount of the DSM center in the east and north directions was greater than 1 m, which was still less than the spatial resolution of the DSM (2.5 m). When the allowable error was less than one pixel, the results of the BOTS algorithm and the ICP algorithm showed a high degree of consistency. Figure 8 shows the spatial distribution of the translational amount of the DSM center after the BOTS algorithm and the ICP algorithm were used for registration optimization.

Table 3.
The translation amount of the geometric center of the DSM in the horizontal direction after registration (unit: m).
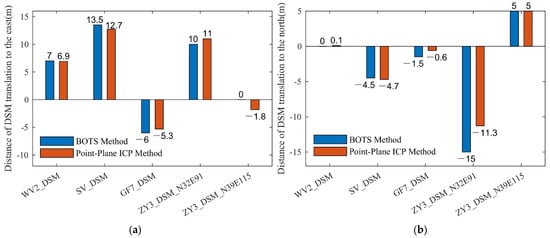
Figure 8.
Registration DSM center horizontal translation amount: (a) is the amount of movement of each DSM center in the east-west direction, and (b) is the amount of movement of each DSM center in the north-south direction).
In the vertical direction, cross-validation and comparative analysis were used to evaluate the effect of the BOTS algorithm. The specific scheme of cross-validation was as follows: in the final ATL03 data screened out, laser points evenly distributed throughout the research area were selected as elevation checkpoints, which were used to count the elevation residuals of the DSM and evaluate the elevation accuracy. These checkpoints were extracted in advance and not used on the DSM fusion.
In Figure 9a–e, two registration algorithms were used to calculate the absolute value of the elevation residuals and the average of the absolute values of the elevation residuals of the five DSMs at each percentile. Figure 10 shows the spatial distribution of elevation checkpoints in each DSM. In general, the elevation residuals of the five DSMs optimized by the two registration algorithms were greatly improved. In the 0~75% percentile of the DSM elevation residual, the residual variation was small, indicating that the distribution of the elevation residual was concentrated. In the 75~100% percentile, the elevation residual changed greatly and the elevation residual distribution was discrete, indicating that the elevation residual in the 75~100% percentile contained abnormal data. The absolute value of the elevation residual and the absolute average value of the elevation residual calculated by the two matching algorithms were close to each other, indicating that the BOTS algorithm can achieve the same accuracy as the ICP algorithm in the vertical direction.
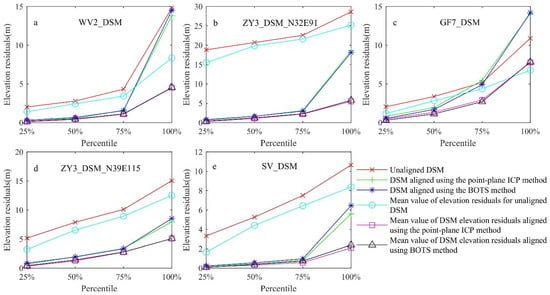
Figure 9.
DSM elevation residual distribution: (a–e) is the absolute value of the elevation residual and the mean of the absolute value of the elevation residual at the quartile before and after the ICP and BOTS algorithms were used for registration.
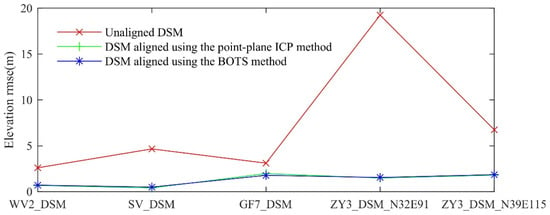
Figure 10.
DSM elevation accuracy evaluation.
According to the analysis results in Figure 9, after removing the abnormal elevation residual data between the 75th and 100th percentiles, the RMSE of the elevation residuals of the two registration algorithms was calculated, as shown in Table 4. Table 4 shows that, after excluding abnormal checkpoints, the residual RMSE value of each unregistered DSM elevation was consistent with the nominal elevation accuracy of the satellite image. After fusing the ICESat-2 data and registering with the BOTS algorithm, the elevation residual RMSE values of WV2_DEM and SV_DEM reached the submeter level. Theoretically, the elevation residual RMSE of GF7_DSM could also reach the submeter level. Since the GF7_DSM area is covered with dense vegetation, which caused the loss of the elevation accuracy of the ATL03 data [47], it resulted in the elevation residual RMSE of GF7_DSM being greater than 1 m. For ZY3_DSM, since the spatial resolution of the data was not high (2.5 m), the elevation residual RMSE value was greater than 1 m.

Table 4.
RMSE statistics of DSM elevation residuals (unit: m).
Figure 10 visually compares the RMSE values of the DSM elevation residuals before and after the optimization of the two registration algorithms for each DSM. In the vertical direction, the elevation residual RMSE calculated by the BOTS algorithm had a clear advantage over the unregistered elevation residual RMSE. Due to the different imaging conditions of each stereo pair, the optimized amplitudes of the five DSMs were different.
5.2. DSM Residual Error Distribution
Figure 11a–e show the spatial distribution of the absolute value of the elevation residual after optimization of WV2_DSM, ZY3_DSM_N32E91, GF7_DSM, ZY3_DSM_N39E115, and SV_DSM based on the terrain similarity (BOTS) DSM registration algorithm. The checkpoints were evenly distributed on each DSM, which ensured the reliability of the DSM elevation accuracy analysis. The checkpoint distribution is shown in Figure 11; the red dot is the position of the checkpoint. The size of the red dot represents the error value; if the point is larger, the error is bigger. The DSM elevation optimization results were greatly affected by the terrain, the type of land cover, and the spatial resolution of the DSM. The points with large elevation residuals in each DSM were mostly distributed in areas with steep terrain and vegetation coverage, while the flat areas had smaller elevation residuals.
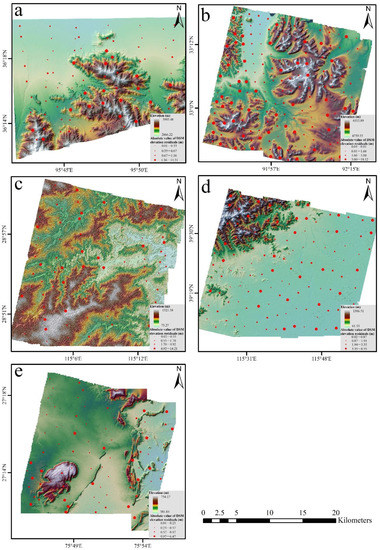
Figure 11.
The spatial distribution of DSM elevation residuals after BOTS algorithm registration (a–e) represents the spatial distribution of the absolute value of the elevation residual after registration by the BOTS algorithm for WV2_DSM, ZY3_DSM_N32E91, GF7_DSM, ZY3_DSM_N39E115, and SV_DSM, respectively.
6. Conclusions
By fusing ICESat-2 laser altimetry data, the elevation accuracy of DSM can be greatly improved, but accurate registration between the two kinds of data is needed. This paper proposes an algorithm for accurate registration of satellite stereo image extraction DSMs and ICESat-2 laser altimetry data based on terrain similarity (BOTS). The effect of the algorithm was verified by applying five pairs of satellite stereo images. The results show that the BOTS algorithm can effectively register the DSM with the ATL03 data by finding the minimum standard deviation of the elevation difference between DSM and ATL03 and improving the elevation accuracy of DSM. After registration, the elevation RMSE of the DSM can reach the submeter level. Among them, the Worldview-2 DSM elevation RMSE was 0.71 m, and the SV-1 DSM elevation RMSE was 0.49 m. For GF-7 DSM, the presence of vegetation reduced the accuracy of ATL03. As a result, the elevation RMSE of the DSM was greater than 1 m, while the elevation RMSE of the two ZY-3 DSMs was 1.55 m and 1.84 m, respectively. After fusing ICESat-2 data, the elevation accuracy of satellite imagery DSM increased 73~92%. Therefore, it can be concluded that the use of ICESat-2 laser point data, after using the BOTS method for accurate registration, can greatly improve the elevation accuracy of DSMs extracted from high-resolution satellite stereo images, which has significant practical value.
In terms of algorithm complexity, the BOTS algorithm makes full use of the elevation information of DSM and ATL03, which is easier to implement than current algorithms. At the same time, the BOTS algorithm belongs to global matching, which avoids the defects of the local optimal solution of the ICP algorithm. Since the BOTS algorithm requires enough points to calculate terrain features, this method is not applicable when the data involved in the calculation is too sparse. For example, when using ATL08 data, the correct results were often not obtained. Therefore, ATL03 data with high laser dot density should be used as much as possible.
Author Contributions
Conceptualization, J.Y.; Data curation, Y.Q. and R.Z.; Methodology, J.Y. and Y.Q.; Software, Y.Q. and J.Y.; Supervision, J.Y.; Visualization, Y.D.; Writing—original draft, J.Y. and Y.Q.; Writing—review and editing, X.L. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Sichuan Science and Technology Program, No. 2019YJ0504; Key Projects of Sichuan Provincial Department of Education, grant No. 17ZA0031.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing does not apply to this article.
Acknowledgments
The authors would like to thank the editors and reviewers for their efforts to help the publication of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Girod, L.; Nuth, C.; Kääb, A.; McNabb, R.; Galland, O. MMASTER: Improved ASTER DEMs for Elevation Change Monitoring. Remote Sens. 2017, 9, 704. [Google Scholar] [CrossRef] [Green Version]
- Albino, F.; Smets, B.; d’Oreye, N.; Kervyn, F. High-resolution TanDEM-X DEM: An accurate method to estimate lava flow volumes at Nyamulagira Volcano (D. R. Congo). J. Geophys. Res. Solid Earth 2015, 120, 4189–4207. [Google Scholar] [CrossRef] [Green Version]
- Bisson, M.; Spinetti, C.; Andronico, D.; Palaseanu-Lovejoy, M.; Fabrizia Buongiorno, M.; Alexandrov, O.; Cecere, T. Ten years of volcanic activity at Mt Etna: High-resolution mapping and accurate quantification of the morphological changes by Pleiades and Lidar data. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102369. [Google Scholar] [CrossRef]
- Kim, J.-W.; Lu, Z.; Qu, F.; Hu, X. Pre-2014 mudslides at Oso revealed by InSAR and multi-source DEM analysis. Geomat. Nat. Hazards Risk 2015, 6, 184–194. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.Y.; Liu, F.Q.; Zhao, C.G.; Dai, J. The study of high resolution stereo mapping satellite. Natl. Remote Sens. Bull. 2021, 25, 1400–1410. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Hu, X. Drift Angle Residual Corrrection Technology in Satellite Photogrammetry. Acta Geod. Cartogr. Sin. 2014, 43, 954–959. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Hu, X.; Su, Z. The on-orbit calibration of geometric parameters of the Tian-Hui 1 (TH-1) satellite. ISPRS J. Photogramm. Remote Sens. 2017, 124, 144–151. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, X.; Gong, J.; Duan, M. The Look-angle Calibration Method for On-orbit Geometric Calibration of ZY-3 Satellite Imaging Sensors. Acta Geod. Cartogr. Sin. 2014, 43, 1039–1045. [Google Scholar] [CrossRef]
- Mi, L.D.W. A Review of High Resolution Optical Satellite Surveying and Mapping Technology. Spacecr. Recovery Remote Sens. 2020, 41, 1–11. [Google Scholar] [CrossRef]
- Anzhu, Y. Research on the Improvement of Georeferencing Accuracy of High Resolution Satellite Imagery; PLA Strategic Support Force Information Engineering University: Zhengzhou, China, 2017; Available online: http://cdmd.cnki.com.cn/Article/CDMD-90005-1018702170.htm (accessed on 1 June 2021).
- Jaud, M.; Passot, S.; Le Bivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the Accuracy of High Resolution Digital Surface Models Computed by PhotoScan® and MicMac® in Sub-Optimal Survey Conditions. Remote Sens. 2016, 8, 465. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.; Lin, X.; Xu, T. Mathematical modeling and accuracy testing of worldview-2 level-1B stereo pairs without ground control points. Remote Sens. 2017, 9, 737. [Google Scholar] [CrossRef] [Green Version]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Babbel, B.J.; Parrish, C.E.; Magruder, L.A. ICESat-2 Elevation Retrievals in Support of Satellite-Derived Bathymetry for Global Science Applications. Geophys. Res. Lett. 2021, 48, 5. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2020GL090629 (accessed on 2 August 2021). [CrossRef] [PubMed]
- Chen, Y.; Zhu, Z.; Le, Y.; Qiu, Z.; Chen, G.; Wang, L. Refraction correction and coordinate displacement compensation in nearshore bathymetry using ICESat-2 lidar data and remote-sensing images. Opt. Express 2021, 29, 2411–2430. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Alexander, P.; Wu, Q.; Tedesco, M.; Shu, S. Characterization of ice shelf fracture features using ICESat-2-A case study over the Amery Ice Shelf. Remote Sens. Environ. 2021, 255, 112266. [Google Scholar] [CrossRef]
- Lai, Y.R.; Wang, L. Monthly Surface Elevation Changes of the Greenland Ice Sheet From ICESat-1, CryoSat-2, and ICESat-2 Altimetry Missions. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F.; Kacimi, S.; Webster, M.A.; Kurtz, N.T.; Petty, A.A. Decay of the Snow Cover Over Arctic Sea Ice from ICESat-2 Acquisitions during Summer Melt in 2019. Geophys. Res. Lett. 2020, 47, e2020GL088209. [Google Scholar] [CrossRef]
- Liu, M.; Popescu, S.C.; Malambo, L. Feasibility of Burned Area Mapping Based on ICESAT-2 Photon Counting Data. Remote Sens. 2020, 12, 24. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Wang, C.; Nie, S.; Pan, F.; Xi, X.; Hu, Z. Mapping forest height using photon-counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA. Ecol. Indic. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.C.; Malambo, L. Using ICESat-2 to Estimate and Map Forest Aboveground Biomass: A First Example. Remote Sens. 2020, 12, 1824. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J.; et al. Fusing simulated GEDI, ICESat-2 and NISAR data for regional aboveground biomass mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Sun, T.; Qi, J.; Huang, H. Discovering forest height changes based on spaceborne lidar data of ICESat-1 in 2005 and ICESat-2 in 2019: A case study in the Beijing-Tianjin-Hebei region of China. For. Ecosyst. 2020, 7, 704–715. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Magruder, L.; Neuenschwander, A.; Klotz, B. Digital terrain model elevation corrections using space-based imagery and ICESat-2 laser altimetry. Remote Sens. Environ. 2021, 264, 112621. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M.; Alonzo, M. Early ICESat-2 on-orbit Geolocation Validation Using Ground-Based Corner Cube Retro-Reflectors. Remote Sens. 2020, 12, 3653. [Google Scholar] [CrossRef]
- Bae, S.; Helgeson, B.; James, M.; Magruder, L.; Sipps, J.; Luthcke, S.; Thomas, T. Performance of ICESat-2 Precision Pointing Determination. Earth Space Sci. 2021, 8, e2020EA001478. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Thomas, T.C.; Pennington, T.A.; Rebold, T.W.; Nicholas, J.B.; Rowlands, D.D.; Gardner, A.S.; Bae, S. ICESat-2 Pointing Calibration and Geolocation Performance. Earth Space Sci. 2021, 8, e2020EA001494. [Google Scholar] [CrossRef]
- Tian, X.; Shan, J. Comprehensive Evaluation of the ICESat-2 ATL08 Terrain Product. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8195–8209. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Boy, J.P. Icesat-2 altimetry as geodetic control. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B3-2020, 1299–1306. [Google Scholar] [CrossRef]
- Wang, M.; Wei, Y.; Yang, B.; Zhou, X. Extraction and Analysis of Global Elevation Control Points from ICESat-2 /ATLAS Data. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 184–192. [Google Scholar] [CrossRef]
- Yang, Q.; Wei, J.; Zheng, J.; Wang, R.; Jia, N.; Qiu, L. Comparison of interpolation methods of digital elevation model using discrete point cloud data. Sci. Surv. Mapp. 2019, 44, 16–23. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Rosenheim, D.; Torlegard, K. Three-Dimensional Absolute Orientation of Stereo Models Using Digital Elevation Models. Photogramm. Eng. Remote Sens. 1988, 54, 1385–1389. [Google Scholar]
- Zhang, T.; Cen, M.; Feng, Y. Comparison of LZD and ICP Algorithms in DEM Matching without Control Points. J. Image Graph. 2006, 11, 714–719. [Google Scholar] [CrossRef]
- Low, K.-L.; Lastra, A. Predetermination of icp registration errors and its application to view planning. In Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling (3DIM 2007), Montreal, QC, Canada, 21–23 August 2007; pp. 73–80. [Google Scholar] [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 4; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 3; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020. [CrossRef]
- Khalsa, S.J.S.; Borsa, A.; Nandigam, V.; Phan, M.; Lin, K.; Crosby, C.; Fricker, H.; Baru, C.; Lopez, L. OpenAltimetry-rapid analysis and visualization of Spaceborne altimeter data. Earth Sci. Inform. 2020. [Google Scholar] [CrossRef]
- Hirschmuller, H. Accurate and efficient stereo processing by semi-global matching and mutual information. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 802, pp. 807–814. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K.; Jelley, B.; Robbins, J.; Klotz, B.; Popescu, S.; Nelson, R.; Harding, D.; Pederson, D. ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 4; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [CrossRef]
- Dong, J.C.; Ni, W.J.; Zhang, Z.Y.; Sun, G.Q. Performance of ICESat-2 ATL08 product on the estimation of forest height by referencing to small footprint LiDAR data. Natl. Remote Sens. Bull. 2021, 25, 1294–1307. [Google Scholar] [CrossRef]
- Ghaderpour, E. Some equal-area, conformal and conventional map projections: A tutorial review. J. Appl. Geod. 2016, 10, 197–209. [Google Scholar] [CrossRef]
- Zabih, R.; Woodfill, J. Non-Parametric Local Transforms for Computing Visual Correspondence; Eklundh, J.-O., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 151–158. [Google Scholar]
- Palaseanu-Lovejoy, M.; Bisson, M.; Spinetti, C.; Buongiorno, M.F.; Alexandrov, O.; Cecere, T. High-Resolution and Accurate Topography Reconstruction of Mount Etna from Pleiades Satellite Data. Remote Sens. 2019, 11, 2983. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X.; Hu, Z. A Ground Elevation and Vegetation Height Retrieval Algorithm Using Micro-Pulse Photon-Counting Lidar Data. Remote Sens. 2018, 10, 1962. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).