Abstract
The network real-time kinematic (RTK) technique uses continuously operating reference stations (CORS) within a geographic area to model the distance dependent errors, allowing users in the area to solve ambiguities. A key step in network RTK is to fix ambiguities between multiple reference stations. When a new satellite rises or when maintenance happens, many unknown parameters are involved in the mathematical model, and traditional methods take some time to estimate the integer ambiguities reliably. The purpose of this study is the single-epoch ambiguity resolution on small-scale CORS network with inter-station distance of around 50 km. A new differencing scheme is developed to explore the full potential of multi-frequency Global Navigation Satellite System (GNSS). In this scheme, a differencing operation is formed between satellites with the closest mapping functions. With the new differencing scheme, tropospheric error can be mostly neglected after the correction, as well as the double-differencing operation. Numerical tests based on two baselines of 49 km and 35 km show that the success rate of ambiguity resolution can reach more than 90%. The single-epoch ambiguity resolution for reference stations brings many benefits to the network RTK service, for example, the instantaneous recovery after maintenance or when a new satellite rises.
1. Introduction
Network real-time kinematic (RTK) uses a number of continuously operating reference stations (CORS) in a large area to model the distance-dependent errors due to satellite orbit, clock, ionosphere, and troposphere [1,2,3]. The distance-dependent errors can be modelled when the integer ambiguities can be fixed, and the ambiguity resolution between reference stations is a key step in the whole data processing chain [4,5]. When a new satellite rises or when maintenance happens, the orbital and propagation errors lead to difficulties in resolving integer ambiguities in observations instantaneously. In practice, the float ambiguity has to be estimated first, and it takes some time to achieve ambiguity resolution between reference stations [6]. The speed of integer ambiguity resolution between static reference stations can be improved with better understanding of these errors, and the single-epoch ambiguity resolution is the ultimate goal. The single epoch ambiguity resolution between reference stations brings great benefits after maintenance or breakdown, or in case of cycle slip, which happens frequently in low- or high-latitude areas during ionospheric scintillations.
In recent years, with the launching of Galileo and BDS, and also with the modernization of GPS and GLONASS [7,8], multi-frequency signals are available for each Global Navigation Satellite System (GNSS). The frequencies available on GNSS signals are summarized in Table 1. The advent of new GNSS constellations and signals on multiple frequencies undoubtedly provides outstanding advantages and benefits, and bring new opportunities for ambiguity resolution at the CORS network sites [7,8], and they also bring new challenges to ambiguity resolution for CORS network.

Table 1.
Observed signals of multiple frequencies.
There are generally two methods for CORS ambiguity resolution. The first is that all ambiguity parameters of all satellites are resolved at one time [6,9]. The other kind is cascading ambiguity resolution including wide-lane ambiguity resolution of Melbourne–Wübbena (MW) combinations, and narrow-lane ambiguity resolution by search. With these two kinds of methods, single epoch CORS ambiguity resolution cannot be realized, mostly due to code noise, ionospheric effects, and tropospheric effects. Another important reason is that these methods are developed for traditional dual-frequency GPS and do not take advantage of multiple GNSS systems and multiple frequency signals.
Thus, in this study, in order to explore the full potential of multi-frequency GNSS, a new method is designed for small CORS with inter-station distances less than 50 km. Similar to previous studies, it is a cascading method including three ambiguity resolution steps: extra-wide lane, wide-lane, and narrow-lane. In the last step, a different differencing scheme is proposed, one that is formed between neighboring satellites with the closest tropospheric mapping functions, and then the remaining tropospheric delay is neglected if the difference of the two mapping functions is less than a predefined value.
In this study, the data used in this study is described first, and the wide-lane combination of GNSS used in the Cascading methods is then introduced. The mathematic models for BDS, Galileo, and GPS are described in detail, respectively, followed by numerical test results. Finally the discussion and conclusions are drawn.
2. Mathematical Model and Data Description
The cascading ambiguity resolution method is widely used to resolve ambiguities in the CORS network. It starts with the extra-wide-lane combination, and goes to the wide-lane and narrow-lane combinations in sequential steps. Suppose that we have five frequencies. The general form for a wide-lane combination can be given by following equations [10]:
where , , ,, and are ambiguity, wavelength, frequency, observable, ionospheric delay, and noise of the combination, respectively. We further have
In the above equations, , , , and are integers and ; is the ionospheric delay at 1575.42 MHz frequency; denotes the standard deviation of measurement noise of the original observables.
The wide-lane combination for each GNSS will be investigated in the next section. They will be evaluated individually based on 24 h observations of two reference stations of the Australian CORS network: HOB2 and SPBY on 12 July 2020, as shown in Figure 1. The receiver types are SEPT POLARX5 and TRIMBLE ALLOY, respectively, and their sample interval of the observations is 1 s. The distance between HOB2 and SPBY is about 49 km.
Figure 1.
Reference stations of HOB2 and SPBY. (https://www.ga.gov.au/scientific-topics/positioning-navigation/geodesy/gnss-networks/station-coordinates-and-maps, accessed on 1 October 2021).
3. Cascading Ambiguity Resolution for GNSS
In this section, the mathematical model is presented for three GNSS constellations including BDS, Galileo, and GPS. For each GNSS constellation, the details of ambiguity resolution for extra-wide lane, wide lane, and narrow are described, and the benefits of the proposed differencing scheme are also presented.
3.1. Mathematical Model of BDS
There are five frequency bands for BDS as shown in Table 1. Most of commercial GNSS receivers support only three of them: L2I, L6I, and L7I. Table 2 lists the optimal extra wide (in bold) and wide-lane combinations of BDS in terms of the ratio of wavelength to observation noise. The details on selection of the optimal wide-lane combination can be found in [10].

Table 2.
Wide-lane combination of BDS.
(1) Extra-wide lane ambiguity resolution
Similar to previous research, the ambiguity resolution method of extra-wide lane is based on MW combination [11]:
and , .
Figure 2 shows the extra-wide lane ambiguity minus correct integer ambiguity, and we can see that most of them are within 0.1 cycle and all are within 0.3 cycle. It can be concluded that single epoch resolution can be achieved with a success rate of 99.999% if the threshold value is set to 0.25 cycle.
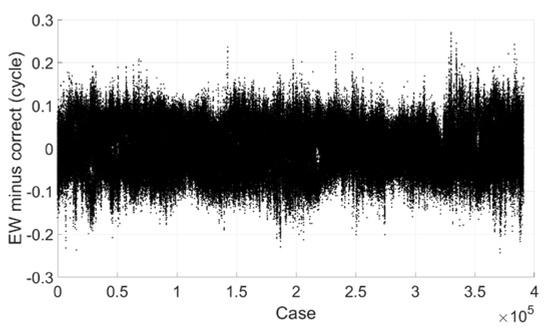
Figure 2.
Extra-wide lane ambiguity minus correct integer ambiguity (BDS).
(2) Wide-lane ambiguity resolution
The wide-lane ambiguity resolution is based on the following equation:
where the weight matrix .
Notice that in the above equation, the tropospheric error is ignored and it caused the bias that can be evaluated based on the following equation:
Figure 3 shows the size of the bias with a simulated tropospheric error from −0.5 m to 0.5 m. The unit of the bias of narrow-lane and wide-lane ambiguity is cycle and the unit of the bias of estimated ionospheric delay is meter. We can see that the biggest bias of wide-lane ambiguity is only about 0.11 cycle with a tropospheric error of 0.5 m. As the remaining tropospheric error is generally no more than 10 cm for medium-distance baseline after being corrected with popular models and double-differenced between stations and satellites, its effect on wide-lane ambiguity resolution can be neglected. Figure 4 is the estimated remaining zenith tropospheric delay of baseline HOB2-SPBY with ambiguities fixed. Though the estimated value is not stable due to observation noise and the effect of multipath, we can see that it should be about, or no more than, 2 cm.
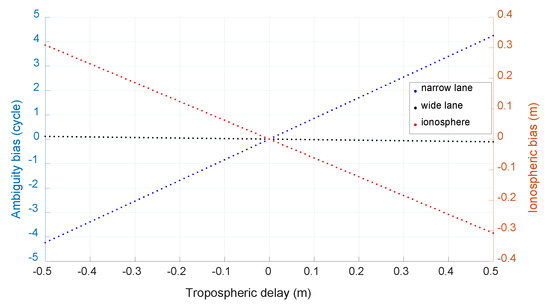
Figure 3.
The caused bias of neglected tropospheric error (BDS).
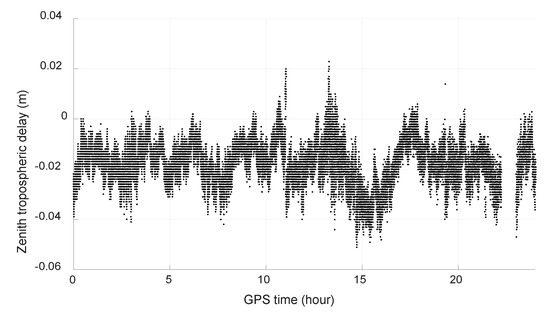
Figure 4.
Estimated zenith tropospheric delay (BDS).
Figure 5 shows the estimated wide-lane ambiguity minus correct integer ambiguity, and we can see that most of them are within 0.2 cycle and all are within 0.6 cycle. If the threshold value is set to 0.25 cycle, 99.9% of epochs can be fixed successfully, and there is no mis-fixed case.
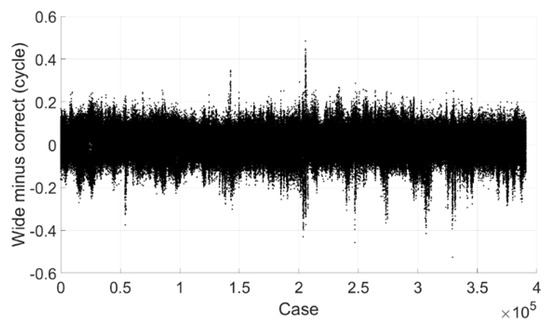
Figure 5.
Wide-lane ambiguity minus correct integer ambiguity (BDS).
(3) Narrow-lane ambiguity resolution
The resolution of narrow-lane ambiguity is based on the following equation:
Note that tropospheric error is also ignored and its effect on ambiguity resolution is studied as shown in Figure 6. We can see that the effects on both ambiguity and ionospheric delay are obvious, the bias of narrow-lane ambiguity can reach 0.924 cycle with ignored tropospheric error of 0.1 m and 0.185 cycle with tropospheric error of 2 cm.
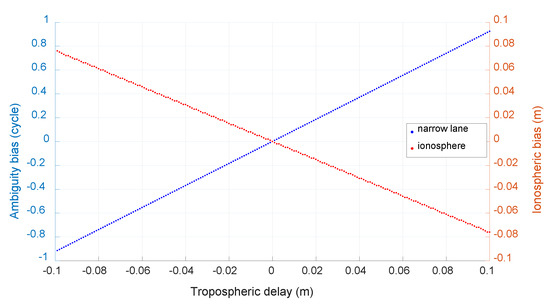
Figure 6.
The caused bias of neglected tropospheric error (BDS).
In order to reduce the effect of tropospheric error on narrow-lane ambiguity resolution, a new differencing scheme between satellites is proposed in which differencing is formed between satellites with closest tropospheric mapping functions. Figure 7 shows the statistics of the mapping function range after differencing between BDS satellites with closest mapping functions and we can see that more than 50% are within 0.25 and about 96% within 1.0. This means that with a zenith tropospheric error of 2 cm, more than half of remaining tropospheric errors, after differencing between satellites, will be within 5 mm and the caused bias of narrow-lane ambiguity resolution will be within 0.046 cycle; and about 96% will be within 2 cm and the caused bias of narrow-lane ambiguity resolution will be within 0.185 cycle.
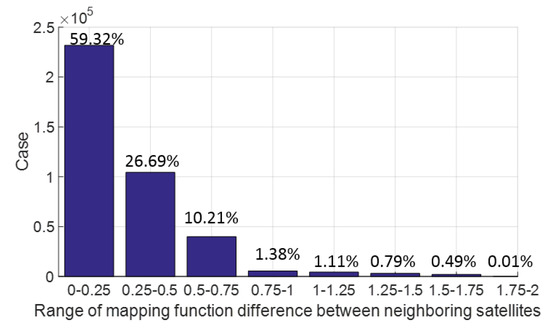
Figure 7.
Statistics of mapping functions after differencing between satellites with closest mapping function (BDS).
Figure 8 shows the estimated narrow-lane ambiguity minus correct integer ambiguity and only those with mapping functions within 1.0 are processed. We can see that most of them are within 0.2 cycle and all are within 0.6 cycle. If the threshold value is set to 0.25 cycle, 98.6% can be fixed successfully, and there is no mis-fixed case.
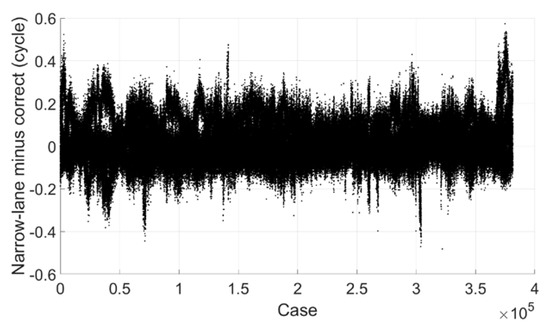
Figure 8.
Narrow-lane ambiguity minus correct integer ambiguity (BDS).
3.2. Mathematical Model of Galileo
Table 3 lists the optimal extra wide (in bold) and wide-lane combinations of Galileo in terms of the ratio of wavelength to observation noise.

Table 3.
Wide-lane combination of Galileo.
(1) Extra-wide lane ambiguity resolution
Similar to BDS, the ambiguity resolution method of extra wide-lane is also based on MW combination [11,12]:
where , , and and are frequencies; and are wavelengths; and are corresponding phase observations; and are corresponding code observations; is estimated integer extra-wide lane ambiguity.
As L5 observation is not available on station SPBY, only the ambiguity resolution performance of extra wide-lane combinations E67, E68, and E78 is tested. Figure 9, Figure 10 and Figure 11 show the ambiguities minus correct integer ones, we can see that for E67 and E68, most of them are within 0.2 cycle, all of them are within 0.6 cycle. For E78 most of them are within 0.1 cycle and all of them are within 0.2 cycle. If the threshold value is set to 0.25 cycle, for E67, 99.5% can be fixed successfully, for E68, it is 97.4%, for E78, it is 100%, and there is no mis-fixed case for all of them. As ambiguity of E68 can be derived from that of E67 and E78, its success rate can also be regarded as 99.5%.
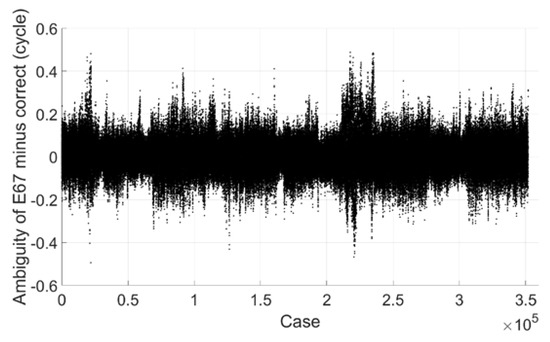
Figure 9.
Extra wide-lane E67 ambiguity minus correct integer ambiguity (Galileo).
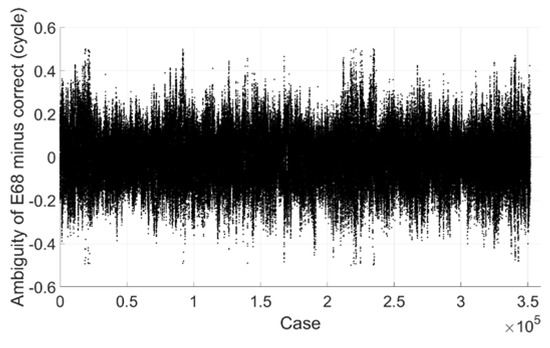
Figure 10.
Extra wide-lane E68 ambiguity minus correct integer ambiguity (Galileo).
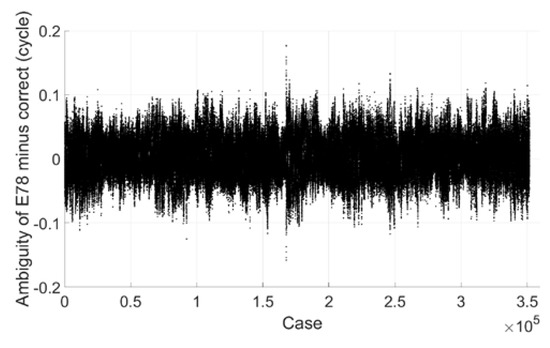
Figure 11.
Extra wide-lane E78 ambiguity minus correct integer ambiguity (Galileo).
(2) Wide-lane ambiguity resolution
The wide-lane ambiguity resolution will be based on the following equation:
where is ambiguity of wide-lane combination E16; , and are fixed extra wide-lane ambiguities. Note that as L5 observation is not available, it is not used in the above equations.
Notice that in the above equations, the tropospheric delay is also ignored and its effect on ambiguity resolution is also investigated with the method same to the above section for BDS case. Figure 12 shows the size of the caused bias with a simulated tropospheric error from −0.5 m to 0.5 m and the unit of the bias of narrow-lane and wide-lane ambiguity is cycle. We can see that the biggest bias of wide-lane ambiguity is only about 0.12 cycle with a tropospheric error of 0.5 m. With a tropospheric error of several cm as shown in Figure 4, its effect on wide-lane ambiguity resolution can be neglected.
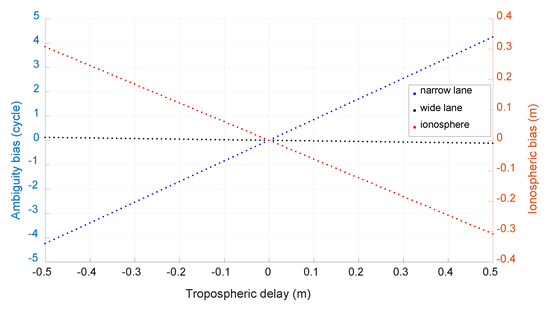
Figure 12.
The caused bias of neglected tropospheric error (Galileo).
Figure 13 shows the estimated wide-lane ambiguity minus correct integer ambiguity, we can see that most of them are within 0.2 cycle and all are within 0.75 cycle. If the threshold value is set to 0.25 cycle, 90.4% can be fixed successfully, and there is no mis-fixed case.
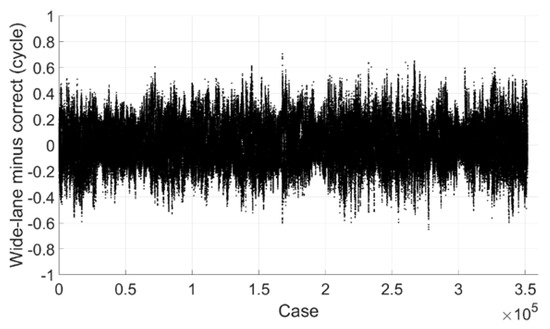
Figure 13.
Wide-lane ambiguity minus correct integer ambiguity (Galileo).
(3) Narrow-lane ambiguity resolution
The resolution of narrow-lane ambiguity will first be based on the following equation:
Note that tropospheric delay is also ignored and its effect on ambiguity resolution is investigated with the same method to BDS case and shown in Figure 14. We can see that the effect is similar to that of BDS and also obvious, the bias of narrow-lane ambiguity can reach 0.922 cycle with tropospheric error of 0.1 m and 0.184 cycle with tropospheric error of 2 cm.
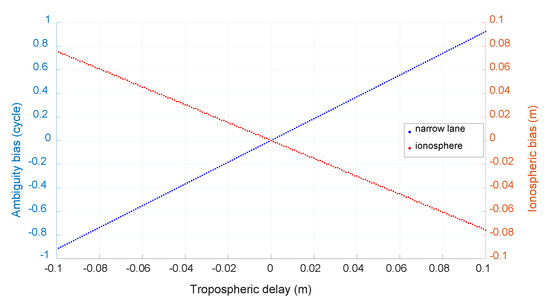
Figure 14.
The caused bias of neglected tropospheric error (Galileo).
In order to reduce the effect of tropospheric error on narrow-lane ambiguity resolution, the difference is also formed between satellites with closest tropospheric mapping functions. Figure 15 is a statistics of the mapping function range after differencing between Galileo satellites with closest mapping functions and we can see that 49.2% are within 0.25 and about 95% within 1.0, which means that with a zenith tropospheric error of 2 cm, about half of remaining tropospheric errors after differencing between satellites will be within 5 mm and the caused bias of narrow-lane ambiguity resolution will be within 0.046 cycle; and about 95% will be within 2 cm and the caused bias of narrow-lane ambiguity resolution will be within 0.184 cycle.
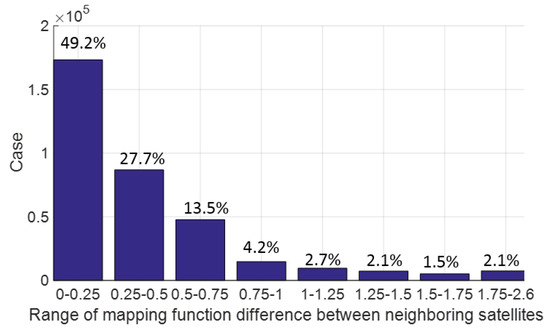
Figure 15.
Statistics of mapping functions after differencing between satellites with closest mapping functions (Galileo).
Figure 16 shows the estimated narrow-lane ambiguity minus correct one and only those with mapping functions within 1.0 are processed. We can see that most of them are within 0.2 cycle and all are within 0.7 cycle. If the threshold value is set to 0.25 cycle, 83.9% can be fixed successfully, and there is no mis-fixed case.
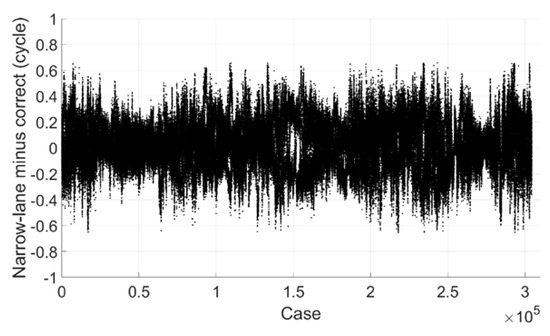
Figure 16.
Narrow-lane ambiguity minus correct integer ambiguity (Galileo).
3.3. Mathematical Model of GPS
As the RINEX files of HOB2 and SPBY have no GPS observations of the frequency band L5, another two stations named BEBR and VILL (shown in Figure 17) from EUREF Permanent GNSS Network are used. These two stations are also two IGS stations in Spain with a distance of about 35 km. The receiver types of the two stations are SEPT POLARX5TR and SEPT POLARX5 and the sample interval of the observations is 1 s. The 24 h observations on 9 May 2020 are used for numerical test in this study.
Figure 17.
The reference stations of CEBR and VILL. (https://www.epncb.oma.be/_networkdata/stationmaps.php, accessed on 1 October 2021).
Table 4 lists the optimal extra wide (in bold) and wide-lane combinations of GPS in terms of the ratio of wavelength to observation noise.

Table 4.
Wide-lane combination of GPS.
(1) Extra-wide lane ambiguity resolution
The ambiguity resolution method of extra-wide lane is based on MW combination [13,14]:
and , , where and are frequencies; and are wavelengths; and are corresponding phase observations; and are corresponding code observations; is estimated integer extra-wide lane ambiguity.
Figure 18 shows the extra-wide lane ambiguity of G25 minus correct integer ambiguity, we can see that most of them are within 0.2 cycle and all are within 0.5 cycle. If the threshold value is set to 0.25 cycle, 99.8% can be fixed successfully.
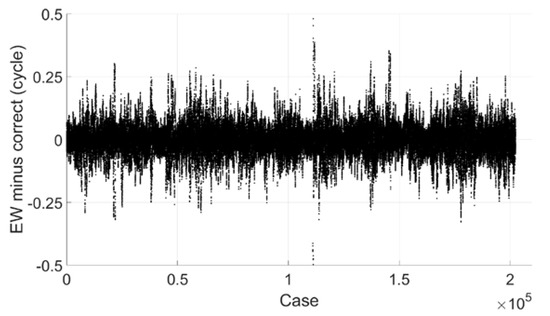
Figure 18.
Extra-wide lane ambiguity minus correct integer ambiguity (GPS).
(2) Wide-lane ambiguity resolution
The wide-lane ambiguity resolution will be based on the following equation:
where is ionospheric delay and , , and are corresponding coefficients; and are ambiguity of frequency bands 2 and 5 and .
Notice that in the above equation, the tropospheric delay is ignored and its effect on ambiguity resolution is also investigated with same method to BDS and Galileo. Figure 19 shows the caused bias by neglected tropospheric error simulated from −0.5 m to 0.5 m and the unit of the bias of narrow-lane and wide-lane ambiguity is cycle. We can see that the biggest bias of wide-lane ambiguity is only about 0.125 cycle with a tropospheric error of 0.5 m. As the remaining tropospheric error is generally no more than 10 cm for medium-distance baseline after being corrected with popular models and double-differenced between stations and satellites, its effect on wide-lane ambiguity resolution can be neglected. For comparison purpose, Figure 20 shows the estimated remaining zenith tropospheric delay of baseline CEBR-VILL with ambiguities fixed. Though the estimated value is not stable due to observation noise and the effect of multipath, we can see that it should be no more than 2 cm.
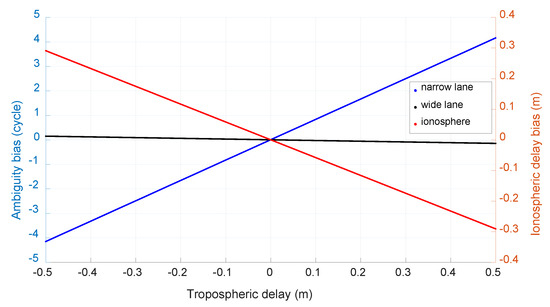
Figure 19.
The caused bias of neglected tropospheric error (GPS).
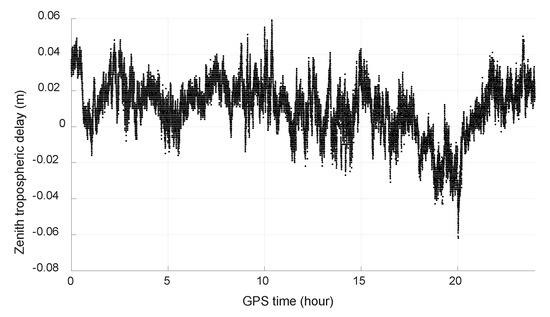
Figure 20.
Estimated tropospheric error of CEBR-VILL (GPS).
Figure 21 shows the estimated wide-lane ambiguity minus correct integer ambiguity, we can see that most of them are within 0.25 cycle and all are within 0.8 cycle. If the threshold value is set to 0.25 cycle, 96.1% can be fixed successfully, and there is no mis-fixed case.
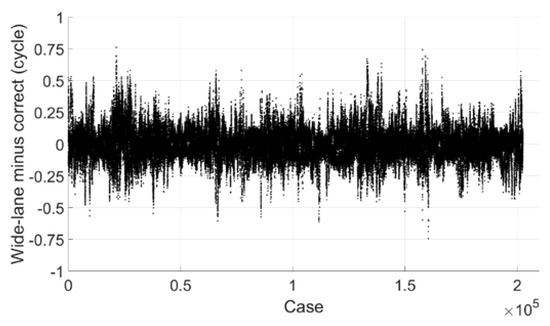
Figure 21.
Wide-lane ambiguity minus correct integer ambiguity (GPS).
(3) Narrow-lane ambiguity resolution
The resolution of narrow-lane ambiguity will first be based on the following equation:
Note that tropospheric delay is also ignored and its effect on ambiguity resolution is shown in Figure 22. We can see that the effect is obvious, the bias of narrow-lane ambiguity can reach about 0.918 cycle with ignored tropospheric delay of 0.1 m and 0.183 cycle with tropospheric delay of 2 cm.
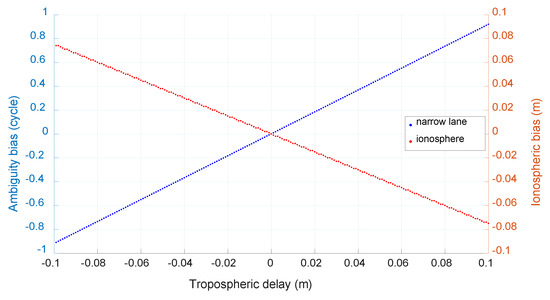
Figure 22.
The caused bias by neglected tropospheric error (GPS).
In order to reduce the effect of tropospheric error on narrow-lane ambiguity resolution, the difference is also formed between GPS satellites with closest tropospheric mapping functions. Figure 23 shows the statistics of the mapping function range after differencing and we can see that 42.9% are within 0.25 and more than 92% within 1.0, which means that with a zenith tropospheric error of 2 cm, about 40% of remaining tropospheric errors after differencing between satellites will be within 5 mm and the caused bias of narrow-lane ambiguity resolution will be within 0.046 cycle; and about 92% will be within 2 cm and the caused bias of narrow-lane ambiguity resolution will be within 0.183 cycle.
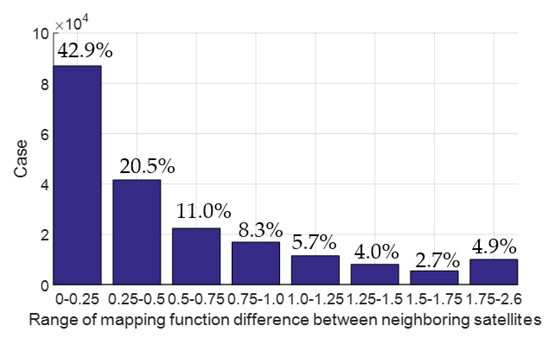
Figure 23.
Statistics of mapping functions after differencing between satellites with closest mapping functions (GPS).
Figure 24 shows the estimated narrow-lane ambiguity minus correct one and only those with mapping functions within 1.0 are processed. We can see that most of them are within 0.25 cycle. If the threshold value is set to 0.25 cycle, 91.33% can be fixed successfully, but due to the effect of multipath, there are mis-fixed cases of about 0.04%.
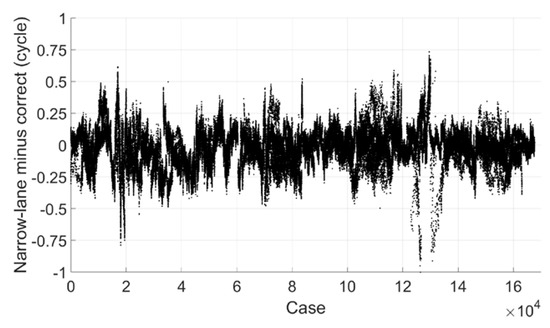
Figure 24.
Narrow-lane ambiguity minus correct integer ambiguity (GPS).
4. Discussion
Table 5 shows the statistics of the ambiguity resolution performance of BDS, Galileo, and GPS. We can see that for extra-wide lane ambiguity resolution, more than 99% can be fixed with single epoch for all three GNSS systems; as to wide-lane ambiguity resolution, it is about 99.9% for BDS, about 90.4% for Galileo, and about 96.1% for GPS; as to narrow-lane, for BDS, it is about 98.6%, about 83.9% for Galileo, and about 91.3% for GPS.

Table 5.
Statistics of ambiguity resolution performance.
The reason why the performance of Galileo is not as good as GPS and BDS may be because the observations of some Galileo satellites suffer from obvious errors due to the effect of multipath. For example, Figure 25 shows the difference of two ionosphere-free combinations and of satellite E21 based on the following formula:
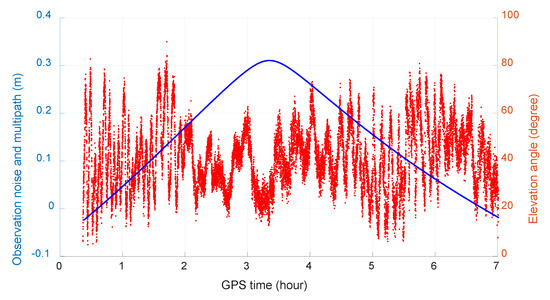
Figure 25.
Observation noise and the effect of multipath of Galileo satellite E21.
We can see that the multipath error for Galileo satellite E21 is obviously large.
5. Conclusions
The objective of this study is to achieve the single-epoch ambiguity resolution on the CORS network. In this paper, a new cascading ambiguity resolution method is proposed for small-scale CORS installed with multiple-frequency GNSS receivers. The distance between stations is about or no more than 50 km. The first step of ambiguity resolution, i.e., extra-wide lane, is to resolve the ambiguity of the MW combination that is traditionally used. The second step of ambiguity resolution, i.e., wide-lane, is based on fixed extra-wide lane where the tropospheric error is neglected in the mathematical model, which is verified with simulation. The third step of ambiguity resolution, i.e., narrow-lane, is based on a differencing scheme in which the differencing operation is formed between satellites with the closest mapping functions, after which, the tropospheric effects can be almost neglected.
The performance of the proposed method is evaluated with 24 h observations of two baselines with distances of about 49 km and 35 km, and the results show that for BDS, about 98.6% can be fixed with single epoch; for Galileo, it is about 83.9%; and for GPS, it is about 91.3%. So, the proposed new method is feasible for small CORS in cases where the remaining tropospheric error is no more than 2 cm after model correction and differencing between stations.
The use of the proposed method is dependent on the understanding of tropospheric delay between CORS stations. Only if we are sure that the tropospheric error is small enough can we use the method safely. While it is also related to the number of observed satellites. With more satellites, the distribution of mapping function becomes denser and the difference between closest ones becomes smaller; hence, even with a bigger zenith one, the tropospheric error can be neglected after differencing between satellites.
In recent years, CORS has become an indispensable infrastructure for positioning and navigation, such as in Hong Kong, Macau, Taiwan, Qingdao, etc., in China, and other cities in the world. Most of these CORS networks have an average distance between reference stations of around 50 km; therefore, the proposed method is expected to be beneficial to the performance of the network RTK.
Author Contributions
Conceptualization, S.J. and D.W.; methodology, S.J.; software, Q.Z.; validation, W.C. and Z.W.; formal analysis, K.H.; investigation, S.J.; resources, W.C.; data curation, S.J.; writing—original draft preparation, S.J.; writing—review and editing, D.W.; visualization, Q.Z.; supervision, W.C.; project administration, Z.W.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
The research was substantially funded by Shenzhen Science and Technology Innovation Commission (Project No. JCYJ20170818104822282), and supported by National Natural Science Foundation of China (Grant No. 42074028, 41704021, and 41701513), Key Program of National Natural Science Foundation of China (Grant No. 41631073), Natural Science Foundation of Shandong Province, China (Grant No. ZR2021MD060, ZR2020MD042, ZR2019MD005, ZR2016DQ01, ZR2017QD002, and ZR2017MD021), the Fundamental Research Funds for the Central Universities (Grant No. 18CX02064A, 18CX02054A, and 16CX02026A), Qingdao National Laboratory for Marine Science and Technology (Grant No. QNLM2016ORP0401), and State Key Laboratory of Earthquake Dynamics (LED2018B03).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
GNSS observation data are provided Regional Reference Frame Sub-Commission for Europe (EUREF) permanent network and Australia CORS network. All the data and products are publicly available through the respective organizations’ websites.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rizos, C. Network RTK research and implementation-a geodetic perspecti. Positioning 2009, 1, 144–150. [Google Scholar] [CrossRef]
- Wielgosz, P.; Kashani, I.; Grejner-Brzezinska, D. Analysis of long-range network RTK during a severe ionospheric storm. J. Geod. 2005, 79, 524–531. [Google Scholar] [CrossRef]
- Shen, Y.; Li, B.; Xu, G. Simplified equivalent multiple baseline solutions with elevation-dependent weights. GPS Solut. 2009, 13, 165–171. [Google Scholar] [CrossRef]
- Hu, G.; Khoo, H.; Goh, P.; Law, C. Development and assessment of GPS virtual reference stations for RTK positioning. J. Geod. 2003, 77, 292–302. [Google Scholar] [CrossRef]
- Dai, L.; Wang, J.; Rizos, C.; Han, S. Predicting atmospheric biases for real-time ambiguity resolution in GPS/GLONASS reference station networks. J. Geod. 2003, 76, 617–628. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J. Improving the speed of CORS Network RTK ambiguity resolution. In Proceedings of the IEEE/ION PLANS 2010, Indian Wells, CA, USA, 4–6 May 2010; pp. 79–84. [Google Scholar] [CrossRef]
- Alkan, R.M.; Karaman, H.; Sahin, M. GPS, GALILEO and GLONASS satellite navigation systems & GPS modernization. In Proceedings of the 2nd International Conference on Recent Advances in Space Technologies, RAST 2005, Istanbul, Turkey, 9–11 June 2005; pp. 390–394. [Google Scholar]
- Gao, W.; Gao, C.; Pan, S. A method of GPS/BDS/GLONASS combined RTK positioning for middle-long baseline with partial ambiguity resolution. Surv. Rev. 2016, 49, 212–220. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P. A theoretical study on the bottlenecks of GPS phase ambiguity resolution in a CORS RTK Network. J. Géod. Sci. 2011, 1, 143–153. [Google Scholar] [CrossRef][Green Version]
- Ji, S.; Chen, W.; Zhao, C.; Ding, X.; Chen, Y. Single epoch ambiguity resolution for Galileo with the CAR and LAMBDA methods. GPS Solut. 2007, 11, 259–268. [Google Scholar] [CrossRef]
- Melbourne, W.G. The case for ranging in GPS-based geodetic systems. In Positioning with GPS-1985: Proceedings, First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; US Department of Commerce: Rockville, MD, USA, 1985; pp. 373–386. [Google Scholar]
- Shengli, W.; Jian, D.; Jikun, O.; Wenfeng, N. Three-step Algorithm for Rapid Ambiguity Resolution between Reference Stations within Network RTK. J. Navig. 2016, 69, 1310–1324. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; He, X.; Zhang, Z.; Miao, W. Models, methods and assessment of four-frequency carrier ambiguity resolution for BeiDou-3 observations. GPS Solut. 2020, 24, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z. Code and phase multipath mitigation by using the observation-domain parameterization and its application in five-frequency GNSS ambiguity resolution. GPS Solut. 2021, 25, 1–14. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).