Retrieval of Arctic Vegetation Biophysical and Biochemical Properties from CHRIS/PROBA Multi-Angle Imagery Using Empirical and Physical Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Ground Data and Spectral Measurements
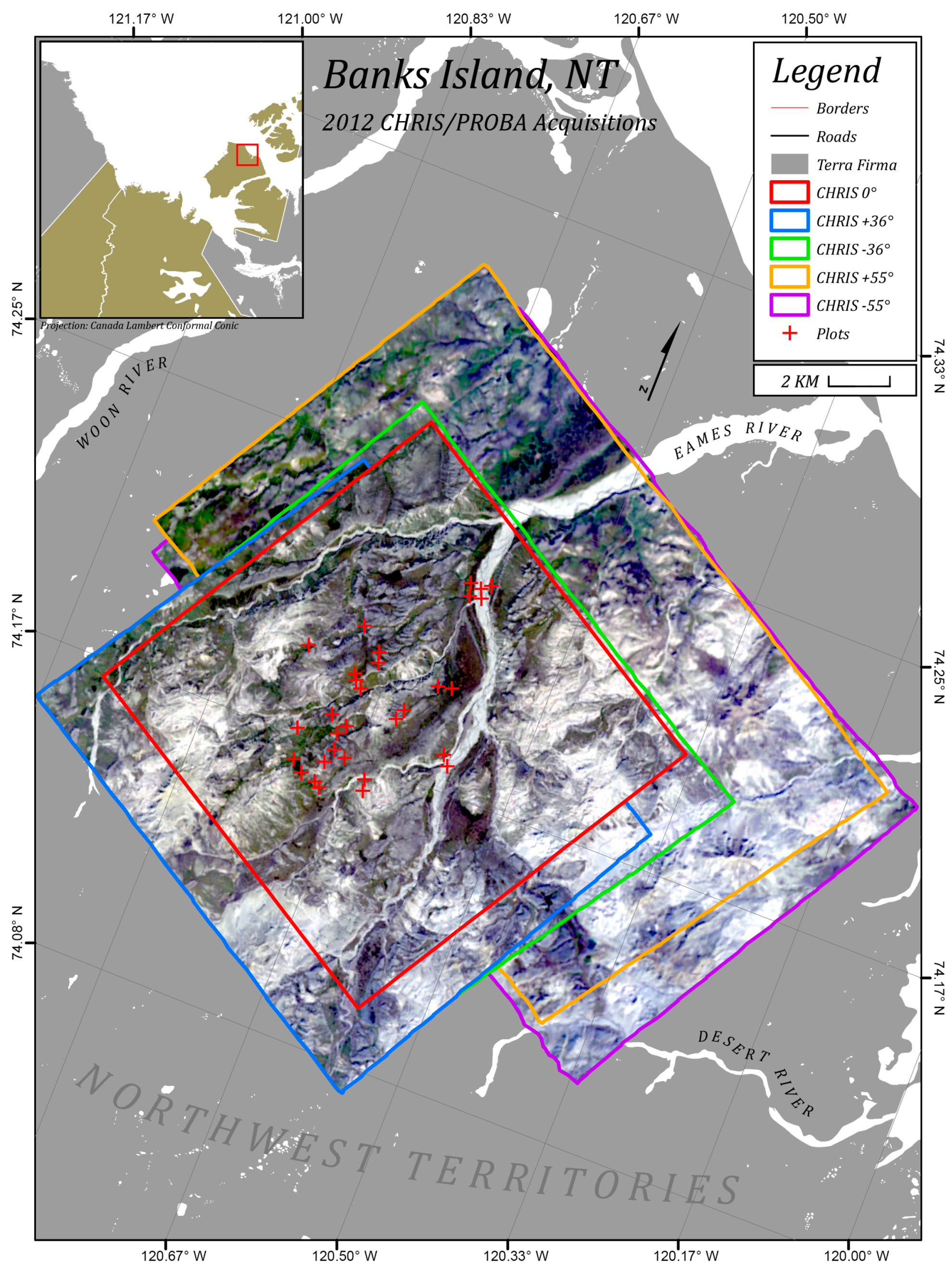
2.3. Satellite Image Acquisition and Pre-Processing
2.4. Parametric and Non-Parametric Regression Modelling
2.5. Physically Based Radiative Transfer Modelling and Inversion
3. Results
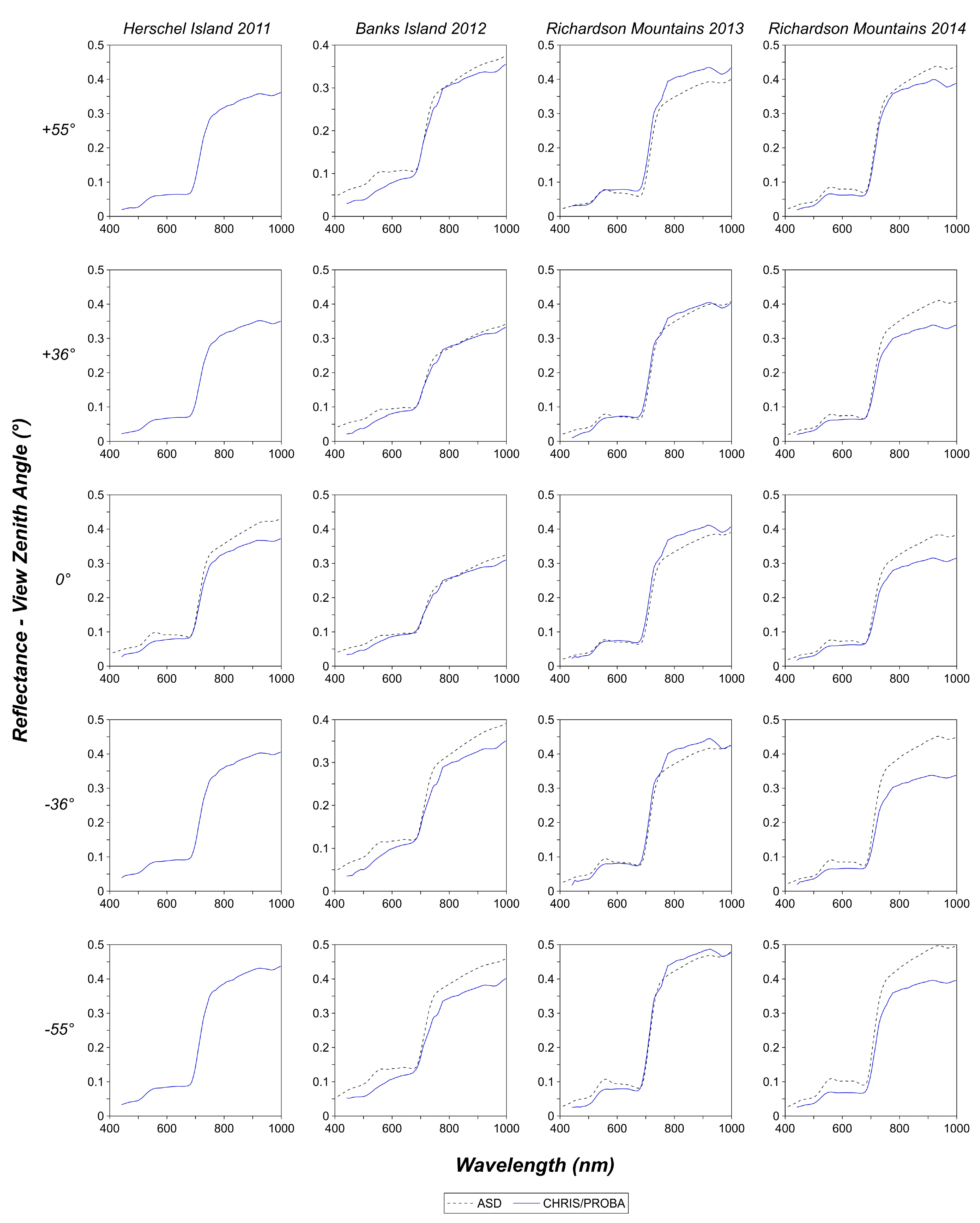
3.1. Comparison of Satellite Derived Surface Reflectance and Ground Measured Reflectance
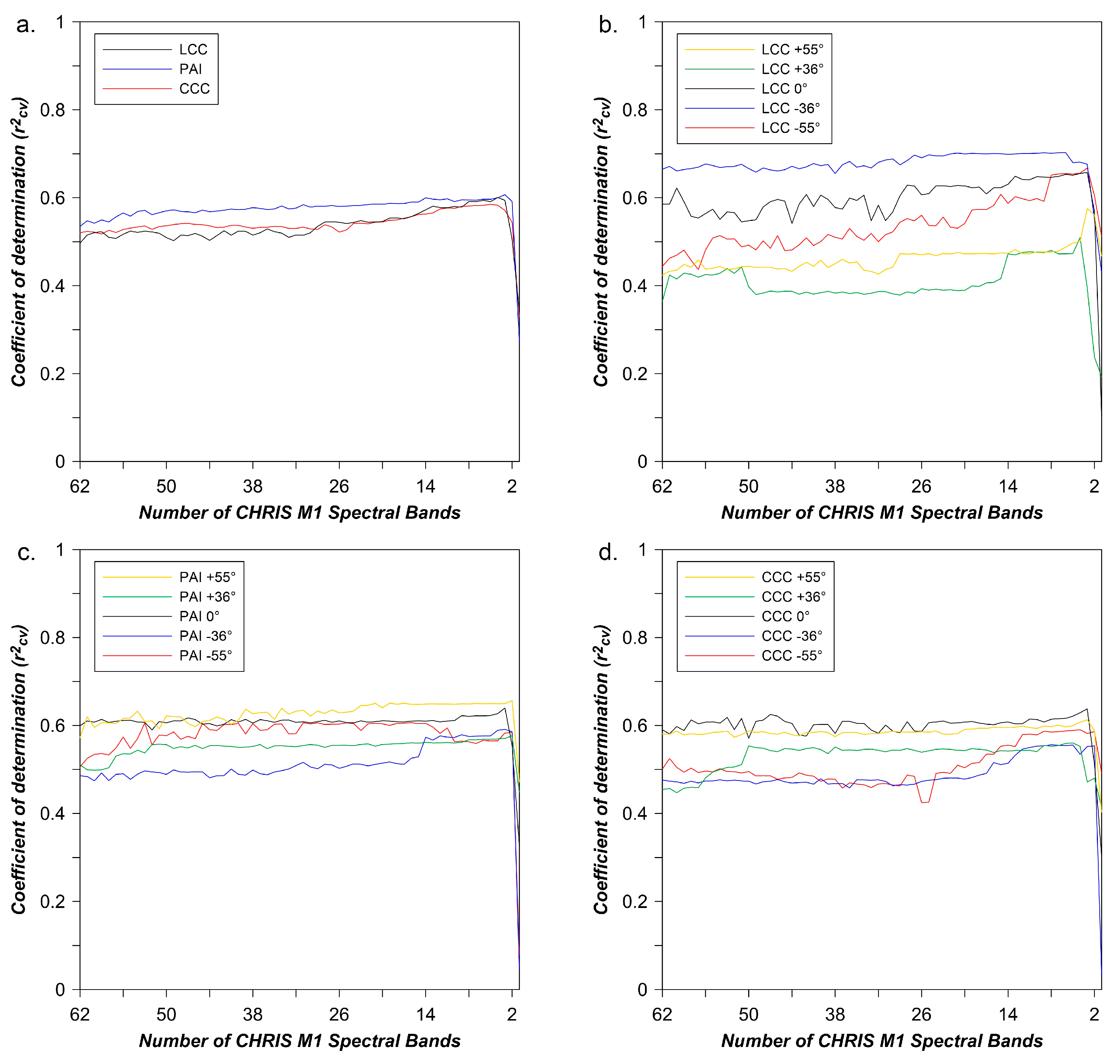
3.2. Parametric Regression: SR and ROSAVI
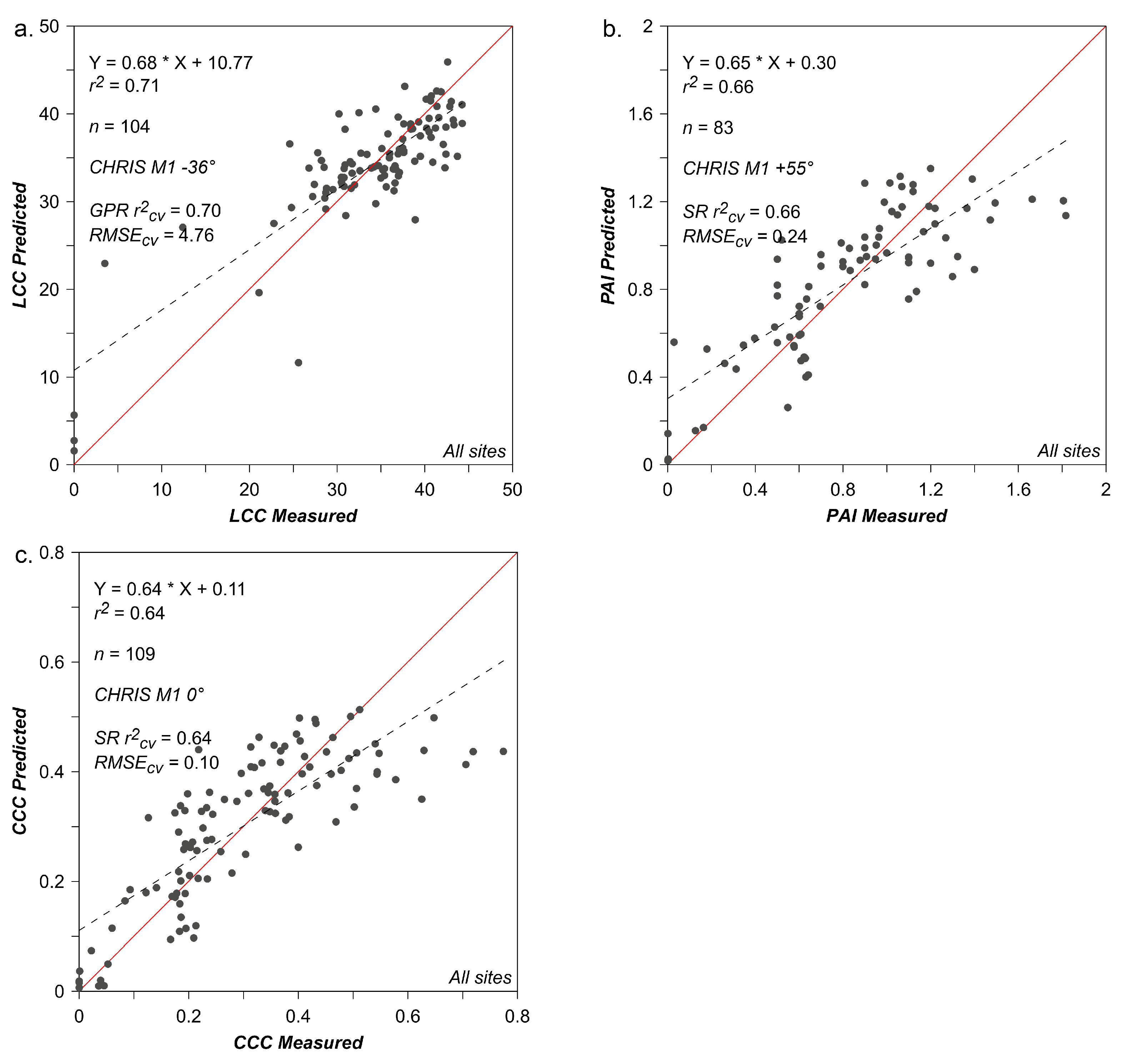
3.3. Non-Parametric Regression: Gaussian Processes Regression (GPR)
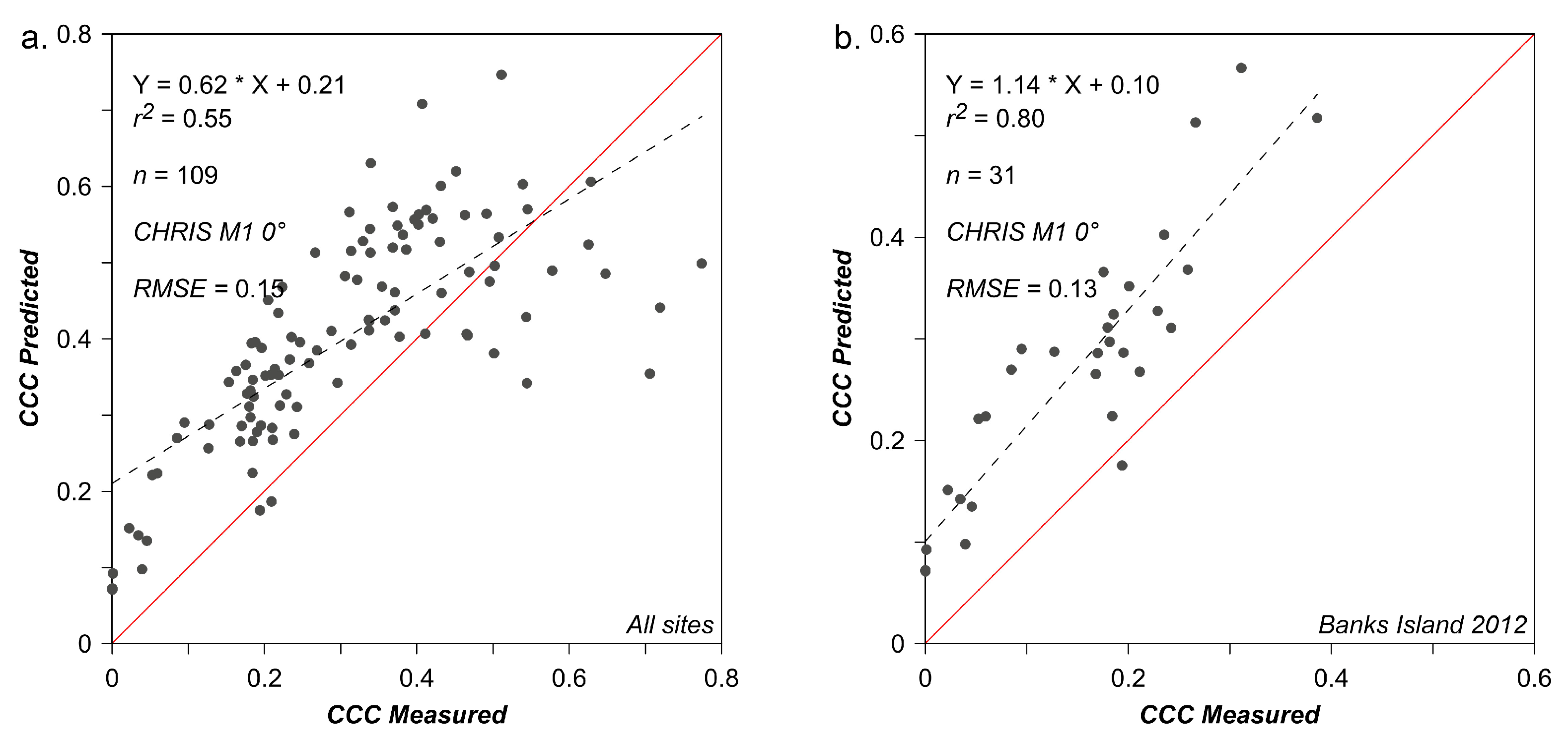
3.4. Physical Modelling: PROSAIL Inversion Using LM and LUT
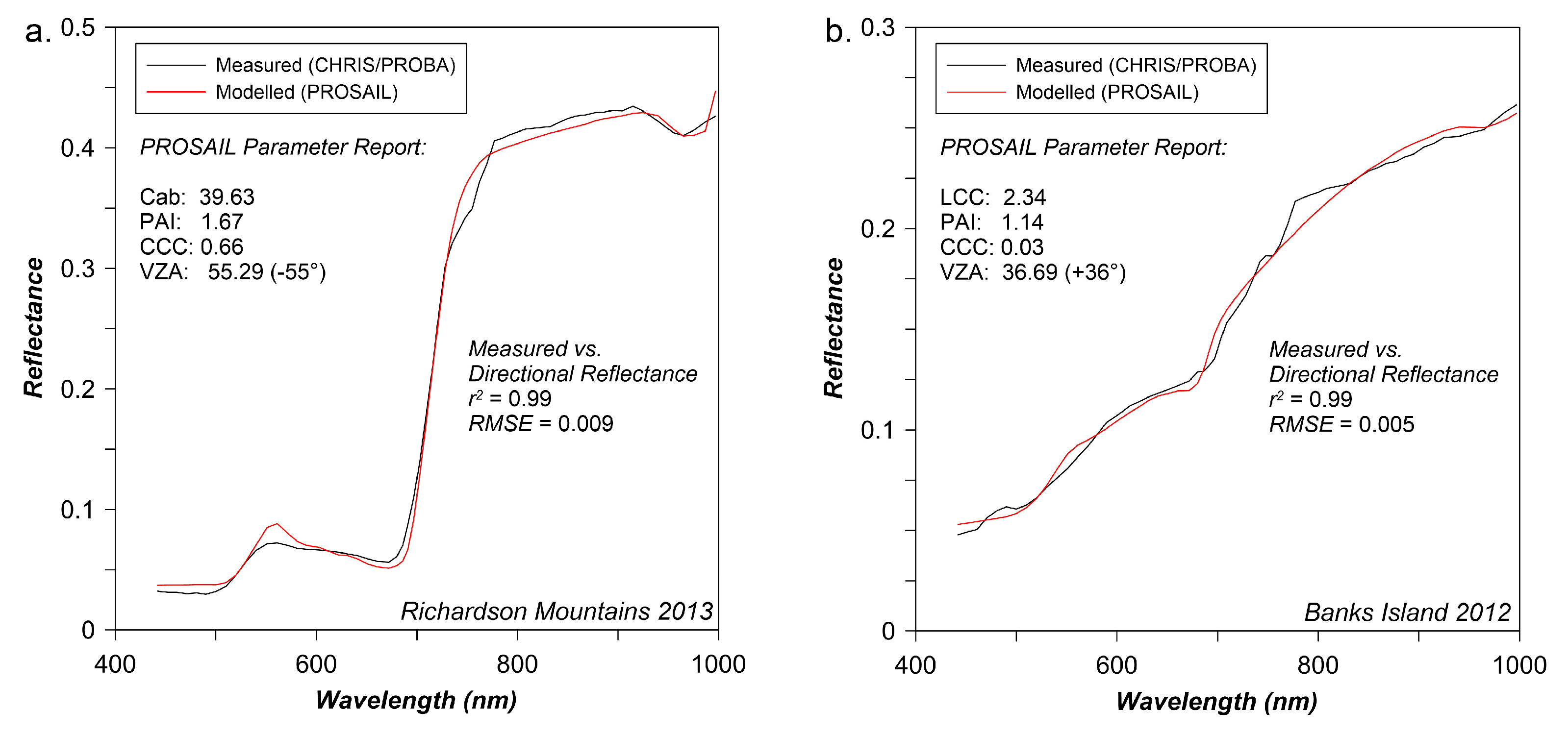
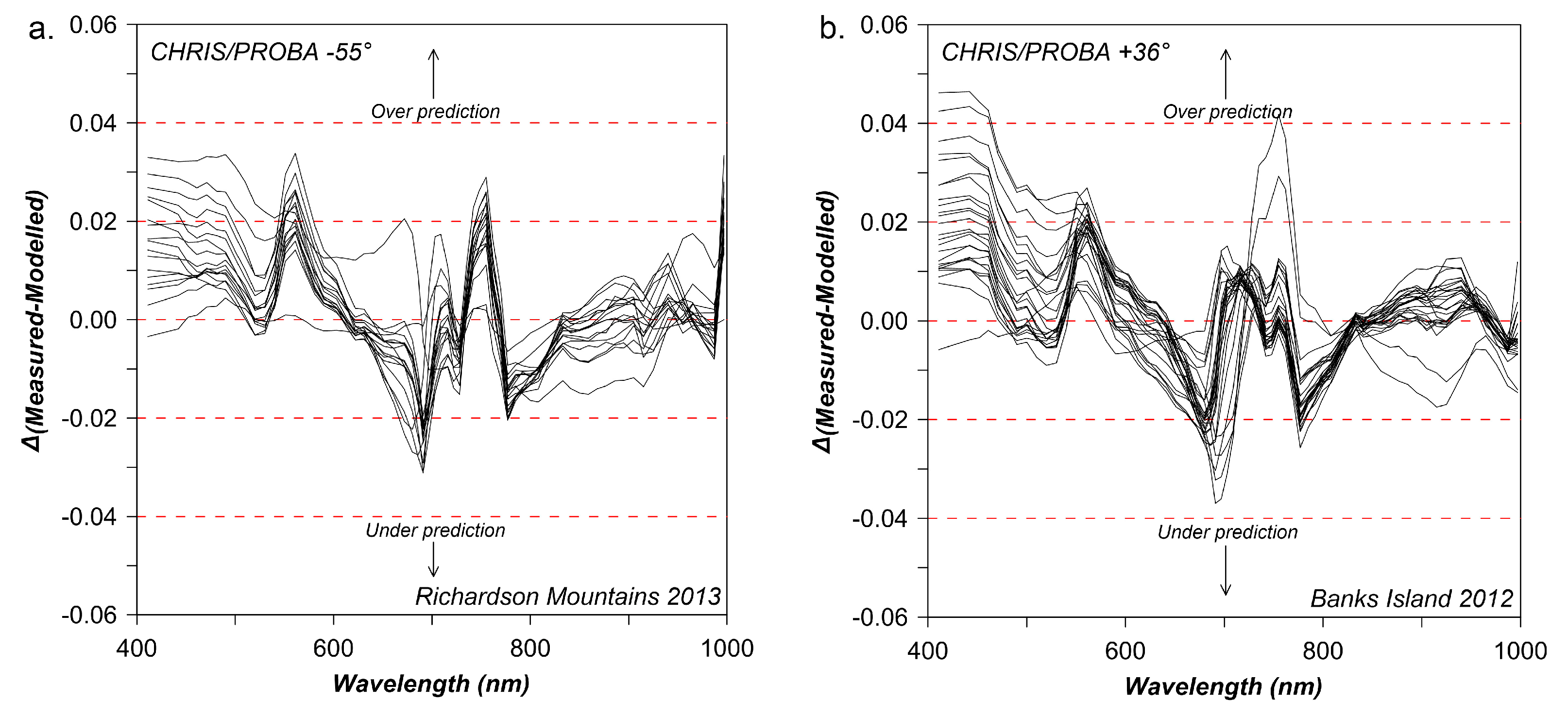
3.4.1. Spectral Curve Fitting Validation Using LM
3.4.2. Vegetation Modelling: PROSAIL Inversion Using LM and LUT
3.5. VZA Synthesis
4. Discussion
4.1. CHRIS M1 TOC Reflectance Spectra
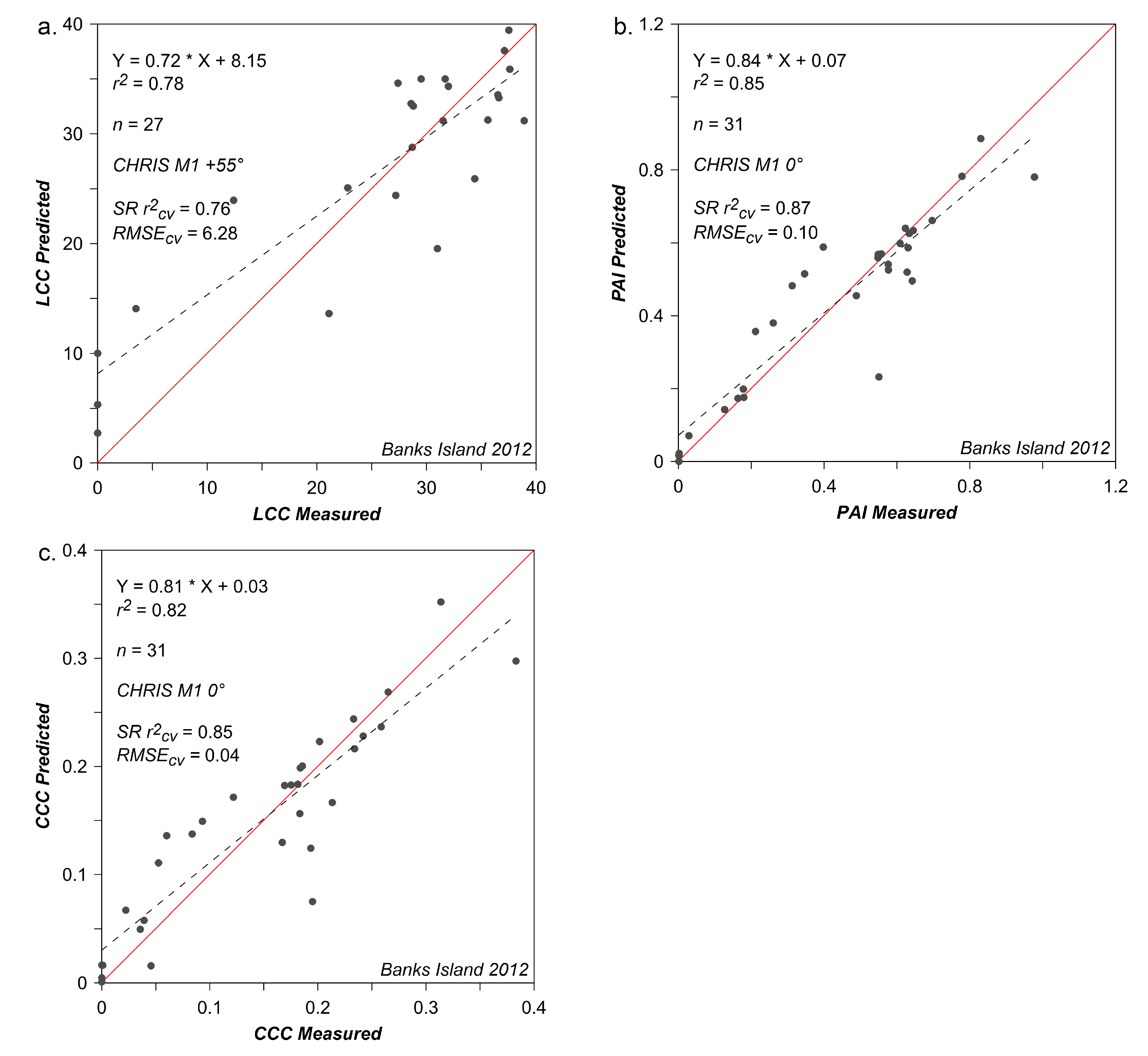
4.2. Empirical Modelling of LCC, PAI and CCC
4.3. Physically Modelling of LCC, CCC and PAI Using PROSAIL
5. Conclusions
- The remote sensing modelling results produced very similar results to the field-based modelling approaches described in Kennedy et al. [14], thus providing confirmation that the spatial sampling methodology employed at the field scale was appropriate for scaling to the remote sensing level.
- The spectroscopy data (comparison of field to CHRIS spectra) demonstrated that sun and sensor geometry are factors controlling the intensity and magnitude of Arctic vegetation reflectance curves. The observed relationships between spectra and surface features (e.g., the percent cover of photosynthetic materials, PAI) highlights the importance of sampling along environmental gradients representative of the greater ecosystem in question. Iteration based empirical modelling methodologies, such as GPR, should be tested further for their ability to compensate for sun-sensor induced variability when estimating leaf and canopy variables in Arctic environments.
- Iteration based empirical modelling methodologies (i.e., SR and GPR) produced the best overall results. Like the field-based approach, optimal weighted multi-angle spectral regions for variable retrievals (LCC, PAI and CCC) were revealed to be largely within expected pigment absorption, red edge and NIR regions.
- The non-iterative empirical approach based on preselected wavelengths used in a soil based VI (i.e., ROSAVI) was shown to produce the least accurate fits/model predictions; however, results were not substantially different from SR and GPR. Further investigation into the use of soil-based VIs is warranted due to the prevalence of gap fractions and non-photosynthetic materials in Arctic tundra canopies. These models should be tested iteratively using the same band selection techniques used with SR in this study.
- The PROSAIL model produced more accurate inversion results when vegetation variables ranges were greater or more separable and produced very similar results to the previous field-scale inversions. The similarity between the field and remote sensing results provides some indication that PROSAIL is capable of being scaled to the remote sensing level in the Arctic. Analysis of the error patterns for the simulated TOC reflectance showed a systematic error pattern across field sites and VZAs. Implications of these results are: (a) it is likely that Arctic tundra canopies violate some of the assumptions behind the physical model, and (b) model calibration (e.g., refractive index and absorption coefficients of leaf constituents) should be explored for Arctic plants/canopies. Future research should consider examining three-dimensional RTMs, as the assumptions behind these approaches may be able to better account for the complex optical properties of Arctic vegetation. For example, the three-dimensional DART model [123] may be able to better simulate the spatial heterogeneity of Arctic vegetation canopies as it relates to species assemblages, senescent vegetation and gap fractions/soil contributions [124].
- VZA-based results for all modelling types demonstrated that nadir (0° VZA) acquisition produced the best predictions of LCC, PAI and CCC; however, retrieval errors varied only slightly, indicating no distinct advantage for any one VZA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Artic Climate Impact Assessment (ACIA). Impacts of a Warming Arctic: Arctic Climate Impact Assessment; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Conservation of Arctic Flora and Fauna (CAFF). Arctic Biodiversity Assessment: Status and Trends in Arctic Biodiversity; Conservation of Arctic Flora and Fauna: Akureyri, Iceland; Narayana Press: Odder, Denmark, 2013. [Google Scholar]
- Sturm, M.; Racine, C.; Tape, K. Increasing shrub abundance in the Arctic. Nature 2001, 411, 546–547. [Google Scholar] [CrossRef]
- Huemmrich, K.F.; Gamon, J.A.; Tweedie, C.E.; Oberbauer, S.F.; Kinoshita, G.; Houston, S.; Kuchy, A.; Hollister, R.D.; Kwon, H.; Mano, M. Remote sensing of tundra gross ecosystem productivity and light use efficiency under varying temperature and moisture conditions. Remote Sens. Environ. 2010, 114, 481–489. [Google Scholar] [CrossRef]
- Huemmrich, K.F.; Kinoshita, G.; Gamon, J.A.; Houston, S.; Kwon, H.; Oechel, W.C. Tundra carbon balance under varying temperature and moisture regimes. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Post, E.; Forchhammer, M.; Bret-Harte, M.; Callaghan, T.; Christensen, T.; Elberling, B.; Fox, A.; Gilg, O.; Hik, D.; Høye, T.; et al. Ecological Dynamics Across the Arctic Associated with Recent Climate Change. Science 2009, 325, 1355–1358. [Google Scholar] [CrossRef] [PubMed]
- Myers-Smith, I.H.; Hik, D.S.; Kennedy, C.; Cooley, D.; Johnstone, J.F.; Kenney, A.J.; Krebs, C.J. Expansion of Canopy-Forming Willows Over the Twentieth Century on Herschel Island, Yukon Territory, Canada. AMBIO 2011, 40, 610–623. [Google Scholar] [CrossRef]
- Fraser, R.H.; Lantz, T.C.; Olthof, I.; Kokelj, S.V.; Sims, R.A. Warming-Induced Shrub Expansion and Lichen Decline in the Western Canadian Arctic. Ecosystems 2014, 17, 1151–1168. [Google Scholar] [CrossRef]
- Fraser, R.H.; Olthof, I.; Kokelj, S.V.; Lantz, T.C.; Lacelle, D.; Brooker, A.; Wolfe, S.; Schwarz, S. Detecting landscape changes in high latitude environments using Landsat trend analysis: 1. Visualization. Remote Sens. 2014, 6, 11533–11557. [Google Scholar] [CrossRef]
- Olthof, I.; Fraser, R.H. Detecting landscape changes in high latitude environments using Landsat trend analysis: 2. Classification. Remote Sens. 2014, 6, 11558–11578. [Google Scholar] [CrossRef]
- Bhatt, U.S.; Walker, D.A.; Raynolds, M.K.; Comiso, J.C.; Epstein, H.E.; Jia, G.; Gens, R.; Pinzon, J.E.; Tucker, C.J.; Tweedie, C.E.; et al. Circumpolar Arctic tundra vegetation change is linked to sea ice decline. Earth Interact. 2010, 14, 1–20. [Google Scholar] [CrossRef]
- Goetz, S.J.; Bunn, A.J.; Fiske, G.J.; Houghton, R.A. Satellite-observed photosynthetic trends across North America associated with climate and fire disturbance. Proc. Natl. Acad. Sci. USA 2005, 102, 13521–13525. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Kennedy, B.E.; King, D.J.; Duffe, J. Comparison of Empirical and Physical Modelling for Estimation of Biochemical and Biophysical Vegetation Properties: Field Scale Analysis across an Arctic Bioclimatic Gradient. Remote Sens. 2020, 12, 3073. [Google Scholar] [CrossRef]
- Stow, D.; Hope, A.; McGuire, D.; Verbyla, D.; Gamon, J.; Huemmrich, F.; Houston, S.; Racine, C.; Sturm, M.; Tape, K.; et al. Remote sensing of vegetation and land-cover change in Arctic Tundra Ecosystems. Remote Sens. Environ. 2004, 89, 281–308. [Google Scholar] [CrossRef]
- Laidler, G.J.; Treitz, P.M.; Atkinson, D.M. Remote Sensing of Arctic Vegetation: Relations between the NDVI, Spatial Resolution and Vegetation Cover on Boothia Peninsula, Nunavut. Arctic 2008, 61, 1–13. [Google Scholar] [CrossRef]
- McFadden, J.P.; Chapin, F.S.; Hollinger, D.Y. Sub grid-scale variability in the surface energy balance of Arctic tundra. J. Geophys. Res. 1998, 103, 28947–28961. [Google Scholar] [CrossRef]
- Gamon, J.A.; Huemmrich, K.F.; Stone, R.S.; Tweedie, C.E. Spatial and temporal variation in primary productivity (NDVI) of coastal Alaskan tundra: Decreased vegetation growth following earlier snowmelt. Remote Sens. Environ. 2013, 129, 144–153. [Google Scholar] [CrossRef]
- Shippert, M.M.; Walker, D.A.; Auerbach, N.A.; Lewis, B.E. Biomass and leaf-area index maps derived from SPOT images for Toolik Lake and Imnavait Creek areas, Alaska. Polar Rec. 1995, 31, 147–154. [Google Scholar] [CrossRef]
- Jacobsen, A.; Hansen, B. Estimation of the soil heat flux/net radiation ratio based on spectral vegetation indexes in high-latitude Arctic areas. Int. J. Remote Sens. 1999, 20, 445–461. [Google Scholar] [CrossRef]
- Dungan, J. Spatial prediction of vegetation quantities using ground and image data. Int. J. Remote Sens. 1998, 19, 267–285. [Google Scholar] [CrossRef]
- Lobo, A.; Moloney, K.; Chic, O.; Chiariello, N. Analysis of fine-scale spatial pattern of a grassland from re-motely-sensed imagery and field collected data. Landsc. Ecol. 1998, 13, 111–131. [Google Scholar] [CrossRef]
- Ostendorf, B.; Reynolds, J.F. A model of Arctic tundra vegetation derived from topographic gradients. Landsc. Ecol. 1998, 13, 187–201. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.E.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P.J. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimated for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.; Schlerf, M. Mapping grassland leaf area index with airborne hyperspectral imagery: A comparison study of statistical approaches and inversion of radiative transfer models. ISPRS J. Photogramm. Remote Sens. 2011, 66, 894–906. [Google Scholar] [CrossRef]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Monitoring canopy biophysical and biochemical parameters in ecosystem scale using satellite hyperspectral imagery: An application on a Phlomis fruticosa Mediterranean ecosystem using multi-angular CHRIS/PROBA observations. Remote Sens. Environ. 2010, 114, 977–994. [Google Scholar] [CrossRef]
- Sykioti, O.; Paronis, D.; Stagakis, S.; Kyparissis, A. Band depth analysis of CHRIS/PROBA data for the study of a Mediterranean natural ecosystem. Correlations with leaf optical properties and ecophysiological parameters. Remote Sens. Environ. 2011, 115, 752–766. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Veroustraete, F.; Munoz-Mari, J.; Clevers, J.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods: A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Jensen, J.R. Introductory Digital Image Processing; Prentice Hall, Pearson Education Inc.: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Barnsley, M.J.; Settle, J.J.; Cutter, M.A.; Lobb, D.R.; Teston, F. The PROBA/CHRIS mission: A low-cost small sat for hyperspectral multiangle observations of the earth surface and atmosphere. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1512–1520. [Google Scholar] [CrossRef]
- Galeazzi, C.; Sacchetti, A.; Cisbani, A.; Babini, G. The PRISMA Program. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. IV-105–IV-108. [Google Scholar]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Liu, N.; Budkewitsch, P.; Treitz, P. Examining spectral reflectance features related to Arctic percent vegetation cover: Implications for hyperspectral remote sensing of Arctic tundra. Remote Sens. Environ. 2017, 192, 58–72. [Google Scholar] [CrossRef]
- Bratsch, S.N.; Epstein, H.E.; Buchhorn, M.; Walker, D.A. Differentiating among four Arctic tundra plant communities at Ivotuk, Alaska using field spectroscopy. Remote Sens. 2016, 8, 51. [Google Scholar] [CrossRef]
- Buchhorn, M.; Walker, D.A.; Heim, B.; Raynolds, M.K.; Epstein, H.E.; Schwieder, M. Ground-based hyperspectral characterization of Alaska tundra vegetation along environmental gradients. Remote Sens. 2013, 5, 3971–4005. [Google Scholar] [CrossRef]
- Davidson, S.; Santos, M.; Sloan, V.; Watts, J.; Phoenix, G.; Oechel, W.; Zona, D. Mapping Arctic Tundra Vegetation Communities using Field Spectroscopy and Multispectral Satellite Data in North Alaska, USA. Remote Sens. 2016, 8, 978. [Google Scholar] [CrossRef]
- Hope, A.S.; Kimball, J.S.; Stow, D.A. The relationship between tussock tundra spectral reflectance properties and biomass and vegetation composition. Int. J. Remote Sens. 1993, 14, 1861–1874. [Google Scholar] [CrossRef]
- Huemmrich, K.F.; Gamon, J.A.; Tweedie, C.E.; Campbell, P.K.; Landis, D.R.; Middleton, E.M. Arctic tundra vegetation functional types based on photosynthetic physiology and optical properties. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 265–275. [Google Scholar] [CrossRef]
- Kushida, K.; Kim, Y.; Tsuyuzaki, S.; Fukuda, M. Spectral vegetation indices for estimating shrub cover, green phytomass and leaf turnover in a sedge-shrub tundra. Int. J. Remote Sens. 2009, 30, 1651–1658. [Google Scholar] [CrossRef]
- Kushida, K.; Hobara, S.; Tsuyuzaki, S.; Kim, Y.; Watanabe, M.; Setiawan, Y.; Harada, K.; Shaver, G.R.; Fukuda, M. Spectral indices for remote sensing of phytomass, deciduous shrubs, and productivity in Alaskan Arctic tundra. Int. J. Remote Sens. 2015, 36, 4344–4362. [Google Scholar] [CrossRef]
- Riedel, S.M.; Epstein, H.E.; Walker, D.A. Biotic controls over spectral reflectance of Arctic tundra vegetation. Int. J. Remote Sens. 2005, 26, 2391–2405. [Google Scholar] [CrossRef]
- Riedel, S.M.; Epstein, H.E.; Walker, D.A.; Richardson, D.L.; Calef, M.P.; Edwards, E.; Moody, A. Spatial and temporal heterogeneity of vegetation properties among four tundra plant communities at Ivotuk, Alaska, USA. Arct. Antarct. Alp. Res. 2005, 37, 25–33. [Google Scholar] [CrossRef]
- Ulrich, M.; Grosse, G.; Chabrillat, S.; Schirrmeister, L. Spectral characterization of periglacial surfaces and geomorphological units in the Arctic Lena Delta using field spectrometry and remote sensing. Remote Sens. Environ. 2009, 113, 1220–1235. [Google Scholar] [CrossRef]
- Tieszen, L.L.; Johnson, P.L. Pigment Structure of Some Arctic Tundra Communities. Ecology 1968, 49, 370–373. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT–4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Juszak, I.; Erb, A.M.; Maximov, T.C.; Schaepman-Strub, G. Arctic shrub effects on NDVI, summer albedo and soil shading. Remote Sens. Environ. 2014, 153, 79–89. [Google Scholar] [CrossRef]
- Buchhorn, M.; Raynolds, M.K.; Walker, D.A. Influence of BRDF on NDVI and biomass estimations of Alaska Arctic tundra. Environ. Res. Lett. 2016, 11, 125002. [Google Scholar] [CrossRef]
- Raynolds, M.K.; Walker, D.A.; Balser, A.; Bay, C.; Campbell, M.; Cherosov, M.M.; Daniëls, F.J.A.; Eidesen, P.B.; Ermokhina, K.A.; Frost, G.V.; et al. A raster version of the Circumpolar Arctic Vegetation Map (CAVM). Remote Sens. Environ. 2019, 232. [Google Scholar] [CrossRef]
- Kennedy, B.; Pouliot, D.; Manseau, M.; Fraser, R.; Duffe, J.; Pasher, J.; Chen, W.; Olthof, I. Assessment of Landsat-based terricolous macrolichen cover retrieval and change analysis over caribou ranges in northern Canada and Alaska. Remote Sens. Environ. 2020, 240. [Google Scholar] [CrossRef]
- Liu, N.; Treitz, P. Modelling high arctic percent vegetation cover using field digital images and high-resolution satellite data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 445–456. [Google Scholar] [CrossRef]
- Stagakis, S.; Vanikiotis, T.; Sykioti, O. Estimating forest species abundance through linear unmixing of CHRIS/PROBA imagery. ISPRS J. Photogramm. Remote Sens. 2016, 119, 79–89. [Google Scholar] [CrossRef]
- Schaepman, M.E. Spectrodirectional remote sensing: From pixels to processes. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 204–223. [Google Scholar] [CrossRef]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Tracking seasonal changes of leaf and canopy light use efficiency in a Phlomis fruticosa Mediterranean ecosystem using field measurements and multi-angular satellite hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2014, 97, 138–151. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.; Koetz, B.; Kneubuhler, M. Angular sensitivity analysis of vegetation indices derived from CHRIS/PROBA data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Vierling, L.A.; Deering, D.W.; Eck, T.F. Differences in Arctic tundra vegetation type and phenology as seen using bidirectional radiometry in the early growing season. Remote Sens. Environ. 1997, 60, 71–82. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: New York, NY, USA, 2006. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Kennedy, B.E. Multi-Angle Spectroscopic Remote Sensing of Arctic Vegetation Biochemical and Biophysical Properties. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2017. [Google Scholar]
- Walker, D.A.; Daniëls, F.J.A.; Alsos, I.; Bhatt, U.S.; Breen, A.L.; Buchhorn, M.; Bültmann, H.; Druckenmiller, L.A.; Edwards, M.E.; Ehrich, D.; et al. Circumpolar Arctic vegetation: A hierarchic review and roadmap toward an internationally consistent approach to survey, archive and classify tundra plot data. Environ. Res. Lett. 2016, 11, 55005. [Google Scholar] [CrossRef]
- Daniëls, F.J.; Gillespie, L.J.; Poulin, M. Plants. In Arctic Biodiversity Assessment. Status and Trends in Arctic Biodiversity; Meltofte, H., Ed.; Conservation of Arctic Flora and Fauna: Akureyri, Iceland; Narayana Press: Odder, Denmark, 2013; pp. 310–353. [Google Scholar]
- Sieg, B.; Drees, B.; Daniëls, F. Vegetation and altitudinal zonation in continental West Greenland. Bioscience 2006, 57, 1–93. [Google Scholar]
- Washburn, A.L. Permafrost features as evidence of climatic change. Earth Sci. Rev. 1980, 15, 327–402. [Google Scholar] [CrossRef]
- Kade, A.; Walker, D.A.; Raynolds, M.K. Plant communities and soils in cryoturbated tundra along a bioclimate gradient in the low Arctic, Alaska. Phytocoenologia 2005, 35, 761–820. [Google Scholar] [CrossRef]
- Frost, G.V.; Epstein, H.E.; Walker, D.A.; Matyshak, G.; Ermokhina, K. Patterned-ground facilitates shrub expansion in low Arctic tundra. Environ. Res. Lett. 2013, 8, 015035. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.; Zhang, X.; Zhang, B.; Tong, Q. Simulation of EO-1 Hyperion data from ALI multispectral data based on the spectral reconstruction approach. Sensors 2009, 9, 3090–3108. [Google Scholar] [CrossRef] [PubMed]
- Cerovic, Z.; Masdoumier, G.; Ghozlen, N.; Latouche, G. A new optical leaf-clip meter for simultaneous non-destructive assessment of leaf chlorophyll and epidermal flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Neumann, H.H.; Den Hartog, G.D.; Shaw, R.H. Leaf-area measurements based on hemispherical photographs and leaf-litter collection in a deciduous forest during autumn leaf-fall. Agric. For. Meteorol. 1989, 45, 325–345. [Google Scholar] [CrossRef]
- Mougin, E.; Demarez, V.; Diawara, M.; Hiernaux, P.; Soumaguel, N.; Berg, A. Estimation of LAI, fAPAR and fCover of Sahel rangelands (Gourma, Mali). Agric. For. Meteorol. 2014, 198, 155–167. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. CAN-EYE V6.4.6 User Manual; L’Institut National de Recherche Agronomique (INRA): Paris, France, 2016; Available online: https://www6.paca.inra.fr/can-eye/ (accessed on 1 November 2016).
- Gitelson, A.A.; Vina, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote Estimation of Canopy Chlorophyll Content in Crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Rivera, J.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple cost functions and regularization options for improved retrieval of leaf chlorophyll content and LAI through inversion of the PROSAIL model. Remote Sens. 2013, 5, 3280–3304. [Google Scholar] [CrossRef]
- Yin, C.; He, B.; Quan, X.; Liao, Z. Chlorophyll content estimation in arid grasslands from Landsat-8 OLI data. Int. J. Remote Sens. 2016, 37, 615–632. [Google Scholar] [CrossRef]
- White, H.P.; Alonso, L. CHRIS-PROBA-Obs-Angle Spreadsheet. ESA BEAM Earth Observation Toolbox and Development Platform Forum—BEAM Toolbox Usage—Updating Metadata Thread. 2016. Available online: http://www.brockmann-consult.de/cms/web/beam/forum/-/message_boards/message/131883 (accessed on 1 November 2016).
- Natural Resources Canada. Atlas of Canada National Scale Data 1:1,000,000; Natural Resources Canada: Ottawa, ON, Canada, 2014; Available online: http://open.canada.ca/data/en/dataset/e9931fc7-034c-52ad-91c5-6c64d4ba0065 (accessed on 1 October 2016).
- Natural Resources Canada. Atlas of Canada, Northern Geodatabase; Natural Resources Canada: Ottawa, ON, Canada, 2012; Available online: http://open.canada.ca/data/en/dataset/7e388083-6b66-5e0e-a264-a3c0eb98a2f0 (accessed on 1 October 2016).
- Gómez-Chova, L.; Alonso, L.; Guanter, L.; Calpe, J.; Moreno, J. Algorithm Theoretical Basis Document for CHRIS/PROBA Noise Reduction; Contract No. 20442/07/I-LG; ESA ESRIN: Rome Italy, 2008. [Google Scholar]
- Gómez-Chova, L.; Alonso, L.; Guanter, L.; Camps-Valls, G.; Calpe, J.; Moreno, J. Correction of systematic spatial noise in push-broom hyperspectral sensors: Application to CHRIS/PROBA images. Appl. Opt. 2008, 47, 46–60. [Google Scholar] [CrossRef]
- Gómez-Chova, L.; Guanter, L.; Alonso, L.; Calpe, J.; Moreno, J. Algorithm Theoretical Basis Document for CHRIS/PROBA Cloud Screening; Contract No. 20442/07/I-LG; ESA ESRIN: Rome Italy, 2008. [Google Scholar]
- Guanter, L.; Alonso, L.; Gómez-Chova, L.; Moreno, J. Algorithm Theoretical Basis Document for CHRIS/PROBA Atmospheric Correction Module; Contract No. 20442/07/I-LG; ESA ESRIN: Rome, Italy, 2008. [Google Scholar]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Hoke, M.L.; Chetwynd, J.H.; Bernstein, L.S.; Shettle, E.P.; Matthew, M.W.; Adler-Golden, S.M. MODTRAN4 Version 3 Revision 1 User’s Manual; Technical Report for Air Force Research Laboratory; Hanscom Air Force Base: Bedford, MA, USA, 2003. [Google Scholar]
- Toutin, T.; Carbonneau, Y.; St. Laurent, L. Image Geometric Corrections. IEEE Trans. Geosci. Remote Sens. 1992, 30, 603–609. [Google Scholar] [CrossRef]
- Toutin, T. Review article: Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Poli, D.; Toutin, T. Review of developments in geometric modelling for high resolution satellite push-broom sensors. Photogramm. Rec. 2012, 27, 58–73. [Google Scholar] [CrossRef]
- Belfiore, O.R.; Parente, C. Comparison of Different Algorithms to Orthorectify WorldView-2 Satellite Imagery. Algorithms 2016, 9, 67. [Google Scholar] [CrossRef]
- Birth, G.; McVey, G. Measuring the Color of Growing Turf with a Reflectance Spectrophotometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping vegetation density in a heterogeneous river floodplain ecosystem using pointable CHRIS/PROBA data. Remote Sens. 2012, 4, 2866–2889. [Google Scholar] [CrossRef]
- Rivera, J.; Verrelst, J.; Alonso, L.; Moreno, J.; Camps-Valls, G. Toward a semi-automatic machine learning retrieval of biophysical parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1249–1259. [Google Scholar]
- Rivera, J.; Verrelst, J.; Delegido, J.; Veroustraete, F.; Moreno, J. On the semi-automatic retrieval of biophysical parameters based on spectral index optimization. Remote Sens. 2014, 6, 4927–4951. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modelling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Verhoef, W. Earth observation modeling based on layer scattering matrices. Remote Sens. Environ. 1985, 17, 165–178. [Google Scholar] [CrossRef]
- Kuusk, A. The Hot-Spot Effect in Plant Canopy Reflectance. In Photon-Vegetation Interactions; Myneni, R.B., Ross, J., Eds.; Springer: New York, NY, USA, 1991; pp. 139–159. [Google Scholar]
- Markwardt, C.B. Non-Linear Least Squares Fitting in IDL with MPFIT. In Proceedings of the Astronomical Data Analysis Software and Systems XVIII, Quebec City, QC, Canada, 2–5 November 2009; Bohlender, D., Dowler, P., Durand, D., Eds.; Astronomical Society of the Pacific: Quebec, QC, Canada, 2009; pp. 251–254. [Google Scholar]
- Baret, F.; Jacquemoud, S. Modeling Canopy Spectral Properties to Retrieve Biophysical and Biochemical Characteristics. In Imaging Spectrometry: A Tool for Environmental Observations; Hill, J., Mégier, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 145–167. [Google Scholar]
- Curran, P.J.; Dungan, J.L.; Macler, B.A.; Plummer, S.E.; Peterson, D.L. Reflectance spectroscopy of fresh whole leaves for the estimation of chemical concentration. Remote Sens. Environ. 1992, 39, 153–166. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S.L.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating leaf biochemistry using the PROSPECT leaf optical properties model. Remote Sens. Environ. 1996, 56, 194–202. [Google Scholar] [CrossRef]
- Deering, D.W.; Eck, T.F.; Banerjee, B. Characterization of the reflectance anisotropy of three boreal forest canopies in spring-summer. Remote Sens. Environ. 1999, 67, 205–229. [Google Scholar] [CrossRef]
- Sandmeier, S.; Muller, C.; Hosgood, B.; Andreoli, G. Physical Mechanisms in Hyperspectral BRDF Data of Grass and Watercress. Remote Sens. Environ. 1998, 66, 222–233. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L.; Liu, X.; Liu, Z. Development of a new BRDF-resistant vegetation index for improving the estimation of leaf area index. Remote Sens. 2016, 8, 947. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Filella, I.; Serrano, I.; Serra, J.; Penuelas, J. Evaluating wheat nitrogen status with canopy reflectance indices and discriminant analysis. Crop Sci. 1995, 35, 1400–1405. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; Le Maire, G. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef]
- Yoder, B.J.; Pettigrew-Crosby, R.E. Predicting nitrogen and chlorophyll content and concentration from reflectance spectra (400–2500 nm) at leaf and canopy scales. Remote Sens. Environ. 1995, 53, 199–211. [Google Scholar] [CrossRef]
- Takebe, M.; Yoneyama, T.; Inada, K.; Murakami, T. Spectral reflectance ratio of rice canopy for estimating crop nitrogen status. Plant Soil 1990, 122, 295–297. [Google Scholar] [CrossRef]
- Walter-Shea, E.A.; Privette, J.; Cornell, D.; Mesarch, M.A.; Hays, C.J. Relations between directional spectral vegetation indices and leaf area and absorbed radiation in alfalfa. Remote Sens. Environ. 1997, 61, 162–177. [Google Scholar] [CrossRef]
- Galvão, L.S.; Roberts, D.A.; Formaggio, A.R.; Numata, I.; Breunig, F.M. View angle effects on the discrimination of soybean varieties and on the relationships between vegetation indices and yield using off-nadir Hyperion data. Remote Sens. Environ. 2009, 113, 846–856. [Google Scholar] [CrossRef]
- Hilker, T.; Galvão, L.S.; Aragão, L.; de Moura, Y.M.; do Amaral, C.H.; Lyapustin, A.I.; Wu, J.; Albert, L.P.; Ferreira, M.J.; Anderson, L.O.; et al. Vegetation chlorophyll estimates in the Amazon from multi-angle MODIS observations and canopy reflectance model. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 278–287. [Google Scholar] [CrossRef]
- Vohland, M.; Mader, S.; Dorigo, W. Applying different inversion techniques to retrieve stand variables of summer barley with PROSPECT + SAIL. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 71–80. [Google Scholar] [CrossRef]
- Preidl, S.; Doktor, D. Comparison of Radiative Transfer Model Inversions to Estimate Vegetation Physiological Status Based on Hyperspectral Data. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011. [Google Scholar]
- Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef] [PubMed]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil-leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.B.; Lopes, M.; Guilleux, J.; Dedieu, G.; et al. Discrete anisotropic radiative transfer (DART 5) for modeling airborne and satellite spectroradiometer and LIDAR acquisitions of natural and urban landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Juszak, I.; Iturrate-Garcia, M.; Gastellu-Etchegorry, J.P.; Schaepman, M.E.; Maximov, T.C.; Schaepman-Strub, G. Drivers of shortwave radiation fluxes in Arctic tundra across scales. Remote Sens. Environ. 2017, 193, 86–102. [Google Scholar] [CrossRef]
- Chapman, J.W.; Thompson, D.R.; Helmlinger, M.C.; Bue, B.D.; Green, R.O.; Eastwood, M.L.; Geier, S.; Olson-Duvall, W.; Lundeen, S.R. Spectral and radiometric calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG). Remote Sens. 2019, 11, 2129. [Google Scholar] [CrossRef]
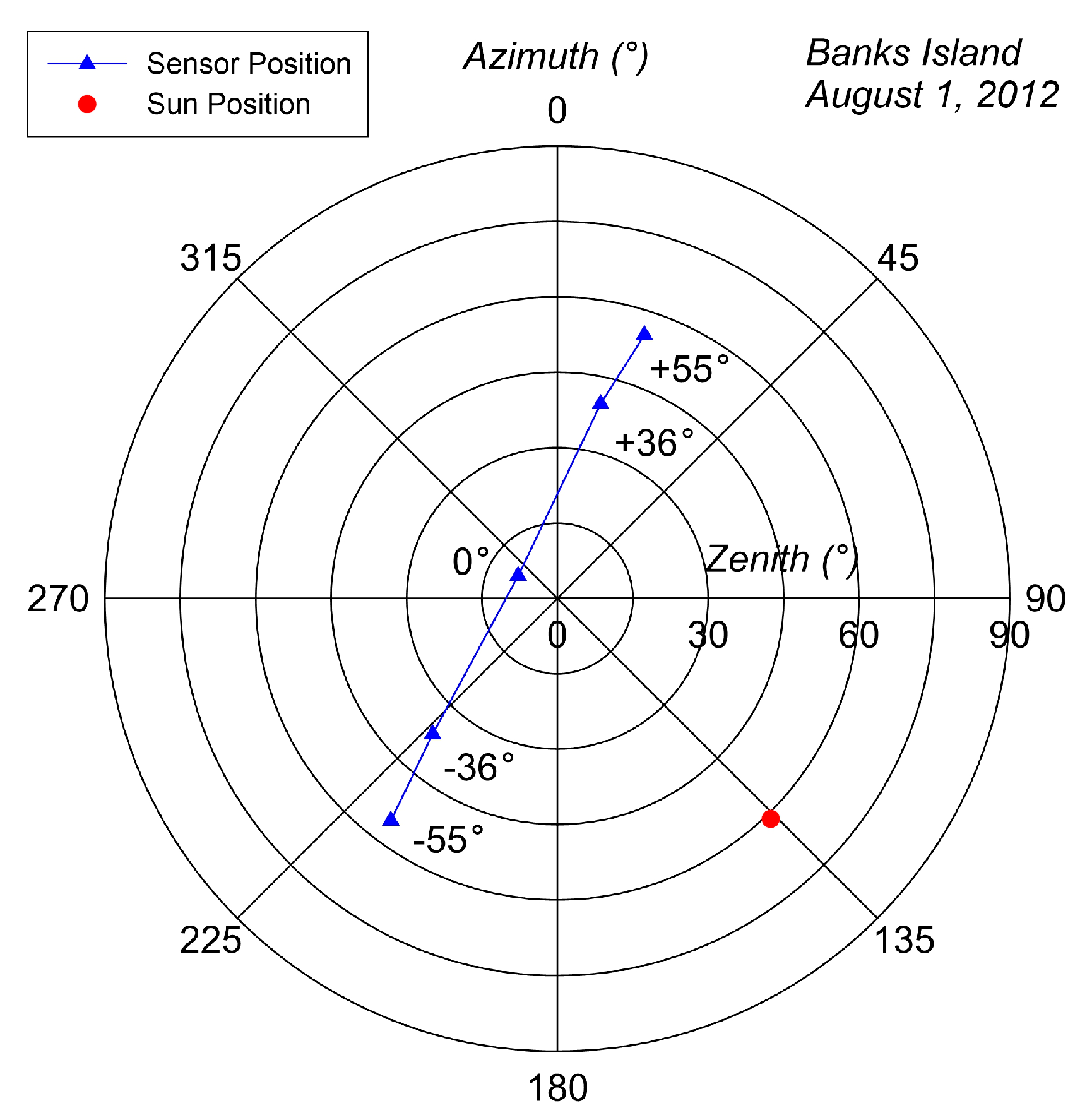

| Image Location | Acquisition Date | Time (UTC) | VZA | VZA * | VAA | SZA | SAA | RAA |
|---|---|---|---|---|---|---|---|---|
| Herschel Island, Yukon | 20 July 2011 | 18:36:55 | +55° | 51.82 | 27.89 | 55.00 | 130.83 | 102.94 |
| 18:37:44 | +36° | 32.22 | 35.14 | 55.00 | 131.05 | 95.91 | ||
| 18:38:33 | 0° | 15.12 | 138.46 | 55.00 | 131.28 | 7.18 | ||
| 18:39:23 | −36° | 34.94 | 176.77 | 55.00 | 131.51 | 45.26 | ||
| 18.40:12 | −55° | 53.23 | 187.49 | 55.00 | 131.73 | 55.76 | ||
| Banks Island, Northwest Territories | 1 August 2012 | 17:25:27 | +55° | 55.22 | 18.28 | 61.00 | 134.40 | 116.12 |
| 17:26:16 | +36° | 36.69 | 12.53 | 61.00 | 134.61 | 122.08 | ||
| 17:27:05 | 0° | 9.00 | 300.05 | 61.00 | 134.83 | 165.22 | ||
| 17:27:54 | −36° | 36.69 | 222.57 | 61.00 | 135.05 | 87.52 | ||
| 17:28:44 | −55° | 55.22 | 216.83 | 61.00 | 135.27 | 81.56 | ||
| Richardson Mountains, Yukon/Northwest Territories | 2 August 2013 | 16:18:06 | +55° | 53.65 | 28.82 | 67.00 | 98.42 | 69.60 |
| 16:19:00 | +36° | 39.67 | 48.62 | 67.00 | 98.42 | 49.80 | ||
| 16:19:43 | 0° | 21.00 | 137.52 | 67.00 | 98.81 | 38.71 | ||
| 16:20:32 | −36° | 38.20 | 167.46 | 67.00 | 99.00 | 68.46 | ||
| 16:21:21 | −55° | 55.29 | 180.44 | 67.00 | 99.19 | 81.25 | ||
| Richardson Mountains, Yukon/Northwest Territories | 6 July 2014 | 00:59:02 | +55° | 55.72 | 145.77 | 56.81 | 248.41 | 102.64 |
| 00:59:51 | +36° | 38.06 | 140.10 | 56.81 | 248.62 | 108.52 | ||
| 01:00:40 | 0° | 21.48 | 42.68 | 56.81 | 248.83 | 153.85 | ||
| 01:01:29 | −36° | 36.51 | 6.93 | 56.81 | 249.03 | 117.90 | ||
| 01:02:18 | −55° | 54.32 | 352.12 | 56.81 | 249.24 | 118.64 |
| SR | ROSAVI | ||||||
|---|---|---|---|---|---|---|---|
| Variable | Angle | r2cv | RMSEcv | NRMSEcv | r2cv | RMSEcv | NRMSEcv |
| LCC | All | 0.61 | 5.39 | 0.13 | 0.50 | 6.12 | 0.14 |
| PAI | All | 0.60 | 0.25 | 0.14 | 0.54 | 0.27 | 0.15 |
| CCC | All | 0.58 | 0.11 | 0.14 | 0.50 | 0.12 | 0.15 |
| LCC | +55° | 0.64 | 5.67 | 0.13 | 0.56 | 6.28 | 0.14 |
| LCC | +36° | 0.43 | 5.58 | 0.13 | 0.36 | 5.89 | 0.13 |
| LCC | 0° | 0.68 | 4.90 | 0.11 | 0.53 | 5.90 | 0.13 |
| LCC | −36° | 0.68 | 4.95 | 0.15 | 0.55 | 5.89 | 0.13 |
| LCC | −55° | 0.61 | 5.87 | 0.13 | 0.50 | 6.66 | 0.15 |
| PAI | +55° | 0.61 | 0.25 | 0.14 | 0.58 | 0.26 | 0.14 |
| PAI | +36° | 0.54 | 0.26 | 0.14 | 0.49 | 0.28 | 0.15 |
| PAI | 0° | 0.63 | 0.24 | 0.13 | 0.56 | 0.26 | 0.14 |
| PAI | −36° | 0.58 | 0.25 | 0.14 | 0.52 | 0.27 | 0.15 |
| PAI | −55° | 0.63 | 0.25 | 0.14 | 0.54 | 0.28 | 0.15 |
| CCC | +55° | 0.58 | 0.11 | 0.14 | 0.55 | 0.12 | 0.15 |
| CCC | +36° | 0.54 | 0.11 | 0.15 | 0.46 | 0.12 | 0.16 |
| CCC | 0° | 0.61 | 0.10 | 0.14 | 0.52 | 0.12 | 0.15 |
| CCC | −36° | 0.57 | 0.11 | 0.14 | 0.49 | 0.12 | 0.15 |
| CCC | −55° | 0.59 | 0.11 | 0.14 | 0.48 | 0.13 | 0.16 |
| All | +55° | 0.61 | - | 0.14 | 0.56 | - | 0.14 |
| All | +36° | 0.50 | - | 0.14 | 0.44 | - | 0.15 |
| All | 0° | 0.64 | - | 0.13 | 0.54 | - | 0.14 |
| All | −36° | 0.61 | - | 0.14 | 0.52 | - | 0.14 |
| All | −55° | 0.61 | - | 0.14 | 0.51 | - | 0.15 |
| GPR | ||||
|---|---|---|---|---|
| Variable | Angle | r2cv | RMSEcv | NRMSEcv |
| LCC | All | 0.62 | 5.49 | 0.12 |
| PAI | All | 0.62 | 0.25 | 0.14 |
| CCC | All | 0.59 | 0.11 | 0.14 |
| LCC | +55° | 0.58 | 6.19 | 0.14 |
| LCC | +36° | 0.51 | 6.03 | 0.14 |
| LCC | 0° | 0.66 | 5.04 | 0.11 |
| LCC | −36° | 0.70 | 4.76 | 0.11 |
| LCC | −55° | 0.67 | 5.42 | 0.12 |
| PAI | +55° | 0.66 | 0.24 | 0.13 |
| PAI | +36° | 0.58 | 0.25 | 0.14 |
| PAI | 0° | 0.64 | 0.23 | 0.13 |
| PAI | −36° | 0.60 | 0.25 | 0.14 |
| PAI | −55° | 0.61 | 0.26 | 0.14 |
| CCC | +55° | 0.61 | 0.11 | 0.14 |
| CCC | +36° | 0.56 | 0.11 | 0.14 |
| CCC | 0° | 0.64 | 0.10 | 0.13 |
| CCC | −36° | 0.56 | 0.11 | 0.14 |
| CCC | −55° | 0.60 | 0.11 | 0.14 |
| All | +55° | 0.62 | - | 0.14 |
| All | +36° | 0.50 | - | 0.14 |
| All | 0° | 0.65 | - | 0.12 |
| All | −36° | 0.62 | - | 0.13 |
| All | −55° | 0.63 | - | 0.13 |
| LM | LUT | ||||||
|---|---|---|---|---|---|---|---|
| Variable | Angle | r2cv | RMSEcv | NRMSEcv | r2cv | RMSEcv | NRMSEcv |
| LCC | All | 0.30 | 7.61 | 0.25 | 0.55 | 7.60 | 0.17 |
| PAI | All | 0.21 | 0.39 | 0.38 | 0.46 | 0.34 | 0.19 |
| CCC | All | 0.32 | 0.13 | 0.18 | 0.48 | 0.14 | 0.18 |
| LCC | +55° | 0.30 | 7.13 | 0.24 | 0.55 | 7.43 | 0.17 |
| LCC | +36° | 0.32 | 7.18 | 0.23 | 0.41 | 7.70 | 0.17 |
| LCC | 0° | 0.34 | 7.64 | 0.24 | 0.62 | 7.46 | 0.17 |
| LCC | −36° | 0.25 | 8.70 | 0.27 | 0.63 | 8.13 | 0.18 |
| LCC | −55° | 0.31 | 7.40 | 0.24 | 0.55 | 7.26 | 0.16 |
| PAI | +55° | 0.21 | 0.40 | 0.39 | 0.40 | 0.32 | 0.18 |
| PAI | +36° | 0.21 | 0.40 | 0.39 | 0.41 | 0.30 | 0.17 |
| PAI | 0° | 0.18 | 0.40 | 0.39 | 0.50 | 0.29 | 0.16 |
| PAI | −36° | 0.26 | 0.40 | 0.39 | 0.51 | 0.29 | 0.16 |
| PAI | −55° | 0.21 | 0.36 | 0.35 | 0.47 | 0.50 | 0.28 |
| CCC | +55° | 0.35 | 0.13 | 0.18 | 0.46 | 0.13 | 0.17 |
| CCC | +36° | 0.30 | 0.15 | 0.22 | 0.48 | 0.14 | 0.18 |
| CCC | 0° | 0.42 | 0.11 | 0.16 | 0.55 | 0.15 | 0.19 |
| CCC | −36° | 0.32 | 0.12 | 0.17 | 0.40 | 0.15 | 0.19 |
| CCC | −55° | 0.22 | 0.12 | 0.16 | 0.51 | 0.13 | 0.17 |
| All | +55° | 0.29 | - | 0.27 | 0.47 | - | 0.17 |
| All | +36° | 0.28 | - | 0.28 | 0.43 | - | 0.17 |
| All | 0° | 0.31 | - | 0.26 | 0.56 | - | 0.17 |
| All | −36° | 0.28 | - | 0.28 | 0.51 | - | 0.18 |
| All | −55° | 0.25 | - | 0.25 | 0.51 | - | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kennedy, B.E.; King, D.J.; Duffe, J. Retrieval of Arctic Vegetation Biophysical and Biochemical Properties from CHRIS/PROBA Multi-Angle Imagery Using Empirical and Physical Modelling. Remote Sens. 2021, 13, 1830. https://doi.org/10.3390/rs13091830
Kennedy BE, King DJ, Duffe J. Retrieval of Arctic Vegetation Biophysical and Biochemical Properties from CHRIS/PROBA Multi-Angle Imagery Using Empirical and Physical Modelling. Remote Sensing. 2021; 13(9):1830. https://doi.org/10.3390/rs13091830
Chicago/Turabian StyleKennedy, Blair E., Doug J. King, and Jason Duffe. 2021. "Retrieval of Arctic Vegetation Biophysical and Biochemical Properties from CHRIS/PROBA Multi-Angle Imagery Using Empirical and Physical Modelling" Remote Sensing 13, no. 9: 1830. https://doi.org/10.3390/rs13091830
APA StyleKennedy, B. E., King, D. J., & Duffe, J. (2021). Retrieval of Arctic Vegetation Biophysical and Biochemical Properties from CHRIS/PROBA Multi-Angle Imagery Using Empirical and Physical Modelling. Remote Sensing, 13(9), 1830. https://doi.org/10.3390/rs13091830






