Integration of Visible and Thermal Imagery with an Artificial Neural Network Approach for Robust Forecasting of Canopy Water Content in Rice
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Digital Image Acquisition
2.3. Thermal Image Acquisition
2.4. Image Segmentation
2.5. Feature Extraction from RGB Images
2.5.1. RGB Color Space Percentage
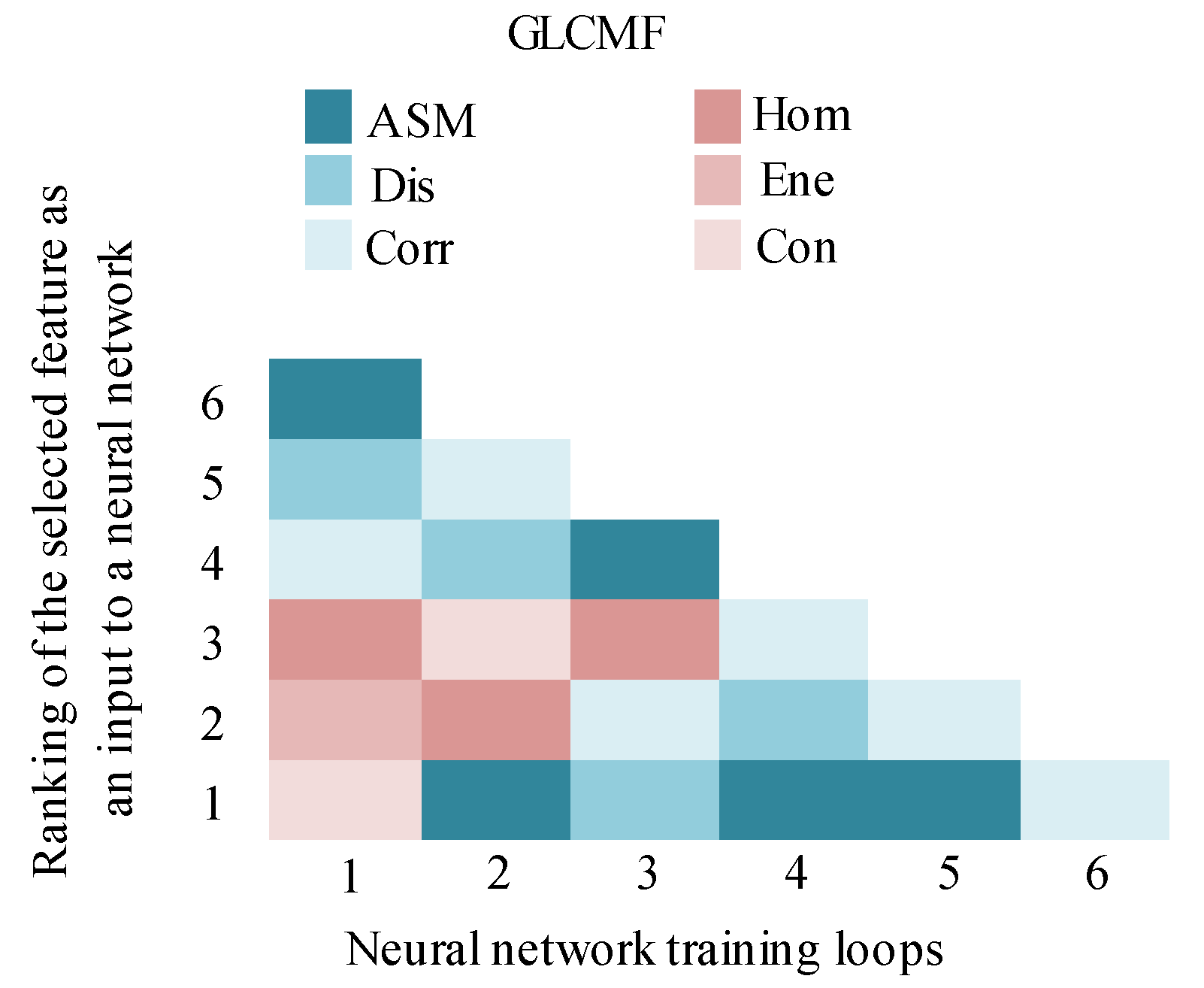
2.5.2. Gray Level Co-Occurrence Matrix-Based Texture Features (GLCMF)
2.6. Feature Extraction from Thermal Images
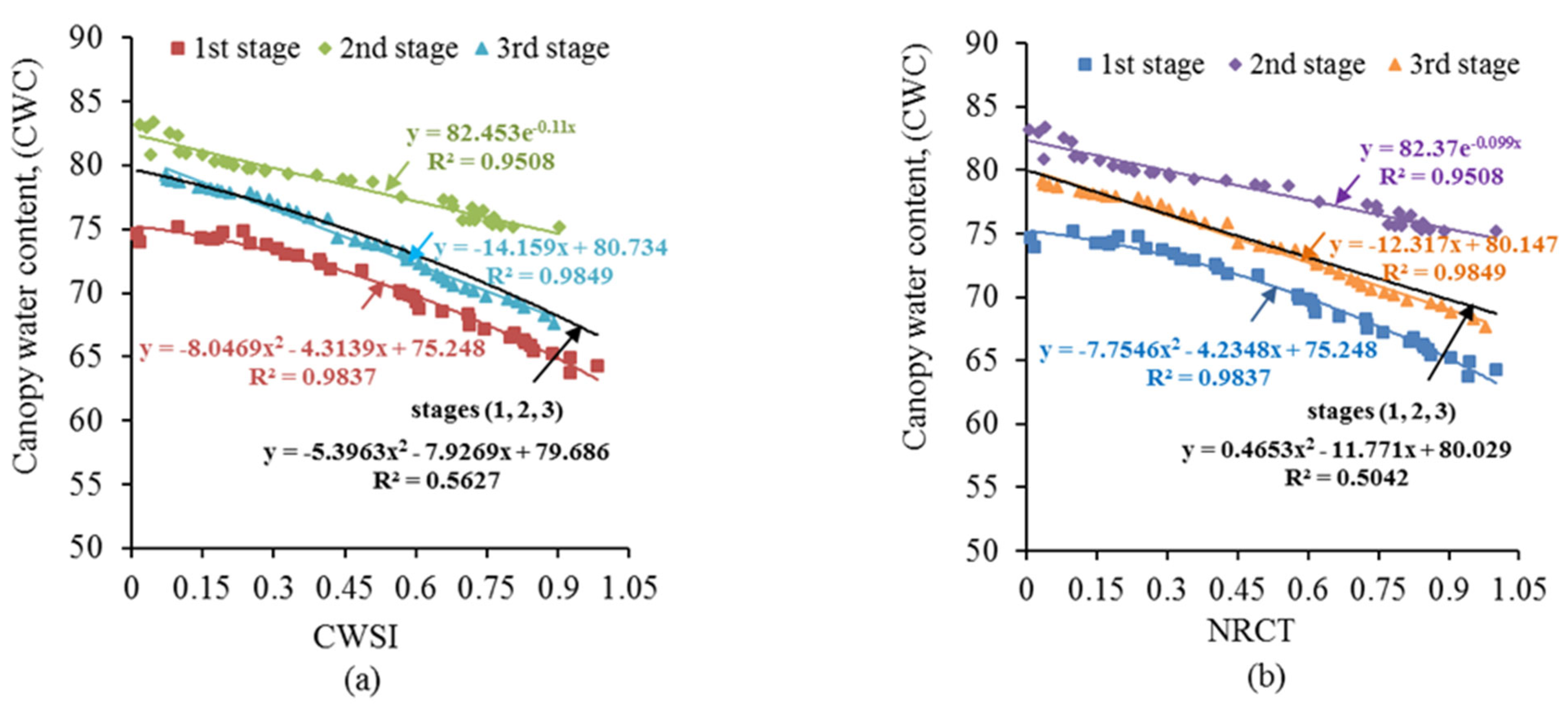
2.6.1. Canopy Temperature-Based Crop Water Stress Index (CWSI)
2.6.2. Normalized Relative Canopy Temperature (NRCT)
2.7. Canopy Water Content Computation
2.8. Dataset and Data Analysis Software
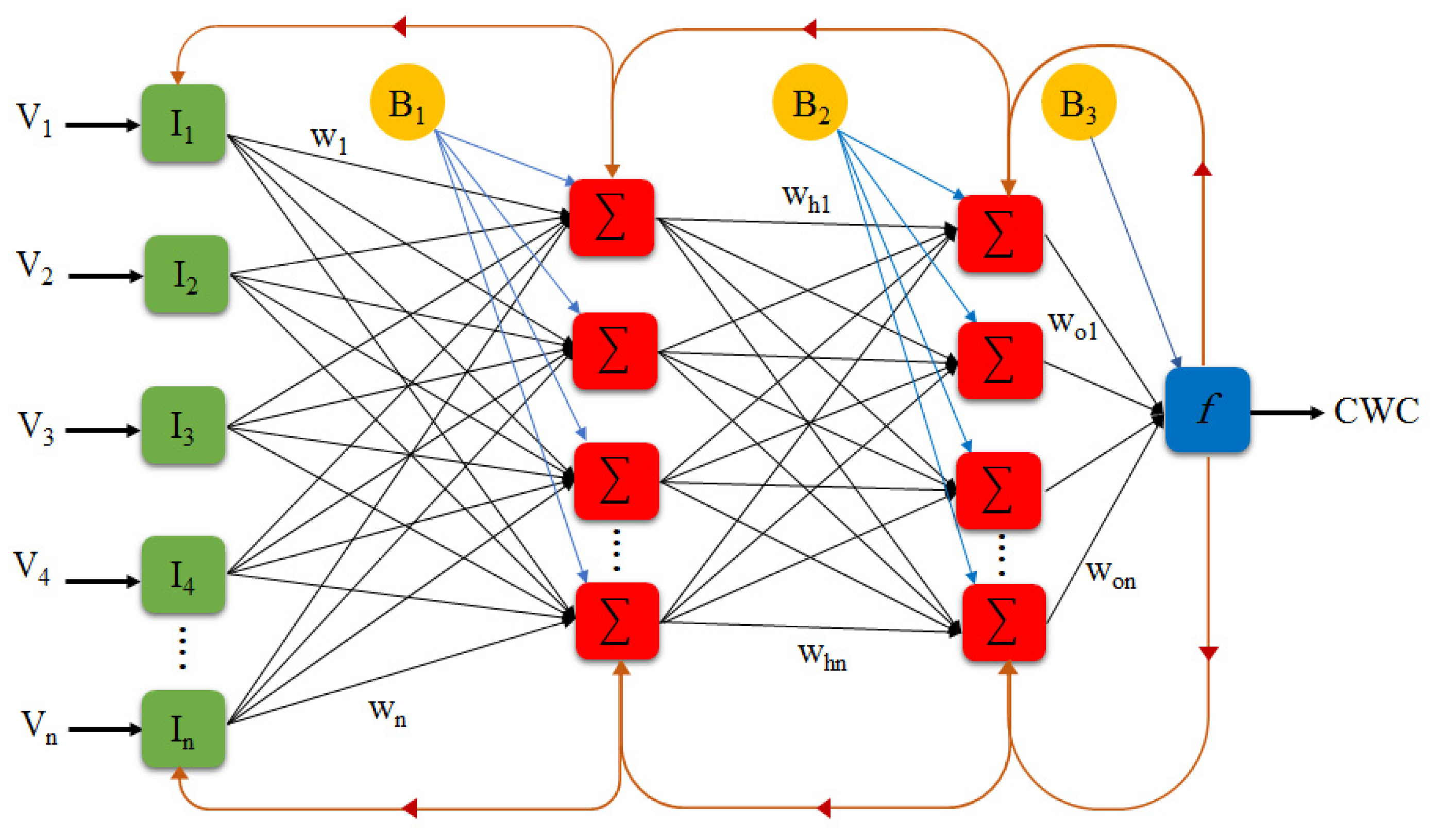
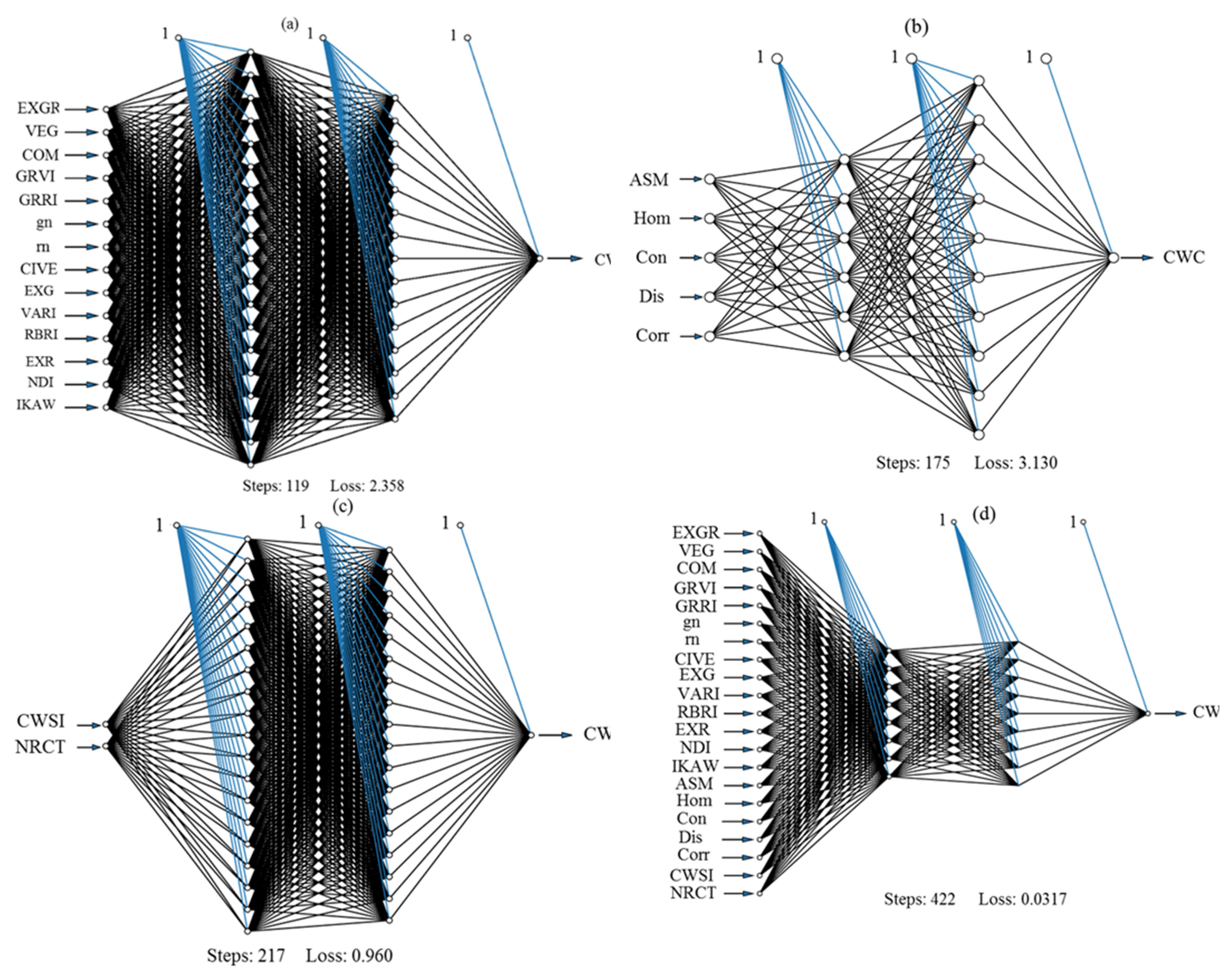
2.9. Implementation of a Backpropagation Neural Network (BPNN)
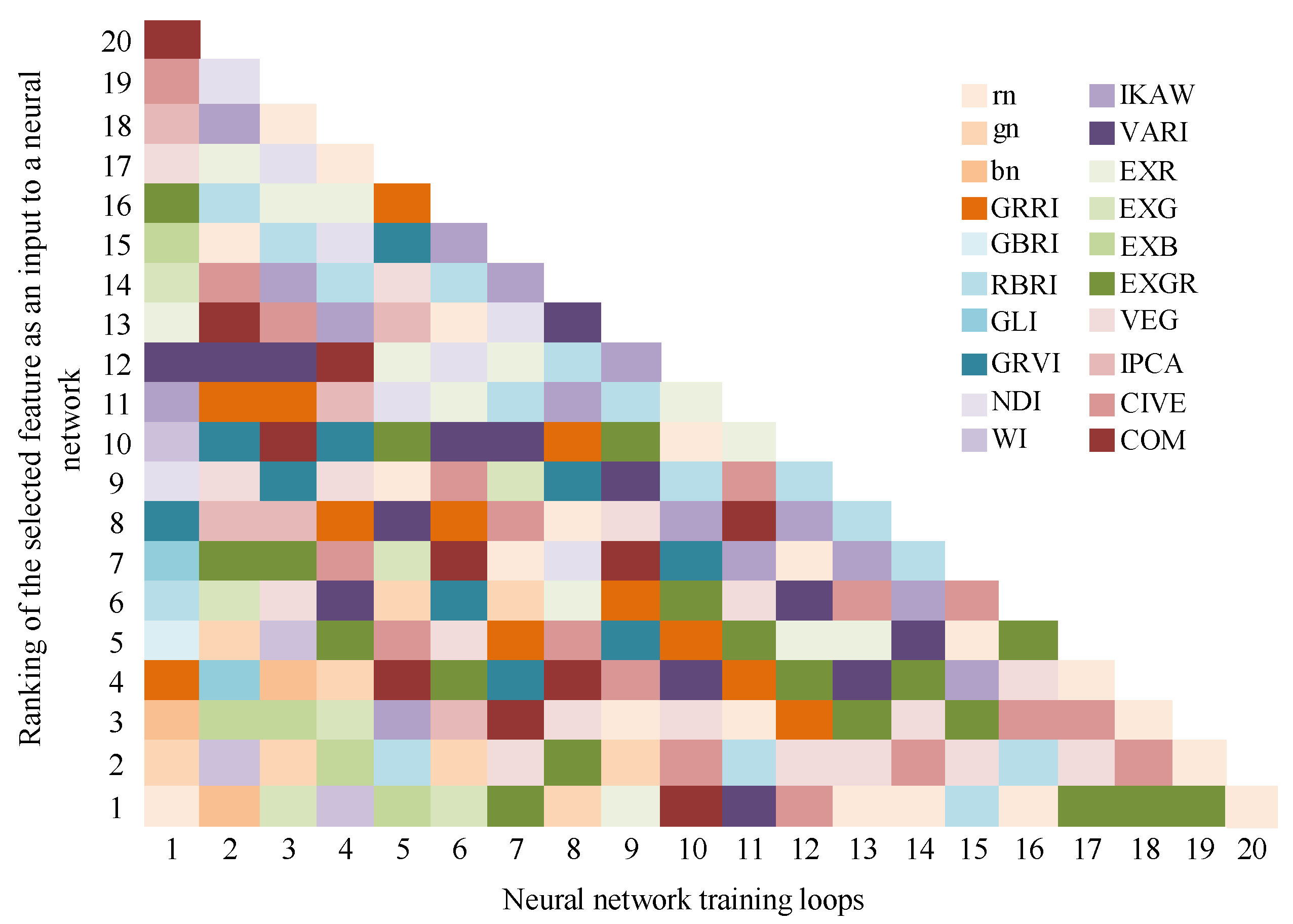
2.10. Hyperparameter Optimization and High-Level Variants Selection
2.11. Statistical Analysis Methods
3. Results
3.1. Optimization Combinations of Independent Variables Selection
3.1.1. Color Vegetation Indices (VI)
3.1.2. GLCM-Based Texture Features (GLCMF)
3.1.3. Thermal Indicators (T)
3.1.4. Best-Combined Features Extracted from Visible and Thermal Imagery
3.2. Neural Network Learning Curves with Super Features
3.3. Neural Network Topology with Higher Variants
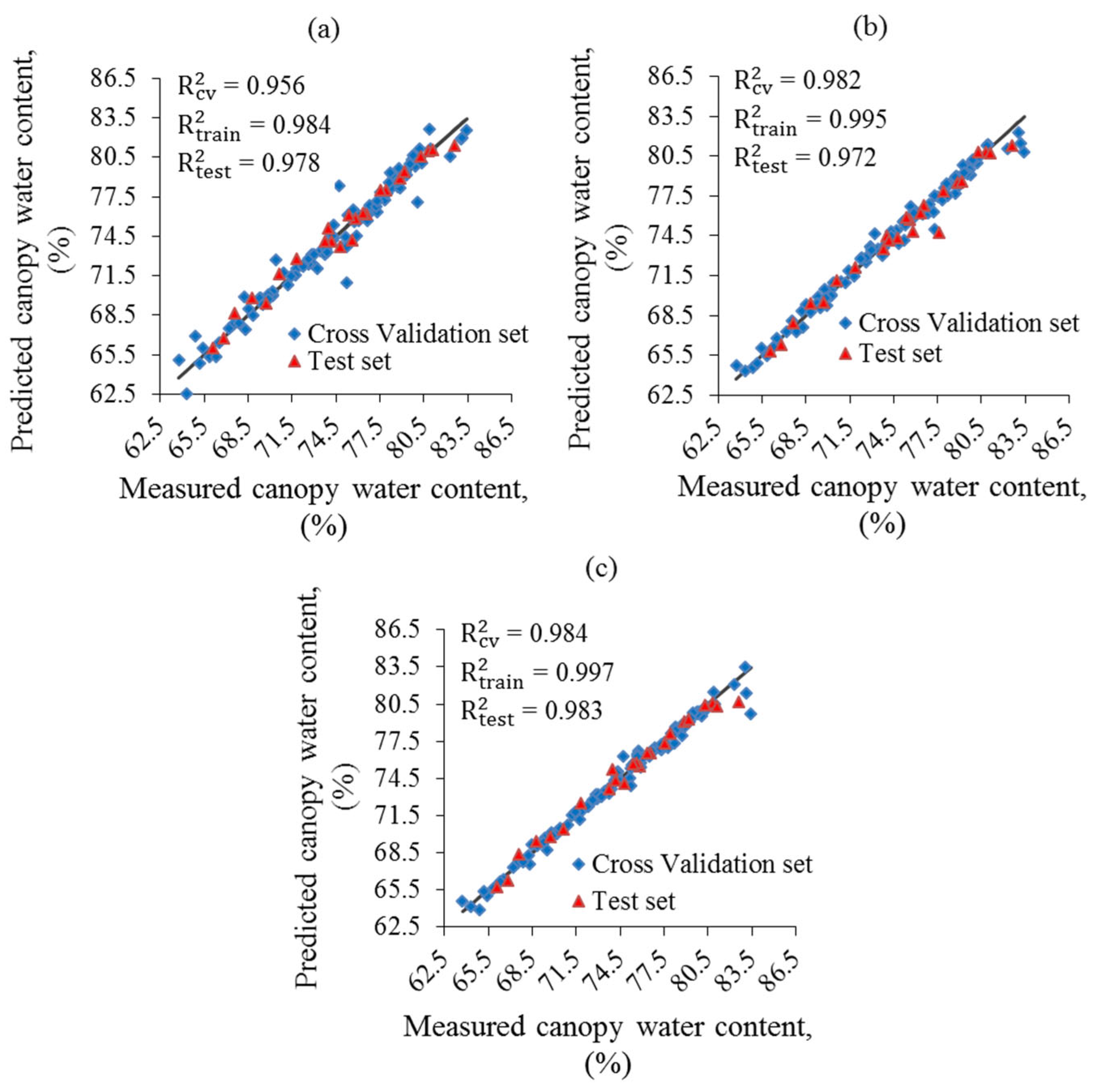
3.4. Canopy Water Content Prediction and Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gilbert, N. Water under pressure. Nat. Cell Biol. 2012, 483, 256–257. [Google Scholar] [CrossRef] [PubMed]
- El-Hendawy, S.; Al-Suhaibani, N.; Salem, A.; Ur Rehman, S.; Schmidhalter, U. Spectral reflectance indices as a rapid nondestructive phenotyping tool forestimating different morphophysiological traits of contrasting spring wheatgermplasms under arid conditions. Turk. J. Agric. For. 2015, 39, 572–587. [Google Scholar] [CrossRef]
- Guerra, L.C.; Bhuiyan, S.I.; Tuong, T.P.; Barker, R. Producing More Rice with Less Water from Irrigated Systems; SWIM Paper 5; IWMI/IRRI: Colombo, Sri Lanka, 1998. [Google Scholar]
- Liu, Y.; Liang, Y.; Deng, S.; Li, F. Effects of irrigation method and radio of organic to inorganic nitrogen on yield ann water use of rice. Plant Nutr. Fertil. Sci. 2012, 18, 551–561. [Google Scholar]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth. Obs. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Serrano, L.; Save, R. Cell wall elasticity and water index (r970nm/r900nm) in wheat under different nitrogen availabilities. Int. J. Remote Sens. 1996, 17, 373–382. [Google Scholar] [CrossRef]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.P.W.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne imaging spectroscopy for sustainable agriculture: Contributions and challenges. Surv. Geophys. 2019, 40, 515–551. [Google Scholar] [CrossRef]
- Peñuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index wi (r900/r970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Elsayed, S.; Darwish, W. Hyperspectral remote sensing to assess the water status, biomass, and yield of maize cultivars under salinity and water stress. Bragantia. 2017, 76, 62–72. [Google Scholar] [CrossRef]
- Scholander, P.F.; Bradstreet, E.D.; Hemmingsen, E.A.; Hammel, H.T. Sap Pressure in Vascular Plants: Negative hydrostatic pressure can be measured in plants. Science. 1965, 148, 339–346. [Google Scholar] [CrossRef]
- Agam, N.; Cohen, Y.; Berni, J.; Alchanatis, V.; Kool, D.; Dag, A.; Yermiyahu, U.; Ben-Gal, A. An insight to the performance of crop water stress index for olive trees. Agric. Water Manag. 2013, 118, 79–86. [Google Scholar] [CrossRef]
- Singh, A.K.; Madramootoo, C.A.; Smith, D.L. Water Balance and Corn Yield under Different Water Table Management Scenarios in Southern Quebec. In Proceedings of the 9th International Drainage Symposium Held Jointly with CIGR and CSBE/SCGAB, Quebec City, QC, Canada, 13–16 June 2010. [Google Scholar]
- Rud, R.; Cohen, Y.; Alchanatis, V.; Levi, A.; Brikman, R.; Shenderey, C.; Heuer, B.; Markovitch, T.; Dar, Z.; Rosen, C.; et al. Crop water stress index derived from multi-year ground and aerial thermal images as an indicator of potato water status. Precis. Agric. 2014, 15, 273–289. [Google Scholar] [CrossRef]
- Dhillon, R.S.; Upadhaya, S.K.; Rojo, F.; Roach, J.; Coates, R.W.; Delwiche, M.J. Development of a continuous leaf monitoring system to predict plant water status. T. ASABE. 2017, 60, 1445–1455. [Google Scholar] [CrossRef]
- Prey, L.; von Bloh, M.; Schmidhalter, U. Evaluating RGB imaging and multispectral active and hyperspectral passive sensing for assessing early plant vigor in winter wheat. Sensors 2018, 18, 2931. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Huang, D. A review of imaging techniques for plant phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef]
- Elsherbiny, O.; Fan, Y.; Zhou, L.; Qiu, Z. Fusion of feature selection methods and regression algorithms for predicting the canopy water content of rice based on hyperspectral data. Agriculture 2021, 11, 51. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE. 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Wang, F.Y.; Wang, K.R.; Wang, C.T.; Li, S.K.; Zhu, Y.; Chen, B. Diagnosis of cotton water status based on image recognition. J. Shihezi Univ. Nat. Sci. 2007, 25, 404–408. [Google Scholar]
- Zakaluk, R.; Sri, R.R. Predicting the leaf water potential of potato plants using RGB reflectance. Can. Biosyst. Eng. 2008, 50. [Google Scholar]
- Wenting, H.; Yu, S.; Tengfei, X.; Xiangwei, C.; Ooi, S.K. Detecting maize leaf water status by using digital RGB images. Int. J. Agric. Biol. Eng. 2014, 7, 45–53. [Google Scholar]
- Shao, Y.; Zhou, H.; Jiang, L.; Bao, Y.; He, Y. Using reflectance and gray-level texture for water content prediction in grape vines. T. ASABE. 2017, 60, 207–213. [Google Scholar]
- Jackson, R.D.; Idso, S.; Reginato, R.; Pinter, P. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Moller, M.; Alchanatis, V.; Cohen, Y.; Meron, M.; Tsipris, J.; Naor, A.; Ostrovsky, V.; Sprintsin, , M.; Cohen , S. Use of thermal and visible imagery for estimating crop water status of irrigated grapevine. J. Exp. Bot. 2006, 58, 827–838. [Google Scholar] [CrossRef]
- Ballester, C.; Jiménez-Bello, M.A.; Castel, J.R.; Intrigliolo, D.S. Usefulness of thermography for plant water stress detection in citrus and persimmon trees. Agric. Forest Meteorol. 2013, 168, 120–129. [Google Scholar] [CrossRef]
- Melis, G.; Dyer, C.; Blunsom, P. On the state of the art of evaluation in neural language models. arXiv 2017, arXiv:1707.05589. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the 30th International Conference on Machine Learning (ICML 2013), Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. JEST 2019, 17, 26–40. [Google Scholar]
- Dawson, T.P.; Curran, P.J.; Plummer, S.E. LIBERTY—Modelling the effects of leaf biochemical concentration on reflectance spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
- Marti, P.; Gasque, M.; Gonzalez-Altozano, P. An artificial neural network approach to the estimation of stem water potential from frequency domain reflectometry soil moisture measurements and meteorological data. Comput. Electron. Agric. 2013, 91, 75–86. [Google Scholar] [CrossRef]
- Abtew, W.; Melesse, A. Evaporation and evapotranspiration: Measurements and estimations. Springer Sci. 2013, 53, 62. [Google Scholar]
- Costa, J.M.; Grant, O.M.; Chaves, M.M. Thermography to explore plant-environment interactions. J. Exp. Bot. 2013, 64, 3937–3949. [Google Scholar] [CrossRef]
- Li, H.; Malik, M.H.; Gao, Y.; Qiu, R.; Miao, Y.; Zhang, M. Proceedings of the Maize Plant Water Stress Detection Based on RGB Image and Thermal Infrared Image, Detroit, MI, USA, 29 July–1 August 2018.
- Yossya, E.H.; Pranata, J.; Wijaya, T.; Hermawan, H.; Budiharto, W. Mango fruit sortation system using neural network and computer vision. Procedia Comput. Sci. 2017, 116, 569–603. [Google Scholar] [CrossRef]
- Kumaseh, M.R.; Latumakulita, L.; Nainggolan, N. Segmentasi citra digital ikan menggunakan metode thresholding. J. Ilmiah Sains. 2013, 13, 74–79. [Google Scholar] [CrossRef][Green Version]
- Kawashima, S.; Nakatani, M. An algorithm for estimating chlorophyll content in leaves using a video camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Kneubuhler, M. Angular sensitivity analysis of vegetation indices derived from CHRIS/PROBA data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Sellaro, R.; Crepy, M.; Trupkin, S.A.; Karayekov, E.; Buchovsky, A.S.; Rossi, C.; Casal, J.J. Cryptochrome as a sensor of the blue/green ratio of natural radiation in Arabidopsis. Plant Physiol. 2010, 154, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Woebbecke, D.; Meyer, G.; Von Bargen, K.; Mortensen, D. Plant Species Identification, Size, and Enumeration using Machine Vision Techniques on Near-Binary Images. In Proceedings of the Optics in Agriculture and Forestry, Boston, MA, USA, 16–17 November 1992; Volume 1836, pp. 208–219. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially located platform and aerial photography for documentation of grazing impacts on wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Mao, W.; Wang, Y.; Wang, Y. Real-Time Detection of between-Row Weeds using Machine Vision. In Proceedings of the 2003 ASAE Annual Meeting, Las Vegas, NV, USA, 27–30 July 2003; p. 1. [Google Scholar]
- Saberioon, M.M.; Amin, M.S.M.; Anuar, A.R.; Gholizadeh, A.; Wayayok, A.; Khairunniza- Bejo, S. Assessment of rice leaf chlorophyll content using visible bands at different growth stages at both the leaf and canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 35–45. [Google Scholar] [CrossRef]
- Guijarro, M.; Pajares, G.; Riomoros, I.; Herrera, P.J.; Burgos-Artizzu, X.P.; Ribeiro, A. Automatic segmentation of relevant textures in agricultural images. Comput. Electron. Agric. 2011, 75, 75–83. [Google Scholar] [CrossRef]
- Ushada, M.; Murase, H.; Fukuda, H. Non-destructive sensing and its inverse model for canopy parameters using texture analysis and artificial neural network. Comput. Electron. Agric. 2007, 57, 149–165. [Google Scholar] [CrossRef]
- Murase, H.; Tani, A.; Nishiura, Y.; Kiyota, M. Growth Monitoring of Green Vegetables Cultured in a Centrifuge Phytotron. In Plant Production in Closed Ecosystems; Goto, E., Kurata, K., Hayashi, M., Sase, S., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1997; pp. 305–319. [Google Scholar]
- Athanasiou, L.S.; Fotiadis, D.I.; Michalis, L.K. Plaque Characterization Methods using Intravascular Ultrasound Imaging. In Atherosclerotic Plaque Characterization Methods Based on Coronary Imaging, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 71–94. [Google Scholar]
- Hall-Beyer, M. GLCM Texture: A Tutorial v. 1.0 through 2.7. Available online: http://hdl.handle.net/1880/51900 (accessed on 4 April 2017).
- Bellvert, J.; Marsal, J.; Girona, J.; Gonzalez-Dugo, V.; Fereres, E.; Ustin, S.L.; Zarco-Tejada, P.J. Airborne thermal imagery to detect the seasonal evolution of crop water status in peach, nectarine and Saturn peach orchards. Remote Sens. 2016, 8, 39. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, Z.H.; Sun, H.; Wang, G.X. Mapping forest ecosystem biomass density for Xiangjiang river basin by combining plot and remote sensing data and comparing spatial extrapolation methods. Remote Sens. 2017, 9, 241. [Google Scholar] [CrossRef]
- Kisi, O.; Demir, V. Evapotranspiration estimation using six different multi-layer perceptron algorithms. Irrig. Drain. Syst. Eng. 2016, 5, 991–1000. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Jensen, J.L.; Kendall, W.S. Networks and Chaos: Statistical and Probabilistic Aspects; Chapman and Hall: London, UK, 1993; Volume 50, p. 48. [Google Scholar]
- Li, J.; Yoder, R.; Odhiambo, L.O.; Zhang, J. Simulation of nitrate distribution under drip irrigation using artificial neural networks. Irrigation Sci. 2004, 23, 29–37. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. Siam J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Schuize, F.H.; Wolf, H.; Jansen, H.W.; Vander, V.P. Applications of artificial neural networks in integrated water management: Fiction or future? Water Sci. Technol. 2005, 52, 21–31. [Google Scholar] [CrossRef]
- Glorfeld, L.W. A methodology for simplification and interpretation of backpropagation-based neural network models. Expert Syst. Appl. 1996, 10, 37–54. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Panigrahi, N.; Das, B.S. Evaluation of regression algorithms for estimating leaf area index and canopy water content from water stressed rice canopy reflectance. Inf. Process. Agric. 2020. [Google Scholar] [CrossRef]
- Meeradevi; Sindhu, N.; Mundada, M.R. Machine learning in agriculture application: Algorithms and techniques. IJITEE 2020, 9, 2278–3075. [Google Scholar]
- Thawornwong, S.; Enke, D. The adaptive selection of financial and economic variables for use with artificial neural networks. Neurocomputing 2004, 56, 205–232. [Google Scholar] [CrossRef]
- Bai, G.; Jenkins, S.; Yuan, W.; Graef, G.L.; Ge, Y. Field-based scoring of soybean iron deficiency chlorosis using RGB imaging and statistical learning. Front. Plant Sci. 2018, 9, 1002. [Google Scholar] [CrossRef]
- Bharati; Manish, H.; Liu, J.J.; MacGregor, J.F. Image texture analysis: Methods and comparisons. Chemometr. Intell. Lab. 2004, 72, 57–71. [Google Scholar] [CrossRef]
- Jana, S.; Basak, S.; Parekh, R. Automatic fruit recognition from natural images using color and texture features. In Proceedings of the 2017 Devices for Integrated Circuit (DevIC), Kalyani, India, 23–24 March 2017; pp. 620–624. [Google Scholar]
- Dubey, S.R.; Jalal, A.S. Fusing color and texture cues to identify the fruit diseases using images. Int. J. Comput. Vis. Image Process. 2014, 4, 52–67. [Google Scholar] [CrossRef]
- Jones, H.G. Plants and Microclimate, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Blum, A.; Mayer, J.; Gozlan, G. Infrared thermal sensing of plant canopies as a screening technique for dehydration avoidance in wheat. Field Crop. Res. 1982, 5, 137–146. [Google Scholar] [CrossRef]
- Alchanatis, V.; Cohen, Y.; Cohen, S.; Moller, M.; Meron, M.; Tsipris, J.; Orlov, V.; Naor, A.; Charit, Z. Fusion of IR and multispectral images in the visible range for empirical and model based mapping of crop water status. In Proceedings of the 2006 ASAE Annual Meeting, Portland, OR, USA, 9–12 July 2006; p. 1. [Google Scholar]
- Leinonen, I.; Jones, H.G. Combining thermal and visible imagery for estimating canopy temperature and identifying plant stress. J. Exp. Bot. 2004, 55, 1423–1431. [Google Scholar] [CrossRef]
- Sun, H.; Feng, M.; Xiao, L.; Yang, W.; Wang, C.; Jia, X.; Zhao, Y.; Zhao, C.; Muhammad, S.K.; Li, D. Assessment of plant water status in winter wheat (Triticum aestivum L.) based on canopy spectral indices. PLoS ONE 2019, 14, e0216890. [Google Scholar] [CrossRef]
- Ge, Y.; Bai, G.; Stoerger, V.; Schnable, J.C. Temporal dynamics of maize plant growth, water use, and leaf water content using automated high throughput RGB and hyperspectral imaging. Comput. Electron. Agric. 2016, 127, 625–632. [Google Scholar] [CrossRef]
- Pandey, P.; Ge, Y.; Stoerger, V.; Schnable, J.C. High throughput in vivo analysis of plant leaf chemical properties using hyperspectral imaging. Front. Plant Sci. 2017, 8, 1348. [Google Scholar] [CrossRef]
- Bhole, V.; Kumar, A.; Bhatnagar, D. Fusion of color-texture features based classification of fruits using digital and thermal images: A step towards improvement. Grenze Int. J. Eng. Technol. 2020, 6, 133–141. [Google Scholar]
- Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Rasmussen, J.; Ntakos, G.; Nielsen, J.; Svensgaard, J.; Poulsen, R.N.; Christensen, S. Are vegetation indices derived from consumer-grade cameras mounted on UAVs sufficiently reliable for assessing experimental plots? Eur. J. Agron. 2016, 74, 75–92. [Google Scholar] [CrossRef]
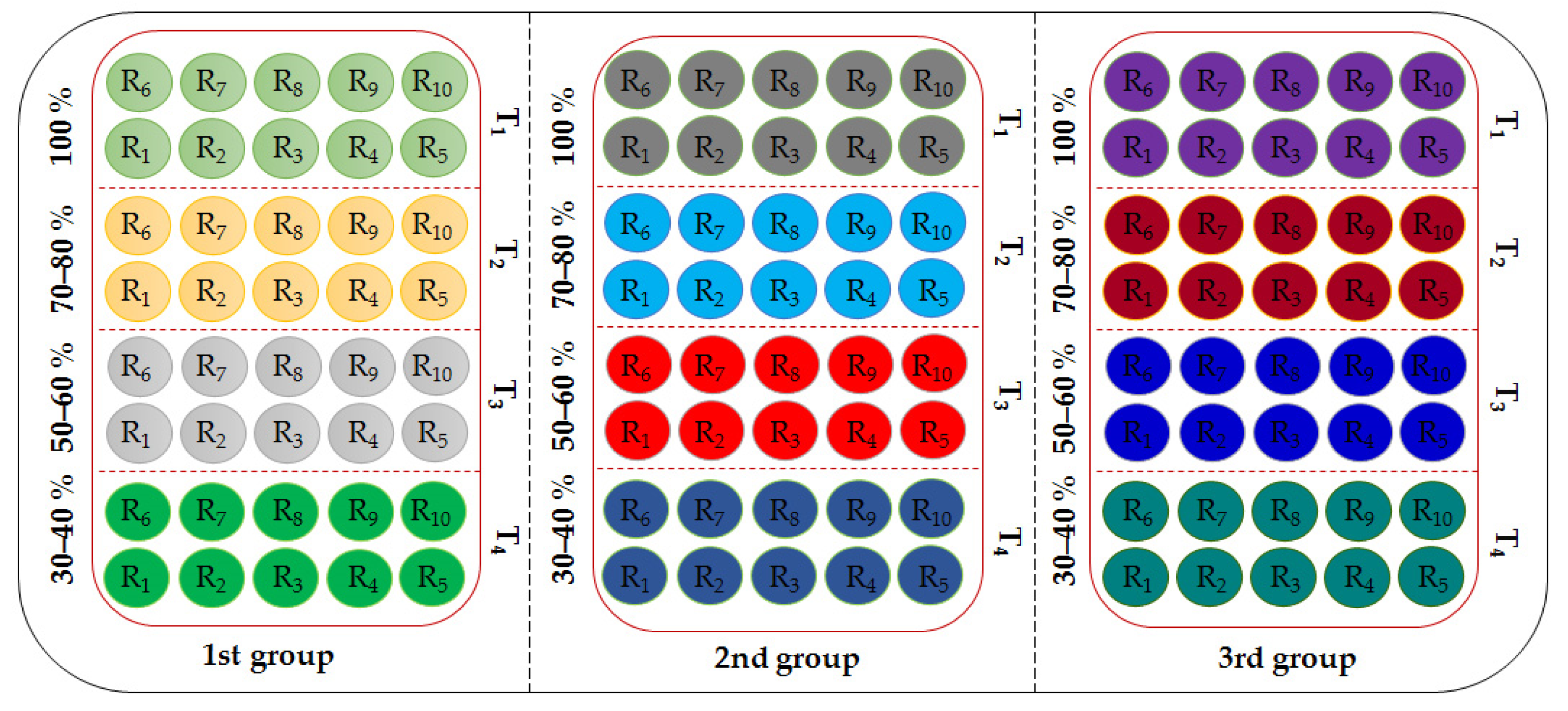



| Date | Temperature (°C) | Relative Humidity (%) | VPD (Kpa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Avg. | Std. | Min. | Max. | Avg. | Std. | ||
| July 10 to August 12 | 24 | 38 | 31 | 5.29 | 41 | 95 | 68 | 20.10 | 1.44 |
| August 13 to August 30 | 23 | 34 | 28.5 | 4.10 | 44 | 97 | 70.5 | 16.97 | 1.15 |
| August 31 to September 21 | 18 | 35 | 26.5 | 5.14 | 41 | 96 | 68.5 | 17.79 | 1.09 |
| RGB Indices | Formula | References |
|---|---|---|
| Normalized red index (rn) | R/(R + G + B) | [36] |
| Normalized green index (gn) | G/(R + G + B) | [36] |
| Normalized blue index (bn) | B/(R + G + B) | [36] |
| Green red ratio index (GRRI) | G/R | [37] |
| Red blue ratio index (RBRI) | R/B | [38] |
| Green blue ratio index (GBRI) | G/B | [38] |
| Normalized difference index (NDI) | (rn − gn)/(rn + gn + 0.01) | [39] |
| Green-red vegetation index (GRVI) | (G − R)/(G + R) | [40] |
| Kawashima index (IKAW) | (R − B)/(R + B) | [36] |
| Woebbecke index (WI) | (G − B)/(R − G) | [18] |
| Green leaf index (GLI) | (2 × G − R − B)/(2 × G + R + B) | [41] |
| Visible atmospherically index (VARI) | (G − R)/(G + R − B) | [42] |
| Excess red vegetation index (EXR) | 1.4 × rn − gn | [43] |
| Excess blue vegetation index (EXB) | 1.4 × bn − gn | [43] |
| Excess green vegetation index (EXG) | 2 × gn − rn − bn | [43] |
| Excess green minus excess red index (EXGR) | EXG − EXR | [43] |
| Principal component analysis index (IPCA) | 0.994 × |R − B| + 0.961 × |G − B| + 0.914 × |G − R| | [44] |
| Color index of vegetation index (CIVE) | 0.441 × R − 0.881 × G + 0.385 × B + 18.78745 | [45] |
| Vegetative index (VEG) | G/(Ra × B(1−a)), a = 0.667 | [45] |
| Combination index (COM) | 0.25 × EXG + 0.3 × EXGR + 0.33 × CIVE + 0.12 × VEG | [45] |
| Variable Type | Formula | Reference |
|---|---|---|
| Contrast | Con = | [49] |
| Dissimilarity | Dis = | |
| Homogeneity | Hom = | |
| Angular second moment | ASM = | |
| Energy | Ene = | |
| Correlation | Corr = |
| nf | (nr1,nr2) | fun | Iter | MSE | RMSE | MAPE (%) | R2 | Acc | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | CV | Test | Train | CV | Test | Train | CV | Test | Train | CV | Test | |||||
| 20 | (14,10) | logistic | 47 | 6.89 | 5.971 | 9.394 | 2.625 | 2.444 | 3.065 | 2.853 | 3.304 | 3.273 | 0.693 | 0.613 | 0.556 | 0.967 |
| 19 | (11,13) | logistic | 45 | 7.017 | 6.150 | 8.486 | 2.649 | 2.480 | 2.913 | 2.868 | 3.353 | 2.948 | 0.687 | 0.577 | 0.599 | 0.971 |
| 18 | (18,18) | logistic | 54 | 7.505 | 7.046 | 7.253 | 2.739 | 2.654 | 2.693 | 3.078 | 3.593 | 2.859 | 0.665 | 0.519 | 0.657 | 0.971 |
| 17 | (2,5) | logistic | 140 | 9.846 | 5.842 | 9.767 | 3.138 | 2.417 | 3.125 | 3.631 | 3.277 | 3.639 | 0.561 | 0.620 | 0.538 | 0.964 |
| 16 | (19,5) | logistic | 65 | 7.689 | 6.969 | 8.758 | 2.773 | 2.639 | 2.959 | 3.104 | 3.558 | 2.979 | 0.657 | 0.525 | 0.586 | 0.970 |
| 15 | (19,16) | tanh | 107 | 7.179 | 7.019 | 8.512 | 2.679 | 2.649 | 2.918 | 3.002 | 3.549 | 2.928 | 0.679 | 0.558 | 0.593 | 0.971 |
| 14 * | (19,15) | logistic | 119 | 4.521 | 5.247 | 7.776 | 2.126 | 2.291 | 2.788 | 2.244 | 3.105 | 2.832 | 0.798 | 0.625 | 0.632 | 0.972 |
| 13 | (13,15) | logistic | 70 | 6.954 | 6.524 | 8.776 | 2.637 | 2.554 | 2.963 | 2.874 | 3.456 | 3.024 | 0.689 | 0.572 | 0.585 | 0.969 |
| 12 | (3,3) | logistic | 174 | 11.201 | 5.609 | 11.499 | 3.347 | 2.369 | 3.391 | 3.657 | 3.235 | 3.503 | 0.500 | 0.598 | 0.456 | 0.964 |
| 11 | (11,6) | logistic | 69 | 7.381 | 6.854 | 8.397 | 2.717 | 2.618 | 2.898 | 3.014 | 3.534 | 2.867 | 0.671 | 0.551 | 0.603 | 0.971 |
| 10 | (6,14) | logistic | 63 | 7.286 | 7.347 | 8.452 | 2.699 | 2.711 | 2.907 | 2.983 | 3.663 | 3.083 | 0.675 | 0.533 | 0.600 | 0.969 |
| 9 | (8,15) | logistic | 104 | 6.729 | 6.722 | 8.393 | 2.594 | 2.593 | 2.897 | 2.858 | 3.496 | 2.861 | 0.699 | 0.531 | 0.603 | 0.971 |
| 8 | (14,14) | logistic | 109 | 6.997 | 6.839 | 9.511 | 2.645 | 2.615 | 3.084 | 2.921 | 3.549 | 3.079 | 0.688 | 0.553 | 0.550 | 0.969 |
| 7 | (17,14) | tanh | 270 | 6.774 | 6.068 | 9.918 | 2.603 | 2.463 | 3.149 | 2.811 | 3.357 | 3.213 | 0.698 | 0.580 | 0.531 | 0.968 |
| 6 | (7,10) | logistic | 86 | 7.484 | 6.364 | 8.983 | 2.736 | 2.523 | 2.997 | 3.069 | 3.403 | 3.059 | 0.666 | 0.565 | 0.575 | 0.969 |
| 5 | (3,11) | logistic | 224 | 7.149 | 6.237 | 7.529 | 2.674 | 2.497 | 2.744 | 2.983 | 3.378 | 2.630 | 0.681 | 0.585 | 0.644 | 0.974 |
| 4 | (10,17) | logistic | 97 | 7.680 | 7.156 | 8.029 | 2.771 | 2.675 | 2.834 | 3.129 | 3.619 | 2.737 | 0.657 | 0.514 | 0.620 | 0.973 |
| 3 | (6,20) | tanh | 150 | 7.685 | 5.961 | 8.297 | 2.772 | 2.442 | 2.881 | 3.065 | 3.311 | 2.922 | 0.657 | 0.602 | 0.607 | 0.971 |
| 2 | (5,15) | logistic | 215 | 7.358 | 5.819 | 9.004 | 2.713 | 2.412 | 3.001 | 2.983 | 3.261 | 2.892 | 0.672 | 0.613 | 0.574 | 0.971 |
| 1 | (8,17) | logistic | 511 | 9.894 | 8.199 | 12.315 | 3.145 | 2.863 | 3.509 | 3.409 | 3.879 | 3.965 | 0.559 | 0.448 | 0.417 | 0.960 |
| nf. | (nr1,nr2) | fun | Iter | MSE | RMSE | MAPE (%) | R2 | Acc | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | CV | Test | Train | CV | Test | Train | CV | Test | Train | CV | Test | |||||
| 6 | (16,10) | relu | 297 | 5.837 | 5.537 | 7.599 | 2.416 | 2.353 | 2.757 | 2.582 | 3.202 | 3.151 | 0.739 | 0.612 | 0.641 | 0.968 |
| 5 * | (6,10) | tanh | 175 | 6.056 | 4.614 | 6.794 | 2.461 | 2.148 | 2.607 | 2.607 | 2.917 | 2.938 | 0.729 | 0.656 | 0.679 | 0.971 |
| 4 | (19,6) | relu | 141 | 6.365 | 5.242 | 6.367 | 2.523 | 2.289 | 2.523 | 2.713 | 3.124 | 2.917 | 0.716 | 0.640 | 0.699 | 0.971 |
| 3 | (7,13) | relu | 185 | 6.339 | 5.335 | 6.127 | 2.518 | 2.309 | 2.475 | 2.671 | 3.133 | 2.949 | 0.717 | 0.615 | 0.710 | 0.971 |
| 2 | (15,3) | tanh | 192 | 7.169 | 5.034 | 10.249 | 2.677 | 2.244 | 3.201 | 3.026 | 3.048 | 3.689 | 0.680 | 0.644 | 0.515 | 0.963 |
| 1 | (19,8) | logistic | 63 | 10.442 | 7.777 | 10.337 | 3.231 | 2.789 | 3.215 | 4.177 | 3.907 | 4.067 | 0.534 | 0.443 | 0.511 | 0.959 |
| nf | (nr1,nr2) | fun | Iter | MSE | RMSE | MAPE (%) | R2 | Acc | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | CV | Test | Train | CV | Test | Train | CV | Test | Train | CV | Test | |||||
| 2 a | (19,18) | logistic | 217 | 2.008 | 1.245 | 4.172 | 1.417 | 1.116 | 2.043 | 1.302 | 1.472 | 1.989 | 0.910 | 0.851 | 0.803 | 0.980 |
| 1 b | (3,5) | logistic | 297 | 9.529 | 6.497 | 10.473 | 3.087 | 2.549 | 3.239 | 3.424 | 3.459 | 3.782 | 0.575 | 0.566 | 0.505 | 0.962 |
| nf | (nr1,nr2) | fun. | Iter | MSE | RMSE | MAPE (%) | R2 | Acc | C.T. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | CV | Test | Train | CV | Test | Train | CV | Test | Train | CV | Test | ||||||
| 7 a | (18,9) | logistic | 275 | 0.119 | 0.199 | 0.583 | 0.346 | 0.447 | 0.764 | 0.366 | 0.599 | 0.668 | 0.995 | 0.982 | 0.972 | 0.993 | 28.158 |
| 16 b | (7,12) | logistic | 130 | 0.355 | 0.437 | 0.455 | 0.596 | 0.661 | 0.674 | 0.604 | 0.891 | 0.682 | 0.984 | 0.956 | 0.978 | 0.993 | 29.977 |
| 21 c | (8,9) | logistic | 422 | 0.063 | 0.130 | 0.359 | 0.251 | 0.361 | 0.599 | 0.251 | 0.480 | 0.564 | 0.997 | 0.984 | 0.983 | 0.994 | 31.911 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsherbiny, O.; Zhou, L.; Feng, L.; Qiu, Z. Integration of Visible and Thermal Imagery with an Artificial Neural Network Approach for Robust Forecasting of Canopy Water Content in Rice. Remote Sens. 2021, 13, 1785. https://doi.org/10.3390/rs13091785
Elsherbiny O, Zhou L, Feng L, Qiu Z. Integration of Visible and Thermal Imagery with an Artificial Neural Network Approach for Robust Forecasting of Canopy Water Content in Rice. Remote Sensing. 2021; 13(9):1785. https://doi.org/10.3390/rs13091785
Chicago/Turabian StyleElsherbiny, Osama, Lei Zhou, Lei Feng, and Zhengjun Qiu. 2021. "Integration of Visible and Thermal Imagery with an Artificial Neural Network Approach for Robust Forecasting of Canopy Water Content in Rice" Remote Sensing 13, no. 9: 1785. https://doi.org/10.3390/rs13091785
APA StyleElsherbiny, O., Zhou, L., Feng, L., & Qiu, Z. (2021). Integration of Visible and Thermal Imagery with an Artificial Neural Network Approach for Robust Forecasting of Canopy Water Content in Rice. Remote Sensing, 13(9), 1785. https://doi.org/10.3390/rs13091785









