A Semi-Automatic Method for Extracting Small Ground Fissures from Loess Areas Using Unmanned Aerial Vehicle Images
Abstract
1. Introduction
2. Methodology of Ground Fissure Extraction
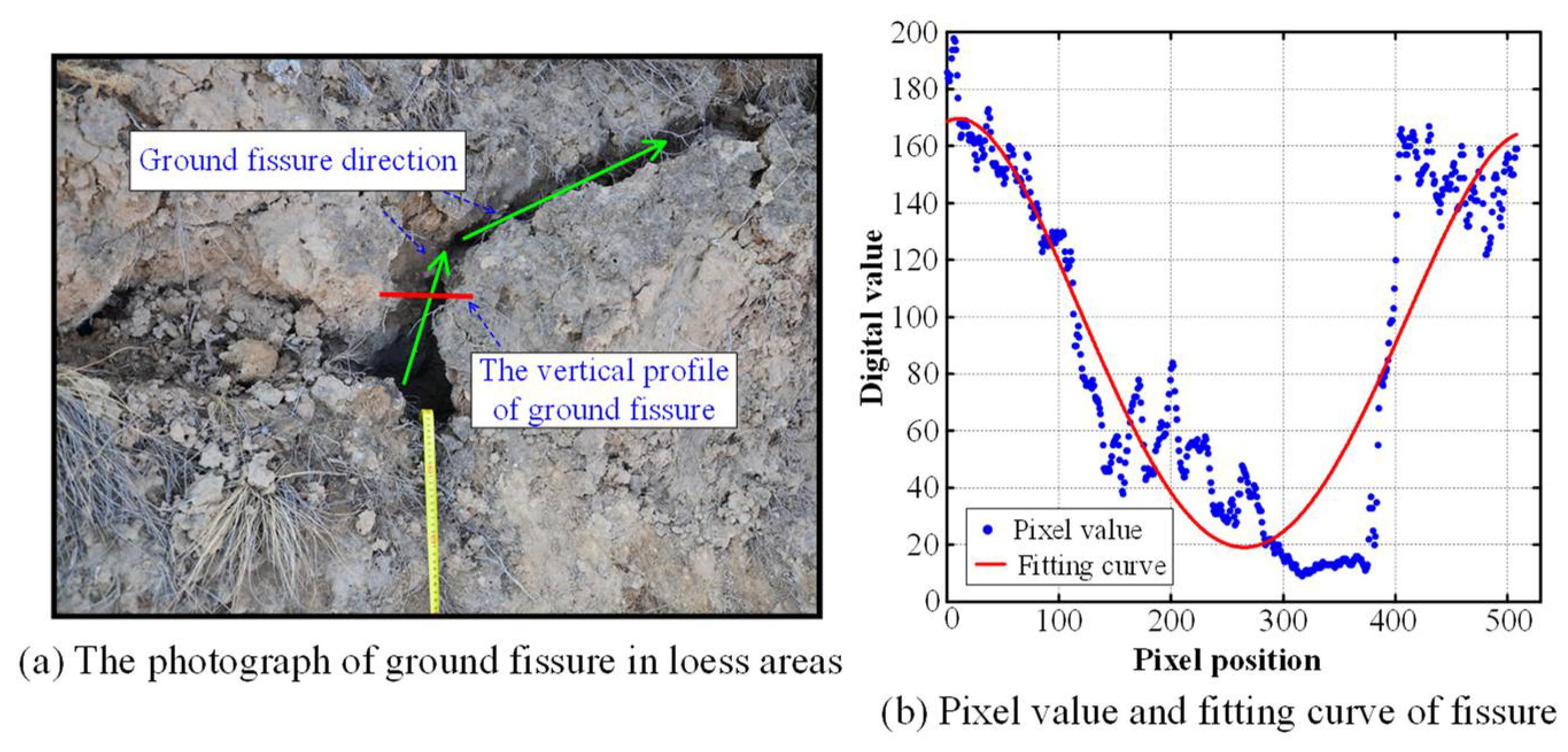
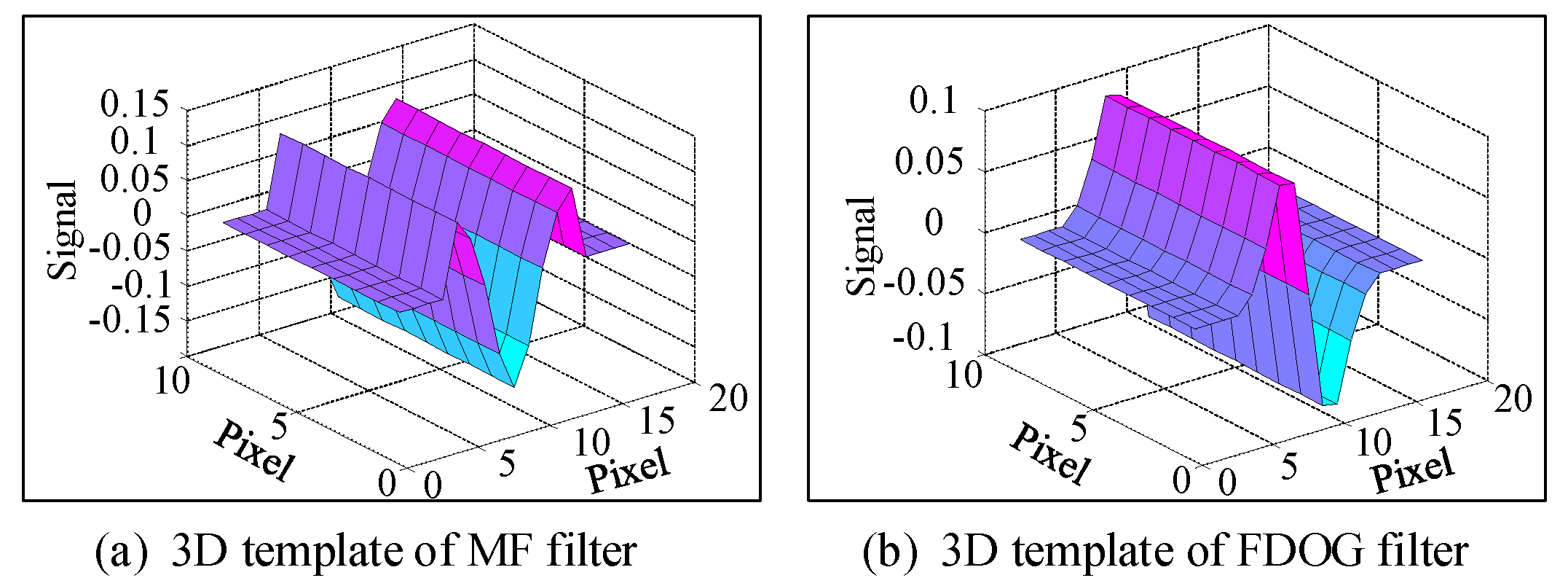
2.1. Modified MF-FDOG Algorithm for Ground Fissure Extraction
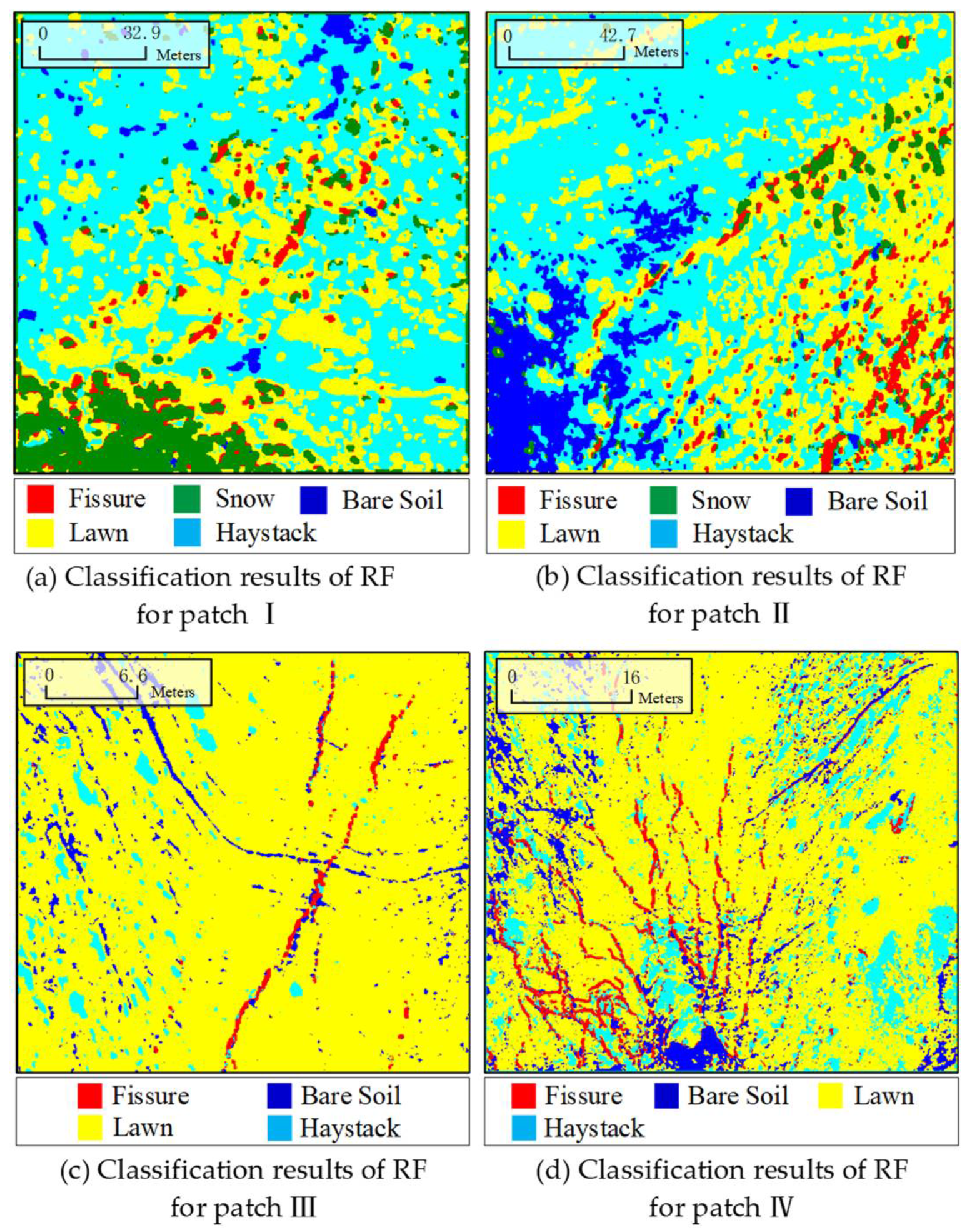
2.2. RF Classification in Loess Landform Areas
3. Post-Processing of Ground Fissure Extraction
3.1. Ground Fissure Connection
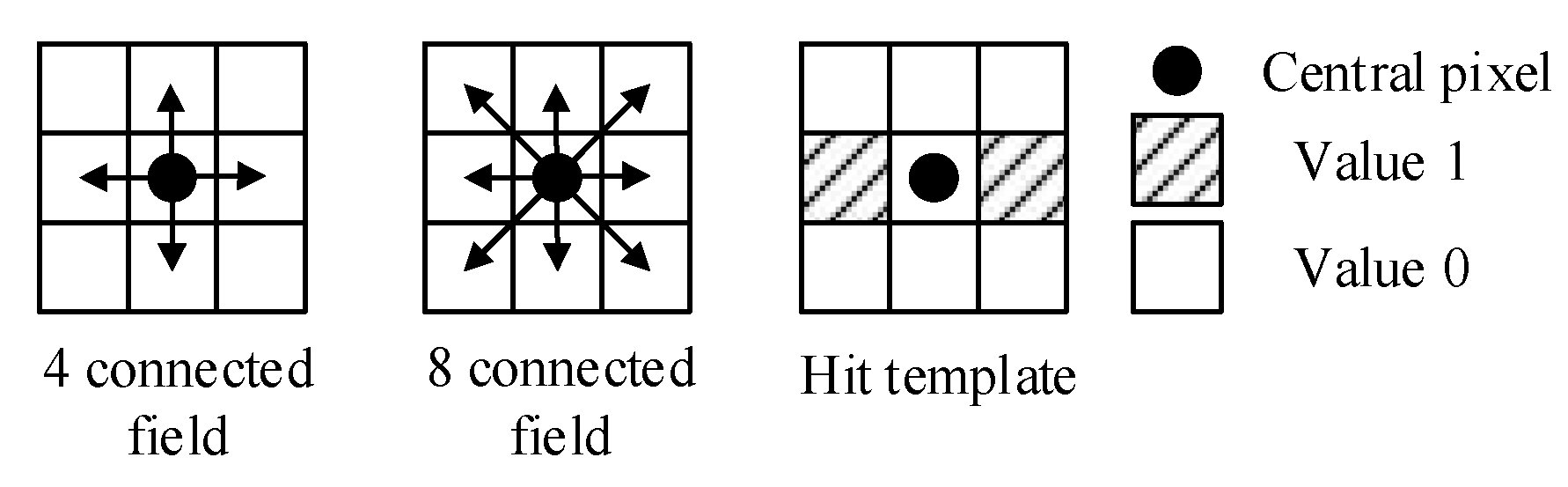
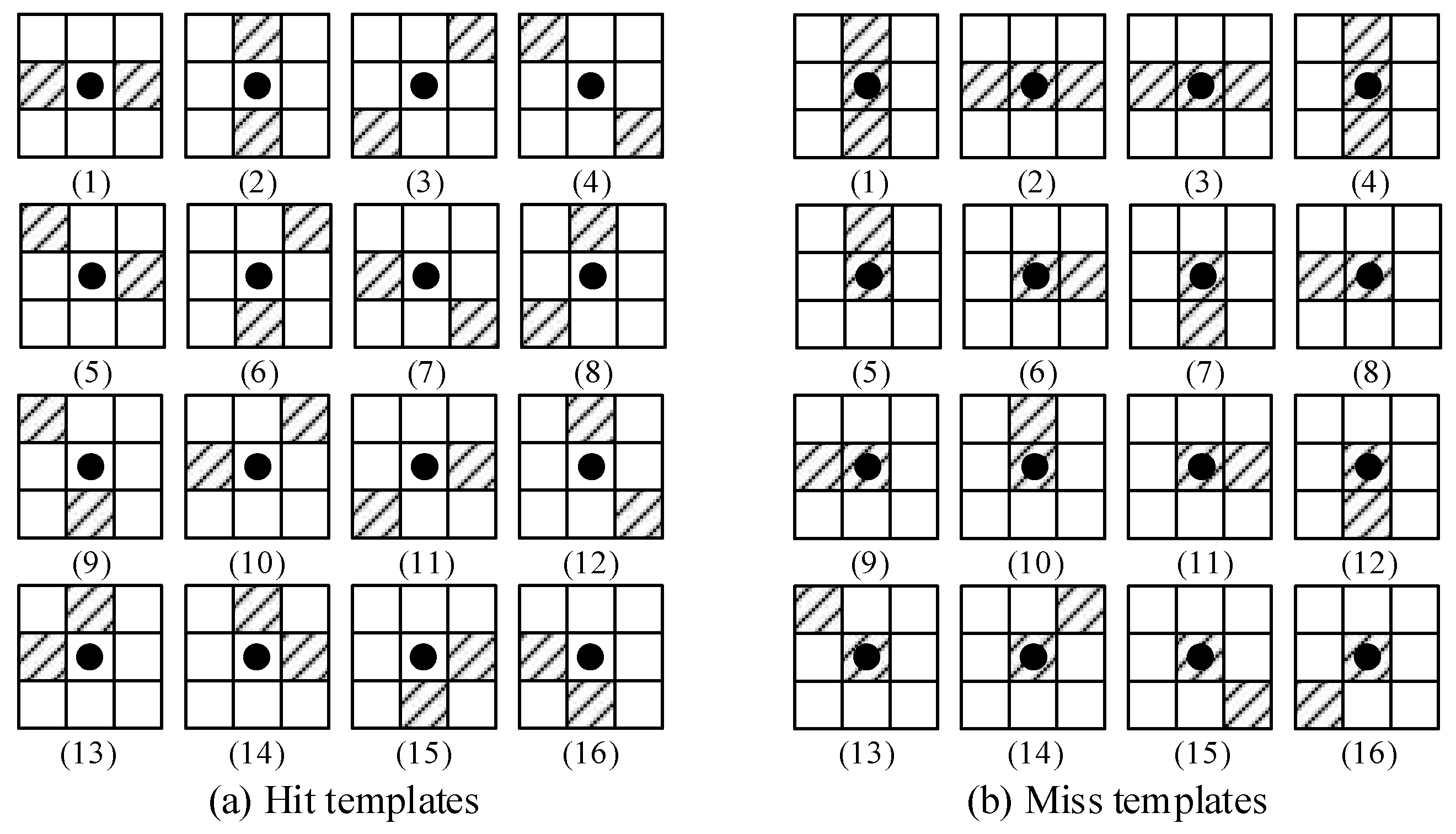
3.2. Fragment Removal from the Ground Fissure Candidates
4. Application of the Ground Fissure Extraction Scheme to the Study Area
4.1. Introduction of the Ground Fissure Extraction Scheme
- Step 1:
- Image acquisition. According to the survey results, the appropriate UAV is selected to obtain the images of the study area. Before flight, the terrain, wind direction and other factors should be considered, and the appropriate flight parameter and the position of the control points should be set. After flight, RTK equipment is used to obtain the coordinates of control points. If image quality is low in some areas, much flight time is added in order to improve the image quality.
- Step 2:
- Image pre-processing. Firstly, the lens parameters will be imported into PixelGrid software to correct the distortion of the original image, in order to reduce the systematic error caused by the lens. After importing the control point data, the geometric correction of images will be processed by PixelGrid software, and the resampling method of three convolutions is selected to ensure the image accuracy. Then, the accuracy evaluation method of PixelGrid will be automatically carried out. Finally, the appropriate filtering and histogram matching method is used to enhance images for conveniently extracting ground fissure.
- Step 3:
- Extraction of ground fissure candidates with the modified MF-FDOG algorithm. According to information obtained from surveying and image analysis, the program is run with suitable parameter settings (i.e., the optimal , , and values) to obtain ground fissure candidates.
- Step 4:
- “Non-ground fissure” target removal. Banded vegetation, edges of remaining snow and shadows from micro-topography will result in several “non-ground fissure” targets in the candidates extracted by step 2. Additionally, UAV images only include red, green, and blue bands. It is difficult to completely remove vegetation targets with such limited spectral information from the candidates. However, the inherent textural features of vegetation are valuable for vegetation information extraction, which is used to eliminate vegetation-induced false ground fissures. Therefore, the RF algorithm is used to classify the images based on both textural and spectral information. Then, the different categories, such as vegetation, are used to create mask files. Applying the mask files to the ground fissure candidate image can exclude non-ground fissure targets and improve the accuracy of ground fissure extraction. Finally, a binary image of the ground fissure is derived.
- Step 5:
- Post-processing. The modified MF-FDOG algorithm is an image processing method based on single pixels. Therefore, the obtained binary image of ground fissures inevitably contains many small gaps and pixel sets whose areas are far less than that of the corresponding true ground fissures. To achieve more accurate results, mathematical morphology was employed to connect broken ground fissures and remove these scattered pixels.
- Step 6:
- Accuracy assessment. In our study, an image classification method was used to identify non-ground fissure targets. The accuracy of image classification significantly affects the final results; thus, the Kappa coefficient and confusion matrix were used to evaluate RF classification accuracy in this study. In addition, the receiver operating characteristic curve (ROC) was used to evaluate the results of ground fissure extraction [35].
4.2. Study Area and Data Source
5. Ground Fissure Extraction Results and Analysis in a Loess Area
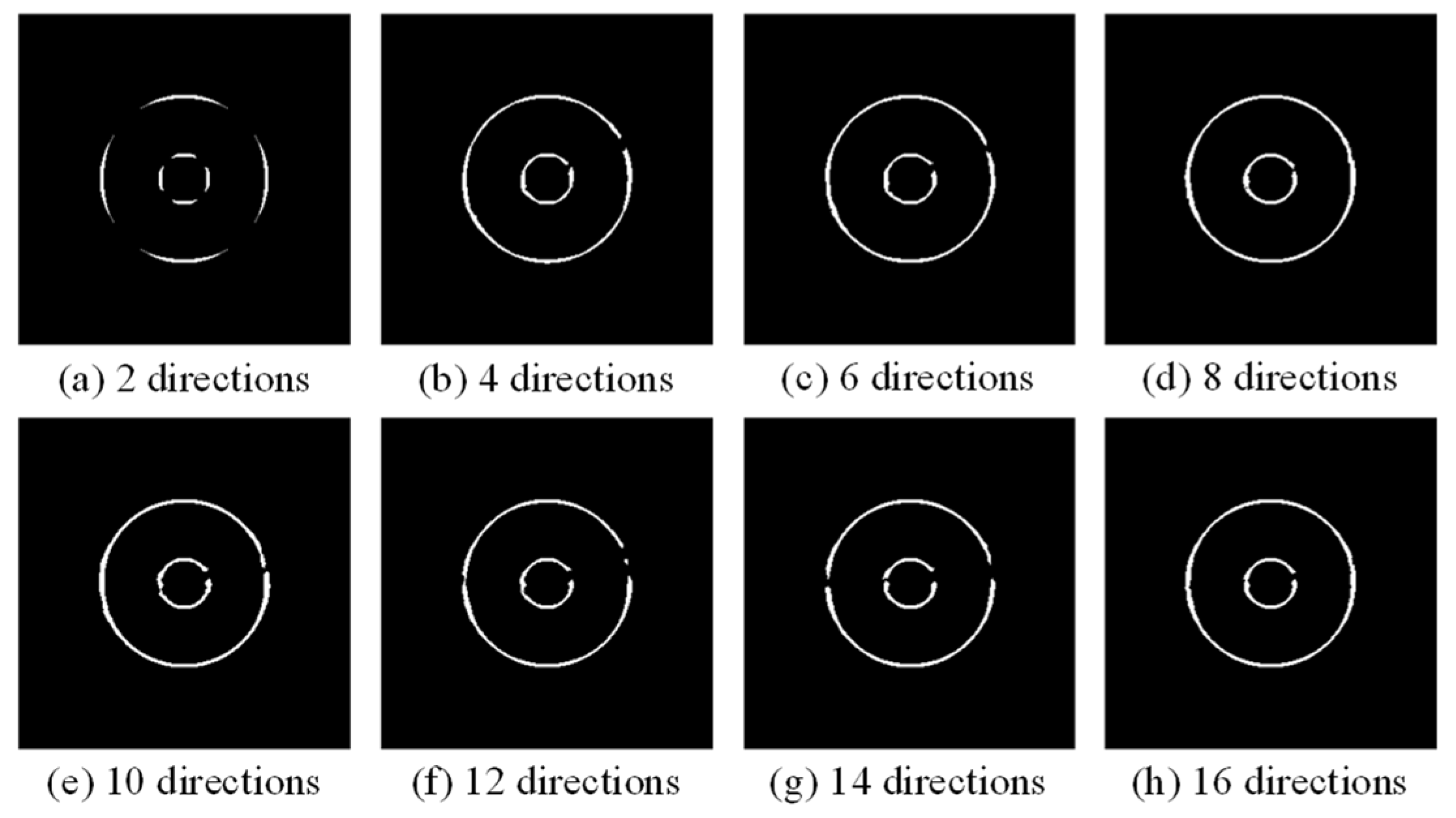
5.1. Selection of Parameter σ and Direction Number in the Template
5.2. Results of Ground Fissure Extraction Based on Modified MF-FDOG Algorithm
5.3. Accuracy Analysis of the Modified MF-FDOG Algorithm
5.4. Accuracy Assessment of the Different Ground Fissure Extraction Algorithms
5.4.1. Self-Assessment of the Modified MF-FDOG Algorithm
5.4.2. Accuracy Comparison of the Different Ground Fissure Extractions Algorithms
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Dong, Y.G.L. Geology and Geomorphology; China Agricultural University Press: Beijin, China, 2013; pp. 257–267. [Google Scholar]
- Chai, H.X.; Cheng, W.M.; Qiao, Y.L. Classification system of 1:1000,000 digital loess geomorphology in China Geo-information. Science 2006, 8, 6–13. [Google Scholar]
- Wang, X.Y.; Mao, S.H.; Zhang, Y.J. Differential Settlement due to Ground Fissures in Xi’an. Adv. Mater. Res. 2015, 1065–1069, 410–413. [Google Scholar] [CrossRef]
- Li, Q.C.; Ye, P.; Shao, G.Z.; Luo, W.B. Integrated Geophysical Detection on Ground Fissure in Shanxi Jingyang Seismostation of National Highway 211. Chin. J. Eng. Geophys. 2014, 11, 106–111. [Google Scholar]
- Wang, Z.F.; Shen, S.L.; Cheng, W.C.; Xu, Y.S. Ground fissures in Xi’an and measures to prevent damage to the Metro tunnel system due to geohazards. Environ. Earth Sci. 2016, 75, 511. [Google Scholar] [CrossRef]
- Stumpf, A.; Niethhammer, U.; Rothmund, S.; Mathieu, A.; Malet, J.P.; Kerle, N.; Joswing, M. Advanced image analysis for automated mapping of landslide surface fissures. Landslide Sci. Pract. 2013, 2, 357–363. [Google Scholar]
- Giuseppe, P.; Nicolai, P. Edge and line oriented contour detection: State of the art. Image Vis. Comput. 2011, 29, 79–103. [Google Scholar]
- Quackenbush, L.J. A review of techniques for extracting linear features from imagery. Photogramm. Eng. Remote Sens. 2004, 70, 1383–1392. [Google Scholar] [CrossRef]
- Shruthi, B.V.; Kerle, N.; Jetten, V.G. Object-based gully feature extraction using high spatial resolution imagery. Geomorphology 2011, 134, 260–268. [Google Scholar] [CrossRef]
- Baruch, A.; Filin, S. Detection of gullies in roughly textured terrain using airborne laser scanning data. J. Photogramm. Remote Sens. 2011, 66, 564–578. [Google Scholar] [CrossRef]
- Jain, R.; Kasturi, R.; Schunck, B.G. Machine Vision; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- Lawrence, G.R. Machine Perception of Three-Dimensional Solids; Institute of Technology: Boston, MA, USA, 1963. [Google Scholar]
- Sobel, I. Camera Models and Machine Perception; California Department of Computer Science, Stanford University: Stanford, CA, USA, 1970. [Google Scholar]
- Prewitt, J.M.S. Object Enhancement and Extraction. Picture Processing and Psychopictorics; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Koenderink, J.J. Theory of “Edge-Detection”. Anal. Sci. Eng. Beyond 2012, 6, 35–49. [Google Scholar]
- Gonzalez, C.I.; Melin, P.; Castro, J.R.; Mendoza, O.; Castillo, O. An improved sobel edge detection method based on generalized type-2 fuzzy logic. Soft Computing—A Fusion of Foundations. Methodol. Appl. 2016, 20, 773–784. [Google Scholar]
- Manasa, N.; Mounica, G. Brain tumor detection based on canny edge detection algorithm and its area calculation. Int. Comput. Math. Sci. 2016, 5, 10–13. [Google Scholar]
- Hu, X. Research on Subway Tunnel Crack Detection Technology Based on Image Processing; Beijing Jiaotong University: Beijing, China, 2014. [Google Scholar]
- Alam, M.A.; Ali, M.M.N.; Syed, M.A.A.; Sorif, N.; Rahaman, M.A. An algorithm to detect and identify defects of industrial pipes using image processing. In Proceedings of the 8th International Conference on Software, Knowledge, Information Management and Applications (SKIMA), Dhaka, Bangladesh, 18–20 December 2014; pp. 1–6. [Google Scholar]
- Khalifa, I.; Aboutabl, A.E.; Barakat, G.S.A. A New Image-Based Model for Predicting Cracks in Sewer Pipes. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 65–71. [Google Scholar] [CrossRef]
- Kirstein, S.; Muller, K.; Walecki, M.N.; Desemo, T.M. Robust adaptive flow line detection in sewer pipes. Autom. Constr. 2012, 21, 24–31. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.L. Geomorphic regionalization and agricultural evaluation of geomorphic featuresin Gansu. J. Gansu Agric. Univ. 1994, 30, 444–449. [Google Scholar]
- Chaudhuri, S.; Chatterjee, S.; Katz, N.; Nelson, M.; Goldbaum, M. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Trans. Med Imaging 1989, 8, 263–269. [Google Scholar]
- Zhang, B.; Zhang, L.; Zhang, L.; Karray, F. Retinal vessel extraction by matched filter with first-order derivative Gaussian. Comput. Biol. Med. 2010, 40, 438–445. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, A.; Malet, J.P.; Kerle, N.; Niethammer, U.; Rothmund, S. Image-based mapping of surface fissures for the investigation of landslide dynamics. Geomorphology 2013, 186, 12–27. [Google Scholar] [CrossRef]
- Breimal, L. Random Forests. Machine Learning; Springer: Berlin/Heidelberg, Germany, 2001; Volume 45, pp. 5–32. [Google Scholar]
- Turin, G. An introduction to matched filters. IRE Trans. Inf. Theory 1960, 6, 311–329. [Google Scholar] [CrossRef]
- Woodward, P.M. Probability and Information Theory with Applications to Radar; Pergamon Press Ltd.: New York, NY, USA, 1953; Volume 41, pp. 59–68. [Google Scholar]
- Nevatla, R.; Babu, K.R. Linear feature extraction and description. Comput. Graph. Image Process. 1980, 13, 257–269. [Google Scholar] [CrossRef]
- Torres, S.J.; Peńa, J.M.; Castro, A.I.D.; López, G.F. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV. Comput. Electron. Agric. 2014, 103, 104–113. [Google Scholar] [CrossRef]
- Rasmussen, J.; Ntakos, G.; Nielsen, J.; Svensgaard, J.; Poulsen, R.N.; Christensen, S. Are vegetation indices derived from consumer-grade cameras mounted on UAVs sufficiently reliable for assessing experimental plots. Eur. J. Agron. 2016, 74, 75–92. [Google Scholar] [CrossRef]
- Hung, C.; Xu, Z.; Sukkarieh, S. Feature learning based approach for weed classification using high resolution aerial images from a digital camera mounted on a UAV. Remote Sens. 2014, 6, 12037–12054. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. UAV remote sensing for urban vegetation mapping using random forest and texture analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef]
- Serra, J. Image Analysis and Mathematical Morphology. Orlando; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Chen, D.M.; Stow, D. The effect of training strategies on supervised classification at different spatial resolutions. Photogramm. Eng. Remote Sens. 2002, 68, 1155–1161. [Google Scholar]
- Emami, H.; Mojaradi, B. A New Method for Accuracy Assessment of Sub-Pixel Classification Results. Am. J Eng. Appl. Sci. 2009, 2, 456–465. [Google Scholar] [CrossRef][Green Version]
- Janssen, L.L.F.; Vanderwel, F.J.W. Accuracy assessment of satellite-derived land-cover data: A review. Photogramm. Eng. Remote Sens. 1994, 60, 419–426. [Google Scholar]
- Tveite, H.; Langaas, S. An accuracy assessment method for geographical line data sets based on buffering. Int. J. Geogr. Inf. 1999, 13, 27–47. [Google Scholar] [CrossRef]
- Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU Computing. IEEE 2008, 96, 879–899. [Google Scholar] [CrossRef]
- Wei, B.W.; Li, T.; Li, G.Y.; Wang, Z.H.; He, M.; Shi, Y.L.; Liu, L.Y.; Zhang, R. Applied analysis of image accelerating distortion correction of OpenCL technology on heterogeneous platform. Comput. Sci. 2016, 43, 167–169. [Google Scholar]





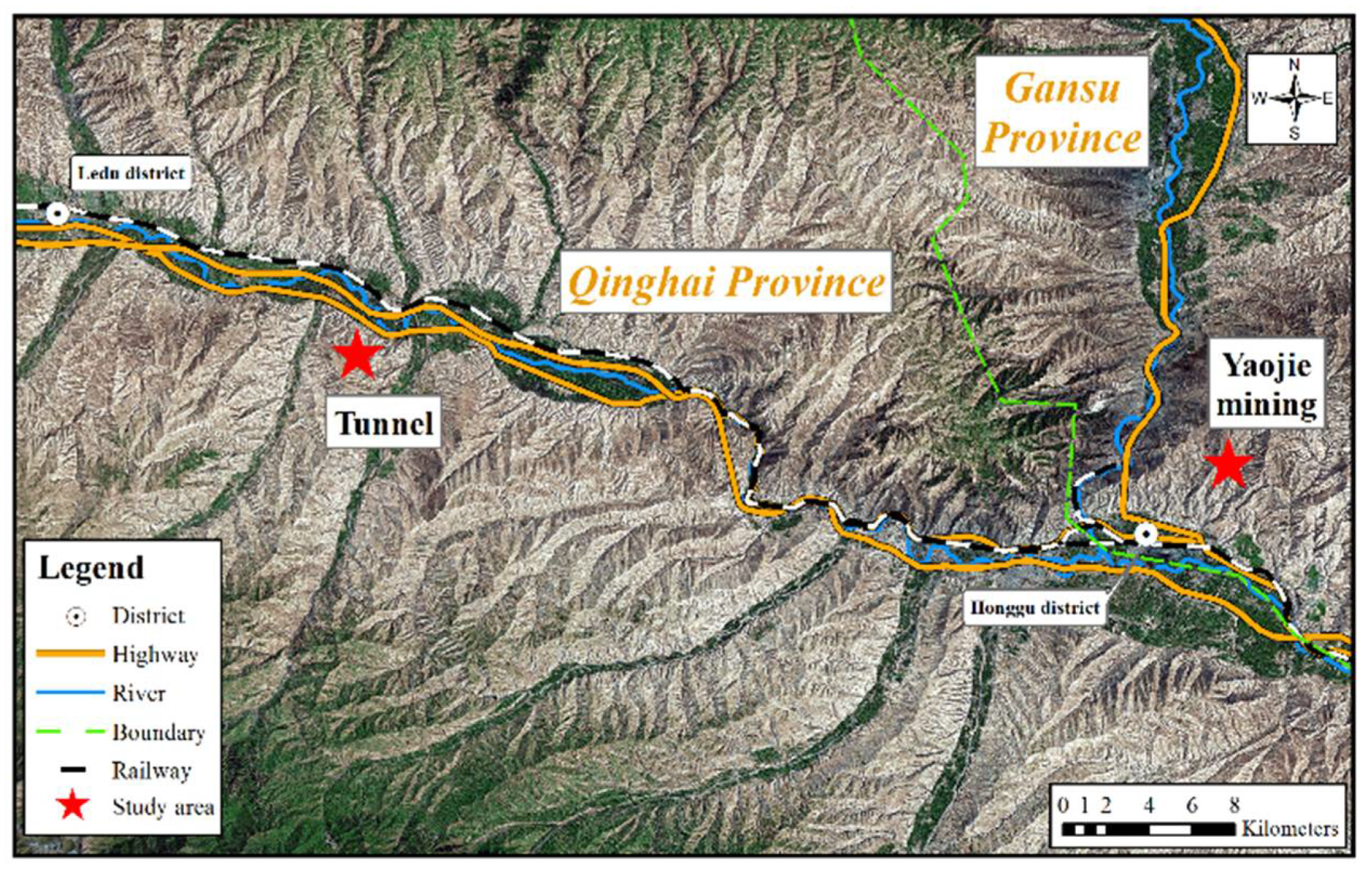













| Tunnel Area | Mining Area | ||
|---|---|---|---|
| Properties of sensor | Model | SONY DSC-RX1 | PHANTOM4 |
| Resolution (dpi) | 6000 × 4000 | 4000 × 2250 | |
| Effective focal length (mm) | 35 | 20 | |
| Photoreceptor size (mm) | 35.8 × 23.9 | 25.4 × 25.4 | |
| UAV platform | Flight height (m) | 3000 | 150 |
| Flight speed (km/h) | 90–120 | 72 | |
| Payload (kg) | 3–5 | – | |
| Resolution (m) | 0.1 | 0.08 | 0.5 |
| (px) | 0.67 | 0.75 | 1.34 |
| Direction | ||||||||
|---|---|---|---|---|---|---|---|---|
| TP | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| Small | 908 | 1667 | 1708 | 1854 | 1979 | 1679 | 1788 | 1880 |
| Large | 1154 | 1938 | 2155 | 2267 | 2331 | 2054 | 2186 | 2132 |
| I | II | III | IV | |
|---|---|---|---|---|
| Overall accuracy/% | 79.81 | 93.10 | 94.98 | 97.22 |
| Kappa accuracy/% | 73.55 | 90.89 | 89.57 | 96.01 |
| - | Tunnel Area | Mining Area | ||||||
|---|---|---|---|---|---|---|---|---|
| Subset I | Subset II | Subset III | Subset IV | |||||
| TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR | |
| Buffer 1 | 0.1195 | 0.0022 | 0.2938 | 0.0080 | 0.2490 | 0.0005 | 0.3387 | 0.0027 |
| Buffer 2 | 0.2489 | 0.0058 | 0.4276 | 0.0177 | 0.4081 | 0.0017 | 0.5165 | 0.0075 |
| Buffer 3 | 0.4323 | 0.0144 | 0.6472 | 0.0357 | 0.5638 | 0.0046 | 0.6537 | 0.0184 |
| Buffer 4 | 0.5338 | 0.0223 | 0.7253 | 0.0513 | 0.6312 | 0.0074 | 0.7090 | 0.0282 |
| Buffer 5 | 0.6150 | 0.0331 | 0.7821 | 0.0710 | 0.6853 | 0.0108 | 0.7547 | 0.0405 |
| Buffer 6 | 0.6767 | 0.0468 | 0.8181 | 0.0936 | 0.7270 | 0.0144 | 0.7872 | 0.0526 |
| Buffer 7 | 0.7135 | 0.0574 | 0.8399 | 0.1104 | 0.7579 | 0.0182 | 0.8141 | 0.0652 |
| Buffer 8 | 0.7534 | 0.0725 | 0.8635 | 0.1330 | 0.7823 | 0.0223 | 0.8384 | 0.0795 |
| Buffer 9 | 0.7895 | 0.0895 | 0.8744 | 0.1444 | 0.8038 | 0.0270 | 0.8581 | 0.0947 |
| Buffer 10 | 0.8218 | 0.1063 | 0.8957 | 0.1803 | 0.8180 | 0.0315 | 0.8750 | 0.1087 |
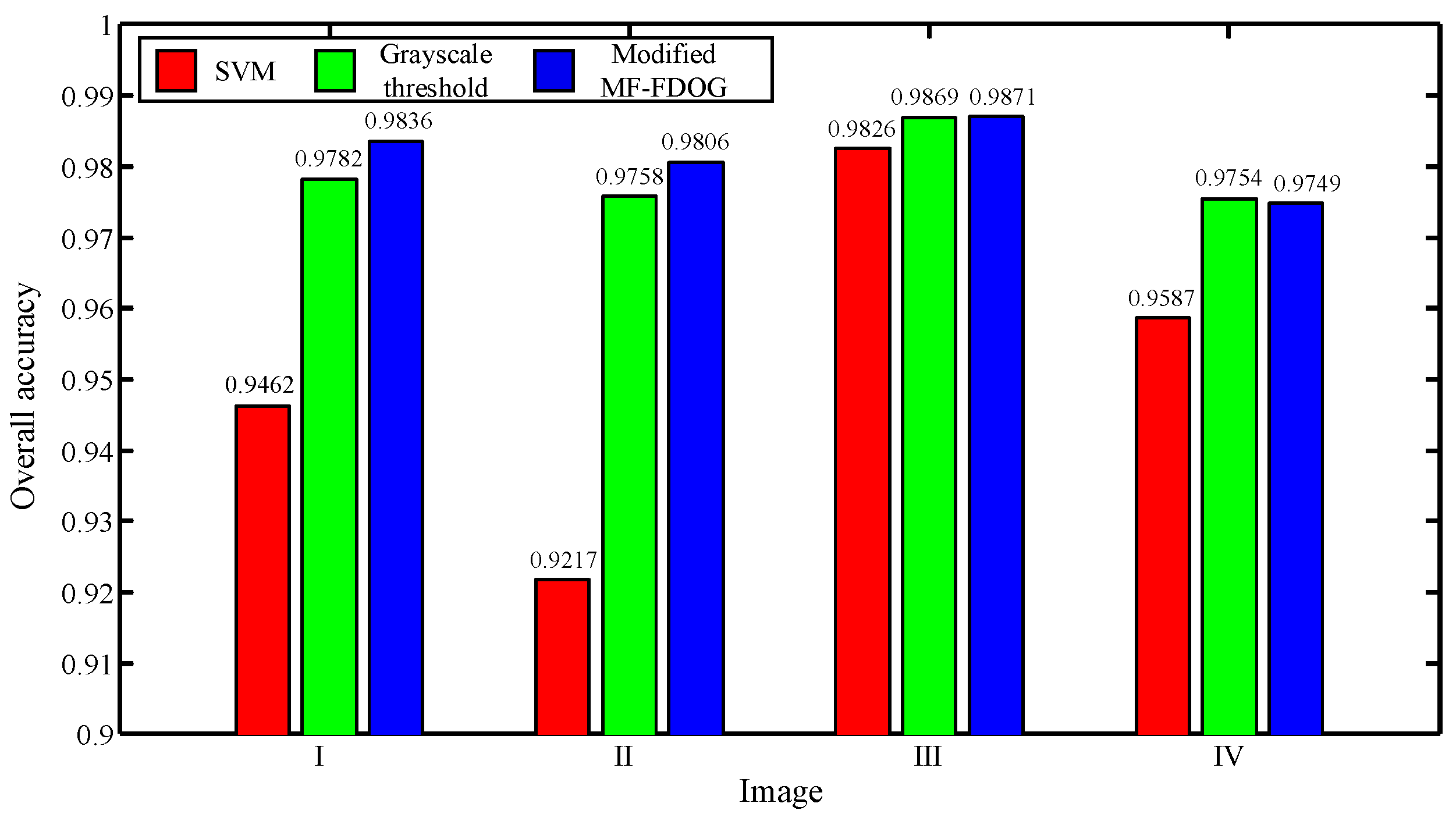
| Subset | SVM Algorithm | Grayscale Threshold Algorithm | The Modified MF-FDOG Algorithm |
|---|---|---|---|
| I | 0.9462 | 0.9782 | 0.9836 |
| II | 0.9217 | 0.9758 | 0.9806 |
| III | 0.9826 | 0.9869 | 0.9871 |
| IV | 0.9587 | 0.9754 | 0.9749 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Wei, B.; Liu, G.; Zhang, R.; Yu, B.; Wu, S. A Semi-Automatic Method for Extracting Small Ground Fissures from Loess Areas Using Unmanned Aerial Vehicle Images. Remote Sens. 2021, 13, 1784. https://doi.org/10.3390/rs13091784
Jia H, Wei B, Liu G, Zhang R, Yu B, Wu S. A Semi-Automatic Method for Extracting Small Ground Fissures from Loess Areas Using Unmanned Aerial Vehicle Images. Remote Sensing. 2021; 13(9):1784. https://doi.org/10.3390/rs13091784
Chicago/Turabian StyleJia, Hongguo, Bowen Wei, Guoxiang Liu, Rui Zhang, Bing Yu, and Shuaiying Wu. 2021. "A Semi-Automatic Method for Extracting Small Ground Fissures from Loess Areas Using Unmanned Aerial Vehicle Images" Remote Sensing 13, no. 9: 1784. https://doi.org/10.3390/rs13091784
APA StyleJia, H., Wei, B., Liu, G., Zhang, R., Yu, B., & Wu, S. (2021). A Semi-Automatic Method for Extracting Small Ground Fissures from Loess Areas Using Unmanned Aerial Vehicle Images. Remote Sensing, 13(9), 1784. https://doi.org/10.3390/rs13091784






