An Accurate Geocoding Method for GB-SAR Images Based on Solution Space Search and Its Application in Landslide Monitoring
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
- GB-SAR original observation dataset. Obtained by GB-SAR by continuous monitoring under specific observation geometry conditions. The azimuth resolution was 2–5 mrad, the maximum range resolution was 0.5 m, and the deformation monitoring accuracy was at the submillimeter level. This was the main dataset used for geocoding in this paper.
- Ground control survey dataset. The azimuth angle of the GB-SAR guide rail was measured by the GNSS or total station and the radar center was combined with ground PCPs in the survey area. The coordinate and angle measurement accuracies reached the centimeter and 0.5 s level, respectively, fully meeting the requirements of GB-SAR coordinate transformation [33,36]. After the measurement, the location point of GB-SAR became the link between the radar and 3D coordinate systems. This dataset was mainly used for the transformation between the two coordinate systems.
- External ancillary 3D information. These data were obtained from aerial photogrammetry or light detection and ranging (LiDAR) carried on UAV. Due to the data gap caused by the shadow of sight, several transformation defects occur during ground-based 3D laser scanning. In this study, UAV aerial photogrammetry technology was used to collect high-resolution images of the monitored area. The PCPs were arranged on the ground to obtain external auxiliary data such as DSM, DOM, and 3D real-scene model (five-lens oblique photogrammetry) using a local unified coordinate system. These data were mainly used to realize the solution space search for geocoding transformation.
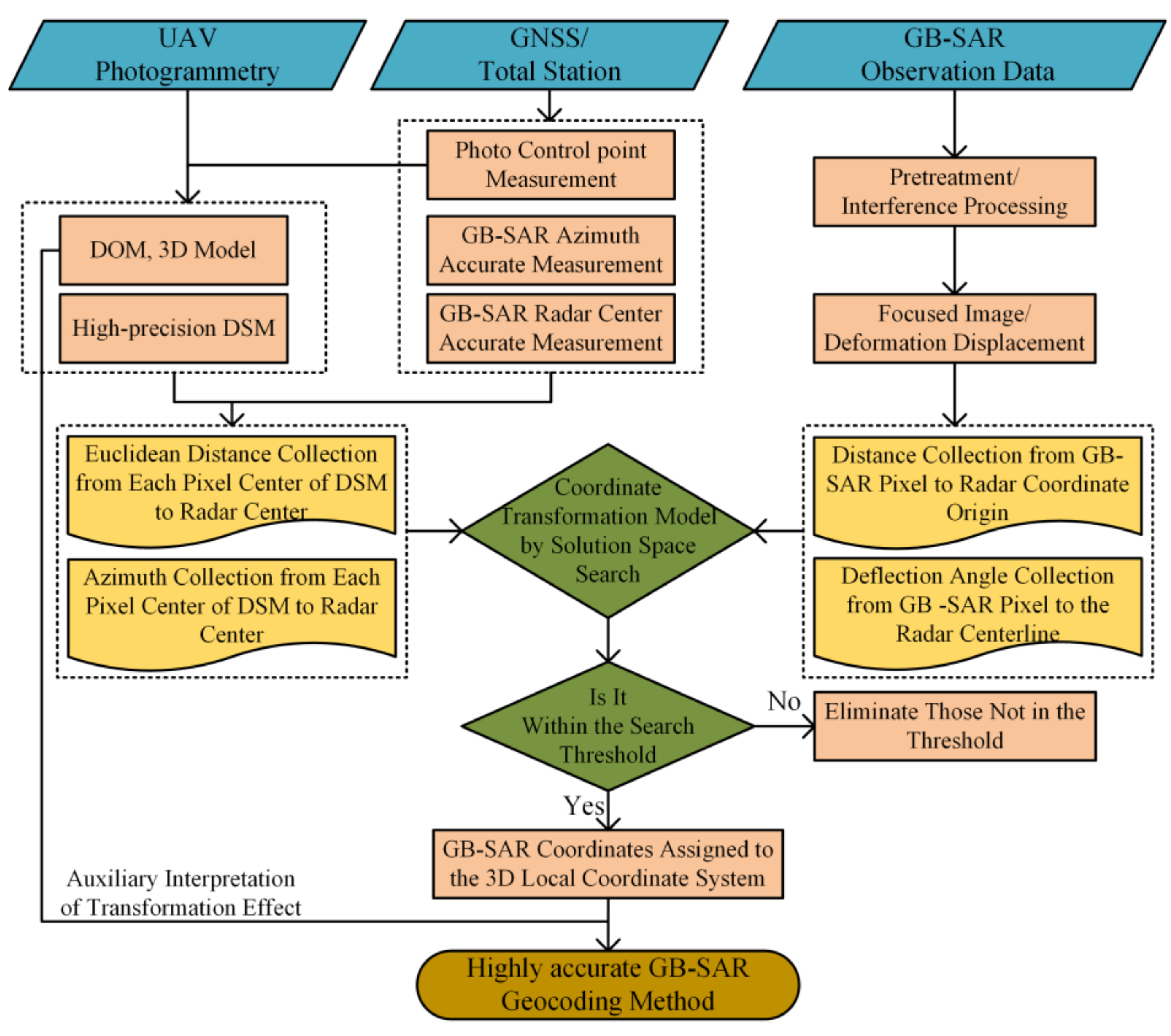
2.2. Solution Space Search Geocoding Model
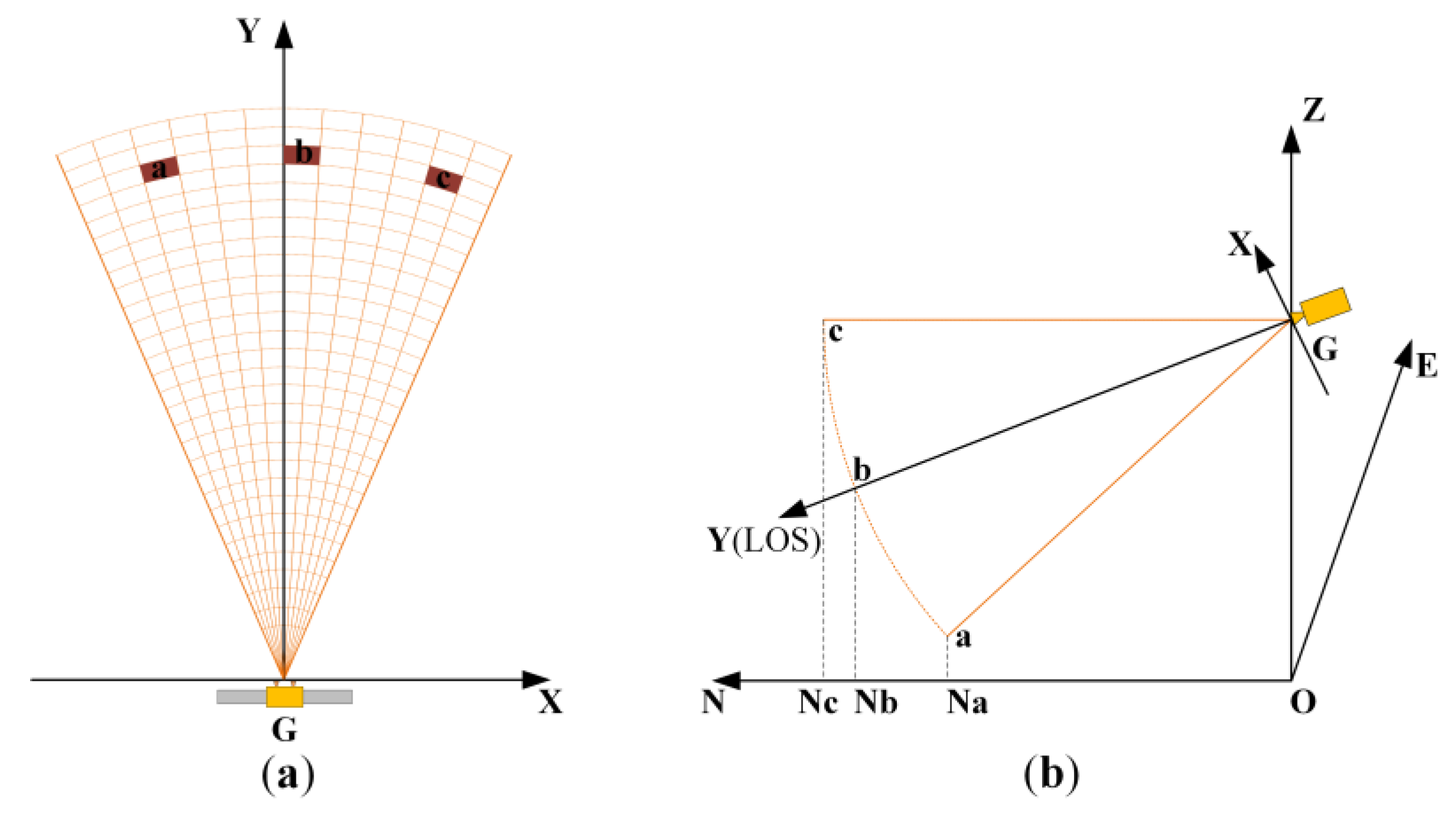
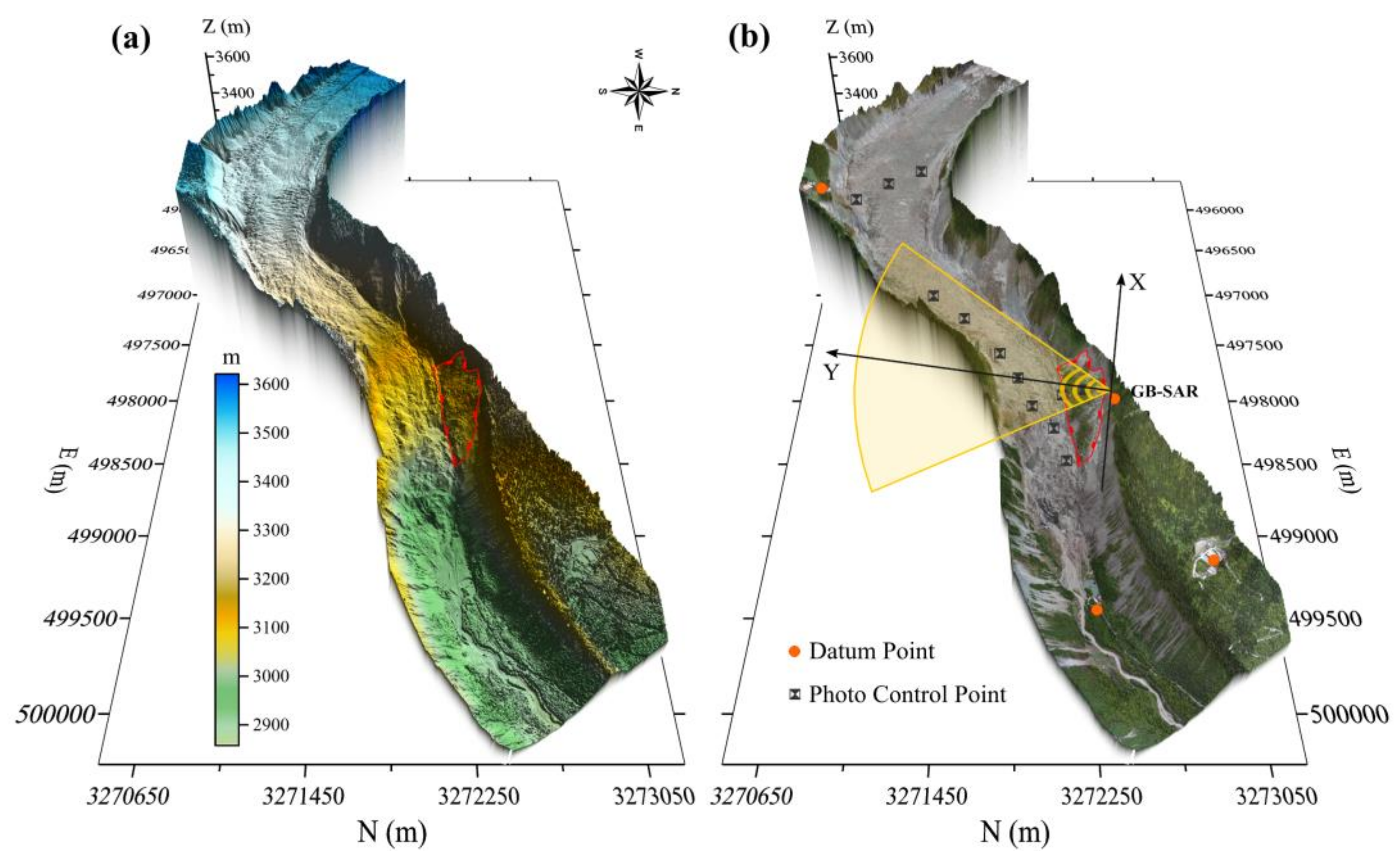
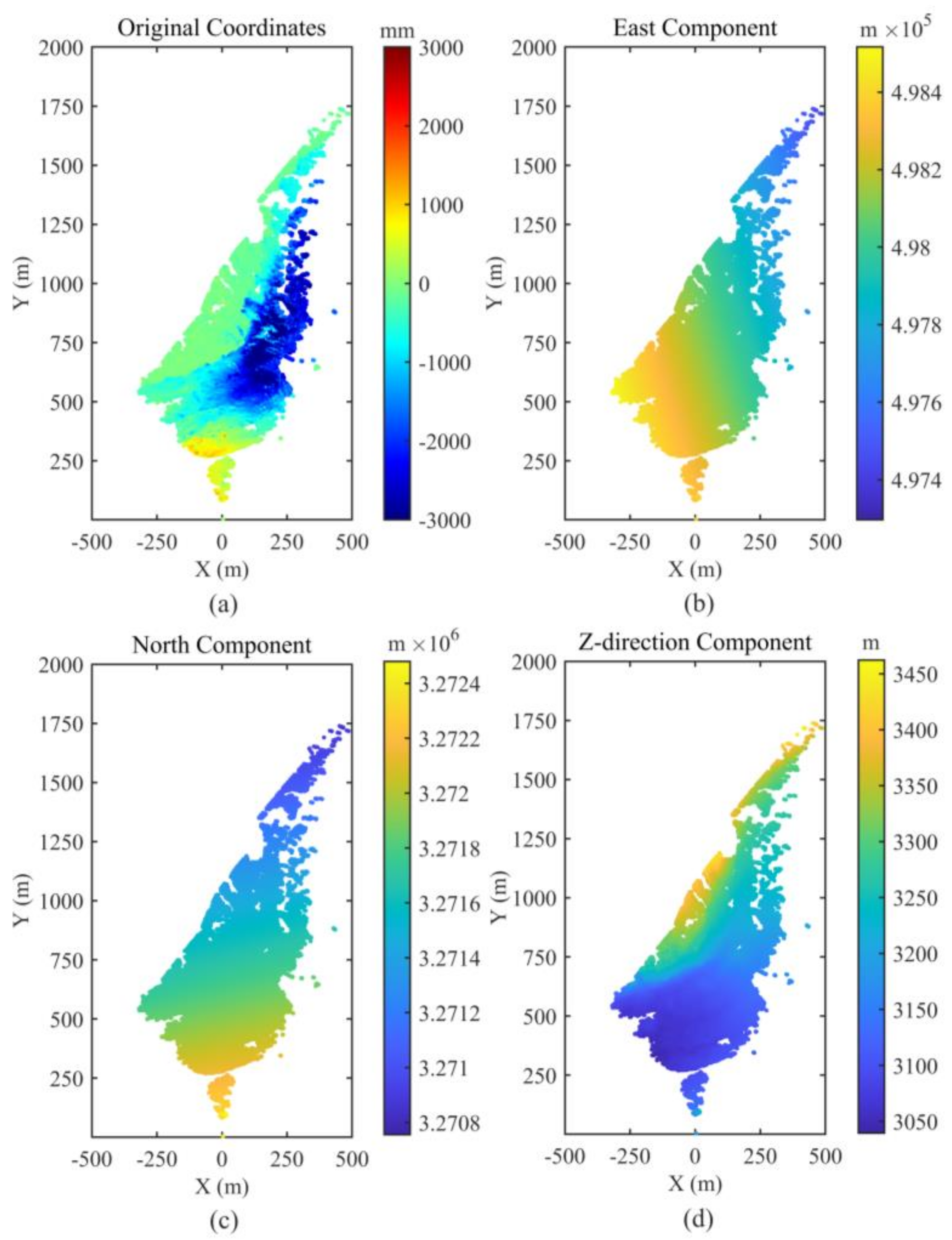
2.2.1. Unified Coordinate System Frame of Each Element
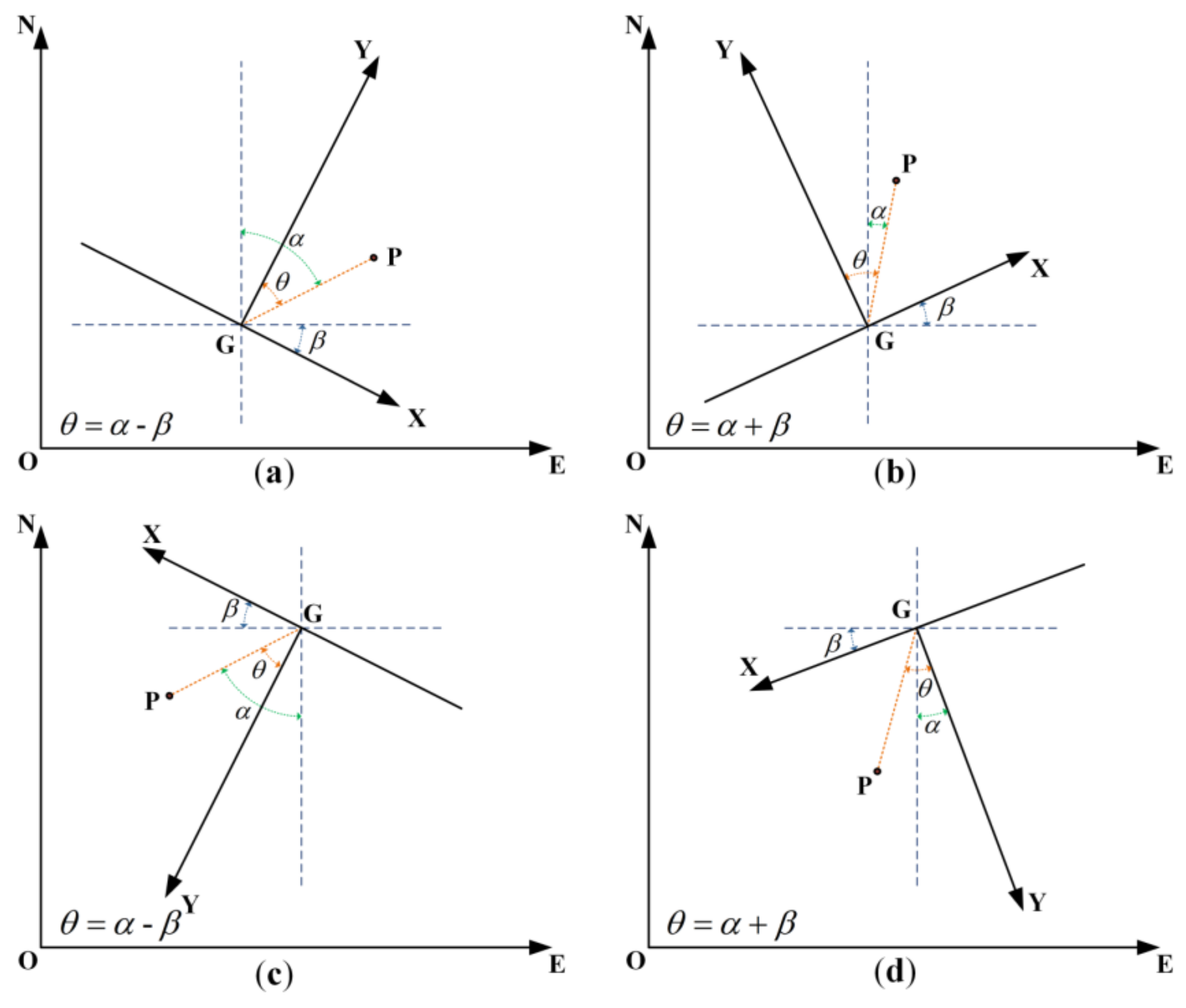
2.2.2. Coordinate Transformation Model
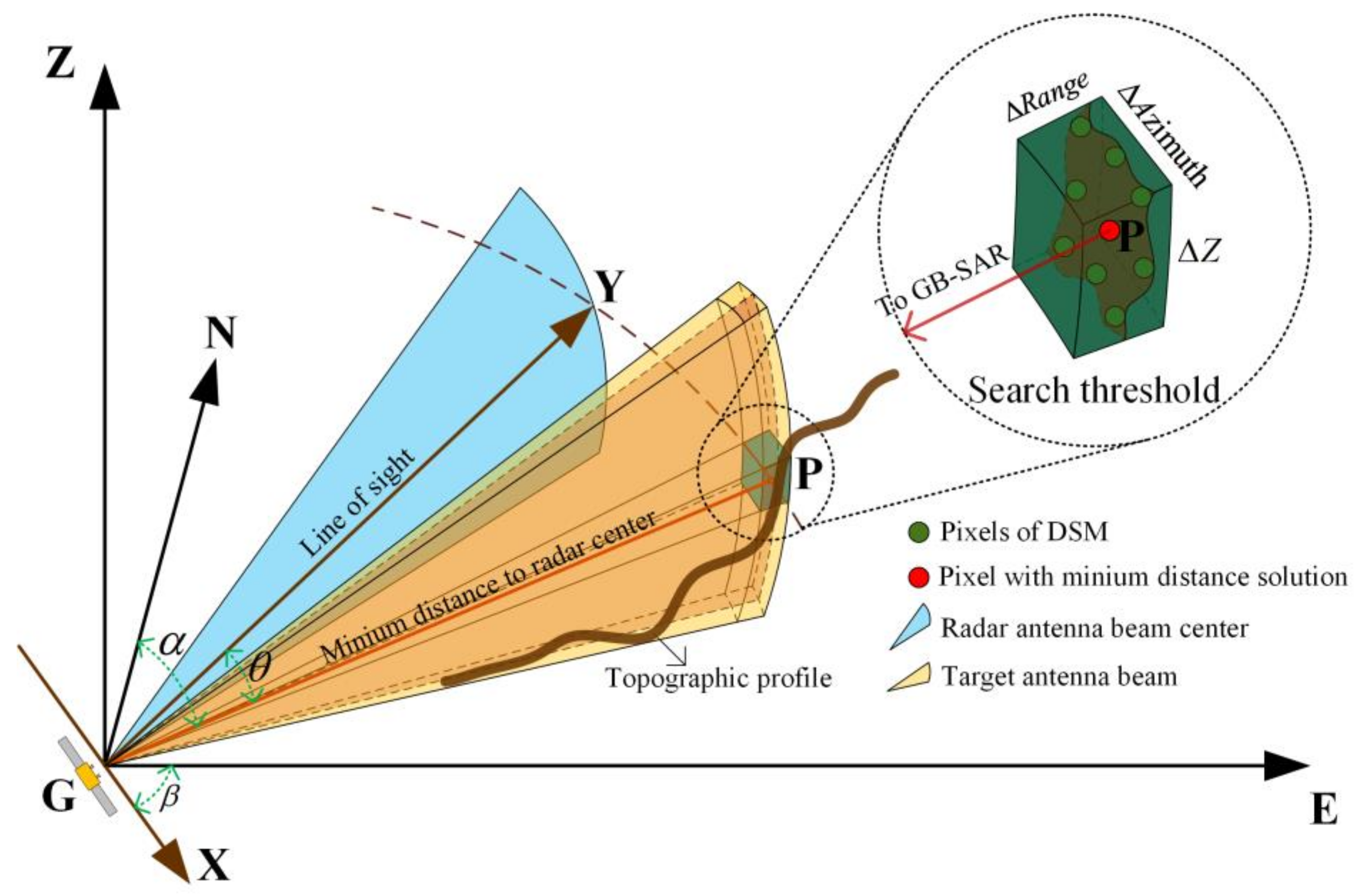
2.2.3. Geocoding Based on Solution Space Search
2.3. Method of Geocoding Accuracy Assessment
3. Experiments
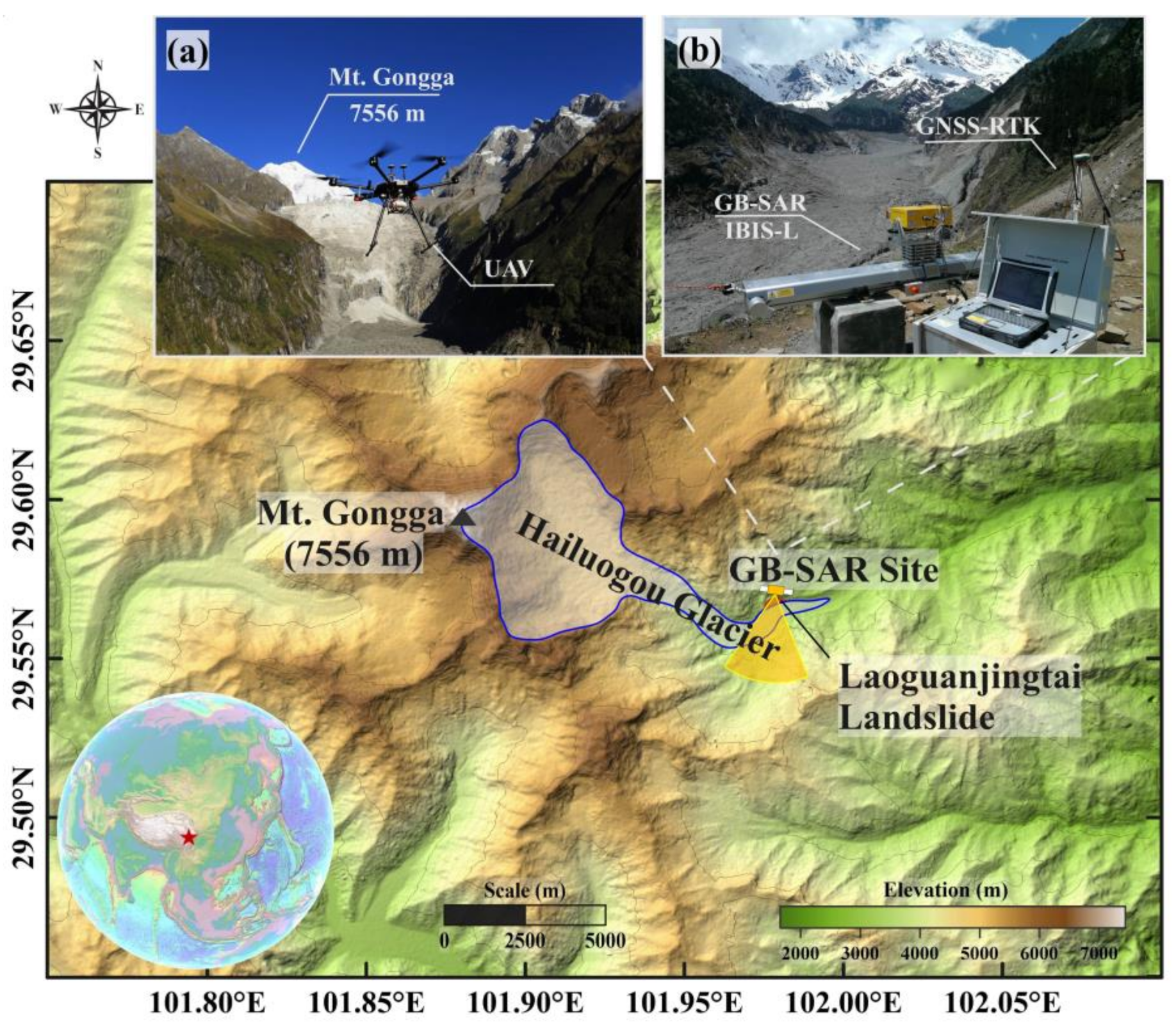
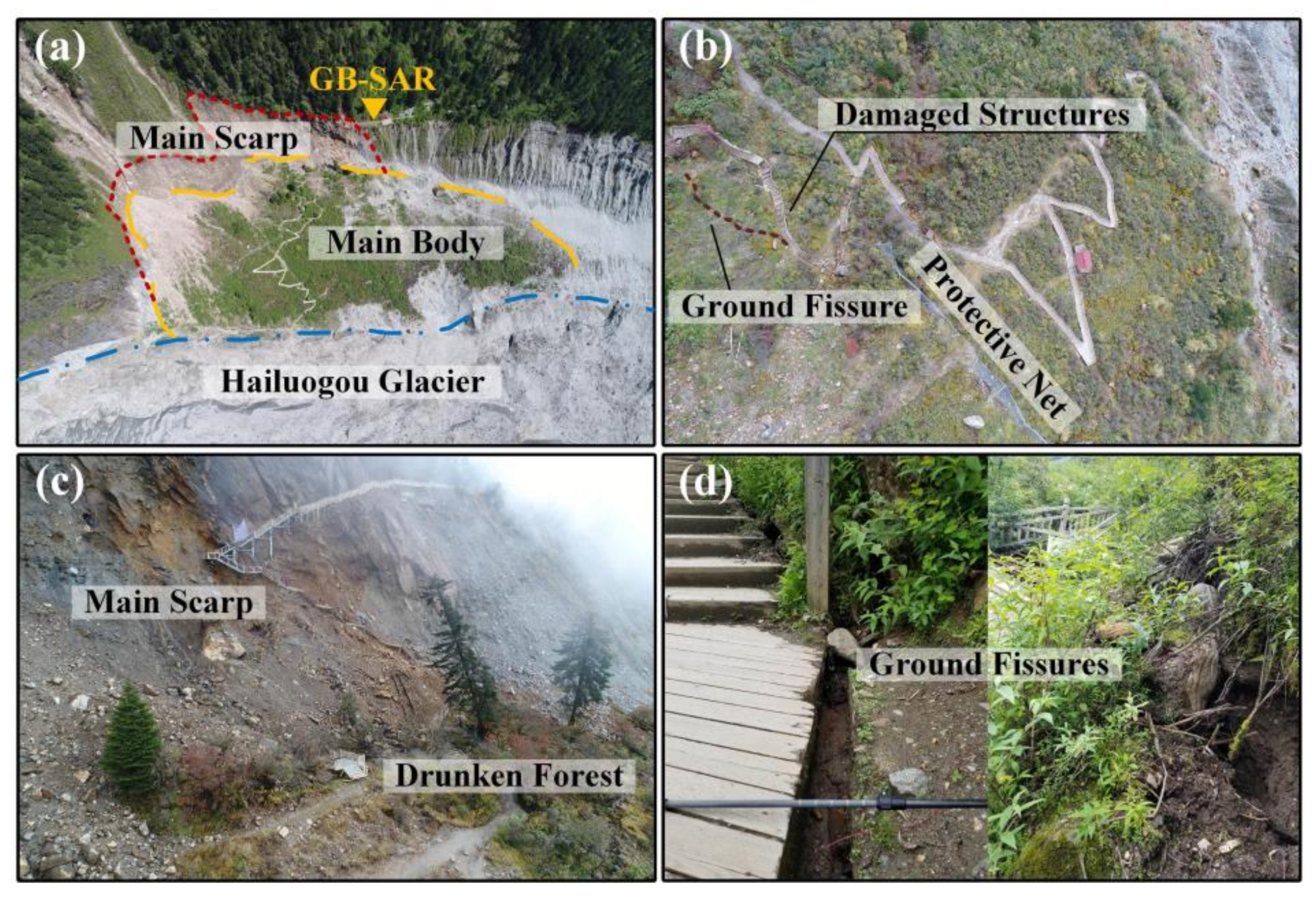
3.1. Overview of the Study Area
3.2. Dataset Acquisition
3.3. Data Processing
3.3.1. DSM and DOM Processing
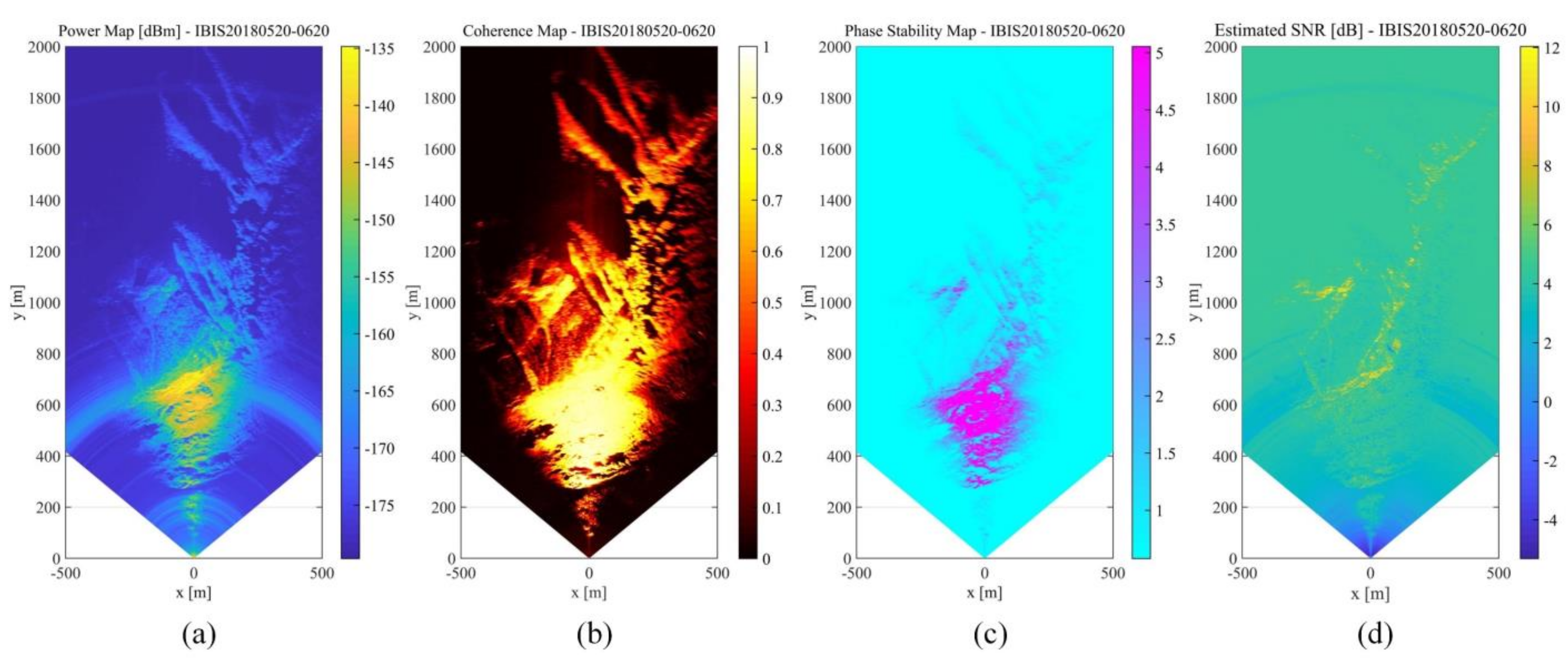
3.3.2. GB-SAR Image Processing
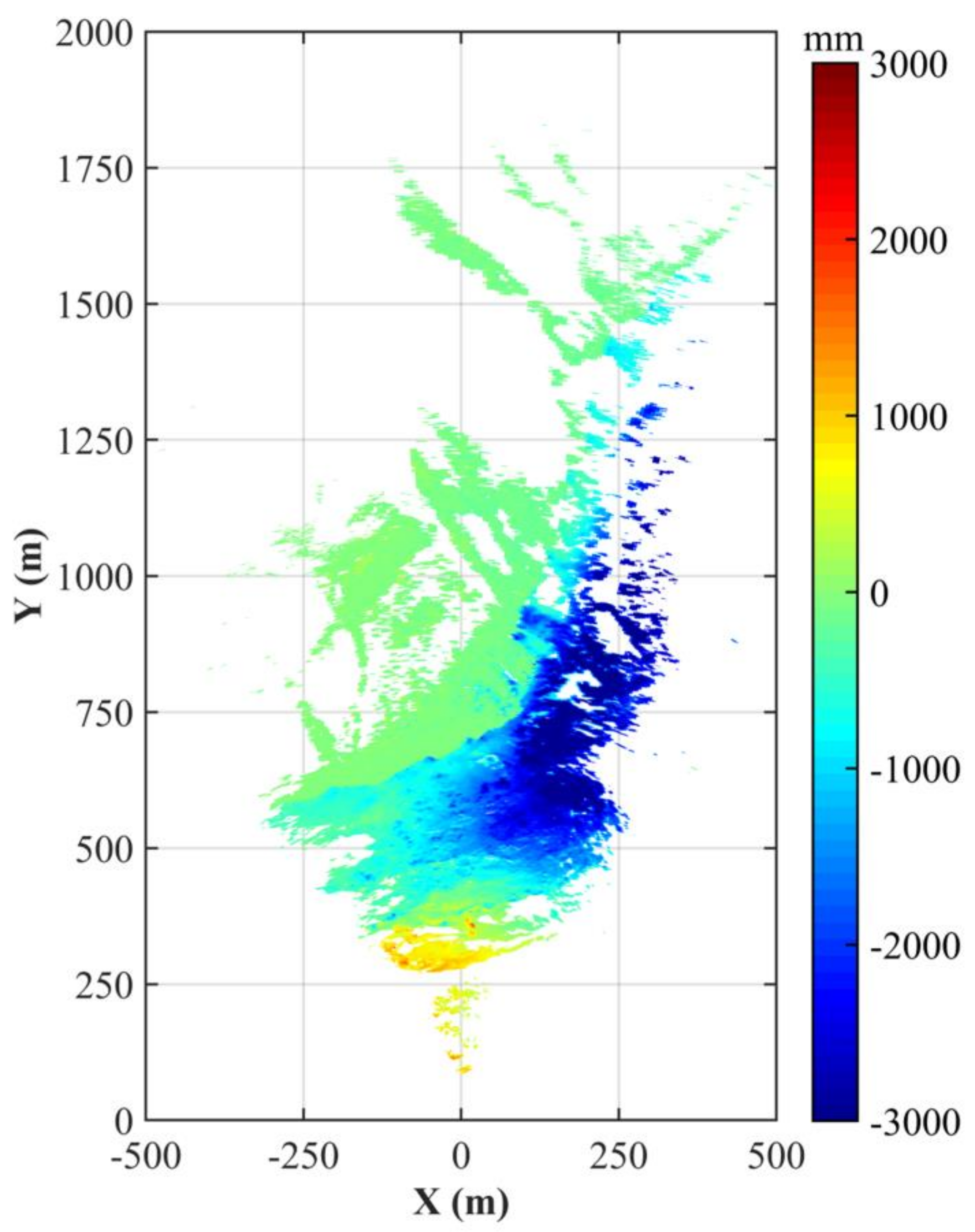
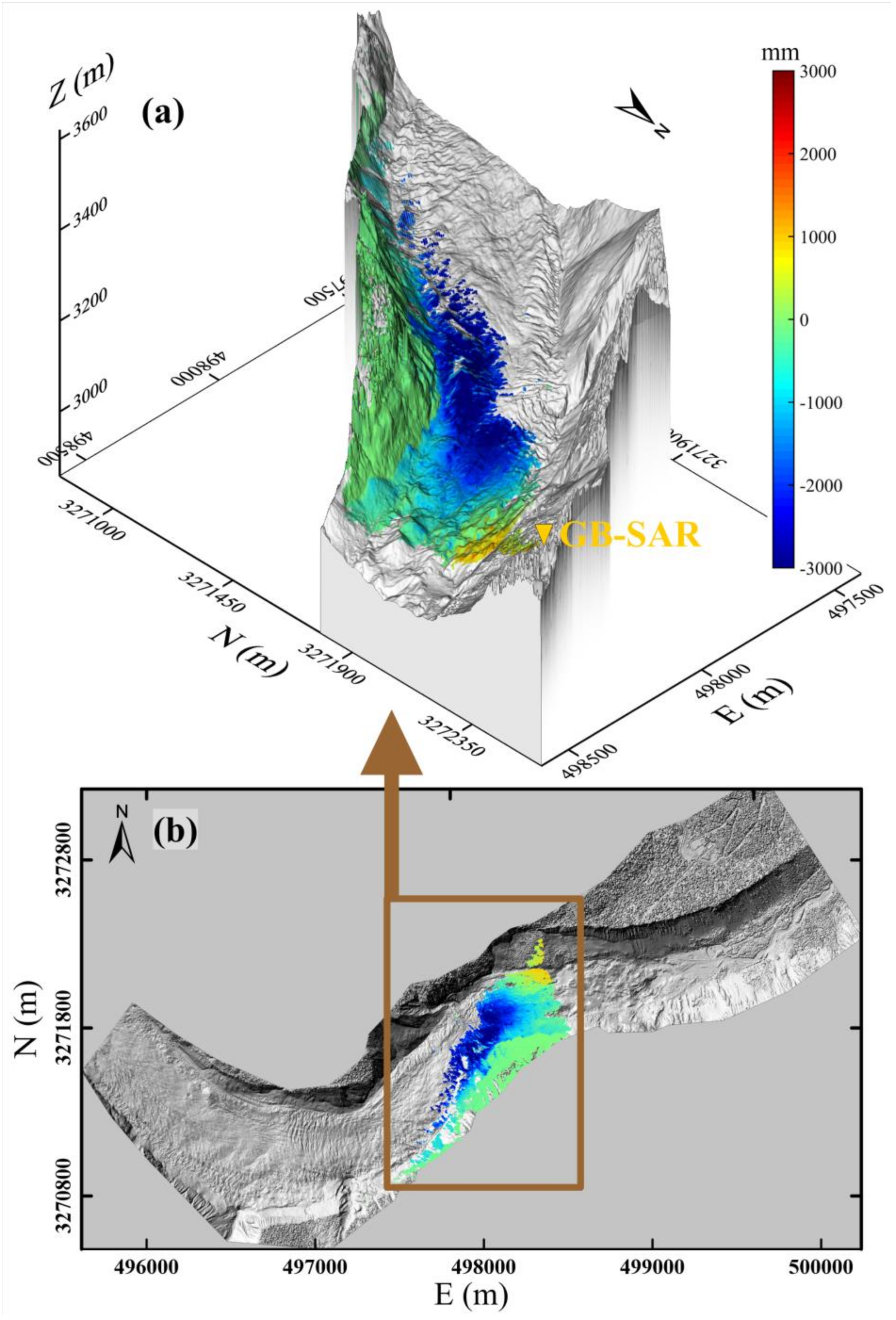
4. Results
5. Discussion
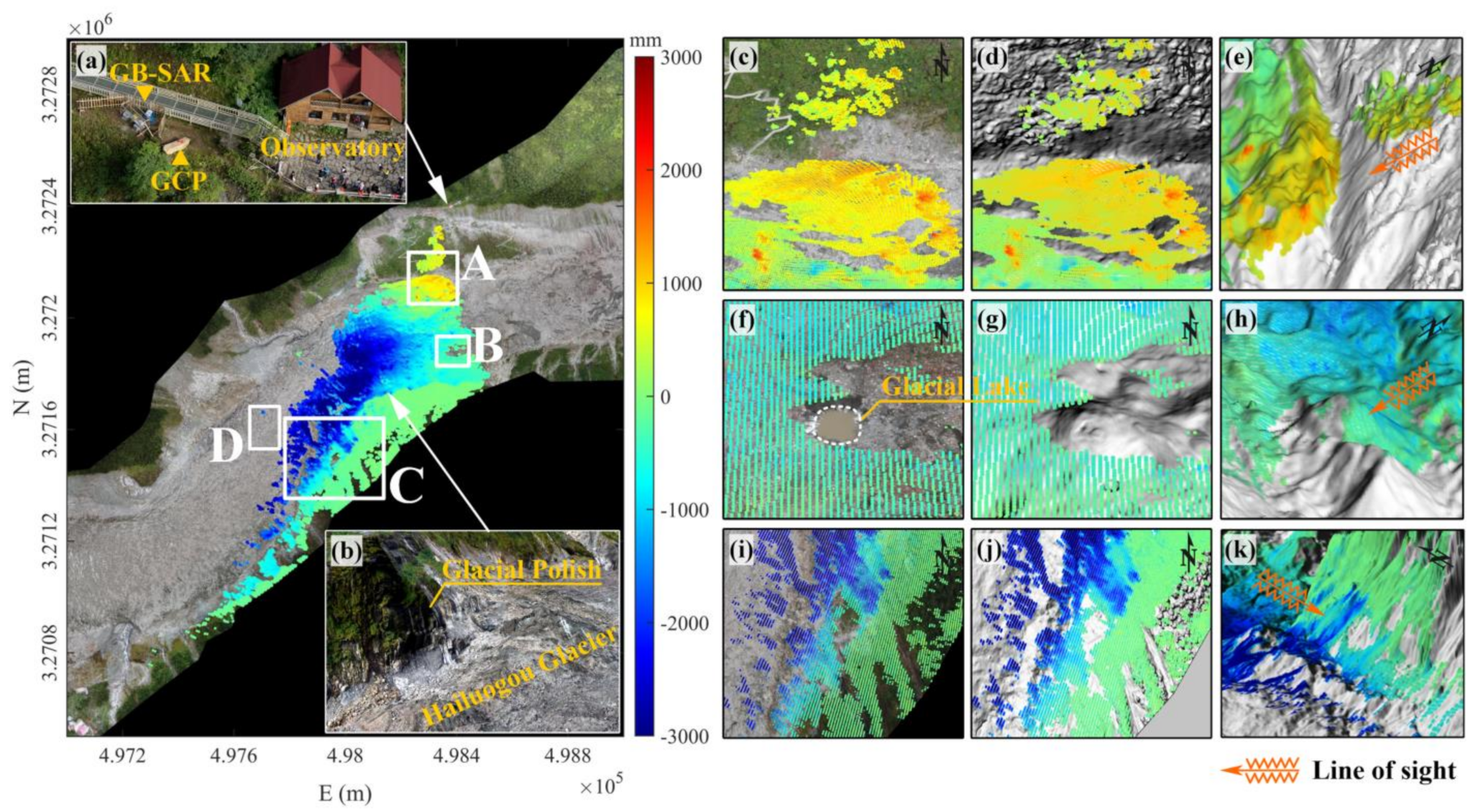
5.1. Discussion on GB-SAR Geocoding Results
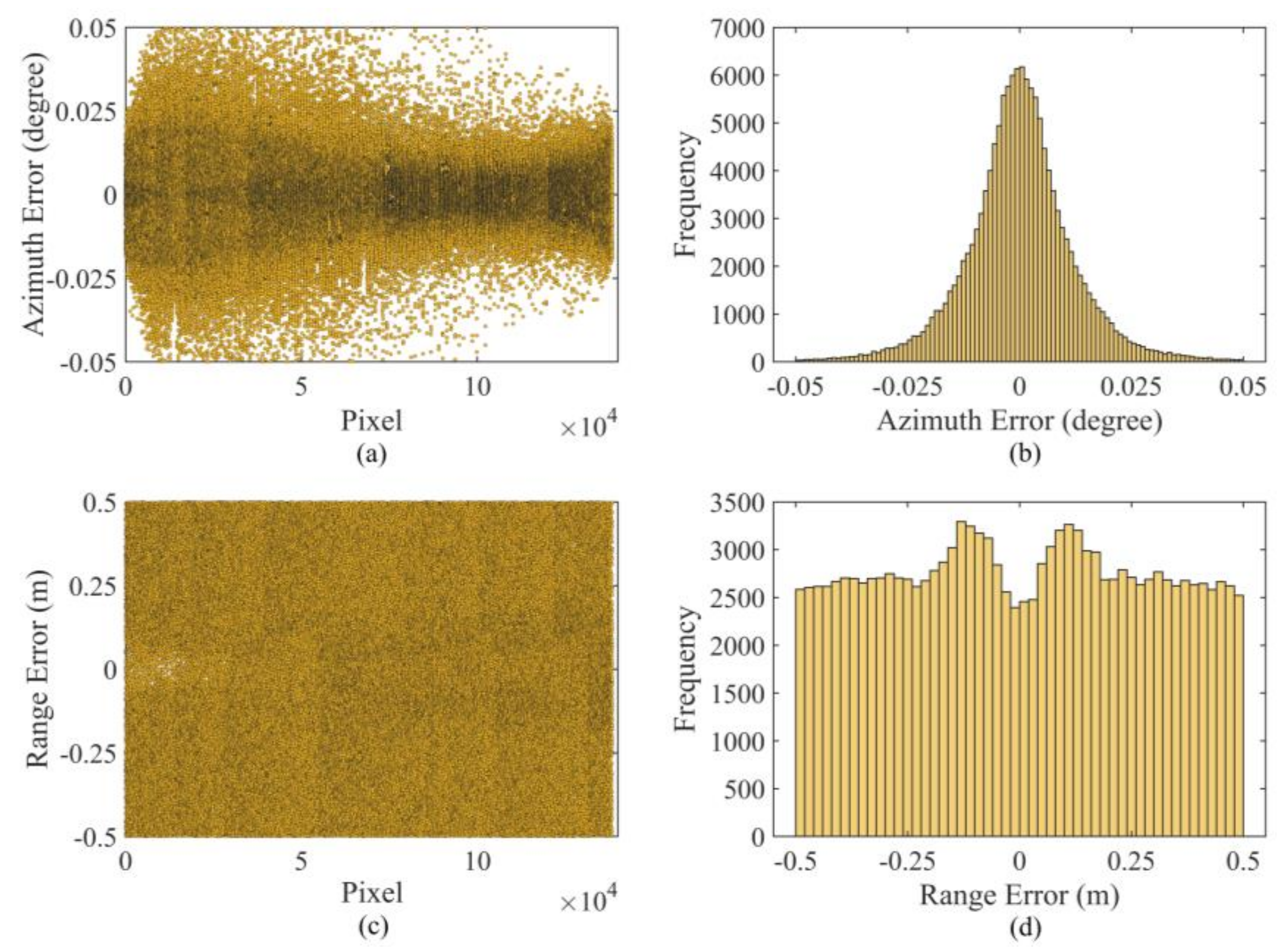
5.2. Assessment of the Geocoding Accuracy
5.3. Landslide Migration Mechanism
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-Based Differential Interferometry SAR: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 43–70. [Google Scholar] [CrossRef]
- Caduff, R.; Schlunegger, F.; Kos, A.; Wiesmann, A. A Review of Terrestrial Radar Interferometry for Measuring Surface Change in the Geosciences. Earth Surf. Process. Landf. 2015, 40, 208–228. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. Ground-based Radar Interferometry: A Bibliographic Review. Remote Sens. 2019, 11, 1029. [Google Scholar] [CrossRef]
- Lingua, A.; Piatti, D.; Rinaudo, F. Remote Monitoring of a Landslide Using an Integration of GB-INSAR and LIDAR Techniques. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 133–139. [Google Scholar]
- Monserrat, O.; Crosetto, M.; Luzi, G. A Review of Ground-based SAR Interferometry for Deformation Measurement. ISPRS-J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef]
- Lowry, B.; Gomez, F.; Zhou, W.; Mooney, M.A.; Held, B.; Grasmick, J. High Resolution Displacement Monitoring of a Slow Velocity Landslide Using Ground Based Radar Interferometry. Eng. Geol. 2013, 166, 160–169. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Mills, J. A New Approach to Selecting Coherent Pixels for Ground-based SAR Deformation Monitoring. ISPRS-J. Photogramm. Remote Sens. 2018, 144, 412–422. [Google Scholar] [CrossRef]
- Atzeni, C.; Barla, M.; Pieraccini, M.; Antolini, F. Early Warning Monitoring of Natural and Engineered Slopes with Ground-Based Synthetic-Aperture Radar. Rock Mech. Rock Eng. 2015, 48, 235–246. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, X.; Ma, H.; Ren, G.; Zhang, K.; Yang, F.; Li, C. Integrated Ground-based SAR Interferometry, Terrestrial Laser Scanner, and Corner Reflector Deformation Experiments. Sensors 2018, 18, 4401. [Google Scholar] [CrossRef] [PubMed]
- Cossu, R.; Schoepfer, E.; Bally, P.; Fusco, L. Near real-time SAR-based processing to support flood monitoring. J. Real-Time Image Process. 2009, 4, 205–218. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, Q.; Hu, X.; Li, Z.; Li, B.; Zhang, J.; Jiang, W.; Luo, Y.; Li, Q.; Ba, R. Detecting the Slope Movement After the 2018 Baige Landslides Based on Ground-based and Space-borne Radar Observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 1–12. [Google Scholar] [CrossRef]
- Casagli, N.; Catani, F.; Ventisette, C.D.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Pieraccini, M.; Casagli, N.; Luzi, G.; Tarchi, D.; Mecatti, D.; Noferini, L.; Atzeni, C. Landslide Monitoring by Ground-based Radar Interferometry: A Field Test in Valdarno (Italy). Int. J. Remote Sens. 2003, 24, 1385–1391. [Google Scholar] [CrossRef]
- Zhang, R.; Song, Y.; Liu, G.; Zhang, H. Landslide Monitoring Based on GB-SAR Interferometry for the Instable Slopes of Yaoji Reservoir. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Atzeni, C.; Mantovani, M.; Marcato, G.; Pasuto, A.; Slivano, S.; Tagliavini, F. Using GB-SAR Technique to Monitor Slow Moving Landslide. Eng. Geol. 2007, 95, 88–98. [Google Scholar] [CrossRef]
- Tarchi, D.; Casagli, N.; Fanti, R.; Leva, D.D.; Luzi, G.; Pasuto, A.; Pieraccini, M.; Slivano, S. Landslide Monitoring by Using Ground-based SAR Interferometry: An Example of Application to the Tessina Landslide in Italy. Eng. Geol. 2003, 68, 15–30. [Google Scholar] [CrossRef]
- Bozzano, F.; Cipriani, I.; Mazzanti, P.; Prestininzi, A. Displacement Patterns of a Landslide Affected by Human Activities: Insights from Ground-based InSAR Monitoring. Nat. Hazards 2011, 59, 1377–1396. [Google Scholar] [CrossRef]
- Xing, C.; Huang, J.; Han, X. Research on the Environmental Effects of GB-SAR for Dam Monitoring. Adv. Mater. Res. 2014, 919, 392–397. [Google Scholar] [CrossRef]
- Wang, P.; Xing, C. Research on Coordinate Transformation Method of GB-SAR Image Supported by 3D Laser Scanning Technology. In Proceedings of the ISPRS TC III Mid-term Symposium, Beijing, China, 7–10 May 2018; pp. 1757–1763. [Google Scholar]
- Rouyet, L.; Kristensen, L.; Derron, M.H.; Michoud, C.; Blikra, L.H.; Jaboyedoff, M.; Lauknes, T.R. Evidence of Rock Slope Breathing Using Ground-based InSAR. Geomorphology 2017, 289, 152–169. [Google Scholar] [CrossRef]
- Frodella, W.; Ciampalini, A.; Gigli, G.; Lombardi, L.; Raspini, F.; Nocentini, M.; Scardigli, C.; Casagli, N. Synergic Use of Satellite and Ground Based Remote Sensing Methods for Monitoring the San Leo Rock Cliff (Northern Italy). Geomorphology 2016, 264, 80–94. [Google Scholar] [CrossRef]
- Liu, B.; Ge, D.; Li, M.; Zhang, L.; Wang, Y.; Zhang, X. Using GB-SAR Technique to Monitor Displacement of Open Pit Slope. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 5986–5989. [Google Scholar]
- Pipia, L.; Fabregas, X.; Aguasca, A.; López-Martínez, C. Polarimetric Temporal Analysis of Urban Environments with a Ground-Based SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2343–2360. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, B.; Zhang, R.; Cai, J.; Fu, Y.; Liu, Q.; Yu, B.; Li, Z. Monitoring Dynamics of Hailuogou Glacier and the Secondary Landslide Disasters Based on Combination of Satellite SAR and Ground-based SAR. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 980–995. [Google Scholar]
- Dematteis, N.; Luzi, G.; Giordan, D.; Zucca, F.; Allasia, P. Monitoring Alpine glacier surface deformations with GB-SAR. Remote Sens. Lett. 2017, 8, 947–956. [Google Scholar] [CrossRef]
- Noferini, L.; Mecatti, D.; Macaluso, G.; Pieraccini, M.; Atzeni, C. Monitoring of Belvedere Glacier Using a Wide Angle GB-SAR Interferometer. J. Appl. Geophys. 2009, 68, 289–293. [Google Scholar] [CrossRef]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Macaluso, G.; Tamburini, A.; Atzeni, C. Monitoring of an Alpine Glacier by Means of Ground-Based SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2007, 4, 495–499. [Google Scholar] [CrossRef]
- Xie, S.; Dixon, T.H.; Voytenko, D.; Deng, F.; Holland, D.M. Grounding Line Migration Through the Calving Season at Jakobshavn Isbræ, Greenland, Observed with Terrestrial Radar Interferometry. Cryosphere 2018, 12, 1–29. [Google Scholar] [CrossRef]
- Wang, P.; Xing, C. A Method of Transforming GB-SAR Image Coordinate to 3D Terrain Coordinate. J. Yangtze River Sci. Res. Inst. 2018, 35, 122–127. [Google Scholar]
- Bardi, F.; Raspini, F.; Ciampalini, A.; Kristensen, L.; Rouyet, L.; Lauknes, T.R.; Frauenfelder, R.; Casagli, N. Space-Borne and Ground-Based InSAR Data Integration: The Aknes Test Site. Remote Sens. 2016, 8, 237. [Google Scholar] [CrossRef]
- Zhou, J.; Tian, J.; Chen, Y.; Mao, Q.; Li, Q. Research on Data Fusion Method of Ground-Based SAR and 3D Laser Scanning. J. Geomat. 2015, 40, 26–30. [Google Scholar]
- Tapete, D.; Casagli, N.; Luzi, G.; Fanti, R.; Gigli, G.; Leva, D. Integrating Radar and Laser-based Remote Sensing Techniques for Monitoring Structural Deformation of Archaeological Monuments. J. Arch. Sci. 2013, 40, 176–189. [Google Scholar] [CrossRef]
- Dematteis, N.; Giordan, D.; Zucca, F.; Luzi, G.; Allasia, P. 4D Surface Kinematics Monitoring Through Terrestrial Radar Interferometry and Image Cross-correlation Coupling. ISPRS-J. Photogramm. Remote Sens. 2018, 142, 38–50. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M. Deformation Measurement Using Terrestrial Laser Scanning Data and Least Squares 3D Surface Matching. ISPRS-J. Photogramm. Remote Sens. 2008, 63, 142–154. [Google Scholar] [CrossRef]
- Tian, W.; Zhao, Z.; Hu, C.; Wang, J.; Zeng, T. GB-InSAR-Based DEM Generation Method and Precision Analysis. Remote Sens. 2019, 11, 997. [Google Scholar] [CrossRef]
- Kuras, P.; Ortyl, Ł.; Owerko, T.; Salamak, M.; Łaziński, P. GB-SAR in the Diagnosis of Critical City Infrastructure—A Case Study of a Load Test on the Long Tram Extradosed Bridge. Remote Sens. 2020, 12, 3361. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, S.; Cao, W. Seasonal Variation of Drainage System in the Lower Ablation Area of a Monsoonal Temperate Debris-covered Glacier in Mt. Gongga, South-eastern Tibet. Water 2018, 10, 1050. [Google Scholar] [CrossRef]
- Hassan, A.; Xu, J.; Zhang, L.; Liu, G.; Schmit, A.; Xing, C.; Xu, Y.; Ouyang, C.; Schwieger, V. Towards Integration of GNSS and GB-SAR Measurements: Exemplary Monitoring of a Rock Fall at the Yangtze River in China. In Proceedings of the Embracing Our Smart World Where the Continents Connect: Enhancing the Geospatial Maturity of Societies, Proceedings of the FIG Congress 2018, Istanbul, Turkey, 6–11 May 2018. [Google Scholar]
- Cai, J.; Zhang, W.; Li, Y.; Ren, S. Landslide Stability Analysis Based on Law of Surface Displacement. Sci. Surv. Mapp. 2016, 41, 96–99. [Google Scholar]
- Liu, G.; Chen, Q.; Luo, X.; Cai, G. Principle and Application of InSAR; Science Press: Chengdu, China, 2019; pp. 237–242. [Google Scholar]
- Yang, H.; Cai, J.; Peng, J.; Wang, J.; Jiang, Q. A Correcting Method About GB-SAR Rail Displacement. Int. J. Remote Sens. 2017, 38, 1483–1493. [Google Scholar] [CrossRef]
- Jiang, M.; Monti-Guarnieri, A. Distributed Scatterer Interferometry with the Refinement of Spatiotemporal Coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3987. [Google Scholar] [CrossRef]
- Jehle, M.; Perler, D.; Small, D.; Schubert, A.; Meier, E. Estimation of Atmospheric Path Delays in TerraSAR-X Data Using Models vs. Measurements. Sensors 2008, 8, 8479–8491. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent Scatterers Analysis for Atmospheric Correction in Ground-based SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Nie, Y.; Pritchard, H.D.; Liu, Q.; Hennig, T.; Wang, W.; Wang, X.; Liu, S.; Nepal, S.; Samyn, D.; Hewitt, K.; et al. Glacial change and hydrological implications in the Himalaya and Karakoram. Nat. Rev. Earth Environ. 2021, 2, 91–106. [Google Scholar] [CrossRef]
- Huggel, C. Recent extreme slope failures in glacial environments: Effects of thermal perturbation. Quat. Sci. Rev. 2009, 28, 1119–1130. [Google Scholar] [CrossRef]
- Huggel, C.; Clague, J.J.; Korup, O. Is climate change responsible for changing landslide activity in high mountains. Earth Surf. Process. Landf. 2012, 37, 77–91. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Liu, S.; He, G. Manifestations and mechanisms of mountain glacier-related hazards. Sci. Cold Arid Reg. 2020, 12, 436–446. [Google Scholar]
| Dataset | Available Equipment | Outputs | Resolutions | Characteristics |
|---|---|---|---|---|
| GB-SAR observation dataset | GB-SAR | SLC/deformation | Azimuth: 2–5 mrad; Range: 0.5 m | The deformation accuracy can reach submillimeter level |
| Ground control survey dataset | GNSS | Coordinates | 10 mm ±1 ppm | Convenient measurement and uniform global accuracy |
| Total station | Coordinates/azimuth | Range: 2 mm + 2 ppm Angle: 0.5″–2″ | High precision, measurement needs intervisibility | |
| External ancillary 3D information | UAV aerial photogrammetry | DSM/DEM/DOM | ≥5 cm | With high precision and rich ground texture |
| Airborne LiDAR | DSM/DEM | ≥5 cm | With high precision and less ground texture | |
| Ground 3D laser scan | DSM/DEM | ≥5 cm | With shadows and inconvenience of interpretation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J.; Jia, H.; Liu, G.; Zhang, B.; Liu, Q.; Fu, Y.; Wang, X.; Zhang, R. An Accurate Geocoding Method for GB-SAR Images Based on Solution Space Search and Its Application in Landslide Monitoring. Remote Sens. 2021, 13, 832. https://doi.org/10.3390/rs13050832
Cai J, Jia H, Liu G, Zhang B, Liu Q, Fu Y, Wang X, Zhang R. An Accurate Geocoding Method for GB-SAR Images Based on Solution Space Search and Its Application in Landslide Monitoring. Remote Sensing. 2021; 13(5):832. https://doi.org/10.3390/rs13050832
Chicago/Turabian StyleCai, Jialun, Hongguo Jia, Guoxiang Liu, Bo Zhang, Qiao Liu, Yin Fu, Xiaowen Wang, and Rui Zhang. 2021. "An Accurate Geocoding Method for GB-SAR Images Based on Solution Space Search and Its Application in Landslide Monitoring" Remote Sensing 13, no. 5: 832. https://doi.org/10.3390/rs13050832
APA StyleCai, J., Jia, H., Liu, G., Zhang, B., Liu, Q., Fu, Y., Wang, X., & Zhang, R. (2021). An Accurate Geocoding Method for GB-SAR Images Based on Solution Space Search and Its Application in Landslide Monitoring. Remote Sensing, 13(5), 832. https://doi.org/10.3390/rs13050832











