Deep Convolutional Denoising Autoencoders with Network Structure Optimization for the High-Fidelity Attenuation of Random GPR Noise
Abstract
1. Introduction
2. Materials and Methods
2.1. Deep Convolutional Denoising Autoencoders
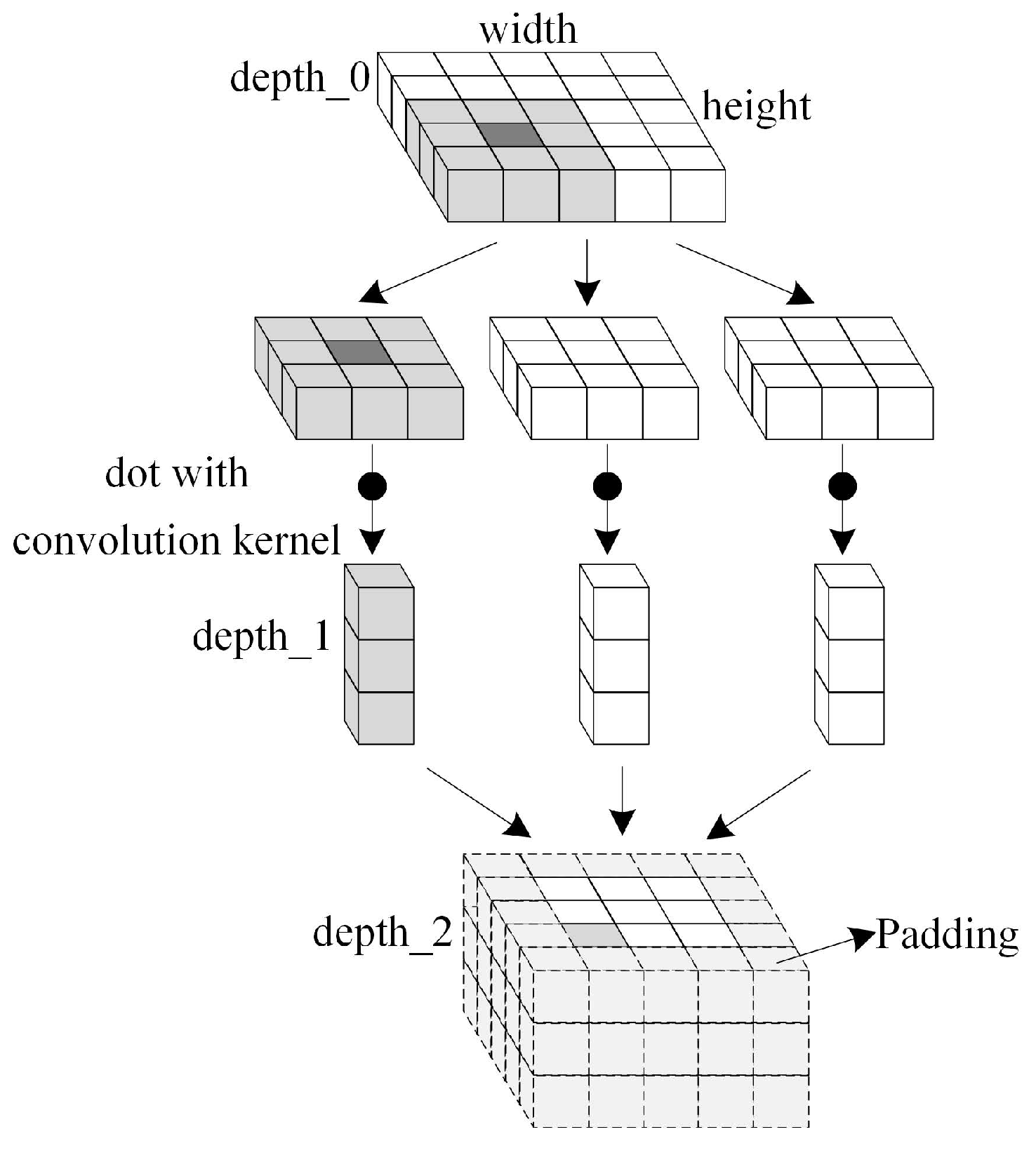
2.2. Convolutional Layer and Max-Pooling Operation
2.3. Implementation of CDAEs
| Algorithm 1 The Training Process for CDAEs |
| Input: Output:
|
3. Network Structure Modification Strategy
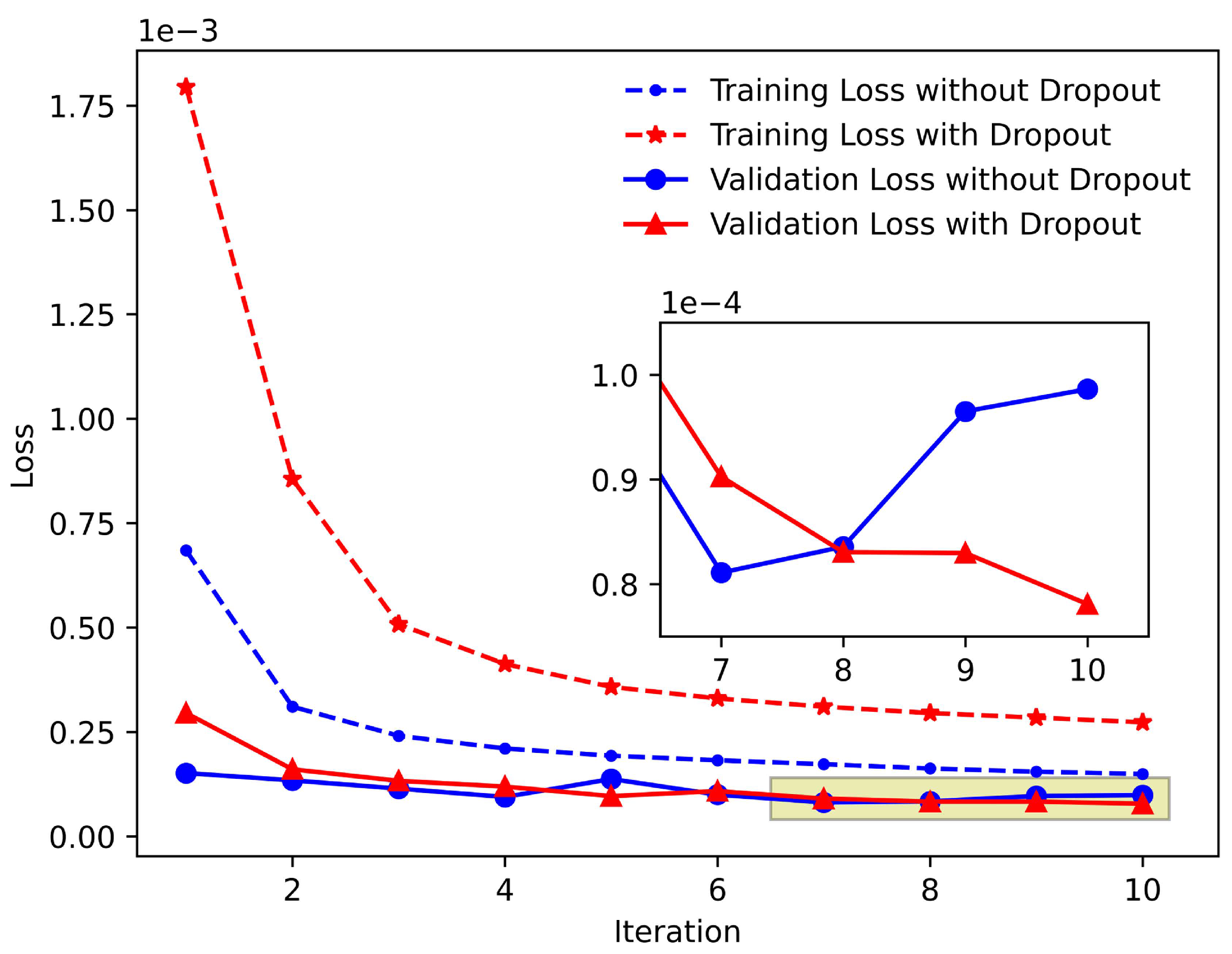
3.1. Overfitting Problem and Dropout Regularization Layer
3.2. Local Receptive Field and Atrous Convolution
3.3. Loss of Detailed Information and Residual Connections
4. Selection of Model Parameters and Model Testing
4.1. Training Dataset and Validation Dataset
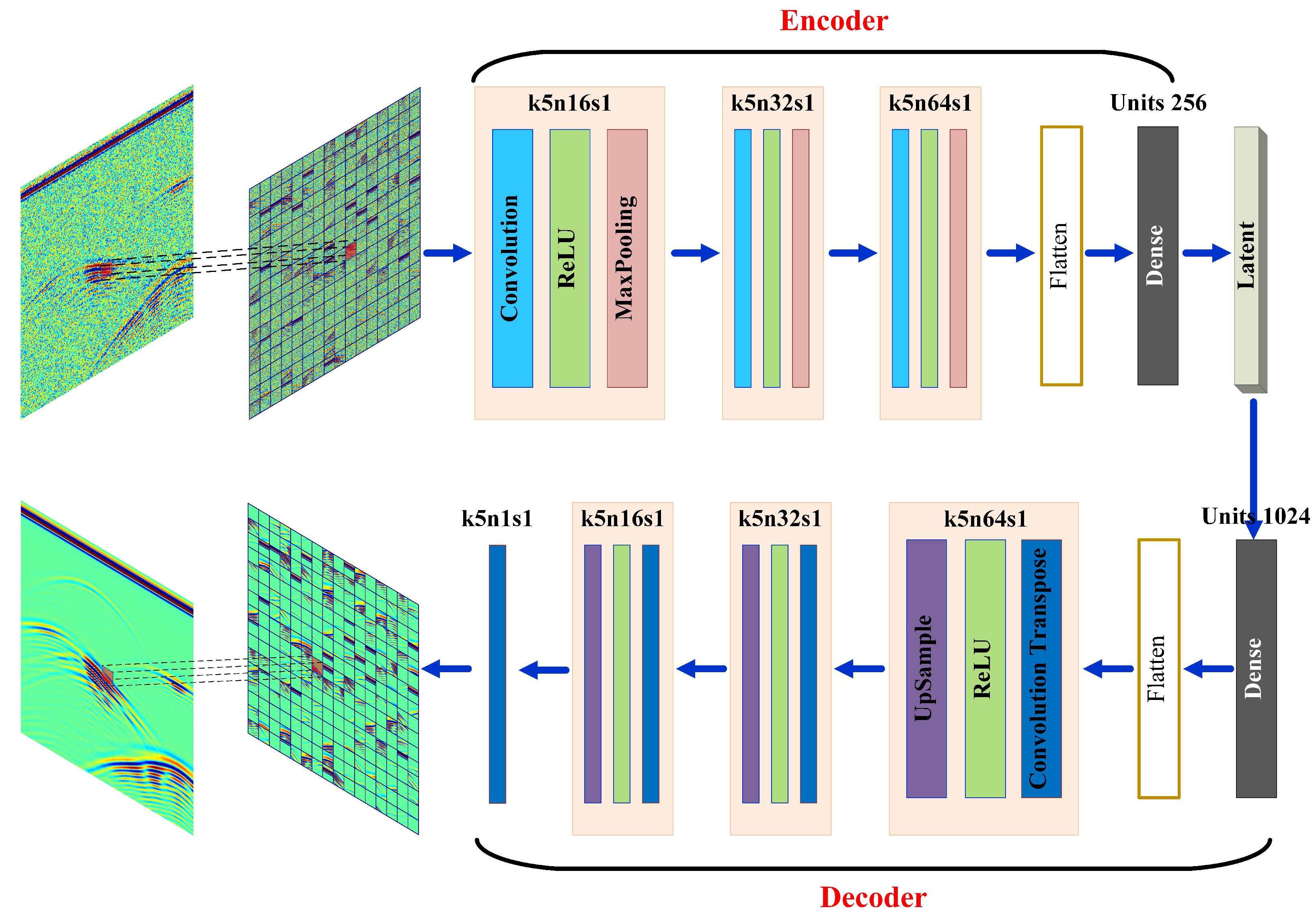
4.2. Structure of the Model
4.3. Selection of Parameters
5. Strategy of Modifying the Network Structure
5.1. Adding the Dropout Regularization Layer
5.2. Replacing Convolution with Atrous Convolution
5.3. Modifying the Network Structure by Residual Connections
5.4. Comparison with Other Typical Noise Attenuation Methods
6. Results
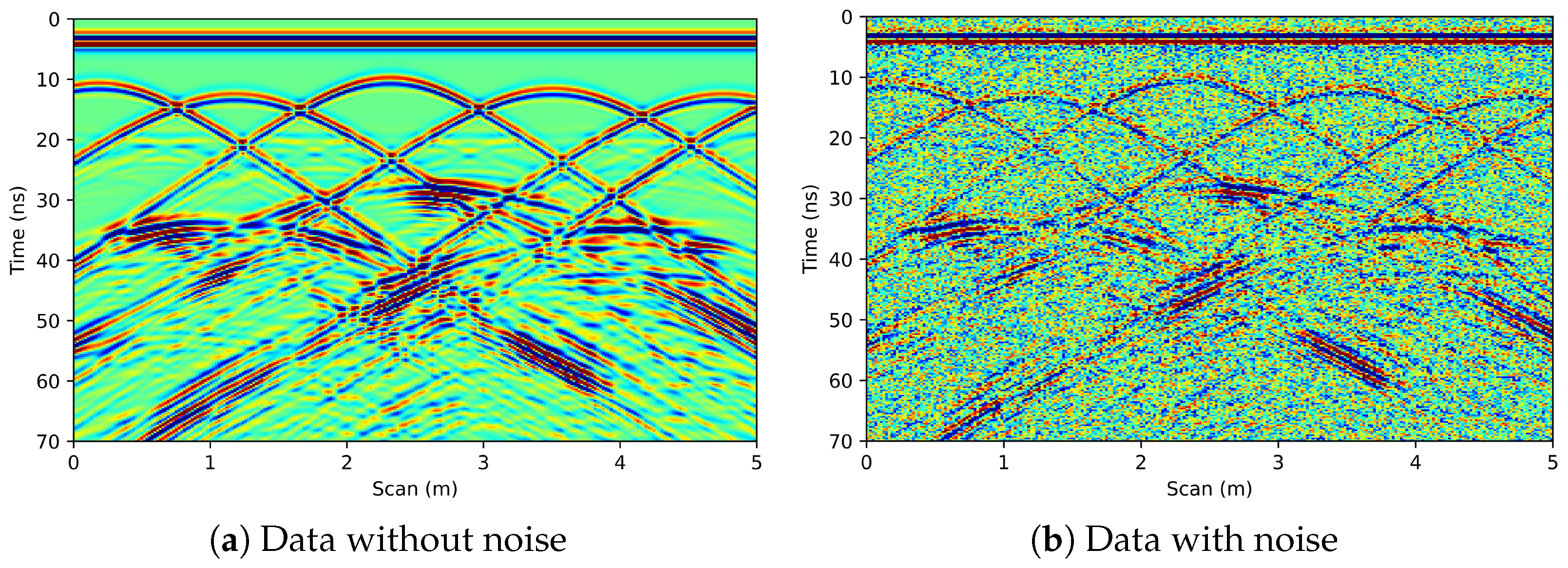
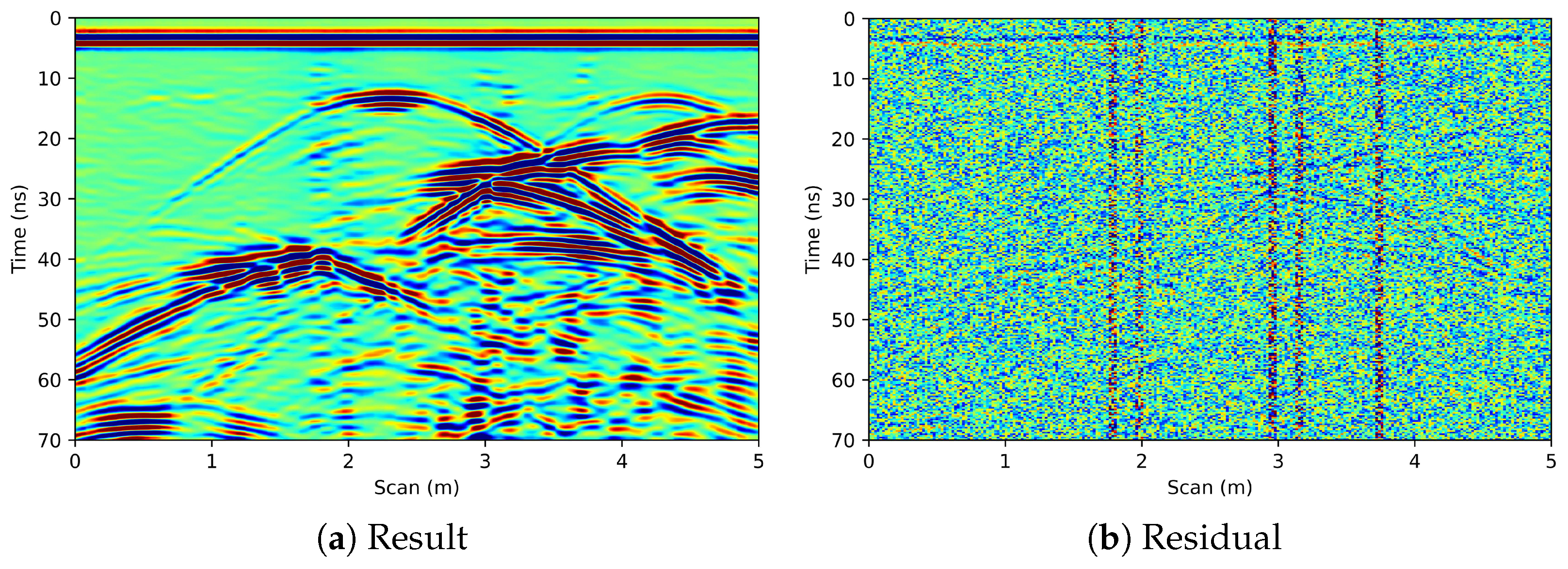
6.1. Synthetic Data
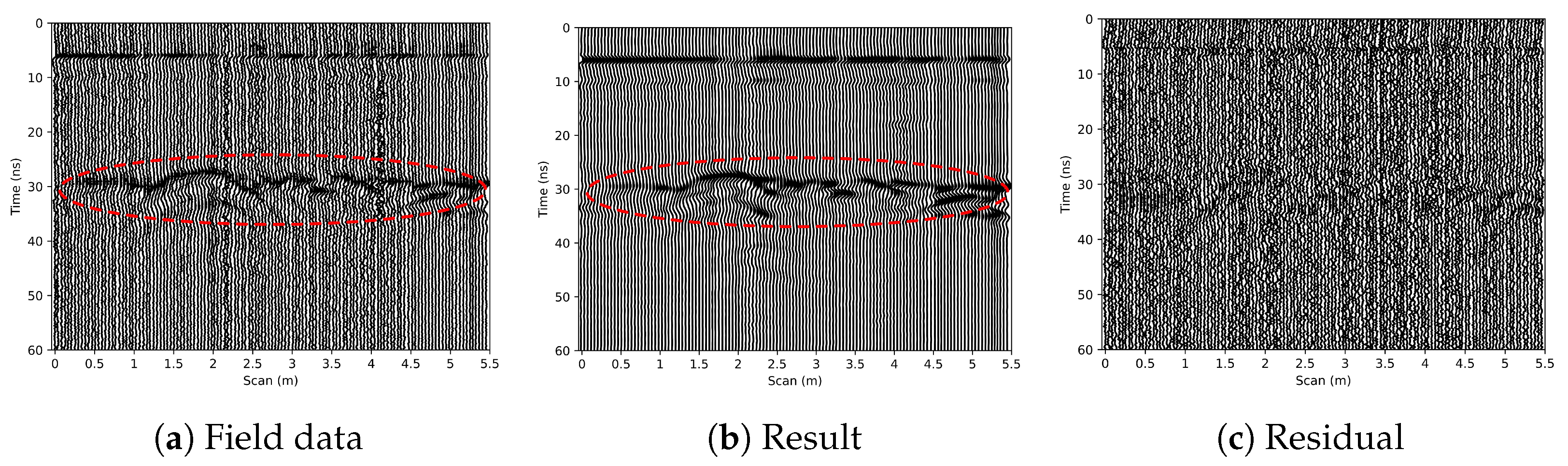
6.2. Field Data
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPR | ground penetrating radar |
| SNR | signal-noise ratio |
| CDAEs | convolutional denoising autoencoders |
| CDAEsNSO | convolutional denoising autoencoders with network structure optimization |
| AD-CDAEs | atrous-dropout convolutional denoising autoencoders |
| ResCDAEs | residual-connection convolutional denoising autoencoders |
| ReLU | rectified linear unit |
| K-SVD | K-singular value decomposition |
References
- Dong, Z.; Ye, S.; Gao, Y.; Fang, G.; Zhang, X.; Xue, Z.; Zhang, T. Rapid detection methods for asphalt pavement thicknesses and defects by a vehicle-mounted ground penetrating radar (GPR) system. Sensors 2016, 16, 2067. [Google Scholar] [CrossRef]
- Khamzin, A.K.; Varnavina, A.V.; Torgashov, E.V. Utilization of air-launched ground penetrating radar (GPR) for pavement condition assessment. Constr. Build. Mater. 2017, 141, 130–139. [Google Scholar] [CrossRef]
- Diamanti, N.; Annan, A.P.; Redman, J.D. Concrete bridge deck deterioration assessment using ground penetrating radar (GPR). J. Environ. Eng. Geophys. 2017, 22, 121–132. [Google Scholar] [CrossRef]
- Solla, M.; Lagüela, S.; Fernández, N. Assessing rebar corrosion through the combination of nondestructive GPR and IRT methodologies. Remote Sens. 2019, 11, 1705. [Google Scholar] [CrossRef]
- Rasol, M.A.; Pérez-Gracia, V.; Fernandes, F.M.; Pais, J.C.; Santos-Assunçao, S.; Santos, C.; Sossa, V. GPR laboratory tests and numerical models to characterize cracks in cement concrete specimens, exemplifying damage in rigid pavement. Measurement 2020, 158, 107662. [Google Scholar] [CrossRef]
- Liu, X.; Dong, X.; Xue, Q. Ground penetrating radar (GPR) detects fine roots of agricultural crops in the field. Plant Soil. 2018, 423, 517–531. [Google Scholar] [CrossRef]
- Lai, W.; Chang, R.K.; Sham, J.F. Blind test of nondestructive underground void detection by ground penetrating radar (GPR). J. Appl. Geophys. 2018, 149, 10–17. [Google Scholar] [CrossRef]
- Terrasse, G.; Nicolas, J.M.; Trouvé, E. Application of the Curvelet Transform for clutter and noise removal in GPR data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 4280–4294. [Google Scholar] [CrossRef]
- He, T.; Shang, H. Direct-wave denoising of low-frequency ground-penetrating radar in open pits based on empirical curvelet transform. Near Surf. Geophys. 2020, 18, 295–305. [Google Scholar] [CrossRef]
- Gan, L.; Zhou, L.; Liu, S.M. A de-noising method for GPR signal based on EEMD. Appl. Mech. Mater. Trans. Tech. Publ. Ltd. 2014, 687, 3909–3913. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Zeng, Z.F.; Chen, L.N. GPR Signal Denoising and Target Extraction with the CEEMD Method. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1615–1619. [Google Scholar]
- Ostoori, R.; Goudarzi, A.; Oskooi, B. GPR random noise reduction using BPD and EMD. J. Geophys. Eng. 2018, 15, 347–353. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Zhang, X. Dip Filter and Random Noise Suppression for GPR B-Scan Data Based on a Hybrid Method in f-x Domain. Remote Sens. 2019, 11, 2180. [Google Scholar] [CrossRef]
- Kobayashi, M.; Nakano, K. A denoising method for detecting reflected waves from buried objects by ground-penetrating radar. Electr. Commun. Jpn. 2013, 96, 1–13. [Google Scholar] [CrossRef]
- Huang, W.L.; Wu, R.S.; Wang, R. Damped dreamlet representation for exploration seismic data interpolation and denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3159–3172. [Google Scholar] [CrossRef]
- Qiao, X.; Fang, F.; Zhang, J. Ground Penetrating Radar Weak Signals Denoising via Semi-soft Threshold Empirical Wavelet Transform. Ingénierie Syst. Inf. 2019, 24, 207–213. [Google Scholar] [CrossRef]
- Chen, L.; Zeng, Z.; Li, J. Research on weak signal extraction and noise removal for GPR data based on principal component analysis. Glob. Geol. 2015, 18, 196–202. [Google Scholar]
- Huang, W.; Wang, R.; Chen, X. Damped sparse representation for seismic random noise attenuation. In SEG Technical Program Expanded Abstracts 2017; Society of Exploration Geophysicists: Tulsa, OK, USA, 2017; pp. 5079–5084. [Google Scholar]
- Deng, L.; Yuan, S.; Wang, S. Sparse Bayesian learning-based seismic denoise by using physical wavelet as basis functions. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1993–1997. [Google Scholar] [CrossRef]
- Bi, W.; Zhao, Y.; An, C. Clutter elimination and random-noise denoising of GPR signals using an SVD method based on the Hankel matrix in the local frequency domain. Sensors 2018, 18, 3422. [Google Scholar] [CrossRef]
- Liu, L.; Ma, J. Structured graph dictionary learning and application on the seismic denoising. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1883–1893. [Google Scholar] [CrossRef]
- Bai, X.; Peng, X. Radar image series denoising of space targets based on Gaussian process regression. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4659–4669. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Li, Y. A Morphological component analysis based on mixed dictionary for signal denoising of ground penetrating radar. Int. J. Simul. Process. Model. 2019, 14, 431–441. [Google Scholar] [CrossRef]
- Li, H.; Wang, R.; Cao, S. Mathematical morphological filtering for linear noise attenuation of seismic data. Geophysics 2016, 81, V159–V167. [Google Scholar] [CrossRef]
- Huang, W.; Wang, R.; Zhang, D. A method for low-frequency noise suppression based on mathematical morphology in microseismic monitoring. Geophysics 2017, 82, V369–V384. [Google Scholar] [CrossRef]
- Li, J.; Le Bastard, C.; Wang, Y.; Gang, W.; Ma, B.; Sun, M. Enhanced GPR Signal for Layered Media Time-Delay Estimation in Low-SNR Scenario. IEEE Geosci. Remote Sens. Lett. 2016, 13, 299–303. [Google Scholar] [CrossRef]
- Gondara, L. Medical image denoising using convolutional denoising autoencoders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 241–246. [Google Scholar]
- Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W. Application of Denoising CNN for Noise Suppression and Weak Signal Extraction of Lunar Penetrating Radar Data. Remote Sens. 2021, 13, 779. [Google Scholar] [CrossRef]
- Grais, E.M.; Plumbley, M.D. Single channel audio source separation using convolutional denoising autoencoders. In Proceedings of the 2017 IEEE global conference on signal and information processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017; pp. 1265–1269. [Google Scholar]
- Meng, Z.; Zhan, X.; Li, J. An enhancement denoising autoencoder for rolling bearing fault diagnosis. Measurement 2018, 130, 448–454. [Google Scholar] [CrossRef]
- Ashfahani, A.; Pratama, M.; Lughofer, E. DEVDAN: Deep evolving denoising autoencoder. Neurocomputing 2020, 390, 297–314. [Google Scholar] [CrossRef]
- Zhu, W.; Mousavi, S.M.; Beroza, G.C. Seismic signal denoising and decomposition using deep neural networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9476–9488. [Google Scholar] [CrossRef]
- Saad, O.M.; Chen, Y. Deep denoising autoencoder for seismic random noise attenuation. Geophysics 2020, 85, V367–V376. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dahl, G.E.; Sainath, T.N.; Hinton, G.E. Improving deep neural networks for LVCSR using rectified linear units and dropout. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–30 May 2013; pp. 8609–9613. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- He, K.; Zhang, X.; Ren, S. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wu, S.; Zhong, S.; Liu, Y. Deep residual learning for image steganalysis. Multimed. Tools Appl. 2018, 77, 10437–10453. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, H.; Gong, J. GPR Detection of Tunnel Lining Cavities and Reverse-time Migration Imaging. Appl. Geophys. 2020, 17, 1–7. [Google Scholar] [CrossRef]
- Zhang, B.; Dai, Q.; Yin, X. A new approach of rotated staggered grid FD method with unsplit convolutional PML for GPR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 52–59. [Google Scholar] [CrossRef]









| Methods | Typical Case |
|---|---|
| fixed transformation basis | curvelet transform, EMD, wavelet transform |
| sparse representation | PCA, SVD, SBL |
| morphological component analysis | MCA, MMF |
| deep learning | FNNs, FCDAEs, DECDAN, DDAE |
| Encoder Part | Decoder Part | ||
|---|---|---|---|
| Layer (Type) | Output Shape | Layer (Type) | Output Shape |
| Input Layer (Input) | (Batch, 32, 32, 1) | Input Layer (Input) | (Amount, 256) |
| Conv2D | (Batch, 32, 32, 16) | Dense | (Batch, 1024) |
| Max-Pooling | (Batch, 16, 16, 16) | Reshape | (Batch, 4, 4, 64) |
| Conv2D | (Batch, 16, 16, 32) | Conv2DTr | (Batch, 4, 4, 64) |
| Max-Pooling | (Batch, 8, 8, 32) | Upsampling | (Batch, 8, 8, 64) |
| Conv2D | (Batch, 8, 8, 64) | Conv2DTr | (Batch, 8, 8, 32) |
| Max-Pooling | (Batch, 4, 4, 64) | Upsampling | (Batch, 16, 16, 32) |
| Flatten | (Batch, 1024) | Conv2DTr | (Batch, 16, 16, 16) |
| Dense (Output) | (Batch, 256) | Upsampling | (Batch, 32, 32, 16) |
| Conv2DTr (Output) | (Batch, 32, 32, 1) | ||
| Filter | Size of Kernel | Length of Latent | Loss | Validation Loss |
|---|---|---|---|---|
| (16, 32, 64) | 256 | |||
| (16, 32, 64) | 256 | |||
| (16, 32, 64) | 512 | |||
| (16, 32, 64) | 512 | |||
| (32, 64, 128) | 256 | |||
| (32, 64, 128) | 256 | |||
| (32, 64, 128) | 512 | |||
| (32, 64, 128) | 512 |
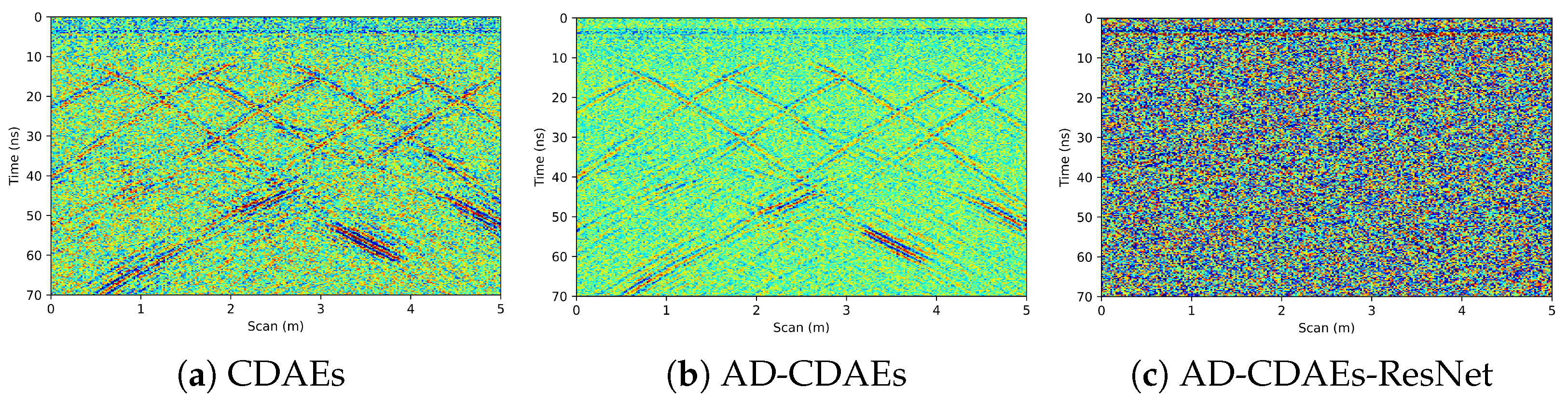
| Strategy | Noise Profile | CDAEs | AD-CDAEs | AD-CDAEs-ResNet |
|---|---|---|---|---|
| SNR | 11.3708 | 17.0944 | 19.7689 | 34.4409 |
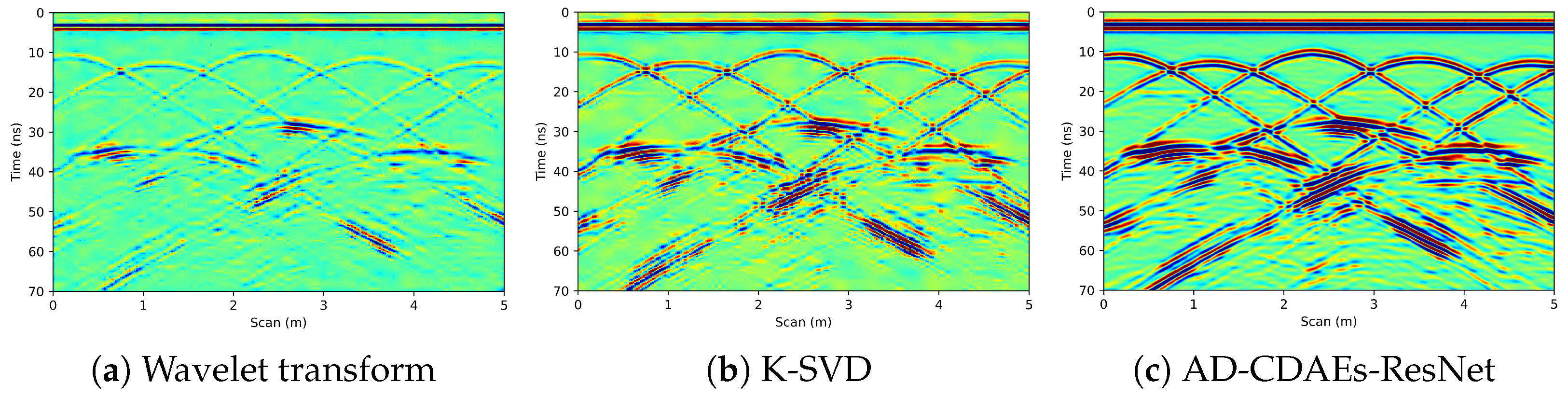
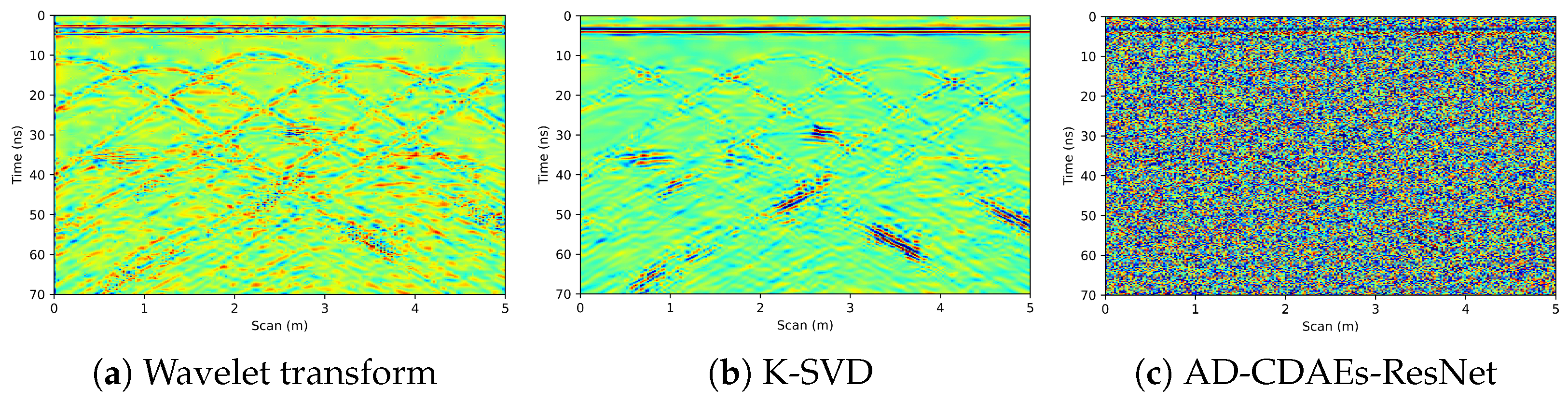
| Strategy | Noise Profile | Wavelet Transform | K-SVD | AD-CDAEs-ResNet |
|---|---|---|---|---|
| SNR | 11.3708 | 19.1945 | 24.5208 | 34.4409 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, D.; Wang, X.; Wang, X.; Ding, S.; Zhang, H. Deep Convolutional Denoising Autoencoders with Network Structure Optimization for the High-Fidelity Attenuation of Random GPR Noise. Remote Sens. 2021, 13, 1761. https://doi.org/10.3390/rs13091761
Feng D, Wang X, Wang X, Ding S, Zhang H. Deep Convolutional Denoising Autoencoders with Network Structure Optimization for the High-Fidelity Attenuation of Random GPR Noise. Remote Sensing. 2021; 13(9):1761. https://doi.org/10.3390/rs13091761
Chicago/Turabian StyleFeng, Deshan, Xiangyu Wang, Xun Wang, Siyuan Ding, and Hua Zhang. 2021. "Deep Convolutional Denoising Autoencoders with Network Structure Optimization for the High-Fidelity Attenuation of Random GPR Noise" Remote Sensing 13, no. 9: 1761. https://doi.org/10.3390/rs13091761
APA StyleFeng, D., Wang, X., Wang, X., Ding, S., & Zhang, H. (2021). Deep Convolutional Denoising Autoencoders with Network Structure Optimization for the High-Fidelity Attenuation of Random GPR Noise. Remote Sensing, 13(9), 1761. https://doi.org/10.3390/rs13091761








