Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications
Abstract
1. Instruction
- The impacts of subset size on the accuracy, integrity and computation load are analyzed in the ideal and practical satellite distribution scenes to illustrate the inefficiency of satellite increase in performance improvement when sufficient satellites have been in use. Consequently, the importance of the satellite selection strategy in RAIM process is confirmed;
- The impacts of a single satellite on the accuracy and integrity of the subset are theoretically evaluated and a cost function is presented according to the performance requirement to choose the valuable satellite for the current subset. This valuable satellite is then used to construct the final subset so that the accuracy and integrity requirements can be both efficiently satisfied;
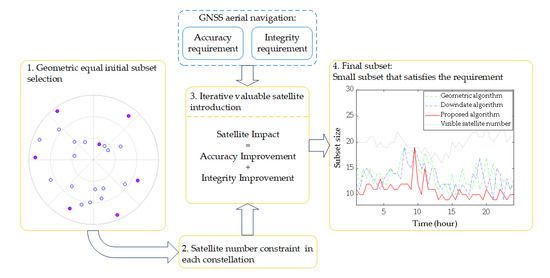
- A performance-requirement-driven fast satellite selection algorithm is raised according to the above investigation. It constructs the initial subset through geometric selection strategy to keep a tolerable accuracy and integrity, then improves the performance by adding a most valuable satellite to the subset until the required performance is met, thus a small size feasible subset is obtained.
2. Problem Statement
2.1. Accuracy and Integrity Models in Weighted Slope-Based RAIM Algorithm
2.1.1. Accuracy Model
2.1.2. Integrity Model
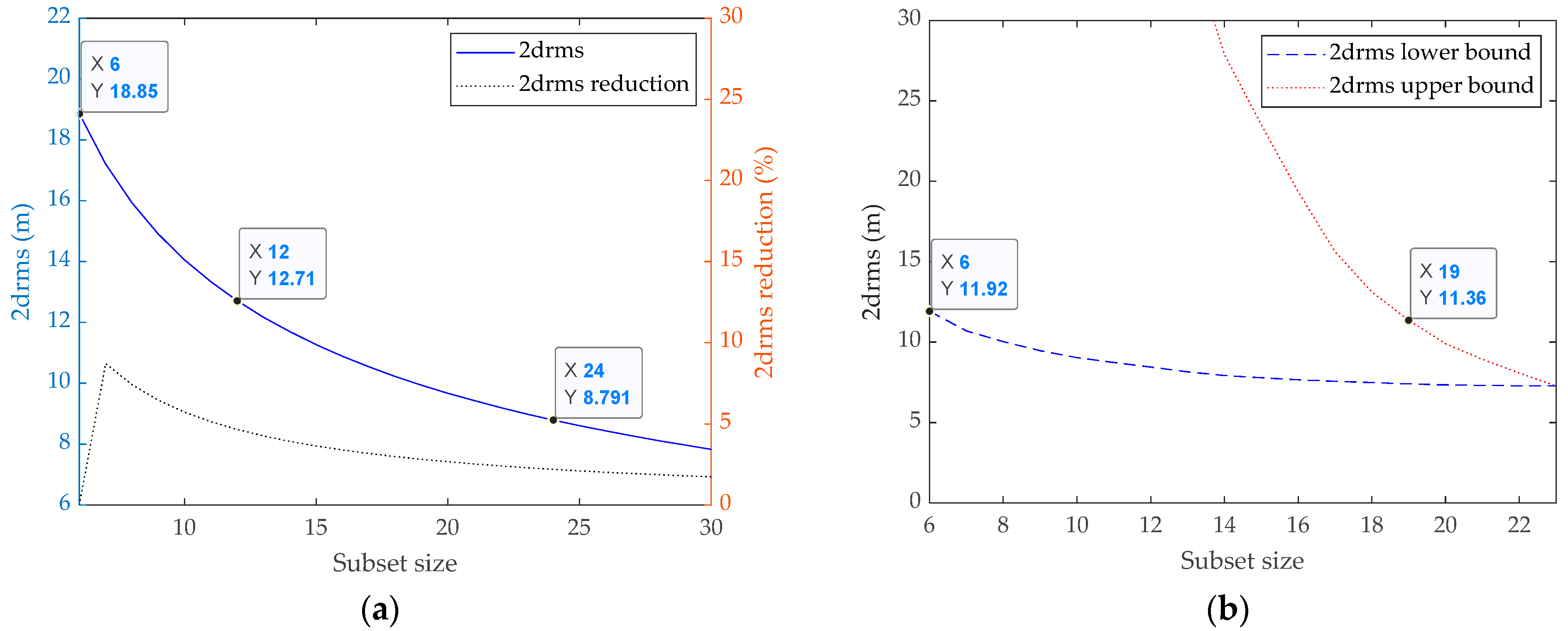
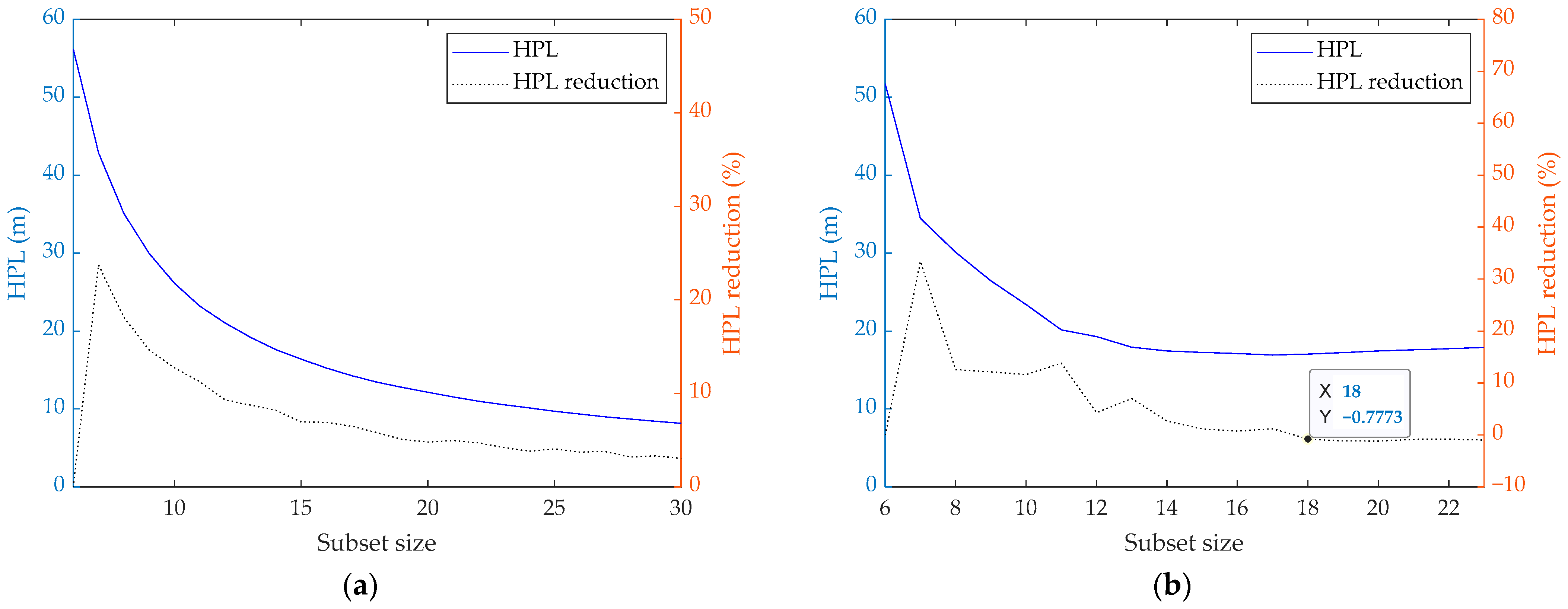
2.2. Impacts of Subset Size on Accuracy and Integrity Performances
2.2.1. Accuracy Performance Improved by Subset Size Growth
2.2.2. Integrity Performance Improved by Subset Size Growth
2.2.3. Computation Load Increased by Subset Size Growth
3. Methodology
3.1. Impacts of Single Satellite on the Accuracy and Integrity of Subset
3.1.1. Impact of Single Satellite on the Accuracy of Subset
3.1.2. Impact of Single Satellite on the Integrity of Subset
3.1.3. Integrated Performance Impact of Single Satellite
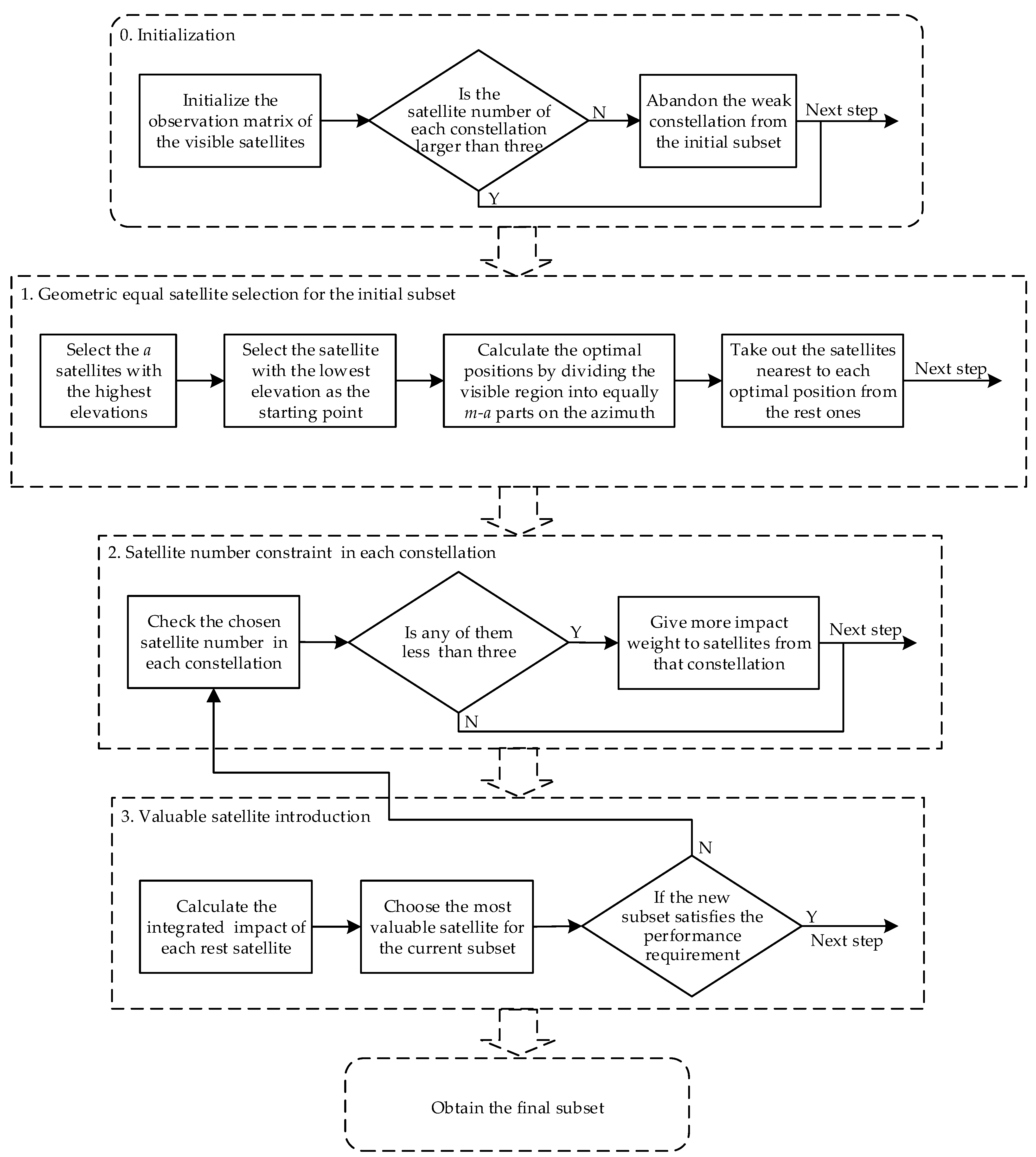
3.2. Performance-Requirement-Driven Fast Satellite Selection Algorithm
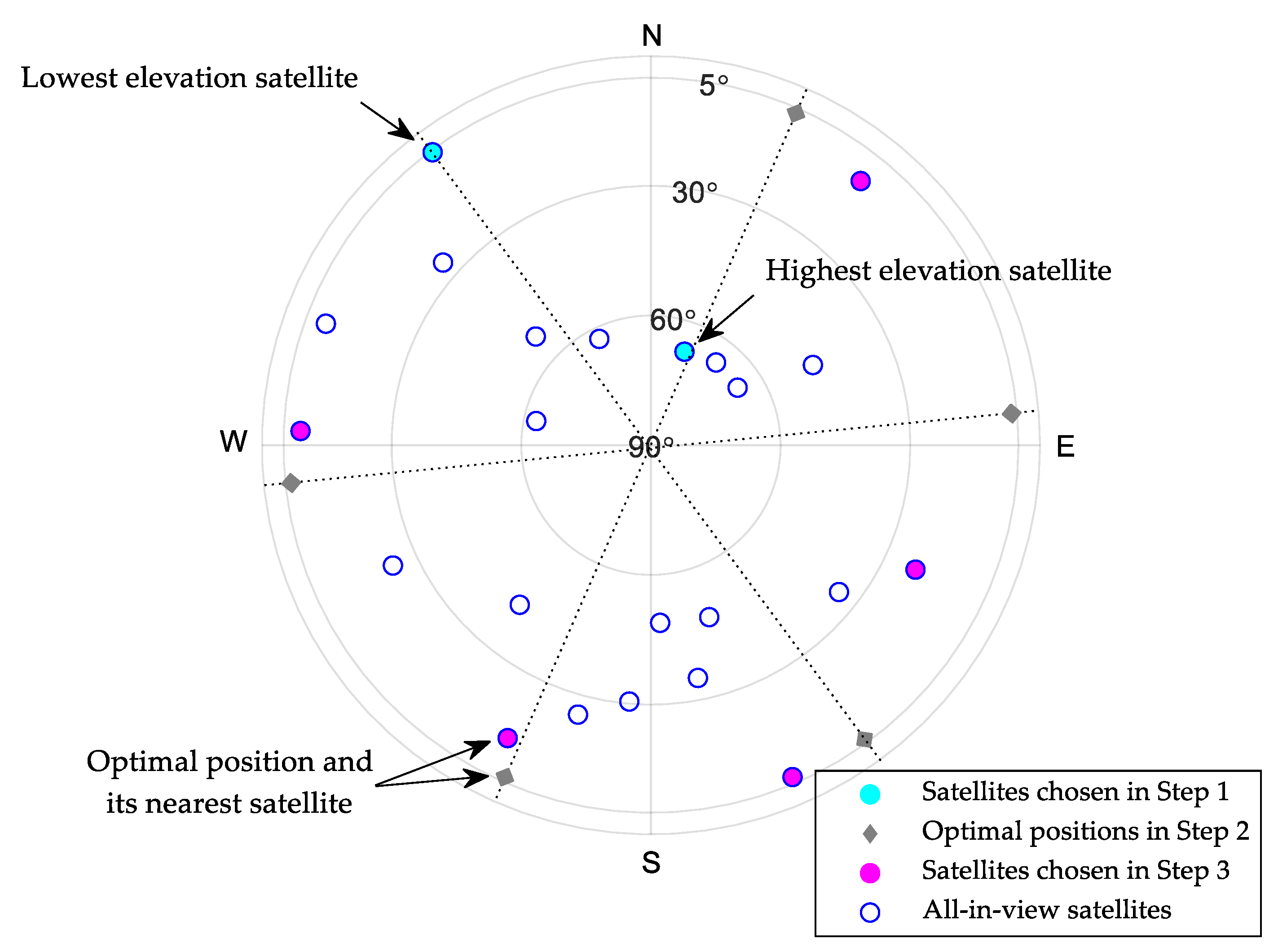
3.2.1. Geometric Equal Satellite Selection for the Initial Subset
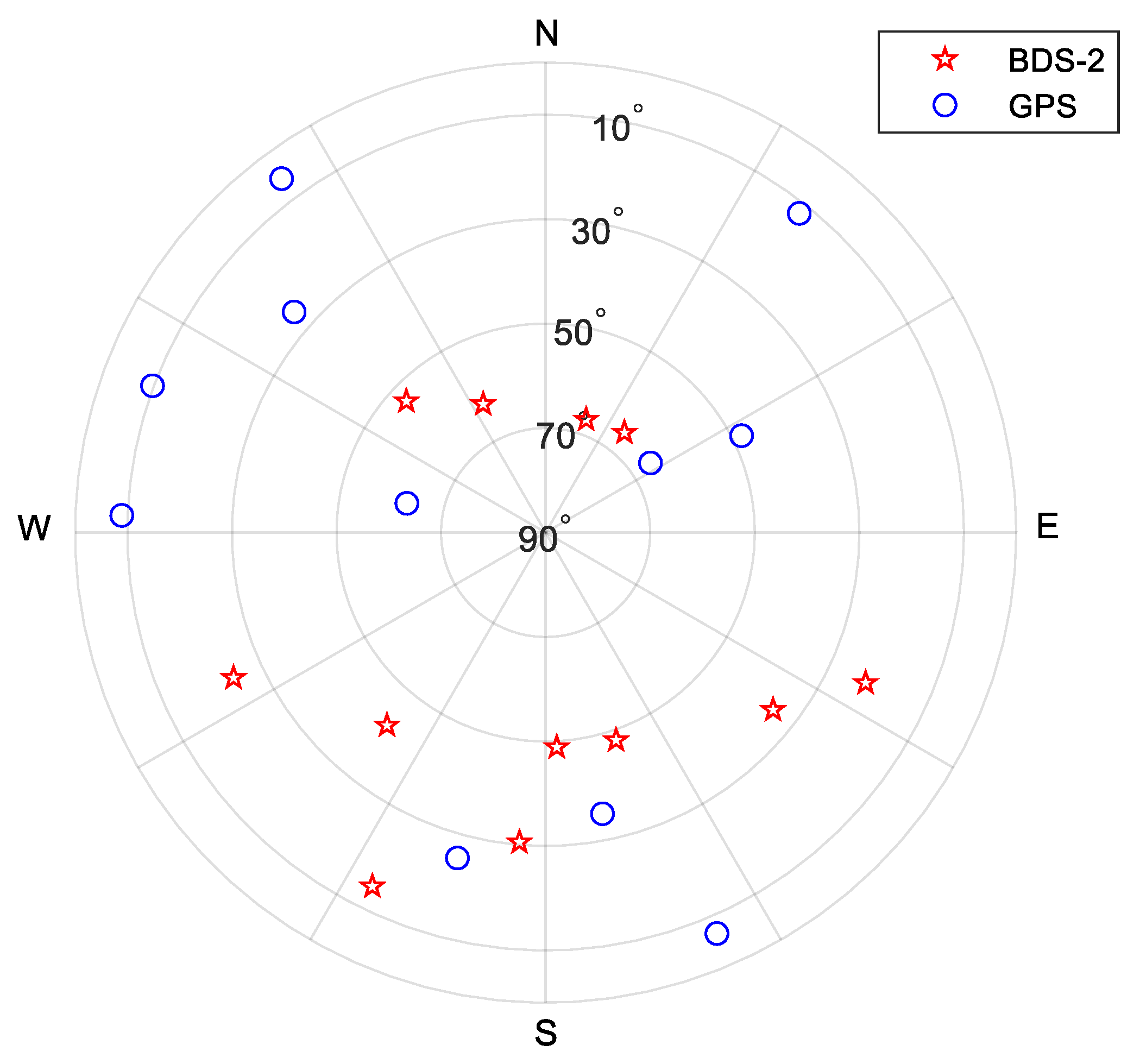
- Selecting the first satellites with the highest elevations then selecting the satellite with the lowest elevation as the starting point of the region partition process in the next step. The chosen satellites are shown as the light cyan points in Figure 3;
- Calculating the optimal positions by dividing the visible region into equally parts on the azimuth from the starting point selected in the previous step. The optimal positions are shown as the grey diamond points in Figure 3;
- Taking out the satellites nearest to each optimal position sequentially from the rest ones, as the manganese violet points in Figure 3. Therefore, the first satellites are selected.
3.2.2. Satellite Number Constraint in Each Constellation
3.2.3. Valuable Satellite Introduction
4. Results and Discussion
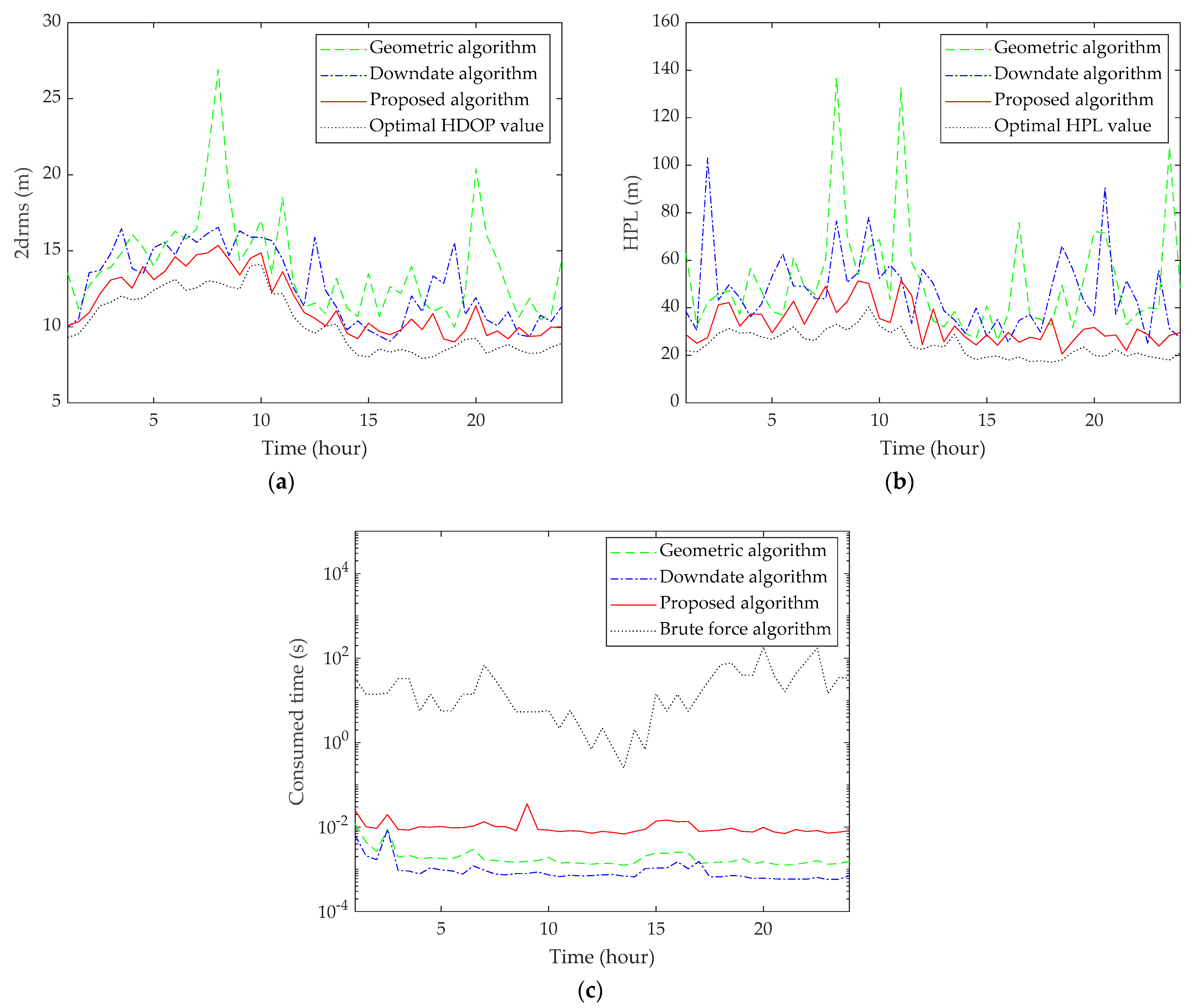
4.1. Fixed Subset Size Simulations
4.2. Minimal Subset Size Simulations
4.3. High Latitudes Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ICAO. Doc 9613, Performance-Based Navigation (PBN) Manual, 4th ed.; ICAO: Montreal, QC, Canada, 2013. [Google Scholar]
- RTCA, Inc. Minimum Aviation System Performance Standards: Required Navigation Performance for Area Navigation; RTCA DO-236B; RTCA: Washington, DC, USA, 2003; pp. 21–24. [Google Scholar]
- Ochieng, W.Y.; Sauer, K.; Walsh, D.; Brodin, G.; Griffin, S.; Denney, M. GPS integrity and potential impact on aviation safety. J. Navig. 2003, 56, 51. [Google Scholar] [CrossRef]
- Nowel, K.; Cellmer, S.; Fischer, A. Validation of GNSS baseline observation models using information criteria. Surv. Rev. 2020. [Google Scholar] [CrossRef]
- Krasuski, K.; Wierzbicki, D. Monitoring Aircraft Position Using EGNOS Data for the SBAS APV Approach to the Landing Procedure. Sensors 2020, 20, 1945. [Google Scholar] [CrossRef]
- Krasuski, K.; Cwiklak, J.; Grzegorzewski, M. Aircraft positioning using GPS/GLONASS code observations. Aircr. Eng. Aerosp. Technol. 2020, 92, 163–171. [Google Scholar] [CrossRef]
- Brown, R.G. A baseline GPS RAIM scheme and a note on the equivalence of three RAIM methods. Navigation 1992, 39, 301–316. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Gebre-Egziabher, D. Kalman filter–based RAIM for GNSS receivers. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2444–2459. [Google Scholar] [CrossRef]
- Sun, Y. RAIM-NET: A Deep Neural Network for Receiver Autonomous Integrity Monitoring. Remote Sens. 2020, 12, 1503. [Google Scholar] [CrossRef]
- Walter, T.; Enge, P. Weighted RAIM for Precision Approach. In Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1995), Palm Springs, CA, USA, 12–15 September 1995; pp. 1995–2004. [Google Scholar]
- Milner, C.D.; Ochieng, W.Y. Weighted RAIM for APV: The Ideal Protection Level. J. Navig. 2011, 64, 61–73. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, J.; Li, R.; Cao, X.; Wang, J. Vision-Aided RAIM: A New Method for GPS Integrity Monitoring in Approach and Landing Phase. Sensors 2015, 15, 22854–22873. [Google Scholar] [CrossRef]
- Sabatini, R.; Moore, T.; Ramasamy, S. Global Navigation Satellite Systems Performance Analysis and Augmentation Strategies in Aviation. Prog. Aeosp. Sci. 2017, 95, 45–98. [Google Scholar] [CrossRef]
- Pan, W.; Zhan, X.; Zhang, X. Fault exclusion method for ARAIM based on tight GNSS/INS integration to achieve CAT-I approach. IET Radar Sonar Navig. 2019, 13, 1909–1917. [Google Scholar] [CrossRef]
- Yeh, S.J.; Jan, S.S. Operational Receiver Autonomous Integrity Monitoring Prediction System for Air Traffic Management System. J. Aircr. 2017, 54, 346–353. [Google Scholar] [CrossRef]
- Nowak, A. The Proposal to “Snapshot” Raim Method for Gnss Vessel Receivers Working in Poor Space Segment Geometry. Pol. Marit. Res. 2015, 22, 3–8. [Google Scholar] [CrossRef]
- Zalewski, P. Integrity Concept for Maritime Autonomous Surface Ships’ Position Sensors. Sensors 2020, 20, 2075. [Google Scholar] [CrossRef]
- Zalewski, P. GNSS Integrity Concepts for Maritime Users. In Proceedings of the 2019 European Navigation Conference (ENC), Warsaw, Poland, 9–12 April 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Feng, S.; Ochieng, W.Y.; Walsh, D.; Ioannides, R. A measurement domain receiver autonomous integrity monitoring algorithm. GPS Solut. 2006, 10, 85–96. [Google Scholar] [CrossRef]
- Joerger, M.; Chan, F.C.; Pervan, B. Solution separation versus residual-based RAIM. Navigation 2014, 61, 273–291. [Google Scholar] [CrossRef]
- Ma, X.; Yu, K.; Montillet, J.P.; He, X. Equivalence Proof and Performance Analysis of Weighted Least Squares Residual Method and Weighted Parity Vector Method in RAIM. IEEE Access 2019, 7, 97803–97814. [Google Scholar] [CrossRef]
- Zhai, Y.; Joerger, M.; Pervan, B. Fault exclusion in multi-constellation global navigation satellite systems. J. Navig. 2018, 71, 1281–1298. [Google Scholar] [CrossRef]
- Luo, S.; Wang, L.; Tu, R.; Zhang, W.; Wei, J.; Chen, C. Satellite selection methods for multi-constellation advanced RAIM. Adv. Space Res. 2020, 65, 1503–1517. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J. A fast satellite selection algorithm: Beyond four satellites. IEEE J. Sel. Top. Signal Process. 2009, 3, 740–747. [Google Scholar] [CrossRef]
- Walter, T.; Blanch, J.; Kropp, V. Satellite selection for multi-constellation SBAS. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 1350–1359. [Google Scholar] [CrossRef]
- Kihara, M.; Okada, T. A satellite selection method and accuracy for the global positioning system. Navigation 1984, 31, 8–20. [Google Scholar] [CrossRef]
- Phatak, M.S. Recursive method for optimum GPS satellite selection. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 751–754. [Google Scholar] [CrossRef]
- Meng, F.; Wang, S.; Zhu, B. GNSS reliability and positioning accuracy enhancement based on fast satellite selection algorithm and RAIM in multiconstellation. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 14–27. [Google Scholar] [CrossRef]
- Huang, P.; Rizos, C.; Roberts, C. Satellite selection with an end-to-end deep learning network. GPS Solut. 2018, 22, 108. [Google Scholar] [CrossRef]
- Du, H.; Hong, Y.; Xia, N.; Zhang, G.; Yu, Y.; Zhang, J. A Navigation Satellites Selection Method Based on ACO with Polarized Feedback. IEEE Access 2020, 8, 168246–168261. [Google Scholar] [CrossRef]
- Gerbeth, D.; Martini, I.; Rippl, M.; Felux, M. Satellite selection methodology for horizontal navigation and integrity algorithms. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 2789–2798. [Google Scholar] [CrossRef]
- Gerbeth, D.; Felux, M.; Circiu, M.S.; Caamano, M. Optimized selection of satellite subsets for a multi-constellation GBAS. In Proceedings of the 2016 International Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 25–28 January 2016; pp. 360–367. [Google Scholar] [CrossRef]
- Gerbeth, D.; Caamano, M.; Circiu, M.S.; Felux, M. Satellite selection in the context of an operational GBAS. Navigation 2019, 66, 227–238. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advanced RAIM user algorithm description: Integrity support message processing, fault detection, exclusion, and protection level calculation. In Proceedings of the 2012 Global Navigation Satellite Systems Conference of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 2828–2849. [Google Scholar]
- Blanch, J.; Walker, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline advanced RAIM user algorithm and possible improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: Boston, MA, USA, 2013; pp. 451–470. [Google Scholar]
- Kaplan, E.D.; Hegarty, C. Understanding GPS/GNSS: Principles and Applications, 3rd ed.; Artech House: Boston, MA, USA, 2017; pp. 661–730. [Google Scholar]
- Li, F.; Li, Z.; Gao, J.; Yao, Y. A Fast Rotating Partition Satellite Selection Algorithm Based on Equal Distribution of Sky. J. Navig. 2019, 72, 1053–1069. [Google Scholar] [CrossRef]
- Abedi, A.A.; Mosavi, M.R.; Mohammadi, K. A new recursive satellite selection method for multi-constellation GNSS. Surv. Rev. 2020, 52, 330–340. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, X.; Pang, C.; Zhang, L.; Feng, B. The influence of satellite configuration and fault duration time on the performance of fault detection in GNSS/INS integration. Sensors 2019, 19, 2147. [Google Scholar] [CrossRef]
- Sturza, M.A.; Brown, A.K. Comparison of fixed and variable threshold RAIM algorithms. In Proceedings of the 3rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1990), Colorado Spring, CO, USA, 19–21 September 1990; pp. 437–443. [Google Scholar]
- Wang, H.; Cheng, Y.; Wei, X.; Li, S.; Wang, H.; Li, Z. A slope-based fast satellite selection algorithm for multi-constellation RAIM. In Proceedings of the 2020 Chinese Automation Congress (CAC 2020), Shanghai, China, 6–8 November 2020. [Google Scholar] [CrossRef]
- RTCA, Inc. Minimum Operational Performance Standards for GPS WAAS Airborne Equipment; RTCA DO-229D; RTCA: Washington, DC, USA, 2006; pp. 41–49. [Google Scholar]


| Type of Operation | HOR./VERT. Accuracy (95%) | Integrity | HAL/VAL | Time to Alert | Continuity | Availability |
|---|---|---|---|---|---|---|
| En Route Oceanic | 3700 m/NA | 1–10−7/h | 7408 m/NA | 5 min | 1–10−4/h to 1–10−8/h | 0.99 to 0.99999 |
| En Route Continental | 3700 m/NA | 1–10−7/h | 3704 m/NA | 5 min | 1–10−4/h to 1–10−8/h | 0.99 to 0.99999 |
| En Route Terminal | 740 m/NA | 1–10−7/h | 1852 m/NA | 15 s | 1–10−4/h to 1–10−8/h | 0.99 to 0.99999 |
| APV-I | 16 m/20 m | 1–2×10−7/App. | 40 m/50 m | 10 s | 1–8×10−6/15 s | 0.99 to 0.999 |
| APV-II | 16 m/8 m | 1–2×10−7/App. | 40 m/20 m | 6 s | 1–8×10−6/15 s | 0.99 to 0.999 |
| Category I | 16 m/4 m | 1–2×10−7/App. | 40 m/10 m | 6 s | 1–8×10−6/15 s | 0.99 to 0.99999 |
| Category II | 6.9 m/2 m | 1–10−9/15 s | 17.3 m/5.3 m | 1 s | 1–4×10−6/15 s | 0.99 to 0.99999 |
| Category III | 6.2 m/2 m | 1–10−9/30 s (H) 1–10−9/15 s (V) | 15.5 m/5.3 m | 1 s | 1–2×10−6/30 s (H) 1–2×10−6/15 s (V) | 0.99 to 0.99999 |
| Calculation Process | ||||
| Multiplication | ||||
| Addition | ||||
| Calculation Process | ||||
| Multiplication | ||||
| Addition | ||||
| Sum | Time Complexity | |||
| Multiplication | ||||
| Addition | ||||
| Requirement | Parameter |
|---|---|
| Accuracy (95%) | 32 m |
| Missed Alert Probability | 0.001 |
| False Alert Probability | 3.33 × 10−7 per sample |
| HAL | 0.1 NM |
| Mask angle | 5 degrees |
| Algorithms | 2drms (m) | HPL (m) | Consumed Time (s) |
|---|---|---|---|
| Geometric algorithm | 13.9855 | 51.6916 | 0.0024 |
| Downdate algorithm | 13.1456 | 48.0024 | 0.0014 |
| Proposed algorithm | 11.4943 | 33.0684 | 0.0123 |
| Brute force algorithm | 10.2619 | 24.4370 | 30.4349 |
| LNAV | APV-I | |||
|---|---|---|---|---|
| Algorithms | Subset Size | Consumed Time (s) | Subset Size | Consumed Time (s) |
| Geometric algorithm | 7.5417 | 0.0043 | 13.7917 | 0.0128 |
| Downdate algorithm | 8.0833 | 0.0023 | 13.3125 | 0.0052 |
| Proposed algorithm | 6.5417 | 0.0062 | 10.7708 | 0.0121 |
| Fixed Subset Size Performance | Minimal Subset Size Performance | |||
|---|---|---|---|---|
| Algorithms | 2drms (m) | HPL (m) | LNAV | APV-I |
| Geometric algorithm | 15.3246 | 65.1377 | 8.1250 | 15.5417 |
| Downdate algorithm | 13.2208 | 53.2312 | 8.1458 | 13.9792 |
| Proposed algorithm | 11.9713 | 37.9720 | 6.8125 | 11.9167 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Cheng, Y.; Cheng, C.; Li, S.; Li, Z. Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications. Remote Sens. 2021, 13, 1725. https://doi.org/10.3390/rs13091725
Wang H, Cheng Y, Cheng C, Li S, Li Z. Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications. Remote Sensing. 2021; 13(9):1725. https://doi.org/10.3390/rs13091725
Chicago/Turabian StyleWang, Huibin, Yongmei Cheng, Cheng Cheng, Song Li, and Zhenwei Li. 2021. "Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications" Remote Sensing 13, no. 9: 1725. https://doi.org/10.3390/rs13091725
APA StyleWang, H., Cheng, Y., Cheng, C., Li, S., & Li, Z. (2021). Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications. Remote Sensing, 13(9), 1725. https://doi.org/10.3390/rs13091725