Deep Learning for Monitoring Agricultural Drought in South Asia Using Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
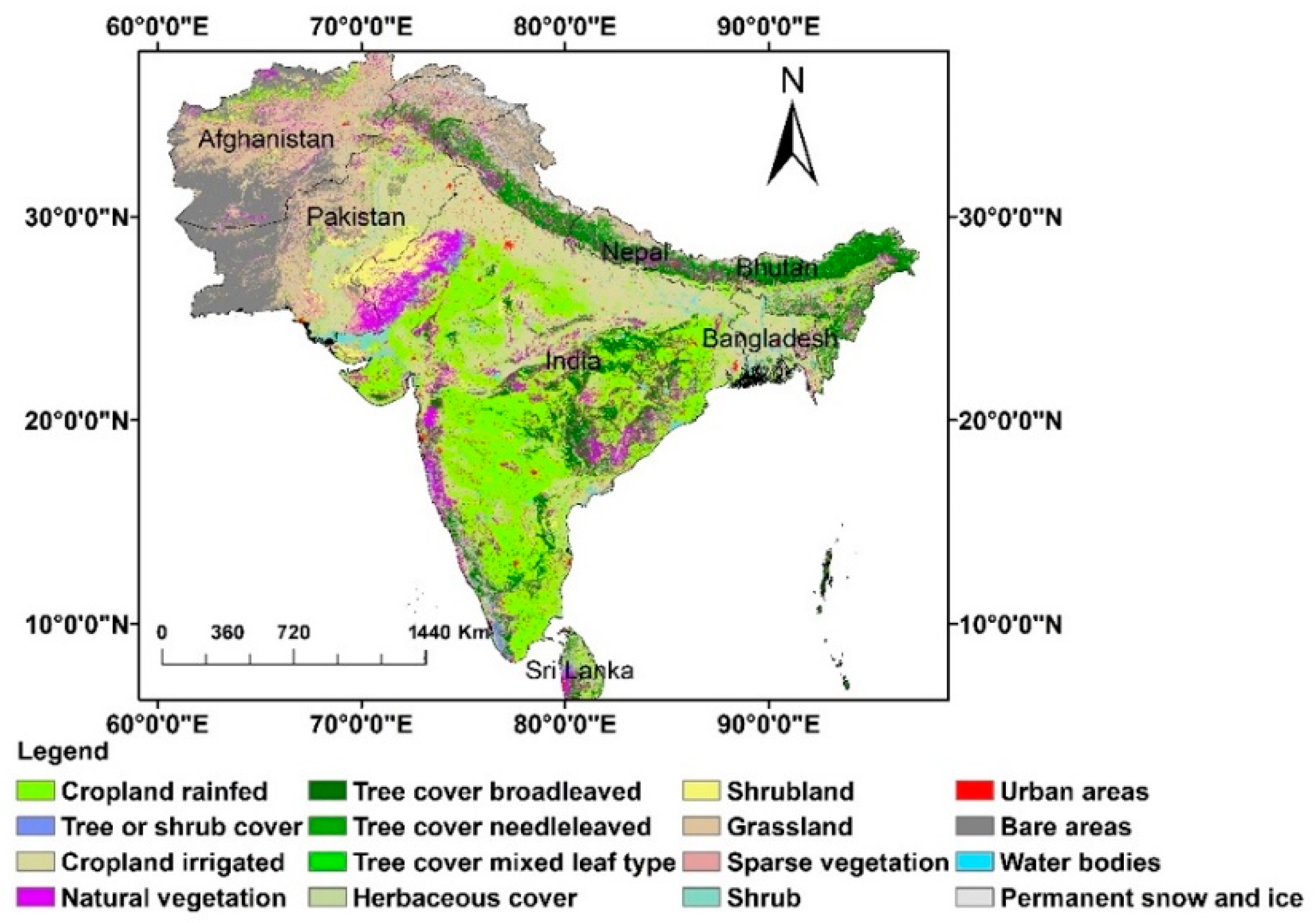
2.1. Study Area
2.2. Data
2.2.1. MODIS Data
2.2.2. GLDAS-NOAH Soil Moisture, Evapotranspiration (ET), Potential Evapotranspiration (PET) Data
2.2.3. CHIRPS Data
2.2.4. GIMMS-NDVI Data
2.2.5. Meteorological Station Data
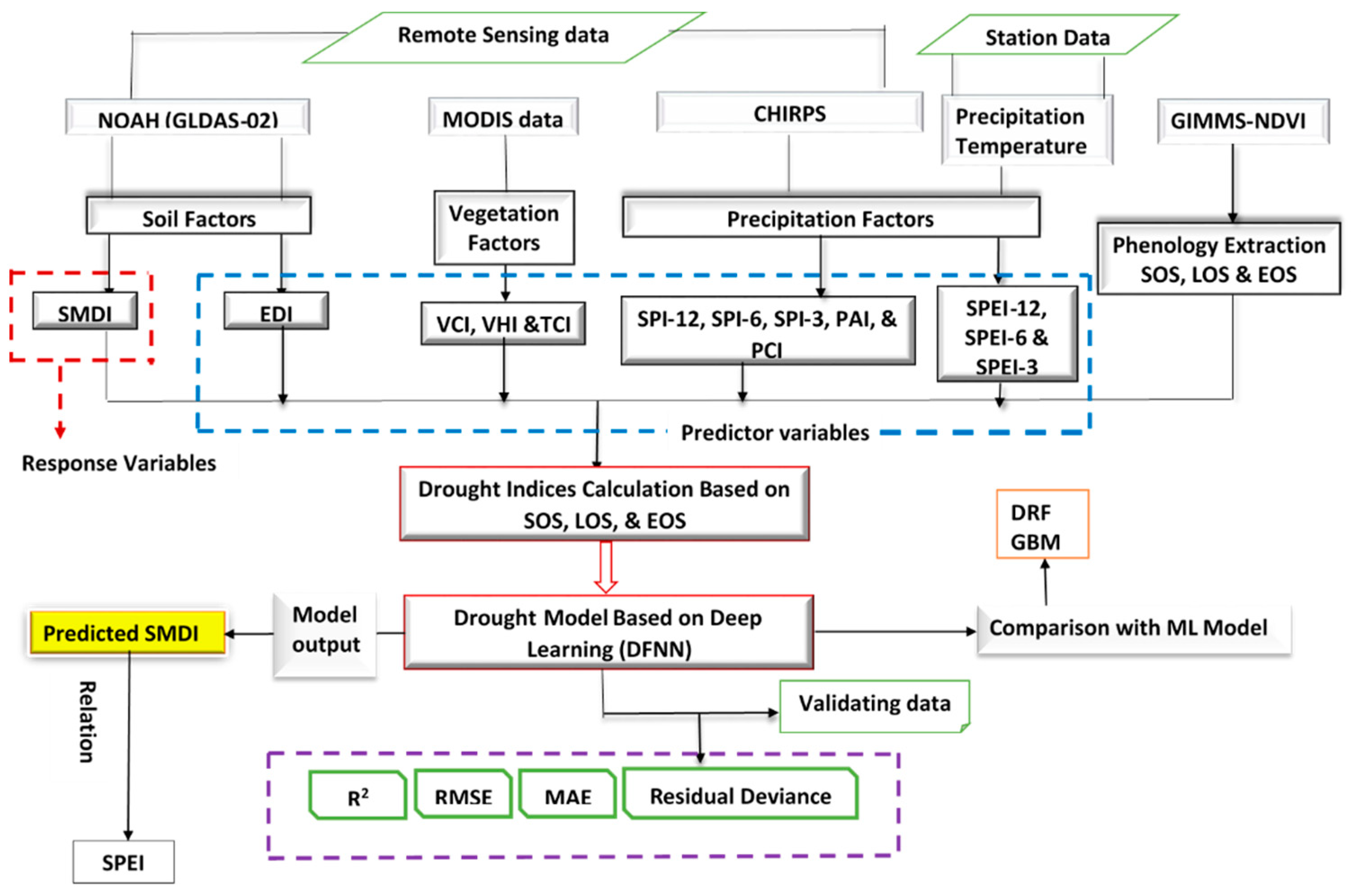
2.3. Model Input Parameter
2.4. Phenology Extraction
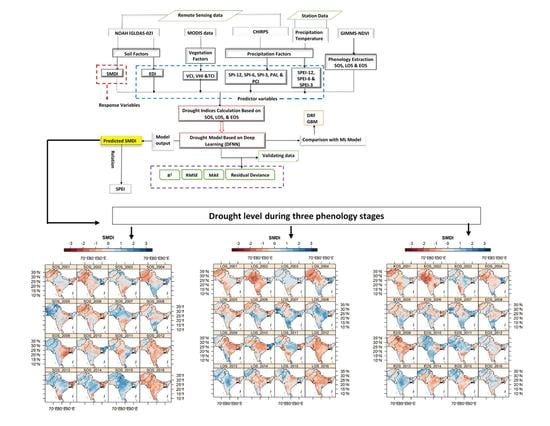
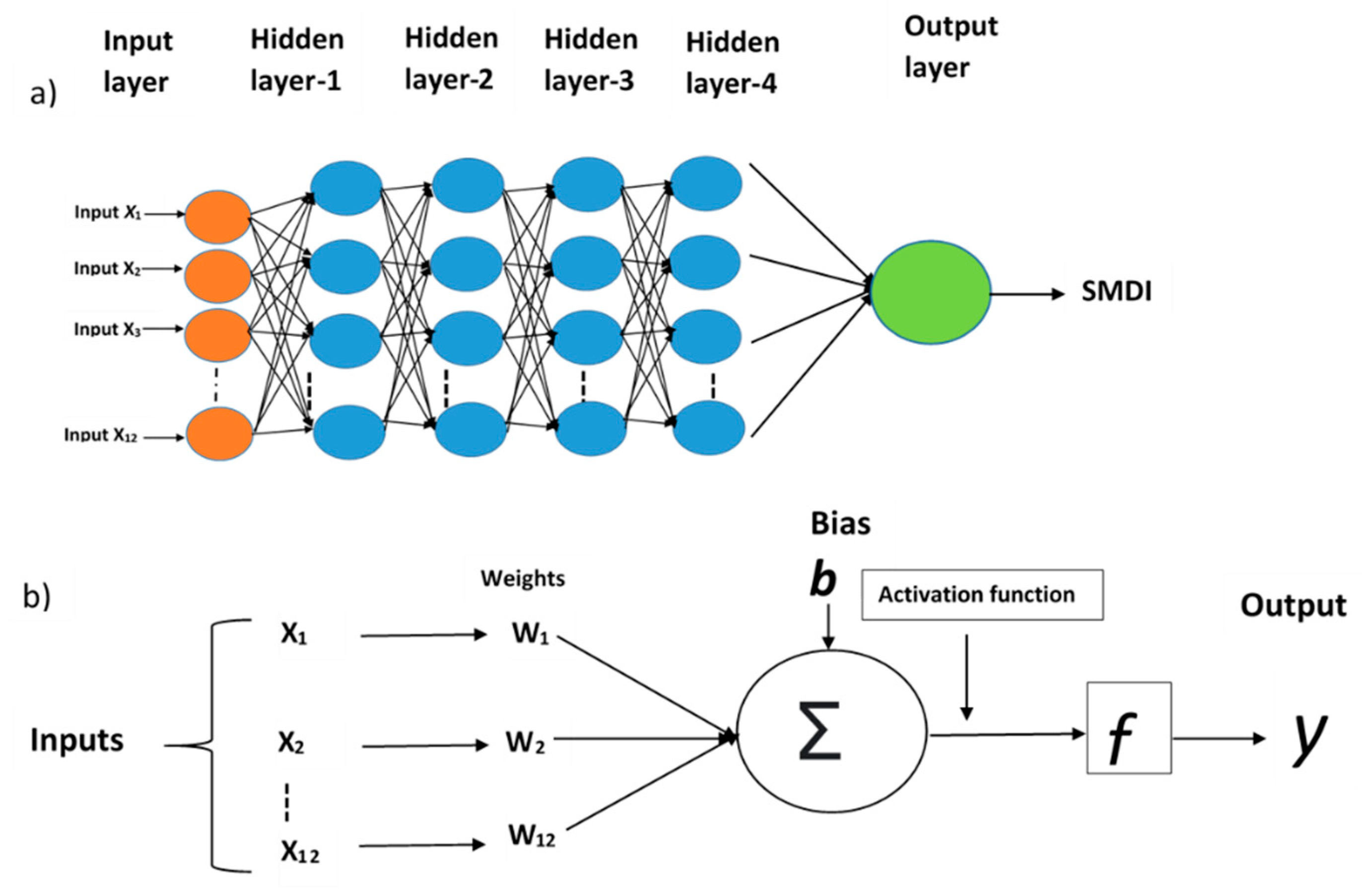
2.5. Construction of Deep Learning Model Using DFNN
2.6. Model Calibration on Training Data Set by Tuning Model Parameter
2.7. Model Validation Using Cross-Validation Data
2.8. Machine Learning Model
2.9. Mann-Kendall Test for Drought Trend Analysis
3. Results
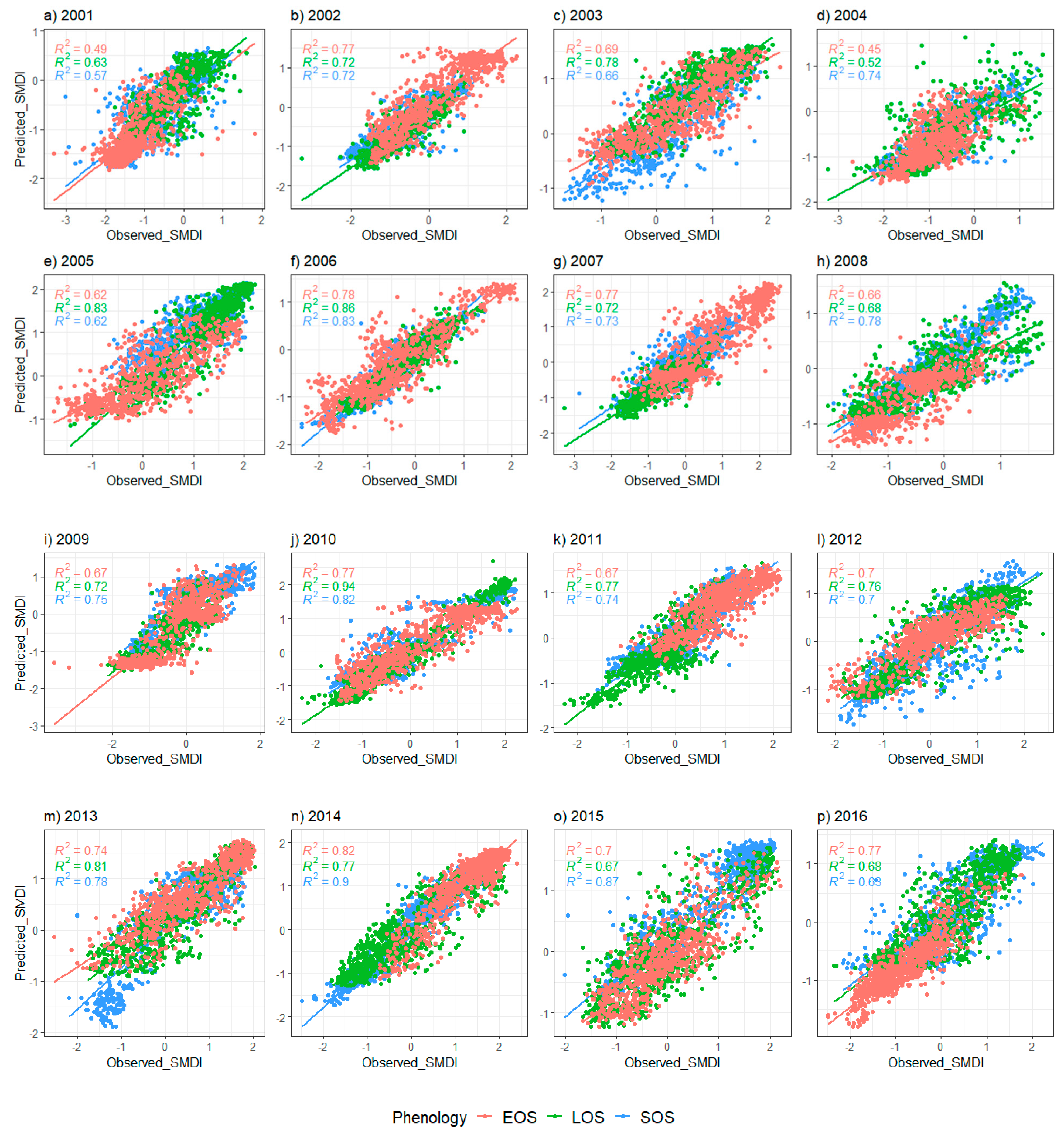
3.1. Deep Learning and Machine Learning Model Performance with Observed Data and Its Statistical Comparison Using Test Data Set in Detecting Drought Pattern
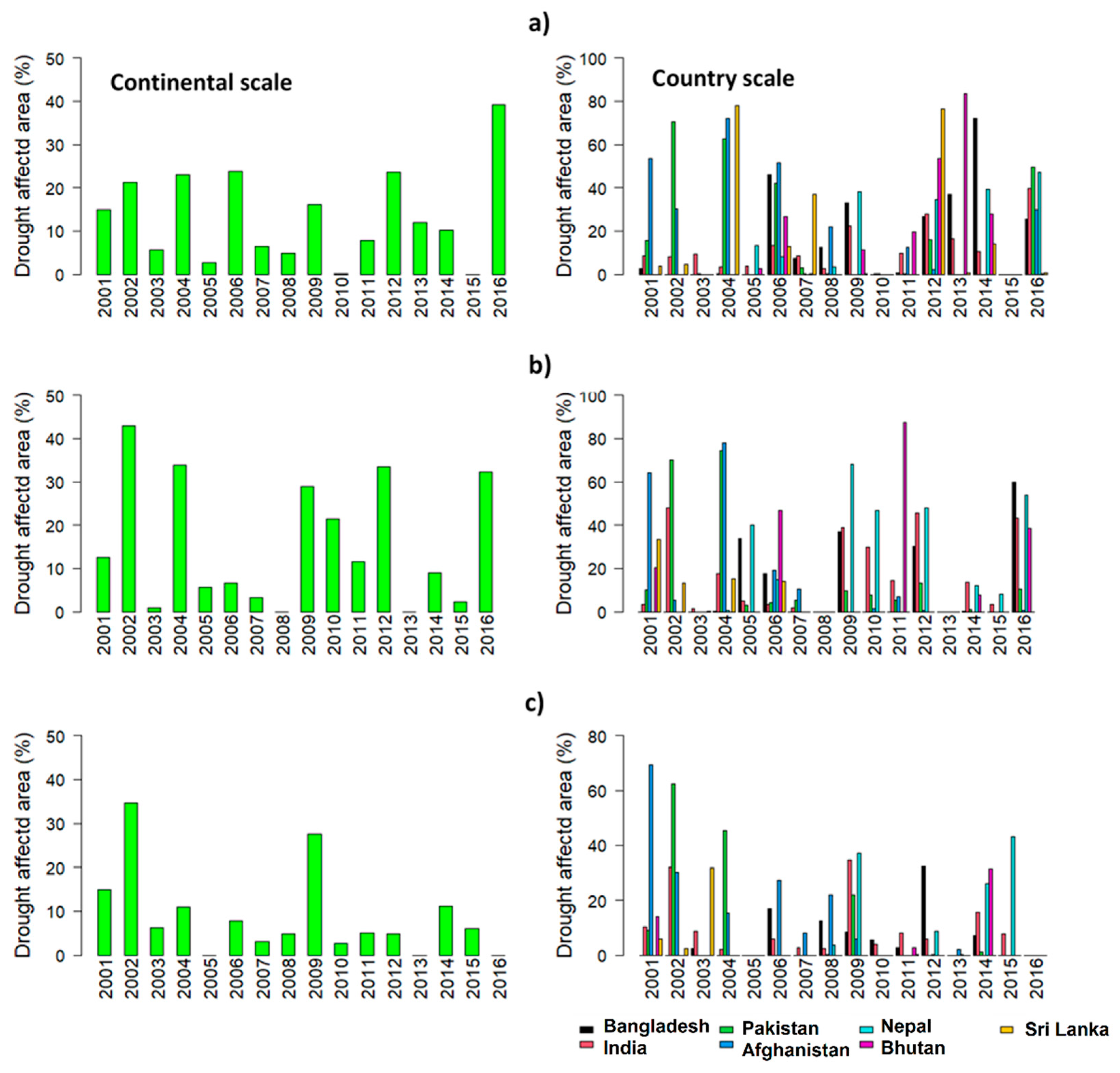
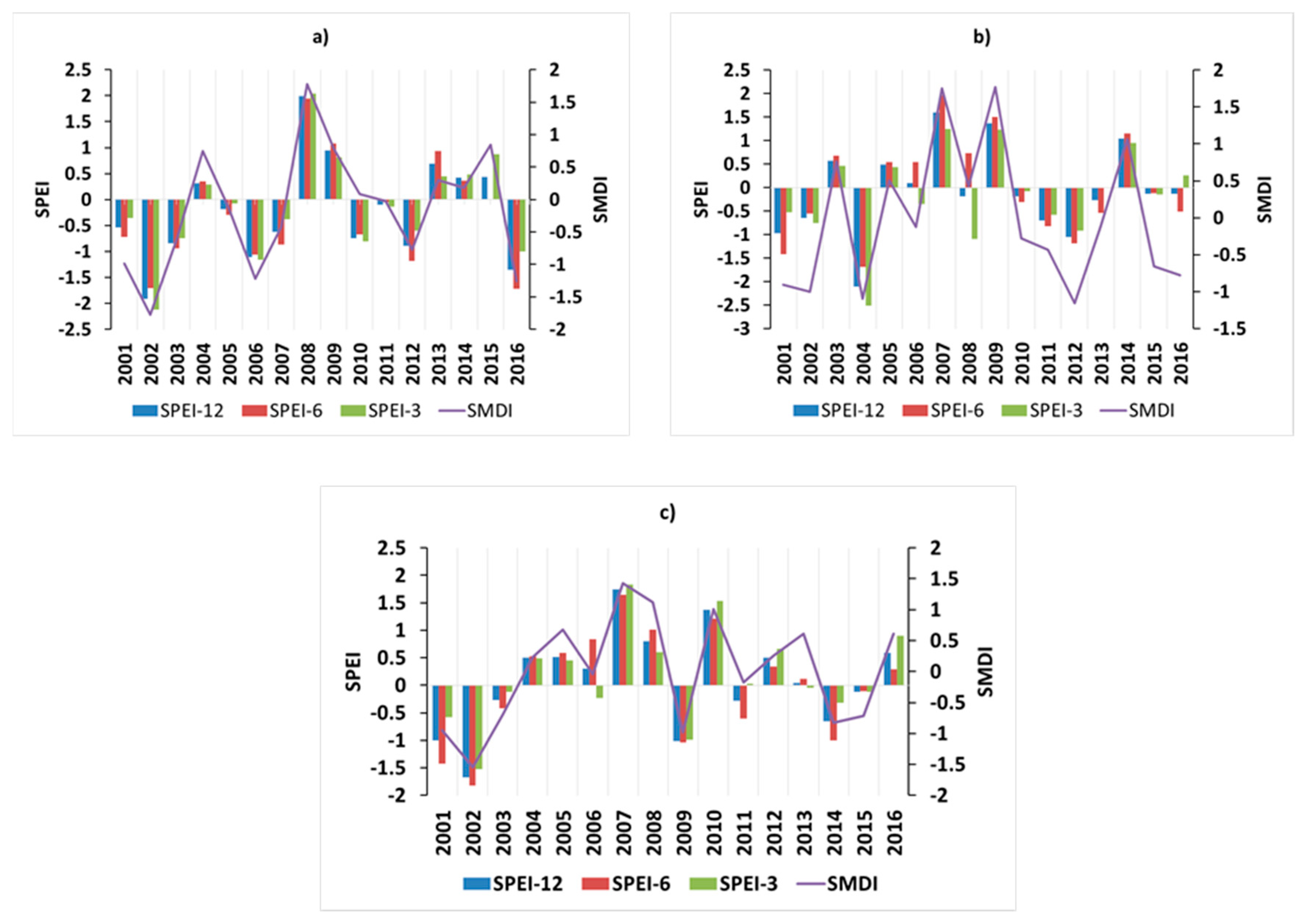
3.2. Spatiotemporal Pattern of Drought Based on SMDI Using a Deep Learning Model during Three Crop Phenology Stages
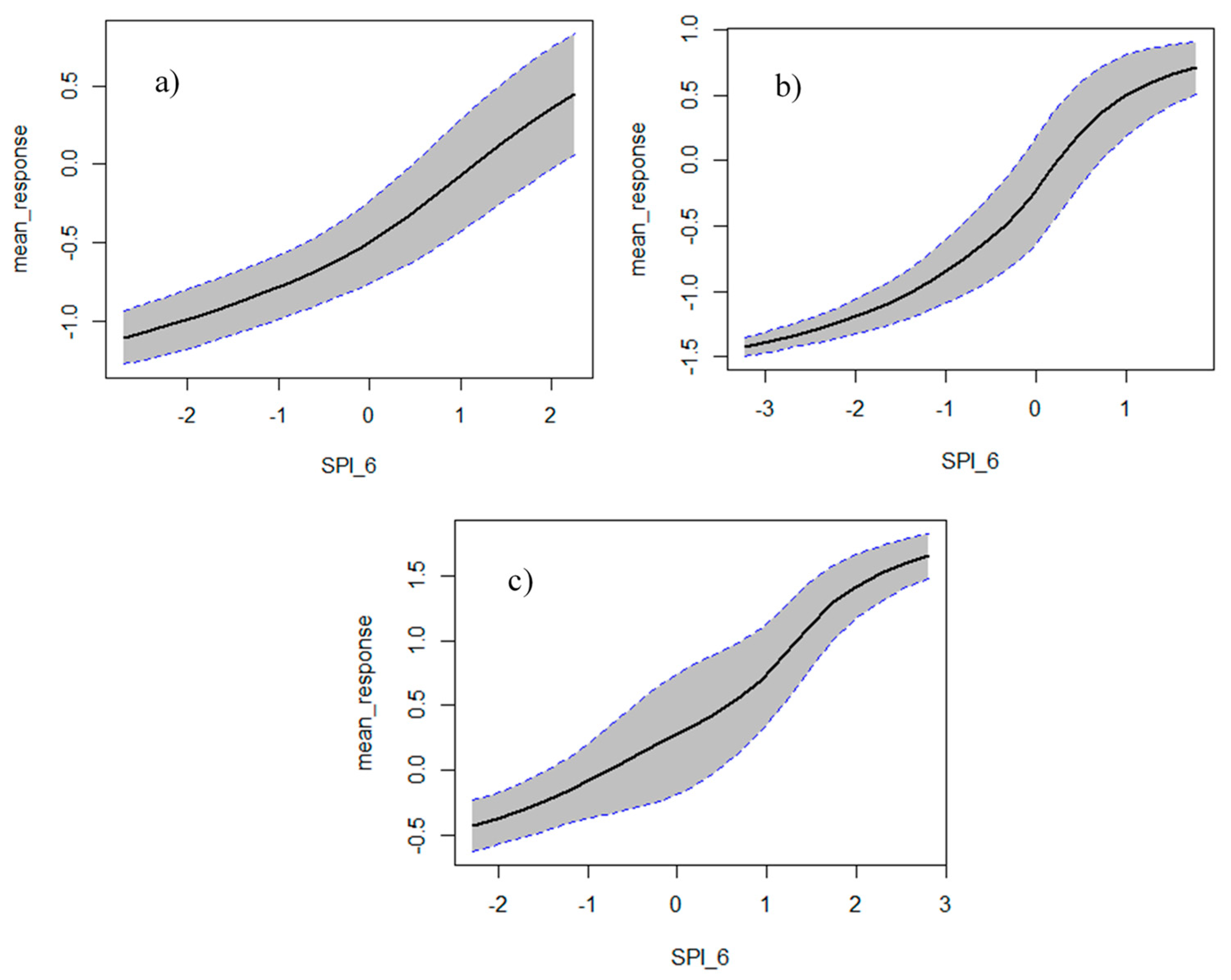
3.3. Uncertainties in SMDI Analysis by DFNN Model
4. Discussion
4.1. Model Comparison and Performance
4.2. Drought Variation in Three Phenology Stages
4.3. SMDI Prediction and Drought Severity Assessment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Model | Parameters |
|---|---|
| DRF | training_frame = train, validation_frame = valid, model_id = “Random forest”, ntrees = 300, learn_rate = 0.3, max_depth = 30, sample_rate = 0.7, col_sample_rate = 0.7, stopping_rounds = 2, stopping_tolerance = 0.001, score_each_iteration = T, nfolds =10, fold_assignment = “Random”, max_depth = 30, keep_cross_validation_fold_assignment = T, seed = 125, stopping_metric = “RMSE” |
| GBM | training_frame = train, validation_frame = valid, ntrees = 300, learn_rate = 0.3, max_depth = 30, sample_rate = 0.7, col_sample_rate = 0.7, stopping_rounds = 2, stopping_tolerance = 0.001, score_each_iteration = T, model_id = “gbm”, nfolds = 10, fold_assignment= “Random”, keep_cross_validation_fold_assignment = T, seed = 125, stopping_metric= “RMSE” |
References
- Heim, R.R., Jr. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A.; Nakhjiri, N.; Farahmand, A. Global integrated drought monitoring and prediction system. Sci. Data 2014, 1, 140001. [Google Scholar] [CrossRef]
- Aadhar, S.; Mishra, V. Data Descriptor: High-resolution near real-time drought monitoring in South Asia. Sci. Data 2017, 4, 170145. [Google Scholar] [CrossRef] [PubMed]
- Wilhite, D.A.; Hayes, M.J.; Knutson, C.L. Drought and Water Crises: Science, Technology, and Management Issues; CRC Press: Boca Raton, FL, USA, 2005; ISBN 9781420028386. [Google Scholar]
- Esfahanian, E.; Nejadhashemi, A.P.; Abouali, M.; Adhikari, U.; Zhang, Z.; Daneshvar, F.; Herman, M.R. Development and evaluation of a comprehensive drought index. J. Environ. Manag. 2017, 185, 31–43. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhou, Z.; Yao, F.; Yang, L.; Hao, C. Validating the modified perpendicular drought index in the North China region using in situ soil moisture measurement. IEEE Geosci. Remote Sens. Lett. 2015, 12, 542–546. [Google Scholar] [CrossRef]
- Tadesse, T.; Champagne, C.; Wardlow, B.D.; Hadwen, T.A.; Brown, J.F.; Demisse, G.B.; Bayissa, Y.A.; Davidson, A.M. Building the vegetation drought response index for Canada (VegDRI-Canada) to monitor agricultural drought: First results. GISci. Remote Sens. 2017, 54, 230–257. [Google Scholar] [CrossRef]
- Bhat, G.S. The Indian drought of 2002—A sub-seasonal phenomenon? Q. J. R. Meteorol. Soc. 2006, 132, 2583–2602. [Google Scholar] [CrossRef]
- Mishra, V.; Aadhar, S.; Asoka, A.; Pai, S.; Kumar, R. On the frequency of the 2015 monsoon season drought in the Indo-Gangetic Plain. Geophys. Res. Lett. 2016, 43, 12102–12112. [Google Scholar] [CrossRef]
- Ali, S.; Henchiri, M.; Yao, F.; Zhang, J. Analysis of vegetation dynamics, drought in relation with climate over South Asia from 1990 to 2011. Environ. Sci. Pollut. Res. 2019, 26, 11470–11481. [Google Scholar] [CrossRef]
- Ahmad, S.; Hussain, Z.; Qureshi, A.S.; Majeed, R.; Saleem, M. Drought Mitigation in Pakistan: Current Status and Options for Future Strategies, 3nd ed.; International Water Management Institute: Colombo, Sri Lanka, 2004. [Google Scholar]
- Dey, N.; Alam, M.; Sajjan, A.; Bhuiyan, M.; Ghose, L.; Ibaraki, Y.; Karim, F. Assessing Environmental and Health Impact of Drought in the Northwest Bangladesh. J. Environ. Sci. Nat. Resour. 2011, 4, 89–97. [Google Scholar] [CrossRef]
- Ali, S.; Tong, D.; Xu, Z.T.; Henchiri, M.; Wilson, K.; Siqi, S.; Zhang, J. Characterization of drought monitoring events through MODIS- and TRMM-based DSI and TVDI over South Asia during 2001–2017. Environ. Sci. Pollut. Res. 2019, 26, 33568–33581. [Google Scholar] [CrossRef] [PubMed]
- Feng, P.; Wang, B.; Liu, D.L.; Yu, Q. Machine learning-based integration of remotely-sensed drought factors can improve the estimation of agricultural drought in South-Eastern Australia. Agric. Syst. 2019, 173, 303–316. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Jang, E.; Rhee, J. Drought assessment and monitoring through blending of multi-sensor indices using machine learning approaches for different climate regions. Agric. For. Meteorol. 2016, 216, 157–169. [Google Scholar] [CrossRef]
- Quiring, S.M.; Ganesh, S. Evaluating the utility of the Vegetation Condition Index (VCI) for monitoring meteorological drought in Texas. Agric. For. Meteorol. 2010, 150, 330–339. [Google Scholar] [CrossRef]
- Hao, C.; Zhang, J.; Yao, F. Combination of multi-sensor remote sensing data for drought monitoring over Southwest China. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 270–283. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, S.; Zhang, H.; Bai, Y.; Zhang, J. Monitoring drought using composite drought indices based on remote sensing. Sci. Total Environ. 2020, 711, 134585. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, X.; Hain, C.R.; Liu, J.; Anderson, M.C. A Method for Objectively Integrating Soil Moisture Satellite Observations and Model Simulations Toward a Blended Drought Index. Water Resour. Res. 2018, 54, 6772–6791. [Google Scholar] [CrossRef]
- Chen, J.; Li, M.; Wang, W. Statistical uncertainty estimation using random forests and its application to drought forecast. Math. Probl. Eng. 2012, 2012, 915053. [Google Scholar] [CrossRef]
- Li, J.; Zhou, S.; Hu, R. Hydrological drought class transition using SPI and SRI time series by loglinear regression. Water Resour. Manag. 2016, 30, 669–684. [Google Scholar] [CrossRef]
- Khadr, M. Forecasting of meteorological drought using Hidden Markov Model (case study: The upper Blue Nile river basin, Ethiopia). Ain Shams Eng. J. 2016, 7, 47–56. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Shen, R.; Huang, A.; Li, B.; Guo, J. Construction of a drought monitoring model using deep learning based on multi-source remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 48–57. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Gong, H.; Li, X.; Wu, X. Soil Drought and Vegetation Response during 2001–2015 in North China Based on GLDAS and MODIS Data. Adv. Meteorol. 2018, 2018. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Borji, M.; Malekian, A.; Salajegheh, A.; Ghadimi, M. Multi-time-scale analysis of hydrological drought forecasting using support vector regression (SVR) and artificial neural networks (ANN). Arab. J. Geosci. 2016, 9, 725. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, G.; Wang, H. Improving meteorological drought monitoring capability over tropical and subtropical water-limited ecosystems: Evaluation and ensemble of the Microwave Integrated Drought Index. Environ. Res. Lett. 2019, 14, 44025. [Google Scholar] [CrossRef]
- Chiang, J.L.; Tsai, Y.S. Reservoir drought prediction using support vector machines. Appl. Mech. Mater. 2012, 145, 455–459. [Google Scholar] [CrossRef]
- Lee, C.S.; Sohn, E.; Park, J.D.; Jang, J.D. Estimation of soil moisture using deep learning based on satellite data: A case study of South Korea. GISci. Remote Sens. 2019, 56, 43–67. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, W.; Huang, W.; Hong, Z.; Meng, L. Upscaling of surface soil moisture using a deep learning model with VIIRS RDR. ISPRS Int. J. Geo-Inf. 2017, 6, 130. [Google Scholar] [CrossRef]
- Agana, N.A.; Homaifar, A. A deep learning based approach for long-term drought prediction. In Proceedings of the SoutheastCon 2017, Concord, NC, USA, 30 March–2 April 2017; pp. 1–8. [Google Scholar]
- Zhai, J.; Mondal, S.K.; Fischer, T.; Wang, Y.; Su, B.; Huang, J.; Tao, H.; Wang, G.; Ullah, W.; Uddin, M.J. Future drought characteristics through a multi-model ensemble from CMIP6 over South Asia. Atmos. Res. 2020, 246, 105111. [Google Scholar] [CrossRef]
- World Bank Population total: South Asia. Available online: https://data.worldbank.org/indicator/SP.POP.TOTL?locations=8S. (accessed on 3 November 2020).
- Miyan, M.A. Droughts in asian least developed countries: Vulnerability and sustainability. Weather Clim. Extrem. 2015, 7, 8–23. [Google Scholar] [CrossRef]
- Han, H.; Bai, J.; Yan, J.; Yang, H.; Ma, G. A combined drought monitoring index based on multi-sensor remote sensing data and machine learning. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (Collection 6); The University of Arizona: Tucson, AZ, USA, 2015. [Google Scholar]
- Park, S.; Park, S.; Im, J.; Rhee, J.; Shin, J.; Park, J.D. Downscaling GLDAS Soil moisture data in East Asia through fusion of Multi-Sensors by optimizing modified regression trees. Water 2017, 9, 332. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Bi, H.; Ma, J.; Zheng, W.; Zeng, J. Comparison of soil moisture in GLDAS model simulations and in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 2658–2678. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.; et al. The common land model. Glob. Chang. Newsl. 2003, 84, 1013–1024. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Jackson, T.J.; Rawls, W.J. Estimating soil water-holding capacities by linking the Food and Agriculture Organization soil map of the world with global pedon databases and continuous pedotransfer functions. Water Resour. Res. 2000, 36, 3653–3662. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Qamer, F.M.; Pedreros, D.; Murthy, M.S.R.; Wahid, S.M.; Shrestha, M. Evaluating the accuracy of Climate Hazard Group (CHG) satellite rainfall estimates for precipitation based drought monitoring in Koshi basin, Nepal. J. Hydrol. Reg. Stud. 2017, 13, 138–151. [Google Scholar] [CrossRef]
- Wu, W.; Li, Y.; Luo, X.; Zhang, Y.; Ji, X.; Li, X. Performance evaluation of the CHIRPS precipitation dataset and its utility in drought monitoring over Yunnan Province, China. Geomat. Nat. Hazards Risk 2019, 10, 2145–2162. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Adv. Glob. Chang. Res. 2020, 69, 625–653. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Hargreaves, G.L.; Hargreaves, G.H.; Paul Riley, J. Irrigation water requirements for senegal river basin. J. Irrig. Drain. Eng. 1985, 111, 265–275. [Google Scholar] [CrossRef]
- Ma, F.; Luo, L.; Ye, A.; Duan, Q. Drought characteristics and propagation in the Semiarid Heihe River Basin in Northwestern China. J. Hydrometeorol. 2019, 20, 59–77. [Google Scholar] [CrossRef]
- Van Loon, A.F. On the Propagation of Drought: How Climate and Catchment Characteristics Influence Hydrological Drought Development and Recovery. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, April 2013. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Du, L.; Tian, Q.; Yu, T.; Meng, Q.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D.; et al. The Drought Monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Vicente-Serrano, S.M.; López-Moreno, J.I. Hydrological response to different time scales of climatological drought: An evaluation of the Standardized Precipitation Index in a mountainous Mediterranean basin. Hydrol. Earth Syst. Sci. 2005, 9, 523–533. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Moorhead, J.E.; Gowda, P.H.; Singh, V.P.; Porter, D.O.; Marek, T.H.; Howell, T.A.; Stewart, B.A. Identifying and Evaluating a Suitable Index for Agricultural Drought Monitoring in the Texas High Plains. J. Am. Water Resour. Assoc. 2015, 51, 807–820. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K.; Zhao, S. Monitoring global land surface drought based on a hybrid evapotranspiration model. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 447–457. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Sp. Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Kogan, F.N. Satellite-observed sensitivity of world land ecosystems to El Niño/La Niña. Remote Sens. Environ. 2000, 74, 445–462. [Google Scholar] [CrossRef]
- Kogan, F.N. Global Drought Watch from Space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Prodhan, F.A.; Zhang, J.; Bai, Y.; Pangali Sharma, T.P.; Koju, U.A. Monitoring of drought condition and risk in bangladesh combined data from satellite and ground meteorological observations. IEEE Access 2020, 8, 93264–93282. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A. Chapter 12 Monitoring Drought Using the Standardized Precipitation Index. Available online: http://digitalcommons.unl.edu/droughtfacpub/70 (accessed on 11 September 2020).
- Guttman, N.B. Comparing the palmer drought index and the standardized precipitation index. J. Am. Water Resour. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Singh, R.P.; Roy, S.; Kogan, F. Vegetation and temperature condition indices from NOAA AVHRR data for drought monitoring over India. Int. J. Remote Sens. 2003, 24, 4393–4402. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef]
- Carrão, H.; Russo, S.; Sepulcre-Canto, G.; Barbosa, P. An empirical standardized soil moisture index for agricultural drought assessment from remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 74–84. [Google Scholar] [CrossRef]
- Bao, G.; Chen, J.; Chopping, M.; Bao, Y.; Bayarsaikhan, S.; Dorjsuren, A.; Tuya, A.; Jirigala, B.; Qin, Z. Geoinformation Dynamics of net primary productivity on the Mongolian Plateau: Joint regulations of phenology and drought. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 85–97. [Google Scholar] [CrossRef]
- Forkel, M.; Wutzler, T. Greenbrown-Land Surface Phenology and Trend Analysis. A Package for the R Software, version 2.2; Wien, Austria. 2015. Available online: http://greenbrown.r-forge.r-project.org/ (accessed on 1 January 2021).
- Nisbet, R.; Elder, J.; Miner, G. Handbook of Statistical Analysis and Data Mining Applications, 2nd ed.; Academic Press: London, UK, 2009; ISBN 9781787284395. [Google Scholar]
- Candel, A.; Parmar, V.; LeDell, E.; Arora, A. Deep Learning with H2O, 5th ed.; H2O. ai Inc.: Mountain View, CA, USA, 2016. [Google Scholar]
- Chang, N.B.; Bai, K. Multisensor Data Fusion and Machine Learning for Environmental Remote Sensing; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781498774345. [Google Scholar]
- Mann, H.B. Non-Parametric Test Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin & Company Limited: London, UK, 1984. [Google Scholar]
- Hossain, M.S.; Roy, K.; Datta, D.K. Spatial and temporal variability of rainfall over the south-west coast of Bangladesh. Climate 2014, 2, 28–46. [Google Scholar] [CrossRef]
- Blain, G.C. The influence of nonlinear trends on the power of the trend-free pre-whitening approach. Acta Sci. Agron. 2015, 37, 21–28. [Google Scholar] [CrossRef]
- Derdous, O.; Bouguerra, H.; Tachi, S.E.; Bouamrane, A. A monitoring of the spatial and temporal evolutions of aridity in northern Algeria. Theor. Appl. Climatol. 2020, 142, 1191–1198. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Radaković, M.G.; Sipos, G.; Mezősi, G.; Gavrilov, G.; Lukić, T.; Basarin, B.; Benyhe, B.; Fiala, K.; Kozák, P.; et al. Aridity in the central and southern Pannonian basin. Atmosphere 2020, 11, 1269. [Google Scholar] [CrossRef]
- Neeti, N.; Eastman, J.R. A Contextual Mann-Kendall Approach for the Assessment of Trend Significance in Image Time Series. Trans. GIS 2011, 15, 599–611. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Evans, M.J.S.; Jeffrey, A.; Evans, S.; Murphy, M.A.; Ram, K. R Package ‘spatialEco’, version 1.3-5. 2021. Available online: https://cran.r-project.org/web/packages/spatialEco/spatialEco.pdf (accessed on 1 January 2021).
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Im, J.; Park, S.; Rhee, J.; Baik, J.; Choi, M. Downscaling of AMSR-E soil moisture with MODIS products using machine learning approaches. Environ. Earth Sci. 2016, 75, 1120. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks, 1st ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1996; ISBN 978-3-642-61068-4. [Google Scholar]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Jain, H.; Serrao, R.; Tripathy, B.K. Hybrid Intelligence Techniques for Handwritten Digit Recognition. In Hybrid Intelligent Techniques for Pattern Analysis and Understanding; Bhattacharyya, S., Mukherjee, A., Pan, I., Dutta, P., Bhaumik, A.K., Eds.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 23–45. ISBN 978-1-4987-6935-8. [Google Scholar]
- Mujumdar, M.; Bhaskar, P.; Ramarao, M.V.S.; Uppara, U.; Goswami, M.; Borgaonkar, H.; Chakraborty, S.; Ram, S. Droughts and Floods. In Assessment of Climate Change over the Indian Region: A Report of the Ministry of Earth Sciences (MoES), Government of India; Krishnan, R., Sanjay, J., Gnanaseelan, C., Mujumdar, M., Kulkarni, A., Chakraborty, S., Eds.; Springer: Singapore, 2020; pp. 117–142. ISBN 9789811543272. [Google Scholar]
- Neena, J.M.; Suhas, E.; Goswami, B.N. Leading role of internal dynamics in the 2009 Indian summer monsoon drought. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Krishnan, R.; Kumar, V.; Sugi, M.; Yoshimura, J. Internal feedbacks from monsoon-midlatitude interactions during droughts in the Indian summer monsoon. J. Atmos. Sci. 2009, 66, 553–578. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Thomas, A.; Simon, A.; Kumar, V. Desert air incursions, an overlooked aspect, for the dry spells of the Indian summer monsoon. J. Atmos. Sci. 2010, 67, 3423–3441. [Google Scholar] [CrossRef]
- Rao, S.A.; Chaudhari, H.S.; Pokhrel, S.; Goswami, B.N. Unusual central Indian drought of summer monsoon 2008: Role of southern tropical Indian Ocean warming. J. Clim. 2010, 23, 5163–5174. [Google Scholar] [CrossRef]
- Roxy, M.K.; Ghosh, S.; Pathak, A.; Athulya, R.; Mujumdar, M.; Murtugudde, R.; Terray, P.; Rajeevan, M. A threefold rise in widespread extreme rain events over central India. Nat. Commun. 2017, 8, 708. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar] [CrossRef]
- Hao, C.; Zhang, J.; Yao, F. Multivariate drought frequency estimation using copula method in Southwest China. Theor. Appl. Climatol. 2017, 127, 977–991. [Google Scholar] [CrossRef]
- Kalisa, W.; Zhang, J.; Igbawua, T.; Ujoh, F.; Ebohon, O.J.; Namugize, J.N.; Yao, F. Spatio-temporal analysis of drought and return periods over the East African region using Standardized Precipitation Index from 1920 to 2016. Agric. Water Manag. 2020, 237, 106195. [Google Scholar] [CrossRef]
- Krishnan, R.; Ramesh, K.V.; Samala, B.K.; Meyers, G.; Slingo, J.M.; Fennessy, M.J. Indian Ocean-monsoon coupled interactions and impending monsoon droughts. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Sinha, A.; Berkelhammer, M.; Stott, L.; Mudelsee, M.; Cheng, H.; Biswas, J. The leading mode of Indian Summer Monsoon precipitation variability during the last millennium. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Mujumdar, M.; Sooraj, K.P.; Krishnan, R.; Preethi, B.; Joshi, M.K.; Varikoden, H.; Singh, B.B.; Rajeevan, M. Anomalous convective activity over sub-tropical east Pacific during 2015 and associated boreal summer monsoon teleconnections. Clim. Dyn. 2017, 48, 4081–4091. [Google Scholar] [CrossRef]
- Krishnan, R.; Sabin, T.P.; Vellore, R.; Mujumdar, M.; Sanjay, J.; Goswami, B.N.; Hourdin, F.; Dufresne, J.L.; Terray, P. Deciphering the desiccation trend of the South Asian monsoon hydroclimate in a warming world. Clim. Dyn. 2016, 47, 1007–1027. [Google Scholar] [CrossRef]
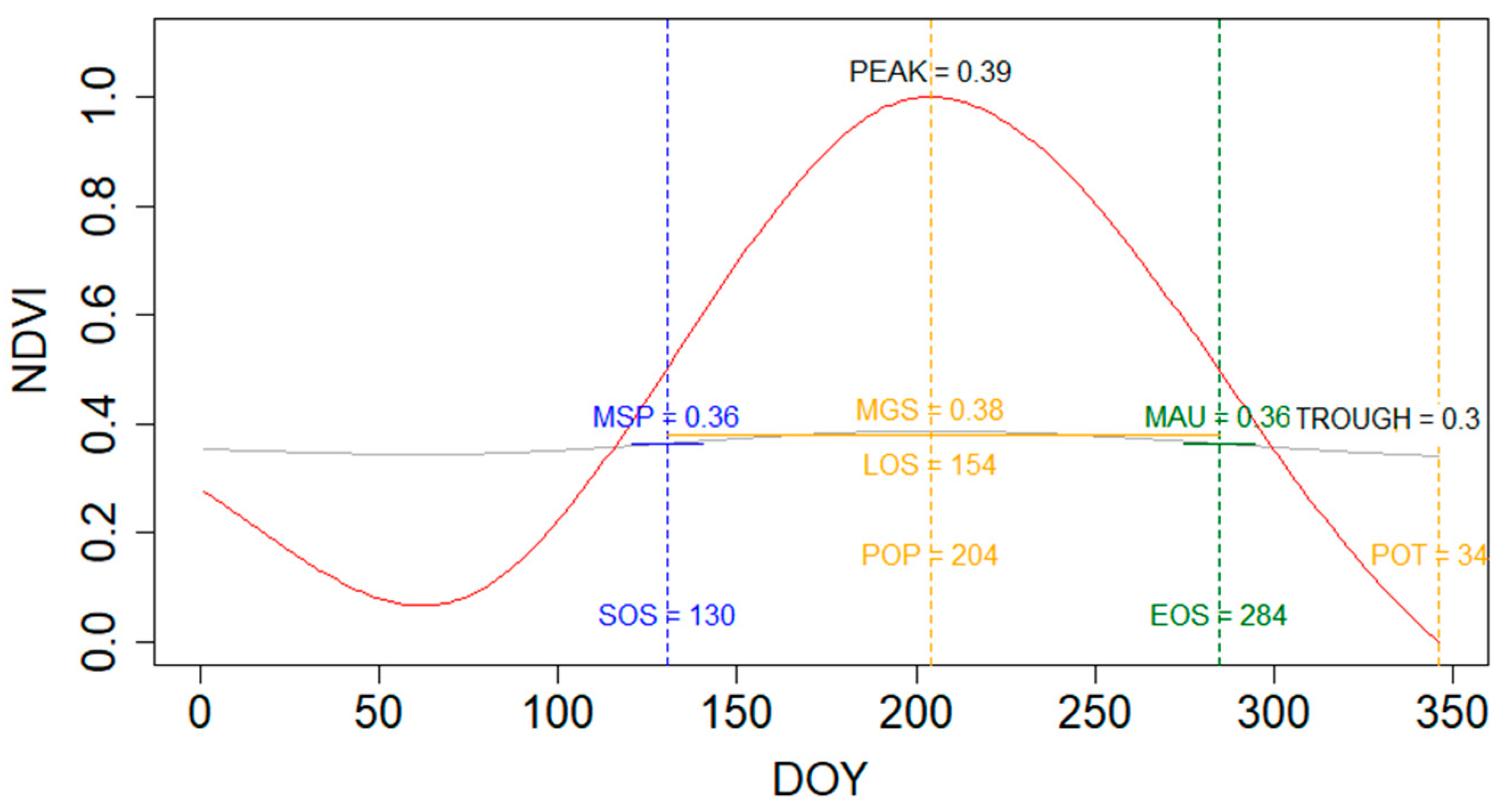






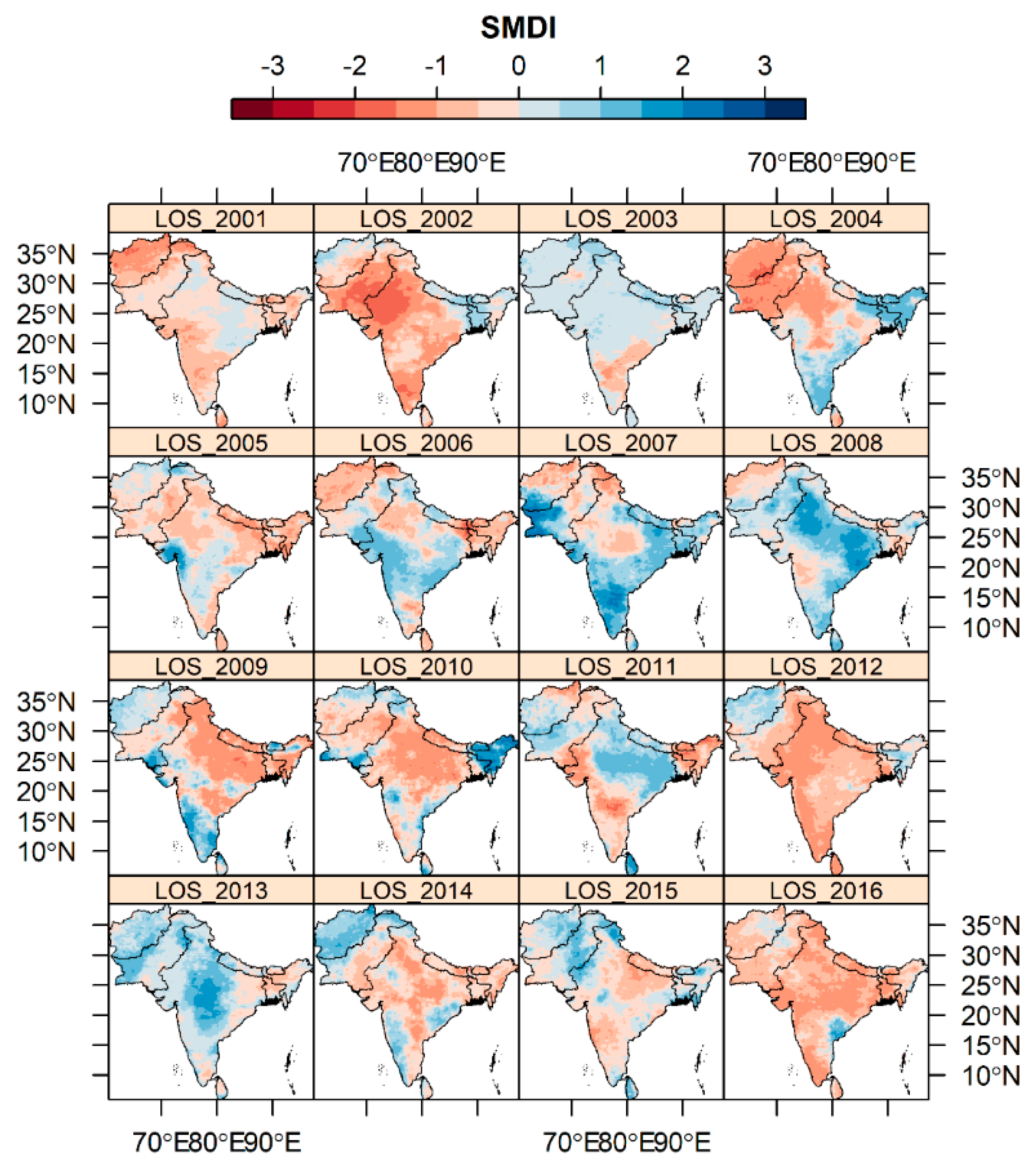
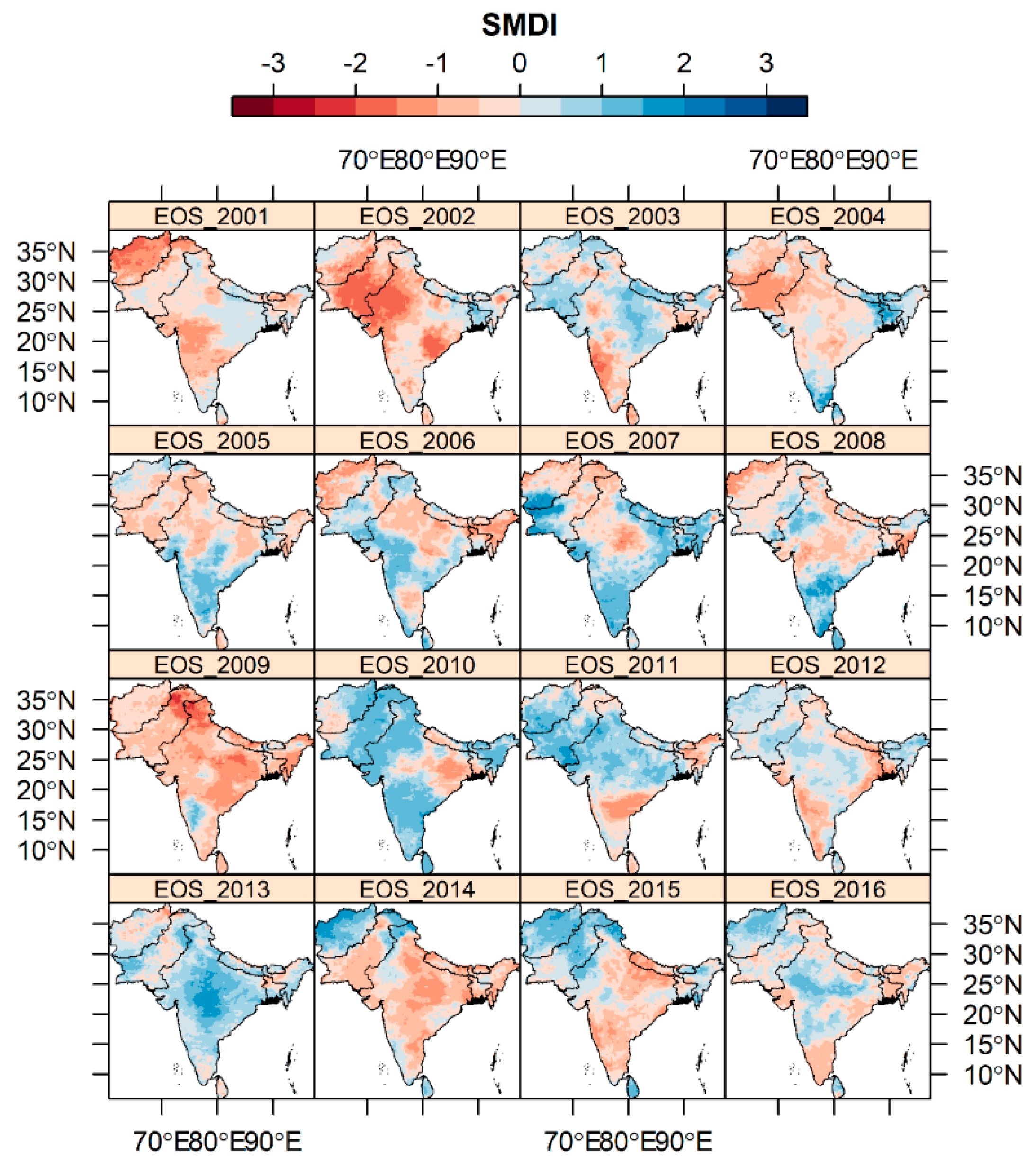
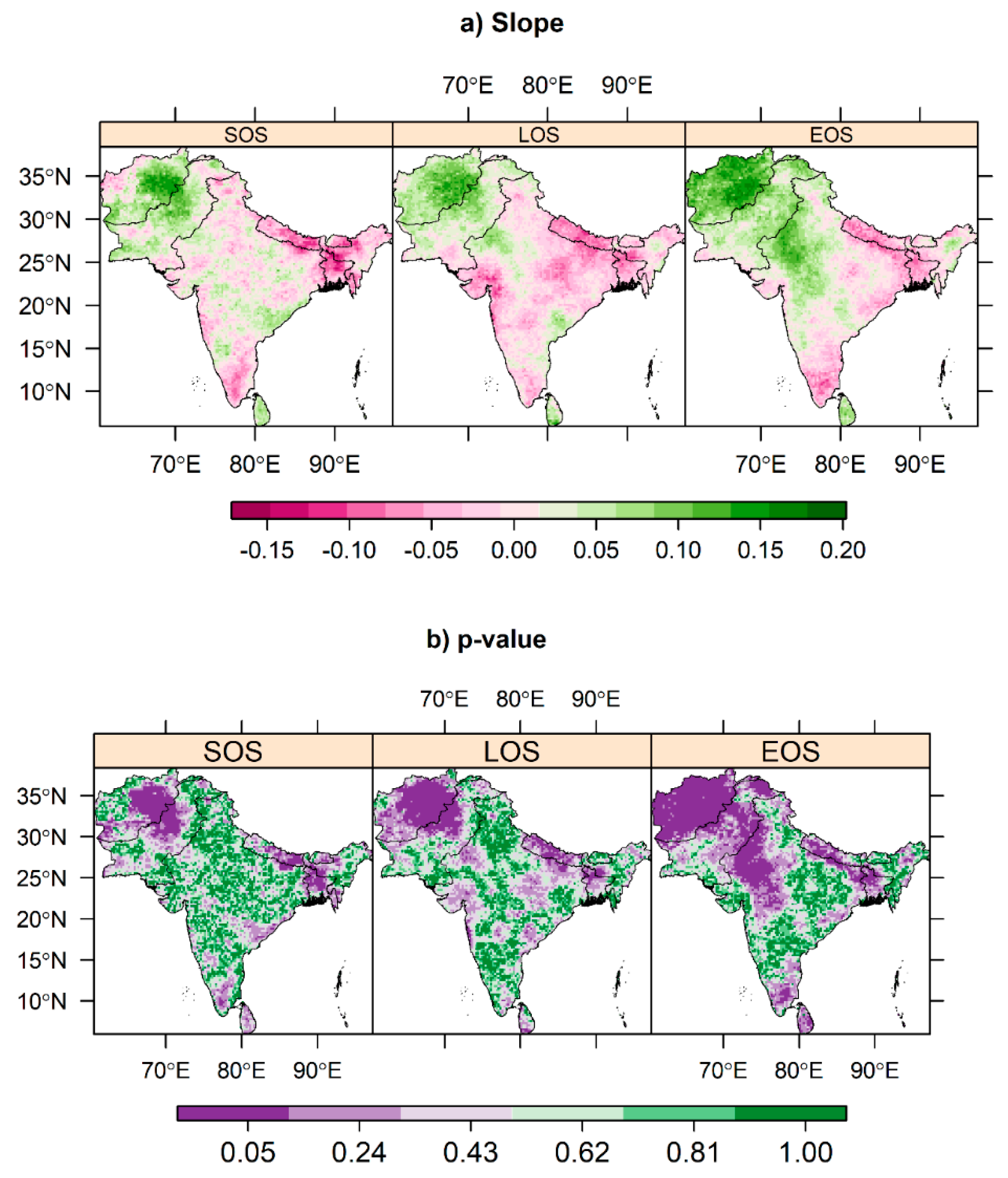

| Data Sources | Data Type | Variables | Temporal Resolution | Spatial Resolution | Coverage |
|---|---|---|---|---|---|
| MODIS | MOD13A1 MOD11A2 | Surface reflectance | 16 days (composite) | 500 m | Global |
| MERIS and SPOT-Vegetation | ESA CCI-LC | Land cover classification | No time series | 300 m | Global |
| GLDAS-NOAA | GLDAS_NOAH025_M_2.1 | Soil moisture, evapotranspiration, and potential evapotranspiration | Monthly | 0.25° × 0.25° | Global |
| CHIRPS from climate hazard center | CHIRPS-2.0 | Precipitation | Monthly | 0.25° × 0.25° | 60N to 60S |
| AVHRR-GIMMS | GIMMS-NDVI | NDVI | 15 days (composite) | 1/12° × 1/12° | Global |
| Type of Variable | Factors | Drought Index | Formula | References |
|---|---|---|---|---|
| Predictor variables | Precipitation | PCI | is the precipitation in a month, and are maximum and minimum precipitation in a month) | [30] |
| PAI | is the precipitation in a month, and is the average annual precipitation in a month) | [25] | ||
|
SPI-3 SPI-6 SPI-12 | (k represents precipitation probability function; , , , , , and are constant) | [56,57] | ||
|
SPEI-3 SPEI-6 SPEI-12 | (w is defined as climatic water balance calculated based on the difference between precipitation and reference evapotranspiration; and | [58,59] | ||
| Soil | EDI | (EDI is evaporative drought index, ET represents evapotranspiration, PET denotes potential evapotranspiration in the corresponding month in the research year) | [60] | |
| Vegetation | VCI | is the NDVI value of a certain month, are the minimum and maximum values of NDVI in the corresponding month in the research year) | [61] | |
| VHI | (α denotes constant value equals to 0.5) | [62] | ||
| TCI | is the LST value of a month, and are the maximum and minimum values of LST for the corresponding month in the study year) | [63] | ||
| Response variable | SMDI | represents the SMDI for first month and denotes soil moisture anomaly of month ) are long term maximum, minimum, and median soil moisture at month ) | [26,27] | |
| Drought Class | SMDI Range |
|---|---|
| Extreme Dry | |
| Severe Dry | |
| Moderate Dry | |
| Near Normal | |
| Wet condition |
| Epoch | Samples | Training Speed (obs/sec) | Training-R2 | Validation-R2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SOS | LOS | EOS | SOS | LOS | EOS | SOS | LOS | EOS | SOS | LOS | EOS | |
| 1 | 5501 | 5499 | 5500 | 592 | 595 | 768 | 0.622 | 0.550 | 0.684 | 0.749 | 0.555 | 0.689 |
| 2 | 11,002 | 10,998 | 11,000 | 671 | 696 | 861 | 0.575 | 0.565 | 0.737 | 0.703 | 0.569 | 0.737 |
| 3 | 16,503 | 16,497 | 16,500 | 724 | 766 | 929 | 0.643 | 0.608 | 0.755 | 0.770 | 0.611 | 0.745 |
| 4 | 22,004 | 21,996 | 22,000 | 770 | 820 | 989 | 0.502 | 0.757 | 0.744 | 0.523 | 0.762 | 0.742 |
| 5 | 27,505 | 27,495 | 27,500 | 808 | 866 | 1041 | 0.694 | 0.808 | 0.759 | 0.720 | 0.801 | 0.752 |
| 6 | 33,006 | 32,994 | 33,000 | 840 | 902 | 1084 | 0.778 | 0.870 | 0.784 | 0.816 | 0.873 | 0.775 |
| 7 | 38,507 | 38,493 | 38,500 | 871 | 937 | 1114 | 0.791 | 0.875 | 0.762 | 0.817 | 0.878 | 0.749 |
| 8 | 44,008 | 43,992 | 44,000 | 900 | 970 | 1151 | 0.798 | 0.881 | 0.769 | 0.815 | 0.878 | 0.754 |
| 9 | 49,509 | 49,491 | 49,500 | 929 | 1001 | 1185 | 0.801 | 0.889 | 0.784 | 0.818 | 0.880 | 0.775 |
| 10 | 55,010 | 54,990 | 55,000 | 956 | 1030 | 1216 | 0.811 | 0.891 | 0.793 | 0.830 | 0.892 | 0.778 |
| 11 | 60,511 | 60,489 | 60,500 | 981 | 1039 | 1244 | 0.809 | 0.881 | 0.778 | 0.828 | 0.886 | 0.761 |
| Phenology | Model | Test Data | ||
|---|---|---|---|---|
| RMSE | MAE | MSE | ||
| SOS | DFNN | 0.417 | 0.310 | 0.174 |
| GBM | 0.439 | 0.330 | 0.193 | |
| DRF | 0.443 | 0.318 | 0.196 | |
| LOS | DFNN | 0.486 | 0.359 | 0.237 |
| GBM | 0.514 | 0.381 | 0.264 | |
| DRF | 0.517 | 0.399 | 0.268 | |
| EOS | DFNN | 0.466 | 0.354 | 0.217 |
| GBM | 0.501 | 0.378 | 0.251 | |
| DRF | 0.514 | 0.403 | 0.265 | |
| Variables | Relative Importance | Percentage | ||||
|---|---|---|---|---|---|---|
| SOS | LOS | EOS | SOS | LOS | EOS | |
| SPI-6 | 1.0 | 1.0 | 1.0 | 15.60 | 20.40 | 19.30 |
| SPI-3 | 0.918 | 0.671 | 0.578 | 8.18 | 9.40 | 6.16 |
| SPI-12 | 0.538 | 0.435 | 0.451 | 6.62 | 4.30 | 5.14 |
| SPEI-6 | 0.910 | 0.387 | 0.453 | 14.20 | 8.70 | 8.71 |
| SPEI-3 | 0.457 | 0.323 | 0.440 | 4.12 | 4.38 | 5.33 |
| SPEI-12 | 0.238 | 0.211 | 0.291 | 3.08 | 2.22 | 3.54 |
| PCI | 0.393 | 0.463 | 0.677 | 5.20 | 9.40 | 13.12 |
| EDI | 0.701 | 0.502 | 0.465 | 10.90 | 10.20 | 9.00 |
| PAI | 0.593 | 0.367 | 0.396 | 9.20 | 7.50 | 7.60 |
| TCI | 0.548 | 0.479 | 0.453 | 8.50 | 9.80 | 8.80 |
| VHI | 0.470 | 0.346 | 0.337 | 7.30 | 7.00 | 6.50 |
| VCI | 0.455 | 0.331 | 0.353 | 7.10 | 6.70 | 6.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prodhan, F.A.; Zhang, J.; Yao, F.; Shi, L.; Pangali Sharma, T.P.; Zhang, D.; Cao, D.; Zheng, M.; Ahmed, N.; Mohana, H.P. Deep Learning for Monitoring Agricultural Drought in South Asia Using Remote Sensing Data. Remote Sens. 2021, 13, 1715. https://doi.org/10.3390/rs13091715
Prodhan FA, Zhang J, Yao F, Shi L, Pangali Sharma TP, Zhang D, Cao D, Zheng M, Ahmed N, Mohana HP. Deep Learning for Monitoring Agricultural Drought in South Asia Using Remote Sensing Data. Remote Sensing. 2021; 13(9):1715. https://doi.org/10.3390/rs13091715
Chicago/Turabian StyleProdhan, Foyez Ahmed, Jiahua Zhang, Fengmei Yao, Lamei Shi, Til Prasad Pangali Sharma, Da Zhang, Dan Cao, Minxuan Zheng, Naveed Ahmed, and Hasiba Pervin Mohana. 2021. "Deep Learning for Monitoring Agricultural Drought in South Asia Using Remote Sensing Data" Remote Sensing 13, no. 9: 1715. https://doi.org/10.3390/rs13091715
APA StyleProdhan, F. A., Zhang, J., Yao, F., Shi, L., Pangali Sharma, T. P., Zhang, D., Cao, D., Zheng, M., Ahmed, N., & Mohana, H. P. (2021). Deep Learning for Monitoring Agricultural Drought in South Asia Using Remote Sensing Data. Remote Sensing, 13(9), 1715. https://doi.org/10.3390/rs13091715