Global Analysis of Atmospheric Transmissivity Using Cloud Cover, Aridity and Flux Network Datasets
Abstract
1. Introduction
2. Data and Methods
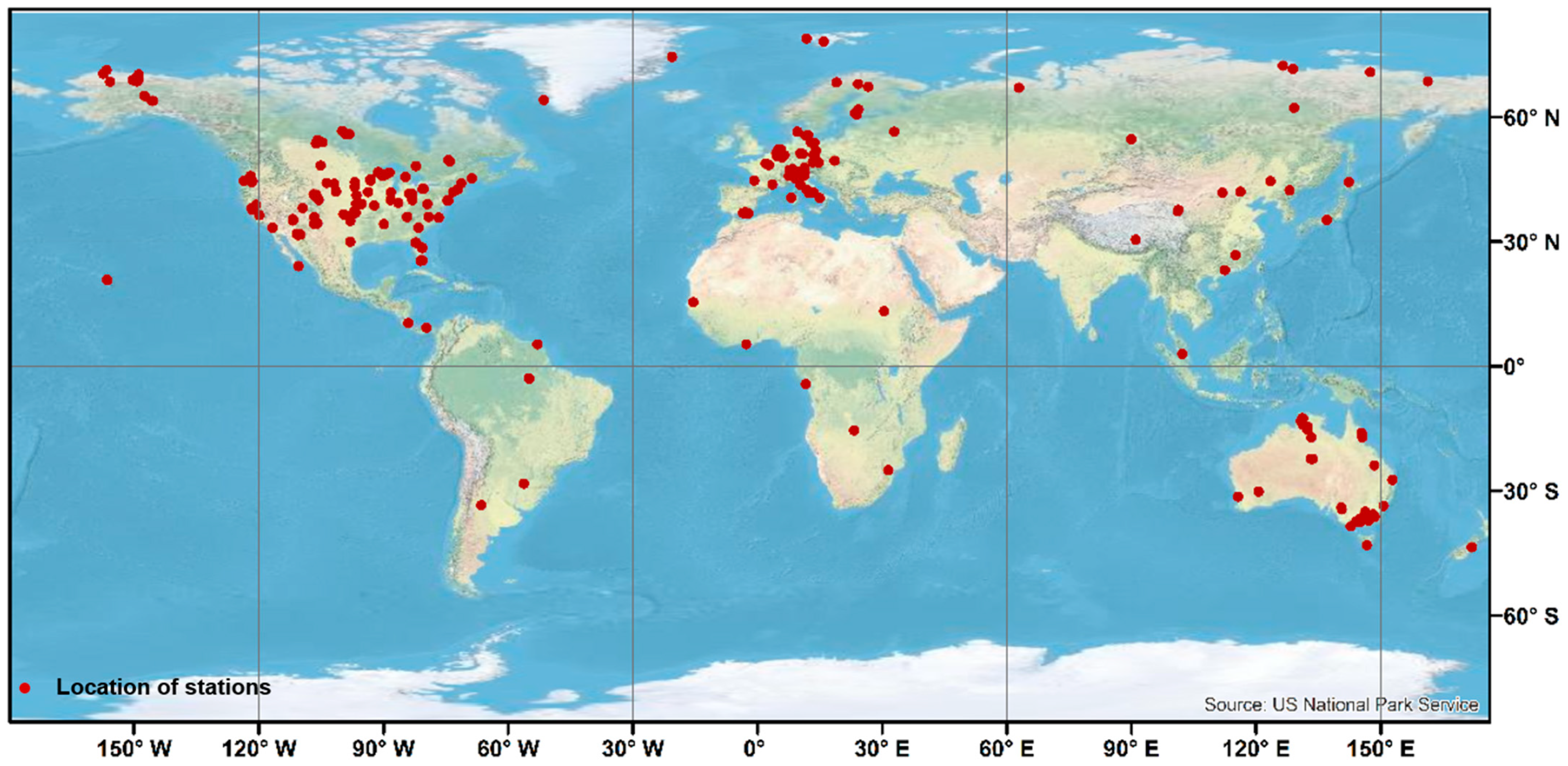
2.1. Data Source
2.2. Method
3. Results and Discussion
3.1. Latitudinal Pattern of Transmissivity and Cloud Cover
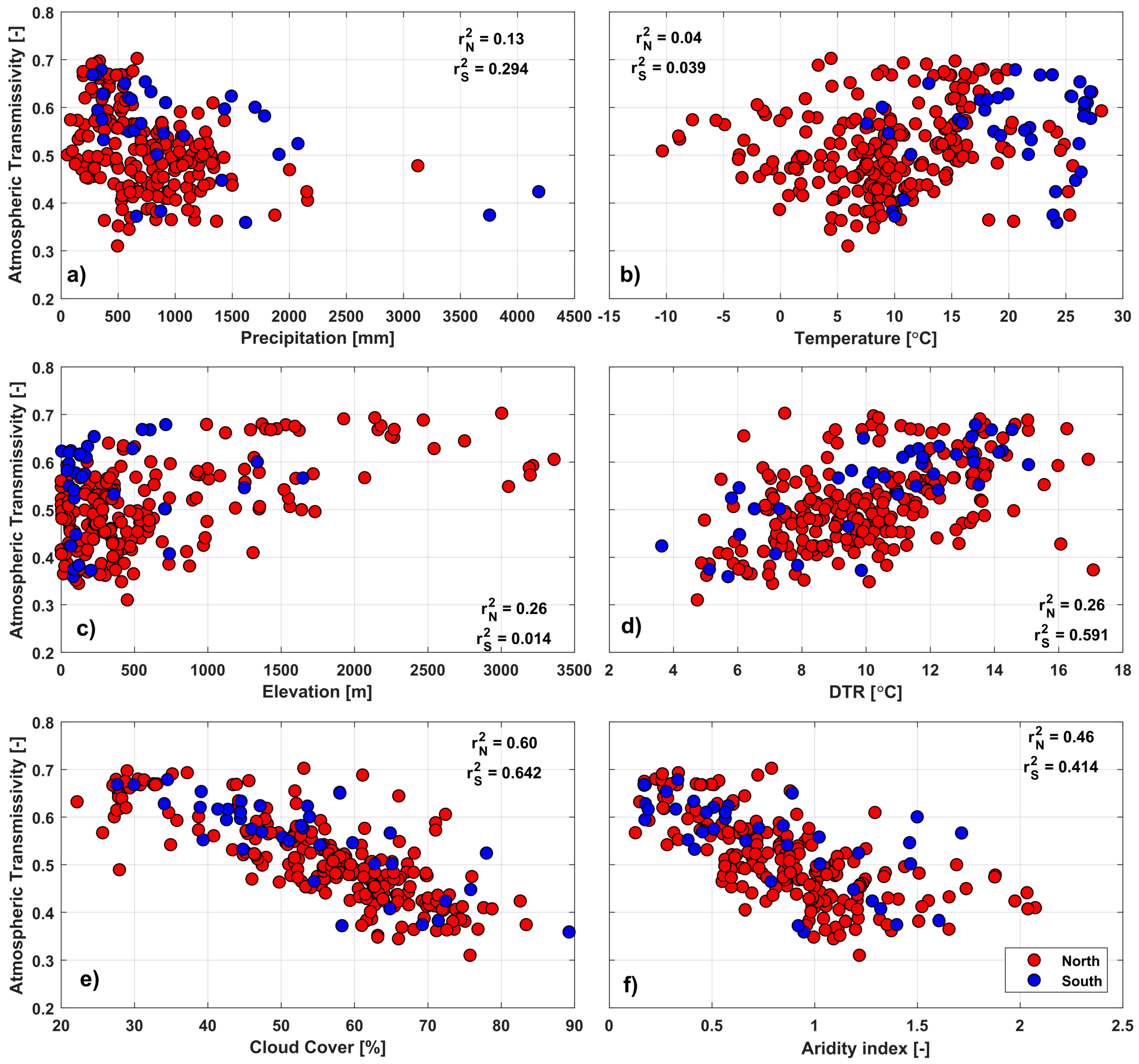
3.2. Transmissivity and Relationship with Other Factors
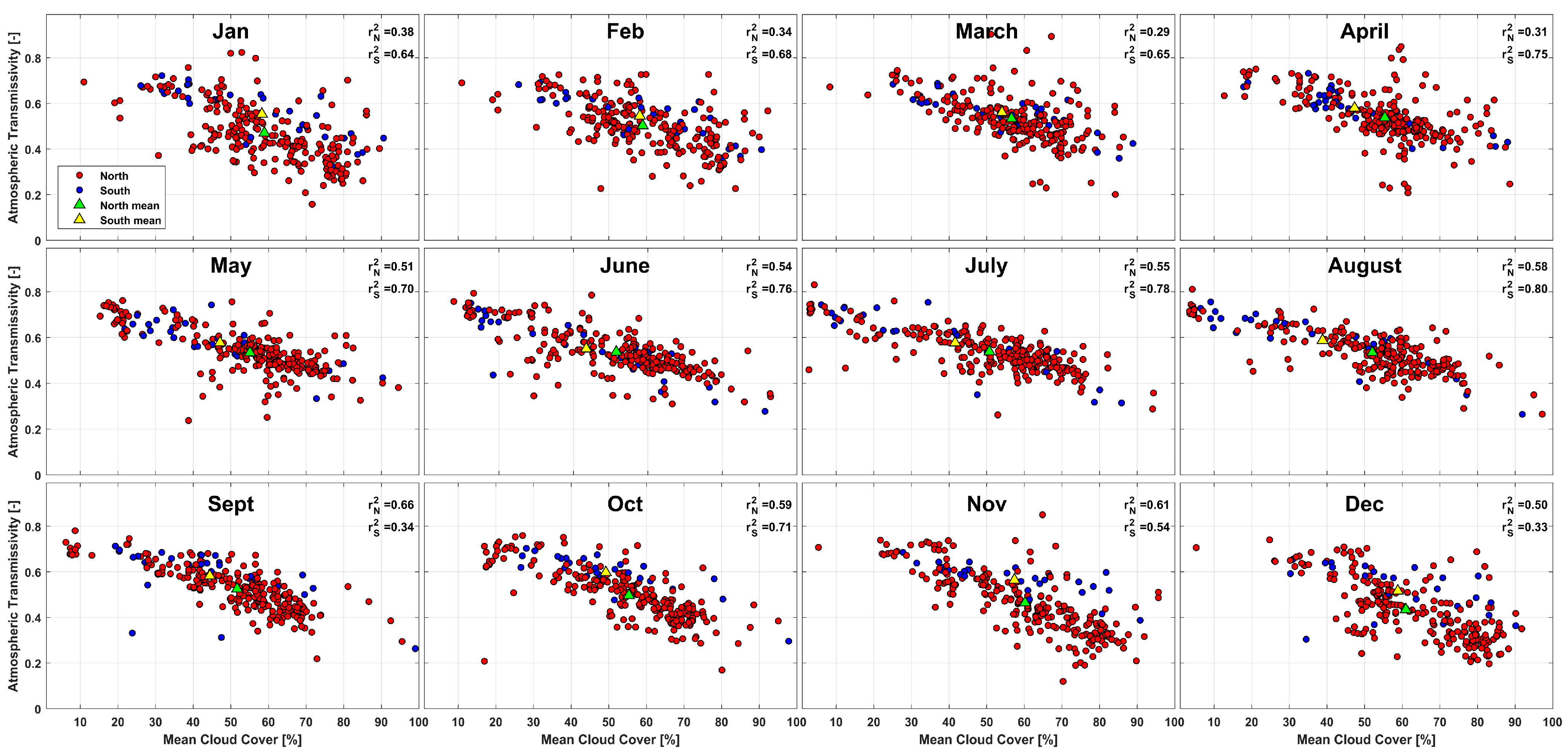
3.3. Monthly Variations of Transmissivity with Cloud Cover
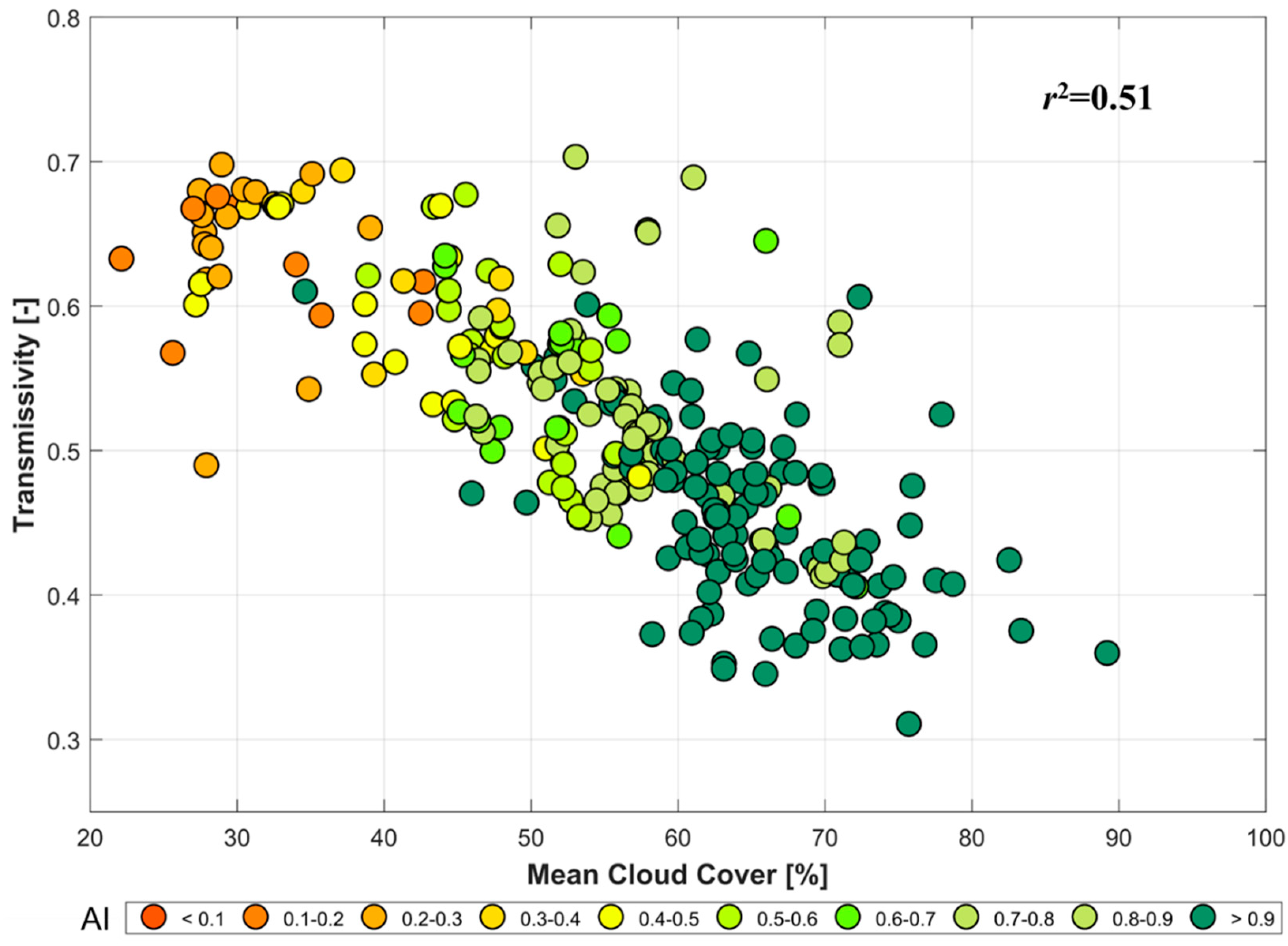
3.4. Embedded Relationship of Aridity and Cloud Cover with Atmospheric Transmissivity
3.5. Atmospheric Transmissivity Based on Köppen Classification
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dickinson, R.E. Land surface processes and climate—Surface albedos and energy balance. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 25, pp. 305–353. [Google Scholar]
- Baigorria, G.A.; Villegas, E.B.; Trebejo, I.; Carlos, J.F.; Quiroz, R. Atmospheric transmissivity: Distribution and empirical estimation around the central Andes. Int. J. Climatol. J. R. Meteorol. Soc. 2004, 24, 1121–1136. [Google Scholar] [CrossRef]
- Arora, V. Modeling vegetation as a dynamic component in soil-vegetation-atmosphere transfer schemes and hydrological models. Rev. Geophys. 2002, 40, 3-1–3-26. [Google Scholar] [CrossRef]
- Bonan, G. Ecological Climatology: Concepts and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Sellers, P.; Dickinson, R.; Randall, D.; Betts, A.; Hall, F.; Berry, J.; Collatz, G.; Denning, A.; Mooney, H.; Nobre, C. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef]
- Kumari, N.; Saco, P.M.; Rodriguez, J.F.; Johnstone, S.A.; Srivastava, A.; Chun, K.P.; Yetemen, O. The Grass Is Not Always Greener on the Other Side: Seasonal Reversal of Vegetation Greenness in Aspect-Driven Semiarid Ecosystems. Geophys. Res. Lett. 2020, 47, e2020GL088918. [Google Scholar] [CrossRef]
- Srivastava, A.; Saco, P.M.; Rodriguez, J.F.; Kumari, N.; Chun, K.P.; Yetemen, O. The role of landscape morphology on soil moisture variability in semi-arid ecosystems. Hydrol. Process. 2021, 35, e13990. [Google Scholar] [CrossRef]
- Hunt, L.; Kuchar, L.; Swanton, C. Estimation of solar radiation for use in crop modelling. Agric. For. Meteorol. 1998, 91, 293–300. [Google Scholar] [CrossRef]
- Mavromatis, T.; Jagtap, S. Estimating solar radiation for crop modeling using temperature data from urban and rural stations. Clim. Res. 2005, 29, 233–243. [Google Scholar] [CrossRef]
- Matsuda, Y.; Fujita, K.; Ageta, Y.; Sakai, A. Estimation of atmospheric transmissivity of solar radiation from precipitation in the Himalaya and the Tibetan Plateau. Ann. Glaciol. 2006, 43, 344–350. [Google Scholar] [CrossRef][Green Version]
- Almorox, J.; Hontoria, C.; Benito, M. Models for obtaining daily global solar radiation with measured air temperature data in Madrid (Spain). Appl. Energy 2011, 88, 1703–1709. [Google Scholar] [CrossRef]
- Moradi, I.; Mueller, R.; Perez, R. Retrieving daily global solar radiation from routine climate variables. Theor. Appl. Climatol. 2014, 116, 661–669. [Google Scholar] [CrossRef]
- Letu, H.; Shi, J.; Li, M.; Wang, T.; Shang, H.; Lei, Y.; Ji, D.; Wen, J.; Yang, K.; Chen, L. A review of the estimation of downward surface shortwave radiation based on satellite data: Methods, progress and problems. Sci. China Earth Sci. 2020, 63, 774–789. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Ibrakhimov, M.; Saito, L. Estimating daily global solar radiation by day of the year in six cities located in the Yucatán Peninsula, Mexico. J. Clean. Prod. 2017, 141, 75–82. [Google Scholar] [CrossRef]
- Zhao, N.; Zeng, X.; Han, S. Solar radiation estimation using sunshine hour and air pollution index in China. Energy Convers. Manag. 2013, 76, 846–851. [Google Scholar] [CrossRef]
- Kirmani, S.; Jamil, M.; Rizwan, M. Empirical correlation of estimating global solar radiation using meteorological parameters. Int. J. Sustain. Energy 2015, 34, 327–339. [Google Scholar] [CrossRef]
- Reddy, K.S.; Ranjan, M. Solar resource estimation using artificial neural networks and comparison with other correlation models. Energy Convers. Manag. 2003, 44, 2519–2530. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.; Sharma, J. Comparison of regression and artificial neural network models for estimation of global solar radiations. Renew. Sustain. Energy Rev. 2015, 52, 1294–1299. [Google Scholar] [CrossRef]
- Sjoberg, R.W.; Horn, B.K. Atmospheric effects in satellite imaging of mountainous terrain. Appl. Opt. 1983, 22, 1702–1716. [Google Scholar] [CrossRef]
- Tyson, P.; Gasse, F.; Bergonzini, L.; D’Abreton, P. Aerosols, atmospheric transmissivity and hydrological modelling of climatic change over Africa south of the equator. Int. J. Climatol. J. R. Meteorol. Soc. 1997, 17, 1651–1665. [Google Scholar] [CrossRef]
- Houghton, E. Climate Change 1995: The Science of Climate Change: Contribution of Working Group I to the Second Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 1996; Volume 2. [Google Scholar]
- Haywood, J.; Ramaswamy, V. Global sensitivity studies of the direct radiative forcing due to anthropogenic sulfate and black carbon aerosols. J. Geophys. Res. Atmos. 1998, 103, 6043–6058. [Google Scholar] [CrossRef]
- Twomey, S. The influence of pollution on the shortwave albedo of clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, cloud microphysics, and fractional cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef]
- Ramaswamy, V.; Boucher, O.; Haigh, J.; Hauglustine, D.; Haywood, J.; Myhre, G.; Nakajima, T.; Shi, G.; Solomon, S. Radiative forcing of climate. Clim. Chang. 2001, 349. [Google Scholar]
- Solomon, S.; Manning, M.; Marquis, M.; Qin, D. Climate Change 2007-the Physical Science Basis: Working Group I Contribution to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007; Volume 4. [Google Scholar]
- Greuell, W.; Genthon, C. Modelling land-ice surface mass balance. In Mass Balance of the Cryosphere: Observations and Modelling of Contemporary and Future Changes; Cambridge University Press: Cambridge, UK, 2004; Volume 117, p. 168. [Google Scholar]
- Angstrom, A. Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Matuszko, D. Influence of the extent and genera of cloud cover on solar radiation intensity. Int. J. Climatol. 2012, 32, 2403–2414. [Google Scholar] [CrossRef]
- Suehrcke, H.; Bowden, R.S.; Hollands, K. Relationship between sunshine duration and solar radiation. Sol. Energy 2013, 92, 160–171. [Google Scholar] [CrossRef]
- Molina, A.; Falvey, M.; Rondanelli, R. A solar radiation database for Chile. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. For. Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Goodin, D.G.; Hutchinson, J.; Vanderlip, R.L.; Knapp, M. Estimating solar irradiance for crop modeling using daily air temperature data. Agron. J. 1999, 91, 845–851. [Google Scholar] [CrossRef]
- Lee, K.H. Constructing a non-linear relationship between the incoming solar radiation and bright sunshine duration. Int. J. Climatol. 2010, 30, 1884–1892. [Google Scholar] [CrossRef]
- Sen, Z. Solar Energy Fundamentals and Modeling Techniques: Atmosphere, Environment, Climate Change and Renewable Energy; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Yu, L.; Zhang, M.; Wang, L.; Qin, W.; Lu, Y.; Li, J. Clear-sky solar radiation changes over arid and semi-arid areas in China and their determining factors during 2001–2015. Atmos. Environ. 2020, 223, 117198. [Google Scholar] [CrossRef]
- Rienecker, M.; Suarez, M.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newsl. 2016, 147, 5–6. [Google Scholar]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Yao, B.; Teng, S.; Lai, R.; Xu, X.; Yin, Y.; Shi, C.; Liu, C. Can atmospheric reanalyses (CRA and ERA5) represent cloud spatiotemporal characteristics? Atmos. Res. 2020, 244, 105091. [Google Scholar] [CrossRef]
- Hänsch, R.; Schulz, K.; Sörgel, U. Machine learning methods for remote sensing applications: An overview. Berlin: Earth Resources and Environmental Remote Sensing/GIS Applications IX. Inter. Soc. Opt. Photo. 2018, 10790, 1079002. [Google Scholar]
- Ma, R.; Letu, H.; Yang, K.; Wang, T.; Shi, C.; Xu, J.; Shi, J.; Shi, C.; Chen, L. Estimation of surface shortwave radiation from Himawari-8 satellite data based on a combination of radiative transfer and deep neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5304–5316. [Google Scholar] [CrossRef]
- Dhungel, R.; Aiken, R.; Evett, S.R.; Colaizzi, P.D.; Marek, G.; Moorhead, J.E.; Baumhardt, R.L.; Brauer, D.; Kutikoff, S.; Lin, X. Energy Imbalance and Evapotranspiration Hysteresis under an Advective Environment: Evidence from Lysimeter, Eddy Covariance, and Energy Balance Modelling. Geophys. Res. Lett. 2021, e2020GL091203. [Google Scholar]
- Mazhar, U.; Jin, S.; Duan, W.; Bilal, M.; Ali, M.; Farooq, H. Spatio-Temporal Trends of Surface Energy Budget in Tibet from Satellite Remote Sensing Observations and Reanalysis Data. Remote Sens. 2021, 13, 256. [Google Scholar] [CrossRef]
- Wilson, A.M.; Silander, J.A., Jr. Estimating uncertainty in daily weather interpolations: A Bayesian framework for developing climate surfaces. Int. J. Climatol. 2014, 34, 2573–2584. [Google Scholar] [CrossRef]
- Jin, M. Analysis of land skin temperature using AVHRR observations. Bull. Am. Meteorol. Soc. 2004, 85, 587–600. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Evan, A.T.; Foster, M.J.; Walther, A. A naive Bayesian cloud-detection scheme derived from CALIPSO and applied within PATMOS-x. J. Appl. Meteorol. Climatol. 2012, 51, 1129–1144. [Google Scholar] [CrossRef]
- Minnis, P.; Sun-Mack, S.; Young, D.F.; Heck, P.W.; Garber, D.P.; Chen, Y.; Spangenberg, D.A.; Arduini, R.F.; Trepte, Q.Z.; Smith, W.L. CERES edition-2 cloud property retrievals using TRMM VIRS and Terra and Aqua MODIS data—Part I: Algorithms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4374–4400. [Google Scholar] [CrossRef]
- Stubenrauch, C.J.; Rossow, W.B.; Kinne, S.; Ackerman, S.; Cesana, G.; Chepfer, H.; Di Girolamo, L.; Getzewich, B.; Guignard, A.; Heidinger, A. Assessment of global cloud datasets from satellites: Project and database initiated by the GEWEX radiation panel. Bull. Am. Meteorol. Soc. 2013, 94, 1031–1049. [Google Scholar] [CrossRef]
- Wylie, D.; Jackson, D.L.; Menzel, W.P.; Bates, J.J. Trends in global cloud cover in two decades of HIRS observations. J. Clim. 2005, 18, 3021–3031. [Google Scholar] [CrossRef]
- Knapp, K.R.; Ansari, S.; Bain, C.L.; Bourassa, M.A.; Dickinson, M.J.; Funk, C.; Helms, C.N.; Hennon, C.C.; Holmes, C.D.; Huffman, G.J. Globally gridded satellite observations for climate studies. Bull. Am. Meteorol. Soc. 2011, 92, 893–907. [Google Scholar] [CrossRef]
- Adaramola, M.S. Estimating global solar radiation using common meteorological data in Akure, Nigeria. Renew. Energy 2012, 47, 38–44. [Google Scholar] [CrossRef]
- Almorox, J.; Bocco, M.; Willington, E. Estimation of daily global solar radiation from measured temperatures at Cañada de Luque, Córdoba, Argentina. Renew. Energy 2013, 60, 382–387. [Google Scholar] [CrossRef]
- Katiyar, A.; Pandey, C.K. Simple correlation for estimating the global solar radiation on horizontal surfaces in India. Energy 2010, 35, 5043–5048. [Google Scholar] [CrossRef]
- Longman, R.J.; Giambelluca, T.W.; Frazier, A.G. Modeling clear-sky solar radiation across a range of elevations in Hawai’i: Comparing the use of input parameters at different temporal resolutions. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Zomer, R.J.; Trabucco, A.; Bossio, D.A.; Verchot, L.V. Climate change mitigation: A spatial analysis of global land suitability for clean development mechanism afforestation and reforestation. Agric. Ecosyst. Environ. 2008, 126, 67–80. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, F.-F.; Zhao, J.-X.; Qi, L.; Ren, H.-L. The possible influence of a nonconventional El Niño on the severe autumn drought of 2009 in Southwest China. J. Clim. 2013, 26, 8392–8405. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Hahn, C.; Warren, S.; Eastman, R. Cloud Climatology for Land Stations Worldwide, 1971–2009 (NDP-026D); Environmental System Science Data Infrastructure for a Virtual Ecosystem, Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2012. [Google Scholar]
- Rubel, F.; Kottek, M. Observed and projected climate shifts 1901–2100 depicted by world maps of the Köppen-Geiger climate classification. Meteorol. Z. 2010, 19, 135. [Google Scholar] [CrossRef]
- Bohn, T.J.; Livneh, B.; Oyler, J.W.; Running, S.W.; Nijssen, B.; Lettenmaier, D.P. Global evaluation of MTCLIM and related algorithms for forcing of ecological and hydrological models. Agric. For. Meteorol. 2013, 176, 38–49. [Google Scholar] [CrossRef]
- Bras, R.L. Hydrology: An Introduction to Hydrologic Science; Addison Wesley Publishing Company: Boston, MA, USA, 1990. [Google Scholar]
- Kopp, G.; Lean, J.L. A new, lower value of total solar irradiance: Evidence and climate significance. Geophys. Res. Lett. 2011, 38, 38. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Process, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Köppen, W.; Geiger, R. Handbuch der Klimatologie; Gebrüder Borntraeger Berlin: Berlin, Germany, 1930; Volume 1. [Google Scholar]
- KOPPEN, W.d. Das geographische system der klimat. Handb. Klimatol. 1936, 46. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Lu, J.; Vecchi, G.A.; Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 2007, 34. [Google Scholar]
- Seidel, D.J.; Fu, Q.; Randel, W.J.; Reichler, T.J. Widening of the tropical belt in a changing climate. Nat. Geosci. 2008, 1, 21–24. [Google Scholar] [CrossRef]
- Tang, Q.; Leng, G. Changes in cloud cover, precipitation, and summer temperature in North America from 1982 to 2009. J. Clim. 2013, 26, 1733–1744. [Google Scholar] [CrossRef]
- Trenberth, K.E. Atmospheric moisture residence times and cycling: Implications for rainfall rates and climate change. Clim. Chang. 1998, 39, 667–694. [Google Scholar] [CrossRef]
- London, J.; Hahn, C.J.; Warren, S.G. Observed variations of total cloudiness and cloud types: Implications for the atmospheric radiation budget. In Atmospheric Radiation; Springer: Berlin/Heidelberg, Germany, 1987; pp. 459–467. [Google Scholar]
- Warren, S.G.; Eastman, R.M.; Hahn, C.J. A survey of changes in cloud cover and cloud types over land from surface observations, 1971–1996. J. Clim. 2007, 20, 717–738. [Google Scholar] [CrossRef]
- Houston, J.; Hartley, A.J. The central Andean west-slope rainshadow and its potential contribution to the origin of hyper-aridity in the Atacama Desert. Int. J. Climatol. J. R. Meteorol. Soc. 2003, 23, 1453–1464. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Wang, J. Temperature effect on the atmospheric transmission function in the 15-μm region. Opt. Lett. 1978, 2, 169–171. [Google Scholar] [CrossRef]
- Kaas, E.; Frich, P. Diurnal temperature range and cloud cover in the Nordic countries: Observed trends and estimates for the future. Atmos. Res. 1995, 37, 211–228. [Google Scholar] [CrossRef]
- Karl, T.R.; Jones, P.D.; Knight, R.W.; Kukla, G.; Plummer, N.; Razuvayev, V.; Gallo, K.P.; Lindseay, J.; Charlson, R.J.; Peterson, T.C. A new perspective on recent global warming: Asymmetric trends of daily maximum and minimum temperature. Bull. Am. Meteorol. Soc. 1993, 74, 1007–1024. [Google Scholar] [CrossRef]
- Dai, A.; Del Genio, A.D.; Fung, I.Y. Clouds, precipitation and temperature range. Nature 1997, 386, 665–666. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Karl, T.R. Effects of clouds, soil moisture, precipitation, and water vapor on diurnal temperature range. J. Clim. 1999, 12, 2451–2473. [Google Scholar] [CrossRef]
- Travis, D.J.; Carleton, A.M.; Lauritsen, R.G. Regional variations in US diurnal temperature range for the 11–14 September 2001 aircraft groundings: Evidence of jet contrail influence on climate. J. Clim. 2004, 17, 1123–1134. [Google Scholar] [CrossRef]
- Roy, S.S.; Balling, R.C., Jr. Analysis of trends in maximum and minimum temperature, diurnal temperature range, and cloud cover over India. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Stanhill, G.; Ianetz, A. Long-term trends in, and the spatial variation of, global irradiance in Israel. Tellus B 1997, 49, 112–122. [Google Scholar] [CrossRef]
- Hartmann, D.L. Radiative effects of clouds on Earth’s climate. In International Geophysics; Elsevier: Amsterdam, The Netherlands, 1993; Volume 54, pp. 151–173. [Google Scholar]
- Lin, L.; Gettelman, A.; Feng, S.; Fu, Q. Simulated climatology and evolution of aridity in the 21st century. J. Geophys. Res. Atmos. 2015, 120, 5795–5815. [Google Scholar] [CrossRef]
- Feng, S.; Fu, Q. Expansion of global drylands under a warming climate. Atmos. Chem. Phys. 2013, 13, 10081–10094. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Poudyal, K.N.; Bhattarai, B.K.; Sapkota, B.; Kjeldstad, B. Estimation of global solar radiation using clearness index and cloud transmittance factor at trans-Himalayan region in Nepal. Energy Power Eng. 2012, 4, 415–421. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic: San Diego, CA, USA, 1974. [Google Scholar]
- Zhang, L.; Dawes, W.; Walker, G. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.; Peña-Arancibia, J.; Sun, F.; Li, H.; Leuning, R. Global variation of transpiration and soil evaporation and the role of their major climate drivers. J. Geophys. Res. Atmos. 2017, 122, 6868–6881. [Google Scholar] [CrossRef]
- Qian, T.; Dai, A.; Trenberth, K.E. Hydroclimatic trends in the Mississippi River basin from 1948 to 2004. J. Clim. 2007, 20, 4599–4614. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, A.; Rodriguez, J.F.; Saco, P.M.; Kumari, N.; Yetemen, O. Global Analysis of Atmospheric Transmissivity Using Cloud Cover, Aridity and Flux Network Datasets. Remote Sens. 2021, 13, 1716. https://doi.org/10.3390/rs13091716
Srivastava A, Rodriguez JF, Saco PM, Kumari N, Yetemen O. Global Analysis of Atmospheric Transmissivity Using Cloud Cover, Aridity and Flux Network Datasets. Remote Sensing. 2021; 13(9):1716. https://doi.org/10.3390/rs13091716
Chicago/Turabian StyleSrivastava, Ankur, Jose F. Rodriguez, Patricia M. Saco, Nikul Kumari, and Omer Yetemen. 2021. "Global Analysis of Atmospheric Transmissivity Using Cloud Cover, Aridity and Flux Network Datasets" Remote Sensing 13, no. 9: 1716. https://doi.org/10.3390/rs13091716
APA StyleSrivastava, A., Rodriguez, J. F., Saco, P. M., Kumari, N., & Yetemen, O. (2021). Global Analysis of Atmospheric Transmissivity Using Cloud Cover, Aridity and Flux Network Datasets. Remote Sensing, 13(9), 1716. https://doi.org/10.3390/rs13091716







