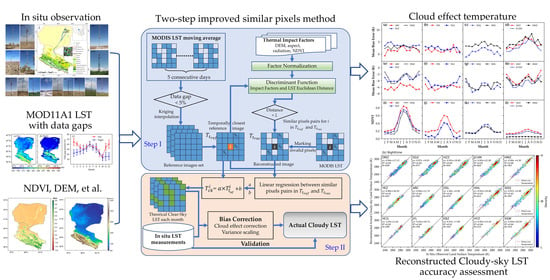
Reconstruction of the Daily MODIS Land Surface Temperature Product Using the Two-Step Improved Similar Pixels Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Data Reprocessing
| Data Sources | Variable | Spatiotemporal Resolution | Date |
|---|---|---|---|
| MODIS/Terra | LST (MOD11A1) | 1 km/daily | January 2013–December 2018 |
| Narrowband emissivity (MOD11B1) | 6 km/daily | ||
| NDVI (MOD13A2) | 1 km/16 day | ||
| SRTM | DEM, slope, aspect | 90 m | |
| Model-based | Theoretical radiation | 1 km/10 min | |
| Ground-based | Upwelling and downwelling longwave radiation | Point/10 min |
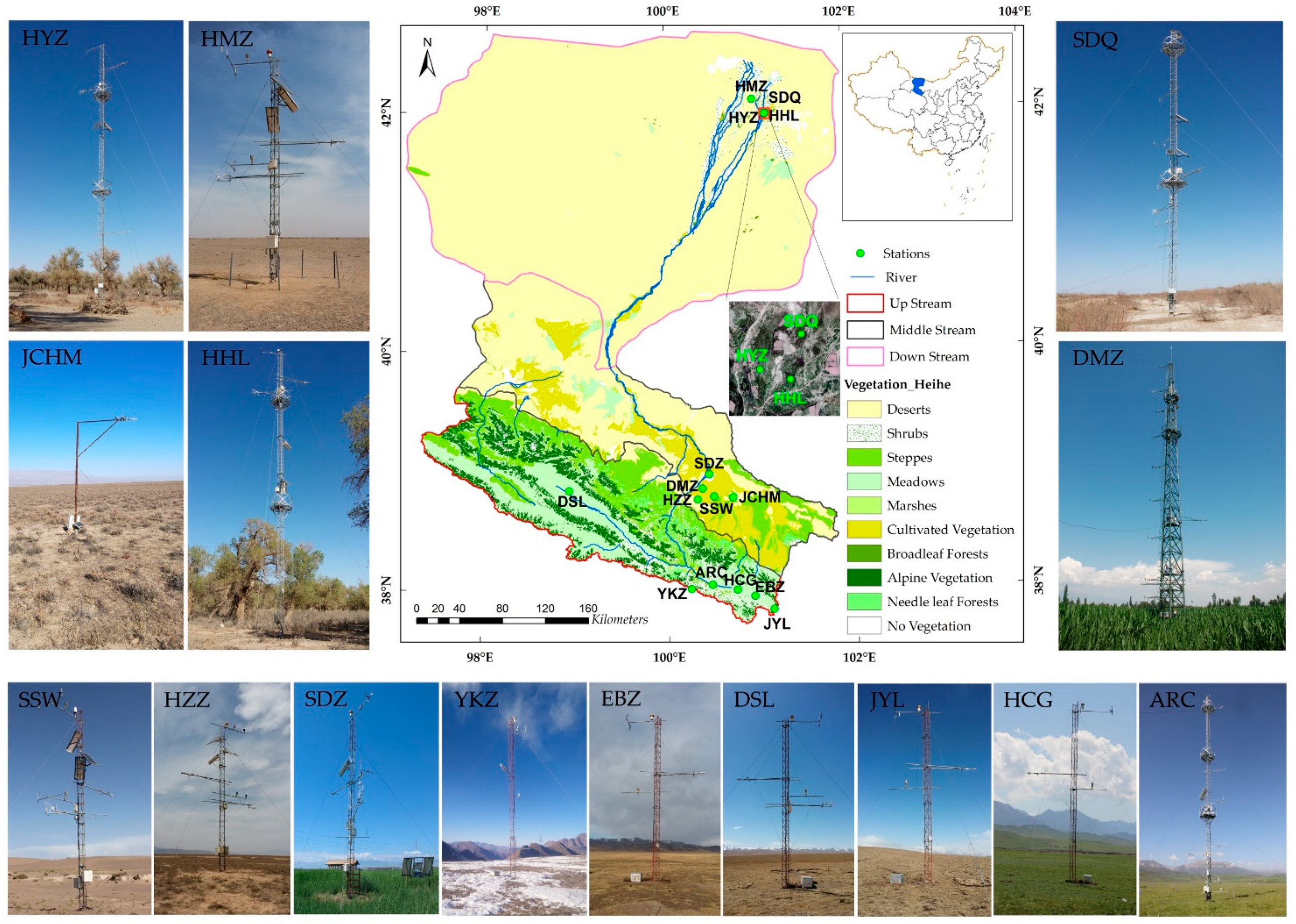
2.2.1. Remote Sensing and Auxiliary Data
2.2.2. Ground LST Estimation
| Station | Longitude | Latitude | Altitude | Land Cover | Date | Sensor | Install Height |
|---|---|---|---|---|---|---|---|
| DMZ * | 100.372°E | 38.866°N | 1556 m | Cropland | 2013–2018 | PSP&PIR | 12 m |
| SDZ * | 100.446°E | 38.975°N | 1460 m | Wetland | 2013–2018 | NR01 | 6 m |
| HZZ * | 100.319°E | 38.765°N | 1726 m | Kalidium foliatum desert | 2013–2018 | CNR1 | 6 m |
| JCHM * | 100.70°E | 38.78°N | 1626 m | Desert steppe | 2013–2018 | CNR4 | 6 m |
| HMZ * | 100.987°E | 42.114°N | 1054 m | Reaumuria desert | 2015–2018 | CNR1 | 6 m |
| YKZ * | 100.242°E | 38.014°N | 4148 m | Alpine meadow | 2014–2018 | CNR4 | 6 m |
| ARC * | 100.464°E | 38.047°N | 3033 m | Alpine meadow | 2013–2018 | CNR4 | 5 m |
| DSL * | 98.941°E | 38.840°N | 3739 m | Marsh alpine meadow | 2013–2018 | CNR1 | 6 m |
| HHL * | 101.134°E | 41.990°N | 874 m | Populus euphratica and Tamarix | 2013–2018 | CNR4 | 24 m |
| SDQ * | 101.137°E | 42.001°N | 873 m | Tamarix | 2013–2018 | CNR4 | 10 m |
| HCG | 100.731°E | 38.003°N | 3137 m | Alpine meadow | 2013–2015 | CNR1 | 6 m |
| JYL | 101.116°E | 37.838°N | 3750 m | Alpine meadow | 2013–2016 | CNR4 | 6 m |
| EBZ | 100.915°E | 37.949°N | 3294 m | Alpine meadow | 2013–2016 | CNR1 | 6 m |
| HYZ | 101.124°E | 41.993°N | 876 m | Populus euphratica | 2013–2015 | CNR4 | 6 m |
| SSW | 100.493°E | 38.789°N | 1594 m | Sand desert | 2013–2015 | CNR1 | 6 m |
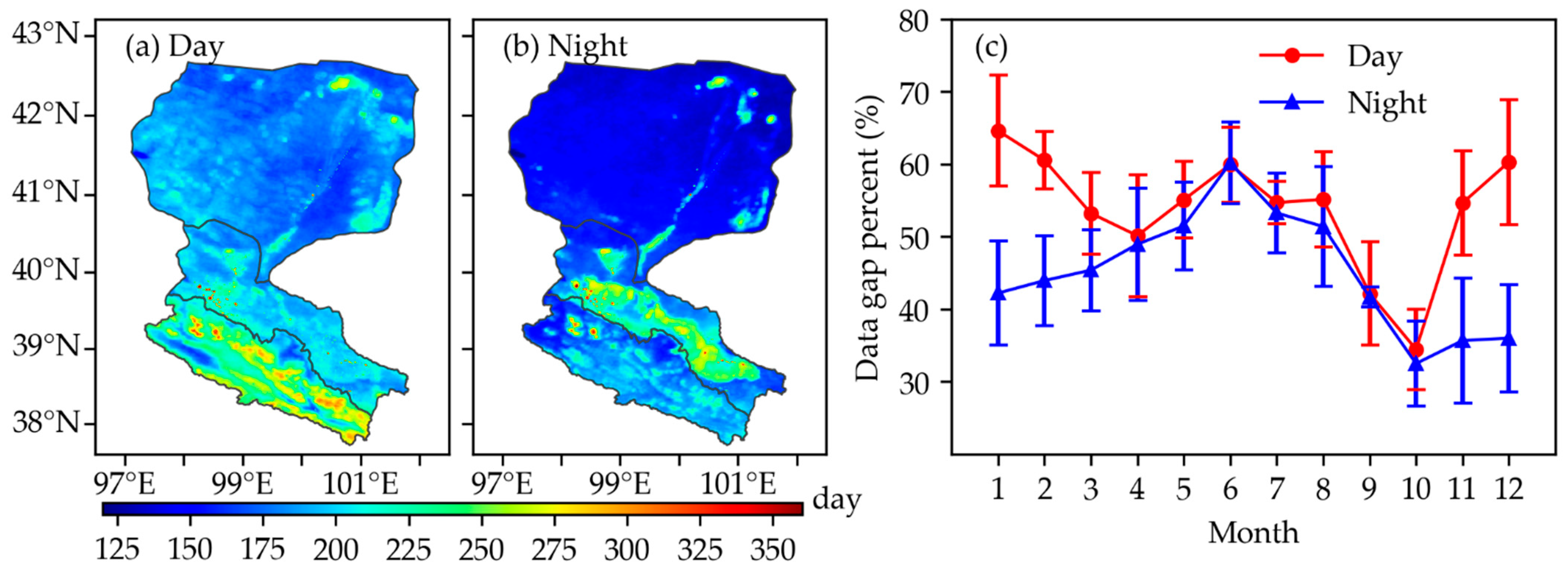
2.2.3. MODIS LST Accuracy
2.3. MODIS LST Reconstruction Method
2.3.1. Reconstruction of Theoretical Clear-Sky LST
2.3.2. Bias Correction of Theoretical Clear-Sky LST
2.4. Evaluation Metrics
3. Results and Discussion
3.1. Generating the Theoretical Clear-Sky LST
3.2. Validation
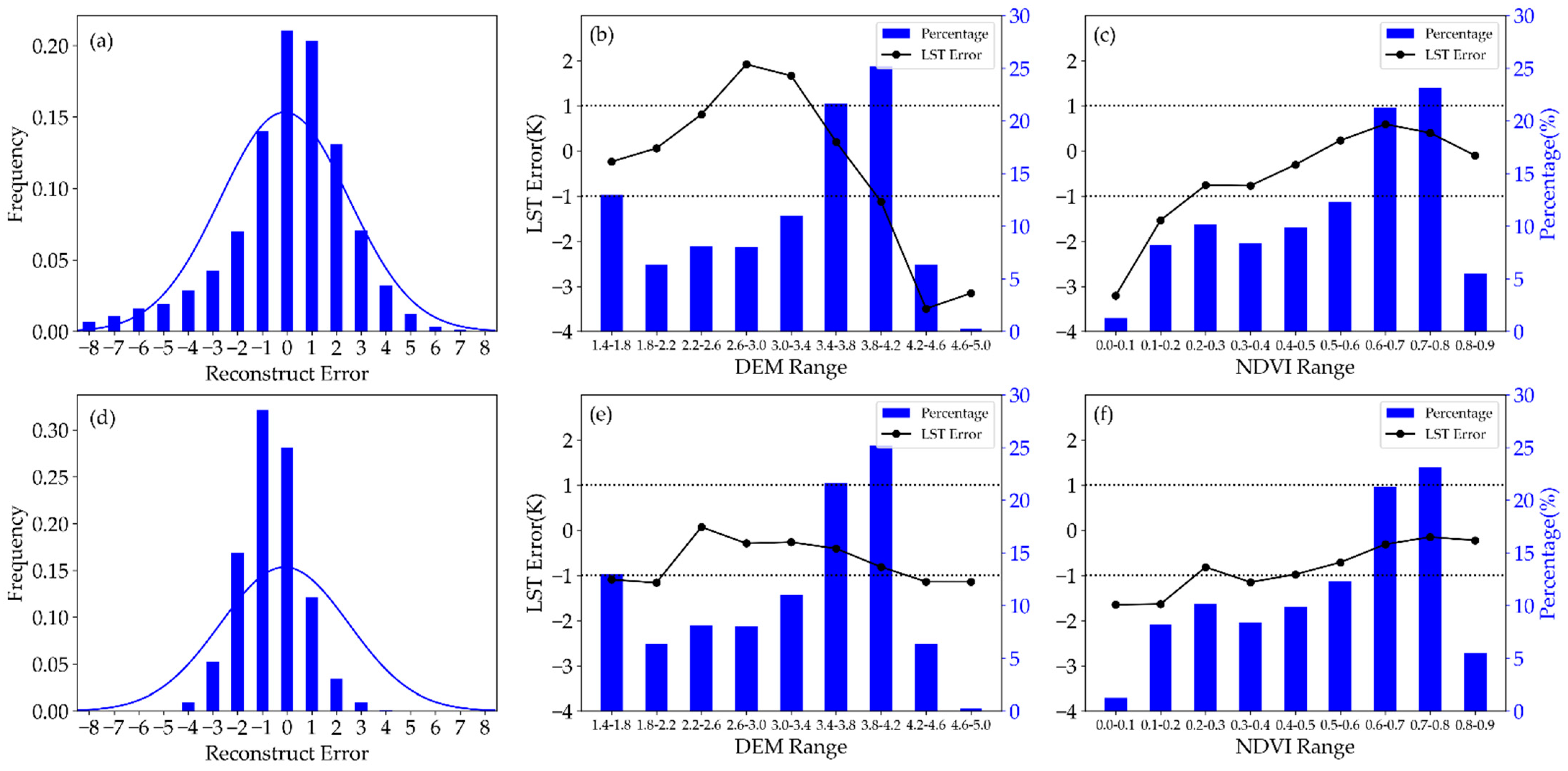
3.3. An Experiment for Testing the Accuracy of the Tck
3.4. Research Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Santer, B.D.; Po-Chedley, S.; Zelinka, M.D.; Cvijanovic, I.; Bonfils, C.; Durack, P.J.; Fu, Q.; Kiehl, J.; Mears, C.; Painter, J.; et al. Human influence on the seasonal cycle of tropospheric temperature. Science 2018, 361, eaas8806. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.Z.; Yan, G.J.; Wan, Z.M.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Kogan, F.N. Operational Space Technology for Global Vegetation Assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Bierkens, M.F.P.; Lutz, A.F.; Immerzeel, W.W. Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 2017, 549, 257–260. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Julien, Y.; García-Monteiro, S. Surface Temperature of the Planet Earth from Satellite Data. Remote Sens. 2020, 12, 218. [Google Scholar] [CrossRef]
- Neteler, M. Estimating Daily Land Surface Temperatures in Mountainous Environments by Reconstructed MODIS LST Data. Remote Sens. 2010, 2, 333–351. [Google Scholar] [CrossRef]
- Singh, S.; Bhardwaj, A.; Singh, A.; Sam, L.; Shekhar, M.; Martín-Torres, F.J.; Zorzano, M.-P. Quantifying the Congruence between Air and Land Surface Temperatures for Various Climatic and Elevation Zones of Western Himalaya. Remote Sens. 2019, 11, 2889. [Google Scholar] [CrossRef]
- Brabyn, L.; Stichbury, G. Calculating the surface melt rate of Antarctic glaciers using satellite-derived temperatures and stream flows. Environ. Monit. Assess 2020, 192, 1–14. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Jin, R.; Guo, J. Remote Sensing of the Mean Annual Surface Temperature and Surface Frost Number for Mapping Permafrost in China. Arct. Antarct. Alp. Res. 2015, 47, 255–265. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Nan, Z.; Che, J.; Sheng, Y.; Wu, Q.; Jin, H.; Luo, D.; Tang, Z.; et al. Mapping the permafrost stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2021, 64, 62–79. [Google Scholar] [CrossRef]
- Jenkins, L.K.; Barry, T.; Bosse, K.R.; Currie, W.S.; Christensen, T.; Longan, S.; Shuchman, R.A.; Tanzer, D.; Taylor, J.J. Satellite-based decadal change assessments of pan-Arctic environments. Ambio 2020, 49, 820–832. [Google Scholar] [CrossRef]
- Retamales-Muñoz, G.; Durán-Alarcón, C.; Mattar, C. Recent land surface temperature patterns in Antarctica using satellite and reanalysis data. J. S. Am. Earth Sci. 2019, 95, 102304. [Google Scholar] [CrossRef]
- McMillin, L.M. Estimation of sea surface temperatures from two infrared window measurements with different absorption. J. Geophys. Res. 1975, 80, 5113–5117. [Google Scholar] [CrossRef]
- Coll, C.; Valor, E.; Galve, J.M.; Mira, M.; Bisquert, M.; García-Santos, V.; Caselles, E.; Caselles, V. Long-term accuracy assessment of land surface temperatures derived from the Advanced Along-Track Scanning Radiometer. Remote Sens. Environ. 2012, 116, 211–225. [Google Scholar] [CrossRef]
- Jiang, G.M.; Li, Z.L. Split-window algorithm for land surface temperature estimation from MSG1-SEVIRI data. Int. J. Remote Sens. 2008, 29, 6067–6074. [Google Scholar] [CrossRef]
- Zhengming, W.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Mao, K.; Yuan, Z.; Zuo, Z.; Xu, T.; Shen, X.; Gao, C. Changes in Global Cloud Cover Based on Remote Sensing Data from 2003 to 2012. Chin. Geogr. Sci. 2019, 20, 306–315. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (Moderate Resolution Imaging Spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Liu, Y.; Key, J.R.; Wang, X. The Influence of Changes in Cloud Cover on Recent Surface Temperature Trends in the Arctic. J. Clim. 2008, 21, 705–715. [Google Scholar] [CrossRef]
- Westermann, S.; Langer, M.; Boike, J. Systematic bias of average winter-time land surface temperatures inferred from MODIS at a site on Svalbard, Norway. Remote Sens. Environ. 2012, 118, 162–167. [Google Scholar] [CrossRef]
- Bechtel, B. A New Global Climatology of Annual Land Surface Temperature. Remote Sens. 2015, 7, 2850–2870. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhong, M.; Zhang, L.; Wu, P. Reconstructing MODIS LST Based on Multitemporal Classification and Robust Regression. IEEE Geosci. Remote Sens. Lett. 2015, 12, 512–516. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, Y. Reconstruction of the land surface temperature time series using harmonic analysis. Comput. Geosci. 2013, 61, 126–132. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Na, F.; Gaodi, X.; Wenhua, L.; Yajing, Z.; Changshun, Z.; Na, L. Mapping Air Temperature in the Lancang River Basin Using the Reconstructed MODIS LST Data. J. Resour. Ecol. 2014, 5, 253–262. [Google Scholar] [CrossRef]
- Kang, J.; Tan, J.; Jin, R.; Li, X.; Zhang, Y. Reconstruction of MODIS Land Surface Temperature Products Based on Multi-Temporal Information. Remote Sens. 2018, 10, 1112. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E. A generalized algorithm for retrieving cloudy sky skin temperature from satellite thermal infrared radiances. J. Geophys. Res. Atmos. 2000, 105, 27037–27047. [Google Scholar] [CrossRef]
- Lu, L.; Venus, V.; Skidmore, A.; Wang, T.; Luo, G. Estimating land-surface temperature under clouds using MSG/SEVIRI observations. Int. J. Appl. Earth. Obs. Geoinf. 2011, 13, 265–276. [Google Scholar] [CrossRef]
- Martins, J.P.A.; Trigo, I.F.; Ghilain, N.; Jimenez, C.; Gottsche, F.M.; Ermida, S.L.; Olesen, F.S.; Gellens-Meulenberghs, F.; Arboleda, A. An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations. Remote Sens. 2019, 11, 3044. [Google Scholar] [CrossRef]
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.-L.; Olesen, F.; Barroso, C.; Camacho-de-Coca, F.; Carrer, D.; Freitas, S.C.; García-Haro, J.; et al. The Satellite Application Facility for Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Prigent, C.; Jimenez, C.; Aires, F. Towards “all weather”, long record, and real-time land surface temperature retrievals from microwave satellite observations. J. Geophys. Res. Atmos. 2016, 121, 5699–5717. [Google Scholar] [CrossRef]
- Long, D.; Yan, L.; Bai, L.; Zhang, C.; Li, X.; Lei, H.; Yang, H.; Tian, F.; Zeng, C.; Meng, X.; et al. Generation of MODIS-like land surface temperatures under all-weather conditions based on a data fusion approach. Remote Sens. Environ. 2020, 246, 111863. [Google Scholar] [CrossRef]
- Zhao, B.; Mao, K.; Cai, Y.; Shi, J.; Li, Z.; Qin, Z.; Meng, X.; Shen, X.; Guo, Z. A combined Terra and Aqua MODIS land surface temperature and meteorological station data product for China from 2003 to 2017. Earth Syst. Sci. Data 2020, 12, 2555–2577. [Google Scholar] [CrossRef]
- Dumitrescu, A.; Brabec, M.; Cheval, S. Statistical Gap-Filling of SEVIRI Land Surface Temperature. Remote Sens. 2020, 12, 1423. [Google Scholar] [CrossRef]
- Weiss, D.J.; Atkinson, P.M.; Bhatt, S.; Mappin, B.; Hay, S.I.; Gething, P.W. An effective approach for gap-filling continental scale remotely sensed time-series. ISPRS J. Photogramm. Remote Sens. 2014, 98, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Zeng, C.; Long, D.; Shen, H.; Wu, P.; Cui, Y.; Hong, Y. A two-step framework for reconstructing remotely sensed land surface temperatures contaminated by cloud. ISPRS J. Photogramm. Remote Sens. 2018, 141, 30–45. [Google Scholar] [CrossRef]
- Yu, W.; Nan, Z.; Wang, Z.; Chen, H.; Wu, T.; Zhao, L. An Effective Interpolation Method for MODIS Land Surface Temperature on the Qinghai-Tibet Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4539–4550. [Google Scholar] [CrossRef]
- Yu, W.; Tan, J.; Ma, M.; Li, X.; She, X.; Song, Z. An Effective Similar-Pixel Reconstruction of the High-Frequency Cloud-Covered Areas of Southwest China. Remote Sens. 2019, 11, 336. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Liu, S.; Li, H.; Xu, Z.; Tan, J.; Zhang, Y.; Ren, Z.; Xiao, L.; Deng, J.; et al. Integrated hydrometeorological, snow and frozen-ground observations in the alpine region of the Heihe River Basin, China. Earth Syst. Sci. Data 2019, 11, 1483–1499. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Xiao, J.; Ma, M. Evapotranspiration components and water use efficiency from desert to alpine ecosystems in drylands. Agric. For. Meteorol. 2021, 298–299, 108283. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Ma, M.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 180072. [Google Scholar] [CrossRef]
- Kumar, L.; Skidmore, A.K.; Knowles, E. Modelling topographic variation in solar radiation in a GIS environment. Int. J. Geogr. Inf. Sci. 1997, 11, 475–497. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Xiao, J.; Ma, M.; Tan, J.; Wang, X.; Geng, L. Carbon fluxes across alpine, oasis, and desert ecosystems in northwestern China: The importance of water availability. Sci. Total Environ. 2019, 697, 133978. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Liang, S. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ. 2009, 113, 1556–1565. [Google Scholar] [CrossRef]
- Li, H.; Li, R.; Yang, Y.; Cao, B.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. Temperature-Based and Radiance-Based Validation of the Collection 6 MYD11 and MYD21 Land Surface Temperature Products Over Barren Surfaces in Northwestern China. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1794–1807. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS LST products in an arid area of Northwest China. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Yu, W.P.; Ma, M.G.; Li, Z.L.; Tan, J.L.; Wu, A.A. New Scheme for Validating Remote-Sensing Land Surface Temperature Products with Station Observations. Remote Sens. 2017, 9, 1210. [Google Scholar] [CrossRef]
- He, Y.; Wang, K. Contrast patterns and trends of lapse rates calculated from near-surface air and land surface temperatures in China from 1961 to 2014. Sci. Bull. 2020, 65, 1217–1224. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–488. [Google Scholar] [CrossRef]
- Jain, S.K.; Goswami, A.; Saraf, A.K. Determination of land surface temperature and its lapse rate in the Satluj River basin using NOAA data. Int. J. Remote Sens. 2008, 29, 3091–3103. [Google Scholar] [CrossRef]
- Tang, Z.; Fang, J. Temperature variation along the northern and southern slopes of Mt. Taibai, China. Agric. For. Meteorol. 2006, 139, 200–207. [Google Scholar] [CrossRef]
- McCune, B.; Keon, D. Equations for potential annual direct incident radiation and heat load. J. Veg. Sci. 2002, 13, 603–606. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Merlin, O.; Gascoin, S.; Gastellu, J.P.; Mattar, C.; Olivera-Guerra, L.; Khabba, S.; Jarlan, L. Normalizing land surface temperature data for elevation and illumination effects in mountainous areas: A case study using ASTER data over a steep-sided valley in Morocco. Remote Sens. Environ. 2017, 189, 25–39. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The impact of the terrain effect on land surface temperature variation based on Landsat-8 observations in mountainous areas. Int. J. Remote Sens. 2019, 40, 1808–1827. [Google Scholar] [CrossRef]
- Yu, Q.; Ji, W.; Pu, R.; Landry, S.; Acheampong, M.; O’Neil-Dunne, J.; Ren, Z.; Tanim, S.H. A preliminary exploration of the cooling effect of tree shade in urban landscapes. Int. J. Appl. Earth. Obs. Geoinf. 2020, 92, 102161. [Google Scholar] [CrossRef]
- Peng, X.; Wu, W.; Zheng, Y.; Sun, J.; Hu, T.; Wang, P. Correlation analysis of land surface temperature and topographic elements in Hangzhou, China. Sci. Rep. 2020, 10, 10451. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.R.; Duan, S.B.; Li, Z.L.; Chang, S.; Xing, Z.F.; Leng, P.; Gao, M.F. Interannual Spatiotemporal Variations of Land Surface Temperature in China From 2003 to 2018. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1783–1795. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Tian, Y.; Wu, L.; Xiao, J.; Chen, F.; Qian, Q. Relationship among land surface temperature and LUCC, NDVI in typical karst area. Sci. Rep. 2018, 8, 641. [Google Scholar] [CrossRef] [PubMed]
- Hope, A.; Engstrom, R.; Stow, D. Relationship between AVHRR surface temperature and NDVI in Arctic tundra ecosystems. Int. J. Remote Sens. 2005, 26, 1771–1776. [Google Scholar] [CrossRef]
- Davies, L.; Gather, U. The identification of multiple outliers. J. Am. Stat. Assoc. 1993, 88, 782–792. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Merchant, C.J.; Ghent, D.; Klüser, L.; Popp, T.; Poulsen, C.; Sogacheva, L. Quantifying Uncertainty in Satellite-Retrieved Land Surface Temperature from Cloud Detection Errors. Remote Sens. 2018, 10, 616. [Google Scholar] [CrossRef]

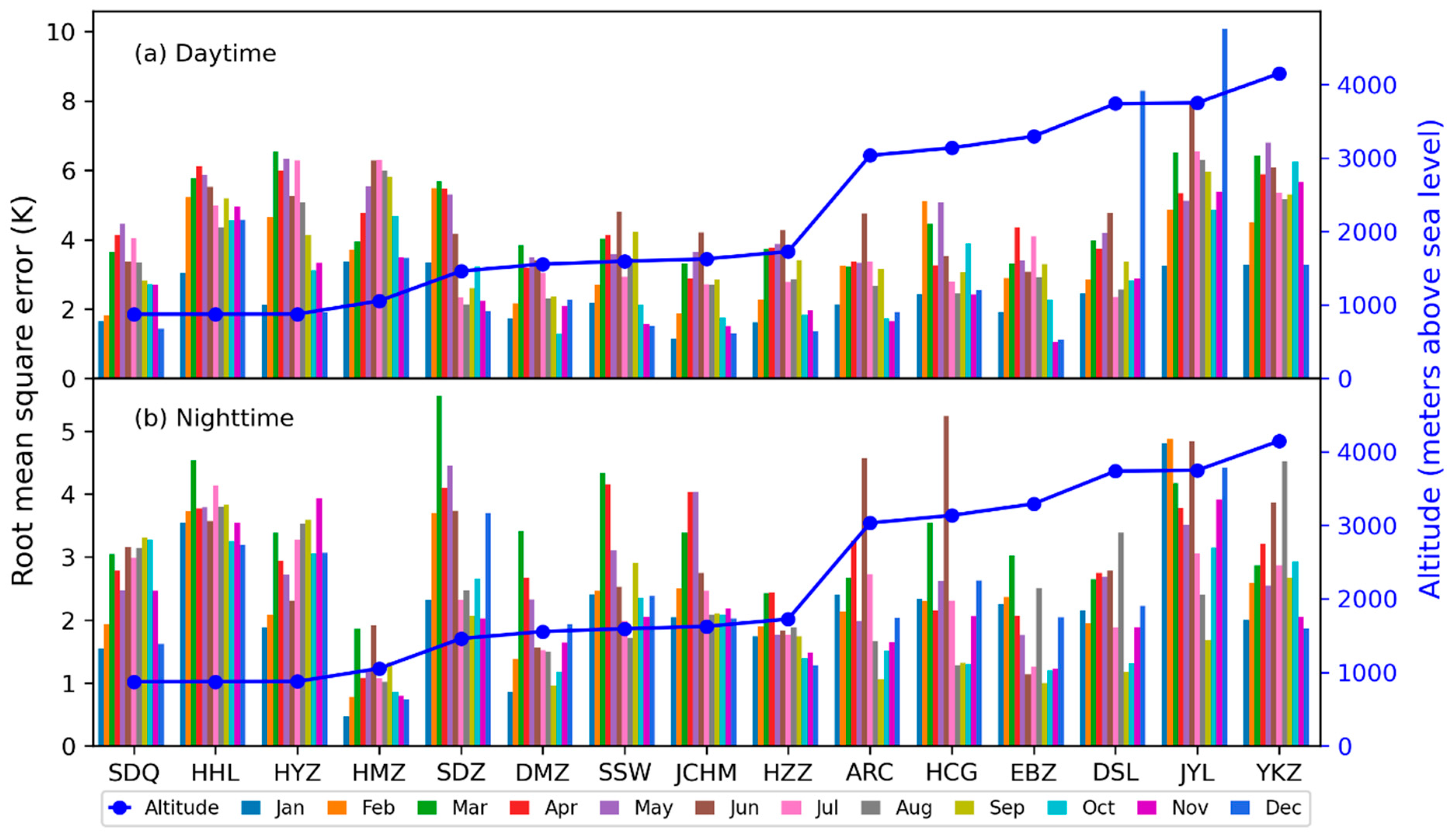

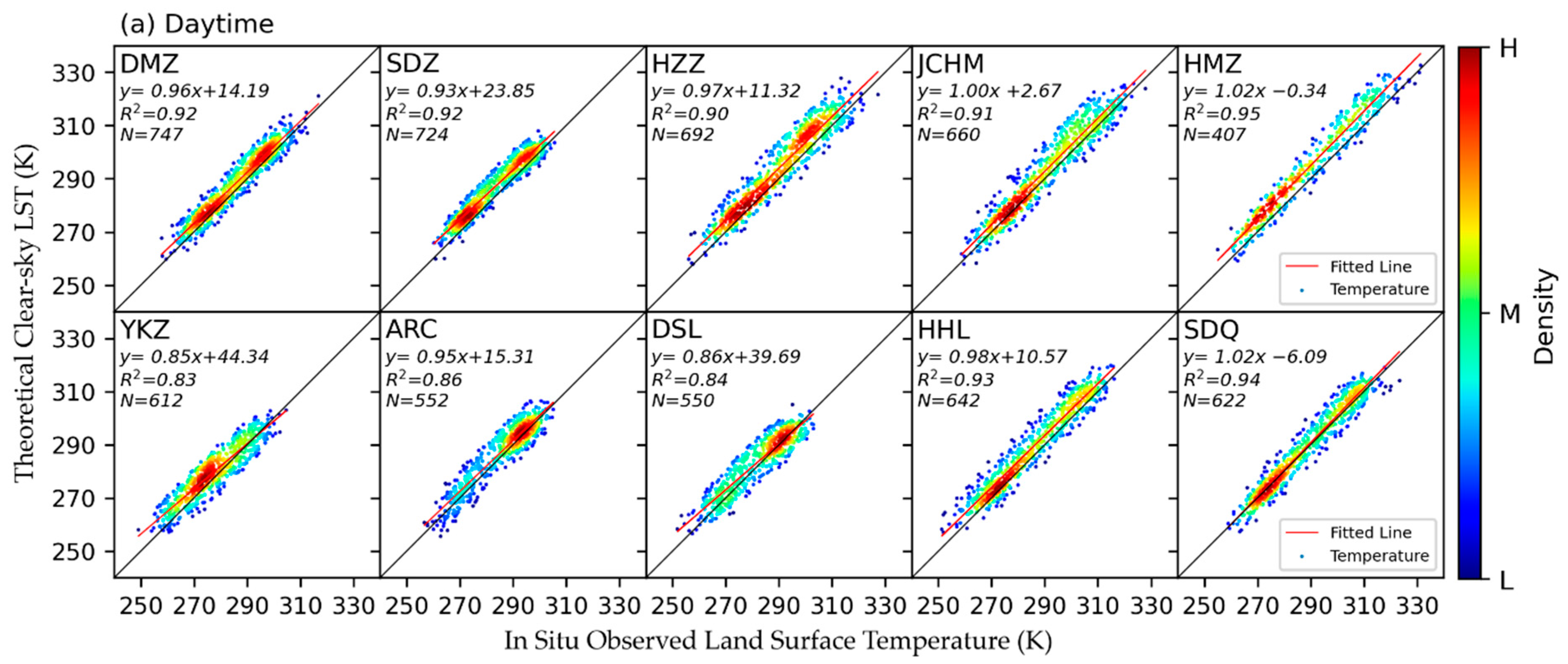
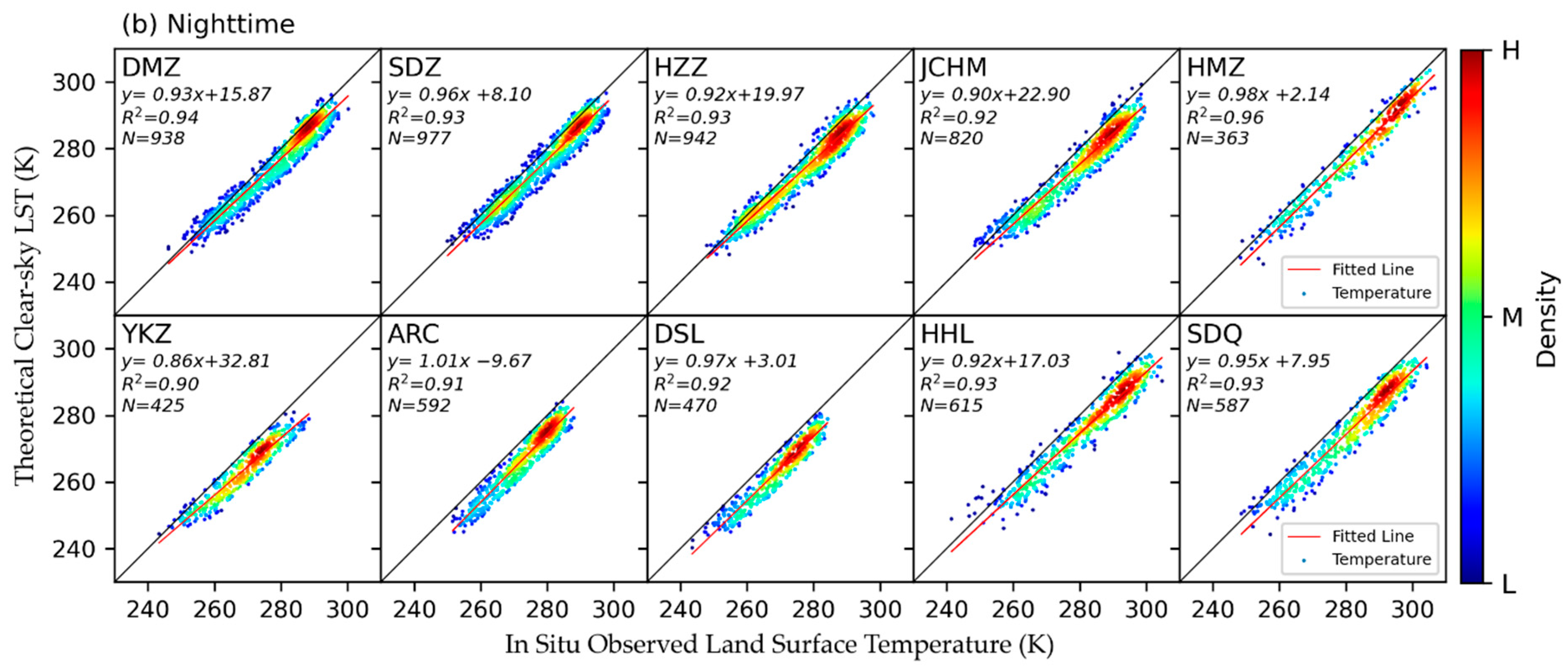
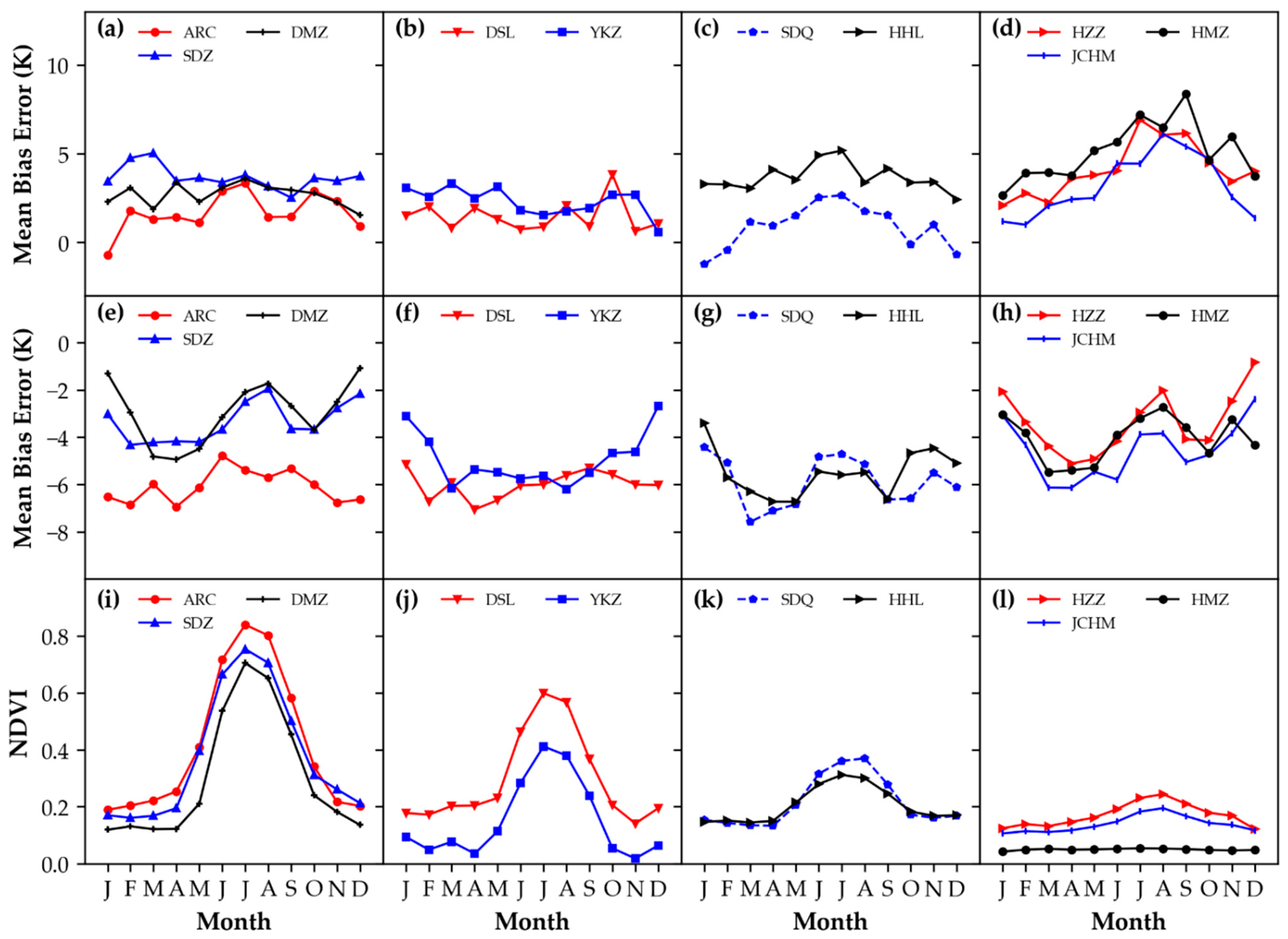
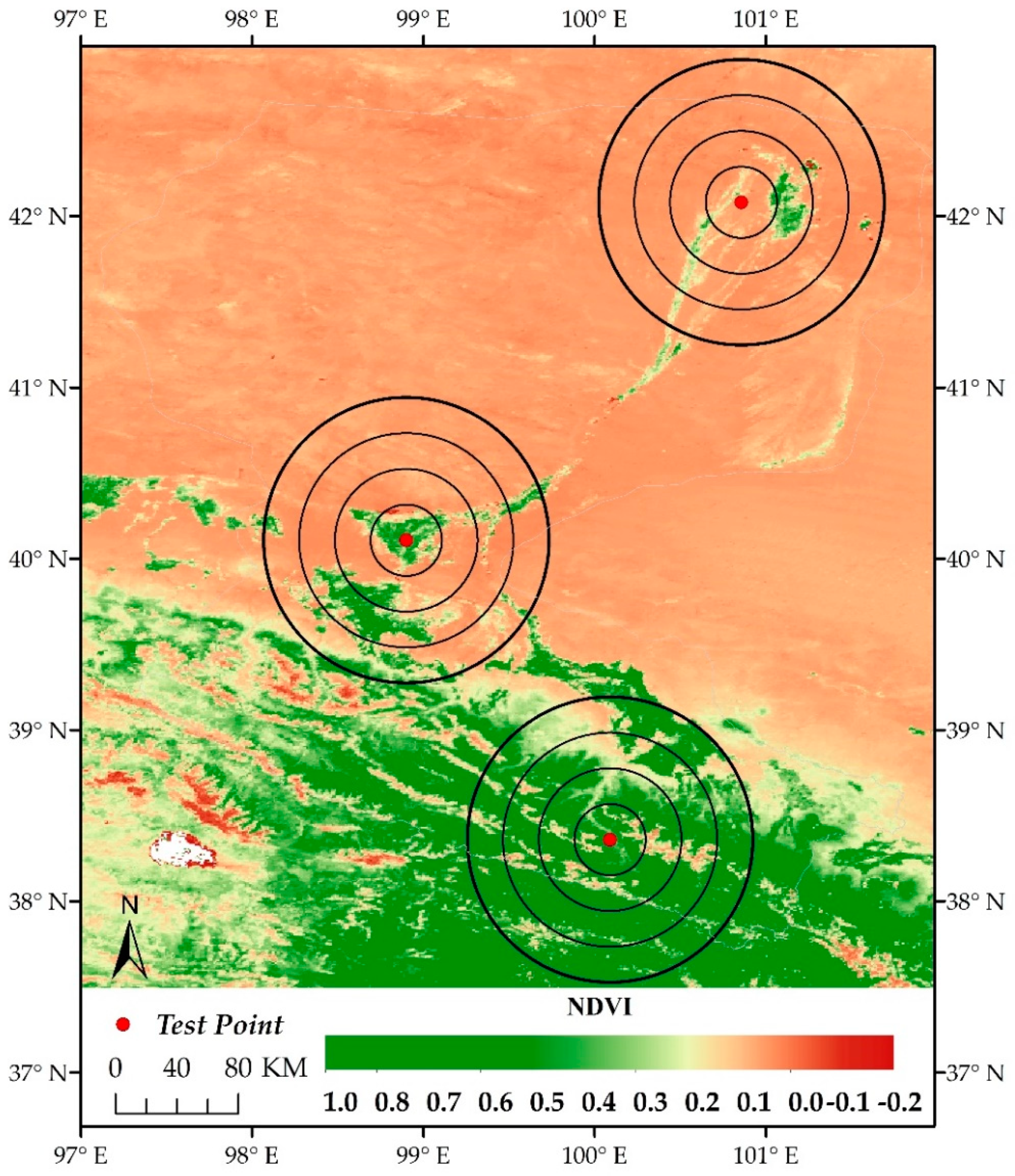
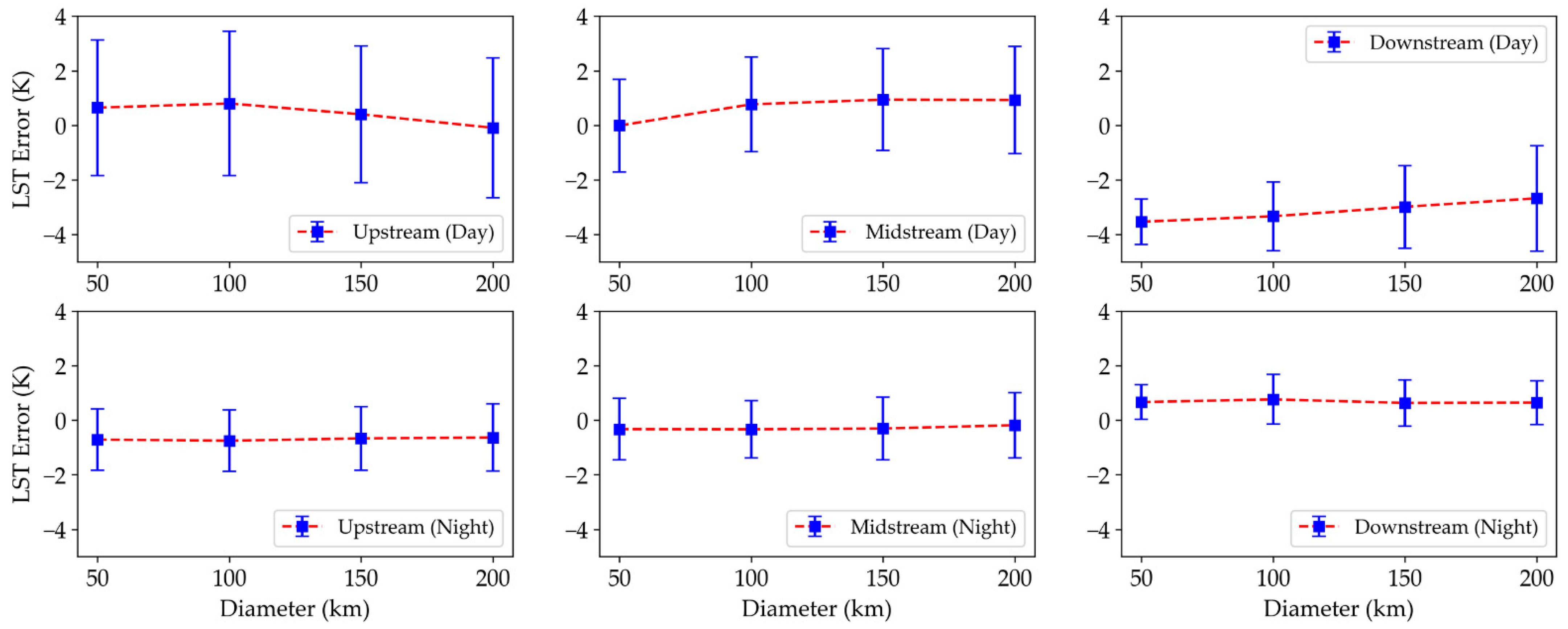
| Station | Daytime | Nighttime | ||||
|---|---|---|---|---|---|---|
| MBE (K) | RMSE (K) | R2 | MBE(K) | RMSE (K) | R2 | |
| DMZ | 2.57 | 4.35 | 0.92 | −2.96 | 4.24 | 0.94 |
| SDZ | 3.73 | 4.94 | 0.92 | −3.33 | 4.50 | 0.93 |
| HZZ | 3.90 | 6.20 | 0.90 | −3.36 | 4.63 | 0.93 |
| JCHM | 2.74 | 5.57 | 0.91 | −4.67 | 5.79 | 0.92 |
| HMZ | 4.91 | 6.42 | 0.95 | −4.08 | 5.03 | 0.96 |
| YKZ | 2.26 | 4.99 | 0.83 | −5.18 | 5.98 | 0.90 |
| ARC | 1.73 | 4.72 | 0.86 | −5.91 | 6.51 | 0.91 |
| DSL | 1.47 | 4.84 | 0.84 | −5.99 | 6.56 | 0.92 |
| HHL | 3.57 | 5.58 | 0.93 | −5.61 | 6.65 | 0.93 |
| SDQ | 0.69 | 3.94 | 0.94 | −5.85 | 6.82 | 0.93 |
| Statistic | Density Vegetation | Medium Vegetation | Sparse Vegetation | Bare Land | ||||
|---|---|---|---|---|---|---|---|---|
| Day | Night | Day | Night | Day | Night | Day | Night | |
| Mean | 2.67 | −4.13 | 1.89 | −5.47 | 2.28 | −5.70 | 4.14 | −3.99 |
| Min | 1.67 | −6.09 | 1.47 | −6.00 | 0.88 | −5.88 | 3.18 | −4.55 |
| Max | 3.68 | −2.95 | 2.30 | −4.59 | 3.67 | −5.52 | 5.12 | −3.38 |
| Station | Daytime | Nighttime | ||||
|---|---|---|---|---|---|---|
| MBE (K) | RMSE (K) | R2 | MBE (K) | RMSE (K) | R2 | |
| DMZ * | −0.01/0.81 | 3.47/2.82 | 0.92/0.94 | 0.19/−1.09 | 2.77/2.00 | 0.95/0.97 |
| SDZ * | 1.13/2.76 | 3.40/3.97 | 0.92/0.92 | −0.22/−2.24 | 2.93/3.41 | 0.94/0.92 |
| HZZ * | 0.04/0.65 | 4.64/3.09 | 0.91/0.95 | 0.92/−1.37 | 3.09/1.86 | 0.94/0.98 |
| JCHM * | −0.98/0.22 | 4.68/2.78 | 0.91/0.97 | −0.28/−2.35 | 3.24/2.78 | 0.93/0.98 |
| HMZ * | 1.02/4.50 | 4.00/5.07 | 0.95/0.99 | 0.29/−0.02 | 2.80/1.14 | 0.96/0.99 |
| YKZ * | 0.39/2.97 | 4.46/5.39 | 0.83/0.78 | 0.43/−0.58 | 2.86/2.80 | 0.91/0.93 |
| ARC * | −0.98/1.08 | 4.23/2.96 | 0.87/0.93 | 0.00/−1.23 | 2.57/2.33 | 0.92/0.96 |
| DSL * | −0.38/−0.18 | 4.60/4.00 | 0.84/0.86 | −0.37/−0.88 | 2.63/2.23 | 0.92/0.96 |
| HHL * | 1.42/3.98 | 4.45/5.13 | 0.93/0.96 | 0.12/−2.91 | 3.47/3.77 | 0.93/0.96 |
| SDQ * | −1.43/0.59 | 3.94/3.28 | 0.94/0.96 | −0.14/−2.30 | 3.40/2.87 | 0.93/0.98 |
| HCG | −0.51/1.42 | 4.80/3.48 | 0.89/0.92 | 0.90/0.09 | 2.69/2.50 | 0.93/0.95 |
| JYL | −0.08/3.80 | 4.05/5.98 | 0.84/0.78 | 0.57/−2.81 | 2.63/3.84 | 0.90/0.93 |
| EBZ | −1.27/0.59 | 4.77/3.10 | 0.85/0.89 | 0.14/−1.08 | 2.49/1.93 | 0.91/0.98 |
| HYZ | −3.56/−2.91 | 5.66/4.91 | 0.93/0.95 | 0.03/−2.59 | 3.01/3.20 | 0.94/0.97 |
| SSW | −1.19/−0.45 | 5.00/3.44 | 0.90/0.94 | −0.36/−2.38 | 3.12/2.91 | 0.94/0.98 |
| All Stations | −0.43/1.32 | 4.41/3.96 | 0.90/0.92 | 0.15/−1.58 | 2.91/2.64 | 0.93/0.96 |
| Station | Daytime | Nighttime | ||||
|---|---|---|---|---|---|---|
| MBE (K) | RMSE (K) | R2 | MBE (K) | RMSE (K) | R2 | |
| Calibration stations | 0.02 | 4.19 | 0.90 | 0.09 | 2.98 | 0.93 |
| Independent stations | −1.32 | 4.86 | 0.88 | 0.26 | 2.79 | 0.92 |
| All stations | −0.43 | 4.41 | 0.90 | 0.15 | 2.91 | 0.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Che, T.; Wang, J.; Liang, J.; Zhang, Y.; Ren, Z. Reconstruction of the Daily MODIS Land Surface Temperature Product Using the Two-Step Improved Similar Pixels Method. Remote Sens. 2021, 13, 1671. https://doi.org/10.3390/rs13091671
Tan J, Che T, Wang J, Liang J, Zhang Y, Ren Z. Reconstruction of the Daily MODIS Land Surface Temperature Product Using the Two-Step Improved Similar Pixels Method. Remote Sensing. 2021; 13(9):1671. https://doi.org/10.3390/rs13091671
Chicago/Turabian StyleTan, Junlei, Tao Che, Jian Wang, Ji Liang, Yang Zhang, and Zhiguo Ren. 2021. "Reconstruction of the Daily MODIS Land Surface Temperature Product Using the Two-Step Improved Similar Pixels Method" Remote Sensing 13, no. 9: 1671. https://doi.org/10.3390/rs13091671
APA StyleTan, J., Che, T., Wang, J., Liang, J., Zhang, Y., & Ren, Z. (2021). Reconstruction of the Daily MODIS Land Surface Temperature Product Using the Two-Step Improved Similar Pixels Method. Remote Sensing, 13(9), 1671. https://doi.org/10.3390/rs13091671