Improved Hydrological Loading Models in South America: Analysis of GPS Displacements Using M-SSA
Abstract
1. Introduction
2. Materials and Methods
2.1. Loading Models
2.1.1. General Circulation Models
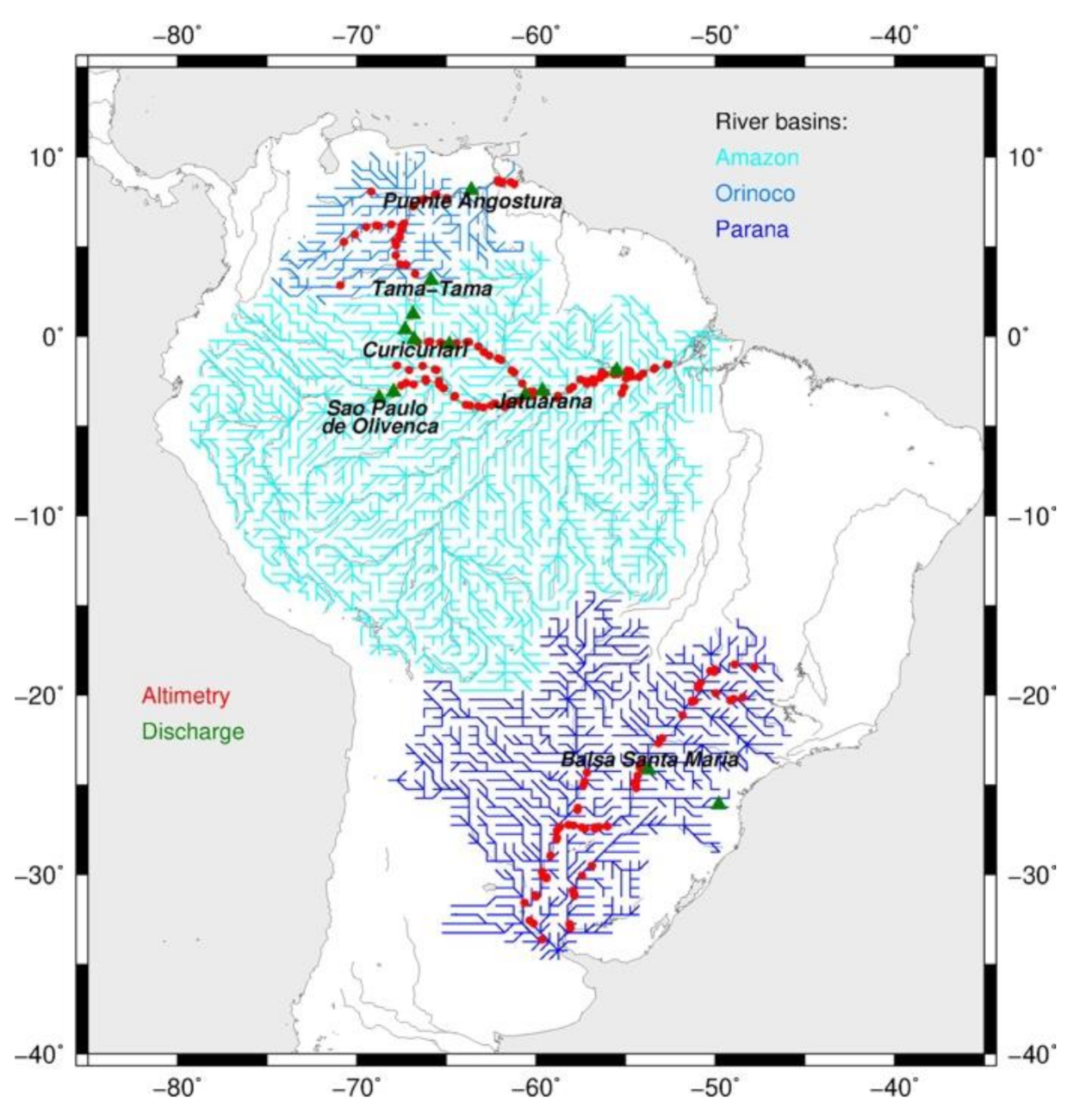
2.1.2. River Modelling
2.1.3. Flow Velocity
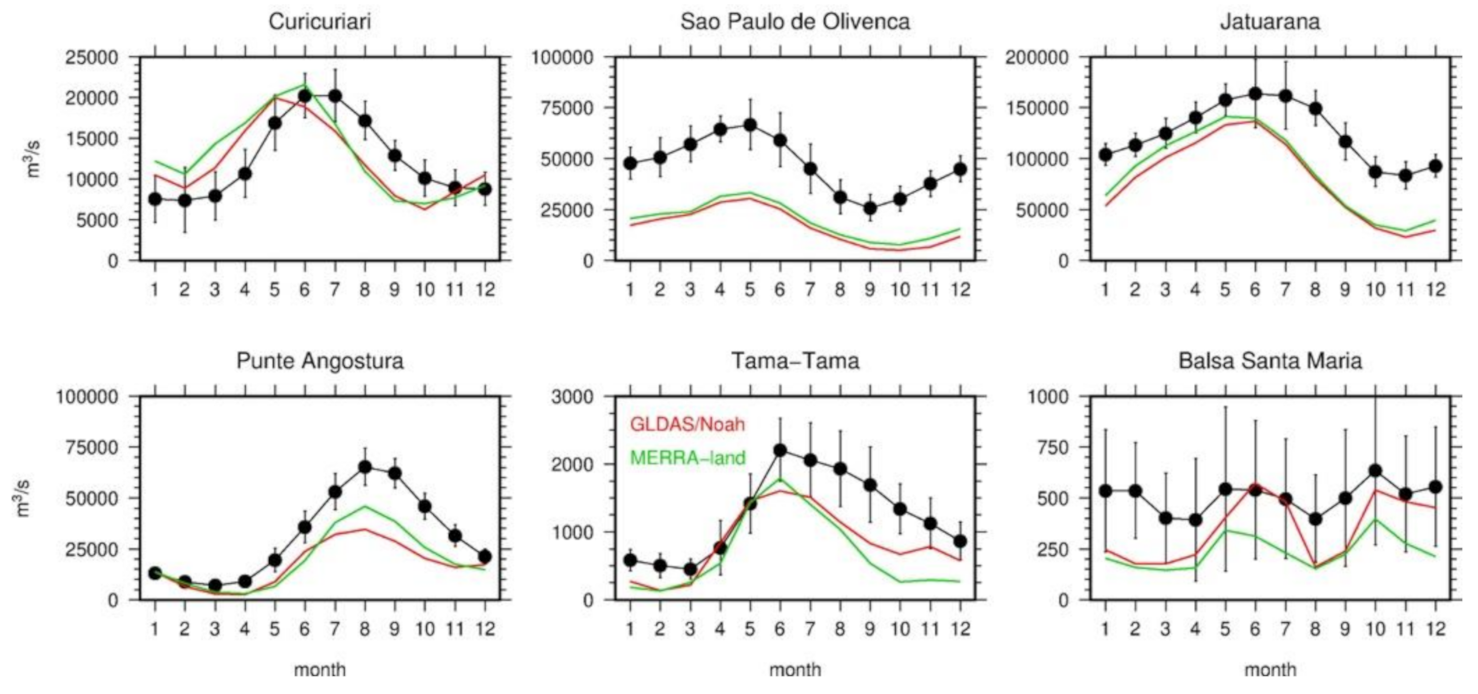
2.1.4. Validation of the River Models
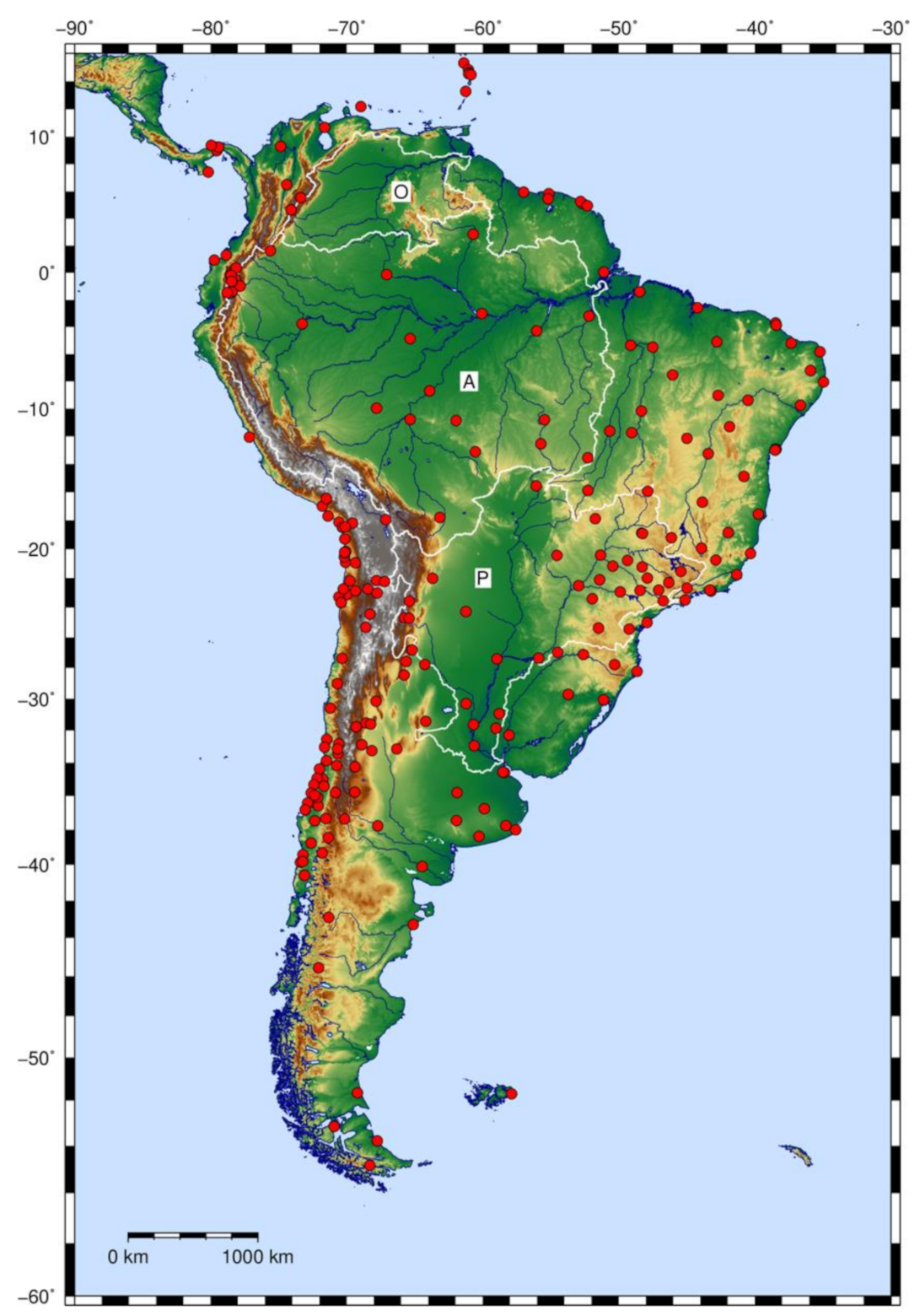
2.2. GNSS Time Series
2.3. Multichannel Singular Spectrum Analysis (M-SSA)
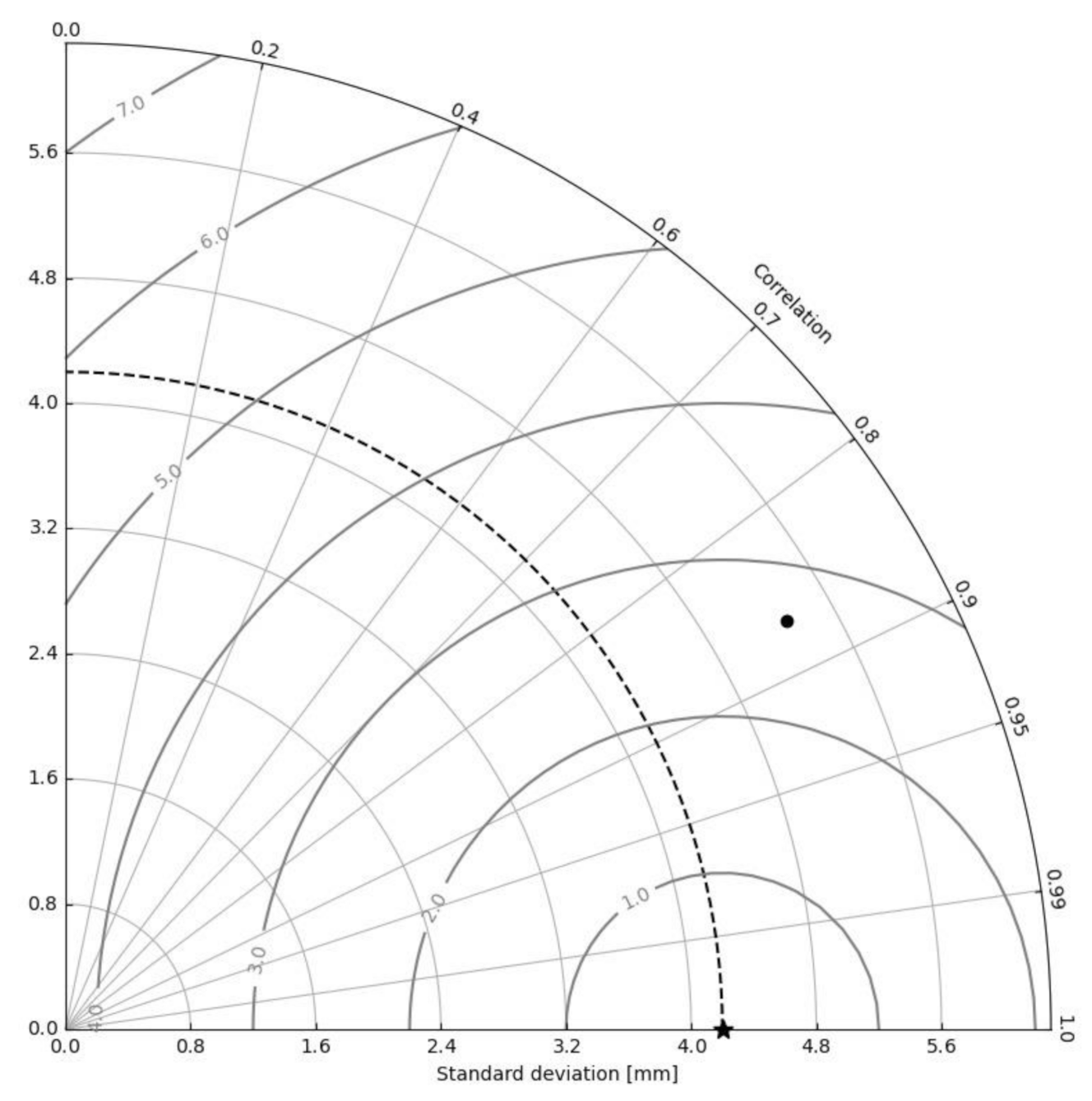
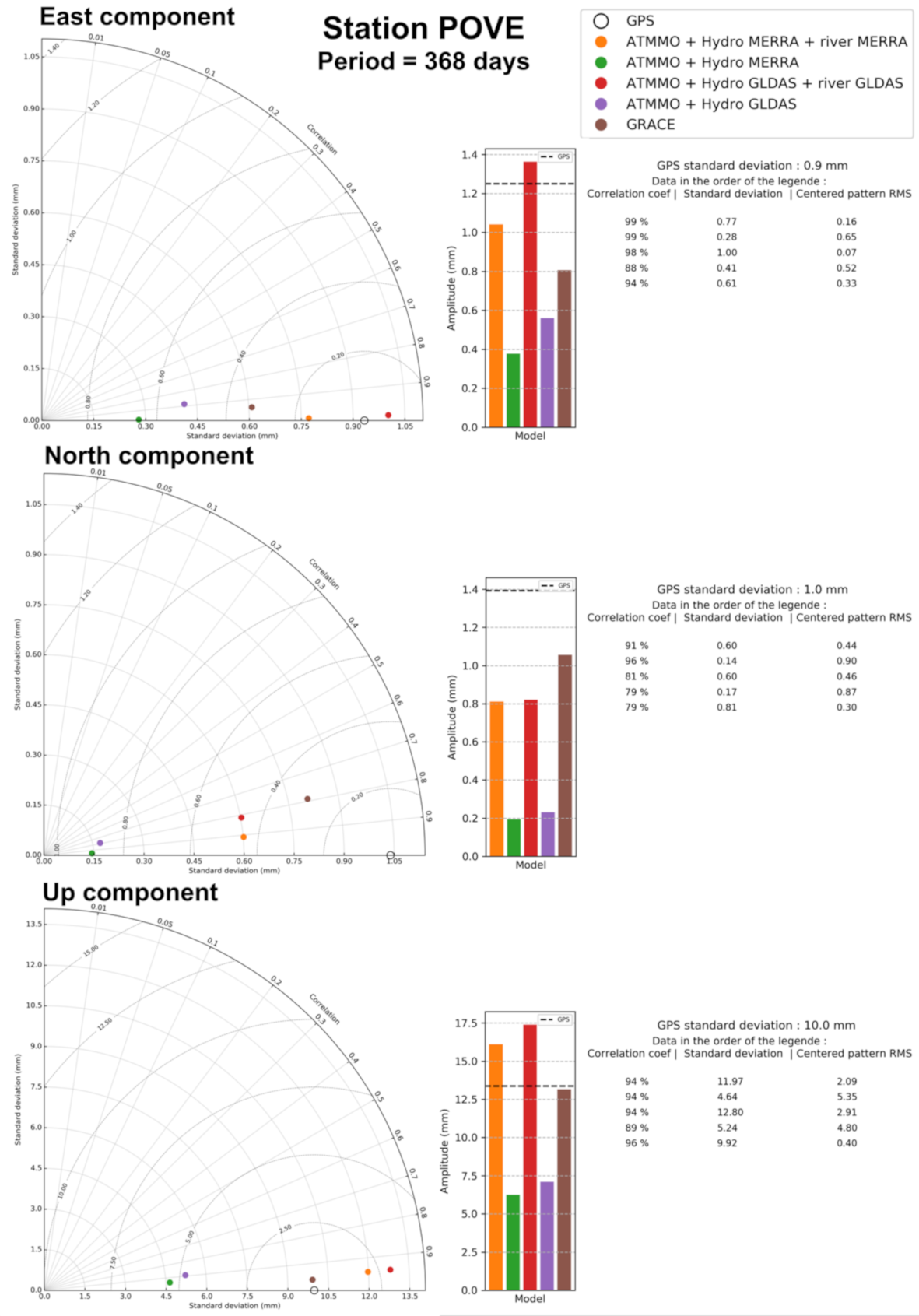
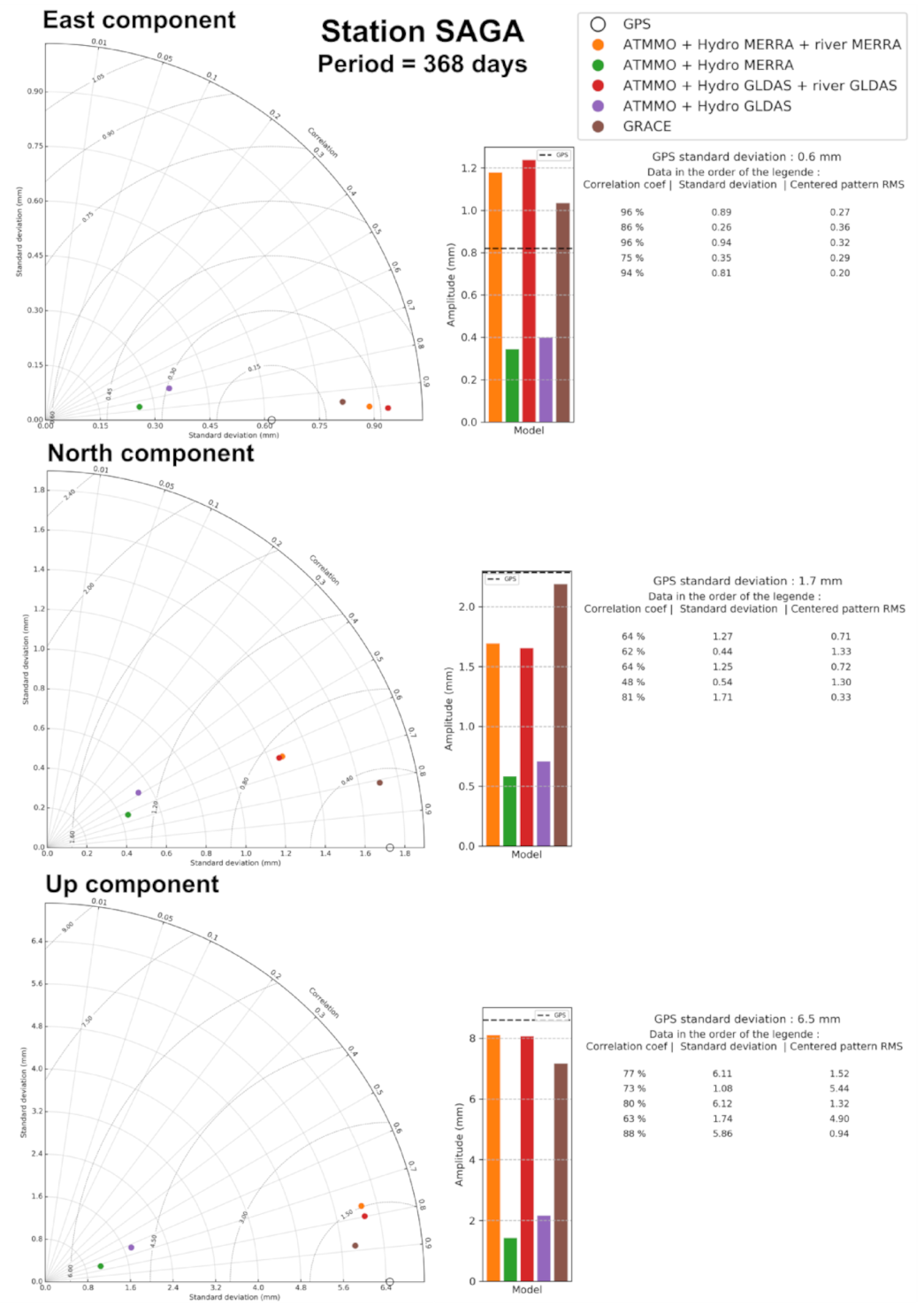
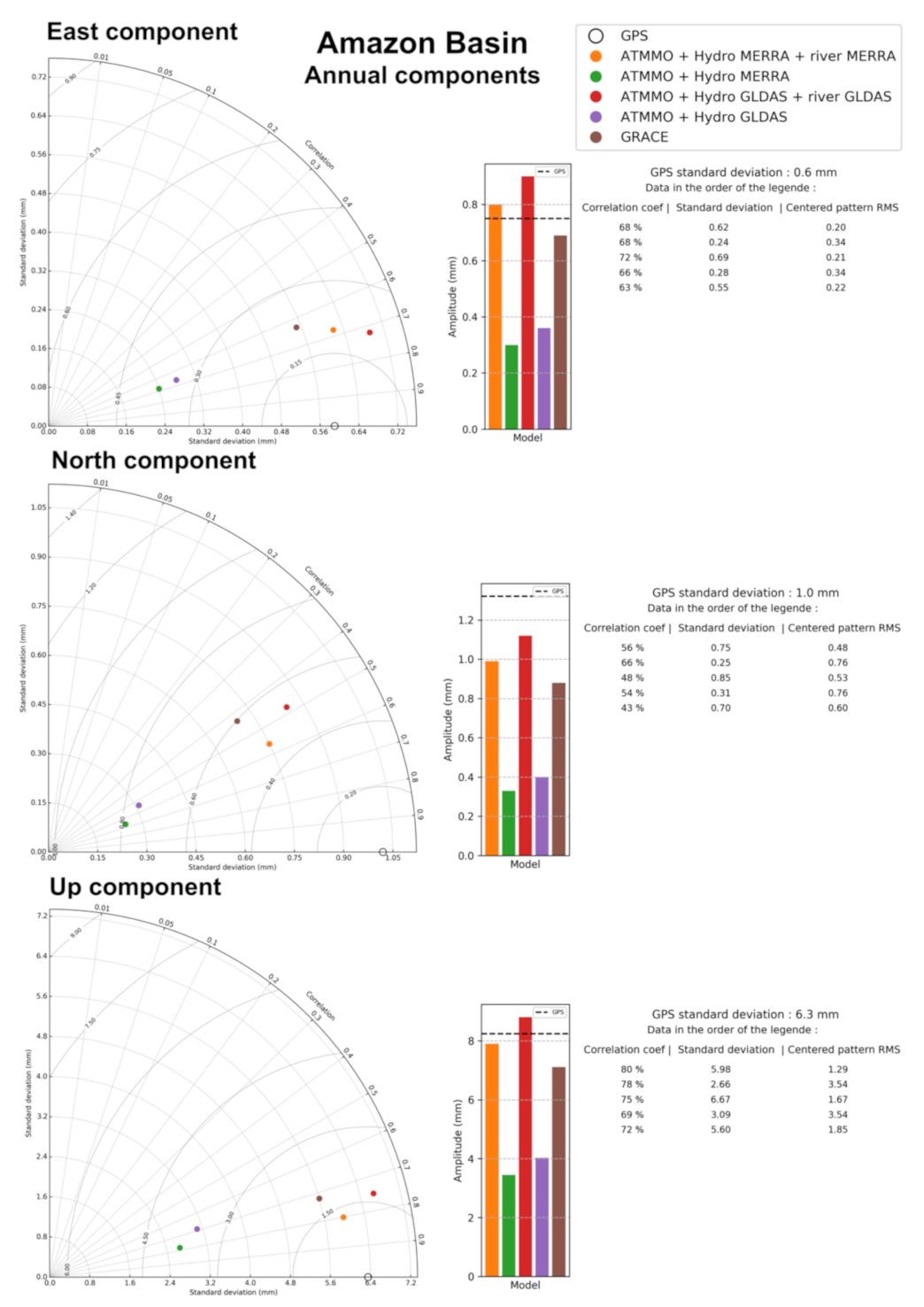
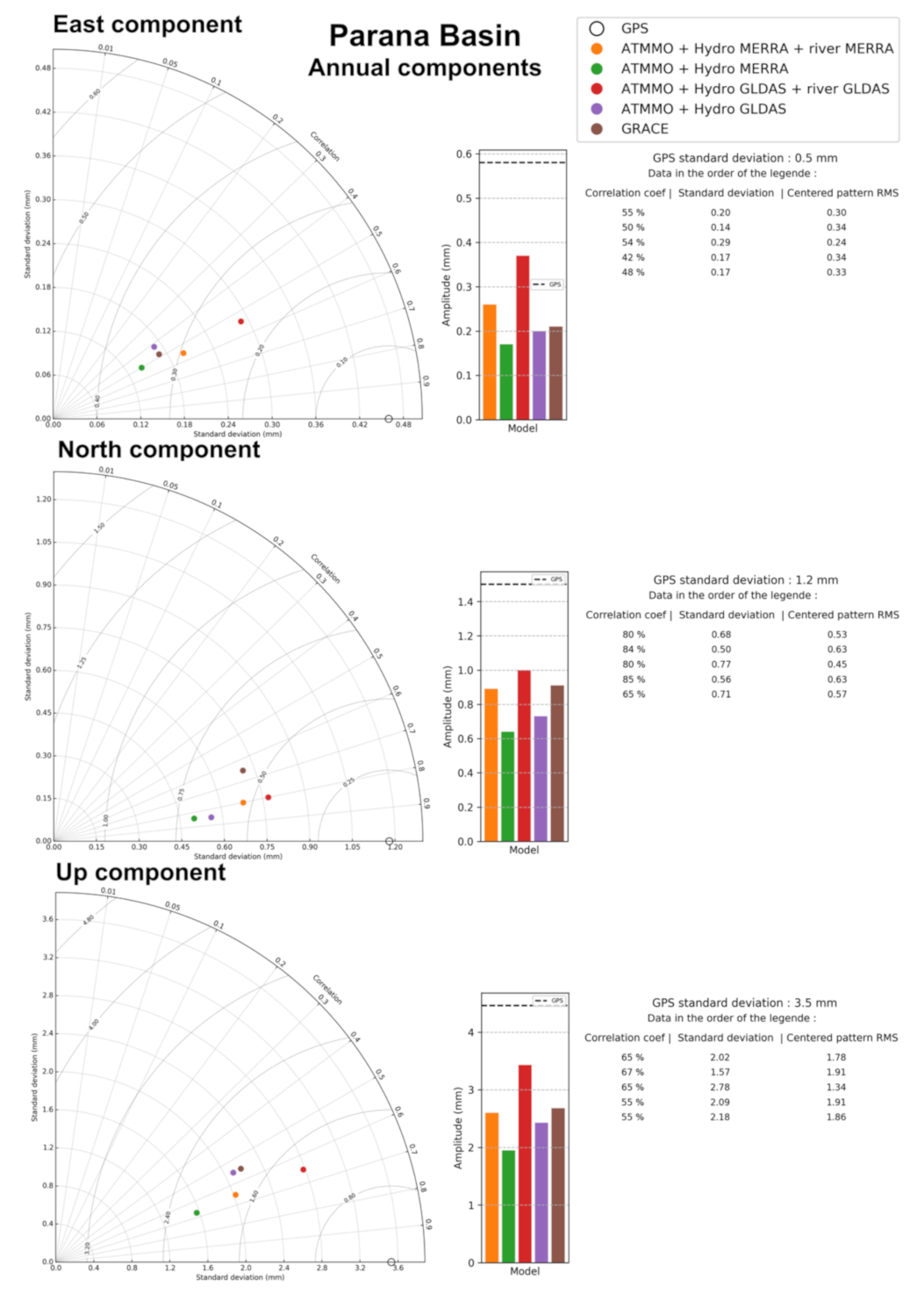
2.4. Taylor Diagram
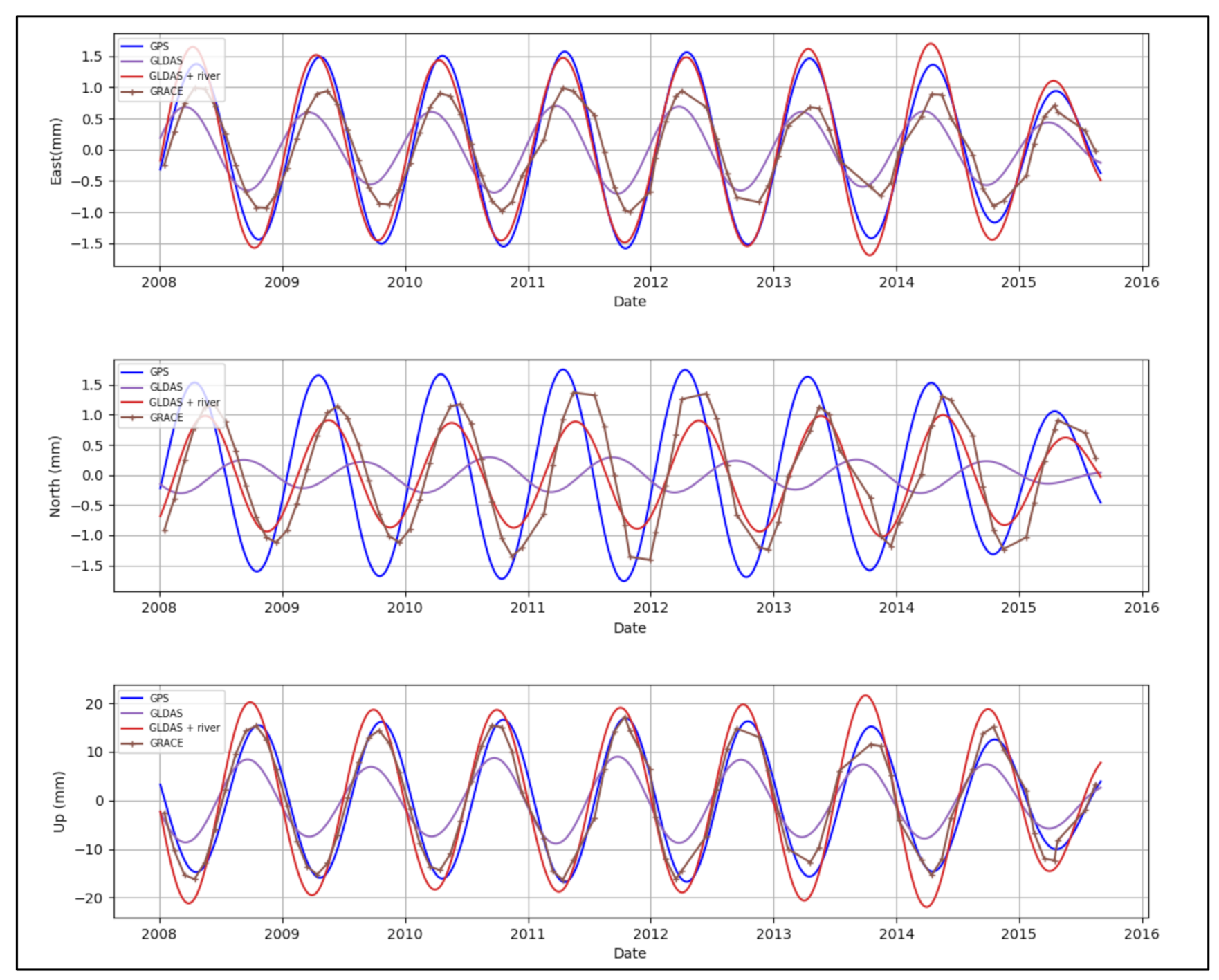
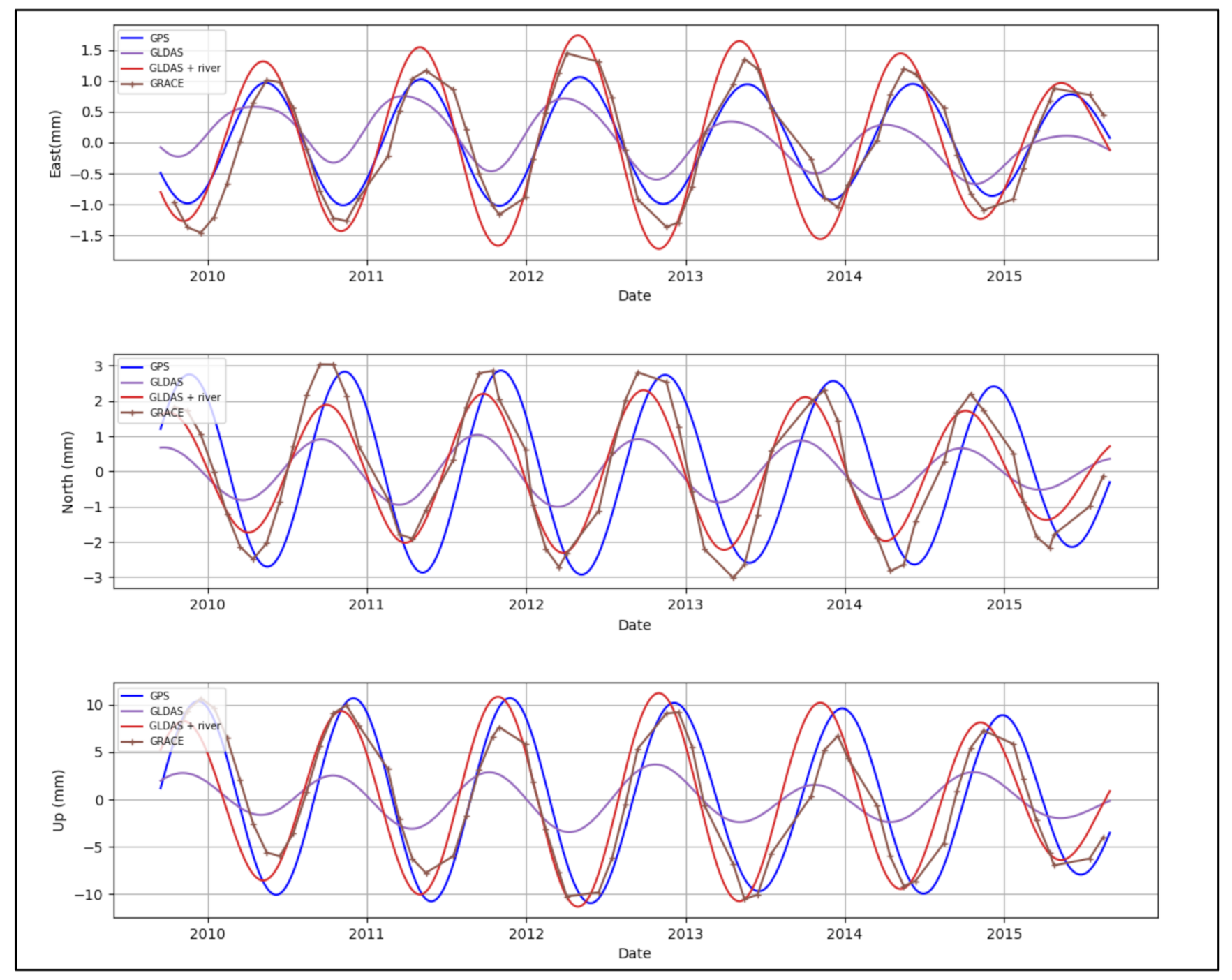
3. Results
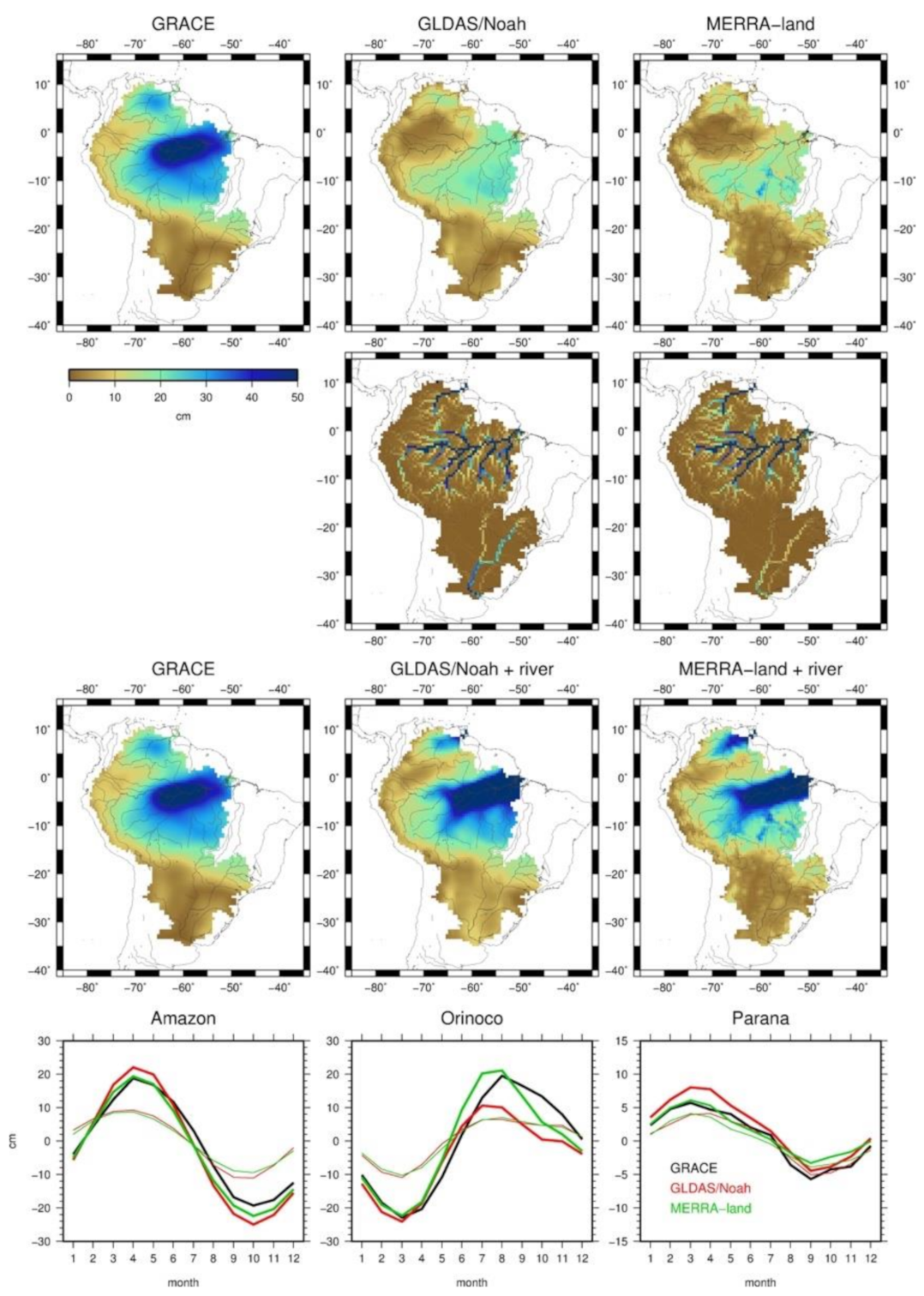
3.1. Annual Signal Amplitude
3.2. Correlation Coefficient between the Models and GPS
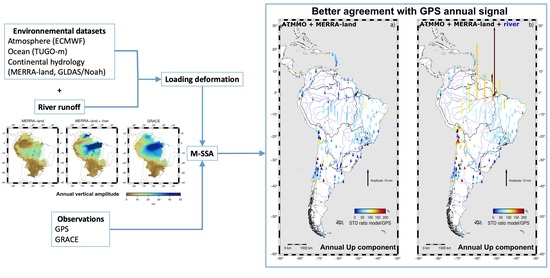
3.3. Model Contribution to Explain GPS Annual Signal
3.4. Centered RMS (CRMS) between the Models and GPS
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A New Global Mode of Earth Deformation: Seasonal Cycle Detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [PubMed]
- King, M.A.; Altamimi, Z.; Boehm, J.; Bos, M.; Dach, R.; Elosegui, P.; Fund, F.; Hernández-Pajares, M.; Lavallee, D.; Mendes Cerveira, P.J.; et al. Improved Constraints on Models of Glacial Isostatic Adjustment: A Review of the Contribution of Ground-Based Geodetic Observations. Surv. Geophys. 2010, 31, 465–507. [Google Scholar] [CrossRef]
- Reager, J.T.; Gardner, A.S.; Famiglietti, J.S.; Wiese, D.N.; Eicker, A.; Lo, M.-H. A Decade of Sea Level Rise Slowed by Climate-Driven Hydrology. Science 2016, 351, 699–703. [Google Scholar] [CrossRef] [PubMed]
- Wöppelmann, G.; Marcos, M. Vertical Land Motion as a Key to Understanding Sea Level Change and Variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Dangendorf, S.; Marcos, M.; Spada, G.; Wöppelmann, G. Uncertainty of the 20th Century Sea-Level Rise Due to Vertical Land Motion Errors. Earth Planet. Sci. Lett. 2017, 473, 24–32. [Google Scholar] [CrossRef]
- Vergnolle, M.; Bouin, M.-N.; Morel, L.; Masson, F.; Durand, S.; Nicolas, J.; Melachroinos, S.A. GPS Estimates of Ocean Tide Loading in NW-France: Determination of Ocean Tide Loading Constituents and Comparison with a Recent Ocean Tide Model. Geophys. J. Int. 2008, 173, 444–458. [Google Scholar] [CrossRef]
- van Dam, T.; Collilieux, X.; Wuite, J.; Altamimi, Z.; Ray, J. Nontidal Ocean Loading: Amplitudes and Potential Effects in GPS Height Time Series. J. Geod. 2012, 86, 1043–1057. [Google Scholar] [CrossRef]
- Tregoning, P.; van Dam, T. Atmospheric Pressure Loading Corrections Applied to GPS Data at the Observation Level. Geophys. Res. Lett. 2005, 32, L22310. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.; Landerer, F.W. Seasonal Variation in Total Water Storage in California Inferred from GPS Observations of Vertical Land Motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Fenoglio-Marc, L.; Scharroo, R.; Annunziato, A.; Mendoza, L.; Becker, M.; Lillibridge, J. Cyclone Xaver Seen by Geodetic Observations. Geophys. Res. Lett. 2015, 42, 9925–9932. [Google Scholar] [CrossRef]
- Penna, N.T.; King, M.A.; Stewart, M.P. GPS Height Time Series: Short-Period Origins of Spurious Long-Period Signals. J. Geophys. Res. Solid Earth 2007, 112, B02402. [Google Scholar] [CrossRef]
- Ferenc, M.; Nicolas, J.; van Dam, T.; Polidori, L.; Rigo, A.; Vernant, P. An Estimate of the Influence of Loading Effects on Tectonic Velocities in the Pyrenees. Stud. Geophys. Geod. 2014, 58, 56–75. [Google Scholar] [CrossRef]
- Collilieux, X.; van Dam, T.; Ray, J.; Coulot, D.; Métivier, L.; Altamimi, Z. Strategies to Mitigate Aliasing of Loading Signals While Estimating GPS Frame Parameters. J. Geod. 2012, 86, 1–14. [Google Scholar] [CrossRef]
- Mémin, A.; Boy, J.-P.; Santamaría-Gómez, A. Correcting GPS Measurements for Non-Tidal Loading. GPS Solut. 2020, 24, 45. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Chen, J.; Famigliett, J.S.; Scanlon, B.R.; Rodell, M. Groundwater Storage Changes: Present Status from GRACE Observations. Surv. Geophys. 2016, 37, 397–417. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G. Contribution of GRACE Satellite Gravimetry in Global and Regional Hydrology, and in Ice Sheets Mass Balance. In Water Resources Management and Modeling; Nayak, P., Ed.; InTech Open: London, UK, 2012. [Google Scholar] [CrossRef][Green Version]
- Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L.; Kusche, J. Does GRACE See the Terrestrial Water Cycle “Intensifying”? J. Geophys. Res. Atmos. 2016, 121, 733–745. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Landerer, F.W. GPS as an Independent Measurement to Estimate Terrestrial Water Storage Variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Borsa, A.A.; Agnew, D.C.; Cayan, D.R. Ongoing Drought-Induced Uplift in the Western United States. Science 2014, 345, 1587–1590. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Terrestrial Water Storage Response to the 2012 Drought Estimated from GPS Vertical Position Anomalies. Geophys. Res. Lett. 2014, 41, 6145–6151. [Google Scholar] [CrossRef]
- Argus, D.F.; Landerer, F.W.; Wiese, D.N.; Martens, H.R.; Fu, Y.; Famiglietti, J.S.; Thomas, B.F.; Farr, T.G.; Moore, A.W.; Watkins, M.M. Sustained Water Loss in California’s Mountain Ranges During Severe Drought From 2012 to 2015 Inferred From GPS. J. Geophys. Res. Solid Earth 2017, 122, 10559–10585. [Google Scholar] [CrossRef]
- Knappe, E.; Bendick, R.; Martens, H.R.; Argus, D.F.; Gardner, W.P. Downscaling Vertical GPS Observations to Derive Watershed-Scale Hydrologic Loading in the Northern Rockies. Water Resour. Res. 2019, 55, 391–401. [Google Scholar] [CrossRef]
- Karegar, M.A.; Dixon, T.H.; Kusche, J.; Chambers, D.P. A New Hybrid Method for Estimating Hydrologically Induced Vertical Deformation From GRACE and a Hydrological Model: An Example From Central North America. J. Adv. Model. Earth Syst. 2018, 10, 1196–1217. [Google Scholar] [CrossRef]
- Carlson, G.; Shirzaei, M.; Werth, S.; Zhai, G.; Ojha, C. Seasonal and Long-Term Groundwater Unloading in the Central Valley Modifies Crustal Stress. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018490. [Google Scholar] [CrossRef]
- Frappart, F.; Minh, K.D.; L’Hermitte, J.; Cazenave, A.; Ramillien, G.; Le Toan, T.; Mognard-Campbell, N. Water Volume Change in the Lower Mekong from Satellite Altimetry and Imagery Data. Geophys. J. Int. 2006, 167, 570–584. [Google Scholar] [CrossRef]
- Han, S.-C.; Yeo, I.-Y.; Alsdorf, D.; Bates, P.; Boy, J.-P.; Kim, H.; Oki, T.; Rodell, M. Movement of Amazon Surface Water from Time-Variable Satellite Gravity Measurements and Implications for Water Cycle Parameters in Land Surface Models. Geochem. Geophys. Geosystems 2010, 11, Q09007. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Bouin, M.-N.; Santamaría-Gómez, A.; Boy, J.-P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; de Linage, C.; et al. Hydrological Deformation Induced by the West African Monsoon: Comparison of GPS, GRACE and Loading Models. J. Geophys. Res. Solid Earth 2012, 117, B05409. [Google Scholar] [CrossRef]
- Dill, R.; Klemann, V.; Dobslaw, H. Relocation of River Storage From Global Hydrological Models to Georeferenced River Channels for Improved Load-Induced Surface Displacements. J. Geophys. Res. Solid Earth 2018, 123, 7151–7164. [Google Scholar] [CrossRef]
- Pinel, S.; Bonnet, M.-P.; Silva, J.S.D.; Sampaio, T.C.; Garnier, J.; Catry, T.; Calmant, S.; Fragoso, C.R.; Moreira, D.; Marques, D.M.; et al. Flooding Dynamics Within an Amazonian Floodplain: Water Circulation Patterns and Inundation Duration. Water Resour. Res. 2020, 56, e2019WR026081. [Google Scholar] [CrossRef]
- Frappart, F.; Seoane, L.; Ramillien, G. Validation of GRACE-Derived Terrestrial Water Storage from a Regional Approach over South America. Remote Sens. Environ. 2013, 137, 69–83. [Google Scholar] [CrossRef]
- Knowles, L.A.; Bennett, R.A.; Harig, C. Vertical Displacements of the Amazon Basin From GRACE and GPS. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018105. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Ferreira, V.G. Assessing Land Water Storage Dynamics over South America. J. Hydrol. 2020, 580, 124339. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing Global Water Storage Variability from GRACE: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, V.G.; Montecino, H.D.; Ndehedehe, C.E.; del Rio, R.A.; Cuevas, A.; de Freitas, S.R.C. Determining Seasonal Displacements of Earth’s Crust in South America Using Observations from Space-Borne Geodetic Sensors and Surface-Loading Models. Earth Planets Space 2019, 71, 84. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Ndehedehe, C.E.; Montecino, H.C.; Yong, B.; Yuan, P.; Abdalla, A.; Mohammed, A.S. Prospects for Imaging Terrestrial Water Storage in South America Using Daily GPS Observations. Remote Sens. 2019, 11, 679. [Google Scholar] [CrossRef]
- Bevis, M.; Alsdorf, D.; Kendrick, E.; Fortes, L.P.; Forsberg, B.; Smalley, R.; Becker, J. Seasonal Fluctuations in the Mass of the Amazon River System and Earth’s Elastic Response. Geophys. Res. Lett. 2005, 32, L16308. [Google Scholar] [CrossRef]
- Moreira, D.M.; Calmant, S.; Perosanz, F.; Xavier, L.; Filho, O.C.R.; Seyler, F.; Monteiro, A.C. Comparisons of Observed and Modeled Elastic Responses to Hydrological Loading in the Amazon Basin. Geophys. Res. Lett. 2016, 43, 9604–9610. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global Models Underestimate Large Decadal Declining and Rising Water Storage Trends Relative to GRACE Satellite Data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef]
- Solman, S.A. Regional Climate Modeling over South America: A Review. Adv. Meteorol. 2013, 2013, 504357. Available online: https://www.hindawi.com/journals/amete/2013/504357/ (accessed on 7 March 2021). [CrossRef]
- Li, Z.; Yue, J.; Li, W.; Lu, D. Investigating Mass Loading Contributes of Annual GPS Observations for the Eurasian Plate. J. Geodyn. 2017, 111, 43–49. [Google Scholar] [CrossRef]
- Klos, A.; Gruszczynska, M.; Bos, M.S.; Boy, J.-P.; Bogusz, J. Estimates of Vertical Velocity Errors for IGS ITRF2014 Stations by Applying the Improved Singular Spectrum Analysis Method and Environmental Loading Models. Pure Appl. Geophys. 2018, 175, 1823–1840. [Google Scholar] [CrossRef]
- Prevost, P.; Chanard, K.; Fleitout, L.; Calais, E.; Walwer, D.; van Dam, T.; Ghil, M. Data-Adaptive Spatio-Temporal Filtering of GRACE Data. Geophys. J. Int. 2019, 219, 2034–2055. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Lannoy, G.J.M.D.; Forman, B.A.; Liu, Q.; Mahanama, S.P.P.; Touré, A. Assessment and Enhancement of MERRA Land Surface Hydrology Estimates. J. Clim. 2011, 24, 6322–6338. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F. Modeling the Barotropic Response of the Global Ocean to Atmospheric Wind and Pressure Forcing—Comparisons with Observations. Geophys. Res. Lett. 2003, 30, 1275. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Sabaka, T.J.; Loomis, B.D.; Arendt, A.A.; McCarthy, J.J.; Camp, J. Antarctica, Greenland and Gulf of Alaska Land-Ice Evolution from an Iterated GRACE Global Mascon Solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Petrov, L.; Boy, J.-P. Study of the Atmospheric Pressure Loading Signal in Very Long Baseline Interferometry Observations. J. Geophys. Res. Solid Earth 2004, 109, B03405. [Google Scholar] [CrossRef]
- Oki, T.; Nishimura, T.; Dirmeyer, P. Assessment of Annual Runoff from Land Surface Models Using Total Runoff Integrating Pathways (TRIP). J. Meteorol. Soc. Jpn. Ser. II 1999, 77, 235–255. [Google Scholar] [CrossRef]
- Miller, J.R.; Russell, G.L.; Caliri, G. Continental-Scale River Flow in Climate Models. J. Clim. 1994, 7, 914–928. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Arsen, A.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A Lake Database to Monitor in the Near Real Time Water Level and Storage Variations from Remote Sensing Data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An Overview of MODIS Land Data Processing and Product Status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006 2015. NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Boy, J.-P. Lake and Reservoir Volume Variations in South America from Radar Altimetry, ICESat Laser Altimetry, and GRACE Time-Variable Gravity. Adv. Space Res. 2020. [Google Scholar] [CrossRef]
- Blewitt, G.; Hammond, W.; Kreemer, C. Harnessing the GPS Data Explosion for Interdisciplinary Science. Eos 2018, 99. [Google Scholar] [CrossRef]
- Bertiger, W.; Bar-Sever, Y.; Dorsey, A.; Haines, B.; Harvey, N.; Hemberger, D.; Heflin, M.; Lu, W.; Miller, M.; Moore, A.W.; et al. GipsyX/RTGx, a New Tool Set for Space Geodetic Operations and Research. Adv. Space Res. 2020, 66, 469–489. [Google Scholar] [CrossRef]
- IERS. IERS Conventions. IERS Technical Note No. 36; Petit, G., Luzum, B., Eds.; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the Global Ocean Tides: Modern Insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS Contribution to ITRF2014. J. Geod. 2016, 90, 611–630. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast Error Analysis of Continuous GNSS Observations with Missing Data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Vautard, R.; Ghil, M. Singular Spectrum Analysis in Nonlinear Dynamics, with Applications to Paleoclimatic Time Series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-Spectrum Analysis: A Toolkit for Short, Noisy Chaotic Signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Ghil, M.; Vautard, R. Interdecadal Oscillations and the Warming Trend in Global Temperature Time Series. Nature 1991, 350, 324–327. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced Spectral Methods for Climatic Time Series. Rev. Geophys. 2002, 40, 1–3. [Google Scholar] [CrossRef]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular Spectrum Analysis for Modeling Seasonal Signals from GPS Time Series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Y.; Wu, S.; Zhang, K. An Enhanced Singular Spectrum Analysis Method for Constructing Nonsecular Model of GPS Site Movement. J. Geophys. Res. Solid Earth 2016, 121, 2193–2211. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Gruszczynska, M. Investigation of Time_changeable Seasonal Components in the GPS Height Time Series: A Case Study for Central Europe. Acta Geodyn. Geomater. 2016, 13, 281–289. [Google Scholar] [CrossRef]
- Klos, A.; Bos, M.S.; Bogusz, J. Detecting Time-Varying Seasonal Signal in GPS Position Time Series with Different Noise Levels. GPS Solut. 2017, 22, 21. [Google Scholar] [CrossRef]
- Golyandina, N. Particularities and Commonalities of Singular Spectrum Analysis as a Method of Time Series Analysis and Signal Processing. WIREs Comput. Stat. 2020, 12, e1487. [Google Scholar] [CrossRef]
- Walwer, D.; Calais, E.; Ghil, M. Data-Adaptive Detection of Transient Deformation in Geodetic Networks. J. Geophys. Res. Solid Earth 2016, 121, 2129–2152. [Google Scholar] [CrossRef]
- Gruszczynska, M.; Rosat, S.; Klos, A.; Gruszczynski, M.; Bogusz, J. Multichannel Singular Spectrum Analysis in the Estimates of Common Environmental Effects Affecting GPS Observations. Pure Appl. Geophys. 2018, 175, 1805–1822. [Google Scholar] [CrossRef]
- Hassani, H.; Mahmoudvand, R.; Zokaei, M. Separability and Window Length in Singular Spectrum Analysis. Comptes Rendus Math. 2011, 349, 987–990. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in Astronomical Time Series Analysis. II—Statistical Aspects of Spectral Analysis of Unevenly Spaced Data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in Astronomical Time Series Analysis. III. Fourier Transforms, Autocorrelation Functions, and Cross-Correlation Functions of Unevenly Spaced Data. Astrophys. J. 1989, 343, 874–887. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Springer, A.; Karegar, M.A.; Kusche, J.; Keune, J.; Kurtz, W.; Kollet, S. Evidence of daily hydrological loading in GPS time series over Europe. J. Geod. 2019, 93, 2145–2153. [Google Scholar] [CrossRef]
- Duan, W.; Maskey, S.; Chaffe, P.L.B.; Luo, P.; He, B.; Wu, Y.; Hou, J. Recent Advancement in Remote Sensing Technology for Hydrology Analysis and Water Resources Management. Remote Sens. 2021, 13, 1097. [Google Scholar] [CrossRef]

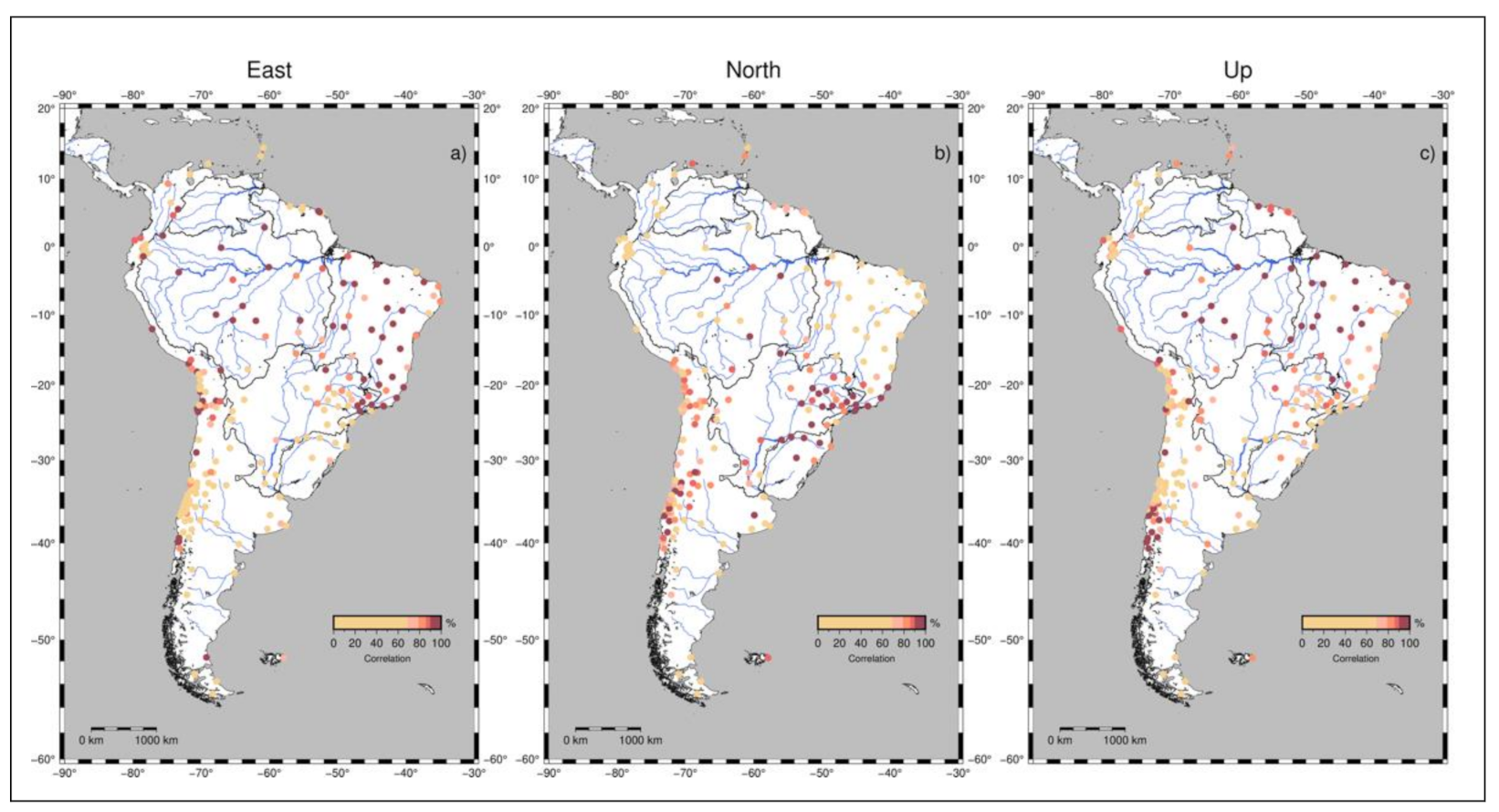
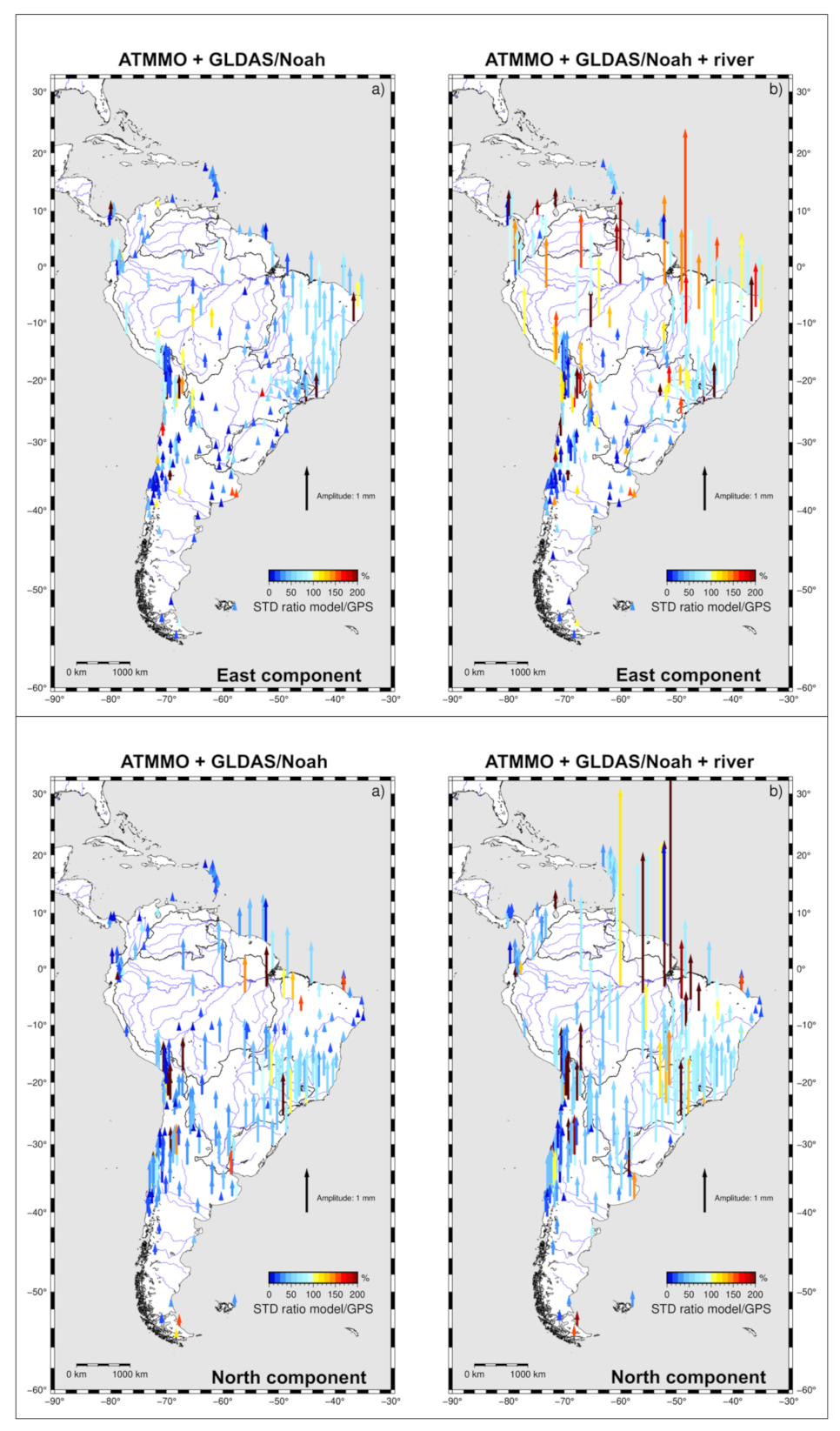
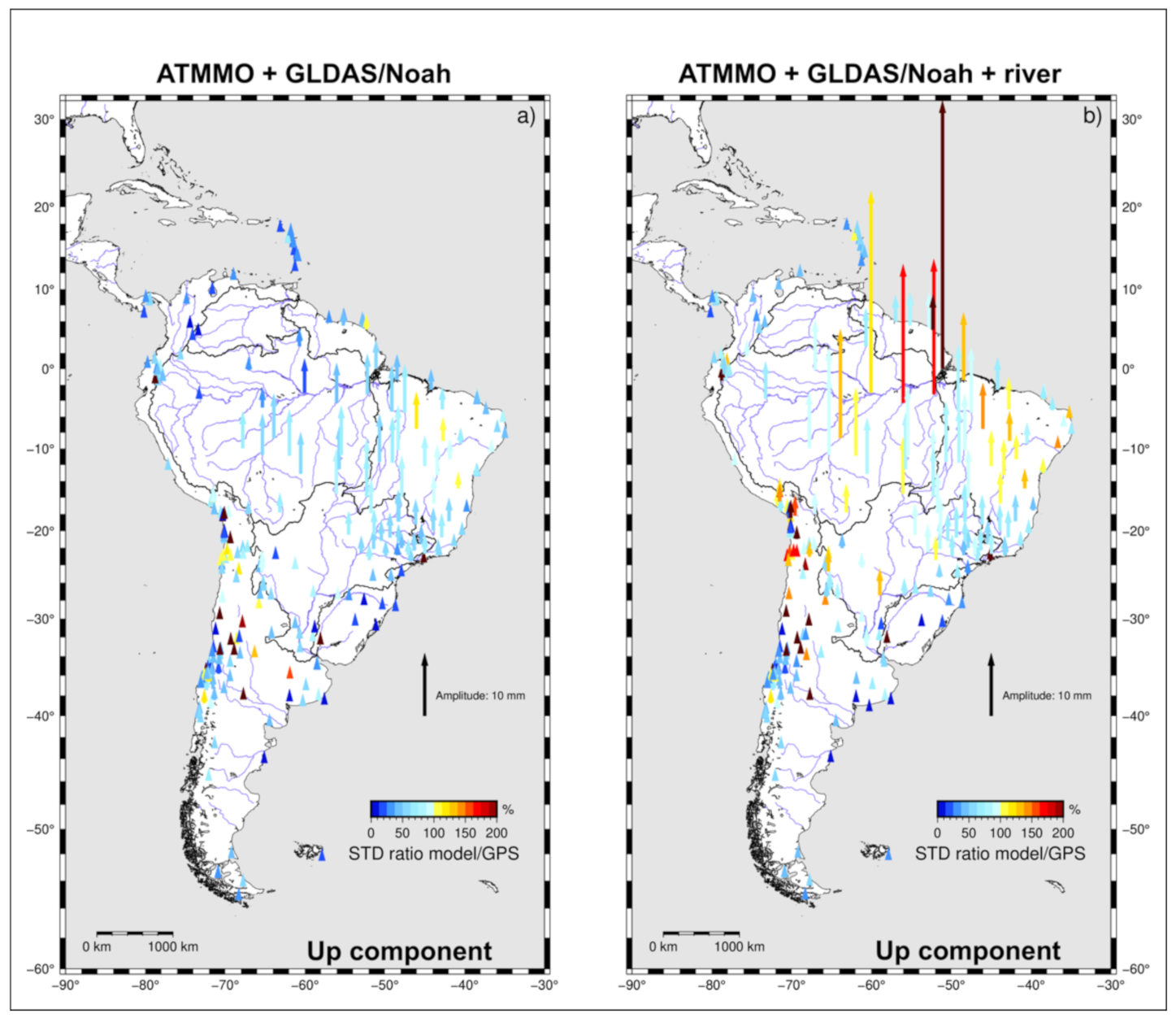
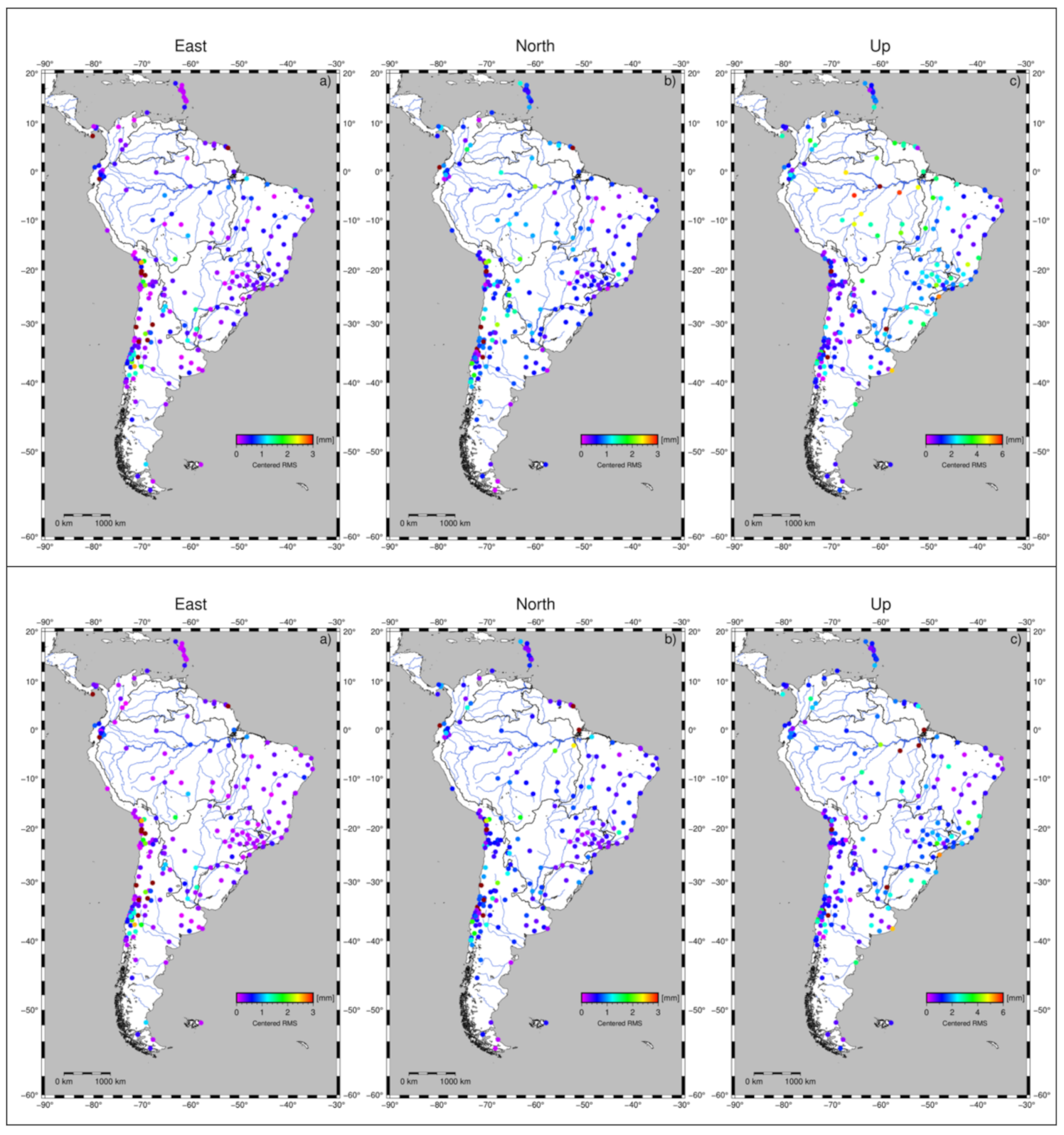
| Model | GRACE | GLDAS/Noah | MERRA-Land | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zone | All | AB | PB | All | AB | PB | All | AB | PB | ||||||
| Class | nR | wR | nR | wR | nR | wR | nR | wR | nR | wR | nR | wR | |||
| East | |||||||||||||||
| ≥90% | 14.2 | 20.0 | 15.0 | 22.7 | 24.7 | 36.0 | 44.0 | 17.5 | 15.0 | 19.4 | 21.1 | 28.0 | 36.0 | 10.0 | 12.5 |
| [80%; 90%[ | 10.5 | 20.0 | 17.5 | 11.7 | 10.9 | 16.0 | 16.0 | 5.0 | 7.5 | 11.7 | 12.1 | 24.0 | 16.0 | 17.5 | 15.0 |
| [70%; 80%[ | 11.7 | 38.0 | 7.5 | 5.7 | 8.1 | 16.0 | 8.0 | 0.0 | 10.0 | 9.3 | 8.5 | 12.0 | 8.0 | 5.0 | 7.5 |
| <70% | 63.6 | 32.0 | 60.0 | 59.9 | 56.3 | 32.0 | 32.0 | 77.5 | 67.5 | 59.5 | 58.3 | 36.0 | 40.0 | 67.5 | 65.0 |
| North | |||||||||||||||
| ≥90% | 4.9 | 4.0 | 15.0 | 26.3 | 15.4 | 20.0 | 8.0 | 55.0 | 37.5 | 30.8 | 20.2 | 24.0 | 12.0 | 50.0 | 42.5 |
| [80%; 90%[ | 9.7 | 12.0 | 20.0 | 14.2 | 18.2 | 4.0 | 12.0 | 15.0 | 27.5 | 18.2 | 17.4 | 12.0 | 4.0 | 20.0 | 15.0 |
| [70%; 80%[ | 14.6 | 8.0 | 17.5 | 12.1 | 14.2 | 4.0 | 8.0 | 12.5 | 12.5 | 13.4 | 15.4 | 12.0 | 4.0 | 15.0 | 20.0 |
| <70% | 70.9 | 76.0 | 47.5 | 47.4 | 52.2 | 72.0 | 72.0 | 17.5 | 22.5 | 37.7 | 47.0 | 52.0 | 80.0 | 15.0 | 22.5 |
| Up | |||||||||||||||
| ≥90% | 15.8 | 44.0 | 12.5 | 12.6 | 17.8 | 16.0 | 40.0 | 0.0 | 0.0 | 22.3 | 26.3 | 36.0 | 40.0 | 5.0 | 12.5 |
| [80%; 90%[ | 15.4 | 8.0 | 22.5 | 20.6 | 19.8 | 28.0 | 20.0 | 12.5 | 25.0 | 19.4 | 17.0 | 20.0 | 24.0 | 25.0 | 20.0 |
| [70%; 80%[ | 10.1 | 4.0 | 7.5 | 14.6 | 14.2 | 16.0 | 12.0 | 25.0 | 25.0 | 15.0 | 12.1 | 16.0 | 12.0 | 30.0 | 25.0 |
| <70% | 58.7 | 44.0 | 57.5 | 52.2 | 48.2 | 40.0 | 28.0 | 62.5 | 50.0 | 43.3 | 44.5 | 38.0 | 24.0 | 40.0 | 42.5 |
| Model | GRACE | GLDAS/Noah | MERRA-Land | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zone | All | AB | PB | All | AB | PB | All | AB | PB | ||||||
| Class | nR | wR | nR | wR | nR | wR | nR | wR | nR | wR | nR | wR | |||
| East | |||||||||||||||
| <50% | 42.1 | 20.0 | 60.0 | 61.1 | 35.6 | 68.0 | 16.0 | 62.5 | 32.5 | 64.8 | 39.7 | 60.0 | 16.0 | 82.5 | 50.0 |
| [50%; 85%[ | 33.6 | 40.0 | 37.5 | 22.3 | 24.7 | 8.0 | 16.0 | 30.0 | 37.5 | 23.1 | 29.6 | 20.0 | 24.0 | 17.5 | 37.5 |
| [85%; 115%[ | 9.7 | 8.0 | 2.5 | 8.5 | 15.4 | 12.0 | 24.0 | 5.0 | 15.0 | 5.7 | 10.5 | 16.0 | 16.0 | 0.0 | 7.5 |
| [115%; 150%[ | 6.1 | 12.0 | 0.0 | 2.4 | 10.5 | 8.0 | 16.0 | 0.0 | 7.5 | 1.6 | 10.9 | 4.0 | 20.0 | 0.0 | 5.0 |
| ≥150% | 8.5 | 20.0 | 0.0 | 5.7 | 13.8 | 4.0 | 28.0 | 2.5 | 7.5 | 4.9 | 9.3 | 0.0 | 24.0 | 0.0 | 0.0 |
| North | |||||||||||||||
| <50% | 49.0 | 32.0 | 27.5 | 71.7 | 42.5 | 84.0 | 32.0 | 52.5 | 22.5 | 74.1 | 46.6 | 84.0 | 44.0 | 62.5 | 25.0 |
| [50%; 85%[ | 31.6 | 36.0 | 57.5 | 15.0 | 36.0 | 4.0 | 40.0 | 37.5 | 57.5 | 13.0 | 34.0 | 4.0 | 28.0 | 32.5 | 62.5 |
| [85%; 115%[ | 4.9 | 12.0 | 5.0 | 4.5 | 6.1 | 0.0 | 8.0 | 5.0 | 7.5 | 4.5 | 4.0 | 4.0 | 8.0 | 2.5 | 5.0 |
| [115%; 150%[ | 4.5 | 4.0 | 4.5 | 2.0 | 4.9 | 4.0 | 8.0 | 0.0 | 7.5 | 2.4 | 5.3 | 4.0 | 8.0 | 0.0 | 5.0 |
| ≥150% | 10.1 | 16.0 | 5.0 | 6.9 | 10.5 | 8.0 | 12.0 | 5.0 | 5.0 | 6.1 | 10.1 | 4.0 | 12.0 | 2.5 | 2.5 |
| Up | |||||||||||||||
| <50% | 34.4 | 8.0 | 42.5 | 42.9 | 25.9 | 40.0 | 0.0 | 32.5 | 12.5 | 52.6 | 29.1 | 56.0 | 0.0 | 52.5 | 35.0 |
| [50%; 85%[ | 34.4 | 36.0 | 40.0 | 38.5 | 33.6 | 52.0 | 36.0 | 57.5 | 47.5 | 32.0 | 40.1 | 40.0 | 48.0 | 42.5 | 52.5 |
| [85%; 115%[ | 17.0 | 44.0 | 17.5 | 10.5 | 21.1 | 4.0 | 40.0 | 7.5 | 30.0 | 6.1 | 13.4 | 0.0 | 28.0 | 2.5 | 7.5 |
| [115%; 150%[ | 6.1 | 8.0 | 0.0 | 2.0 | 9.3 | 0.0 | 12.0 | 0.0 | 7.5 | 4.5 | 8.9 | 0.0 | 20.0 | 2.5 | 5.0 |
| ≥150% | 8.1 | 4.0 | 0.0 | 6.1 | 10.1 | 4.0 | 12.0 | 2.5 | 2.5 | 4.9 | 8.5 | 4.0 | 4.0 | 0.0 | 0.0 |
| Model | GRACE | GLDAS/Noah | MERRA-Land | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zone | All | AB | PB | All | AB | PB | All | AB | PB | ||||||
| Class | nR | wR | nR | wR | nR | wR | nR | wR | nR | wR | nR | wR | |||
| East | |||||||||||||||
| <1 mm | 84.6 | 88.0 | 92.5 | 83.8 | 84.6 | 88.0 | 88.0 | 92.5 | 92.5 | 83.4 | 84.6 | 84.0 | 88.0 | 83.4 | 92.5 |
| [1 mm; 2 mm[ | 7.3 | 8.0 | 7.5 | 8.1 | 7.3 | 8.0 | 8.0 | 7.5 | 7.5 | 8.5 | 7.3 | 12.0 | 8.0 | 8.5 | 7.5 |
| [2 mm; 3 mm[ | 2.4 | 0.0 | 0.0 | 2.4 | 2.4 | 0.0 | 0.0 | 0.0 | 0.0 | 2.4 | 2.4 | 0.0 | 0.0 | 2.4 | 0.0 |
| ≥3 mm | 5.7 | 4.0 | 0.0 | 5.7 | 5.7 | 4.0 | 4.0 | 0.0 | 0.0 | 5.7 | 5.7 | 4.0 | 4.0 | 5.7 | 0.0 |
| North | |||||||||||||||
| <1 mm | 80.2 | 80.0 | 85.0 | 77.3 | 83.4 | 60.0 | 84.0 | 87.5 | 95.0 | 78.5 | 85.0 | 64.0 | 88.0 | 85.0 | 92.5 |
| [1 mm; 2 mm[ | 15.0 | 20.0 | 15.0 | 17.0 | 10.9 | 36.0 | 12.0 | 12.5 | 5.0 | 15.8 | 9.7 | 32.0 | 12.0 | 15.0 | 7.5 |
| [2 mm; 3 mm[ | 0.8 | 0.0 | 0.0 | 1.6 | 1.2 | 4.0 | 4.0 | 0.0 | 0.0 | 1.6 | 0.8 | 4.0 | 0.0 | 0.0 | 0.0 |
| ≥3 mm | 4.0 | 0.0 | 0.0 | 4.0 | 4.5 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | 4.5 | 0.0 | 0.0 | 0.0 | 0.0 |
| Up | |||||||||||||||
| <3 mm | 89.5 | 80.0 | 87.5 | 84.6 | 92.3 | 48.0 | 84.0 | 87.5 | 95.0 | 83.8 | 91.1 | 48.0 | 88.0 | 82.5 | 90.0 |
| [3 mm; 6 mm[ | 7.3 | 12.0 | 10.0 | 12.6 | 4.0 | 48.0 | 8.0 | 10.0 | 2.5 | 12.6 | 6.1 | 40.0 | 12.0 | 15.0 | 7.5 |
| [6 mm; 9 mm[ | 0.8 | 0.0 | 0.0 | 0.8 | 1.6 | 0.0 | 8.0 | 0.0 | 0.0 | 1.6 | 0.8 | 8.0 | 0.0 | 0.0 | 0.0 |
| ≥9 mm | 2.4 | 8.0 | 2.5 | 2.0 | 2.0 | 4.0 | 0.0 | 2.5 | 2.5 | 2.0 | 2.0 | 4.0 | 0.0 | 2.5 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolas, J.; Verdun, J.; Boy, J.-P.; Bonhomme, L.; Asri, A.; Corbeau, A.; Berthier, A.; Durand, F.; Clarke, P. Improved Hydrological Loading Models in South America: Analysis of GPS Displacements Using M-SSA. Remote Sens. 2021, 13, 1605. https://doi.org/10.3390/rs13091605
Nicolas J, Verdun J, Boy J-P, Bonhomme L, Asri A, Corbeau A, Berthier A, Durand F, Clarke P. Improved Hydrological Loading Models in South America: Analysis of GPS Displacements Using M-SSA. Remote Sensing. 2021; 13(9):1605. https://doi.org/10.3390/rs13091605
Chicago/Turabian StyleNicolas, Joëlle, Jérôme Verdun, Jean-Paul Boy, Louis Bonhomme, Ayoub Asri, Adélie Corbeau, Antoine Berthier, Frédéric Durand, and Peter Clarke. 2021. "Improved Hydrological Loading Models in South America: Analysis of GPS Displacements Using M-SSA" Remote Sensing 13, no. 9: 1605. https://doi.org/10.3390/rs13091605
APA StyleNicolas, J., Verdun, J., Boy, J.-P., Bonhomme, L., Asri, A., Corbeau, A., Berthier, A., Durand, F., & Clarke, P. (2021). Improved Hydrological Loading Models in South America: Analysis of GPS Displacements Using M-SSA. Remote Sensing, 13(9), 1605. https://doi.org/10.3390/rs13091605