NRTK, PPP or Static, That Is the Question. Testing Different Positioning Solutions for GNSS Survey

Abstract

Worldwide, the determination of the coordinates from a Global Navigation Satellite System (GNSS) survey (in Network Real Time Kinematic, Precise Point Positioning, or static mode) has been analysed in several scientific and technical applications. Many of those have been carried out to compare Precise Point Positioning (PPP), Network Real Time Kinematic (NRTK), and static modes’ solutions, usually, using the latter as the true or the most plausible solution. This approach is not always possible as the static mode solution depends on several parameters (baseline length, acquisition time, ionospheric, and tropospheric models, etc.) that must be considered to evaluate the accuracy of the method. This work aims to show the comparison among the GNSS survey methods mentioned above, using some benchmark points. The tests were carried out by comparing the survey methods in pairs to check their solutions congruence. The NRTK and the static solutions refer to a local GNSS CORS network’s analysis. The NRTK positioning has been obtained with different methods (VRS, FKP, NEA) and the PPP solution has been calculated with two different software (RTKLIB and CSRS-PPP). A statistical approach has been performed to check if the distribution frequencies of the coordinate’s residual belong to the normal distribution, for all pairs analysed. The results show that the hypothesis of a normal distribution is confirmed in most of the pairs and, specifically, the Static vs. NRTK pair seems to achieve the best congruence, while involving the PPP approach, pairs obtained with CSRS software achieve better congruence than those involving RTKLIB software.

1. Introduction

The coordinates from a Global Navigation Satellite Systems (GNSS) survey, as it is known throughout literature, can be computed with different approaches (relative and differential techniques, or absolute precise point positioning method). Traditionally, according to the relative survey, there are many differences distinguishing the static and the kinematic modes (RTK, real time kinematic or NRTK, network-based RTK). Specifically, the static mode allows reaching the highest precisions, despite the time involved for the survey and the data post-processing could limit its application [1,2,3,4]. Using the kinematic mode, the distance between the master and the rover receivers needs to be low, generally less than 20 km to solve the ambiguity phase fixing with “on the fly” procedure in order to retrieve the centimetre accuracy of the static positioning [5]. To overcome the above mentioned constrain, in the last few years, the GNSS Continuously Operating Reference Stations (CORS) networks have been widely used for real time positioning with high-precision. The presence of widely spread GNSS CORS networks encouraged the use of the NRTK technique that allows overcoming the limits of the distances among the stations. The use of GNSS CORS network, also, allows applying differential corrections more reliable on wide areas, such as the Virtual Reference Station (VRS) approach [6], the Multi Reference Station (MRS) approach [7], the Flächen Korrektur Parameter (FKP) approach or other surface correction approaches [8,9]. Several authors [10,11,12] demonstrated that the NRTK technique allows reaching centimeter accuracy, comparable with the accuracy of the static measurements.

The fundamentals of the PPP method were presented in [13] and in [14]. Many other research have discussed this methodology, to establish a geodetic survey control network [15] and to verify the possibilities of multi-constellation measurements for both static and kinematic acquisitions, to improve the convergence of PPP solutions [16,17,18,19]. The accuracy of PPP method has also been studied comparing the outcomes from online web services using different software and satellite ephemerides products [20], evaluating the performances of online free available PPP services for static positioning and tropospheric delay estimation [21,22]. Other works have also analyzed the possibility to achieve high positioning accuracy with PPP using a short period of observations [17,23,24,25].

A very prominent segment of PPP applications, known to the scientific community as GNSS-Ionosphere, has been developed to measure the ionospheric total electron content (TEC) aiming monitoring the global ionospheric climate. The TEC observations record regional ionospheric perturbations due to earthquakes/tsunamis, or geomagnetic storms, typhoon, and eclipses.

Moreno et al. [26] examined the relation between large changes in the rate of TEC with positioning errors in single PPP epochs, at equatorial latitudes during post-sunset hours, establishing that estimated altitudes have errors up to several meters for a single-epoch positioning. Results have been validated via the online CSRS-PPP software using three International GNSS Services (IGS) stations. Afraimovich et al. [27] report that the total GPS L2 phase slipped during the recovery phase of a geomagnetic storm due to GPS signal scattering on field aligned irregularities, both for the lines-of-sight aligned to the magnetic field line (the field of aligned scattering) and across the magnetic field line (the field of across scattering). Demyanov et al. [28] observed that the signal carrier phase scintillations can be caused by the ionospheric irregularities and also by a satellite oscillator anomalies and troposphere. The authors also reports that the parameter sensitivity crucially depends on the GPS receiver hardware and the carrier phase data sampling rate. A second-order derivative of the GPS signal phase is suggested as a mean to detect small-scale ionospheric irregularities. It was found that a 50 Hz data sampling rate is an adequate time resolution to reveal small-scale irregularities responsible for the ionospheric scintillations. More recently, Jin et al. [29], by analyzing a decade long observations of Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC), estimated the long-term variations of the plasmaspheric total electron content (PTEC).

The above-mentioned studies propose methodologies and mathematical approaches to analyze peculiar environmental conditions (magnetic storms, solar flares, atmospheric storms, and ionospheric scintillations) inducing positioning inaccuracies as highlighted in the suggested references, which may be referred to for further details, without claiming to be exhaustive.

In this work, we aim to compare NRTK, PPP and static methodologies to retrieve the coordinates of several benchmarks. The NRTK and static solutions have been performed using the GNSS CORS network of University of Palermo (UNIPA) located in the western-part of Sicily (Italy) included in the national Topcon Italy GNSS CORS network (TopNET live, [30]). The PPP solutions were carried out using two different software: the Canadian Spatial Reference System Precise Point Positioning (CSRS-PPP) online Web service and the open source program package RTKLIB. To compare Static and PPP solutions, only an hour of observations was considered.

In the assessment of NRTK or PPP positioning, most scientific studies use as reference the results obtained by the comparison with static mode positioning, especially if the processing is performed with scientific software (Bernese, GAMIT (GNSS at MIT, Massachusetts Institute of Technology), GBLOCK (Global Kalman filter), GIPSY-OASIS (GNSS-Inferred Positioning System and Orbit Analysis Simulation Software)) in which it is possible the errors’ components modelling (final ephemeris, tropospheric, ionospheric). Based on results from similar tests (short baselines, 10–30 kilometres in length, observed for a hour), it has been demonstrated that the commercial software packages performs better than a scientific one (e.g., Bernese) [31,32].

However, in this study, the static observations are relatively short (about an hour) and the static processing was processed with a commercial software; these conditions are not able to guarantee the best performance of static positioning, since, as reported by [20,31], the results of the processing can be different from each other (difference of a few centimetres), in the three geodetic components, depending on the software used.

For these reasons, the best strategy, used by the authors of this work, established the comparison between all different modes (NRTK, PPP, static) in order to provide a congruence analysis of the results obtained with different approaches.

The paper is organized as follows. A description of the UNIPA GNSS CORS network, the benchmark tests and a short introduction to the software involved for the analyses are discussed in Section 2. A synopsis of the results is presented and discussed in Section 3, and finally, concluding remarks and future applications are reported in Section 4.

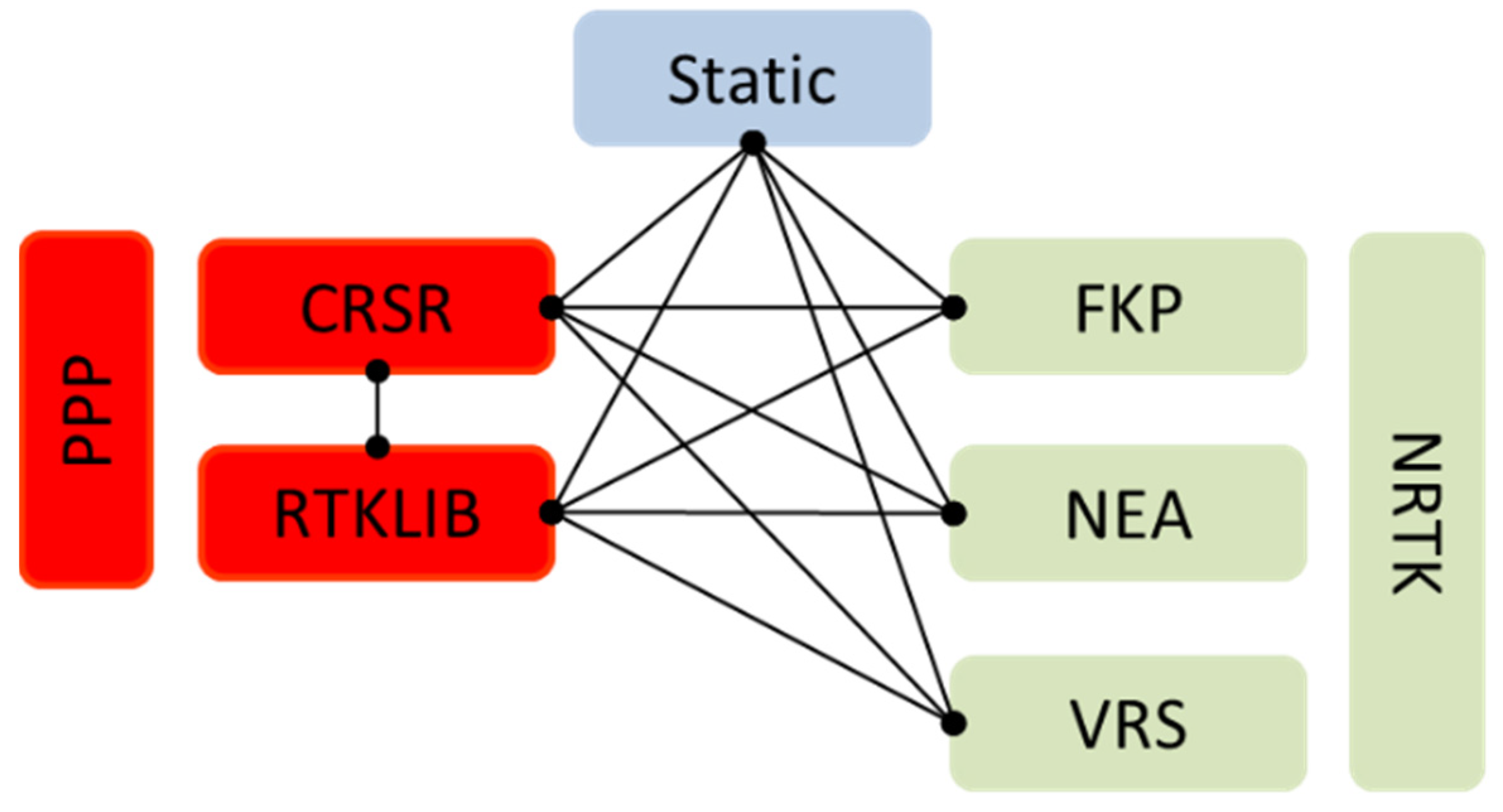
2. Materials and Methods

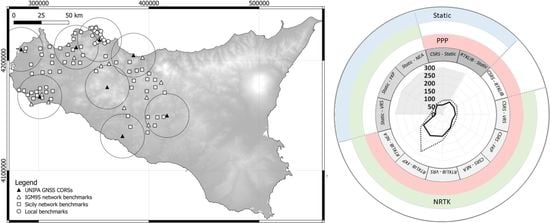
2.1. UNIPA GNSS CORS Network

The UNIPA GNSS CORS network has been materialized in 2006 for scientific purposes by University of Palermo [33]. It is made up of eight CORSs located in western Sicily with inter-distances ranging between 22 and 80 km, equipped with Topcon NET G-3 GPS and GLONASS enabled receivers.

Up to 2012, the Control Centre (CC) was at the Department of Engineering of University of Palermo and the GNSS − State Monitoring and Representation Technique (GNSMART) software by Geo++ was used to manage the CORS network and to produce the NRTK corrections. From 2013, all reference stations were included in the NetGEO GNSS CORS network, managed by Topcon Italy. The network provides daily RINEX data (30”), hourly raw data (1”) and real-time GNSS data streams code, Nearest Station (hereinafter NEA), VRS and FKP.

Preliminary, the coordinates of the reference stations were established in ITRF05 and ETRF89 (epoch 1989.0) frames. Recently, six CORSs have been included in the Italian GNSS dynamic network denominated Rete Dinamica Nazionale (RDN), that is a Regional Reference Frame sub-commission for Europe (EUREF) European sub-network, aiming to monitor the reference system variations [34]. The RDN network is computed in the ETRF2000 reference frame (epoch 2008.0) using the Bernese 5.0 software; thus, the coordinates of the UNIPA GNSS CORS network have been also calculated in this frame. Data from UNIPA GNSS CORS network have been also included within a European regional integration of long-term national dense network solutions [35] for the positions and velocities of more than 3000 stations.

In the last few years, the UNIPA GNSS CORS network has been involved for scientific applications in different fields, including the electromagnetic pollution monitoring via a GPS-GIS integrated system [36], the trajectories calculation of Mobile Mapping System (MMS) [37,38], the dams monitoring with integrated InSAR and GNSS techniques [39,40], the geodetic measurements of the stalactite elevation in geological analyses [41], the use of unmanned aerial vehicles for soil moisture characterization [42], the positioning and guidance of agricultural machines via GNSS [43], the monitoring of active faulting, with integrated geodetic and InSAR techniques [44,45].

2.2. Static, NRTK Survey and Software Processing

In the last years, several projects were carried out to evaluate the performance of the UNIPA GNSS CORS network using several GPS reference benchmarks. These reference benchmarks have been also used for our tests since they have good-excellent sky visibility and therefore were suitable for GPS-GLONASS observations. In order to use permanently materialized points, easily reachable and detectable without specific arrangements, the GNSS reference benchmarks have been chosen among the points belonging to the national and local static GNSS networks in Sicily. Fourteen of those belong to the national static GNSS network (IGM95 network), and fifty-seven to the local GNSS network. The IGM95 network was developed by Italian Military Geographic Institute (IGM) in the nineties using differential techniques and it was calculated in the European ETRS89 system, using the EUREF points available in the country [46]. The network is connected with the levelling geodetic networks and it is made up of 3000 distributed points (177 are located in Sicily), approximately distant 20 km with a Root-Mean-Square Error (RMSE) of ±5 cm. The local static GNSS regional network in Sicily was mainly developed for technical applications and it is made up of 523 points, spaced 7–9 km from each other. Benchmarks have been stabilized in various modes, including concrete pier with aluminum plate, stainless steel, stainless steel mast, and roof mounted on buildings, according to national regulations.

The coordinates of the local static GNSS network have been computed with observations of three independent bases in relation to the points of the IGM95 network. All these points are distributed on the area covered by the UNIPA GNSS CORS network and they have been used for the tests of this work (Figure 1); in addition, some new reference points (fifteen points) were also materialized (mostly around the city of Palermo) and used for the tests.

Preliminarily, the coordinates of all GNSS reference benchmarks were computed in ITRF05 frame performing the static survey with dual-frequency GNSS receivers Topcon HiPer-Pro and Topcon GR3, equipped with controller FC-100 and FC-200. The occupation time was about 60 min. We chose a one hour observations since distances from CORSs to benchmarks were about 15–20 km at most (≈80% of the benchmarks), and according to literature [31,32] this occupation time is sufficient at these distances. A maximum distance of ≈30 Km characterizes an IGM95 benchmark. The elevation mask was set to 10 degrees, the epoch/logging rate to 15 s, and the maximum PDOP was fixed to 6.

The Topcon Tools package ver. 8.2.3 by Topcon Corporation was used for the static measurements. The software allows the data processing from different devices such as total stations, digital levels and GNSS receivers, and it is used in several technical-scientific applications [47,48]. Topcon Tools uses the Modified Hopfield Model for the tropospheric corrections [49]. The employed positioning mode was Code-based differential (“CODE DIFF”), the time range and the cut-off angle were set to 15 s and 10 degrees, respectively. Each GPS reference benchmark was measured with three independent baselines from the nearest permanent stations. The precision of all GNSS reference benchmark coordinates in ITRF05 frame is approximately few millimeters.

The survey was verified by recalculating the coordinates of the benchmark, belonging to the IGM95 and local network in Sicily, in the ETRF89 frame (epoch 1989.0) and then the results were compared with the official coordinates; the differences between the results were in the same order of magnitude of the intrinsic accuracy of the geodetic networks. For the NRTK processing was used GNSMART (GNSS − State Monitoring and Representation Technique), developed by Geo++ GmbH (Garbsen, Germany). It is one of the earliest systems guaranteeing an uniform coverage for the absolute positioning in real time with centimeter precision [50]. The GNSS observations (GPS and GLONASS, in this study) are stored in RTCM 2.3 (Radio Technical Commission for Maritime Services) format, able to send the differential corrections (VRS, FKP, NEA). GNSMART uses the same tropospheric delay model of Topcon Tools (the modified Hopfield model) [51], with two scaling parameter/station, while regarding the ionospheric delay a single layer model with polynomial, one bias per satellite (vertical delay), with 3D Gauss–Markov process (one bias per receiver−satellite combination) [50]. Also used Meridiana ver. 2011, developed by GEOPRO s.r.l. (Ancona, Italy), only for recording data from the different NRTK corrections (VRS, FKP, NEA).

The NRTK positioning was carried out using a scientific protocol given by [52]. Specifically, it is based on taking measurements during the weekdays from 8:00 am to 6:00 pm, without a preliminary check about the geometric configuration of the satellites or the stations efficiency and using dual-frequency geodetic GNSS receivers Topcon Hiper-Pro (by Topcon Corporation, Japan) with controller FC-100. Two separate sessions are recorded for each benchmark to obtain independent satellite configurations; for each session, four independent tests (from the startup to the turning off of the instruments) for each network solution, were analyzed (VRS, FKP, NEA). The results, recorded at the fifth epoch, were accepted with both phase solution and ambiguity phase fixed, while the solution is considered rejected when the ambiguity phase fixing did not occur within five minutes since the connection with the software (float or stand-alone solution).

Overall, 86 GNSS reference benchmarks have been measured in NRTK survey (out over 100 benchmarks); indeed, some benchmarks during the investigation were damaged and not detectable. Also, the computation of the VRS, FKP, and NEA solutions was not possible for all points. The NEA solution has been only used for GNSS reference benchmarks distant less than about 20 km from the nearest reference station. An evaluation between valid tests, in which the NRTK corrections were obtained, and failed tests, in which the receiver has not received the network corrections, showed that the VRS correction was achieved for 72% of GNSS benchmarks, the FKP for 61% and the NEA for 59%. Totally, the benchmarks used to detect the differential corrections were 61, 52, and 50 in VRS, FKP, and NEA modes, respectively.

2.3. PPP Software Processing

The PPP processing was carried out using one-hour of static acquisitions and two different packages, CSRS-PPP and RTKLib.

CSRS-PPP is an on-line service developed by Geodetic Survey Division of Natural Resources Canada that allows an easy access to the Canadian Spatial Reference System (CSRS). The CSRS-PPP allows GPS users in Canada (and abroad) to achieve accurate positioning by submitting GPS observations from a single receiver over the Internet. It can process GNSS observations from single or dual-frequency GPS receivers operating in static or kinematic mode. The aim to this software is the use of precise GNSS orbit and clock products generated through international collaborations [53,54,55]. CSRS-PPP uses the Estimate ZTD (Zenith Total Delay) model for tropospheric corrections, with the IGS final (Repro1) orbits and Observations Frequency Mode Phase and Code Double Static in which the elevation cut-off is 15°.

Within this research, the raw data of all 86 benchmarks were sent by email; the computation reports, by the software online, included the coordinates in the ITRF05 frame and the associated plots.

RTKLib (version 2.4.2 p13) is an open source program package used for standard and precise positioning with GNSS (Takasu and Yasuda 2009) [56]. This software is widely used in scientific research for smartphone in static and kinematic modes [57], although the performance of GPS-only, BeiDou Navigation Satellite System (BDS)-only, and combination of BDS/GPS have been analyzed recently [58]. The NRTK corrections to the raw data have been also applied to a GNSS CORS of the mass market receivers [59,60]. However, the Pseudo-VRS technique incorporates high-precision GNSS positioning methods, for instance in the developments of vehicle-to-vehicle communication [61]. The software was used for static and kinematic surveys using GNSS multi-constellation receivers acquiring GPS, GLONASS and Galileo Open Service (OS) [62]; more recently, its performance using the GNSS multi-constellation PPP technique in static mode has been also analyzed [19].

The processing with RTKLib was performed by selecting the Ionospheric Iono-Free LC model and the Estimate ZTD to correct the ionospheric and the tropospheric influence, respectively; and the IGS (International GNSS Service) ephemerids to correct orbit and clock, in accordance with a similar studies conduct recently by Angrisano et al. [19]. In particular:

-

GDOP threshold is set to reject solutions with GDOP values higher than 30°, and a mask-angle equal to 10° is applied.

-

No ambiguity resolution strategy is used, since the PPP-AR (Ambiguity Resolution) function selectable in RTKLib software, was experimental at experimental at the time of data processing, providing unstable and inaccurate solution with respect to standard PPP according to the RTKLib manual. A detailed description of Ambiguity Resolution, in particular using GLONASS, is reported in [63].

-

The Phwindup (phase wind-up) option is set to correct the delay caused by the relative rotation between the satellite and receiver antennas.

-

Reject Ecl, is set to exclude the GPS Block IIA eclipsed satellites, that degrade the PPP solutions due to unpredicted behavior of yaw-attitude.

-

RAIM (Receiver Autonomous Integrity Monitoring Receiver Autonomous Integrity Monitoring) FDE (Fault Detection Fault Detection and Exclusion) detect and exclude possible outliers from the measurements set used for the solution computation.

-

Sat PCV (phase center variations) and Rec PVC, were set to consider the phase center variations of the satellite and the receiver, respectively. It requires the so-called “igs14.atx” file, provided by the IGS (International GNSS Service), containing the correction parameters of several types of antenna.

The Ionospheric Iono-Free model and the estimated zenith total delay (ZTD) option were selected to correct the ionospheric and the tropospheric influence, respectively, while through the IGS ephemerids we accounts for the orbit and clock corrections [19].

The Saastamoinen model [64] computes the tropospheric delay $T_r$ using the following expression (1):

$$T_r=\frac{0.002277}{\cos (z)}\left[p+\left(\frac{1255}{T}+0.05\right)e-ta{n}^2\left(z\right)\right]$$

(1)

where: p, is the total pressure; T, is the absolute temperature of the air; e, is the partial pressure of water vapor; z, is the zenith angle.

In the Saastamoinen model [64], a standard atmosphere is considered as a reference, the geodetic height is approximated to the ellipsoidal height, and a humidity percentage is fixed to 70%.

The model considers the troposphere as divided into two layers. The first layer, from the earth surface to 10 km on it, has a constant descent rate of temperature of 6.5 °C km⁻¹. The second layer, from 10 to 70 km on the earth surface, has assumed having a constant temperature value. Therefore, for atmospheric refraction integral, the function of refractive index can be computed based on the zenith distance trigonometric functions and term wise integration. In this way, the ZTD is expressed as (2)–(4):

$$ZTD=0.002277\frac{(P_0+\left(0.05+\frac{1255}{P_0+273.15}\right)e_0{}^{}}{f\left(\phi ,h\right)}$$

(2)

$$e_0=r_h·r_h·6.11·{10}^{\frac{7.5T_0}{T_0+273.3}}$$

(3)

$$f\left(\phi ,Z\right)=1-0.00266\cos 2\phi -0.00028Z$$

(4)

where P₀, T₀, and e₀ are, respectively, the surface pressure, the surface temperature, and the water vapor pressure at the surface level, r_h is the relative humidity, f($\phi$, Z) is the correction of gravity acceleration caused by the rotation of the earth, and $\phi$ and Z are the point latitude and altitude, respectively.

The Estimate ZTD model computes the tropospheric delay starting from the expression of the Saastamoinen model with the zenith angle and relative humidity equal to zero and employing the NMF (Niell Mapping Function), based on receiver geographical coordinates and measurement time [65]. The mapping function in terms of the elevation (El) and the azimuth (Az) angles between the satellite and the receiver is expressed as:

$$M\left(El\right)=M_w\left(E\right)\{1+\cot \left(El\right)·(G_N\cos \left(El\right)·(G_N\cos \left(\mathrm{Az}\right)+G_E\sin (Az))\}$$

(5)

$$T_{r,z}=M_h\left(El\right)·Z_H+M\left(El\right)\left(Z_T-Z_H\right)$$

(6)

where, Z_T accounts for the tropospheric zenith total delay that is estimated from the extended Kalman filter together with the north (G_N) and the east (G_E) components of the tropospheric gradient. Z_H accounts for the tropospheric zenith hydro-static delay computed using a tropospheric model, such as Saastamoinen, Hopfield [51], or modified Hopfield models with the zenith angle and relative humidity equal to zero. M_h (El) and M_w (El) are, respectively, the hydro-static and wet mapping-functions.

Niell [65] kept the basic form of the Herring (MTT model, [66]) mapping function adding a height correction term and assuming that the elevation dependence is a function of only geographical parameters (if we accept that, in a way, the day of the year is also a constant and independent parameter) and proposed the function (7):

$$m\left(\upsilon \right)=\frac{1+\frac{a}{1+\frac{b}{1+c}}}{\sin \left(\upsilon \right)+\frac{a}{\sin \left(\upsilon \right)+\frac{b}{\sin \left(\upsilon \right)+c}}}+\Delta m\left(\upsilon \right)$$

(7)

The wet delay parameters $a,b,c$are given at tabular latitude ${\phi }_i$ 15°, 30°, 45°, 60° and 75°. The hydrostatic parameters $a_h,b_h,and{c}_h$ at time in UT days is calculated as (8):

$$a_h\left({\varphi }_i,t\right)=a_{avg}\left({\varphi }_i\right)-a_{amp}\left({\varphi }_i\right)\cos \left(2\pi \frac{t-T_0}{365.25}\right)$$

(8)

where $a_{avg}$ and $a_{amp}$ are given at tabular latitude ${\phi }_i$ 15°, 30°, 45°, 60° and 75°, and $T_0$ is the adopted phase, DOY 28 as described in [66]

The height correction is given by (9) as a function of the coefficients a_h, b_h, and c_h and the orthometric height:

$$\mathsf{\Delta }m\left(\upsilon \right)=\frac{1}{\sin \left(\upsilon \right)}-\frac{1+\frac{a_h}{1+\frac{b_h}{1+c_h}}}{\sin \left(\upsilon \right)+\frac{a_h}{\sin \left(\upsilon \right)+\frac{b_h}{\sin \left(\upsilon \right)+c_h}}}\times H$$

(9)

2.4. Data Analysis

The aim of this work is to evaluate the congruence of different positioning solutions obtained with alternative GNSS methodologies. The solutions’ congruence was assessed by statistically analyzing the coordinate’s differences on selected benchmarks. The analysis was performed by considering separately each coordinate component, North (N), East (E) and Ellipsoidal Height (Z). The static results were compared to NRTK solutions, namely VRS, FKP and NEA, and PPP solutions by CSRS and RTKLIB. The NRTK solutions were compared to the two PPP solutions; in additional, the two PPP solutions (CSRS and RTKLIB) were compared with each other. Totally, twelve different comparisons have been carried out (Figure 2): Static vs. CSRS, Static vs. RTKLIB, CSRS vs. RTKLIB, CSRS vs. VRS, CSRS vs. FKP, CSRS vs. NEA, RTKLIB vs. VRS, RTKLIB vs. FKP, RTKLIB vs. NEA, Static vs. VRS; Static vs. FKP and finally Static vs. NEA.

The procedure used for statistical analysis aimed to remove the extreme values (considered as possible outliers), if occurring. Indeed, some authors analyzed the statistical distribution of GNSS errors [67] using a normal distribution as discussed and justified by [68]. A normal distribution was fitted to the empirical frequency under the hypotheses of equal mean and standard deviation. According to Specht [67], values exceeding 95.4% in the cumulative frequency, corresponding to a span of ±2 standard deviations from the mean, were considered possible outliers and removed from the comparison. Although it can be considered a poorly conservative threshold [69], it allows dealing with relatively small sets of observations. The normal distribution is considered separately from each of the measured coordinates [67]. The correlation between coordinate components is neglected in the univariate analysis, moreover multivariate analyses of outliers tend to reject less data samples than univariate under the same confidence level [70]. Despite these approximations, univariate analysis occurs in a relatively straightforward examination with the identification of possible outliers [70].

Several statistical tests can be applied to examine the consistency of empirical distribution with the theoretical normal distribution, including the Anderson–Darling [71], Cramér-von Mises [72], Kolmogorov–Smirnov [73], and Lilliefors [74] tests.

Two tests were selected being the most frequently applied to verify if the empirical distribution of the solutions differences, once removed the possible outliers, follows a normal distribution, namely the Kolmogorov–Smirnov (KS) and the Anderson–Darling (AD) tests. The KS test is a non-parametric method and it was used to assess whether the empirical distribution frequency of the coordinates differences belongs to a reference normal distribution (the null hypothesis, H₀) against the alternative hypothesis (H₁) that the empirical distribution does not fit the theoretical distribution [75]. The null hypothesis was evaluated for rejection at a significance level α, by comparing the KS value, resulting from the test, with the critical value, KSC. As well as the two-sample KS test, the two-sample AD test is used to test whether the two samples originate from the same distribution [76]. The AD test can be considered a modification of the KS test and it weighs more the tails than the KS test does.

The mean values, μ, and the standard deviations, σ, of the coordinates differences, ΔN, ΔE and Δh, were compared, as well, to the corresponding value prior removing extreme values. Another two statistical indices, the sample skewness, S, and the kurtosis index, K, [77], evaluated before and after extreme values removal, allowed assessing whether and how much the empirical frequency distribution gets more symmetricity and mesokurticity.

After removing extreme values, the determination coefficient, r², between the empirical frequency and the corresponding values of the fitted normal distribution, was used to measure the strength of a linear relation between the corresponding values. All correlations are classified according to Evans [78].

3. Results and Discussion

The first analysis aimed to check the range of variability of coordinates differences for all pairs involved (

Table 1. Range of variability of the coordinate differences (min – max in mm).

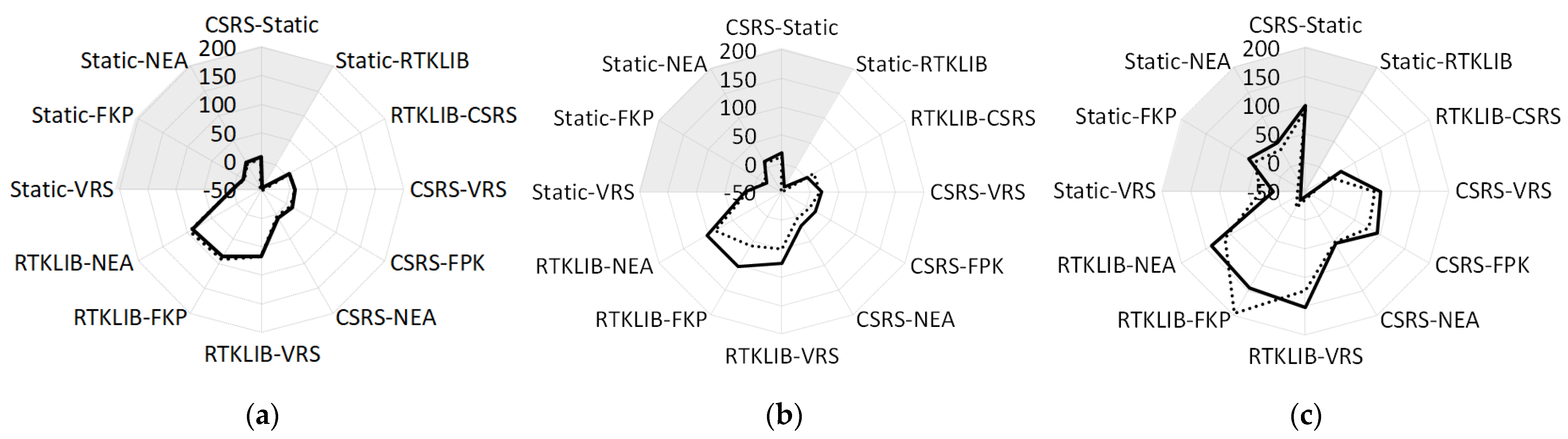
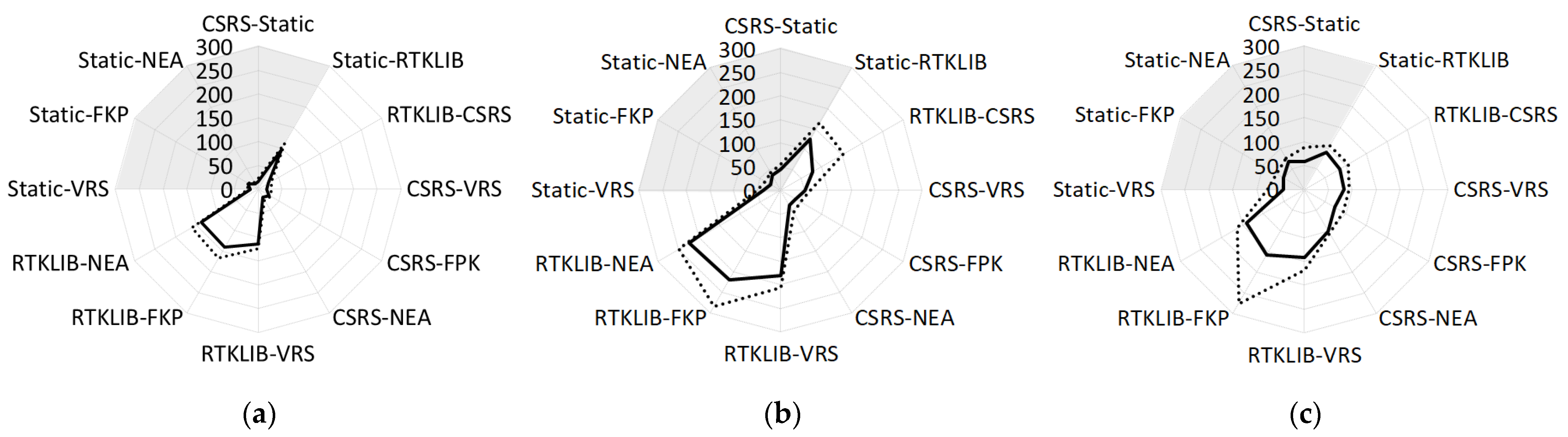
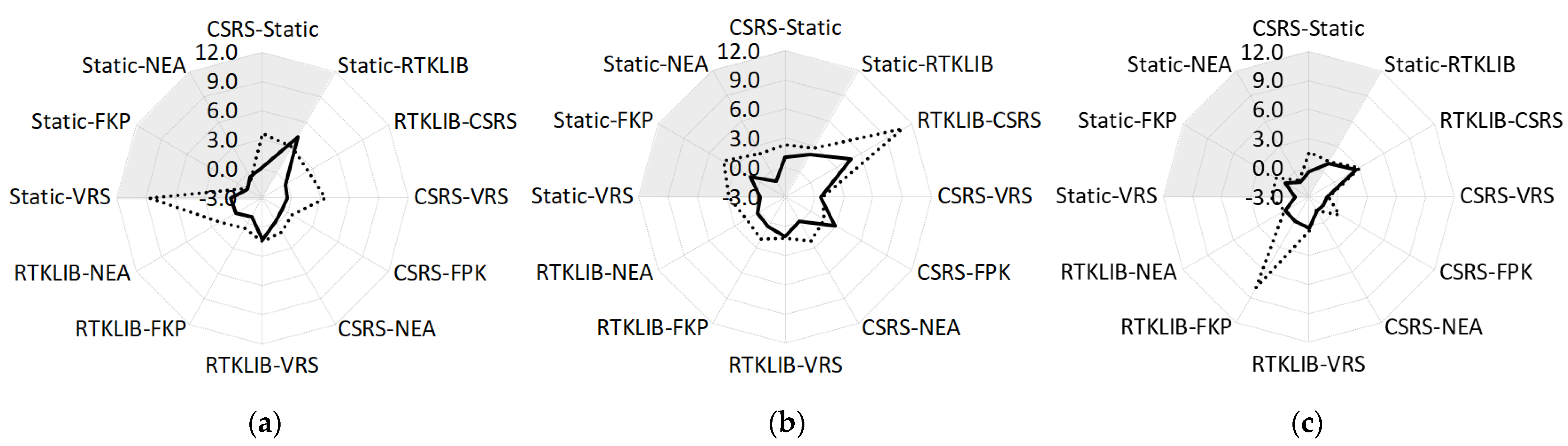
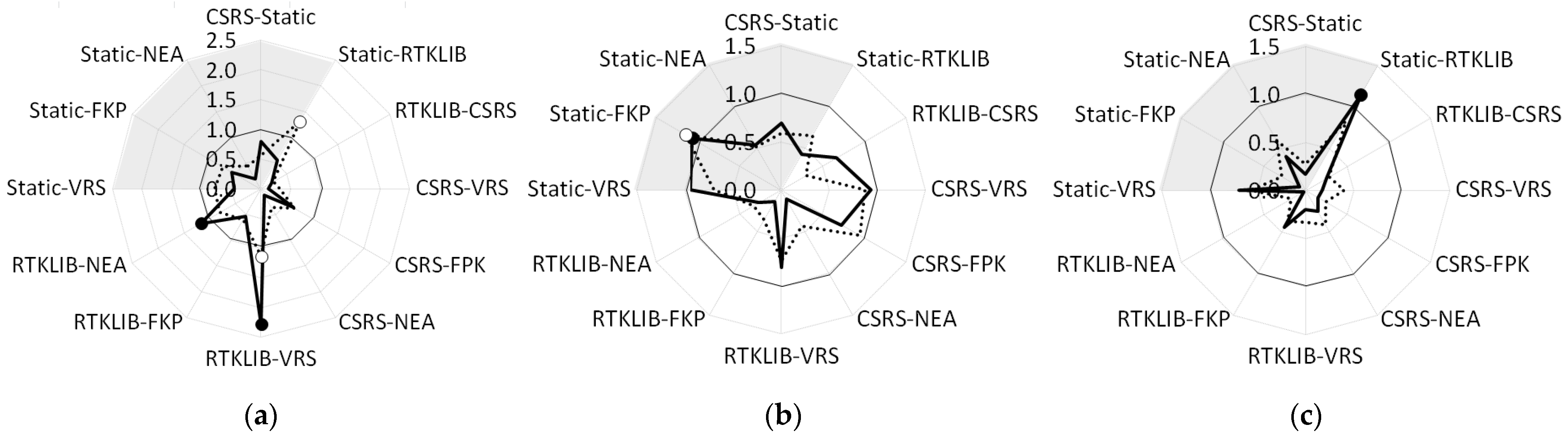
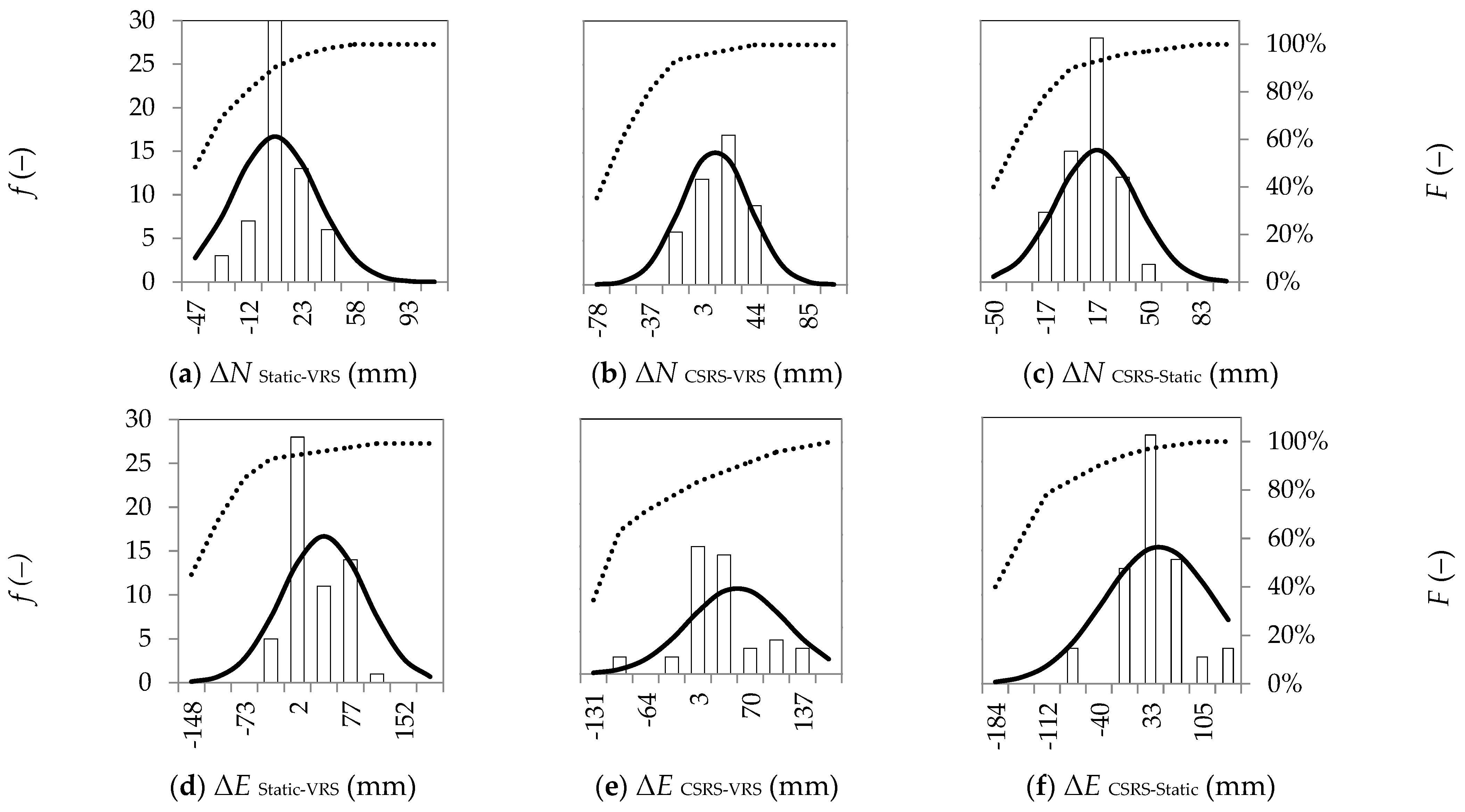
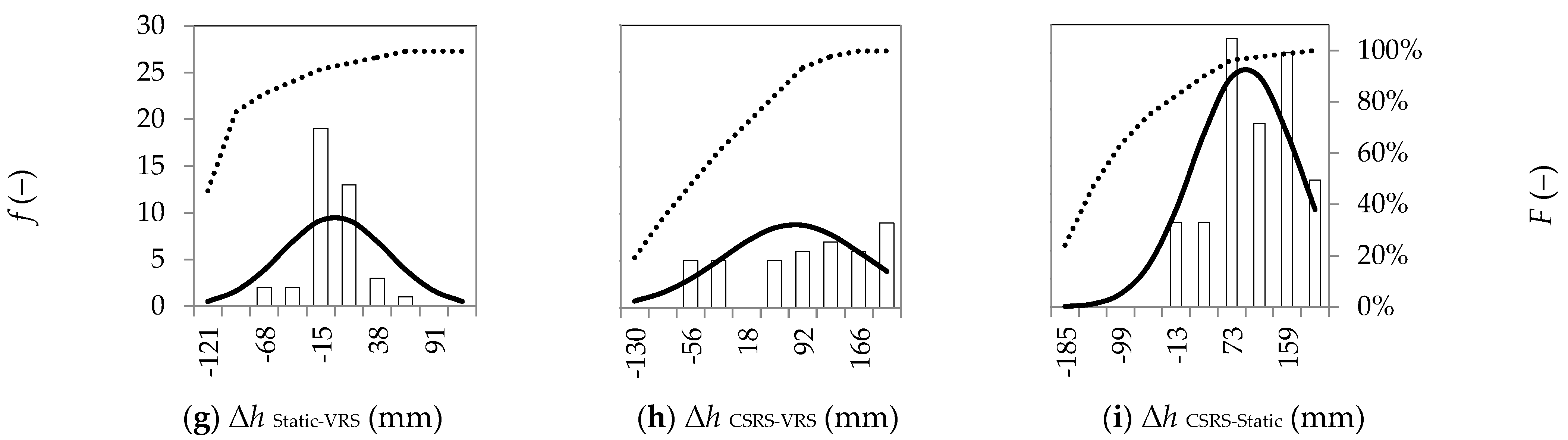
Min Max (mm)	Static CSRS	Static RTKLIB	RTKLIB CSRS	Static VRS	Static FKP	Static NEA	CSRS VRS	CSRS FKP	CSRS NEA	RTKLIB VRS	RTKLIB FKP	RTKLIB NEA
ΔN	−50 100	−409 133	−107 116	−47 110	−60 36	−32 41	−78 105	−70 56	−75 54	−85 433	−209 585	−82 652
ΔE	−184 141	−606 462	−603 745	−148 190	−121 118	−149 78	−131 170	−106 122	−169 101	−492 580	−782 583	−697 653
Δh	−185 346	−375 219	−402 298	−206 187	−137 173	−135 174	−130 203	−170 208	−120 210	−318 504	−166 1328	−245 480

). This analysis shows that the variability of the pairs involving RTKLIB is always much higher than the other, as confirmed by the range always higher than 500 mm, 1000 mm and 500 mm for N, E and h components. In the other cases the range of variability is less than 400 mm, excluding the differences for h component in the comparisons Static vs. CSRS and Static vs. RTKLIB, where the values are 531 mm and 594 mm, respectively. A suitable comparison of the results should require the removal of any outliers, if occurring. So, as discussed in the previous section, assuming that the coordinates’ differences belong to a normal distribution, the extreme values can be considered possible outliers and then removed. Some statistics descriptors of the ΔN, ΔE and Δh algebraic differences among different pairs of solutions were applied to discuss if and to what extent different solutions lead to comparable results.

The mean values μ of the coordinates differences, calculated before and after outliers removal, were compared for the different cases (Figure 3). Once extreme values were removed, it was observed that μ of ΔN, ΔE and Δh increases while oppositely decreases in other cases, depending on the values and the number of extreme values removed. As already highlighted, in the analysis of the range of variability, the pairs involving RTKLIB behave differently than the remaining pairs except for the comparison RTKLIB vs. CSRS which shows similar values to the other cases. Specifically, μ for the RTKLIB vs. NRTK (VRS, FPK and NEA) comparison was on average 85, 65 and 144 mm in the pre outliers removal and 81, 93, and 146 in the post outliers removal, respectively, for of ΔN, ΔE, and Δh, while in the Static vs. RTKLIB comparison was −53, −52, and −83 mm in the pre outliers removal and −47, −40, and −68 in the post outliers removal. For the other observations the mean values on average was 3, 8 and 51 mm in the pre outliers’ removal and 5, 11, and 59 mm in the post outliers removal respectively for ΔN, ΔE, and Δh.

Also, for the standard deviation σ, a similar behavior can be observed. Generally, σ are higher for the pairs involving RTKLIB (RTKLIB vs. NRTK and Static vs. RTKLIB) compared to the remaining pairs, 119, 212, and 164 mm on average for ΔN, ΔE, and Δh, respectively, compared to the remaining pairs (25, 50, and 26 mm for ΔN, ΔE, and Δh, respectively) (Figure 4). The lowest σ were always obtained for Static vs. NRTK pairs (σ of 22, 44 and 73 mm, on the average in the pre outliers removal and of 18, 33, and 54 mm in post outliers removal). As expected, σ is often reduced after removing the extreme values; the reduction is more evident for ΔN and Δh than for ΔE.

The highest skewness characterizes the ΔN component of the Static vs. VRS and Static vs. CSRS differences (S ≈ 1.54 and 0.78, Figure 5, panel a, continuous line) and the ΔE component of the Static vs. VRS and Static vs. FKP differences (S ≈ 0.51 and 0.55). The extreme values removal generally reduces the asymmetry of the differences frequency distribution (Figure 5), except for the ΔN component of Static vs. NEA and the Δh component of CSRS vs. VRS, CSRS vs. FKP and Static vs. VRS. The reductions for CSRS vs. Static, CSRS vs. NEA and Static vs. FKP were 57, 58 and 50%, respectively. Static vs. NEA and Static vs. PPP (CSRS and RTKLIB) exhibited the lowest average skewness (S ≈ 0.07 and 0.06, respectively) after the extreme values removal, while CSRS vs. FKP showed the highest average skewness (S ≈ 0.58).

The highest leptokurticity characterizes the Static vs. VRS for the ΔN component (K ≈ 8.6), RTKLIB vs. CSRS for the ΔE component (K ≈ 10.9) and RTKLIB vs. FKP for the Δh component (K ≈ 7.8) before extremes removal (Figure 6, continuous lines). Once extreme values were removed (dashed lines), the abovementioned pairs loose leptokurticity (K ≈ 0.3, 4.7, and –0.1 for ΔN, ΔE and Δh, respectively).

According to the KS test, the differences belong to a normal distribution at a significance level α (Figure 7 panel a, α = 0.05) except for ΔE for the Static vs. FKP pair, and ΔN for the Static vs. RTKLIB and RTKLIB vs. VRS pairs, where the null hypothesis is rejected and the ratio KS/KSC is greater than unity (1.16, 1.31, and 1.14). The lowest values of KS/KSC characterize the RTKLIB vs. CSRS pair (0.27, on the average). According to these results, the AD test shows that the differences belong to a normal distribution (Figure 7 panel b, α = 0.05) excluding one more time ΔE in the Static vs. FKP pair, ΔN in the RTKLIB vs. VRS and RTKLIB vs. NEA differences, and ΔZ in the Static vs. RTKLIB pair (AD/ADC = 1.07, 2.28, 1.17, and 1.15, respectively). The lowest value of AD/ADC was achieved for the CSRS vs. NEA differences (0.16 on the average). If the variables (e.g., ΔN, ΔE and Δh) are normally distributed and independent, this implies they are “jointly normally distributed”, i.e., their pairs must have multivariate normal distribution [79].

The determination coefficients are used to corroborate the assumption that after removing the extreme values, the normal distribution well describes the empirical distribution. At least, only the pairs Static vs. CSRS, RTKLIB vs. CSRS and CSRS vs. NEA exhibit moderate correlation for all components. Analyzing the ΔN differences, results shown that, CSRS vs. Static, RTKLIB vs. CSRS, CSRS vs. VRS and Static vs. VRS pairs exhibit very strong correlations (r² = 0.81, 0.93, 0.74 and 0.67, respectively) (

Table 2. Determination coefficient, r², between empirical and normal frequencies of ΔN, ΔE and Δh differences among pairs of processing techniques (after extreme values removal): very strong correlations (r² > 0.62) are highlighted in bold, correlations assumed as strong are in the following range (0.35 < r² ≤ 0.62), moderate correlations (0.16 ≤ r² < 0.35) are reported in grey, very weak and weak correlations (r² < 0.15) were removed.

R2	Static CSRS	Static RTKLIB	RTKLI CSRS	Static VRS	Static FKP	Static NEA	CSRS VRS	CSRS FKP	CSRS NEA	RTKLIB VRS	RTKLIB FKP	RTKLIB NEA
ΔN	0.81		0.93	0.67		0.30	0.74		0.45
ΔE	0.57	0.30	1.00	0.39	0.20		0.29	0.23	0.58		0.34	0.21
Δh	0.43	0.21	0.59	0.69	0.84				0.23	0.54	0.64	0.77

). Considering the ΔE differences, only, RTKLIB vs. CSRS exhibits the maximum value of r² (r² = 1.00), while the Δh differences exhibit very strong correlation for the pairs RTKLIB vs. FKP, RTKLIB vs. NEA, Static vs. VRS and Static vs. FKP (r² = 0.64, 0.77, 0.69 and 0.85, respectively). Very weak and weak correlations were removed from Table 2.

Finally, once removing extreme values, a comparison between the best fitting normal distribution and the empirical distribution frequencies has been performed for the Static vs. VRS, CSRS vs. VRS and CSRS vs. Static coordinates differences (Figure 8). The minima and maxima x-axis values change for different pairs according to the corresponding range of variability. From the comparison, the best fitting seems to characterize the ΔN differences. The maximum range of variability is ~ ± 80 mm (CSRS vs. VRS, panel b). The distributions of the empirical frequencies of ΔE CSRS vs. Static and Δh CSRS vs. VRS show many gaps, while those of ΔE Static vs. VRS and Δh CSRS vs. Static highlight a secondary peak. By visually interpreting the empirical frequency distributions of the ΔN and ΔE differences: the ΔN Static vs. VRS, CSRS vs. VRS and CSRS vs. Static well represent the bell shape. Meanwhile, ΔE Static vs. VRS, Static vs. CSRS relatively well represent the bell shape. Considering the altimetric component Δh, only the Static vs. VRS rather well represents the bell shape.

The range of variability of the 5 pairs involving RTKLIB remains higher than that of the remaining 7 pairs (

Table 3. Range of variability minima – maxima values, min – max (mm), for ΔN, ΔE and Δh differences, post removal of the extreme values.

Min Max (mm)	Static CSRS	Static RTKLIB	RTKLIB CSRS	Static VRS	Static FKP	Static NEA	CSRS VRS	CSRS FKP	CSRS NEA	RTKLIB VRS	RTKLIB FKP	RTKLIB NEA
ΔN	−24 54	−353 46	−42 67	−38 40	−52 29	−20 31	−23 52	−33 56	−37 43	−42 355	−124 374	−36 431
ΔE	−92 141	−418 258	−201 341	−43 118	−82 34	−51 78	−106 151	−32 122	−42 101	−173 580	−481 583	−269 653
Δh	−33 212	−204 219	−120 298	−61 69	−44 173	−49 174	−69 203	−23 208	−96 210	−76 504	−166 511	−120 480

), even after removing the extreme values for all computation schemes. The average ΔN, ΔE and Δh indeed were 374, 791, and 540 mm being reduced of ~102 mm, while they were slightly reduced for the latter seven being 76, 170, and 232 mm. The lowest range of variability min–max pre extremes value removal were obtained for Static vs. NRTK pairs (109, 268, and 337 mm for ΔN, ΔE, and Δh, on the average), and it remains the lowest also after removal (70, 135, and 190 mm).

4. Conclusions

As a result of this work, the coordinates retrieved with different GNSS approaches (static, NRTK, and PPP) were compared. It is commonly accepted that the static survey guarantees the best results in terms of precision, increasing the occupation time, but it needs a long time to post-process data. The NRTK technique allows the measurements of coordinates in real-time, but strictly depends on the network configuration and the active reference stations during the processing. Finally, the PPP approach is automatized with online software, but needs the implementation of ultra-precise ephemerides and post-processing elaboration.

Some statistics descriptors of the north, east, and ellipsoidal height differences among different pairs of solutions were analyzed, among the Static, NRTK, and PPP methodologies.

Among the twelve pairs of evaluated solutions, those five involving RTKLIB exhibited a different behavior compared to the others and they often did not belong to a normal distribution.

Once extreme values were removed, the Static vs. NRTK pair showed the lowest range of variability and the lowest standard deviation (≈−70, 135, 190 mm and 18, 33, and 54 mm on average, respectively, for the ΔN, ΔE and Δh).

The analysis of Kurtosis highlighted that, on the average, the frequency distribution loses leptokurticity tending to the normal distribution (particularly the CSRS vs. Static, CSRS vs. VRS, RTKLIB vs. NEA and Static vs. FKP pairs). The standard deviation of the differences for the N, E and h components of pairs which did not involve RTKLIB was ~20, ~40, and ~70 mm, respectively, while the standard deviation of the differences for the ΔN, ΔE, and Δh components of pairs involving RTKLIB was ~100, ~170, and ~120 mm, respectively.

Two statistic tests, the Kolmogorov–Smirnov and the Anderson–Darling, were implemented to verify if the frequency distribution of the differences belonged to a normal distribution. Both showed that excluding the ΔE in the Static vs. FKP comparison, and some pairs including RTKLIB (Static vs. RTKLIB for ΔN and Δh, Static vs. VRS and Static vs. NEA for N), for which the null hypothesis is rejected, mostly the distribution frequency of the differences among pairs belonged to a normal distribution, at a significance threshold of 0.05. In particular, according to the Kolmogorov–Smirnov test, the best values were found for the differences CSRS vs. Static and CSRS vs. NEA, while in agreement with the Anderson–Darling test, the best values were found for Static vs. NEA and once again for PPP vs. NEA differences.

The coefficient of determination between the empirical and the theoretical frequency distributions provided a measure of how well observed frequencies were replicated by the theoretical frequencies. The analysis highlighted that CSRS vs. Static, RTKLIB vs. CSRS and Static vs. VRS exhibited the highest correlations (~0.6 – 0.9) while Static vs. FKP, Static vs. NEA, CSRS vs. VRS, and CSRS vs. FKP exhibited weak correlations.

Need to be remarked that the aim of this work was to analyze the congruence of the solutions obtained with different methodologies (Static, PPP and NRTK), nor to judge software packages. Although the lowest congruencies seem characterizing the pairs involving RTKLIB, this result should not be considered a criticism on the performance of this well-known open access program, which undoubtedly is one among of the most useful PPP processing software available, given its very straightforward applicability, considering also that our analysis is limited to one hour of data.

With extended observation times, the congruence among different solutions could be enhanced. Moreover, enlarging the number of benchmarks, the accuracy of the NRTK positioning compared to PPP and Static should be improved, in turn affecting related congruencies.

Other analyses are required to further investigate the performances of different solutions and to test other methods for GNSS network solutions (such as the Master Auxiliary Concepts, MAC). In addition, the recent development of Galileo and Beidou-3 constellations could give more indications than those obtained in this study with only GPS and GLONASS constellations.

In the last few years, several applications have been developed employing the IGS stations in static mode. Specifically, the available online services and packages include the Automatic Precise Positioning Service (APPS), GPS Analysis and Positioning Software, the Canadian Spatial Reference System precise point positioning service, and the Magic-PPP [17,23,24,25], or the comparative analysis of ZTD-estimates obtained with six different software packages (JPL’s APPS [80], CSRS-PPP, MagicGNSS [81], European Space Agency and Barcelona’s tech GNSSLab Tool (gLAB) [82], RTKLIB, the University of Nottingham’s POINT) respect the ZTD-estimates obtained from the IGS tropospheric product [17,23,24,25]. Moreover, these applications and services could be engaged to analyze the PPP positioning compared to other solutions.NRTK, PPP, or Static, that is the question!