1. Introduction
The computational demands of scientific research are constantly increasing. In the field of radio astronomy, observation has evolved from the single telescope to the interferometer arrays, which is currently under development. At the same time, the Very Long Baseline Interferometry (VLBI) technology, which increases the accuracy of observation by extending the distance between the stations, has also been rapidly developed. They are all developed based on interferometric technology, but the data processing methods of them are different.
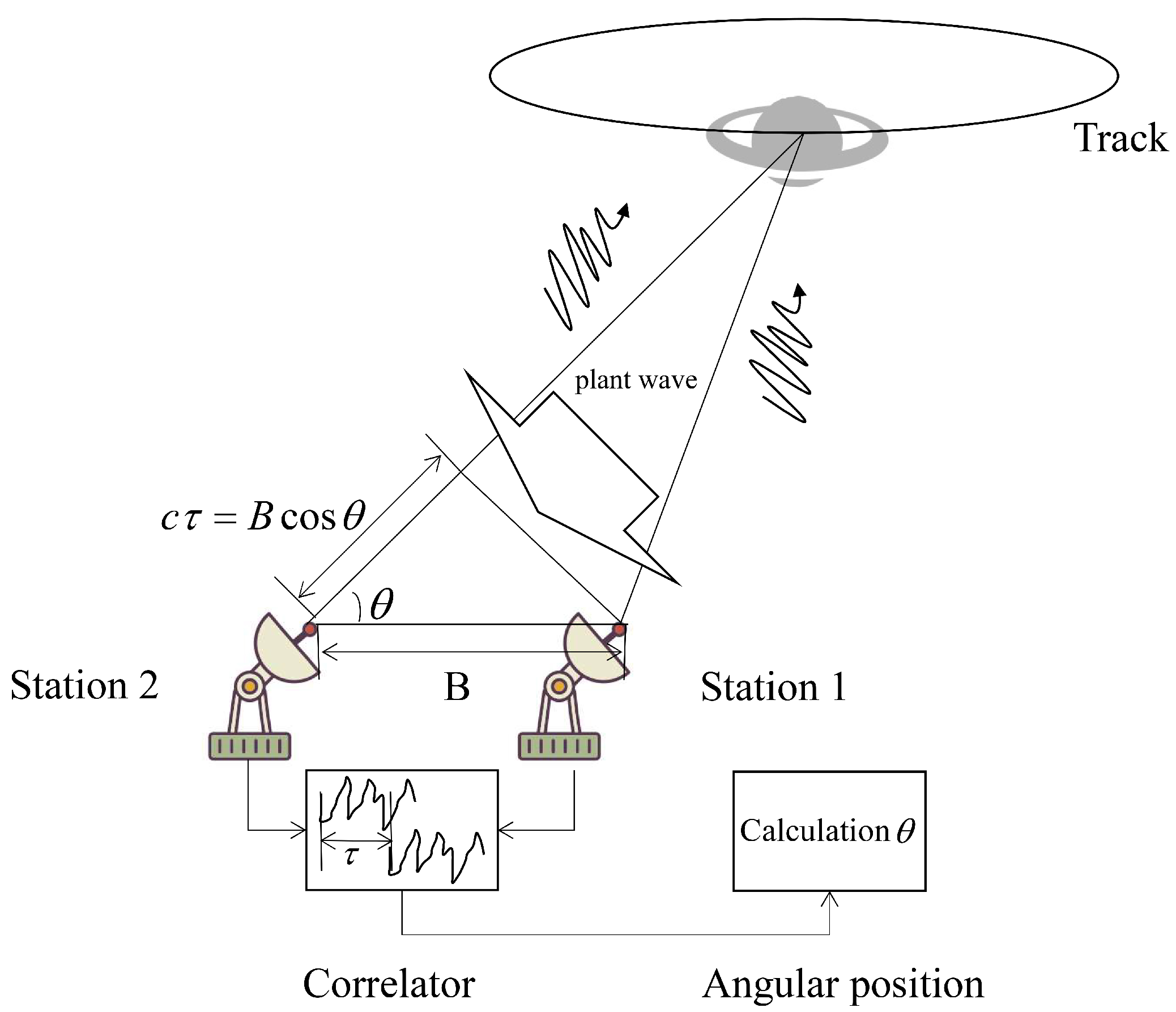
VLBI plays a key role in deep space exploration and astronomical observation due to the capability of high accurate angular measurement. The technology performs correlation calculations on the observation data of multiple radio telescopes, thus synthesizing multiple telescopes into a synthetic aperture telescope with an equivalent diameter of the longest baseline length [
1,
2]. Until now, the VLBI has been widely used in many fields, such as geodetic survey, astrophysics, detector positioning, and so on [
3,
4]. With the increase of VLBI stations and the observation bandwidth, there is a strong demand for fast correlation processing [
5,
6].
For the interferometric technology, the most important part is the design of correlators. In the past few decades, many correlators based on dedicated hardware have been developed. Among various dedicated hardware, application specific integrated circuit (ASIC), digital signal processing (DSP) and field-programmable gate arrays (FPGA) are usually employed in the development of VLBI correlators. A. R. Whitney et al. [
7] implemented a VLBI system based on the the custom-VLSI chip and the DSP. Compared with ASIC, FPGA has a shorter design cycle, lower development cost and more flexible design. Rurik A. Primiani et al. [
8] designed a new VLBI correlator, which replaced the previously-coined ASIC correlator. Hitoshi Kiuchi et al. [
9] proposed six preset correlation processing system on the basis of FPGA. In order to avoid programming, testing and debugging issues in the traditional FPGA development process, Gan et al. [
10] adopted the OpenCL tool flow to convert the OpenCL kernel function into customized FPGA hardware accelerator files, automatically. DSP is more suitable for processing computing tasks, and the FPGA is better for logic operations. Shanghai Astronomical Observatory (SHAO) developed the third-generation Chinese VLBI Data Acquisition System (CDAS), and then equipped the DSP board with Xilinx XC7K480T FPGA for data processing [
11]. The joint research activity in the RadioNet FP7 Programme designed a generic high-performance computing platform based on DSP and FPGA for radio astronomy, named UniBoard [
12]. Although the methods based on dedicated chips can effectively implement the VLBI correlator, their economic costs and scalability are still insufficient.
A recent trend is to correlate in software instead of dedicated hardware. With the rapid development of high-performance computing technology [
13,
14,
15,
16], the correlators have begun to be developed on the general CPU platform. In the earlier work, VLBI software correlators are implemented based on a single CPU [
17], e.g., the VLBI correlator from National Radio Astronomy Observatory (NRAO) was developed based on an IBM 360/50 [
18]. Furthermore, the VLBI correlators are implemented on CPU clusters to achieve higher efficiency, such as the Chinese VLBI Network (CVN) Earth software developed by Shanghai Astronomical Observatory of the Chinese Academy of Sciences [
19] and DiFX VLBI correlator proposed by Swinburne University of Technology [
20]. Extensive experiments verify that the CPU cluster can realize real-time VLBI data processing at a medium data rate, and it is easier to design and develop compared with the dedicated chips.
The emergence of the graphics processing unit (GPU) and the compute unified device architecture (CUDA) provide new opportunities for accelerating VLBI correlators [
21,
22]. GPU has been developed as a high-performance device with the characteristics of high parallelism, multithreading, many-cores, huge bandwidth capacity, and hundreds of computing cells. But they only discussed how to deploy the algorithm on heterogeneous platforms and analyze the processing results of the software. In recent years, for the interferometric array observation technology, some correlators have been accomplished on the GPU. Thomas Hobiger et al. [
23] discussed the feasibility of implementing correlator on GPU. The Cobalt project implemented a GPU-based correlator for LOFAR [
24]. However, the GPU-based parallel acceleration method of VLBI algorithm has not been studied yet. Besides, GPU has been widely used in the field of remote sensing for big data processing [
25,
26,
27,
28]. Inspired by the remote sensing applications and correlators of interferometric array observation technology on GPU, we try to implement a high efficient GPU-based VLBI correlator considering hierarchical optimization strategies.
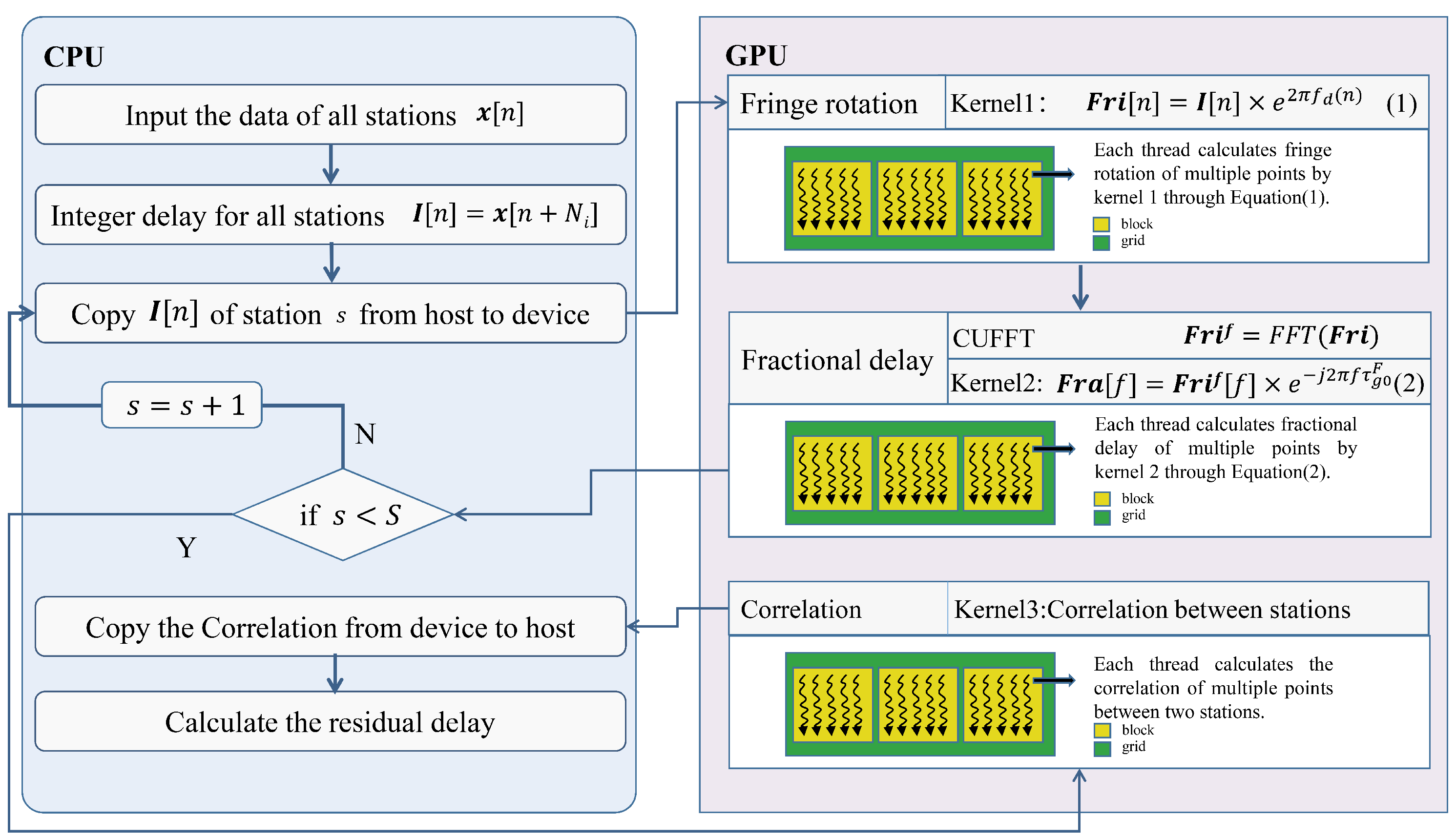
In order to meet real-time processing at high data rate, we propose a parallel implementation of VLBI algorithm on the CPU-GPU heterogeneous platform. To solve the computation-intensive issue, the VLBI algorithm is implemented in GPU massively parallel mode, and is designed to realize the fine-grained task partitioning and calculation. Further, to deal with the data-intensive problem, the multi-level GPU optimization strategies have been introduced to improve the efficiency of data access and processing pipeline. Finally, the proposed method has been evaluated by the actual observation data. It is proved that the GPU implementation can meet the demands of high data rate real-time calculation, and is superior to the serial CPU method and multi-core CPU method.
In all, compared with previous works, we make the following contributions.
- (1)
GPU parallelization of the VLBI algorithm is presented. According to the characteristics of the GPU, multi-point calculation tasks are allocated to GPU threads to make full use of the computing capability of the threads and the hardware resources of the GPU.
- (2)
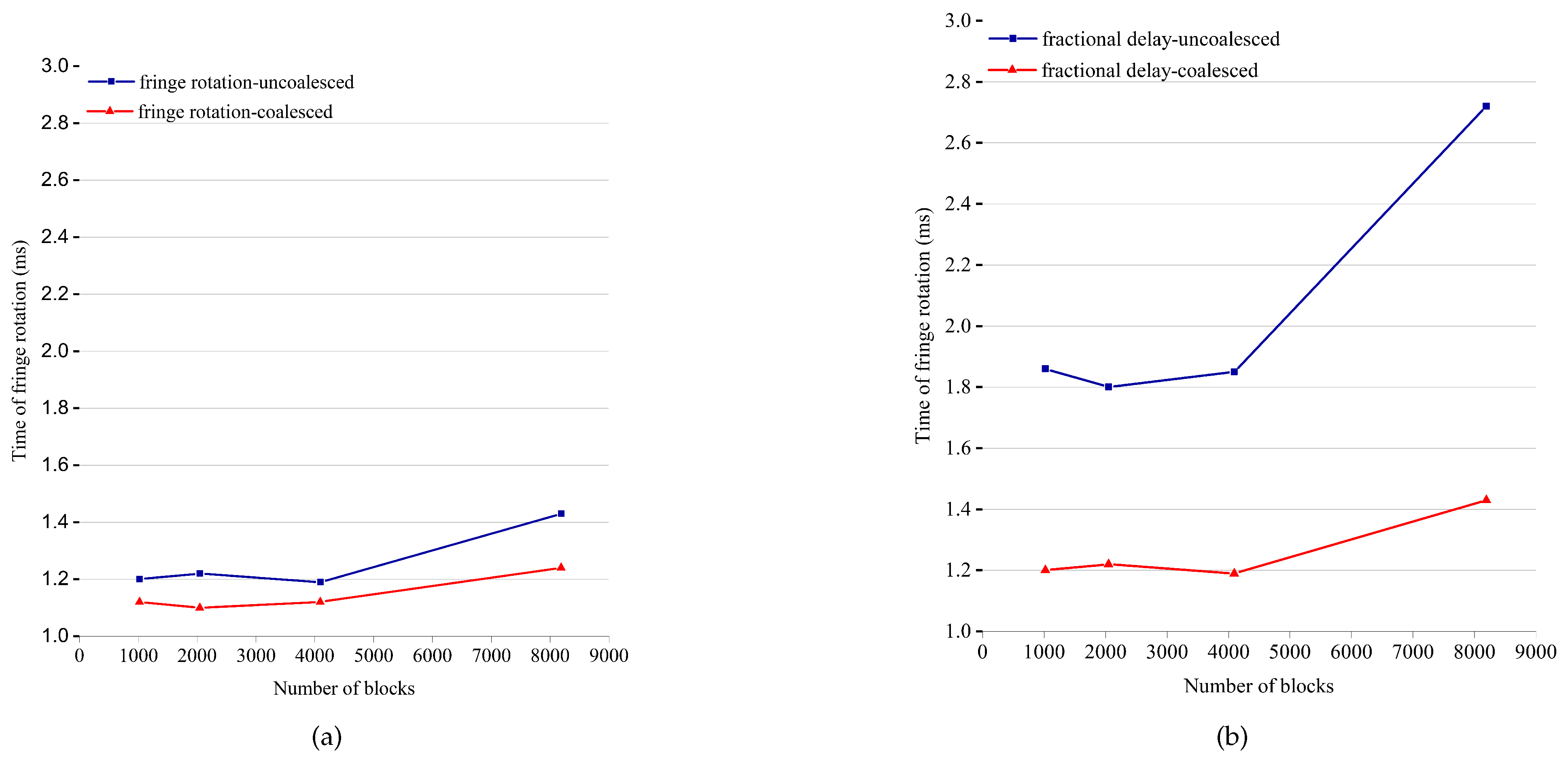
Shared memory is used to solve the uncoalescing problem encountered when accessing global memory.
- (3)
According to the characteristics of VLBI data, CUDA stream is used to optimize the data transmission between CPU and GPU.
The remainder of this paper is organized as follows. Section II presents the calculation flow of the VLBI algorithm and analyzes the algorithm complexity. Section III gives the details of the proposed GPU-based parallel VLBI method. Experimental results are shown and analyzed in Section IV. Conclusions and perspectives are given in Section V.
5. Conclusions
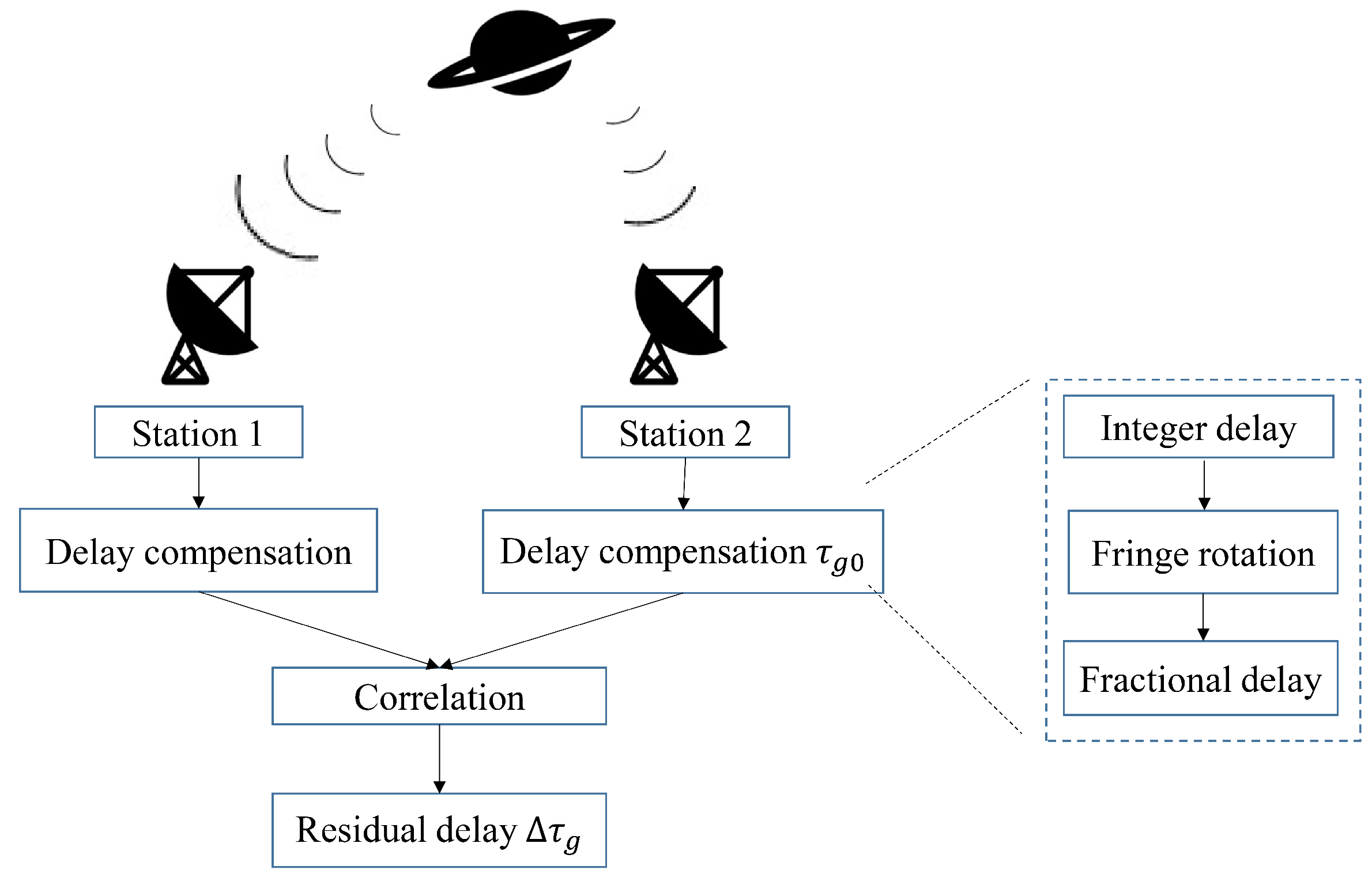
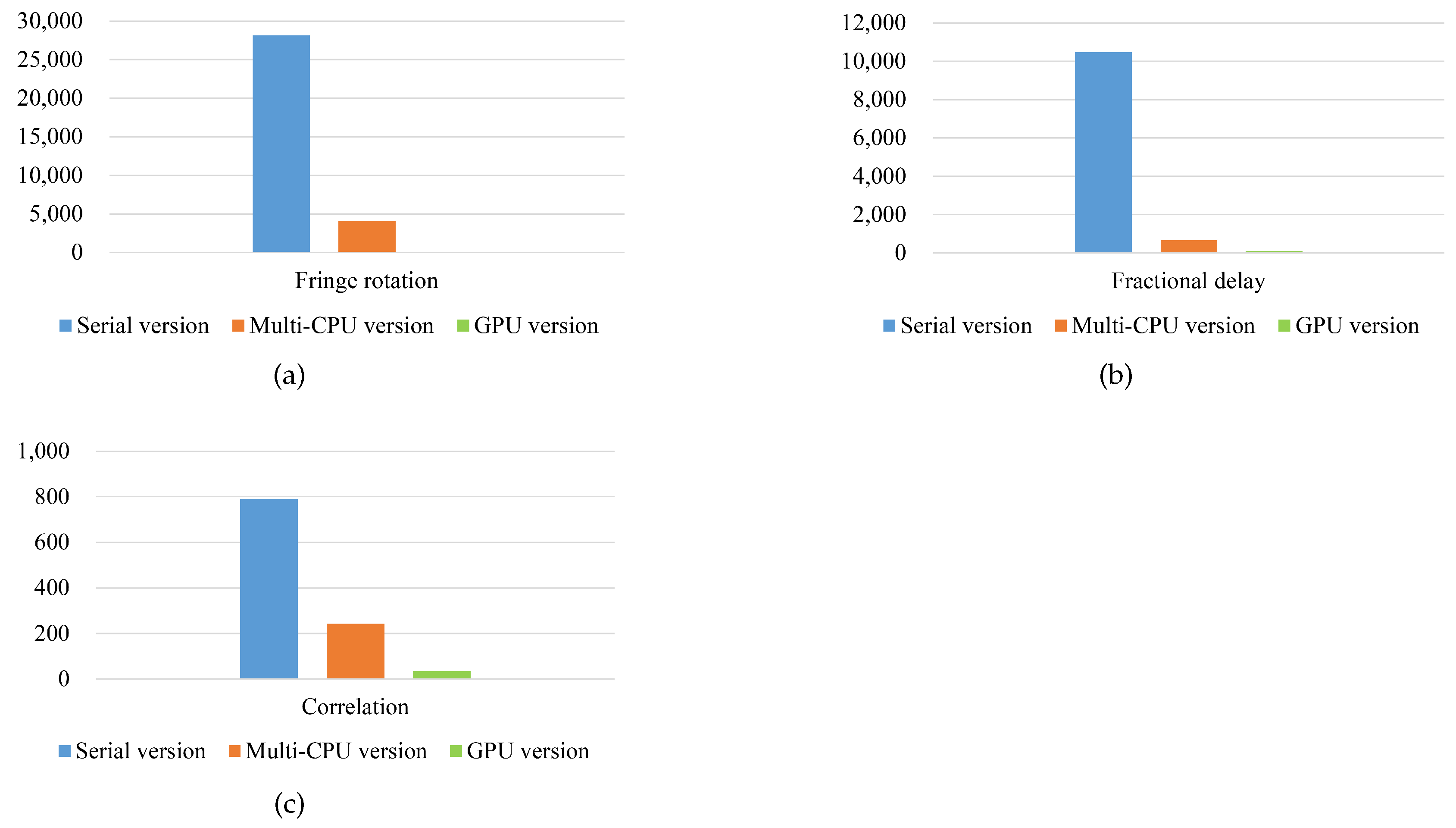
In this paper, a GPU-based VLBI parallel correlator is proposed to meet the growing demands for high computing power. Through the algorithm complexity analysis, the targets of the parallel acceleration are determined, namely calculations of the fringe rotation, fractional delay and the correlation. By assigning the multi-point calculation as single thread task, the VLBI algorithm is massively parallelized. As a kind of computing-intensive and data-intensive issue, the GPU-based VLBI algorithm is further optimized in terms of data transfer. Through multi-level optimization strategies, namely data transmission rules, coalescing access and concurrent pipelines, the efficiency is increased by 2-fold. Under the premise of ensuring the calculation accuracy, compared with the serial version, the calculation part and the overall calculation have reached the speedups of and , respectively. Compared with the multi-CPU version, the corresponding parts have achieved speedups of and . In addition, the data processing rate of the GPU-based correlator can reach 712 Mbps, which can far meet the current ground station processing needs. The GPU-based correlator outperforms the actual multi-CPU-based correlator in terms of computing performance and data rate. In the future work, we will study the multi-GPU-based VLBI algorithm and deploy it to the better performance CPU cluster to further improve the data processing capability for deep space exploration.