Abstract
Grottoes, with caves and statues, are an important part of immovable heritage. Statues in a particular grotto setting are often similar in geometric form and artistic style, and identifying the similarity between these statues can help provide important references for value recognition, condition assessment, repair, and the virtual restoration of statues. Traditionally, such reference information mainly depended on expert empirical judgment, which is highly subjective, lacks quantitative analysis, and cannot provide effective scientific support for the virtual restoration of grotto statues. This paper presents a similarity index based approach for identifying similarities between grotto statues by studying 11 small Buddhist statues carved on the 18th cave in the Yungang Grottoes, located in Datong, China. The similarity index is determined according to the hash values calculated based on the pHash method using the orthophoto images of Buddhist statues to identify similar statues. Similar feature points between the identified statues are then matched using the Scale Invariant Feature Transform (SIFT) operator to support the repair and reconstruction of damaged statues. The experimental results show that the variation of similarity index values confirms the visual inspection of the statues’ appearance in the orthophotos. The additional analysis of three-dimensional (3D) point clouds also confirms that the similarity index based approach is accurate in the initial screening of similar grotto statues.
1. Introduction
Grottoes, with caves and statues, are an important symbol of Chinese Buddhism and an important part of immovable heritage. China has a large number of grottoes that have been excavated and filled with invaluable manuscripts, artwork, and statues, and these grottoes are widely distributed across the country. The history of these grottoes goes back to the time between the 3rd and 8th centuries CE. Chinese grottoes are also important for studying Chinese politics, economy, culture, architecture, art, and music during past dynasties [1]. However, the condition of these grottoes has deteriorated over time due to human activities (e.g., coal mining and tourism) and natural weathering (Guo and Jiang, 2015; Liu et al., 2011) [2]. As such, the protection and documentation of these grottoes has become increasingly urgent.
According to the Venice Charter for the Conservation and Restoration of Monuments and Sites, “Replacements of missing parts must integrate harmoniously with the whole” [3]. The challenge to the conservation and restoration of grottoes is to identify the proper references and provide scientific evidence needed for the recording and reconstruction of grotto statues to support virtual restoration, rather than just relying on subjective and empirical judgment without quantitative analysis by experts. Virtual restoration is the scientific process of the study and reconstruction of historically significant or damaged objects, which records aspects before their damage or degradation and reconstructs them after. Considerable efforts have been made in both areas.
Reconstructing damaged objects or restoring missing parts of cultural heritage using similar characteristics of an identified reference object has been studied previously. The methods fall into two types. The first type applies to symmetric objects that can be divided into two or more identical pieces, so undamaged pieces can be used as the basis for reconstructing damaged pieces. This type of method has been studied on small portable symmetric antiquities such as potteries and vases [4,5,6] and sizeable immovable grotto Buddhist statues such as the Thousand-hand Bodhisattva in Dazu, China [7,8,9,10]. The second type of method focuses on a cluster of heritage objects, such as the terracotta warriors in China [11] and the human face statues of the Bayon temple in Cambodia [12,13], which may be similar or have similar or repetitive parts that can be used as references for reconstruction. Studies have been done on identifying symmetric pieces and similar objects, especially on the similarity of the Buddhist statues in the grottoes [7,8,9,10,14], based on matching three-dimensional (3D) point clouds, copying with axis of symmetry, and analyzing clusters with self-similarity. However, these methods did not develop any similarity index as a quantitative measure.
The purpose of this paper is to study and propose a similarity index based approach for identifying similar grotto statues to support the virtual restoration of damaged statues. The study used 11 small Buddhist statues carved on the main Buddhist statue in the 18th cave of the Yungang Grottoes, located in Datong, Shanxi Province, China, as shown in Figure 1. Included in the World Cultural Heritage List by UNESCO in December 2001, the Yungang Grottoes, with 252 caves and 51,000 statues, represent an outstanding achievement of Buddhist cave art in China during the 5th and 6th centuries [15]. It is one of the three most famous ancient Buddhist sculptural sites in China. The grottoes are royal grottoes, because the Northern Wei Dynasty used Buddhism to serve the ruling class, and are closely related to the national policy of the Northern Wei Dynasty [16]. The Yungang Grottoes are unique in the sense that they embody many foreign artistic features such as those found in Greece and Rome and in Indian architecture and Gandhara art, and they represent a major milestone in the birth and artistic trend of Chinese Mahayana Buddhism [17]. The early Yungang Grottoes had apparent artistic features of Gandhara and Mathura art from ancient India, and the Buddhist statues had noticeable Xianbei cultural features. Later, to alleviate social and ethnic conflicts and promote cultural exchanges between the north and the south, Han culture was added to Buddhism, and the grotto statues after that had characteristics of the Han culture. The excavation of the Yungang Grottoes promoted the cultural exchange and integration of various nationalities in the Northern Wei Dynasty, gradually localizing Buddhism in China. It carried forward the traditional Chinese architectural style [18]. The Yungang Grottoes are the product of the cultural exchange between China and the west, the integration of Hu and Han cultures, and the influence of court and folk culture. They are also the embodiment of the cultural integration of Confucianism and Buddhism and the artistic expression of historical features of the Northern Wei Dynasty [19].

Figure 1.
Small statues carved onto the statues in the 18th cave of the Yungang Grottoes, China.
Attempts at the restoration and repair of the Yungang Grottoes have been made on deficient parts of some statues in the past [15]. Besides the main Buddhist statues, the artisans also built many small Buddhist statues with similar styles. Some of them have been damaged by human activities (e.g., coal mining and tourism) and natural weathering over time [20], while others are relatively well preserved and can be used as references for restoration. However, selecting the right Buddhist statue as a reference for restoration traditionally was based on either the personal experience of experts or the record and inference of ancient sources (texts, graphics, etc.), which are now mostly lost. Therefore, identifying new and scientific restoration evidence plays an essential role in reconstructing damaged statues [21].
The rest of the paper is organized as follows: Section 2 reviews the previous works related to the virtual restoration of grotto statues. Section 3 describes the study area and discusses the methods used in this study. Section 4 presents our experiment’s results on determining similarity index values and matching the feature points of identified similar statues, followed by some discussions in Section 5. Finally, Section 6 provides some concluding remarks and prospects for future research.
2. Background and Related Work
The protection of the Yungang Grottoes has a long history. The Grottoes have been repaired many times. According to the great Cave Temple’s stele record, rebuilt in the XiJing Wuzhou mountain of the Jin Dynasty, the most extensive restoration was carried out during the Liao Dynasty (1060 A.D.), and the aim of the project was mainly to build wooden eaves in front of the grottoes [22,23]. According to the stele records of rebuilding the great stone Buddhist Temple in Yungang, the Grottoes were also repaired during the Qing Dynasty. The eaves and some damaged Buddhist statues of the 5th and 6th caves in the Grottoes were rebuilt between 1651 and 1873 [24].
During the period of the Republic of China, some experts carried out a comprehensive investigation of the Yungang Grottoes. In 1933, some well-recognized architects, Sicheng Liang, Huiyin Lin, and the others, went to Datong to investigate the local ancient buildings and the Yungang Grottoes and made a special investigation on the Yungang Grottoes from the perspective of architectural history [25,26]. During World War II, the Japanese also conducted a comprehensive investigation and research on the Grottoes, and produced a 16-volume report “Yungang Grottoes”, which provided a large amount of reliable mapping data and precious photos of the Grottoes, which have become important evidence for the later studies of the Grottoes [27,28].
Since the beginning of the People’s Republic of China, the Yungang Grottoes have been fully protected. In 1955, the Yungang Grottoes Protection Institute (now the Yungang Grottoes Research Institute) was established. Since the mid-1960s, researchers have tried to innovate and improve the chemical protection methods and traditional reinforcement technology used in the Grottoes. In the 1970s, the focus of the Grottoes’ protection was to prevent cave collapses. Through emergency reinforcement, many caves and sculptures on the verge of collapse were saved, and the stability problem of the main caves and statues was virtually solved. In the 1980s, the Grottoes entered a period of comprehensive maintenance. Within this period, almost all the grottoes were repaired, and meteorological stations and grotto protection laboratories were established.
In recent years, the Yungang Grottoes began to be digitally protected. In 2011, Zhejiang University and the Yungang Grottoes Cultural Research Institute used Scanning Electron Microscope (SEM), Fourier Transform Infrared Spectrometer (FTIR), X-Ray Diffraction (XRD), and Energy Dispersive Analysis X-Ray (EDAX) to study the potential hazards (dust deposit, salt crystallization, and black crust) to the grottoes and the conservation methods that could be used to help guide remediation efforts directed at reducing the weathering problem [20]. In 2015, the Yungang Grottoes Research Institute conducted 3D scanning of the 18th cave in the Yungang Grottoes, established a large 3D GIS platform for the Grottoes, and preserved digital mapping data of the 18th cave of the Grottoes [29]. In 2017, Zhejiang University successfully replicated cave 3 and cave 12 of the Grottoes by using 3D printing technology [30]. Beijing University of Civil Engineering and Architecture also completed 3D printing of cave 18 in 2018, which is one of the earliest caves of the Grottoes and has the richest carving content [31]. In 2020, Yan et al. carried-out 3D reconstruction based on the multi-view images of Cave 15 and Cave 16 of the Grottoes and quantitatively analyzed weathering effect on the Grottoes [32].
From the restoration history of the Yungang Grottoes, it is clear that ancient conservation projects could only rely on workers to repair by hands because they were limited by the level of science and technology. In recent years, the protection of the Grottoes has focused on the eave’s restoration and the grottoes’ stability, but quantitative judgment of the similarity of the Buddhist statues in the Grottoes has not attracted much attention from researchers.
The best evidence for the restoration of damaged cultural heritage ideally is the original documentation, such as survey data and photos. However, these documents have been mostly lost over time. In the case of the Yungang Grottoes, pictures and deterioration survey data were available in the book, Yungang Grottoes, published by Japanese scholar Toshio Nagahiro in the 1950s [20,27]. On the other hand, cultural heritage, especially grottoes and statues, of the same period tend to have a unified style. Therefore, searching for similar objects may provide an economical and scientific means to restore damaged heritage objects.
As mentioned in Section 1, the methods for identifying references are mainly based on symmetric pieces of the same object and similar objects of a group of objects. For symmetric objects, the undamaged part is determined as the reference, and the damaged part is reconstructed or repaired based on the reference parts. The Shape Laboratory of Brown University (USA) launched a Semantic Interoperability to access Cultural Heritage (STITCH) project, which mainly studied the automatic splicing and virtual restoration of movable cultural heritage objects based on similarity. Brown et al. presented an inexpensive system for acquiring information from small objects, such as fragments of wall paintings, and associated metadata [33]. In addition, they introduced a novel 3D matching algorithm that registered two-dimensional (2D) scans to 3D geometry and computed normals from 2D scans. Their algorithm efficiently searched for matching fragments using the scanned geometry. Other scholars virtually reconstructed the broken heritage objects by utilizing their own axes, generatrices, and other geometric features [3,5,34]. Fantini carried out human-machine interactive virtual restoration of damaged ancient skulls, damaged pottery figurines, and stone statues [6,34,35], where the symmetry was obvious. According to the above studies, the symmetry axis can be used as evidence for cultural heritage restoration, but it may not be suitable for grotto statues.
For immovable heritage objects such as grotto statues, Hou’s team at Beijing University of Civil Engineering and Architecture studied the digital reconstruction of the broken fingers of the Thousand-hand Bodhisattva stone inscription in Dazu, Chongqing, China [9,10]. They proposed a method for reconstructing missing Bodhisattva fingers based on regression model prediction. First, a complete “Bodhisattva hand”, similar to a broken Bodhisattva hand, was found, according to the symmetry of the whole Thousand-hand Bodhisattva. A skeleton line of the similar Bodhisattva hand was constructed through the differential geometry contraction principle. A regression model was established to predict the size information of the damaged finger. With this method, the geometric symmetry and palm skeleton line comparison of all 830 hands of the Thousand-hand Bodhisattva were used as the basis of similarity discrimination, but the similarity comparison of palm texture and other details was not possible.
In order to search for similar objects in a group of objects through cluster analysis, the team of Tokyo University of Japan studied type statistical recognition using 3D point cloud data of face sculptures in the Bayon temple, Cambodia [36,37,38]. They used the measured 3D geometric model to align 3D faces in the same coordinate system, direction, and normalization; captured the depth image of each face; and finally classified them through clustering analysis and other statistical methods. The classification method was more general, only classified similar face sculptures into one category, and did not define the objective threshold for each classification. Zhou’s team from Northwest University (China) extracted the outlines and surface salient features of the fragments of terra cotta warriors and horses and classified and established a template library [11,39]. By querying and comparing the standard models in the template library makes the subsequent virtual splicing of fragments possible. However, their study focused on classifying the fragments of terracotta warriors and horses according to the pre-established template and did not calculate the similarity between different fragments.
There are several methods used for 2D image similarity discrimination. They include:
- Structural Similarity Index Measurement (SSIM): SSIM is an index for the quality evaluation of full reference images, which measures image similarity from brightness, contrast, and structure. SSIM values range from 0 to 1. The larger the value, the smaller the image distortion. This method is usually used to measure the distortion of a compressed image, rather than calculating the similarity between two images [40].
- Cosine Similarity: Cosine Similarity is used to represent the image as a vector and calculate the cosine distance between the vectors to represent the similarity of the two images. According to our testing, this method took a long time to calculate the similarity between small Buddhists on the Thousand Buddhist cassock [41].
- Histogram Method: Histograms can describe the global distribution of colors in an image, which is a basic method for image similarity calculation. However, the histogram is too simple to capture the similarity of color information without any more information. As long as the color distribution is similar, it can be judged that the similarity between the two is high. For Buddhist statues, the stone color is almost the same, so it is obviously unreasonable to use the histogram method to judge whether images are similar [42].
- Mutual Information Method: Calculating the mutual information of two images can represent the similarity between them. If the size of the two images is the same, the similarity of the two images can be represented to a certain extent. However, in most cases, the size of the image is not the same. If the two images are adjusted to the same size, some original information is lost, making it less suitable for determining image similarity [43].
- Hash value: The hash method normalizes images to a certain size, calculates a sequence as the hash value of this image, and then compares the same number of bits in the hash value sequence of two images [44,45]. The lower the number of different data bits, the higher the similarity of the two images. According to the pre-defined threshold value, the similarity of the two images can be tested. Compared with other forms of similarity discrimination, this method takes less time. Furthermore, the algorithm is hardly affected by image resolution and color and has better robustness.
After analyzing the above image similarity discrimination methods and considering the current needs of this study, i.e., to obtain a stable and accurate objective similarity index of Buddhist statues [46,47], this paper chose the hash value method for determining similarities between small Buddhist statue images. Subsequently, the identified similar small Buddhist statue images are matched by the Scale Invariant Feature Transform (SIFT) operator [48,49] to visualize the similar feature points.
3. Materials and Methods
The overall process of assessing the similarity between different small Buddhist statues and obtaining the similarity index to match the similar feature points is shown in Figure 2. First, an orthophoto image of the experimental area was preprocessed to segment single Buddhist images. Then, the hash value of any two images was obtained by the pHash algorithm and the difference between the hash values was compared by the Hamming distance. After that, the similarity index was obtained. The larger the value, the more similar the two images are. When repairing a small Buddhist statue, the Buddhist statue with a larger similarity index can be selected as a reference, and then the SIFT operator can be used to find and match similar feature points.
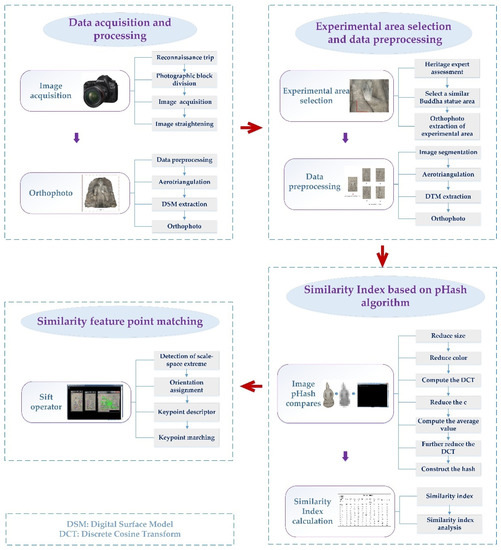
Figure 2.
The overall process of the proposed approach.
3.1. Study Area and Data Acquisition
In this paper, the selected study area is the “Thousand Buddhist cassocks” on the main Buddhist statue in the 18th cave of the Yungang Grottoes (see the red box area in Figure 1). The area includes both well-preserved small Buddhist statues and damaged ones. To assess the similarity between individual statues, an orthophoto image of the study area, created using the commercial software Concept Capture to 300 DPI, was preprocessed and segmented, and the image of each small statue was saved independently. The images were further rotated to avoid the influence of the inconsistent postures of the small statues under comparison (Figure 3).

Figure 3.
Rotation of preprocessed and segmented image of Buddhist statues.
Given the dimensions and the characteristics of the Buddhist statues, a Canon 5D Mark IV digital camera was used to capture the original orthophoto of the 18th cave of the Yungang Grottoes. The highest resolution of a single photo is 6720 × 4480 pixels, and the effective number of pixels is 30.4 million, which meets the basic requirements for generating high-resolution orthophoto images with 300dpi. According to [50], the distortion of the photos taken with the 50mm lens is small, so the orthophotos were collected with the 50 mm lens. Considering data quality, volume, and post-processing, the vertical and horizontal overlaps of adjacent photos were set at no less than 30%, which not only ensured the sufficient overlap of adjacent photos but also avoided the post-processing difficulties caused by the high overlap and redundancy of the collected photos.
When collecting orthophoto images, to ensure the consistency of the picture overlap and reduce the picture jitter and residual image caused by the camera operator, a tripod, slide rail, and shutter line were used as auxiliary photographic equipment. Scaffolding was also set up to facilitate the photo shooting at different heights. In setting the camera, the exposure mode was set to “m” file and the image quality was set to raw + JPEG large/excellent for later processing. According to the weather conditions, the color temperature value was set between 5200 K and 6500 K. The ISO speed was generally set to 200, and the aperture was set to F10.
Where there was insufficient light in the grottoes, a flashlight was used to ensure the exposure, and outdoor shooting was conducted with natural light. Before shooting, the facade of the 18th cave was divided into 16 areas (red dotted box in Figure 4). In each segmented area, an “s” shaped track was used to take the grotto images layer by layer (as shown by the blue arrow in Figure 4). At the joints of adjacent areas, the overlapping degree of the photos (shown by yellow and green arrows in Figure 4) were appropriately increased to avoid the omission of photos and ensure the quality of data acquisition. To ensure that the photos taken could meet the requirements of creating orthophoto images and three-dimensional model texture, the angle of image shooting was set such that the angle between the lens and the main Buddhist statue was constant at 90 degrees. If the panorama was taken from the front, part of the panorama was taken first and the rest were shot one by one. Choosing a time when the light was softer and more uniform avoided backlight shooting. Considering the characteristics of the Yungang Grottoes, the side texture was also photographed using the same principle, except for the front side, in turn. The texture images of each facade, ceiling, and ground of the 18th cave were obtained by multi-angle photography.

Figure 4.
Orthophoto acquisition sequence (arrow indicates camera moving direction).
3.2. Quantitative Analysis of Existing Algorithms
Considering that the application of three-dimensional data needs high-cost equipment and data processing is also very complex, this paper uses orthophoto images of Buddhist statues as the data source to distinguish the 2D image similarity of different Buddhist statues to replace manual identification and ensure the scientific and objective judgment results and references. With respect to the image recognition algorithm, it is supposed to have high timeliness, accuracy, and robustness, and not be affected by image resolution and color. Moreover, it should be able to determine whether the orthophotos of the two Buddhist statues are similar or not by presetting threshold and carrying out quantitative analysis.
According to [51,52,53], there are three hash algorithms: average hash (aHash), different hash (dHash), and perceptual hash (pHash) (see Table 1). The aHash algorithm is based on pixel domain design, which runs fast, and image size scaling has little effect on its results. However, the gamma correction or histogram equalization of an image has a more significant impact on the image hash value, which is more suitable for original image retrieval based on thumbnails. The pHash algorithm is based on the frequency domain and retains the image’s low-frequency components by Discrete Cosine Transform (DCT). While the aHash is quick and easy, it may be too rigid to make a comparison. For example, it can generate false-misses if a gamma correction or a color histogram is applied to the image because the colors move along a non-linear scale—changing where the “average” is located and where bits are above/below the average. A more robust algorithm is used by pHash. The pHash algorithm can tolerate images with rotation and size changes of less than 25% and avoid the influence of gamma correction or color histogram adjustment. However, DCT is quite time-consuming, so the speed of pHash is the slowest among the three algorithms. The dHash algorithm is based on pixel difference and is sensitive to image rotation and deformation. In terms of recognition effect, the dHash algorithm is better than the aHash algorithm but is not as good as the pHash algorithm. In terms of implementation speed, the dHash algorithm is better than the pHash algorithm, but not as fast as the aHash algorithm.

Table 1.
Comparison results of the three hash algorithms.
In this study, an orthophoto image of a small Buddhist statue was selected as the original image, and the size, brightness, chroma, contrast, sharpness, blur degree, and angle of the original image were subsequently adjusted (Figure 5). Then, the accuracy and efficiency of the different hash algorithms were tested by using the original image and seven transformed images (The test program was written in Python language).

Figure 5.
Original image and transformed image. (a) image (original); (b) image (light); (c) image (resize); (d) image (contrast); (e) image (sharp); (f) image (blur); (g) image (color); (h) image (rotate).
The pHash algorithm was selected for determining the similarity index because it is more accurate, though less efficient, compared with the dHash algorithm, as shown in Table 1. This is because the objects studied are the small Buddhist statues on the Thousand Buddhist cassock, and the degree of degradation of the small Buddhist statues is the main factor affecting the similarity index of the Buddhist statues.
The similarity index of Buddhist statues can only be used to judge whether the Buddhist statues are similar or not. Its disadvantage is that it only generates the numerical values that are used to express the similarity degree of Buddhist statues and does not identify the matching feature points between two similar Buddhist statues. Therefore, it is necessary to identify and match the feature points of similar Buddhist statues.
The main process of feature point matching is as follows:
Key points are detected; description vectors are extracted and feature matching is performed:
- Construct local feature descriptor;
- Feature matching.
There are many algorithms for feature point matching, such as SIFT operator, Surf operator, Brisk operator, and Orb operator. The matching speed, accuracy, and robustness should be considered comprehensively for algorithm selection (see Table 2). According to [54,55,56,57,58,59], SIFT operator and Surf operator have high accuracy, and the results are relatively stable. SIFT is more accurate than Surf, but the running speed is slower. The Brisk operator and Orb operator are relatively fast, but the accuracy is poor. Again, considering the characteristics of small grotto statues, accuracy is a more important factor; thus, SIFT operator was selected as the feature point matching algorithm in this study.

Table 2.
Comparison of four feature point matching algorithm.
3.3. pHash Algorithm and Similarity Index
The similarity index is based on the pHash algorithm [53,60], which can form a group of hash data after image processing and is often used to search similar images using the original image. During the image search, the hash algorithm firstly extracts the input image features and then generates a set of hash values represented by a two-dimensional array. Then, the hash value is compared with the hash value of the target image to find the matching image [60].
The processing steps of the pHash algorithm are illustrated in Figure 6:

Figure 6.
Flow chart of pHash algorithm.
- Reduce size: The fastest way to remove high frequencies and detail is to shrink the image. In this case, pHash starts with a small image; 32 × 32 pixels is a suitable size. This is really done to simplify the Discrete Cosine Transform (DCT) computation and not because it is needed to reduce the high frequencies.
- Reduce color: The image was reduced to grayscale to further simplify the number of computations.
- Compute the DCT: The DCT separated the image into a collection of frequencies and scalars. We used a 32 × 32 pixel DCT during this process.
- Reduce the DCT: While the DCT is 32 × 32 pixels, the top-left is kept to 8 × 8 and the lowest frequencies in the picture are represented.
- Compute the average value.
- Reduce the DCT further.
According to the 8 × 8 pixel DCT matrix, we set the 64-bit hash value to 0 or 1. To be specific, “1” was set if it was greater than or equal to the average value of DCT, and “0” was set if it was less than the average value of DCT. The results did not show the true low frequency but only roughly showed the relative proportion of the frequency relative to the average value. If the overall structure of the image remained unchanged, the hash result value remained unchanged. It could therefore avoid the influence of gamma correction or color histogram adjustment.
3.3.1. Compute the Average Value
In this step, the hash value was obtained. In the 32 × 32 matrix generated after DCT transformation, most of the information was in the 8 × 8 matrix in the upper left corner. Therefore, it is only necessary to compare the 8 × 8 matrix elements with the average value of DCT. If the value was greater than or equal to the average value, it was recorded as 0, and then a 64-bit hash value composed of “0” and “1” was obtained.
In the above algorithm, the two-dimensional DCT was obtained according to the coefficient sub-matrix of 8 × 8 in the matrix:
G—N * N image pixels;
G—threshold matrix in N * N matrix;
A—cosine coefficient matrix.
After getting the 64-bit hash value, we needed to compare it with the hash value of the target image and calculate the number of different characters in the corresponding position between the 64-bit hash values of the two images through calculating the “Hamming distance”. Therefore, the range of pHash value was 0 to 64. The smaller the value, the smaller the difference between the images, and the more similar the two images are [53].
3.3.2. Compute the Cultural Heritage Similarity Index
First, the Buddhist statue images were numbered in sequence from 1 onwards after separating the experiment area. We then compared the 1st Buddhist statue image with the rest of the Buddhist images and recorded the similarity index after each comparison and entered it into the table. After the first round of comparisons, we compared the next Buddhist statue images with the rest of the Buddhist images and completed the above process. This process was iterated until the image of each Buddhist statues had been compared with the other Buddhist statue images. Finally, the similarity index was obtained according to the following formula:
S—similarity index
I—pHash value between two Buddhist statues images
It can be seen from the above formula that the higher the similarity index, the more similar the two pictures are. From this, we can judge the degree of similarity between the two Buddhist statues.
3.4. SIFT Operator and Feature Point Matching
To understand the similarities between the small Buddhist statue to be restored and the selected standard reference Buddhist statue, the SIFT operator can be used to obtain the matching feature points. The full name of the SIFT operator is Scale Invariant Feature Transform, which was first published by David Lowe at the International Conference on computer vision in 1999 and then improved in 2004 [48]. The SIFT operator has the invariability of image rotation and scale transformation and has good robustness to affine transformation, brightness transformation, and noise. It has often been used to match the feature points between images to extract the facial feature points of Buddhist statues, realize the objective evaluation of the similarities of Buddhist statues, and provide a scientific basis for the entity restoration of cultural heritage.
The SIFT operator obtains the point set of feature points through detecting the feature points of the input image; it then matches the feature points of different images to obtain similar feature points. The core content of the SIFT operator is the construction and detection of feature points, and its main steps are shown in Figure 7 [49]:
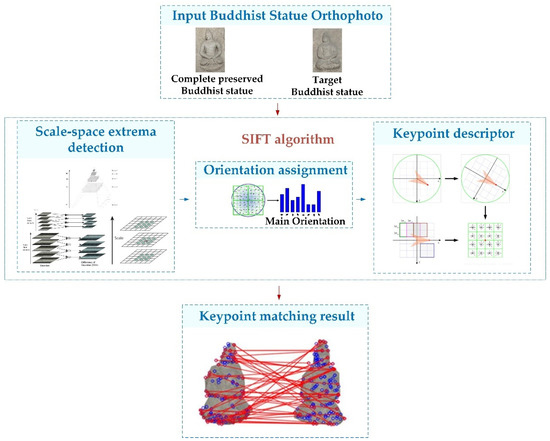
Figure 7.
Flow chart of SIFT algorithm.
- Constructing scale space;
- Searching for an extremum in scale space;
- Determining the accurate location of extreme points;
- Construct direction parameters of feature points.
4. Results
As shown in Figure 8, this paper first uses the method of close-range photogrammetry to generate the orthophoto image of the main Buddhist statue of the 18th cave of the Yungang Grottoes and then preprocesses the orthophoto image to cut out the area shown in Figure 1 from the Thousand Buddhist cassock. This is the research area of this paper.

Figure 8.
The main Buddhist Orthophoto of the 18th cave of the Yungang Grottoes.
As seen in Table 1, image rotation will affect the accuracy of the pHash algorithm. To avoid the influence of the posture of the small Buddhist statue on the similarity results, it is also necessary to uniformly adjust the posture of the small Buddhist statue and delete the background of the Buddhist statue (Figure 3) to ensure that the similarity discrimination is not affected by other factors.
Figure 9 shows the Hamming distance from the pHash algorithm between Buddhist statue No. 3 and Buddhist statue No. 2. As shown in Figure 10, the preprocessed images of eleven small Buddhist statues are selected as experimental data in the demonstration area. The results after executing the hash algorithm are shown in Table 3.

Figure 9.
Numerical value generated by pHash algorithm.

Figure 10.
The experimental object in this paper. (a) Orthophoto of Buddhist statue No. 1; (b) Orthophoto of Buddhist statue No. 2; (c) Orthophoto of Buddhist statue No. 3; (d) Orthophoto of Buddhist statue No. 4; (e) Orthophoto of Buddhist statue No. 5; (f) Orthophoto of Buddhist statue No. 6; (g) Orthophoto of Buddhist statue No. 7; (h) Orthophoto of Buddhist statue No. 8; (i) Orthophoto of Buddhist statue No. 9; (j) Orthophoto of Buddhist statue No. 10; (k) Orthophoto of Buddhist statue No. 11.

Table 3.
Statistics of experimental results.
Table 3 lists the similarity index between different small Buddhist statues. Taking the small Buddhist statue No. 2 as an example, the most similar one is the small Buddhist statue No. 3, with a similarity index of 97%. Therefore, small Buddhist statue No. 3 can be selected as the reference object for the restoration of small Buddhist statue No. 2.
As shown in Figure 11, we selected several Buddhist images with the highest similarity index to perform the SIFT algorithm matching experiment. The similarity index values are 94%, 97%, 97%, and 97%, respectively, between Buddhist statue No. 1 and Buddhist statue No. 2, between Buddhist statue No. 2 and Buddhist statue No. 3, between Buddhist statue No. 4 and Buddhist statue No. 9, and between Buddhist statue No. 4 and Buddhist statue No. 10. The red circle connected by the red line is the similar feature point of the two images, and the blue circle is the detected feature point.
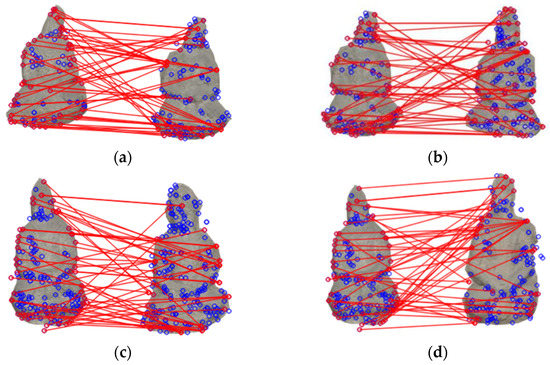
Figure 11.
Extracting detail feature points of similar Buddhist statues using the SIFT algorithm. (a) Feature point matching of Buddhist Image No. 1 and Buddhist Image No. 2; (b) Feature point matching of Buddhist Image No. 2 and Buddhist Image No. 3; (c) Feature point matching of Buddhist Image No. 4 and Buddhist Image No. 9; (d) Feature point matching of Buddhist Image No. 4 and Buddhist Image No. 10.
To verify the reliability of the similarity index proposed in this paper, we selected Buddhist statue No. 2 and Buddhist statue No. 3, with the highest similarity index of 97%, to perform the deviation analysis of the 3D point clouds. The 3D point clouds of Buddhist statues No. 2 and No. 3 were obtained using the RIEGL VZ-1000 3D scanner, and the point cloud accuracy is 5mm. We used Geomagic software for 3D modelling and the best fitting of the Buddhist statue point cloud, carrying out multiple processing such as denoising, modelling, segmentation, and accuracy analysis. First, the 3D models of the two Buddhist statues were superimposed, and then the deviation of the two models was analyzed. As shown in Figure 12, the maximum 3D deviation of the two Buddhist statue models is ±0.0129m, the average 3D deviation is + 0.0028m and -0.0034m, the standard deviation is 0.0041m, and the Root Mean Squared Estimate (RMSE) is 0.0042m. It can also be seen from the deviation chromatogram that the chromatograms of the two small Buddha statues are green, light blue, and light yellow, which proves that the deviation is within the acceptable range. Therefore, it can be considered that the similarity index of Buddhist statues No. 2 and No. 3 is consistent with the actual situation.

Figure 12.
Three-dimensional (3D) model deviation analysis of Buddhist statues No. 2 and No.3.
5. Discussion
In recent years, image processing technology and 3D scanning technology have been prevalent in the digital protection of cultural heritage [61]. Although orthophoto and 3D point clouds of the Yungang Grottoes were captured simultaneously during digital documentation, in this paper, orthophoto was finally selected as the basic data to explore the similarity index of the Buddhist statues.
There are two reasons for this:
- The Yungang Grottoes are large, complex, and immovable cultural heritage with a huge volume, and they lack independent high-precision scanning of individual Buddhist statues. Although high precision 3D scanning can provide more details, it will provide huge amounts of point cloud data, which involves complex data processing and high costs. In order to reduce the difficulty of 3D data processing, instead of using 3D data we chose 2D photos, which are simpler and more economical.
- The objective of this paper was to develop a quick and convenient way to judge the similarity of cultural relic objectively. Using 2D photo as a data source, people can use a consumer digital camera to collect data, which brings down the data collection barrier.
As shown in the results (Table 3), the larger the similarity index, the more similar the two Buddhist statues are. For a group of small Buddhist statues whose similarity index is too low, we cannot simply consider that they are two completely different small Buddhist statues. We should combine the actual situation, where the hash value is different due to the missing part of the Buddhist statues, resulting in the low similarity index. The prior knowledge of cultural relic experts is also very important. Especially when there are Buddhist statues with the same similarity index, as shown in Table 3; the similarity index between Buddhist statue No. 1 and Buddhist statue No. 2 or No. 3 are both 94%. In this situation, the prior knowledge of experts should be taken into consideration to make an appropriate choice.
After obtaining the similarity index, we selected the SIFT operator to match the similarity features of Buddhist statue images because the similarity index can only give objective values. This is because, in the real restoration of Buddhist statues, it is always necessary to analyze the similar parts visually. Although there are many methods for matching similar features, there are some common operators, such as the Surf operator improved by the SIFT operator, the Brisk operator, and the Orb operator. However, after referring to the research literature and comparing the operation efficiency, robustness, matching accuracy, and other indicators, we finally selected the SIFT operator with the highest matching accuracy (Table 2). Because this paper’s research objects are single Buddhist statues, the amount of data to be processed is small, and the slight difference in running speed can be ignored. However, the surface features of grotto statues are not obvious due to weathering, so a SIFT operator with high accuracy is needed to perform feature point matching to avoid missing similar feature points.
6. Conclusions
This paper presents an approach for quantitatively judging the similarity of Buddhist statues using the similarity index. With this approach, archaeologists, restorers, conservator, and scientists can quantitatively judge the similarity of Buddhist statues for the quick screening of similar statues. It solves two problems. One is that the similarity judgment of Buddha images used to depend on the subjective evaluation of experts, and the other one is the lack of quantitative similarity assessment. In this study, a method of automatic identification of similar Buddhist statue images by combining a pHash algorithm with a SIFT operator. The unique “hash fingerprint” can be generated quickly and accurately based on the pHash algorithm. Moreover, the SIFT operator is used to match the similarity feature points of similar Buddhist statue images to provide a reference for experts.
At present, the identification of Buddhist statues with similar artistic models remains in the empirical identification, and there is a lack of scientific quantitative identification methods. This paper provides quantitative evidence for the virtual and physical restoration of grottoes by using orthophoto images, so that people can quickly judge the similarity between different Buddhist statues, accurately locate similar feature points, and assist experts in repairing Buddha statues.
From the results, the similarity of No. 1 and No. 2, No. 1 and No. 3, No. 2 and No. 3, No. 4 and No. 9, and No. 4 and No. 10 is more than 90%. These Buddhist statues are considered very similar and can be selected as the reference Buddhist statues for other damaged Buddhist statues. The 3D point cloud was also used to generate the models of Buddhist statues No. 2 and No. 3. It was found that their deviation was very small; the Root Mean Squared Estimate (RMSE) is only 0.0042m, which confirms the similarity index of Buddhist statues No. 2 and No. 3 of 97%.
The results were based on a limited number of small grotto statues of the Yungang Grottoes using only orthophoto images of Buddhist statues. Although judging the similarity of Buddhist statues by orthophoto images is more efficient than using 3D point cloud data in quickly generating similarity index in terms of data acquisition and processing speed and algorithms, the method works better for the preliminary screening of similar statues. Further investigation on the methods that integrate both 2D images and 3D point cloud data may provide a more complete and automatic solution from preliminary screening to the final identification of the reference statues because high-precision 3D data can describe the details of Buddhist statues more accurately.
Author Contributions
Conceptualization, W.H.; methodology, W.H., M.H., and S.L.; software, W.H.; resources, Y.Q.; writing—original draft preparation, W.H.; writing—review and revisions, S.X. and S.L.; supervision, M.H.; project administration, M.H. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China, grant number 2019YFC1520800.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to confidentiality.
Acknowledgments
The authors would like to gratefully thank the Yungang Grottoes Research Institute for providing all the required data and information. We would also like to thank all reviewers for their constructive comments that helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Su, B. Study on China’s Grottoes Temple; Cultural relics Press: Beijing, China, 1996. [Google Scholar]
- Guo, F.; Jiang, G. Investigation into rock moisture and salinity regimes: Implications of sandstone weathering in Yungang Grottoes, China. Carbonates Evaporites 2015, 30, 1–11. [Google Scholar] [CrossRef]
- Charter Venice. International Charter for the Conservation and Restoration of Monuments and Sites. In IInd International Congress of Architects and Technicians of Historic Monuments, Venice; Charter Venice: Venice, Italy, 1964; pp. 25–31. [Google Scholar]
- Kashihara, K. Three-dimensional reconstruction of artifacts based on a hybrid genetic algorithm. In Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Seoul, Korea, 14–17 October 2012; pp. 900–905. [Google Scholar]
- Bilde, P.G.; Handberg, S. Ancient Repairs on Pottery from Olbia Pontica. Am. J. Archaeol. 2012, 116, 461–481. [Google Scholar] [CrossRef]
- Fantini, M.; De Crescenzio, F.; Persiani, F.; Benazzi, S.; Gruppioni, G. 3D restitution, restoration and prototyping of a medieval damaged skull. Rapid Prototyp. J. 2008, 14, 318–324. [Google Scholar] [CrossRef]
- Hou, M.; Zhang, X.; Wu, Y.; Hu, Y. 3D Laser Scanning Modeling and Application on Dazu Thousand-hand Bodhisattva in China. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, XL-4, 81–85. [Google Scholar] [CrossRef]
- Hou, M.; Yang, S.; Hu, Y.; Wu, Y.; Shu, Z.; Zhang, X. A novel method for the virtual restoration of cultural relics based on a 3D fine model. DYNA-Ingeniería e Industria 2015, 90, 307–313. [Google Scholar]
- Hou, M.; Li, S.; Jiang, L.; Wu, Y.; Hu, Y.; Yang, S.; Zhang, X. A New Method of Gold Foil Damage Detection in Stone Carving Relics Based on Multi-Temporal 3D LiDAR Point Clouds. ISPRS Int. J. Geo Inf. 2016, 5, 60. [Google Scholar] [CrossRef]
- Hou, M.; Yang, S.; Hu, Y.; Wu, Y.; Jiang, L.; Zhao, S.; Wei, P. Novel Method for Virtual Restoration of Cultural Relics with Complex Geometric Structure Based on Multiscale Spatial Geometry. ISPRS Int. J. Geo Inf. 2018, 7, 353. [Google Scholar] [CrossRef]
- Zhou, M.; Geng, G.; Wu, Z.; Shui, W. A Virtual Restoration System for Broken Pottery. In Proceedings of the Conference on Pattern Recognition, Quebec, QC, Canada, 11–15 August 2002; Volume 11, p. 15. [Google Scholar]
- Lu, M.; Kamakura, M.; Zheng, B.; Takamatsu, J.; Nishino, K.; Ikeuchi, K. Clustering Bayon face towers using restored 3D shape models. In Proceedings of the 2011 Second International Conference on Culture and Computing IEEE, Kyoto, Japan, 20–22 October 2011; pp. 39–44. [Google Scholar]
- Lu, M.; Zheng, B.; Takamatsu, J.; Nishino, K.; Ikeuchi, K. Preserving the khmer smile: Classifying and restoring the faces of bayon. In Proceedings of the 12th International conference on Virtual Reality, Archaeology and Cultural Heritage, Prato, Italy, 18–21 October 2011; pp. 161–168. [Google Scholar]
- Wang, H.; He, Z.; He, Y.; Chen, D.; Huang, Y. Average-face-based virtual inpainting for severely damaged statues of Dazu Rock Carvings. J. Cult. Heritage 2019, 36, 40–50. [Google Scholar] [CrossRef]
- UNESCO, Yungang Grottoes, Word Heritage List. Available online: https://whc.unesco.org/en/list/1039/ (accessed on 1 March 2021).
- Liu, X. An analysis of the development of Yungang Grottoes art in the Northern Wei Dynasty. J. Jinzhong Univ. 2020, 5, 63–69+92 . [Google Scholar]
- Zhang, Z. Focusing on the musical cultural value of Yungang Grottoes. Chin. Musicol. 2019, 2, 11. [Google Scholar]
- Liu, D. The cultural function of Yungang Grottoes in the Northern Wei Dynasty. Sci. Educ. Guide 2020, 9, 156–157. [Google Scholar]
- Peng, S. The model of Yungang Grottoes statues bred by multi culture. Art Obs. 2018, 1, 117–121. [Google Scholar]
- Liu, R.Z.; Zhang, B.J.; Zhang, H.; Shi, M.F. Deterioration of Yungang Grottoes: Diagnosis and research. J. Cult. Heritage 2011, 12, 494–499. [Google Scholar] [CrossRef]
- Fryskowska, A.; Stachelek, J. A no-reference method of geometric content quality analysis of 3D models generated from laser scanning point clouds for hBIM. J. Cult. Heritage 2018, 34, 95–108. [Google Scholar] [CrossRef]
- Bai, S. The discovery and research of the stele records of the great Cave Temple rebuilt in Xi jing Wuzhou mountain of Jin Dynasty -- discussing some problems about Yungang Grottoes with Professor Nagahiro Toshio of Japan. J. Peking Univ. 1982, 2, 30–50. [Google Scholar]
- Li, Y. The discovery of the stele records of the great Cave Temple rebuilt in Xi jing Wuzhou mountain of Jin Dynasty. Chin. Cult. Heritage 2007, 5, 40–43. [Google Scholar]
- Yan, W. Research on Yungang Grottoes; Guangxi Normal University Press: Guilin, China, 2003. [Google Scholar]
- Liang, S.; Lin, H.; Liu, D. Architecture of Northern Wei Dynasty in Yungang Grottoes. Buddh. Cult. 2014, 5, 108–115. [Google Scholar]
- Liang, S.; Liu, D.; China construction, society. Investigation Report on Ancient Architecture in Datong: The Northern Wei Dynasty Architecture in Yungang Grottoes; Society for the Study of Chinese Architecture: Beijing, China, 1936. [Google Scholar]
- Mizuno, S.; Nagahiro, T.; Kang, Y. The Buddhist Cave Temples of the Fifth Century AD in North China, 16 Vols; Kyoto University: Kyoto, Japan, 1952–1956. (In Japanese) [Google Scholar]
- Nagahiro Toshio. Yungang Diary: A Survey of Buddhist Grottoes During the War; Cultural relics Press: Beijing, China, 2009. [Google Scholar]
- Wu, Y. Application of digital technology in cave 18 of Yungang Grottoes. Urban Surv. 2015, 6, 89–93. [Google Scholar]
- Diao, C.; Li, Z.; Zhang, Z.; Ning, B.; He, Y. To achieve real immersion: The 3d virtual and physical reconstruction of cave 3 and cave 12 of Yungang Grottoes. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, XLII-2/W9, 297–303. [Google Scholar] [CrossRef]
- Li, L.; Wang, J. Application of 3D laser scanning technology and 3D printing technology in reproduction of Yungang Grottoes. Surv. World 2020, 5, 88–92. [Google Scholar]
- Yan, K. Quantitative Study on Weathering Disease of Yungang Grottoes by Multi View Image 3D Reconstruction Technology; Minzu University of China: Beijing, China, 2020. [Google Scholar]
- Brown, B.J.; Toler-Franklin, C.; Nehab, D.; Burns, M.; Dobkin, D.; Vlachopoulos, A.; Weyrich, T. A system for high-volume acquisition and matching of fresco fragments: Reassembling Theran wall paintings. ACM Trans. Graph. (TOG) 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Di Paola, F.; Milazzo, G.; Spatafora, F. Computer Aided Restoration Tools to Assist the Conservation of AN Ancient Sculpture. The Colossal Statue of ZEUS Enthroned. ISPRS-International Archives of the Photogrammetry. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2017, XLII-2/W5, 177–184. [Google Scholar] [CrossRef]
- Arbace, L.; Sonnino, E.; Callieri, M.; Dellepiane, M.; Fabbri, M.; Idelson, A.I.; Scopigno, R. Innovative uses of 3D digital technologies to assist the restoration of a fragmented terracotta statue. J. Cult. Heritage 2013, 14, 332–345. [Google Scholar] [CrossRef]
- Kamakura, M.; Oishi, T.; Takamatsu, J.; Ikeuchi, K. Classification of Bayon faces using 3D models. Virtual Syst. Multimed. 2005, 751–760. [Google Scholar]
- Lu, M.; Zheng, B.; Takamatsu, J.; Nishino, K.; Ikeuchi, K. 3D shape restoration via matrix recovery. In Asian Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 306–315. [Google Scholar]
- Lanitis, A.; Stylianou, G.; Voutounos, C. Virtual restoration of faces appearing in byzantine icons. J. Cult. Heritage 2012, 13, 404–412. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Chen, X.; Zhang, S.; Geng, G. A multi feature fusion method for reassembly of 3D cultural heritage artifacts. J. Cult. Heritage 2018, 33, 191–200. [Google Scholar] [CrossRef]
- Hassan, M.; Bhagvati, C. Structural Similarity Measure for Color Images. Int. J. Comput. Appl. 2012, 43, 7–12. [Google Scholar] [CrossRef]
- Xia, P.; Zhang, L.; Li, F. Learning similarity with cosine similarity ensemble. Inf. Sci. 2015, 307, 39–52. [Google Scholar] [CrossRef]
- Jeong, S.; Won, C.S.; Gray, R.M. Image retrieval using color histograms generated by Gauss mixture vector quantization. Comput. Vis. Image Underst. 2004, 94, 44–66. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M.; Song, Z. Multi-Modal Image Registration Based on Multi-Feature Mutual Information. J. Med Imaging Heal. Informatics 2019, 9, 153–158. [Google Scholar] [CrossRef]
- Chamoso, P.; Rivas, A.; Martín-Limorti, J.J.; Rodríguez, S. A hash based image matching algorithm for social networks. In International Conference on Practical Applications of Agents and Multi-Agent Systems; Springer: Cham, Switzerland, 2017; pp. 183–190. [Google Scholar]
- Yang, B.; Gu, F.; Niu, X. Block mean value based image perceptual hashing. In Proceedings of the 2006 International Conference on Intelligent Information Hiding and Multimedia, Pasadena, CA, USA, 18–20 December 2006; pp. 167–172. [Google Scholar]
- Howarth, P.; Rüger, S. Robust texture features for still-image retrieval. IEE Proc. Vision Image Signal Process. 2005, 152, 868. [Google Scholar] [CrossRef]
- Eitz, M.; Hildebrand, K.; Boubekeur, T.; Alexa, M. Sketch-Based Image Retrieval: Benchmark and Bag-of-Features Descriptors. IEEE Trans. Vis. Comput. Graph. 2011, 17, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Gu, M.; Zhang, D.; Liu, J. Image Sensing Hash Algorithms Based on Cluster Analysis and SIFT. Data Commun. 2015, 3, 36–40. [Google Scholar]
- Hua, W.; Hu, Y.; Hou, M.; Zhang, X. Research on partition method of mural photo collection. Geogr. Inf. World 2017, 3, 107–112. [Google Scholar]
- Huang, J.; Li, X.; Chen, B.; Yang, D. A Comparative Study on Image Similarity Algorithms Based on Hash. J. Dali Univ. 2017, 12, 8. [Google Scholar]
- Christoph, Z. Implementation and Benchmarking of Perceptual Image hash Functions. 2010. Available online: http://phash.org/docs/pubs/thesis_zauner.pdf (accessed on 22 March 2021).
- Monga, V.; Evans, B.L. Robust perceptual image hashing using feature points. In Proceedings of the 2004 International Conference on Image Processing, 2004. ICIP’04, Singapore, 24–27 October 2004; pp. 677–680. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Karami, E.; Prasad, S.; Shehata, M. Image matching using SIFT, SURF, BRIEF and ORB: Performance comparison for distorted images. arXiv 2017, arXiv:1710.02726. [Google Scholar]
- Chien, H.J.; Chuang, C.C.; Chen, C.Y.; Klette, R. When to use what feature? SIFT, SURF, ORB, or A-KAZE features for monocular visual odometry. In Proceedings of the 2016 International Conference on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016; pp. 1–6. [Google Scholar]
- Tareen, S.A.K.; Saleem, Z. A comparative analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; pp. 1–10. [Google Scholar]
- Dang, Q.B.; Le, V.P.; Luqman, M.M.; Coustaty, M.; Tran, C.D.; Ogier, J.M. Camera-based document image retrieval system using local features-comparing SRIF with LLAH, SIFT, SURF and ORB. In Proceedings of the 2015 13th International Conference on Document Analysis and Recognition (ICDAR), Tunis, Tunisia, 23–26 August 2015; pp. 1211–1215. [Google Scholar]
- Rong, G.; Xu, G.; Xing, G.; Jiang, J.; Sun, Y. Feature point matching algorithm based on SIFT, Orb, Ransac. J. Xinyu Univ. 2019, 24, 33–37. [Google Scholar]
- Wang, T.; Yu, X.; Liu, Z. Fast Image Matching Algorithm Base on Hash. J. Chongqing Univ. Sci. Technol. 2017, 3, 75–78. [Google Scholar]
- Lerones, P.M.; Llamas, J.; Gómez-García-Bermejo, J.; Zalama, E.; Oli, J.C. Using 3D digital models for the virtual restoration of polychrome in interesting cultural sites. J. Cult. Heritage 2014, 15, 196–198. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).