Integration of a Wearable Mobile Mapping Solution and Advance Numerical Simulations for the Structural Analysis of Historical Constructions: A Case of Study in San Pedro Church (Palencia, Spain)
Abstract
1. Introduction
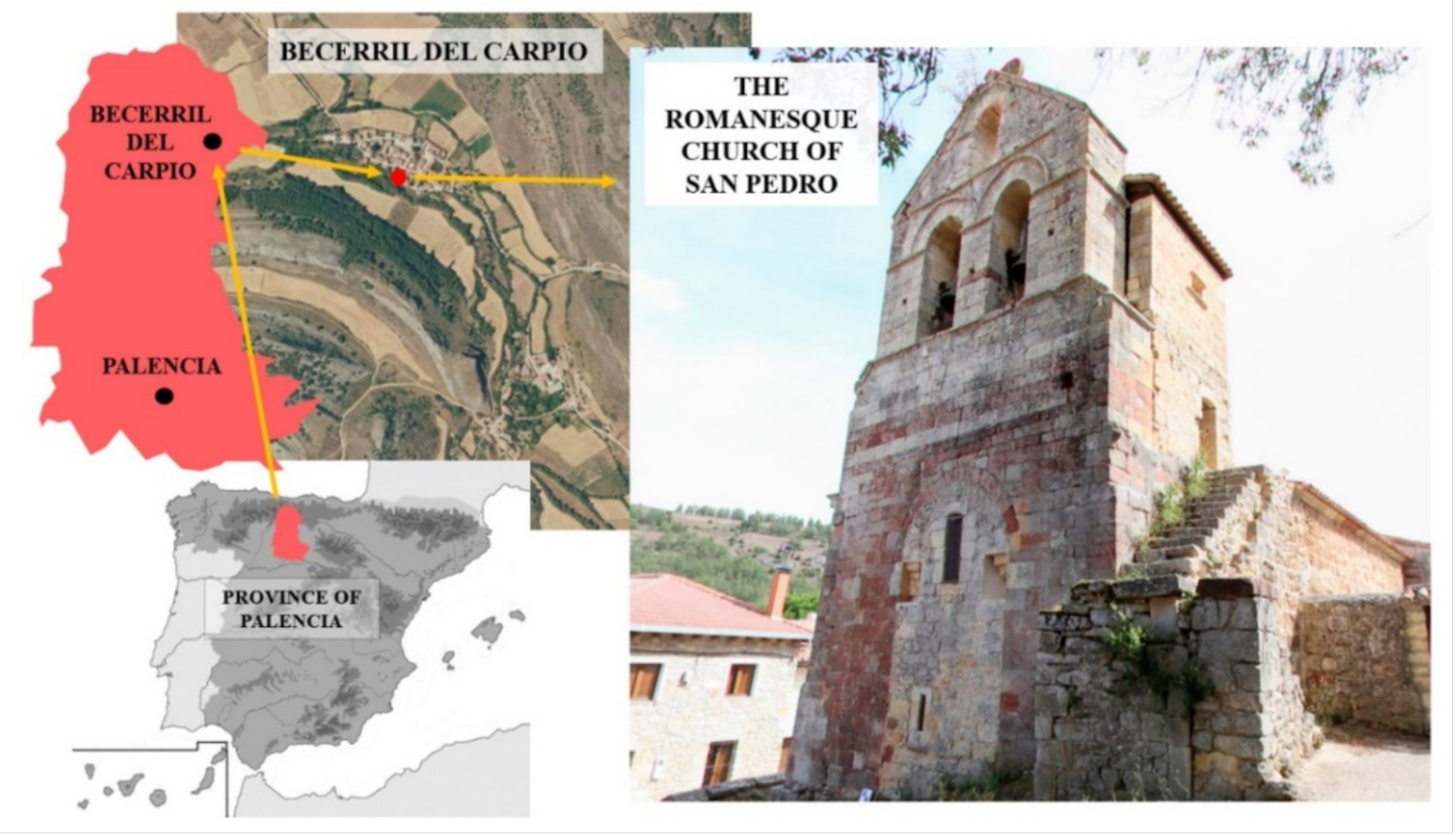
2. The Romanesque Church of San Pedro (Becerril del Carpio, Palencia, Spain)
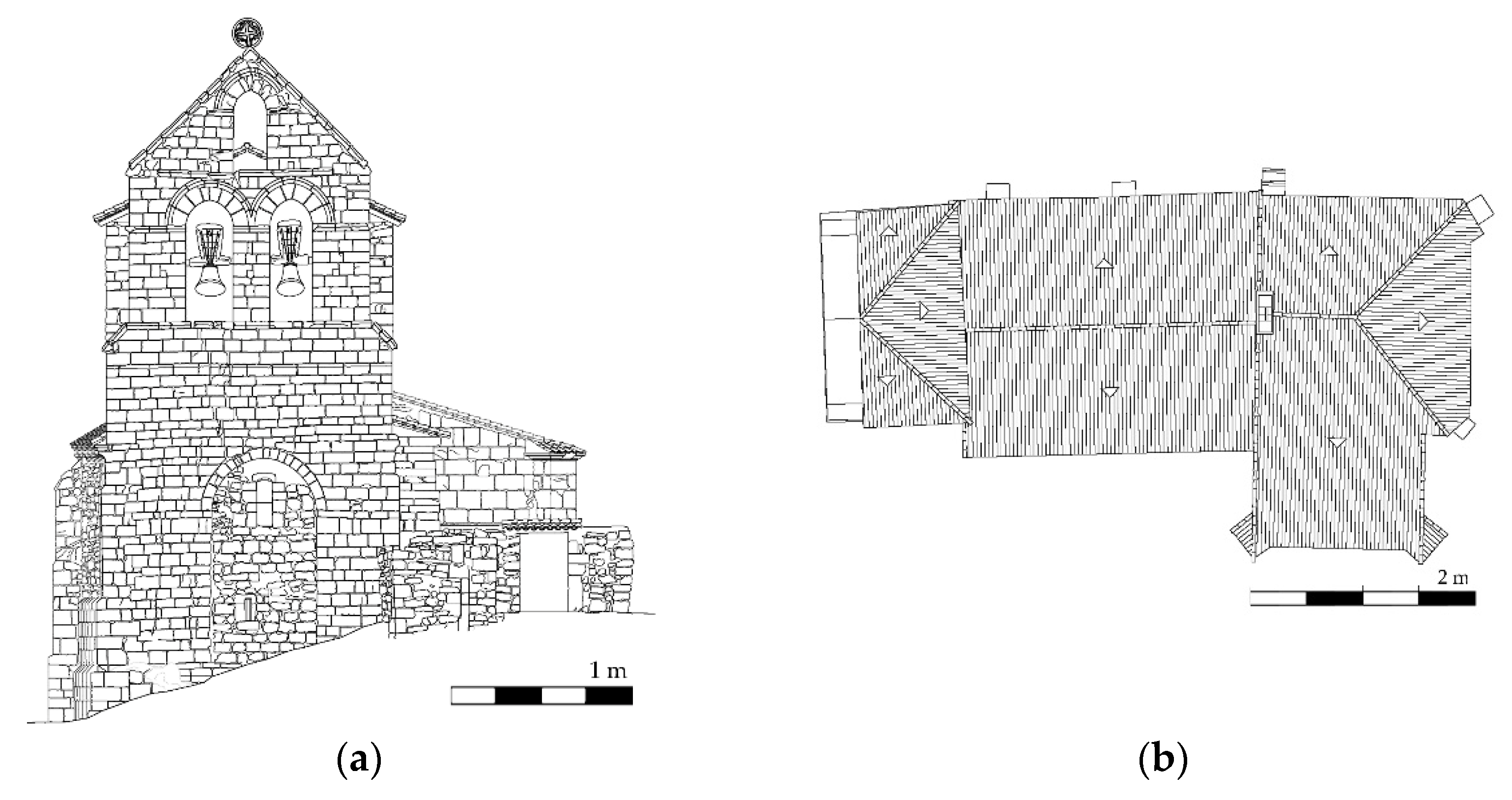
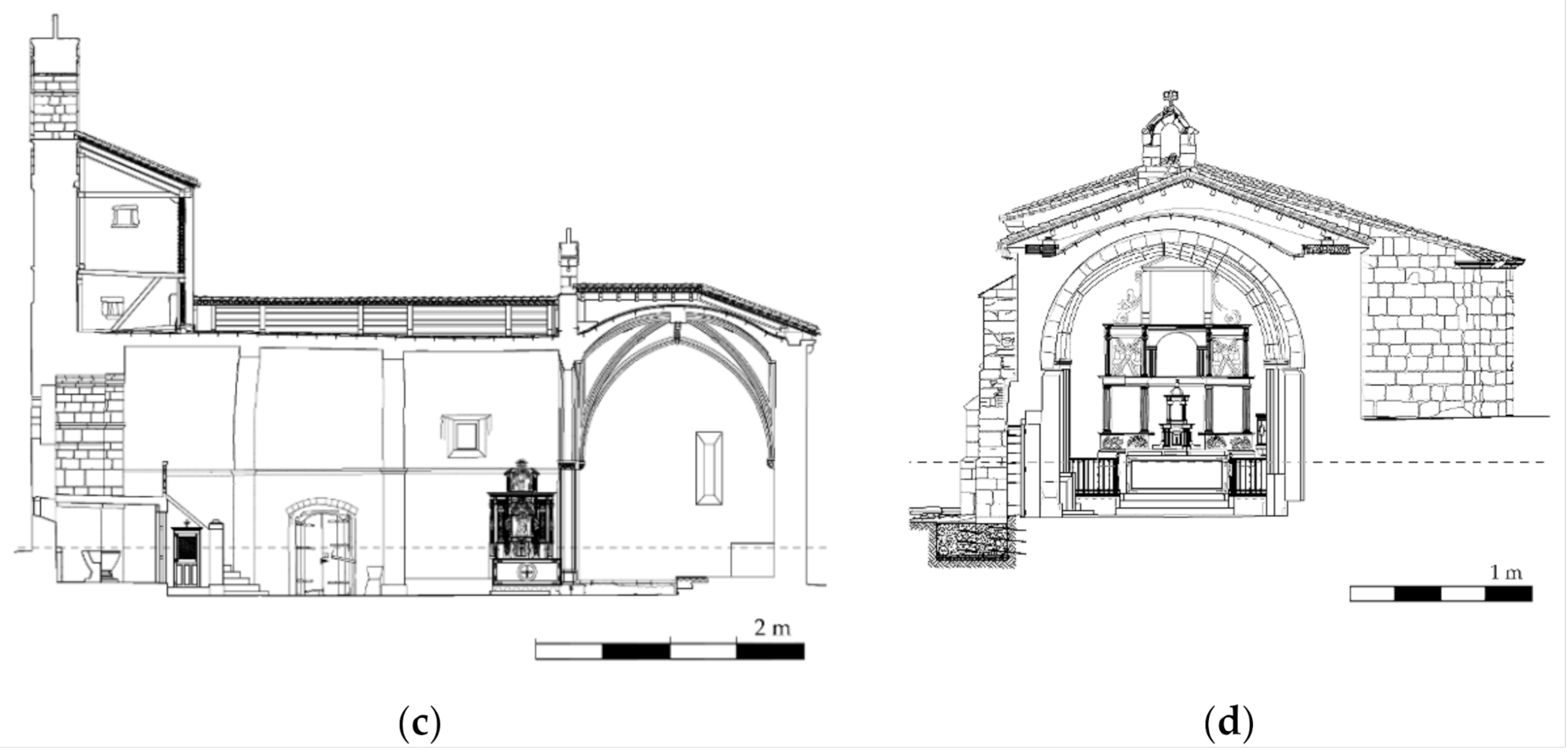
2.1. Description of the Structure
2.2. Intervention Works Carried Out during 2011
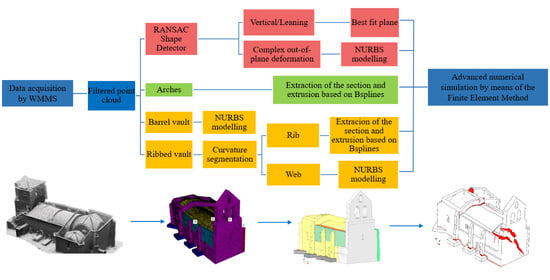
3. From the Point Cloud to the As-Built CAD Model
3.1. Wearable Mobile Mapping System (WMMS)
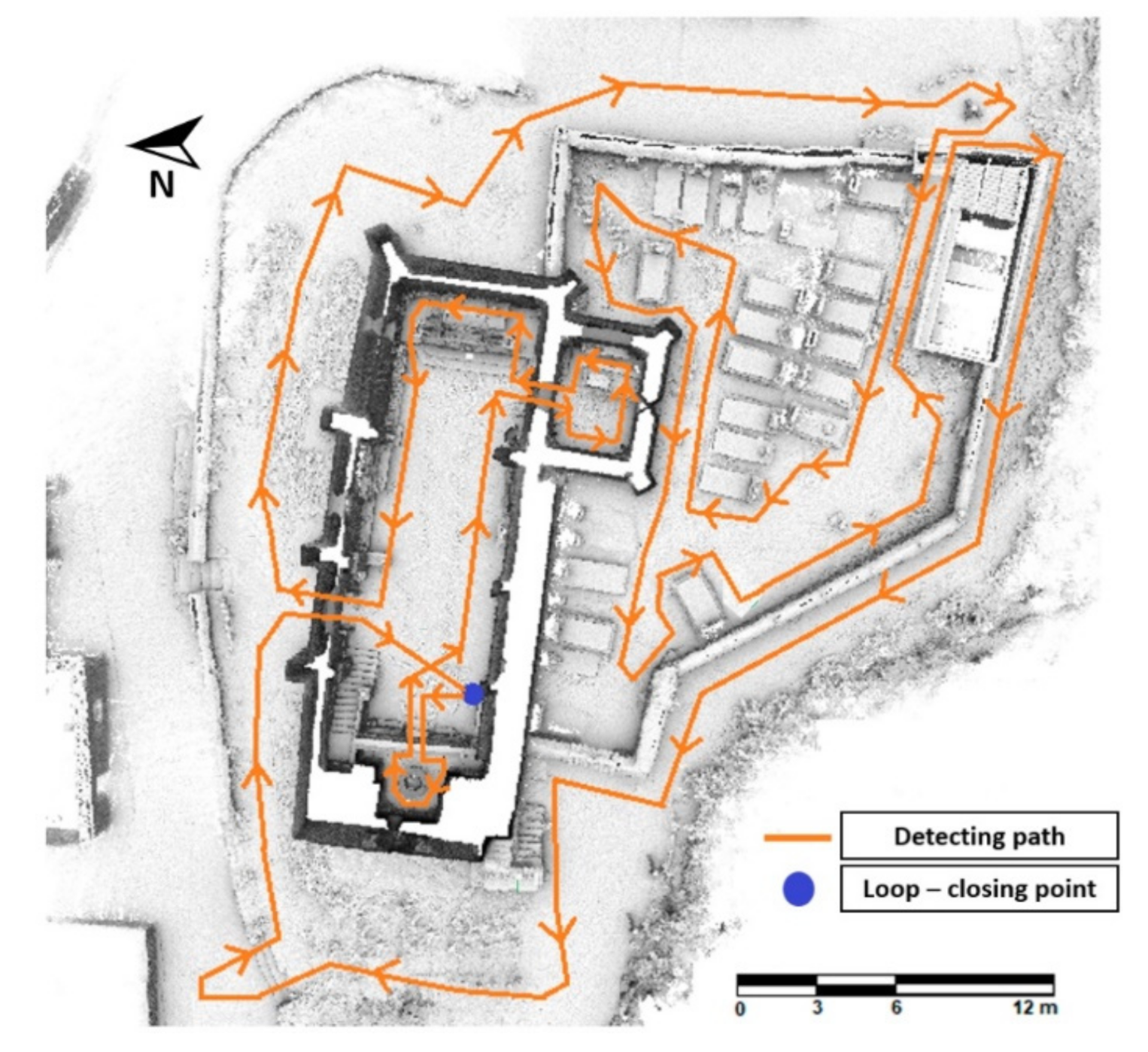
3.2. Digitalization of the Structure
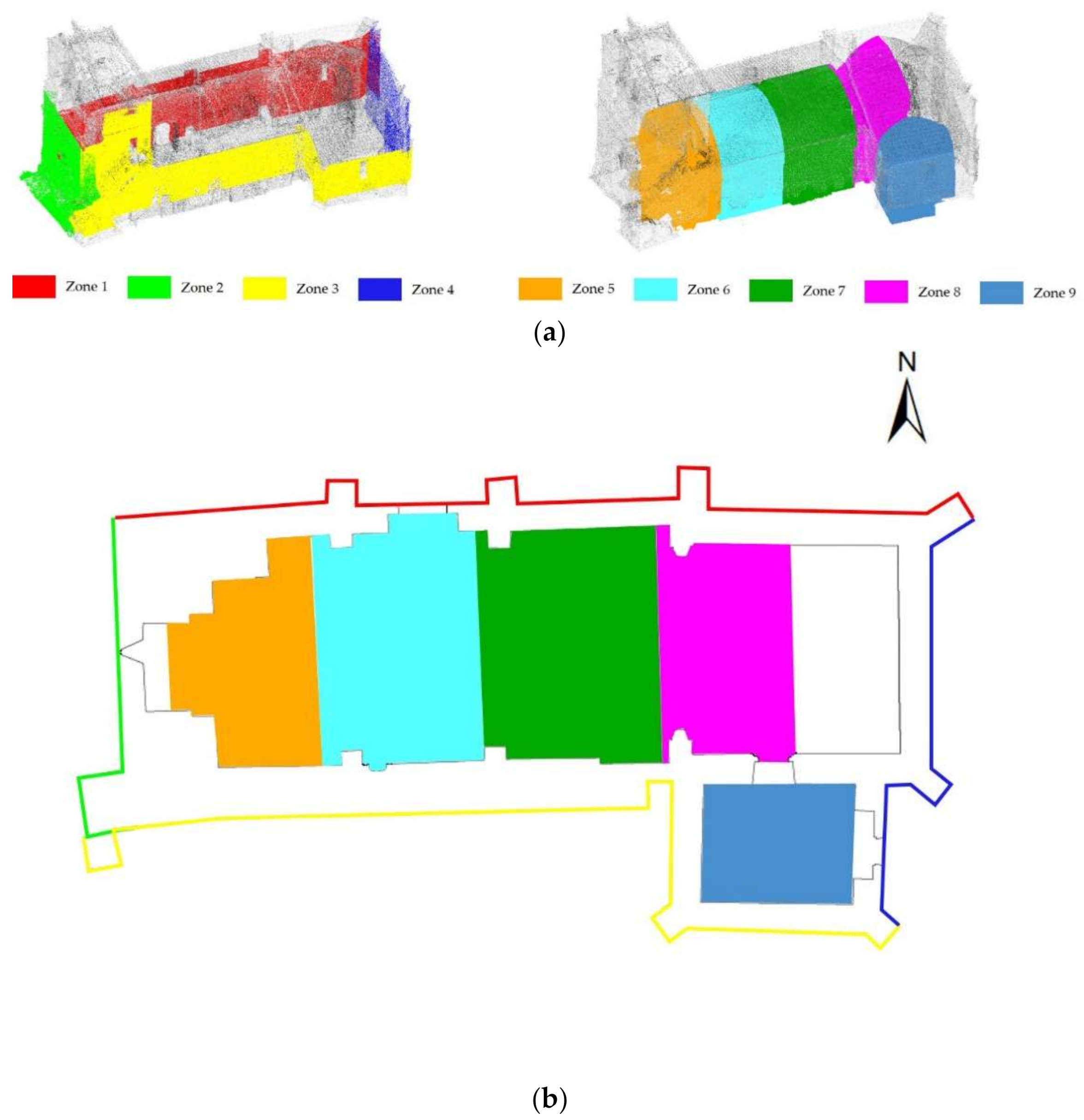
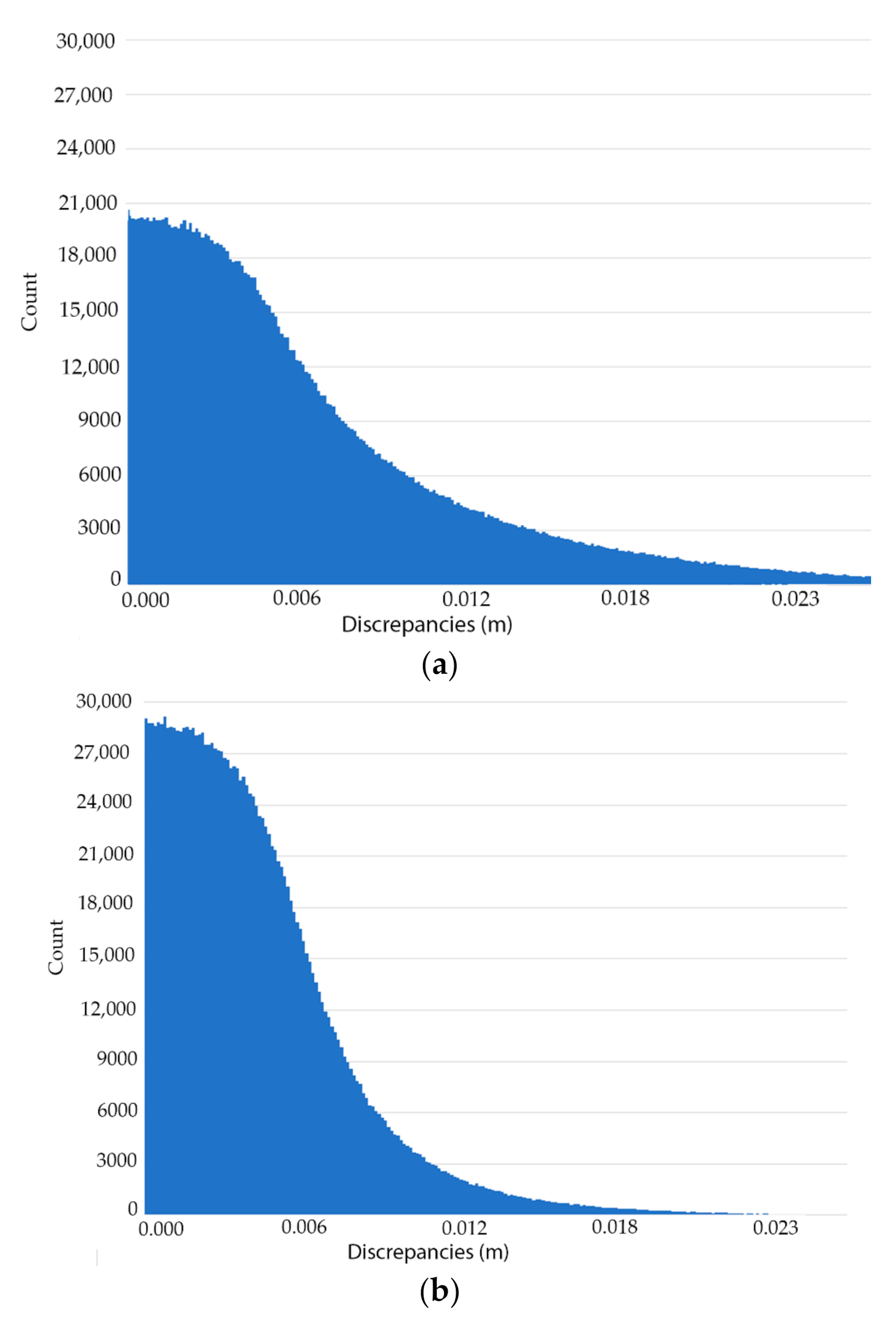
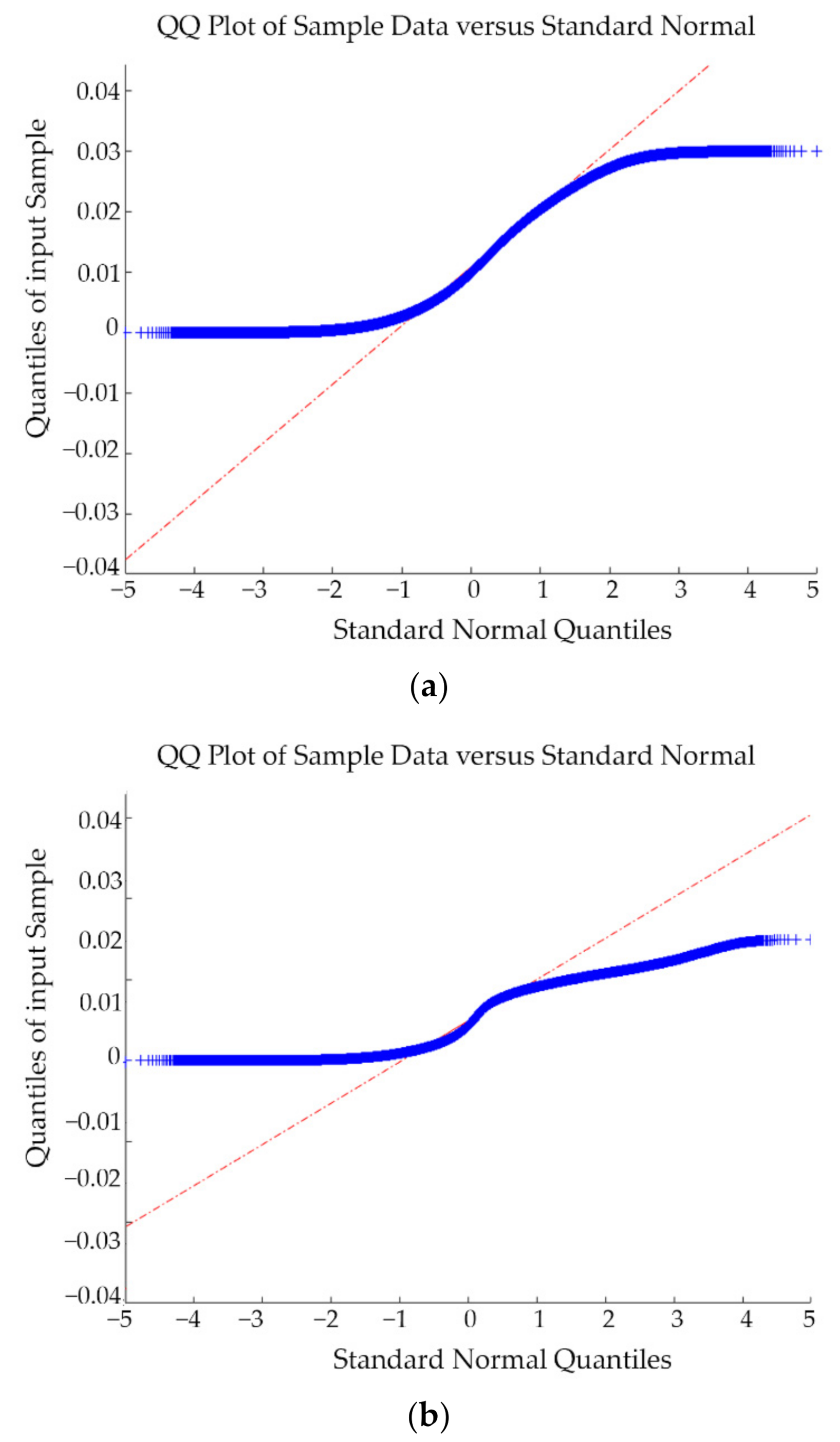
3.3. Point Cloud Post-Processing
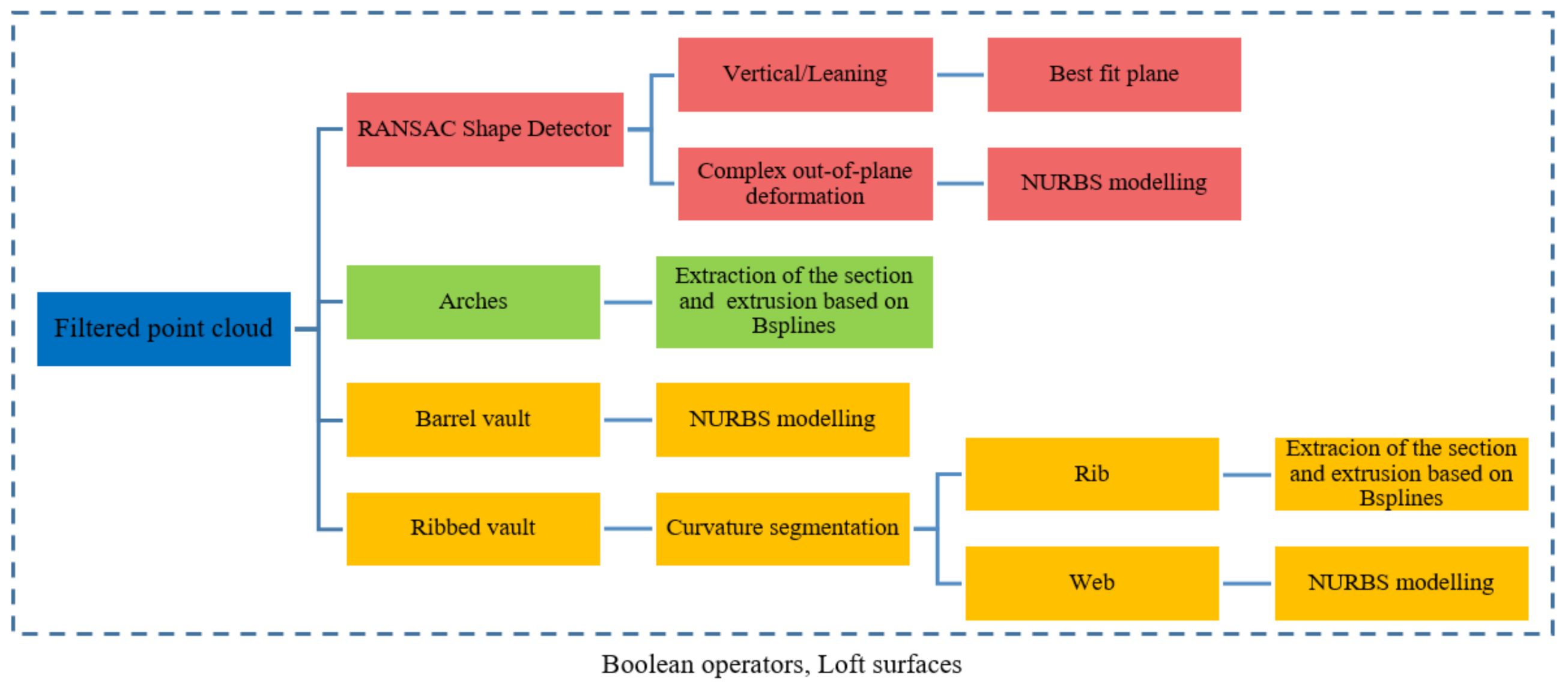
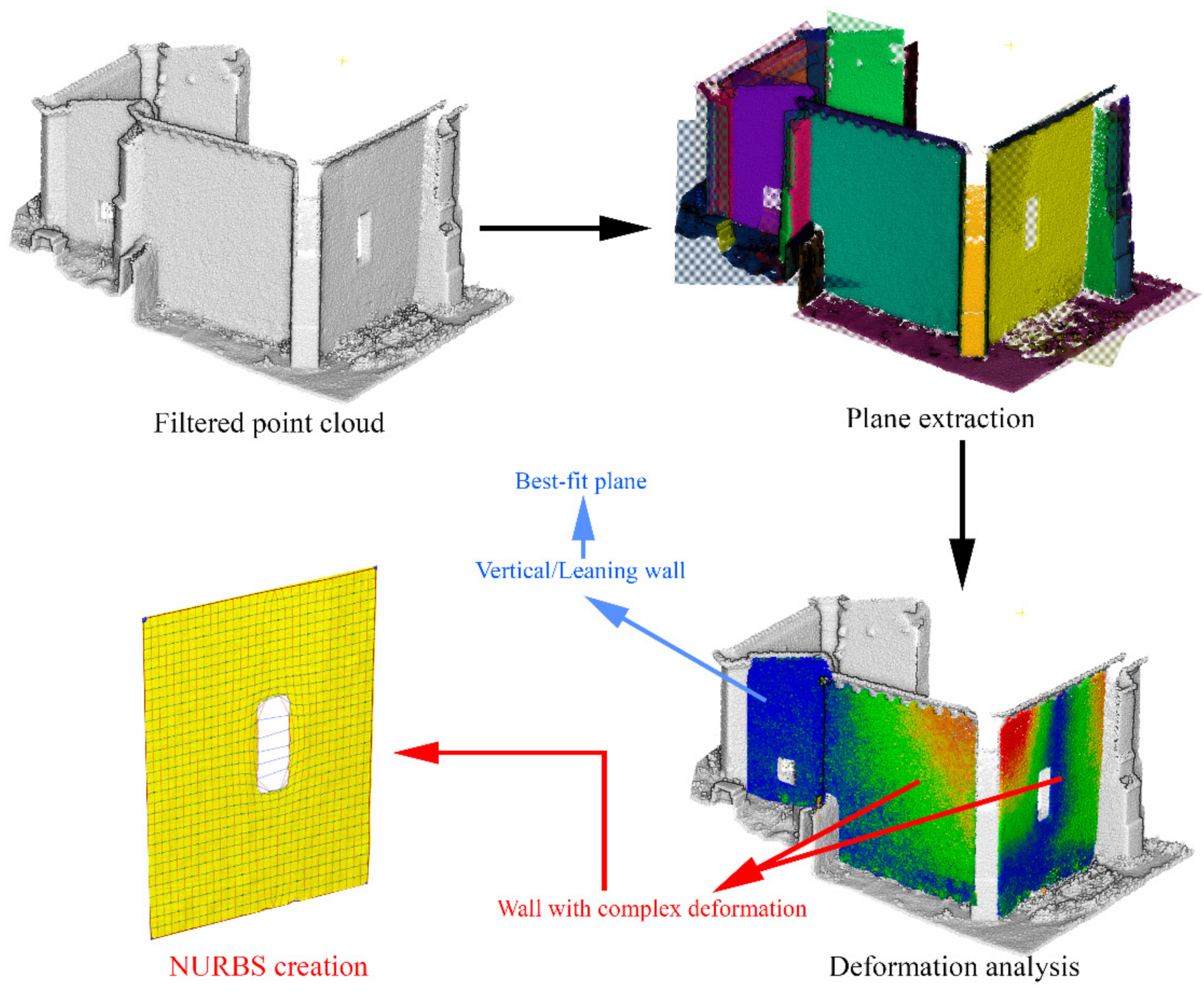
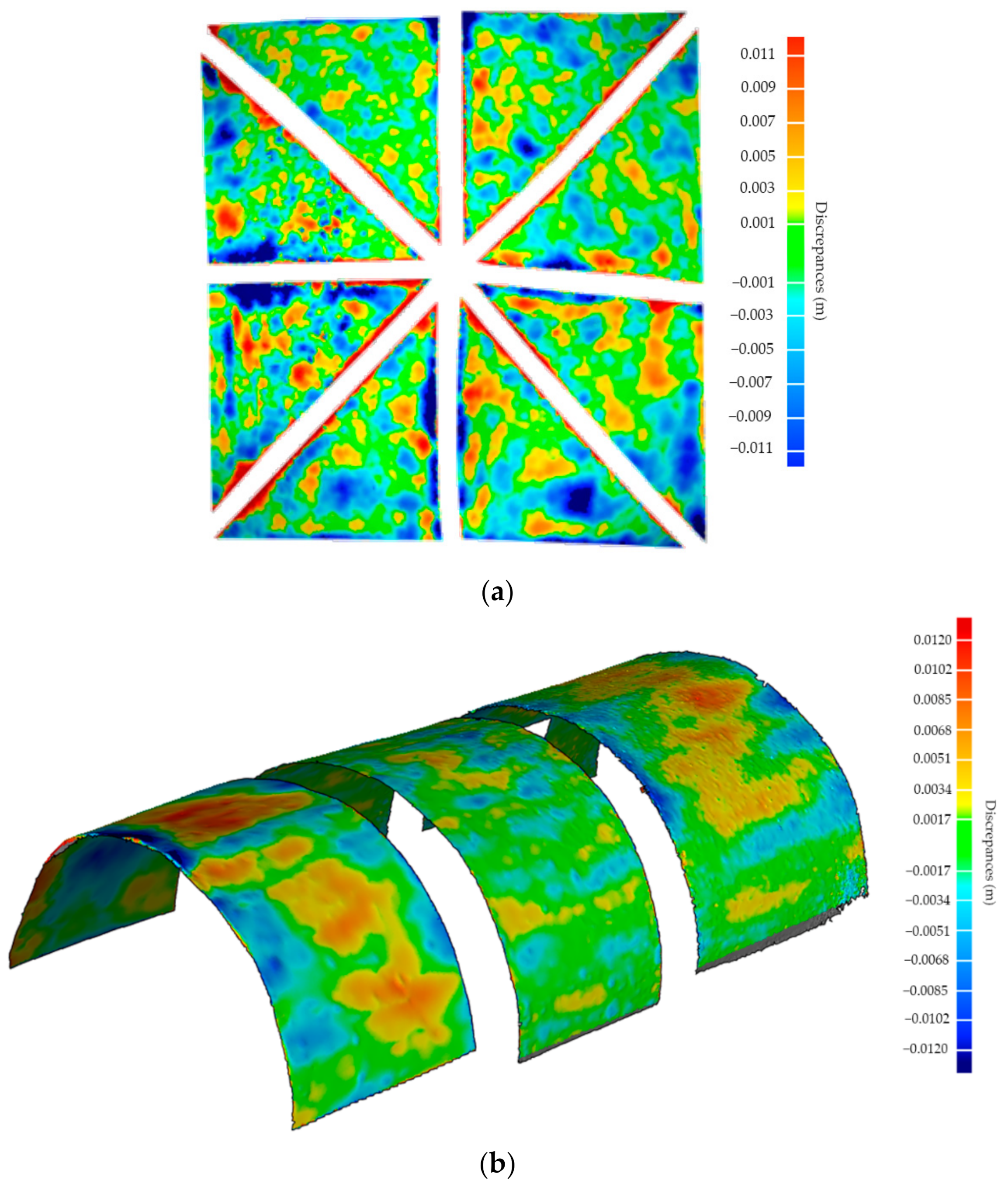
3.4. Reverse Engineering
4. Structural Analysis
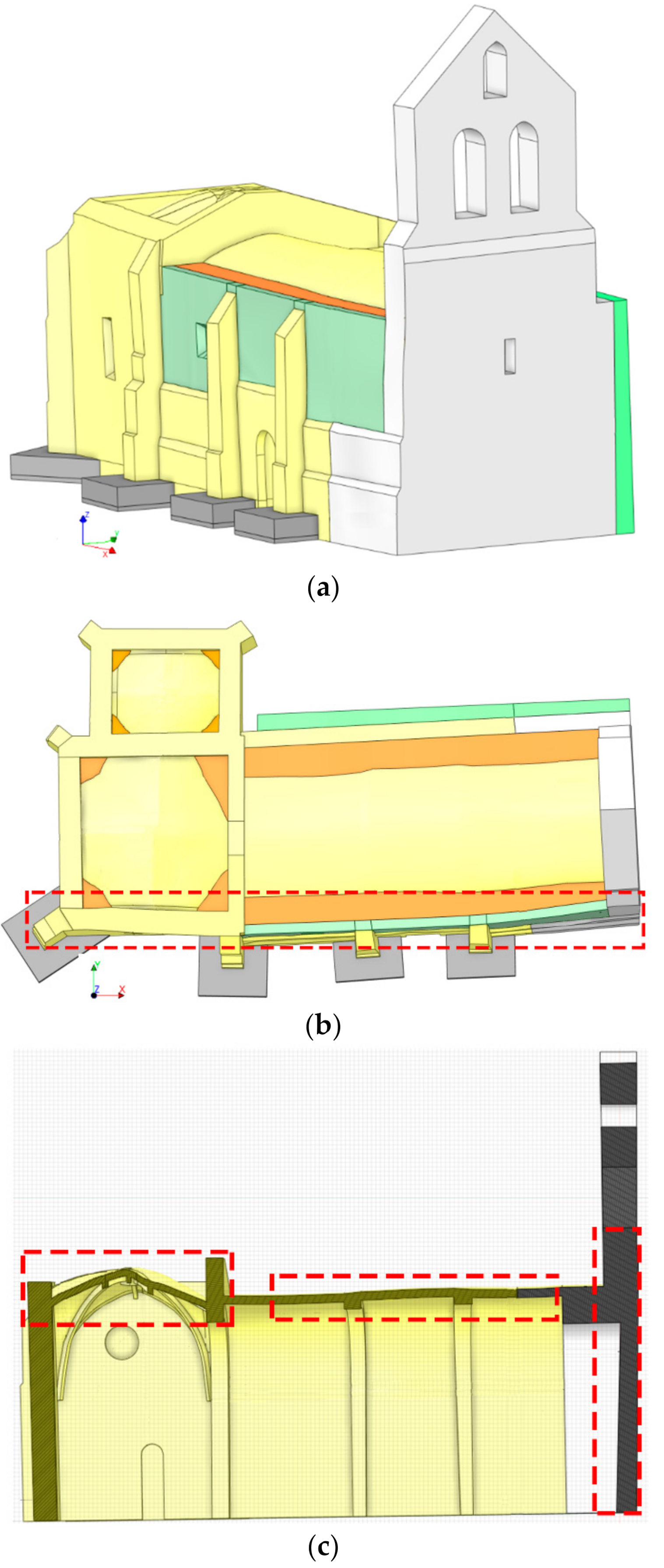
4.1. Numerical Mesh
4.2. Constitutive Models and Material Properties
4.3. Structural Impact of the TRM Layers
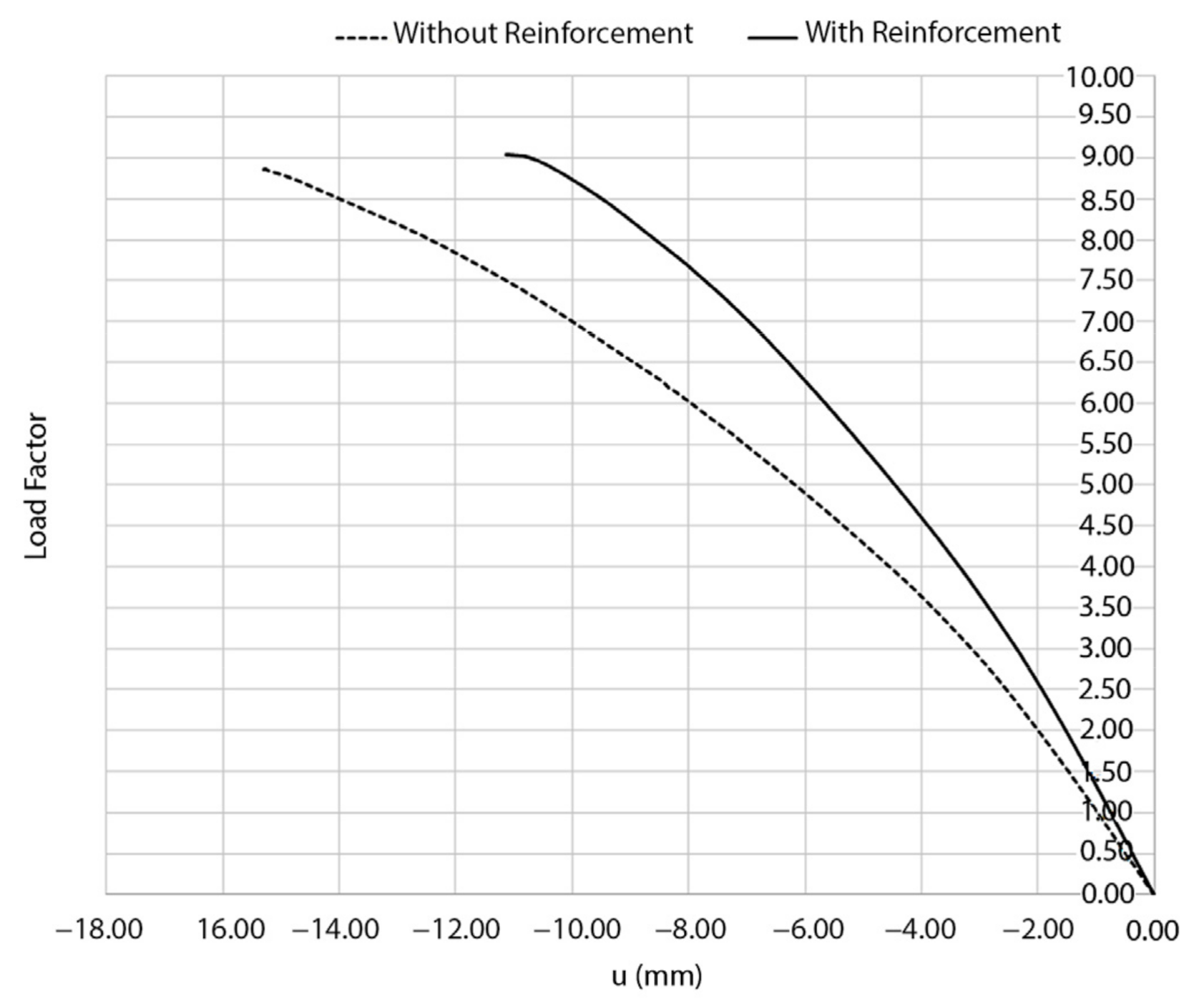
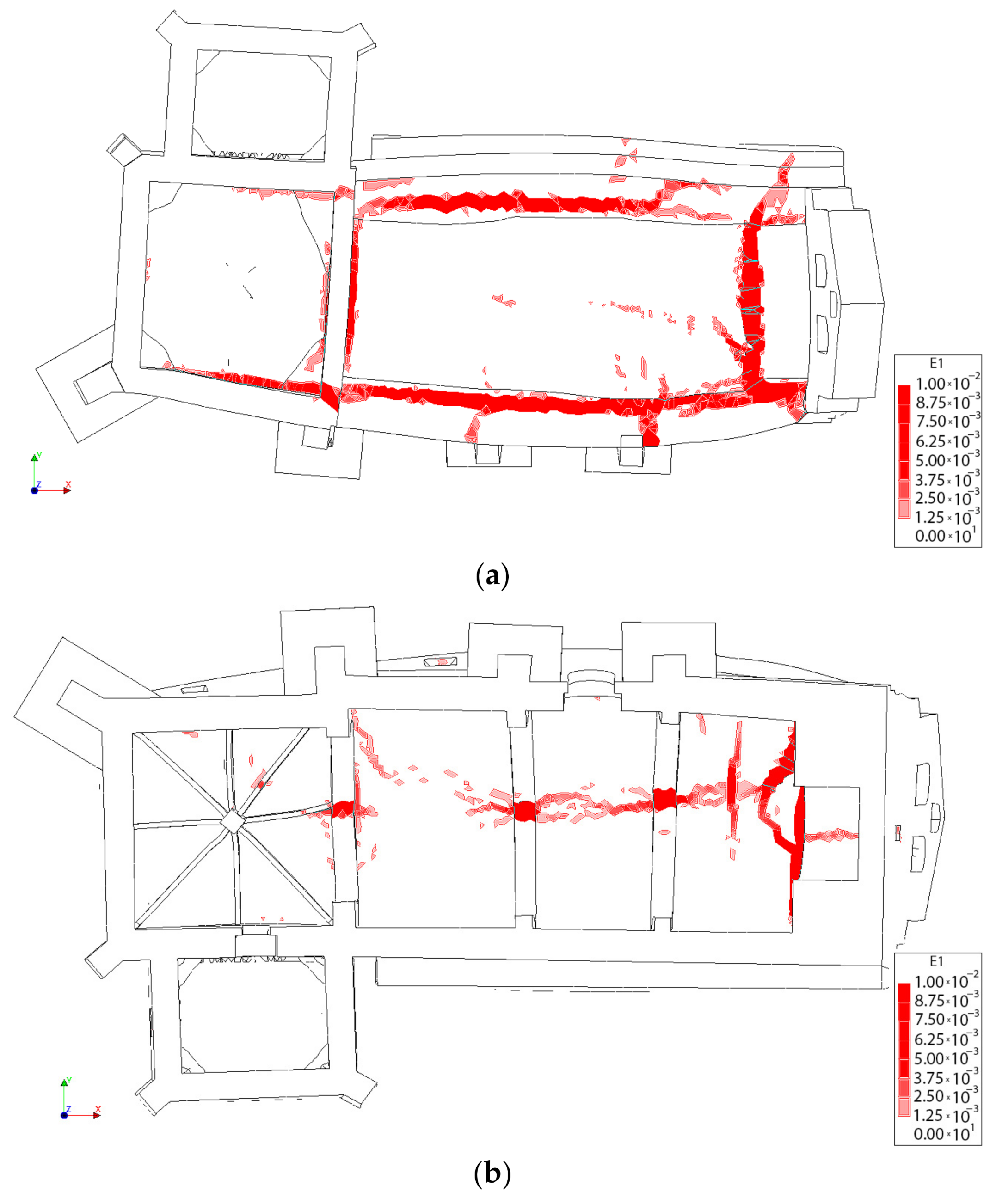
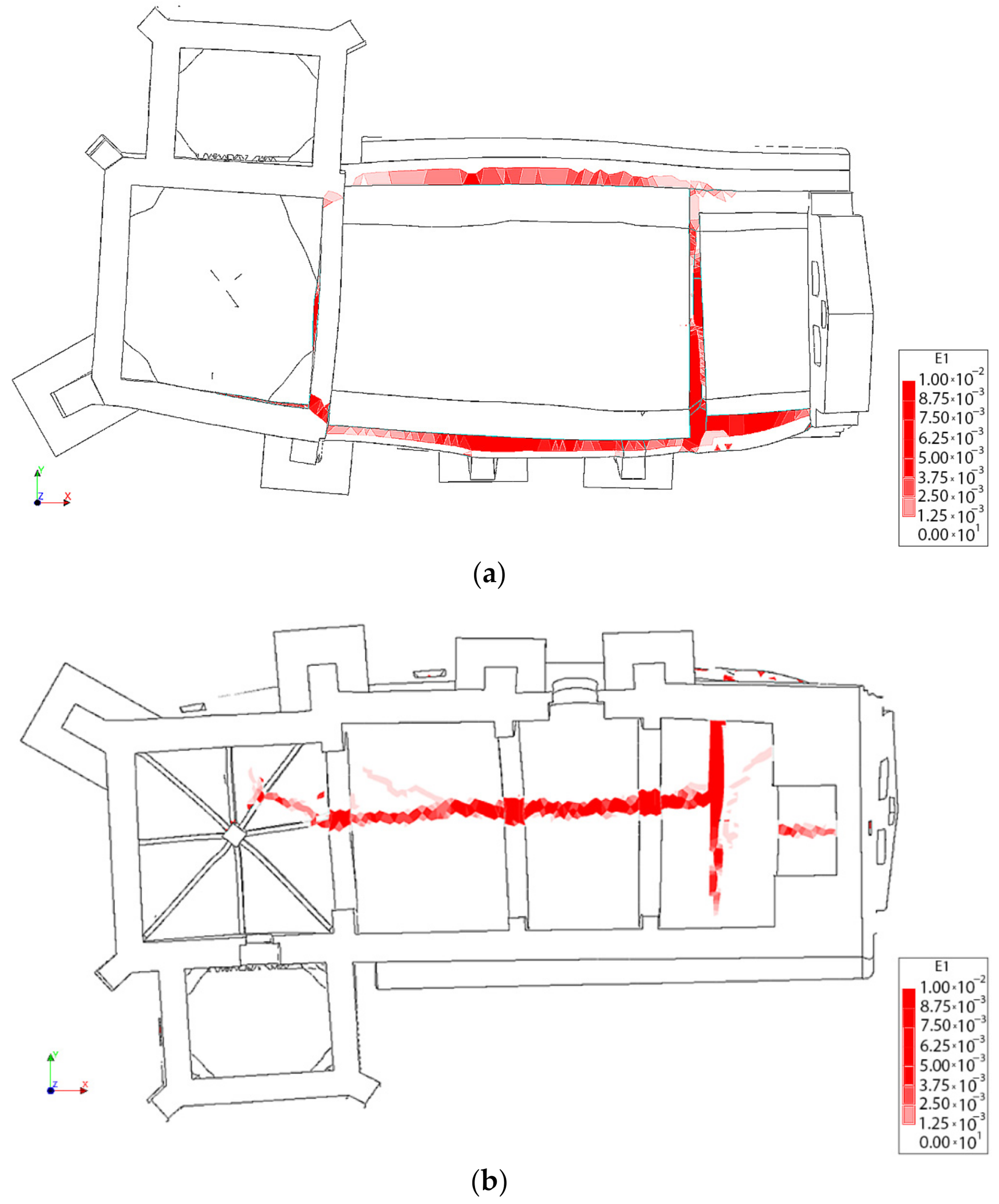
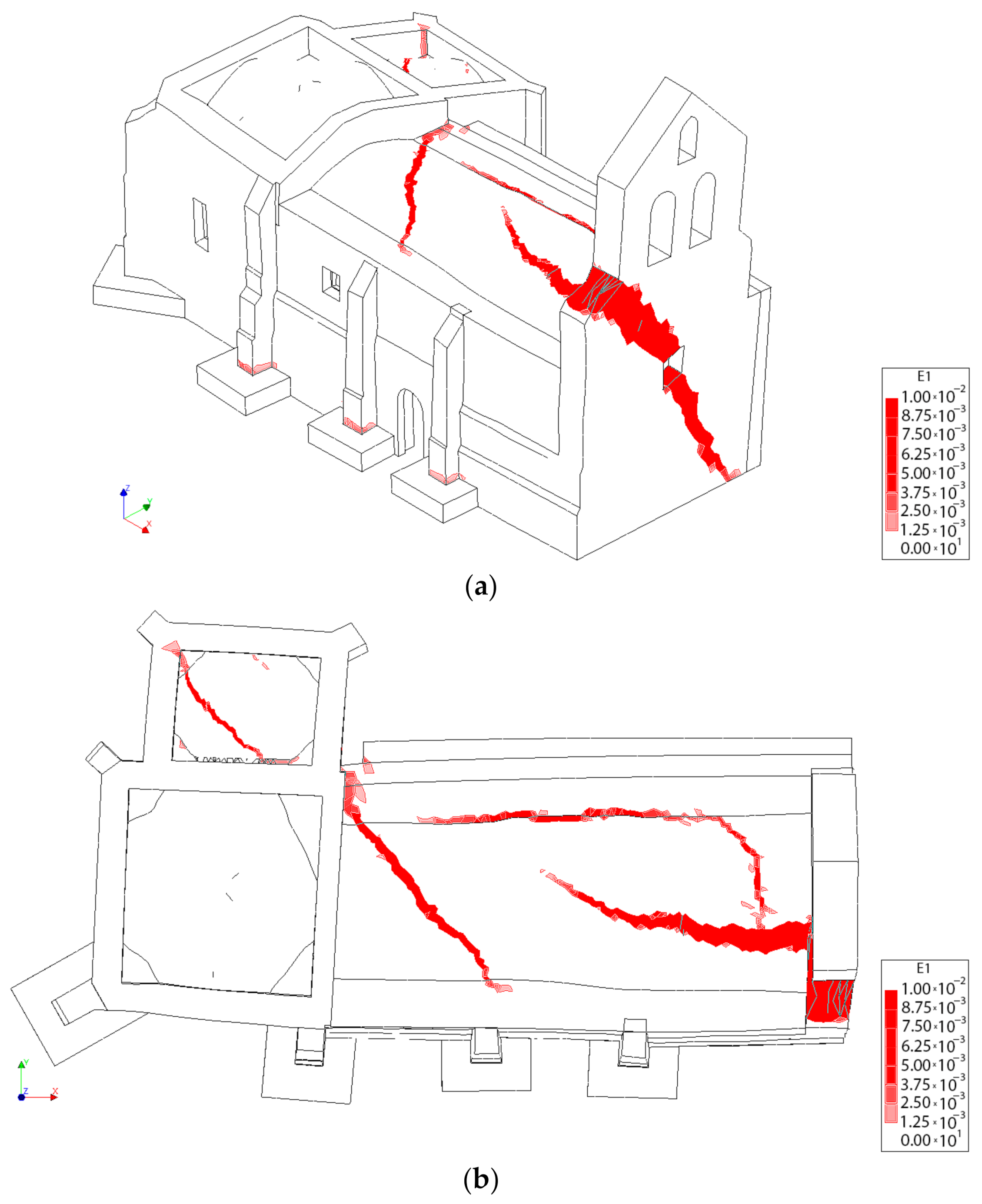
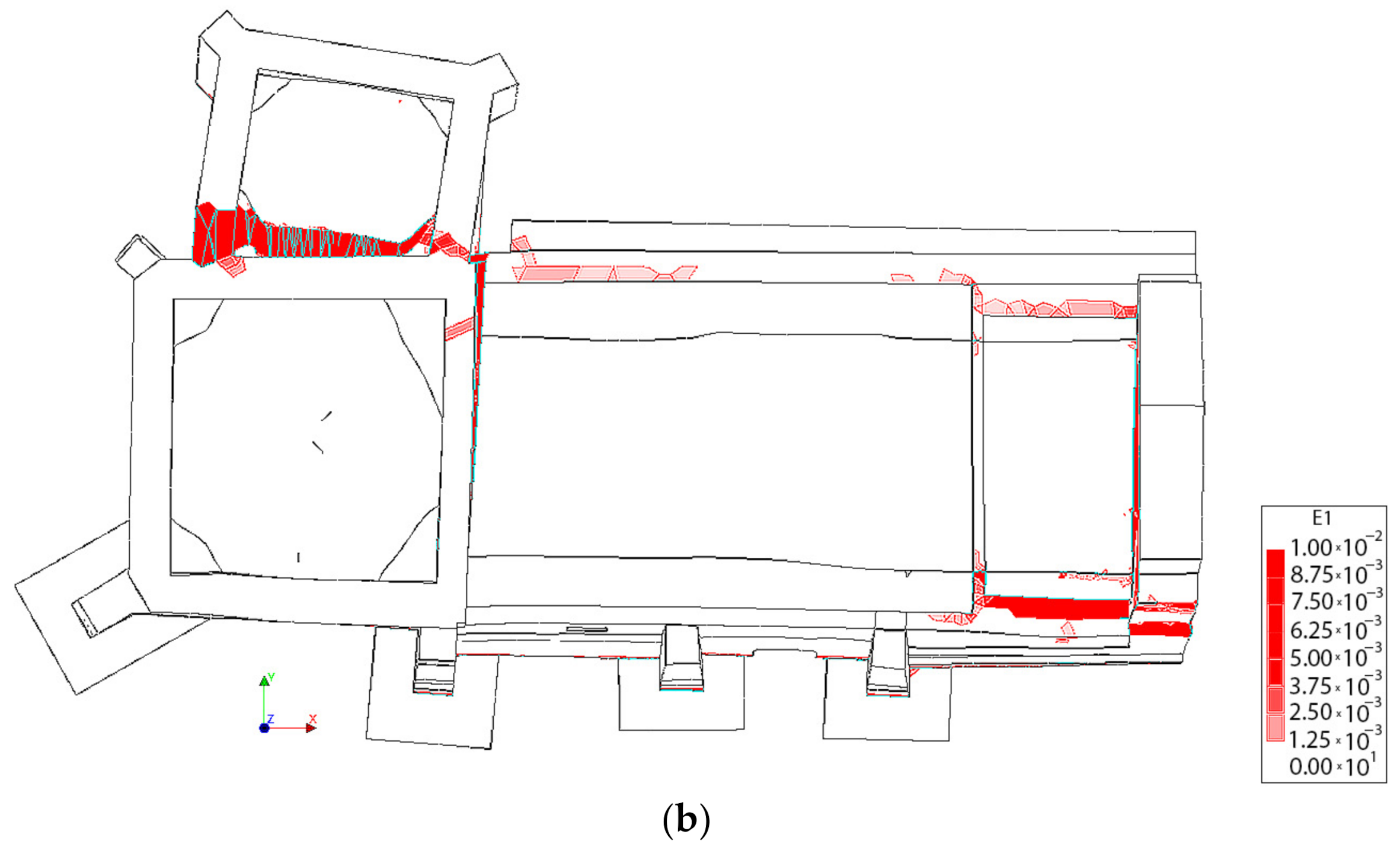
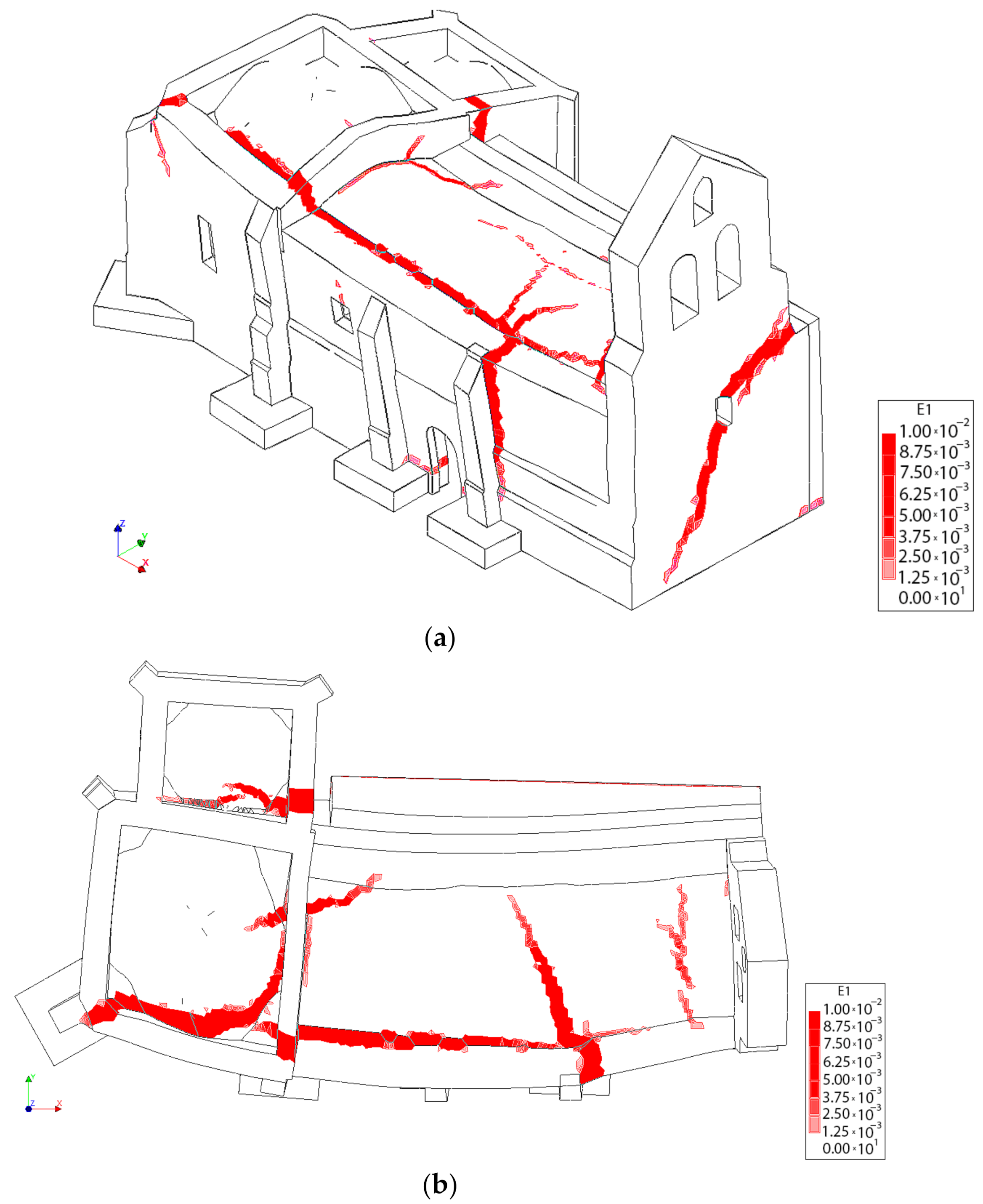
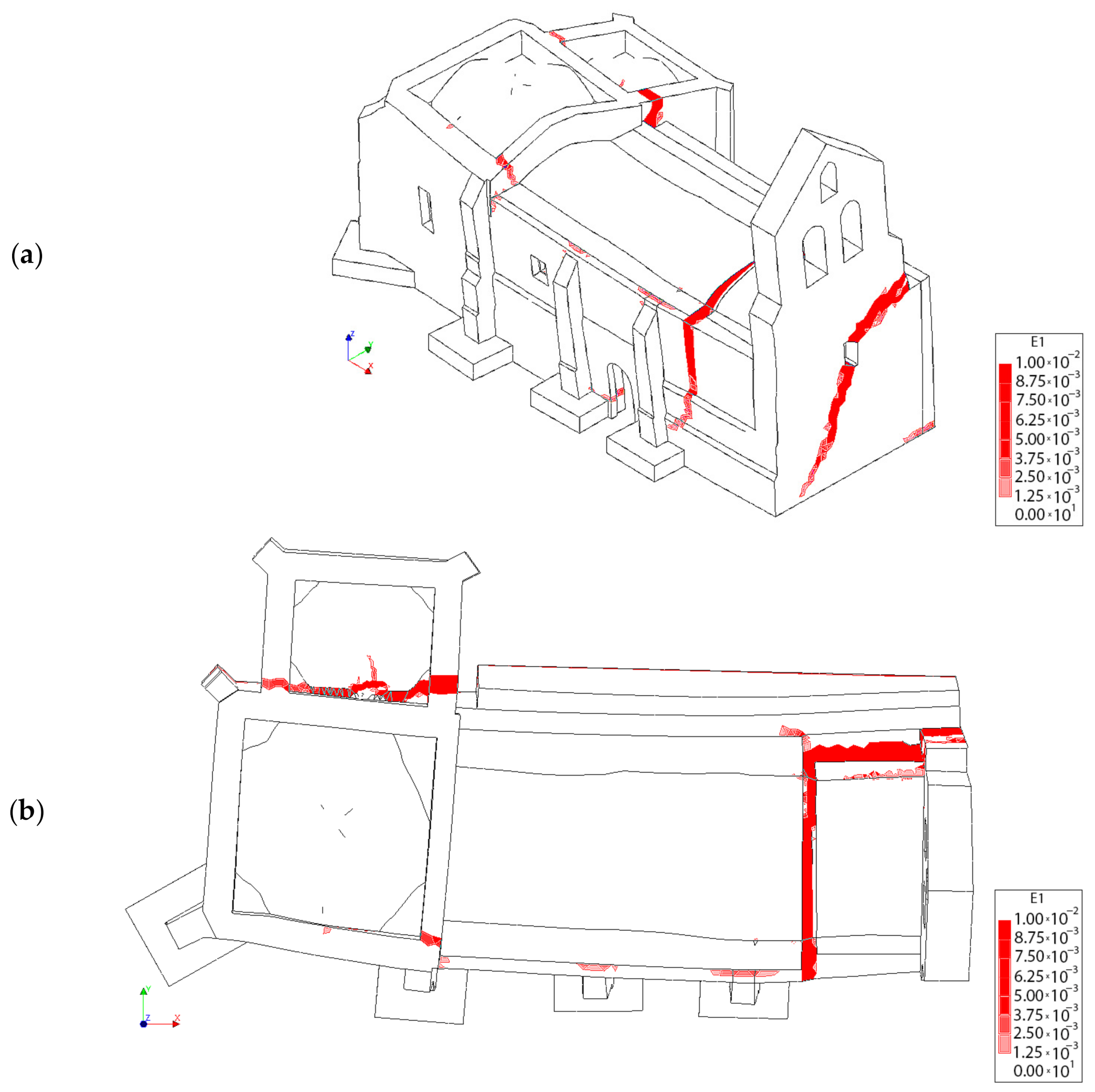
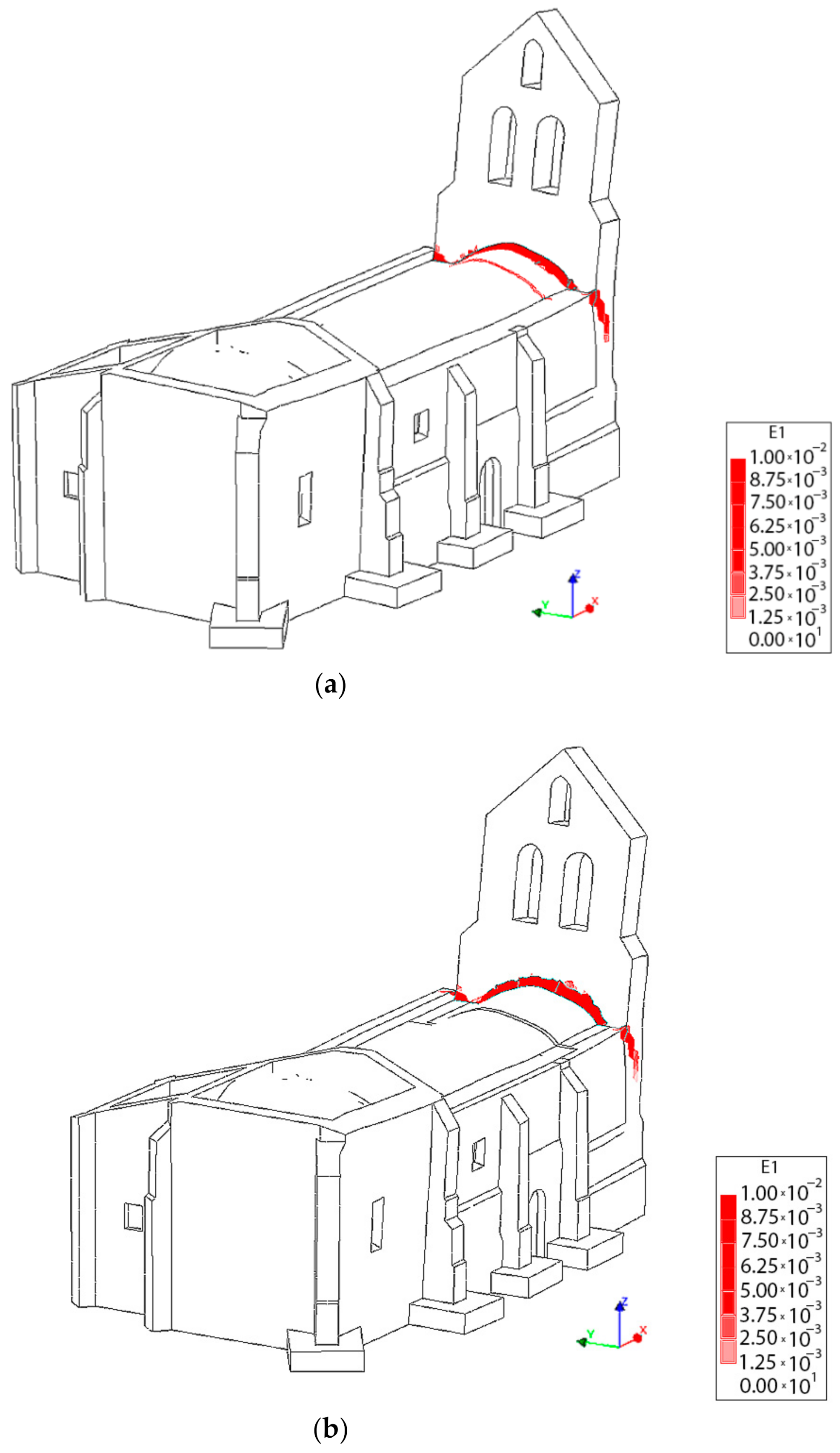
4.3.1. Results Obtained from the Static Non-Linear Analysis
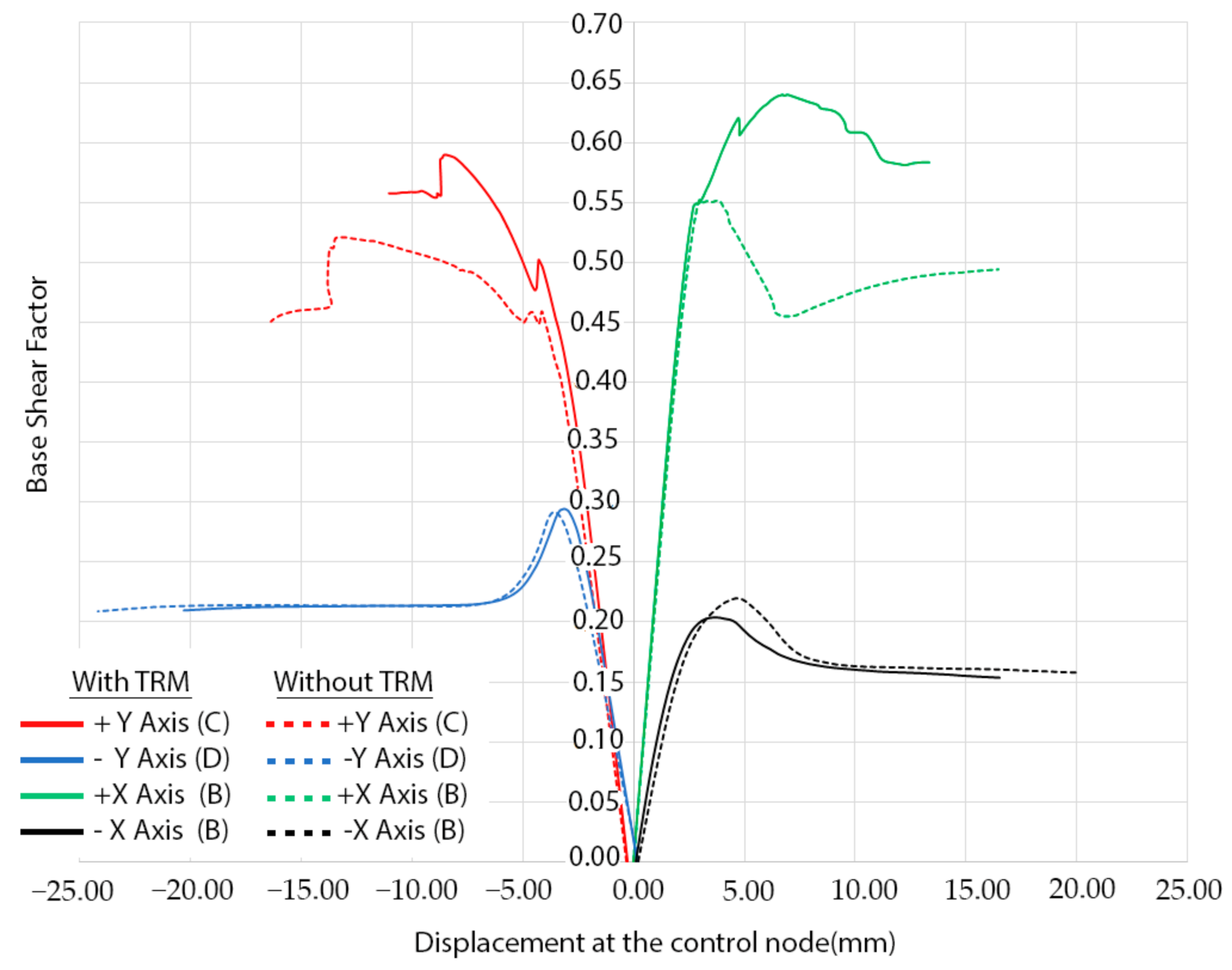
4.3.2. Results Obtained from the Seismic Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roca, P.; Cervera, M.; Gariup, G.; Pela’, L. Structural analysis of masonry historical constructions. Classical and advanced approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef]
- Aguilar, R.; Noel, M.F.; Ramos, L.F. Integration of reverse engineering and non-linear numerical analysis for the seismic assessment of historical adobe buildings. Autom. Constr. 2019, 98, 1–15. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Bautista-De Castro, Á.; Conde, B.; Carrasco, P.; Ramos, L.F. Non-destructive means and methods for structural diagnosis of masonry arch bridges. Autom. Constr. 2019, 104, 360–382. [Google Scholar] [CrossRef]
- Masciotta, M.G.; Pellegrini, D.; Brigante, D.; Barontini, A.; Lourenço, P.B.; Girandi, M.; Padovani, C.; Fabbrocino, G. Dynamic characterization of progressively damaged segmental masonry arches with one settled support: Experimental and numerical analyses. Frat. Integrità Strutt. 2019, 14, 423–441. [Google Scholar] [CrossRef]
- Lagomarsino, S. Damage assessment of churches after L’Aquila earthquake (2009). Bull. Earthq. Eng. 2012, 10, 73–92. [Google Scholar] [CrossRef]
- Fuentes, D.D.; Baquedano Julià, P.A.; D’Amato, M.; Laterza, M. Preliminary seismic damage assessment of mexican churches after september 2017 earthquakes. Int. J. Archit. Herit. 2019. [Google Scholar] [CrossRef]
- Clementi, F. Failure analysis of apennine masonry churches severely damaged during the 2016 central Italy seismic sequence. Buildings 2021, 11, 58. [Google Scholar] [CrossRef]
- Yurdakul, M.; Yılmaz, F.; Artar, M.; Can, Ö.; Öner, E.; Daloğlu, A.T. Investigation of time-history response of a historical masonry minaret under seismic loads. Structures 2021, 30, 265–276. [Google Scholar] [CrossRef]
- Kassotakis, N.; Sarhosis, V.; Riveiro, B.; Conde, B.; D’Altri, A.M.; Mills, J.; Milani, G.; de Miranda, S.; Castellazzi, G. Three-dimensional discrete element modelling of rubble masonry structures from dense point clouds. Autom. Constr. 2020, 119, 103365. [Google Scholar] [CrossRef]
- Pepe, M.; Costantino, D.; Restuccia Garofalo, A. An Efficient pipeline to obtain 3D model for HBIM and structural analysis purposes from 3D point clouds. Appl. Sci. 2020, 10, 1235. [Google Scholar] [CrossRef]
- Bassoli, E.; Vincenzi, L.; D’Altri, A.M.; de Miranda, S.; Forghieri, M.; Castellazzi, G. Ambient vibration-based finite element model updating of an earthquake-damaged masonry tower. Struct. Control Health Monit. 2018, 25, e2150. [Google Scholar] [CrossRef]
- Castellazzi, G.; D’Altri, A.M.; de Miranda, S.; Ubertini, F. An innovative numerical modeling strategy for the structural analysis of historical monumental buildings. Eng. Struct. 2017, 132, 229–248. [Google Scholar] [CrossRef]
- Gonizzi, S.; Politecnico, B.; Milano, D.; Guidi, G.; Di Milano, P.; Gonizzi Barsanti, S.; Guidi, G. A geometric processing workflow for transforming reality-based 3D models in volumetric meshes suitable for FEA. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W3, 331–338. [Google Scholar] [CrossRef]
- Bautista-De Castro, Á.; Sánchez-Aparicio, L.J.; Ramos, L.F.; Sena-Cruz, J.; González-Aguilera, D. Integrating geomatic approaches, Operational Modal Analysis, advanced numerical and updating methods to evaluate the current safety conditions of the historical Bôco Bridge. Constr. Build. Mater. 2018, 158, 961–984. [Google Scholar] [CrossRef]
- Barazzetti, L.; Banfi, F.; Brumana, R.; Previtali, M. Creation of parametric BIM objects from point clouds using nurbs. Photogramm. Rec. 2015, 30, 339–362. [Google Scholar] [CrossRef]
- Nocerino, E.; Pablo, R.-G.; Menna, F. Introduction to Mobile Mapping with Portable Systems; CRC Press: Boca Raton, FL, USA, 2019; ISBN 9781351018869. [Google Scholar]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–108. [Google Scholar] [CrossRef]
- Nocerino, E.; Menna, F.; Kessler, F.B.; Fondazione, F.R.; Kessler, B.; Remondino, F.; Toschi, I.; Rodríguez-Gonzálvez, P. Investigation of indoor and outdoor performance of two portable mobile mapping systems. SPIE Opt. Metrol. 2017. [Google Scholar] [CrossRef]
- di Filippo, A.; Sánchez-Aparicio, L.J.; Barba, S.; Martín-Jiménez, J.A.; Mora, R.; Aguilera, D.G. Use of a wearable mobile laser system in seamless indoor 3D mapping of a complex historical site. Remote Sens. 2018, 10, 1897. [Google Scholar] [CrossRef]
- Barba, S.; di Filippo, A.; Limongiello, M.; Messina, B. Integration of active sensors for geometric analysis of the Chapel of the Holy Shroud. In Proceedings of the 27th CIPA International Symposium “Documenting the Past for a Better Future”, Ávila, Spain, 1–5 September 2019; Volume XLII-2/W15, pp. 149–156. [Google Scholar]
- Sánchez-Aparicio, L.; Conde, B.; Maté-González, M.A.; Mora, R.; Sánchez-Aparicio, M.; García-Álvarez, J.; González-Aguilera, D. A comparative study between WMMS and TLS for the stability analysis of the San Pedro Church Barrel vault by means of the finite element method. In Proceedings of the 27th CIPA International Symposium “Documenting the Past for a Better Future”, Ávila, Spain, 1–5 September 2019; Volume XLII-2/W15; pp. 1047–1054. [Google Scholar]
- Nocerino, E.; Menna, F.; Toschi, I.; Morabito, D.; Remondino, F.; Rodríguez-Gonzálvez, P. Valorisation of history and landscape for promoting the memory of WWI. J. Cult. Herit. 2018, 29, 113–122. [Google Scholar] [CrossRef]
- Maté-González, M.Á.; Sánchez-Aparicio, L.J.; Sáez Blázquez, C.; Carrasco García, P.; Álvarez-Alonso, D.; de Andrés-Herrero, M.; García-Davalillo, J.C.; González-Aguilera, D.; Hernández Ruiz, M.; Jordá Bordehore, L.; et al. On the combination of remote sensing and geophysical methods for the digitalization of the san lázaro middle paleolithic rock shelter (Segovia, Central Iberia, Spain). Remote Sens. 2019, 11, 2035. [Google Scholar] [CrossRef]
- Roca, P.; Lourenço, P.B.; Gaetani, A. Historic Construction and Conservation. Materials, Systems and Damage; Routledge: London, UK, 2019; ISBN 978-0-429-05276-7. [Google Scholar]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Ghiassi, B.; Allahvirdizadeh, R.; Wang, X.; Mininno, G.; Silva, R.A. Macromodeling approach for pushover analysis of textile-reinforced mortar-strengthened masonry. In Numerical Modeling of Masonry and Historical Structures: From Theory to Application; Elsevier: Amsterdam, The Netherlands, 2019; pp. 745–778. ISBN 9780081024393. [Google Scholar]
- Gunes, B.; Cosgun, T.; Sayin, B.; Ceylan, O. Structural rehabilitation of a Middle Byzantine ruin and the masonry building constructed above the ruin. Part I: The ruin. Eng. Fail. Anal. 2019, 105, 503–517. [Google Scholar] [CrossRef]
- Bru, D.; Ivorra, S.; Baeza, F.J. Seismic behavior of a masonry chimney retrofitted with composite materials: A preliminary aproach. Int. J. Saf. Secur. Eng. 2017, 7, 486–497. [Google Scholar] [CrossRef]
- Europan Committee for Standardization. Eurocode 2: Design of Concrete Strucures; European Committee for Standardization: Brussels, Belgium, 1992. [Google Scholar]
- GeoSLAM A Survey REVOlution. Introducing the ZEB-REVO Mobile Indoor Mapping System. Available online: https://gpserv.com/wp-content/uploads/2017/01/ZEB-REVO-Brochure-v1.0.3.pdf (accessed on 15 December 2020).
- GeoSLAM ZEB Go—GeoSLAM. Available online: https://geoslam.com/solutions/zeb-go/ (accessed on 1 September 2020).
- Quigley, M.; Gerkey, B.; Conley, K.; Faust, J.; Foote, T.; Leibs, J.; Berger, E.; Wheeler, R.; Ng, A. ROS: An open-source robot operating system. ICRA Work. Open Source Softw. 2009, 3, 5. [Google Scholar]
- Balta, H.; Velagic, J.; Bosschaerts, W.; De Cubber, G.; Siciliano, B. Fast statistical outlier removal based method for large 3D Point clouds of outdoor environments. IFAC-PapersOnLine 2018, 51, 348–353. [Google Scholar] [CrossRef]
- Guerrero, P.; Kleiman, Y.; Ovsjanikov, M.; Mitra, N.J. PCPNet learning local shape properties from raw point clouds. Comput. Graph. Forum 2018, 37, 75–85. [Google Scholar] [CrossRef]
- Rakotosaona, M.; La Barbera, V.; Guerrero, P.; Mitra, N.J.; Ovsjanikov, M. PointCleanNet: Learning to denoise and remove outliers from dense point clouds. Comput. Graph. Forum 2020, 39, 185–203. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Xu, Z.; Foi, A. Anisotropic denoising of 3D point clouds by aggregation of multiple surface-adaptive estimates. IEEE Trans. Vis. Comput. Graph. 2019. [Google Scholar] [CrossRef] [PubMed]
- CloudCompare: 3D point cloud and mesh processing software Open Source Project. Available online: http://www.cloudcompare.org/ (accessed on 15 December 2020).
- Rodríguez-Gonzálvez, P.; Jiménez Fernández-Palacios, B.; Muñoz-Nieto, Á.; Arias-Sanchez, P.; Gonzalez-Aguilera, D. Mobile LiDAR system: New possibilities for the documentation and dissemination of large cultural heritage sites. Remote Sens. 2017, 9, 189. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Del Pozo, S.; Ramos, L.F.; Arce, A.; Fernandes, F.M. Heritage site preservation with combined radiometric and geometric analysis of TLS data. Autom. Constr. 2018, 85, 24–39. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- TNO DIANA BV DIANA—Finite Element Analysis. User’s Manual. Available online: https://dianafea.com/diana-manuals (accessed on 10 November 2020).
- Lourenço, P.B.; Greco, F.; Barontini, A.; Pia Ciocci, M.; Karanikoloudis, G. Seismic Retrofitting Project: Modeling of Prototype Buildings; The Getty Conservation Institute: Los Angeles, CA, USA, 2019. [Google Scholar]
- Ciocci, M.P.; Sharma, S.; Lourenço, P.B. Engineering simulations of a super-complex cultural heritage building: Ica Cathedral in Peru. Meccanica 2018, 53, 1931–1958. [Google Scholar] [CrossRef]
- Illampas, R.; Ioannou, I.; Lourenço, P.B. Seismic appraisal of heritage ruins: The case study of the St. mary of carmel church in cyprus. Eng. Struct. 2020, 224, 111209. [Google Scholar] [CrossRef]
- Norme Tecniche per le Costruzioni (NTC-08). Available online: http://www.ingegneriasoft.com/pdf/Norme_Tecniche_Costruzioni_2008_cap1-12.pdf (accessed on 10 November 2020).
- Lourenço, P.B. Structural Masonry Analysis: Recent Developments and Prospects. In Proceedings of the 14th International Brick and Block Masonry Conference, Sydney, Australia, 17–20 February 2008. [Google Scholar]
- Kariou, F.A.; Triantafyllou, S.P.; Bournas, D.A.; Koutas, L.N. Out-of-plane behaviour of TRM strengthened masonry walls. In Proceedings of the SMAR 2017-Fourth Conference on Smart Monitoring Assessment and Rehabilitation of Civil Structures, Zurich, Switzerland, 13–15 September 2017. [Google Scholar]
- O’Hearne, N.; Mendes, N.; Lourenço, P.B. Seismic analysis of the San Sebastian Basilica (Philippines). In Proceedings of the 40th IABSE Symposium: Tomorrow’s Megastructures, Nantes, France, 19–21 September 2018. [Google Scholar]
- Seismic Standards Standing Committee Seismic construction standard: General and building (NCSE-02). Available online: https://www.mitma.gob.es/recursos_mfom/0820200.pdf (accessed on 10 November 2020).







| WMLS Zeb REVO | |
|---|---|
| Measuring principle | Time of flight |
| Operating time | 4 h |
| Field of view | 270° (H) × 360° (V) |
| Wavelength (nm) | 905 |
| Scanner resolution (°) | 0.625 H × 1.8 V |
| Orientations system | MEMS IMU |
| Scanner dimensions (mm) | 86 × 113 × 287 |
| Total weight (kg) | 4.10 |
| Scanner weight (kg) | 1.00 |
| Dimensions (mm) | 220 × 180 × 470 |
| Working range (m) | 0.60–30 m indoors |
| 0.60–15 outdoors | |
| Measurement rate | 40,000 points per second |
| Accuracy (cm) | 1–3 |
| Without Noise Reduction | With Noise Reduction | |||
|---|---|---|---|---|
| Cases | Bias | Dispersion | Bias | Dispersion |
| Median (m) | NMAD (m) | Median (m) | NMAD (m) | |
| Case 1 | 0.005 | ±0.004 | 0.003 | ±0.002 |
| Case 2 | 0.005 | ±0.004 | 0.003 | ±0.003 |
| Case 3 | 0.005 | ±0.004 | 0.004 | ±0.003 |
| Case 4 | 0.005 | ±0.005 | 0.004 | ±0.003 |
| Case 5 | 0.005 | ±0.005 | 0.003 | ±0.003 |
| Case 6 | 0.005 | ±0.005 | 0.002 | ±0.002 |
| Case 7 | 0.010 | ±0.009 | 0.008 | ±0.005 |
| Case 8 | 0.007 | ±0.007 | 0.005 | ±0.005 |
| Case 9 | 0.014 | ±0.011 | 0.010 | ±0.009 |
| Parameter | Regular Masonry (Limestone) with Infill Core | Irregular Masonry (Sandstone and Tuff) with Infill Core | Tuff Masonry (Vaults) |
|---|---|---|---|
| Young modulus (Gpa) | 1.44 | 1.02 | 1.08 |
| Poisson ration (-) | 0.20 | 0.20 | 0.20 |
| Density (kg/m3) | 2000 | 2000 | 1600 |
| Tensile strength (N/mm2) | 0.10 | 0.10 | 0.10 |
| Fracture energy in tensile regime (N·mm) | 0.05 | 0.05 | 0.05 |
| Compressive strength (N/mm2) | 2.22 | 1.48 | 1.41 |
| Fracture energy in compressive regime (N·mm) | 3.55 | 2.45 | 2.34 |
| Properties | Value | |
|---|---|---|
| Mortar | Young modulus (GPa) | 4.00 |
| Poisson ratio (-) | 0.20 | |
| Thickness (m) | 0.03 | |
| Density (kg/m3) | 1850 | |
| Compressive strength (MPa) | 2.50 | |
| Fracture energy (N/mm) | 3.44 | |
| Tensile strength (MPa) | 0.55 | |
| Plateau and strain | 0.0016 | |
| Power c | 0.6 | |
| Carbon fibre | Young modulus (GPa) | 160 |
| Poisson ratio (-) | 0.20 | |
| Reinforcement ratio (mm2/m) | 44 | |
| Density (kg/m3) | 1780 | |
| Tensile strength (Mpa) | 4300 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Aparicio, L.J.; Mora, R.; Conde, B.; Maté-González, M.Á.; Sánchez-Aparicio, M.; González-Aguilera, D. Integration of a Wearable Mobile Mapping Solution and Advance Numerical Simulations for the Structural Analysis of Historical Constructions: A Case of Study in San Pedro Church (Palencia, Spain). Remote Sens. 2021, 13, 1252. https://doi.org/10.3390/rs13071252
Sánchez-Aparicio LJ, Mora R, Conde B, Maté-González MÁ, Sánchez-Aparicio M, González-Aguilera D. Integration of a Wearable Mobile Mapping Solution and Advance Numerical Simulations for the Structural Analysis of Historical Constructions: A Case of Study in San Pedro Church (Palencia, Spain). Remote Sensing. 2021; 13(7):1252. https://doi.org/10.3390/rs13071252
Chicago/Turabian StyleSánchez-Aparicio, Luis Javier, Rocío Mora, Borja Conde, Miguel Ángel Maté-González, María Sánchez-Aparicio, and Diego González-Aguilera. 2021. "Integration of a Wearable Mobile Mapping Solution and Advance Numerical Simulations for the Structural Analysis of Historical Constructions: A Case of Study in San Pedro Church (Palencia, Spain)" Remote Sensing 13, no. 7: 1252. https://doi.org/10.3390/rs13071252
APA StyleSánchez-Aparicio, L. J., Mora, R., Conde, B., Maté-González, M. Á., Sánchez-Aparicio, M., & González-Aguilera, D. (2021). Integration of a Wearable Mobile Mapping Solution and Advance Numerical Simulations for the Structural Analysis of Historical Constructions: A Case of Study in San Pedro Church (Palencia, Spain). Remote Sensing, 13(7), 1252. https://doi.org/10.3390/rs13071252