Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
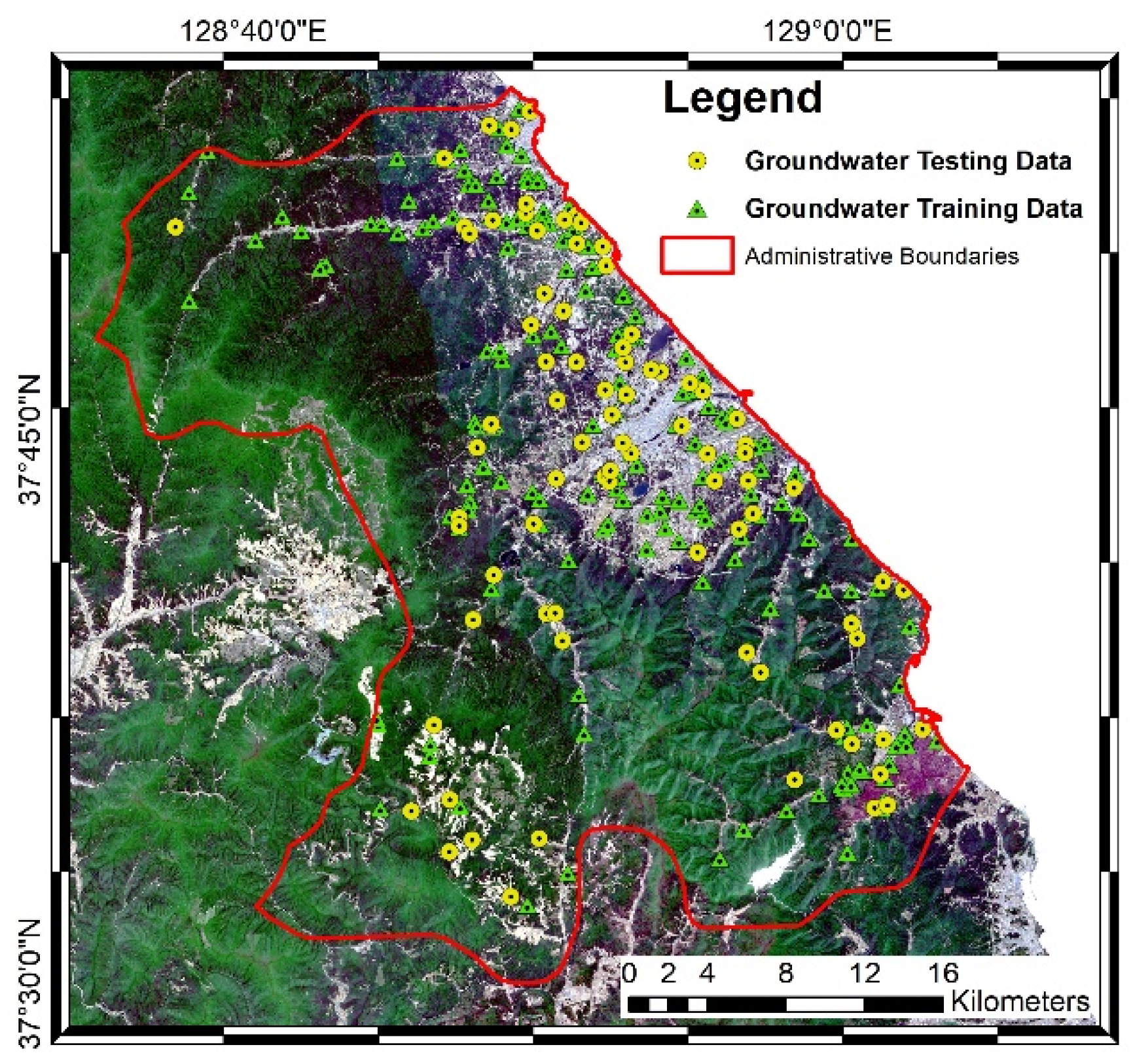
2.2. Groundwater Datasets
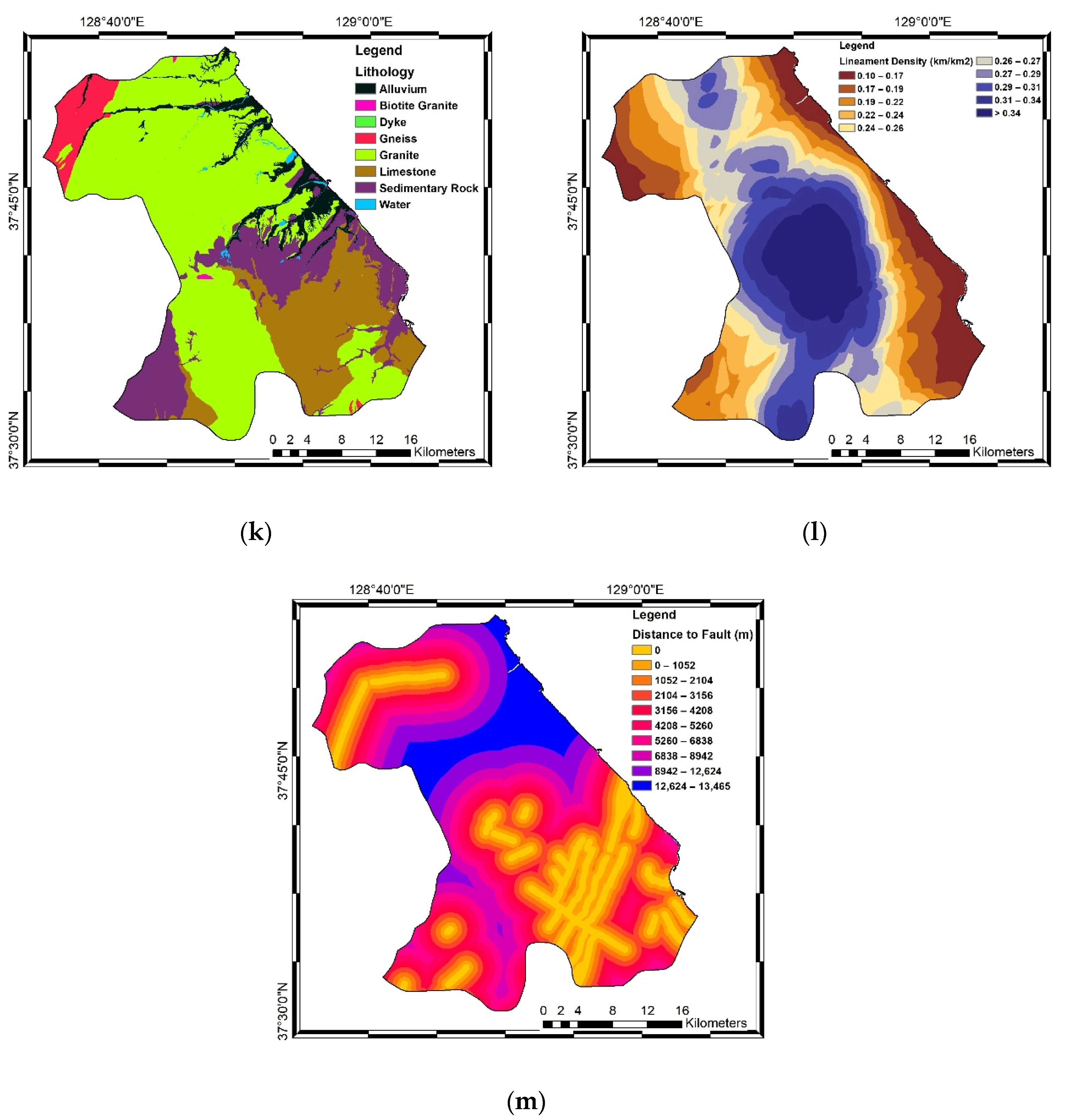
2.3. Selection of Groundwater-Related Factors
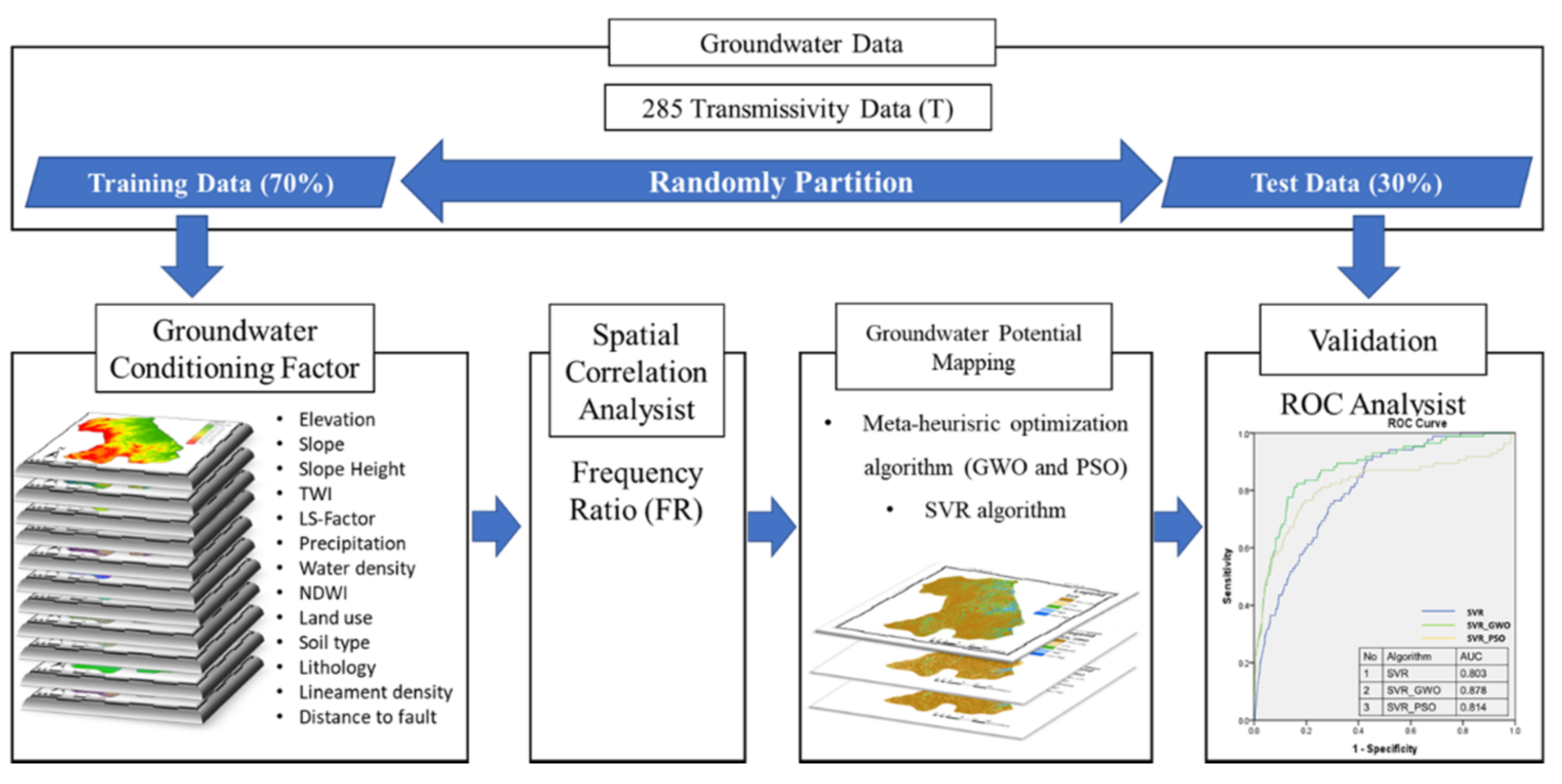
2.4. Methodology
2.5. Support Vector Regression
2.6. Grey Wolf Optimization
2.7. Particle Swarm Optimization
3. Results
3.1. Relationships between Groundwater and Related Factors
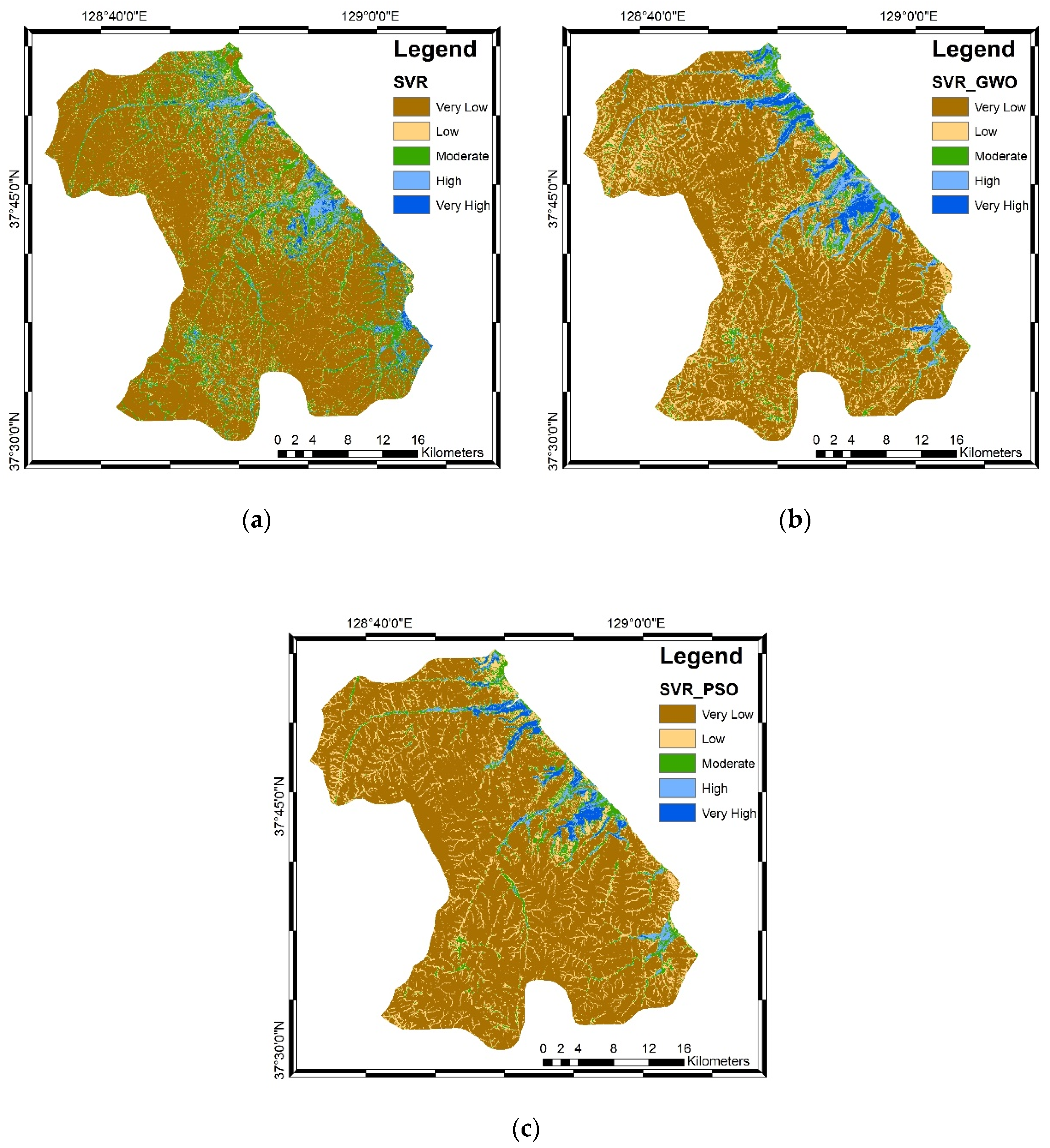
3.2. Construction of Groundwater Potential Maps
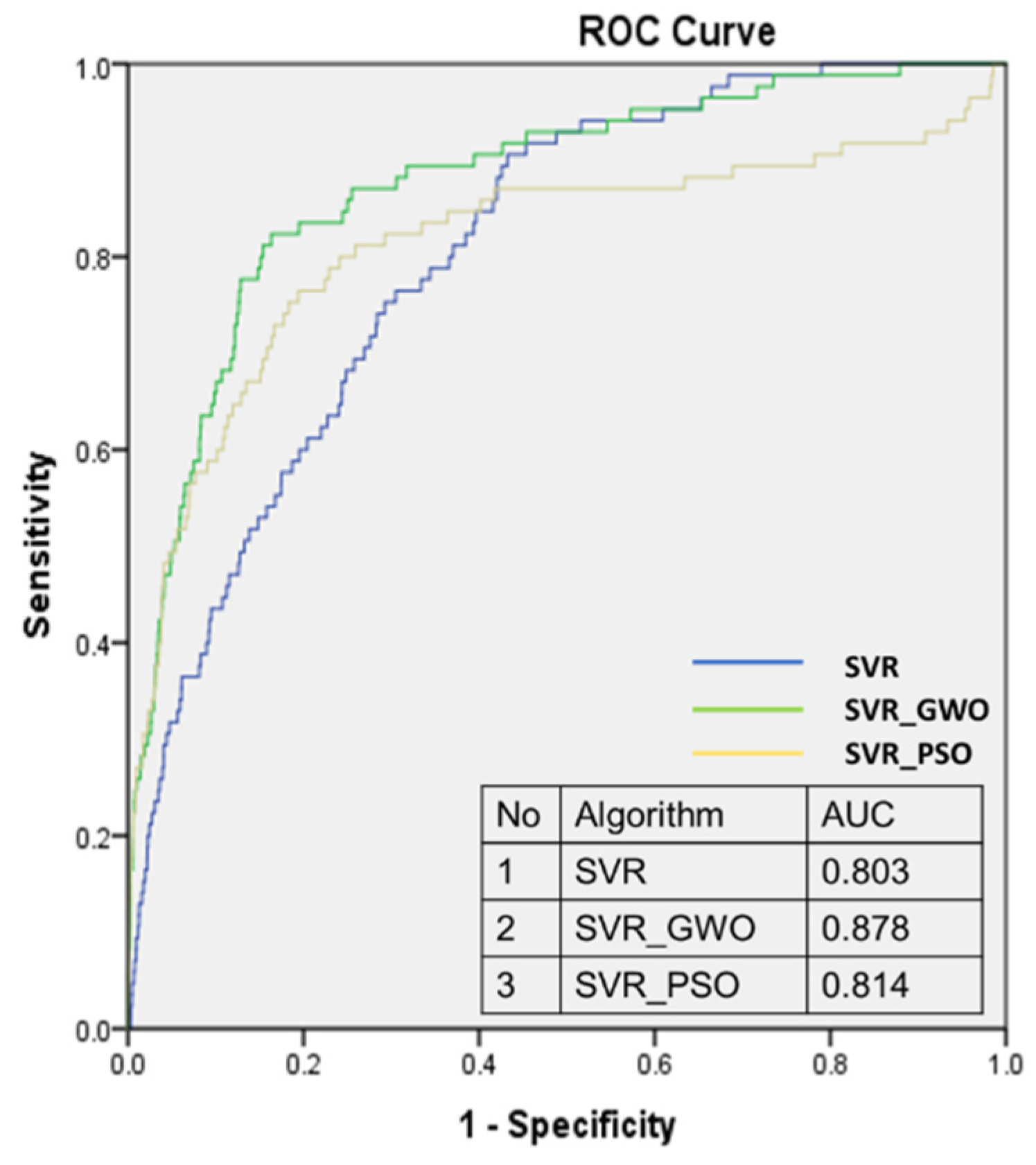
3.3. Sensitivity Analysis
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press (CUP): Cambridge, UK, 2013. [Google Scholar]
- WWDR. The United Nations World Water Development Report, 2017: Wastewater: The Untapped Resource; UNESCO: Paris, France, 2017; ISBN 978-92-3-100201-4. [Google Scholar]
- Zandi, J.; Ghazvinei, P.T.; Hashim, R.; Yusof, K.B.W.; Ariffin, J.; Motamedi, S. Mapping of regional potential groundwater springs using Logistic Regression statistical method. Water Resour. 2016, 43, 48–57. [Google Scholar] [CrossRef]
- Mohamaden, M.I.I.; Ehab, D. Application of electrical resistivity for groundwater exploration in Wadi Rahaba, Shalateen, Egypt. NRIAG J. Astron. Geophys. 2017, 6, 201–209. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.P.; Bera, A. Delineating groundwater potential zones of agriculture dominated landscapes using GIS based AHP techniques: A case study from Uttar Dinajpur district, West Bengal. Environ. Earth Sci. 2020, 79, 302. [Google Scholar] [CrossRef]
- Kim, J.C.; Jung, H.S.; Lee, S. Groundwater productivity potential mapping using frequency ratio and evidential belief function and artificial neural network models: Focus on topographic factors. J. Hydroinformatics 2018, 20, 1436–1451. [Google Scholar] [CrossRef]
- Ministry of Land, Transport and Maritime Affairs. National Groundwater Monitoring Network in Korea Annual Report 2016; MLTM: Seoul, Korea, 2016.
- Manap, M.A.; Nampak, H.; Pradhan, B.; Lee, S.; Sulaiman, W.N.A.; Ramli, M.F. Application of probabilistic-based frequency ratio model in groundwater potential mapping using remote sensing data and GIS. Arab. J. Geosci. 2014, 7, 711–724. [Google Scholar] [CrossRef]
- Muchingami, I.; Chuma, C.; Gumbo, M.; Hlatywayo, D.; Mashingaidze, R. Review: Approaches to groundwater exploration and resource evaluation in the crystalline basement aquifers of Zimbabwe. Hydrogeol. J. 2019, 27, 915–928. [Google Scholar] [CrossRef]
- Yin, H.; Shi, Y.; Niu, H.; Xie, D.; Wei, J.; Lefticariu, L.; Xu, S. A GIS-based model of potential groundwater yield zonation for a sandstone aquifer in the Juye Coalfield, Shangdong, China. J. Hydrol. 2018, 557, 434–447. [Google Scholar] [CrossRef]
- Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.M.; Jung, H.S. GIS-based groundwater potential mapping using artificial neural network and support vector machine models: The case of Boryeong city in Korea. Geocarto Int. 2018, 33, 847–861. [Google Scholar] [CrossRef]
- Díaz-Alcaide, S.; Martínez-Santos, P. Review: Advances in groundwater potential mapping. Hydrogeol. J. 2019, 27, 2307–2324. [Google Scholar] [CrossRef]
- Altafi Dadgar, M.; Zeaieanfirouzabadi, P.; Dashti, M.; Porhemmat, R. Extracting of prospective groundwater potential zones using remote sensing data, GIS, and a probabilistic approach in Bojnourd basin, NE of Iran. Arab. J. Geosci. 2017, 10, 1–11. [Google Scholar] [CrossRef]
- Duan, H.; Deng, Z.; Deng, F.; Wang, D. Assessment of groundwater potential based on multicriteria decision making model and decision tree algorithms. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Adeyeye, O.A.; Ikpokonte, E.A.; Arabi, S.A. GIS-based groundwater potential mapping within Dengi area, North Central Nigeria. Egypt. J. Remote Sens. Sp. Sci. 2019, 22, 175–181. [Google Scholar] [CrossRef]
- Achmad, A.R.; Lee, S.; Park, S.; Eom, J.; Lee, C.W. Estimating the potential risk of the Mt. Baekdu Volcano using a synthetic interferogram and the LAHARZ inundation zone. Geosci. J. 2020, 24, 755–768. [Google Scholar] [CrossRef]
- Hakim, W.L.; Lee, C.-W. A Review on Remote Sensing and GIS Applications to Monitor Natural Disasters in Indonesia. Korean J. Remote Sens. 2020, 36, 1303–1322. [Google Scholar]
- Elmahdy, S.I.; Mohamed, M.M. Probabilistic frequency ratio model for groundwater potential mapping in Al Jaww plain, UAE. Arab. J. Geosci. 2015, 8, 2405–2416. [Google Scholar] [CrossRef]
- Jothibasu, A.; Anbazhagan, S. Spatial mapping of groundwater potential in Ponnaiyar River basin using probabilistic-based frequency ratio model. Model. Earth Syst. Environ. 2017, 3, 1–12. [Google Scholar] [CrossRef]
- Falah, F.; Zeinivand, H. GIS-Based Groundwater Potential Mapping in Khorramabad in Lorestan, Iran, using Frequency Ratio (FR) and Weights of Evidence (WoE) Models. Water Resour. 2019, 46, 679–692. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C.; et al. GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef]
- Tahmassebipoor, N.; Rahmati, O.; Noormohamadi, F.; Lee, S. Spatial analysis of groundwater potential using weights-of-evidence and evidential belief function models and remote sensing. Arab. J. Geosci. 2016, 9, 1–18. [Google Scholar] [CrossRef]
- Khoshtinat, S.; Aminnejad, B.; Hassanzadeh, Y.; Ahmadi, H. Groundwater potential assessment of the Sero plain using bivariate models of the frequency ratio, Shannon entropy and evidential belief function. J. Earth Syst. Sci. 2019, 128, 1–16. [Google Scholar] [CrossRef]
- Sokeng, V.-C.J.; Kouamé, F.K.; Ngounou Ngatcha, B.; Dibi N’da, H.; Akpa You, L.; Rirabe, D. Delineating Groundwater Potential Zones in Western Cameroon Highlands Using GIS Based Artificial Neural Networks Model and Remote Sensing Data. Int. J. Innov. Appl. Stud. 2016, 15, 747–749. [Google Scholar]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of Support Vector Machine, Random Forest, and Genetic Algorithm Optimized Random Forest Models in Groundwater Potential Mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Park, S.; Hamm, S.-Y.; Jeon, H.-T.; Kim, J. Evaluation of Logistic Regression and Multivariate Adaptive Regression Spline Models for Groundwater Potential Mapping Using R and GIS. Sustainability 2017, 9, 1157. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Pradhan, B.; Saharkhiz, M.A.; Lee, S. Groundwater aquifer potential modeling using an ensemble multi-adoptive boosting logistic regression technique. J. Hydrol. 2019, 579, 124172. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Chapi, K.; Shahabi, H.; Pradhan, B.; Pham, B.T.; Singh, V.P.; Chen, W.; Khosravi, K.; Ahmad, B.B.; et al. A hybrid computational intelligence approach to groundwater spring potential mapping. Water 2019, 11, 2013. [Google Scholar] [CrossRef]
- Chen, W.; Tsangaratos, P.; Ilia, I.; Duan, Z.; Chen, X. Groundwater spring potential mapping using population-based evolutionary algorithms and data mining methods. Sci. Total Environ. 2019, 684, 31–49. [Google Scholar] [CrossRef]
- Toth, E.; Brath, A.; Montanari, A. Comparison of short-term rainfall prediction models for real-time flood forecasting. J. Hydrol. 2000, 239, 132–147. [Google Scholar] [CrossRef]
- Al-Fugara, A.; Ahmadlou, M.; Shatnawi, R.; AlAyyash, S.; Al-Adamat, R.; Al-Shabeeb, A.A.R.; Soni, S. Novel hybrid models combining meta-heuristic algorithms with support vector regression (SVR) for groundwater potential mapping. Geocarto Int. 2020. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Al-Fugara, A.; Ahmadlou, M.; Al-Shabeeb, A.R.; AlAyyash, S.; Al-Amoush, H.; Al-Adamat, R. Spatial mapping of groundwater springs potentiality using grid search-based and genetic algorithm-based support vector regression. Geocarto Int. 2020, 1–20. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Najah Ahmed, A.; Kisi, O.; El-Shafie, A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. J. Hydrol. 2020, 582, 124435. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266–267, 198–207. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B. Bin Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of landslide susceptibility using hybrid support vector regression (SVR) and the adaptive neuro-fuzzy inference system (ANFIS) with various metaheuristic algorithms. Sci. Total Environ. 2020, 741, 139937. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Statistics Korea. Complete Enumeration Results of the 2010 Population and Housing Census; Statistics Korea: Daejon, Korea, 2011. [Google Scholar]
- Ali, A.; Kim, K.Y. Seismic site conditions in Gangneung, Korea, based on Rayleigh-wave dispersion curves and topographic data. Geosci. J. 2016, 20, 781–791. [Google Scholar] [CrossRef]
- Kim, M.G.; Lee, Y. Il The stratigraphy and correlation of the upper Paleozoic Pyeongan Supergroup of southern Korean Peninsula—A review. J. Geol. Soc. Korea 2017, 53, 321–338. [Google Scholar] [CrossRef]
- Ministry for Food, Agriculture, Forestry and Fisheries. Rural Groundwater Survey Report (Gangneung-si); MFAFF: Seoul, Korea, 2010.
- Lee, S.; Hyun, Y.; Lee, S.; Lee, M.-J. Groundwater Potential Mapping Using Remote Sensing and GIS-Based Machine Learning Techniques. Remote Sens. 2020, 12, 1200. [Google Scholar] [CrossRef]
- Razack, M.; Huntley, D. Assessing Transmissivity from Specific Capacity in a Large and Heterogeneous Alluvial Aquifer. Ground Water 1991, 29, 856–861. [Google Scholar] [CrossRef]
- Arabameri, A.; Roy, J.; Saha, S.; Blaschke, T.; Ghorbanzadeh, O.; Tien Bui, D. Application of Probabilistic and Machine Learning Models for Groundwater Potentiality Mapping in Damghan Sedimentary Plain, Iran. Remote Sens. 2019, 11, 3015. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerdà, A.; Conoscenti, C.; Kalantari, Z. A comparison of statistical methods and multi-criteria decision making to map flood hazard susceptibility in Northern Iran. Sci. Total Environ. 2019, 660, 443–458. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Lerner, D.N.; Harris, B. The relationship between land use and groundwater resources and quality. Land Use policy 2009, 26, S265–S273. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Evaluating the relationship between topography and groundwater using outputs from a continental-scale integrated hydrology model. Water Resour. Res. 2015, 51, 6602–6621. [Google Scholar] [CrossRef]
- Duan, H.; Deng, Z.; Deng, F. Classification of groundwater potential in Chaoyang area based on QUEST algorithm. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; Institute of Electrical and Electronics Engineers Inc.: Pistacaway, NJ, USA, 2016; pp. 890–893. [Google Scholar]
- Serele, C.; Pérez-Hoyos, A.; Kayitakire, F. Mapping of groundwater potential zones in the drought-prone areas of south Madagascar using geospatial techniques. Geosci. Front. 2020, 11, 1403–1413. [Google Scholar] [CrossRef]
- Snowdon, A.P.; Sykes, J.F.; Normani, S.D. Topography scale effects on groundwater-surface water exchange fluxes in a Canadian Shield setting. J. Hydrol. 2020, 585, 124772. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M. Assessment of a data-driven evidential belief function model and GIS for groundwater potential mapping in the Koohrang Watershed, Iran. Geocarto Int. 2015, 30, 662–685. [Google Scholar] [CrossRef]
- Oikonomidis, D.; Dimogianni, S.; Kazakis, N.; Voudouris, K. A GIS/Remote Sensing-based methodology for groundwater potentiality assessment in Tirnavos area, Greece. J. Hydrol. 2015, 525, 197–208. [Google Scholar] [CrossRef]
- Preeja, K.R.; Joseph, S.; Thomas, J.; Vijith, H. Identification of Groundwater Potential Zones of a Tropical River Basin (Kerala, India) Using Remote Sensing and GIS Techniques. J. Indian Soc. Remote Sens. 2011, 39, 83–94. [Google Scholar] [CrossRef]
- Sørensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Kumar, P.K.D.; Gopinath, G.; Seralathan, P. Application of remote sensing and GIS for the demarcation of groundwater potential zones of a river basin in Kerala, southwest coast of India. Int. J. Remote Sens. 2007, 28, 5583–5601. [Google Scholar] [CrossRef]
- Das, S.; Pardeshi, S.D.; Kulkarni, P.P.; Doke, A. Extraction of lineaments from different azimuth angles using geospatial techniques: A case study of Pravara basin, Maharashtra, India. Arab. J. Geosci. 2018, 11, 1–13. [Google Scholar] [CrossRef]
- Singh, K.V.; Setia, R.; Sahoo, S.; Prasad, A.; Pateriya, B. Evaluation of NDWI and MNDWI for assessment of waterlogging by integrating digital elevation model and groundwater level. Geocarto Int. 2015, 30, 650–661. [Google Scholar] [CrossRef]
- Yeh, H.F.; Cheng, Y.S.; Lin, H.I.; Lee, C.H. Mapping groundwater recharge potential zone using a GIS approach in Hualian River, Taiwan. Sustain. Environ. Res. 2016, 26, 33–43. [Google Scholar] [CrossRef]
- Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping Groundwater Potential Using a Novel Hybrid Intelligence Approach. Water Resour. Manag. 2019, 33, 281–302. [Google Scholar] [CrossRef]
- Lee, S.; Hyun, Y.; Lee, M.-J. Groundwater Potential Mapping Using Data Mining Models of Big Data Analysis in Goyang-si, South Korea. Sustainability 2019, 11, 1678. [Google Scholar] [CrossRef]
- Nhu, V.H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Geertsema, M.; Kress, V.R.; Karimzadeh, S.; Kamran, K.V.; et al. Landslide detection and susceptibility modeling on cameron highlands (Malaysia): A comparison between random forest, logistic regression and logistic model tree algorithms. Forests 2020, 11, 830. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.-W. Application of Decision-Tree Model to Groundwater Productivity-Potential Mapping. Sustainability 2015, 7, 13416–13432. [Google Scholar] [CrossRef]
- Thapa, R.; Gupta, S.; Guin, S.; Kaur, H. Assessment of groundwater potential zones using multi-influencing factor (MIF) and GIS: A case study from Birbhum district, West Bengal. Appl. Water Sci. 2017, 7, 4117–4131. [Google Scholar] [CrossRef]
- Mandal, U.; Sahoo, S.; Munusamy, S.B.; Dhar, A.; Panda, S.N.; Kar, A.; Mishra, P.K. Delineation of Groundwater Potential Zones of Coastal Groundwater Basin Using Multi-Criteria Decision Making Technique. Water Resour. Manag. 2016, 30, 4293–4310. [Google Scholar] [CrossRef]
- Sander, P. Lineaments in groundwater exploration: A review of applications and limitations. Hydrogeol. J. 2007, 15, 71–74. [Google Scholar] [CrossRef]
- Benjmel, K.; Amraoui, F.; Boutaleb, S.; Ouchchen, M.; Tahiri, A.; Touab, A. Mapping of Groundwater Potential Zones in Crystalline Terrain Using Remote Sensing, GIS Techniques, and Multicriteria Data Analysis (Case of the Ighrem Region, Western Anti-Atlas, Morocco). Water 2020, 12, 471. [Google Scholar] [CrossRef]
- Hakim, W.; Achmad, A.; Lee, C.-W. Land Subsidence Susceptibility Mapping in Jakarta Using Functional and Meta-Ensemble Machine Learning Algorithm Based on Time-Series InSAR Data. Remote Sens. 2020, 12, 3627. [Google Scholar] [CrossRef]
- Pradhan, B.; Abokharima, M.H.; Jebur, M.N.; Tehrany, M.S. Land subsidence susceptibility mapping at Kinta Valley (Malaysia) using the evidential belief function model in GIS. Nat. Hazards 2014, 73, 1019–1042. [Google Scholar] [CrossRef]
- Moung-Jin, L.; Won-Kyong, S.; Joong-Sun, W.; Inhye, P.; Saro, L. Spatial and temporal change in landslide hazard by future climate change scenarios using probabilistic-based frequency ratio model. Geocarto Int. 2014, 29, 639–662. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Wu, W.; Zucca, C.; Muhaimeed, A.S.; Al-Shafie, W.M.; Fadhil Al-Quraishi, A.M.; Nangia, V.; Zhu, M.; Liu, G. Soil salinity prediction and mapping by machine learning regression in Central Mesopotamia, Iraq. Land Degrad. Dev. 2018, 29, 4005–4014. [Google Scholar] [CrossRef]
- Azeez, O.; Pradhan, B.; Shafri, H. Vehicular CO Emission Prediction Using Support Vector Regression Model and GIS. Sustainability 2018, 10, 3434. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid Modified Firefly Algorithm and Support Vector Regression model for accurate Short Term Load Forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S.; et al. Spatial prediction of landslide susceptibility using GIS-based data mining techniques of ANFIS with whale optimization algorithm (WOA) and grey wolf optimizer (GWO). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Pradhan, M.; Roy, P.K.; Pal, T. Oppositional based grey wolf optimization algorithm for economic dispatch problem of power system. Ain Shams Eng. J. 2018, 9, 2015–2025. [Google Scholar] [CrossRef]
- Soleimani, H.; Kannan, G. A hybrid particle swarm optimization and genetic algorithm for closed-loop supply chain network design in large-scale networks. Appl. Math. Model. 2015, 39, 3990–4012. [Google Scholar] [CrossRef]
- Tien Bui, D.; Bui, Q.T.; Nguyen, Q.P.; Pradhan, B.; Nampak, H.; Trinh, P.T. A hybrid artificial intelligence approach using GIS-based neural-fuzzy inference system and particle swarm optimization for forest fire susceptibility modeling at a tropical area. Agric. For. Meteorol. 2017, 233, 32–44. [Google Scholar] [CrossRef]
- Arabameri, A.; Nalivan, O.A.; Pal, S.C.; Chakrabortty, R.; Saha, A.; Lee, S.; Pradhan, B.; Bui, D.T. Novel machine learning approaches for modelling the gully erosion susceptibility. Remote Sens. 2020, 12, 2833. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Notti, D.; Mateos, R.M.; Monserrat, O.; Devanthéry, N.; Peinado, T.; Roldán, F.J.; Fernández-Chacón, F.; Galve, J.P.; Lamas, F.; Azañón, J.M. Lithological control of land subsidence induced by groundwater withdrawal in new urban AREAS (Granada Basin, SE Spain). Multiband DInSAR monitoring. Hydrol. Process. 2016, 30, 2317–2331. [Google Scholar] [CrossRef]
- Costall, A.R.; Harris, B.D.; Teo, B.; Schaa, R.; Wagner, F.M.; Pigois, J.P. Groundwater Throughflow and Seawater Intrusion in High Quality Coastal Aquifers. Sci. Rep. 2020, 10, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Jasechko, S.; Perrone, D.; Seybold, H.; Fan, Y.; Kirchner, J.W. Groundwater level observations in 250,000 coastal US wells reveal scope of potential seawater intrusion. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Hounsinou, S.P. Assessment of potential seawater intrusion in a coastal aquifer system at Abomey—Calavi, Benin. Heliyon 2020, 6, e03173. [Google Scholar] [CrossRef] [PubMed]
- Floris, M.; Fontana, A.; Tessari, G.; Mulè, M. Subsidence Zonation through Satellite Interferometry in Coastal Plain Environments of NE Italy: A Possible Tool for Geological and Geomorphological Mapping in Urban Areas. Remote Sens. 2019, 11, 165. [Google Scholar] [CrossRef]
- Maskooni, E.K.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R. Application of advanced machine learning algorithms to assess groundwater potential using remote sensing-derived data. Remote Sens. 2020, 12, 2742. [Google Scholar] [CrossRef]

| Factor | Class | Total % | Event % | Frequency Ratio |
|---|---|---|---|---|
| Elevation (m) | 0–100 | 9.88 | 52.72 | 5.34 |
| 100–222 | 10.47 | 21.74 | 2.08 | |
| 222–356 | 11.11 | 8.70 | 0.78 | |
| 356–495 | 9.92 | 5.98 | 0.60 | |
| 495–623 | 10.00 | 3.80 | 0.38 | |
| 623–735 | 9.90 | 1.09 | 0.11 | |
| 735–846 | 9.73 | 2.17 | 0.22 | |
| 846–968 | 9.83 | 3.26 | 0.33 | |
| 968–1119 | 9.71 | 0.00 | 0.00 | |
| >1119 | 9.54 | 0.54 | 0.06 | |
| Slope (degrees) | 0–3.95 | 10.66 | 51.09 | 4.79 |
| 3.95–9.64 | 10.02 | 30.43 | 3.04 | |
| 9.64–14.84 | 10.15 | 11.41 | 1.12 | |
| 14.84–19.29 | 9.94 | 4.89 | 0.49 | |
| 19.29–23.50 | 9.89 | 1.09 | 0.11 | |
| 23.50–27.46 | 9.95 | 0.54 | 0.05 | |
| 27.46–31.17 | 10.02 | 0.54 | 0.05 | |
| 31.17–34.88 | 9.79 | 0.00 | 0.00 | |
| 34.88–39.34 | 9.85 | 0.00 | 0.00 | |
| >39.34 | 9.74 | 0.00 | 0.00 | |
| Slope height (m) | 0–6.37 | 9.99 | 24.46 | 2.45 |
| 6.37–10.61 | 10.00 | 15.76 | 1.58 | |
| 10.61–12.74 | 10.00 | 25.00 | 2.50 | |
| 12.74–14.86 | 10.00 | 30.43 | 3.04 | |
| 14.86–23.36 | 10.00 | 3.26 | 0.33 | |
| 23.36–33.98 | 10.00 | 0.54 | 0.05 | |
| 33.98–48.85 | 10.00 | 0.00 | 0.00 | |
| 48.85–70.09 | 10.00 | 0.54 | 0.05 | |
| 70.09–108.32 | 10.00 | 0.00 | 0.00 | |
| >108.32 | 10.00 | 0.00 | 0.00 | |
| TWI | 1.65–4.74 | 10.00 | 0.00 | 0.00 |
| 4.74–5.14 | 10.00 | 0.00 | 0.00 | |
| 5.14–5.54 | 10.00 | 0.00 | 0.00 | |
| 5.54–6.04 | 10.00 | 1.09 | 0.11 | |
| 6.04–6.74 | 10.00 | 2.17 | 0.22 | |
| 6.74–7.64 | 10.00 | 5.98 | 0.60 | |
| 7.64–9.24 | 10.00 | 6.52 | 0.65 | |
| 9.24–12.53 | 10.00 | 12.50 | 1.25 | |
| 12.53–13.93 | 10.00 | 28.26 | 2.83 | |
| 13.93–27.21 | 10.00 | 43.48 | 4.35 | |
| LS-factor | 0–3.59 | 10.66 | 51.09 | 4.79 |
| 3.59–7.18 | 9.94 | 25.54 | 2.57 | |
| 7.18–10.78 | 9.93 | 10.33 | 1.04 | |
| 10.78–14.37 | 9.93 | 5.98 | 0.60 | |
| 14.37–17.97 | 9.93 | 3.26 | 0.33 | |
| 17.97–21.56 | 9.93 | 1.09 | 0.11 | |
| 21.56–26.36 | 9.92 | 1.63 | 0.16 | |
| 26.36–32.25 | 9.92 | 0.54 | 0.05 | |
| 32.35–38.73 | 9.92 | 0.00 | 0.00 | |
| >38.73 | 9.92 | 0.54 | 0.05 | |
| Precipitation (mm/year) | 1198–1245 | 4.30 | 0.00 | 0.00 |
| 1245–1275 | 6.96 | 2.72 | 0.39 | |
| 1275–1294 | 6.23 | 7.61 | 1.22 | |
| 1294–1309 | 9.37 | 6.52 | 0.70 | |
| 1309–1322 | 12.12 | 4.89 | 0.40 | |
| 1322–1335 | 14.84 | 5.98 | 0.40 | |
| 1335–1350 | 13.31 | 6.52 | 0.49 | |
| 1350–1367 | 12.30 | 14.67 | 1.19 | |
| 1367–1383 | 13.47 | 30.43 | 2.26 | |
| 1383–1410 | 7.10 | 20.65 | 2.91 | |
| Water density (km/km2) | 0 | 14.10 | 8.15 | 0.58 |
| 0–1.58 | 9.54 | 5.98 | 0.63 | |
| 1.58–2.77 | 9.54 | 4.89 | 0.51 | |
| 2.77–3.96 | 9.54 | 5.43 | 0.57 | |
| 3.96–5.15 | 9.54 | 6.52 | 0.68 | |
| 5.15–6.34 | 9.55 | 11.41 | 1.20 | |
| 6.34–7.52 | 9.55 | 8.70 | 0.91 | |
| 7.52–9.11 | 9.55 | 8.70 | 0.91 | |
| 9.11–11.49 | 9.55 | 13.59 | 1.42 | |
| >11.49 | 9.54 | 26.63 | 2.79 | |
| NDWI | −0.57–−0.04 | 10.00 | 37.50 | 3.75 |
| −0.04–0.02 | 10.00 | 29.89 | 2.99 | |
| 0.02–0.08 | 10.00 | 13.04 | 1.30 | |
| 0.08–0.15 | 10.00 | 8.15 | 0.82 | |
| 0.15–0.23 | 10.00 | 4.89 | 0.49 | |
| 0.23–0.32 | 10.00 | 3.26 | 0.33 | |
| 0.32–0.41 | 10.00 | 1.09 | 0.11 | |
| 0.41–0.5 | 10.00 | 1.09 | 0.11 | |
| 0.5–0.61 | 10.01 | 0.54 | 0.05 | |
| >0.61 | 10.01 | 0.54 | 0.05 | |
| Land use | Urban | 3.61 | 21.58 | 5.98 |
| Agricultural | 11.95 | 57.55 | 4.82 | |
| Forest | 78.19 | 11.87 | 0.15 | |
| Grassland | 3.28 | 4.68 | 1.42 | |
| Marsh | 0.29 | 0.72 | 2.51 | |
| Water body | 1.52 | 2.52 | 1.65 | |
| Bare ground | 1.16 | 1.08 | 0.93 | |
| Soil type | Common paddy | 0.60 | 6.52 | 10.81 |
| Immature paddy | 0.35 | 4.89 | 13.91 | |
| Sandy paddy | 3.85 | 26.09 | 6.78 | |
| Wet paddy | 2.48 | 11.41 | 4.60 | |
| Common field | 5.24 | 23.37 | 4.46 | |
| Immature field | 1.80 | 3.80 | 2.11 | |
| Sandy field | 1.25 | 2.72 | 2.17 | |
| Red/yellow forest soil | 1.04 | 2.17 | 2.10 | |
| Volcanic ash soil | 2.22 | 3.26 | 1.47 | |
| Rock/soil | 78.97 | 13.59 | 0.17 | |
| Other | 2.20 | 2.17 | 0.99 | |
| Lithology | Alluvium | 5.82 | 28.06 | 4.82 |
| Biotite granite | 0.10 | 0.00 | 0.00 | |
| Dyke | 0.01 | 0.00 | 0.00 | |
| Gneiss | 4.35 | 0.00 | 0.00 | |
| Granite | 54.83 | 43.88 | 0.80 | |
| Limestone | 17.89 | 3.60 | 0.20 | |
| Sedimentary rock | 16.34 | 24.46 | 1.50 | |
| Water | 0.66 | 0.00 | 0.00 | |
| Lineament density (km/km2) | 0.10–0.17 | 99.62 | 242.11 | 2.43 |
| 0.17–0.19 | 100.57 | 173.68 | 1.73 | |
| 0.19–0.22 | 100.64 | 100.00 | 0.99 | |
| 0.22–0.24 | 100.66 | 89.47 | 0.89 | |
| 0.24–0.26 | 100.66 | 68.42 | 0.68 | |
| 0.26–0.27 | 100.65 | 42.11 | 0.42 | |
| 0.27–0.29 | 100.66 | 36.84 | 0.37 | |
| 0.29–0.31 | 100.63 | 60.82 | 0.60 | |
| 0.31–0.34 | 100.67 | 81.29 | 0.81 | |
| >0.34 | 100.67 | 73.68 | 0.73 | |
| Distance to fault (m) | 0 | 10.05 | 6.52 | 0.65 |
| 0–1052 | 10.02 | 8.15 | 0.81 | |
| 1052–2104 | 10.00 | 7.07 | 0.71 | |
| 2104–3156 | 10.00 | 5.43 | 0.54 | |
| 3156–4208 | 10.00 | 9.24 | 0.92 | |
| 4208–5260 | 9.99 | 12.50 | 1.25 | |
| 5260–6838 | 10.00 | 6.52 | 0.65 | |
| 6838–8942 | 9.99 | 11.41 | 1.14 | |
| 8942–12,624 | 10.00 | 14.67 | 1.47 | |
| >12,624 | 9.96 | 18.48 | 1.86 |
| Factors | Mapping Accuracy Values (%) | |||||
|---|---|---|---|---|---|---|
| SVR | Variation | SVR_GWO | Variation | SVR_PSO | Variation | |
| All factors | 0.803 | 0.878 | 0.814 | |||
| Elevation | 0.8 | –0.3 | 0.866 | –1.2 | 0.803 | –1.1 |
| Slope | 0.783 | –2 | 0.872 | –0.6 | 0.805 | –0.9 |
| Slope height | 0.788 | –0.5 | 0.872 | –0.6 | 0.807 | –0.7 |
| TWI | 0.788 | –0.5 | 0.878 | 0 | 0.81 | –0.4 |
| LS | 0.782 | –2.1 | 0.877 | –0.2 | 0.808 | –0.6 |
| Precipitation | 0.807 | 0.4 | 0.882 | 0.3 | 0.82 | 0.6 |
| Water density | 0.788 | –0.5 | 0.879 | 0.1 | 0.808 | –0.6 |
| NDWI | 0.792 | –1.1 | 0.866 | –1.3 | 0.797 | –1.7 |
| Land use | 0.752 | –5.1 | 0.87 | –0.9 | 0.811 | –0.3 |
| Soil type | 0.777 | –2.6 | 0.865 | –1.3 | 0.804 | –1 |
| Lithology | 0.78 | –2.3 | 0.871 | –0.7 | 0.8 | –1.4 |
| Lineament Density | 0.782 | –2.1 | 0.874 | –0.4 | 0.807 | –0.7 |
| Distance to fault | 0.806 | 0.3 | 0.878 | 0 | 0.815 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fadhillah, M.F.; Lee, S.; Lee, C.-W.; Park, Y.-C. Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea. Remote Sens. 2021, 13, 1196. https://doi.org/10.3390/rs13061196
Fadhillah MF, Lee S, Lee C-W, Park Y-C. Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea. Remote Sensing. 2021; 13(6):1196. https://doi.org/10.3390/rs13061196
Chicago/Turabian StyleFadhillah, Muhammad Fulki, Saro Lee, Chang-Wook Lee, and Yu-Chul Park. 2021. "Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea" Remote Sensing 13, no. 6: 1196. https://doi.org/10.3390/rs13061196
APA StyleFadhillah, M. F., Lee, S., Lee, C.-W., & Park, Y.-C. (2021). Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea. Remote Sensing, 13(6), 1196. https://doi.org/10.3390/rs13061196










