Abstract
Deep convolutional neural networks (CNNs) are widely used in hyperspectral image (HSI) classification. However, the most successful CNN architectures are handcrafted, which need professional knowledge and consume a very significant amount of time. To automatically design cell-based CNN architectures for HSI classification, we propose an efficient continuous evolutionary method, named CPSO-Net, which can dramatically accelerate optimal architecture generation by the optimization of weight-sharing parameters. First, a SuperNet with all candidate operations is maintained to share the parameters for all individuals and optimized by collecting the gradients of all individuals in the population. Second, a novel direct encoding strategy is devised to encode architectures into particles, which inherit the parameters from the SuperNet. Then, particle swarm optimization is used to search for the optimal deep architecture from the particle swarm. Furthermore, experiments with limited training samples based on four widely used biased and unbiased hyperspectral datasets showed that our proposed method achieves good performance comparable to the state-of-the-art HSI classification methods.
1. Introduction
A hyperspectral image (HSI) has a high spectral and spatial resolution, which provides rich information about ground truths [1]. Hyperspectral sensors mounted on different space platforms, i.e., imaging spectrometers, are used to capture images in the ultraviolet, visible, near-infrared, and mid-infrared regions of the electromagnetic spectrum, where tens to hundreds of continuous and subdivided spectral bands simultaneously image the target area. The exploitation of HSI signatures is a powerful tool for observing the surface of the Earth. Therefore, there are a wide range of processing techniques to explore HSI data [2,3,4], and HSI classification is one of the most popular techniques for HSI data exploitation. HSI classification is widely applied in many fields, such as agricultural applications [5], forestry and environmental management [6], water and maritime resource management [7], and military and defense applications [8].
Compared to traditional HSI classification algorithms, convolutional neural networks (CNNs) can not only explore spectral information, but can also combine spatial information with spectral information [9]. Moreover, because of the share of parameters to tackle the curse of dimensionality [10] and the local receptive field to learn spatial information [11], CNNs show good performance in HSI band selection [12,13], feature extraction and classification [14]. There are many CNN models used as HSI classifiers, including the spectral CNN [15,16], the spatial CNN [17,18], and the spectral–spatial CNN [19,20]. With the advance of remote sensing technology, better classifiers are being developed to further improve the classification performance and the complexity of CNNs. On the one hand, some new types of CNNs have been introduced for HSI classification, such as the dense CNN using shortcut connections between layers [21] and the deep residual network with skip connections [22]. On the other hand, some other techniques have been combined with CNNs, such as the attention mechanism [23], sparse representation [24], multi-scale fusion [25], and discriminant embedding [26].
Although the aforementioned CNN models have achieved remarkable progress in HSI classification tasks in recent years, there are two major problems that should be considered when applying these CNN models for HSI classification. On the one hand, designing state-of-the-art successful CNN architectures requires substantial professional knowledge of human experts and consume a significant amount of time for repeated debugging. For example, ResNet [27] and DesNet [21] were carefully handcrafted by taking into consideration the manual domain knowledge. On the other hand, manually optimizing a CNN when applying it to different data sources may take days or even weeks and should always be fine-tuned; additionally, this process results in a heavy computational burden, and is not affordable for most researchers and developers [28].
To overcome the problems of handcrafting CNN models, neural architecture search (NAS) [29] is an import method to automatically design neural architectures. Since Zoph et al. [30] successfully discovered a neural network architecture that can achieve comparable performance to handcrafted CNNs, there has been a growing interest in designing a robust and well-performing neural architecture from the predefined search space by NAS. There are many different search strategies that can be used to design a proper CNN architecture, including evolutionary algorithms (EAs), reinforcement learning (RL), and gradient-based methods. Recently, Chen et al. [31] proposed the automatic design of CNNs for HSI classification, based on the gradient descent method, and the automatic CNNs achieved better performance compared to some state-of-the-art deep learning methods. However, the method based on gradient descent easily converges to the local optimal, and it cannot be used when there is a vanishing gradient problem or an exploding gradient problem. EAs search globally, and population-based optimization affords EAs a very good global search ability. To address the NAS problem, a global search technique is required, which has always been a topic of interest for discovering the neural architecture by the EA search strategy. Junior et al. [32] found good chain CNN architectures based on the particle swarm optimization (PSO) search strategy using nine datasets, which can only search simple chain-CNNs. Real et al. [33] proposed AmoebaNet-A and found comparable cell-based neural architectures to some state-of-the-art ImageNet models using the CIFAR-10 dataset, showing that they consumed a significant time without weight-sharing. An alternative architecture optimization method is neuroevolution, which is inspired by the evolution of natural brains. Stanley et al. [34] proposed a classic neuroevolutionary approach, NEAT, Neural Networks through Augmenting Topologieswhich can modify weights and add nodes and connections in neural networks. HyperNEAT [35,36] is an improvement of NEAT, which uses an indirect encoding method named CPPNs [37] that can generate the patterns of weights in neural networks themselves to evolve into bigger network.
To automatically search for CNN architectures for HSI classification, we propose an NAS method named PSO-Net, which is based on PSO and consumes a significant amount of time to search for the optimal architecture. To further accelerate optimal architecture generation, we propose CPSO-Net with weight-sharing parameter optimization based on PSO-Net. We propose two cell-based CNN architecture search methods by PSO, capable of searching globally, compared to the gradient descent method. The main contributions of this paper are summarized as follows:
- (1)
- Two methods based on PSO are explored to automatically design the CNN architecture for HSI classification.
- (2)
- A novel encoding strategy is devised that can be used to encode architectures into arrays with the information of the connections and basic operations types between the nodes in computation cells.
- (3)
- To improve the search efficiency, CPSO-Net maintains continuous SuperNet sharing parameters for all particles and optimizes by collecting the gradients of all individuals in the population.
- (4)
- PSO-Net and CPSO-Net are tested on four biased and unbiased hyperspectral datasets with limited training samples, showing comparable performance to the state-of-the-art CNN classification methods.
The remainder of this paper is structured as follows. Detailed related work about neural architecture search and PSO is presented in Section 2. Section 3 introduces the proposed PSO-Net and CPSO-Net in detail. Section 4 summarizes and analyzes a series of experiments performed for HSI classification. Section 5 provides the main conclusions and perspectives of this work.
2. Related Work
In this section, we introduce two methods related to the method we proposed, namely neural architecture search and particle swarm optimization.
2.1. Neural Architecture Search
NAS aims to design a well-performing neural network architecture by selecting and combining basic operations and connections from a predefined search space.
There are three main parts in NAS, namely the search space, the search strategy, and the performance estimation strategy. The search space is a set of all possible architectures. The search strategy then automatically finds the optimal architecture from the search space. The estimation of performance aims to find the architectures with high predictive performance by training and validation based on data.
The search space should be predefined with the information of all basic operations and connection nodes. The search space mainly includes two types. The first is to directly construct the global search space of the entire neural network architecture, including the chain architecture search space [38] and the multi-branch architecture search space [30]; the second is to construct parts of the neural network architecture by repeating certain specific structures, such as the cell-based search space [39].
The search strategy contains gradient-based search and RL- and EA-based approaches. Gradient-based approaches [40,41,42] convert the discrete architecture space into a continuous space and find the optimal architecture using the gradient method in the continuous space. RL-based methods [30,39] set the state–action space as the NAS search space and set the policy function as the recurrent network to finish the search process. The validation accuracy of each individual is used as the fitness to evolve the next generation. In EA-based approaches [43,44], the population is composed of a group of candidate network structures, and individuals generate new network architectures through evolutionary algorithms. To improve the search efficiency of EA-based approaches, Yang et al. [45] maintained a SuperNet that is trained by the gradient descent method and shares parameters for all architectures.
The core of the estimation of performance is the weight parameter optimization step, which can be divided into two categories, namely individual and weight-sharing optimization. Individual weight parameter optimization often learns each network separately, typically incurring a heavy computational burden and taking a significant amount of time. Therefore, weight-sharing parameter optimization methods are used to accelerate training [43,46], which can be divided into two categories according to the search strategies, i.e., weight-sharing heuristic search strategies and weight-sharing differentiable search strategies. Weight-sharing heuristic search strategies [47,48] always train one SuperNet that includes all candidate operations first, and then focuses on each individual inherit parameter from the SuperNet. Rather than training all individuals, the SuperNet is optimized only once during one iteration, which dramatically reduces the computational complexity by separately learning each network. Weight-sharing differentiable search strategies [40] relax one architecture to one SuperNet, with the weights of all candidate operations being optimized by the gradient descent method.
2.2. Particle Swarm Optimization
PSO is a kind of evolutionary computation, which is derived from research on the predation behavior of birds [49]. The main idea of particle swarm optimization is to find the optimal solution through the cooperation and information-sharing among individuals from the swarm. In PSO, each candidate solution can be thought of as a bird in the solution space, which is called a particle. The optimal solution of itself in the past is the , and the current global optimal solution in the swarm is the . At every iteration, particles update themselves by tracking two extremes: and . Each particle is updated according to the following rule of PSO:
where is the velocity of the i-th particle, is the current particle position of the i-th particle, w is a constant called momentum that controls how much the previous velocity affects the velocity at the current time step, , and are yjr constants defined beforehand, representing the weight of yjr particles approaching the and , and and are random numbers in [0, 1).
One of the positive characteristics of PSO is that it is capable of fast convergence [50] when compared to other evolutionary approaches, such as genetic algorithms. Due to the fact that searching CNNs takes a lot time, even on the most powerful computers, a faster converging characteristic can have a positive impact in terms of obtaining the optimal CNN architecture.
3. Proposed Method
In this section, we propose a cell-based CNN architecture search method by particle swarm optimization at first, named PSO-Net. To make the search stage more efficient and to reduce the time consumed, we developed another novel continuous PSO approach for searching neural architectures, namely CPSO-Net.
The two proposed methods are all based on the PSO architecture search step, including four procedures to search for the optimal CNN architecture: Construction of the search space, initialization of the architectures, weight optimization of the neural network constructed by the architectures, fitness evaluation of the individual particles, and particle update. CPSO-Net is an improvement based on PSO-Net, and the two methods have different procedures for the parameter optimization of architectures. The weight optimization of the former is the individual weight optimization of all particles, and the latter is weight-sharing by the inherited weights from the SuperNet.
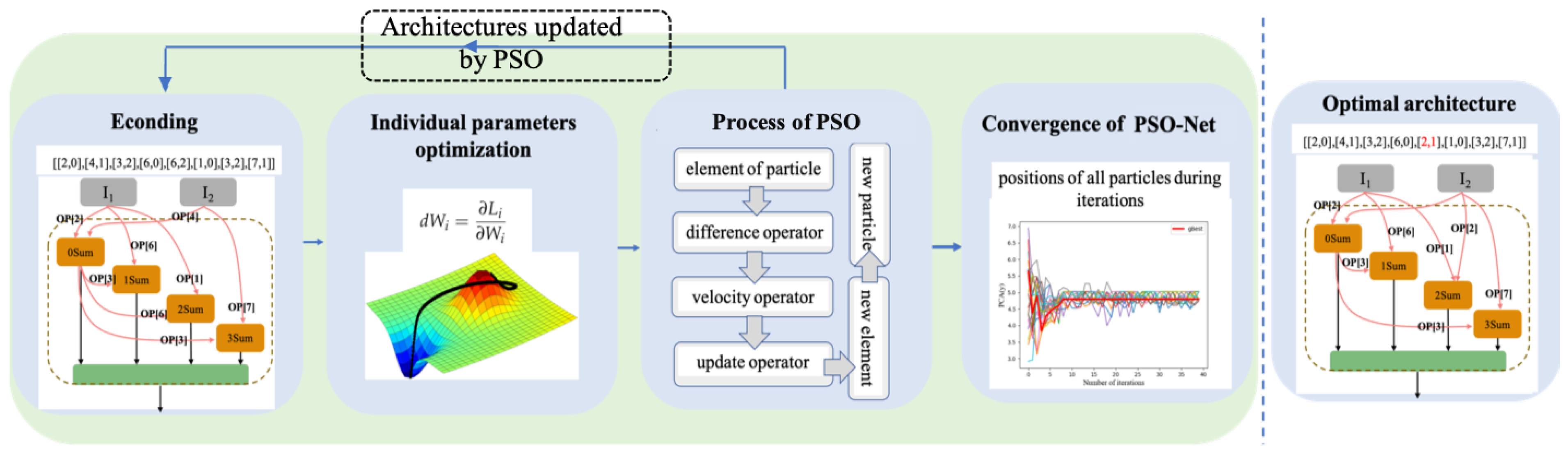
Figure 1 shows the framework of the stages of PSO-Net. From the framework, one can see that network architectures are encoded into arrays. Then, the gradient descent method is used separately to obtain the weight parameters for all architectures, and PSO is used as the architecture search method to optimize the architectures by the fitness of all particles. Finally, the optimal architecture is found after reaching the number of iterations.
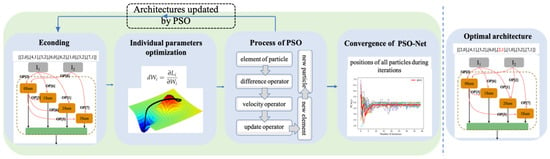
Figure 1.
Framework of the stages of particle swarm optimization PSO-Net. The constructed network architectures from the search space are encoded into arrays, and populations are initialized. The gradient descent method is used to obtain the weight parameters for all architectures separately, and PSO is used to optimize the architectures and to search for the optimal architecture until reaching the number of iterations. The output is the optimal architecture.
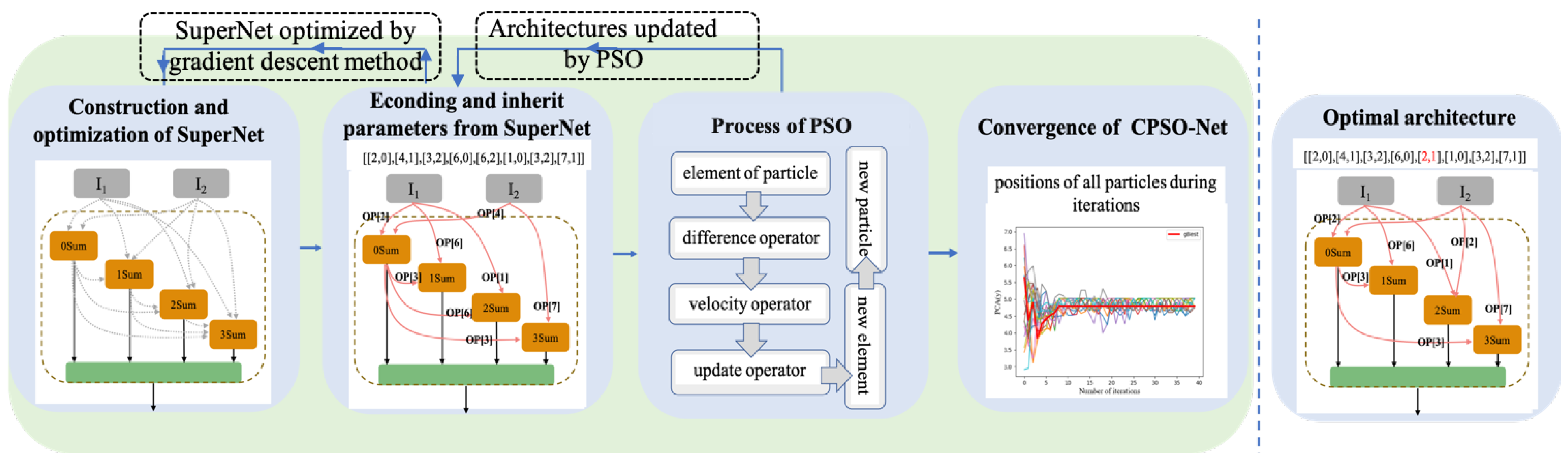
Figure 2 shows the framework of the stages of CPSO-Net, which is proposed-based PSO-Net. The main difference of Figure 2 is the procedure of the parameter optimization of architectures. To accelerate the optimal architecture generation, a SuperNet is maintained to share the parameters for all particles and is optimized by collecting the gradients of all individuals in the population. Rather than training all the individuals of PSO-Net, the SuperNet of CPSO-Net is optimized only once during one iteration, which dramatically reduces the computational complexity by separately learning each network.
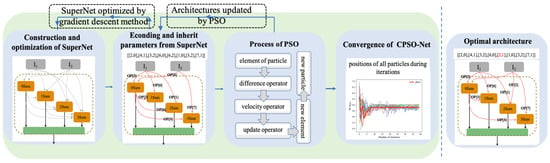
Figure 2.
Framework of CPSO-Net. A continuous SuperNet that contains all candidate operations and can be trained by gradient descent is maintained first. Then, all architectures are encoded into an array, inheriting the parameters from the SuperNet, and search for the optimal architecture by PSO. Finally, the optimal architecture is found.
All the operations of PSO-Net and CPSO-Net are detailed in the following subsections.
3.1. Construction of the Search Space
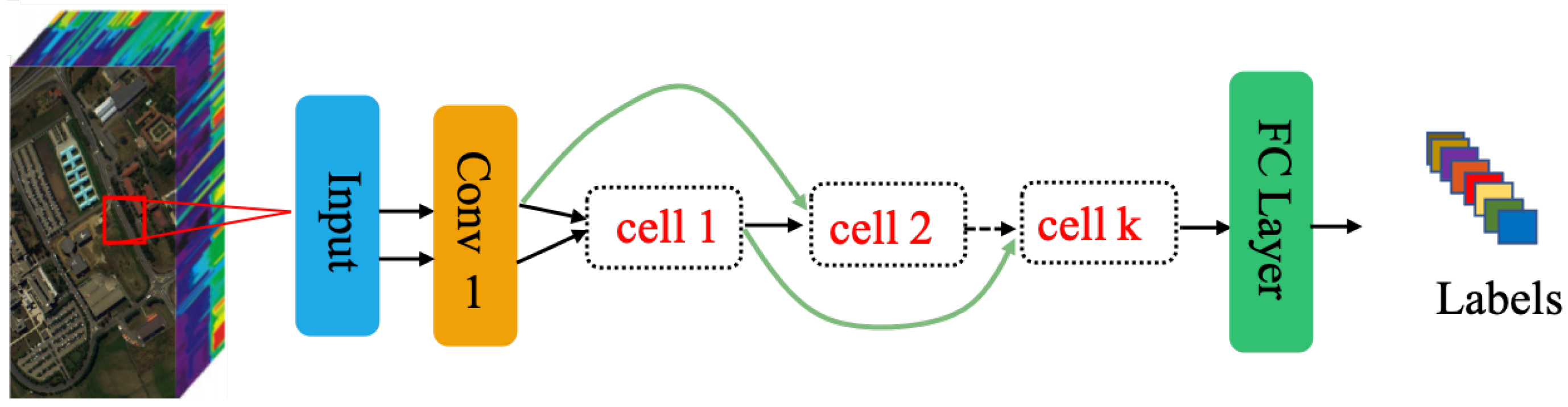
The search space contains two parts, namely all candidate basic operations and connection nodes. On the one hand, there are three main basic operation types: Convolution operations, pooling operations, and nonlinear operations. All candidate basic operations are placed into the operations list named to prepare for the next encoding strategy. On the other hand, the cell-based search space is used to design CNN architectures in the algorithm we proposed. Each neural network architecture is built by stacking two types of k number computation cells, which includes normal cells and one reduction cell. Each cell consists of an ordered sequence with two input nodes, n intermediate nodes, and one output node. The input of the input nodes are the cell outputs in the previous two cells, and the output of the cell is a cascade by the n intermediate nodes, each of which is calculated by the sum of two computations. Additionally, each computation is based on a random one operation of the basic operations computing on a random one node of its previous nodes. Each computation is defined as an element, which is composed of the basic operation and the computed node. Therefore, there are 2n elements in each cell with n intermediate nodes. Figure 3 shows the general architecture stacking by the automatically designed computation cells by PSO-Net and CPSO-Net.
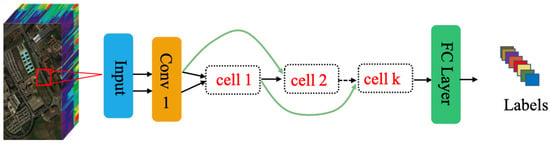
Figure 3.
The general architecture stacking by the automatically designed computation cells by PSO-Net and CPSO-Net. The bottleneck convolution layer and the fully connected layer in Figure 3 are designed for data preprocessing and classification with human knowledge.
3.2. Initialization of the Swarm
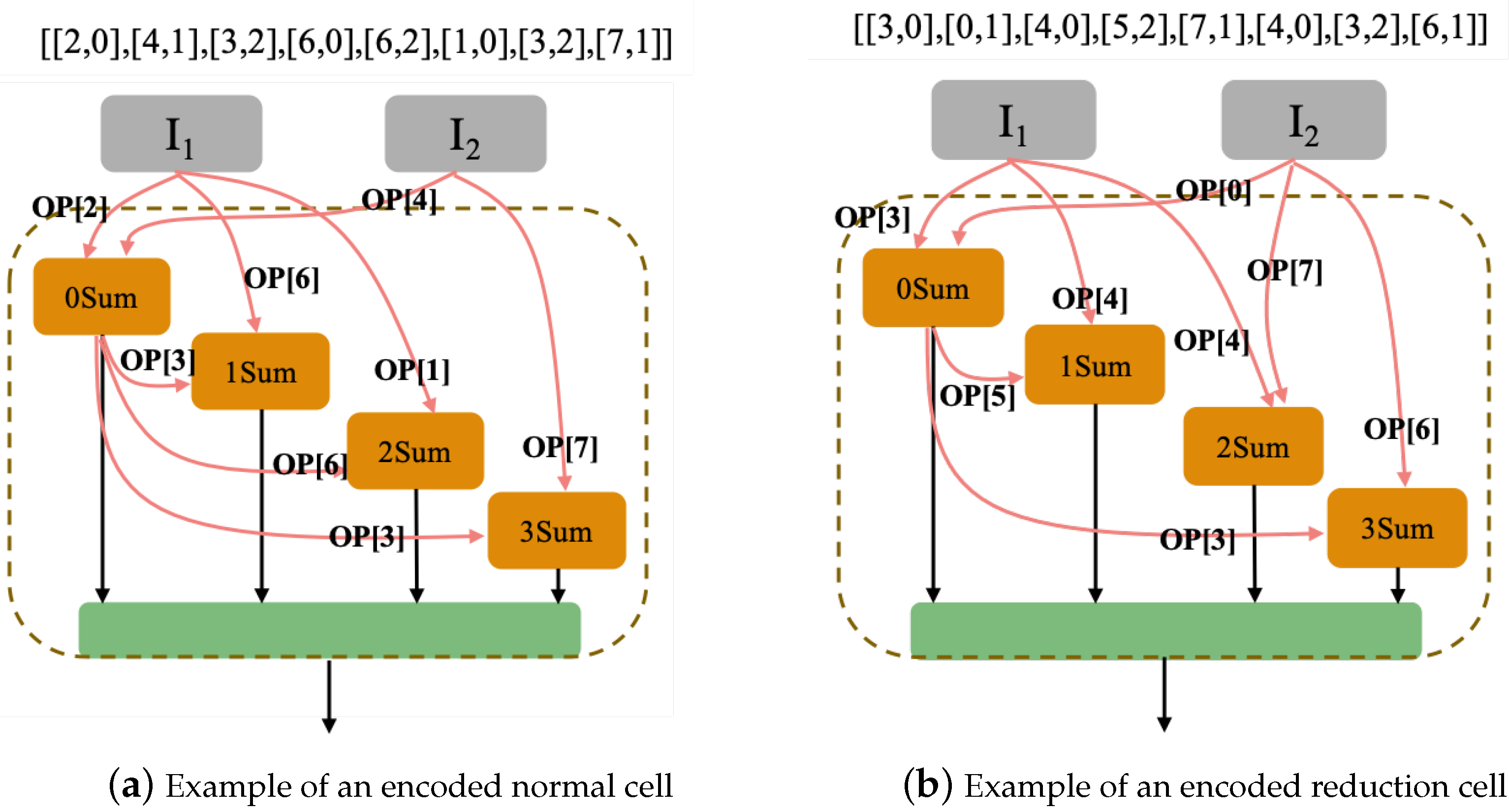
Particle encoding is the core of the initialization of architectures. A novel encoding strategy was devised that can be used to encode architectures into arrays with the information of all of the basic operations and connections between the nodes in computation cells—where the first and second input node is numbered the 0th and 1th in all nodes, and the n intermediate nodes are numbered in cells successively following the number of two input nodes. First, an array with a shape of (2, 2n, 2) is built, which represents an architecture. The first dimension of the array represents two types of computation cells, namely normal cells and reduction cells. The second dimension of the array represents the 2n elements (defined in Section 3.1) in each cell with n intermediate nodes. The third dimension of the array is composed of the index of basic operations list and the computed node. Next, P particles of the swarm are initialized by the above encoding strategy. Figure 4 shows an example of an encoded architecture, including an encoded normal cell and a reduction cell with four intermediate nodes.
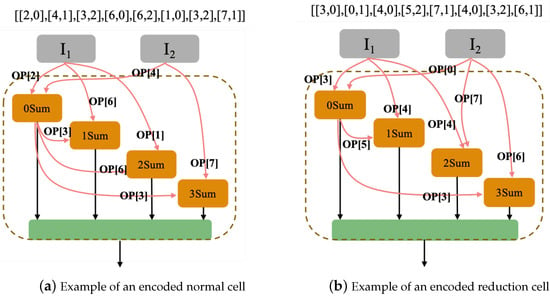
Figure 4.
An example of an encoded architecture, including an encoded normal cell and a reduction cell with four intermediate nodes. There are eight elements in each cell with four intermediate nodes. (a) An example of an encoded normal cell. The 0th intermediate node, as well the 2th node in the cell, are calculated by the sum of two elements [2] computed based on the 0th node in the cell and [4] computed based on the 1th node in the cell, where the 0th and 1th nodes in the cell are the two input nodes. All the remaining intermediate nodes are encoded into arrays in the same way. (b) An example of an encoded reduction cell.
3.3. The Weight Optimization of the Neural Network Constructed by Architectures
The weight of the neural network constructed by architectures should be optimized, when receiving information of the connection and basic operation type between the nodes in computation cells.
3.3.1. Individual Parameter Optimization of PSO-Net
The parameter optimization of PSO-Net involves training individual particles by the gradient descent method. Each network we searched can be represented by the particle P and a set of full precision parameters , where P is the population size. The training dataset X is denoted as the input data, and is the prediction of the i-th network . The loss can be expressed as , where is the criterion and Y is the target. The parameter of can be optimized by:
3.3.2. Weight-Sharing Parameter Optimization of CPSO-Net
To further accelerate optimal network generation, we built a SuperNet that includes all candidate operations and sharing parameters W for all particles. Each particle is regarded as a subnet and inherits the weight parameters from the fixed SuperNet, which can be optimized by the gradient descent method. Therefore, there is no need to train each particle from the beginning to the end, and the search time can therefore be greatly reduced. After the parameters have converged, the architecture could alternately be optimized by the PSO algorithm.
Sampling from the SuperNet , the different network is a part of , and the parameter W of can be inherited from W. Therefore, W can be represent as , where ⊙ is the mask operation that retains the parameters of the corresponding nodes of particle . Therefore, the gradient of also can be calculated as:
The SuperNet shares W for all different architectures, so the gradient of parameter W should be calculated by collecting the gradients of all individuals in the population:
Inspired by the mini-batch samples idea of stochastic gradient descent for updating parameters, we used mini-batch architectures to accumulate the gradients of all individuals for updating the shared weight W.
3.4. Fitness Evaluation
Fitness evaluation is performed using the HSI classification accuracy of the optimized neural network on the validation set, and aimed to estimate the performance of the architectures. Each particle is evaluated as a solution by the fitness evaluation function. Its optimal solution in the past is the , and the current global optimal solution in the swarm is the . By the fitness of PSO-Net and CPSO-Net, we can find the and .
3.5. Particle Update
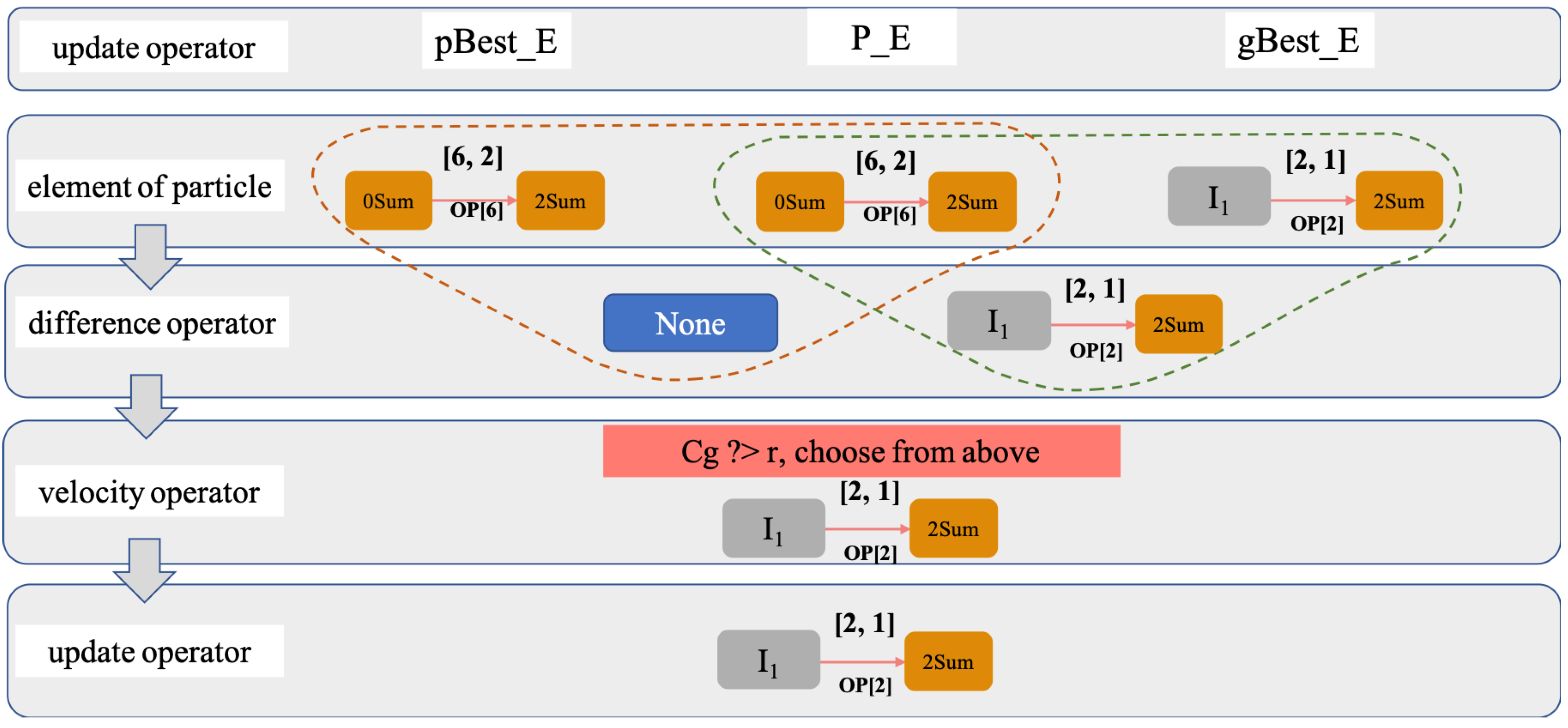
The difference and the velocity operator are devised based on PSO to update the particles. The particle P is updated element by element until all elements of the particle have been updated, so the particle update problem is transformed into the element update problem. Before being able to update an element, the difference between two elements with the same index in two particles needs to be measured, and the velocity of the element needs to be computed.
The difference is calculated by comparing and . If both elements are the same, the difference is “None”, which means no difference. If the two elements are different, the result of is .
The velocity of any given element of a particle is based on the two differences: and , where , , and P have the same index in a particle. Each element velocity is chosen from the two differences based on the decision factor and a number r obtained at random from [0,1). If , the algorithm selects from the difference . Otherwise, the algorithm selects from the difference .
Each element is updated according to its element velocity. If its element velocity is “None”, the element remains the same, otherwise it should be displaced by its velocity. Particles are modified element by element according to the element velocity. Figure 5 shows the update of an element of a particle.
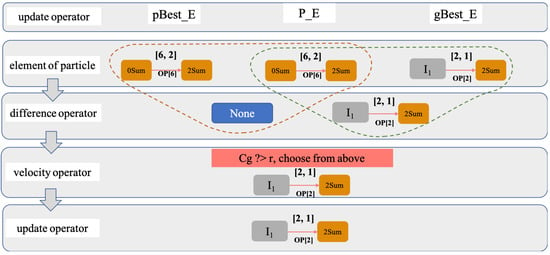
Figure 5.
The update process for an element in a particle. This example shows an update of an element of the intermediate node. Before being able to update the element of a particle, the difference between or by the different, and the velocity of the element needs to be computed using the velocity operator.
The essence of the role of a particle update is that a particle update can be converted to an element update in the particle. We assumed that the elements of and can obtain good fitness, so that and can achieve good fitness. Therefore, we compared P to and element by element, and determined whether the element P needs to be replaced by or . Figure 4 shows the update process of particles.
4. Experimental Results and Analysis
In this section, we explain the experimental setting of the method proposed and a comparative algorithm, followed by the empirical results, to confirm the effectiveness of the proposed method for automatically designing CNNs for HSI classification based on four HSI datasets with biased and unbiased data. The experimental conditions were as follows: A NVIDIA GTX1080 Ti GPU, a E5-2620 CPU, and a memory of 32 GB.
4.1. Datasets
In this section, we used four standard hyperspectral datasets to evaluate the methods we proposed. As shown in Table 1, the four datasets were Salinas Valley in California in the USA (Salinas), a mixed vegetation site over the Indian Pines test area in northwestern Indiana in the USA (Indian Pines), an urban site over the University of Pavia in Italy (Pavia), and the Kennedy Space Center (KSC) in Florida in the USA. The detailed training samples of each class are shown in Table 1.

Table 1.
Number of samples in the Salinas Valley (Salinas), Indian Pines, University of Pavia (Pavia), and Kennedy Space Center (KSC) hyperspectral datasets.
The first dataset, Salinas, was collected by the Airborne Visible Infrared Imaging Spectrometer (AVIRIS) with 224-band over Salinas Valley, California, which is of a high spatial resolution (3.7 m/pixels). The available dataset consists of 204 bands with pixels after discarding the 20 water absorption bands and the 16 land cover classes.
The second dataset, Indian Pines, was captured by the AVIRIS sensor with 220-band over the Indian Pines test area. The available dataset consists of 200 bands with pixels after removing the water absorption bands. The ground reference map covers 16 classes of interest.
The third dataset, University of Pavia, was collected by the ROSIS-3 sensor with 115-band over the University of Pavia, which is of a high spatial resolution (1.3 m/pixels) to avoid mixed pixels. The available dataset consists of 103 bands with pixel vectors after removing the noisy bands. The ground reference map covers nine classes of interest.
The fourth dataset, KSC, was captured by the airborne AVIRIS sensor over KSC, Florida, at an altitude of approximately 20 km with a spatial resolution of 18 m. The available dataset consists of 176 bands with pixels after removing the water absorption and noisy bands. The ground reference map covers 13 classes of interest.
4.2. Comparative Experiment
To evaluate the performance of the two methods we proposed, some CNN classification methods, including handcrafted CNN models and automatically designed CNN models based on spatial–spectral information, were employed to achieve a comprehensive comparison with the PSO-Net and CPSO-Net methods. We chose several handcrafted CNN models that have reported results in the spectral–spatial information hyperspectral datasets to test the proposed algorithms. The CNN [51] was conducted, which is a sample CNN designed to tackle the problem of HSI spectral–spatial classification. The spectral–spatial residual network (SSRN) [22] and ResNet [27] are residual-based methods, which can achieve good classification performance. DesNet [21] using shortcut connections between layers was used for comparison. Moreover, an automatically designed CNN method, namely Auto-CNN, was introduced, which explores the automatic design of CNNs for HSI classification by the gradient descent and achieved good performance. To demonstrate the performance of the two methods we proposed, we made a comparison in the classification accuracy and the computational complexity with handcrafted and automatically designed CNN models. To further illustrate the search effectiveness of PSO-Net and CPSO-Net, we compared them with a peer, the automatically designed method Auto-CNN, in terms of time complexity.
4.3. Experimental Settings
In this section, we explain the detailed parameter setting for our experiments. For the automatically designed algorithms, including Auto-CNN, PSO-Net, and CPSO-Net, the search space should be predefined. We set the number of computation cells k to 3 and the intermediate nodes n to 4, and the basic operation list includes the following candidate basic operations: None; 3 × 3 max pooling, abbreviated as max_3 × 3; 3 × 3 average pooling, abbreviated as avg_3 × 3; skip connection, abbreviated as skip; 3 × 3 separable convolution, abbreviated as sep_3 × 3; 5 × 5 separable convolution, abbreviated as sep_5 × 5; 3× 3 dilated convolution, abbreviated as dil_3 × 3; 5 × 5 dilated convolution, abbreviated as dil_5 × 5. For HSI classification, the general architecture of automatically designed CNNs includes three parts. First, hyperspectral datasets as an input pass one 1 × 1 bottleneck convolution layers to set the number of HSI bands to 10 for the next computation cells. Then, two normal cells with padding and setting stride to 1, and reduction cells with padding and setting stride to 2 are stacked to complete the CNN. Finally, the final labels can be obtained by the fully connected layer.
For all the experiments in this work, we split the labeled samples of the HSI datasets into three subsets by sampling without replacement, namely the training, validation, and test sets. To ensure that all classes are included in the training, validation, and test dataset, we choose samples including all classes based on the proportion of every class in whole dataset and samples in each class are randomly selected with the same probability in this class. Based on the rule above, we chose 200 samples, including all classes as the training set and 600 samples as the validation set for each dataset. To demonstrate the stability of the two proposed methods, we conducted the experiments five times with random split datasets. Details of the training samples of each class of the four datasets are shown in Table 1. All the remaining labeled samples served as the test set to evaluate the capability of the network. The training set was used to train the network, and the validation set was used to evaluate the performance of the architectures found and to search for the optimal architecture for all the automatic design algorithms.
For biased datasets, we chose 7 × 7 × B neighborhoods of a pixel as input, where B is the number of HSI bands. For unbiased datasets, samples with 32 × 32 slides were not enough to divide into the training and validation datasets, so we chose 7 × 7 neighborhoods of a pixel, and none of the samples were overlapping. For all the CNN models designed by hand, i.e., 3-D CNN, SSRN, ResNet, DesNet, we set the training epochs to 100 epochs. The learning rate for the weights of all these models was 0.025. For 3-D Auto-CNN, we set the training epochs in the architecture search and test process both to 100 epochs. The learning rate for the weights in the search and test process was 0.025 and 0.05, respectively. For PSO-Net, we set the swarm size to 100, the number of iterations to 40, to 0.5, the training epochs in the architecture search and test process both to 100 epochs, and the learning rate for the weights in the architecture search and test process to 0.025. For CPSO-Net, only the training epochs in the architecture search were different from above, inspired by the mini-batch architecture idea of stochastic gradient descent for updating parameters, with only one epoch achieving good performance. For the test process, the experimental settings for the different methods can be found in Table 2.

Table 2.
Experimental settings for the different methods. CNN, convolutional neural network.
4.4. Results Analysis
In this section, we analyze the classification results and compare our algorithm with other methods in terms of classification accuracy, parameters, and time complexity on biased hyperspectral datasets to illustrate the effectiveness of our algorithms. We also demonstrate the optimal architectures searched by our methods, and analyze the convergence to illustrate the feasibility of the methods we proposed. Finally, we conduct experiments on unbiased hyperspectral datasets to further show our algorithms’ advantages.
4.4.1. Classification Accuracy
Table 3, Table 4, Table 5 and Table 6 show the detailed classification results on test datasets of the two methods we proposed and the other comparative algorithm. As shown in Table 3, Table 4, Table 5 and Table 6, it is obvious that PSO-Net and CPSO-Net achieved a big improvement classification accuracy over the handcraft methods, including CNN, SSRN, ResNet, and DesNet. Therefore, we mainly compared the methods with Auto-CNN, which is an automatically designed method as well. For the University of Pavia dataset, CPSO-Net improved the OA, AA, and Kappa of Auto-CNN by 1.34%, 0.64%, and 0.0185, respectively, and PSO-Net exhibited the best OA, AA, and Kappa, with improvements of 1.78%, 2.31%, and 0.0221 over Auto-CNN. respectively. For the Salinas dataset, PSO-Net and CPSO-Net performed almost the same, and CPSO-Net exhibited the best OA, AA and Kappa, with improvements of 1.22%, 1.95% and 0.0221 over Auto-CNN, respectively. For the Indian Pines dataset, both PSO-Net and CPSO-Net achieved higher classification results than the other algorithms. CPSO-Net exhibited the best AA and Kappa, while PSO-Net exhibited the best OA, with improvements of 1.88%, 0.0171, and 1.37% over Auto-CNN, respectively. For the KSC dataset, similar results to the other datasets were obtained. Obviously, CPSO-Net dramatically accelerated the optimal network generation and achieved quality performance comparable to PSO-Net. For the Salinas, Indian Pines, and KSC datasets, CPSO-Net achieved even better classification performance than PSO-Net, with some improvement over PSO-Net in terms of AA, OA, and Kappa. There may be some significant differences in every class accuracy. For example, CPSO-Net achieved particularly improvement of 12.98% over Auto-CNN in the first-class classification on Salinas. In addition, Table 7 shows the detailed average rankings of the classification accuracy on four datasets through the minimize performance measure based Friedman test [52], which is a statistical test for the homogeneity of multiple samples. From Table 7, we can see that the proposed approaches get almost similar ranking and rank higher than other comparative algorithms in terms of OA, AA, and Kappa.

Table 3.
Classification accuracy with bolding the best accuracy based on the biased Pavia dataset, run five times.

Table 4.
Classification accuracy with bolding the best accuracy based on the biased Salinas dataset, run five times.

Table 5.
Classification accuracy with bolding the best accuracy based on the biased Indian Pines dataset, run five times.

Table 6.
Classification accuracy with bolding the best accuracy based on the biased KSC dataset, fun five times.

Table 7.
Average rankings of Friedman test on four datasets in terms of OA, AA and Kappa, bold the best results.
To sum up from the classification accuracy analysis above, we can draw two conclusions. On the one hand, the PSO-Net and CPSO-Net algorithms made significant improvements over the state-of-the-art CNN models designed by hand, including CNN, SSRN, ResNet, and DesNet. Additionally, the proposed approaches are able to find better architectures than Auto-CNN optimized by the gradient descent. On the other hand, the two methods proposed herein achieved almost the same classification performance, while CPSO-Net dramatically reduced the time computation.
In addiction, taking CPSO-Net as example, we made a sensitivity hyperparameter analysis of the cell numbers with an additional two and four cells, intermediate nodes with an additional three and five nodes, and a population size with an additional 60 and 140. From Figure 6a,b, it can be seen that fewer number of cells or intermediate nodes achieved a lower OA, but the models with a higher number of cells or intermediate nodes did not necessarily lead to better performance. The main reason is that the models with simple architectures may not be able to extract deep features, and complex models may cause an overfitting problem with limited training samples. From Figure 6c, we can see that a small population may make architectures fall into the local optimal, but a large population will not greatly improve the classification performance when spending much more time.

Figure 6.
Classification results of different models searched by CPSO-Net with different numbers of cells, intermediate nodes, and population sizes based on four biased hyperspectral image (HSI) datasets.
4.4.2. Complexity Analysis
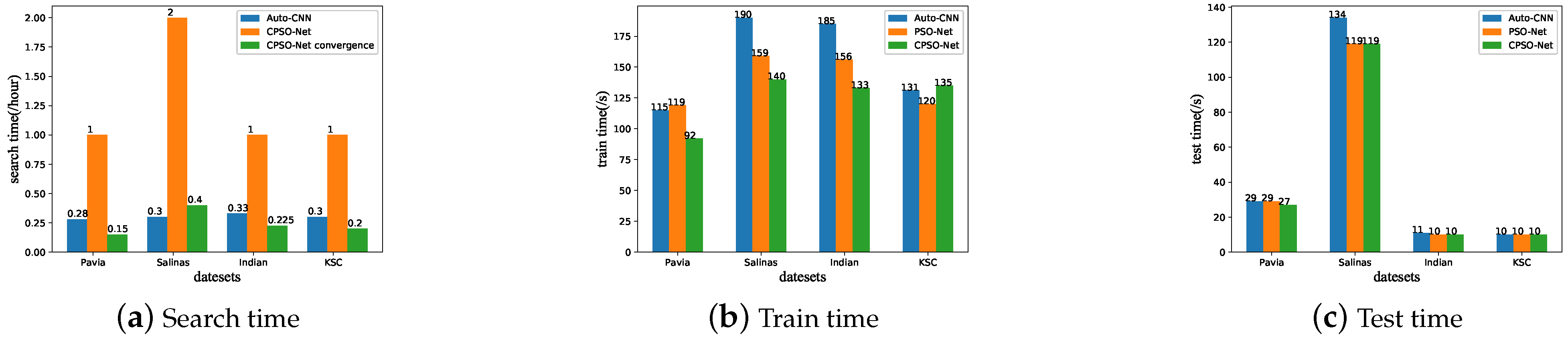
To analyze the complexity of the method we proposed, the results of several trainable parameters compared to both human-designed and automatically designed CNNs are shown in the bottom row of Table 3, Table 4, Table 5 and Table 6, and the time consumed compared to the peer automatically designed method are shown in Figure 7. From Table 3, Table 4, Table 5 and Table 6, it is obvious that the models searched by PSO-Net and CPSO-Net achieved better results with the state-of-the-art CNNs designed by human experts while having significantly less parameters, which means less time and computational complexity to train the CNN models. There are two main reasons for the above results. First, a CNN model with a high number of trainable parameters may cause an overfitting problem with limited training samples. Second, automatically designed methods can search CNNs more suitably for specific HSI datasets. For the automatically designed methods Auto-CNN, PSO-Net, and CPSO-Net, even though they had the same search space, CPSO-Net and PSO-Net performed better than Auto-CNN. However, there was no consistent pattern between the number of parameters of the models searched by the three automatically designed methods.
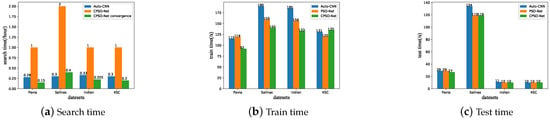
Figure 7.
Time consumed in the different stages of the different automatically designed CNNs methods based on four biased HSI datasets.
To further compare the search effectiveness of these automatically designed methods, Figure 7 shows the time consumed in the different stages of the peer automatically designed CNN methods based on four biased HSI datasets. PSO-Net consumed approximately 15 h to converge, which is a significant time compared to the other two automatically designed methods. Therefore, Figure 7a only shows the search time of Auto-CNN, CPSO-Net, and CPSO-Net convergence. From Table 3, Table 4, Table 5 and Table 6 and Figure 7a, we can see that CPSO-Net and PSO-Net achieved better performance with a big improvement for Auto-CNN, but CPSO-Net dramatically reduced the search time by the weight-sharing parameters from the SuperNet compared to PSO-Net. The time of the total iteration of CPSO-Net consumed more time than Auto-CNN, while it converged at six, eight, nine, and eight iterations (the detailed convergence analysis can be seen is Section 4.4.3) based on Pavia, Salinas, Indian Pines, and KSC, respectively. CPSO-Net only consumed approximately 15 min to converge, which is almost close to and even less than Auto-CNN. From Figure 7b, we can see that the training time of the CNNs searched by CPSO-Net was less than that of PSO-Net and Auto-CNN based on the Pavia, Salinas, and Indian Pines datasets. From Figure 7c, the three automatic-designed method, i.e., Auto-CNN, PSO-Net, and CPSO-Net, consumed almost the same time to test all the data of the CNNs searched.
To sum up, from Figure 7, we can see that PSO-Net consumed a significant amount of time to converge, while CPSO-Net dramatically accelerated the search generation. The time CPSO-Net consumed to converge was almost same as and even less than Auto-CNN.
4.4.3. Convergence Analysis
To dramatically accelerate optimal network generation, CPSO-Net shared the weights of SuperNet for all particles based on PSO-Net and achieved quality performance comparable to PSO-Net. Therefore, we mainly analyze the convergence of CPSO-Net in this section. The convergence of the architectures was different from the other solutions, and it is not enough only to consider the fitness of particles. The fitness was determined by the HSI classification accuracy of the optimized neural network, which was composed of the architectures and weight parameters. However, the number of parameters of the architectures and the position of the particles were only related to architecture. Therefore, the architecture convergence analysis of CPSO-Net took the number of parameters of the architectures and the position of all the particles as important criteria.
The number of parameters of the architectures were closely related to the operations in said architectures. With the alter of the operations in the architectures, the number of parameters changed accordingly, representing the architectures converging when the number of parameters remained the same during the generations. Figure 8 shows the accuracy and number of parameters of during iterations based on four datasets by CPSO-Net. From the number of parameters of , we can see that the architectures converged at six, eight, nine, and eight iterations based on the Pavia, Salinas, Indian Pines, and KSC datasets, respectively. The accuracy of the validation dataset still increased after the convergence of architectures. The main reason is that the parameters of the architectures inherited from the SuperNet continued to be optimized, while SuperNet was trained until reaching the maximum iterations.

Figure 8.
The accuracy and parameters of during the iterations based on four biased datasets by CPSO-Net.
We further visualized the position of 20 particles selected randomly and during the iterations based on four datasets by CPSO-Net in Figure 9. The position of the particles was projected from the array (encoding from the architectures) into one-dimensional space using principal component analysis (PCA). As we can see, all particles divided globally at initialization, gradually tended toward focusing on global exploration with the iteration, toward the best particle position found thus far, and the position of converged at the same iteration as the number of parameters of , as shown in Figure 8.

Figure 9.
Positions of 20 particles and during the iterations based on four biased HSI datasets by CPSO-Net.
4.4.4. Optimal Architecture
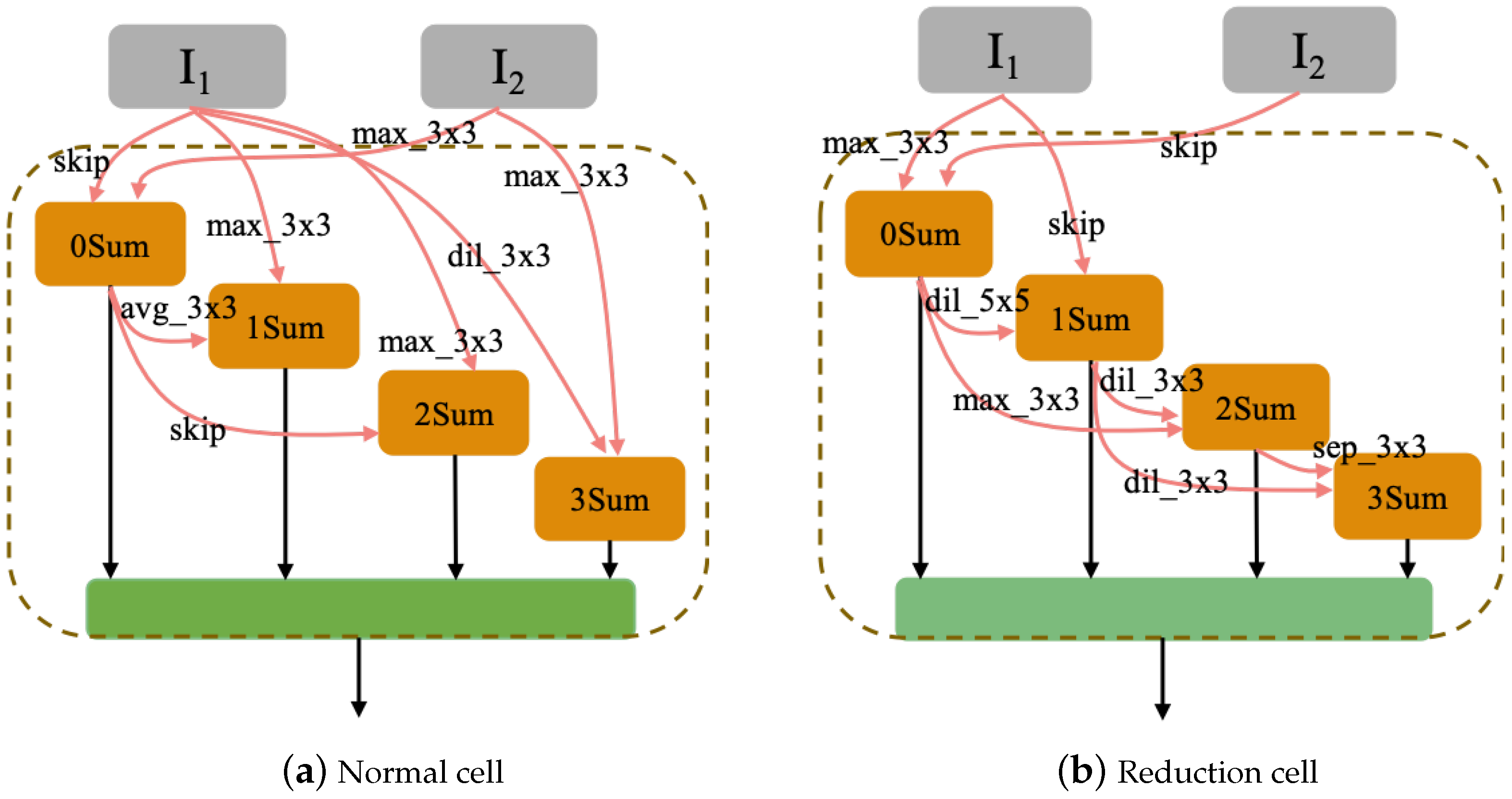
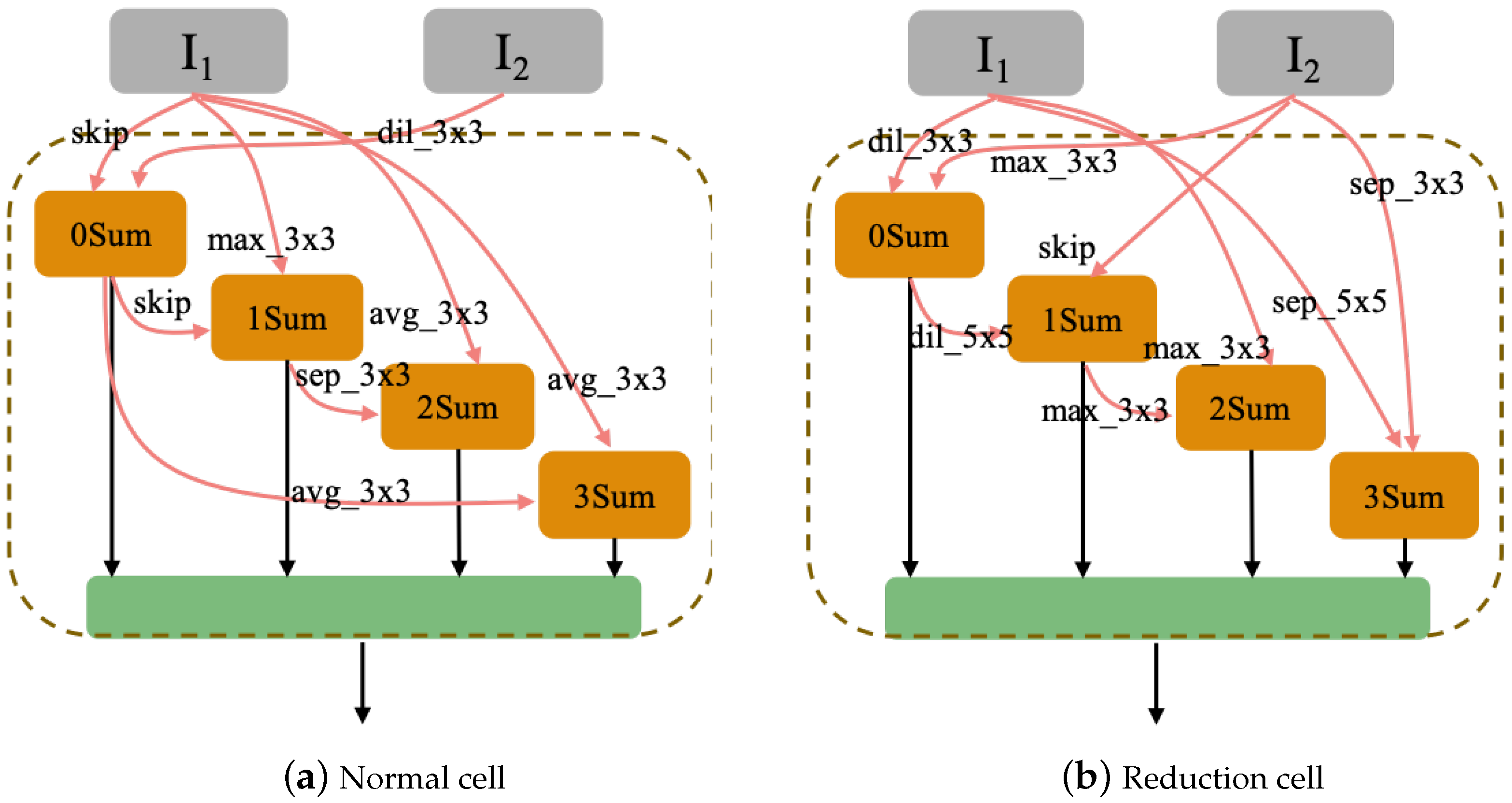
To find the optimal architecture is the main purpose of the method we proposed, the optimal architecture can be searched at the end of the algorithms. After searching, the optimal architecture can be used to classify all the data. Herein, we took PSO-Net based on biased the University of Pavia dataset and CPSO-Net based on the biased Salinas dataset as examples. The architectures of the optimal CNN architectures found by the proposed PSO-Net and CPSO-Net are shown in Figure 10 and Figure 11. Compared to the handcraft CNNs, PSO-Net and CPSO-Net designed the optimal architectures in a predefined search space without professional knowledge of human experts and without spending significant time on repeated debugging. The search space is constructed by incorporating typical properties of successful architectures designed by hand. Therefore, the optimal architectures searched includes some typical properties of handcraft CNNs. For example, inspired by the ResNet, the optimal architectures in Figure 10 and Figure 11 introduced skip connections.
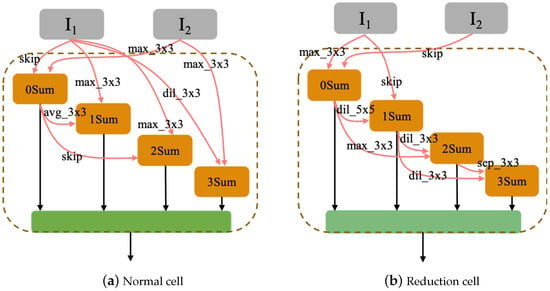
Figure 10.
Optimal architecture of PSO-Net for the biased Pavia dataset.
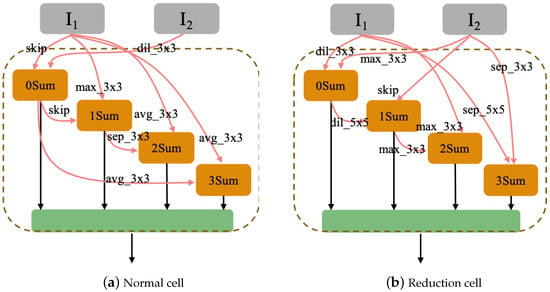
Figure 11.
Optimal architecture of CPSO-Net for the biased Salinas dataset.
4.4.5. Classification Maps
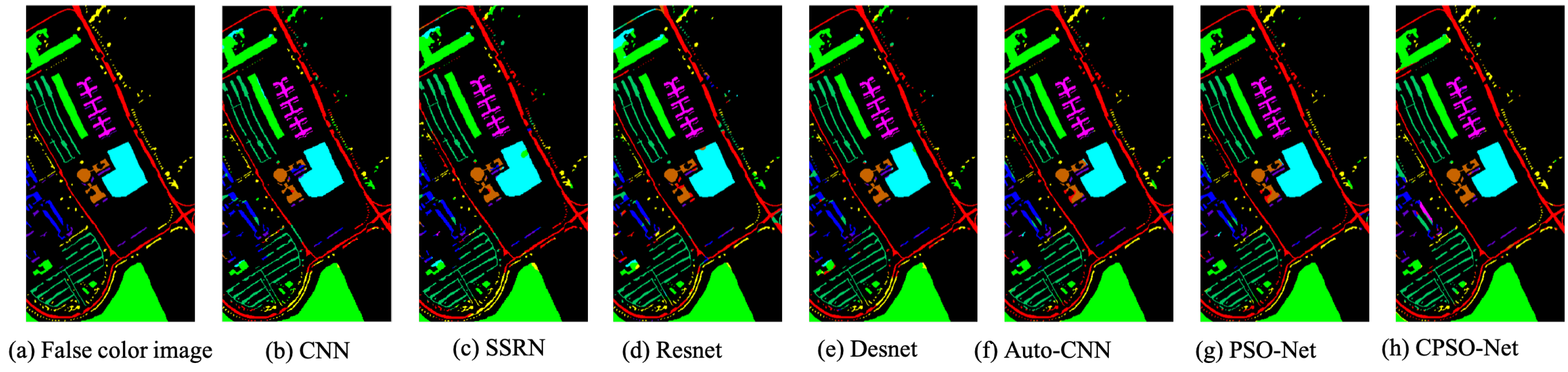
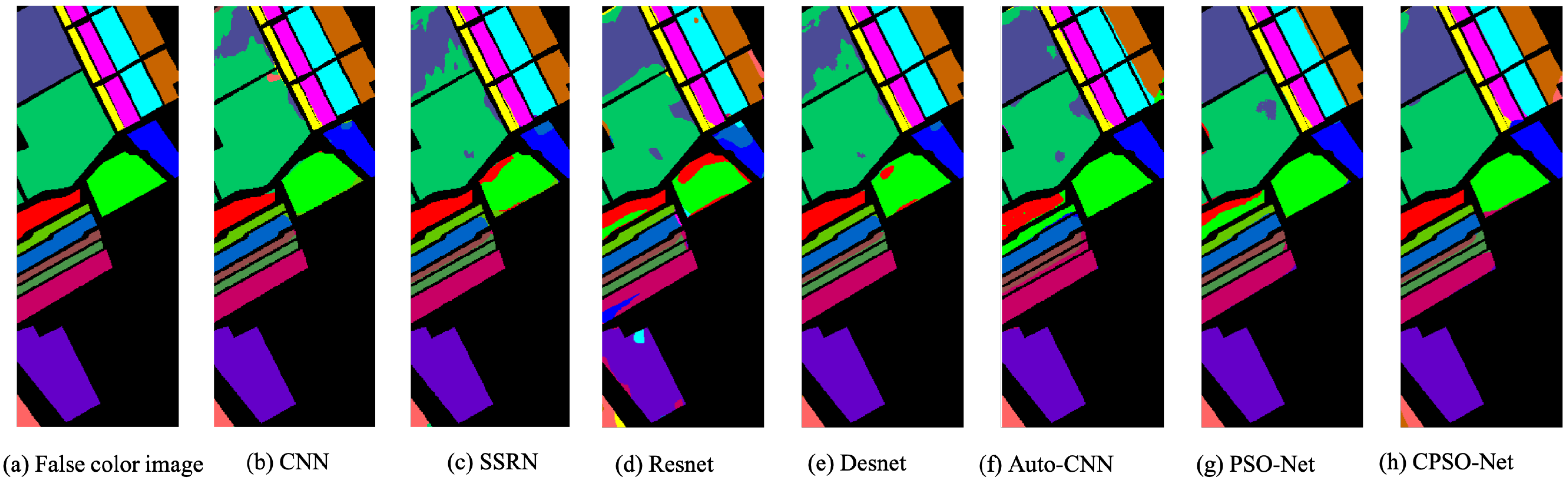
To clearly represent the classification results, we plotted the whole image classification maps of all the models. The classification maps obtained by the different models based on four biased datasets are shown in Figure 12, Figure 13, Figure 14 and Figure 15. We evaluated the classification accuracies from the noise scatter in the visual perspective. From the results, we can see that CPSO-Net achieved less scatter in the class with the largest area compared to the other models, which means that CPSO-Net can obtain more precise classification accuracy in this class. From the resulting images, we figured out how the different classification methods affected the classification results. Obviously, the automatically designed CNNs had less noise than the handcrafted CNN model, which demonstrates the feasibility of designing CNN models automatically. It is obvious that the CNN search by the methods we proposed had less scatter than the automatically design method Auto-CNN for HSI classification, which further demonstrates the effectiveness of PSO-Net and CPSO-Net.
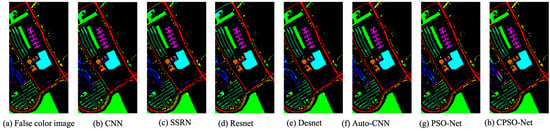
Figure 12.
Classification Maps on biased Pavia dataset.
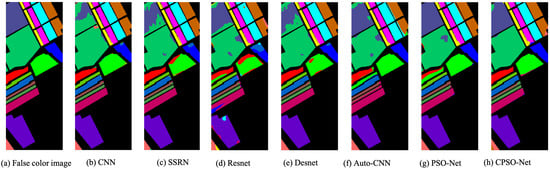
Figure 13.
Classification maps based on the biased Salinas dataset.

Figure 14.
Classification maps based on the biased Indian Pines dataset.

Figure 15.
Classification maps based on the biased KSC dataset.
4.5. Unbiased HSI Classification
There may be pixel overlapping and training-test information leakage problems on biased datasets which lead to over-optimistic results for spectral-spatial methods. Therefore, to further demonstrate the effectiveness of PSO-Net and CPSO-Net, we conducted some more experiments on the unbiased hyperspectral datasets and tested the two methods in comparison to CNN, SSRN, ResNet, DesNet, and Auto-CNN based on the four biased HSI datasets of Pavia, Salinas, Indian Pines, and KSC. There are some methods to split training and test datasets without pixels overlapping and training-test information leakage, such as patch-based [53] and set-to-sets distance based [54] methods.
For the unbiased datasets, samples with 32 × 32 slides were not enough for dividing into the training and test datasets, so we chose 7 × 7 neighborhoods of a pixel according to the patch-based [53] method, and none of the samples were overlapping. When the All other experimental settings were the same with the aforementioned biased datasets.
From Table 8, Table 9, Table 10 and Table 11, it is obvious to see that PSO-Net and CPSO-Net performed much better than the other models, and the improvements of PSO-Net and CPSO-Net were significant. In particular, the performance of CPSO-Net was better and consumed much less time than PSO-Net. However, the results of different unbiased spatial-based HSI classification methods were all lower than the performance of the biased methods.

Table 8.
Classification accuracy with bolding the best accuracy based on the unbiased Pavia dataset, run five times.

Table 9.
Classification accuracy with bolding the best accuracy based on the unbiased Salinas dataset, run five times.

Table 10.
Classification accuracy with bolding the best accuracy based on the unbiased Indian Pines dataset, run five times.

Table 11.
Classification accuracy with bolding the best accuracy based on the unbiased KSC dataset, run five times.
5. Conclusions
In this paper, we proposed two novel evolutionary-based search methods, PSO-Net and CPSO-Net, which use particle swarm optimization as the search strategy to search for the optimal architecture. For PSO-Net, the gradient descent method was used to obtain the weight parameters for all architectures separately, and PSO was used to optimize the architectures and search for the optimal architecture until reaching the maximum number of iterations. To accelerate the optimal network generation, CPSO-Net made an improvement based on the PSO-Net parameter optimization of architectures. For CPSO-Net, we maintained a SuperNet with all candidate operations and shared the weight parameters for all individuals. There was no need to train each particle from the beginning to the end, so the search time was reduced greatly. Our results showed that PSO-Net and CPSO-Net can achieve better classification accuracies compared to the state-of-the-art algorithms of the automatic design of CNNs for HSI classification, and CPSO-Net can obtain almost the same results with much less time consumed than PSO-Net.
For future works, we will consider multiple complementary objectives, such as the number of parameters and the classification accuracy to achieve the Pareto optimal front. To further demonstrate the effectiveness of the methods we proposed herein, we will test these methods on the same common image classification datasets.
Author Contributions
Conceptualization, X.L. and C.Z.; methodology, X.L.; software, X.L. and C.Z.; validation, X.L., C.Z., and Z.C.; formal analysis, X.L.; investigation, C.Z.; resources, X.L. and Z.C.; data curation, C.Z.; writing—original draft preparation, C.Z.; writing—review and editing, X.L., Z.C., J.Y., Z.Z., and X.G.; visualization, C.Z.; supervision, X.L.; project administration, X.L. and Z.C.; funding acquisition, X.L. All authors read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China (grant numbers 61973285, 62076226, 61873249, and 61773355) and the Open Research Project of the Hubei Key Laboratory of Intelligent Geo-Information Processing (grant number KLIGIP-2019A04).
Acknowledgments
The authors would like to thank M. Graa, M.A. Veganzons, and B. Ayerdi for the hyperspectral image datasets used in this paper, and Y. Chen for the Auto-CNN source codes.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Yi, C.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral image super-resolution based on spatial and spectral correlation fusion. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4165–4177. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Haut, J.M.; Bernabé, S.; Paoletti, M.E.; Fernandez-Beltran, R.; Plaza, A.; Plaza, J. LowChigh-power consumption architectures for deep-learning models applied to hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 776–780. [Google Scholar] [CrossRef]
- Teke, M.; Deveci, H.S.; Haliloglu, O.; Gürbüz, S.Z.; Sakarya, U. A short survey of hyperspectral remote sensing applications in agriculture. In Proceedings of the 2013 6th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 16 August 2013; pp. 171–176. [Google Scholar]
- Shang, X.; Chisholm, L.A. Classification of australian native forest species using hyperspectral remote sensing and machine-learning classification algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2481–2489. [Google Scholar] [CrossRef]
- Han, Y.; Li, J.; Zhang, Y.; Hong, Z.; Wang, J. Sea ice detection based on an improved similarity measurement method using hyperspectral data. Sensors 2017, 17, 1124. [Google Scholar]
- El-Sharkawy, Y.H.; Elbasuney, S. Hyperspectral imaging: Anew prospective for remote recognition of explosive materials. Remote Sens. Appl. Soc. Environ. 2019, 13, 31–38. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3d convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Luo, Y.; Zou, J.; Yao, C.; Zhao, X.; Li, T.; Bai, G. Hsi-cnn: A novel convolution neural network for hyperspectral image. In Proceedings of the International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 16–17 July 2018; pp. 464–469. [Google Scholar]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS Net: Band-adaptive spectral-spatial feature learning neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, X.; Cai, Z. BS-Nets: An end-to-end framework for band selection of hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1969–1984. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, Z.; Cai, Z.; Liu, X.; Jiang, X.; Yan, Q. Graph convolutional subspace clustering: A robust subspace clustering framework for hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Feng, J.; Wang, L.; Yu, H.; Jiao, L.; Zhang, X. Divide-and-conquer dual-architecture convolutional neural network for classification of hyperspectral images. Remote Sens. 2019, 11, 484. [Google Scholar] [CrossRef]
- Charmisha, K.; Sowmya, V.; Soman, K. Dimensionally reduced features for hyperspectral image classification using deep learning. In Proceedings of the International Conference on Communications and Cyber Physical Engineering (ICCCE), Hyderabad, India, 24–25 January 2018; pp. 171–179. [Google Scholar]
- Du, J.; Li, Z. A hyperspectral target detection framework with subtraction pixel pair features. IEEE Access. 2018, 6, 45562–45577. [Google Scholar] [CrossRef]
- Jia, P.; Zhang, M.; Yu, W.; Shen, F.; Shen, Y. Convolutional neural network based classification for hyperspectral data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5075–5078. [Google Scholar]
- Haut, J.; Paoletti, M.; Plaza, J.; Plaza, A. Hyperspectral image classification using random occlusion data augmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1751–1755. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Geng, Y.; Zhang, Z.; Li, X.; Du, Q. Unsupervised spatial-spectral feature learning by 3d convolutional autoencoder for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6808–6820. [Google Scholar] [CrossRef]
- Sellami, A.; Farah, M.; Farah, I.R.; Solaiman, B. Hyperspectral imagery classification based on semi-supervised 3-d deep neural network and adaptive band selection. Expert Syst. Appl. 2019, 129, 246–259. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep&Dense convolutional neural network for hyperspectral image classification. Remote Sens. 2018, 10, 1454. [Google Scholar]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J. Hyperspectral images classification based on dense convolutional networks with spectral-wise attention mechanism. Remote Sens. 2019, 11, 159. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Safari, K.; Prasad, S.; Labate, D. A multiscale deep learning approach for high-resolution hyperspectral image classification. IEEE Geosci. Remote Sens Lett. 2021, 18, 167–171. [Google Scholar] [CrossRef]
- Shao, W.; Du, S. Spectral-spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl. Based Syst. 2021, 212, 1–27. [Google Scholar] [CrossRef]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1–21. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2017, arXiv:1611.01578. [Google Scholar]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, G.; Benediktsson, J.A. Automatic design of convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]
- Junior, F.; Erivaldo, F.; Yen, G. Particle swarm optimization of deep neural networks architectures for image classification. Swarm Evol. Comput. 2019, 49, 62–74. [Google Scholar] [CrossRef]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the Conference on Artificial Intelligence (AAAI), Honolulu, HI, USA, 27 January–1 February 2019; pp. 4780–4789. [Google Scholar]
- Stanley, K.O.; Miikkulainen, R. Evolving neural networks through augmenting topologies. IEEE Trans. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef]
- Gauci, J.; Stanley, K.O. Autonomous evolution of topographic regularities in artificial neural networks. Neural Comput. 2010, 22, 1860–1898. [Google Scholar] [CrossRef] [PubMed]
- Stanley, K.O.; D’Ambrosio, D.B.; Gauci, J. A hypercube-based indirect encoding for evolving large-scale neural networks. Artif. Life 2009, 15, 185–212. [Google Scholar] [CrossRef]
- Stanley, K.O. Compositional pattern producing networks: A novel abstraction of development. Genet. Program Evol. Mach. 2007, 8, 131–162. [Google Scholar] [CrossRef]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing Neural Network Architectures Using Reinforcement Learning. arXiv 2017, arXiv:1611.02167. [Google Scholar]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 8697–8710. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2019, arXiv:1806.09055. [Google Scholar]
- Xie, S.; Zheng, H.; Liu, C.; Lin, C. Snas: Stochastic neural architecture search. arXiv 2019, arXiv:1812.09926. [Google Scholar]
- Wu, B.; Dai, X.; Zhang, P.; Wang, Y.; Sun, F.; Wu, Y.; Tian, Y.; Vajda, P.; Jia, Y.; Keutzer, K. Fbnet: Hardware-aware efficient convnet design via differentiable neural architecture search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10734–10742. [Google Scholar]
- Pham, H.; Guan, M.Y.; Zoph, B.; Le, Q.V.; Dean, J. Efficient neural architecture search via parameter sharing. In Proceedings of the Internation Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 6522–6531. [Google Scholar]
- Xie, L.; Yuille, A. Genetic cnn. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1388–1397. [Google Scholar]
- Yang, Z.; Wang, Y.; Chen, X.; Shi, B.; Xu, C.; Xu, C.; Tian, Q.; Xu, C. CARS: Continuous evolution for efficient neural architecture search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 1829–1838. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Efficient multi-objective neural architecture search via lamarckian evolution. arXiv 2019, arXiv:1804.09081. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Smash: One-shot model architecture search through hypernetworks. arXiv 2017, arXiv:1708.05344. [Google Scholar]
- Saxena, S.; Verbeek, J. Convolutional neural fabrics. In Proceedings of the Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 4060–4068. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science (MHS), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Sahu, A.; Panigrahi, S.K.; Pattnaik, S. Fast convergence particle swarm optimization for functions optimization. Procedia Technol. 2012, 4, 319–324. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 30, 86–92. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Validating hyperspectral image segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1264–1268. [Google Scholar] [CrossRef]
- Cao, X.; Ren, M.; Zhao, J.; Lu, H.; Jiao, L. Non-overlapping classification of hyperspectral imagery based on set-to-sets distance. Neurocomputing 2020, 378, 422–434. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).