1. Introduction
Vertically-resolved cloud amount is essential for understanding Earth’s radiation budget. Cloud radiative forcing varies from positive to negative, depending on cloud properties, and their location in the 3D troposphere [
1]. Chepfer et al. [
2] argue that as the climate warms and clouds adjust to new conditions, the vertical cloud profile will provide a clearer indication of the change than the column-integrated cloud amount. Early evidence of this has already been noted by Norris et al. [
3], who reported a statistically significant increase in cloud top height globally.
The majority of methods that are used in cloud remote sensing exploit column-integrated radiances. In such cases, information about clouds at various altitudes is inferred indirectly: by studying cloud top properties [
4]. However, limitations inherent in passive imaging and sounding techniques have led to disagreement in the global cloud amount estimation. Depending on the considered dataset, mean cloud amount at low, mid, and high levels varies from 26 to 62%, 12 to 55%, and 10 to 18%, respectively [
5]. In practice, the detection and accurate parametrization of multi-layered cloud remains a challenge for even the most advanced imagers and sounders [
6].
Two satellites have been launched that improve our knowledge of cloud vertical distribution: CloudSat and Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO). The former carries a Cloud Profiling Radar (CPR), operating at 94 GHz, while the latter hosts the Cloud-Aerosol Lidar with an Orthogonal Polarization (CALIOP) instrument, that profiles the atmosphere at 532 nm and 1064 nm wavelengths [
7,
8].
Both lidar and radar are active sensing instruments: they send a radiation pulse towards the nadir, then receive the backscattered signal. The analysis of the echo can directly detect the presence of cloud along the line of sight, and this operating principle represents a considerable improvement over cloud imagers/sounders [
9]. Importantly, lidar and radar are complementary techniques. The CALIOP signal is fully attenuated when cloud optical thickness exceeds five [
10]. On the other hand, CloudSat “misses” thin clouds, but successfully penetrates optically thick layers, as far down as Earth’s surface (except for dense hydrometeors, e.g., some precipitating convective clouds).
Launched together in 2006, CloudSat and CALIPSO were placed on almost-identical sun-synchronous orbits with an equatorial crossing time of 13:30 local solar time (ascending node). Between June 2006 and April 2011, the pair of satellites flew in close orbital formation, sampling the same region of the atmosphere only 10–15 seconds apart. Joint processing of lidar and radar backscattered signals resulted in a dataset of vertically-resolved cloud amount that, to date, remains one-of-a-kind. In 2011, the CloudSat and CALIPSO tandem was temporarily interrupted. Although the satellites were reunited a year later, they never regained their initial operational functionality [
11].
CloudSat and CALIPSO’s ability to penetrate cloud is a trade-off for their instruments’ swath width—both sensors only collect data along their overlapping ground tracks (~1 km wide). The track repeats every 16 days, meaning a location is sampled 22–23 times per year, or never (if outside the ground track). This unusual configuration introduces a significant source of uncertainty for any climate-related statistic derived from the CloudSat–CALIPSO dataset.
Various dedicated, theoretical formalisms have been developed (e.g. [
12,
13,
14,
15,
16,
17]) to assess an area’s cloud fraction from a finite sample (a transect line in the case of profiling instruments). For instance, van de Poll et al. [
14] used a Bayesian Inference Algorithm to calculate the a posteriori probability distribution of clouds, based on a priori assumptions of the size and organization of clouds and cloud gaps, as well as the assumed cloud fraction at the time of observation.
However, these theoretical models have not been widely adopted in practice, and the “conventional” definition of cloud amount remains the preferred approach: the ratio of cloudy pixels to all pixels along a transect of predefined length. The resulting CloudSat and/ or CALIPSO climatologies are usually limited to the mean cloud amount and neglect statistical uncertainty assessments [
14]. If it is considered, uncertainty is expressed in terms of standard deviation (e.g. [
18,
19]), and only occasionally as a confidence interval [
20,
21,
22].
The goal of this study, therefore, is to provide a quantitative assessment of uncertainties related to the vertically-resolved mean cloud amount calculated from joint CloudSat–CALIPSO lidar–radar cloud profiles (2006–2011). We follow the conventional (i.e., the most widely used) definition of cloud amount, so that our results can be directly applied to existing and future CloudSat–CALIPSO climatologies. We focus on an empirical dataset, consisting of five years of observations, rather than purely theoretical considerations.
The obtained results allow us to answer the question of whether it is possible to obtain a mean cloud amount from joint CloudSat–CALIPSO observations, at a known accuracy (1% or 5%), with a high confidence level (>0.95), and at fine spatial resolution (1°–2.5°). The results of our calculations are reported here, to help the scientific community interpret various lidar/radar cloud climatologies.
2. Materials and Methods
2.1. Satellite Data
In this study, we focus on a particular CloudSat–CALIPSO data product: the radar-lidar geometrical profile “2B-GEOPROF-LIDAR” (version P2_R05), also occasionally codenamed “RL-GEOPROF” [
10,
23]. The product considers CloudSat and CALIPSO missions as a single observing system and combines their data streams. In particular, the following products are merged:
CALIPSO’s “Vertical Feature Mask” (VFM). The lidar profiles the atmosphere every ⅓ km along the ground track, however such spatial detail is only available below 8.2 km. In the upper troposphere (8.2–20.2 km), samples are averaged to 1 km. Similarly, the vertical resolution varies from 30 to 60 m, respectively. “Features” in the atmosphere are detected using the Selective Interacted Boundary Locator (SYBIL) algorithm [
24], and the tropospheric domain considers two classes: “cloud” and “aerosol” (sub-types are also provided);
CloudSat’s “Geometrical Profiling” (2B-GEOPROF) product. The radar has a 1.4 × 1.7 km
2 footprint, and samples the atmosphere every 1.1 km along the track with a vertical resolution of 480 m (oversampled to 240 m). The measured return power is examined to distinguish between hydrometeors and the noise of clear atmosphere. The resulting cloud mask is provided as a probability, reflecting the confidence level (ranging from 0 to 40) that a particular atmospheric volume features a hydrometeor [
25].
During the cloud mask merge, CloudSat’s coarse geometry serves as a reference for the final product: the horizontal spacing of joint profiles is set to ~1.1 km, while the vertical resolution remains at 240 m. The 2B-GEOPROF-LIDAR product reports up to five cloud layers, separated by no less than four “clear” CloudSat volumes (i.e., 960 m in altitude). Each layer is characterized by two science data variables: “LayerBase” and “LayerTop”, indicating the geometric altitude of the layer base and the layer top, respectively. Details of the merging strategy can be found in Mace et al. [
23], while further improvements are reported in Mace and Zhang [
10].
The availability of the 2B-GEOPROF-LIDAR product is constrained by CloudSat’s performance. For the first five years after its launch, the satellite operated nominally, sampling the atmosphere 10–15 seconds ahead of CALIPSO. In 2011, a battery problem resulted in it losing synchronization with CALIPSO, and the joint mission temporarily ceased. After a year-long recovery effort, CloudSat resumed observations with CALIPSO. However, technical issues required the adoption of a new mode of action: Daylight Only Operations (DO-Op).
While it still follows CALIPSO, CloudSat is only able to sense the atmosphere during the daylight portion of its orbit, i.e., for ~60 of the 99 minutes that make up a full orbit [
11,
26]. As a result, ~40% of scientific data are lost. The missing data relate to nighttime, hence any cloud climatology developed with CloudSat data after 2012 features a significant bias, especially over the oceans [
27]. In its DO-Op configuration, CALIPSO data overlap with degraded CloudSat data, due to fewer orbit adjustment maneuvers for the latter. The temporal separation between the two spacecrafts has increased to ~100 seconds [
28].
Considering the history of CloudSat–CALIPSO joint operations, and the quality of the lidar–radar overlap post-2012, we decided to only evaluate the 2006–2011 part of the 2B-GEOPROF-LIDAR product. Using the terminology provided by CloudSat’s scientific team, the dataset spans the period Epoch 00 (starting 2 June 2006) and Epoch 04 (ending 17 April 2011). It comprises the longest homogenous lidar–radar cloud profile record available for climate studies to date. Nonetheless, the approach used in this study can be also successfully applied to DO-Op data, for applications that require/accept a limited dataset.
Our CloudSat–CALIPSO data were accessed from the CloudSat Data Processing Center, operated by the Cooperative Institute for Research in the Atmosphere (CIRA), a research institute at Colorado State University (
http://www.cloudsat.cira.colostate.edu).
2.2. Cloud Amount
This study adopts the most widely-used definition of cloud amount (cloud fraction): the ratio of cloudy observations to all valid observations. Whether a particular level of a lidar–radar profile was “clear” or “cloudy”, was determined from “LayerBase” and “LayerTop” variables given in the 2B-GEOPROF-LIDAR product. We only considered those profiles for which the “Data_quality” flag was set to “0” (“data of good quality”).
Since we investigated vertically-resolved cloud amount, calculations were made with respect to an atmospheric volume. This 3-dimensional space in the atmosphere is 480 m high (i.e., the original CloudSat vertical resolution), and has a width determined by the grid box size. For instance, a 1° grid resulted in 2,592,000 atmospheric volumes.
During a single CloudSat–CALIPSO overpass, a volume was sampled along a transect. The exact number of lidar–radar profiles constituting the transect varied, depending on the grid box size, and the transect orientation with respect to the center. The total number of transects per volume, for the whole 2006–2011 timeframe, depended on the spatial resolution. For example, values ranged from ~300 close to the equator, increasing poleward up to ~4500 when 1° data were considered (
Table 1).
Since the grid resolution used for the spatiotemporal aggregation of profiles could have an impact on the final statistics, all calculations were performed simultaneously at four spatial scales: 1.0°, 2.5°, 5.0°, and 10.0°. The influence of temporal averaging was acknowledged by considering three domains: the annual mean, the seasonal (autumn) mean, and the monthly mean (September). Although the choice of season and month was somewhat arbitrary, results for other seasons/ months showed the same patterns.
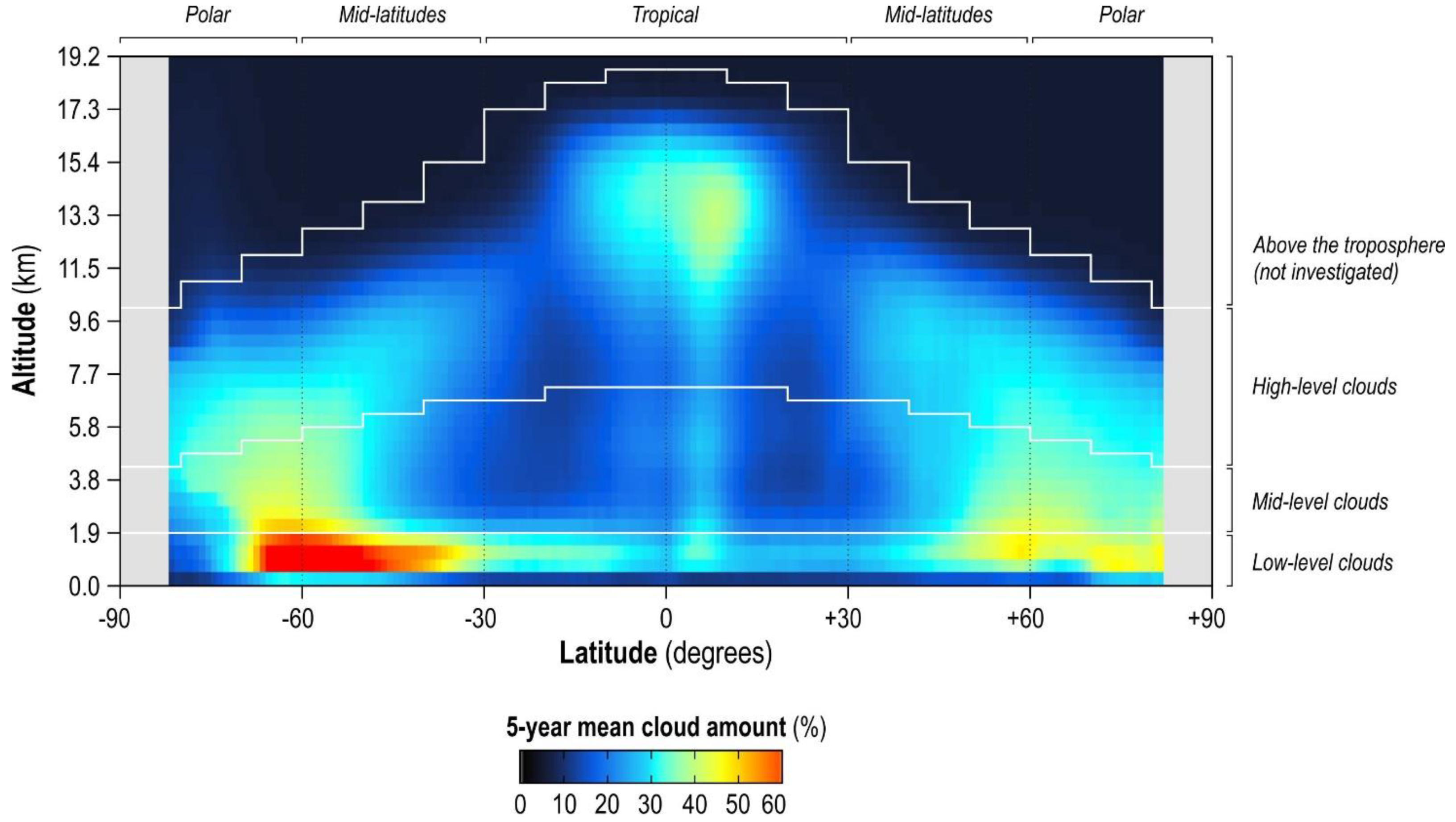
Only atmospheric volumes located below 19.2 km (the troposphere) were analyzed. Statistics are reported for the whole tropospheric profile, and the common cloud levels (low, mid, high) defined by the World Meteorological Organization (WMO;
Figure 1). The WMO divides clouds into three levels, based on the altitude range where the genera occur most frequently. The upper and lower bounds of a level vary with latitude, as the cloud regime changes towards the poles (at the tropopause the height decreases). For instance, mid-level clouds occur between 2 and 8 km in the tropics, at 2–7 km in mid latitudes, and 2–4 km in polar regions. Clouds below 2 km are always classified as low level, regardless of the latitude [
29]. Since CALIPSO reports clouds with respect to sea level, our definition of cloud levels also refers to sea level (
Figure 1).
Mean cloud amount was the point estimate under evaluation in this study. Our goal was to assign a confidence level to the mean, taking into account the specific sampling scheme of the CloudSat-CALIPSO joint mission, and the empirical data. Uncertainty in mean cloud amount was evaluated in terms of the confidence interval (CI). Upper and lower bounds were identified using a non-parametric bootstrap approach [
30,
31,
32]. The procedure was as follows.
First, a cloud amount was calculated for each of n CloudSat–CALIPSO transects within a volume. The resulting n-element sample was then randomly re-sampled (with replacement) 10,000 times, to compute a mean cloud amount. The 10,000 bootstrap means were normally distributed, with standard error SE*, and mean t*. The latter represents the final (bootstrapped) estimate of the mean cloud amount for an atmospheric volume.
The CI for the mean was derived from the bootstrapped distribution, and accounted for bias (
b), i.e., the difference between the sample mean (
t0), and the bootstrapped mean (
t*):
where:
t0—mean cloud amount in the original sample;
b—bias in the mean estimate, b = t* − t0;
t*—bootstrapped estimate of mean cloud amount;
zα—1 − α/2 quantile of the standard normal distribution;
SE*—standard error of the bootstrapped estimate.
The estimation of the CI required a confidence level (CL) to be set prior to the calculation. The choice of the CL impacts the width of the CI: higher CLs produce wider CIs. In order to gain a deeper insight into how the choice of CL determines uncertainty in cloud amount estimates, we simultaneously investigated four possibilities: CL = 0.85, CL = 0.90, CL = 0.95, and CL = 0.99. All calculations used the “bootstrap” package of the R statistical environment.
For some volumes, the CI could not be calculated due to a monotonic variable: cloud amount for all of
n observations was 0% (
Table 1). This mostly occurred in the cloud-free upper atmosphere, especially the tropics. For these volumes, CI = 0% was assigned. For some volumes the CI formula resulted in upper/ lower bound estimates above/ below the possible range of cloud amount (0–100%). This was corrected by assigning 0% to negative values, and 100% to overestimates.
3. Results
The average width of the CI for the CloudSat–CALIPSO-based estimation of mean cloud amount was 8.27%. This figure refers to the annual mean, calculated using data gridded at 1° spatial resolution, and assuming a CL of 0.95. The statistic varied as a function of grid size, and CL (
Table 2).
Mean CI across all considered scenarios was relatively high: 26.21%. We observed the broadest CI (27.59%) when mean monthly cloud amount was investigated at 1° resolution and CL = 0.99. On the other hand, lidar–radar data processed with a 10° grid box and CL = 0.85 resulted in the narrowest interval: 1.38%. At the same time, we noted three distinct patterns that influenced CI widths.
Considering the change in the spatial scale of a grid box, we observed that CI width increased approximately four times, as the spatial resolution increased from 1° to 10°. The pattern was identical regardless of the CL. For instance, if the CL was limited to 0.95, the CI width was 1.88% at the coarsest spatial resolution, and 8.27% at the finest resolution.
Changing the CL over the range CL = 0.85 to CL = 0.99 almost doubled the CI width. With data gridded at 1° resolution, the absolute CI width was 6.10% at CL = 0.85 and increased to 10.81% at the higher CL (0.99). Here again, the same regularity was observed among all considered resolutions (
Table 2).
We also investigated the magnitude of the change in CI width as a consequence of extending the timeframe. Statistics revealed that it nearly tripled when the number of data-months used in the calculation increased from one (monthly mean) to twelve (annual mean). For example, values increased from 8.27% to 21.87% for 1° data, and CL = 0.95.
Seasonal and monthly statistics featured the same regularities as annual data: a four-fold widening of the CI with increasing spatial resolution, and a narrowing of the CI, by half, as the CL fell.
Table 2 reports data for September, and the autumn period (September to November). As results for other months and seasons did not differ from those presented by more than ±1% of cloud amount, they are intentionally omitted.
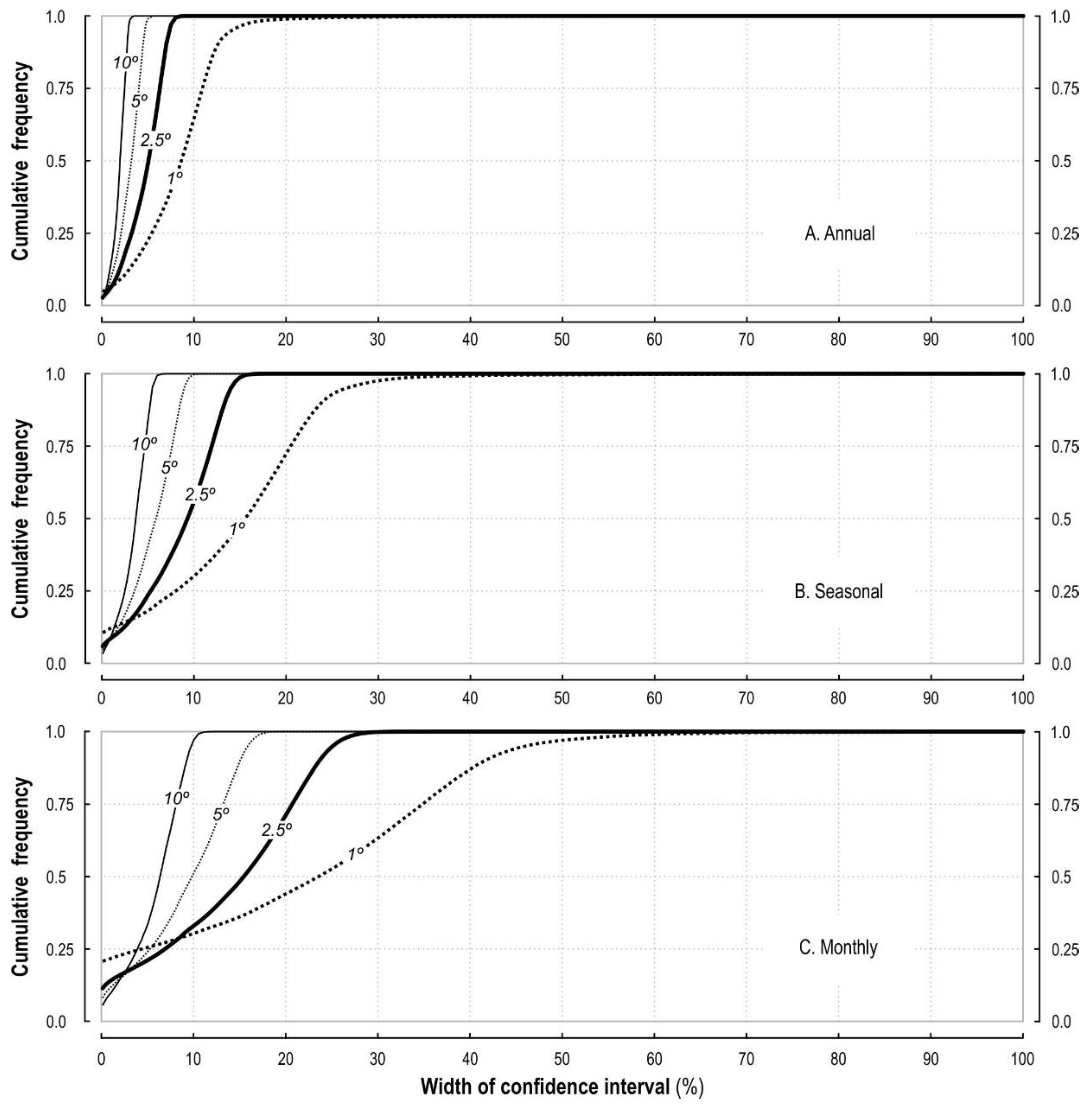
A single, global average CI width does not tell us much about the variability of actual CI values for individual locations in the atmosphere (i.e., individual 3D volumes for which CloudSat–CALIPSO estimates the cloud amount). This detailed information can be found when histograms of CI width are considered (
Figure 2).
These plots confirm that shifts in CI width are consistent with a change in CL, grid box size, and the number of months used for the calculation. However, we observed that the same parameters also influenced the shape of the CI distribution: it became broader with an increase in grid box size and/ or CL, and with a decrease in the number of months considered. Consequently, CI width variability spanned over ~60% for the monthly mean, ~40% for the seasonal mean, and ~20% for the annual mean (1° data, CL = 0.95;
Figure 2A–C). At 2.5° resolution these ranges were noticeably smaller: ~30%, ~20%, and ~10%, respectively (
Figure 2D–F).
The distribution of CI widths revealed two maxima. The first corresponded to the average, while the second was located close to 0%. The latter maximum reflected the frequency of monotonic observations, i.e., cases where cloud amount was constant or nearly constant throughout a year/season/month. For the annual statistic, the maximum at 0% was secondary, but became primary for seasonal and, especially, monthly calculations.
The bi-modal distribution was particularly noticeable at the finest spatial scale (grid box of 1°). A decrease in spatial resolution produced fewer monotonic observations; therefore, the magnitude of the 0% maximum fell sharply. It was not observed at all with 10° data, regardless of the CL, or the number of months included in the calculation (
Figure 2J–L). For intermediate resolutions, the maximum only appeared at seasonal and monthly scales (
Figure 2D–I).
Our results showed that the width of the mean cloud amount CI varied with geographic location. We observed a possible impact of both the number of CloudSat–CALIPSO observations, and cloud regime.
Figure 3 shows the spatial variability of the column-averaged CI width at 2.5° spatial resolution and CL = 0.95. Patterns observed for other grid box sizes and CLs were similar.
Mid-latitude CI were broadest (5%), especially close to ~50°N/S. Poleward, as the density of satellite passes per grid cell increases, the CI width becomes narrower, and eventually reaches 1% at ~85°N/S. On the other hand, the CI narrows towards lower latitudes, compared to values observed at mid-latitudes. However, in this case, the decrease is less significant (down to 3%) and is followed by an increase in CI width over locations along the Intertropical Convergence Zone (ITCZ).
Variation in CI widths within 30°N/S partially resembled the spatial distribution of low clouds (e.g., marine stratocumulus). Therefore, we recalculated the column-averaged CI width, but considering each cloud level—low, middle, high—separately.
The pattern we observed for the lower troposphere (
Figure 3B) differed noticeably from those obtained for mid- and high-levels (
Figure 3C,D). First, we noted no increase in CI width due to the ITCZ. Second, locations associated with tropical marine stratocumulus featured higher CI widths in the lower troposphere (~5%), than in middle or upper parts (~2–3%).
When considering only high-level clouds (
Figure 3D), CI widths were greatest (>5%) along the ITCZ. The tropical upper atmosphere was also the region in which variability in CI width was largest: between 0% and 8% (for 2.5° data, CL = 0.95). Given that the middle and upper atmosphere constitutes the majority of the atmospheric volume, patterns noted for these highest levels dominated column-averaged statistics (
Figure 3A).
4. Discussion
In this study, we investigated uncertainties associated with mean cloud amount calculated from joint CloudSat–CALIPSO mission data. Rather than taking a purely theoretical approach (e.g., van de Poll et al. 2006), we evaluated actual uncertainties as they exist in the empirical dataset. The magnitude of uncertainty, expressed by the width of the CI, varied with grid box size, CL, and the number of observations. Whether these uncertainties are significant for climate studies depends on the application.
The Global Climate Observing System (GCOS) and the US National Institute of Standards and Technology (NIST) have proposed some general requirements for satellite-based data products. In particular, the NIST recommends 1% accuracy for global mean cloud cover [
33], while the GCOS has adopted a wider range of target accuracies: 1% to 5%. The higher value refers to optically thin clouds, the lower value to optically thick clouds [
34]. The GCOS also calls for cloud data to be available globally, every three hours, at a spatial resolution of 50 km (0.5° at the equator). Neither the NIST nor the GCOS give requirements for vertically resolved mean cloud amount, solely focusing on column-integrated values.
The requirements given in the NIST and GCOS guidelines are parameter-oriented, meaning that they do not provide instructions on how to (technically) design an observing system as such. Any configuration is allowed, as long as the requirements are met. As parameters are investigated globally, it is unlikely that a single sensor (or a single observatory) could produce a dataset that fulfils all of the spatial and temporal requirements. As we will demonstrate, that is also true for the CloudSat–CALIPSO joint mission. Therefore, we used the NIST/GCOS requirements as a general benchmark for characterizing the performance of a lidar–radar mission with a 16-day revisit period.
CloudSat and CALIPSO circle Earth on Sun-synchronous orbits, hence they always sample the atmosphere at the same local solar time. The configuration makes it impossible to capture a diurnal cycle of the cloud amount and does not meet the GCOS temporal requirements of eight observations per day. The diurnal cycle of cloud profiles can be resolved with a single lidar mission, but only when the orbit is not Sun-synchronous. This was the case for the Cloud-Aerosol Transport System (CATS) lidar that operated onboard the International Space Station [
27]. CATS data made it possible to compute the cloud amount at a given time of the day, but only as a multi-annual mean (a mean diurnal cycle). Three-hour data were not available every day—unlike data provided by the International Satellite Cloud Climatology Project (ISCCP) [
35]. Such high temporal frequency sampling is beyond the capacity of any existing or planned lidar/ radar profiling mission. On the other hand, although ground-based lidar/ radar systems are capable of providing atmospheric profiles at very high temporal and vertical resolution, this is only possible for a limited number of fixed locations.
The footprint of the CloudSat–CALIPSO product is ~1 km, therefore the GCOS requirement of 50 km spatial resolution is, theoretically, met. Unfortunately, the narrow swath of both the lidar and the radar only allow sampling of locations along the ground track. The distance between adjacent paths leads to large data gaps. This can be mitigated by increasing the size of the grid box used for data integration. Nevertheless, a gap-free map would require a resolution below 1° (~100 km at the equator), as demonstrated in this study. For this reason, global CloudSat and/ or CALIPSO products are released at coarse resolution. For instance, the “CALIPSO-GOCCP GCM Oriented Cloud CALIPSO Product”, designed to evaluate cloudiness in Global Circulation Models is delivered at 2° resolution [
36].
Our findings only allow us to assess cloud amount accuracy requirements in the context of the CloudSat–CALIPSO joint mission. Here, we assume that “accuracy” can be approximated by the width of the CI, since the absolute (“true”) value of cloud amount is never known. We were able to calculate how many CloudSat–CALIPSO atmospheric volumes featured an estimated mean cloud amount with a CI ≤ 1%, 5%, and 10%. Statistics were calculated based on data that assumed a CL = 0.95.
Our results show (
Figure 4) that the requirement of 1% accuracy (CI = 1%) is met by ~6.5% of CloudSat–CALIPSO volumes in the troposphere, regardless of whether a 1° or 2.5° grid is used. Lowering the expected accuracy to 5% allowed more volumes to meet the requirement: 22.5% of volumes at 1° resolution, or 48.9% at 2.5° resolution. On the other hand, if the requirement is to have at least 99% of volumes meet the accuracy criterion, the criterion itself would have to be 20% for 1° data, or 8% for 2.5° data.
The extent to which the accuracy requirement can be met varies spatially (
Figure 5). Fewer than half of volumes in the atmospheric column met the 5% requirement at mid-latitudes and in the ITCZ (
Figure 5B,E). On the other hand, almost all volumes (>80%) met the 5% requirement in polar regions and in the tropics. At high latitudes, this was due to frequent sampling by the lidar and radar, while the tropics featured an almost-constantly cloud-free atmosphere (except for shallow convection in the lower troposphere).
Our statistics clearly suggest that 1% accuracy (i.e., CI = 1%) for annual mean cloud amount is not achievable with a mission that uses the CloudSat–CALIPSO configuration, even with a five-year time series. In order to have >99% of mean cloud amount estimations in the troposphere, with CI = 1%, the spatial resolution of the cloud climatology would have to be below 10°. However, 5% accuracy is achievable for almost all regions of the troposphere at 5° resolution. Meeting the requirements at seasonal (
Figure 4B) and monthly (
Figure 4C) scales is more challenging.
An alternative approach to evaluating the degree of uncertainty is to test whether uncertainties are smaller than the climate change signal predicted by cloud amount trends. Chepfer et al. [
2] used climate models to produce lidar-like cloud profiles for the present-day climate, and for a future, warmer atmosphere (i.e., a +4 K increase in global air temperature). The latter authors only used lidar data, distinguishing between optically thick and thin clouds. This was a slightly different configuration to the one evaluated in this study (joint CloudSat–CALIPSO profiles, all clouds).
Nevertheless, we applied our CLs to the differences between the present and the warmer climates reported by Chepfer et al. [
2]. Specifically, we compared the vertical change in CI width from our research with the vertical change in cloud amount anomaly reported in
Figure 3 in Chepfer et al. [
2]. The “anomaly” was defined as the difference between the future and the present CALIPSO-like cloud amount profile (the authors considered two models: the CanAM4 model, and the HadGEM2 model). Whenever the cloud amount anomaly at a given altitude was greater than the CI width for that altitude, we concluded that the climate signal exceeded the uncertainty (noise) level.
We found that the magnitude of uncertainty in the CloudSat–CALIPSO 5-year climatology makes it impossible to detect statistically significant changes in cloud amount at most atmospheric levels. Considering thin clouds, the only detectable changes are in the upper troposphere (>10 km), regardless of the latitude. For thick clouds, a statistically significant change may be expected at altitudes of between 8 km and 12 km in the tropics, and below 5 km in polar regions. Again, it should be emphasized that we investigated joint lidar–radar profiles, while Chepfer et al. [
2] only evaluated lidar-like observations.
We evaluated the width of the CL for mean cloud amount. Various factors that influence this width were investigated: the cloud regime (average cloudiness, its variability), geography (longitude, latitude, altitude), and technical/ statistical aspects (CL, the number of observations, grid size). An interesting question was which of these factors (or group of factors) had the largest influence on CI width. To find this out, we used a multivariate regression model, followed by a decomposition of the resulting coefficient of determination (R2).
Although regression models require regressors to be independent, we intentionally decided to not exclude any variable (
Table 3). This was because our goal was not to develop a typical, predictive model, but rather to gain a general insight into the contribution of different variables to CI widths. The contribution was calculated using the relative importance (‘realimpo’) package developed by Grömping [
37] and implemented in the ‘R’ statistical environment. First, we constructed a linear multivariate regression model, then each individual regressor’s contribution to the model’s R
2 was calculated following the method given in Lindeman et al. [
38].
For our CloudSat–CALIPSO dataset, the considered model (
Table 3) explained 65.3% of CI variability at 1° resolution, and >87% at coarser resolutions. As expected, the cloud regime was the dominating factor, since cloud amount and its standard deviation directly impact the bootstrap’s standard error, and thus the CI width. The only unknown was the relative impact of the cloud regime. The analysis found that the factor constituted as much as ~60–70% of R
2, regardless of the spatial resolution of the grid. Of the “statistical” variables, a predefined CL was always twice as important as the number of observations, and together they contributed ~30% to R
2. Geographical factors were practically irrelevant.
The results of our assessment of the relative importance of different factors leads us to conclude that, on a global scale, the sampling frequency of the CloudSat–CALIPSO mission is sufficient to provide reliable cloud amount statistics. A higher sampling frequency would not result in a narrower CI, as it is primarily determined by the cloud regime—a factor that is not controlled by humans (unlike an orbit design). On the other hand, the statistic given in
Table 3 is globally-averaged, meaning that for some locations the actual number of observations is much smaller than the global average and, for those volumes, the number of observations will be higher. Additionally, the global statistics is, to some extent, biased by the number of cloud-free and almost-cloud-free volumes located in the mid- and upper-troposphere at low latitudes. These volumes were characterized by narrow CIs regardless of the number of observations, as the variation in cloud amount was very small, even monotonic.
5. Summary and Conclusions
Our study evaluated uncertainties in vertically-resolved cloud amount, resulting from the unique, joint CloudSat–CALIPSO climatology (2B-GEOPROF-LIDAR product, version P2_R05). Our dataset covered the pre-Daylight Only Operations era of the CloudSat mission, i.e., the longest unbiased record of joint radar–lidar observations. Uncertainties were examined in terms of the CI, calculated with the bootstrap approach. In order to obtain a comprehensive insight into factors that control CI widths, we simultaneously considered four spatial resolutions (1.0°, 2.5°, 5.0°, and 10.0°), four confidence levels (0.85, 0.90, 0.95, and 0.99), and three time scales (annual, seasonal, and monthly). Additional statistics were provided for the more generalized low-, mid-, and high-levels defined by the WMO. We found that:
average CI width was 8.27% at 1° resolution, and CL = 0.95. However, CI widths: (1) decreased four times as the spatial resolution increased from 1° to 10°, (2) doubled as the CL increased from 0.85 to 0.99, and (3) tripled as the number of data-months increased from one (monthly mean) to twelve (annual mean);
mean CI width was largest in the mid-latitudes and decreased towards the poles and the equator. The greatest range of CI width variability occurred in the tropics and resembled the spatial pattern of marine stratocumulus and the ITCZ. Regions of tropical stratocumulus were correlated with higher CI widths in the low troposphere, and the opposite trend was observed in overlying levels. In the ITZC, CI widths could only be calculated for the mid and high troposphere;
based on a general analysis of relative importance, the cloud regime (mean cloud amount, and its standard deviation) was the most important factor impacting overall CI width. On a global scale, the number of observations was an order of magnitude less significant than the cloud regime, or the assumed confidence level. This suggests that uncertainties in the CloudSat–CALIPSO annual climatology result from the cloud regime (i.e., the typical cloud amount and cloud amount variability at a specific location), rather than the current sampling strategy.
The central question of our study was to establish whether it is possible to obtain a mean cloud amount from joint CloudSat–CALIPSO observations, at 1 or 5% accuracy, with a high level of confidence (>0.95), and at a fine spatial resolution (1–2.5°). Using CI width as an indicator of accuracy, we demonstrated that the answer is negative, either at 1% or 5% accuracy. The 1% requirement can only be satisfied if profiles are spatiotemporally averaged at 10° resolution, and only for a five-year mean. The looser criterion of 5% can only be met at four times lower resolution (5°).
Existing uncertainties are unlikely to prevent the detection of a climate change signal in high clouds globally, but only for thin clouds. Change in thick clouds may only be detectable in the tropics, above 8 km, or in polar regions, below 5 km. For other locations, altitudes and cloud types, the CI widths we noted were larger than model-predicted change in cloud amount. Although our findings need to be confirmed in more detailed studies, we were able to compare our results with lidar-only cloud change scenarios.