1. Introduction
Although traditional global navigation satellite systems (GNSSs), as sophisticated and complex systems, are widely used in navigation, positioning, and timing, GNSSs still cannot overcome their own bottlenecks, such as their weak signal power (only 20 W power interference can cause denial of a cell’s GNSS signal [
1]), coupled with multiple paths, especially in challenging environments, such as lush forests, canyons, cities with tall buildings, indoor locations, and polar regions. GNSS signals are easily blocked, and the number of visible satellites decreases as the visible elevation angle increases, leading to unusable multisatellite positioning. There are also deficiencies in the accuracy, reliability, availability, and anti-interference.
In recent years, a program to provide global internet access based on broadband low earth orbit (LEO) constellations has been reproposed. The purpose of this program is to provide truly global and robust broadband coverage and access, to expand the coverage of geosynchronous (GEO) satellites to polar regions, and to improve the user positioning accuracy [
2]. Compared with traditional GNSSs, LEO constellations offer the advantages of a large number of satellites, high accuracy, and high availability and the LEO system can be used for communication, cm-level navigation enhancement, and positioning services. In addition, LEO satellites are closer to the earth, which means that less path loss and the stronger signal power undoubtedly enhance the anti-interference ability of the system, and they are considered to be an important direction for future development. Radio communication and navigation have many similar technical foundations, but they have different needs in terms of information transmission and signal measurement and have evolved along their own routes. With the rise of concepts such as the internet and autonomous driving, positioning and communication functions have become inseparable, and the necessity of communication and navigation integration has become a consensus. Therefore, the concept of integration of the technology of positioning, navigation, timing, remote sensing, and communication (PNTRC) has been proposed in recent years [
3] PNTRC can be used as a space-based internet access station to solve global internet access problems, but also as a navigation and communication information source to achieve the rapid convergence of precise positioning, communication, and navigation realized by only one link. Therefore, the study of LEO constellation single-satellite positioning technology solutions based on PNTRC has the outstanding advantage of a high availability, thereby providing an opportunity to solve the problem of location services in the challenging environments mentioned above.
To apply the LEO constellation to the field of navigation and realize the PNTRC, many scholars have made bold attempts and provided many creative solutions. Reference [
4] studied the feasibility and performance of the LEO constellation as a potential navigation enhancement platform and evaluated and analyzed the comprehensive performance, coverage rate, and signal strength of the LEO constellation. The results show that the LEO system has a better performance than GNSSs and can be used as a navigation enhancement platform in challenging environments. Reference [
5] Based on PNTRC, the LEO communication satellite signal and the E-911 ground cellular signal have been integrated to provide positioning services. Reference [
6] The new ideas and functions of PNTRC have been integrated into the signal system, and the basic technology of PNTRC has been researched at the signal-design level. To realize the benefits of PNTRC to enhance the GNSS system and improve the usability of LEO constellations, reference [
7] proposed a global navigation enhancement system based on the LEO constellation. To improve the navigation availability and attain a better anti-jamming ability, reference [
8] (from the perspective of a signal design system) proposed a frequency-hopping binary offset carrier (BOC) modulation scheme with a strong anti-interference ability, in order to improve the anti-jamming capability of LEO constellation navigation at the signal-design level.
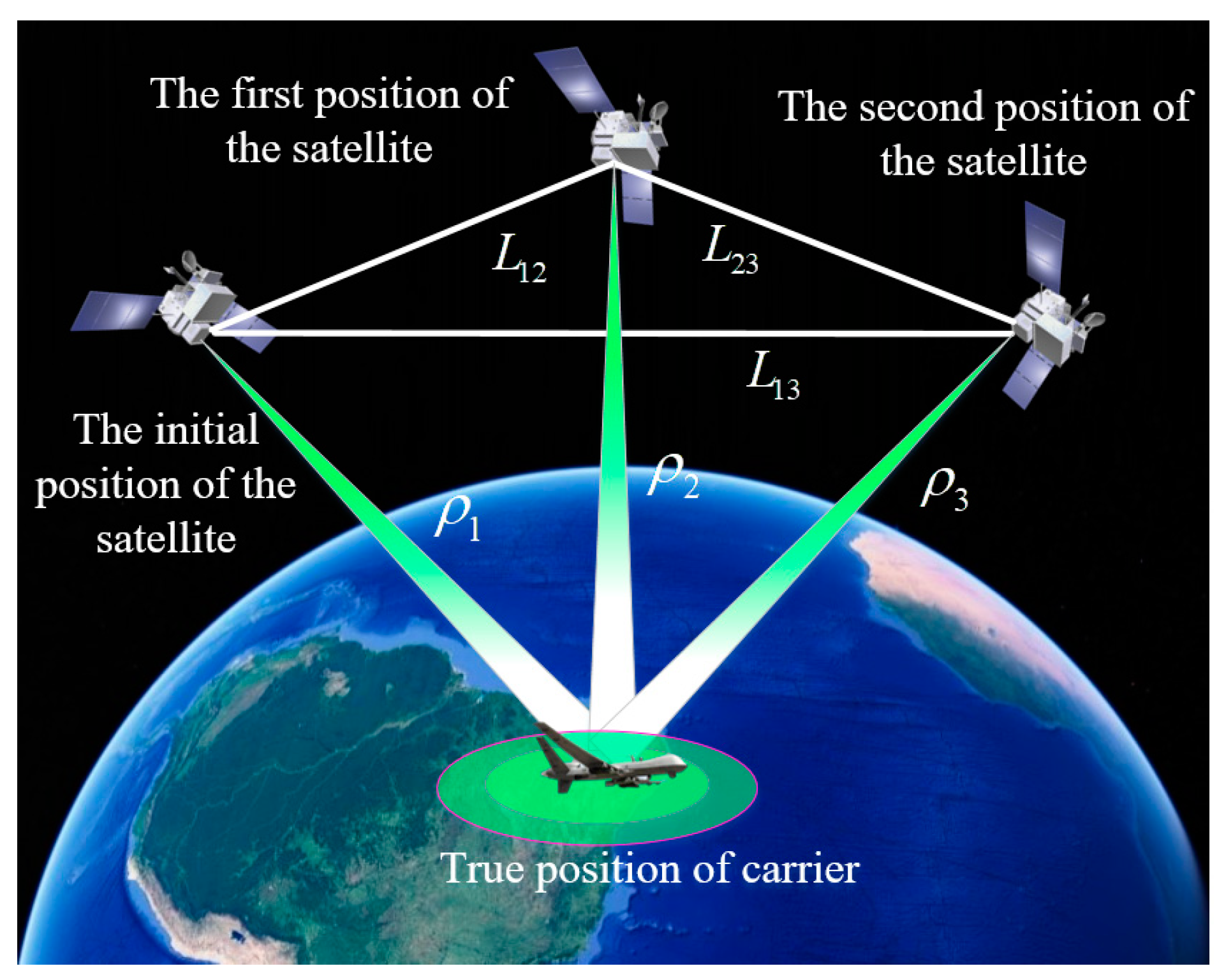
For exploration of the application of a single satellite in navigation and positioning, references [
9,
10,
11] located the radiation source by measuring the phase difference or frequency of the incoming wave. Additionally, references [
12,
13] proposed a positioning method based on a single-satellite Doppler integral, which has a high positioning accuracy for static targets, but the positioning accuracy decreases rapidly for dynamic targets. To overcome this problem, reference [
12,
13,
14] proposed a scheme based on integrated navigation. Moreover, reference [
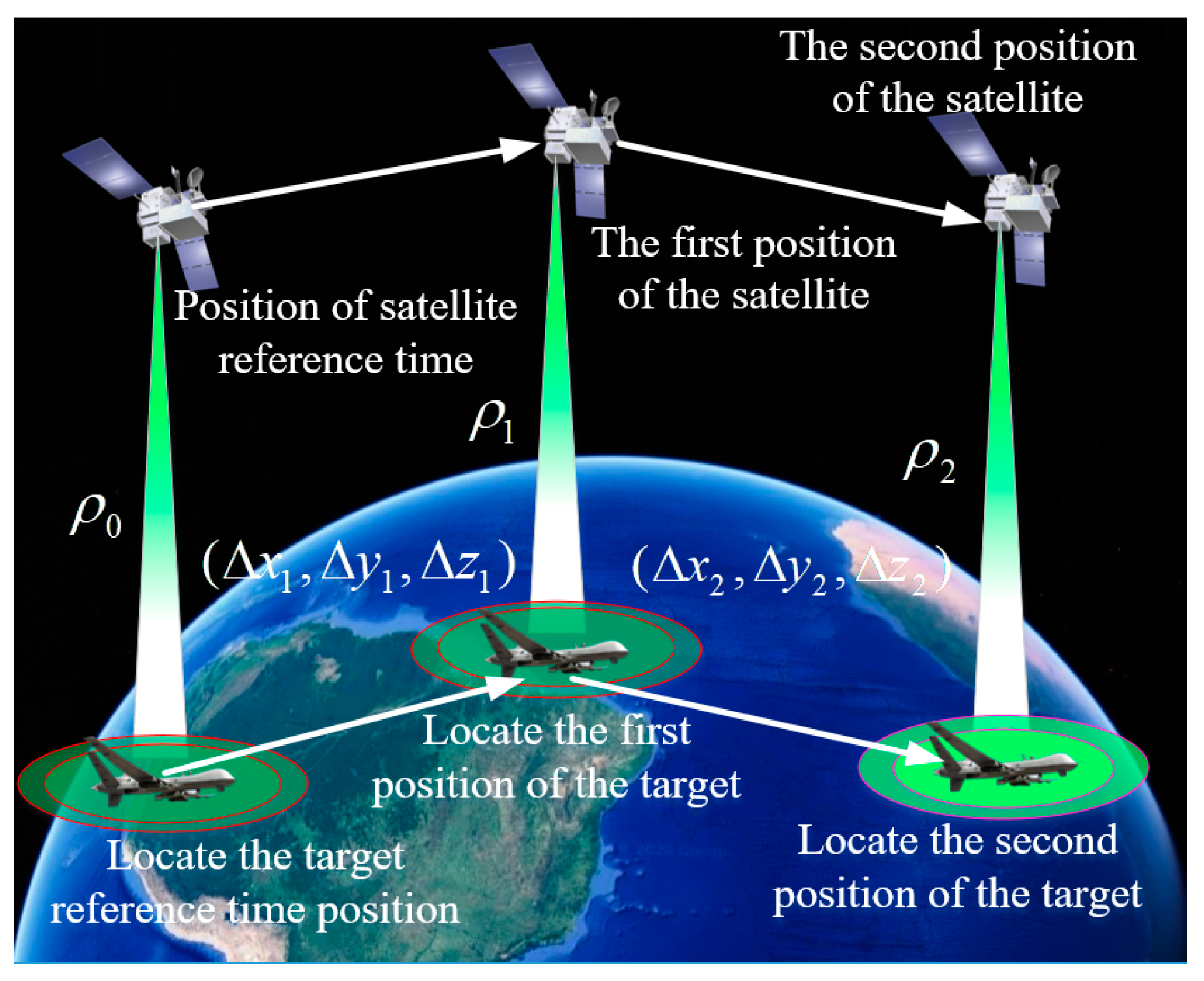
15] proposed a single-satellite positioning method based on the inertial navigation system (INS) and Doppler pseudorange difference. To solve the problem of parameter estimation and target location being divided into two independent stages in traditional single-satellite positioning, a single-satellite passive location method using spatial sparsity is proposed in [
16].
To cope with the demand for location services under challenging environmental conditions, different scholars have provided different solutions in different positioning situations. Reference [
17] developed an INS that can be used by a navigation vehicle to assist INS through Doppler measurements and tightly coupled LEO satellite signals when GNSS signals are not available. Furthermore, reference [
18] pointed out that under the condition of global coverage, users may have 1–3 visible satellites in different times and places and proposed that under different conditions, only Doppler observations should be used for positioning solutions. Reference [
19] proposed a Doppler positioning algorithm based on a LEO satellite system in a complex environment when the GPS signal is accidentally blocked. To improve the dynamic positioning accuracy of single-satellite positioning in emergencies, reference [
20] proposed an INS-aided single-satellite positioning algorithm in the case of GNSS system rejection. This INS-aided single-satellite positioning algorithm can provide certain space-based positioning services for dynamic targets.
The new single-satellite integrated navigation and positioning algorithm based on broadband LEO constellation communication links offers a low-cost approach, a strong engineering practicability, and an anti-jamming scheme. The accuracy of navigation and positioning is better than the accuracy of navigation and positioning of the traditional algorithm of single-satellite and MEO constellation algorithms, and effectively overcomes the problem of INS divergence. The new single-satellite integrated navigation and positioning algorithm can provide a cm-level navigation scheme for relevant personnel engaged in outdoor tourism, exploration, or scientific research in challenging environments, such as lush forests, canyons, high latitude areas, and polar regions, without relying on GNSS.
In
Section 2, based on introducing the traditional single-satellite positioning algorithm, we give the principle of our algorithm and compare it with the traditional algorithm. Next, in
Section 3, we model and analyze the errors involved in the system. In
Section 4, based on the unscented Kalman filter (UKF), we model the state and observation vectors of the algorithm and give the corresponding state and observation equations. Finally, in
Section 5, we simulate the algorithm and perform qualitative and quantitative analysis for different scenarios, comparing our algorithm with the traditional single-satellite navigation algorithm, and present our conclusion in the last section.
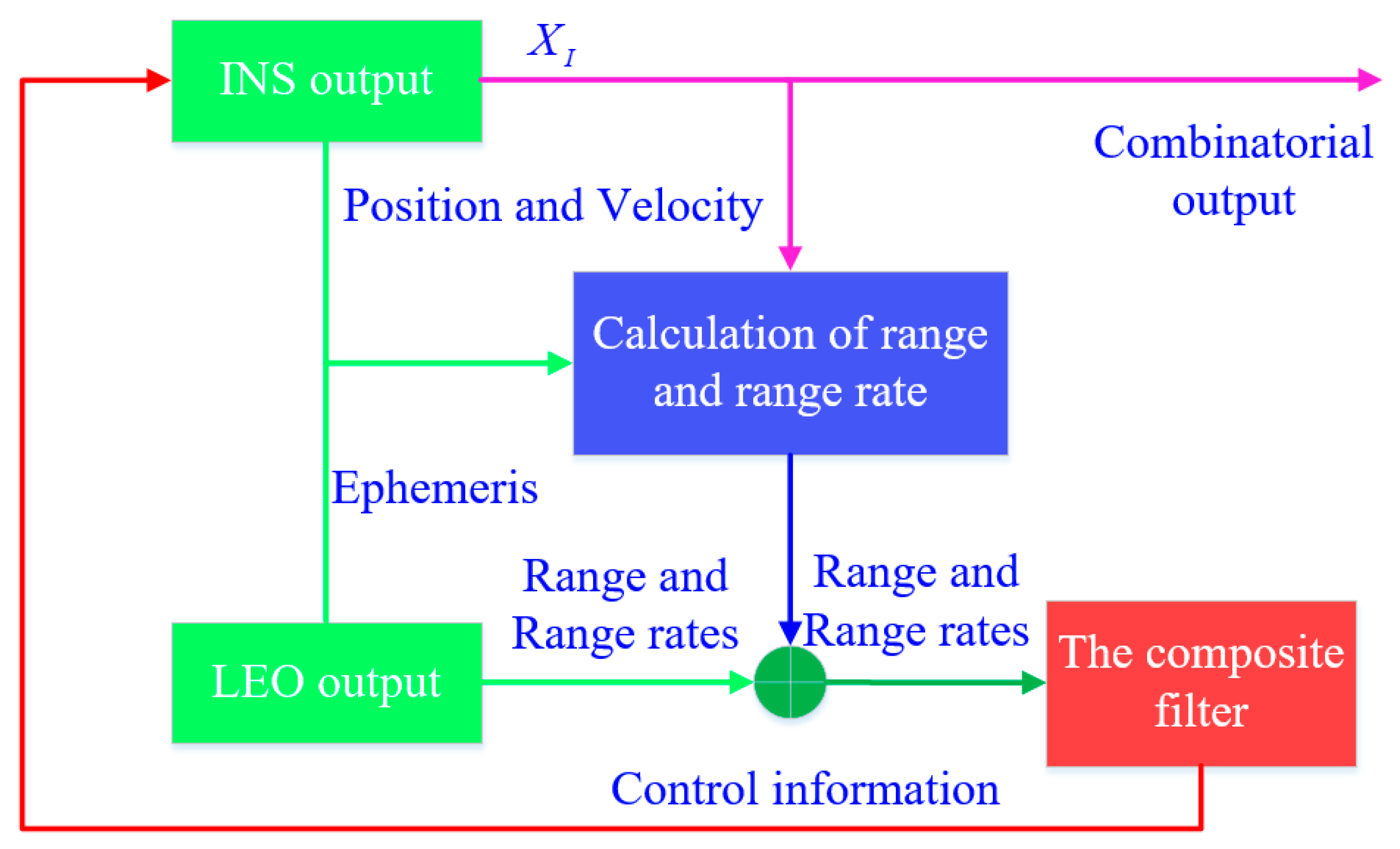
4. State Modeling of a Single-Satellite Integrated Navigation Positioning Algorithm Based on Broadband LEO Constellation Communication Links
Since the loose combination requires the GNSS solution result, at least four visible satellites are required. In some places, due to occlusion or a challenging environment, the number of visible satellites cannot be satisfied. At this time, the loose combination cannot be used. However, the close combination is a high-level combination mode. In the close combination mode, not only will the GNSS correct the INS, but the INS will also correct the GNSS. This bidirectional auxiliary method makes the positioning accuracy significantly higher than the positioning accuracy of the loose combination. Even if the number of visible satellites is fewer than four, the tightly integrated mode can work stably for a period of time.
Therefore, to match our algorithm, we use tight integrated navigation to analyze and employ the UKF algorithm for filtering.
4.1. State Equation of Single-Satellite Integrated Navigation and Positioning Algorithm Based on Broadband LEO Constellation Communication Links
When designing the algorithm of an integrated navigation system, we usually use the indirect filtering method. The state variables of the system include two parts, namely, the error of INS and the error of GNSS. However, the scene applied to the integrated navigation algorithm in this paper is the three-dimensional position navigation and positioning of aircraft under a LEO constellation. Since the state equation of GNSS is similar to that of INS, only INS error is listed here.
In the process of selecting the state variables of the INS state equation, according to
Section 3.1, the attitude error, velocity error, position error of INS, first-order Markov drift, and Markov offset of the gyroscope and accelerometer can be gathered together to obtain the state variables as follows:
where
and
denote the longitude error and altitude error, respectively.
The error state equation of INS is as follows:
The 15-dimensional state variables
are shown in Equation (32), and the process noise vector is
where
,
, and
represent the random drift noise of the gyroscope in the NED direction, and
,
, and
represent the random drift noise of the accelerometer in the NED direction.
The state transition matrix is a -dimensional parameter matrix, and is a -dimensional noise driving matrix.
Similarly, the noise drive matrix
is as follows:
According to the above analysis, the state equation of the INS is as follows:
where
,
,
and
.
4.2. Observation Equation of Single-Satellite Integrated Navigation and Positioning Algorithm Based on Broadband LEO Constellation Communication Links
Generally, the loose combination observation equation is based on the position and velocity combination, and the close combination observation equation is based on pseudorange and pseudorange rates. For the aircraft navigation and positioning in the incomplete observation mode of GNSS, the loose combination mode is not applicable. Therefore, the single-satellite integrated navigation and positioning algorithm based on broadband LEO constellation communication links adopts the tight combination mode, and the observation equation is introduced below.
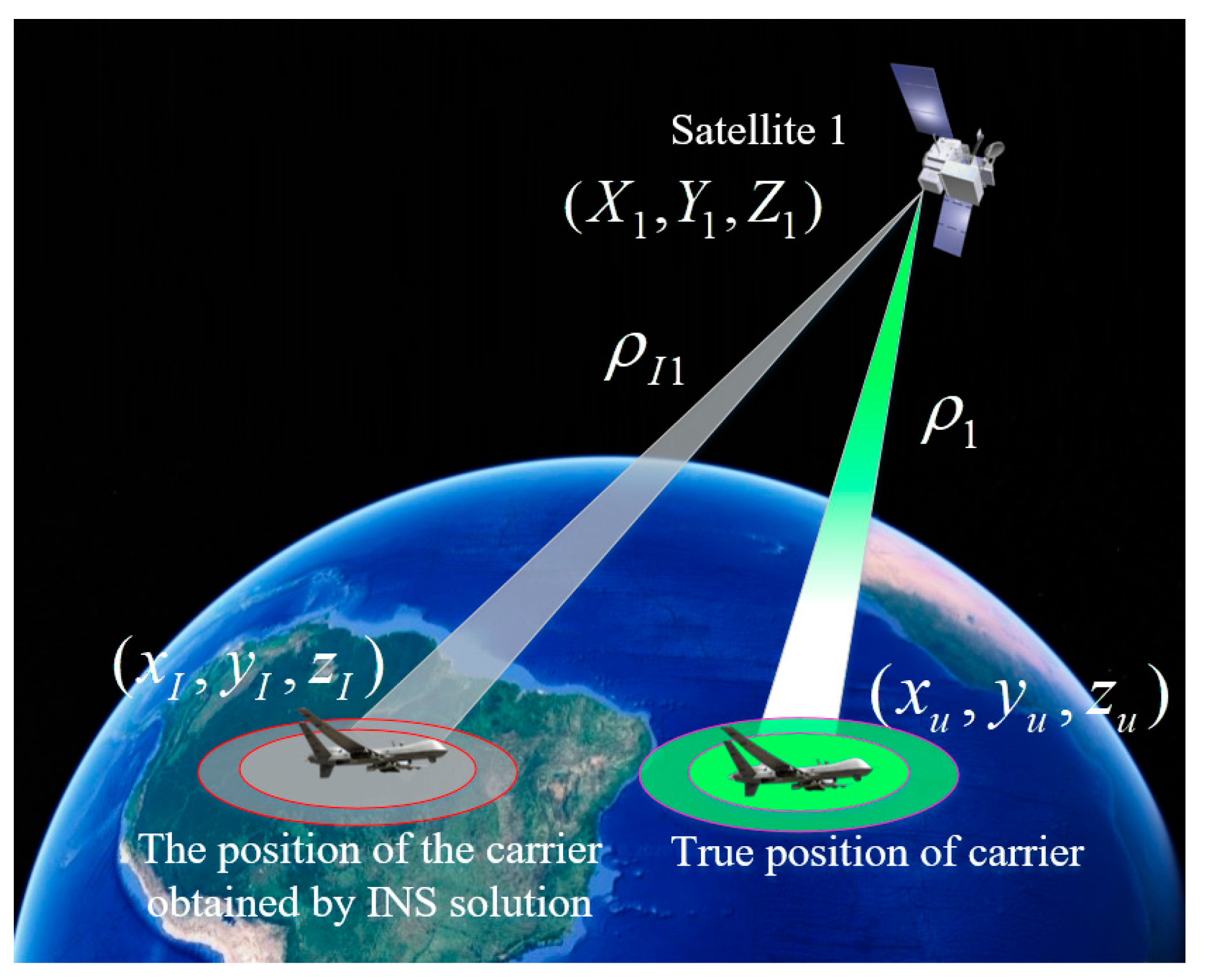
In the ECEF coordinate system, the carrier position calculated by INS is assumed to be , the satellite position calculated by LEO satellite ephemeris is , and the real position of the carrier is .
The pseudorange from the carrier to the GNSS satellite obtained by INS is as follows:
where the superscript
denotes the
th satellite.
Let Equation (37) be expanded by the Taylor series at the true value. Taking the first and second order derivatives, we can obtain
where
is the true distance from the carrier to satellite
.
Let
. Then, Equation (38) can be expressed as follows:
The pseudorange measured by the GNSS receiver is as follows:
where
is the pseudorange measurement white noise of the
th satellite
.
According to Equation (39) and Equation (40), the pseudorange difference observation equation of INS and GNSS can be calculated:
According to the previous discussion, the position state variables of the geographical coordinate system are
,
, and
, while the position state variables of the ECEF coordinate system are
,
, and
. Through the coordinate transformation matrix
, the transformation of position state variables can be completed. The position expression of the transformed ECEF coordinate system is as follows:
Then, after omitting the infinitesimal in Equation (42), the two sides of the equation take the differential at the same time, and the state transfer matrix of the error from the geographical system to the ECEF coordinate system is obtained:
In the GNSS/INS integrated navigation system, if the number of satellites is
, then the pseudorange observation equation obtained from Equation (41) is as follows:
where
In the same way, the pseudorange rate from the carrier to the GNSS satellite calculated by INS is as follows:
The pseudorange rate that is output by the GNSS receiver can be obtained by deriving the pseudorange
in Equation (40):
By combining Equation (47) with Equation (48), the pseudorange rate difference observation equation of INS and GNSS can be obtained:
Similar to the pseudorange error, the velocity error in the geographical coordinate system must be converted into the velocity error in the ECEF coordinate system, as shown in the following formula:
By comparing this with Equation (44), the measurement equation of the pseudorange rate can be obtained as follows:
where
By combining the observation equations of the pseudorange and pseudorange rate information, we can obtain the closely combined observation equation:
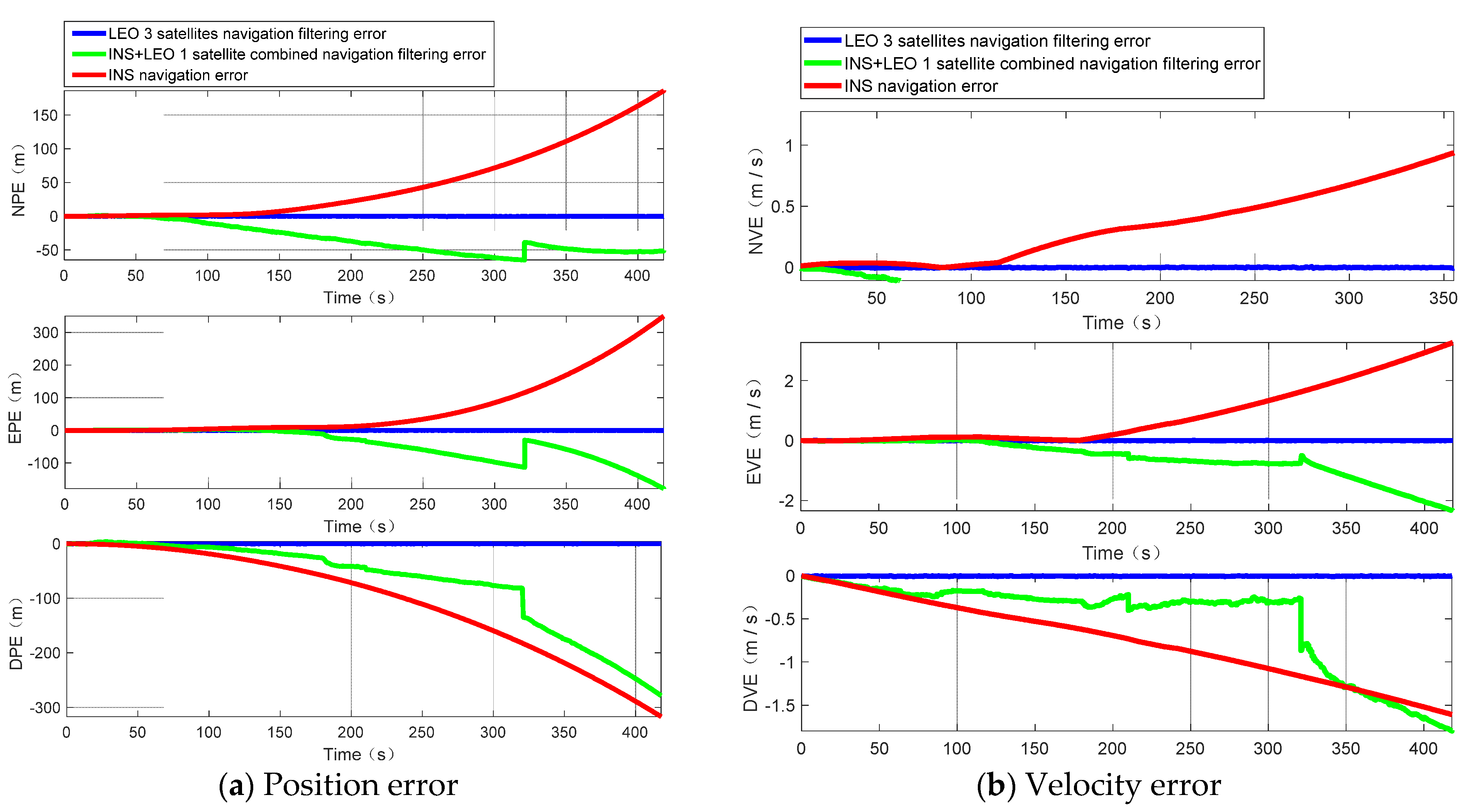
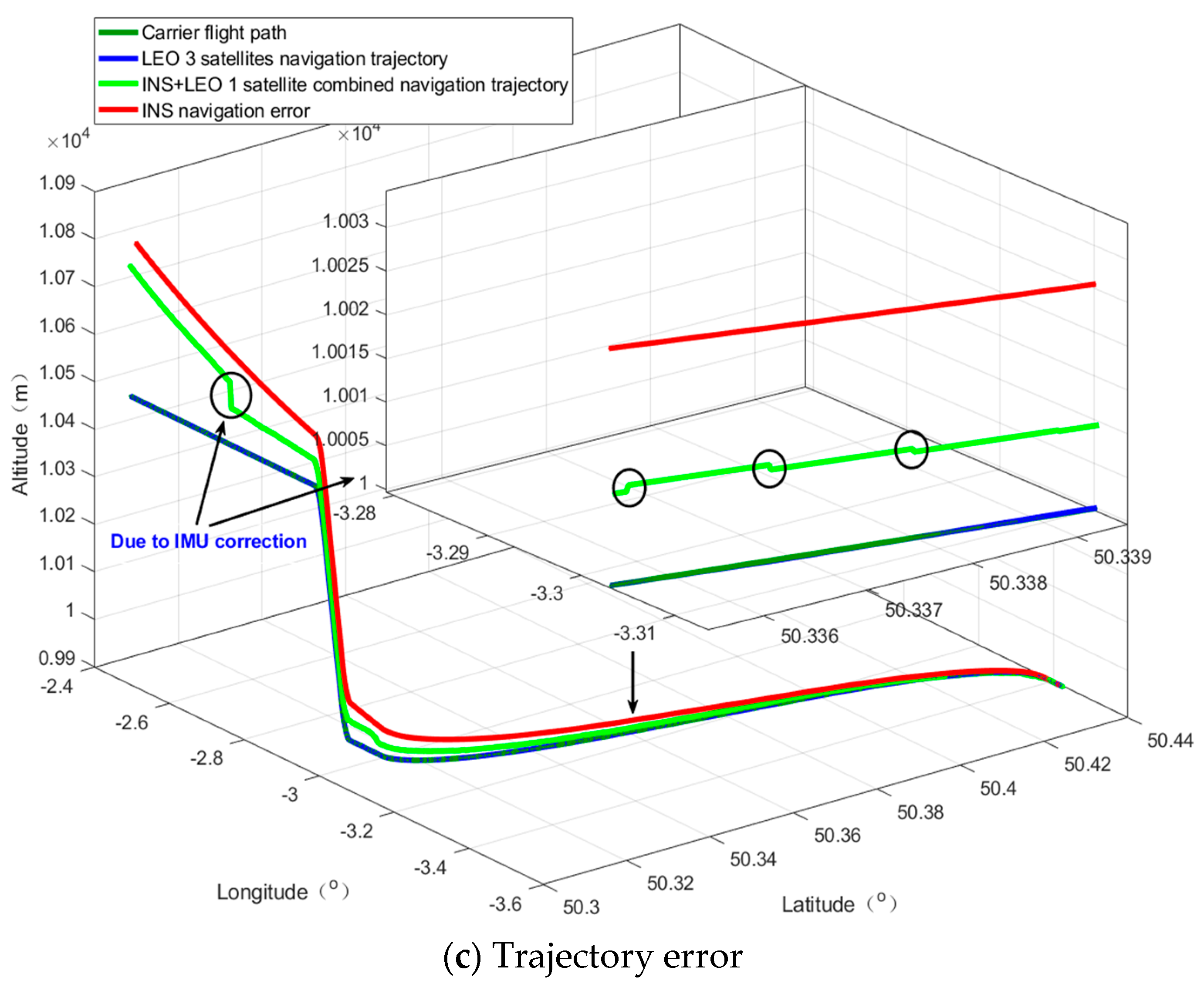
6. Results
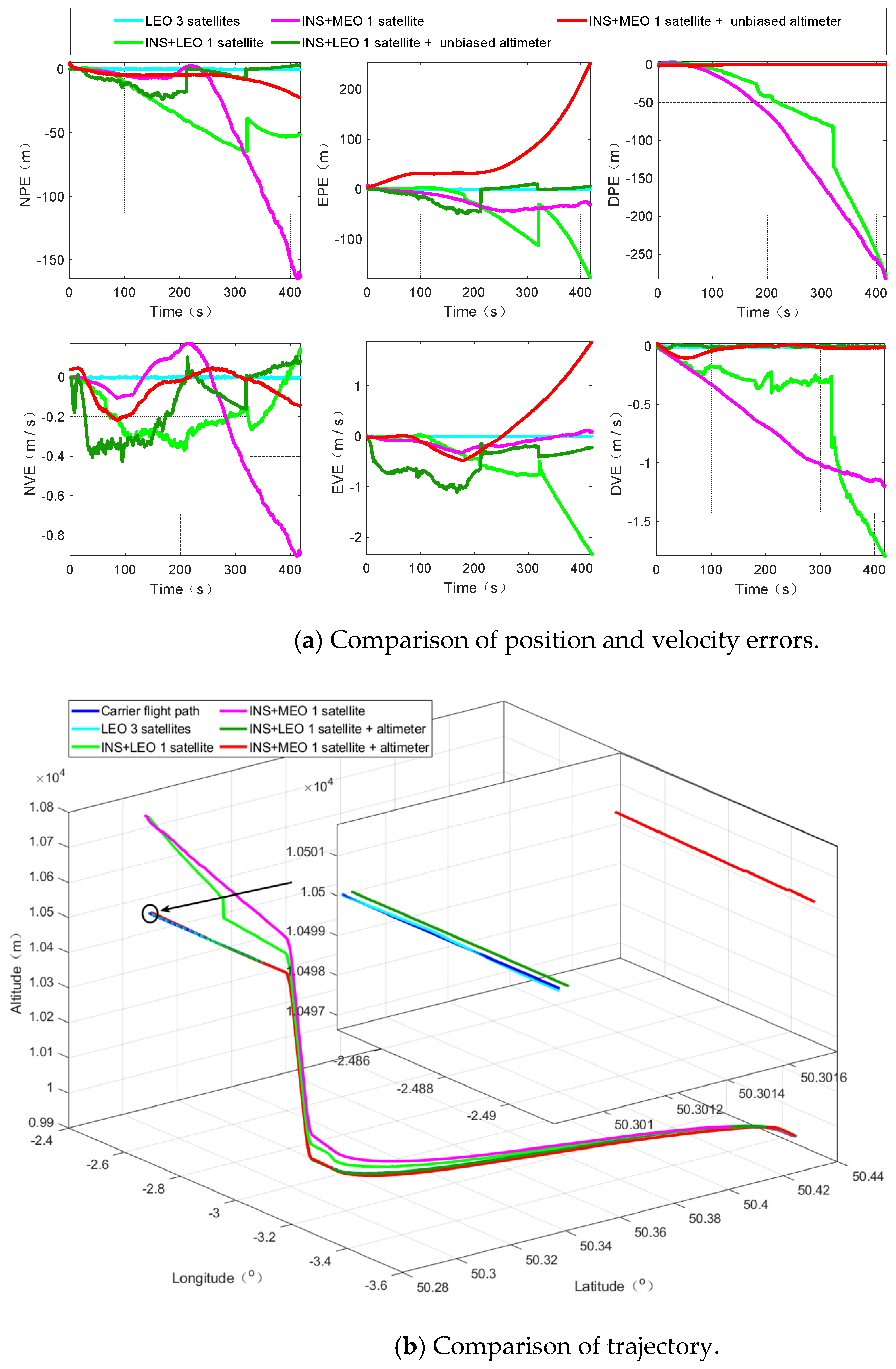
This paper presents a low-cost, high engineering ease-of-use, and strong anti-jamming capability tool for the high-precision and real-time positioning requirements in challenging environments. Our algorithm is based on the LEO giant constellation. It has a realistic material basis and actual needs. Space X, OneWeb, and Telesat are intensively conducting research and subsequent prototype satellite launches, striving to achieve seamless internet interconnection in any corner of the world and high-precision positioning at a cm level.
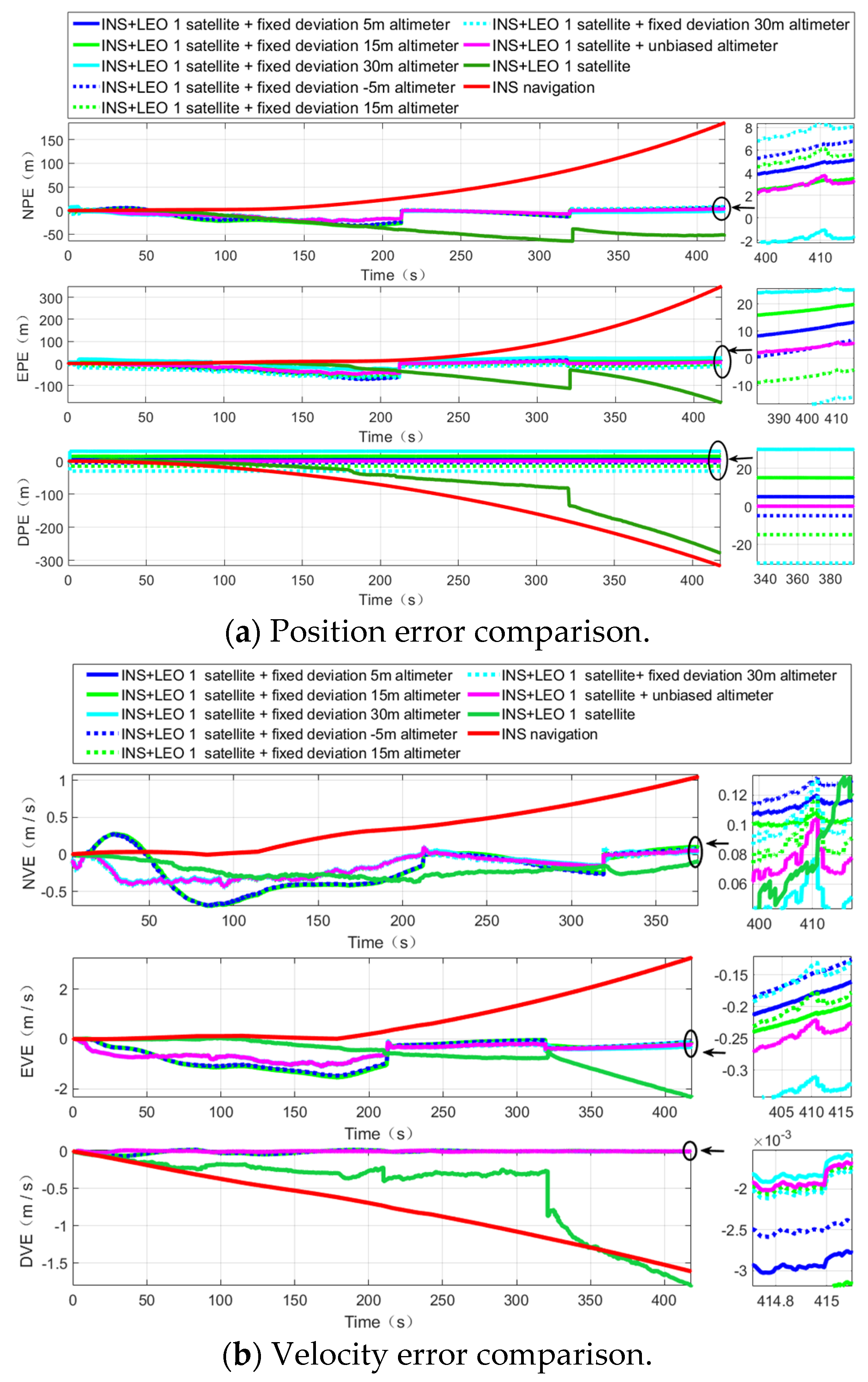
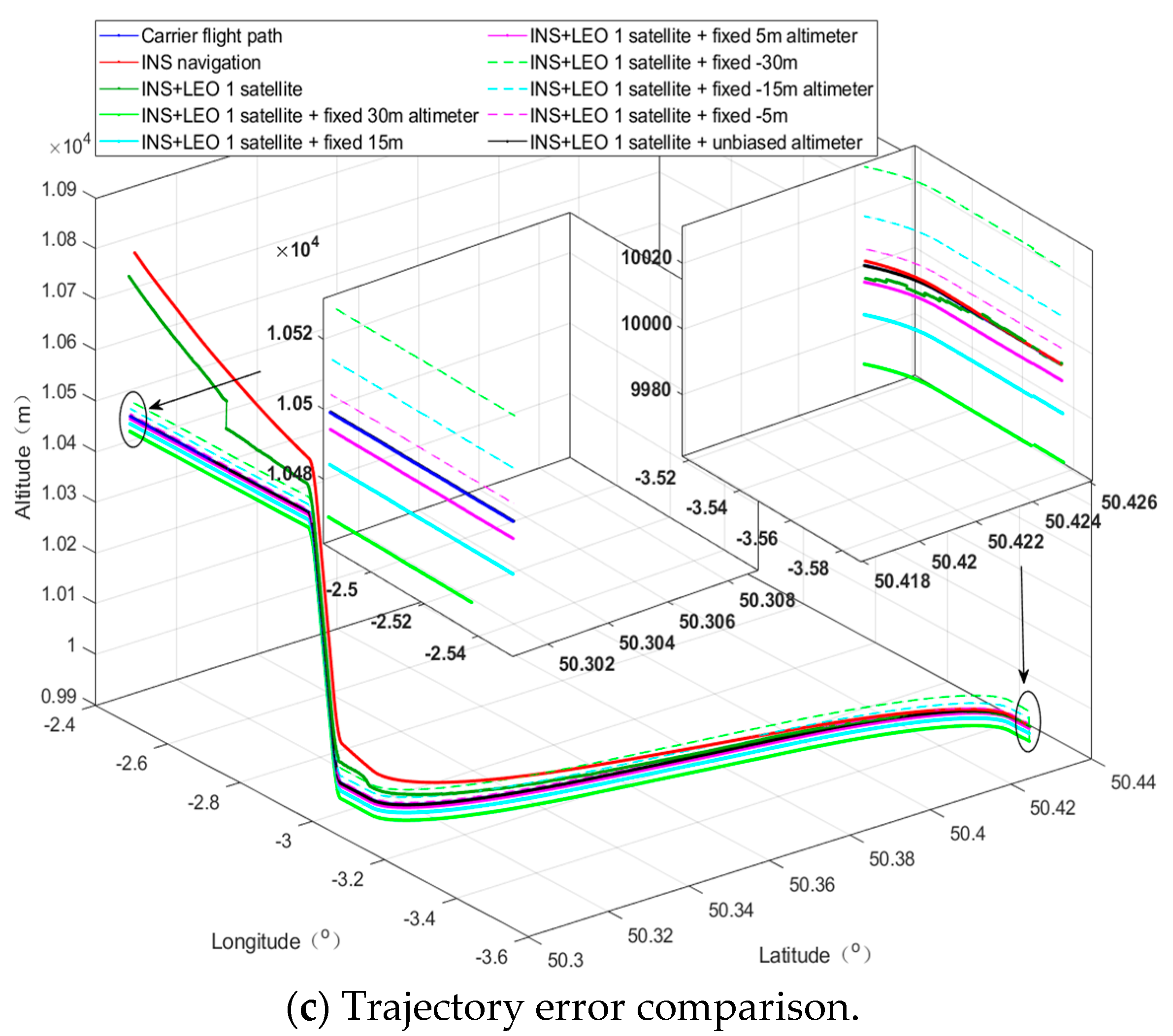
Through our research, we can find that, even in the scenario without an altimeter, our algorithm can provide basic location services; when combined with an altimeter, it can effectively overcome the divergence problem of INS and significantly improve the navigation and positioning accuracy in challenging environments, and when the altimeter deviation is small, the positioning accuracy can be further improved. With the advancement of modern electronic technology, it is not difficult to obtain an altimeter with a smaller deviation; in addition, we also verified from the perspective of simulation that the LEO constellation is more suitable for the implementation of the PNTRC scheme, which benefits from the advantages and potential advantages of the LEO constellation. Compared with the traditional single-satellite positioning algorithm, our algorithm is an implementation scheme of PNTRC, which eliminates the clock bias. Additionally, there is no need to exchange time redundancy for spatial redundancy for positioning, there is no positioning delay, and the positioning accuracy is significantly better than that of traditional algorithms.
Therefore, there are various signs that our algorithm can satisfy the requirement for location services in challenging environments, such as lush forests, canyons, cities with towering buildings, etc.