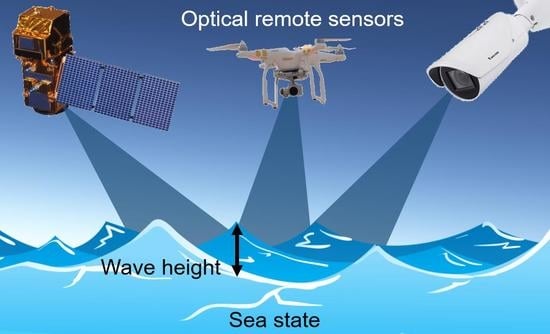
Sea State from Single Optical Images: A Methodology to Derive Wind-Generated Ocean Waves from Cameras, Drones and Satellites
Abstract
1. Introduction
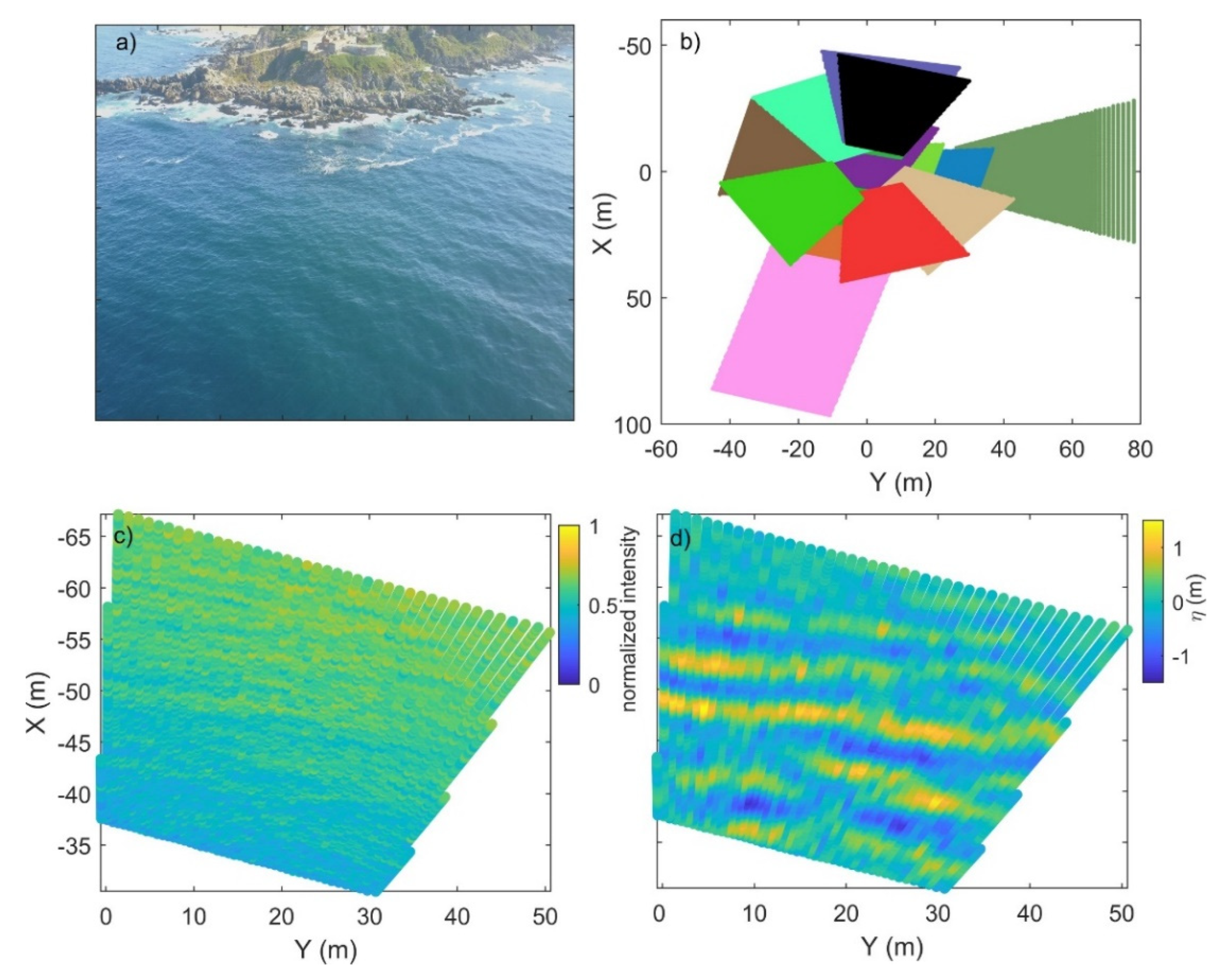
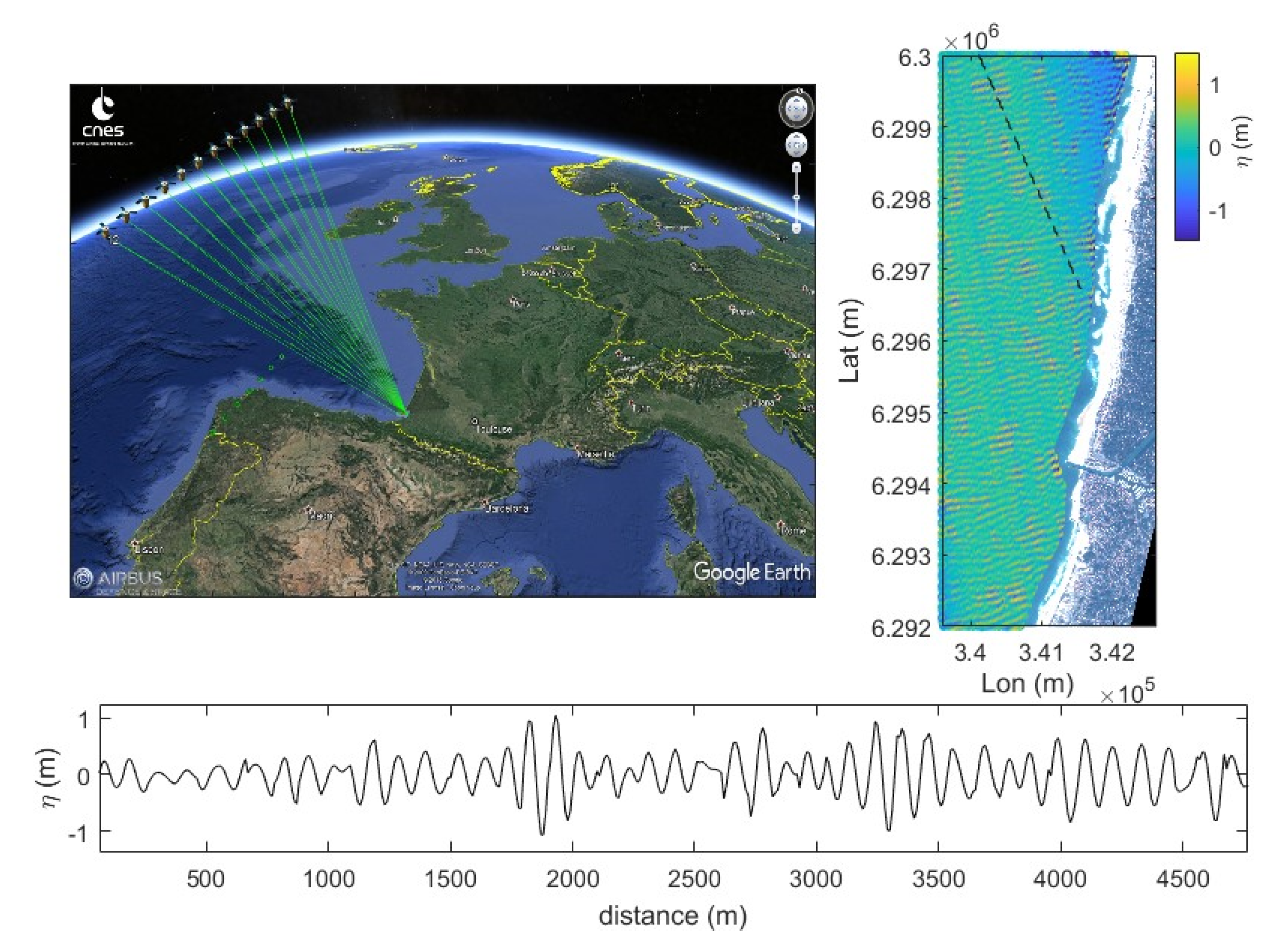
2. Datasets
3. Method
η(ρ, γ) = δρ S(ρ, γ)
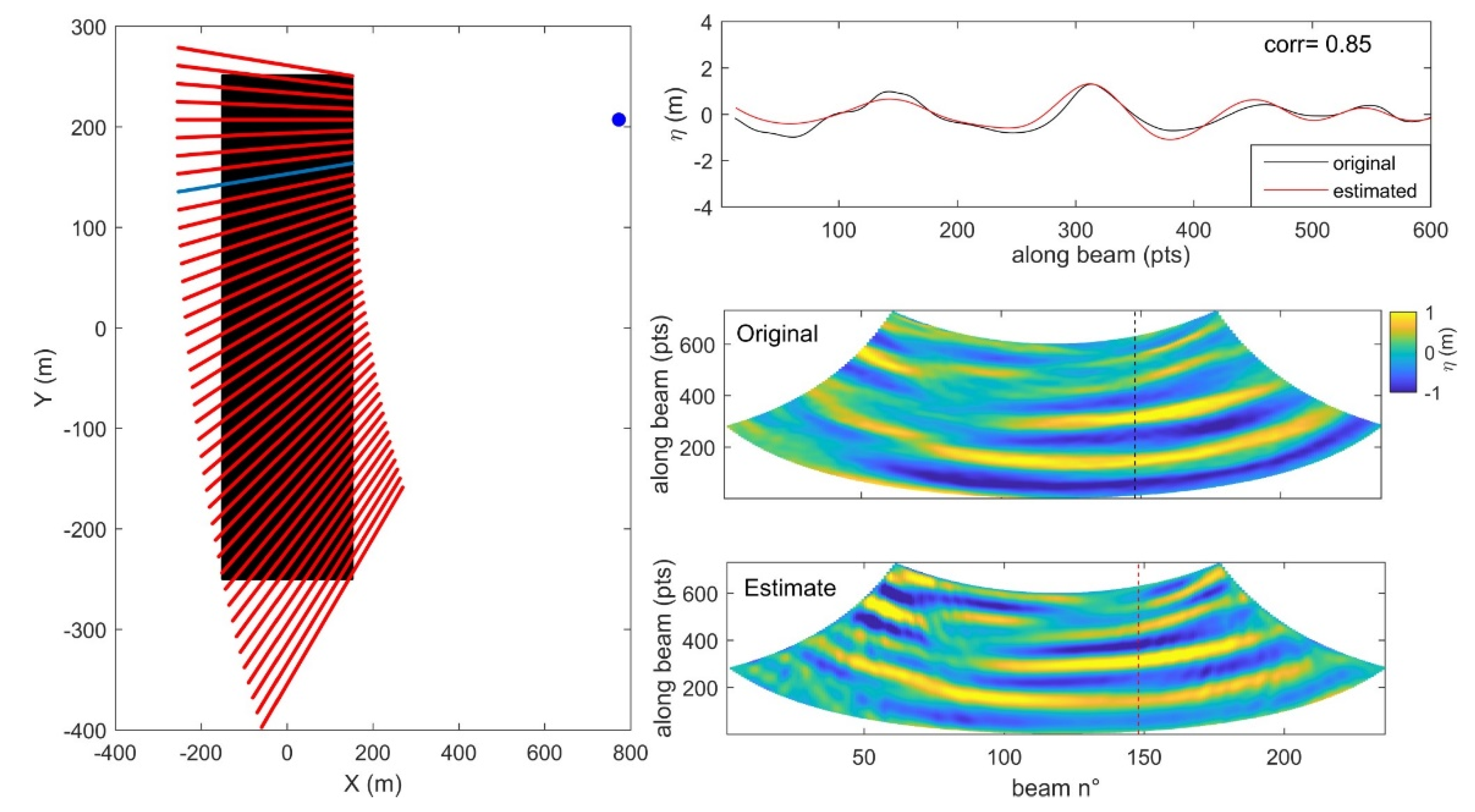
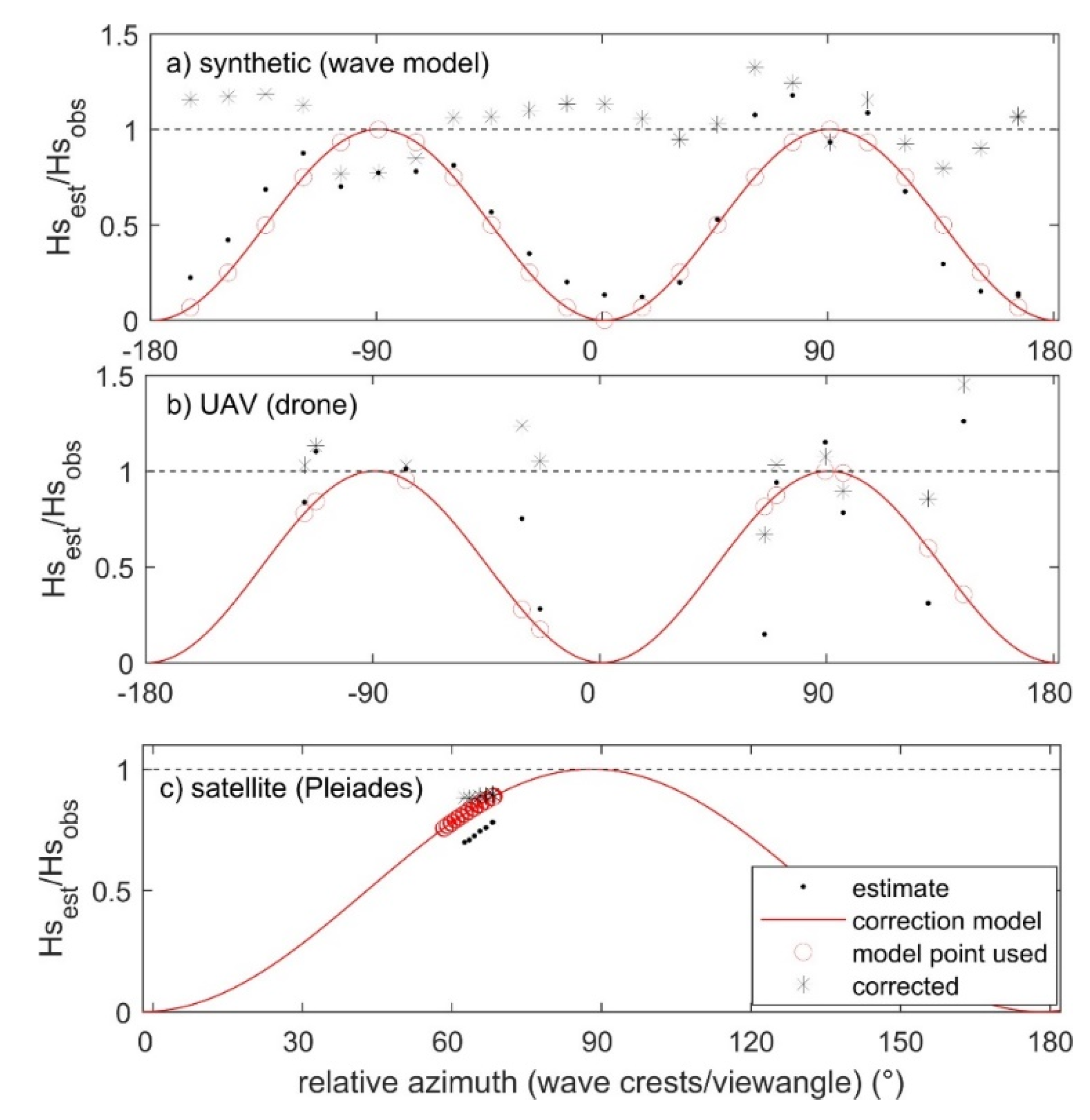
4. Results
5. Conclusions and Way Forward
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ardhuin, F.; Stopa, J.E.; Chapron, B.; Collard, F.; Husson, R.; Jensen, R.E.; Johannessen, J.; Mouche, A.; Passaro, M.; Quartly, G.D.; et al. Observing Sea States. Front. Mar. Sci. 2019, 6, 124. [Google Scholar] [CrossRef]
- Holman, R.; Brodie, K.; Spore, N. Surf zone characterization using a small quadcopter: Technical issues and procedures. IEEE Trans. Geosci. Rem. Sens. 2017, 55, 2017–2027. [Google Scholar] [CrossRef]
- Brodie, K.; Palmsten, M.; Hesser, T.; Dickhudt, P.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Appl. Opt. 2018, 136, 147–160. [Google Scholar] [CrossRef]
- Chickadel, C. Remote Measurements of Waves and Currents over Complex Bathymetry. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2007. [Google Scholar]
- Chapman, R.; Irani, G. Errors in estimating slope spectra from wave images. Appl. Opt. 1994, 20, 3645–3652. [Google Scholar] [CrossRef] [PubMed]
- Jaihne, B.; Klinke, J.; Waas, S. Imaging of short ocean wind waves: A critical theoretical 186 review. Opt. Soc. Am. A 1994, 11, 2197–2209. [Google Scholar] [CrossRef]
- Perugini, E.; Soldini, L.; Palmsten, M.L.; Calantoni, J.; Brocchini, M. Linear depth inversion 188 sensitivity to wave viewing angle using synthetic optical video. Coast. Eng. 2019, 152, 103535. [Google Scholar] [CrossRef]
- Bechle, A.J.; Wu, C.H. Virtual wave gauges based upon stereo imaging for measuring surface wave characteristics. Coast. Eng. 2011, 58, 305–316. [Google Scholar] [CrossRef]
- Buscombe, D.; Carini, R.J.; Harrison, S.R.; Chickadel, C.C.; Warrick, J.A. Optical wave gauging using deep neural networks. Coast. Eng. 2020, 155, 103593. [Google Scholar] [CrossRef]
- De Vries, S.; Hill, D.; de Schipper, M.; Stive, M. Using stereo photogrammetry to measure coastal waves. J. Coast. Res. 2009, SI 56, 1484–1488. [Google Scholar]
- Almar, R.; Cienfuegos, R.; Catalán, P.; Michallet, H.; Castelle, B.; Bonneton, P.; Marieu, V.A. new breaking wave height direct estimator from video imagery. Coast. Eng. 2012, 61, 42–48. [Google Scholar] [CrossRef]
- Andriolo, U.; Mendes, D.; Taborda, R. Breaking Wave Height Estimation from Time Images: Two Methods for Coastal Video Monitoring Systems. Remote Sens. 2020, 12, 204. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. cBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. Ocean. 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R.; de Almeida, L.P.M.; Sall, M. On the Operational Use of UAVs for Video-Derived Bathymetry. Coast. Eng. 2019, 152, 103527. [Google Scholar] [CrossRef]
- Thuan, D.H.; Almar, R.; Marchesiello, P.; Viet, N.T. Video Sensing of Nearshore Bathymetry Evolution with Error Estimate. Remote Sens. 2019, 7, 233. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Yurovskaya, M.; Chapron, B.; Collard, F.; Donlon, C. Sun glitter imagery of ocean surface waves. Part 1: Directional spectrum retrieval and validation. J. Geophys. Res. Ocean. 2017, 122, 1369–1383. [Google Scholar] [CrossRef]
- Almar, R.; Bergsma, E.; Maisongrande, P.; Melo de Almeida, L. Coastal bathymetry from 214 optical submetric satellite video sequence: A showcase with Pleiades persistent mode. Remote Sens. Environ. 2019, 231, 111263. [Google Scholar] [CrossRef]
- Almar, R.; Bergsma, E.W.; Gawehn, M.; Aarninkhof, S.; Benshila, R. High-frequency Tem-poral Wave-pattern Reconstruction from a Few Satellite Images: A New Method towards Estimating Regional Bathymetry. J. Coast. Res. 2020, 95, 996–1000. [Google Scholar] [CrossRef]
- Almar, R.; Michallet, H.; Cienfuegos, R.; Bonneton, P.; Tissier, M.; Ruessink, G. On the use of the Radon Transform in studying nearshore wave dynamics. Coast. Eng. 2014, 92, 24–30. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R.; Maisongrande, P. Radon-Augmented Sentinel-2 Satellite Imagery to Derive Wave-Patterns and Regional Bathymetry. Remote Sens. 2019, 11, 1918. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almar, R.; Bergsma, E.W.J.; Catalan, P.A.; Cienfuegos, R.; Suarez, L.; Lucero, F.; Lerma, A.N.; Desmazes, F.; Perugini, E.; Palmsten, M.L.; et al. Sea State from Single Optical Images: A Methodology to Derive Wind-Generated Ocean Waves from Cameras, Drones and Satellites. Remote Sens. 2021, 13, 679. https://doi.org/10.3390/rs13040679
Almar R, Bergsma EWJ, Catalan PA, Cienfuegos R, Suarez L, Lucero F, Lerma AN, Desmazes F, Perugini E, Palmsten ML, et al. Sea State from Single Optical Images: A Methodology to Derive Wind-Generated Ocean Waves from Cameras, Drones and Satellites. Remote Sensing. 2021; 13(4):679. https://doi.org/10.3390/rs13040679
Chicago/Turabian StyleAlmar, Rafael, Erwin W. J. Bergsma, Patricio A. Catalan, Rodrigo Cienfuegos, Leandro Suarez, Felipe Lucero, Alexandre Nicolae Lerma, Franck Desmazes, Eleonora Perugini, Margaret L. Palmsten, and et al. 2021. "Sea State from Single Optical Images: A Methodology to Derive Wind-Generated Ocean Waves from Cameras, Drones and Satellites" Remote Sensing 13, no. 4: 679. https://doi.org/10.3390/rs13040679
APA StyleAlmar, R., Bergsma, E. W. J., Catalan, P. A., Cienfuegos, R., Suarez, L., Lucero, F., Lerma, A. N., Desmazes, F., Perugini, E., Palmsten, M. L., & Chickadel, C. (2021). Sea State from Single Optical Images: A Methodology to Derive Wind-Generated Ocean Waves from Cameras, Drones and Satellites. Remote Sensing, 13(4), 679. https://doi.org/10.3390/rs13040679