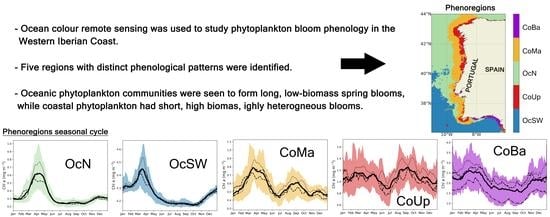
Assessing Phytoplankton Bloom Phenology in Upwelling-Influenced Regions Using Ocean Color Remote Sensing
Abstract
1. Introduction
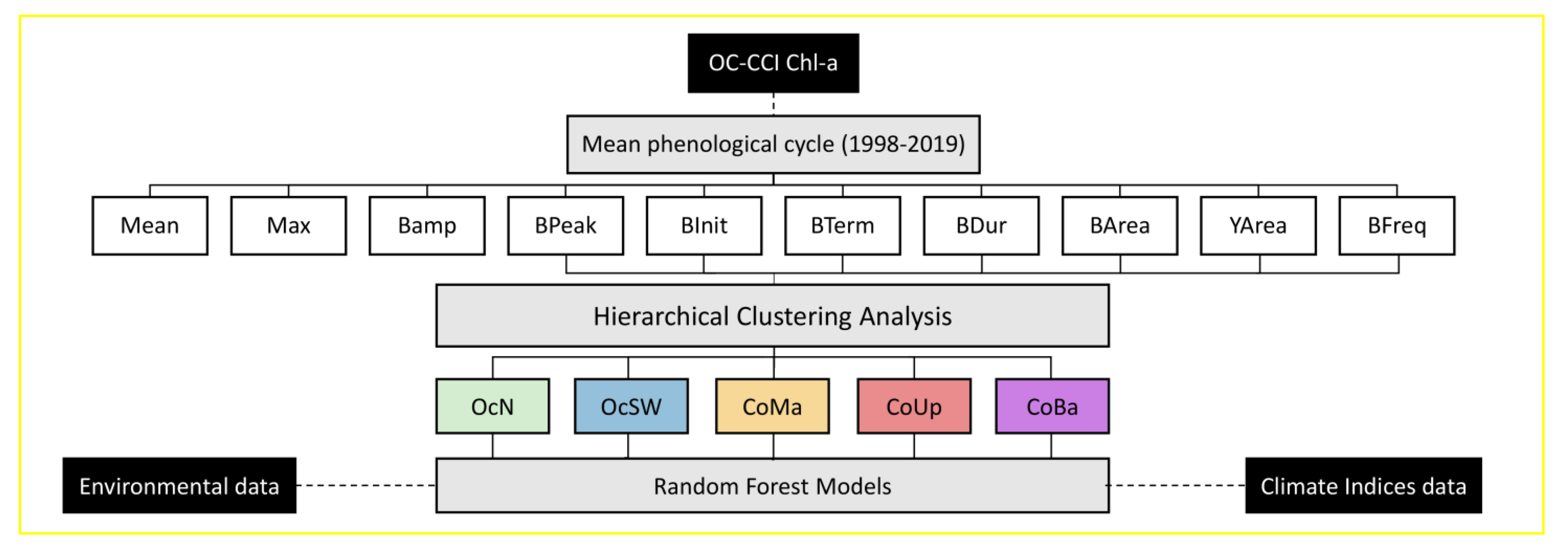
2. Data and Methods
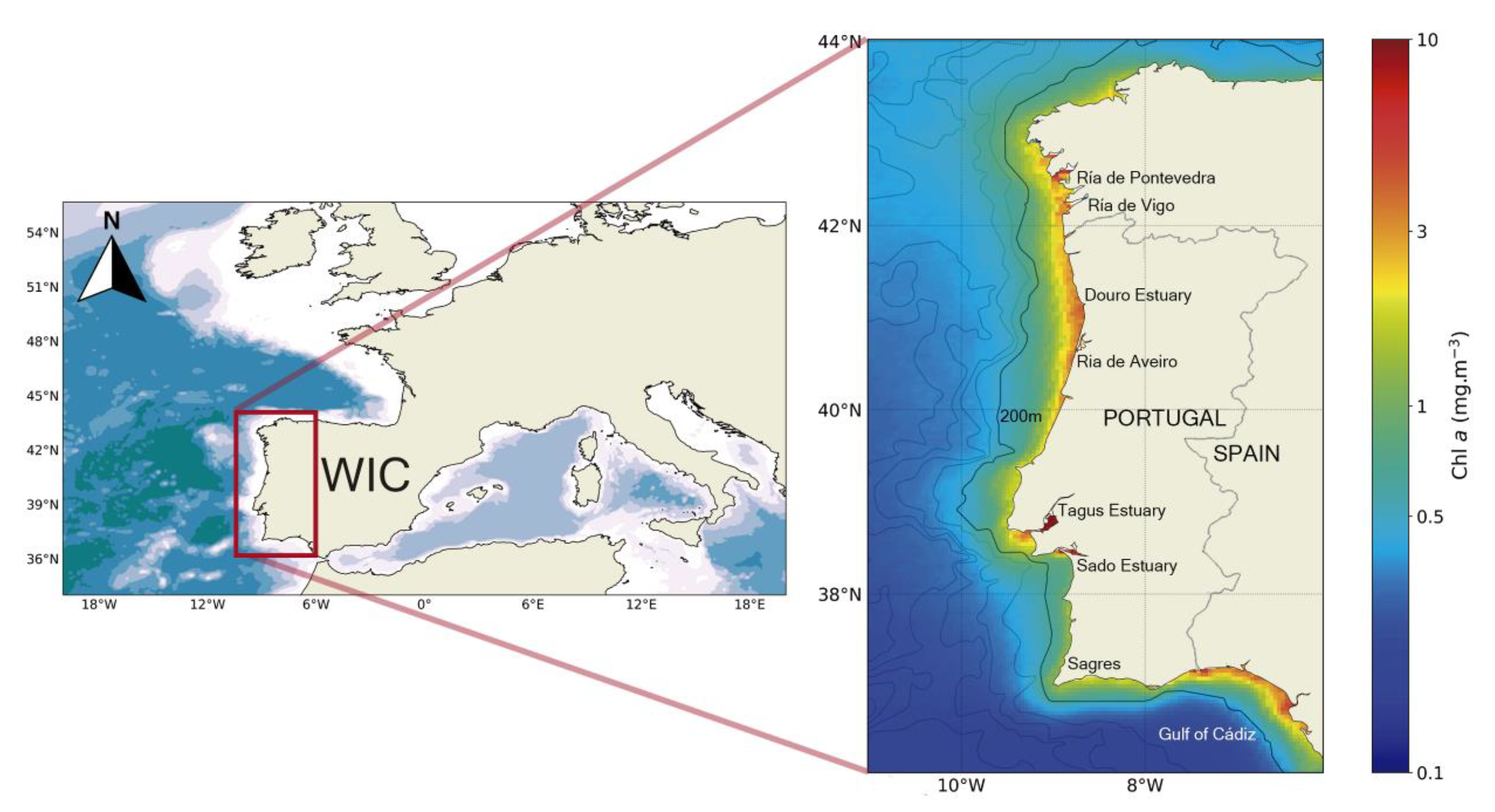
2.1. Study Area
2.2. Chl-a Data
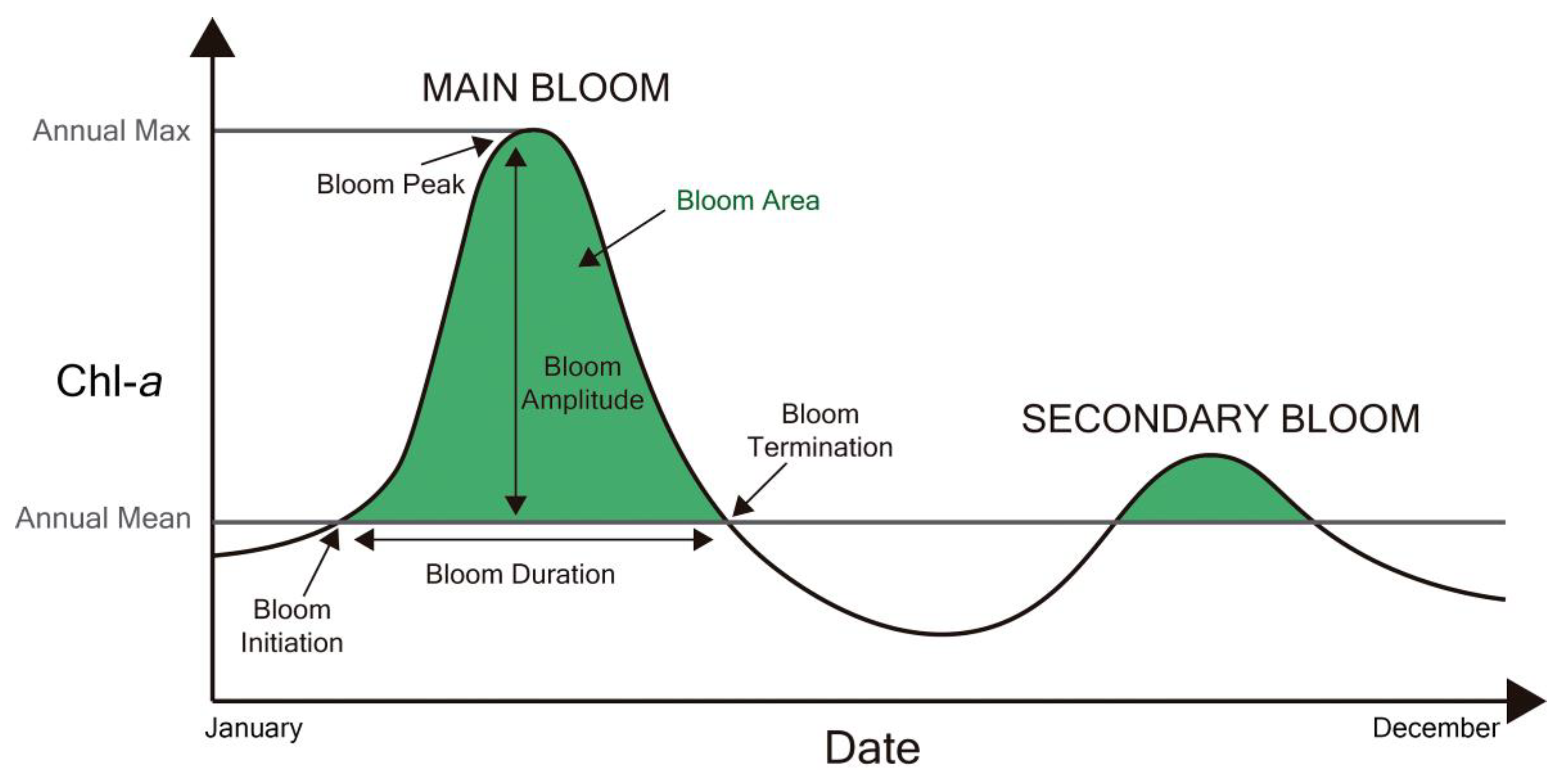
2.3. Estimating Bloom Phenology
2.4. Regional Analysis of Bloom Phenology
2.5. Environmental Data Products
2.6. Random Forest Analysis
3. Results
3.1. Phytoplankton biomass off Western Iberia
3.2. Bloom Phenology Metrics
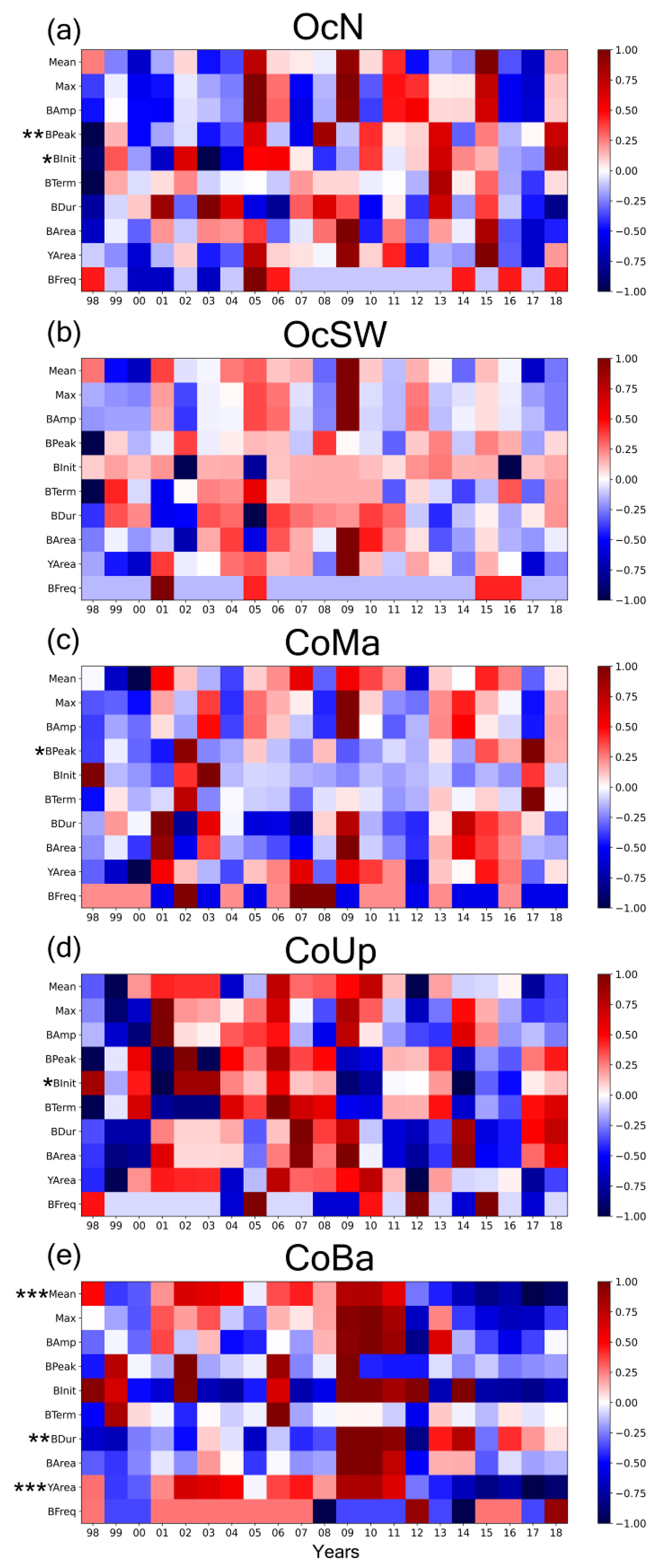
3.3. Regional Patterns of Bloom Phenology
3.4. Drivers of Bloom Phenology
4. Discussion
4.1. Phytoplankton Bloom Phenology in the WIC
4.2. Drivers of Bloom Phenology
4.3. Remote Sensing as a Tool for Assessing Bloom Phenology in Coastal Regions
5. Final Considerations
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Lutz, M.J.; Caldeira, K.; Dunbar, R.B.; Behrenfeld, M.J. Seasonal rhythms of net primary production and particulate organic carbon flux to depth describe the efficiency of biological pump in the global ocean. J. Geophys. Res. Oceans. 2007, 112. [Google Scholar] [CrossRef]
- Palevsky, H.I.; Quay, P.D. Influence of biological carbon export on ocean carbon uptake over the annual cycle across the North Pacific Ocean. Glob. Biogeochem. Cycles 2017, 31, 81–95. [Google Scholar] [CrossRef]
- Koeller, P.; Fuentes-Yaco, C.; Platt, T.; Sathyendranath, S.; Richards, A.; Ouellet, P.; Orr, D.; Skúladóttir, U.; Wieland, K.; Savard, L.; et al. Basin-scale coherence in phenology of shrimps and phytoplankton in the North Atlantic Ocean. Science 2009, 8, 791–793. [Google Scholar] [CrossRef]
- Platt, T.; Fuentes-Yaco, C.; Frank, K.T. Spring algal bloom and larval fish survival. Nature 2003, 423, 398–399. [Google Scholar] [CrossRef] [PubMed]
- Asch, R.G.; Stock, C.A.; Sarmiento, J.L. Climate change impacts on mismatches between phytoplankton blooms and fish spawning phenology. Glob. Chang. Biol. 2019, 25, 2544–2559. [Google Scholar] [CrossRef] [PubMed]
- Henson, S.A.; Cole, H.S.; Hopkins, J.; Martin, A.P.; Yool, A. Detection of climate change-driven trends in phytoplankton phenology. Glob. Chang. Biol. 2018, 24, e101–e111. [Google Scholar] [CrossRef]
- Sverdrup, H. On conditions for the vernal blooming of phytoplankton. J. Cons. Int. Explor. Mer. 1953, 18, 287–295. [Google Scholar] [CrossRef]
- Siegel, D.; Doney, S.; Yoder, J. The north atlantic spring phytoplankton bloom and Sverdrup’s critical depth hypothesis. Science 2002, 296, 730–733. [Google Scholar] [CrossRef]
- Lindemann, C.; St John, M.A. A seasonal diary of phytoplankton in the north atlantic. Front. Mar. Sci. 2014, 1, 37. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Ji, R.; Browman, H.I. Revisiting Sverdrup’s critical depth hypothesis. ICES J. Mar. Sci. 2015, 72, 1892–1896. [Google Scholar] [CrossRef]
- Racault, M.F.; Le Quéré, C.; Buitenhuis, E.; Sathyendranath, S.; Platt, T. Phytoplankton phenology in the global ocean. Ecol. Indic. 2012, 14, 152–163. [Google Scholar] [CrossRef]
- Kahru, M.; Brotas, V.; Manzano-Sarabia, M.; Mitchell, B.G. Are phytoplankton blooms occurring earlier in the Arctic? Glob. Chang. Biol. 2011, 17, 1733–1739. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining phytoplankton diversity from ocean color: A scientific roadmap for future development. Front. Mar. Sci. 2017, 4, 55. [Google Scholar] [CrossRef]
- Racault, M.-F.; Sathyendranath, S.; Menon, N.; Platt, T. Phenological responses to ENSO in the global oceans. In Integrative Study of the Mean Sea Level and Its Components; Cazenave, A., Champollion, N., Paul, F., Benveniste, J., Eds.; Springer: Cham, Swizerland, 2017; pp. 281–297. [Google Scholar]
- Krug, L.A.; Platt, T.; Sathyendranath, S.; Barbosa, A.B. Patterns and drivers of phytoplankton phenology off sw iberia: A phenoregion based perspective. Prog. Oceanogr. 2018, 165, 233–256. [Google Scholar] [CrossRef]
- Gittings, J.A.; Raitsos, D.E.; Kheireddine, M.; Racault, M.-F.; Claustre, H.; Hoteit, I. Evaluating tropical phytoplankton phenology metrics using contemporary tools. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Salgado-Hernanz, P.; Racault, M.-F.; Font-Munõz, J.; Basterretxea, G. Trends in phytoplankton phenology in the mediterranean sea based on ocean-colour remote sensing. Remote Sens. Environ. 2019, 221, 50–64. [Google Scholar] [CrossRef]
- Soppa, M.A.; Völker, C.; Bracher, A. Diatom phenology in the Southern Ocean: Mean patterns, trends and the role of climate oscillations. Remote Sens. 2016, 8, 420. [Google Scholar] [CrossRef]
- Friedland, K.D.; Mouw, C.B.; Asch, R.G.; Ferreira, A.S.A.; Henson, S.; Hyde, K.J.; Morse, R.E.; Thomas, A.C.; Brady, D.C. Phenology and time series trends of the dominant seasonal phytoplankton bloom across global scales. Glob. Ecol. Biogeogr. 2018, 27, 551–569. [Google Scholar] [CrossRef]
- Louw, D.C.; van der Plas, A.K.; Mohrholz, V.; Wasmund, N.; Junker, T.; Eggert, A. Seasonal and interannual phytoplankton dynamics and forcing mechanisms in the Northern Benguela upwelling system. J. Mar. Syst. 2016, 157, 124–134. [Google Scholar] [CrossRef]
- Mahadevan, A. The impact of submesoscale physics on primary productivity of plankton. Annu. Rev. Mar. Sci. 2016, 8, 161–184. [Google Scholar] [CrossRef]
- Häder, D.P.; Gao, K. Interactions of anthropogenic stress factors on marine phytoplankton. Front. Env. Sci. 2015, 3, 14. [Google Scholar] [CrossRef]
- Marić, D.; Kraus, R.; Godrijan, J.; Supić, N.; Djakovac, T.; Precali, R. Phytoplankton response to climatic and anthropogenic influences in the north-eastern Adriatic during the last four decades. Estuar. Coast. Shelf Sci. 2012, 115, 98–112. [Google Scholar] [CrossRef]
- Brody, S.R.; Lozier, M.S.; Dunne, J.P. A comparison of methods to determine phytoplankton bloom initiation. J. Geophys. Res. Oceans 2013, 118, 2345–2357. [Google Scholar] [CrossRef]
- Ferreira, A.S.; Visser, A.W.; MacKenzie, B.R.; Payne, M.R. Accuracy and precision in the calculation of phenology metrics. J. Geophys. Res. Oceans 2014, 119, 8438–8453. [Google Scholar] [CrossRef]
- Rolinski, S.; Horn, H.; Petzoldt, T.; Paul, L. Identifying cardinal dates in phytoplankton time series to enable the analysis of long-term trends. Oecologia 2007, 153, 997–1008. [Google Scholar] [CrossRef]
- Navarro, G.; Ruiz, J. Spatial and temporal variability of phytoplankton in the gulf of cádiz through remote sensing images. Deep Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 1241–1260. [Google Scholar] [CrossRef]
- Goela, P.; Danchenko, S.; Icely, J.; Lubian, L.M.; Cristina, S.; Newton, A. Using chemtax to evaluate seasonal and interannual dynamics of the phytoplankton community off the south-west coast of Portugal. Estuar. Coast. Shelf Sci. 2014, 151, 112–123. [Google Scholar] [CrossRef]
- Krug, L.A.; Platt, T.; Sathyendranath, S.; Barbosa, A.B. Unravelling region-specific environmental drivers of phytoplankton across a complex marine domain (off sw iberia). Remote Sens. Environ. 2017, 203, 162–184. [Google Scholar] [CrossRef]
- Ferreira, A.; Garrido-Amador, P.; Brito, A.C. Disentangling environmental drivers of phytoplankton biomass off western Iberia. Front. Mar. Sci. 2019, 6, 44. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Figueiras, F.G.; Lorenzo, L.M.; Arbones, B. Phytoplankton composition, photosynthesis and primary production during different hydrographic conditions at the Northwest Iberian upwelling system. Mar. Ecol. Prog. Ser. 2003, 252, 89–104. [Google Scholar] [CrossRef]
- Relvas, P.; Barton, E.D.; Dubert, J.; Oliveira, P.B.; Peliz, A.; Da Silva, J.; Santos, A.M.P. Physical oceanography of the western Iberia ecosystem: Latest views and challenges. Prog. Oceanogr. 2007, 74, 149–173. [Google Scholar] [CrossRef]
- Garrido, S.; Silva, A.; Marques, V.; Figueiredo, I.; Bryére, P.; Mangin, A.; Santos, A.M.P. Temperature and food-mediated variability of european atlantic sardine recruitment. Prog. Oceanogr. 2017, 159, 267–275. [Google Scholar] [CrossRef]
- Vidal, T.; Calado, A.J.; Moita, M.T.; Cunha, M.R. Phytoplankton dynamics in relation to seasonal variability and upwelling and relaxation patterns at the mouth of Ria de Aveiro (West Iberian Margin) over a four-year period. PLoS ONE 2017, 12, e0177237. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, P.; Amorim, F.; Dubert, J.; Nolasco, R.; Moita, T. Phytoplankton distribution and physical processes off NW iberia during two consecutive upwelling seasons. Cont. Shelf Res. 2019, 190, 103987. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Brewin, R.J.; Brockmann, C.; Brotas, V.; Calton, B.; Chuprin, A.; Cipollini, P.; Couto, A.B.; Dingle, J.; Doerffer, R.; et al. An Ocean-Colour Time Series for Use in Climate Studies: The Experience of the Ocean-Colour Climate Change Initiative (OC-CCI). Sensors 2019, 19, 4285. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef]
- Jackson, T.; Sathyendranath, S.; Mélin, F. An improved optical classification scheme for the Ocean Colour Essential Climate Variable and its applications. Remote Sens. Environ. 2017, 203, 152–161. [Google Scholar] [CrossRef]
- Ocean Colour Climate Change Initiative Dataset, Version 4.2., European Space Agency. Available online: http://www.esa-oceancolour-cci.org/ (accessed on 13 May 2020).
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Taberner, M.; Antoine, D.; Arnone, R.; Balch, W.M.; Barker, K.; et al. A compilation of global bio-optical in situ data for ocean-colour satellite applications-version two. Earth Syst. Sci. Data 2019, 11, 1037–1068. [Google Scholar] [CrossRef]
- Sá, C.; D’Alimonte, D.; Brito, A.; Kajiyama, T.; Mendes, C.; Vitorino, J.; Oliveira, P.; Da Silva, J.; Brotas, V. Validation of standard and alternative satellite ocean-color chlorophyll products off western iberia. Remote Sens. Environ. 2015, 168, 403–419. [Google Scholar] [CrossRef]
- Racault, M.-F.; Sathyendranath, S.; Platt, T. Impact of missing data on the estimation of ecological indicators from satellite ocean-colour time-series. Remote Sens. Environ. 2014, 152, 15–28. [Google Scholar] [CrossRef]
- Cole, H.; Henson, S.; Martin, A.; Yool, A. Mind the gap: The impact of missing data on the calculation of phytoplankton phenology metrics. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Greve, W.; Prinage, S.; Zidowitz, H.; Nast, J.; Reiners, F. On the phenology of north sea ichthyoplankton. ICES J. Mar. Sci. 2005, 62, 1216–1223. [Google Scholar] [CrossRef]
- Sasaoka, K.; Chiba, S.; Saino, T. Climatic forcing and phytoplankton phenology over the subarctic North Pacific from 1998 to 2006, as observed from ocean color data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Balcan, M.-F.; Liang, Y.; Gupta, P. Robust hierarchical clustering. J. Mach. Learn. Res. 2014, 15, 3831–3871. [Google Scholar]
- Autret, E.; Tandéo, P.; Paul, F.; Prévost, C.; Piollé, J. Product user manual for level 4 ODYSSEA reprocessed SST product over the European North West Shelf/Iberia Biscay Irish Seas. EU Copernicus Marine Service, 1.1 ed.. 2019. Available online: https://resources.marine.copernicus.eu/documents/PUM/CMEMS-SST-PUM-010-026.pdf (accessed on 13 May 2020).
- Amo, A.B.; Gutknecht, E.; Sotillo, M.G. Product user manual for Atlantic—Iberian Biscay Irish—biogeochemistry multi-year non-assimilative hindcast product. EU Copernicus Marine Service, 3.2 ed.. 2019. Available online: https://resources.marine.copernicus.eu/documents/PUM/CMEMS-IBI-PUM-005-003.pdf (accessed on 13 May 2020).
- Amo, A.B.; Levier, B.; Sotillo, M.G. Product user manual for Atlantic—Iberian Biscay Irish—Ocean physics reanalysis product. EU Copernicus Marine Service, 3.2 ed.. 2019. Available online: https://cmems-resources.cls.fr/documents/PUM/CMEMS-IBI-PUM-005-002.pdf (accessed on 13 May 2020).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Wei, C.L.; Rowe, G.T.; Escobar-Briones, E.; Boetius, A.; Soltwedel, T.; Caley, M.J.; Soliman, Y.; Huettmann, F.; Qu, F.; Yu, Z.; et al. Global patterns and predictions of seafloor biomass using random forests. PLoS ONE 2010, 5, e15323. [Google Scholar] [CrossRef] [PubMed]
- Kruk, C.; Devercelli, M.; Huszar, V.L.; Hernández, E.; Beamud, G.; Diaz, M.; Silva, L.H.; Segura, A.M. Classification of reynolds phytoplankton functional groups using individual traits and machine learning techniques. Freshw. Biol. 2017, 62, 1681–1692. [Google Scholar] [CrossRef]
- Hu, S.; Liu, H.; Zhao, W.; Shi, T.; Hu, Z.; Li, Q.; Wu, G. Comparison of machine learning techniques in inferring phytoplankton size classes. Remote Sens. 2018, 10, 191. [Google Scholar] [CrossRef]
- Liu, X.; Feng, J.; Wang, Y. Chlorophyll a predictability and relative importance of factors governing lake phytoplankton at different timescales. Sci. Total Environ. 2019, 648, 472–480. [Google Scholar] [CrossRef]
- Scornet, E.; Biau, G.; Vert, J.-P. Consistency of random forests. Ann. Stat. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C.; Villa-Vialaneix, N. Random forests for big data. Big Data Res. 2017, 9, 28–46. [Google Scholar] [CrossRef]
- Parr, T.; Turgutlu, K.; Csiszar, C.; Howard, J. Beware Default Random Forest Importances. 2018. Available online: https://explained.ai/rf-importance/ (accessed on 13 May 2020).
- Riley, G.A. Phytoplankton of the north central Sargasso sea, 1950–52 1. Limnol. Oceanogr. 1957, 2, 252–270. [Google Scholar] [CrossRef]
- Longhurst, A. Seasonal cycles of pelagic production and consumption. Prog. Oceanogr. 1995, 36, 77–167. [Google Scholar] [CrossRef]
- González Taboada, F.; Anadón, R. Seasonality of north atlantic phytoplankton from space: Impact of environmental forcing on a changing phenology (1998–2012). Glob. Chang. Biol. 2014, 20, 698–712. [Google Scholar] [CrossRef] [PubMed]
- Beca-Carretero, P.; Otero, J.; Land, P.; Groom, S.; Alvarez-Salgado, X.A. Seasonal and inter-annual variability of net primary production in the nw iberian margin (1998–2016) in relation to wind stress and sea surface temperature. Prog. Oceanogr. 2019, 178, 102135. [Google Scholar] [CrossRef]
- Krug, L.A.; Platt, T.; Barbosa, A.B. Delineation of ocean surface provinces over a complex marine domain (off SW Iberia): An objective abiotic-based approach. Reg. Stud. Mar. Sci. 2018, 18, 80–96. [Google Scholar] [CrossRef]
- Sousa, M.C.; de Castro, M.; Alvarez, I.; Gomez-Gesteira, M.; Dias, J.M. Why coastal upwelling is expected to increase along the western iberian peninsula over the next century? Sci. Total Environ. 2017, 592, 243–251. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Palma, S.; Oliveira, P.B.; Moita, M.T. Composition and interannual variability of phytoplankton in a coastal upwelling region (Lisbon Bay, Portugal). J. Sea Res. 2009, 62, 238–249. [Google Scholar] [CrossRef]
- Pitcher, G.C.; Figueiras, F.G.; Hickey, B.M.; Moita, M.T. The physical oceanography of upwelling systems and the development of harmful algal blooms. Prog. Oceanogr. 2010, 85, 5–32. [Google Scholar] [CrossRef] [PubMed]
- Varela, R.; Alvarez, I.; Santos, F.; de Castro, M.; Gómez-Gesteira, M. Has upwelling’ strengthened along worldwide coasts over 1982–2010? Sci. Rep. 2015, 5, 1–15. [Google Scholar] [CrossRef] [PubMed]
- González-García, C.; Forja, J.; González-Cabrera, M.C.; Jiménez, M.P.; Lubián, L.M. Annual variations of total and fractionated chlorophyll and phytoplankton groups in the Gulf of Cadiz. Sci. Total Environ. 2018, 613, 1551–1565. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Enri, J.; Escudier, R.; Pascual, A.; Mañanes, R. Heavy Guadalquivir River discharge detection with satellite altimetry: The case of the eastern continental shelf of the Gulf of Cadiz (Iberian Peninsula). Adv. Space Res. 2015, 55, 1590–1603. [Google Scholar] [CrossRef]
- IOCCG. Synergy between Ocean Colour and Biogeochemical/Ecosystem Models; Dutkiewicz, S., Ed.; IOCCG Report Series; 2020. No. 19; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2020; p. 184. [Google Scholar]
- Novoa, S.; Doxaran, D.; Ody, A.; Vanhellemont, Q.; Lafon, V.; Lubac, B.; Gernez, P. Atmospheric corrections and multi-conditional algorithm for multi-sensor remote sensing of suspended particulate matter in low-to-high turbidity levels coastal waters. Remote Sens. 2017, 9, 61. [Google Scholar] [CrossRef]
- Guerreiro, S.B.; Birkinshaw, S.; Kilsby, C.; Fowler, H.J.; Lewis, E. Dry getting drier–the future of transnational river basins in Iberia. J. Hydrol. Reg. Stud. 2017, 12, 238–252. [Google Scholar] [CrossRef]
- Lehahn, Y.; d’Ovidio, F.; Lévy, M.; Heifetz, E. Stirring of the northeast Atlantic spring bloom: A Lagrangian analysis based on multisatellite data. J. Geophys. Res. Oceans. 2007, 112. [Google Scholar] [CrossRef]
- Zampieri, M.; Toreti, A.; Schindler, A.; Scoccimarro, E.; Gualdi, S. Atlantic multi-decadal oscillation influence on weather regimes over Europe and the Mediterranean in spring and summer. Glob. Planet. Chang. 2017, 151, 92–100. [Google Scholar] [CrossRef]
- Fraga, F. Upwelling off the galician coast, northwest Spain. In Coastal Upwelling; Francis, A.R., Ed.; American Geophysical Union: Washington, DC, USA, 1981; Volume 1, pp. 176–182. [Google Scholar]
- Peliz, A.; Dubert, J.; Santos, A.M.P.; Oliveira, P.B.; Le Cann, B. Winter upper ocean´ circulation in the western iberian basin fronts, eddies and poleward flows: An overview. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 621–646. [Google Scholar] [CrossRef]
- Arístegui, J.; Barton, E.D.; Álvarez-Salgado, X.A.; Santos, A.M.P.; Figueiras, F.G.; Kifani, S.; Hernández-León, S.; Mason, E.; Machú, E.; Demarcq, H. Sub-regional ecosystem variability in the Canary Current upwelling. Prog. Oceanogr. 2009, 83, 33–48. [Google Scholar] [CrossRef]
- Bakun, A.; Black, B.A.; Bograd, S.J.; Garcia-Reyes, M.; Miller, A.J.; Rykaczewski, R.R.; Sydeman, W.J. Anticipated effects of climate change on coastal upwelling ecosystems. Curr. Clim. Chang. Rep. 2015, 1, 85–93. [Google Scholar] [CrossRef]
- Wang, D.; Gouhier, T.C.; Menge, B.A.; Ganguly, A.R. Intensification and spatial homogenization of coastal upwelling under climate change. Nature 2015, 518, 390–394. [Google Scholar] [CrossRef]
- Sousa, M.C.; Ribeiro, A.; Des, M.; Gomez-Gesteira, M.; de Castro, M.; Dias, J.M. NW Iberian peninsula coastal upwelling future weakening: Competition between wind intensification and surface heating. Sci. Total Environ. 2020, 703, 134808. [Google Scholar] [CrossRef] [PubMed]
- Bograd, S.J.; Schroeder, I.; Sarkar, N.; Qiu, X.; Sydeman, W.J.; Schwing, F.B. Phenology of coastal upwelling in the california current. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Trigo, R.M.; Pozo-Vázquez, D.; Osborn, T.J.; Castro-Díez, Y.; Gámiz-Fortis, S.; Esteban-Parra, M.J. North Atlantic oscillation influence on precipitation, river flow and water resources in the Iberian Peninsula. Int. J. Climatol. 2004, 24, 925–944. [Google Scholar] [CrossRef]
- Groom, S.B.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, B.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.K.; Chuprin, A.; et al. Satellite ocean colour: Current status and future perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef]
- Chavez, F.P.; Messié, M. A comparison of eastern boundary upwelling ecosystem. Prog. Oceanogr. 2009, 83, 80–96. [Google Scholar] [CrossRef]
- Brito, A.C.; Garrido-Amador, P.; Gameiro, C.; Nogueira, M.; Moita, T.; Cabrita, M.T. Integrating In Situ and Ocean Color Data to Evaluate Ecological Quality under the Water Framework Directive. Water 2020, 12, 3443. [Google Scholar] [CrossRef]
- Garrido, S.; Ben-Hamadou, R.; Oliveira, P.B.; Cunha, M.E.; Chícharo, M.A.; van der Lingen, C.D. Diet and feeding intensity of sardine Sardina pilchardus: Correlation with satellite-derived chlorophyll data. Mar. Ecol. Prog. Ser. 2008, 354, 245–256. [Google Scholar] [CrossRef]
- Sherman, K.; O’Reilly, J.; Belkin, I.M.; Melrose, C.; Friedland, K.D. The application of satellite remote sensing for assessing productivity in relation to fisheries yields of the world’s large marine ecosystems. ICES J. Mar. Sci. 2011, 68, 667–676. [Google Scholar] [CrossRef][Green Version]
- Brotas, V.; Couto, A.B.; Sá, C.; Amorim, A.; Brito, A.; Laanen, M.; Peters, S.; Poser, K.; Eleveld, M.; Miller, P.; et al. Deriving Aquaculture indicators from Earth Observation in the AQUA-USERS project (AQUAculture USEr driven operational Remote Sensing information Services). Ocean Opt. XXII 2014, 1–9. [Google Scholar] [CrossRef]
- Gomes, M.; Correia, A.; Pinto, L.; Sá, C.; Brotas, V.; Mateus, M. Coastal Water Quality in an Atlantic Sea Bass Farm Site (Sines, Portugal): A First Assessment. Front. Mar. Sci. 2020, 7, 175. [Google Scholar] [CrossRef]
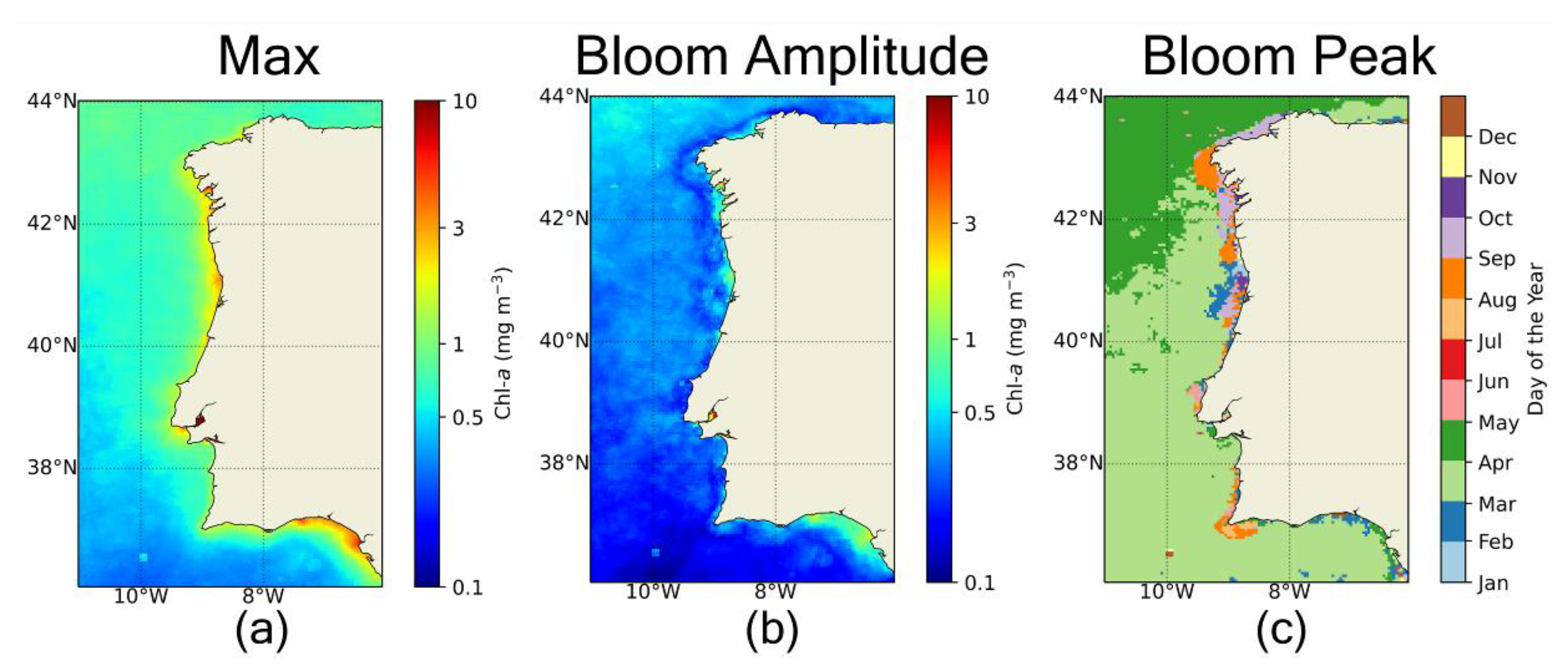
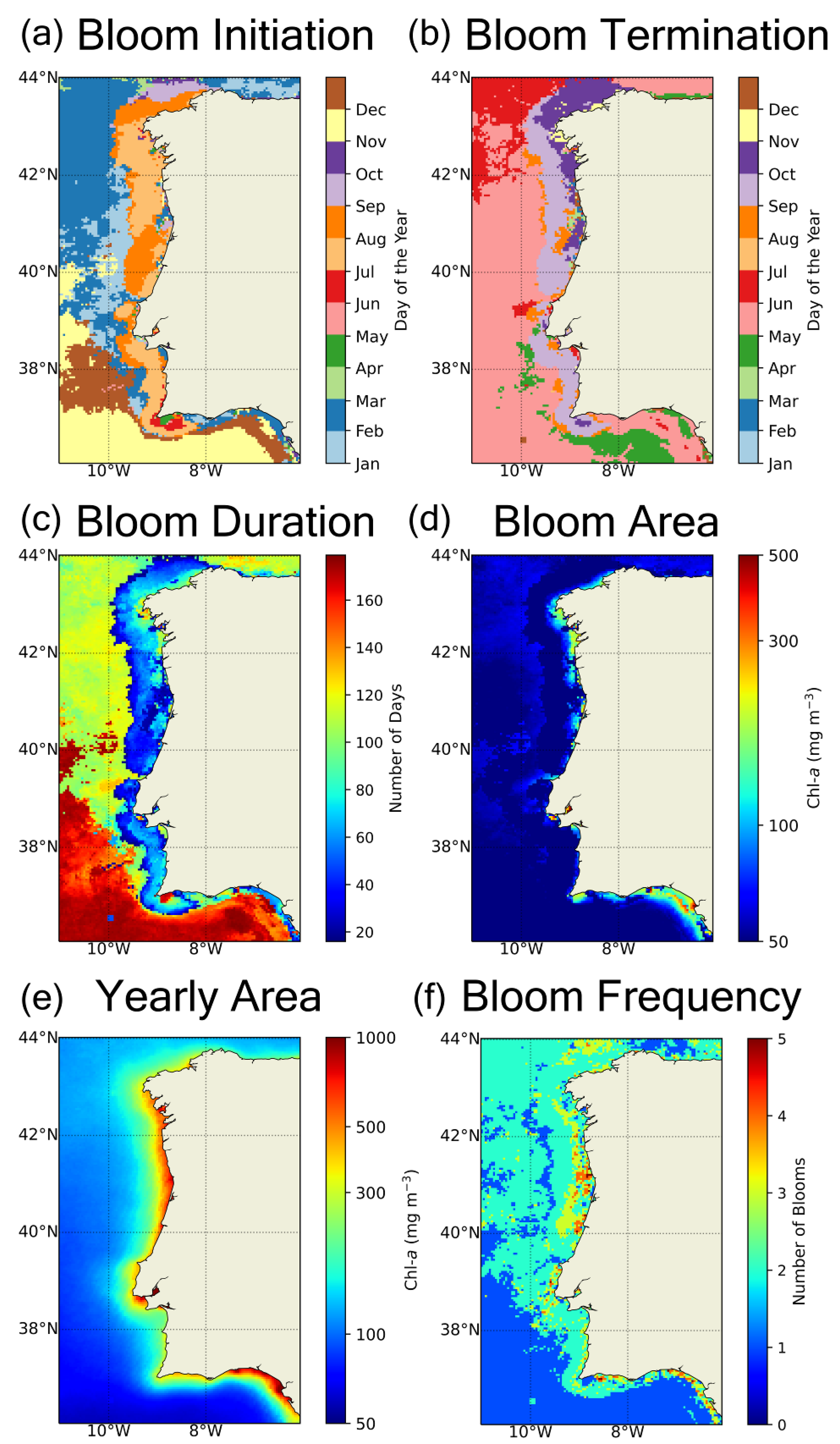
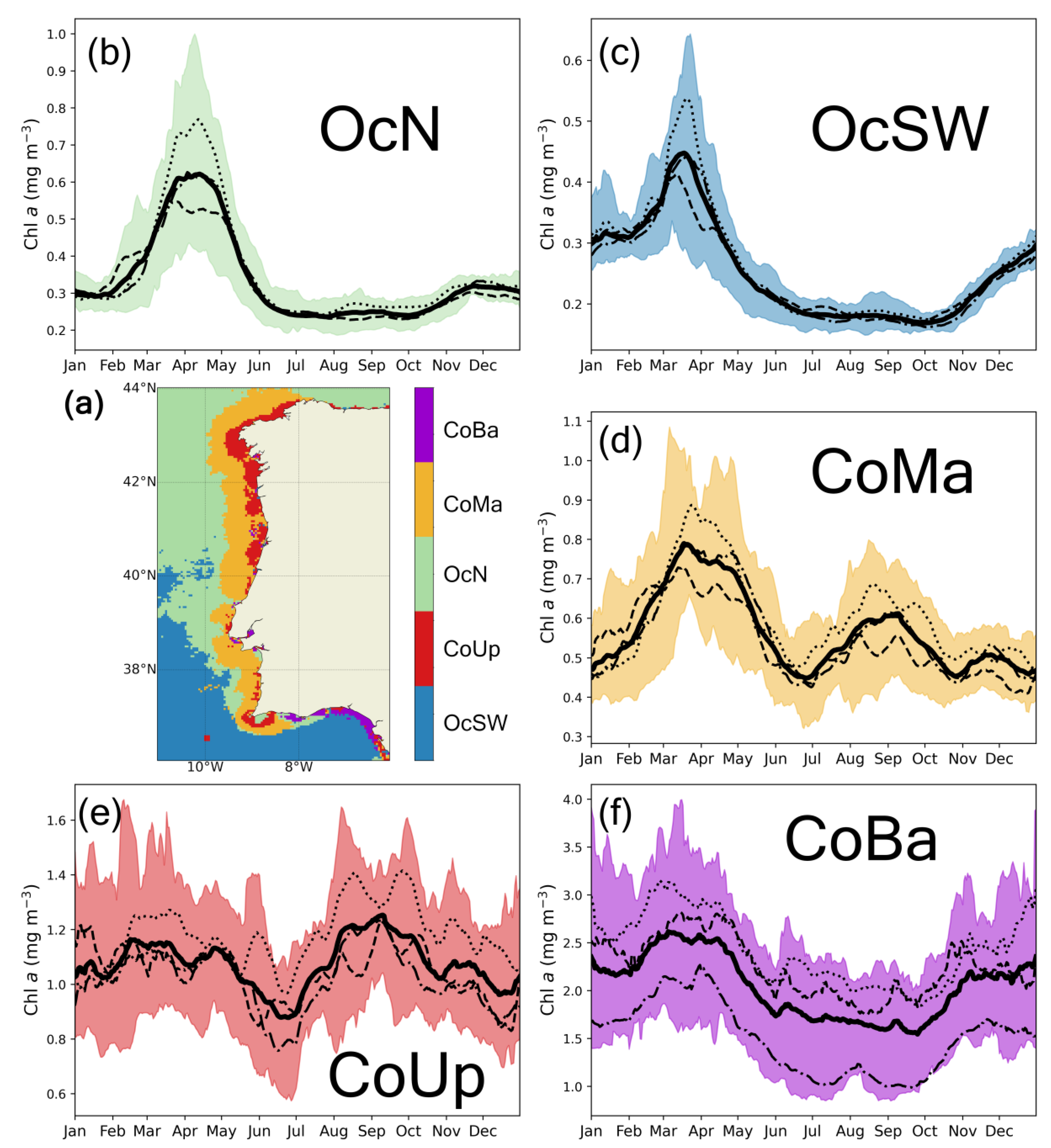
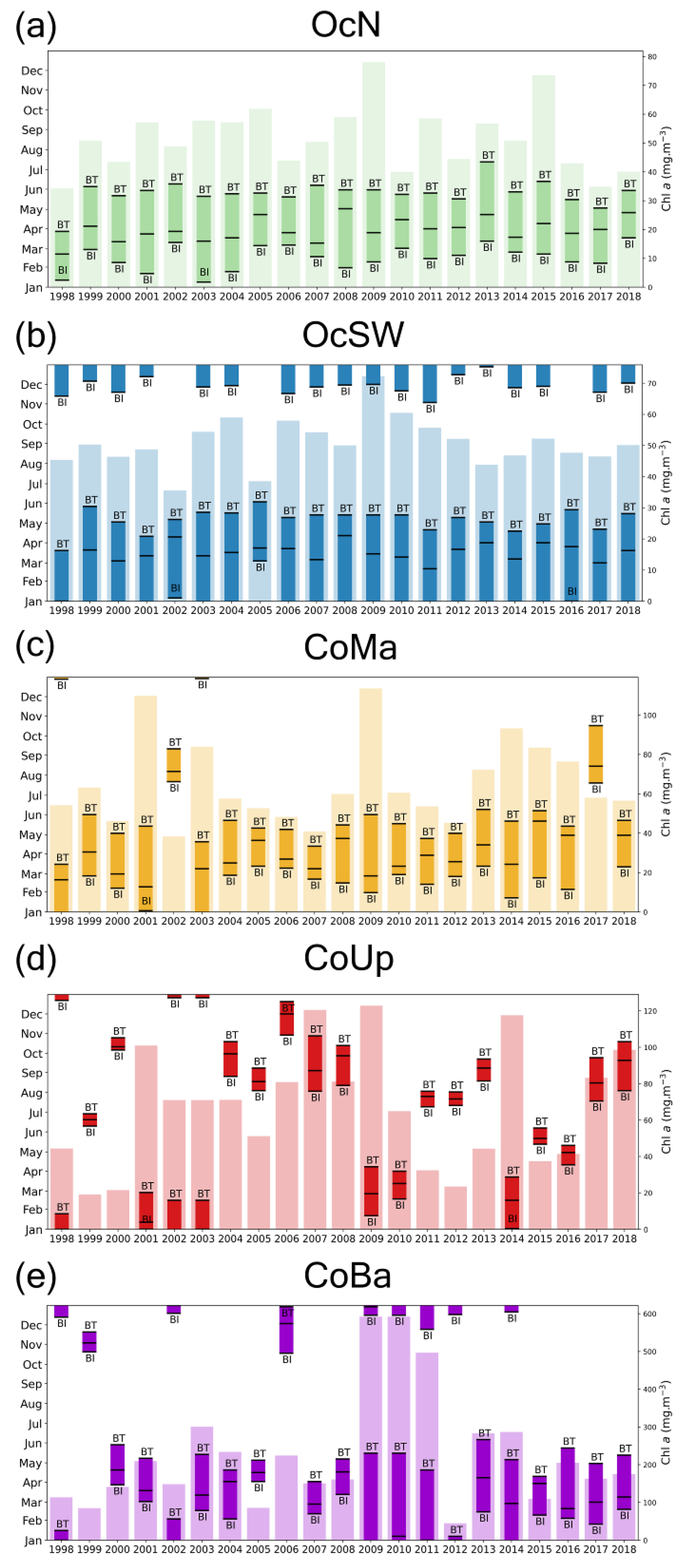
| Metric | Full Name | Unit | Description |
| Mean | Chl a mean | mg m−3 | Mean Chl a concentration of the seasonal cycle |
| Max | Chl a maximum | mg m−3 | Maximum Chl a concentration of the seasonal cycle |
| BAmp | Bloom amplitude | mg m−3 | Difference between Chl a maximum and mean |
| BPeak | Bloom peak | - | DOY of Chl a Maximum |
| BInit | Bloom initiation | - | DOY of initiation of the main bloom in the seasonal cycle |
| BTerm | Bloom termination | - | DOY of termination of the main bloom in the seasonal cycle |
| BDur | Bloom duration | days | Duration of the main bloom in the seasonal cycle |
| BArea | Bloom area | mg m−3 | Biomass of the main bloom in the seasonal cycle |
| YArea | Yearly area | mg m−3 | Total biomass accumulated during the seasonal cycle |
| BFreq | Bloom Frequency | blooms year−1 | Number of blooms in the seasonal cycle |
| Metric | Full Name | Unit |
|---|---|---|
| SST | Sea surface temperature | °C |
| MLD | Mixed layer depth | m |
| SAL | Salinity | (unitless) |
| SSH | Sea surface height | m |
| Vo | Meridional component of water transport | m s−1 |
| Uo | Zonal component of water transport | m s−1 |
| DIN | Dissolved inorganic nitrogen (nitrate + ammonium) concentration | µM |
| PO43− | Phosphate concentration | µM |
| Si | Silicon concentration | µM |
| Zeu | Euphotic zone depth | m |
| NAO | North Atlantic Oscillation index | (unitless) |
| AMO | Atlantic Meridional Oscillation index | (unitless) |
| MEI | Multivariate El-Niño Southern Oscillation index | (unitless) |
| OcN | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | BAmp | BPeak | Binit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.34 | 0.73 | 0.39 | 90 (March) | 47 (February) | 146 (May) | 100 | 51.64 | 123.97 | 2.19 |
| Min | 0.3 | 0.49 | 0.19 | 52 (February) | 9 (January) | 87 (March) | 73 | 34.25 | 111.18 | 1 |
| Max | 0.39 | 1.11 | 0.73 | 122 (May) | 77 (March) | 194 (July) | 132 | 78.05 | 144 | 4 |
| Stdev | 0.02 | 0.18 | 0.16 | 17 | 19 | 18 | 18 | 11.18 | 8.98 | 0.73 |
| P10 | 0.31 | 0.53 | 0.21 | - | - | - | 75 | 39.98 | 114.89 | 1 |
| P90 | 0.38 | 1.01 | 0.62 | - | - | - | 122 | 61.83 | 139.29 | 3 |
| Mode | - | - | - | March | February | May | - | - | - | - |
| Trend | - | - | - | 1.32** | 1.20* | - | - | - | - | - |
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.76 | 0.69 | 0.6 | 0.98 | ||||||
| Max | 1 | 0.66 | 0.79 | |||||||
| BAmp | 0.64 | 0.73 | ||||||||
| BPeak | 0.59 | 0.54 | ||||||||
| Binit | 0.55 | −0.48 | 0.49 | |||||||
| BTerm | 0.47 | 0.53 | ||||||||
| BDur | 0.62 | −0.69 | ||||||||
| Barea | 0.67 | |||||||||
| YArea | ||||||||||
| BFreq | ||||||||||
| OcSW | ||||||||||
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.25 | 0.51 | 0.26 | 74 (March) | 339 (December) | 127 (May) | 152 | 50.88 | 92.53 | 1.24 |
| Min | 0.22 | 0.34 | 0.09 | 1 (January) | 1 (January) | 79 (March) | 91 | 35.54 | 80.93 | 1 |
| Max | 0.3 | 0.99 | 0.69 | 102 (April) | 362 (December) | 154 (June) | 174 | 72.27 | 110.66 | 3 |
| Stdev | 0.02 | 0.14 | 0.13 | 20 | 24 | 16 | 22 | 7.73 | 6.49 | 0.53 |
| P10 | 0.23 | 0.4 | 0.16 | - | - | - | 121 | 43.82 | 84.27 | 1 |
| P90 | 0.27 | 0.64 | 0.38 | - | - | - | 172 | 58.99 | 98.58 | 2 |
| Mode | - | - | - | Mar | Nov | May | - | - | - | - |
| Trend | - | - | - | - | - | - | - | - | - | - |
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.79 | 0.74 | 0.47 | 0.96 | ||||||
| Max | 1 | 0.58 | 0.84 | |||||||
| BAmp | 0.58 | 0.79 | ||||||||
| BPeak | 0.69 | |||||||||
| Binit | 0.54 | 0.51 | ||||||||
| BTerm | ||||||||||
| BDur | 0.7 | −0.54 | ||||||||
| Barea | 0.63 | |||||||||
| YArea | ||||||||||
| BFreq | ||||||||||
| CoMa | ||||||||||
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.57 | 0.99 | 0.41 | 90 (March) | 48 (February) | 137 (May) | 86 | 65.16 | 207.83 | 2.71 |
| Min | 0.46 | 0.76 | 0.23 | 40 (February) | 3 (January) | 75 (March) | 51 | 38.39 | 167.73 | 2 |
| Max | 0.64 | 1.46 | 0.83 | 227 (August) | 363 (December) | 290 (October) | 131 | 113.54 | 231.82 | 4 |
| Stdev | 0.05 | 0.17 | 0.15 | 44 | 44 | 40 | 22 | 20.67 | 17.01 | 0.7 |
| P10 | 0.5 | 0.78 | 0.26 | - | - | - | 59 | 45.28 | 182.63 | 2 |
| P90 | 0.63 | 1.17 | 0.61 | - | - | - | 119 | 93.27 | 228.91 | 4 |
| Mode | - | - | - | Mar | Feb | May | - | - | - | - |
| Trend | - | - | - | 3.00* | - | - | - | - | - | - |
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.64 | 0.99 | ||||||||
| Max | 0.97 | 0.67 | 0.67 | −0.45 | ||||||
| BAmp | 0.66 | 0.47 | −0.51 | |||||||
| BPeak | 0.87 | |||||||||
| Binit | ||||||||||
| BTerm | ||||||||||
| BDur | 0.93 | −0.51 | ||||||||
| Barea | −0.55 | |||||||||
| YArea | ||||||||||
| BFreq | ||||||||||
| CoUp | ||||||||||
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 1.11 | 1.62 | 0.51 | 274 (October) | 242 (August) | 292 (October) | 47 | 66.61 | 405.09 | 3.14 |
| Min | 0.9 | 1.11 | 0.09 | 1 (January) | 1 (January) | 25 (January) | 19 | 19.05 | 327.99 | 2 |
| Max | 1.27 | 2.2 | 0.99 | 365 (December) | 360 (December) | 354 (December) | 86 | 122.84 | 463.26 | 5 |
| Stdev | 0.11 | 0.28 | 0.22 | 106 | 106 | 126 | 21 | 32.12 | 39.51 | 0.94 |
| P10 | 0.95 | 1.25 | 0.25 | - | - | - | 21 | 23.48 | 345.57 | 2 |
| P90 | 1.21 | 2 | 0.81 | - | - | - | 76 | 117.59 | 442.96 | 5 |
| Mode | - | - | - | September | August | October | - | - | - | - |
| Trend | - | - | - | - | −6.88* | - | - | - | - | - |
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.65 | 1 | ||||||||
| Max | 0.93 | 0.45 | 0.63 | 0.65 | ||||||
| BAmp | −0.45 | 0.45 | 0.6 | |||||||
| BPeak | 0.46 | 0.75 | ||||||||
| Binit | ||||||||||
| BTerm | ||||||||||
| BDur | 0.97 | −0.59 | ||||||||
| Barea | −0.54 | |||||||||
| YArea | ||||||||||
| BFreq | ||||||||||
| CoBa | ||||||||||
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 2.15 | 3.61 | 1.46 | 49 (February) | 19 (January) | 110 (April) | 78 | 228.66 | 781.85 | 2.57 |
| Min | 1.29 | 2.21 | 0.33 | 1 (January) | 26 (January) | 7 (January) | 21 | 44.9 | 472.94 | 1 |
| Max | 2.83 | 5.67 | 2.83 | 365 (December) | 355 (December) | 363 (December) | 151 | 592.12 | 1035.39 | 4 |
| Stdev | 0.51 | 1.03 | 0.68 | 50 | 48 | 55 | 41 | 151.6 | 183.3 | 0.79 |
| P10 | 1.43 | 2.25 | 0.81 | - | - | - | 33 | 85.73 | 522.32 | 2 |
| P90 | 2.7 | 5.35 | 2.68 | - | - | - | 147 | 496.57 | 987.45 | 3 |
| Mode | - | - | - | April | Feb | May | - | - | - | - |
| Trend | −0.05*** | - | - | - | - | - | 3.17** | - | −16.66*** | - |
| Mean | Max | BAmp | BPeak | BInit | BTerm | BDur | BArea | YArea | BFreq | |
| Mean | 0.81 | 0.48 | 0.48 | 0.49 | 1 | |||||
| Max | 0.9 | 0.51 | 0.81 | 0.82 | ||||||
| BAmp | 0.69 | 0.85 | 0.5 | −0.44 | ||||||
| BPeak | 0.5 | |||||||||
| Binit | ||||||||||
| BTerm | ||||||||||
| BDur | 0.89 | −0.46 | ||||||||
| Barea | 0.52 | |||||||||
| YArea | ||||||||||
| BFreq |
| OcN | ||||
|---|---|---|---|---|
| Metric | R2 | RMSE | Model Predictors | Response to main predictors increase |
| Mean | 0.75 | 0.01 | DIN *, AMO, Uo, MEI, Fe, NAO | + |
| Max | 0.75 | 0.09 | Si *, MLD, NAO, DIN, Sal, MEI, SSH | − |
| BAmp | 0.76 | 0.08 | Si *, NAO, MLD, DIN, Sal | − |
| BPeak | 0.71 | 9.2 | MLD *, Fe, Vo | + |
| BInit | 0.63 | 11.45 | DIN *, Vo | + |
| BTerm | 0.8 | 8.39 | AMO *, Fe, NAO, DIN, Sal, Vo | − |
| BDur | 0.73 | 9.33 | AMO *, Si, Uo, MLD | − |
| BArea | 0.87 | 4.09 | Si *, Uo | − |
| YArea | 0.77 | 4.3 | DIN *, AMO, Uo | + |
| BFreq | 0.61 | 0.45 | AMO *, MEI *, Vo * | + 0 − |
| OcSW | ||||
| Metric | R2 | RMSE | Model Predictors | Response to main predictors increase |
| Mean | 0.63 | 0.01 | MEI *, NAO *, Si | + − |
| Max | 0.69 | 0.08 | DIN *, Si, SST, NAO, Sal, Vo, Fe, Uo, SSH | + |
| BAmp | 0.7 | 0.07 | DIN *, SST, Si, Vo, Sal, NAO, SSH, Uo, Fe | + |
| BPeak | 0.8 | 9.07 | Sal *, Si *, SST, DIN, SSH | 0 − |
| BInit | 0.47 | 79.19 | MEI * | − |
| BTerm | 0.51 | 11.56 | SST *, Si | + |
| BDur | 0.65 | 13.3 | Fe *, NAO | + |
| BArea | 0.82 | 3.24 | Fe *, SST *, Sal *. Si *, NAO, MEI, Uo, Vo | + + + − |
| YArea | 0.63 | 3.95 | DIN *, Si*, NAO, Vo, Uo | + − |
| BFreq | 0.8 | 0.23 | Si *, SST *, Fe, Vo | − 0 |
| CoMa | ||||
| Metric | R2 | RMSE | Model Predictors | Response to main predictors increase |
| Mean | 0.65 | 0.03 | Vo *, DIN, MLD, SSH, Sal, Si | + |
| Max | 0.63 | 0.1 | DIN *, Sal, MLD | + |
| BAmp | 0.63 | 0.09 | DIN *, Sal, MLD, Uo | + |
| BPeak | 0.53 | 32.61 | SSH *. Fe *, Sal | + − |
| BInit | 0.84 | 39.78 | MLD *, AMO, Fe, SST, NAO, Si, MEI, SSH, Vo, Sal | − |
| BTerm | 0.43 | 34.65 | DIN *, SSH *, Fe, AMO, Sal | − + |
| BDur | 0.71 | 11.94 | SSH *, Sal *, DIN, AMO | 0 − |
| BArea | 0.68 | 11.78 | SSH *. Sal *, Si, DIN, Uo, MLD | 0 |
| YArea | 0.86 | 6.38 | SSH *, Vo *, MLD, DIN, Sal, Si, Uo | + + |
| BFreq | 0.64 | 0.42 | MEI *, Sal *, MLD, DIN | + + |
| CoUp | ||||
| Metric | R2 | RMSE | Model Predictors | Response to main predictors increase |
| Mean | 0.69 | 0.06 | Sal * | + |
| Max | 0.86 | 0.1 | Sal *, MEI *, Zeu, Vo, Uo, DIN, SST | + + |
| BAmp | 0.66 | 0.13 | MEI *, DIN, NAO, Uo, Fe | + |
| BPeak | 0.7 | 59.52 | SSH *, Zeu | − |
| BInit | 0.72 | 57.42 | DIN *, MEI *, Uo *, SST, AMO, Sal, Si, NAO | − + 0 |
| BTerm | 0.87 | 36.17 | SSH *, NAO, Uo, AMO, Fe, MEI, Si | − |
| BDur | 0.56 | 13.83 | Uo *, MLD, Si | + |
| BArea | 0.58 | 20.83 | Uo *, MLD | − |
| YArea | 0.69 | 22 | Sal * | + |
| BFreq | 0.59 | 0.6 | Sal *. Fe | + |
| CoBa | ||||
| Metric | R2 | RMSE | Model Predictors | Response to main predictors increase |
| Mean | 0.73 | 0.26 | Sal *, Uo* | + − |
| Max | 0.58 | 0.67 | Sal * | + |
| BAmp | 0.61 | 0.43 | Si *, Uo, SSH, Sal, Fe | − |
| BPeak | 0.66 | 67.7 | SST *, NAO, Vo, MEI | + |
| BInit | 0.6 | 89.81 | NAO *, Si *, Zeu *, AMO | − − − |
| BTerm | 0.48 | 57.33 | Si *, SST *, NAO, SSH | 0 + |
| BDur | 0.71 | 21.62 | Uo *, Si, MLD | + |
| BArea | 0.5 | 106.92 | Uo *, MLD | + |
| YArea | 0.73 | 96.11 | Sal *, Uo | + |
| BFreq | 0.6 | 0.5 | MEI *, Zeu, Uo, Si, MLD, SST | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, A.; Brotas, V.; Palma, C.; Borges, C.; Brito, A.C. Assessing Phytoplankton Bloom Phenology in Upwelling-Influenced Regions Using Ocean Color Remote Sensing. Remote Sens. 2021, 13, 675. https://doi.org/10.3390/rs13040675
Ferreira A, Brotas V, Palma C, Borges C, Brito AC. Assessing Phytoplankton Bloom Phenology in Upwelling-Influenced Regions Using Ocean Color Remote Sensing. Remote Sensing. 2021; 13(4):675. https://doi.org/10.3390/rs13040675
Chicago/Turabian StyleFerreira, Afonso, Vanda Brotas, Carla Palma, Carlos Borges, and Ana C. Brito. 2021. "Assessing Phytoplankton Bloom Phenology in Upwelling-Influenced Regions Using Ocean Color Remote Sensing" Remote Sensing 13, no. 4: 675. https://doi.org/10.3390/rs13040675
APA StyleFerreira, A., Brotas, V., Palma, C., Borges, C., & Brito, A. C. (2021). Assessing Phytoplankton Bloom Phenology in Upwelling-Influenced Regions Using Ocean Color Remote Sensing. Remote Sensing, 13(4), 675. https://doi.org/10.3390/rs13040675