Analysis of the Snow Water Equivalent at the AEMet-Formigal Field Laboratory (Spanish Pyrenees) During the 2019/2020 Winter Season Using a Stepped-Frequency Continuous Wave Radar (SFCW)
Abstract
1. Introduction
1.1. Snow Water Equivalent Importance
1.2. Instrumentation and Techniques
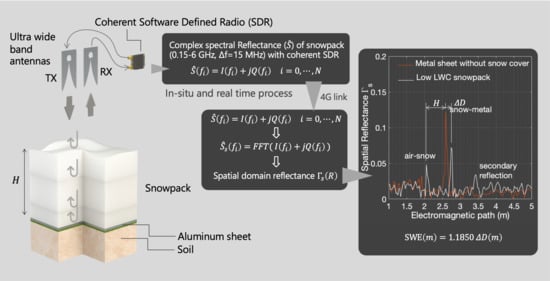
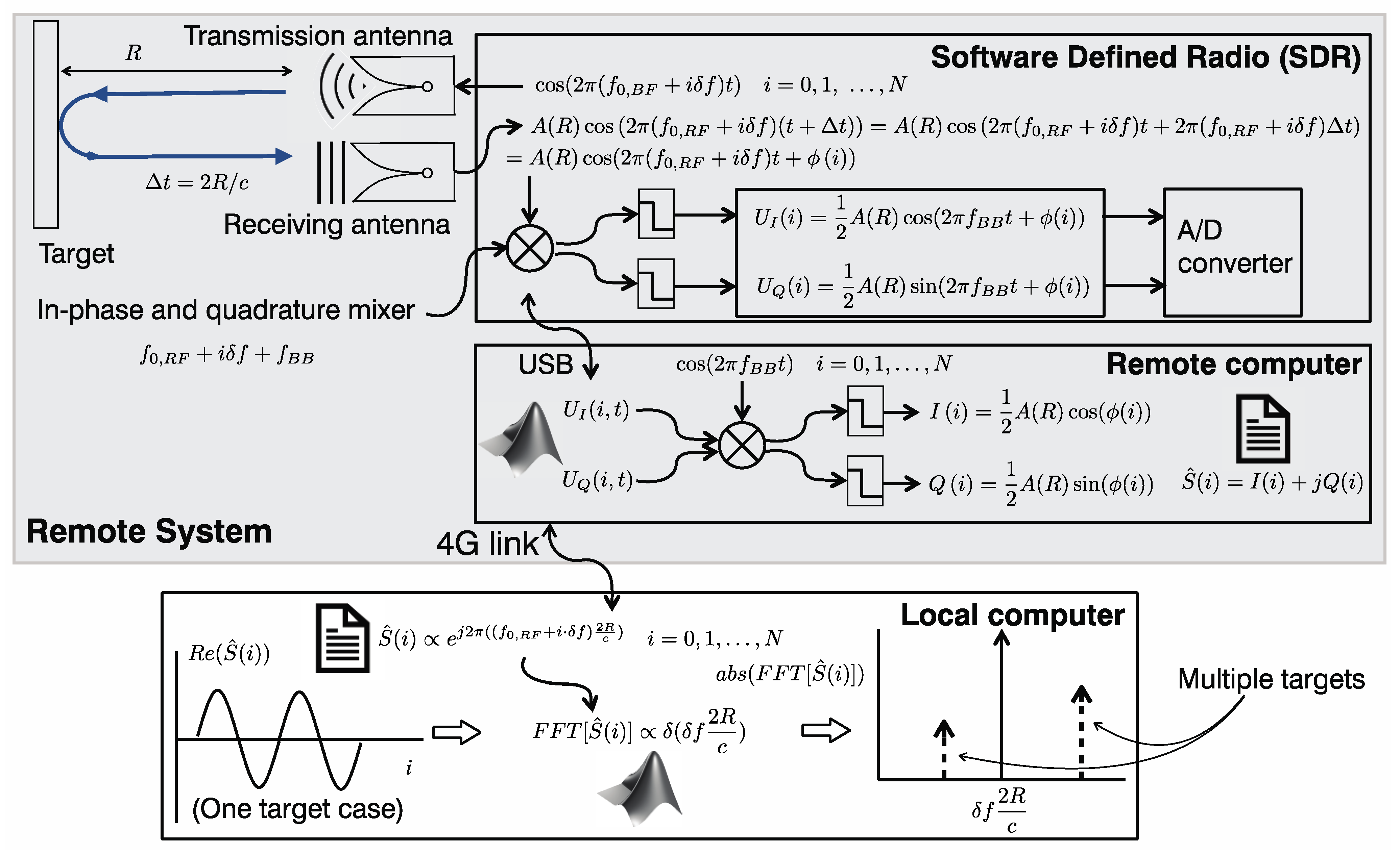
2. Theory of the SFCW Radar
2.1. Measurement Principle
3. Snowpack Electromagnetic Model
3.1. Matricial Multilayer Snowpack Electromagnetic Model
3.2. Reflectance Calculation for the Snowpack Multilayer
3.3. Spectral and Spatial Reflectance of Snowpack
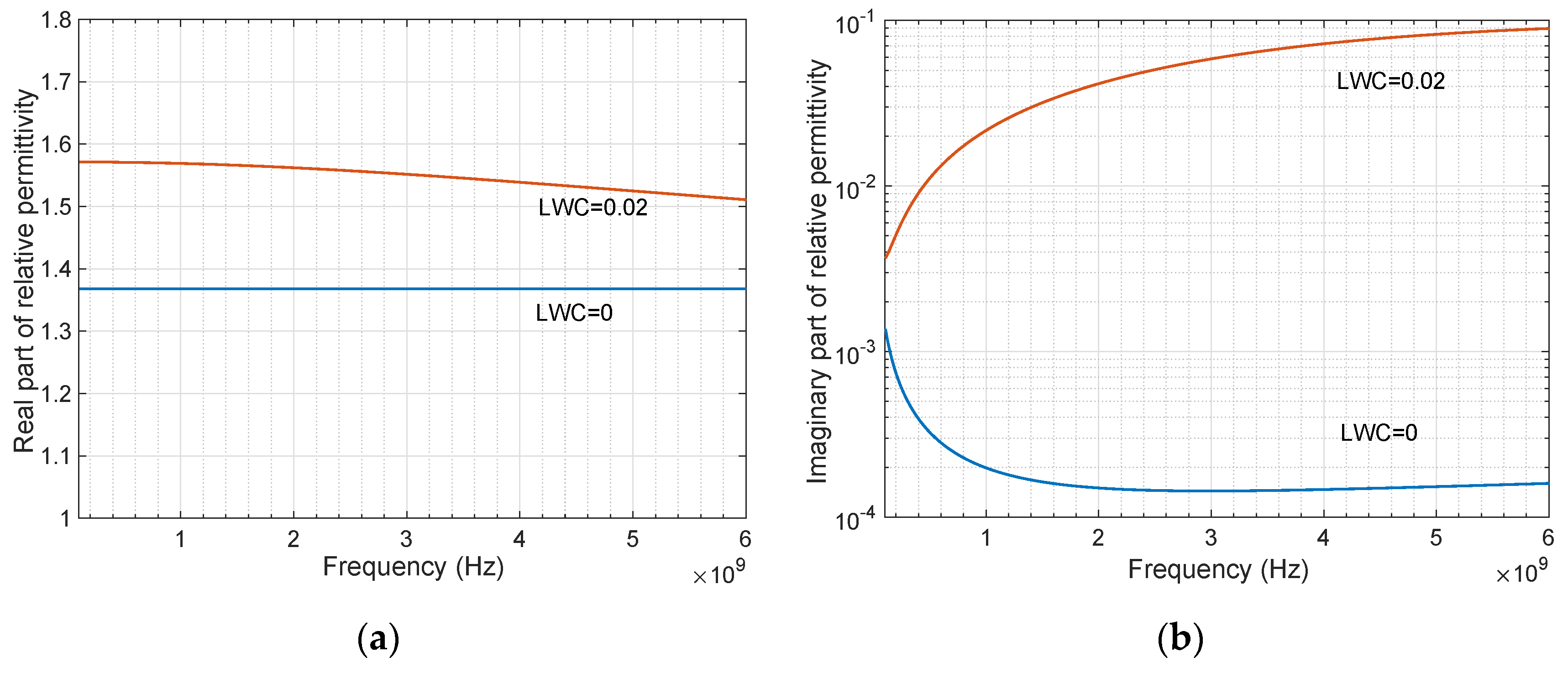
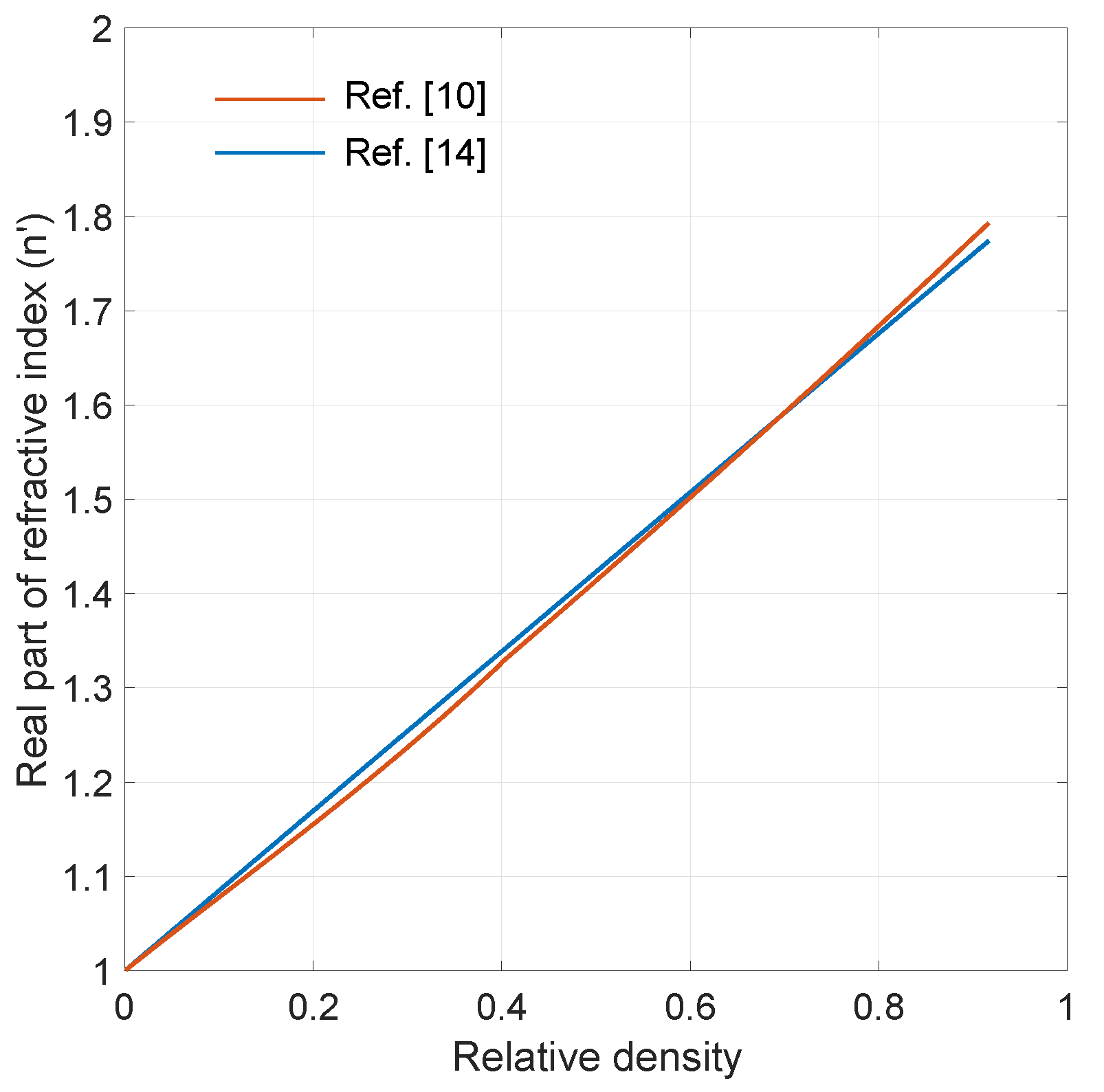
3.4. Complex Dielectric Constant of Dry and Wet Snow
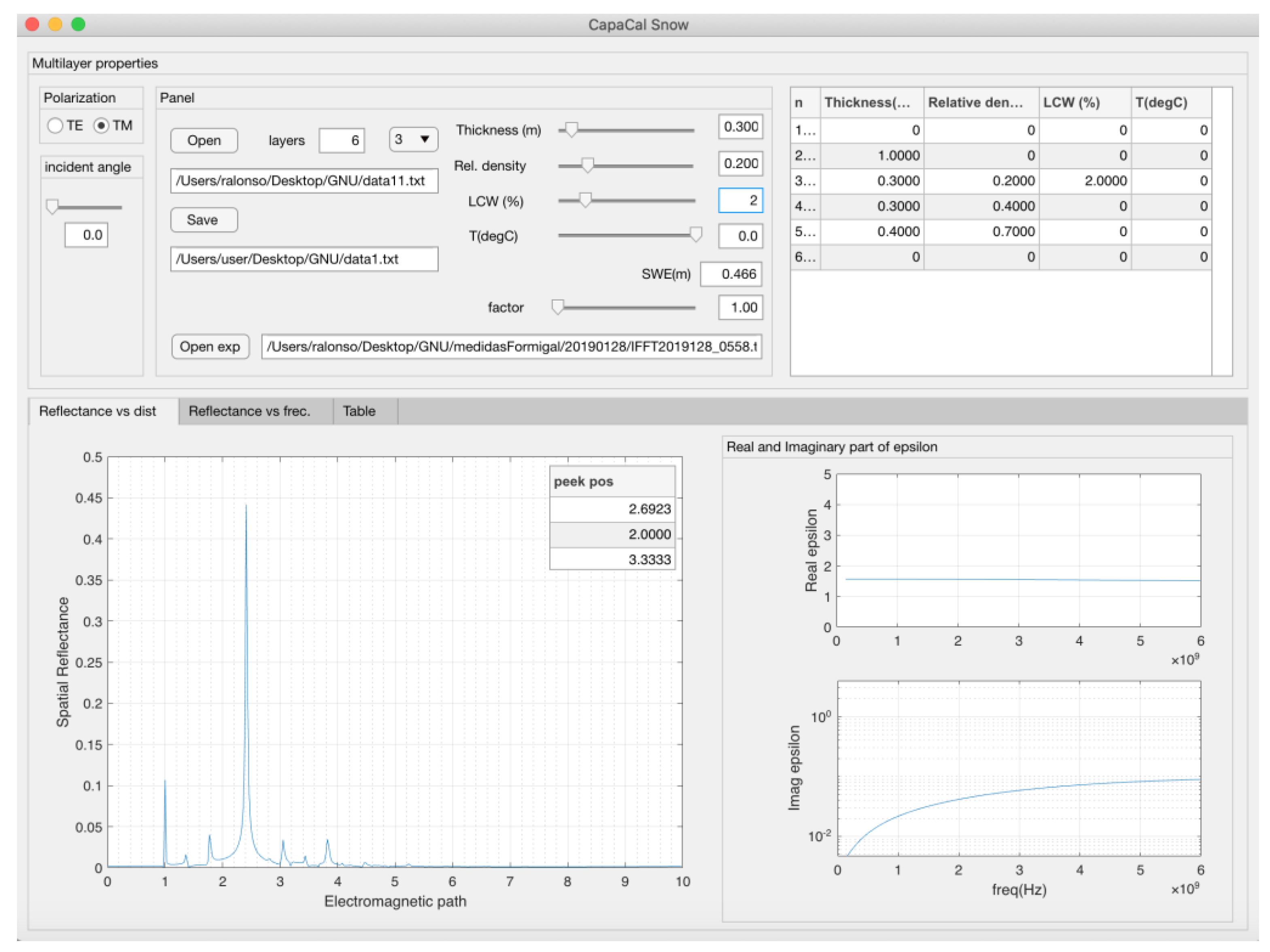
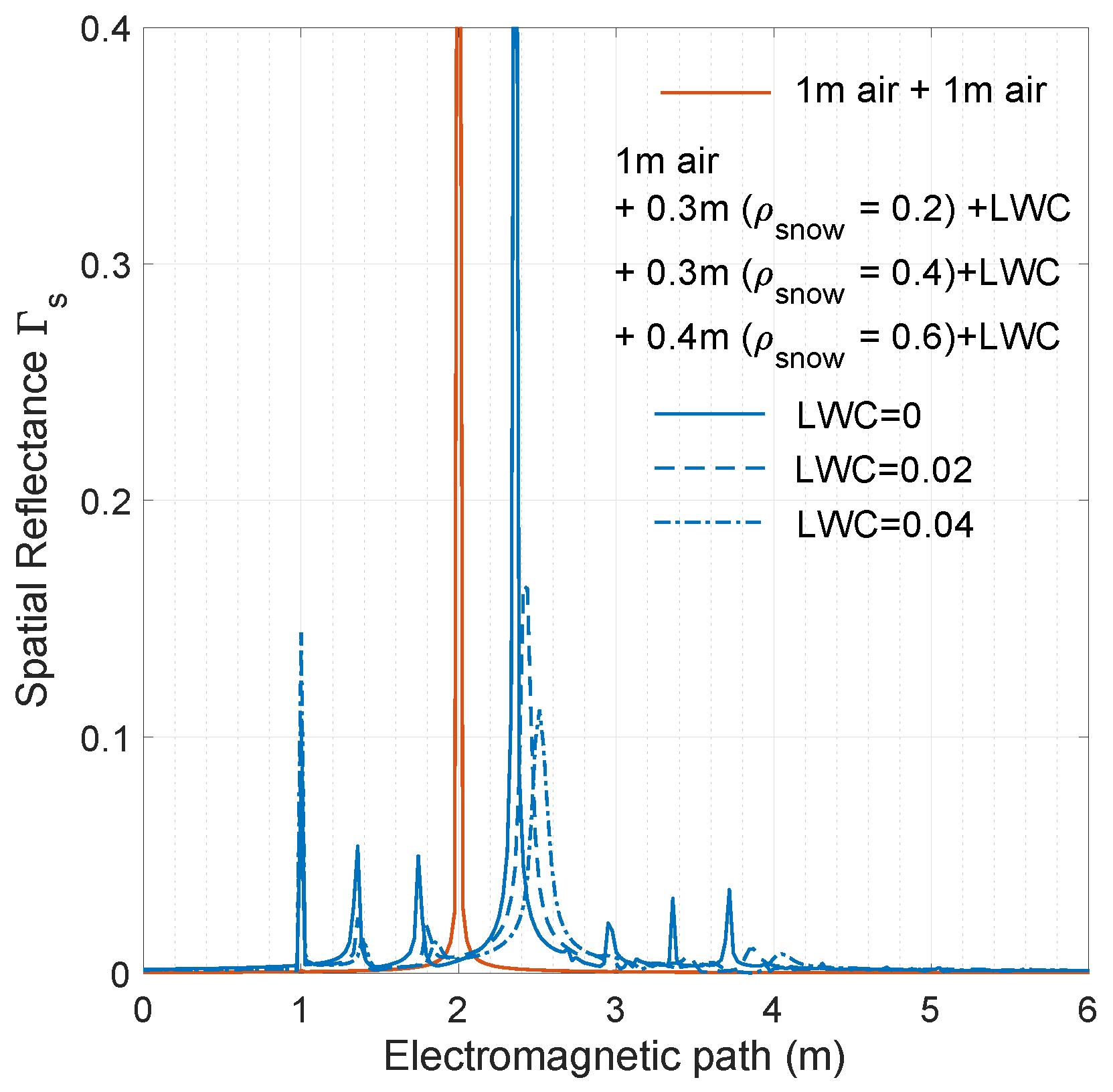
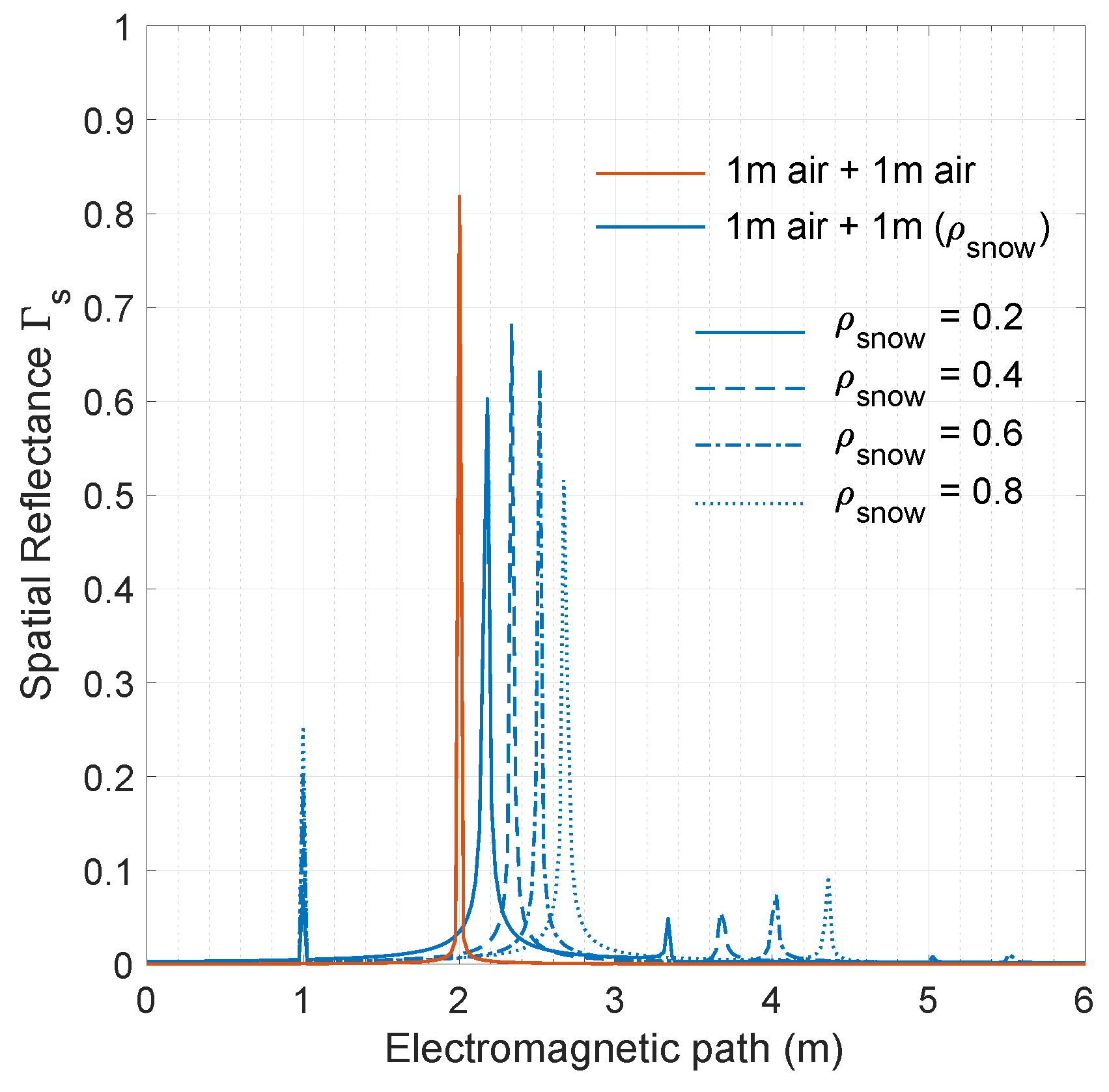
3.5. Simulations of Snowpack Reflectance
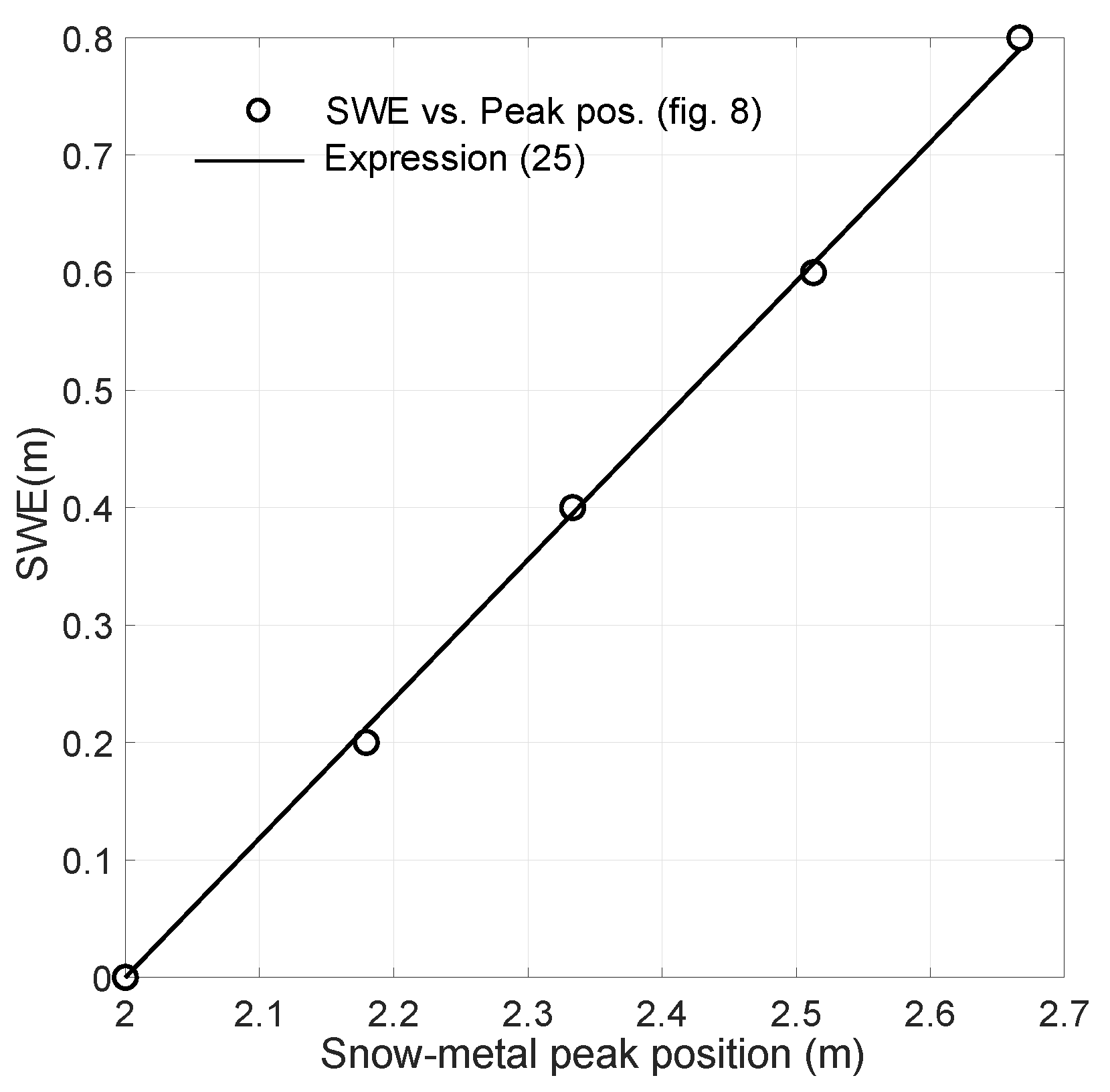
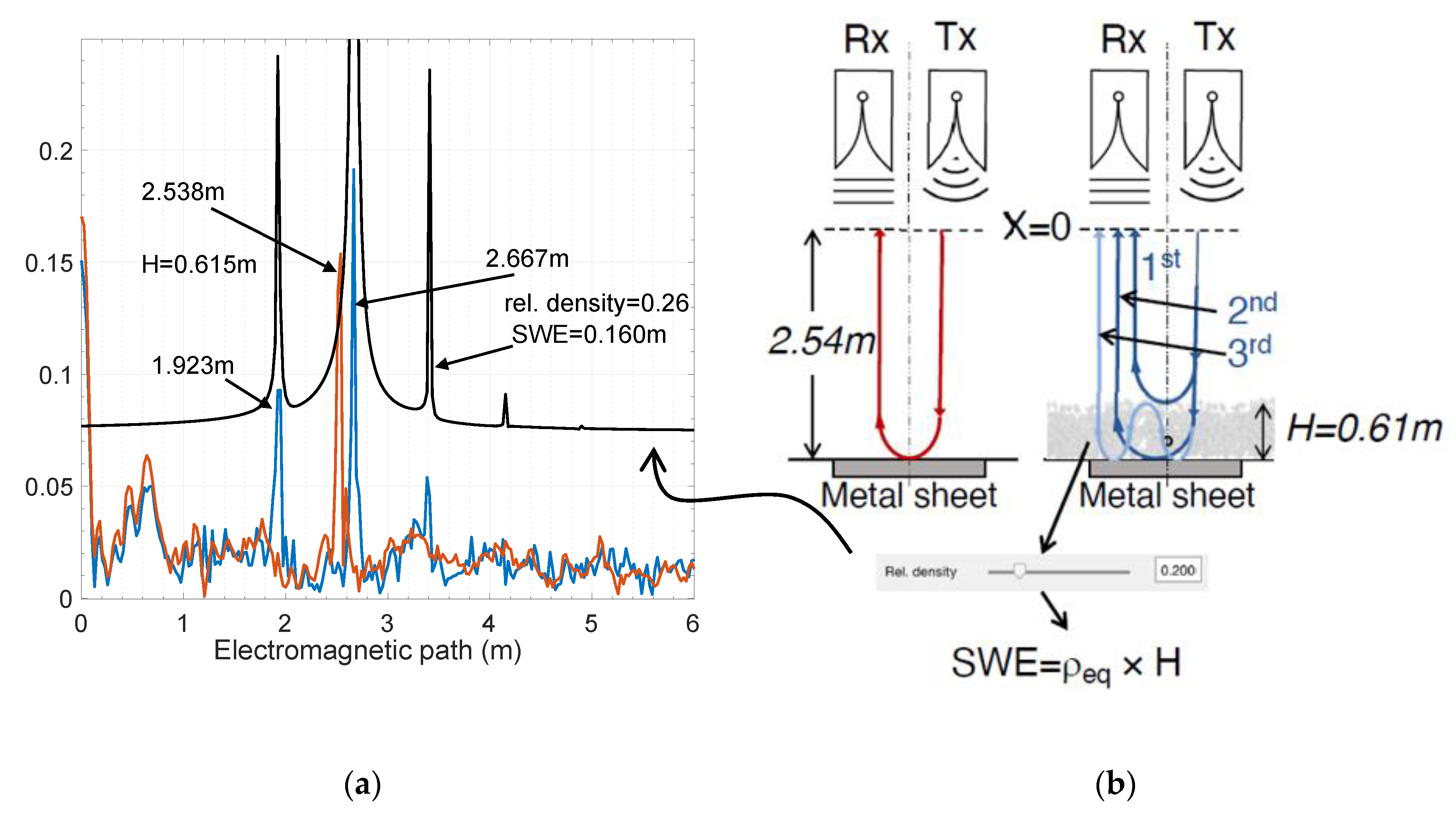
3.6. Estimation Procedure of SWE
4. Materials and Methods
4.1. Test Site Description
4.2. Field Measurement Radar Setup
4.3. Measurement Process
4.4. Milimeter Wave Radar Depth Sensor
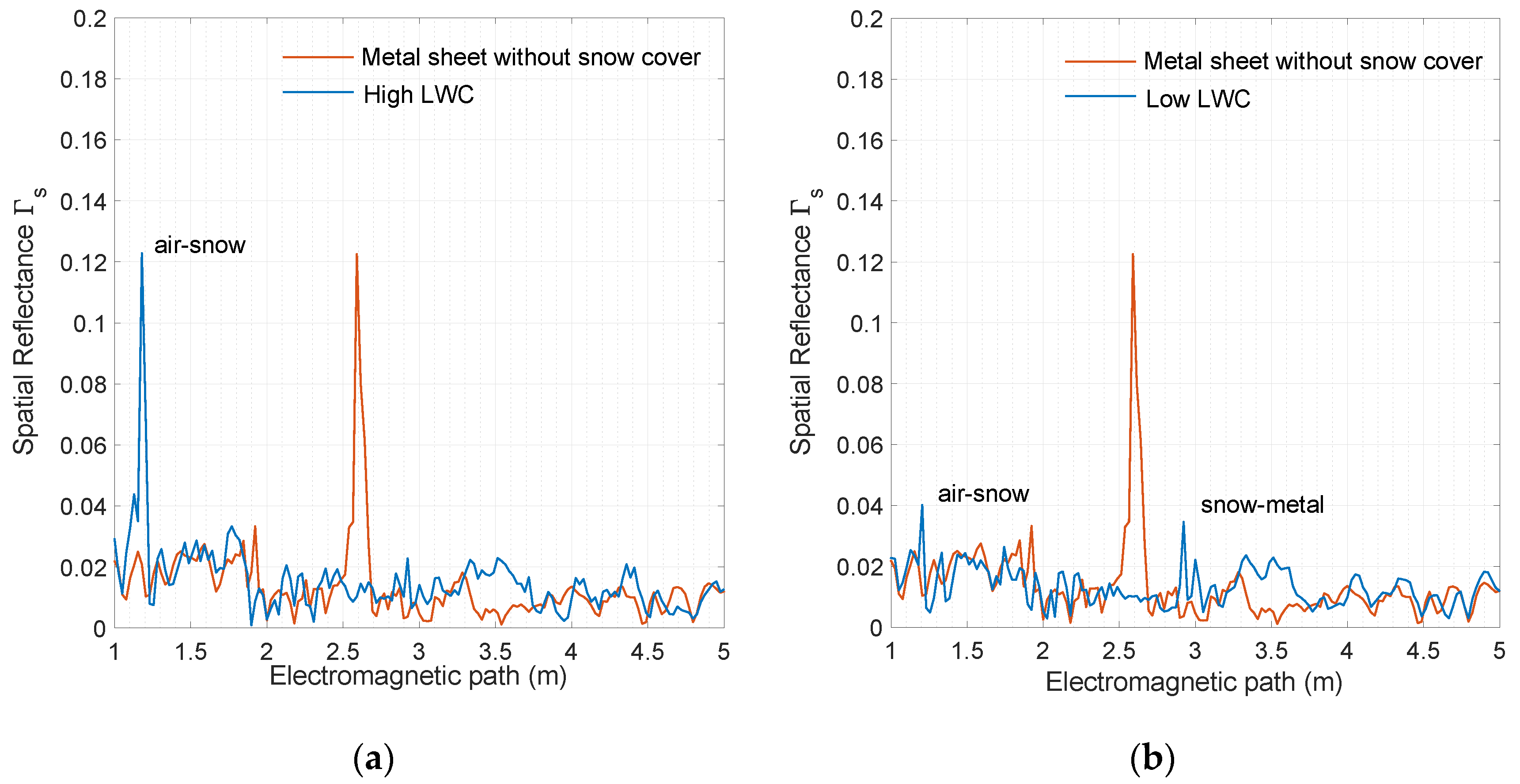
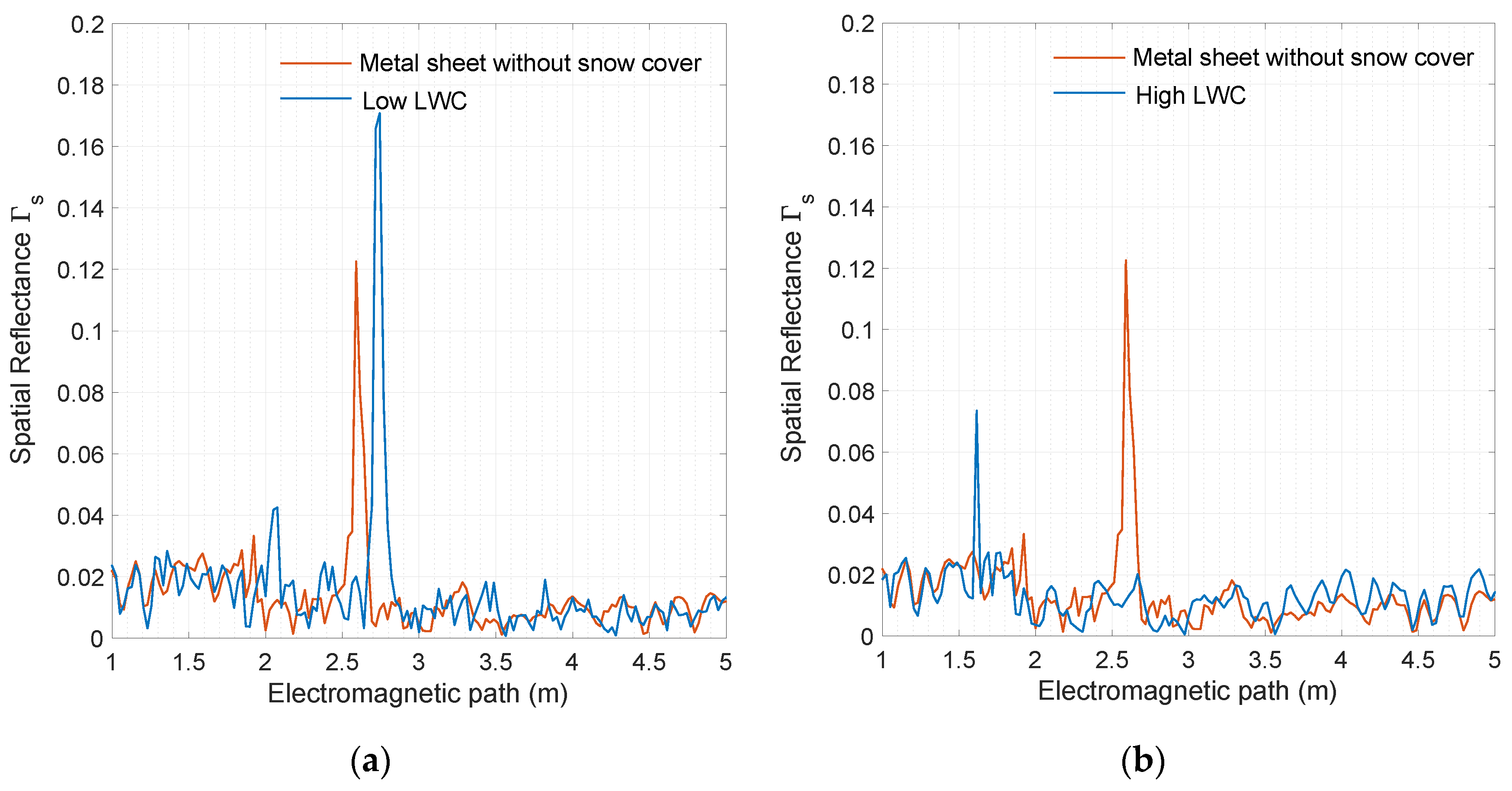
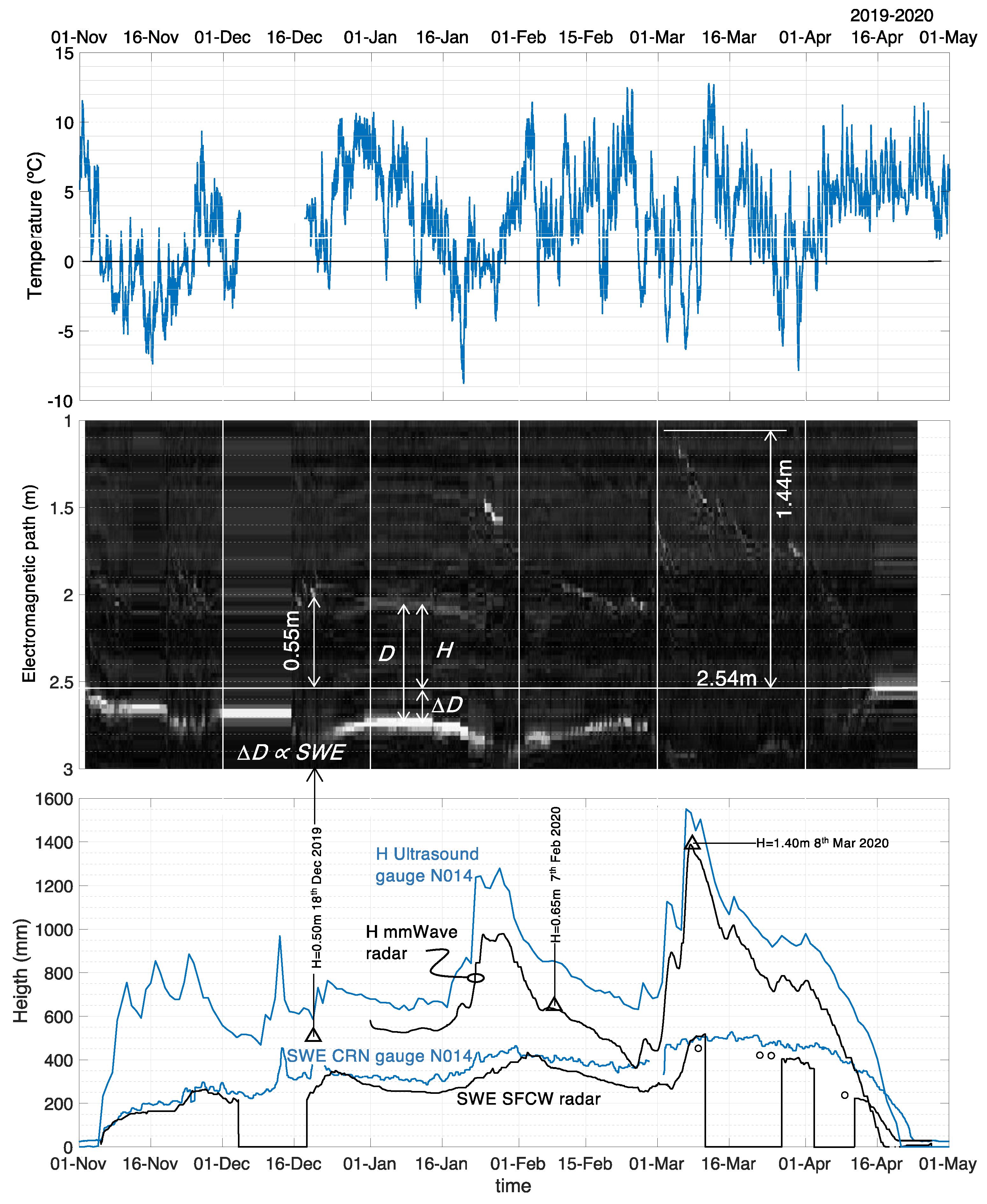
5. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dutra, E.; Viterbo, P.; Miranda, P.M.A.; Balsamo, G. Complexity of snow schemes in a climate model and its impact on Surface energy and hydrology. J. Hydrometeorol. 2012, 13, 521–538. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Gray, D.M.; Brown, T.; Hedstrom, N.R.; Quinton, W.L.; Granger, R.J.; Carey, S.K. The cold regions hydrological model: A platform for basing process representation and model structure on physical evidence. Hydrol. Processes 2007, 21, 2650–2667. [Google Scholar] [CrossRef]
- Marks, D.; Dozier, J. Climate and energy exchange at the snow surface in the alpine region of the Sierra Nevada: 2. Snow cover energy balance. Water Resour. Res. 1992, 28, 3043–3054. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Russi, T.; Stökli, U.; Zimmerli, M. SNOWPACK model calculations for avalanche warning based upon a new network of weather and snow stations. Cold Reg. Sci. Technol. 1999, 30, 145–157. [Google Scholar] [CrossRef]
- Kinar, N.J.; Pomeroy, J.W. Measurement of the physical properties of the snowpack. Rev. Geophys. 2015, 53, 481–544. [Google Scholar] [CrossRef]
- Paquet, E.; Laval, M.; Basalaev, L.M.; Belov, A.; Eroshenko, E.; Kartyshov, V.; Struminsky, A.; Yanke, V.L. An Application of Cosmic-Ray Neutron Measurements to the Determination of the Snow Water Equivalent. In Proceedings of the 30th International Cosmic Ray Conference, Merida, Mexico, 3–11 July 2007; Universidad Nacional Autónoma de México: Mexico City, Mexico, 2008; Volume 1, pp. 761–764. [Google Scholar]
- Kodama, M.; Nakai, K.; Kawasaki, S.; Wada, M. An application of cosmic-ray neutron measurements to the determination of the snow-water equivalent. J. Hydrol. 1979, 41, 85–92. [Google Scholar] [CrossRef]
- Kinar, N.J.; Pomeroy, J.W. Automated Determination of Snow Water Equivalent by Acoustic Reflectometry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3161–3167. [Google Scholar] [CrossRef]
- Pielmeier, C.; Schneebeli, M. Developments in the stratigraphy of snow. Surv. Geophys. 2003, 24.5-6, 389–416. [Google Scholar] [CrossRef]
- Tiuri, M.; Sihvola, A.; Nyfors, E.; Hallikaiken, M. The complex dielectric constant of snow at microwave frequencies. IEEE J. Ocean. Eng. 1984, 9, 377–382. [Google Scholar] [CrossRef]
- Sihvola, A.; Tiuri, M. Snow Fork for Field Determination of the Density and Wetness Profiles of a Snow Pack. IEEE Trans. Geosci. Remote Sens. 1986, GE-24.5, 717–721. [Google Scholar] [CrossRef]
- Denoth, A.; Foglar, A.; Weiland, P.; Mätzler, C.; Aebischer, H.; Tiuri, M.; Sihvola, A. A comparative study of instruments for measuring the liquid water content of snow. J. Phys. D 1984, 56, 2154–2160. [Google Scholar] [CrossRef]
- Mätzler, C. Applications of the interaction of microwaves with the natural snow cover. Remote Sens. Rev. 1987, 2, 259–387. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Microwave Emission Model of Layered Snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Lundberg, A.; Thunehed, H.; Bergström, J. Impulse Radar Snow Surveys -Influence of Snow Density. Nord. Hydrol. 2000, 31, 1–14. [Google Scholar] [CrossRef]
- Lundberg, A.; Thunehed, H. Snow Wetge Influence on Impulse Radar Snow Surveys. Theoretical and Laboratory study. Nord. Hydrol. 2000, 31, 89–106. [Google Scholar] [CrossRef]
- Gubler, H.; Hiller, M. The use of Microwave FMCW Radar in Snow and Avalanche Research. Cold Reg. Sci. Technol. 1984, 9, 109–119. [Google Scholar] [CrossRef]
- Holmgren, J.; Sturm, M.; Yankielun, N.E.; Koh, G. Extensive measurements of snow depth using FMCW radar. Cold Reg. Sci. Technol. 1998, 27.1, 17–30. [Google Scholar] [CrossRef]
- Marshall, H.P.; Koh, G. FMCW radars for snow research. Cold Reg. Sci. Technol. 2008, 52, 118–131. [Google Scholar] [CrossRef]
- Okorn, R.; Brunnhofer, G.; Platzer, T.; Heilig, A.; Schmid, L.; Mitterer, C.; Schweizer, J.; Eisen, O. Upward-looking L-band FMCW radar for snow cover monitoring. Cold Reg. Sci. Technol. 2014, 103, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Yankieluna, N.; Rosenthalb, W.; Davis, R.E. Alpine snow depth measurements from aerial FMCW radar. Cold Reg. Sci. Technol. 2004, 40, 123–134. [Google Scholar] [CrossRef]
- Pasian, M.; Barbolini, M.; Dell’Acqua, F.; Espín-López, P.F.; Silvestri, L. Snowpack Monitoring Using a Dual-Receiver Radar Architecture. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1195–1204. [Google Scholar] [CrossRef]
- Marshall, H.P.; Schneebeli, M.; Koh, G. Snow stratigraphy measurements with high-frequency FMCW radar: Comparison with snow micro-penetrometer. Cold Reg. Sci. Technol. 2007, 47, 108–117. [Google Scholar] [CrossRef]
- Panzer, B.; Gomez-Garcia, D.; Leuschen, C.; Paden, J.; Rodriguez-Morales, F.; Patel, A.; Markus, T.; Holt, B.; Gogineni, P. An ultra-wideband, microwave radar for measuring snow thickness on sea ice and mapping near-surface internal layers in polar firn. J. Glaciol. 2013, 59, 244–254. [Google Scholar] [CrossRef]
- Available online: https://www.ettus.com (accessed on 7 February 2021).
- Costanzo, S.; Spadafora, F.; Di Massa, G.; Borgia, A.; Costanzo, A.; Aloi, G.; Pace, P.; Loscrì, V.; Moreno, H.O. Potentialities of usrp-based software defined radar systems. Prog. Electromagn. Res. B 2013, 53, 417435. [Google Scholar] [CrossRef]
- Carey, S.C.; Scott, W.R. Software defined radio for stepped frequency, Ground Penetrating Radar. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4825–4828. [Google Scholar] [CrossRef]
- Marimuthu, J.; Bialkowski, K.S.; Abbosh, A.M. Software-Defined Radar for Medical Imaging. IEEE Trans. Microw. Theory Technol. 2016, 64, 643–652. [Google Scholar] [CrossRef]
- Prabaswara, A.; Munir, A.; Suksmono, A.B. GNU Radio based software-defined FMCW radar for weather surveillance application. In Proceedings of the 6th International Conference on Telecommunication Systems, Services, and Applications (TSSA), Bali, Indonesia, 20–21 October 2011; pp. 227–230. [Google Scholar] [CrossRef]
- Alonso, R.; Pozo, J.M.G.d.; Peruga, I.; Buisán, S.; Álvarez, J.A. Analysis Of Snow Water Equivalent (Swe) Of Snowpack By An Ultra Wide Band Step Frequency Continuous Wave Radar (Sfcw). In Proceedings of the 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Nguyen, C.; Park, J. Stepped-Frequency Radar Sensors. Theory, Analysis and Design; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-319-12271-7. [Google Scholar]
- Øyan, M.J.; Hamran, S.E.; Hanssen, L.; Berger, T.; Plettemeier, D. Ultrawideband gated step frequency ground-penetrating radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 212–220. [Google Scholar] [CrossRef]
- Taylor, J.D. Ultrawideband Radar Applications and Design; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9781420089868. [Google Scholar]
- Kurosawa, K.; Pierce, R.M.; Ushioda, S.; Hemminger, J.C. Raman-scattering and attenuated-total-reflection studies of surface-plasmon polaritons. Phys. Rev. B 1986, 33, 789–798. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1975; ISBN 978-0-521-64222-4. [Google Scholar]
- Buisán, S.T.; Earle, M.E.; Collado, J.L.; Kochendorfer, J.; Alastrué, J.; Wolff, M.; Smith, C.D.; López-Moreno, J.I. Assessment of snowfall accumulation underestimation by tipping bucket gauges in the Spanish operational network. Atmos. Meas. Tech. 2017, 10, 1079–1091. [Google Scholar] [CrossRef]
- Available online: http://www.saihebro.com/saihebro/index.php?url=/datos/ficha/estacion:N014 (accessed on 7 February 2021).
- Available online: https://siliconradar.com/products/single-product/120-ghz-radar-transceiver/ (accessed on 7 February 2021).







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Start frequency | 150 MHz | Stop frequency | 6 GHz |
| Number of steps (N) | 390 | Stepped-frequency, δf | 15 MHz |
| Chirp period | ≈80 s | Unambiguous range, Ru 2 | 10 m |
| Resolution (in vacuum), δR 1 | ≈2.5 cm | Intermediate frequency (IF) | 31.250 kHz |
| Sampling rate | 3.125 MS/s | Antennas wide band | 675 MHz–12 GHz |
| Directivity of antennas | 11dBi@2.4GHz | FOV 3 of Tx and Rx antennas | <15° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso, R.; Pozo, J.M.G.d.; Buisán, S.T.; Álvarez, J.A. Analysis of the Snow Water Equivalent at the AEMet-Formigal Field Laboratory (Spanish Pyrenees) During the 2019/2020 Winter Season Using a Stepped-Frequency Continuous Wave Radar (SFCW). Remote Sens. 2021, 13, 616. https://doi.org/10.3390/rs13040616
Alonso R, Pozo JMGd, Buisán ST, Álvarez JA. Analysis of the Snow Water Equivalent at the AEMet-Formigal Field Laboratory (Spanish Pyrenees) During the 2019/2020 Winter Season Using a Stepped-Frequency Continuous Wave Radar (SFCW). Remote Sensing. 2021; 13(4):616. https://doi.org/10.3390/rs13040616
Chicago/Turabian StyleAlonso, Rafael, José María García del Pozo, Samuel T. Buisán, and José Adolfo Álvarez. 2021. "Analysis of the Snow Water Equivalent at the AEMet-Formigal Field Laboratory (Spanish Pyrenees) During the 2019/2020 Winter Season Using a Stepped-Frequency Continuous Wave Radar (SFCW)" Remote Sensing 13, no. 4: 616. https://doi.org/10.3390/rs13040616
APA StyleAlonso, R., Pozo, J. M. G. d., Buisán, S. T., & Álvarez, J. A. (2021). Analysis of the Snow Water Equivalent at the AEMet-Formigal Field Laboratory (Spanish Pyrenees) During the 2019/2020 Winter Season Using a Stepped-Frequency Continuous Wave Radar (SFCW). Remote Sensing, 13(4), 616. https://doi.org/10.3390/rs13040616