DSM Generation from Single and Cross-Sensor Multi-View Satellite Images Using the New Agisoft Metashape: The Case Studies of Trento and Matera (Italy)

Abstract

DSM generation from satellite imagery is a long-lasting issue and it has been addressed in several ways over the years; however, expert and users are continuously searching for simpler but accurate and reliable software solutions. One of the latest ones is provided by the commercial software Agisoft Metashape (since version 1.6), previously known as Photoscan, which joins other already available open-source and commercial software tools. The present work aims to quantify the potential of the new Agisoft Metashape satellite processing module, considering that to the best knowledge of the authors, only two papers have been published, but none considering cross-sensor imagery. Here we investigated two different case studies to evaluate the accuracy of the generated DSMs. The first dataset consists of a triplet of Pléiades images acquired over the area of Trento and the Adige valley (Northern Italy), which is characterized by a great variety in terms of geomorphology, land uses and land covers. The second consists of a triplet composed of a WorldView-3 stereo pair and a GeoEye-1 image, acquired over the city of Matera (Southern Italy), one of the oldest settlements in the world, with the worldwide famous area of Sassi and a very rugged morphology in the surroundings. First, we carried out the accuracy assessment using the RPCs supplied by the satellite companies as part of the image metadata. Then, we refined the RPCs with an original independent terrain technique able to supply a new set of RPCs, using a set of GCPs adequately distributed across the regions of interest. The DSMs were generated both in a stereo and multi-view (triplet) configuration. We assessed the accuracy and completeness of these DSMs through a comparison with proper references, i.e., DSMs obtained through LiDAR technology. The impact of the RPC refinement on the DSM accuracy is high, ranging from 20 to 40% in terms of LE90. After the RPC refinement, we achieved an average overall LE90 <5.0 m (Trento) and <4.0 m (Matera) for the stereo configuration, and <5.5 m (Trento) and <4.5 m (Matera) for the multi-view (triplet) configuration, with an increase of completeness in the range 5–15% with respect to stereo pairs. Finally, we analyzed the impact of land cover on the accuracy of the generated DSMs; results for three classes (urban, agricultural, forest and semi-natural areas) are also supplied.

1. Introduction

Digital Surface Models (DSMs) are a discrete mathematical representation of the Earth’s surface through a regular array of Z-values (heights), all referenced to a common datum [1]. DSMs represent the topographic surface visible from space or air which includes vegetation, buildings, infrastructures and generally all human-made objects. Thus, they provide an essential source of information for several engineering, environmental, Earth sciences, safety and security applications.

Presently, thanks to the growing numbers of satellite sensors such as WorldView, GeoEye and Pléiades, more and more high-resolution optical imagery are available. The increasing accessibility of these high-resolution optical satellite data has attracted considerable interest in DSM generation and a wide literature has been produced [2,3,4,5,6]. Furthermore, many commercial software tools are now able to generate DSMs from optical data. Among these, OrthoEngine, the photogrammetric module of Geomatica (PCI Geomatics) [7], ENVI Opticalscape (L3Harris Geospatial) [8], ERDAS IMAGINE (Hexagon Geospatial) [9] and SAT-PP (4DiXplorer) [10] are the most used.

Since version 1.6, released in January 2020, Agisoft Metashape [11] (previously known as Photoscan)—a photogrammetric 3D modelling software based on the Structure from Motion technique—supports the processing of satellite imagery, in addition to standard digital images. This new option, integrated into the standard multi-view workflow, allows generating all the typical products, such as dense clouds, DSMs, orthomosaics and tiled polygonal models from satellite optical imagery. Specifically, Metashape can process panchromatic and multispectral satellite images, provided that sufficiently accurate Rational Polynomial Coefficients (RPCs) are available for each image [12].

This paper aims at deeply investigating and testing the Agisoft Metashape satellite processing capabilities, by continuing the work started in [13]. Indeed, it is worth noticing that to the best of our knowledge, the Agisoft Metashape satellite processing module has been only very partially investigated in previous works [13,14]. Han et al. [14] compared the performance of three software solutions for DSM generation, including Agisoft Metashape; they assessed the accuracy of DSMs generated using a WorldView-3 multi-view satellite dataset. In [13] only preliminary results were discussed and, also in this case, none with cross-sensor imagery. Therefore, a complete and detailed analysis of Agisoft Metashape performance is still missing, especially with cross-sensor imagery, which is quite standard when wide areas covered by multiple scenes captured by different sensors (possibly in short time intervals) are considered.

The standard Rational Polynomial Functions (RPFs) model has been widely adopted for imagery orientation in technical and scientific applications. The RPCs for these functions are usually supplied by the satellite companies, as part of the image metadata, to enable direct image orientation without the knowledge of camera information, satellite attitude and ephemeris; in this sense, they allow the satellite companies to hide the physical sensor models. Furthermore, as the RPCs implicitly provide the interior and exterior sensor orientation, the availability of Ground Control Points (GCPs) is no longer required [15].

In the present work, we used the original RPCs provided in the imagery metadata and we also refined them through an original terrain independent approach [16]. We recall here that an image orientation approach based on RPFs is referred to as “terrain independent” when the original RPCs are used and refined using (a few) suitable GCPs, whereas it is referred to as “terrain dependent” when all the RPCs are directly estimated from scratch, using a high number of GCPs. It is well known that the terrain dependent approach must be avoided because it is costly (for the high number of required GCPs) and very sensitive to GCP outliers. On the contrary, the new original approach generates a new set of RPCs starting from the original one, but using a few suitable GCPs, differently from the standard terrain independent approach which just estimates a correction for the original RPC set through a simple (shift or affine) 2D transformation [15]. To generate the refined RPCs, we used a set of GCPs adequately distributed across the regions of interest. This refinement guarantees that all the used imagery are georeferenced in a unique reference frame (the same as the reference DSM used to assess the quality of the generated DSMs), removing possible georeferencing biases among different imagery, which can severely impact the quality of the generated DSMs. Therefore, we tested the potential of the Agisoft Metashape satellite processing module using both the original and the refined RPCs to evaluate the impact of the refinement on DSM accuracy. We investigated the procedure using single and cross-sensor multi-view satellite images. Specifically, we adopted a triplet of Pléiades images and a triplet composed of a WorldView-3 stereo pair and a GeoEye-1 image and we evaluated the accuracy of the generated DSMs using LiDAR DSMs as reference. We also analyzed the impact of land use on the generated DSMs using the CORINE (coordination of information on the environment) Land Cover (CLC) inventory [17].

The paper is organized as follows: Section 2 gives a description of the study areas and the adopted datasets; Section 3 presents the standard DSM generation procedure using Agisoft Metashape and provides technical details about the performed processing; Section 4 illustrates the DSM assessment using the LiDAR ground truths. Finally, in Section 5 some conclusions and final considerations are drawn.

2. Study Areas and Optical Datasets

The analyzed study areas include two different regions: Trento and the Adige valley (Northern Italy) and Matera (Southern Italy). The former shows a great variety in terms of land cover and land use (such as urban and agricultural areas, forested hills and mountains), slope and altitude (which ranges from 200 to 1500 m). The area heterogeneity is strictly related to variations in terms of frequency of surface irregularities (such as buildings, isolated trees and so on). The latter includes part of the urban area of Matera, one of the oldest settlements in the world (Sassi of Matera), and a very rugged morphology in the surroundings including the slope of the rocky ravine created by the Gravina stream. Because of this, the region of interest, despite being quite limited, is highly heterogeneous and irregular. It presents a dense urban area, with both ancient and modern dwellings that perfectly fit with the morphology of the territory, which is suddenly interrupted by the ravine or one of the deep gorges with steep walls created by rainwater over thousands of years [18]. In terms of extension, the Trento area considered for the DSM accuracy assessment corresponds to the extension of the LiDAR DSM used as reference, which ranges from 659,989.5 m to 668,010.5 m E and from 5,097,989.5 m to 5,108,010.5 m N (Coordinate Reference System CRS: EPSG:32632-WGS 84/UTM zone 32N-Projected). Specifically, the reference LiDAR DSM, captured in 2014, is characterized by a grid step of 0.5 × 0.5 m and a noise that ranges from 0.05 to 0.10 m; the elevations are orthometric heights with respect to the Italian official geoid ITALGEO 2005. This DSM is freely available on the website of the Provincia Autonoma di Trento [19]. The Matera area ranges from 635,415.5 m to 637,197.0 m E and from 4,501,771.5 m to 4,503,758.5 m N (CRS: EPSG:32633-WGS 84/UTM zone 33N-Projected), that is again the region covered by the reference LiDAR DSM used for comparison. The grid step of this DSM, acquired in July 2013, amounts to 0.5 × 0.5 m and the noise ranges from 0.03 to 0.05 m; the elevations are ellipsoidal heights with respect to WGS84 ellipsoid.

As far as concerns the optical dataset, it consists of a triplet captured in along-track mode by the Pléiades sensor over the area of Trento and a triplet acquired by the WorldView-3 and GeoEye-1 satellites over Matera.

The DSM generation was based on pairs and triplets processing. For each pair, the intersection angle ${\beta }_{ij}$ between the i-$th$ and j-$th$ images was computed using the standard formula:

$${\beta }_{ij}=arccos\left(\frac{e_i·e_j}{\left|\right|e_i\left|\right|·\left|\right|e_j\left|\right|}\right)$$

(1)

where $e_i=(sin{\alpha }_{i}cos{\zeta }_i,cos{\alpha }_{i}cos{\zeta }_i,sin{\zeta }_i)$ refers to the satellite average position during the acquisition of the i-$th$ image, according to the local ENU Cartesian coordinate system, and ${\alpha }_i$ and ${\zeta }_i$ are the corresponding satellite azimuth and elevation. If the information about the satellite elevation is not available, $\zeta$ can be replaced by the incidence angle $\iota$, since $\zeta =90°-\iota$.

The images composing the Pléiades triplet, hereafter called image 1, image 2, and image 3, were acquired on 28 August 2012 in the North-South scan direction. The boundaries of each image are displayed in

Table 1. Boundaries of the Trento Pléiades triplet.

	Image 1		Image 2		Image 3
Corner	Longitude (°)	Latitude (°)	Longitude (°)	Latitude (°)	Longitude (°)	Latitude (°)
LL	11.05	46.02	11.06	46.02	11.06	46.02
UL	11.06	46.11	11.06	46.11	11.06	46.11
UR	11.19	46.11	11.19	46.11	11.19	46.11
LR	11.19	46.02	11.19	46.02	11.19	46.02

, whereas the average acquisition features for the Pléiades triplet are recalled in

Table 2. Acquisition features (average values) of the Trento Pléiades triplet.

	Image 1	Image 2	Image 3
Azimuth Angle (°)	180.0	180.0	180.0
Cross-Track View Angle (°)	3.0	1.8	1.5
In-Track View Angle (°)	−12.7	12.4	17.3
Off-Nadir View Angle (°)	13.0	12.5	17.4
In-Track Incidence Angle (°)	13.4	−13.7	−19.0
Cross-Track Incidence Angle (°)	−6.3	0.9	2.5
Incidence Angle (°)	14.7	13.7	19.2
Sun Azimuth (°)	158.3	157.9	157.9
Sun Elevation (°)	51.8	51.8	51.8
Native Mean GSD (m)	0.73	0.73	0.76

.

All the images are oversampled and supplied to the user with a 0.50 m GSD (the native mean GSDs are shown in Table 2). The three images are analyzed by pairs, testing all the possible combinations, and all together as described below:

• pair 1, composed of images 1 and 3 (intersection angle of $32.4°$);
• pair 2, composed of images 1 and 2 (intersection angle of $27.1°$);
• pair 3, composed of images 2 and 3 (intersection angle of $5.3°$);
• pair 1–pair 2 (that is, the triplet obtained by merging pairs 1 and 2—see Section 3 for more details);
• pair 1–pair 3 (as before);
• pair 2–pair 3 (as before).

For Matera, the three 16 bit BGRN images used in the present study were captured between March 2017 (WorldView-3 stereo pair) and May 2017 (GeoEye-1 image). In the present work, we refer to the WorldView-3 pair and GeoEye-1 image as WorldView-3 1, WorldView-3 2, and GeoEye-1, respectively. In

Table 3. Boundaries of the Matera WorldView-3 stereo pair and the GeoEye-1 image.

	WorldView-3 1		WorldView-3 2		GeoEye-1
Corner	Longitude (°)	Latitude (°)	Longitude (°)	Latitude (°)	Longitude (°)	Latitude (°)
LL	16.56	40.62	16.56	40.62	16.57	40.63
UL	16.57	40.71	16.57	40.71	16.57	40.70
UR	16.70	40.70	16.70	40.70	16.65	40.69
LR	16.69	40.62	16.69	40.62	16.65	40.63

, the boundaries of the three images are recalled. The three products, however, are provided to the user in a projected CRS (that is, EPSG:32633-WGS 84/UTM zone 33N-Projected): it is worth noticing that the image projection was carried out through a flat digital model associated with the average elevation of the area covered by each image. In addition to the average values of the main acquisition parameters shown in

Table 4. Acquisition features (average values) of the Matera WorldView-3 stereo pair and the GeoEye-1 image.

	WorldView-3 1	WorldView-3 2	GeoEye-1
ROI Average Elevation (m)	379.47	379.47	363.49
Scan Direction (-)	Forward	Forward	Reverse
Cross-Track View Angle (°)	−5.9	−7.8	−3.8
In-Track View Angle (°)	9.2	−28.4	−1.2
Off-Nadir View Angle (°)	11.0	29.4	4.0
Satellite Azimuth (°)	338.1	205.0	260.8
Satellite Elevation (°)	78.1	57.2	85.6
Sun Azimuth (°)	162.0	162.5	149.7
Sun Elevation (°)	51.7	51.8	62.8
Native Mean GSD (m)	0.32	0.40	0.42

, we must mention that the images were all acquired in full swath mode and that they were resampled to 0.40 m.

Also in this case, the images were analyzed both by pairs, testing all the possible combinations, and all together. Hereafter the combinations will be referred to as:

• pair 1, composed of images WorldView-3 1 and GeoEye-1 (intersection angle of $11.7°$);
• pair 2, composed of images WorldView-3 1 and WorldView-3 2 (intersection angle of $41.7°$);
• pair 3, composed of images WorldView-3 2 and GeoEye-1 (intersection angle of $30.5°$);
• pair 1–pair 2–pair 3 (that is, the triplet obtained by merging the DSMs generated from the aforementioned pairs, according to a sub-optimal procedure external to Agisoft Metashape—see Section 3 for more details).

3. DSM Generation Procedure

To produce the DSMs presented in this paper, we followed the standard Agisoft Metashape procedure described in [12] (the used version of the software was 1.6.5.11249—Professional Edition). We can summarize it as follows: for the satellite imagery, the first steps to generate a DSM are essentially those required to produce a 3D model through a common digital camera, namely image alignment and dense cloud generation. To calibrate the satellite images, the software relies on the RPCs which are loaded automatically if they are present in the RPC coefficient tag of the image EXIF data. Alternatively, they can be loaded from supplementary .txt or .rpb files. For all the imagery, the RPCs were stored in .xml files, which were converted to .txt, including the inverse model coefficients only (from ground coordinates—$(\varphi ,\lambda ,h)$—to image ones—$(I,J)$).

As already mentioned, for the processing of stereo pairs both the original and refined RPCs were used, so that two versions were produced for each of the DSMs to be validated: the first with the original RPCs and the second with the refined ones. The RPCs were refined using a set of 19 and 11 uniformly distributed GCPs for the case studies of Trento and Matera, respectively. Two kinds of processing were considered: all the possible pairs and the two triplets to fully exploit the imagery information content. The six tests on the stereo pairs (pair 1, pair 2 and pair 3 of the Trento study area and pair 1, pair 2 and pair 3 of the Matera study area) were carried out both with the original and the refined RPCs, using the same processing parameters [12]:

• the alignment accuracy was set to “High”;
• the alignment was optimized with respect to the $(cx,cy)$ parameters on all the tie points found in the previous step;
• the dense cloud was built with “Ultra High” quality.

The two tests on the triplets gave different results. For Pléiades triplet of the Trento area it was not possible to proceed with a standard multi-view approach, since the overall alignment of the three images was not achieved. Therefore, all the pairs were firstly aligned in separate chunks (using only the refined RPCs). Then, for each chunk, the alignment was optimized and a dense cloud was built with “Ultra High” quality. Finally, the chunks were aligned two by two (pair 1–pair 2, pair 1–pair 3 and pair 2–pair 3)—based on the respective tie points—and merged. The resulting point cloud was the union of the original “parent” point clouds.

For the mixed triplet of the Matera area, neither a multi-view approach nor an approach based on chunk alignment as done for Pléiades triplet was successful. Therefore, the final DSM coming from the three images was obtained with a simple procedure external to Agisoft, computing a weighted mean of the three DSMs obtained from the three different pairs. In details, the weighting criterion was based on the intersection angles $\beta$ of the three pairs, following the dependence of height precision on the satellite base-to-altitude ratio in the standard normal case [20]:

$$h_w^{i,j}=\frac{{\sum }_{k=1}^n{tan}^2\left({\beta }_k\right)·h_k^{i,j}}{{\sum }_{k=1}^n{tan}^2\left({\beta }_k\right)}$$

(2)

where $h_w^{i,j}$ is the weighted height of the $(i,j)$-$th$ pixel, $h_k^{i,j}$ is the height of the $(i,j)$-$th$ pixel of the DSM generated from the $k-th$ pair and $n\in \{1,2,3\}$ is the number of DSMs contributing to the estimate of the weighted height. It is evident that this simple procedure is general but sub-optimal; in fact, the final DSM is not derived from an overall optimization of the alignment of all images, but only through a combination of different DSMs, each containing a possible bias due to the geometry of the pair from which it is generated.

The following stage of DSM generation was the same for all the tests: each DSM was generated from the respective dense cloud as source data, in a geographic CRS (the WGS 84/UTM zone 32N + EGM96 coordinate system for the Trento study area, the WGS 84/UTM zone 33N coordinate system for the Matera study area).

Table 5. DSM optimal resolution computed by Agisoft Metashape—case study of Trento.

Test	DSM Optimal Resolution (m)
pair 1	0.52
pair 2	0.51
pair 3	0.52
pairs 1-2	0.52
pairs 1-3	0.52
pairs 2-3	0.52

and

Table 6. DSM optimal resolution computed by Agisoft Metashape—case study of Matera.

Test	DSM Optimal Resolution (m)
pair 1	0.40
pair 2	0.40
pair 3	0.36

refer to the DSM optimal resolution automatically computed by Agisoft Metashape for each image set, being not dependent on the RPC refinement. During the DSM generation stage, no interpolation was carried out for the non-reconstructed areas.

4. Accuracy and Completeness Assessment

To evaluate the accuracy of the generated DSMs, we compared them to the corresponding LiDAR reference for each study area. First of all, we resampled all the obtained DSMs to the reference DSM resolution (0.5 m) using a cubic interpolation. Then, we computed the elevation differences for each pixel according to the following equation:

$$\Delta Z_i=Z_{DSM,i}-Z_{REF,i}$$

(3)

where $Z_{DSM,i}$ is the $i-th$ pixel elevation of the generated DSM and $Z_{REF,i}$ is the $i-th$ pixel elevation of the LiDAR DSM.

Then, we used a threshold $\Delta Z$ of 20 m to remove the values out of the range $(-\Delta Z,\Delta Z)$ considered outliers. We computed the standard statistical indicators of the elevation differences (mean, standard deviation, root mean square error—RMSE, median, normalized median absolute deviation—NMAD, LE68 and LE90) which are usually adopted for the assessment of the global DSMs [21]. We assessed the results using the entire tile and considering the different land covers and morphologies separately. 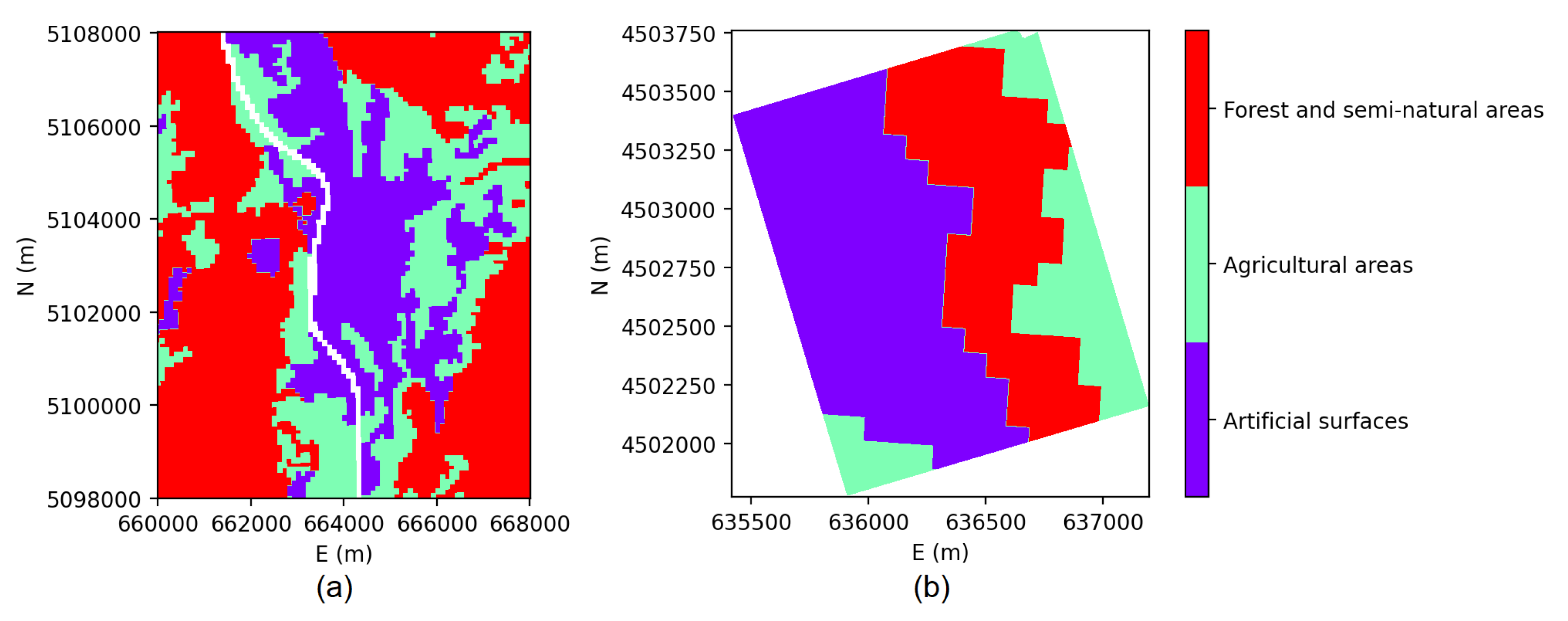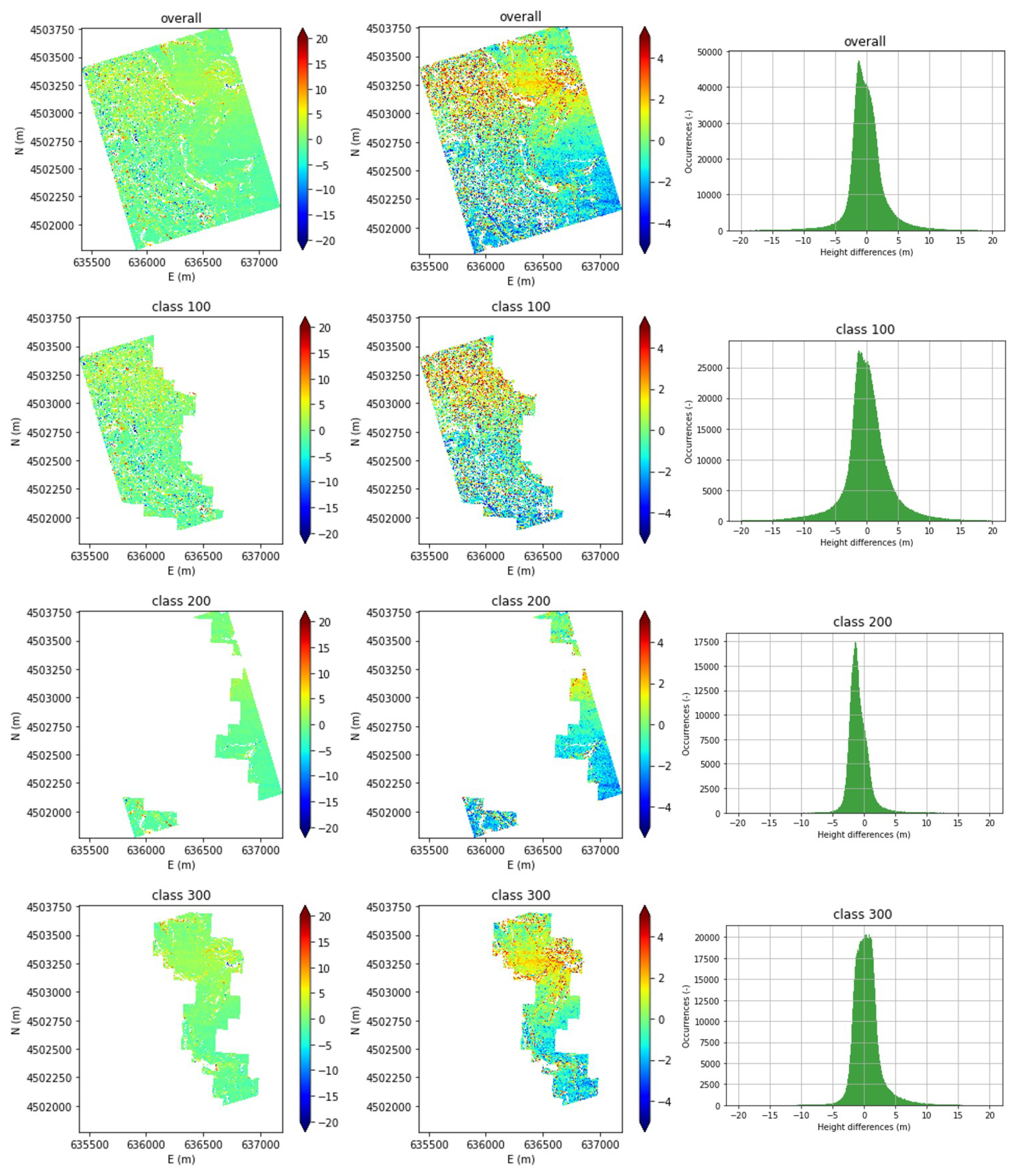For local assessment, we adopted the CLC inventory at epoch 2012 (Figure 1), resampled to the resolution of the reference LiDAR DSMs, to distinguish the artificial surfaces (class 100), agricultural (class 200) and forest and semi-natural areas (class 300).

The completeness, dependent on the occlusions and therefore on the terrain morphology and intersection angles, was evaluated as the ratio (percentage) of filled pixels over total pixels.

4.1. The Study Case of Trento

For Trento, the urban tile is characterized by small adjacent buildings and narrow streets, whereas the mountainous one by very steep slopes [22]. The results of the Pléiades pairs over the area of Trento obtained using the original and the refined RPCs are shown in

Table 7. Statistical indicators for DSM accuracy assessment over Trento—pair DSMs—original RPCs.

Pair, Compl., Int. Ang.	Tile	Mean	Std. Dev.	RMSE	Median	NMAD	LE68	LE90
(-, %, °)	(-)	(m)	(m)	(m)	(m)	(m)	(m)	(m)
pair 1 78.23% $32.4°$	Overall	1.81	3.97	4.36	2.43	2.13	2.78	6.46
	Artificial surfaces	2.55	3.78	4.55	2.78	1.43	2.03	6.37
	Agricultural areas	2.35	2.94	3.76	2.64	1.40	1.61	4.42
	Forest and semi-natural areas	0.78	4.61	4.68	1.17	3.77	3.94	7.45
pair 2 85.27% $27.1°$	Overall	2.01	4.22	4.67	2.62	2.37	3.06	6.97
	Artificial surfaces	2.74	3.97	4.82	2.98	1.54	2.19	6.79
	Agricultural areas	2.57	3.12	4.04	2.85	1.48	1.72	4.80
	Forest and semi-natural areas	1.10	4.88	5.01	1.41	4.06	4.25	7.98
pair 3 95.98% $5.3°$	Overall	0.31	4.29	4.30	0.92	2.97	3.46	7.08
	Artificial surfaces	0.93	3.82	3.93	1.37	2.19	2.59	6.29
	Agricultural areas	0.94	3.19	3.32	1.26	1.93	2.13	4.99
	Forest and semi-natural areas	−0.40	4.93	4.95	0.00	4.30	4.45	8.15

and

Table 8. Statistical indicators for DSM accuracy assessment over Trento—pair DSMs—refined RPCs.

Pair, Compl., Int. Ang.	Tile	Mean	Std. Dev.	RMSE	Median	NMAD	LE68	LE90
(-, %, °)	(-)	(m)	(m)	(m)	(m)	(m)	(m)	(m)
pair 1 79.33% $32.4°$	Overall	−0.80	3.30	3.39	−0.41	1.95	2.31	5.09
	Artificial surfaces	−0.09	3.16	3.16	0.00	1.27	1.62	4.99
	Agricultural areas	−0.38	2.79	2.82	−0.21	1.59	1.74	4.10
	Forest and semi-natural areas	−1.66	3.58	3.95	−1.38	2.85	2.96	5.56
pair 2 86.92% $27.1°$	Overall	−0.92	3.07	3.20	−0.45	1.66	2.04	4.57
	Artificial surfaces	−0.22	2.98	2.99	−0.03	1.09	1.44	4.52
	Agricultural areas	−0.57	2.41	2.48	−0.31	1.27	1.43	3.40
	Forest and semi-natural areas	−1.62	3.37	3.74	−1.22	2.48	2.61	5.14
pair 3 94.74% $5.3°$	Overall	−1.42	4.79	5.00	−1.09	4.32	4.47	7.83
	Artificial surfaces	−0.20	3.54	3.54	−0.01	2.74	2.83	5.57
	Agricultural areas	−0.14	4.25	4.25	−0.10	3.68	3.78	6.90
	Forest and semi-natural areas	−2.82	5.28	5.98	−3.02	5.21	5.20	8.59

, respectively. The same Tables include the intersection angle and the DSM completeness for each pair.

Table 7 and Table 8 clearly highlight that some outliers are still present: mean and median but also standard deviation and NMAD are different, being median and NMAD representative of the standard situation without outliers. Furthermore, the benefit of RPC refinement is clearly visible by comparing the median and NMAD values of pairs 1 and 2 in the two Tables. For pair 3 the situation is different since this is the pair with the minimum intersection angle ($5.3°$) and the weakest geometry (that is clear by comparing the LE90 values for the three pairs). However, its contribution is useful for the completeness of the final DSM, since it is the least impacted by occlusions. The overall gain of the refinement in terms of LE90 is in the range 20–35%, being the overall LE90 around 4.5–5.0 m and the best LE90 for the agricultural areas class around 3.5–4.0 m (Table 8). The forest and semi-natural areas class is the most critical since it is the most prone to temporal variations over time (imagery were acquired in 2012 and LiDAR in 2014). The best result was obtained with pair 2, with overall LE90 around 4.5 m, the best LE90 for the class of the agricultural areas around 3.5 m, and completeness at 86.9%.

Considering the improvement brought by refinement, only the refined RPCs were used to generate DSMs from the Pléiades triplet (

Table 9. Statistical indicators for DSM accuracy assessment over Trento—triplet DSMs—refined RPCs.

Pairs, Compl.	Tile	Mean	Std. Dev.	RMSE	Median	NMAD	LE68	LE90
(-, %)	(-)	(m)	(m)	(m)	(m)	(m)	(m)	(m)
pair 1–pair 2, 90.85%	Overall	−1.18	3.30	3.51	−0.71	2.00	2.33	4.98
	Artificial surfaces	−0.38	3.20	3.22	−0.16	1.28	1.64	4.99
	Agricultural areas	−0.78	2.75	2.85	−0.46	1.59	1.74	3.94
	Forest and semi-natural areas	−1.96	3.52	4.03	−1.62	2.71	2.83	5.42
pair 1–pair 3, 97.30%	Overall	−1.75	3.47	3.88	−1.25	2.55	2.79	5.37
	Artificial surfaces	−1.01	3.09	3.25	−0.53	1.71	2.05	4.73
	Agricultural areas	−1.21	3.06	3.29	−0.84	2.05	2.25	4.72
	Forest and semi-natural areas	−2.47	3.72	4.46	−2.22	3.14	3.20	5.83
pair 2–pair 3, 97.79%	Overall	−1.78	3.34	3.79	−1.26	2.46	2.68	5.08
	Artificial surfaces	−1.00	3.02	3.18	−0.50	1.65	1.98	4.53
	Agricultural areas	−1.26	2.84	3.11	−0.87	1.97	2.11	4.22
	Forest and semi-natural areas	−2.52	3.60	4.40	−2.21	3.01	3.07	5.60

). The accuracy results are consistent with those for pairs 1 and 2, but the quite positive contribution brought by pair 3 to completeness is clear. The best combination is pairs 2 and 3, minimizing the sum of the intersection angles: the overall LE90 is around 5.0 m and the best LE90 for the agricultural areas class around 4.2 m, with completeness at 97.8%. The benefit of the triplet including the best pair for accuracy (pair 2) and the best pair for completeness (pair 3) is therefore evident, getting an overall similar accuracy and gain (higher than 10%) in completeness with respect to pair 2.

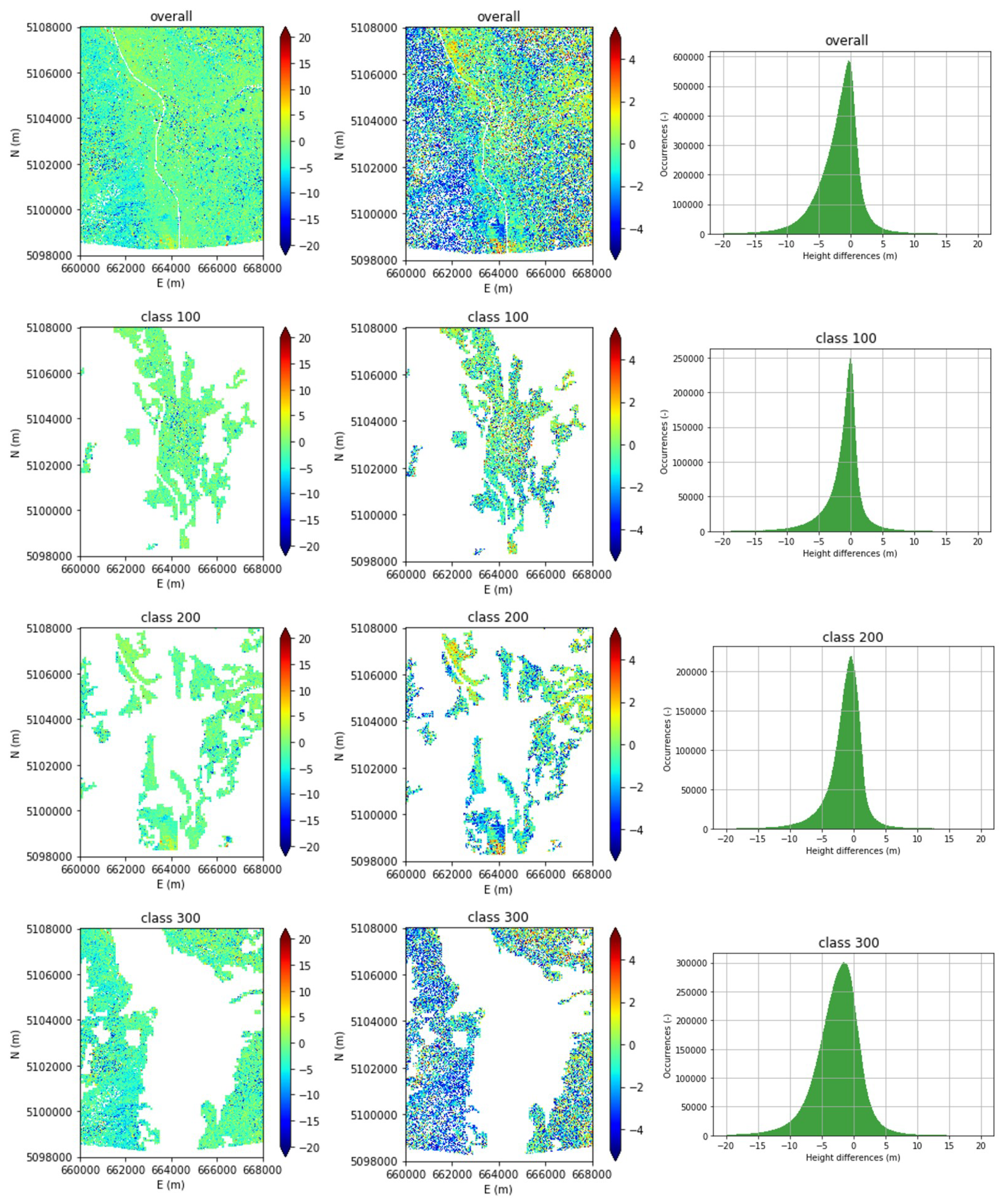
To provide an overview of the error distribution and to better highlight and explain the main error sources, we selected the best DSMs (based on accuracy and completeness) obtained from our tests using the refined RPCs (both for the stereo and multi-view case) and produced the error maps and histograms for the overall DSM and for each tile. The results obtained are shown in Figure 2 and Figure 3. All the histograms display a negative asymmetry, confirmed by the majority of bluish vs. reddish pixels in the corresponding maps. This is probably due to the growth of built areas and forests between the epoch of acquisition of Pléiades images (2012) and the epoch of the reference LiDAR DSM release (2014).

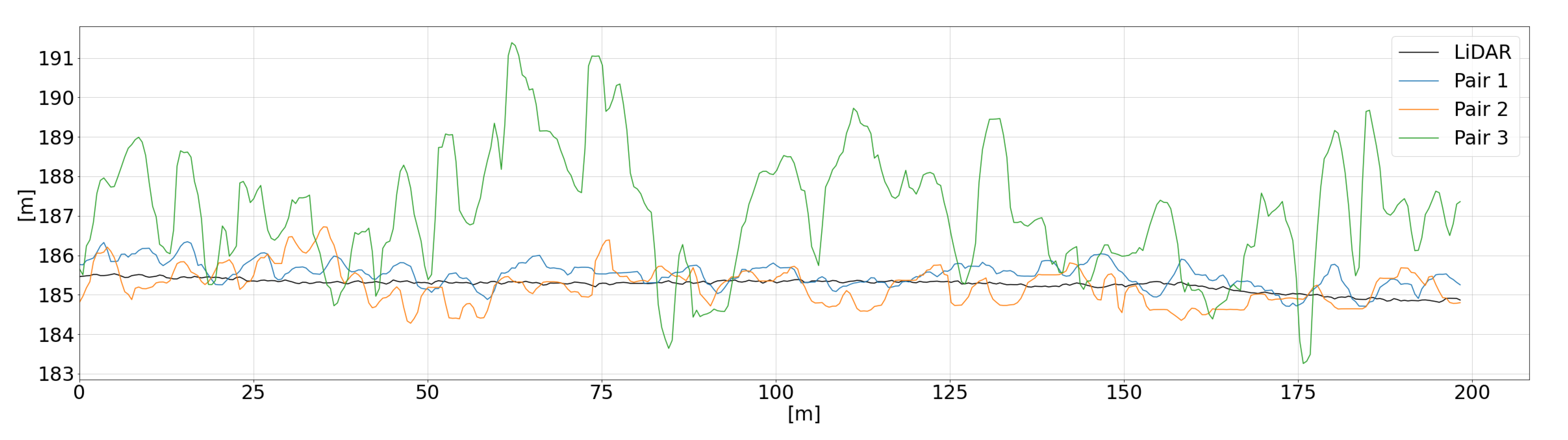
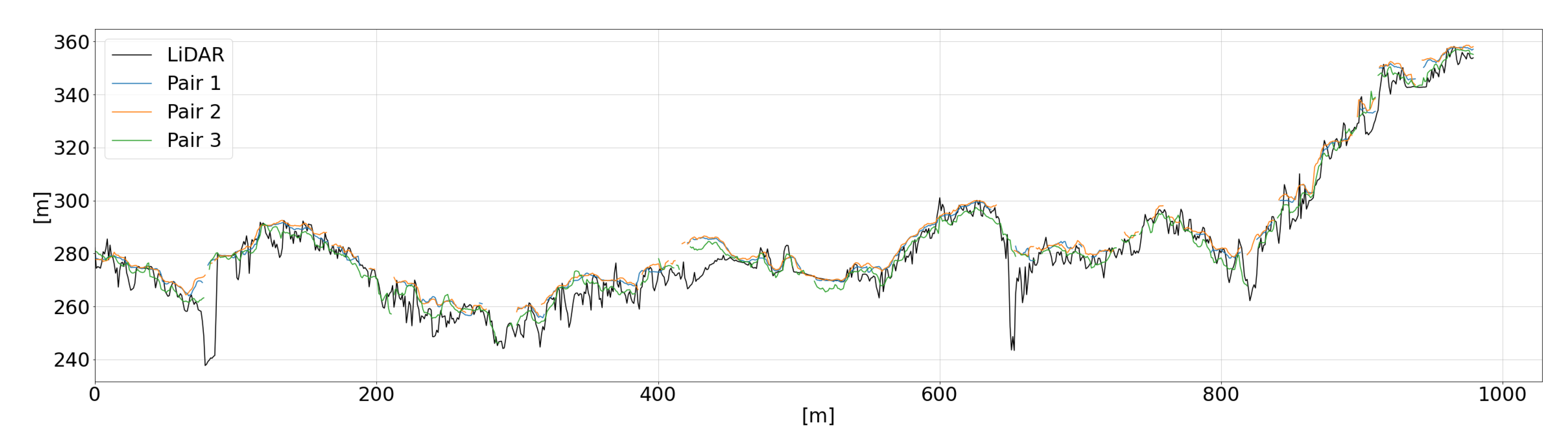
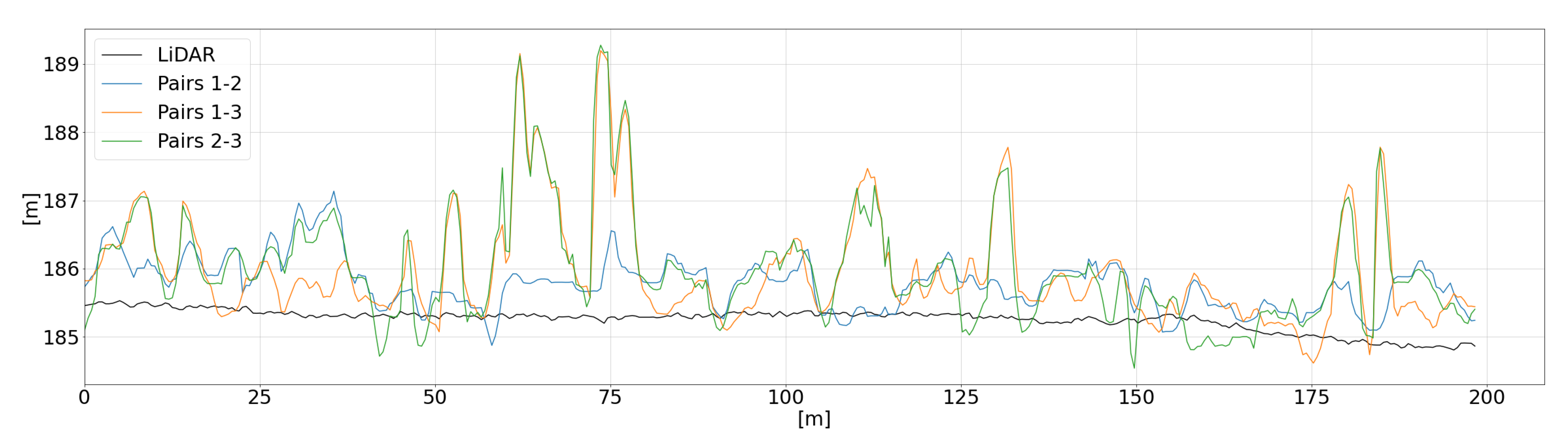
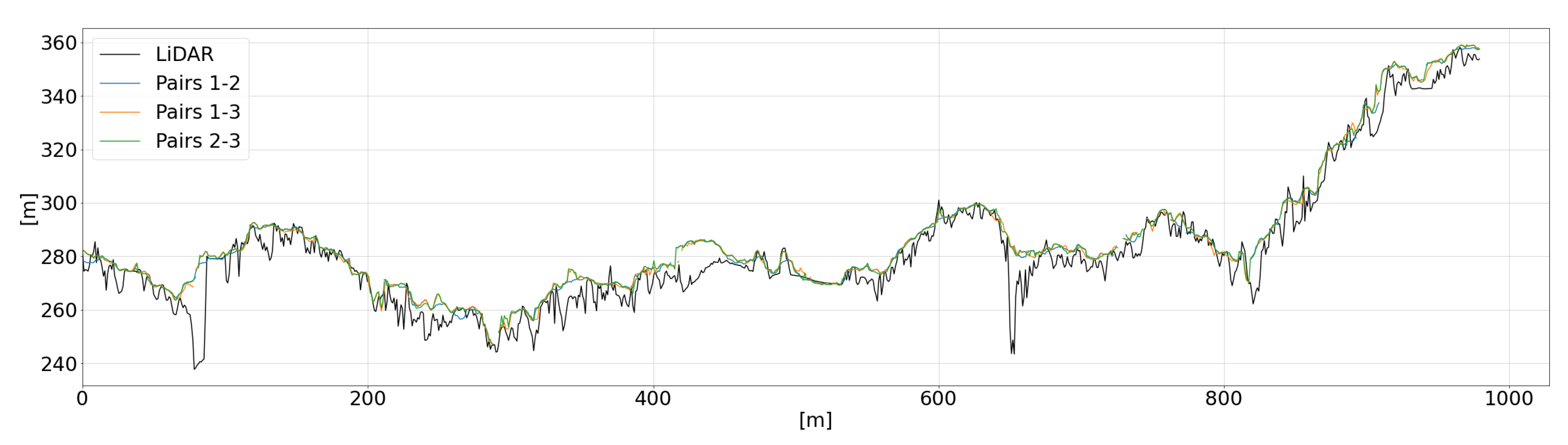
Finally, to examine the results more closely, we extracted the DSM height values along the sections shown in Figure 4 (the sections always start at point A and end at point B; all the section profiles are represented accordingly). In particular, we focused on three regions:

• S1T—a smooth area without occlusions, corresponding to the local airport runway, to highlight the DSM inner noise;
• S2T—a forested valley to monitor possible vegetation variations in the above mentioned period 2012-2014;
• S3T—a wider region, including both a hill and part of the city centre, to assess the reconstruction quality both for high and low frequencies.

The analysis included the DSMs generated from the three image pairs (Figure 5, Figure 6 and Figure 7) and the three image triplets obtained by merging two image pairs (Figure 8, Figure 9 and Figure 10). For all the sections, we used the DSMs generated with the refined RPCs.

As previously anticipated, Figure 5 and Figure 8 (corresponding to a smooth area without occlusions) are quite useful to highlight the noise of the generated DSMs, represented by the NMAD (dispersion without the effect of outliers) recalled in Table 8 and Table 9. As expected, the overall best result is obtained with pair 2, followed by the triplet with pairs 1 and 2 having the two highest intersection angles. Here pair 3 is useless, since there are no occlusions, and its weak geometry impacts negatively the results.

If we consider the other two regions (S2T and S3T), instead, and we visualize them at a lower scale (Figure 6, Figure 7, Figure 9 and Figure 10), we can draw the following general conclusions:

• at low-middle frequencies, the profiles are reconstructed quite well; higher frequencies due to narrow streets in the urban area or to vegetation are significantly lost; occlusions in the urban area and local variations that occurred between 2012 and 2014 (such as vegetation growth or new buildings) are also shown;
• the DSMs generated from the triplets are more complete than those generated from the single pairs, as expected, and mainly those benefiting from the inclusion of pair 3, with the smallest intersection angle.

4.2. The Study Case of Matera

For the second study area (Matera), the assessment of the DSMs generated from the image pairs using the original and the refined RPCs is shown in

Table 10. Statistical indicators for DSM accuracy assessment over Matera—pair DSMs—original RPCs.

Pair, Compl., Int. Ang.	Tile	Mean	Std. Dev.	RMSE	Median	NMAD	LE68	LE90
(-, %, °)	(-)	(m)	(m)	(m)	(m)	(m)	(m)	(m)
pair 1 96.11% $11.7°$	Overall	−3.79	3.85	5.41	−4.22	2.22	2.58	6.12
	Artificial surfaces	−3.50	4.71	5.87	−3.85	3.03	3.62	8.00
	Agricultural areas	−4.30	2.46	4.95	−4.75	1.31	1.51	3.40
	Forest and semi-natural areas	−3.94	2.93	4.90	−4.22	1.95	2.06	4.36
pair 2 77.77% $41.7°$	Overall	−0.72	3.78	3.85	−1.30	1.61	2.23	6.33
	Artificial surfaces	−0.68	5.07	5.12	−1.50	3.22	4.29	8.74
	Agricultural areas	−1.02	1.70	1.98	−1.38	0.53	0.75	2.09
	Forest and semi-natural areas	−0.57	2.39	2.45	−0.96	1.39	1.52	3.48
pair 3 85.49% $30.5°$	Overall	−1.61	3.99	4.30	−1.17	2.08	2.69	6.86
	Artificial surfaces	−2.42	5.05	5.60	−1.88	3.66	4.35	8.77
	Agricultural areas	−0.77	1.93	2.08	−0.89	0.82	0.97	2.48
	Forest and semi-natural areas	−0.90	2.67	2.82	−0.91	1.72	1.84	3.77

and

Table 11. Statistical indicators for DSM accuracy assessment over Matera—pair DSMs—refined RPCs.

Pair, Compl., Int. Ang.	Tile	Mean	Std. Dev.	RMSE	Median	NMAD	LE68	LE90
(-, %, °)	(-)	(m)	(m)	(m)	(m)	(m)	(m)	(m)
pair 1 90.06% $11.7°$	Overall	0.02	3.00	3.00	−0.21	1.96	1.98	4.23
	Artificial surfaces	0.09	3.71	3.71	−0.08	2.43	2.57	5.80
	Agricultural areas	−0.82	1.86	2.03	−1.08	1.24	1.29	2.32
	Forest and semi-natural areas	0.43	2.27	2.31	0.24	1.68	1.62	3.16
pair 2 70.01% $41.7°$	Overall	−0.66	2.68	2.76	−0.97	0.89	1.05	3.47
	Artificial surfaces	−0.37	3.62	3.64	−0.69	1.20	1.64	5.86
	Agricultural areas	−1.23	1.39	1.85	−1.37	0.60	0.60	1.51
	Forest and semi-natural areas	−0.61	1.79	1.89	−0.89	0.72	0.78	2.46
pair 3 73.84% $30.5°$	Overall	−1.48	2.59	2.99	−1.32	1.03	1.10	3.66
	Artificial surfaces	−1.64	3.58	3.94	−0.96	1.40	2.14	5.95
	Agricultural areas	−1.53	1.26	1.98	−1.68	0.64	0.67	1.38
	Forest and semi-natural areas	−1.24	1.50	1.94	−1.32	0.75	0.82	1.88

, respectively.

Again, the statistical indicators reveal the persistence of some outliers, due to the difference between mean and median and between standard deviation and NMAD. The DSM accuracy clearly benefits from the refinement of the RPCs: indeed, by comparing Table 10 and Table 11, we can notice an improvement practically for all the indicators and all the image pairs. Moreover, the gaps between mean and median and between standard deviation and NMAD are always reduced (even if not always at class level). In the case of the DSMs generated from the pairs with the original RPCs, the DSM corresponding to pair 1 is the best in terms of overall LE90 (6.12 m), followed by the DSM produced with pair 2 (overall LE90 of 6.33 m) and finally by the DSM generated with pair 3 (LE90 of 6.86 m). The overall standard deviation is approximately the same (about 4 m) for all the pairs. Also in this case, the median of differences is in general slightly higher, in absolute value, than the mean in all the LC classes over all the pairs. Moreover, the LC “Artificial surfaces” is the one with the worst statistical indicators over all the pairs. In terms of completeness, we still notice a correlation between the intersection angle and the DSM completeness: the lower the intersection angle, the more complete the final DSM (even if less accurate, according to the RMSE). Also for the study area of Matera, the RPC refinement reduced the bias and the noise in all the LC classes over all the pairs (Table 11), with an overall RMSE always lower than 3 m. The positive effect of the RPC refinement is visible on the LE90 too: indeed, the LE90 is reduced by 41%, on average, for the whole tile, 31% for the artificial surfaces, 35% for the agricultural areas and 36% for the forested and semi-natural ones. The overall LE90 amounts to 3.5–4.5 m and the best LE90 for the class of the agricultural areas (the most accurate class) is around 1.5–2.5 m (Table 11). The positive effect is even more evident analyzing the values of the median and NMAD, which in general are lower than 1 m and 2 m, respectively, in all the LC classes for all the pairs. The artificial surfaces class is the most critical one, due to the high urban density.

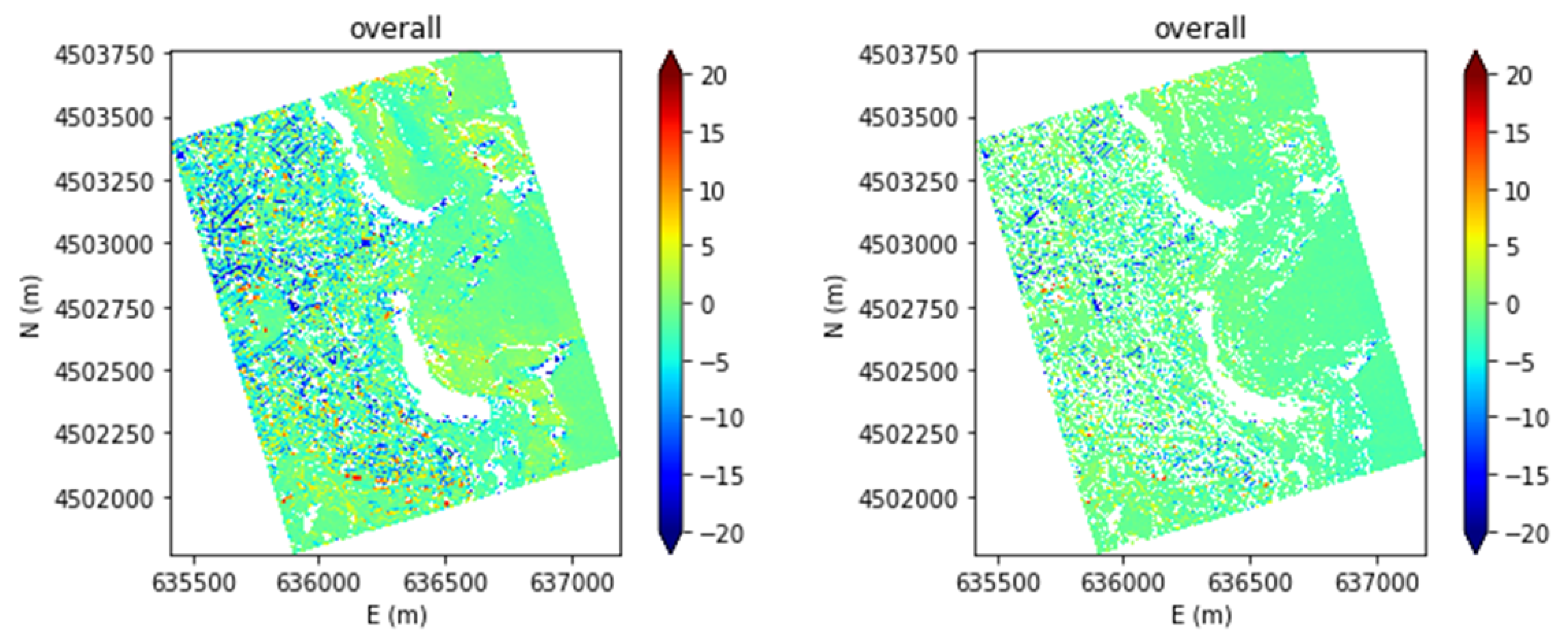
On the other hand, the DSM completeness decreases by 5–15%, which can be explained, at least partially, with the improvement of the median in the urban tile for all the pairs. Since the urban tile is the worst class, in terms of accuracy, both for the tests with original and refined RPCs, due to the narrow streets that characterize the city of Matera, we could deduce that a relevant part of the urban tile, poorly reconstructed through the originals RPCs (several bluish pixels in Figure 11-left), is even harder to reconstruct based on the new image configuration determined by the refined RPCs. As a consequence, many urban areas previously reconstructed (even with considerable errors) may have been considered outliers under this new configuration, and thus excluded from the statistics and completeness computation (many bluish pixels in Figure 11-left become void pixels in Figure 11-right). Figure 11 shows this effect comparing the error maps for pair 3 which suffers the highest decrease in terms of completeness before and after the RPC refinement.

All considered, the best result was obtained with pair 1, with overall LE90 around 4.2 m and completeness at 90.1%.

As to the multi-view case,

Table 12. Statistical indicators for DSM accuracy assessment over Matera—pair 1–pair 2–pair 3—refined RPCs.

Pairs, Compl.	Tile	Mean	Std. Dev.	RMSE	Median	NMAD	LE68	LE90
(-, %)	(-)	(m)	(m)	(m)	(m)	(m)	(m)	(m)
pair 1 – pair 2 – pair 3 95.53%	Overall	−0.64	2.95	3.02	−0.79	1.26	1.51	4.33
	Artificial surfaces	−0.65	3.74	3.80	−0.61	1.84	2.30	6.20
	Agricultural areas	−1.17	1.52	1.92	−1.35	0.72	0.72	1.66
	Forest and semi-natural areas	−0.31	2.11	2.13	−0.59	0.92	1.09	2.83

summarizes the accuracy assessment of the DSM generated with the refined RPCs using the simple but sub-optimal merging procedure carried out outside of Agisoft Metashape (see Section 3).

As expected, the final DSM, even if more accurate than those obtainable with the original RPCs, is slightly less accurate than the best models generated from image pairs with refined RPCs (the LE90 amounts to 4.3 m). This is mainly due to the fact that it is not derived from an overall optimization of the alignment of all images but from a combination of different DSMs and it inherits the respective biases and noises. However, this drawback is balanced by the gain in terms of completeness that amounts to 95.5%. All considered, we can conclude that the proposed solution, even though sub-optimal, allows taking the best from the still accurate outputs generated through Agisoft Metashape.

As for the case study of Trento, in Figure 12 and Figure 13 we show the error maps and histograms of the most accurate and complete DSMs obtained from our tests using the refined RPCs (both for the stereo and multi-view case), for the overall DSM and each LC tile.

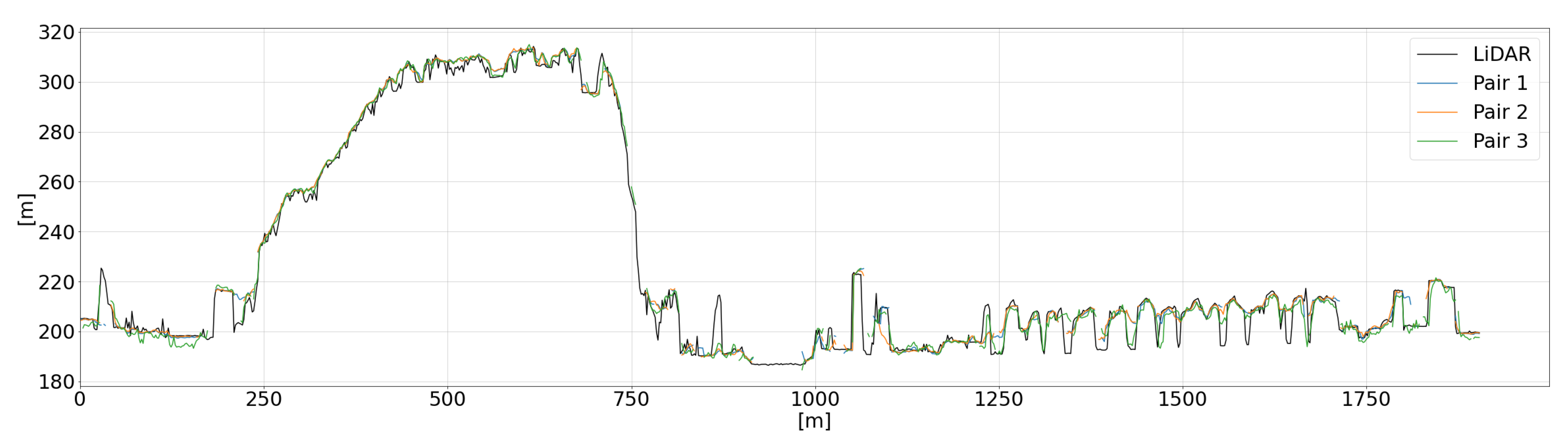
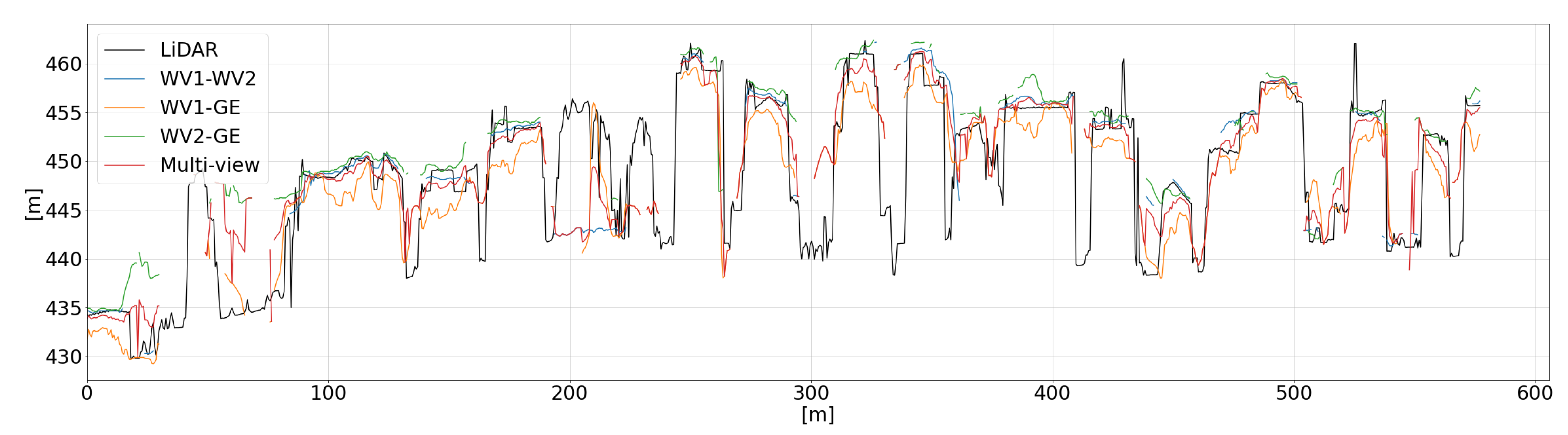
Finally, we extracted the DSM height values along the vertical sections (Figure 14) which include the old city center and the ravine (S1M) and the modern city (S2M). Also in this case, the sections start at point A and end at point B, and all the section profiles are represented accordingly. It is worth highlighting that both the regions are characterized by high urban density, which makes them very challenging in terms of reconstruction completeness for Agisoft Metashape. In this case, the analysis focuses on the DSMs generated using the three image pairs and the triplet with the refined RPCs. The extracted profiles are shown in Figure 15 and Figure 16.

Again, as for Trento, the DSM obtained from the triplet seems much more complete than the others (a few parts are missing, mainly related to occluded areas). Moreover, as proven by Table 11 and Table 12, the artificial surface reconstruction is the least precise among all the LC classes and for all the tests. This is particularly evident by comparing, for section S1M, the forested area and the artificial one in terms of completeness, or by considering the number of missing parts and the surface noise in section S2M.

5. Conclusions

The goal of this work was to quantify the potential of the new Agisoft Metashape satellite image processing module. We investigated two different case studies to evaluate the accuracy of the generated DSMs, using single and cross-sensor multi-view optical satellite imagery: a triplet of Pléiades images acquired over Trento and a triplet composed of a WorldView-3 stereo pair and a GeoEye-1 image over Matera. We processed the images using the original RPCs—provided as part of the image metadata—and the RPCs refined using an original terrain independent approach. We assessed the accuracy, precision and completeness of the generated DSMs using LiDAR ground truths. We performed the assessment both over the entire tile and considering different land covers. For local assessment, we adopted the CLC inventory to distinguish artificial surfaces, agricultural areas and forest and semi-natural areas. Furthermore, for visual comparison with the LiDAR reference, we extracted the DSM height values along sections corresponding to different land covers.

In general, the results highlight the high impact of the RPC refinement on the accuracy of the generated DSMs (ranging from 20 to 40% in terms of LE90), especially in the urban areas, usually very challenging for the DSM production from satellite images, and for both the case studies of Trento and Matera. Specifically, with the refined RPCs, the DSMs were generated both in a stereo and multi-view (triplet) configuration. We achieved an average overall LE90 <5.0 m (Trento) and <4.0 m (Matera) for the stereo configuration, and <5.5 m (Trento) and <4.5 m (Matera) for the multi-view (triplet) configuration, with an increase of completeness in the range 5–15% with respect to stereo pairs. Therefore, at least for the stereo processing of satellite pairs, Agisoft Metashape has been demonstrated to be a software able to leverage the potentialities of the input images, even when they are captured from different satellites, as in the case of some of the pairs used in this work.

As regards the multi-view processing, Agisoft Metashape cannot be considered, at present, a stable solution, both for single sensor and cross-sensor images. Indeed, if on one hand it is possible to rely on Metashape outputs to generate more complete digital models than those produced using the mere image pairs (partially avoiding the problem of occlusions), on the other hand it does not provide a clear pipeline to obtain accurate DSMs. As to the Pléiades triplet, in fact, it was necessary to align separate image pairs to obtain an accurate DSM (average overall LE90 lower than 5.5 m) and comparable to the ones generated from stereo pairs, since the alignment based on the whole triplet led to very inaccurate DSMs.

As to the case study of Matera, instead, neither the triplet nor the chunk alignment successfully produced an accurate and complete DSM; to simultaneously exploit the information contained in all the three images, at least partially, we relied on an external procedure, computing a weighted mean of the three DSMs obtained from the three different pairs, based on the respective intersection angles. The proposed solution, even though sub-optimal, allows taking the best from the still accurate outputs generated through Agisoft Metashape: indeed, the final DSM matches both the accuracy (LE90 = 4.3 m) and the completeness of the stereo configuration.

Finally, despite the issues encountered with the triplet processing, the results achieved with Agisoft Metashape remain encouraging. Indeed, the DSMs obtained for the Trento area are characterized by a better accuracy than the DSMs generated through the commercial software PCI Geomatica and the open-source software DATE [2] using the very same Pléiades triplet: the RMSE over all the whole tile is indeed lower than 4 m for all the pair combinations (Table 9) and therefore better than the 4.7 m of DATE and the 5.6 m of PCI Geomatica [2]. Nevertheless, further analyses are needed for both the locations considered in this work to investigate the impact of different variables such as the use of imagery from other suppliers and the effect of the illumination and of the image angles and overlap.