Abstract
Air temperature is an important physical indicator for urban and architectural environments; however, it is difficult to obtain its distributive characteristics by field measurements owing to the limitations of current measuring instruments. In this context, this study was conducted to demonstrate whether a small and portable ground-based thermal infrared spectroradiometer can be used to estimate the horizontal air temperature distribution in built spaces. For this estimation, we first calculated a forward model using radiative transfer simulations, and the air temperature distribution was inversely estimated from the observed radiance using the model. To regularize the estimated air temperature, we used the maximum a posteriori method, which uses prior information. To verify this estimation method, we conducted measurement experiments in two types of built spaces that had different air temperature distributions within spaces that were approximately 20 m long. Moreover, we conducted a parametric case study on the prior information. As a result, we were able to estimate the air temperature distribution with an average root mean square error (RMSE) of 1.3 °C for all cases when the average RMSE of the prior information for all cases was 2.1 °C. This improvement in the RMSE indicates that this method is able to remotely estimate the horizontal air temperature distribution in built spaces.
1. Introduction
Air temperature is an important physical indicator that influences the design and functionality of urban and built environments. To realize thermal comfort in urban spaces, it is important to understand the thermal environment at the pedestrian level where people are active [1]. It is also important to monitor the horizontal thermal environment within or between rooms where occupants live to achieve thermal comfort in buildings [2]. Thus, determining the horizontal distribution of air temperature is an important subject of research. In these spaces, even if they are relatively small, the presence of a sensible heat source/sink can cause large air temperature differences. For example, in urban spaces, in shaded areas of high-rise buildings [3] and street canyons [4], low-temperature ground surfaces and building walls act as heat sinks during the day, and a reduction in air temperature of more than 2 °C has been confirmed in some cases. In buildings, depending on the location of the air conditioning vents, a large air temperature distribution is generated in the room (e.g., Huang et al. [5] reported a temperature irregularity of approximately 2.4 °C), which affects the comfort of the occupants. Another example of a large indoor temperature distribution is that at a data center [6]. In a data center, it is important to control the air conditioning by properly determining the air temperature distribution caused by the exhaust heat of the servers, which is a sensible heat source, to ensure stability and reduce the energy consumption of the equipment. Therefore, knowing the air temperature distribution is imperative for urban climates and indoor environments.
There are several methods to measure the air temperature in the field of building engineering and urban climatology. All these methods involve the positioning of measuring instruments (for example, thermometers, thermistors, and thermocouples) at the measurement location [7,8]. These fixed-point observations were carried out based on the assumption that the observation-point measurement adequately represents the ambient temperature of the space; however, it has been pointed out that it is difficult to ensure representativeness in urban areas [9]. Moreover, the above-mentioned methods also suffer from problems such as the necessity of implementing forced ventilation via erecting a solar radiation shield because the measurement sensors are easily affected by solar radiation [10]. Additionally, the time constant of measurement is not very sensitive because of the sensor heat capacity [10]. Meanwhile, mobile observations are sometimes carried out to obtain the spatial distributions of the air temperature in urban sites [3,11,12]. However, temporal variations in the meteorological conditions (e.g., dominant wind, solar radiation, and air temperature) during the observations make it difficult to comprehensively understand the spatial variations. In addition, mobile observations are limited to ground-level applications because the sensors are held by people or mounted on bicycles/automobiles.
In contrast, in the field of remote sensing, researchers have measured the vertical air temperature distribution through atmospheric layers with the use of satellite-based spectroradiometers [13,14]. Besides, commercial thermal infrared spectroradiometers have become available for use in urban and architectural applications in recent years [15]. In this context, this study proposes a thermal-infrared-spectroradiometer-based method to estimate the air temperature distribution of comparatively short horizontal paths in built spaces. Thus, the application of this remote sensing method to urban and built environments can enable the remote estimation of the air temperature distribution and solve the problem of representativeness in built space measurements.
Although there are many reports on measuring the vertical air temperature distribution of long measurement paths through atmospheric layers [16,17], no research has been conducted on the horizontal short-path air temperature distribution. There are two significant differences between the inverse estimation of the atmospheric air temperature distribution (via satellites) and the air temperature distribution in built spaces. First, as mentioned above, the parameter of interest in built spaces is often the horizontal temperature distribution. Meanwhile, we note that when considering vertical paths from a satellite, the temperature sensitivity is maximized at the middle of the path owing to the trade-off between the properties of the gas components and the transmittance decreasing: the gas concentration decreases with altitude, with the atmospheric transmittance decreasing with distance from the satellite [18]. On the other hand, when the horizontal path is considered as the object of interest, we note that the gas component concentration is uniform in comparison with the case of the vertical path. Second, in built spaces, relatively short paths are considered in comparison with those considered for satellite observations. The paths of interest usually span – m within buildings or – m in the case of urban climate studies. For short paths, the contribution from the air is relatively small, which makes the estimation of the air temperature difficult. Therefore, the feasibility of the remote sensing method in measuring the air temperature distribution in urban and built environments has not been suitably explored. In this study, we first show the theoretical aspects of inverse estimation of air temperature distribution, we demonstrate its feasibility for built spaces by conducting experiments in two types of built spaces that had different air temperature distributions within spaces that were approximately 20 m long.
2. Methods
2.1. Target Phenomena and Accuracy
Our spectroradiometer-based method is applied to built spaces in this study, wherein the observation parameters are the air temperature distributions in a room and the outdoor microclimate. We assumed the spatial scales of 10– m for indoors and – m for outdoors. We set the target accuracy in this study to 1 °C for the following reasons: In indoor environments, we are often interested in the effect of the air temperature on the thermal comfort of the human body. For example, thermal comfort indices such as the standard effective temperature (SET*) or the predicted mean vote (PMV) are highly influenced by the air temperature [19]. In addition, the air temperature difference that can be detected by humans is approximately 1 °C [20]. Meanwhile, regarding the outdoor microclimate, the “park cool island” (PCI) effect of a greened area can reduce the air temperature by up to 1–5 °C when compared with the surrounding environment [21]. In general, thermocouples, thermometers, and electrical resistance thermometers are used to measure indoor environments or outdoor microclimates. The accuracy of these thermometers is generally about 0.5 °C [22]. In this regard, it has been pointed out that an error of 1–2 °C is generated in urban and architectural environment measurements because of the effect of solar radiation [23]. In the air conditioning control of buildings, the target accuracy is often set to approximately 1 °C.
The estimation method of the air temperature distribution from a spectroradiometer consists of two processes. The first involves the physical modeling of the relationship between the atmospheric properties and radiance measurements, which is called the forward model or observation equation. In the forward model, given the atmospheric properties, the observed radiance values are uniquely determined. More details on this aspect of the process are provided in Section 2.2. The second process is called inverse estimation or the retrieval method, which estimates the atmospheric properties (in this study, the air temperature distribution of the path) from the recorded radiance data. More details are provided in this regard in Section 2.3.
2.2. Observation Equation
The observational equation expressing the relationship between the radiance incident on a sensor and the radiation from the atmosphere can be described as
where represents the incident radiance of wavelength on the sensor (at position s); the Planck function at temperature T; and the air temperatures at position and the boundary surface, respectively; and the transmittance from position 0 to position s. The first item on the right-hand side represents the radiance from the boundary surface, and the second item represents that from the air. Generally, a simplified representation between the observed value and the unknown parameter is used to formulate the retrieval algorithm. The observation Equation (1) is discretized in space and simplified, and the relation between the observed spectra and the air temperature distribution can be obtained as
where represents the measurement vector consisting of the observed spectra, the true air temperature distribution, the forward model, the measurement error, and all the other parameters of the observation equation.
In this study, we assume the following as prerequisites for the calculation of the horizontal temperature distribution in built spaces.
- The surface temperature and emissivity of a boundary surface are known.
- The physical properties of the atmosphere other than the air temperature are known (e.g., distribution of concentrations of CO and HO).
- The scattering of radiation by gas molecules in the atmosphere is negligible.
Regarding Assumption 1, if the material of the boundary surface is known, the emissivity can be calculated by using the literature values and the surface temperature can be calculated only by means of an thermal infrared spectroradiometer used for temperature distribution estimation with the application of the split-window method [24,25]. Regarding Assumption 2, it is generally rare that the concentration distributions of CO and HO are perfectly known in built spaces; however, the concentrations of these gases are roughly known (e.g., in an indoor heating, ventilation, and air conditioning (HVAC) system, the CO and HO concentrations are measured to control the amount of outside air or indoor environmental quality). In this regard, we plan to conduct a sensitivity analysis of the effect of estimation bias in the gas concentration on air temperature estimation using simulations in our future studies. Regarding Assumption 3, it is well known that atmospheric scattering is negligible in the thermal infrared region [26].
2.3. Retrieval Methodology
In this section, we discuss the retrieval process. As regards Equation (2), to obtain the air temperature distribution, we first obtain when is given. However, in practice, is extremely unstable in that a small change in the measurement can significantly affect the estimation of . This phenomenon is often observed in inverse estimation and is referred to as an ill-posed or ill-conditioned problem [27,28]. Therefore, in this study, we use the maximum a posteriori (MAP) method to stabilize the solution with a Bayesian approach, which is widely used in satellite remote sensing [14,29]. The MAP method uses probabilistic information (prior distribution) known before the observation of the target air temperature for regularization, and the temperature distribution that maximizes the posterior distribution given by the Bayes theorem is considered as the MAP solution.
The flow of inverse estimation with the use of the MAP method is shown in Figure 1. First, we assume prior distribution of the air temperature for the target built spaces. Second, observations are recorded with a thermal infrared spectroradiometer to obtain radiance . Finally, we estimate the air temperature distribution where posterior distribution is maximized with the use of the observational radiance , prior distribution , and Jacobian (derivative of the forward model). Maximizing the posterior distribution corresponds to minimizing the following cost function . Thus, we have
where denotes the variance–covariance matrix of the observation error, the expected value of the prior distribution, and the variance–covariance matrix of the prior distribution. In this study, we did not consider spatial correlations (i.e., the variance–covariance matrix is a diagonal matrix). Although there is a spatial correlation in the distribution of the air temperature in actual physical phenomena, when the spatial correlation is not taken into account, the solution is always estimated on the side of caution. The air temperature distribution can be estimated by determining the temperature distribution minimizing cost function with the Gaussian–Newton method via the following iterative equation [29],
where represents the i th estimate of the air temperature distribution and is the Jacobian matrix, which is the derivative of the forward model with respect to .
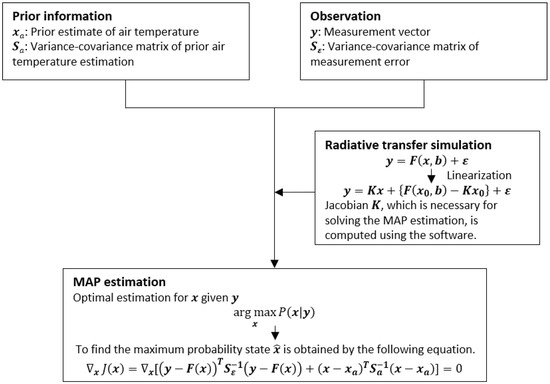
Figure 1.
Flow of the inverse estimation of the air temperature distribution.
To evaluate the MAP solution, we introduce averaging kernel . The averaging kernel represents the sensitivity of MAP solution to true state . Averaging kernel is the product of gain matrix and Jacobian matrix :
With this averaging kernel, we can express the MAP solution as [29]
where denotes the identity matrix. The averaging kernel is a weighting factor for the relative contributions of true state and prior distribution to MAP solution . That is, represents the contribution of true state to MAP solution , represents the contribution from prior distribution , and represents the contribution from the observational error [30]. Therefore, the influence of the true air-temperature distribution increases as the averaging kernel approaches the identity matrix. In this manner, the averaging kernel indicates the extent to which it reflects the true air temperature distribution.
3. Experiment
3.1. Experiment Outline
To verify the efficacy of the proposed method in estimating the temperature distribution in built spaces, we conducted experiments considering two scenarios. One scenario involved an experiment to estimate the horizontal temperature distribution between two rooms with a temperature difference (the indoor experiment), and the other involved an experiment to estimate the horizontal temperature distribution for a temperature difference existing inside and outside a building (the outdoor experiment). Our experiments were carried out at the Tokyo Institute of Technology Suzukakedai campus (lat 35°30′45″N. long 139°29′5″E.) in Kanagawa Prefecture, Japan, in winter (21 December 2016). The factors that affect the proposed method (due to seasonal or daily variations) are the concentration of atmospheric gases and the air temperature. As shown in Section 3.4, humidity has a dominant effect on the spectra selected for this experiment. Regarding humidity, it is expected that measurements during the winter season will be disadvantageous because the emission of thermal infrared radiation from atmospheric gases is low under low humidity conditions. Regarding air temperature, there are largely seasonal and daily variations in both outdoor and indoor spaces. When considering general air conditioning in indoor spaces, large temperature differences (e.g., between a room and corridor, between indoor and outdoor spaces, etc.) occur in winter due to heating and non-heating conditions. We selected the winter season considering the above conditions. Moreover, because solar radiation may cause errors in the thermohygrometer, which measures the true value, the outdoor experiment was conducted in the evening when there was no solar radiation. Figure 2 and Figure 3 show the floor plans corresponding to the indoor and outdoor experiments, respectively.
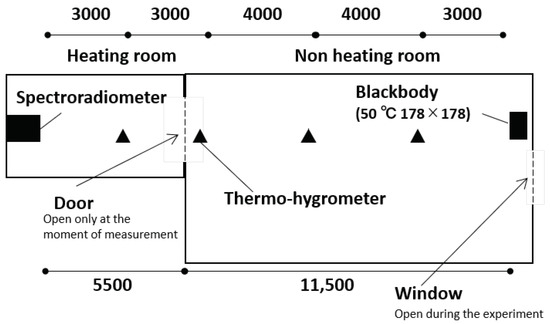
Figure 2.
Overview of the indoor experiment. The dimensions are indicated in millimeters.
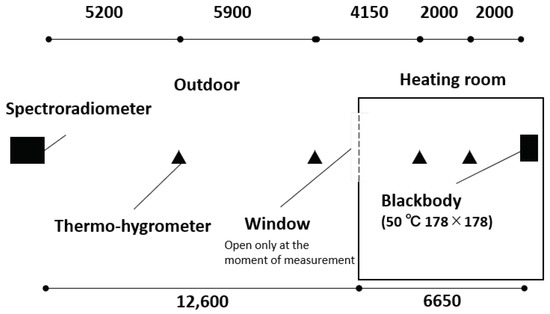
Figure 3.
Overview of the outdoor experiment. The dimensions are indicated in millimeters.
In these experiments, a thermal infrared spectroradiometer was installed at the observation point, and a planar blackbody furnace set at 50 °C was installed at the boundary. The field of view of the spectroradiometer used was 7 mrad, which corresponds to a circular footprint of about 12–13 cm in diameter on the blackbody surface. The size of the blackbody was 17.8 cm × 17.8 cm; therefore, the entire footprint was covered by the blackbody. We note here that the air temperature distribution is considered to be estimated regardless of the boundary surface temperature in this method. Although the boundary surface temperature is considered to be close to the surrounding air temperature in general built spaces without solar irradiance, in this experiment, the boundary surface temperature was intentionally set to 50 °C with a difference from the air temperature to confirm that the estimated air temperature distribution was not an estimate of the boundary surface temperature. In other words, if the temperature coincides with the boundary surface temperature, it cannot be determined whether the estimated temperature is the air temperature or the boundary surface temperature. In both sets of experiments, to verify this estimation method, the temperature and humidity were measured with the use of thermohygrometers at four points along the line-of-sight path of the thermal infrared spectroradiometer. Each thermohygrometer sensor was placed in a fan-aspirated radiation shield to improve the time constant and exclude the effect of radiation, and it was installed at a height of approximately 1.1 m from the floor. In our study, we used the RTR-503 thermohygrometer (T&D, Matsumoto, Japan), and its measurement interval was set at 10 s.
In the indoor experiment, the observation-point-side room was heated by an air conditioner, and a window was opened to the cooler outdoor atmosphere in the boundary-surface-side room to ensure a large temperature difference between the two rooms. The path length in the heating room was 5.5 m and that in the non-heating room was 11.5 m. The boundary between the heating room and the non-heating room contained a door, and it was opened only at the moment of measurement; the mixing of air in two rooms was avoided as best as possible. At the time of measurement, the room temperature of the heating room was approximately 25 °C, and its humidity was approximately 25%rh (5.8 g m), whereas the room temperature of the nonheating room was approximately 18 °C, with the humidity being approximately 35%rh (5.4 g m).
The outdoor experiment was carried out after sunset. The spectroradiometer was installed outdoors, and the blackbody furnace was installed indoors. The outdoor air temperature and humidity were approximately 13 °C and 60%rh (6.8 g m), respectively. The room temperature and humidity in the heating room were approximately 27 °C and 20%rh (5.2 g m), respectively. The windows separating the indoor and outdoor areas were opened only at the moment of observation. The height setting and conditions of the thermohygrometer were the same as the counterpart ones of the indoor experiment. According to the nearest meteorological observatory, the weather was slightly cloudy, and the wind speed was 1.3 m s at the time of the outdoor experiment.
3.2. Instrument
A spectroradiometer with a high spectral resolution is often used for atmospheric sounding. In the thermal–infrared wavelength range, a spectral resolution of the order of 0.1 µm is obtained by using a filter, and a 10-times higher resolution is obtained by using a diffraction grating. If a still greater resolution is desired, Fourier transform spectroscopy can be used [13]. The current generation of spectroradiometers mounted on artificial satellites exhibit high spectral resolution because they use Fourier transform spectrometers, in which the accuracy (noise equivalent temperature difference) is as high as 0.2 K [14]. However, as regards our approach, it is important to verify the accuracy of commonly available equipment to practically apply this method in built spaces. In this study, we used a commercially available, relatively small, and portable thermal infrared spectroradiometer that has recently become available for use in building engineering and urban climatology.
Table 1 lists the specifications of the spectroradiometer used in this study (SR-5000N, CI Systems, Carrollton, TX, USA [31]), and Figure 4 shows the photographs of the various instruments used. This spectroradiometer uses a circular variable filter method, and the spectral resolution is not very high (<0.2% of the wavelength) when compared with those used in satellites (e.g., the spectral resolution of thermal and near-infrared sensor for carbon observation Fourier transform Spectrometer (TANSO-FTS) attached to the greenhouse gases observing satellite (GOSAT) is 0.2 cm [32].). Here, we note that the spectral resolution is strongly correlated with the spatial resolution of the temperature distribution: a higher wavelength resolution corresponds to a greater spatial resolution. Considering these differences between the satellite- and ground-based use of spectroradiometers, here, we experimentally verify the feasibility of this method for application to built spaces.

Table 1.
Summary of spectroradiometer specifications.

Figure 4.
(a) Spectroradiometer (SR-5000N, CI-Systems, USA [31]). (b) Blackbody (SR-800N CI-Systems, USA [33]).
Here, we first describe a method to convert the raw signal data acquired by the spectroradiometer into radiance. First, the response function defined by Equation (8) was obtained by using the reference measurement data with the spectroradiometer in close contact with the planar blackbody furnace.
where
Here, represents the Planck function at temperature T at wavelength and the emissivity of an external blackbody (0.97). is the internal blackbody temperature at observation, is that of the reference observation, and is the temperature of the external blackbody (50 °C). Next, in this measurement, the radiance is obtained by the raw signal data and the response function, as expressed in Equation (7). To reduce the random error, we performed 10 consecutive scans in 1 measurement and used the average value.
3.3. MAP Method Conditions
The MAP method uses a Bayesian approach to regularize the solution, and therefore it is necessary to set a prior distribution. The prior distribution in this study refers to the probabilistic distribution known by the observer before the observation of the air temperature. As the setting of the prior distribution depends on the physical phenomena related to the measurement object (e.g., heat-island effect and indoor air-conditioning control), in our investigations, we carried out a parametric study by setting the prior distribution generally used for the urban and built environments. Table 2 lists the conditions pertaining to the MAP methods.

Table 2.
Conditions related to the MAP method. For the case studies, the mean air temperature of the prior distribution in both the indoor and outdoor experiments was set to 2 °C higher (cases A1, A2, B1, and B2) and 2 °C lower (cases A3, A4, B3, and B4) than the actual value measured by the thermohygrometer. In addition, the uncertainty of the prior information was calculated in two cases: when the standard deviation of the prior information of air temperature (i.e., square root of the diagonal component of ) was 3 °C (cases A1, A3, B1, and B3) and when it was 5 °C (cases A2, A4, B2, and B4). In the indoor experiment, the air temperature in the heating room was 25.2 °C and that in the non-heating room was 18.3 °C. In the outdoor experiment, the outdoor air temperature was 13.0 °C, and the heating room air temperature was 27.4 °C.
In both the indoor and outdoor experiments, we set the prior information of air temperature as 2 °C higher (Cases A1, A2, B1, and B2) and 2 °C lower (Cases A3, A4, B3, and B4) than the value measured by the thermohygrometer. These case studies assume that the prior information of air temperature can be estimated with an error of 2 °C. We also conducted case studies on the standard deviation of the prior information of air temperature (i.e., square root of the diagonal component of ) at 3 °C (Cases A1, A3, B1, and B3) and 5 °C (Cases A2, A4, B2, and B4). The standard deviation of the observation error (i.e., square root of the diagonal component of ) was obtained as 5% of the observed value. This value was obtained by means of preliminary experiments. We assumed that the observation error included spectral noise, forward model error (including the uncertainty of water vapor concentration), and representation error (reflecting the mismatch between the model resolution and the measurement location) [30].
In both experiments, the observed paths consisted of two spaces with temperature differences. The discretization boundary was set to coincide with the boundary of these spaces. The path was discretized into four layers, considering that in the urban climate and architectural fields, the control of air conditioning and micrometeorology investigations require spatial resolutions of the order of several meters. In this way, we can change the number and width of layers arbitrarily according to the target phenomenon.
In our study, the Jacobian was calculated by using MODTRAN 5.4 (Spectral Sciences Incorporated, USA) [34]. The initial value of the air temperature for the Jacobian calculation was given by the mean of the prior distribution, and the Jacobian was updated for each convergence calculation. Although the discretization intervals of the generated Jacobian and the spectroradiometer channels were different, the smoothness of the two channels was confirmed to be nearly the same, and the spectroradiometer data were adjusted to the generated Jacobian by linear interpolation. The water vapor concentration for the Jacobian calculation was given by the observed value of the thermohygrometer. Here, it is noted that in many cases, it is not possible to measure water vapor directly, but it is possible to obtain some prior information.
3.4. Channel Selection Using Mutual Information
The data of several channels can be obtained simultaneously in spectroradiometer observations. Therefore, when the least-squares method is directly used, the accuracy of the MAP solution appears to improve with increase in the number of channels. However, in actual observations, it is known that the MAP solution is easily affected by systematic errors when using more channels than necessary [35]. Therefore, in this study, the error effect on the MAP solution is reduced by selecting only the channels necessary for the inverse estimation of the temperature. Thus, we adopted a previously proposed method for selecting channels in order of the mutual information quantity [36]. Based on this method, we selected the number of channels as 10. All the selected wavelengths were in the wavelength band of water vapor. The information corresponding to 81% of the entire observation range was included in these 10 selected channels (Figure 5).
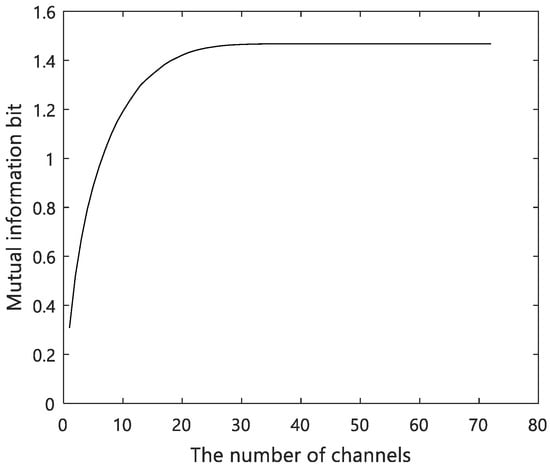
Figure 5.
Ascending cumulative graph of mutual information of channels. The information corresponding to 81% of the entire observation range is included in the first 10 channels.
4. Results
Figure 6a depicts the Jacobian corresponding to the indoor experiment (Case A1–A4), whereas Figure 6b shows that of the outdoor experiment (Case B1–B4). In both the indoor and outdoor experiments, we observed a large Jacobian value for every channel in the first layer. In contrast, this value decreased gradually beyond the second layer. As expected, this result indicates that the contribution from the first layer is larger than those of the other layers in the observed radiance. The observed spectra of the indoor and outdoor experiments and the spectra obtained by the forward model simulation are shown in Figure 7. Here, we used the mean of the prior information as the air temperature distribution of the forward model simulation. The simulated spectra of Cases A1, A2, B1, and B2 tend to be slightly lager in terms of magnitude than those of Cases A3, A4, B3, and B4. This is because the prior information of the former cases is assumed to be 2 °C higher than the room temperature measured by the thermohygrometer, and that of the latter cases is assumed to be 2 °C lower. Overall, the observed values are consistent with the spectra constructed by using the forward model. Next, we attempt to confirm whether a appropriate result can be obtained in the MAP solution.
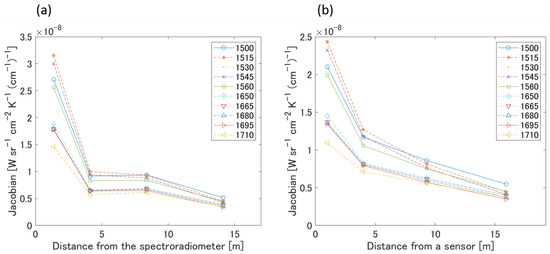
Figure 6.
Simulated Jacobian (10 selected channels). For any channel, the first-layer value is particularly large and tends to monotonically decrease with distance. (a) Indoor experiment (Cases A1–A4). (b) Outdoor experiment (Cases B1–B4).
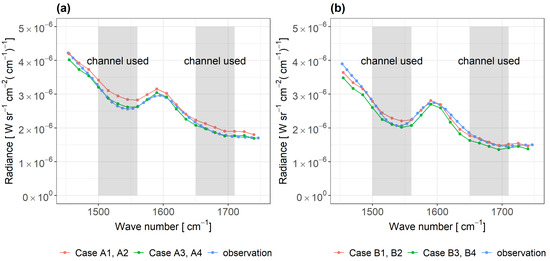
Figure 7.
Simulated spectra (Cases A1–A4, B1–B4) and observed spectra. We used the mean of the prior information as the air temperature distribution of the forward-model-simulated spectra. (a) Indoor experiment (Cases A1–A4), (b) Outdoor experiment (Cases B1–B4).
Figure 8 shows the MAP solution (i.e., the estimated value of the air temperature distribution) of the indoor experiment whereas Figure 9 shows that of the outdoor experiment. In Cases A1–A4, the first and second layers correspond to the heating room and the third and fourth layers correspond to the non-heating room. Moreover, in Cases B1–B4, the first-to-third layers were outdoors, and only the fourth layer corresponded to the heating room. We note that in all cases, the MAP solution is able to estimate the air temperature distribution in the two spaces of interest. In Cases A1 and A2 of the indoor experiment, the MAP solutions for the first layer are 23.1 °C and 22.4 °C, respectively, which are approximately 2.1–2.8 °C lower than the nearest true value of 25.2 °C. In Cases A3, A4, and B1–B4, the MAP solutions lie close to the true value throughout the entire path when compared with the mean value of the prior distribution. In all cases, the MAP solution approaches the mean of the prior distribution as the distance from the spectroradiometer increases. Additionally, there is no significant difference between the cases with standard deviations of the prior distribution of 3 °C and 5 °C (i.e., the comparison of A1 and A2, A3 and A4, B1 and B2, and B3 and B4).
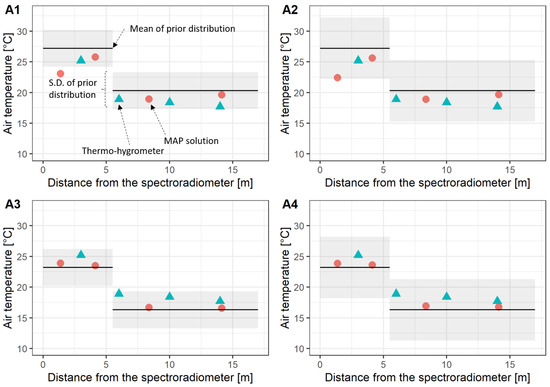
Figure 8.
MAP solution in Cases (A1–A4). The solid line indicates the mean of the prior information given by the normal distribution. The mean of the prior information in Cases A1 and A2 were set 2 °C higher, whereas those of Cases A3 and A4 were set 2 °C lower than the measured value of the thermohygrometer. The shaded region represents the standard deviation of the prior information (i.e., square root of the diagonal component of ) set in Table 2.
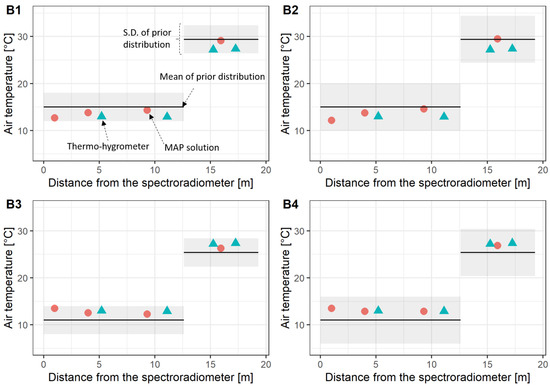
Figure 9.
MAP solution in Cases (B1–B4). The solid line indicates the mean of the prior information given by the normal distribution. The mean of the prior information in Cases B1 and B2 were set 2 °C higher, whereas those of Cases B3 and B4 were set 2 °C lower than the measured value of the thermohygrometer before conducting the experiments. The shaded region represents the standard deviation of the prior information (i.e., square root of the diagonal component of ) set in Table 2.
Table 3 lists the root mean square error (RMSE) of the MAP solution along with that of the prior information. The center position of each layer in the MAP solution differs from that of the point measured by the thermohygrometer. Thus, to calculate the RMSE, the measured value was linearly complemented in each space (i.e., heating room, non-heating room, or outdoor). In the range of extrapolation, the nearest-neighbor value was used. The air temperature was estimated within the error range of 0.3 to 2.2 °C. The RMSE was reduced when compared with the prior distribution in all cases. The mean RMSE of the prior information for all cases was 2.1 °C, whereas the estimated air temperature distribution was 1.3 °C, thereby indicating that the RMSE of the estimated air temperature distribution was reduced by 0.8 °C. In particular, the RMSEs of Cases B3 and B4, in which the mean of the prior distribution was set to 2 °C lower than the true value, were less than 1 °C, thereby achieving the target accuracy.

Table 3.
Comparison of RMSEs of prior information and MAP solution. Fractions may not match due to rounding.
The averaging kernels for the indoor and outdoor experiments are shown in Figure 10. The standard deviation of the prior distribution is 3 °C in Cases A1, A3, B1, and B3 (Figure 10a,c) as compared with 5 °C in Cases A2, A4, B2, and B4 (Figure 10b,d), that is, the averaging kernel is larger in the latter cases. As can be inferred from Equation (3), the uncertainty of the prior information becomes large (i.e., increased standard deviation of the prior distribution), and the MAP solution is relatively weighted by the observation. In all cases, the averaging kernels exhibit peak values in the first layer, whereas no peak values are observed in the second-to-fourth layers. This result indicates that it is easier to estimate the air temperature closer to the sensor. We discuss this point in detail in the discussion section.
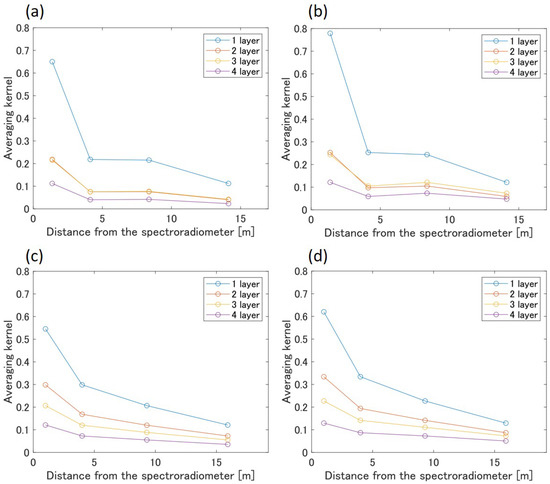
Figure 10.
Averaging kernel considered in the study. The MAP solution consists of both the observed air temperature distribution and prior information, with a higher value of the averaging kernel indicating a higher weight from the observed air temperature distribution. (a) Cases A1 and A3, (b) cases A2 and A4, (c) cases B1 and B3, and (d) cases B2 and B4.
5. Discussion
5.1. Estimation Accuracy of Horizontal Air Temperature Distribution
From the results of our experiments, we found that the RMSEs of the estimated air temperature were reduced when compared with those of the prior distribution, even for the relatively short paths of dozens of meters assumed in built spaces when using the thermal infrared spectroradiometer (Table 3). Furthermore, it was possible to reproduce the temperature distribution of the paths with a temperature difference existing between the heating and non-heating rooms and between the indoor and outdoor spaces (Figure 8 and Figure 9). Here, we recall that the target accuracy was set as 1 °C in our study. In our experiments, the RMSEs were determined to lie in the range of 0.3–2.2 °C, and our target was achieved in some cases (Cases B3 and B4). In this regard, it has been reported that the average bias is −0.7 K in the case of vertical air temperature distribution observations with the use of an aircraft-based spectroradiometer from an altitude of approximately 8.9 km [37]. Meanwhile, it is already known that the error of the MAP solution is represented by the (1) error of observed spectra, (2) error due to discretization, and (3) error between the observation equation and the true physical phenomenon (including parameters of the observation equation, such as the composition of gases) [30].
If there was no bias in the forward-model simulations, the observed radiance should have ranged between those of Cases A1–A2 and A3–A4; however, the observation radiance was lower than those of the two forward-model simulations in the range of 1500–1545 cm (Figure 7a). Thus, there was a possibility of a low bias in the forward model of the indoor experiment at 1500–1545 cm. Here, we note that this spectral band corresponds to the absorption band of water vapor, and the measurement bias of water vapor may have affected the results. Moreover, the accuracy of the thermohygrometer used in these experiments was 5%rh. When we set water vapor with 5%rh higher than the observed value, the RMSE of the MAP solution in Cases A3 and A4 was better than that of the prior distribution. As a result, the RMSE of Case A3 was reduced from 1.3 to 1.1 and that of Case A4 was reduced from 1.2 to 0.9. Therefore, because this method is affected by the concentration of water vapor, it is necessary to use channels other than those used in this study (Table 2) when observing phenomena where the concentration of water vapor is highly uncertain. Despite this kind of bias in some cases, overall, the mean RMSE decreased from 2.1 °C to 1.3 °C (Table 3).
In our study, we used the commercial thermal infrared spectroradiometer with a relatively low spectral resolution to examine the applicability of the equipment to built spaces. A further improvement of the estimation accuracy can be expected upon using a high-spectral resolution spectroradiometer based on an interferometer.
5.2. Influence of Prior Distribution on the Estimation of the Air Temperature Distribution
The MAP method uses prior information to regularize the solution. Therefore, the estimated temperature distribution (i.e., MAP solution) includes the contribution from the observation by the spectroradiometer and the prior information. In fact, the MAP solution tended to asymptotically approach the prior distribution with increasing distance from the sensor (Figure 8 and Figure 9). Therefore, to verify the accuracy of the estimated value of the temperature distribution obtained by the MAP method, it is necessary to quantitatively analyze both the error with the reference thermometer and the influence of prior information on the MAP solution; the averaging kernel is useful for such analysis [29]. A larger averaging kernel corresponds to the greater influence of the observation on the MAP solution.
In all cases, the averaging kernel exhibited a peak value in the first layer (Figure 10). On the other hand, no maximum value was observed in the second-to-fourth layers. This result indicates that it is easy to estimate the temperature near the spectroradiometer; however, it is difficult to estimate the temperature at increasing distances from the sensor. In this study, we selected the spectral channels according to the mutual information. Although this method maximizes the amount of information in the entire observation, this was not necessarily the optimal approach to obtain information from a distance. The lack of information on distant air temperature is a limitation when this method is applied to built spaces. In the future, we plan to investigate ways to select the channel that will increase the air temperature information at more distant locations.
Here, we also note that it is possible to overcome the difficulty of estimating the air temperature as a function of the distance by devising an observation method in built spaces. For example, for the heat island effect, we can install spectroradiometers on the rooftops of several buildings. For the indoor environment (especially large spaces such as stadiums or domes), we can install these on opposite walls. Consequently, spectroradiometer observations from both directions may be used to supplement the information as a function of the distance. Furthermore, by installing multiple spectroradiometers at different heights, we can obtain a three-dimensional air temperature distribution, which can contribute to more advanced air conditioning control and elucidation of boundary layer meteorology.
In addition, although the boundary surface temperature is known in this study, it is often unknown in actual measurements. As described in Section 2.2, by using the split-window method [24,25], we can obtain the boundary surface temperature with only the spectroradiometer used for observation.
In our investigations, we conducted a case study on the prior distribution, which has a significant impact on the estimated solution of the MAP method, after removing as much bias as possible, for example, the channel selection method based on the information content criterion. The influence of the bias on water vapor assumed in the forward model was also discussed. We showed that in 20 m long built spaces, the horizontal air temperature distribution can be estimated with an RMSE of 1.3 °C, which is comparable to the required accuracy. Estimating the horizontal air temperature distribution is a new and challenging application of remote sensing techniques in urban and built environments. Therefore, its feasibility needs to be tested both experimentally and theoretically, as done during the development of new satellite sensors. We believe that the present study is the first important step toward the general application of the method. To apply our method to various built spaces with different lengths, temperature distributions, humidity, and land surface conditions, sensitivity analysis and improvement of the method will be conducted in a future study.
6. Conclusions
In this study, we showed that the method used to estimate the vertical air temperature distribution of the atmosphere from artificial satellites and aircraft can be used to estimate the horizontal air temperature distribution for comparatively short paths in urban and built spaces based on experiments with a ground-based thermal infrared spectroradiometer. For our estimation, we first calculated a forward model using radiative transfer simulations, and the air temperature distribution was estimated from the observed radiance using this model. To regularize the estimated value, we used a Bayesian approach called the MAP method. A case study was carried out to confirm the effect of the prior distribution used in the MAP method on the estimated value of the air temperature. The mean RMSE of the prior information for all cases was 2.1 °C, whereas the estimated air temperature distribution (MAP solution) was 1.3 °C, thereby indicating that the RMSE of the estimated air temperature distribution was reduced by 0.8 °C. In some cases, the target accuracy of 1 °C was achieved. In the estimation using the MAP method, for a distance of 20 m (discretized into four layers), we were able to estimate the air temperature difference and reduce the estimation error from the prior information before observation. Our findings suggest the possibility of remotely estimating the air temperature distribution in built spaces. We believe that the present study is the first important step toward the general application of the method to built spaces. To apply our method to various built spaces having different lengths, temperature distributions, and humidity, sensitivity analysis and improvement of the method will be conducted in a future study.
Author Contributions
Conceptualization, R.T. and T.A.; methodology, R.T., T.A., and H.O.; software, R.T. and H.O.; validation, R.T.; formal analysis, R.T.; investigation, R.T. and T.A.; resources, R.T. and T.A.; data curation, R.T.; writing—original draft preparation, R.T.; writing—review and editing, R.T., T.A., and H.O.; visualization, R.T.; supervision, T.A. and H.O.; project administration, R.T. and T.A.; funding acquisition, T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JSPS KAKENHI Grant Number 17H03353.
Data Availability Statement
Inquiries regarding programming code and experiment data should be made by contacting the first and corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Dounis, A.; Caraiscos, C. Advanced control systems engineering for energy and comfort management in a building environment—A review. Renew. Sustain. Energy Rev. 2009, 13, 1246–1261. [Google Scholar] [CrossRef]
- Oshio, H.; Chen, K.; Asawa, T. Airborne and Terrestrial Observations of the Thermal Environment of Urban Areas Surrounding a High-Rise Building during the Japanese Winter. Sensors 2020, 20, 517. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ng, E.; An, X.; Ren, C.; Lee, M.; Wang, U.; He, Z. Sky view factor analysis of street canyons and its implications for daytime intra-urban air temperature differentials in high-rise, high-density urban areas of Hong Kong: A GIS-based simulation approach. Int. J. Climatol. 2010, 32, 121–136. [Google Scholar] [CrossRef]
- Huang, C.; Zou, Z.; Li, M.; Wang, X.; Li, W.; Huang, W.; Yang, J.; Xiao, X. Measurements of indoor thermal environment and energy analysis in a large space building in typical seasons. Build. Environ. 2007, 42, 1869–1877. [Google Scholar] [CrossRef]
- Wang, C.H.; Tsui, Y.Y.; Wang, C.C. On cold-aisle containment of a container datacenter. Appl. Therm. Eng. 2017, 112, 133–142. [Google Scholar] [CrossRef]
- Chojer, H.; Branco, P.; Martins, F.; Alvim-Ferraz, M.; Sousa, S. Development of low-cost indoor air quality monitoring devices: Recent advancements. Sci. Total Environ. 2020, 727, 138385. [Google Scholar] [CrossRef] [PubMed]
- Coulby, G.; Clear, A.; Jones, O.; Godfrey, A. A Scoping Review of Technological Approaches to Environmental Monitoring. Int. J. Environ. Res. Public Health 2020, 17, 3995. [Google Scholar] [CrossRef]
- Muller, C.L.; Chapman, L.; Grimmond, C.S.B.; Young, D.T.; Cai, X. Sensors and the city: A review of urban meteorological networks. Int. J. Climatol. 2013, 33, 1585–1600. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Instruments and Methods of Observation Volume I: Measurement of Meteorological Variables, 2018 ed.; WMO: Geneva, Switzerland, 2018. [Google Scholar]
- Oke, T.; Maxwell, G. Urban heat island dynamics in Montreal and Vancouver. Atmos. Environ. (1967) 1975, 9, 191–200. [Google Scholar] [CrossRef]
- Tsin, P.K.; Knudby, A.; Krayenhoff, E.S.; Ho, H.C.; Brauer, M.; Henderson, S.B. Microscale mobile monitoring of urban air temperature. Urban Clim. 2016, 18, 58–72. [Google Scholar] [CrossRef]
- Rees, W.G. Physical Principles of Remote Sensing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2012; ISBN 9781139017411. [Google Scholar]
- Menzel, W.P.; Schmit, T.J.; Zhang, P.; Li, J. Satellite-Based Atmospheric Infrared Sounder Development and Applications. Bull. Am. Meteorol. Soc. 2018, 99, 583–603. [Google Scholar] [CrossRef]
- Cabib, D.; Orr, H. Circular variable filters (CVF) at CI, progress and new performance. Proc. SPIE—Int. Soc. Opt. Eng. 2012, 8542. [Google Scholar] [CrossRef]
- Yang, J.; Min, Q. Retrieval of Atmospheric Profiles in the New York State Mesonet Using One-Dimensional Variational Algorithm. J. Geophys. Res. Atmos. 2018. [Google Scholar] [CrossRef]
- Wark, D.Q. On indirect temperature soundings of the stratosphere from satellites. J. Geophys. Res. 1961, 66, 77–82. [Google Scholar] [CrossRef]
- Liou, K.N. An Introduction to Atmospheric Radiation, 2nd ed.; Academic Press: Cambridge, MA, USA, 2002; p. 583. [Google Scholar]
- ASHRAE. Thermal Environmental Conditions for Human Occupancy; Number ANSI/ASHRAE Standard 55-2017 in ASHRAE Standard; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- Tamura, T. A review of studies on regional differences of thermal and humidity sensitivity on human skin surface. Jpn. J. Sens. Eval. 2007, 11, 81–88. (In Japanese) [Google Scholar]
- Jamei, E.; Rajagopalan, P.; Seyedmahmoudian, M.; Jamei, Y. Review on the impact of urban geometry and pedestrian level greening on outdoor thermal comfort. Renew. Sustain. Energy Rev. 2016, 54, 1002–1017. [Google Scholar] [CrossRef]
- T&D. TR-7wb/nw Series Thermo Recorder Manual; T&D: Matsumoto, Japan, 2019. [Google Scholar]
- Melnikova, I.N.; Vasilyev, A.V. Short-Wave Solar Radiation in the Earth’s Atmosphere: Calculation, Observation, Interpretation; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–303. [Google Scholar] [CrossRef]
- Ulivieri, C.; Castronuovo, M.; Francioni, R.; Cardillo, A. A split window algorithm for estimating land surface temperature from satellites. Adv. Space Res. 1994, 14, 59–65. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Petty, G.W. A First Course in Atmospheric Thermodynamics; Sundog Publishing: Madison, WI, USA, 2008. [Google Scholar]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Menke, W. Geophysical Data Analysis: Discrete Inverse Theory, matlab ed.; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2000. [Google Scholar]
- Brasseur, G.P.; Jacob, D.J. Modeling of Atmospheric Chemistry; Cambridge University Press: Cambridge, UK, 2017; p. 560. [Google Scholar]
- Cabib, D.; Orr, H. Circular Variable Filters (CVF) at CI, progress and new performance. In Electro-Optical Remote Sensing, Photonic Technologies, and Applications VI; Kamerman, G.W., Steinvall, O., Bishop, G.J., Gonglewski, J., Lewis, K.L., Hollins, R.C., Merlet, T.J., Gruneisen, M.T., Dusek, M., Rarity, J.G., Eds.; SPIE: Bellingham, WA, USA, 2012. [Google Scholar] [CrossRef]
- Kuze, A.; Urabe, T.; Suto, H.; Kaneko, Y.; Hamazaki, T. The instrumentation and the BBM test results of thermal and near-infrared sensor for carbon observation (TANSO) on GOSAT. In Infrared Spaceborne Remote Sensing XIV; Strojnik, M., Ed.; SPIE: Bellingham, WA, USA, 2006. [Google Scholar] [CrossRef]
- CI-Systems. SR-800N Superior Accuracy Blackbody. Available online: https://www.ci-systems.com/Files/Source-SR-800N.pdf (accessed on 9 October 2020).
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Hoke, M.L.; et al. MODTRAN5: 2006 update. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII; Shen, S.S., Lewis, P.E., Eds.; SPIE: Bellingham, WA, USA, 2006. [Google Scholar] [CrossRef]
- Saitoh, N.; Imasu, R.; Ota, Y.; Niwa, Y. CO2 retrieval algorithm for the thermal infrared spectra of the Greenhouse Gases Observing Satellite: Potential of retrieving CO2 vertical profile from high-resolution FTS sensor. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Rodgers, C.D. Information content and optimization of high-spectral-resolution measurements. In Optical Spectroscopic Techniques and Instrumentation for Atmospheric and Space Research II; Hays, P.B., Wang, J., Eds.; SPIE: Bellingham, WA, USA, 1996. [Google Scholar] [CrossRef]
- Allen, G.; Illingworth, S.M.; O’Shea, S.J.; Newman, S.; Vance, A.; Bauguitte, S.J.B.; Marenco, F.; Kent, J.; Bower, K.; Gallagher, M.W.; et al. Atmospheric composition and thermodynamic retrievals from the ARIES airborne TIR-FTS system—Part 2: Validation and results from aircraft campaigns. Atmos. Meas. Tech. 2014, 7, 4401–4416. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).