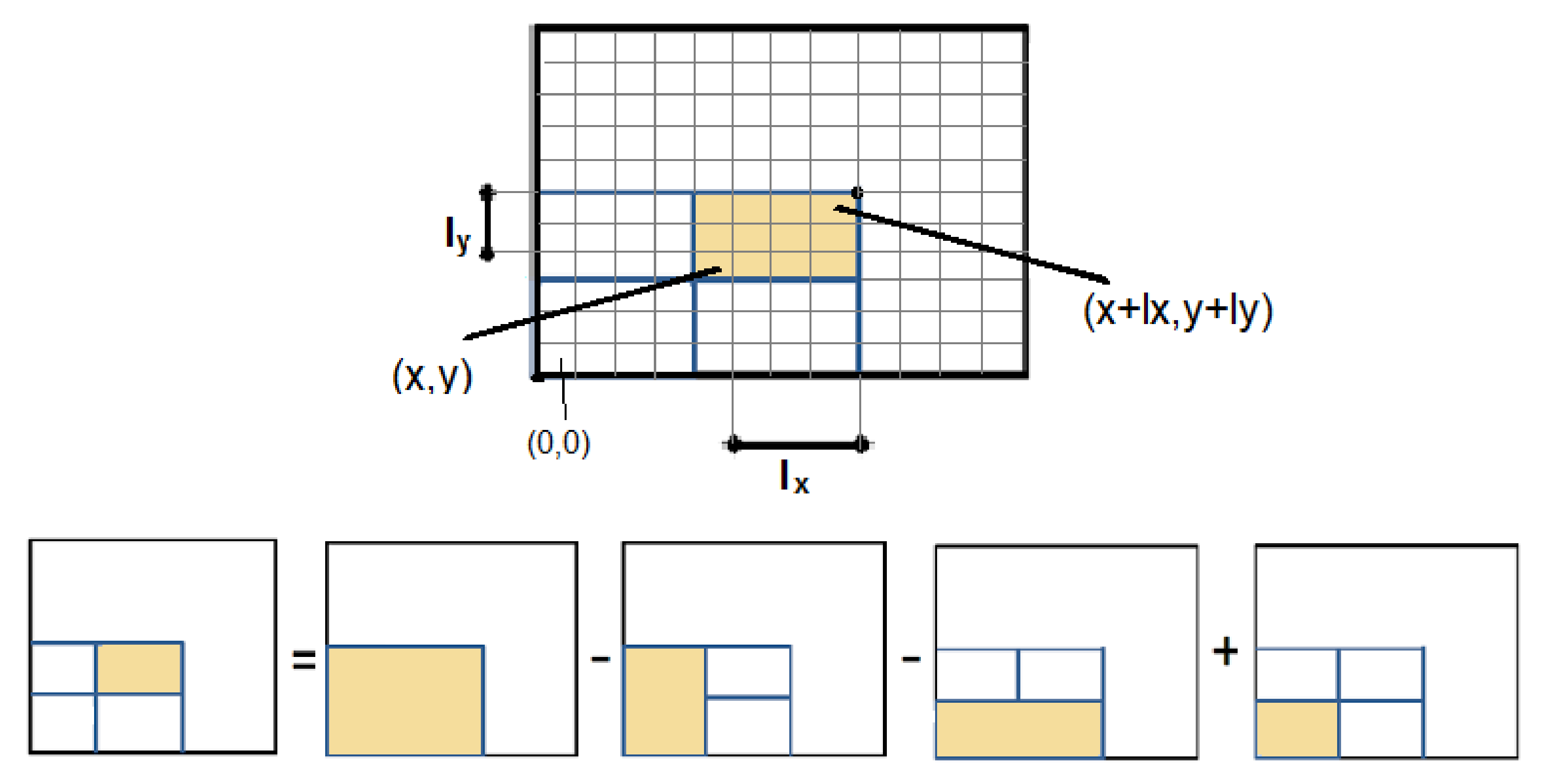
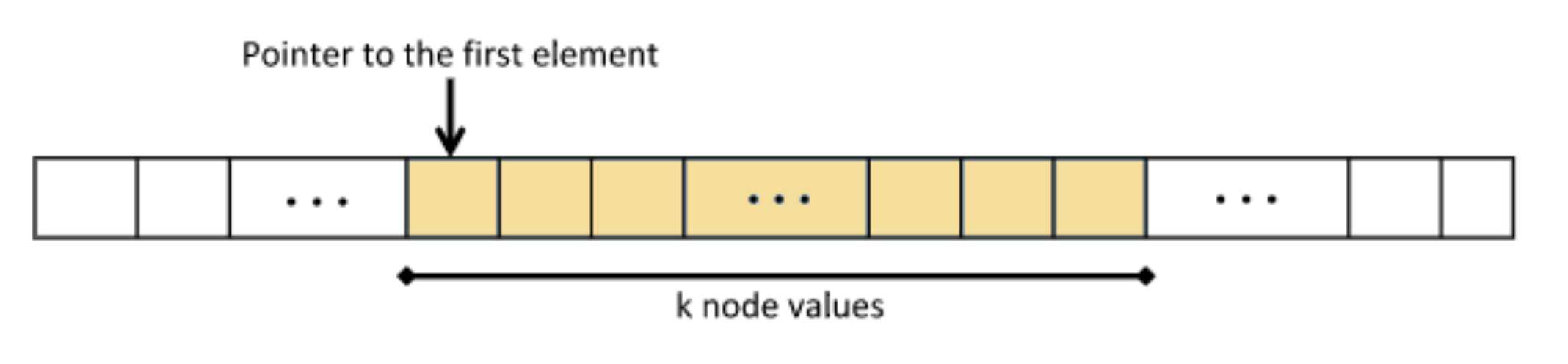
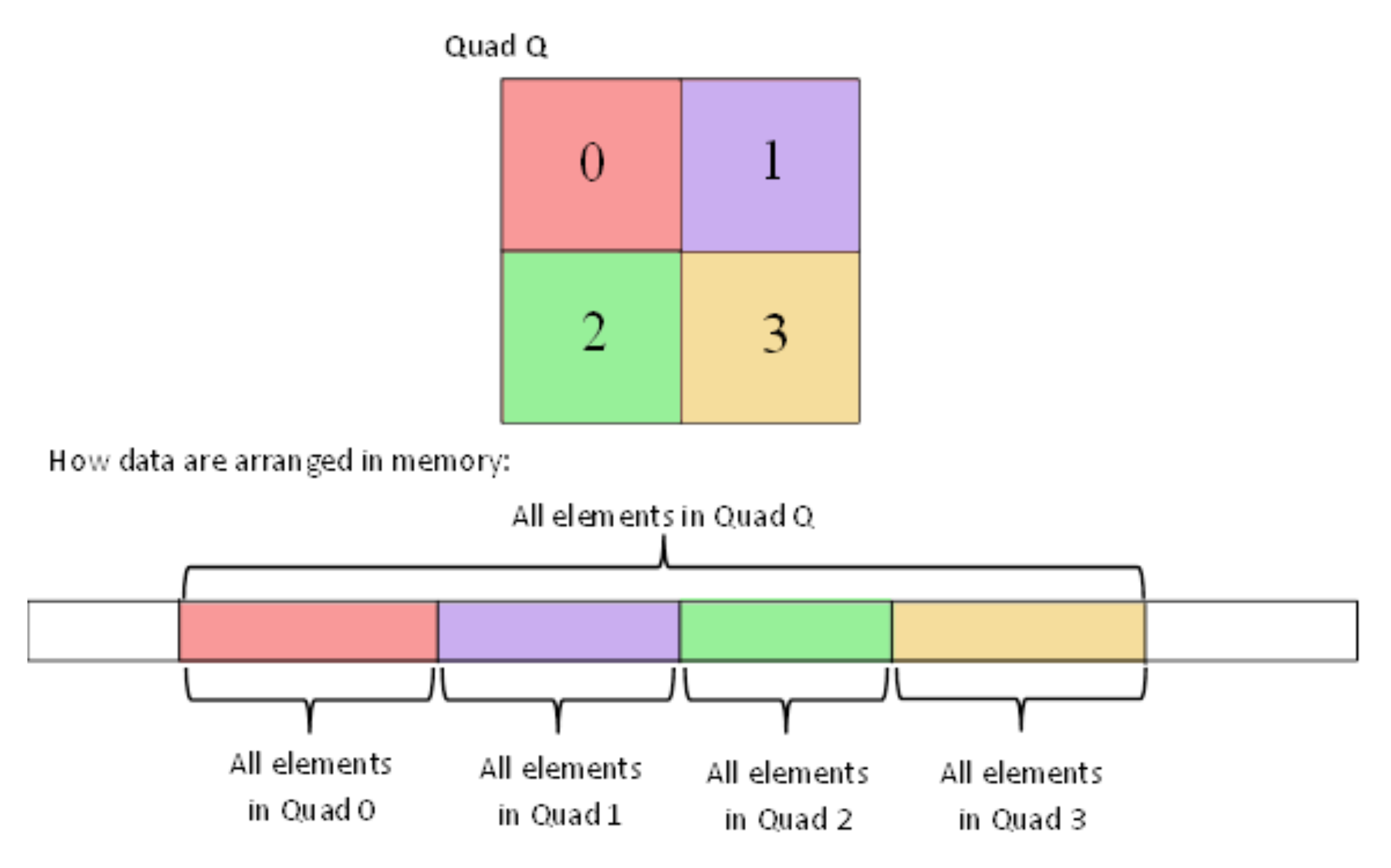
1. Introduction
LiDAR systems acquire distance information and contributed substantially in forest monitoring due to their ability to record information from below the tree canopy. There are used to be two types of LiDAR data: discrete and the full-waveform (FW) [
1]. The discrete LiDAR systems recorded a few peak laser returns, while the FW LiDAR systems record the entire backscattered signal digitised and discretised at equal distances. The results are a set of multiple returns equally spaced, defined as the “wave samples” according to the LAS file specifications [
2]. The state-of-art airborne LiDAR sensors are full-waveform. Peak points are extracted from the waveforms after the acquisition in post processing and delivered in discrete LiDAR file formats [
3]. Therefore, nowadays delivered LAS1.0, LAS1.1 or LAS1.2 data may contain “peak points extracted from waveform data” that do not come with all the downside discrete systems had, e.g., minimum distance between two returns and maximum number of returns per pulse. This is confusing though, since the data are delivered in discrete LiDAR file formats but contain processed waveform data (peak points extracted) [
4]. Despite that, the waveform data still contain extra information due to the waveform samples that exist between the peak points.
Even though, extraction of peak returns from the waveform data has been widely used, there are still very few uses of the waveform samples, also named as Hyper Point Clouds [
5]. The Airborne Research Facility of the National Environment Research Council in the UK (NERC-ARF) has been acquiring airborne data for the UK and overseas since 2010 and has more than 100 clients of new and archived data. Many clients request that FW LiDAR data to be acquired when planning a flight but, despite the significant number of acquisitions, the majority of research still only uses discrete LIDAR. Some of the factors underlying this slow uptake are:
Traditional ways of interpreting the full-waveform LiDAR data suggest echo decomposition for detecting peak points and interpreting the point clouds extracted [
7]. Both SPDlib [
8] and FullAnalyse [
9] visualise either the peak extracted points or the raw waveform samples. SPDlib visualises the samples with intensity above a given threshold as points, while FullAnalyse generates a sphere per sample, with its radius directly correlated to the intensity of each wave sample. Similarly, Pulsewaves visualise a number of waveforms with different transparency according to their intensity [
10].
On the one hand, visualising all the wave samples makes understanding of data difficult due to high noise. On the other hand, peak point extraction identifies significant features but the FW LiDAR data also contain information about the width of peaks in the returns. This information can be accumulated from multiple shots into a voxel array, building up a 3D discrete density volume [
11].
Voxelisation of FW LiDAR data was introduced by Persson et al. [
12] who used it to visualise small scanned areas (15 m × 15 m). The waveforms samples were inserted into a 3D voxelised space and the voxels were visualised using different transparencies according to their intensity. Similarly, Miltiadou et al. [
13] adopted voxelisation for 3D polygonal model creation and applied it to larger areas. Once the 3D density volume is generated, an algebraic object is defined. Nevertheless, visualising algebraic objects is not straightforward, since they contain no discrete values. This problem can either be addressed by ray-tracing [
14] or by iso-surface extraction [
15]. Iso-surface is the equivalent to a contour line in 3D. In other words, it is a surface that represents a set of points given a constant value, the iso-level. Once an algebraic representation of the FW LiDAR data is defined, an iso-surface can be extracted for a given iso-level. In this paper, the iso-surface extraction approach is investigated.
Even though iso-surface extraction has not been intensively research for modelling FW LiDAR data, there are many related applications in medical visualisation [
16,
17] and visual effects [
18,
19]. Research work exists on optimising both ray-tracing and iso-surface extraction (surface reconstruction) and it can be categorised into three groups: surface-tracking, parallelisation and data structures. Those approaches are discussed below along with their benefits and limitations with respect to voxelised FW LiDAR data.
Surface-tracking was applied at Rodrigues de Araujo and Pires Jorge [
20] and Hartmann [
21]. Starting from a seed point, the surface is expanded according to the local curvature of the implicit object. This method is considered to be faster and more efficient in comparison to the Marching Cubes algorithm since huge empty spaces are ignored. It further opens up possibilities for finer surface reconstruction at areas with high gradient changes. Nevertheless, surface-tracking algorithms cannot be applied with real laser scanning data because these data are neither manifold nor closed. For example, in a forest scene, a tree canopy may be detached from the ground due to missing information about its trunk. Therefore, by tracking the surface, the algorithm may converge at a single tree instead of the entire forest.
Hansen and Hinker proposed parallelising the polygonisation process of BlobTree trees on Single Instruction, Multiple Data (SIMD) machines [
22]. The Instruction is a series of commands to be executed. The longer the series of the commands is, the greater the speed up is. BlobTree trees represent implicit objects as a combination of primitives and operations [
23]. As the depth of the tree increases, the length of the parallelised instruction increases as well and therefore a good speed up is achieved. Nevertheless, the function for the implicit representation of the FW LiDAR data at [
13] executes in constant time, making it harder to achieve speed up using SIMD machines. Further, according to the C++ Coding Standards when optimisation is required, it is better to seek an algorithmic approach first because it is simpler to maintain and less likely to contain bugs [
24].
It worth highlighting that this paper investigates the performance of six data structures perform on iso-surface extraction (3D polygonal model creation) of voxelised full-waveform LiDAR data. Even though the performance of the algorithm is tested on the algorithm implemented by the authors at [
13], there are many distinct and acknowledged approaches on 3D forest modelling and segmentation [
25]. Except for forest related applications, 3D modelling was applied and has also been applied on urban environments [
26,
27]. The literature in urban modelling may differ, but the usage of data structures is relevant.
4. Discussion
To briefly sum up, the following six data structures have been implemented and their performance has been tested for reconstructing 3D polygonal models from voxelised FW LiDAR data:
1D-Array: Simple array that keeps data coherent in memory for quick access.
Voxel Hashing: A hashed table is used for storing the intensity values of the voxels [
33].
Octree: Simple hierarchical structure, but it is scanline implementation (i.e., it cannot identify and ignore big chunks of empty voxels).
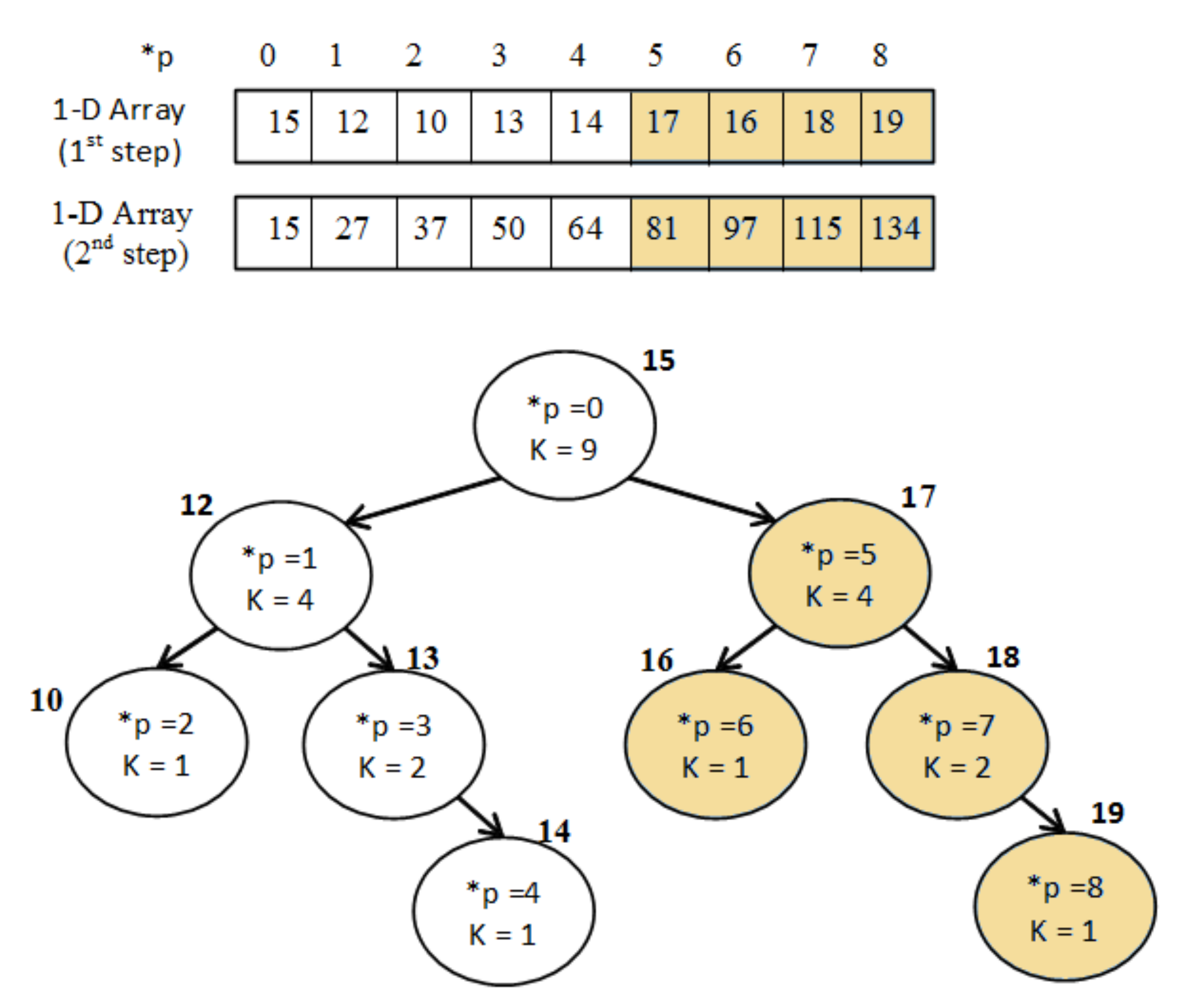
Integral Volumes: Extension of “Integral Images” that allows finding the sum of any cuboid area in constant time. It is used for quickly identifying and ignoring empty areas during polygonisation.
Octree Max/Min: The polygonisation is embedded into an hierarchical data structure [
37]. The max and min values of each branch are stored to identify and ignore branches that either only contain low level noise or are completely inside the algebraic object.
Integral Octree: new data structure proposed at this paper and an attempt to preserve properties from both “Octree Max/Min” and “Integral Volumes”.
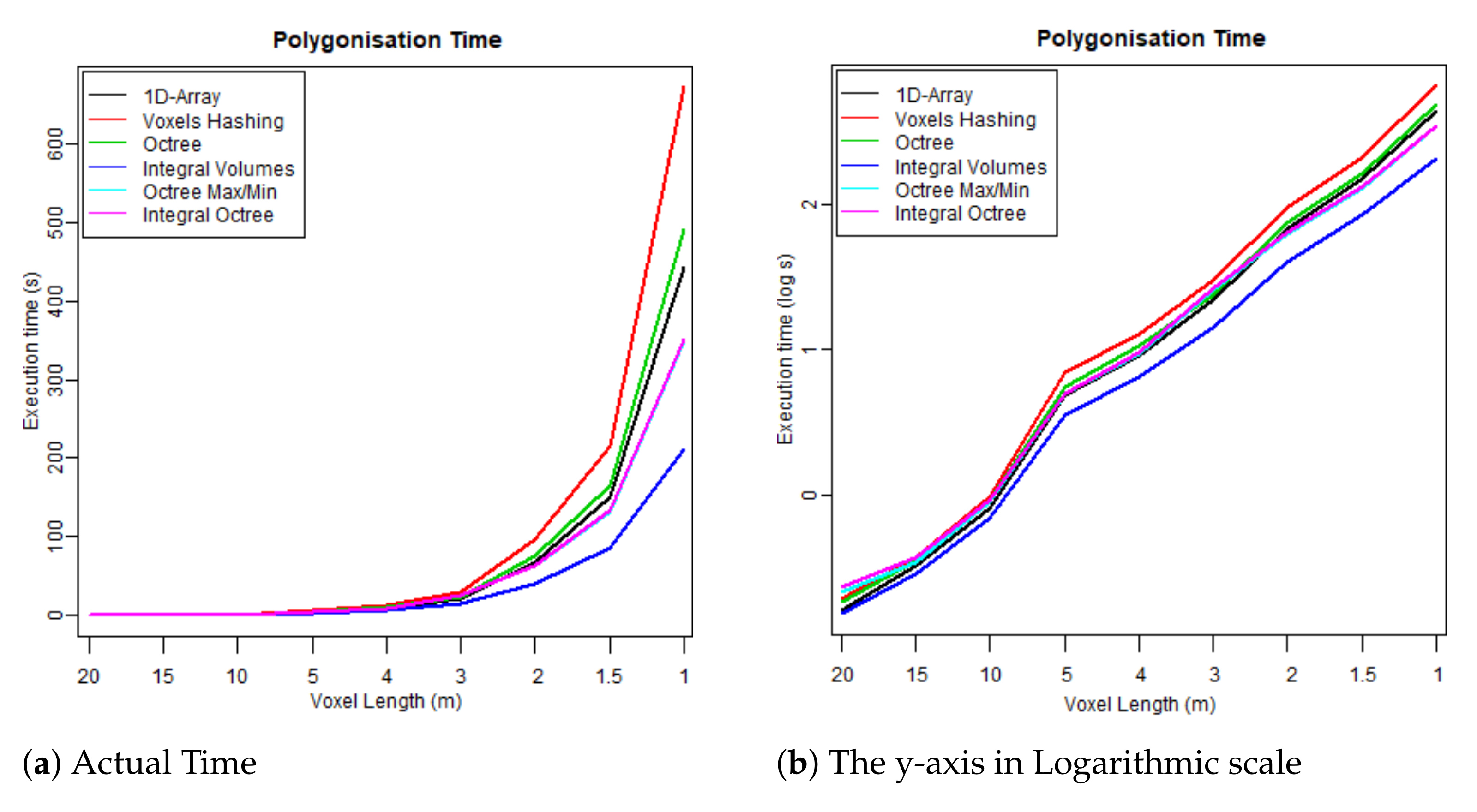
Each one of the aforementioned data structures has different properties. The first three implementations are scanline algorithms, which means that polygonisation is linear and all the voxels, including the empty ones, are checked for generating triangles primitives. Some data structures are taken from the literature to test how well they perform on this specific datasets while others are new and presented into this paper.
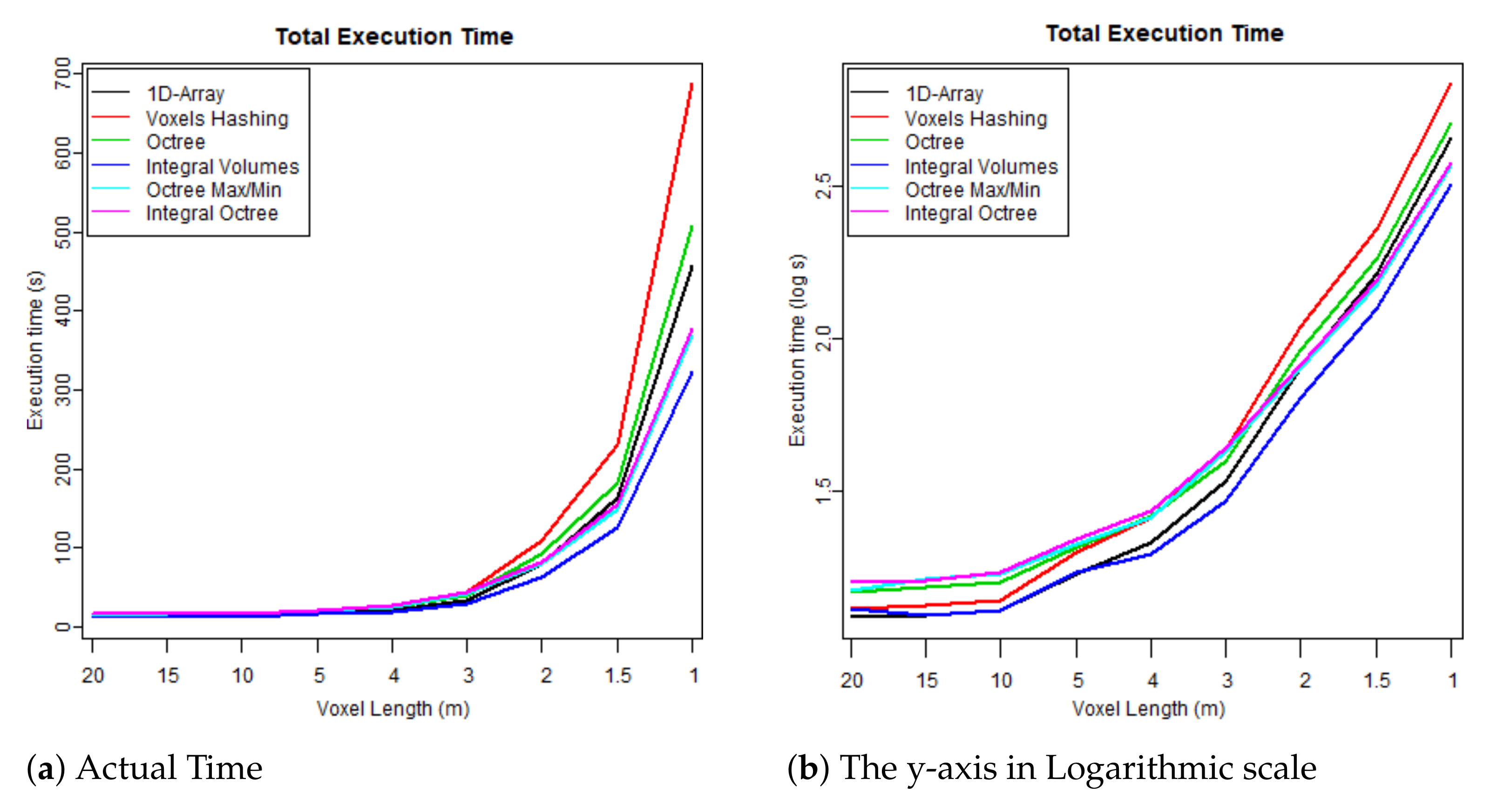
Table 6 summarises their properties and the problems each data structure attempts to resolve.
Before proceeding to the comparison of the data structures, it is worth mentioning a limitation. Even though noisy points are classified during preprocessing by NERC-ARF-DAN, the tools we implement use the limits stored inside the LAS files for defining the size of the voxelised space [
11]. This implies that the noisy points are ignored during voxelisation but the voxelised space is not resized. Therefore, hierarchical structures—that do not store empty voxels—has been benefited from the removal of the noisy waveforms, but structures that require to store the values of all the voxels are not. This may be resolved by reading the LAS files twice: once for defining the size of the voxelised space and once for the voxelisation process. This will increase construction time and it should, therefore, be considered according to the type of the structure to be used and the size of the data to be loaded.
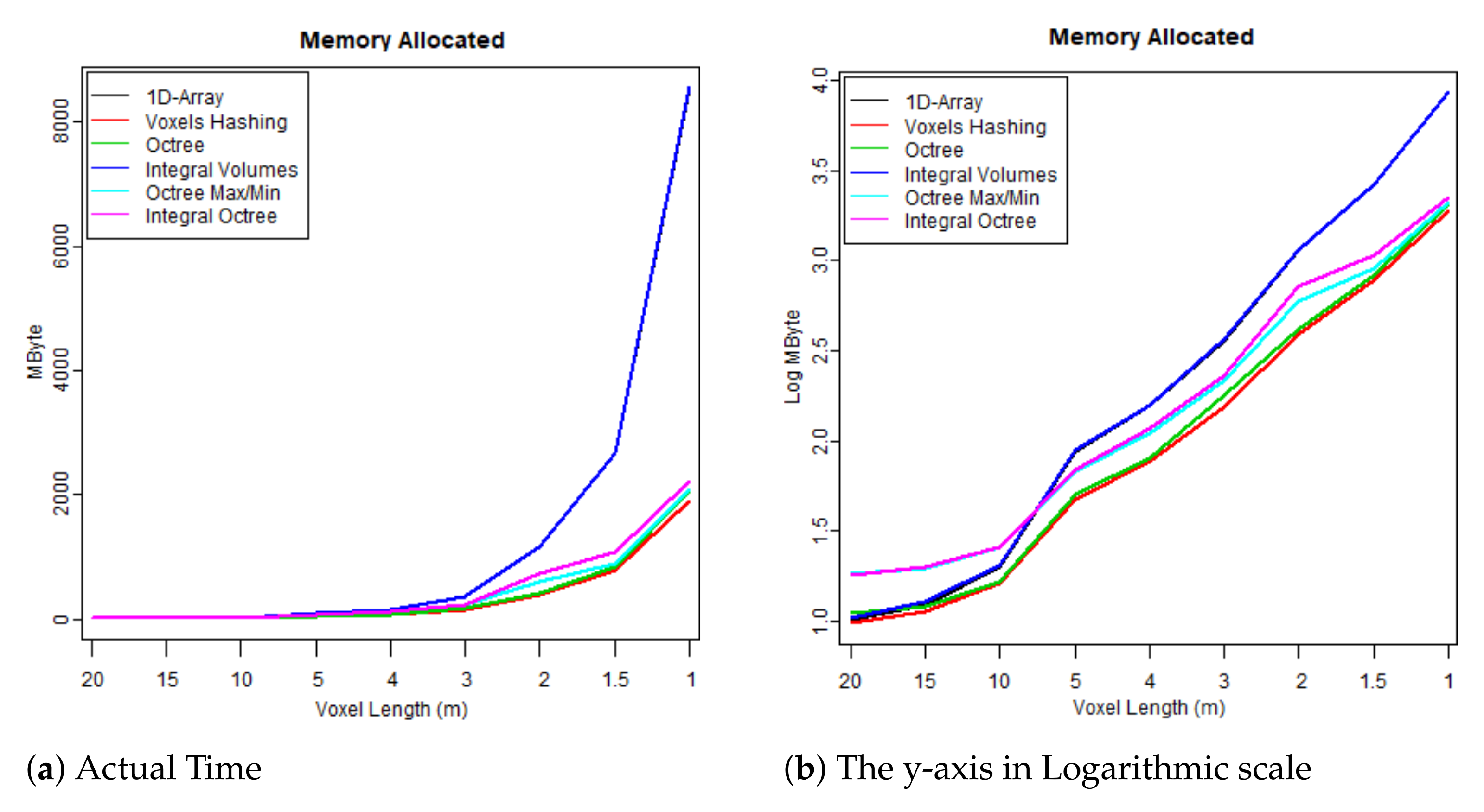
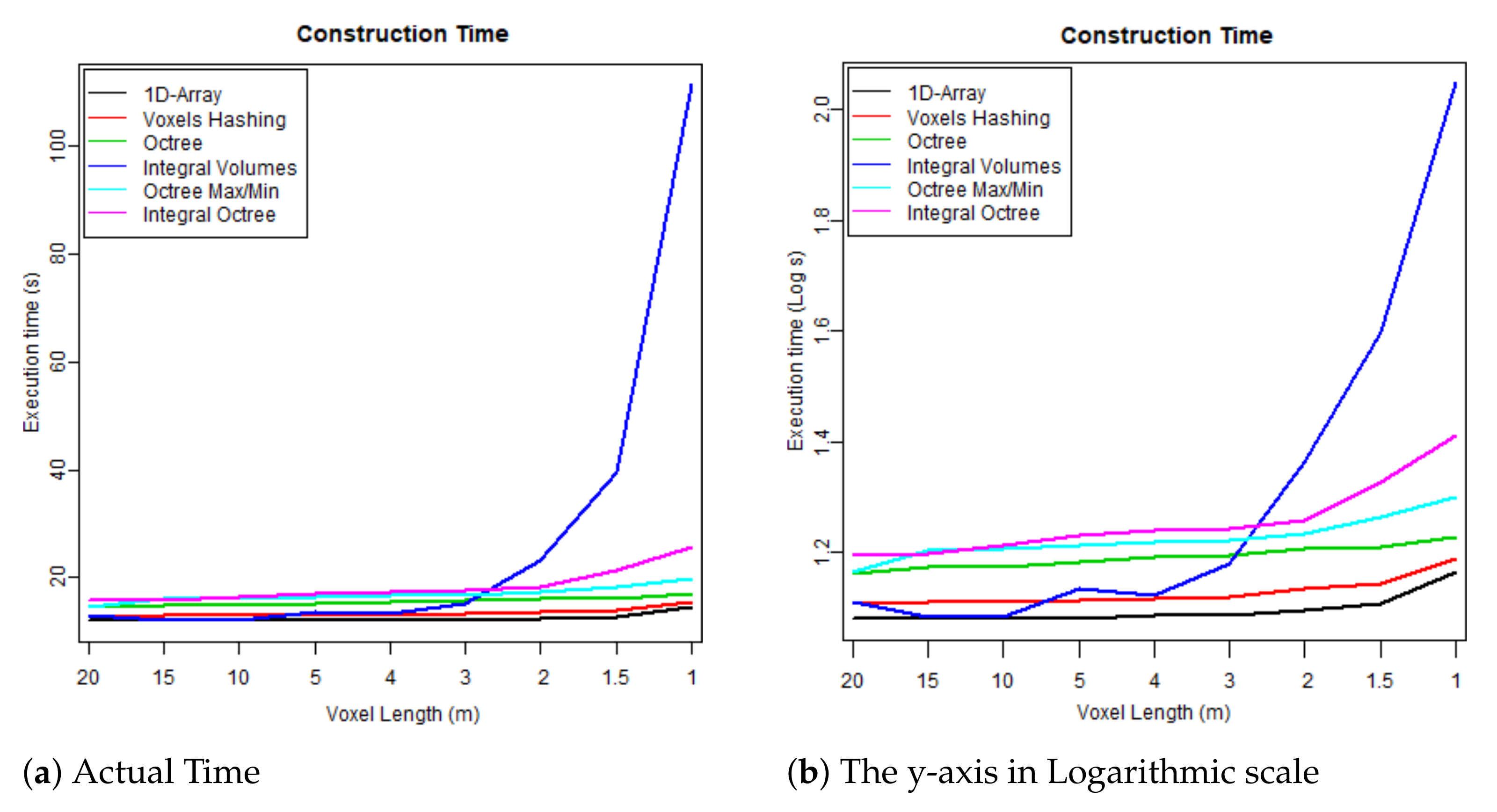
Overall, “Integral Volumes” is the fastest one but it consumes as much memory as the original “1D-Array”. Its performance is better than the “Octree Max and Min” because:
Elements are accessed in constant time while traversing a tree requires at least time, when the tree is balanced, and up to for unbalanced trees.
The size of the volume is the original cuboid while any octree data structure requires a cubic space that is a power of two. This results into extending the boundaries of the 3D voxelised FW LiDAR data, including big empty areas and building deeper and unbalanced trees (increased traversal time).
Neighbour-finding is faster than octrees since no backtracking is required.
Checking whether a surface is crossing the edges of an empty area is much faster using the “Integral Volumes” because the sum of any volume is calculated in constant time. Therefore, checking whether the neighbours of an empty cell are also empty is trivial. In contrast, the “Octree Max/Min” and “Integral Tree” data structures must loop through all the voxels at the edges of an empty branch to avoid generating holes.
Regarding the “Voxel Hashing”, faster results were expected than the “Octree” because it does not require traversal for reaching elements, but it is very likely to have more memory jumps, considering that the implementation of the octree structures keeps the children of every branch coherent in memory for faster interpretation. Additionally, during the expansion of hashed tables, many reallocation occurs.
Furthermore, “Octree Max and Min” and the “Integral Octree” have similar results. In the tests, the isolevel was set lower than the noise threshold and for that reason the empty branches were the ones discarded at the tests (Line 6 of Algorithm 3). If the isolevel was lower than the noise threshold, then the low level noise would have affected the “Octree Max and Min” less than the “Integral Octree”; the “Octree Max and Min” check whether the max value is below the threshold, while the “Integral Octree” the sum of the leaves. Additionally, “Integral Octree” consumes more memory for saving the leaves into an 1D-array, but even though “Integral Octree” generally performed worse than the “Octree Max/Min” in the tests of
Table 4 and
Table 5, it should be beneficial in multiresolution direct volumetric rendering and blurring the volume for noise removal.
It further worth mentioning that even though this specific paper tested the performance of the data structures using FW LiDAR data, this research has a bigger application domain. Firstly, the data structures can be used for interpreting a variety of voxel-based datasets. Secondly, iso-surface extraction is a big field in Computer Graphics used in Medical imaging [
38] and Animation Production [
39]. Therefore, this research is not restricted to the usage of LiDAR data but has multiple applications.
5. Conclusions
Advances in Remote Sensing, Medical Imagery and Animation production raises the need for efficient data management. In respect to airborne LiDAR technologies, the full-waveform (FW) airborne LiDAR data are 5 to 10 times larger than discrete LiDAR data. Most existing workflows only support handling of discrete LiDAR or peak points extracted from FW LiDAR, since the increased amount of information recorded makes handling difficult. This paper investigated the performance of six data structures for managing voxelised FW LiDAR data during 3D polygonal model creation. The six data structures are (1) 1D-Array, (2) Voxel Hashing, (3) Octree, (4) Integral Volumes, (5) Octree Max/Min, (6) Integral Octree. The “Integral Octree” is proposed in this paper and it is an attempt to preserve the properties of “Integral Volumes” in an hierarchical structure. According to the results, “Integral Volumes”, which are able to return the sum of any cuboid area at constant time, is the fastest data structure for the 3D polygonal model creation of voxelised FW LiDAR data, but it consumes the most memory, equal to the “1D-Array” data structure. It is, therefore, concluded that each data structure has different properties and both memory consumption and time efficiency need to be taken into consideration, as well as the type of the interpretation to be performed. Finally, even though this paper investigates the performance of these data structures for interpreting voxelised FW LiDAR data, the application domain is much bigger since it could be utilised in any type of volumetric data.