Deep Localization of Static Scans in Mobile Mapping Point Clouds
Abstract
1. Introduction
Contributions of the Research
- Considering TLS data are less related to MLS data initially, a stable method was proposed to recognize the coarse related MLS place, in which simple, reliable features (i.e., cylinder-like primitives) are extracted to describe general characteristics of a local urban scene. Moreover, to overcome variant features of cylinder-like objects extracted from MLS and TLS due to point density, occlusions and/or seasonal changes in vegetation, a decision-making strategy based on a probabilistic framework is developed to select the best related MLS point clouds.
- A novel patch-based convolution neural network is proposed for further pose refinement, which can deal with a large-scale complicated scene by introducing patch instead of a single point as a calculation unit. In addition, after the processing of neural network, a global refinement for prediction based on patches are applied to improve the accuracy and stability of a transformation estimation.
2. Related Works
2.1. Place Recognition
2.2. Related Literature of Pose Refinement
3. Instruments and Data Capturing
3.1. Data Acquisition and Experimental Data
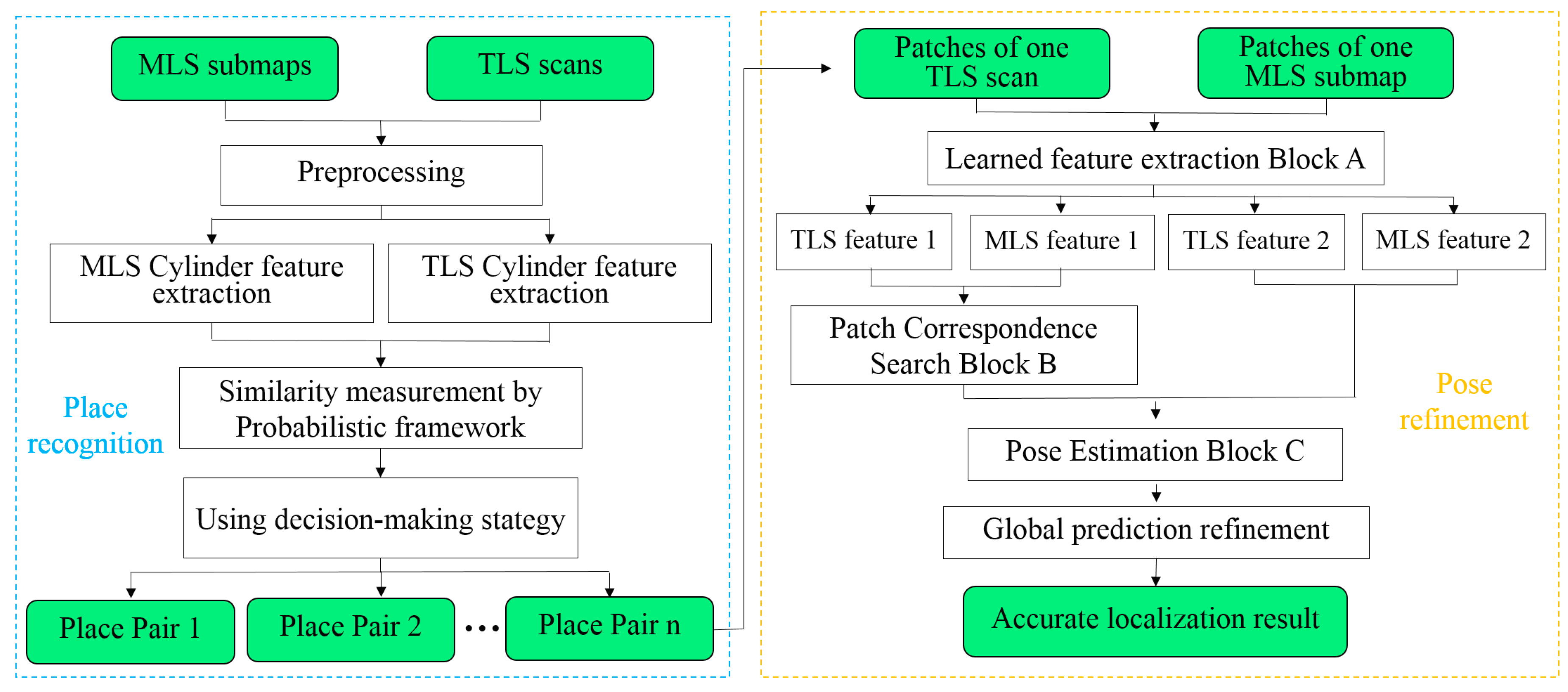
4. Methods
4.1. Cylinder Object-Based Place Recognition
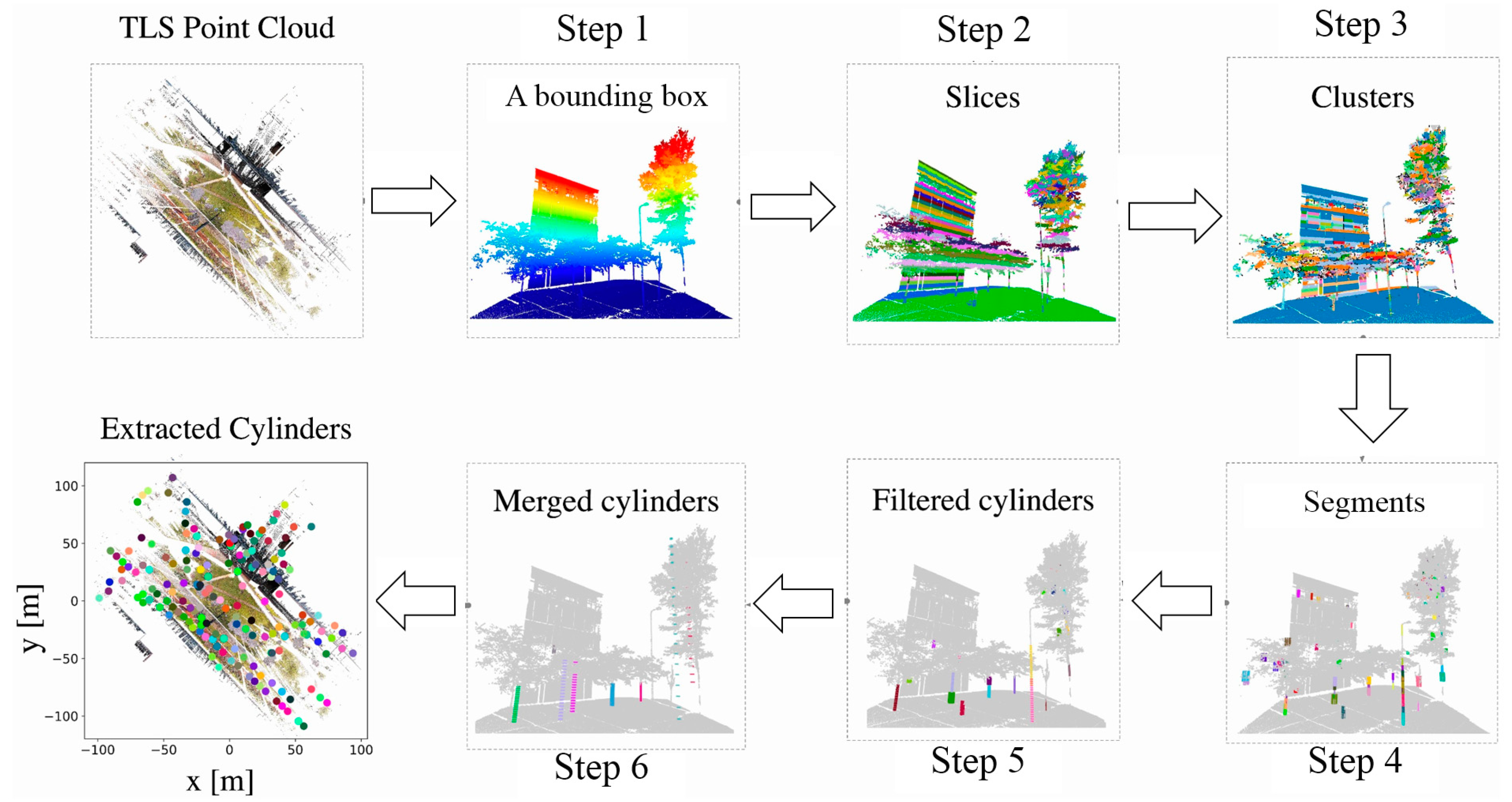
4.1.1. Cylinder Features Extraction
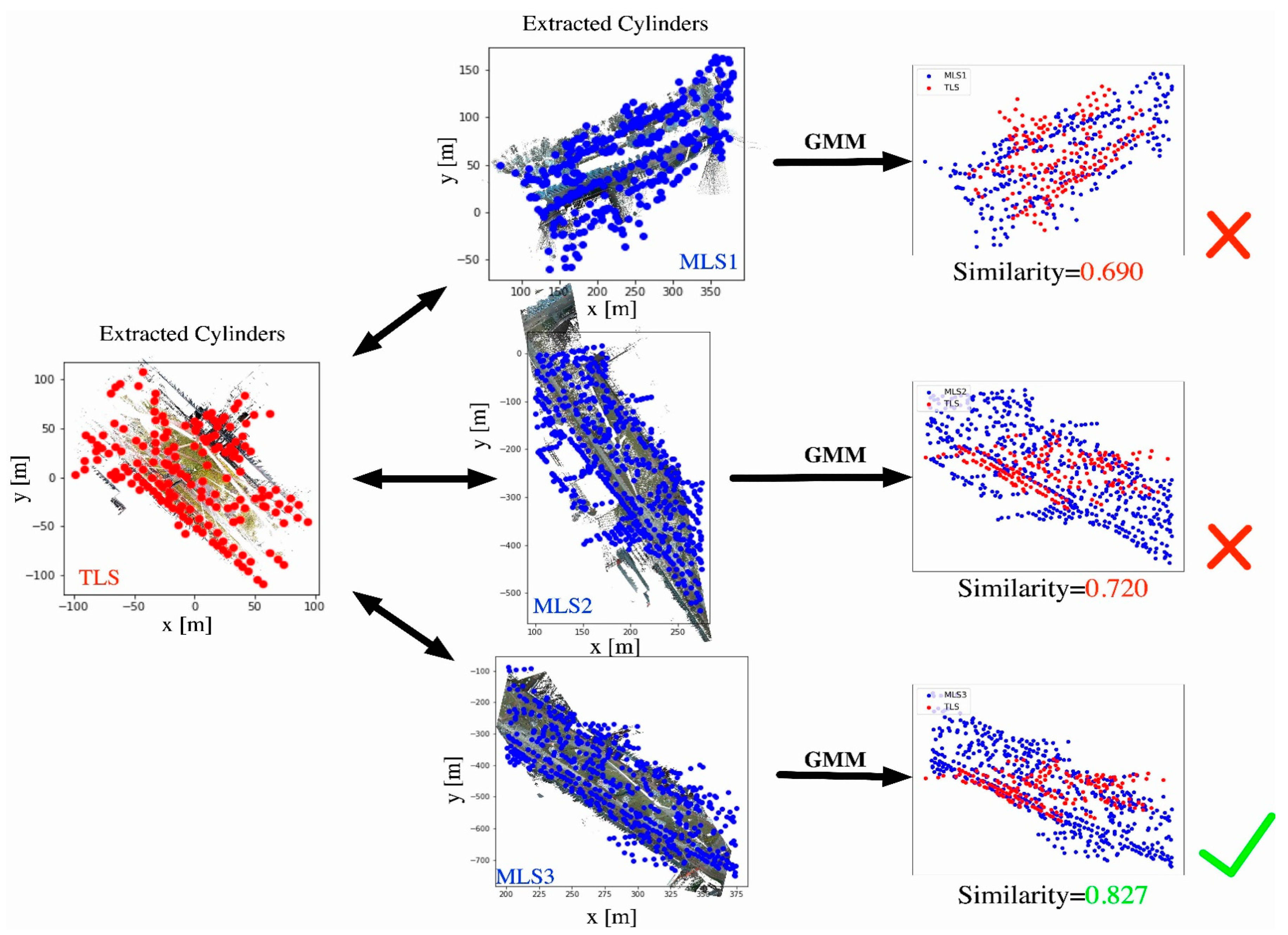
4.1.2. Probabilistic Framework for Similarity Measurement
4.1.3. Decision-Making Strategy
4.2. Deep Learning-based Pose Refinement
4.2.1. Patch-based Neural Network for Pose Refinement
4.2.2. Design of Loss Function
4.2.3. Global Prediction Refinement
5. Experimental Results
5.1. Experimental Setup
5.1.1. Data Preparation
5.1.2. Evaluation Criteria
- Confusion matrix w.r.t. patch and batch
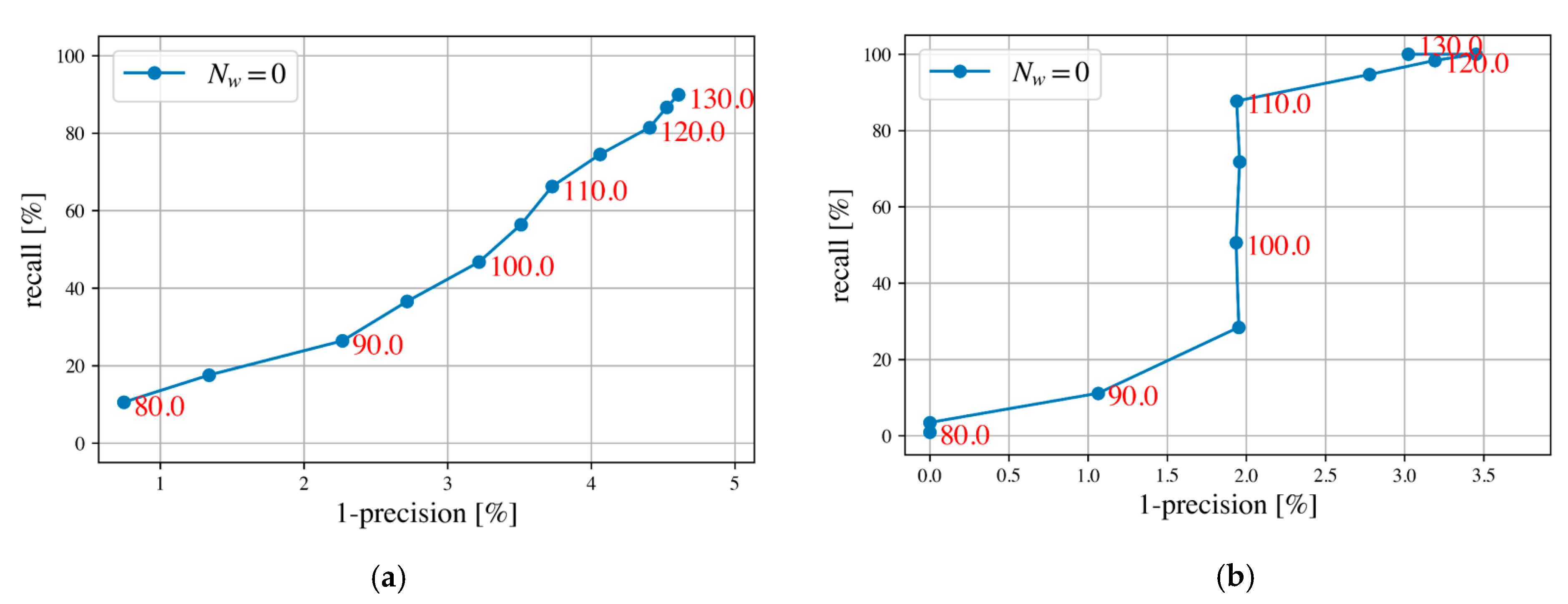
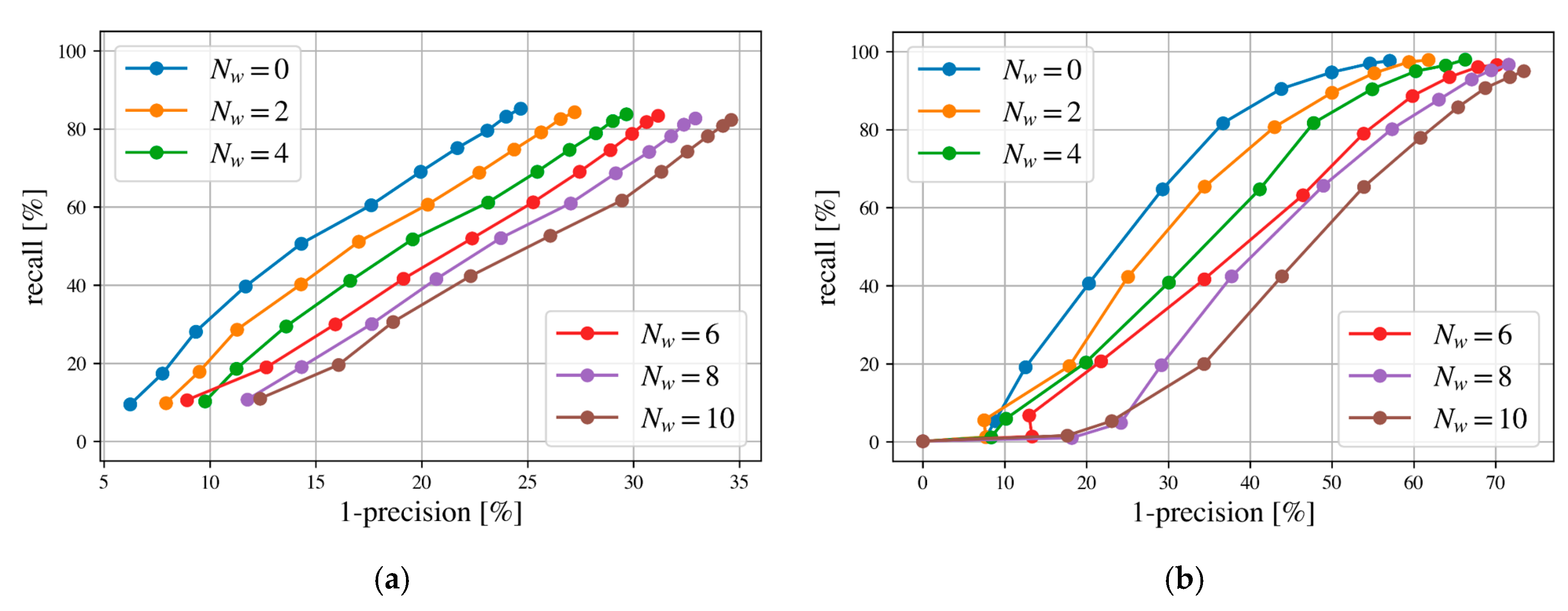
- Precision–Recall Curve
5.1.3. Implementation Environment
5.2. Place Recognition Results
5.2.1. Cylinder Feature Extraction Results
5.2.2. Recognized Results Based on Extracted Features
5.2.3. Overview of Place Recognition
5.3. Pose Refinement Results and Evaluation
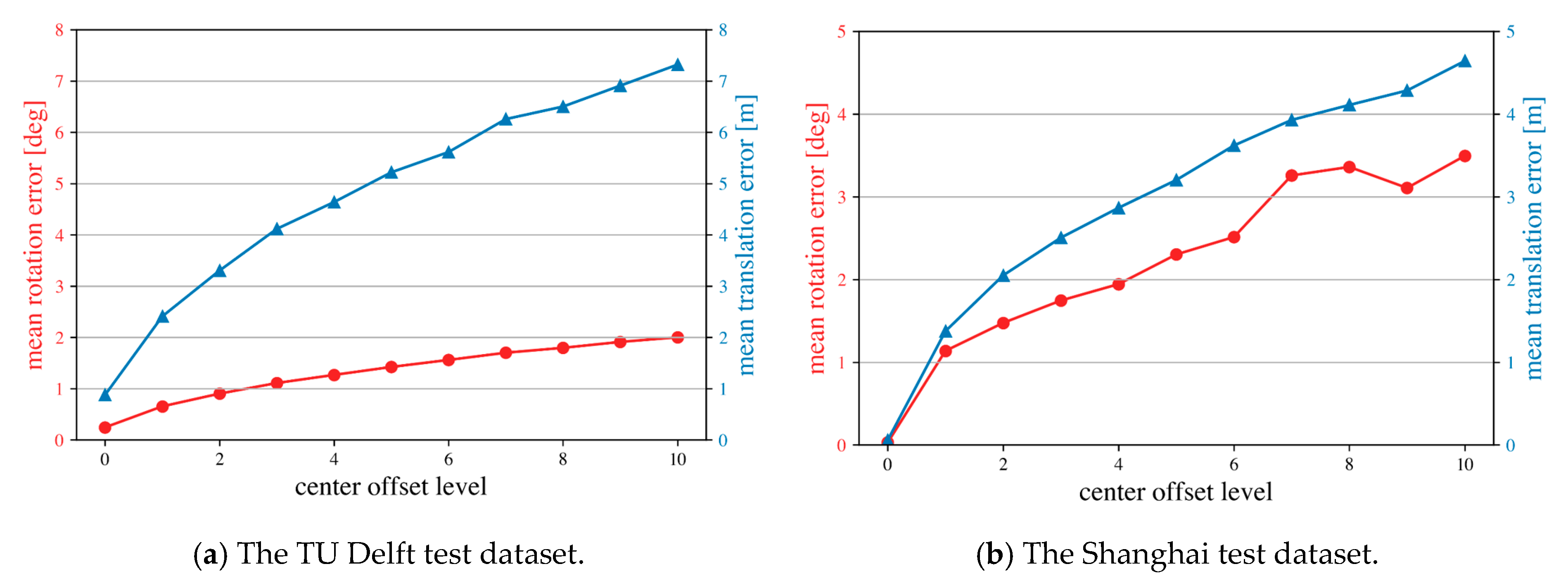
5.3.1. Performance of Thresholds in the Correspondence Search Block
5.3.2. Overview of Pose Refinement Results
6. Discussion and Analysis
6.1. Evaluation of Correspondence Search Block
6.2. Evaluation of Pose Estimation Block and Global Prediction Refinement
6.3. Comparison between the Proposed Method and Traditional Methods
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drawil, N.M.; Amar, H.M.; Basir, O.A. GPS localization accuracy classification: A context-based approach. IEEE Trans. Intell. Transp. Syst. 2012, 14, 262–273. [Google Scholar] [CrossRef]
- Vivacqua, R.; Vassallo, R.; Martins, F. A low cost sensors approach for accurate vehicle localization and autonomous driving application. Sensors 2017, 17, 2359. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Du, S.; Li, G.; Li, H. Integrate Point-Cloud Segmentation with 3D LiDAR Scan-Matching for Mobile Robot Localization and Mapping. Sensors 2020, 20, 237. [Google Scholar] [CrossRef] [PubMed]
- Che, E.; Jung, J.; Olsen, M.J. Object recognition, segmentation, and classification of mobile laser scanning point clouds: A state of the art review. Sensors 2019, 19, 810. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Chin, T.J.; Bustos, A.P.; Schindler, K. Practical optimal registration of terrestrial LiDAR scan pairs. ISPRS J. Photogramm. Remote. Sens. 2019, 147, 118–131. [Google Scholar] [CrossRef]
- Avidar, D.; Malah, D.; Barzohar, M. Local-to-Global Point Cloud Registration Using a Dictionary of Viewpoint Descriptors. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 891–899. [Google Scholar]
- Liang, F.; Yang, B.; Dong, Z.; Huang, R.; Zang, Y.; Pan, Y. A novel skyline context descriptor for rapid localization of terrestrial laser scans to airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2020, 165, 120–132. [Google Scholar] [CrossRef]
- Elbaz, G.; Avraham, T.; Fischer, A. 3D Point Cloud Registration for Localization Using a Deep Neural Network Auto-Encoder. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4631–4640. [Google Scholar]
- Nagy, B.; Benedek, C. Real-Time Point Cloud Alignment for Vehicle Localization in a High Resolution 3D Map. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 1–2. [Google Scholar]
- Angelina Uy, M.; Lee, G.H. Pointnetvlad: Deep Point Cloud Based Retrieval for Large-Scale Place Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4470–4479. [Google Scholar]
- Yin, H.; Tang, L.; Ding, X.; Wang, Y.; Xiong, R. LocNet: Global Localization in 3D Point Clouds for Mobile Vehicles. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 728–733. [Google Scholar]
- Landsiedel, C.; Wollherr, D. Global localization of 3D point clouds in building outline maps of urban outdoor environments. Int. J. Intell. Robot. Appl. 2017, 1, 429–441. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y. Two-step adaptive extraction method for ground points and breaklines from lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Isa, S.M.; Shukor, S.A.; Rahim, N.A.; Maarof, I.; Yahya, Z.R.; Zakaria, A.; Wong, R. Point Cloud Data Segmentation Using RANSAC and Localization. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Perlis, Malaysia, 7–8 November 2019; Volume 705, p. 012004. [Google Scholar]
- Von Hansen, W.; Gross, H.; Thoennessen, U. Line-based registration of terrestrial and airborne LIDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 161–166. [Google Scholar]
- Cheng, L.; Tong, L.; Li, M.; Liu, Y. Semi-automatic registration of airborne and terrestrial laser scanning data using building corner matching with boundaries as reliability check. Remote Sens. 2013, 5, 6260–6283. [Google Scholar] [CrossRef]
- Hauglin, M.; Lien, V.; Næsset, E.; Gobakken, T. Geo-referencing forest field plots by co-registration of terrestrial and airborne laser scanning data. Int. J. Remote Sens. 2014, 35, 3135–3149. [Google Scholar] [CrossRef]
- Yang, B.; Zang, Y.; Dong, Z.; Huang, R. An automated method to register airborne and terrestrial laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 109, 62–76. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, S.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of laser scanning point clouds: A review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Scaioni, M.; Li, H.; Li, N.; Lu, M.; Liu, C. Feature-constrained registration of building point clouds acquired by terrestrial and airborne laser scanners. J. Appl. Remote Sens. 2014, 8, 083587. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep Learning on Point Sets for 3d Classification and Segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & Efficient Point Cloud Registration Using Pointnet. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 7163–7172. [Google Scholar]
- Vinit, S.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. PCRNet: Point Cloud Registration Network Using Pointnet Encoding. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; Volume 2, p. 3. [Google Scholar]
- Lu, W.; Wan, G.; Zhou, Y.; Fu, X.; Yuan, Y.; Song, Y. Deepvcp: An End-to-End Deep Neural Network for Point Cloud Registration. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 12–21. [Google Scholar]
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3DRegNet: A Deep Neural Network for 3D Point Registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–18 June 2020; pp. 7193–7203. [Google Scholar]
- Akiyoshi, K.; Yusuke, S.; Kohta, I.; Hideo, S. Corsnet: 3d Point Cloud Registration by Deep Neural Network. In Proceedings of the IEEE Robotics and Automation Letters, Paris, France, 31 May 2020; Volume 5, pp. 3960–3966. [Google Scholar]
- Qi, C.R.; Li, Y.; Su, H.; Guibas, L.J. Pointnet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chen, Y.; Medioni, G. Object Modeling by Registration of Multiple Range Images. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 2724–2729. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-Icp. Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2009; p. 435. [Google Scholar]
- Dong, J.; Peng, Y.; Ying, S.; Hu, Z. LieTrICP: An improvement of trimmed iterative closest point algorithm. Neurocomputing 2014, 140, 67–76. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point Set Registration: Coherent Point Drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Koguciuk, D. Parallel RANSAC for point cloud registration. Found. Comput. Decis. Sci. 2017, 42, 203–217. [Google Scholar] [CrossRef]
- Aissou, B.; Aissa, A.B. An Adapted Connected Component Labeling for Clustering Non-Planar Objects from Airborne LIDAR Point Cloud. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 191–195. [Google Scholar] [CrossRef]
- Poux, F.; Ponciano, J.J. Self-Learning Ontology for Instance Segmentation of 3d Indoor Point Cloud. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 309–316. [Google Scholar] [CrossRef]
- Koreň, M.; Mokroš, M.; Bucha, T. Accuracy of tree diameter estimation from terrestrial laser scanning by circle-fitting methods. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 122–128. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, X.; Hu, H. Point cloud segmentation for complex microsurfaces based on feature line fitting. Multimed. Tools Appl. 2020, 1, 1–26. [Google Scholar]
- Date, H.; Wakisaka, E.; Moribe, Y.; Kanai, S. TLS point cloud registration based on ICP algorithm using point quality. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 963–968. [Google Scholar] [CrossRef]
- Sorkine-Hornung, O.; Michael, R. Least-squares rigid motion using SVD. Computing 2017, 1, 1–5. [Google Scholar]
- Makovetskii, A.; Voronin, S.; Kober, V.; Tihonkih, D. An efficient point-to-plane registration algorithm for affine transformations. Applications of Digital Image Processing XL. Int. Soc. Opt. Photonics 2017, 10396, 103962J. [Google Scholar]







| Equipment Types | MLS System | TLS Scanner | MLS System |
|---|---|---|---|
| Riegl VQ 250 | Leica Geosystems P40 | Optech Lynx HS300 | |
| Main technical specifications | Max. range: 180 m; Range accuracy: 5 mm; Measurement rate: 300 kHz; Scan frequency: 100 scans/s; Laser wavelength: near infrared; Beam divergence: 0.35 mrad; Field of view: 360°; Camera: Ladybug 3. | Max. range: 270 m; Range accuracy: 1.2 mm; 3D position accuracy: 3 mm/50 m, 6 mm/100 m; Scan frequency: 1 million points/s; Beam divergence: <0.23 mrad; Field of view: 360°. | Max. range: 250 m; Range accuracy: 5 mm; Absolute accuracy: 2 cm; Measurement rate: 150–1600 kHz; Scan frequency: 600 lines/s; Field of view: 360°; Camera: FLIR ladybug. |
| Data Types | Covered Area (km2) | Point num.(Million) | Collection Time | Point Density (pts./m2) | Characteristics | |
|---|---|---|---|---|---|---|
| TU Delft Campus data | MLS | 1.26 | 63.7 | 2016.02 | 593 | Various cylinder objects (e.g., tree and street lamp), has many similar local scenes with repetitive structures |
| TLS | 0.15 | 55.2 | 2020.05 | 782 | ||
| Shanghai urban data | MLS | 3.12 | 212.4 | 2020.07 | 566 | Has lots of moving objects that leads to occlusions, density variations, noise, etc. |
| Simulated TLS | 0.045 | 25.6 | 2020.07 | 566 | ||
| Hyperparameters | TU Delft Campus Dataset | Shanghai Urban Dataset |
|---|---|---|
| Number of batches | 3968 as training set | 2560 as training set |
| 992 as holdout set | 640 as holdout set | |
| 1600 as test set | 1000 as test set | |
| Number of points/batch | 10 (patches) × 256 (points) | 10 (patches) × 256 (points) |
| Patch size w.r.t. (x, y, z) axis | 5 m × 5 m × 3 m | 5 m × 5 m × 3 m |
| Rotation range w.r.t. (x, y, z) axis | ||
| translation range w.r.t. (x, y, z) axis |
| TU Delft Dataset | Num. of Extracted Façade Lines | Num. of Extracted Cylinders | Façade Line Extraction Time (s) | Cylinder Extraction Time (s) | Correct Extraction Ratio of Cylinders (%) | |
|---|---|---|---|---|---|---|
| MLS | Scene1 | 2 | 298 | 9.5 | 25.9 | 81.6 |
| Scene2 | 86 | 522 | 35.8 | 41.5 | 78.9 | |
| Scene3 | 137 | 641 | 47.0 | 53.1 | 93.5 | |
| Scene4 | 100 | 498 | 41.0 | 40.0 | 89.5 | |
| Scene5 | 35 | 467 | 27.4 | 45.3 | 84.0 | |
| TLS | Scan1 | 26 | 191 | 6.3 | 12.4 | 85.6 |
| Scan2 | 115 | 159 | 8.5 | 11.6 | 81.0 | |
| Scan3 | 49 | 235 | 6.4 | 11.0 | 95.8 | |
| Scan4 | 110 | 168 | 7.7 | 12.2 | 92.5 | |
| MLS1 | MLS2 | MLS3 | MLS4 | MLS5 | |
|---|---|---|---|---|---|
| TLS1 | (0.45 a,16.2 a) | (0.60 b,10.6 a) | (0.60 b,10.1 a) | (0.51 a,18.6 a) | (0.56 a,11.3 a) |
| TLS2 | (0.62,10.5 a) | (0.63,8.8) | (0.73 c,7.5) | (0.63,11.6 a) | (0.63,8.5) |
| TLS3 | (0.69,7.2) | (0.72,6.7) | (0.77,5.9) | (0.83 b,5.5) | (0.82 b,5.3) |
| TLS4 | (0.63,8.9) | (0.68,7.7) | (0.69,7.6) | (0.64,8.9) | (0.79 c,6.1) |
| (a) Initialization: outlier removal | |||||
| Decision | MLS1 | MLS2 | MLS3 | MLS4 | MLS5 |
| TLS1 | 0 | 0 | 0 | 0 | 0 |
| TLS2 | 0 | 0 | 1 | 0 | 0 |
| TLS3 | X | X | 0 | X | X |
| TLS4 | X | X | 0 | X | X |
| (b) 1st decision-making result | |||||
| Decision | MLS1 | MLS2 | MLS3 | MLS4 | MLS5 |
| TLS1 | 0 | 0 | 0 | 0 | 0 |
| TLS2 | 0 | X | X | 0 | X |
| TLS3 | X | X | X | X | X |
| TLS4 | X | X | X | X | X |
| (c) 2nd decision-making result | |||||
| Decision | MLS1 | MLS2 | MLS3 | MLS4 | MLS5 |
| TLS1 | 0 | 1 | 0 | 0 | 0 |
| TLS2 | 0 | 0 | 1 | 0 | 0 |
| TLS3 | 0 | 0 | 0 | 1 | 0 |
| TLS4 | 0 | 0 | 0 | 0 | 1 |
| (d) 3rd decision-making result | |||||
| Decision | MLS1 | MLS2 | MLS3 | MLS4 | MLS5 |
| TLS1 | 0 | 0 | 0 | 0 | 0 |
| TLS2 | 0 | 0 | 1 | 0 | 0 |
| TLS3 | 0 | 0 | 0 | 1 | 0 |
| TLS4 | 0 | 0 | 0 | 0 | 1 |
| Classical Methods | Parameter Setting |
|---|---|
| ICP_P2Po and ICP_P2Pl | Down-sampling voxel size: 1.0 m |
| source batch size: ∼35,000 points | |
| target batch size: ∼65,000 points | |
| maximum correspondence points-pair distance: 5.0 m | |
| maximum number of iterations: 20,000 | |
| number of neighbors for normal computation: 30 | |
| relative root mean square error (RMSE): 1.0 × 10−6 | |
| FPFH + RANSAC | number of neighbors for FPFH feature extraction: 30 |
| number of correspondences to fit RANSAC: 4 | |
| CPD registration method | source batch size: 2560 points |
| target batch size: 2560 points | |
| relative difference ∆ of the objective function: 0.1 | |
| maximum number of iterations: 20 |
| Methods | Mean Rotation Error (deg) | Mean Translation Error (m) | Max Rotation Error (deg) | Max Translation Error (m) | Run Time on 8 Million pts/s |
|---|---|---|---|---|---|
| ICP_P2Po | 0.40 | 1.94 | 0.40 | 1.95 | 380.16 |
| ICP_P2Pl | 0.34 | 1.76 | 0.35 | 1.76 | 179.27 |
| FPFH+RANSAC | / | / | / | / | 922.76 |
| CPD | 0.27 | 0.95 | 1.09 | 5.02 | >1000 |
| Predicted Network A | 8.16 | 9.40 | 8.81 | 36.02 | 26.00 |
| Predicted Network B | 6.66 | 13.66 | 7.43 | 24.94 | 26.33 |
| Corrected Network A | 0.25 | 0.88 | 1.26 | 4.07 | 36.97 |
| Corrected Network B | 0.24 | 0.88 | 1.26 | 4.06 | 35.98 |
| Methods | Mean Rotation Error (deg) | Mean Translation Error (m) | Max Rotation Error (deg) | Max Translation Error (m) | Run Time on 8 Million pts/s |
|---|---|---|---|---|---|
| ICP_P2Po | / | / | / | / | >1000 |
| ICP_P2Pl | / | / | / | / | >1000 |
| CPD | / | / | / | / | >1000 |
| Predicted Network A | 16.15 | 21.23 | 65.98 | 94.97 | 17.26 |
| Predicted Network B | 23.85 | 22.35 | 66.12 | 41.11 | 16.97 |
| Corrected Network A | 0.03 | 0.06 | 0.14 | 0.34 | 23.42 |
| Corrected Network B | 0.03 | 0.07 | 0.18 | 0.36 | 23.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, Y.; Meng, F.; Lindenbergh, R.; Truong-Hong, L.; Li, B. Deep Localization of Static Scans in Mobile Mapping Point Clouds. Remote Sens. 2021, 13, 219. https://doi.org/10.3390/rs13020219
Zang Y, Meng F, Lindenbergh R, Truong-Hong L, Li B. Deep Localization of Static Scans in Mobile Mapping Point Clouds. Remote Sensing. 2021; 13(2):219. https://doi.org/10.3390/rs13020219
Chicago/Turabian StyleZang, Yufu, Fancong Meng, Roderik Lindenbergh, Linh Truong-Hong, and Bijun Li. 2021. "Deep Localization of Static Scans in Mobile Mapping Point Clouds" Remote Sensing 13, no. 2: 219. https://doi.org/10.3390/rs13020219
APA StyleZang, Y., Meng, F., Lindenbergh, R., Truong-Hong, L., & Li, B. (2021). Deep Localization of Static Scans in Mobile Mapping Point Clouds. Remote Sensing, 13(2), 219. https://doi.org/10.3390/rs13020219







