A New Combined Adjustment Model for Geolocation Accuracy Improvement of Multiple Sources Optical and SAR Imagery
Abstract
1. Introduction
2. Basic Principle of the RFM
3. Methodology
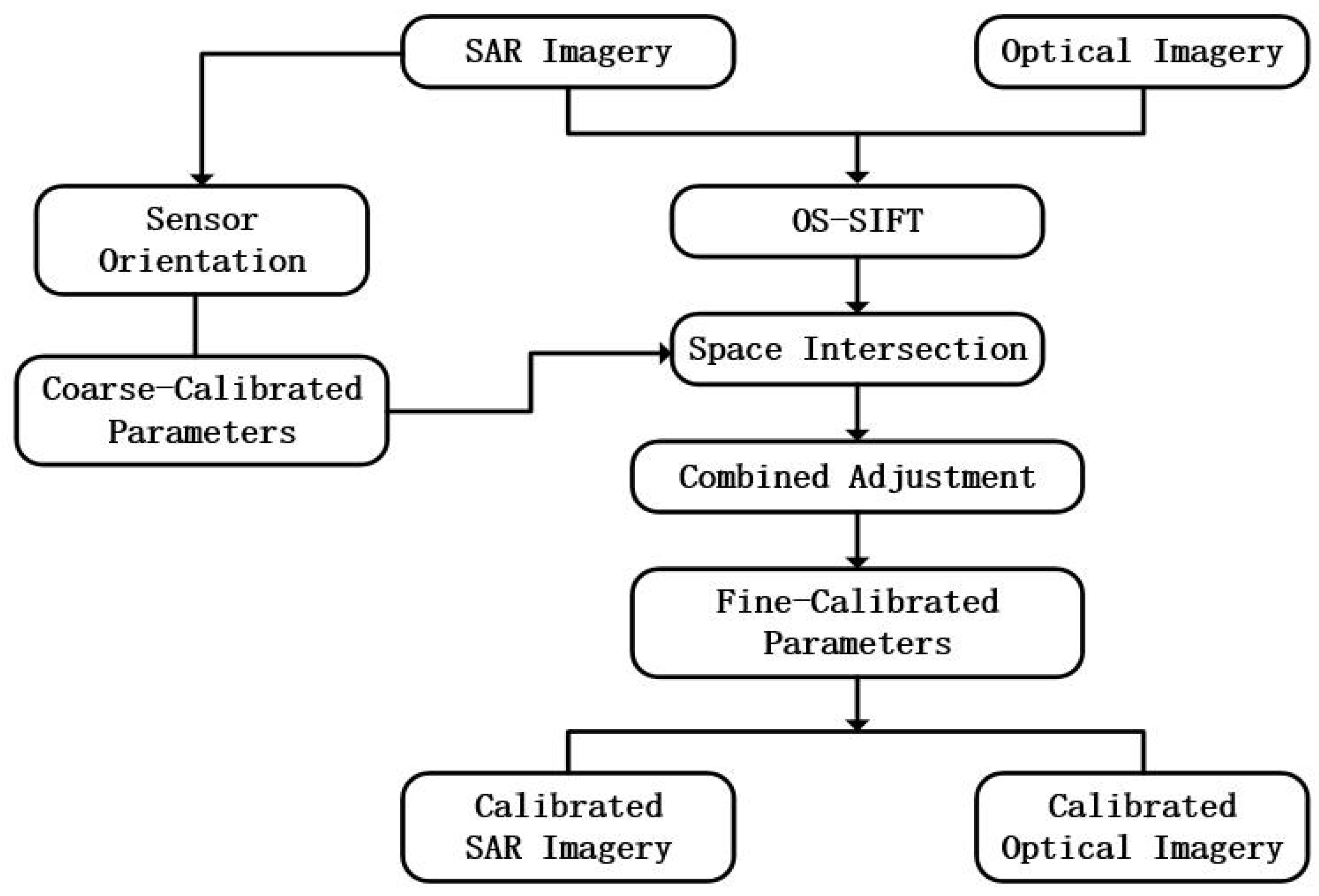
3.1. Overview
3.2. Sensor Orientation of SAR Imagery
3.3. Combined Adjustment Model
3.3.1. Unification of Coordinate System
3.3.2. Combined Normal Equations
3.3.3. Heterogeneous Weight Strategy
4. Experimental Results and Analysis
4.1. Experimental Dataset
4.2. Performance of the Combined Adjustment
5. Discussions and Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Rupnik, E.; Pierrot-deseilligny, M.; Delorme, A. 3D reconstruction from multi-view VHR-satellite images in MicMac. ISPRS J. Photogramm. Remote Sens. 2018, 139, 201–211. [Google Scholar] [CrossRef]
- Hégarat-Mascle, S.L.; Ottlé, C.; Guérin, C. Land cover change detection at coarse spatial scales based on iterative estimation and previous state information. Remote Sens. Environ. 2018, 95, 464–479. [Google Scholar] [CrossRef]
- Tokarczyk, P.; Wegner, J.D.; Walk, S.; Schindler, K. Features, Color Spaces, and Boosting: New Insights on Semantic Classification of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 280–295. [Google Scholar] [CrossRef]
- Luo, L.; Wang, X.; Guo, H.; Lasaponara, R.; Zong, X.; Masini, N.; Wang, G.; Shi, P.; Khatteli, H.; Chen, F.; et al. Airborne and spaceborne remote sensing for archaeological and cultural heritage applications: A review of the century (1907–2017). Remote Sens. Environ. 2019, 232, 111280. [Google Scholar] [CrossRef]
- Zhihua, X.; Lixin, W.; Yonglin, S.; Fashuai, L.; Qiuling, W. Tridimensional Reconstruction Applied to Cultural Heritage with the Use of Camera-Equipped UAV and Terrestrial Laser Scanner. Remote Sens. 2014, 6, 10413–10434. [Google Scholar]
- Meyer, D.; Fraijo, E.; Lo, E.; Rissolo, D.; Kuester, F. Optimizing UAV systems for rapid survey and reconstruction of large scale cultural heritage sites. Digit. Herit. 2015. Available online: https://ieeexplore.ieee.org/document/7413857 (accessed on 28 January 2021).
- Hadjimitsis, D.G.; Themistocleous, K.; Michaelides, S.; Papadavid, G.; Themistocleous, K.; Ioannides, M.; Agapiou, A.; Hadjimitsis, D.G. The methodology of documenting cultural heritage sites using photogrammetry, UAV, and 3D printing techniques: The case study of Asinou Church in Cyprus. In Proceedings of the SPIE—Third International Conference on Remote Sensing and Geoinformation of the Environment, Paphos, Cyprus, 16 March 2015. [Google Scholar]
- Erenoglua, R.C.; Akcaya, O.; Erenoglub, O. An UAS-assisted multi-sensor approach for 3D modeling and reconstruction of cultural heritage site. Remote Sens. Environ. 2017, 26, 79–90. [Google Scholar] [CrossRef]
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the 2013 International Conference on 3DV-Conference, Seattle, WA, USA, 29 June–1 July 2013. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef]
- Cheng, C.; Zheng, S.; Liu, X.; Han, J. Space-Borne SAR Image Geo-Location in Mountain Area with Sparse GCP. In Proceedings of the International Symposium on Image and Data Fusion, Tengchong, China, 9–11 August 2011; pp. 1–4. [Google Scholar]
- Zhang, W.S.; Wang, Y.M.; Wang, C.; Jin, S.L.; Zhang, H. Precision Comparison of Several Algorithms for Precise Rectification of Linear Array Push-Broom Middle or High Resolution Imagery on the Plainness and Small Areas. OPT Tech. 2006. Available online: https://www.researchgate.net/publication/291743025_Precision_comparison_of_several_algorithms_for_precise_rectification_of_linear_array_push-broom_middle_or_high_resolution_imagery_on_the_plainness_and_small_areas (accessed on 28 January 2021).
- Cao, J.; Fu, J.; Yuan, X.; Gong, J. Nonlinear bias compensation of ZiYuan-3 satellite imagery with cubic splines. ISPRS J. Photogramm. Remote Sens. 2017, 133, 174–185. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Cen, M.; Guo, H.; Zhang, T.; Zhao, C. SRTM DEM-Aided Mapping Satellite-1 Image Geopositioning without Ground Control Points. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2137–2141. [Google Scholar] [CrossRef]
- Hong, Z.; Tong, X.; Liu, S.; Chen, P.; Xie, H.; Jin, Y. A Comparison of the Performance of Bias-Corrected RSMs and RFMs for the Geo-Positioning of High-Resolution Satellite Stereo Imagery. Remote Sens. 2015, 7, 16815–16830. [Google Scholar] [CrossRef]
- Shen, X.; Liu, B.; Li, Q.Q. Correcting bias in the rational polynomial coefficients of satellite imagery using thin-plate smoothing splines. ISPRS J. Photogramm. Remote Sens. 2017, 125. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, G.; Li, D.; Tang, X.; Jiang, Y.; Pan, H.; Zhu, X. Planar Block Adjustment and Orthorectification of ZY-3 Satellite Images. Photogramm. Eng. Remote Sens. 2014, 80, 559–570. [Google Scholar] [CrossRef]
- Teo, T.A.; Chen, L.C.; Liu, C.L.; Tung, Y.C.; Wu, W.Y. DEM-Aided Block Adjustment for Satellite Images With Weak Convergence Geometry. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1907–1918. [Google Scholar]
- Choi, S.Y.; Kang, J.M. Accuracy Investigation of RPC-based Block Adjustment Using High Resolution Satellite Images GeoEye-1 and WorldView-2. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2012, 30, 107–116. [Google Scholar] [CrossRef][Green Version]
- Ding, C.; Liu, J.; Lei, B.; Qiu, X. Preliminary Exploration of Systematic Geolocation Accuracy of GF-3 SAR Satellite System. J. Radars 2017, 6, 11–16. [Google Scholar]
- Schwerdt, M.; Bräutigam, B.; Bachmann, M.; Döring, B.; Schrank, D.; Gonzalez, J.H. Final TerraSAR-X Calibration Results Based on Novel Efficient Methods. IEEE Trans. Geosci. Remote Sens. 2010, 48, 677–689. [Google Scholar] [CrossRef]
- Shimada, M.; Isoguchi, O.; Tadono, T.; Isono, K. PALSAR Radiometric and Geometric Calibration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3915–3932. [Google Scholar] [CrossRef]
- Covello, F.; Battazza, F.; Coletta, A.; Lopinto, E.; Fiorentino, C.; Pietranera, L.; Valentini, G.; Zoffoli, S. COSMO-SkyMed an existing opportunity for observing the Earth. J. Geodyn. 2010, 49, 171–180. [Google Scholar] [CrossRef]
- Jiao, N.; Wang, F.; You, H.; Qiu, X.; Yang, M. Geo-Positioning Accuracy Improvement of Multi-Mode GF-3 Satellite SAR Imagery Based on Error Sources Analysis. Sensors 2018, 18, 2333. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Wang, T.; Zhao, R.; Deng, M.; Jiang, B.; Li, X.; Wang, H.; Zhu, Y.; Li, F.; et al. Block Adjustment without GCPs for Chinese Spaceborne SAR GF-3 Imagery. Sensors 2018, 18, 4023. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.; Zhang, G.; Zhao, R.; Li, S.; Li, J. Improvement of gaofen-3 absolute positioning accuracy based on cross-calibration. Sensors 2017, 17, 2903. [Google Scholar] [CrossRef]
- Niangang, J.; Feng, W.; Hongjian, Y.; Xiaolan, Q. Geolocation Accuracy Improvement of Multiobserved GF-3 Spaceborne SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1–5. [Google Scholar]
- Wang, M.; Wang, Y.; Run, Y.; Cheng, Y.; Jin, S. Geometric accuracy analysis for GaoFen3 stereo pair orientation. IEEE Geosci. Remote Sens. Lett. 2018, 15, 92–96. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, G. Multi-Mode GF-3 Satellite Image Geometric Accuracy Verification Using the RPC Model. Sensors 2017, 17, 2005. [Google Scholar] [CrossRef]
- Tao, C.V.; Hu, Y. 3D reconstruction methods based on the rational function model. Photogramm. Eng. Remote Sens. 2002, 68, 705–714. [Google Scholar]
- Jiang, W.; Yu, A.; Dong, Z.; Wang, Q. Comparison and Analysis of Geometric Correction Models of Spaceborne SAR. Sensors 2016, 16, 973. [Google Scholar] [CrossRef]
- Cheng, C.; Zheng, S.; Liu, X.; Han, J. Geometric Rectification of Small Satellite Remote Sensing Images. In Proceedings of the 2010 International Conference on Remote Sensing (ICRS), Hangzhou, China, 5 October 2010; pp. 324–327. [Google Scholar]
- Schulz, S.; Renner, U. DLR-TUBSAT: A microsatellite for interactive earthobservation. In Proceedings of the Small Satellite Systems and Services, Hong Kong, China, 9–14 June 2000. [Google Scholar]
- Xiong, W.; Shen, W.; Wang, Q.; Shi, Y.; Xiao, R.; Fu, Z. Research on HJ-1A/B satellite data automatic geometric precision correction design. Eng. Sci. 2014, 5, 90–96. [Google Scholar] [CrossRef]
- Wu, B.; Tang, S.; Zhu, Q.; Yuen Tong, K.; Hu, H.; Li, G. Geometric integration of high-resolution satellite imagery and airborne LiDAR data for improved geopositioning accuracy in metropolitan areas. ISPRS J. Photogramm. Remote Sens. 2015, 109, 139–151. [Google Scholar]
- Bagheri, H.; Schmitt, M.; Angelo, P.; Zhu, X.X. A framework for SAR-optical stereogrammetry over urban areas. ISPRS J. Photogramm. Remote Sens. 2018, 146, 389–408. [Google Scholar]
- Tang, S.; Wu, B.; Zhu, Q. Combined adjustment of multi-resolution satellite imagery for improved geo-positioning accuracy. ISPRS J. Photogramm. Remote Sens. 2016, 114, 125–136. [Google Scholar] [CrossRef]
- Niangang, J.; Feng, W.; Hongjian, Y.; Jiayin, L.; Xiaolan, Q. A generic framework for improving the geopositioning accuracy of multi-source optical and SAR imagery. ISPRS J. Photogramm. Remote Sens. 2020, 169, 377–388. [Google Scholar]
- Jeong, J.; Yang, C.; Kim, T. Geo-positioning accuracy using multiple-satellite images: IKONOS, QuickBird, and KOMPSAT-2 stereo images. Remote Sens. 2015, 7, 4449–4564. [Google Scholar] [CrossRef]
- Ma, Z.; Gong, Y.; Cui, C.; Deng, J.; Cao, B. Geometric positioning of multi-source optical satellite imagery for the island and reef area with sparse ground control points. In Proceedings of the Oceans 2017, Aberdeen, UK, 9 June 2017. [Google Scholar]
- Pi, Y.; Yang, B.; Li, X.; Wang, M.; Cheng, Y. Large-Scale Planar Block Adjustment of GaoFen1 WFV Images Covering Most of Mainland China. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1368–1379. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; You, H. OS-SIFT: A Robust SIFT-Like Algorithm for High-Resolution Optical-to-SAR Image Registration in Suburban Areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Guo, J.-W.; Li, Y.-S. Study on the precision of block adjustment based on UAV imagery data. In Proceedings of the 2017 2nd International Conference on Frontiers of Sensors Technologies, Shenzhen, China, 16 April 2017. [Google Scholar]
- Qiu, X.; Han, C.; Liu, J.; Radars, J. A Method for Spaceborne SAR Geolocation Based on Continuously Moving Geometry. J. Radars 2013, 2, 54–59. [Google Scholar] [CrossRef]
- Tao, C.V.; Hu, Y. Use of the Rational Function Model for Image Rectification. Can. J. Remote Sens. 2001, 27, 593–602. [Google Scholar] [CrossRef]
- Zhang, G.; Fei, W.; Li, Z.; Zhu, X.; Tang, X. Analysis and test of the substitutability of the RPC model for the rigorous sensor model of spaceborne SAR imagery. Acta Geod. Cartogr. Sin. 2010, 39, 264–270. [Google Scholar]




| Platform | Acquisition Date | Orbit | Incidence Angle () | Size (Pixels) | Resolution (m) |
|---|---|---|---|---|---|
| JL-104-1 | 2 April 2018 | DEC | 8.73 | 11,516 × 12,143 | 0.93 × 0.94 |
| JL-104-2 | 23 June 2018 | DEC | 4.33 | 11,506 × 12,148 | 0.92 × 0.92 |
| JL-104-3 | 29 October 2018 | DEC | 0.84 | 11,518 × 12,120 | 0.92 × 0.92 |
| JL-105-1 | 15 June 2018 | DEC | −0.52 | 11,518 × 12,056 | 0.92 × 0.92 |
| JL-105-2 | 10 October 2018 | DEC | 5.19 | 11,518 × 12,008 | 0.92 × 0.94 |
| JL-106-1 | 7 June 2018 | DEC | 1.38 | 11,530 × 12,007 | 0.92 × 0.92 |
| JL-107-1 | 31 March 2018 | DEC | 1.97 | 11,513 × 11,991 | 0.92 × 0.92 |
| GF3-1 | 28 December 2016 | DEC | 37.43 | 16,215 × 21,531 | 2.24 × 2.86 |
| GF3-2 | 14 November 2019 | DEC | 24.68 | 21,625 × 23,354 | 1.12 × 2.61 |
| GF3-3 | 20 December 2019 | ASC | 41.43 | 18,124 × 20,316 | 2.24 × 3.03 |
| Images | Before Calibration | After Calibration | ||
|---|---|---|---|---|
| X | Y | X | Y | |
| GF3-1 | 11.11 | 8.09 | 1.56 | 8.09 |
| GF3-2 | 10.96 | 7.84 | 1.73 | 7.84 |
| GF3-3 | 12.37 | 8.21 | 1.61 | 8.21 |
| Items | Before Adjustment | After Adjustment | After Weighted Adjustment | |||
|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | |
| RFM | 146.36 | 111.75 | 61.97 | 72.23 | 2.97 | 4.78 |
| Proposed | 146.36 | 111.75 | 59.43 | 71.89 | 2.65 | 4.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, N.; Wang, F.; You, H. A New Combined Adjustment Model for Geolocation Accuracy Improvement of Multiple Sources Optical and SAR Imagery. Remote Sens. 2021, 13, 491. https://doi.org/10.3390/rs13030491
Jiao N, Wang F, You H. A New Combined Adjustment Model for Geolocation Accuracy Improvement of Multiple Sources Optical and SAR Imagery. Remote Sensing. 2021; 13(3):491. https://doi.org/10.3390/rs13030491
Chicago/Turabian StyleJiao, Niangang, Feng Wang, and Hongjian You. 2021. "A New Combined Adjustment Model for Geolocation Accuracy Improvement of Multiple Sources Optical and SAR Imagery" Remote Sensing 13, no. 3: 491. https://doi.org/10.3390/rs13030491
APA StyleJiao, N., Wang, F., & You, H. (2021). A New Combined Adjustment Model for Geolocation Accuracy Improvement of Multiple Sources Optical and SAR Imagery. Remote Sensing, 13(3), 491. https://doi.org/10.3390/rs13030491








