Next Article in Journal
Subpixel Change Detection Based on Radial Basis Function with Abundance Image Difference Measure for Remote Sensing Images
Next Article in Special Issue
Multi-Epoch and Multi-Imagery (MEMI) Photogrammetric Workflow for Enhanced Change Detection Using Time-Lapse Cameras
Previous Article in Journal
Evaluation and Hydrological Utility of the GPM IMERG Precipitation Products over the Xinfengjiang River Reservoir Basin, China
Previous Article in Special Issue
A New Combined Adjustment Model for Geolocation Accuracy Improvement of Multiple Sources Optical and SAR Imagery
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 5
10.3390/rs13050867
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Improved Real-Time Natural Hazard Monitoring Using Automated DInSAR Time Series

by
Krisztina Kelevitz
1,*,
Kristy F. Tiampo
2 and
Brianna D. Corsa
2
1
School of Earth and Environment, University of Leeds, COMET, Leeds LS2 9JT, UK
2
Cooperative Institute for Research in Environmental Sciences, University of Colorado, CIRES, Boulder, CO 80309, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(5), 867; https://doi.org/10.3390/rs13050867
Submission received: 30 December 2020 / Revised: 11 February 2021 / Accepted: 19 February 2021 / Published: 25 February 2021
(This article belongs to the Special Issue Advances in Photogrammetry and Remote Sensing: Data Processing and Innovative Applications)
Browse Figures
Versions Notes

Abstract

:
As part of the collaborative GeoSciFramework project, we are establising a monitoring system for the Yellowstone volcanic area that integrates multiple geodetic and seismic data sets into an advanced cyber-infrastructure framework that will enable real-time streaming data analytics and machine learning and allow us to better characterize associated long- and short-term hazards. The goal is to continuously ingest both remote sensing (GNSS, DInSAR) and ground-based (seismic, thermal and gas observations, strainmeter, tiltmeter and gravity measurements) data and query and analyse them in near-real time. In this study, we focus on DInSAR data processing and the effects from using various atmospheric corrections and real-time orbits on the automated processing and results. We find that the atmospheric correction provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) is currently the most optimal for automated DInSAR processing and that the use of real-time orbits is sufficient for the early-warning application in question. We show analysis of atmospheric corrections and using real-time orbits in a test case over the Kilauea volcanic area in Hawaii. Finally, using these findings, we present results of displacement time series in the Yellowstone area between May 2018 and October 2019, which are in good agreement with GNSS data where available. These results will contribute to a baseline model that will be the basis of a future early-warning system that will be continuously updated with new DInSAR data acquisitions.

1. Introduction

Natural catastrophes occur at a variety of spatial and temporal scales. In particular, solid earth hazards, such as large earthquakes and volcanic eruptions, often have very long inter-event times and this makes it difficult to forecast their behavior. Today, we monitor a significant number of active volcanoes around the world, collecting geodetic data in the form of GNSS and SAR data, in conjunction with ground-based measurements from strainmeters, tiltmeters and gravity instruments with the goal of providing early warning and reducing risk and losses. In addition, in many areas, we also collect seismic data, thermal measurements and/or perform sampling of local gas emissions. While the term “big data” is widely used today, it is not simply about volume, but also about the variability in data types, the latency with which data is generated and transmitted, and the veracity, or accuracy of the models that ingest data [1]. Natural volcano observatories that collect large volumes of variable data over long time periods provide a unique opportunity to develop a framework that integrates modern data sources and advanced computational algorithms. This is essential to both early detection of volcanic activity and forecasting eruptions on intermediate- and short-term time scales.
Modern forecasting tools for volcanic eruptions primarily rely on some combination of probabilistic studies of geologic records of activity and eruption and comprehensive monitoring networks that incorporate seismic, geodetic, thermal and gas measurements into modern computational tools [2,3,4,5,6,7,8,9]. In particular, recent developments in differential interferometric synthetic aperture radar (DInSAR) and Global Navigation Satellite System (GNSS) geodes have promoted significant advances in monitoring of volcanic hazards, providing high-resolution ground deformation data with dense spatiotemporal coverage. DInSAR can be used to map ground deformation with high spatial resolution and sub-centimeter precision over large areas, and is a suitable tool for ground deformation monitoring of active volcanic regions [10,11,12,13,14,15]. The unprecedented volumes of SAR data provided by modern satellites such as Sentinel-1A/B from the European Space Agency (ESA), ALOS-2 from the Japan Aerospace Exploration Agency (JAXA) and the upcoming NISAR (NASA-ISRO Synthetic Aperture Radar) mission from the US National Aeronautics and Space Administration (NASA) and the Indian Space Research Organization present both an important opportunity and a significant challenge for observation of the large number of active volcanoes around the world that are not currently monitored by volcano observatories [6,8]
A number of research groups around the world are developing high-performance computing and cloud-based methods for rapid processing of both SAR and DInSAR images. These include, among others, the Advanced Rapid Imaging and Analysis (ARIA) project [16,17,18], the Alaskan Satellite Facility (ASF) [19,20,21], the Centre for the Observation and Modelling of Earthquakes, Volcanoes and Tectonics (COMET) [22,23] and the UNAVCO GeoSciFramework project [24]. The natural extension of these efforts focuses on the longer-term monitoring of specific regions, such as the national ground motion service for Norway (Annual Report, Geological Survey of Norway, https://www.ngu.no/en/topic/insar-norway accessed on 23 February 2021), and specific phenomena, including volcanic activity in South America [25].
Acquisition and processing of satellite SAR data and GNSS data (sampling over time frames of days-to-years) can be used to study strain accumulation in Earth’s crust, allowing us to model and invert for the underlying physical cause of that strain, including changes in magma composition, storage and movement. Recent developments in remote sensing make it feasible to continuously monitor and predict natural hazards. In particular, with the Sentinel missions of the European Space Agency (ESA), remote sensing data is becoming freely available to researchers everywhere [26]. The Sentinel-1 missions are providing SAR measurements for the entire globe with an unprecedented repeatability of 12 days. When combining Sentinel 1A and Sentinel 1B acquisitions, the repeatability becomes 6 days. These repeatedly acquired SAR data from a single sensor can be used to obtain the Line-of-Sight (LOS) time series of ground deformation using DInSAR methods [14,27,28,29,30].
As part of the GeoSciFramework project [31] (https://www.unavco.org/projects/major-projects/earthcube/geosciframework/geosciframework.html accessed on 23 February 2021), we are focusing on modeling and monitoring ground motion in the Yellowstone volcanic area. The ultimate goal of the project is to continuously monitor this area using newly acquired DInSAR and GNSS data and, in conjunction with thermal and gas observations and strainmeter, tiltmeter and gravity measurements, integrate that data into machine learning approaches to identify precursory patterns and inform eruption forecasts. Here, we process DInSAR images for Yellowstone into time series, then include them in the time series stream integrated with GNSS data; this provides 3D surface motions, improves the accuracy of the SAR-derived time series and derives high-resolution time series maps, complete with the corresponding horizontal and vertical errors [32].
In this paper, we discuss details of the DInSAR data processing for this project with specific focus on the effect of using real time orbits and standard atmospheric corrections in the automated processing. When monitoring a region of potential natural hazard such as a volcano, it is necessary to use real-time orbits when processing DInSAR data, as these orbits are available weeks earlier than the precise orbits. Therefore, it is important to understand the potential limitations and accuracy of DInSAR data processed with these orbits. DInSAR data can be noisy due to atmospheric effects and it is essential that we apply atmospheric corrections during the processing. In this paper, we explore the use of atmospheric corrections from two providers: European Centre for Medium-Range Weather Forecasts (ECMWF), a correction that is widely used [33], and the Generic Atmospheric Correction Online Service (GACOS), which integrates ECMWF and continuous GNSS tropospheric delay estimates [34]. While GACOS might become the state-of-the-art atmospheric correction in the coming years, it is not yet implemented for automated processing, and for the near-real time application that we discuss in this paper, it could be more beneficial to use the ECMWF correction that can be applied automatically during the processing flow.
Because the Yellowstone region is challenging for DInSAR data processing due to its dense vegetation and regular snow coverage, we tested the accuracy of DInSAR data with different orbits over the Big Island of Hawaii. Hawaii is a simpler case for DInSAR data processing, is well-instrumented over the entire island, and there are other studies available for comparison with our results. We apply these results to an initial study of Yellowstone caldera [35].

2. Materials and Methods

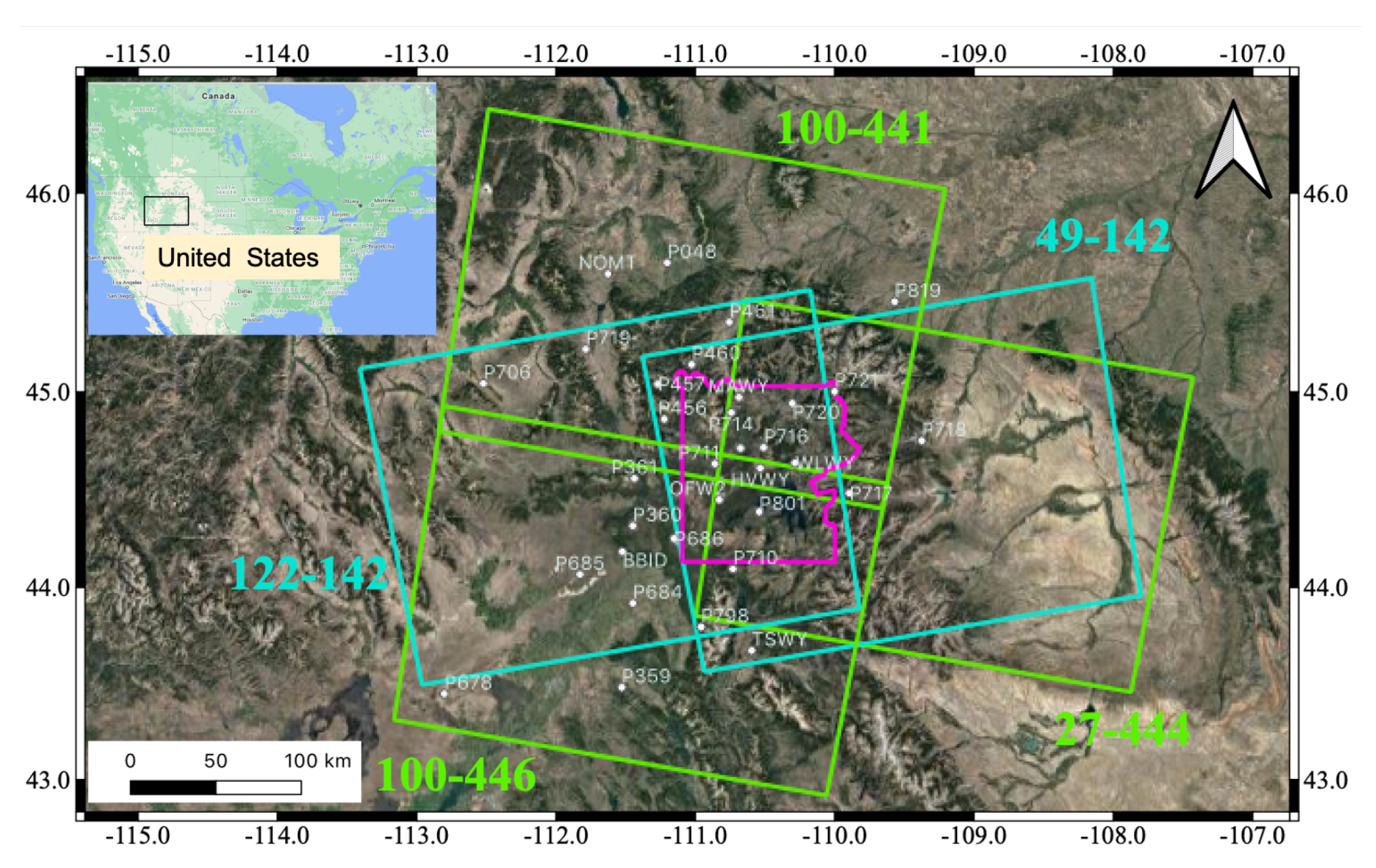
2.1. The Yellowstone and Hawaiian Volcanic Areas

The Yellowstone caldera is a long-lived, silicic volcanic system located on the eastern edge of the Basin and Range province. Fed by a deep-seated mantle plume that is responsible for its long-term activity, there have been three caldera-forming eruptions, at 2.0, 1.3 and 0.64 Ma BP, at this intraplate hotspot. That most recent eruption released almost 1000 km 3 of material and collapsed into a 45 by 70 km caldera [36,37,38,39]. Considered one of the most potentially dangerous volcanoes in the world [40], the caldera is characterized by very high heat flow, widespread seismicity, extensive hydrothermal activity, and ongoing episodes of surface uplift and subsidence [38]. For example, since 2004, there have been two episodes of surface deformation with uplift rates of as much as 7 cm/year. Modeling of that deformation identified an expanding sill at 7–10 km in depth [41].
Spatial and temporal variations of Yellowstone ground movement are correlated with changes in seismic and hydrothermal activity in and around the caldera [38,41,42,43]. Because of the dynamic nature of the caldera and the significant volcanic and seismic hazard, there is a substantial monitoring effort at Yellowstone, including continuous GNSS, borehole strain, and seismic networks. Figure 1 shows the Sentinel-1 frames that cover the Yellowstone area.
The island of Hawaii is formed by five volcanoes, among them the youngest and most active is the Kilauea volcano. An active shield volcano that was created as the Pacific plate moved over the Hawaiian hotspot [44], Kilauea was formed at least 300,000 years ago, reaching above sea-level about 100,000 years ago [45]. The volcano has been continuously active in modern history, producing a stream of explosive and effusive eruptions [46].
The island and Kilauea volcano has been extensively studied and is continuously monitored by the USGS Hawaiian Volcano Observatory. The monitoring networks consist of more than 100 field stations with instruments that record and measure earthquakes, ground movement, volcanic gases, sound waves, lava advancement, inferred magma volume below ground, and visual changes in eruptive activity. In addition, remote sensing, especially DInSAR data, can provide an additional large spatial and temporal-scale overview [47,48].
In Figure 2, we show the descending frame of the Sentinel-1 DInSAR data coverage from the data we use in this paper. This is not a complete image of the DInSAR coverage over the Hawaii area.

2.2. DInSAR Data

We acquired Sentinel-1 data through the Alaskan Satellite Facility (ASF) and processed them using the GMT5SAR DInSAR data processing package [49]. We generated time series of displacement using the GIAnT toolbox [50]. We processed 43 scenes of Sentinel-1 DInSAR data between 4 January 2017 and 16 June 2018 of the descending frame of Path 87, Frame 527 (Figure 2). We generated every possible combination of interferograms with less than 50 days of temporal baseline. Because the spatial repeatability of the Sentinel-1 acquisitions does not vary significantly over the 18 months of the period that we were interested in, we did not impose any spatial baseline limits.
We processed all available Sentinel-1 SAR data covering the Yellowstone volcanic area. Four frames are fully or partially covering the Yellowstone National Park and the surrounding areas (Figure 1). We used the GMT5SAR [49] toolbox for DInSAR processing and the GIAnT [50] toolbox for displacement time series calculation. These were carried out using the Summit high-performance research computing facilities at the University of Colorado, Boulder.
We used all available SAR acquisitions between January 2017 and December 2018, and formed all possible interferograms with a maximum temporal baseline of 50 days. We did not impose any spatial baseline limit, as the Sentinel-1 mission is designed to have a great repeatability in terms of spatial coverage of the same frame. Details of data processing of each frame are shown in Table 1.
Details of data processed in this study for both the Hawaii and Yellowstone areas are shown in Table 1.

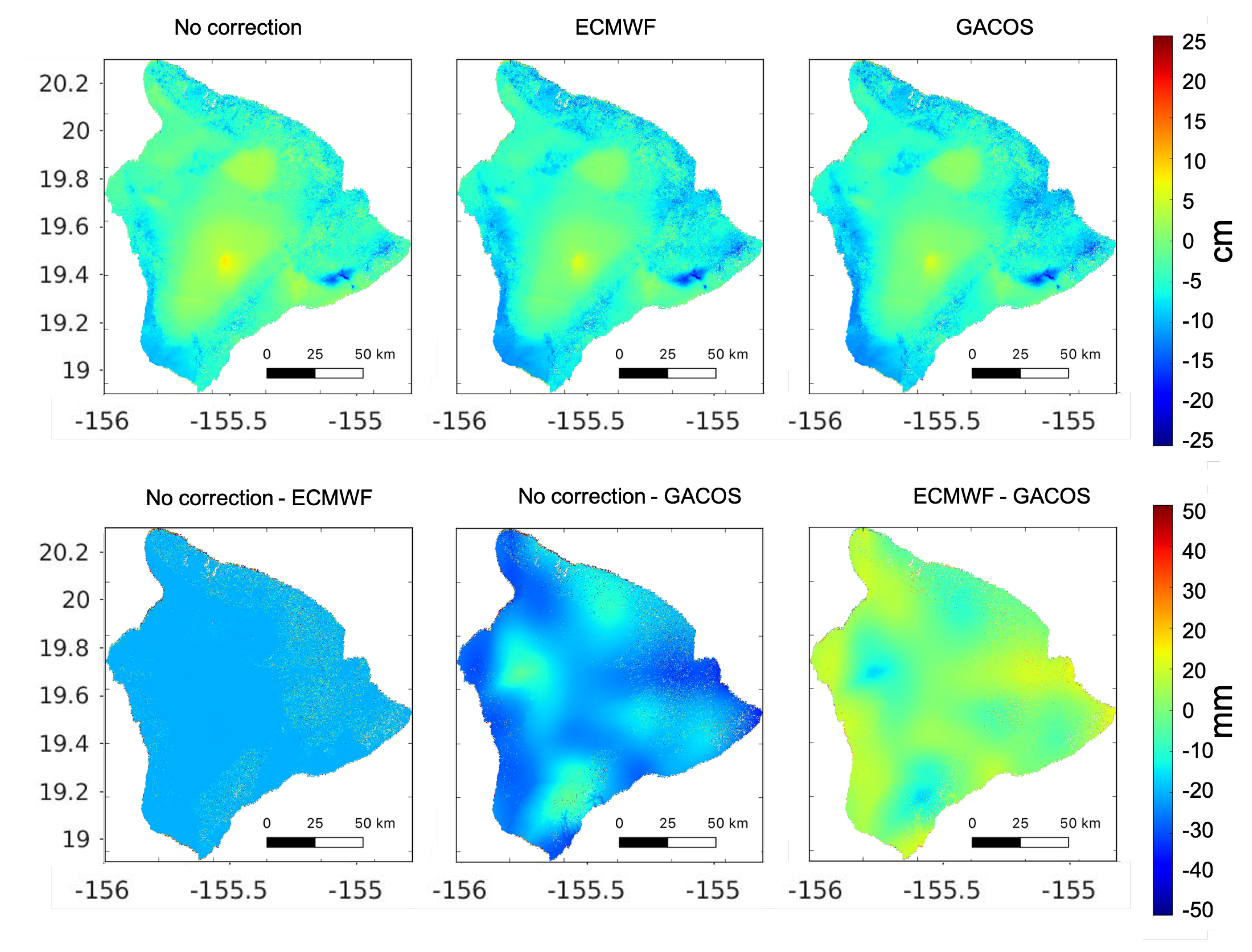
2.3. Atmospheric Correction and Displacement Time Series

The atmosphere varies greatly both in space and time, and radar signals that propagate through the various layers of the atmosphere are significantly affected. The atmosphere can introduce errors of over ten centimeters in the measured ground deformation [51]. Atmospheric effects can be mitigated based on external data, such as meteorological observations [52,53], GNSS observations [54,55], high-resolution meteorological models [56], or water vapor (MODIS [57] or MERIS [55]) data. Correction can also be applied based on techniques developed for DInSAR data analysis, such as correlation analysis [58,59], pair-wise logic [60], PSInSAR technique [61,62] or stacking [61,63].
Various atmospheric corrections are available. In this paper, we explore the application of two of them, both based on external datasets, such as meteorological observations and GNSS data.
We assess, using the ECMWF [33] and the GACOS [34], atmospheric corrections based on their effectiveness and availability. The ECMWF (European Centre for Medium-Range Weather Forecasts) is based on an 80 km resolution weather model, and the GACOS correction is incorporating the ECMWF weather data with continuous GNSS measurements.
To calculate displacement time series, we use the Generic InSAR Analysis Toolbox (GIAnT) software package [50]. GIAnT is used for rapid generation of time-series of surface displacement using DInSAR data based on either the Small BAseline Subset (SBAS) or the New Small BAseline Subset (NSBAS) methods.
The SBAS technique is appropriate to apply when the differential interferograms have a small spatial baseline [27], that is typically the case with the Sentinel-1 mission data. The observation equation of the SBAS method is Equation (1).
Φ i j = ∑ n = i j − 1 δ φ n
where Φ i j is the phase of the interferogram combining acquisitions i and j and δ φ n is the phase increment between acquisitions n and n + 1 . The cumulative phase can be obtained by solving a linear least squares inversion problem, but it solves only for coherent pixels, and this can result in a small number of pixels in the final solution.
The NSBAS method uses the same principle as the SBAS method but it (1) estimates DEM errors as well and (2) accommodates missing observations, and therefore, has been optimized for the monitoring of transient ground motion that has small amplitude and takes place over large areas and in natural settings [64]. The observation equation becomes as in Equation (2):
0 = ∑ n = 1 k δ φ n − f ( Δ t k ) + e B p e r p k ( k = 2 , 3 , ⋯ N )
where f ( Δ t k ) is the deformation and e B p e r p k is the DEM error. We expect this method to be appropriate to employ in the long-term monitoring of the Yellowstone area, but plan to explore other methods before the system becomes operational in order to optimize the output in terms of accuracy and processing time. For example, a new technique, Multidimensional Small Baseline Subset (MSBAS), allows us to incorporate DInSAR results from different satellites and wavelengths into one time series [65].

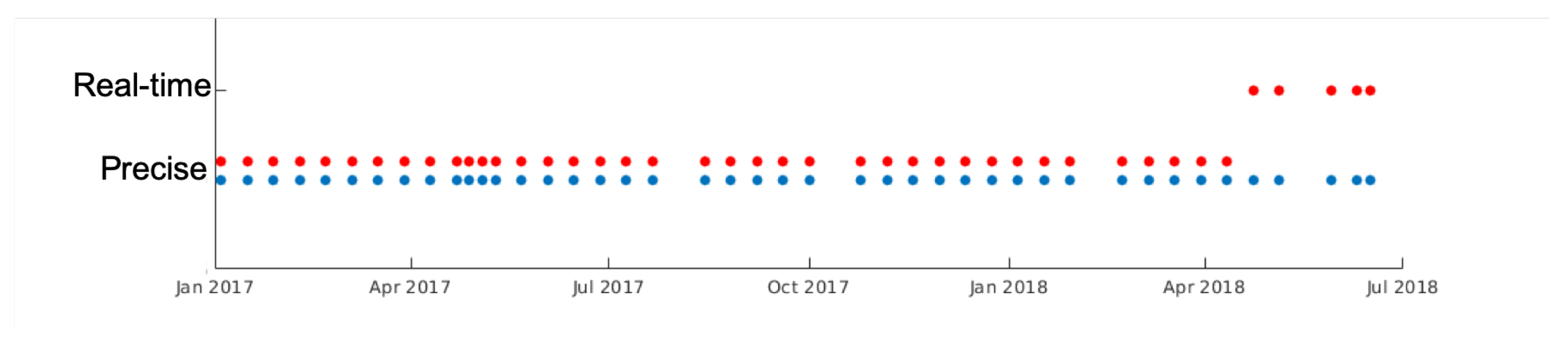
2.4. Real-time and Precise Orbits

We use the same Kilauea dataset as described in Section 2.3. We applied de-ramping and ECMWF atmospheric corrections [33]. Using these interferograms, we computed time series of displacements between 4 January 2017 and 16 June 2018 with the NSBAS technique, which is appropriate for a selected combination of interferograms with small spatial baselines between the images [64].
To compare results with precise and real-time orbits, we carried out the described processing sequence twice. In the first case, we used precise orbits for all the scenes and in the second case, we replaced the precise orbits with real-time ones for the last five scenes (Figure 3). This simulates a scenario of processing DInSAR data in near-real time, when for the past 20 days, there are only real-time orbits available but for older scenes there are the calculated precise orbits available. When operational, we will ingest new data when acquired and use real-time orbits with the newest DInSAR scenes, while at the same time, we will reprocess older scenes for which precise orbits became available since the last processing.

3. Results

3.1. Atmospheric Correction

Figure 4 shows results of three cases of processed DInSAR data over the Hawaii area: no atmospheric correction applied, ECMWF atmospheric correction applied [33], and GACOS atmospheric correction applied [34]. We find that both atmospheric corrections help remove apparent uplift signal (red) at the highest elevations of the island and keep the subsidence signal (blue) close to the southeast shoreline that is related to the 2018 Kilauea eruptions. Applying the ECMWF correction yields a smoother image than the GACOS correction.
Figure 5 shows the locations of selected GNSS stations and the corresponding time series of relative displacements derived from the DInSAR dataset. We selected three GNSS stations on the island of Hawaii that offer a comprehensive analysis of the corrections applied. At PMAU station, there is no expected ground motion; however, the ECMWF and GACOS cumulative displacement results seem to differ. MOKP station, which is close to the summit of Mauna Loa, is far enough from the volcanic activity that only small ground motion can be expected. Thirdly, at PUOC station, where ground motion is expected due to volcanic activity in 2018. We selected a single pixel closest to the location of each of these GNSS stations. Since some smoothing is already applied in the NSBAS process, we did not average among a number of pixels around the GNSS location. The DInSAR time series start at zero, and the GNSS time series are shifted to be shown overlaying the DInSAR time series. These GNSS time series are acquired from the Nevada Geodetic Laboratory and they span from 2000 for MOKP and from 2006 for both PUOC and PMAU, up until the present day [66].
We find that both ECMWF and GACOS perform similarly in terms of fit to the GNSS data, and even when no correction is applied, the uncorrected DInSAR results approximately match the corrected ones. In addition, we calculated the fit between the presented DInSAR and GNSS time series using the Dynamic Time Warping method (DTW) [67,68]. This technique calculates the similarities of time series of different sampling and gives the Euclidean distance between the two time series [69], d, as shown in each panel in Figure 5. The smaller the distance, the more similar the time series are. While none of the tests is best in every case, at the location of the 2018 volcanic activities (PUOC GNSS station), the ECMWF correction gives the smallest d value. Future studies should apply similar tests to larger suites of data to better assess under what conditions each method is preferred.
For further use in the GeoSciFramework project, we chose to use the ECMWF correction, as it is possible to include this in automatic processing chains as opposed to GACOS, which requires an individual data request for each scene. The DTW comparison shows that both ECMWF and GACOS perform very similarly, and as GACOS is planned to be automatically available in the future, we will consider this comparison in greater depth before the Yellowstone monitoring system becomes operational.

3.2. Real-Time and Precise Orbits

After processing 43 DInSAR acquisitions, we compare the two sets of results: one where we only used precise orbits, and one in which we replaced the orbits of the last five acquisitions with real-time orbits. Individual interferograms show some pixel-to-pixel difference, but the broad image of ground deformation and its interpretation do not differ between the two cases (Figure 6). These two interferograms show the deformation of the active area that corresponds to the rift eruption and collapse of Kilauea volcano during spring and summer of 2018 [70].
We find similarly non-significant differences when assessing the comparison between cumulative displacements as a result of the two scenarios (Figure 7). Differences at time steps 1, 15, 30 and 42 are shown in Figure 8. The 42nd time step is the final one, also corresponding to the interferogram in Figure 6. Because the first 38 acquisitions are the same in both processing sequences, we do not expect any disparities in the first 37 time-steps. However, as we carried out the processing and time series generation separately, and as the solution to the displacement history is non-unique, we still see some pixel-to-pixel differences at earlier time steps. The difference between the two sets of processing become larger and larger as we assess later and later timesteps; however, we find that these differences are due to the non-uniqueness of the solution for the displacement time series rather than a consequence of the real-time orbits used. If we assess the last five time-steps, where in one case, we use precise and in the other case, real-time orbits, we do not observe a change in the rate of increasing differences.

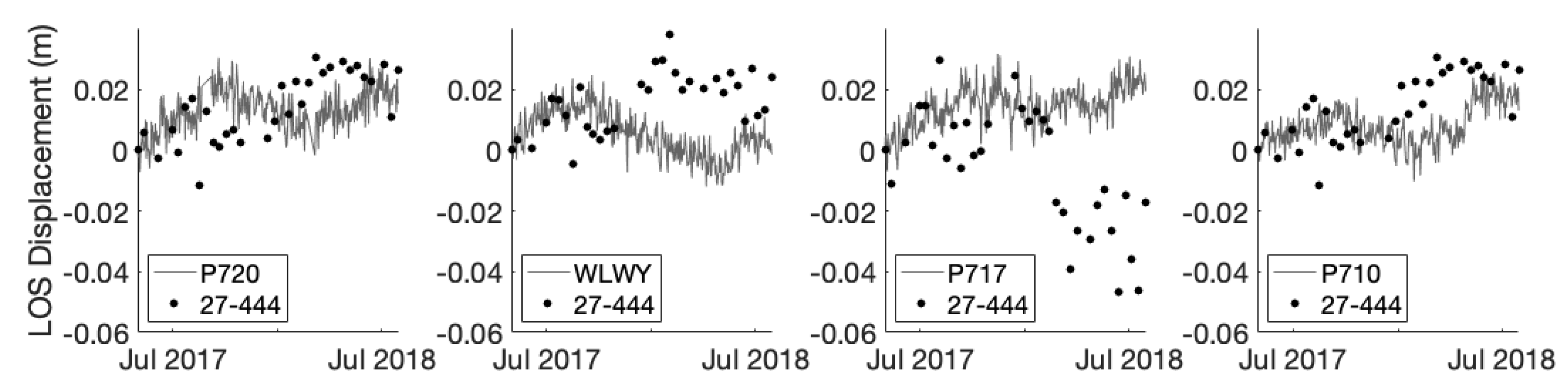
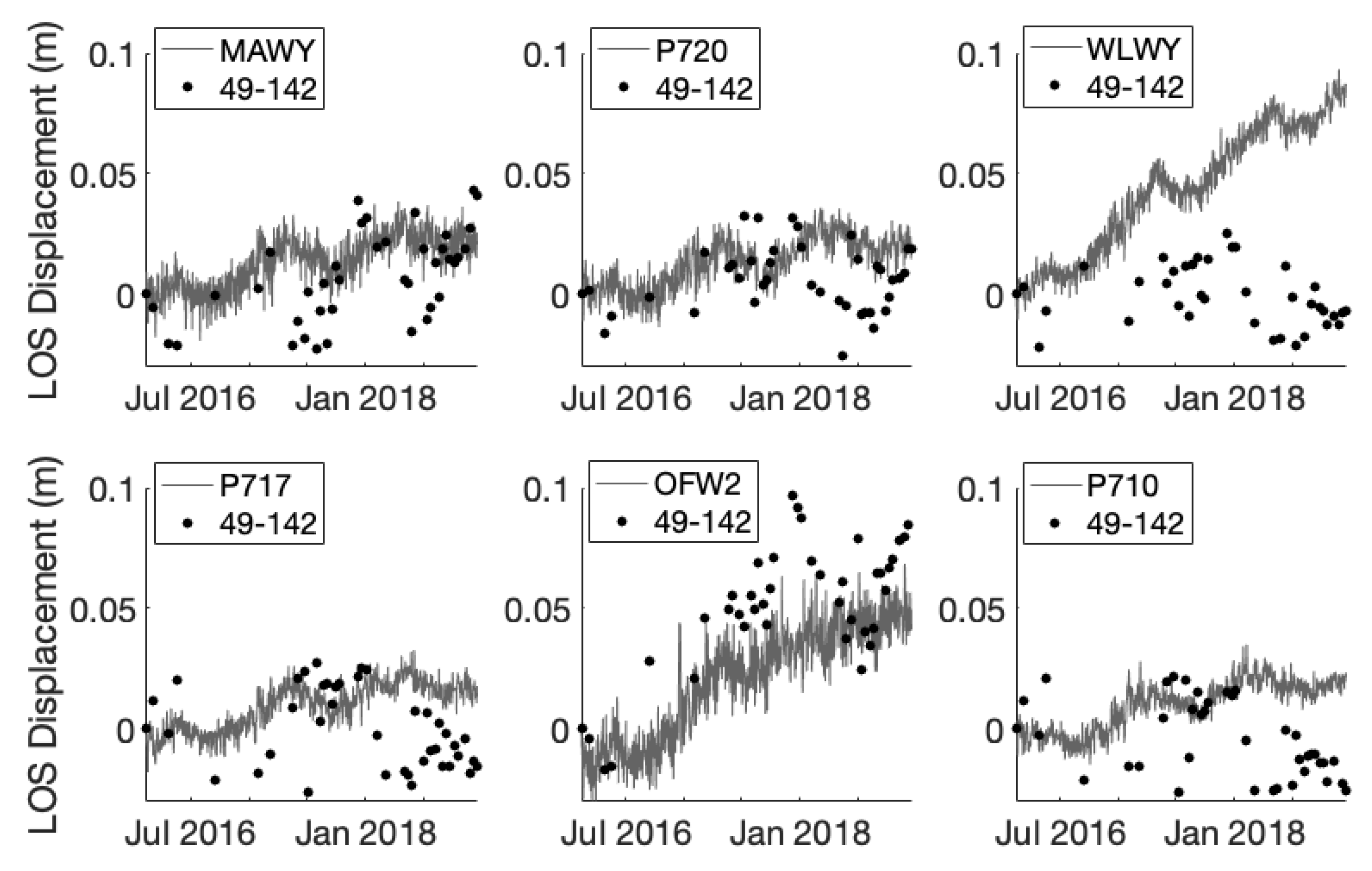
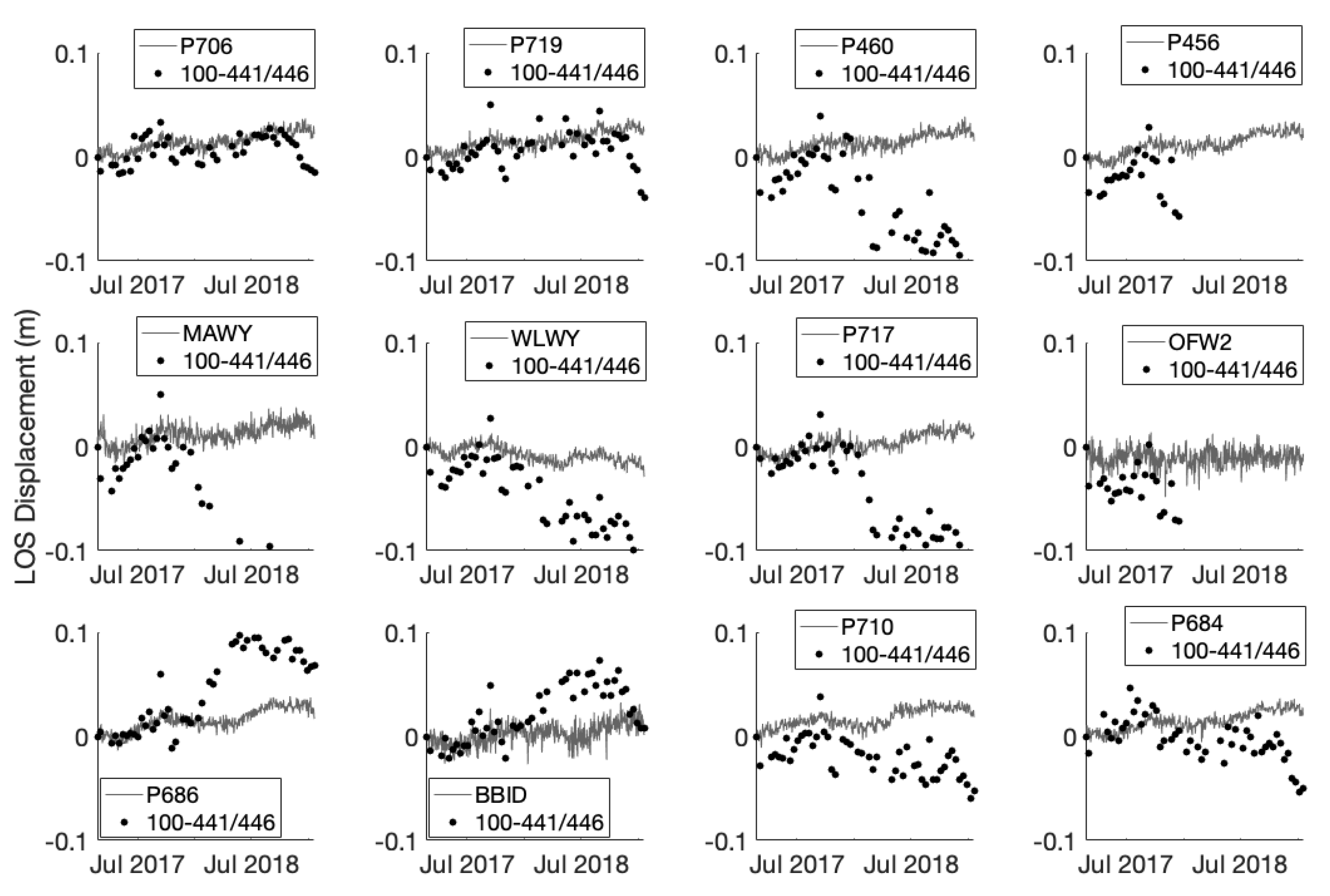
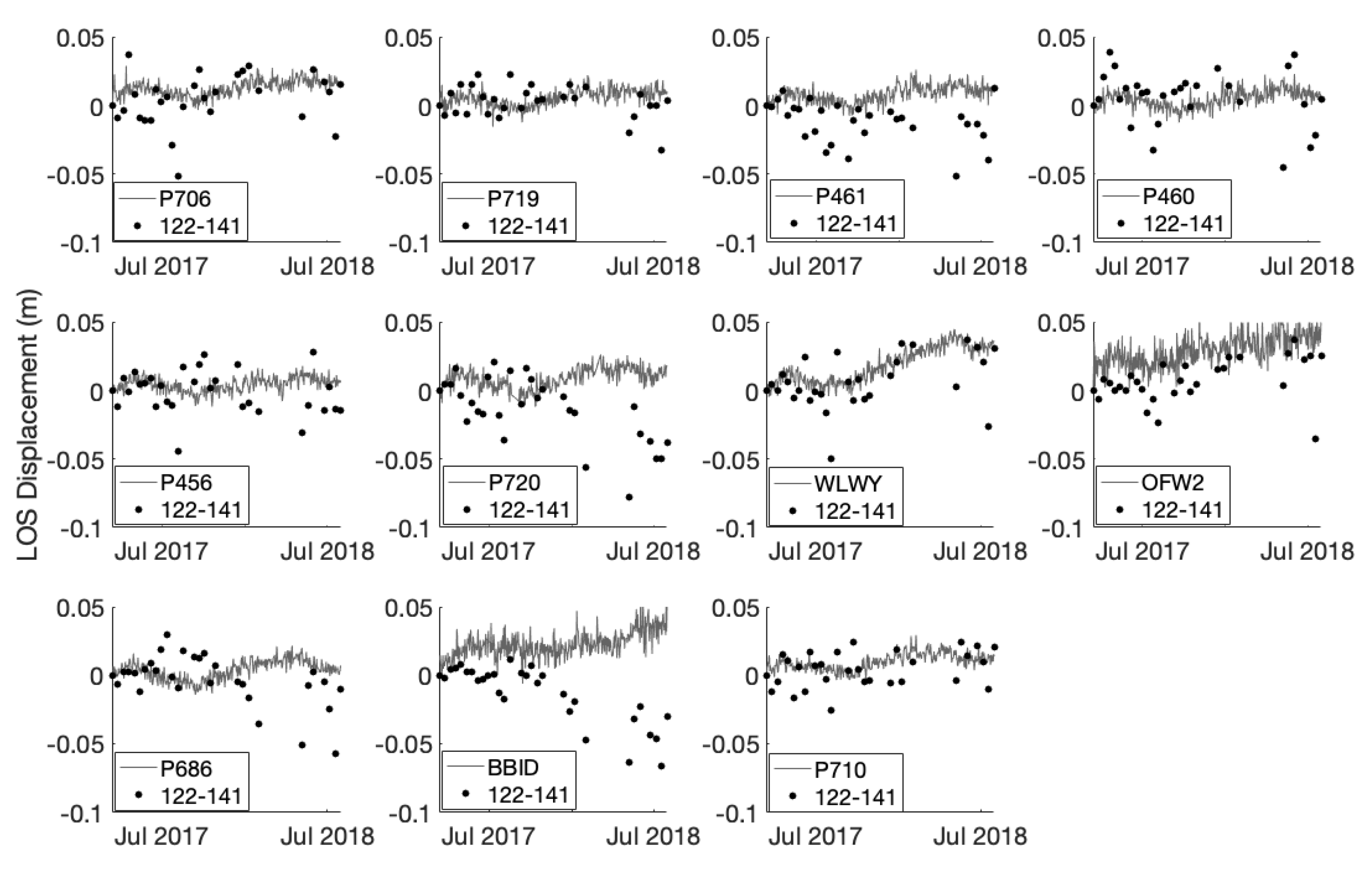
3.3. Yellowstone Results

We acquired Sentinel-1 data between January 2017 and December 2018 for the frames covering the Yellowstone National park (Figure 1). In the case of frames 100–441 and 100–446, we merged and cropped away the northern half of 100–441 and the southern half of 100–446, and processed the mid-section as one frame.
Based on the results from the atmospheric correction study over Hawaii and the findings over the deforming area, we applied the ECMWF correction or each of the frames we processed in the Yellowstone area. Figure 9 shows different atmospheric corrections applied for the 49–142 frame.
We used precise orbits since they are available to process past data. We show cumulative displacements between May 2017 and August 2018 for all frames, as some data were not available between January 2017 and April 2017 and between September 2018 and December 2018 (Figure 10).
These initial results show that some residual apparent uplift (red) is present in many cases, which is most likely due to a DEM or atmospheric correction error as they clearly coincide with steep topography gradients in the region. This apparent uplift marked with red is most prominent in the Path 49, Frame 142 image (top right panel on Figure 10). Subsidence in these images is marked with blue and we see a consistent signal in the southwest corner of the Yellowstone National Park on all four cumulative displacement images (black circles on Figure 10). This is the region where the Yellowstone volcano is most active, marked with geysers and hot springs and gas emission activities.
We collected and analysed the available continuous GNSS data and compared it to displacements derived from the DInSAR analysis. Figure 11, Figure 12, Figure 13 and Figure 14 show comparison between (1) the displacement derived from GNSS time series in the LOS direction of the DInSAR acquisition and (2) the LOS displacement extracted from the DInSAR solution at the location corresponding to the GNSS station. In this comparison, we include all available DInSAR time series between January 2017 and December 2018. Some stations show better fit (MAWY, P720, or OFW2) than others (WLWY or P710). It is difficult to gain a general idea of the quality of the fit between GNSS and DInSAR displacement, because these permanent GNSS stations are present only at the area of the Yellowstone National Park, and most of the DInSAR frame do not have any ground truth data to compare with.
Further DInSAR results are shown in the Appendix A: examples of interferograms and their location are shown in Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5.

4. Discussion

We have compared the effects of applying two different atmospheric corrections, the ECMWF and GACOS corrections. The ECMWF correction is based on weather forecast and meteorological modelling only, while the GACOS also includes GNSS measurements. We found the two corrections similar in both cumulative displacement results and when we compared time series of individual pixels to GNSS data. An advantage of the ECMWF correction is that it is possible to extract the atmospheric information automatically through the processing, while the GACOS correction requires that we request the data and wait times can be up to 24 h. For the GeoSciFramework project purposes to provide early warning of changes in volcanic activities in the Yellowstone volcanic area, the ECMWF correction and its automated setup is better suited to the current computational structure. We will revisit this issue when GACOS becomes available on a similar automated basis.
Analysis at Hawaii for the time period January 2017 through June 2018 provides an assessment of the potential effect of using atmospheric corrections on hazard evaluation. Figure 4 shows the estimated change in height associated with atmospheric corrections in Hawaii, and the differences between the two methods. Note that the difference in estimated displacements between the ECMWF and no correction and the ECMWF and GACOS corrections range from 2.5 to 5 cm in those locations associated with either significant topography or magma motion. In the case of the former, this could result in overestimating potential hazard, while in the latter, it could mean inaccurate estimation of the size and location of the magma source, resulting in underestimation of the potential hazard. Future work will include assessment of these effects for a wider variety of hazard types and associated models.
We found that using real-time orbits instead of precise ones does not significantly affect the results of cumulative displacement over the Kilauea case study. There are pixel-to-pixel differences, but they do not change the overall results and interpretation of the DInSAR analysis. Therefore, it is possible to use these measurements in near-real time as they are acquired and processed, which is essential for early-warning purposes, as in the case of monitoring the Yellowstone volcanic area. As precise orbits are being continuously calculated and updated, the DInSAR displacement results can be refined for past acquisitions and real-time orbits employed for the most recent ones.
The important conclusion here is that the use of real-time orbits will not significantly impact the estimate of surface displacements (Figure 7 and Figure 8) and, as such, not adversely affect the associated hazard estimates or evaluation, regardless of the hazard type.
Real-time orbits are available within two hours of the DInSAR image acquisition, and we expect to have updated ground motion and displacement results approximately eight hours after each new SAR image is available over the Yellowstone area. This estimation includes the time it takes to pull the new image data, wait the two hours for the real-time orbit to become available, complete the processing through GMT5SAR software, and apply the final GIAnT time series inversion. The new image would be interfered against only the most recent acquisitions contained within the 50-day threshold. This suggests that 6–12 new interferograms would be processed each time and then added to the continuously updating model of the Yellowstone volcanic area, together with other remote sensing observations from the GNSS network and ground-based borehole strain and seismic measurements. Through machine learning techniques, it is possible to ingest a large amount of data and set up a warning system that will provide alerts to any change in seismic activity or surface deformation.
The initial cumulative displacement calculations (Figure 10) will contribute towards the baseline model that will be set up over the course of the GeoSciFramework project. Future work in the GeoSciFramework project includes implementing a faster processing chain described by Zebker [35], merging DInSAR observations from different acquisition frames [65] and optimizing integration of the different types of observations with their varying spatial and temporal acquisition rates.
It would be beneficial to install some GNSS stations across these frames outside of the Yellowstone National Park area, and acquire further ground truth data. This could contribute to the analysis of the displacements and could provide explanation to some of the apparent uplift that correlates with the topography.

Author Contributions

K.K. has performed the majority of data-processing, analysis and writing. B.D.C. gave significant contributions into the processing of the data and K.F.T. gave significant contributions to the interpretation and writing of this manuscript. All authors have read and agree to the published version of the manuscript.

Funding

This research was funded by NSF Grant No. 1835566, Collaborative Research:Framework: Data:NSCI:HDR:GeoSCIFramework:Scalable Real-Time Streaming Analytics and Machine Learning for Geoscience and Hazards Research.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://scihub.copernicus.eu (accessed on 23 February 2021).

Acknowledgments

We thank the European Space Agency (ESA) for acquiring and the National Aeronautics and Space Administration (NASA) and ASF for distributing Sentinel-1 SAR data. Figures were plotted using Matlab, Google Earth Pro, GIAnT and QGIS (a free and open source geographic information system, https://www.qgis.org/en/site/ (accessed on 23 February 2021)).

Conflicts of Interest

The authors declare no conflict of interest.

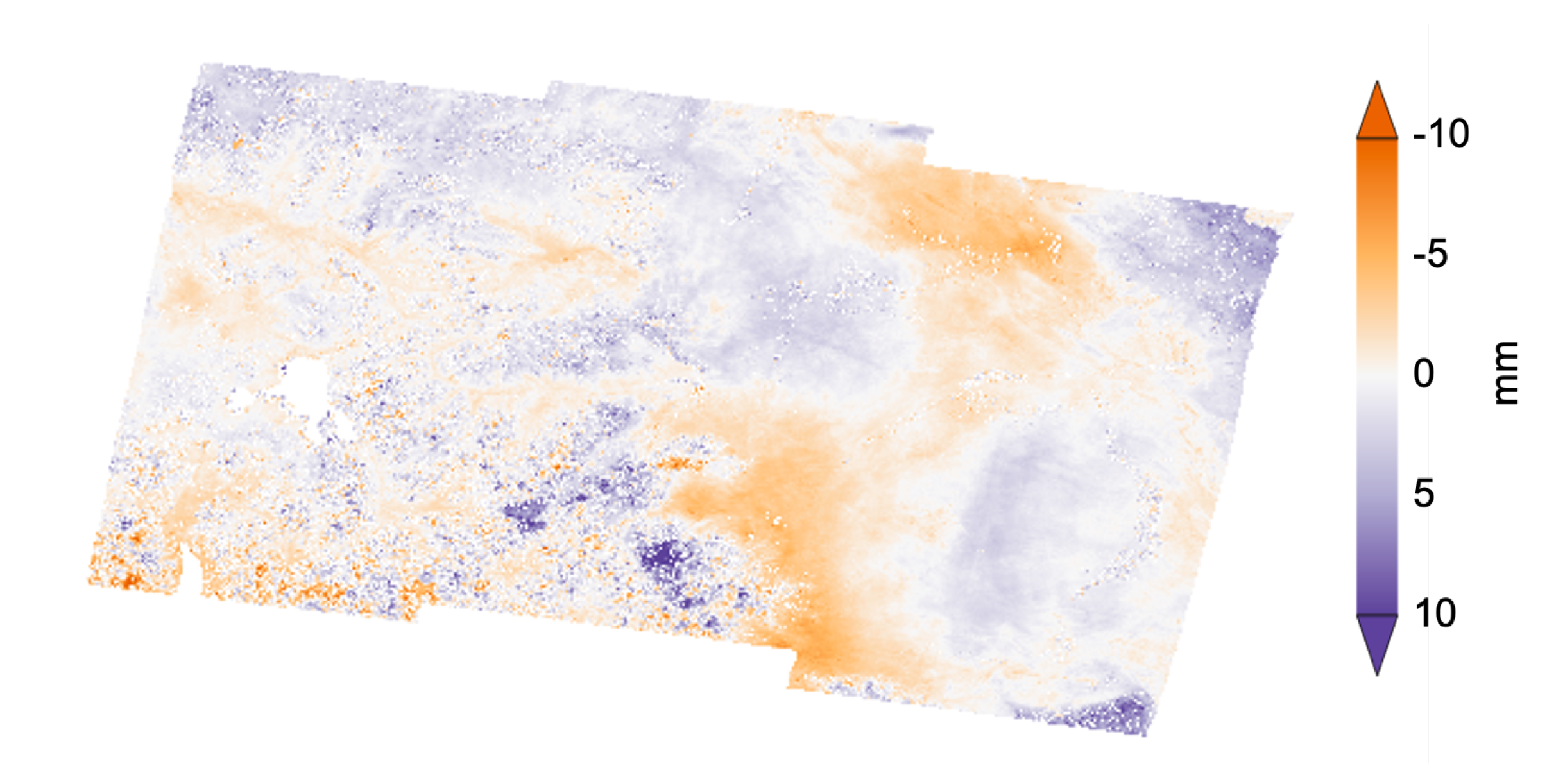
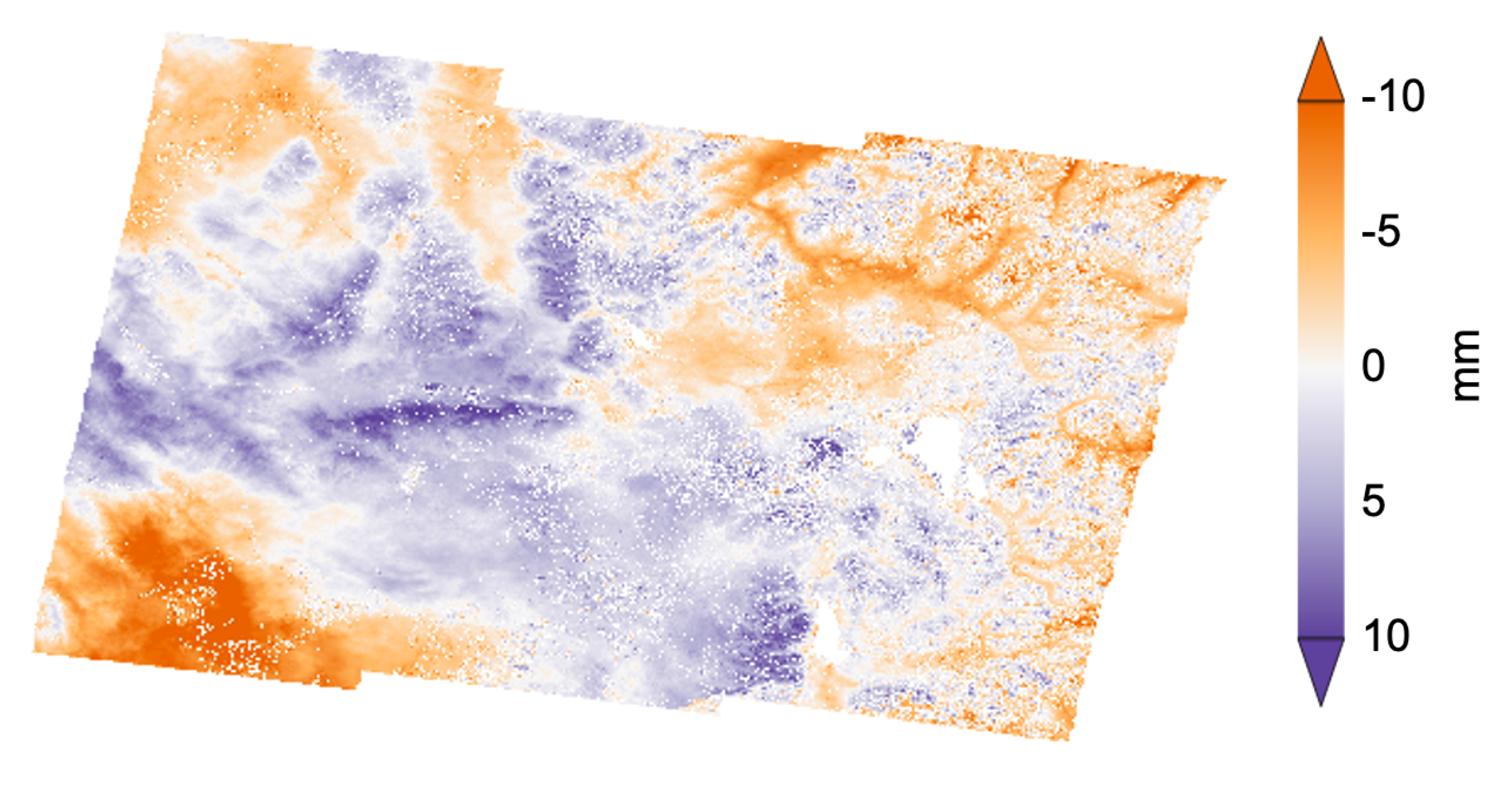
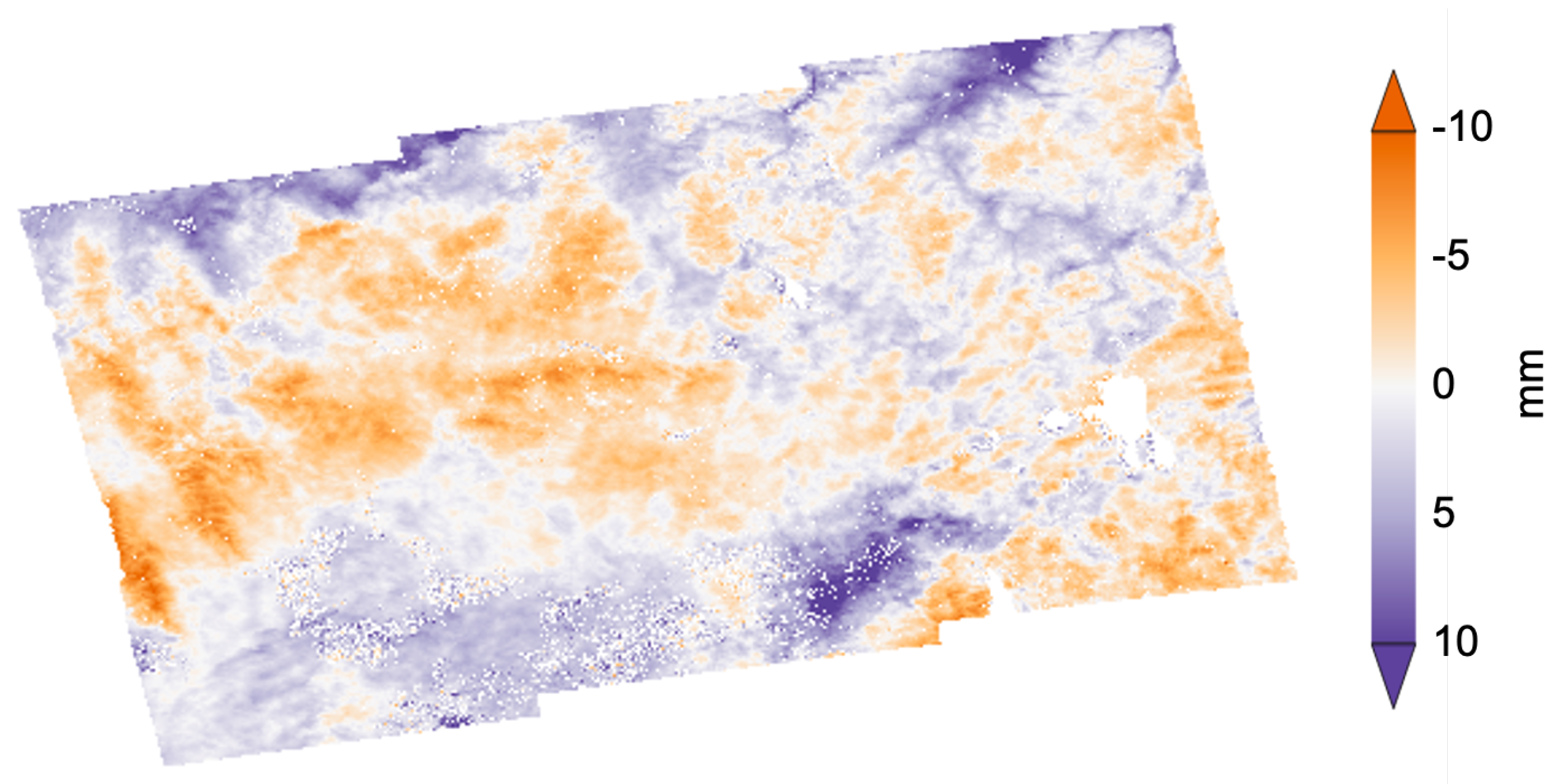
Appendix A. Examples of Interferograms from the Yellowstone Data Processing

Remotesensing 13 00867 g0a1 550
Figure A1. Location of the DInSAR frames and continuously recording GNSS stations. The outline of the Yellowstone national park is shown with magenta.
Figure A1. Location of the DInSAR frames and continuously recording GNSS stations. The outline of the Yellowstone national park is shown with magenta.
Remotesensing 13 00867 g0a1
Remotesensing 13 00867 g0a2 550
Figure A2. Track 27, Frame 444, 20170816-20171003.
Figure A2. Track 27, Frame 444, 20170816-20171003.
Remotesensing 13 00867 g0a2
Remotesensing 13 00867 g0a3 550
Figure A3. Track 100, Frame 441/446, 20170914-20171101.
Figure A3. Track 100, Frame 441/446, 20170914-20171101.
Remotesensing 13 00867 g0a3
Remotesensing 13 00867 g0a4 550
Figure A4. Track 122, Frame 141, 20170724-20170910.
Figure A4. Track 122, Frame 141, 20170724-20170910.
Remotesensing 13 00867 g0a4
Remotesensing 13 00867 g0a5 550
Figure A5. Track 49, Frame 142, 20180515-20180702.
Figure A5. Track 49, Frame 142, 20180515-20180702.
Remotesensing 13 00867 g0a5

References

  1. Tiampo, K.F.; McGinnis, S.; Kropivnitskaya, Y.; Qin, J.; Bauer, M.A. Big data challenges and hazards modeling. In Risk Modeling for Hazards and Disasters; Elsevier: Amsterdam, The Netherlands, 2018; pp. 193–210. [Google Scholar]
  2. Dzurisin, D. A comprehensive approach to monitoring volcano deformation as a window on the eruption cycle. Rev. Geophys. 2003, 41, 1001. [Google Scholar] [CrossRef]
  3. Aiuppa, A.; Moretti, R.; Federico, C.; Giudice, G.; Gurrieri, S.; Liuzzo, M.; Papale, P.; Shinohara, H.; Valenza, M. Forecasting Etna eruptions by real-time observation of volcanic gas composition. Geology 2007, 35, 1115–1118. [Google Scholar] [CrossRef]
  4. Marzocchi, W.; Sandri, L.; Selva, J. BET_EF: A probabilistic tool for long-and short-term eruption forecasting. Bull. Volcanol. 2008, 70, 623–632. [Google Scholar] [CrossRef] [Green Version]
  5. Marzocchi, W.; Garcia-Aristizabal, A.; Gasparini, P.; Mastellone, M.L.; Di Ruocco, A. Basic principles of multi-risk assessment: A case study in Italy. Nat. Hazards 2012, 62, 551–573. [Google Scholar] [CrossRef]
  6. Loughlin, S.C.; Sparks, R.S.J.; Sparks, S.; Brown, S.K.; Jenkins, S.F.; Vye-Brown, C. Global Volcanic Hazards and Risk; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
  7. Newhall, C.G.; Pallister, J.S. Using multiple data sets to populate probabilistic volcanic event trees. In Volcanic Hazards, Risks and Disasters; Elsevier: Amsterdam, The Netherlands, 2015; pp. 203–232. [Google Scholar]
  8. Gaddes, M.; Hooper, A.; Bagnardi, M. Using machine learning to automatically detect volcanic unrest in a time series of interferograms. J. Geophys. Res. Solid Earth 2019, 124, 12304–12322. [Google Scholar] [CrossRef] [Green Version]
  9. Poland, M.P.; Anderson, K.R. Partly Cloudy With a Chance of Lava Flows: Forecasting Volcanic Eruptions in the Twenty-First Century. J. Geophys. Res. Solid Earth 2020, 125, e2018JB016974. [Google Scholar] [CrossRef]
  10. Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
  11. Amelung, F.; Jónsson, S.; Zebker, H.; Segall, P. Widespread uplift and ?trapdoor?faulting on Galapagos volcanoes observed with radar interferometry. Nature 2000, 407, 993–996. [Google Scholar] [CrossRef]
  12. Wadge, G. A strategy for the observation of volcanism on Earth from space. Philos. Trans. R. Soc. London. Ser. Math. Phys. Eng. Sci. 2003, 361, 145–156. [Google Scholar] [CrossRef] [PubMed]
  13. Fernández, J.; Tizzani, P.; Manzo, M.; Borgia, A.; González, P.; Martí, J.; Pepe, A.; Camacho, A.; Casu, F.; Berardino, P.; et al. Gravity-driven deformation of Tenerife measured by InSAR time series analysis. Geophys. Res. Lett. 2009, 36, L04306. [Google Scholar] [CrossRef] [Green Version]
  14. Samsonov, S.V.; d’Oreye, N.; González, P.J.; Tiampo, K.F.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the Greater Vancouver region from two decades of ERS-ENVISAT-RADARSAT-2 DInSAR measurements. Remote. Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef] [Green Version]
  15. Samsonov, S.V.; Feng, W.; Peltier, A.; Geirsson, H.; d?Oreye, N.; Tiampo, K.F. Multidimensional Small Baseline Subset (MSBAS) for volcano monitoring in two dimensions: Opportunities and challenges. Case study Piton de la Fournaise volcano. J. Volcanol. Geotherm. Res. 2017, 344, 121–138. [Google Scholar] [CrossRef]
  16. Hua, H.; Owen, S.E.; Yun, S.H.; Agram, P.S.; Manipon, G.; Starch, M.; Sacco, G.F.; Bue, B.D.; Dang, L.B.; Linick, J.P.; et al. Large-scale Sentinel-1 processing for solid earth science and urgent response using cloud computing and machine learning. AGUFM 2017, 2017, G33A-02. [Google Scholar]
  17. Bekaert, D.; Agram, P.; Owen, S.; Karim, M.; Dang, L.; Manipon, G.; Linick, J.; Hua, H.; Gurrola, E.; Simons, M.; et al. Development of Standardized Interferometric Products and Online Processing Capabilities. AGUFM 2018, 2018, G32A-02. [Google Scholar]
  18. Bekaert, D.P.; Karim, M.; Linick, J.P.; Hua, H.; Sangha, S.; Lucas, M.; Malarout, N.; Agram, P.S.; Pan, L.; Owen, S.E.; et al. Development of open-access Standardized InSAR Displacement Products by the Advanced Rapid Imaging and Analysis (ARIA) Project for Natural Hazards. AGUFM 2019, 2019, G23A-04. [Google Scholar]
  19. Meyer, F.J.; Arko, S.A.; Hogenson, K.; McAlpin, D.B.; Whitley, M.A. A cloud-based system for automatic hazard monitoring from Sentinel-1 SAR data. In Proceedings of the 2017 AGU Fall Meeting, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
  20. Garron, J.; Stoner, C.; Meyer, F. Cloud-based oil detection processing pipeline prototype for C-band synthetic aperture radar data. In Proceedings of the OCEANS 2017-Anchorage, Aberdeen, UK, 18–21 September 2017; pp. 1–7. [Google Scholar]
  21. Logan, T.A.; Nicoll, J.B. Automated RTC and INSAR Stack-Processing at the Alaska Satellite Facility. In Proceedings of the 2018 AGU Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
  22. Wright, T.; Gonzalez, P.; Walters, R.; Hatton, E.; Spaans, K.; Hooper, A. LiCSAR: Tools for automated generation of Sentinel-1 frame interferograms. In Proceedings of the 2016 AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
  23. Wright, T.J.; Hooper, A.J.; Spaans, K.; Hatton, E.L.; González, P.J.; Bhattarai, S.; Biggs, J.; Crippa, P.; Ebmeier, S.K.; Elliott, J.R.; et al. COMET-LICSAR: Systematic Deformation Monitoring of Fault Zones and Volcanoes with the Sentinel-1 Constellation. In Proceedings of the 2017 AGU Fall Meeting, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
  24. Corsa, B.D.; Tiampo, K.F.; Kelevitz, K.; Baker, S.; Meertens, C. Automated Processing, Streaming, and Integration of InSAR Time Series and GNSS Data; as part of the Collaborative GeoSciFramework Research Project. AGUFM 2019, 2019, G13C-0574. [Google Scholar]
  25. Reath, K.; Pritchard, M.; Poland, M.; Delgado, F.; Carn, S.; Coppola, D.; Andrews, B.; Ebmeier, S.; Rumpf, E.; Henderson, S.; et al. Thermal, deformation, and degassing remote sensing time series (CE 2000–2017) at the 47 most active volcanoes in Latin America: Implications for volcanic systems. J. Geophys. Res. Solid Earth 2019, 124, 195–218. [Google Scholar] [CrossRef] [Green Version]
  26. Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote. Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
  27. Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote. Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
  28. Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote. Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
  29. Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef] [Green Version]
  30. Usai, S. A least squares database approach for SAR interferometric data. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef] [Green Version]
  31. Corsa, B.; Tiampo, K.; Kelevitz, K.; Baker, S.; Meertens, C. Comparison of Insar Time Series Generation Techniques as Part of the Collaborative Geosciframework Research Project. In Proceedings of the 2020 AGU Fall Meeting, Online, 7–11 December 2020. [Google Scholar]
  32. Samsonov, S.; Tiampo, K. Analytical optimization of a DInSAR and GPS dataset for derivation of three-dimensional surface motion. IEEE Geosci. Remote. Sens. Lett. 2006, 3, 107–111. [Google Scholar] [CrossRef]
  33. Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
  34. Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for Interferometric Synthetic Aperture Radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
  35. Zebker, H.A. User-friendly InSAR data products: Fast and simple timeseries processing. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 2122–2126. [Google Scholar] [CrossRef]
  36. Christiansen, R.L. The Quaternary and Pliocene Yellowstone Plateau Volcanic Field of Wyoming, Idaho, and Montana; U.S. Geological Survey: Denver, CO, USA, 2001. [Google Scholar]
  37. Yuan, H.; Dueker, K. Teleseismic P-wave tomogram of the Yellowstone plume. Geophys. Res. Lett. 2005, 32, L07304. [Google Scholar] [CrossRef] [Green Version]
  38. Smith, R.B.; Jordan, M.; Steinberger, B.; Puskas, C.M.; Farrell, J.; Waite, G.P.; Husen, S.; Chang, W.L.; O’Connell, R. Geodynamics of the Yellowstone hotspot and mantle plume: Seismic and GPS imaging, kinematics, and mantle flow. J. Volcanol. Geotherm. Res. 2009, 188, 26–56. [Google Scholar] [CrossRef] [Green Version]
  39. Russo, E.; Waite, G.; Tibaldi, A. Evaluation of the evolving stress field of the Yellowstone volcanic plateau, 1988 to 2010, from earthquake first-motion inversions. Tectonophysics 2017, 700, 80–91. [Google Scholar] [CrossRef]
  40. Newhall, C.; Self, S.; Robock, A. Anticipating future Volcanic Explosivity Index (VEI) 7 eruptions and their chilling impacts. Geosphere 2018, 14, 572–603. [Google Scholar] [CrossRef] [Green Version]
  41. Chang, W.L.; Smith, R.B.; Farrell, J.; Puskas, C.M. An extraordinary episode of Yellowstone caldera uplift, 2004–2010, from GPS and InSAR observations. Geophys. Res. Lett. 2010, 37, L23302. [Google Scholar] [CrossRef] [Green Version]
  42. Waite, G.P.; Smith, R.B. Seismic evidence for fluid migration accompanying subsidence of the Yellowstone caldera. J. Geophys. Res. Solid Earth 2002, 107, ESE-1. [Google Scholar] [CrossRef] [Green Version]
  43. Chang, W.; Smith, R.; Wicks, C.; Puskas, C.; Farrell, J. Accelerated uplift and source models of the Yellowstone caldera, 2004–2006, from GPS and InSAR observations. Science 2007, 318, 952–956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Sherrod, D.R.; Sinton, J.M.; Watkins, S.E.; Brunt, K.M. Geologic map of the State of Hawaii. US Geol. Surv. Open File Rep. 2007, 1089, 83. [Google Scholar]
  45. Quane, S.; Garcia, M.; Guillou, H.; Hulsebosch, T. Magmatic history of the East Rift Zone of Kilauea Volcano, Hawaii based on drill core from SOH 1. J. Volcanol. Geotherm. Res. 2000, 102, 319–338. [Google Scholar] [CrossRef]
  46. Holcomb, R.T. Eruptive history and long-term behavior of Kilauea Volcano. US Geol. Surv. Prof. Pap 1987, 1350, 261–350. [Google Scholar]
  47. Montgomery-Brown, E.K.; Sinnett, D.; Poland, M.; Segall, P.; Orr, T.; Zebker, H.; Miklius, A. Geodetic evidence for en echelon dike emplacement and concurrent slow slip during the June 2007 intrusion and eruption at Kīlauea volcano, Hawaii. J. Geophys. Res. Solid Earth 2010, 115, B07405. [Google Scholar] [CrossRef] [Green Version]
  48. Jung, H.S.; Lu, Z.; Won, J.S.; Poland, M.P.; Miklius, A. Mapping three-dimensional surface deformation by combining multiple-aperture interferometry and conventional interferometry: Application to the June 2007 eruption of Kilauea volcano, Hawaii. IEEE Geosci. Remote. Sens. Lett. 2010, 8, 34–38. [Google Scholar] [CrossRef]
  49. Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. Eos Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef] [Green Version]
  50. Agram, P.S.; Jolivet, R.; Riel, B.; Lin, Y.N.; Simons, M.; Hetland, E.; Doin, M.-P.; Lasserre, C. New radar interferometric time series analysis toolbox released. Eos, Transactions American Geophysical Union 2013, 94, 69–70. [Google Scholar] [CrossRef] [Green Version]
  51. Ding, X.l.; Li, Z.w.; Zhu, J.j.; Feng, G.c.; Long, J.P. Atmospheric effects on InSAR measurements and their mitigation. Sensors 2008, 8, 5426–5448. [Google Scholar] [CrossRef] [Green Version]
  52. Hanssen, R.; Feijt, A. A first quantitative evaluation of atmospheric effects on SAR interferometry. Ers Sar Interferom. 1997, 406, 277. [Google Scholar]
  53. Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
  54. Li, Z.; Ding, X.; Huang, C.; Wadge, G.; Zheng, D. Modeling of atmospheric effects on InSAR measurements by incorporating terrain elevation information. J. Atmos. Sol. Terr. Phys. 2006, 68, 1189–1194. [Google Scholar] [CrossRef]
  55. Li, Z.; Fielding, E.J.; Cross, P.; Muller, J.P. Interferometric synthetic aperture radar atmospheric correction: GPS topography-dependent turbulence model. J. Geophys. Res. Solid Earth 2006, 111, B02404. [Google Scholar] [CrossRef]
  56. Webley, P.; Wadge, G.; James, I. Determining radio wave delay by non-hydrostatic atmospheric modelling of water vapour over mountains. Phys. Chem. Earth Parts A B C 2004, 29, 139–148. [Google Scholar] [CrossRef]
  57. Li, Z.; Muller, J.P.; Cross, P. Tropospheric correction techniques in repeat-pass SAR interferometry. In Proceedings of the FRINGE 2003 Workshop, Frascati, Italy, 1–5 December 2003; pp. 1–5. [Google Scholar]
  58. Sarti, F.; Vadon, H.; Massonnet, D. A Method for Automatic Characterisation of Atmospheric Artifacts in SAR Interferograms by Correlation of Multiple Interferograms over the same Site. Eur. Space Agency Publ. Esa SP 1998, 441, 545–556. [Google Scholar]
  59. Fruneau, B.; Sarti, F. Detection of ground subsidence in the city of Paris using radar interferometry: Isolation of deformation from atmospheric artifacts using correlation. Geophys. Res. Lett. 2000, 27, 3981–3984. [Google Scholar] [CrossRef]
  60. Massonnet, D.; Feigl, K.L. Discrimination of geophysical phenomena in satellite radar interferograms. Geophys. Res. Lett. 1995, 22, 1537–1540. [Google Scholar] [CrossRef]
  61. Ferretti, A.; Prati, C.; Rocca, F. Multibaseline InSAR DEM reconstruction: The wavelet approach. IEEE Trans. Geosci. Remote. Sens. 1999, 37, 705–715. [Google Scholar] [CrossRef]
  62. Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
  63. Williams, S.; Bock, Y.; Fang, P. Integrated satellite interferometry: Tropospheric noise, GPS estimates and implications for interferometric synthetic aperture radar products. J. Geophys. Res. Solid Earth 1998, 103, 27051–27067. [Google Scholar] [CrossRef]
  64. Doin, M.P.; Guillaso, S.; Jolivet, R.; Lasserre, C.; Lodge, F.; Ducret, G.; Grandin, R. Presentation of the small baseline NSBAS processing chain on a case example: The Etna deformation monitoring from 2003 to 2010 using Envisat data. In Proceedings of the Fringe Symposium, Frascati, Italy, 19–23 September 2011; pp. 3434–3437. [Google Scholar]
  65. Samsonov, S.; d’Oreye, N. Multidimensional time-series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar]
  66. Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99, 1–2. [Google Scholar] [CrossRef]
  67. Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech, Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef] [Green Version]
  68. Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series; KDD Workshop: Seattle, WA, USA, 1994; Volume 10, pp. 359–370. [Google Scholar]
  69. Cassisi, C.; Montalto, P.; Aliotta, M.; Cannata, A.; Pulvirenti, A. Similarity measures and dimensionality reduction techniques for time series data mining. Adv. Data Min. Knowl. Discov. Appl. 2012, 71–96. [Google Scholar]
  70. Neal, C.; Brantley, S.; Antolik, L.; Babb, J.; Burgess, M.; Calles, K.; Cappos, M.; Chang, J.; Conway, S.; Desmither, L.; et al. The 2018 rift eruption and summit collapse of Kīlauea Volcano. Science 2019, 363, 367–374. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 13 00867 g001 550
Figure 1. Sentinel-1 frames covering the Yellowstone area. The Yellowstone National Park boundaries are outlined with magenta. White markers show the locations of permanent GNSS stations in the area covered by the frames.
Figure 1. Sentinel-1 frames covering the Yellowstone area. The Yellowstone National Park boundaries are outlined with magenta. White markers show the locations of permanent GNSS stations in the area covered by the frames.
Remotesensing 13 00867 g001
Remotesensing 13 00867 g002 550
Figure 2. Coverage of the descending frame of Path 87, Frame 527. White markers show the locations of permanent GNSS stations that we used in this study.
Figure 2. Coverage of the descending frame of Path 87, Frame 527. White markers show the locations of permanent GNSS stations that we used in this study.
Remotesensing 13 00867 g002
Remotesensing 13 00867 g003 550
Figure 3. Acquisitions processed, blue and red dots mark which orbit were used when discussing precise orbit and realtime orbit processing, respectively.
Figure 3. Acquisitions processed, blue and red dots mark which orbit were used when discussing precise orbit and realtime orbit processing, respectively.
Remotesensing 13 00867 g003
Remotesensing 13 00867 g004 550
Figure 4. Top row: Cumulative displacement over the big island of Hawaii between January 2017 and June 2018 with no atmospheric correction applied (left), European Centre for Medium-Range Weather Forecasts (ECMWF) (middle) and Generic Atmospheric Correction Online Service (GACOS) (right) atmospheric correction applied. In the cumulative displacement plots, high (red) values mark an uplift, while low (blue) values mark subsidence. Bottom row: Differences between each of the cumulative displacement results.
Figure 4. Top row: Cumulative displacement over the big island of Hawaii between January 2017 and June 2018 with no atmospheric correction applied (left), European Centre for Medium-Range Weather Forecasts (ECMWF) (middle) and Generic Atmospheric Correction Online Service (GACOS) (right) atmospheric correction applied. In the cumulative displacement plots, high (red) values mark an uplift, while low (blue) values mark subsidence. Bottom row: Differences between each of the cumulative displacement results.
Remotesensing 13 00867 g004
Remotesensing 13 00867 g005 550
Figure 5. Left: Location of the three GNSS stations that we used for the comparison. Right panels: Comparison of GNSS time series and the displacement time series of the corresponding DInSAR pixel. Grey lines show the GNSS displacement converted to the satellite Line-of-Sight (LOS), and yellow, orange and blue symbols show the DInSAR time series for the different atmospheric corrections applied: no correction applied, the ECMWF correction applied and the GACOS correction applied, respectively. The Euclidean distance, d, is shown in each panel, where the smaller value represents a better fit between the time series.
Figure 5. Left: Location of the three GNSS stations that we used for the comparison. Right panels: Comparison of GNSS time series and the displacement time series of the corresponding DInSAR pixel. Grey lines show the GNSS displacement converted to the satellite Line-of-Sight (LOS), and yellow, orange and blue symbols show the DInSAR time series for the different atmospheric corrections applied: no correction applied, the ECMWF correction applied and the GACOS correction applied, respectively. The Euclidean distance, d, is shown in each panel, where the smaller value represents a better fit between the time series.
Remotesensing 13 00867 g005
Remotesensing 13 00867 g006 550
Figure 6. Interferograms computed between 10 June 2018 and 16 June 2018 using real-time (left) and precise (middle) orbits. The (right) panel shows the difference, note the change of scale. On this plot, we show the unwrapped phase where high (purple) values represent an LOS increase in distance from the satellite, which means subsidence on the ground. Consequently, low (orange) values mark a decrease in the LOS distance, which means uplift on the ground.
Figure 6. Interferograms computed between 10 June 2018 and 16 June 2018 using real-time (left) and precise (middle) orbits. The (right) panel shows the difference, note the change of scale. On this plot, we show the unwrapped phase where high (purple) values represent an LOS increase in distance from the satellite, which means subsidence on the ground. Consequently, low (orange) values mark a decrease in the LOS distance, which means uplift on the ground.
Remotesensing 13 00867 g006
Remotesensing 13 00867 g007 550
Figure 7. Cumulative displacement over the big island of Hawaii between January 2017 and June 2018 using real-time (left) and precise (right) orbits.
Figure 7. Cumulative displacement over the big island of Hawaii between January 2017 and June 2018 using real-time (left) and precise (right) orbits.
Remotesensing 13 00867 g007
Remotesensing 13 00867 g008 550
Figure 8. Using the same dataset from Figure 7: Differences in cumulative displacements at time-steps ((a) 1, (b) 15, (c) 30 and (d) 42, the entire processing time).
Figure 8. Using the same dataset from Figure 7: Differences in cumulative displacements at time-steps ((a) 1, (b) 15, (c) 30 and (d) 42, the entire processing time).
Remotesensing 13 00867 g008
Remotesensing 13 00867 g009 550
Figure 9. Top row: Cumulative displacement calculated from Frame 49-142 between May 2017 and August 2018 with no atmospheric correction applied (left), ECMWF (middle) and GACOS (right) atmospheric correction applied. In the cumulative displacement plots, high (red) values mark an uplift, while low (blue) values mark subsidence. Bottom row: Differences between each of the cumulative displacement results.
Figure 9. Top row: Cumulative displacement calculated from Frame 49-142 between May 2017 and August 2018 with no atmospheric correction applied (left), ECMWF (middle) and GACOS (right) atmospheric correction applied. In the cumulative displacement plots, high (red) values mark an uplift, while low (blue) values mark subsidence. Bottom row: Differences between each of the cumulative displacement results.
Remotesensing 13 00867 g009
Remotesensing 13 00867 g010 550
Figure 10. Cumulative displacements between May 2017 and August 2018 over the Yellowstone area (see details about each frame in Table 1) obtained from four different acquisition frames of Sentinel-1 data. Red areas show uplift, which is apparently coinciding with steep valleys. Blue areas represent subsidence; black circles identify consistent subsidence on all four images.
Figure 10. Cumulative displacements between May 2017 and August 2018 over the Yellowstone area (see details about each frame in Table 1) obtained from four different acquisition frames of Sentinel-1 data. Red areas show uplift, which is apparently coinciding with steep valleys. Blue areas represent subsidence; black circles identify consistent subsidence on all four images.
Remotesensing 13 00867 g010
Remotesensing 13 00867 g011 550
Figure 11. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 27-444 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Figure 11. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 27-444 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Remotesensing 13 00867 g011
Remotesensing 13 00867 g012 550
Figure 12. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 49-142 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Figure 12. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 49-142 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Remotesensing 13 00867 g012
Remotesensing 13 00867 g013 550
Figure 13. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 100-441/446 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Figure 13. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 100-441/446 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Remotesensing 13 00867 g013
Remotesensing 13 00867 g014 550
Figure 14. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 122-141 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Figure 14. Comparison of GNSS displacement with displacement derived from the corresponding DInSAR pixel in the 122-141 frame. The displacements are shown in the LOS direction of the DInSAR data acquisition.
Remotesensing 13 00867 g014
Table
Table 1. Details of the Sentinel-1 DInSAR data presented in this paper.
Table 1. Details of the Sentinel-1 DInSAR data presented in this paper.
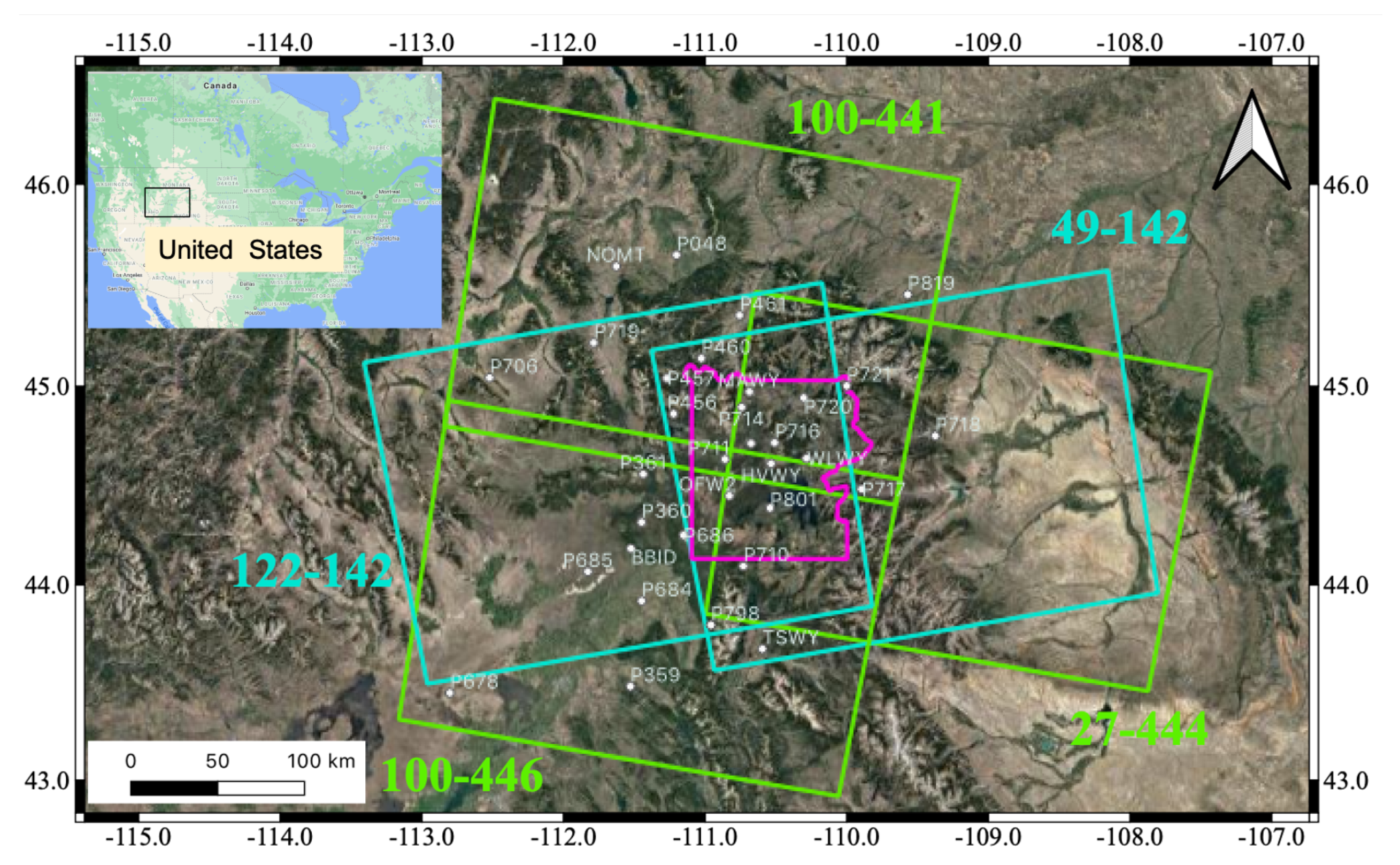
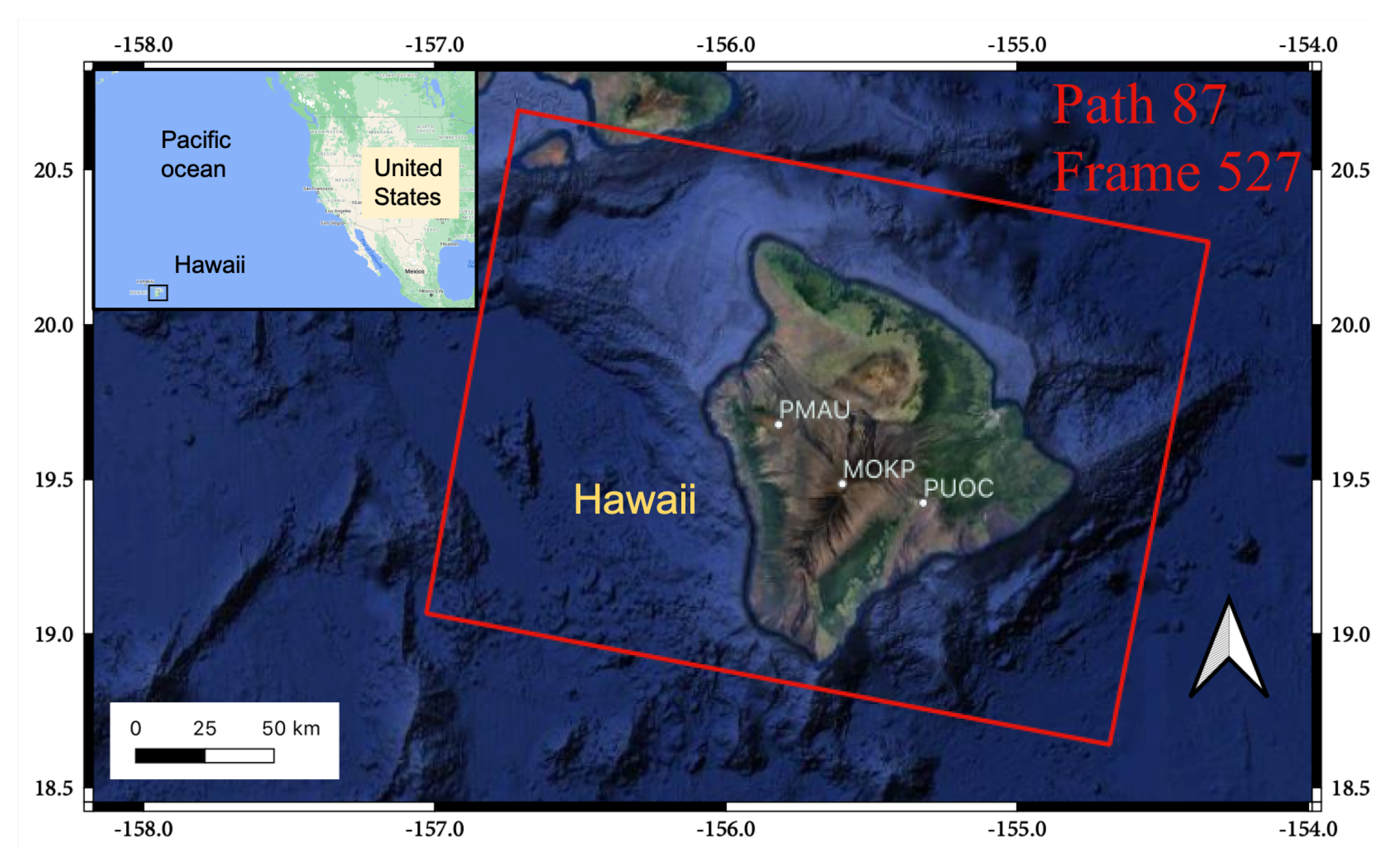
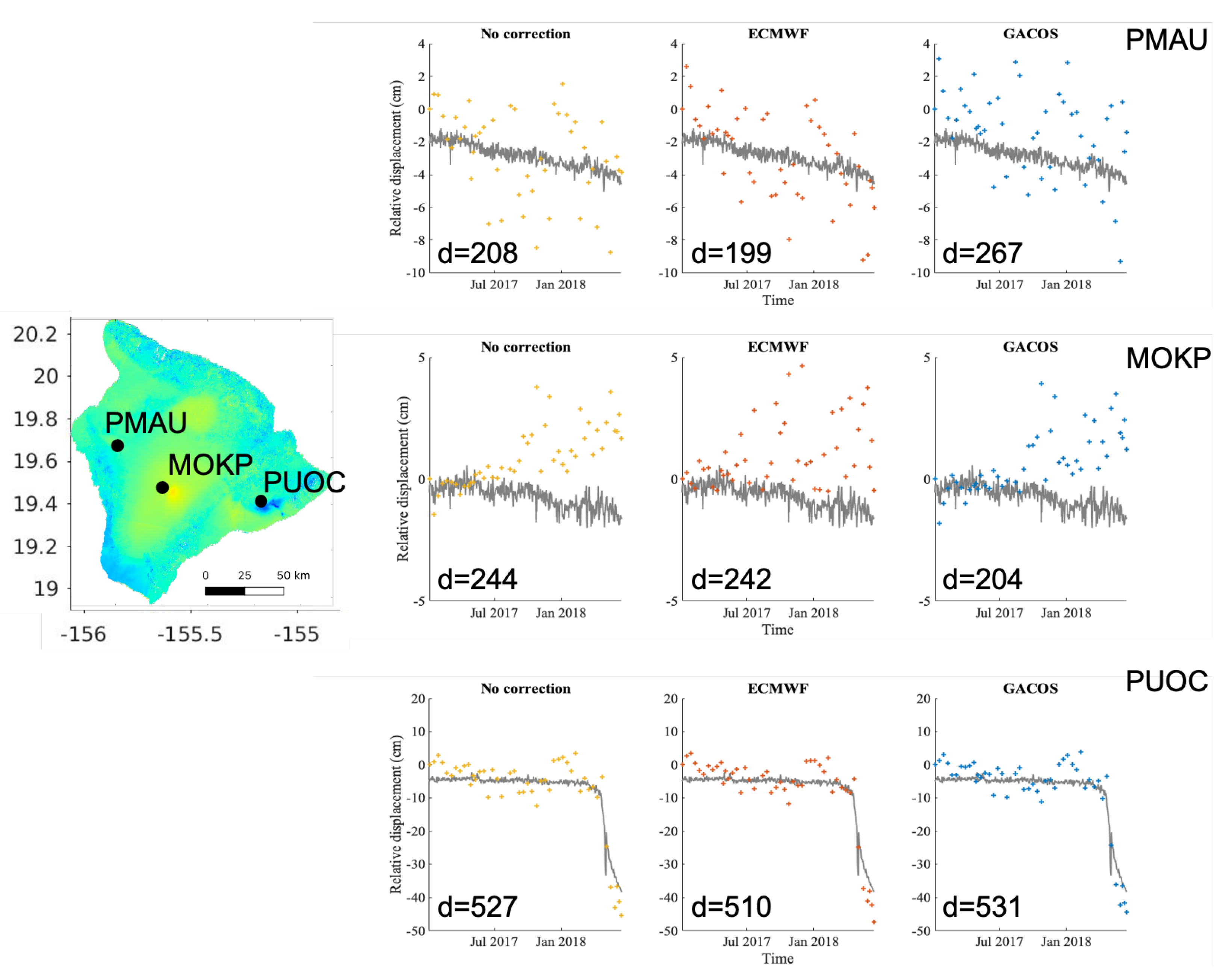
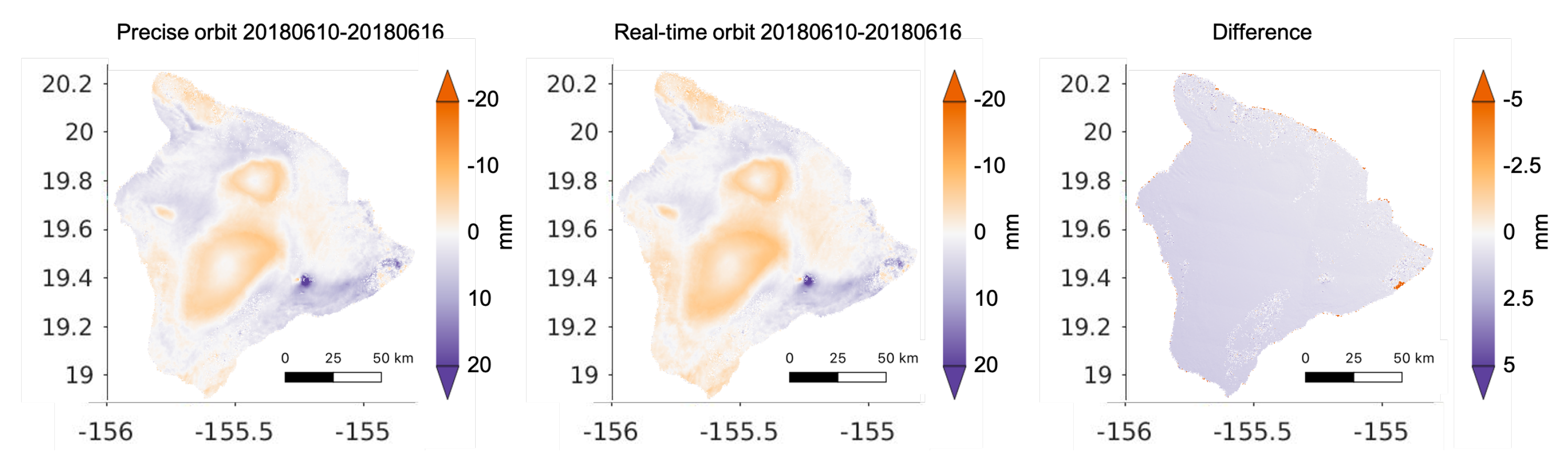
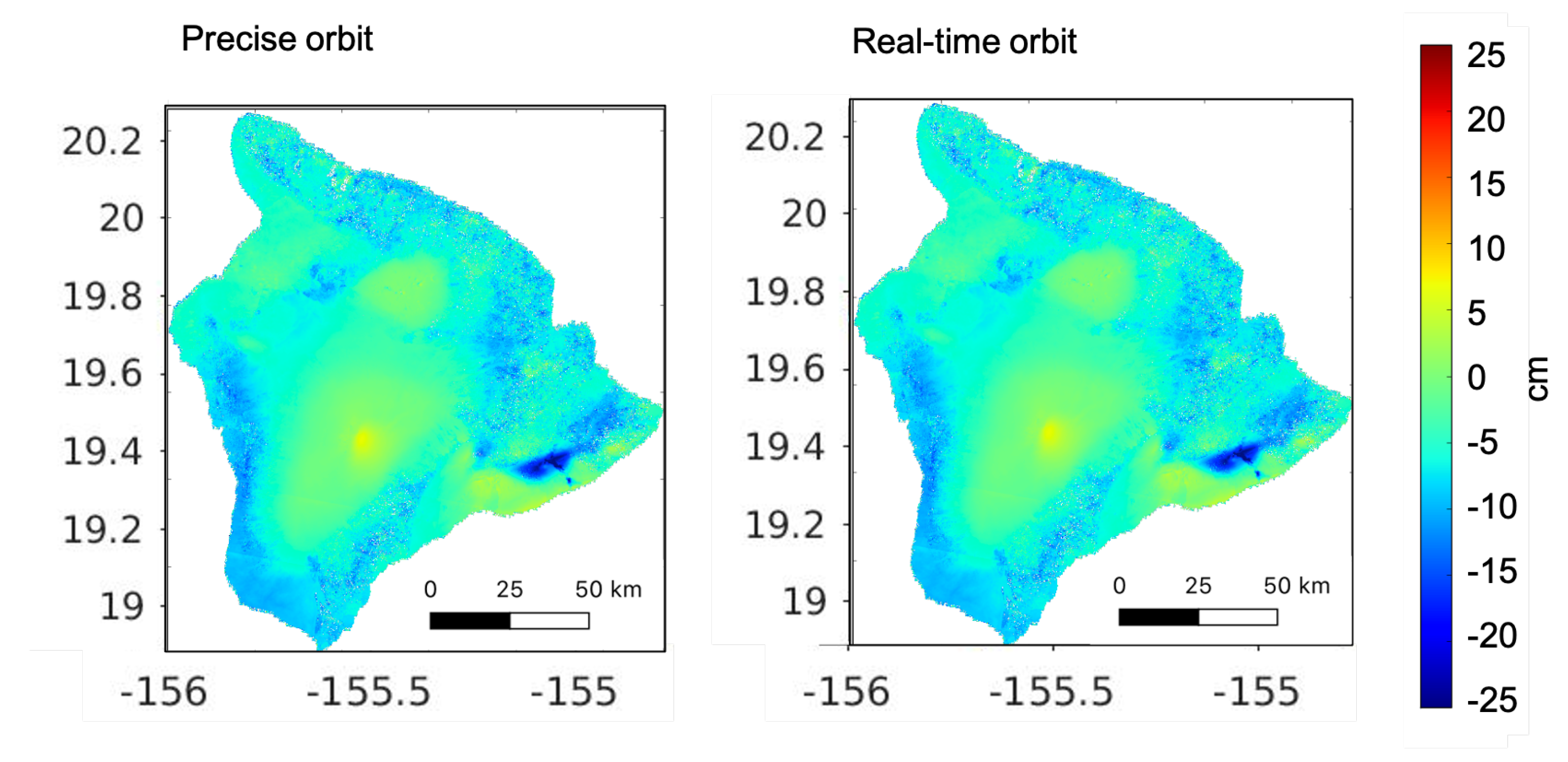
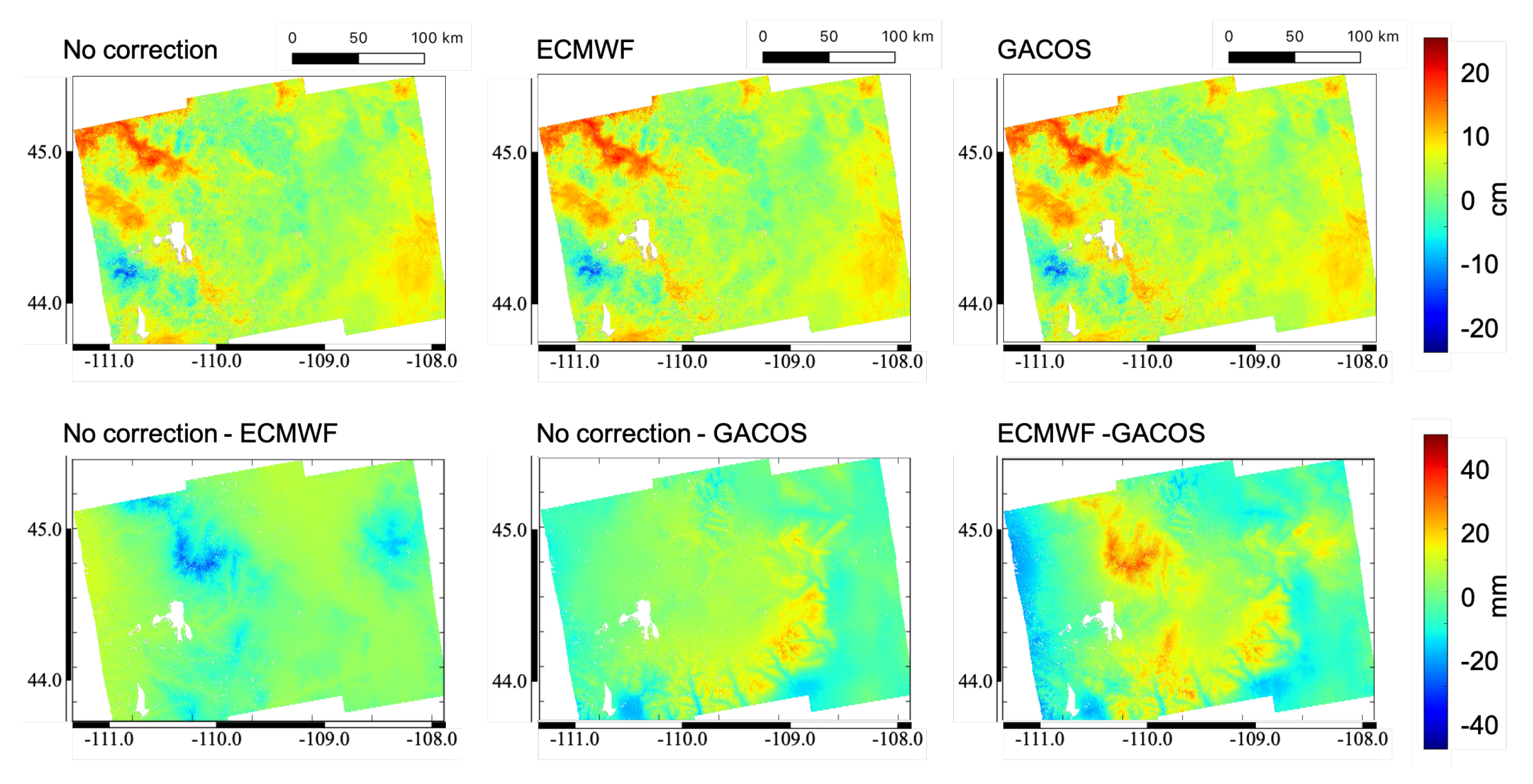
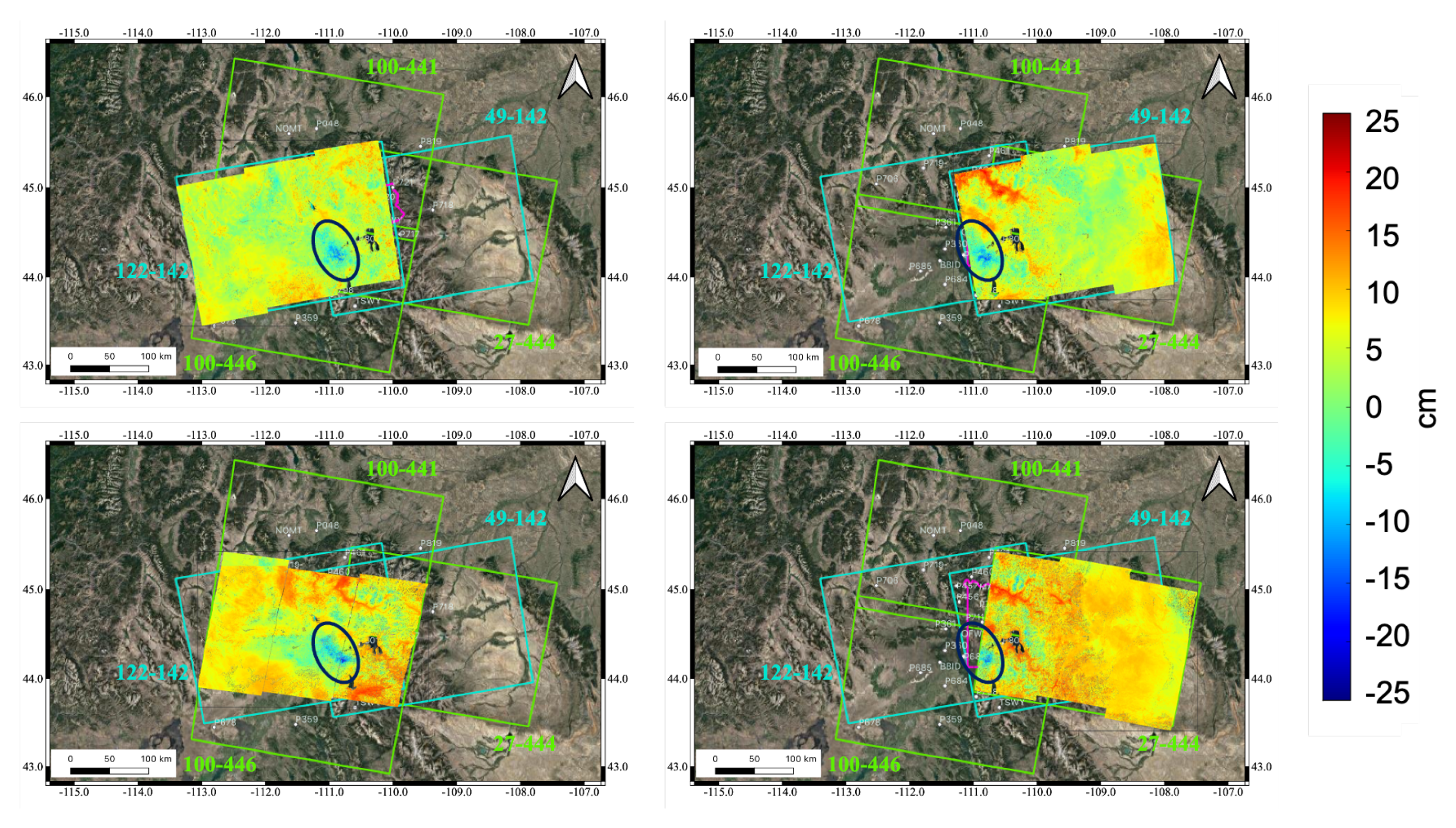
LocationKilaueaYellowstoneYellowstoneYellowstoneYellowstone
Directiondescendingascendingascendingdescendingdescending
Track874912210027
Frame527142141441/446444
Time range start4 January 20178 January 201714 March 201722 February 201730 April 2017
Time range end16 June 201817 December 201831 July 201819 January 201930 July 2018
No. of scenes4541304933
No. of IFGs114947912170
master image3 June 201715 May 201824 July 201714 September 201716 August 2017
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Kelevitz, K.; Tiampo, K.F.; Corsa, B.D. Improved Real-Time Natural Hazard Monitoring Using Automated DInSAR Time Series. Remote Sens. 2021, 13, 867. https://doi.org/10.3390/rs13050867

AMA Style

Kelevitz K, Tiampo KF, Corsa BD. Improved Real-Time Natural Hazard Monitoring Using Automated DInSAR Time Series. Remote Sensing. 2021; 13(5):867. https://doi.org/10.3390/rs13050867

Chicago/Turabian Style

Kelevitz, Krisztina, Kristy F. Tiampo, and Brianna D. Corsa. 2021. "Improved Real-Time Natural Hazard Monitoring Using Automated DInSAR Time Series" Remote Sensing 13, no. 5: 867. https://doi.org/10.3390/rs13050867

APA Style

Kelevitz, K., Tiampo, K. F., & Corsa, B. D. (2021). Improved Real-Time Natural Hazard Monitoring Using Automated DInSAR Time Series. Remote Sensing, 13(5), 867. https://doi.org/10.3390/rs13050867

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop