Unmanned Aerial Vehicle Depth Inversion to Monitor River-Mouth Bar Dynamics
Abstract
1. Introduction
2. Video Acquisition and Rectification
2.1. Field Site: Suruga Coast (Japan)
2.2. Image Acquisition and Rectification
3. Depth Estimation Method
3.1. Depth Inversion
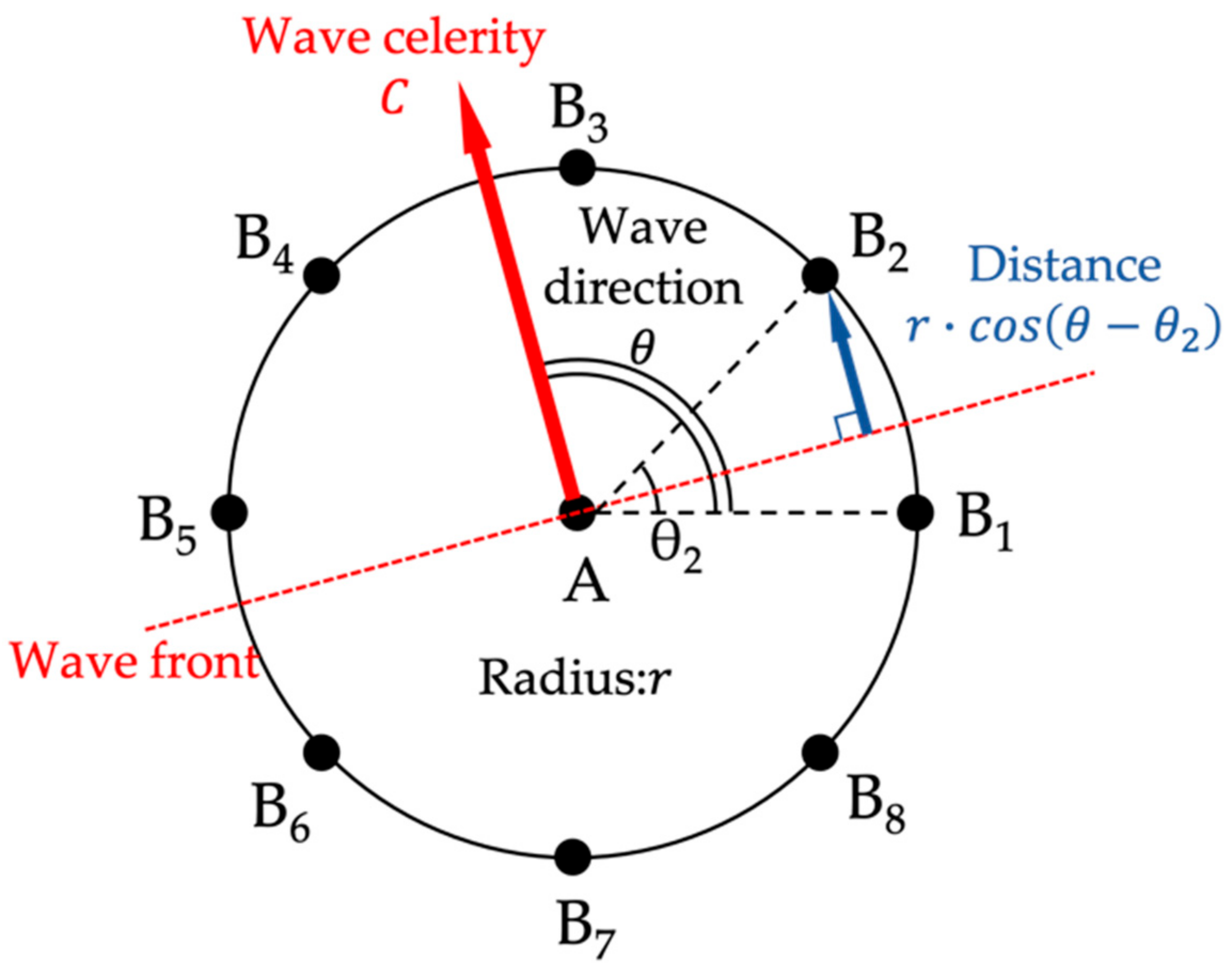
3.2. Estimation of Wave Celerity and Direction
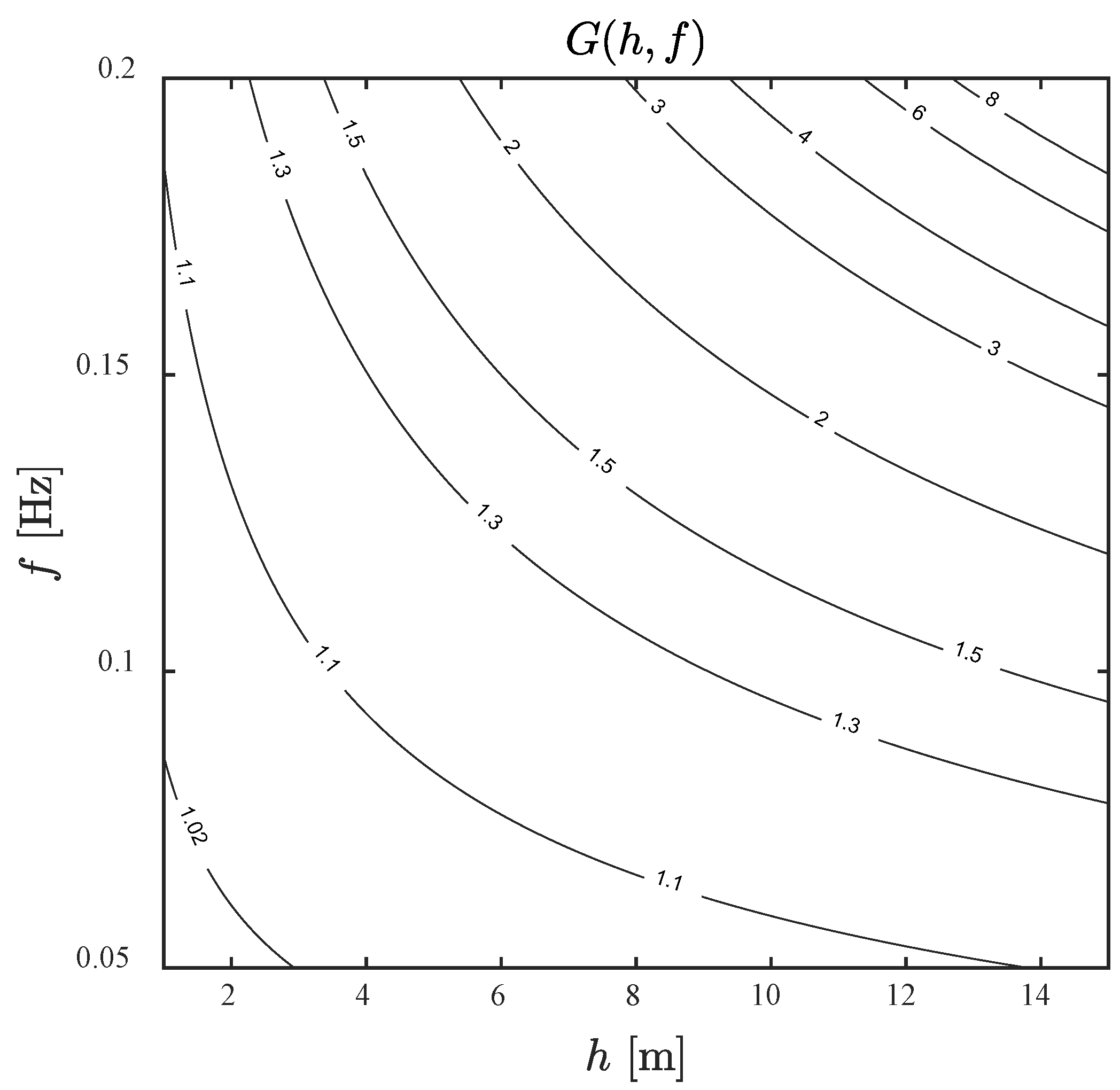
3.3. Estimation of Wave Frequency
4. Results
4.1. Estimated Bathymetry
4.2. Validation
5. Discussion
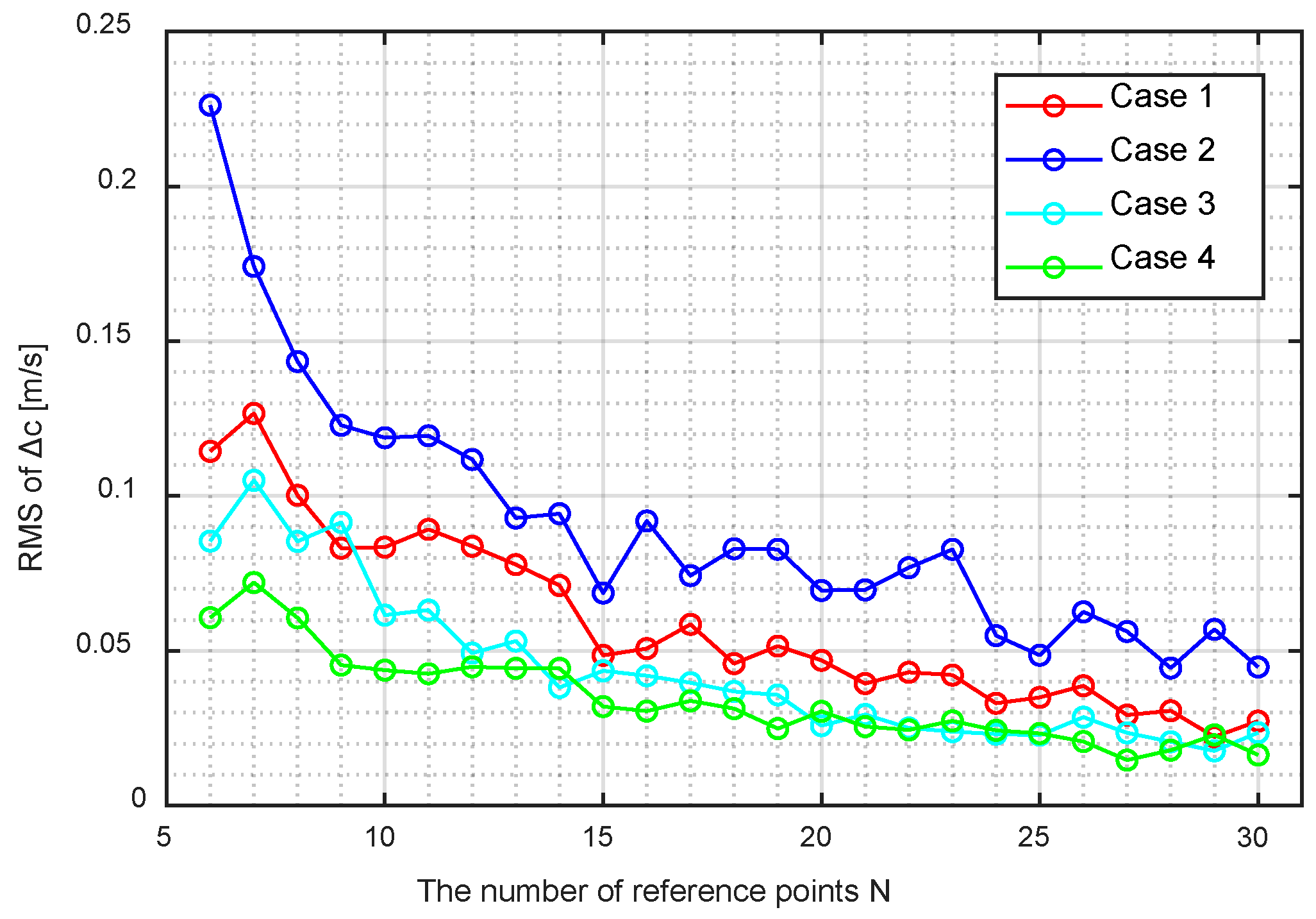
5.1. Optimal Estimation Parameters
5.2. Required Video Length
5.3. Applicability to Bathymetry Monitoring
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Δxp | 3 m | Pixel cross-shore spacing |
| Δyp | 5 m | Pixel along-shore spacing |
| Δt | 0.167 s | Time series sampling interval |
| Δxm | 6 m | Cross-shore analysis point spacing |
| Δym | 10 m | Alongshore analysis point spacing |
| Lx | 18 m | Analysis smoothing scale in x |
| Ly | 30 m | Analysis smoothing scale in y |
| κ | 2 | Smoothing scale expansion at outer boundary |
| hmin | 0.25 m | Minimum acceptable depth |
| smin | 0.5 | Minimum acceptable skill |
| λ | 10 | Minimum acceptable normalised eigenvalue |
| f | [1/18, 1/50, 1/4] | Analysis of frequency bins |
| Nkeep | 4 | Number of frequency bins to retain |
References
- Vitousek, S.; Barnard, P.L.; Limber, P. Can beaches survive climate change? J. Geophys. Res. Earth Surf. 2017, 122, 1060–1067. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy coastlines under threat of erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Wright, L. Sediment transport and deposition at river mouths: A synthesis. Geol. Soc. Am. Bull. 1977, 88, 857–868. [Google Scholar] [CrossRef]
- Warrick, J. Littoral sediment from rivers: Patterns, rates and processes of river mouth morphodynamics. Front. Earth Sci. 2020, 8, 355. [Google Scholar] [CrossRef]
- Nienhuis, J.H.; Ashton, A.D.; Nardin, W.; Fagherazzi, S.; Giosan, L. Alongshore sediment bypassing as a control on river mouth morphodynamics. J. Geophys. Res. Earth Surf. 2016, 121, 664–683. [Google Scholar] [CrossRef]
- Lippmann, T.C.; Holman, R.A. The spatial and temporal variability of sand bar morphology. J. Geophys. Res. Oceans 1991, 95, 11575–11590. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. Oceans 2000, 105, 22015–22033. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. cBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. Oceans 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D.; Luque, P.; Orfila, A.; Ribas, F. UBathy: A New Approach for Bathymetric Inversion from Video Imagery. Remote Sens. 2019, 11, 2722. [Google Scholar] [CrossRef]
- Bos, C. Wave Characteristics Derived from Video. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave celerity from video imaging: A new method. In Proceedings of the 31st Conference on Coastal Engineering, Humburg, Germany, 31 August–5 September 2008; Smith, J.M., Ed.; World Scientific: Singapore, 2009; pp. 661–673. [Google Scholar]
- Ondoa, G.A.; Almar, R.; Castelle, B.; Testut, L.; Léger, F.; Sohou, Z.; Bonou, F.; Bergsma, E.W.J.; Meyssignac, B.; Larson, M. Sea level at the coast from video-sensed waves: Comparison to tidal gauges and satellite altimetry. J. Atmos. Ocean. Technol. 2019, 36, 1591–1603. [Google Scholar] [CrossRef]
- Thuan, D.H.; Binh, L.T.; Viet, N.T.; Hanh, D.K.; Almar, R.; Marchesiello, P. Typhoon impact and recovery from continuous video monitoring: A case study from Nha Trang Beach, Vietnam. J. Coast. Res. 2016, 75, 263–267. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef]
- Radermacher, M.; De Schipper, M.A.; Reniers, A.J.H.M. Sensitivity of rip current forecasts to errors in remotely-sensed bathymetry. Coast. Eng. 2018, 135, 66–76. [Google Scholar] [CrossRef]
- Holman, R.A.; Brodie, K.L.; Spore, N.J. Surf zone characterization using a small quadcopter: Technical issues and procedures. IEEE T. Geosci. Remote. 2017, 55, 2017–2027. [Google Scholar] [CrossRef]
- Brodie, K.L.; Bruder, B.L.; Slocum, R.K.; Spore, N.J. Simultaneous mapping of coastal topography and bathymetry from a lightweight multicamera UAS. IEEE T. Geosci. Remote. 2019, 57, 6844–6864. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Almar, R.; de Almeida, L.P.M.; Sall, M. On the operational use of UAVs for video-derived bathymetry. Coast. Eng. 2019, 152, 103527. [Google Scholar] [CrossRef]
- Tsukada, F.; Shimozono, T.; Matsuba, Y. UAV-based mapping of nearshore bathymetry over broad areas. Coast. Eng. J. 2020, 62, 285–298. [Google Scholar] [CrossRef]
- Suzuki, T.; Tajima, Y.; Watanabe, M.; Tsuruta, N.; Takagi, H.; Takabatake, T.; Suzuki, K.; Shimozono, T.; Shigihara, Y.; Shibayama, T.; et al. Post-event survey of locally concentrated disaster due to 2019 Typhoon Faxai along the western shore of Tokyo Bay, Japan. Coast. Eng. J. 2020, 62, 146–158. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A.; Lippmann, T.C.; Stanley, J.; Plant, N. Practical use of video imagery in nearshore oceanographic field studies. IEEE J. Ocean. Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Matsuba, Y.; Sato, S. Nearshore bathymetry estimation using UAV. Coast. Eng. J. 2018, 60, 51–59. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R. Video-based depth inversion techniques, a method comparison with synthetic cases. Coast. Eng. 2018, 138. [Google Scholar] [CrossRef]
- Andriolo, U. Nearshore Wave Transformation Domains from Video Imagery. J. Mar. Sci. Eng. 2019, 7, 186. [Google Scholar] [CrossRef]
- Thuan, D.H.; Almar, R.; Marchesiello, P.; Viet, N.T. Video Sensing of Nearshore Bathymetry Evolution with Error Estimate. J. Mar. Sci. Eng. 2019, 7, 233. [Google Scholar] [CrossRef]
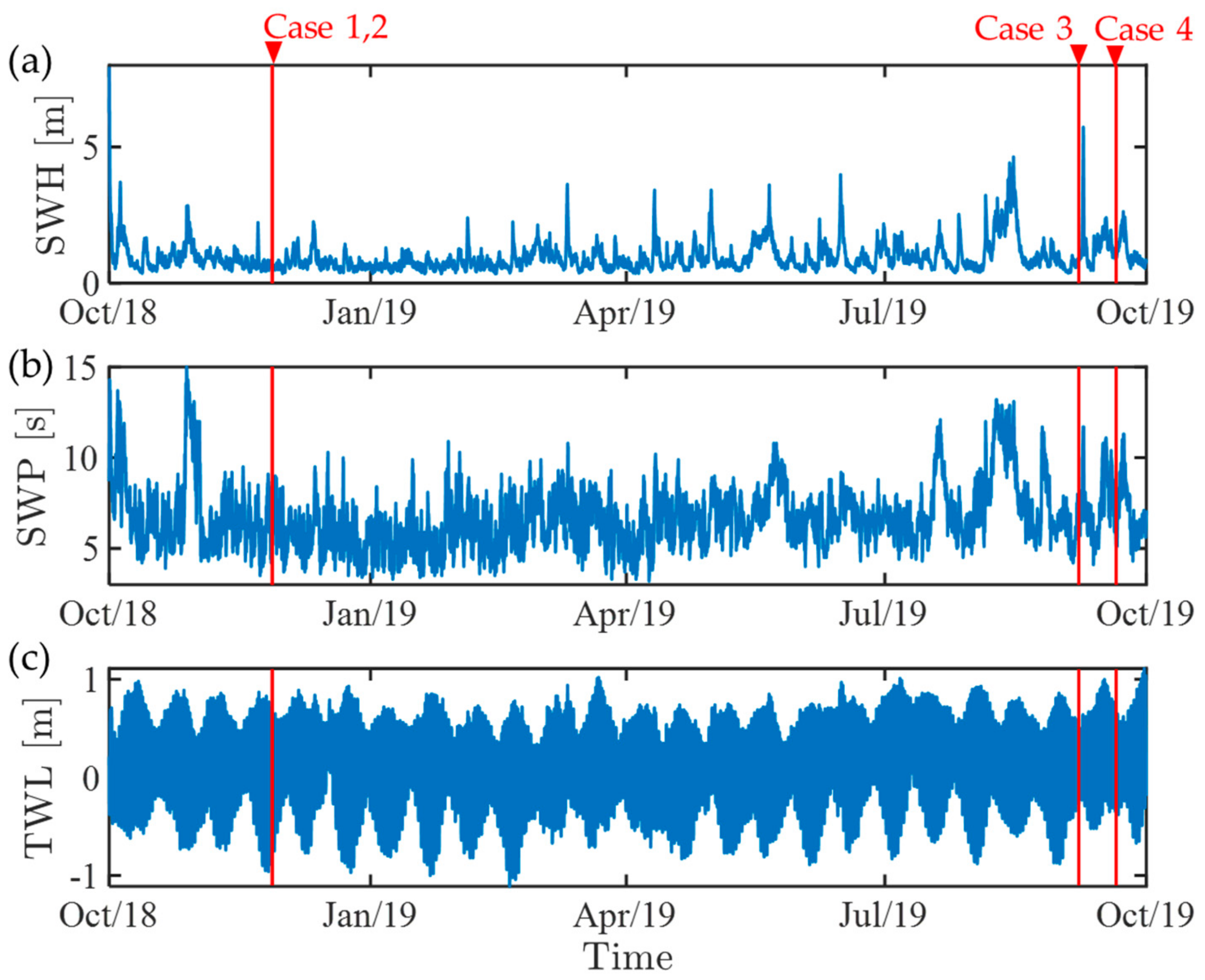


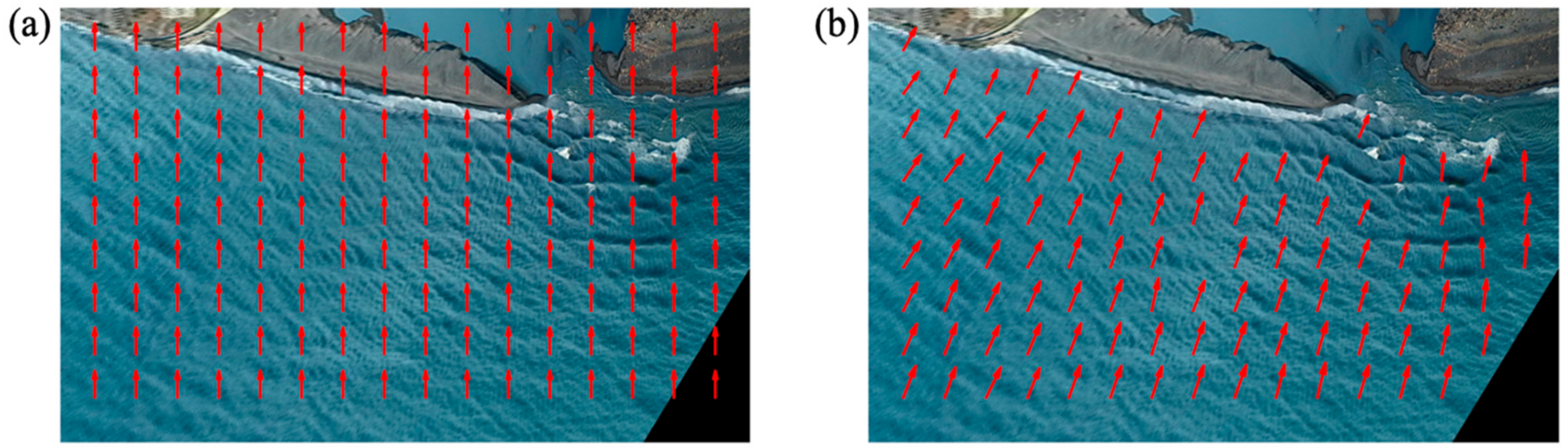
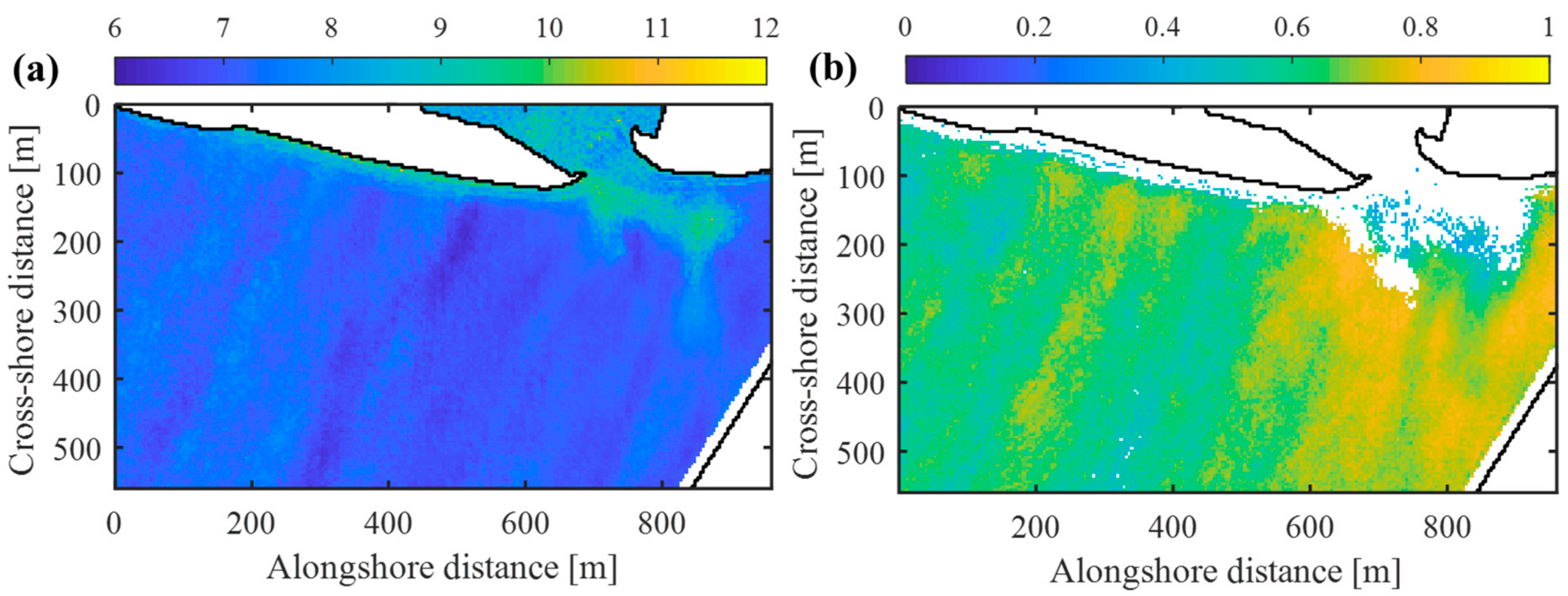

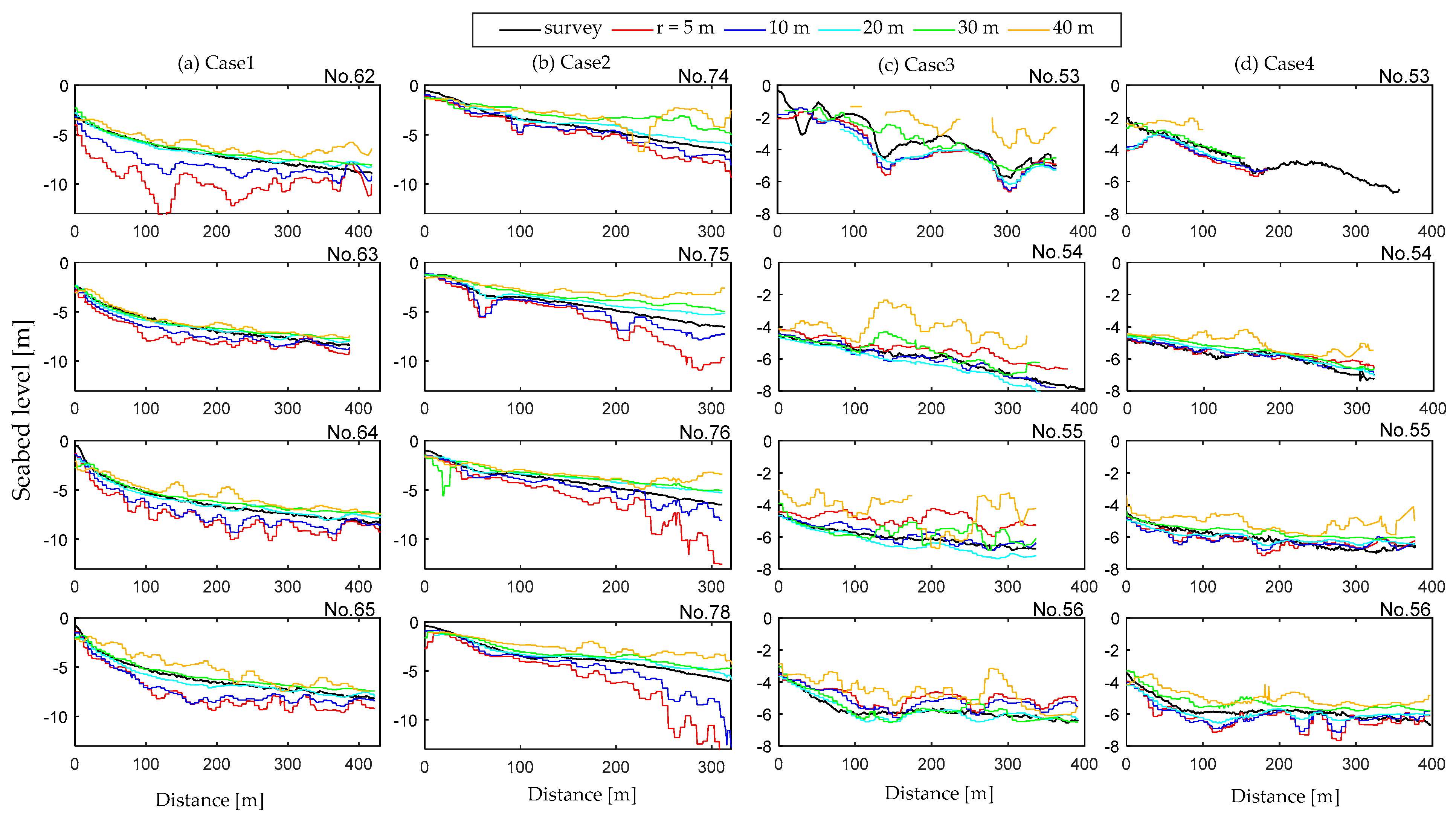
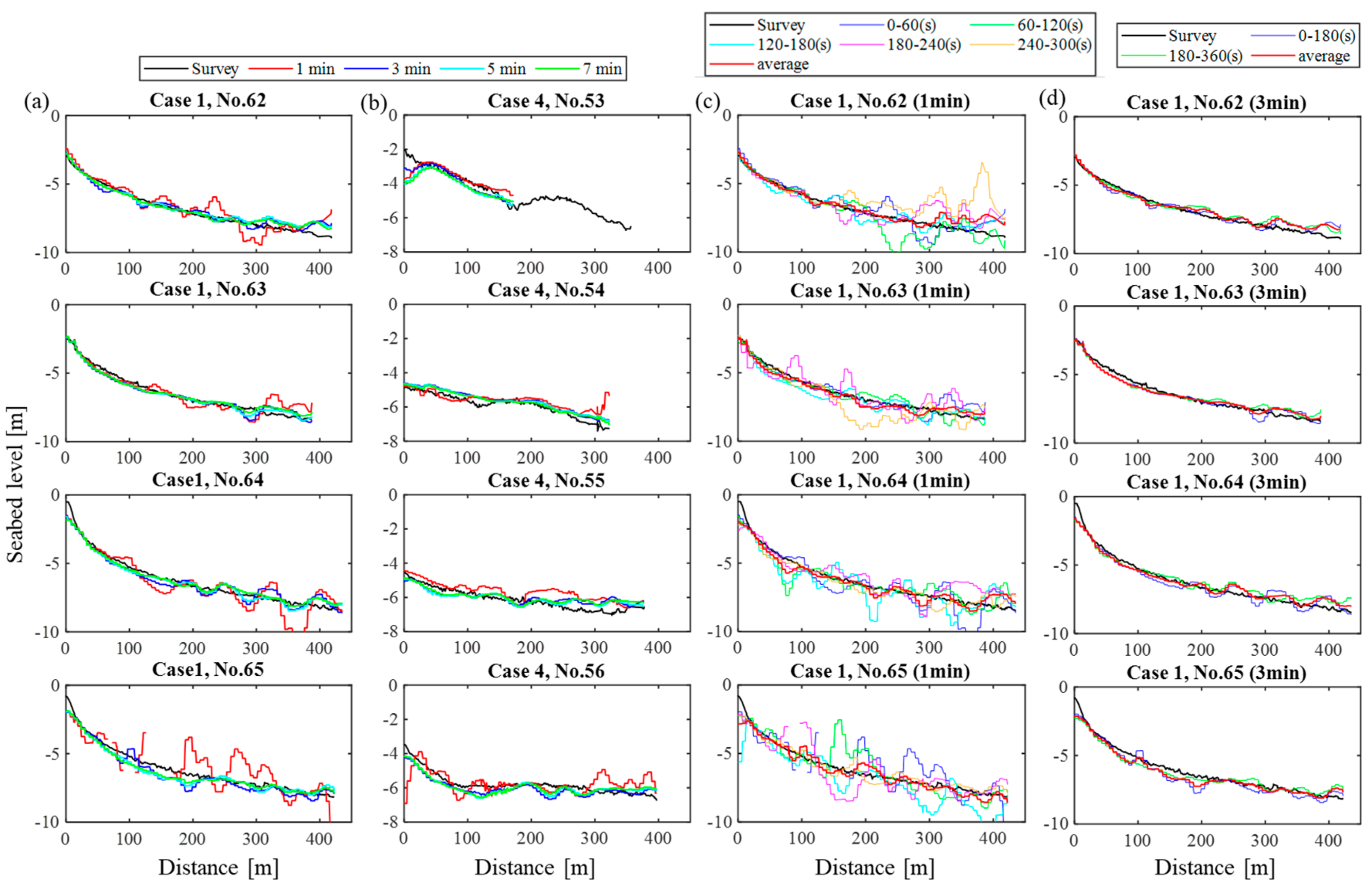

| Case | Area | Date/Time (JST) | SWH | SWP | TWL | Solar Angles 1 (Azimuth, Elevation) |
|---|---|---|---|---|---|---|
| Case 1 | A1 | 27 November 2018/8:41 | 0.60 m | 7.8 s | +0.67 m | (136.8°, 20.6°) |
| Case 2 | A2 | 27 November 2018/10:51 | 0.61 m | 8.6 s | +0.59 m | (168.0°, 33.2°) |
| Case 3 | A3 | 7 September 2019/6:08 | 0.89 m | 7.1 s | −0.31 m | (88.0°, 8.3°) |
| Case 4 | A3 | 20 September 2019/9:31 | 1.06 m | 5.5 s | +0.49 m | (130.9°, 44.9°) |
| Case | Area | Video Length | Mean Camera Position (longitude, Latitude, Altitude 1) | Mean Camera Angle 2 (Azimuth, Elevation) |
|---|---|---|---|---|
| Case 1 | A1 | 422 s | (138.2789°, 34.7609°, 153.6 m) | (184.8°, 34.8°) |
| Case 2 | A2 | 741 s | (138.2479°, 34.7431°, 100.9 m) | (100.9°, 61.5°) |
| Case 3 | A3 | 278 s | (138.2970°, 34.7721°, 142.4 m) | (202.6°, 76.6°) |
| Case 4 | A3 | 500 s | (138.2964°, 34.7701°, 145.0 m) | (210.3°, 66.9°) |
| Case | RMSE (present) | RMSE (cBathy) | Domain-Averaged Tr | Domain-Averaged R | Video-Shooting Date | Survey Date |
|---|---|---|---|---|---|---|
| Case 1 | 0.33 m | 0.47 m | 8.2 s | 0.68 | 27 November 2018 | 24 October 2018 |
| Case 2 | 0.52 m | 0.56 m | 8.6 s | 0.53 | 27 November 2018 | 24 October 2018 |
| Case 3 | 0.49 m | 0.65 m | 7.4 s | 0.64 | 7 September 2019 | 3 September 2019 |
| Case 4 | 0.35 m | 0.38 m | 7.5 s | 0.68 | 20 September 2019 | 30 September 2019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashimoto, K.; Shimozono, T.; Matsuba, Y.; Okabe, T. Unmanned Aerial Vehicle Depth Inversion to Monitor River-Mouth Bar Dynamics. Remote Sens. 2021, 13, 412. https://doi.org/10.3390/rs13030412
Hashimoto K, Shimozono T, Matsuba Y, Okabe T. Unmanned Aerial Vehicle Depth Inversion to Monitor River-Mouth Bar Dynamics. Remote Sensing. 2021; 13(3):412. https://doi.org/10.3390/rs13030412
Chicago/Turabian StyleHashimoto, Kana, Takenori Shimozono, Yoshinao Matsuba, and Takumi Okabe. 2021. "Unmanned Aerial Vehicle Depth Inversion to Monitor River-Mouth Bar Dynamics" Remote Sensing 13, no. 3: 412. https://doi.org/10.3390/rs13030412
APA StyleHashimoto, K., Shimozono, T., Matsuba, Y., & Okabe, T. (2021). Unmanned Aerial Vehicle Depth Inversion to Monitor River-Mouth Bar Dynamics. Remote Sensing, 13(3), 412. https://doi.org/10.3390/rs13030412








