Continuous Multi-Angle Remote Sensing and Its Application in Urban Land Cover Classification
Abstract
1. Introduction
2. Characteristics of the Experimental Data
2.1. Differences between CMARS Data and Traditional RS Data
- similar solar radiation;
- similar solar incident angle;
- similar atmospheric conditions; and,
- same ground objects except for the moving objects (for example, vegetation in summer and winter is totally different, and dry soil is different after rain).
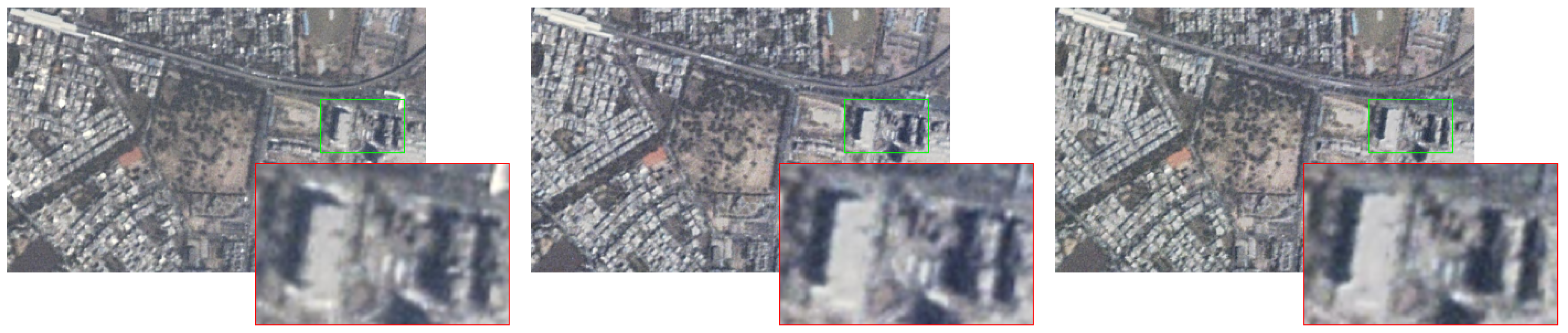
2.2. Experimental Data
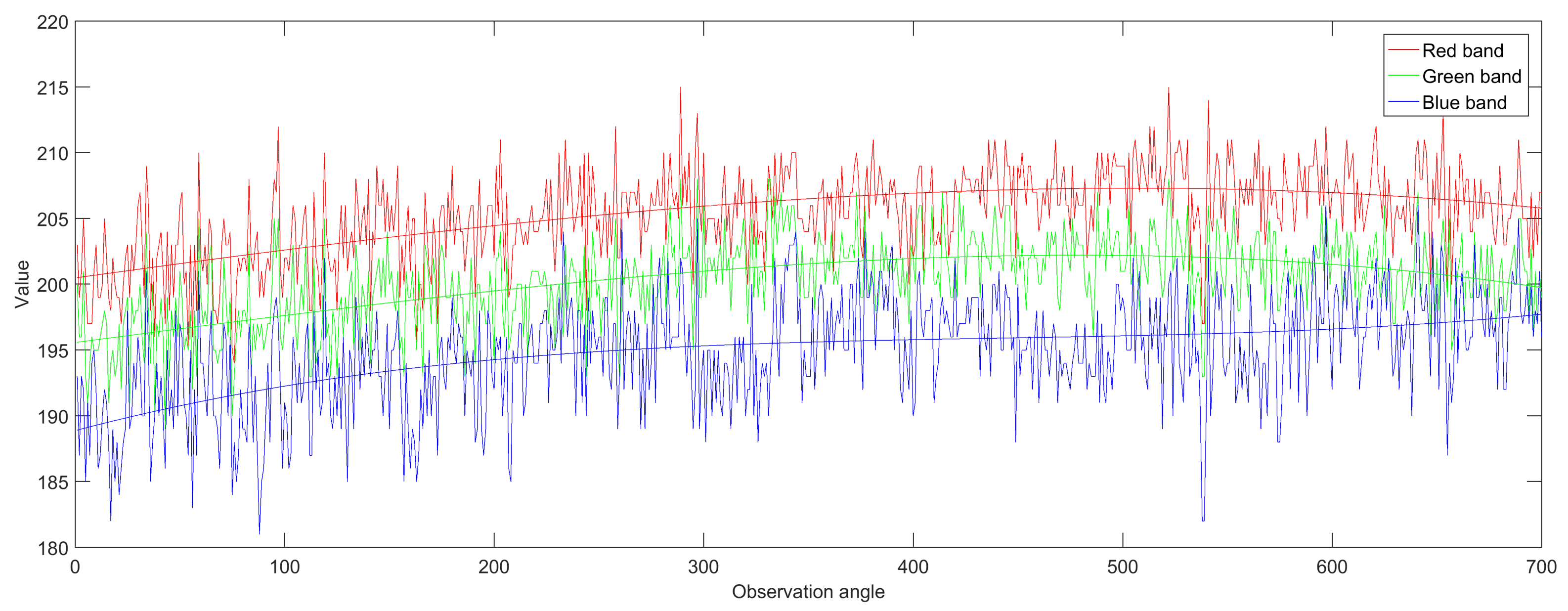
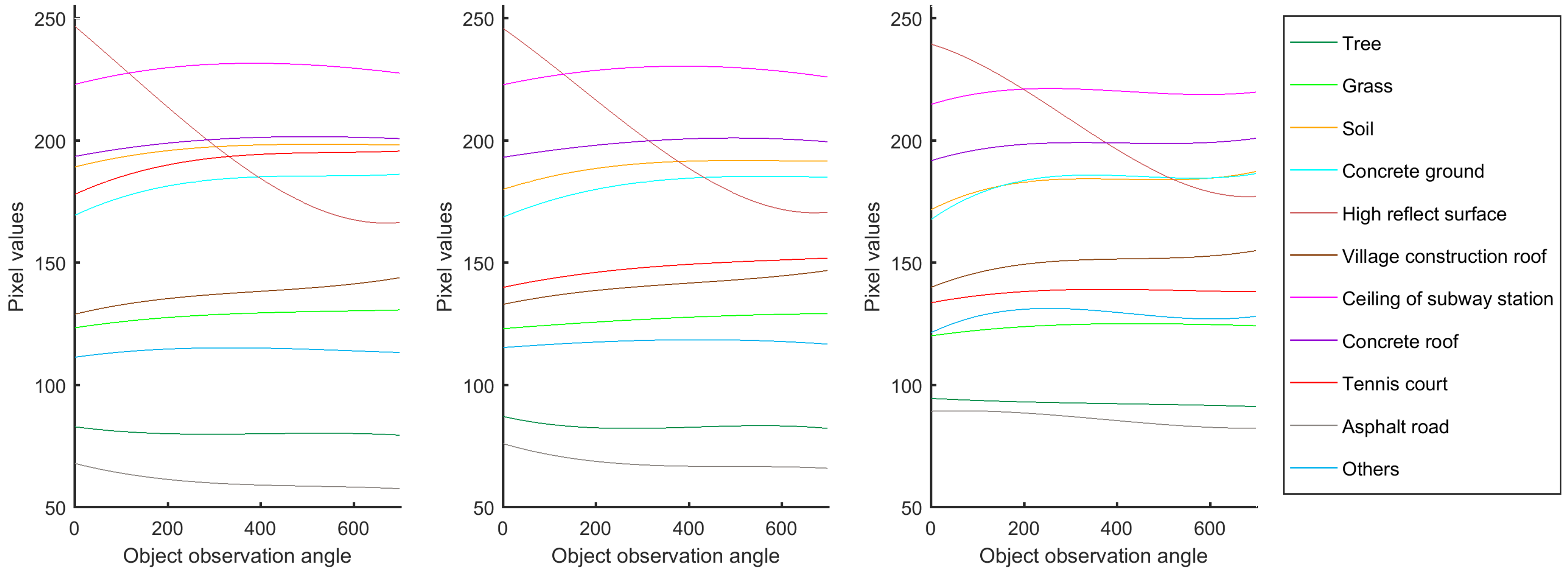
2.3. Pixel Level Analysis
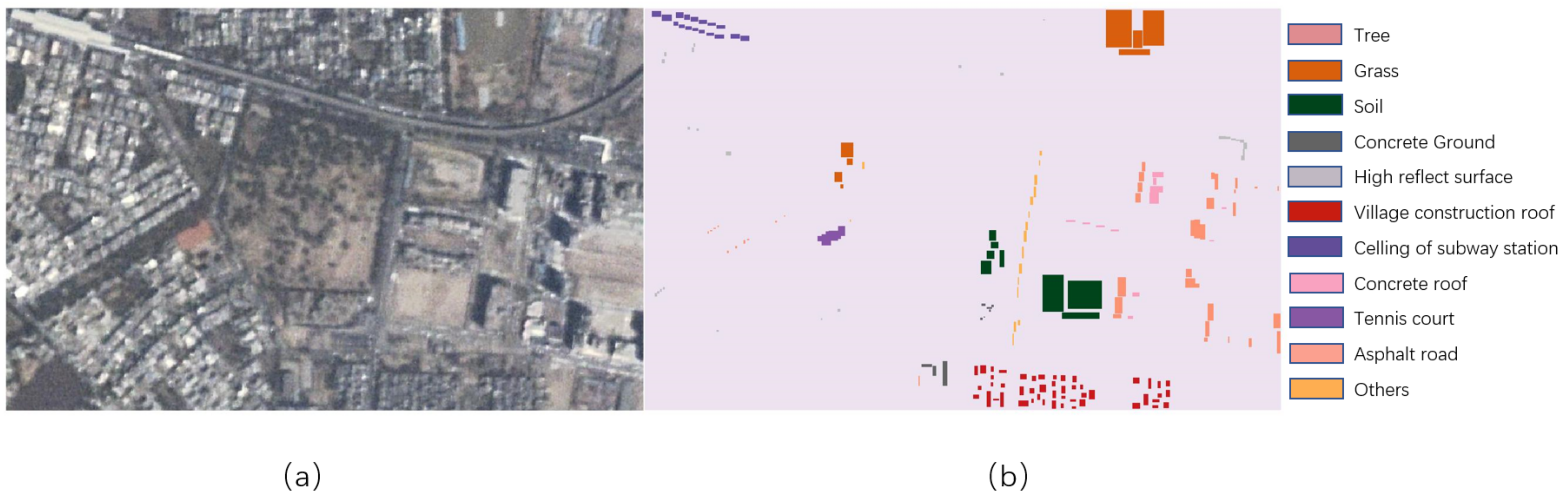
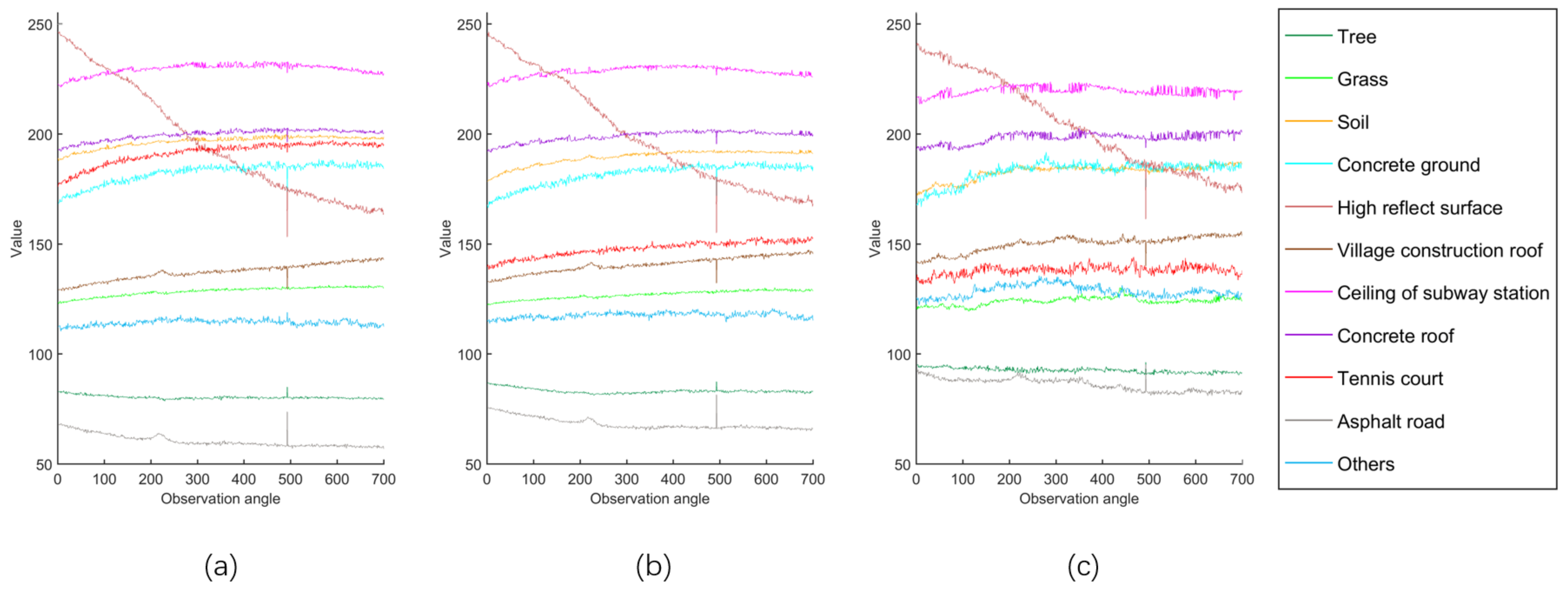
2.4. Analysis of Multiple Classes
3. Results
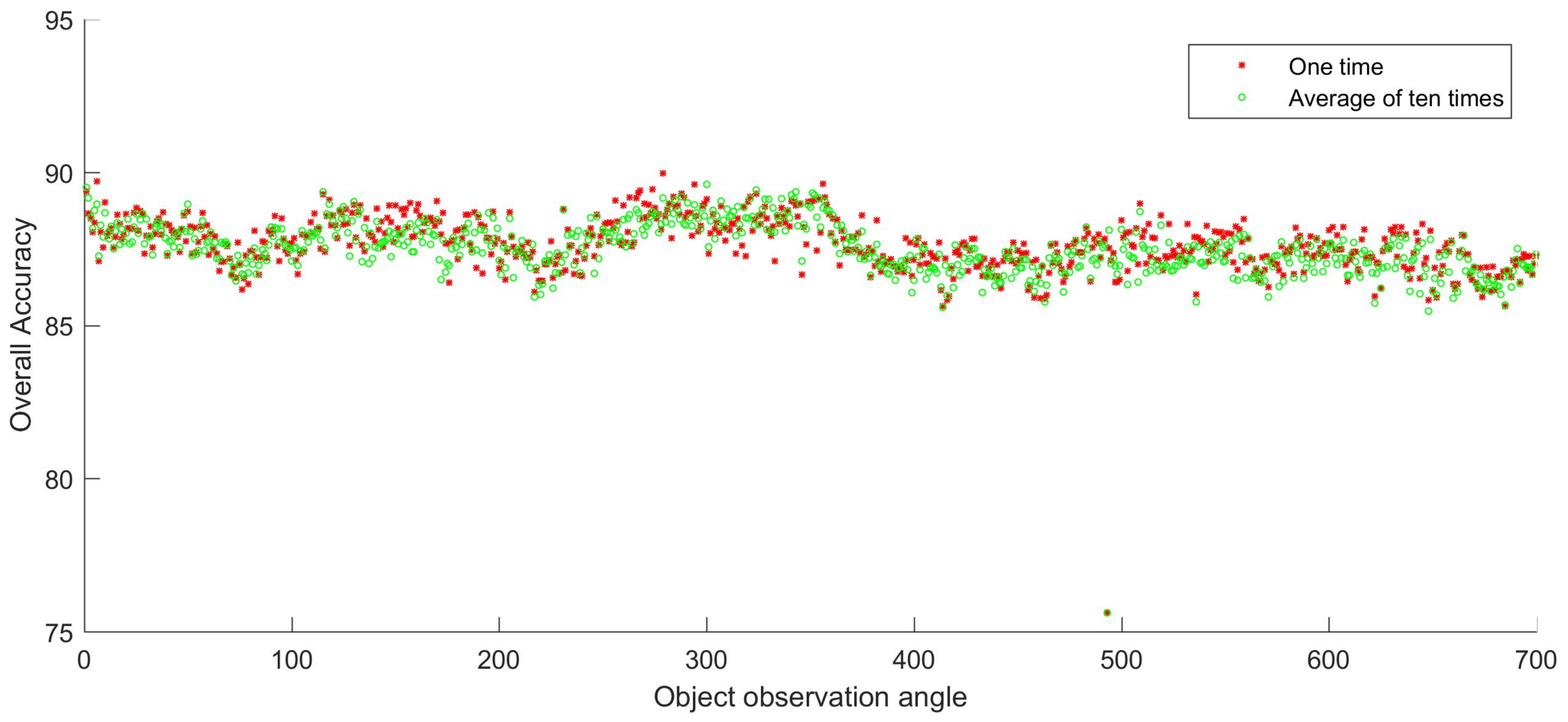
3.1. Single-Angle Classification on Raw Data
3.2. Multiple-Angle Classification on Raw Data
3.3. Classification with Extracted Geometric Features
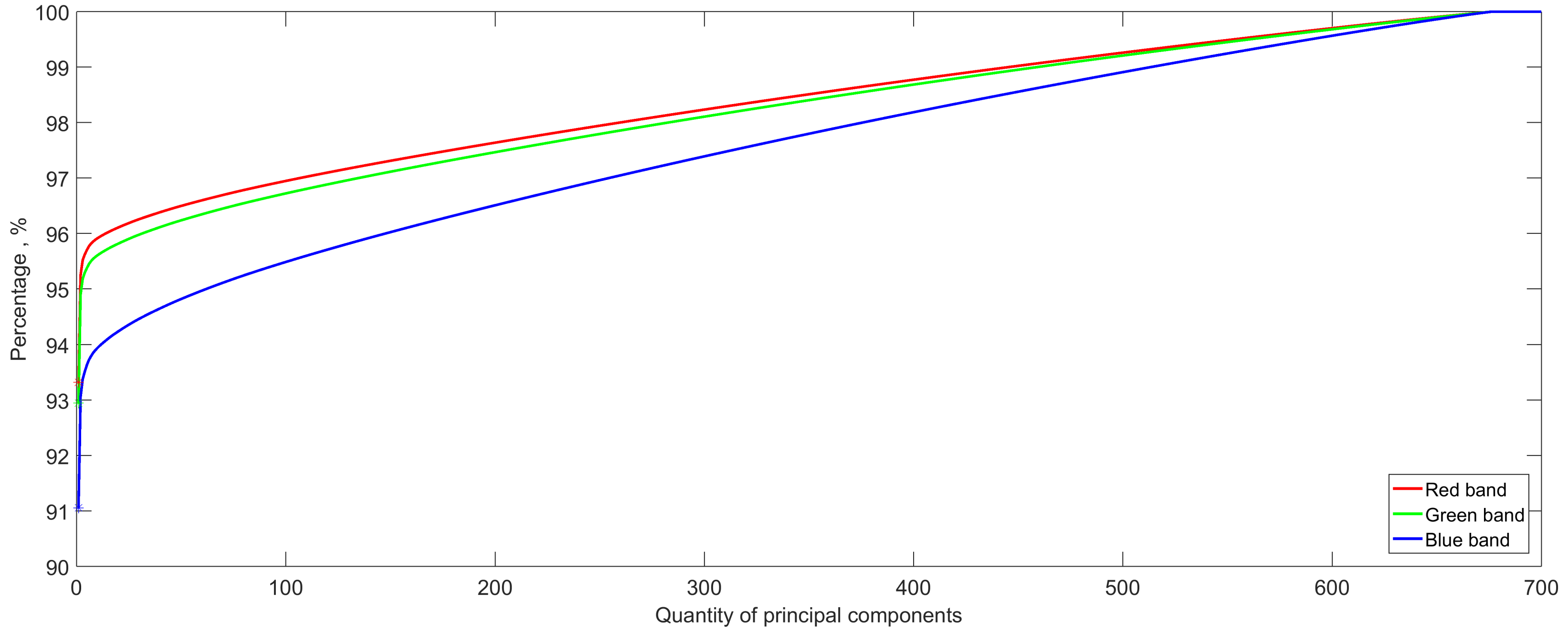
3.4. Classification Via PCA
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toth, C.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Lautenbacher, C.C. The global earth observation system of systems (GEOSS). In Proceedings of the 2005 IEEE International Symposium on Mass Storage Systems and Technology, Sardinia, Italy, 20–24 June 2005; pp. 47–50. [Google Scholar]
- Zhang, H.; Yang, Z.; Zhang, L.; Shen, H. Super-resolution reconstruction for multi-angle remote sensing images considering resolution differences. Remote Sens. 2014, 6, 637–657. [Google Scholar] [CrossRef]
- Huang, X.; Chen, H.; Gong, J. Angular difference feature extraction for urban scene classification using ZY-3 multi-angle high-resolution satellite imagery. ISPRS J. Photogramm. Remote Sens. 2018, 135, 127–141. [Google Scholar] [CrossRef]
- Molini, A.B.; Valsesia, D.; Fracastoro, G.; Magli, E. DeepSUM: Deep neural network for Super-resolution of Unregistered Multitemporal images. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3644–3656. [Google Scholar] [CrossRef]
- Shao, Z.; Tang, P.; Wang, Z.; Saleem, N.; Yam, S.; Sommai, C. BRRNet: A fully convolutional neural network for automatic building extraction from high-resolution remote sensing images. Remote Sens. 2020, 12, 1050. [Google Scholar] [CrossRef]
- Shao, Z.; Zhou, Z.; Huang, X.; Zhang, Y. MRENet: Simultaneous Extraction of Road Surface and Road Centerline in Complex Urban Scenes from Very High-Resolution Images. Remote Sens. 2021, 13, 239. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Rogan, J.; Kellndorfer, J. Assessment of spectral, polarimetric, temporal, and spatial dimensions for urban and peri-urban land cover classification using Landsat and SAR data. Remote Sens. Environ. 2012, 117, 72–82. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, B. Spatial and temporal classification of synthetic satellite imagery: Land cover mapping and accuracy validation. Geo-Spat. Inf. Sci. 2014, 17, 1–7. [Google Scholar] [CrossRef]
- Kong, F.; Li, X.; Wang, H.; Xie, D.; Li, X.; Bai, Y. Land cover classification based on fused data from GF-1 and MODIS NDVI time series. Remote Sens. 2016, 8, 741. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, C.; Cai, M.; Edward, N.Y.Y.; Wu, T. Classification of local climate zones using ASTER and Landsat data for high-density cities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3397–3405. [Google Scholar] [CrossRef]
- Chen, B.; Huang, B.; Xu, B. Multi-source remotely sensed data fusion for improving land cover classification. ISPRS J. Photogramm. Remote Sens. 2017, 124, 27–39. [Google Scholar] [CrossRef]
- Xu, K.; Jiang, Y.; Zhang, G.; Zhang, Q.; Wang, X. Geometric potential assessment for ZY3-02 triple linear array imagery. Remote Sens. 2017, 9, 658. [Google Scholar] [CrossRef]
- Hall, F.G.; Hilker, T.; Coops, N.C.; Lyapustin, A.; Huemmrich, K.F.; Middleton, E.; Margolis, H.; Drolet, G.; Black, T.A. Multi-angle remote sensing of forest light use efficiency by observing PRI variation with canopy shadow fraction. Remote Sens. Environ. 2018, 112, 3201–3211. [Google Scholar] [CrossRef]
- Chen, C.; Knyazikhin, Y.; Park, T.; Yan, K.; Lyapustin, A.; Wang, Y.; Yang, B.; Myneni, R.B. Prototyping of lai and fpar retrievals from modis multi-angle implementation of atmospheric correction (maiac) data. Remote Sens. 2017, 9, 370. [Google Scholar] [CrossRef]
- Li, D.; Yao, Y.; Shao, Z.; Wang, L. From digital Earth to smart Earth. Chin. Sci. Bull. 2014, 59, 722–733. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J.; Wang, Z. Smart monitoring cameras driven intelligent processing to big surveillance video data. IEEE Trans. Big Data 2017, 4, 105–116. [Google Scholar] [CrossRef]
- Zhang, G.; Li, L.T.; Jiang, Y.H.; Shi, X.T. On-orbit relative radiometric calibration of optical video satellites without uniform calibration sites. Int. J. Remote Sens. 2019, 40, 5454–5474. [Google Scholar] [CrossRef]
- Kopsiaftis, G.; Karantzalos, K. Vehicle detection and traffic density monitoring from very high resolution satellite video data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1881–1884. [Google Scholar]
- Yang, T.; Wang, X.; Yao, B.; Li, J.; Zhang, Y.; He, Z.; Duan, W. Small moving vehicle detection in a satellite video of an urban area. Sensors 2016, 16, 1528. [Google Scholar] [CrossRef]
- Li, H.; Man, Y. Moving ship detection based on visual saliency for video satellite. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1248–1250. [Google Scholar]
- Li, H.; Chen, L.; Li, F.; Huang, M. Ship detection and tracking method for satellite video based on multiscale saliency and surrounding contrast analysis. J. Appl. Remote Sens. 2019, 13, 026511. [Google Scholar] [CrossRef]
- Wu, J.; Wang, T.; Yan, J.; Zhang, G.; Jiang, X.; Wang, Y.; Bai, Q.; Yuan, C. Satellite video point-target tracking based on Hu correlation filter. Chin. Space Sci. Technol. 2019, 39, 55–63. [Google Scholar] [CrossRef]
- Joe, J.F. Enhanced sensitivity of motion detection in satellite videos using instant learning algorithms. In Proceedings of the IET Chennai 3rd International Conference on Sustainable Energy and Intelligent Systems (SEISCON 2012), Tiruchengode, India, 27–29 December 2012; pp. 424–429. [Google Scholar]
- Platias, C.; Vakalopoulou, M.; Karantzalos, K. Automatic Mrf-Based Registration of High resolution satellite video data. In Proceedings of the ISPRS Annals of the Photogrammetry Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 121–128. [Google Scholar]
- Xie, Q.; Yao, G.; Liu, P. Super-resolution reconstruction of satellite video images based on interpolation method. In Proceedings of the 7th International Congress of Information and Communication Technology (ICICT), Sanya, China, 1–2 January 2017; pp. 454–459. [Google Scholar]
- Mou, L.; Zhu, X. Spatiotemporal scene interpretation of space videos via deep neural network and tracklet analysis. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1823–1826. [Google Scholar]
- Chang Guang Satellite Technology Co., Ltd. Corporate Information. Available online: http://www.charmingglobe.com/EWeb/about_tw.aspx?id=9 (accessed on 23 January 2021).
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Cao, X.; Xu, L.; Meng, D.; Zhao, Q.; Xu, Z. Integration of 3-dimensional discrete wavelet transform and Markov random field for hyperspectral image classification. Neurocomputing 2017, 226, 90–100. [Google Scholar] [CrossRef]
- Du, P.; Xia, J.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple classifier system for remote sensing image classification: A review. Sensors 2012, 12, 4764–4792. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal component analysis and factor analysis. In Principal Component Analysis; Springer: New York, NY, USA, 1986; pp. 115–128. ISBN 978-1-4757-1906-2. [Google Scholar]
- Mackiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral-spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Ma, J.; Ma, Y.; Li, C. Infrared and visible image fusion methods and applications: A survey. Inf. Fusion 2019, 45, 153–178. [Google Scholar] [CrossRef]
| Item | Detail |
|---|---|
| Data source | Jilin-1 video satellite |
| Center coordinate | North , East , New Delhi, India. |
| Size of data | pixels |
| Ground resolution | 1.13 m (approximate value) |
| Band width | Blue: 437–512 nm, Green: 489–585 nm, Red: 580–723 nm |
| Dynamic range | 8 bits (0–255) |
| Time of duration | 28 s |
| Number of observation angles | 700 angles |
| Class Name | Number of Samples | |
|---|---|---|
| 1 | Tree | 4394 |
| 2 | Grass | 5314 |
| 3 | Soil | 5364 |
| 4 | Concrete ground | 490 |
| 5 | High reflective surface | 538 |
| 6 | Village construction roof | 2910 |
| 7 | Roof of subway station | 1278 |
| 8 | Concrete roof | 899 |
| 9 | Tennis court | 652 |
| 10 | Asphalt road | 3521 |
| 11 | Others | 651 |
| Reference | Tree | Grass | Soil | Concrete Ground | High Reflective Surface | Village Construction Roof | Roof of Subway Station | Concrete Roof | Tennis Court | Asphalt Road | Others | Total | User’s Accuracy (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Result of Classification | ||||||||||||||
| Tree | 3827 | 80 | 0 | 0 | 0 | 30 | 0 | 0 | 0 | 333 | 38 | 4308 | 88.83 | |
| Grass | 108 | 4368 | 6 | 3 | 0 | 52 | 0 | 2 | 0 | 3 | 45 | 5087 | 95.69 | |
| Soil | 0 | 2 | 5047 | 62 | 0 | 0 | 0 | 36 | 15 | 0 | 0 | 5162 | 97.77 | |
| Concrete ground | 0 | 2 | 16 | 349 | 0 | 44 | 1 | 67 | 0 | 0 | 0 | 479 | 72.86 | |
| High reflective surface | 0 | 0 | 0 | 0 | 458 | 0 | 5 | 0 | 0 | 0 | 0 | 463 | 98.92 | |
| Village construction roof | 18 | 85 | 0 | 30 | 0 | 2437 | 0 | 27 | 0 | 1 | 336 | 2934 | 83.06 | |
| Roof of subway station | 0 | 0 | 0 | 0 | 53 | 0 | 1175 | 46 | 0 | 0 | 0 | 1274 | 92.23 | |
| Concrete roof | 0 | 2 | 22 | 21 | 0 | 12 | 33 | 676 | 0 | 0 | 0 | 766 | 88.25 | |
| Tennis court | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 604 | 0 | 0 | 609 | 99.18 | |
| Asphalt road | 212 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2999 | 0 | 3211 | 93.40 | |
| Others | 9 | 9 | 0 | 0 | 0 | 189 | 0 | 0 | 0 | 9 | 199 | 415 | 47.95 | |
| Total | 4174 | 5048 | 5096 | 465 | 511 | 2764 | 1214 | 854 | 619 | 3345 | 618 | 0 | 0 | |
| Producer’s Accuracy (%) | 91.69 | 96.43 | 99.04 | 75.05 | 89.63 | 88.17 | 96.79 | 79.16 | 97.58 | 89.66 | 32.20 | 0 | 0 | |
| Training-Set Ratio | 1% | 2.5% | 5% | 10% | 20% | 40% | 80% | |
|---|---|---|---|---|---|---|---|---|
| Number of Angles | ||||||||
| 2 | 87.74 * | 90.86 | 91.95 | 92.81 | 93.51 | 93.86 | 93.83 | |
| +1.273 | 0.7933 | 0.7784 | 0.8140 | 0.8069 | 0.6349 | 0.7723 | ||
| 4 | 91.23 | 93.31 | 94.29 | 94.71 | 95.55 | 95.68 | 95.90 | |
| 0.7680 | 0.5886 | 0.5447 | 0.5716 | 0.5074 | 0.5340 | 0.4517 | ||
| 8 | 93.07 | 94.72 | 95.52 | 96.00 | 96.53 | 96.81 | 97.07 | |
| 0.5482 | 0.4378 | 0.3326 | 0.4261 | 0.2785 | 0.2141 | 0.2826 | ||
| 16 | 94.23 | 95.72 | 96.10 | 96.72 | 97.31 | 97.69 | 98.12 | |
| 0.3917 | 0.3153 | 0.2127 | 0.1859 | 0.1686 | 0.1644 | 0.1925 | ||
| 32 | 95.35 | 96.31 | 96.83 | 97.32 | 98.02 | 98.48 | 98.92 | |
| 0.3560 | 0.2178 | 0.1586 | 0.1506 | 0.1400 | 0.1239 | 0.1339 | ||
| 64 | 95.84 | 96.82 | 97.56 | 98.04 | 98.59 | 99.19 | 99.62 | |
| 0.2638 | 0.1561 | 0.1360 | 0.1344 | 0.1104 | 0.0887 | 0.0799 | ||
| 128 | 95.97 | 97.19 | 98.03 | 98.56 | 99.12 | 99.67 | 99.87 | |
| 0.1192 | 0.1252 | 0.1064 | 0.0985 | 0.0901 | 0.0592 | 0.0315 | ||
| 256 | 96.14 | 97.37 | 98.26 | 98.84 | 99.45 | 99.84 | 99.91 | |
| 0.1196 | 0.0670 | 0.0875 | 0.0703 | 0.0504 | 0.0252 | 0.0257 | ||
| 512 | 96.26 | 97.50 | 98.39 | 99.04 | 99.57 | 99.89 | 99.93 | |
| 0.0721 | 0.0331 | 0.0434 | 0.0368 | 0.0266 | 0.0122 | 0.0151 | ||
| 700 | 96.23 | 97.47 | 98.41 | 99.13 | 99.58 | 99.91 | 99.94 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Training-Set Ratio | 1% | 2.5% | 5% | 10% | 20% | 40% | 80% | |
|---|---|---|---|---|---|---|---|---|
| Parameters | ||||||||
| Two- piece linear function | 94.31 | 94.03 | 94.74 | 95.34 | 96.67 | 96.62 | 96.85 | |
| Cubic curve function | 91.01 | 93.53 | 94.05 | 94.33 | 95.17 | 95.02 | 95.62 | |
| Training-Set Ratio | 1% | 2.5% | 5% | 10% | 20% | 40% | 80% | |
|---|---|---|---|---|---|---|---|---|
| Number of Principal Components | ||||||||
| 1 | 94.36 | 96.20 | 97.18 | 97.32 | 97.40 | 97.92 | 98.14 | |
| 2 | 94.98 | 96.74 | 97.92 | 98.06 | 98.31 | 98.79 | 99.23 | |
| 4 | 95.29 | 97.29 | 98.43 | 98.75 | 99.16 | 99.42 | 99.65 | |
| 8 | 95.76 | 97.41 | 98.48 | 98.87 | 99.35 | 99.62 | 99.73 | |
| 16 | 95.68 | 97.61 | 98.63 | 98.94 | 99.53 | 99.69 | 99.83 | |
| 32 | 96.10 | 97.68 | 98.62 | 99.04 | 99.66 | 99.78 | 99.87 | |
| 64 | 96.21 | 97.62 | 98.68 | 99.14 | 99.67 | 99.88 | 99.85 | |
| 128 | 96.12 | 97.63 | 98.68 | 99.15 | 99.66 | 99.90 | 99.87 | |
| 256 | 96.12 | 97.57 | 98.64 | 99.12 | 99.66 | 99.90 | 99.92 | |
| 512 | 96.21 | 97.48 | 98.49 | 99.11 | 99.63 | 99.90 | 99.94 | |
| 700 | 96.23 | 97.47 | 98.41 | 99.13 | 99.58 | 99.91 | 99.94 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Leung, Y.; Fung, T.; Shao, Z.; Lu, J.; Meng, D.; Ying, H.; Zhou, Y. Continuous Multi-Angle Remote Sensing and Its Application in Urban Land Cover Classification. Remote Sens. 2021, 13, 413. https://doi.org/10.3390/rs13030413
Yao Y, Leung Y, Fung T, Shao Z, Lu J, Meng D, Ying H, Zhou Y. Continuous Multi-Angle Remote Sensing and Its Application in Urban Land Cover Classification. Remote Sensing. 2021; 13(3):413. https://doi.org/10.3390/rs13030413
Chicago/Turabian StyleYao, Yuan, Yee Leung, Tung Fung, Zhenfeng Shao, Jie Lu, Deyu Meng, Hanchi Ying, and Yu Zhou. 2021. "Continuous Multi-Angle Remote Sensing and Its Application in Urban Land Cover Classification" Remote Sensing 13, no. 3: 413. https://doi.org/10.3390/rs13030413
APA StyleYao, Y., Leung, Y., Fung, T., Shao, Z., Lu, J., Meng, D., Ying, H., & Zhou, Y. (2021). Continuous Multi-Angle Remote Sensing and Its Application in Urban Land Cover Classification. Remote Sensing, 13(3), 413. https://doi.org/10.3390/rs13030413







