Towards Semantic SLAM: 3D Position and Velocity Estimation by Fusing Image Semantic Information with Camera Motion Parameters for Traffic Scene Analysis
Abstract
1. Introduction
- Unlike previous approaches that are end-to-end data driven solutions, we introduce a hybrid solution that, on one hand, leverages deep learning algorithms to detect different cars in the scene and, on the other hand, describes the dynamic motion of these cars in an analytical way that can be used within the framework of a Bayesian filter where we fuse the discrepancy between the virtual image, obtained using a 3D CAD model, and the actual image, with camera motion parameters measured by the sensors on board. In this way we estimate not only car positions but also their velocities, which is important for safe navigation;
- Our approach will be able to keep predicting the motion parameters of the cars even in the case of full occlusion because we involve the dynamics of their motion in the estimation process. Previous approaches cannot predict the position of the car in the case of full occlusion.
2. Related Work
2.1. 2D Object Detection
2.2. Semantic SLAM without Using 3D CAD Model
2.3. Image Based 3D Object Detection Using 3D CAD Models
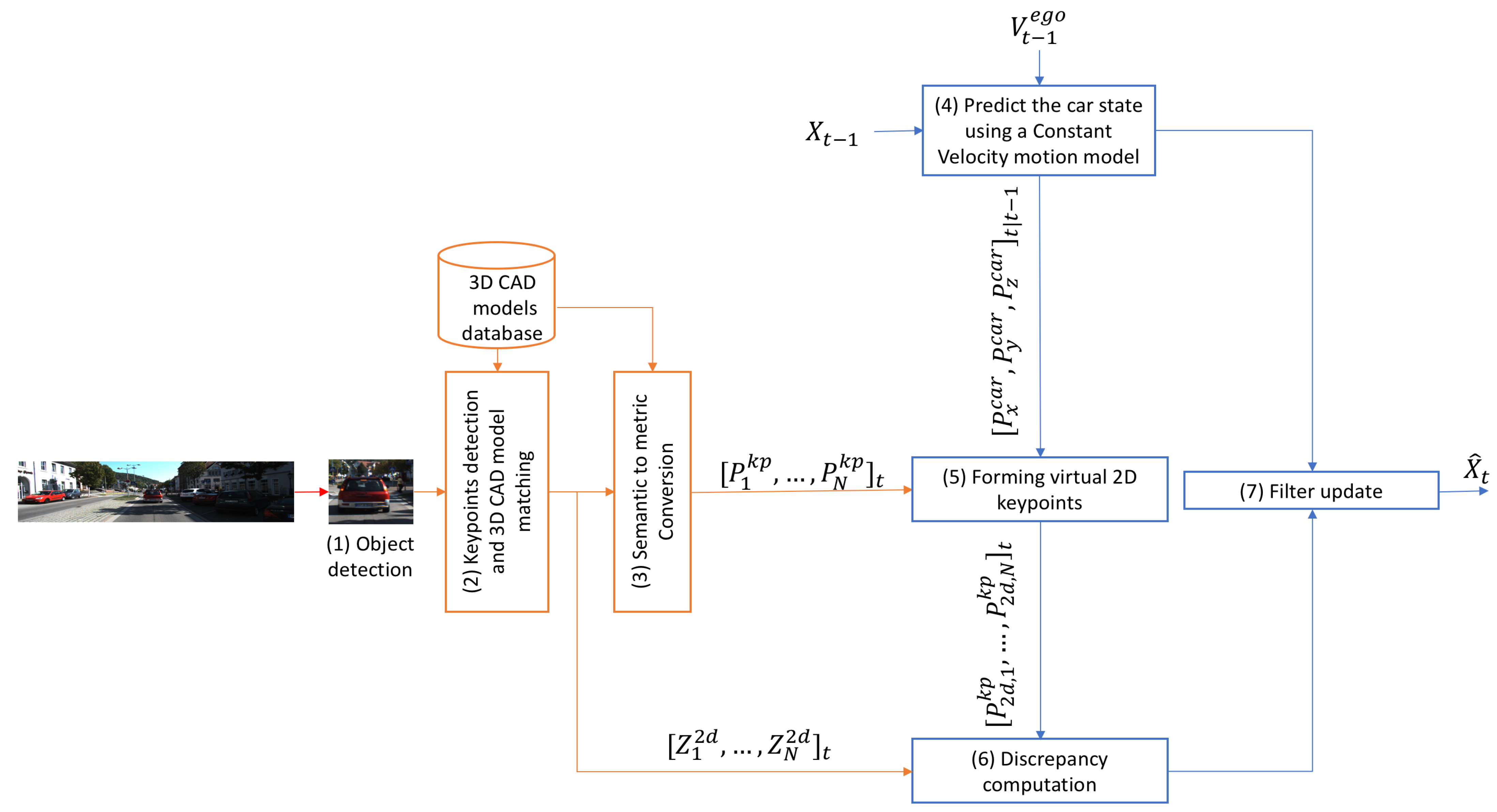
3. Proposed Approach
3.1. Proposed Pipeline
3.1.1. Object Detection
3.1.2. Key Points Detection and 3D CAD Model Matching
3.1.3. Semantic to Metric Information Conversion
3.1.4. State Prediction
3.1.5. Forming Virtual 2D Key Points
3.1.6. Discrepancy Formulation
3.1.7. Temporal Fusing of the Discrepancy with the Motion Parameters of the Camera (Filter Update)
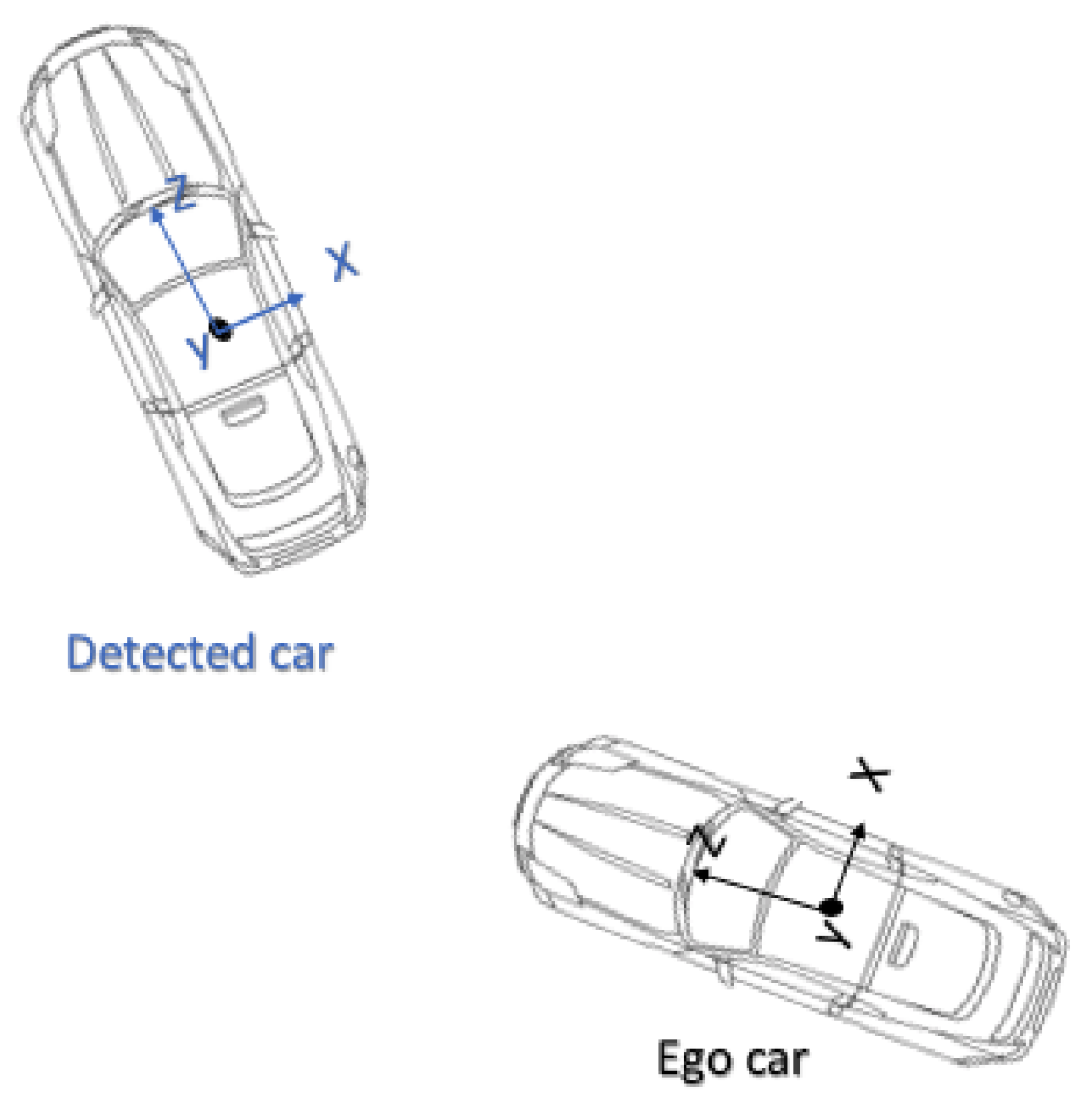
3.2. Problem Statement and Its Solution
3.2.1. Motion Model
3.2.2. Observation Model and Semantic Information Fusing
3.2.3. Solution Using EKF
- Prediction
- Updatewhere
| Algorithm 1: Temporal semantic fusion. |
| Result: Initialize ;  |
4. Results
5. Discussion
- This fusion allows the algorithm to work even in the case of full occlusion as shown in Figure 6. During occlusion, the estimation error grows. However, after the image comes back, the algorithm converges quickly;
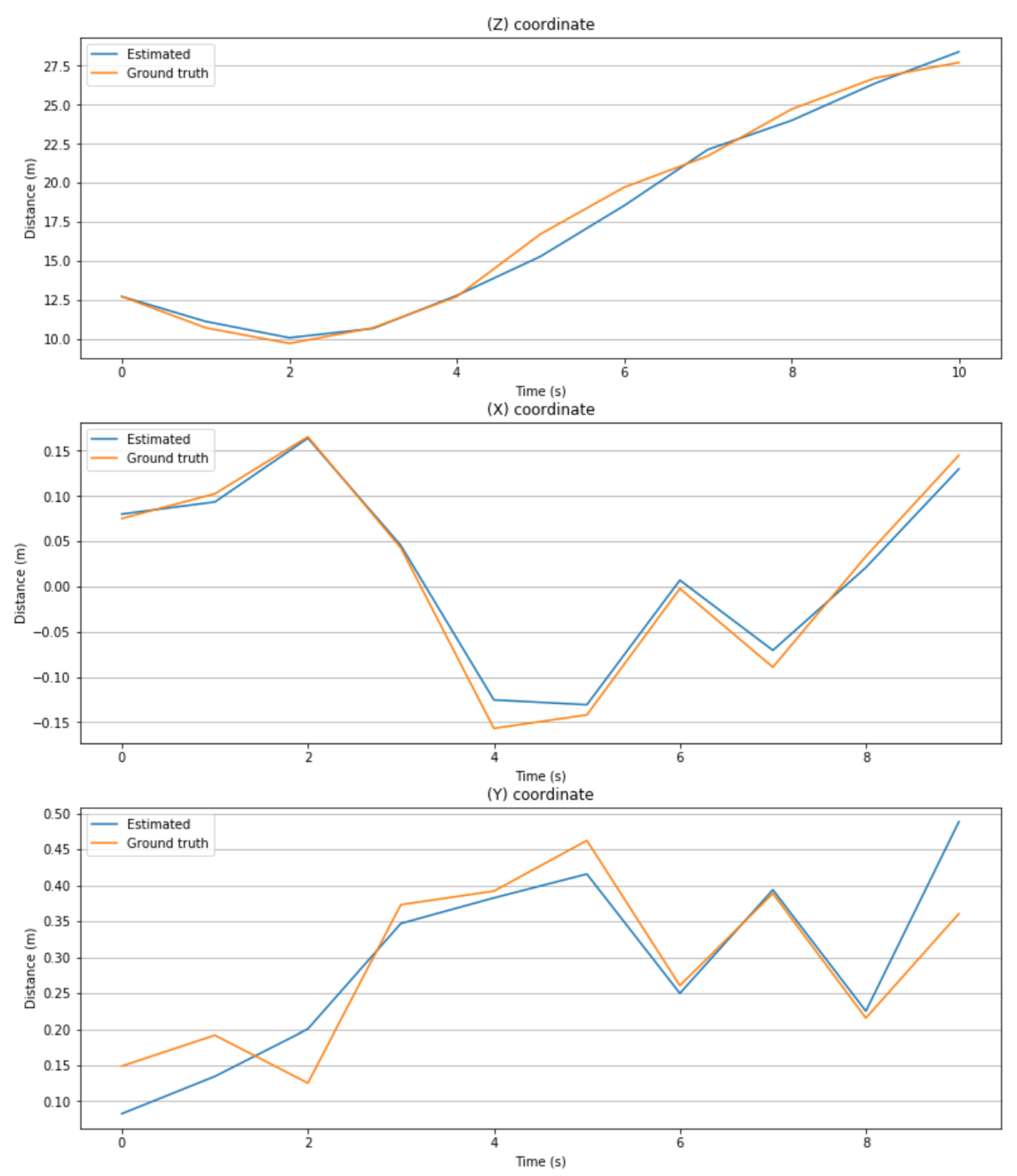
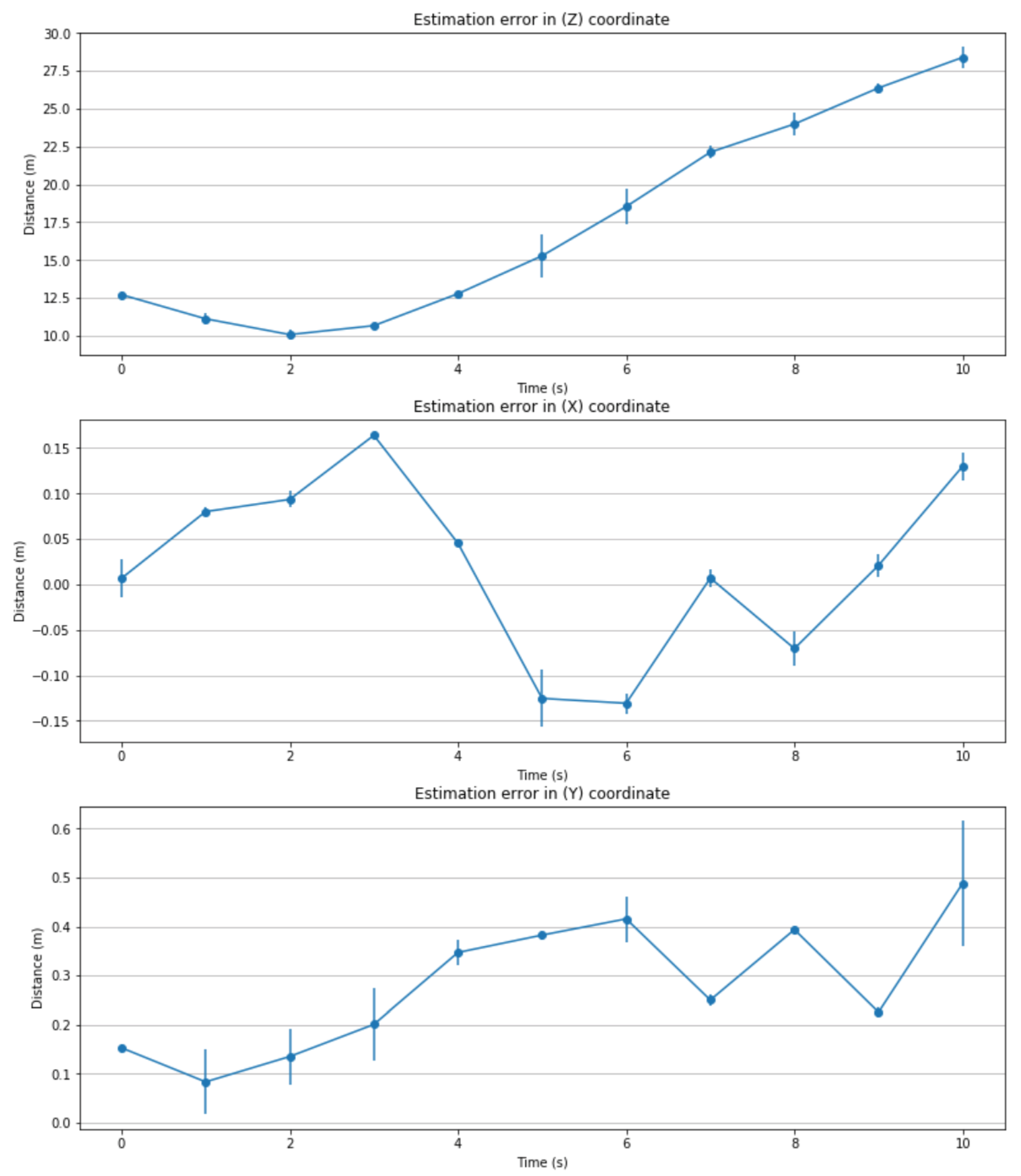
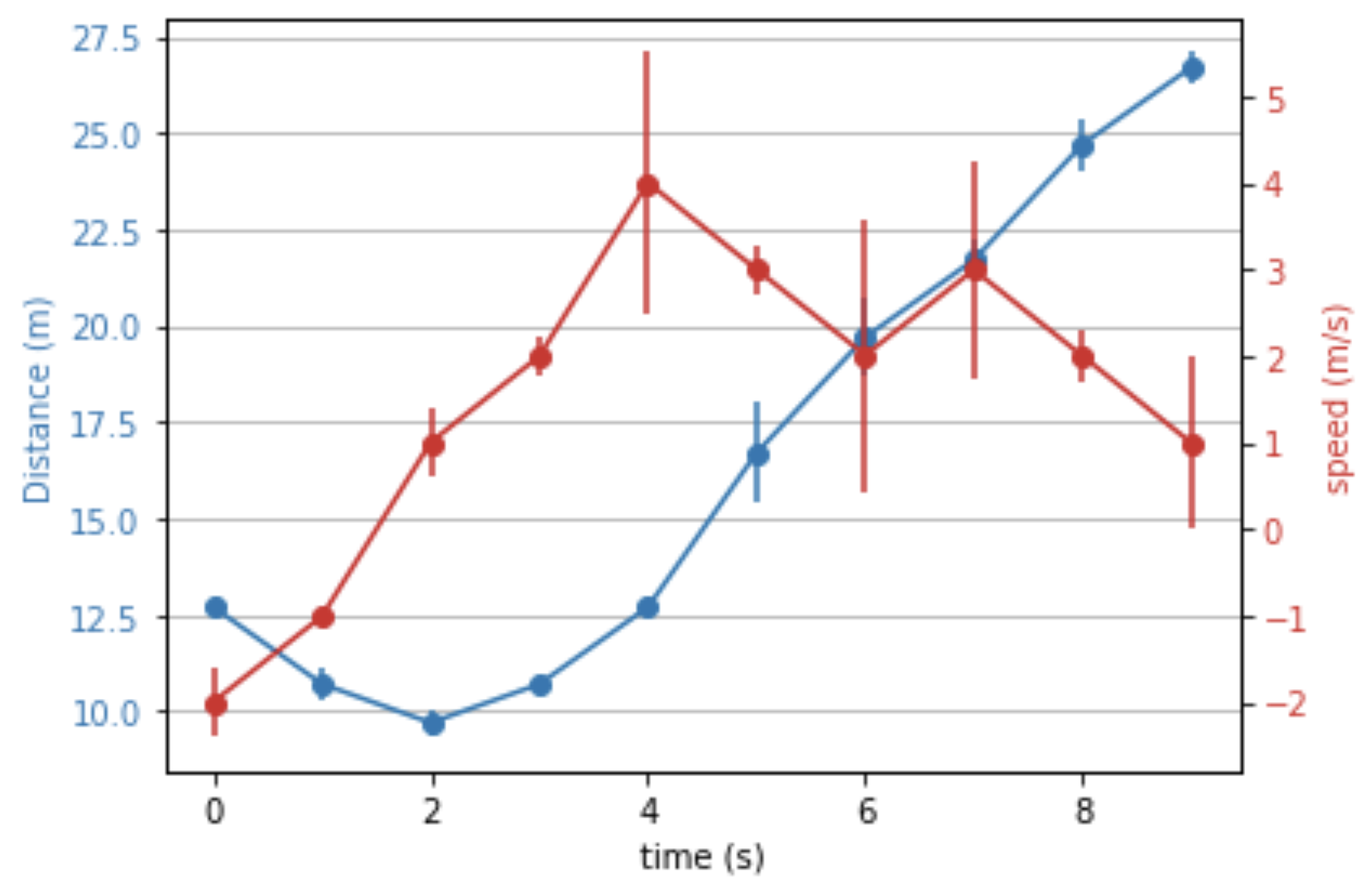
- In this paper, we used the Kitti dataset which has real driving scenarios. The results of the proposed algorithm are compared with the ground truth values obtained by the 2 cm accuracy 3D LiDAR to evaluate estimation error. Figure 4 presents the estimated 3D position using the proposed approach and its corresponding ground truth using the 3D LiDAR. Figure 5 and Figure 7 present estimation errors in 3D position and longitudinal velocity, respectively. These results show that the proposed approach can work in real driving scenarios;
- To the best of our knowledge, the existing works use 3D CAD models to estimate the position using one shot estimation [6,7,23]. The proposed approach has an advantage over the existing ones in the following aspects:
- -
- Other approaches do not take into account the dynamic motion constraints of the detected cars while the proposed approach fuses these motion constraints with semantic information to increase estimation accuracy;
- -
- Other approaches do not depend on temporal fusing. They depend on one shot estimation which does not work in the case of occlusion. In contrast, our approach depends on temporal fusing which allows it to predict car position and velocity in the case of occlusion;
- -
- Unlike other approaches which estimate the 3D position of a detected car only, the proposed approach estimates the velocity as well. Including car velocity in the state vector increases the accuracy of the estimation process due to the natural correlation between position and velocity of a detected car.
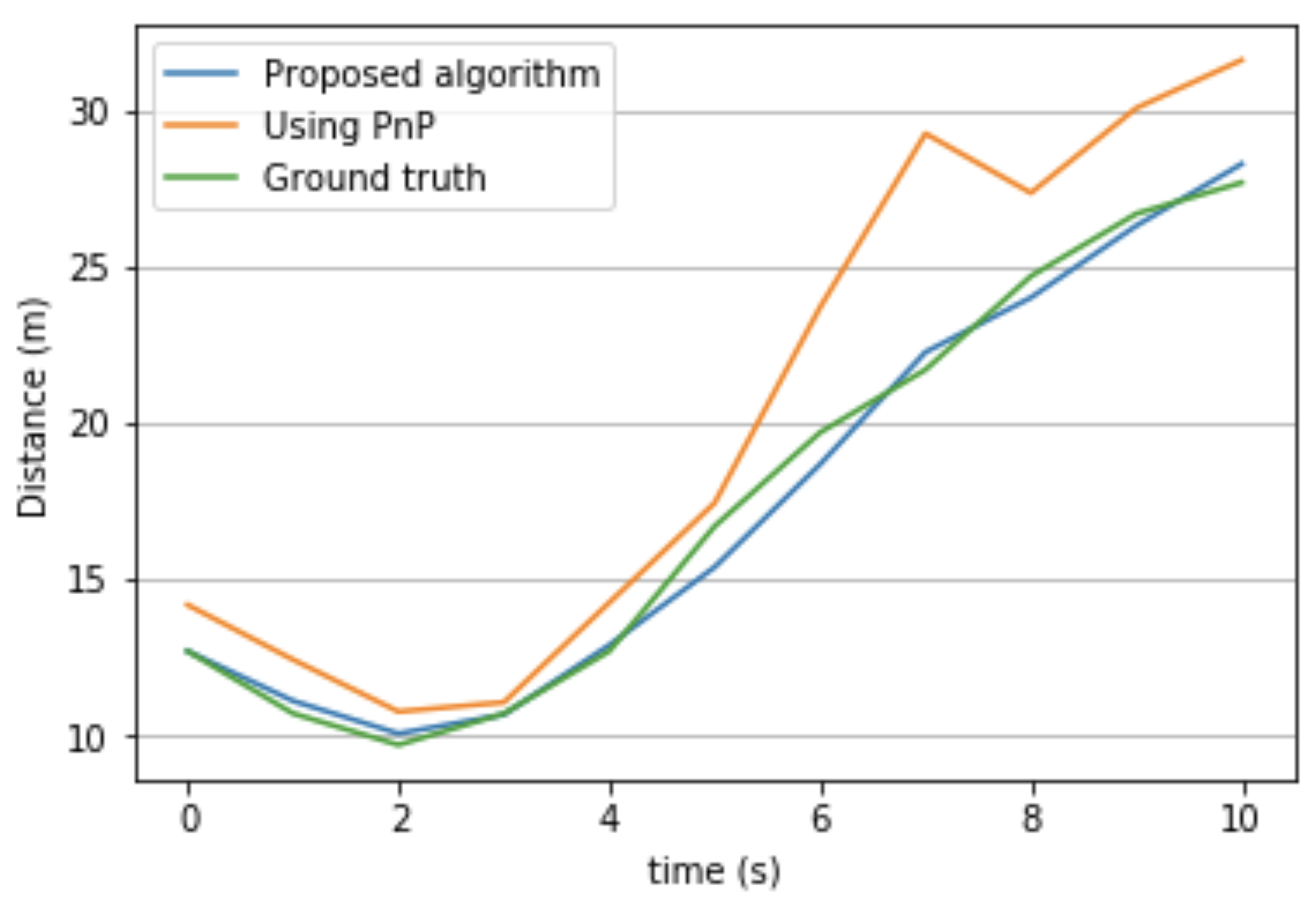
- A comparison between the proposed algorithm and the EPnP algorithm to estimate a detected car position using the KiTTi dataset is presented in Figure 8. The EPnP algorithm is one of the algorithms that depend on one shot estimation [23]. It estimates object position by minimizing the discrepancy between a virtual and a real image using the Levenberg–Marquardt method and is used in many other one-shot based algorithms [6]. From Figure 8, we can notice that the proposed approach slightly outperforms EPnP for distances up to 17 m. However, for distances greater than 17 m, the proposed approach has a better accuracy compared to EPnP algorithm. In addition, it is worth mentioning that EPnP, as well as other one shot-based approaches, will not work in the case of occlusion while the proposed approach can still predict the car position as presented in Figure 6;
- The experiments show that the algorithm can be used for short ranges and long ranges to get an idea of the traffic scene;
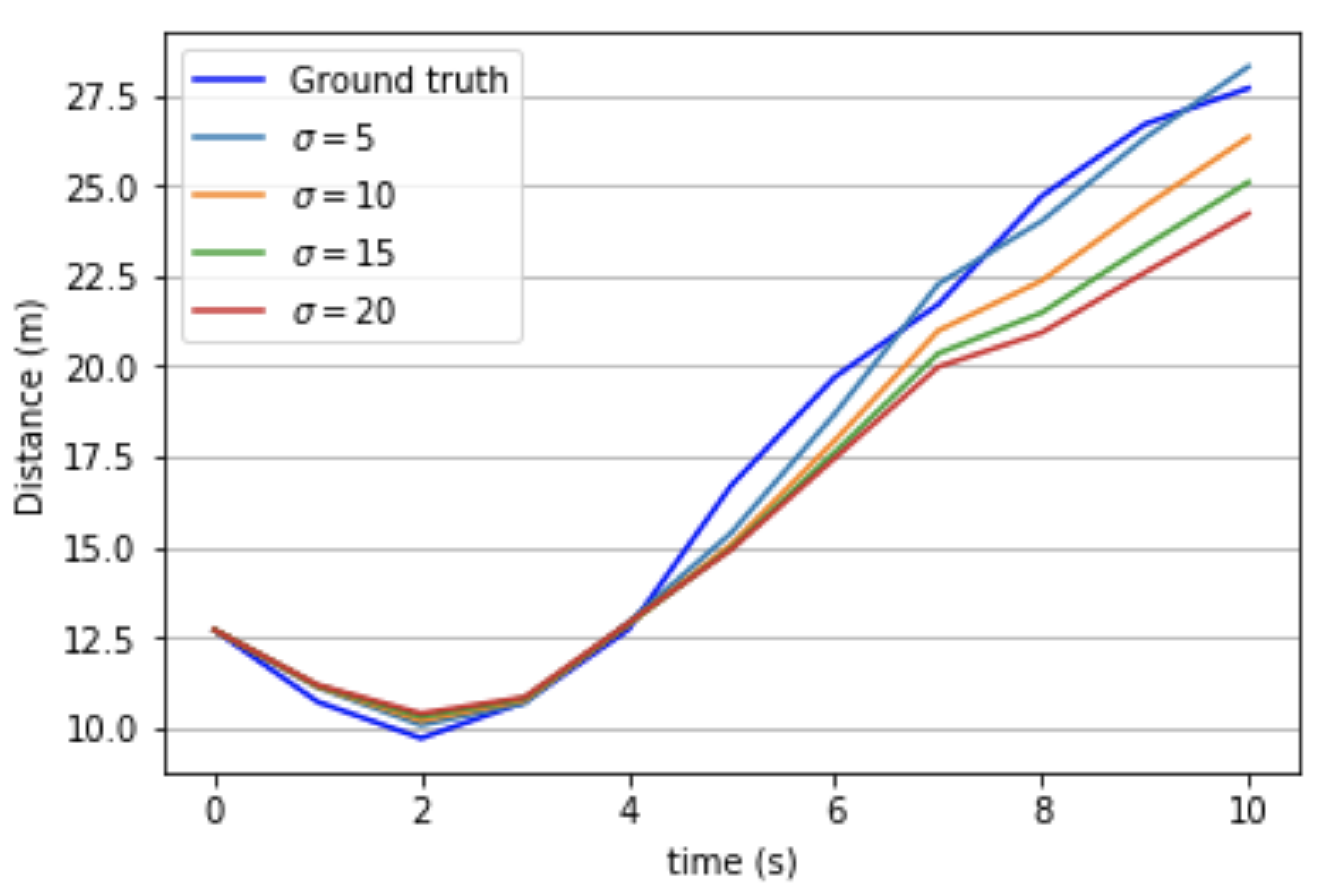
- According to Figure 9, the proposed algorithm is robust against different levels of measurement noise for distances up to 17 m. However, for distances greater than 17 m, the increase in measurements uncertainties will affect the estimation accuracy;
- The proposed algorithm depends on an object detection algorithm and a 3D CAD model matching algorithm to get a class ID and a matched 3D CAD model ID, respectively. In this paper, we assumed that the results of the object detection algorithm and the matching algorithm are correct. However, in real life, the results may be wrong. This introduces a limitation to the proposed approach as any errors in the class ID and/or the model ID will affect the estimation accuracy. It is possible to overcome this limitation by taking into account the uncertainties in class and model IDs during the estimation process. This can be done by augmenting the state vector to include, in addition to position and velocity variables, a class ID and a model ID and consider them as random variables to be estimated. The implementation of this point is out of the scope of the current paper and will be considered in future work;
- In this paper, Singer’s model (constant velocity model) was used to describe the dynamic motion of the detected car. This model is not enough to describe the motion in some cases, as it leads to incorrect results when the constant velocity condition is violated like in the case of turns. A more robust solution can be achieved by using Interacting Multiple Model filter (IMM filter) [25] where several motion models can be used to describe different types of motion scenarios. This point will be investigated in future work.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardos, J. Probabilistic Semi-Dense Mapping from Highly Accurate Feature-Based Monocular SLAM. In Proceedings of the Robotics: Science and Systems XI, Sapienza University of Rome, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Campos, C.E.M.; Elvira, R.; Rodríguez, J.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial and Multi-Map SLAM. arXiv 2020, arXiv:2007.11898. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.E.; Fu, C.; Berg, A.C. SSD: Single Shot MultiBox Detector. arXiv 2015, arXiv:1512.02325. [Google Scholar]
- Chabot, F.; Chaouch, M.; Rabarisoa, J.; Teulière, C.; Chateau, T. Deep MANTA: A Coarse-to-fine Many-Task Network for joint 2D and 3D vehicle analysis from monocular image. arXiv 2017, arXiv:1703.07570. [Google Scholar]
- Kundu, A.; Li, Y.; Rehg, J.M. 3D-RCNN: Instance-level 3D Object Reconstruction via Render-and-Compare. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Wu, D.; Zhuang, Z.; Xiang, C.; Zou, W.; Li, X. 6D-VNet: End-To-End 6-DoF Vehicle Pose Estimation From Monocular RGB Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPR), Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Song, X.; Wang, P.; Zhou, D.; Zhu, R.; Guan, C.; Dai, Y.; Su, H.; Li, H.; Yang, R. ApolloCar3D: A Large 3D Car Instance Understanding Benchmark for Autonomous Driving. arXiv 2018, arXiv:1811.12222. [Google Scholar]
- Manhardt, F.; Kehl, W.; Gaidon, A. ROI-10D: Monocular Lifting of 2D Detection to 6D Pose and Metric Shape. arXiv 2018, arXiv:1812.02781. [Google Scholar]
- He, T.; Soatto, S. Mono3D++: Monocular 3D Vehicle Detection with Two-Scale 3D Hypotheses and Task Priors. arXiv 2019, arXiv:1901.03446. [Google Scholar] [CrossRef]
- Qin, Z.; Wang, J.; Lu, Y. MonoGRNet: A Geometric Reasoning Network for Monocular 3D Object Localization. arXiv 2018, arXiv:1811.10247. [Google Scholar] [CrossRef]
- Barabanau, I.; Artemov, A.; Burnaev, E.; Murashkin, V. Monocular 3D Object Detection via Geometric Reasoning on Keypoints. arXiv 2019, arXiv:1905.05618. [Google Scholar]
- Ansari, J.A.; Sharma, S.; Majumdar, A.; Murthy, J.K.; Krishna, K.M. The Earth ain’t Flat: Monocular Reconstruction of Vehicles on Steep and Graded Roads from a Moving Camera. arXiv 2018, arXiv:1803.02057. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. arXiv 2013, arXiv:1311.2524. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.B.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bowman, S.L.; Atanasov, N.; Daniilidis, K.; Pappas, G.J. Probabilistic data association for semantic SLAM. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1722–1729. [Google Scholar]
- Doherty, K.; Fourie, D.; Leonard, J. Multimodal Semantic SLAM with Probabilistic Data Association. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2419–2425. [Google Scholar]
- Doherty, K.; Baxter, D.; Schneeweiss, E.; Leonard, J.J. Probabilistic Data Association via Mixture Models for Robust Semantic SLAM. arXiv 2019, arXiv:1909.11213. [Google Scholar]
- Davison, A.J. FutureMapping: The Computational Structure of Spatial AI Systems. arXiv 2018, arXiv:1803.11288. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An accurate O(n) solution to the PnP problem. Int. J. Comput. Vis. 2009, 81. [Google Scholar] [CrossRef]
- Singer, R.A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets. IEEE Trans. Aerosp. Electron. Syst. 1970, AES-6, 473–483. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory, Algorithms and Software; John Wiley & Sons Ltd.: Chichester, UK, 2001. [Google Scholar]
- Stepanov, O.A. Optimal and Sub-Optimal Filtering in Integrated Navigation Systems. In Aerospace Navigation Systems; Nebylov, A., Watson, J., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2016; pp. 244–298. [Google Scholar]
- Sabattini, L.; Levratti, A.; Venturi, F.; Amplo, E.; Fantuzzi, C.; Secchi, C. Experimental comparison of 3D vision sensors for mobile robot localization for industrial application: Stereo-camera and RGB-D sensor. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012; pp. 823–828. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Multi-Object Tracking Benchmark. The KITTI Vision Benchmark Suite. Available online: http://www.cvlibs.net/datasets/kitti/eval_tracking.php (accessed on 10 August 2020).
- OXTS. RT v2 GNSS-Aided Inertial Measurement Systems; Revision 180221; Oxford Technical Solutions Limited: Oxfordshire, UK, 2015. [Google Scholar]
- Mansour, M.; Davidson, P.; Stepanov, O.; Raunio, J.P.; Aref, M.M.; Piché, R. Depth estimation with ego-motion assisted monocular camera. Gyroscopy Navig. 2019, 10, 111–123. [Google Scholar] [CrossRef]
- Davidson, P.; Mansour, M.; Stepanvo, O.; Piché, R. Depth estimation from motion parallax: Experimental evaluation. In Proceedings of the 26th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 27–29 May 2019. [Google Scholar]
- Mansour, M.; Davidson, P.; Stepanov, O.; Piché, R. Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach. Remote Sens. 2019, 11, 1990. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansour, M.; Davidson, P.; Stepanov, O.; Piché, R. Towards Semantic SLAM: 3D Position and Velocity Estimation by Fusing Image Semantic Information with Camera Motion Parameters for Traffic Scene Analysis. Remote Sens. 2021, 13, 388. https://doi.org/10.3390/rs13030388
Mansour M, Davidson P, Stepanov O, Piché R. Towards Semantic SLAM: 3D Position and Velocity Estimation by Fusing Image Semantic Information with Camera Motion Parameters for Traffic Scene Analysis. Remote Sensing. 2021; 13(3):388. https://doi.org/10.3390/rs13030388
Chicago/Turabian StyleMansour, Mostafa, Pavel Davidson, Oleg Stepanov, and Robert Piché. 2021. "Towards Semantic SLAM: 3D Position and Velocity Estimation by Fusing Image Semantic Information with Camera Motion Parameters for Traffic Scene Analysis" Remote Sensing 13, no. 3: 388. https://doi.org/10.3390/rs13030388
APA StyleMansour, M., Davidson, P., Stepanov, O., & Piché, R. (2021). Towards Semantic SLAM: 3D Position and Velocity Estimation by Fusing Image Semantic Information with Camera Motion Parameters for Traffic Scene Analysis. Remote Sensing, 13(3), 388. https://doi.org/10.3390/rs13030388







