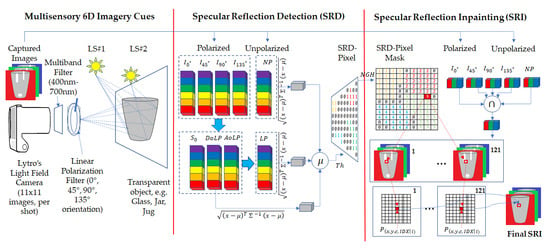
Specular Reflection Detection and Inpainting in Transparent Object through MSPLFI
Abstract
1. Introduction
2. Related Works
2.1. Specular Reflection Detection (SRD)
2.2. Specular Reflection Inpainting (SRI)
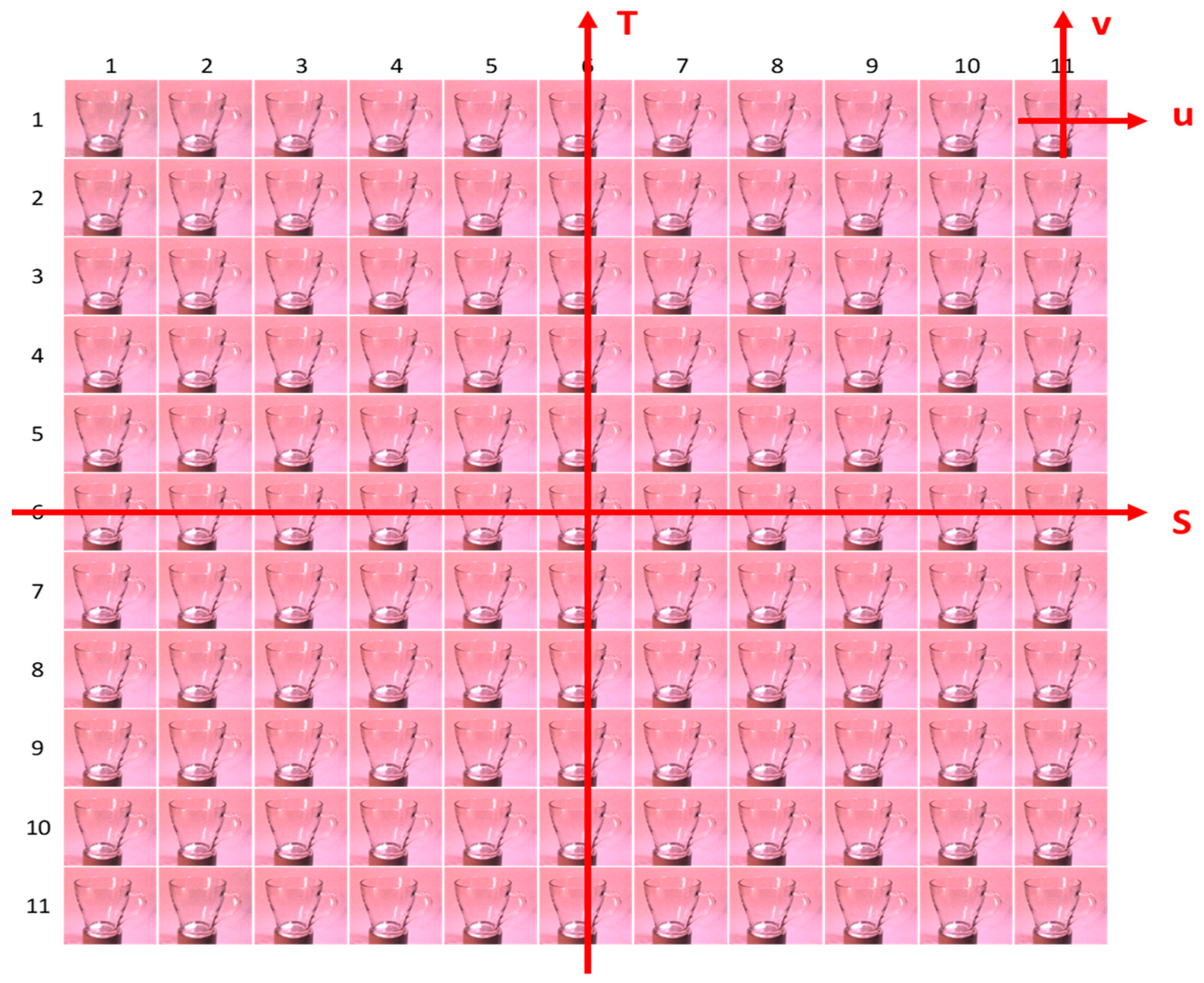
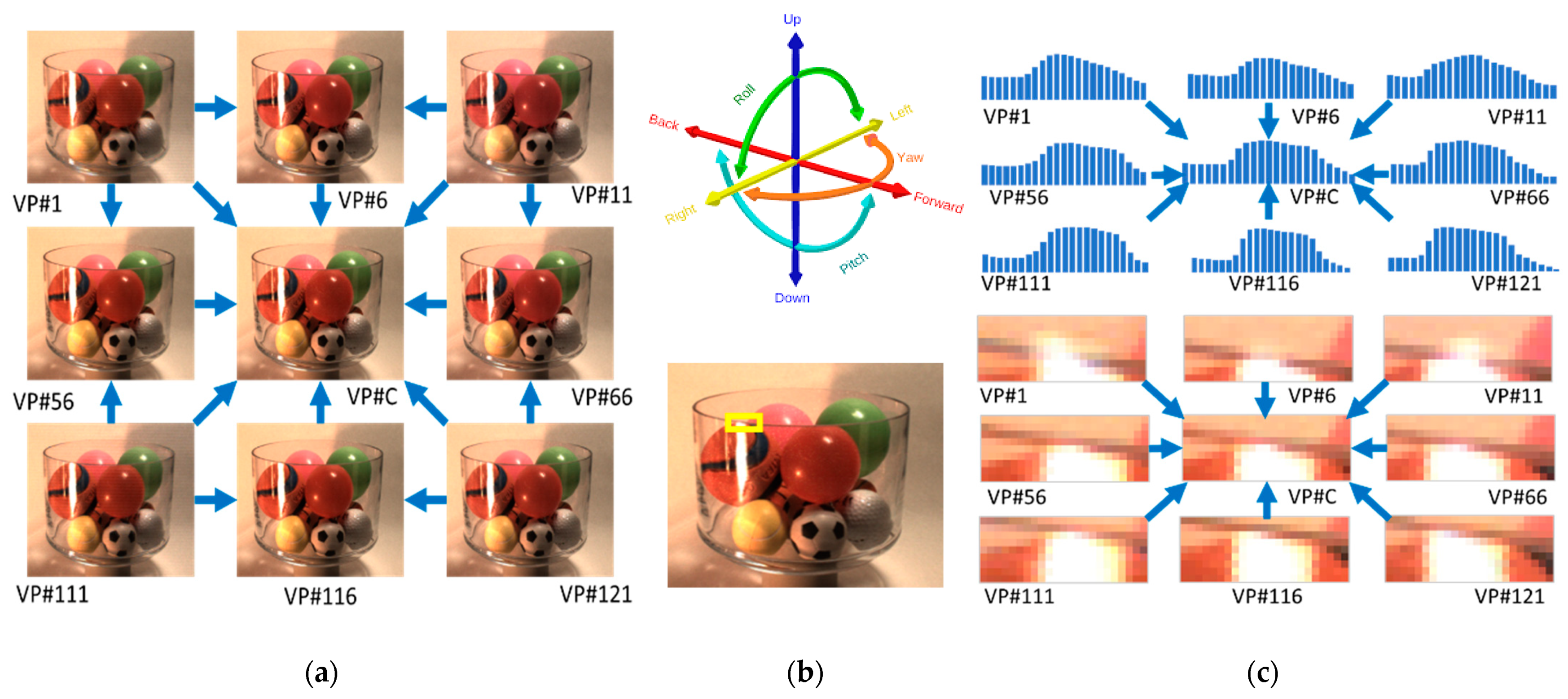
3. Analysis of MSPLFI Transparent Object Dataset
3.1. Experimental Setup
3.2. MSPLFI Transparent Object Dataset
3.3. Degrees of Freedom
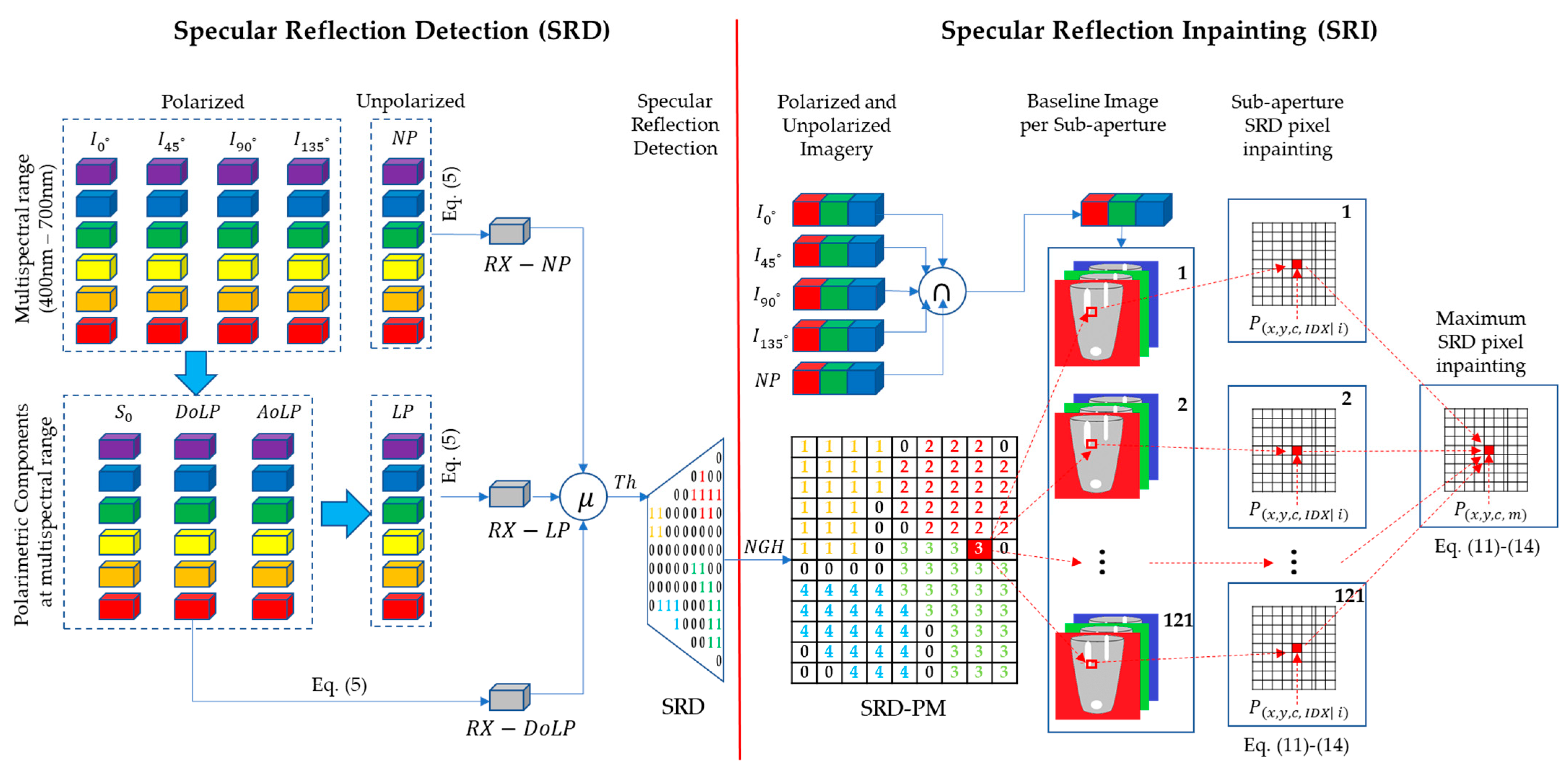
4. Proposed Two-fold SRDI Framework
4.1. Specular Reflection Detection (SRD)
| Algorithm 1. SRD in Transparent Object |
| Input: MSPLFI Object Dataset |
| Output: SRD Pixel in Binary |
| 1: for all lenslet (.LFR) image do |
| 2: Decode raw lenslet (.LFR) multiband polarized and unpolarized images into 4D () LF images |
| 3: Remove and clip unwanted images and pixels |
| 4: end for |
| 5: for all sub-aperture image do |
| 6: for all multiband do |
| 7: Calculate as in Equations (7)–(10) |
| 8: if type ( = “unpolarized” then |
| 9: Convert multiband image into corresponding grayscale Store multiband grayscale image as column vector |
| 10: else if type ( = “polarized” then |
| 11: Store multiband image as column vector |
| 12: end if |
| 13: end for |
| 14: Calculate mean () and covariance () per sub-aperture index of LF |
| 15: Calculate Mahalanobis distance as in Equation (5) |
| 16: Reshape distance vector as 2D image which represents SRD per sub-aperture image |
| 17: end for |
| 18: Calculate maximum changes/specularities observed in all sub-aperture indexes for object type “” |
| 19: repeat steps 5–18 for object type = “” and object type= “” |
| 20: Calculate mean () specularity of object type: , and |
| 21: Apply threshold () to binarize SRD pixels |
4.2. Specular Reflection Inpainting (SRI)
| Algorithm 2. SRI in Transparent Object |
| Input: MSPLFI Object Dataset, SRD-PM |
| Output: SRD Pixel Inpainting in RGB |
| 1: Strengthen SRD-PM (output from Algorithm 1) by labeling all neighboring pixels as SRD ones |
| 2: Compute connected components and label them |
| 3: Calculate baseline image per sub-aperture index by taking minimum pixel intensities of both polarized and unpolarized images in RGB channels |
| 4: for all common sub-aperture images do |
| 5: for all labels do |
| 6: for all pixel patterns () in SRD-PM do |
| 7: if labels (SRD-PMs) exist then |
| 8: Compute distances () among 4-connected neighbors not in SRD-PM in each channel, as in Equation (11), and store them in 2D-matrix (), as in Equation (12) |
| 9: Winning pixel pattern is index () of pixel pattern corresponding to column-wise minimum sum of , as in Equations (13) and (14) for inpainting of specular reflections |
| 10: end if |
| 11: end for |
| 12: end for |
| 13: end for |
| 14: repeat steps 4 to 13 to calculate maximum specular reflection in suppressed image of transparent object from already suppressed sub-apertures |
5. Experimental Results
5.1. Selection of Performance Evaluation Metric
5.1.1. Selection of SRD Metric
5.1.2. Selection of Inpainting Quality Metric
5.2. Generation of Ground Truth
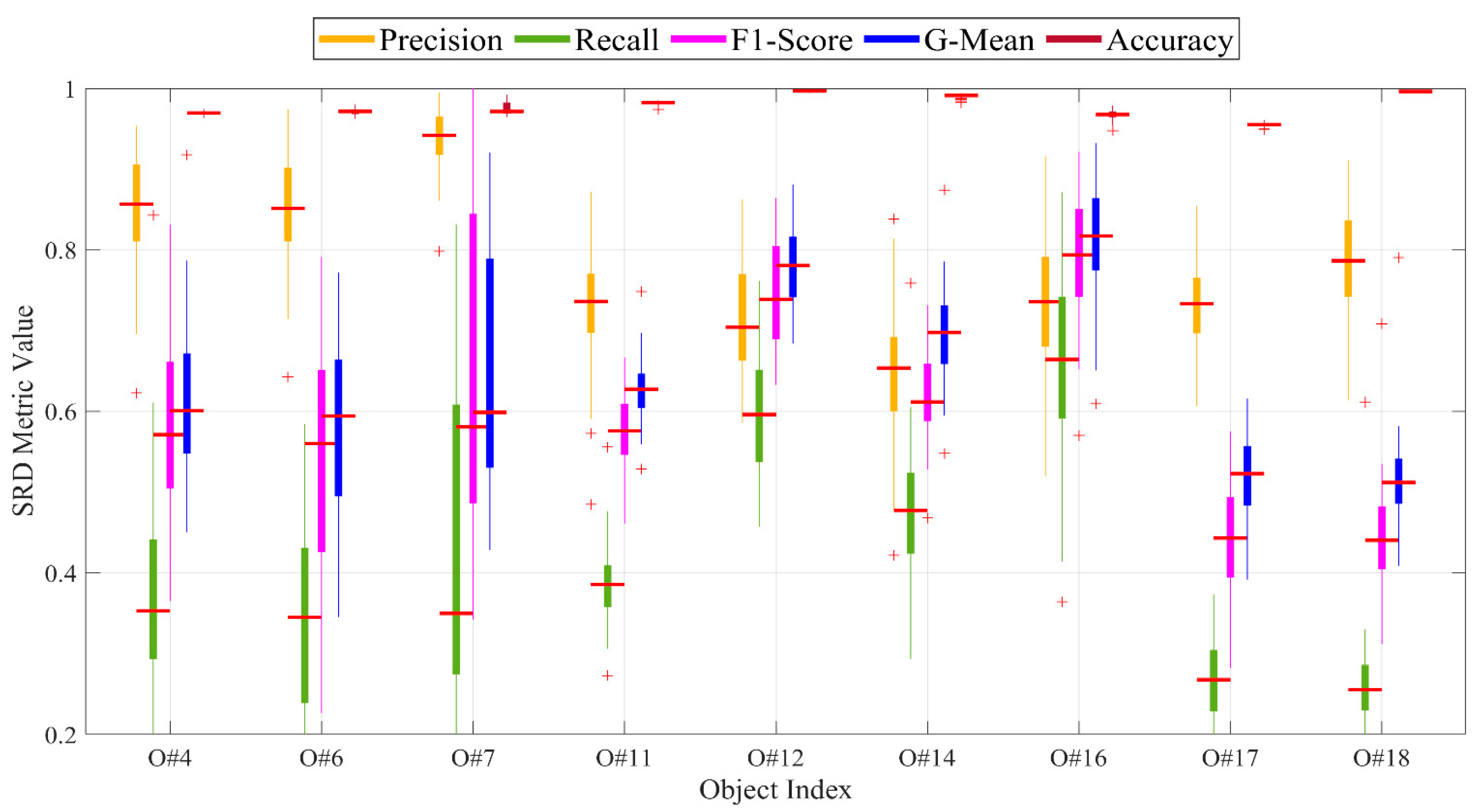
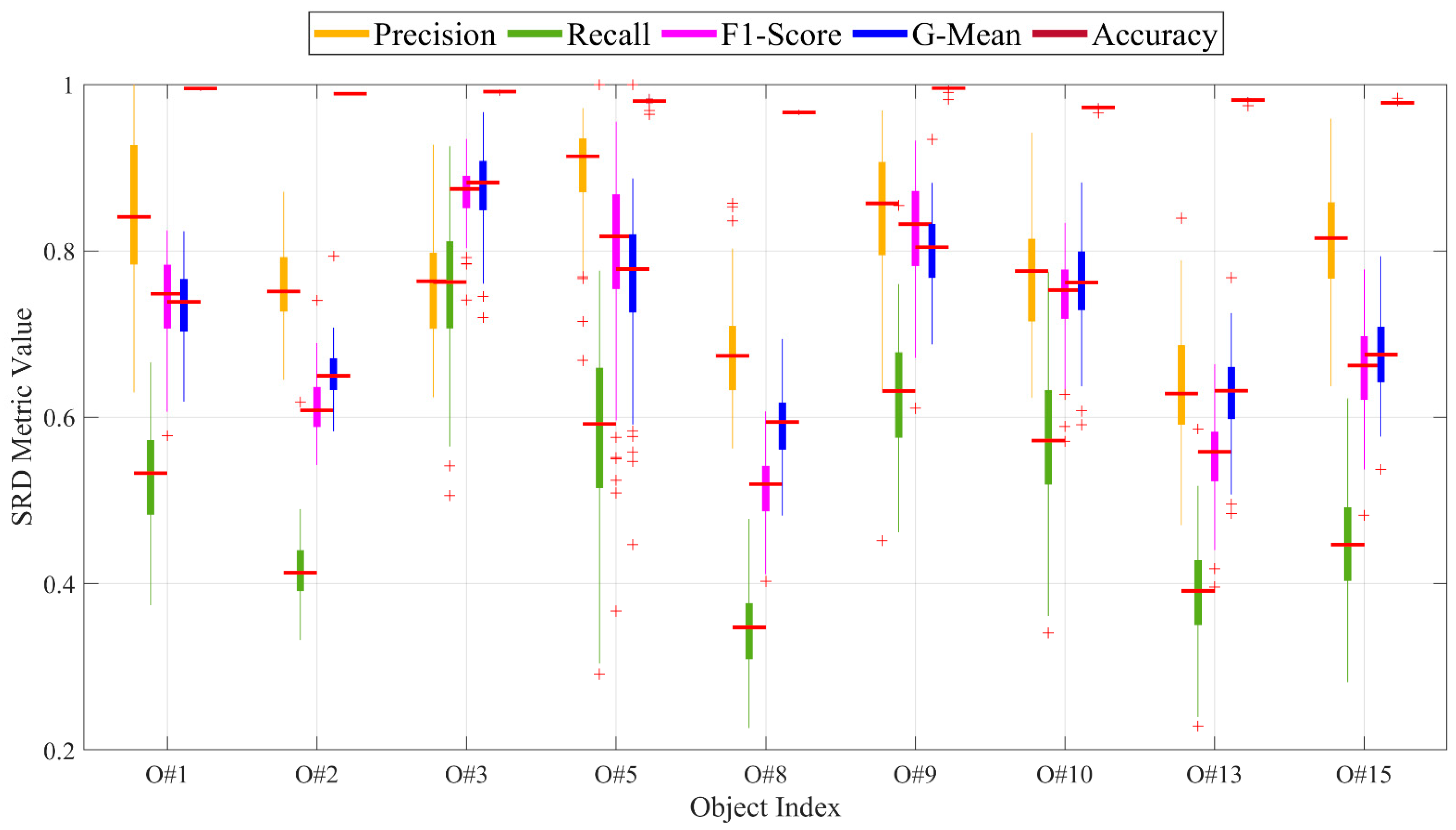
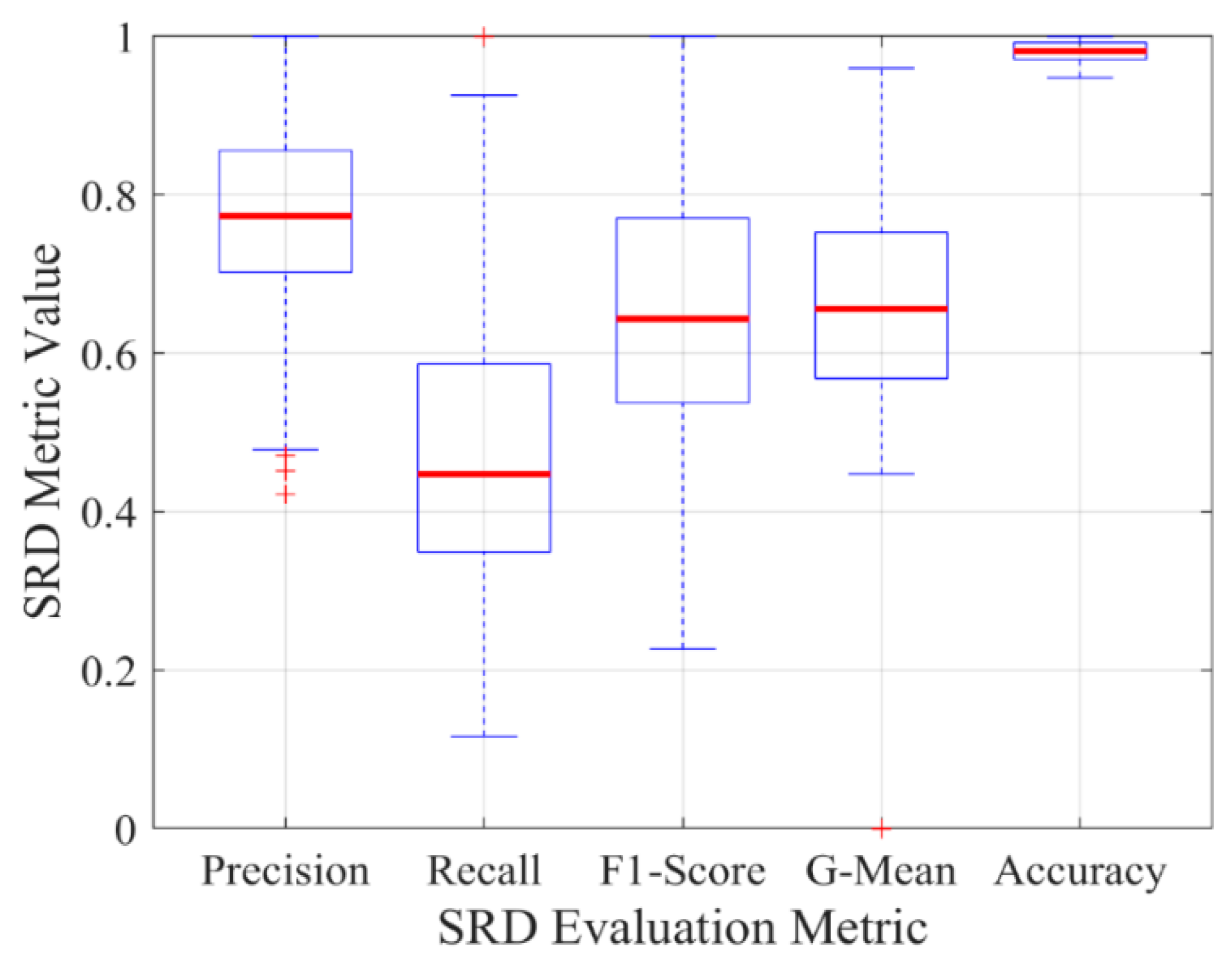
5.3. Performance Evaluation of SRD
5.3.1. Analysis of SRD Rate
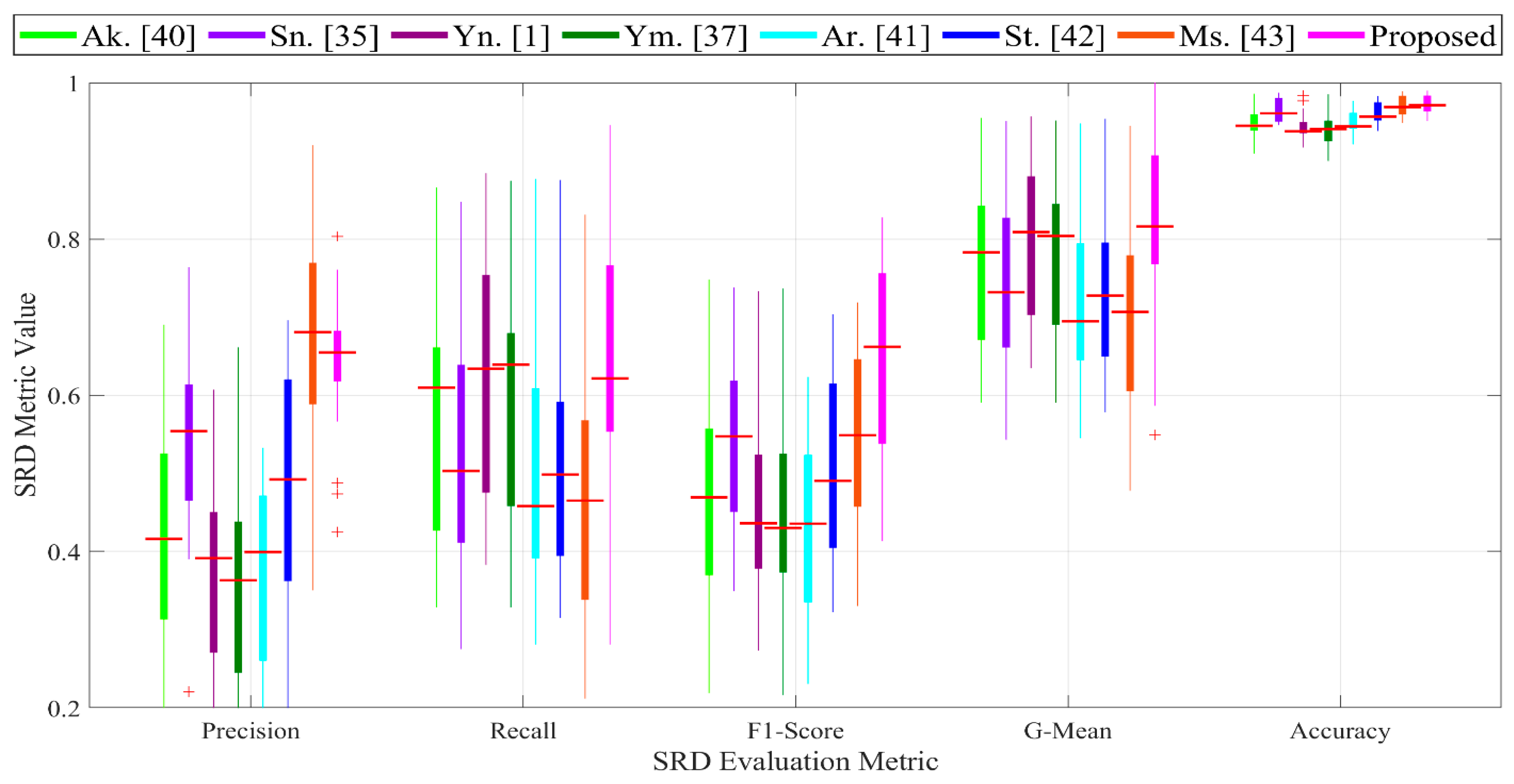
5.3.2. Comparison of SRD Rates of Proposed Method and Those in Literature
5.3.3. Visualization of SRD Rates of Different Methods
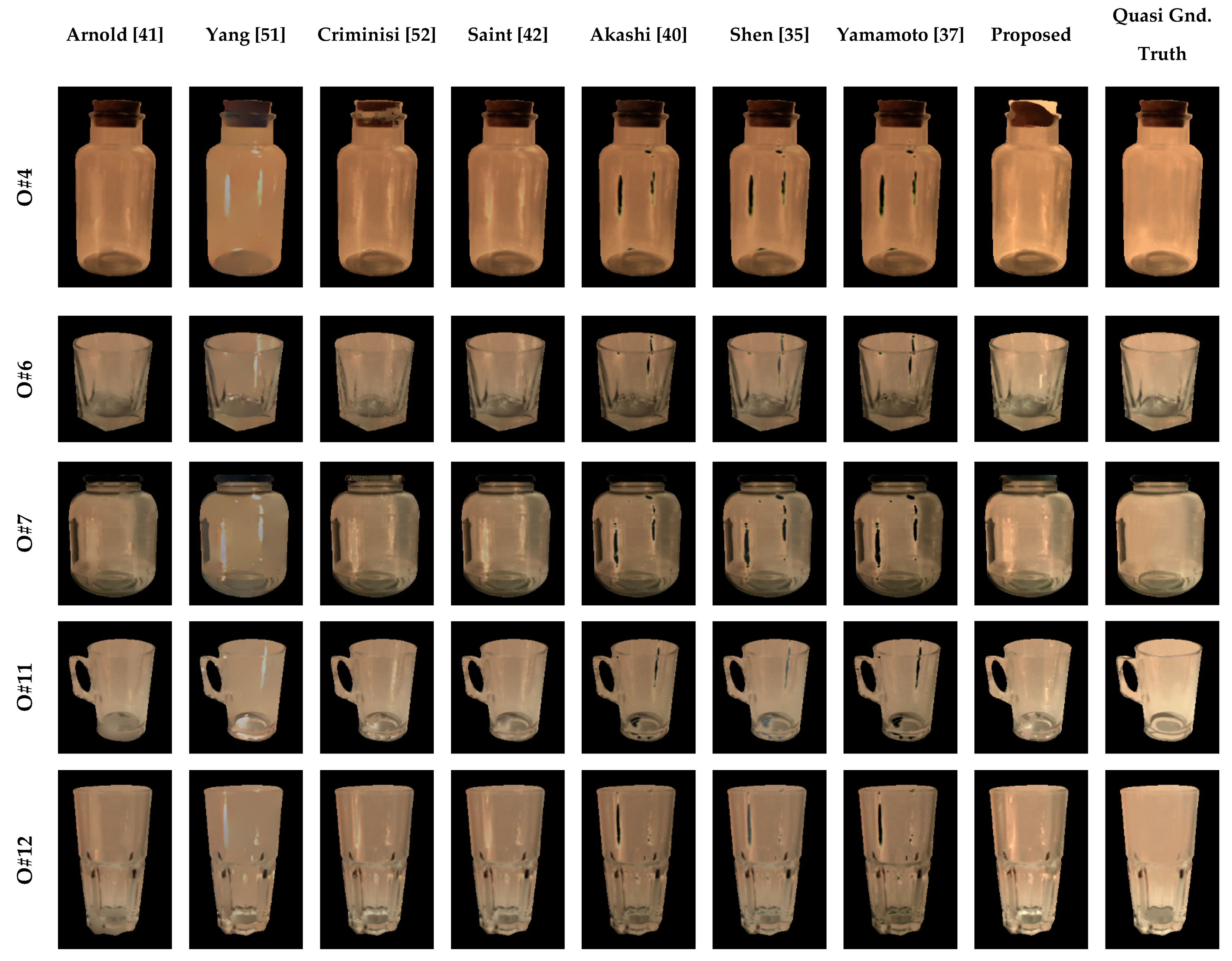
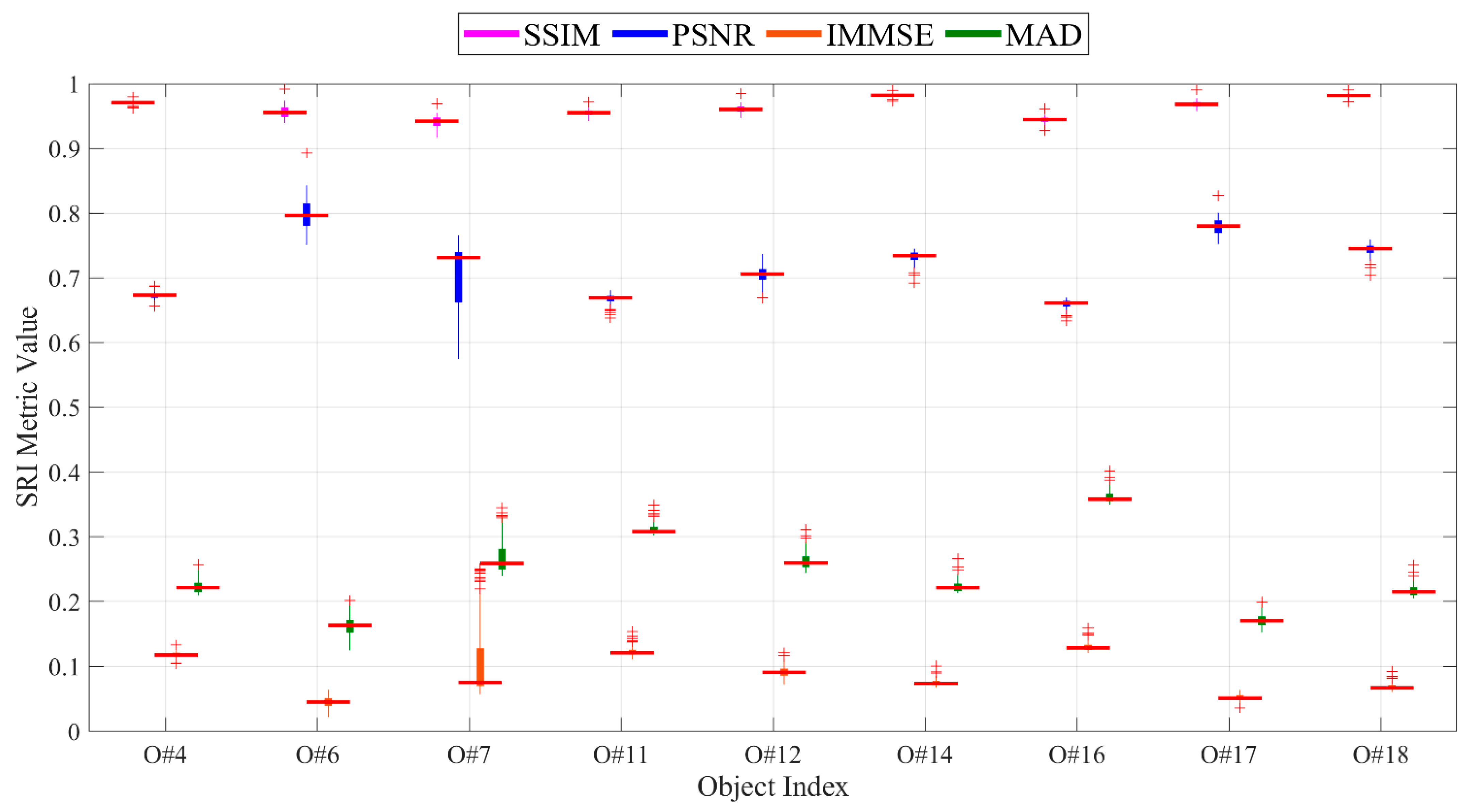
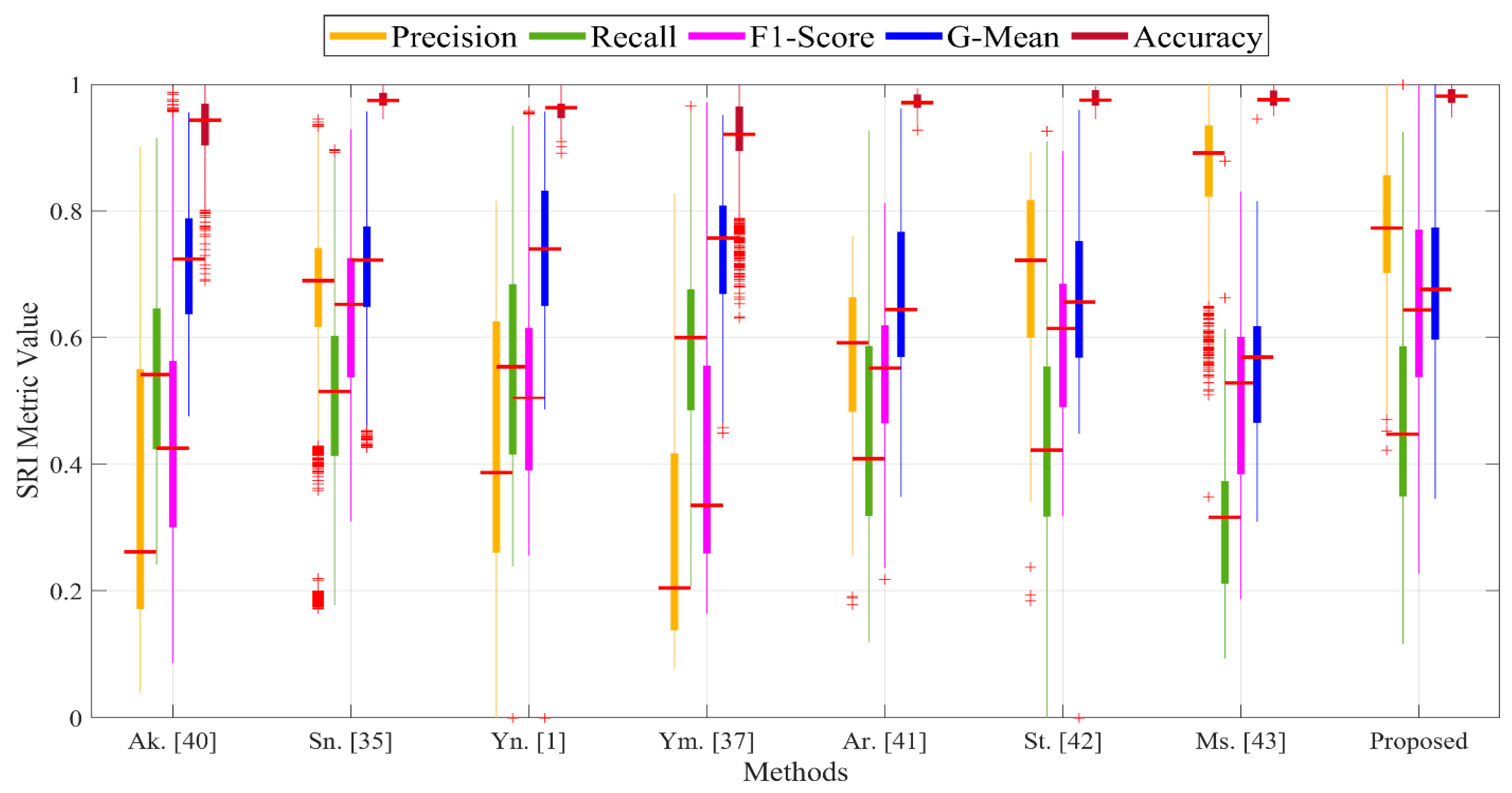
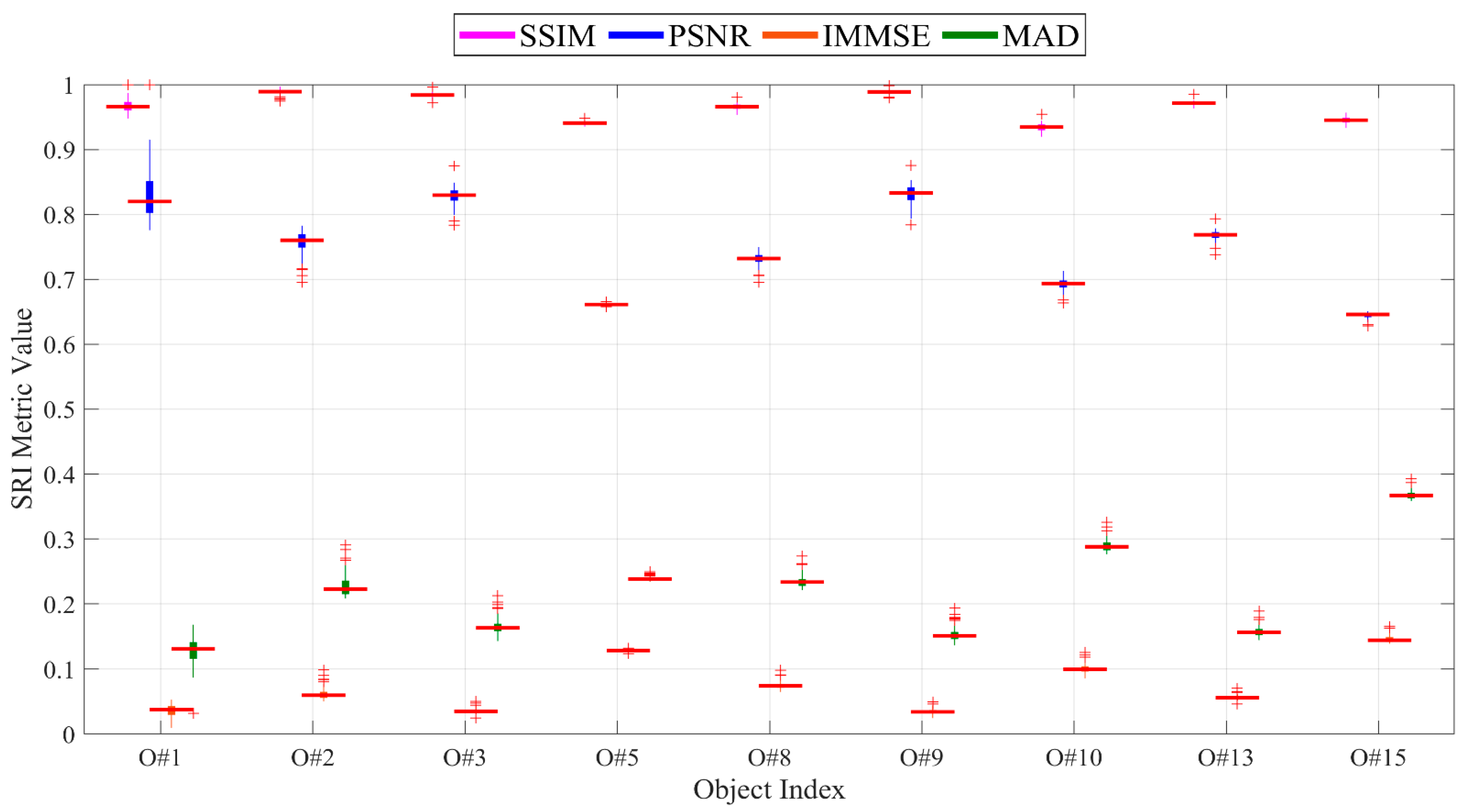
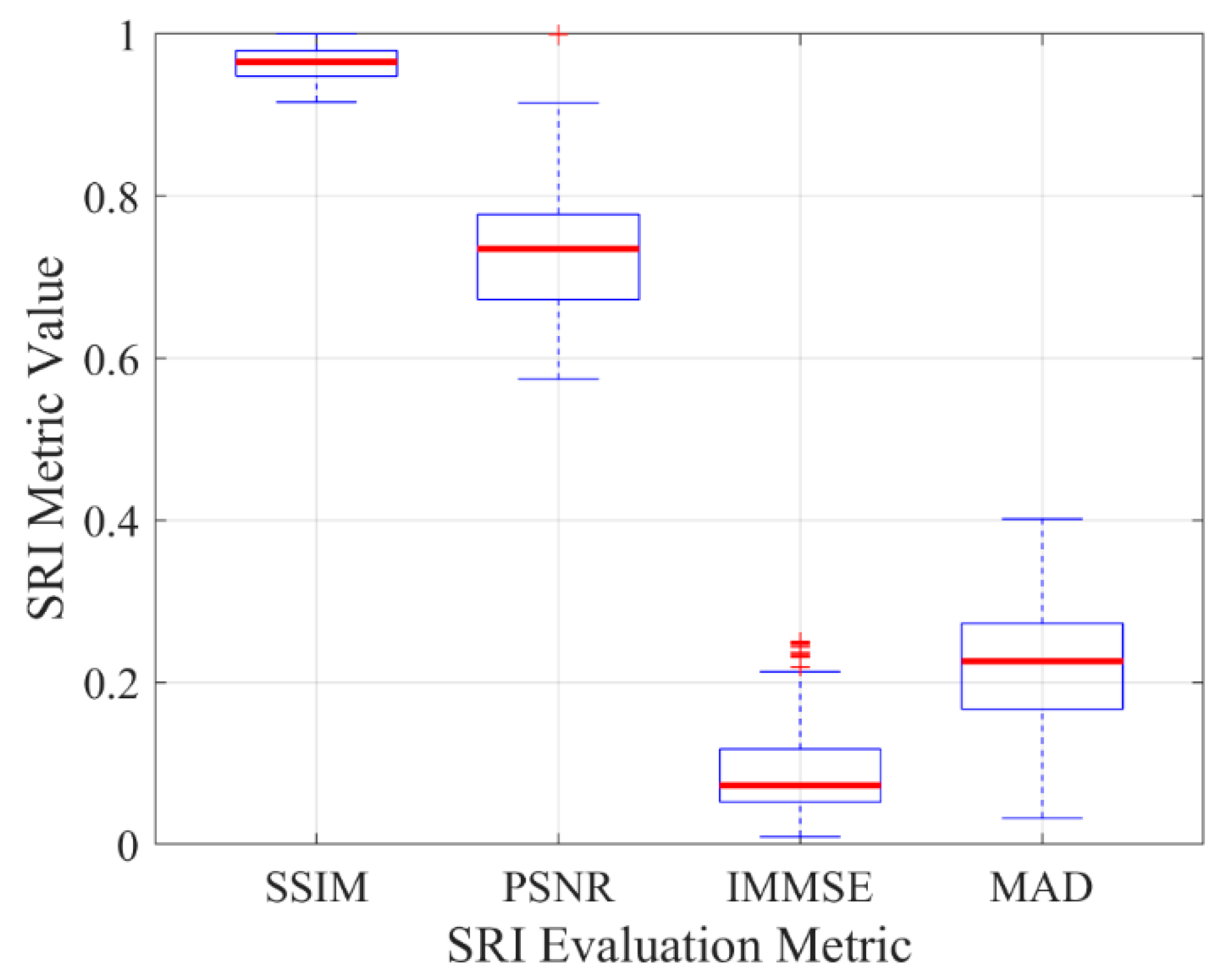
5.4. Performance Evaluation of SRI
5.4.1. Analysis of SRI Quality
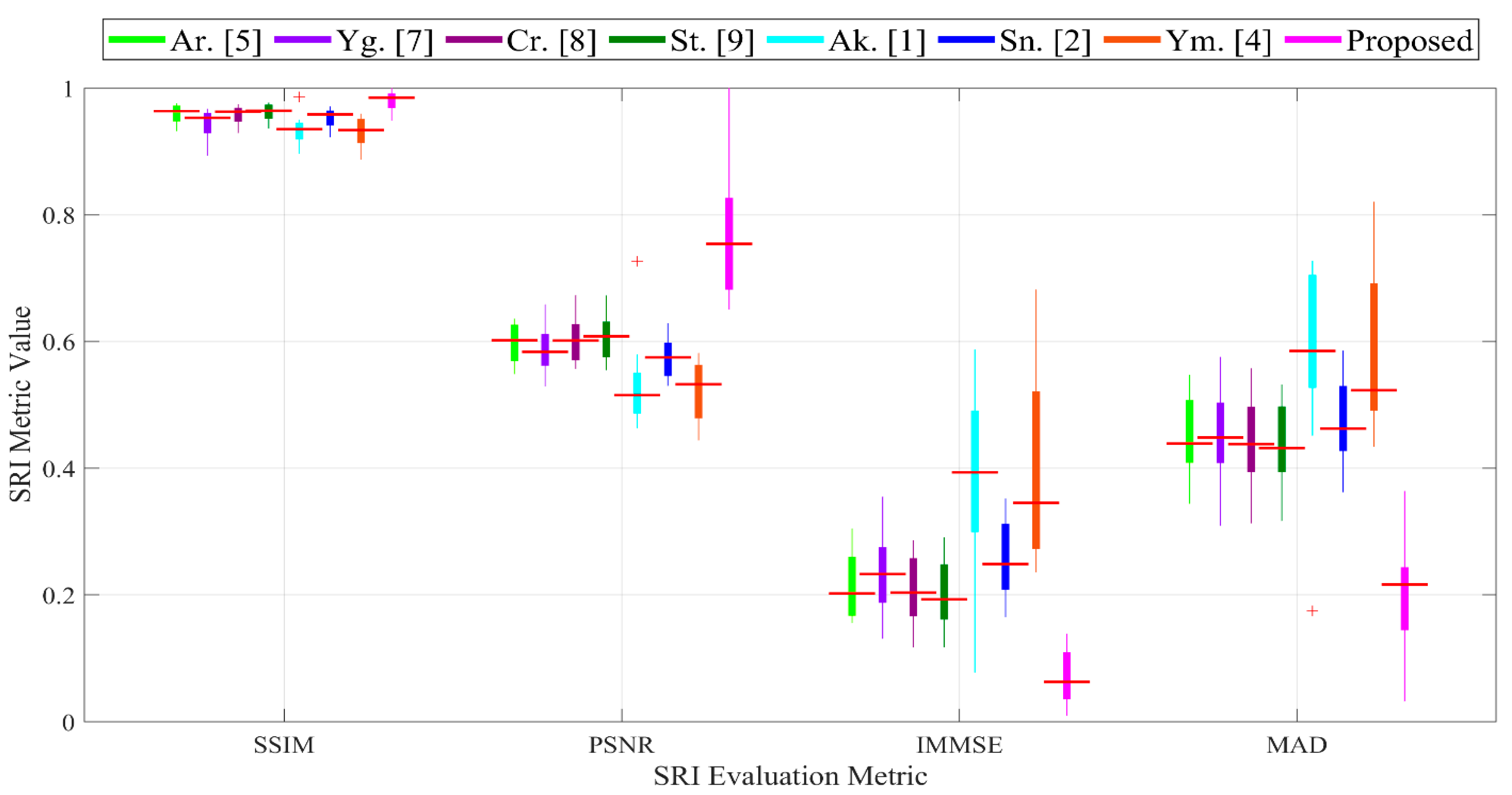
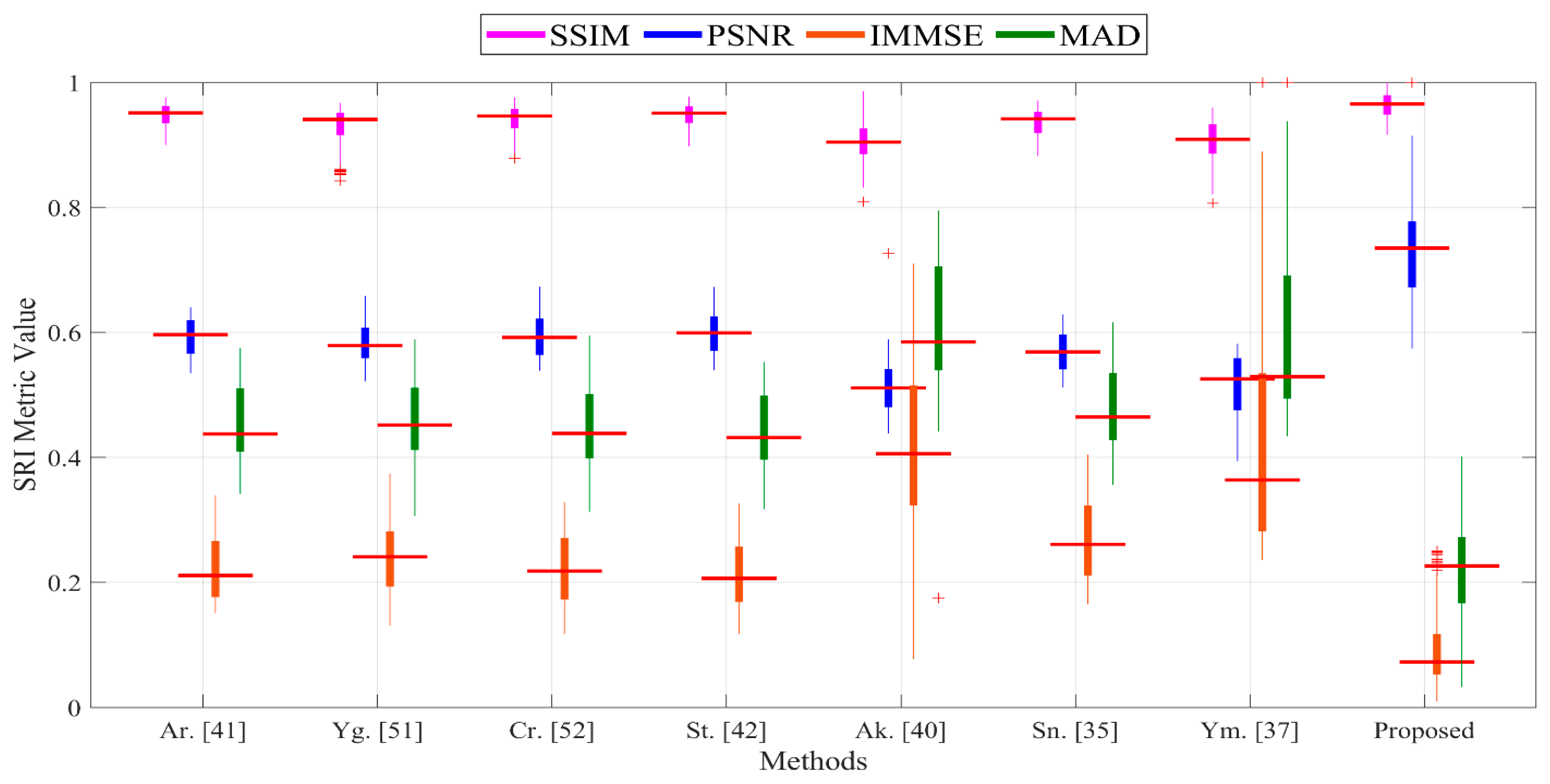
5.4.2. Comparison of SRI Rates of Proposed Method and Those in Literature
5.4.3. Visualization of SRI Quality Assessment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


Appendix B

References
- Yang, Q.; Wang, S.; Ahuja, N. Real-time specular highlight removal using bilateral filtering. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 6–9 September 2010. [Google Scholar]
- Xin, J.H.; Shen, H.L. Accurate color synthesis of three-dimensional objects in an image. JOSA A 2004, 21, 713–723. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Lee, S.W. Estimation of diffuse and specular appearance. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999. [Google Scholar]
- Hara, K.; Nishino, K.; Ikeuchi, K. Determining reflectance and light position from a single image without distant illumination assumption. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 3 April 2008. [Google Scholar]
- Tan, R.T.; Ikeuchi, K. Separating reflection components of textured surfaces using a single image. In Proceedings of the Digitally Archiving Cultural Objects, Nice, France, 14–17 October 2003. [Google Scholar]
- Kalra, A.; Taamazyan, V.; Rao, S.K.; Venkataraman, K.; Raskar, R.; Kadambi, A. Deep polarization cues for transparent object segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Tyo, J.S.; Goldstein, D.L.; Chenault, D.B.; Shaw, J.A. Review of passive imaging polarimetry for remote sensing applications. Appl. Opt. 2006, 45, 5453–5469. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Shen, X.; Xu, L.; Zhuo, S.; Zhang, X.; Shen, L.; Jia, J. Crossfield joint image restoration via scale map. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013. [Google Scholar]
- Schaul, L.; Fredembach, C.; Susstrunk, S. Color image dehazing using the near-infrared. In Proceedings of the 16th IEEE International Conference on Image Processing (ICIP), Chiang Mai, Thailand, 7 November 2009. [Google Scholar]
- Salamati, N.; Larlus, D.; Csurka, G.; Süsstrunk, S. Semantic image segmentation using visible and near-infrared channels. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Berns, R.S.; Imai, F.H.; Burns, P.D.; Tzeng, D.Y. Multispectral-based color reproduction research at the Munsell Color Science Laboratory. In Proceedings of the Electronic Imaging: Processing, Printing, and Publishing in Color, Proceedings of the SPIE, Zurich, Switzerland, 7 September 1998. [Google Scholar]
- Thomas, J.B. Illuminant estimation from uncalibrated multispectral images. In Proceedings of the 2015 Colour and Visual Computing Symposium (CVCS), Gjovik, Norway, 25–26 August 2015. [Google Scholar]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of green-red vegetation index for remote sensing of vegetation phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. Remote sensing of vegetation structure using computer vision. Remote. Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef]
- Rfenacht, D.; Fredembach, C.; Süsstrunk, S. Automatic and accurate shadow detection using near-infrared information. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1672–1678. [Google Scholar] [CrossRef] [PubMed]
- Sobral, A.; Javed, S.; Ki Jung, S.; Bouwmans, T.; Zahzah, E.H. Online stochastic tensor decomposition for background subtraction in multispectral video sequences. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Islam, M.N.; Tahtali, M.; Pickering, M. Hybrid Fusion-Based Background Segmentation in Multispectral Polarimetric Imagery. Remote Sens. 2020, 12, 1776. [Google Scholar] [CrossRef]
- Nayar, S.K.; Fang, X.-S.; Boult, T. Separation of reflection components using color and polarization. Int. J. Comput. Vis. 1997, 21, 163–186. [Google Scholar] [CrossRef]
- Wolff, L.B. Polarization-based material classification from specular reflection. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 1059–1071. [Google Scholar] [CrossRef]
- Atkinson, G.A.; Hancock, E.R. Shape estimation using polarization and shading from two views. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2001–2017. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, J.; Zhang, Y. Target detection for polarized hyperspectral images based on tensor decomposition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 674–678. [Google Scholar] [CrossRef]
- Goudail, F.; Terrier, P.; Takakura, Y.; Bigue, L.; Galland, F.; DeVlaminck, V. Target detection with a liquid-crystal-based passive stokes polarimeter. Appl. Opt. 2004, 43, 274–282. [Google Scholar] [CrossRef] [PubMed]
- Denes, L.J.; Gottlieb, M.S.; Kaminsky, B.; Huber, D.F. Spectropolarimetric imaging for object recognition. In Proceedings of the 26th AIPR Workshop: Exploiting New Image Sources and Sensors, Washington, DC, USA, 1 March 1998. [Google Scholar]
- Romano, J.M.; Rosario, D.; McCarthy, J. Day/night polarimetric anomaly detection using SPICE imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 5014–5023. [Google Scholar] [CrossRef]
- Islam, M.N.; Tahtali, M.; Pickering, M. Man-made object separation using polarimetric imagery. In Proceedings of the SPIE Future Sensing Technologies, Tokyo, Japan, 12–14 November 2019. [Google Scholar]
- Zhou, P.C.; Liu, C.C. Camouflaged target separation by spectral-polarimetric imagery fusion with shearlet transform and clustering segmentation. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Imaging Sensors and Applications, Beijing, China, 21 August 2013. [Google Scholar]
- Maeno, K.; Nagahara, H.; Shimada, A.; Taniguchi, R.I. Light field distortion feature for transparent object recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Xu, Y.; Maeno, K.; Nagahara, H.; Shimada, A.; Taniguchi, R.I. Light field distortion feature for transparent object classification. Comput. Vision Image Underst. 2015, 139, 122–135. [Google Scholar] [CrossRef]
- Xu, Y.; Nagahara, H.; Shimada, A.; Taniguchi, R.I. Transcut: Transparent object segmentation from a light-field image. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Shafer, S.A. Using color to separate reflection components. Color Res. Appl. 1985, 10, 210–218. [Google Scholar] [CrossRef]
- Tan, R.T.; Ikeuchi, K. Reflection components decomposition of textured surfaces using linear basis functions. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Yoon, K.J.; Choi, Y.; Kweon, I.S. Fast separation of reflection components using a specularity-invariant image representation. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006. [Google Scholar]
- Sato, Y.; Ikeuchi, K. Temporal-color space analysis of reflection. JOSA A 1994, 11, 2990–3002. [Google Scholar] [CrossRef]
- Lin, S.; Shum, H.Y. Separation of diffuse and specular reflection in color images. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Shen, H.L.; Cai, Q.Y. Simple and efficient method for specularity removal in an image. Appl. Opt. 2009, 48, 2711–2719. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Vo, Q.N.; Yang, H.J.; Kim, S.H.; Lee, G.S. Separation of specular and diffuse components using tensor voting in color images. Appl. Opt. 2014, 53, 7924–7936. [Google Scholar] [CrossRef]
- Yamamoto, T.; Nakazawa, A. General improvement method of specular component separation using high-emphasis filter and similarity function. ITE Trans. Media Technol. Appl. 2019, 7, 92–102. [Google Scholar] [CrossRef]
- Mallick, S.P.; Zickler, T.; Belhumeur, P.N.; Kriegman, D.J. Specularity removal in images and videos: A PDE approach. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006. [Google Scholar]
- Quan, L.; Shum, H.Y. Highlight removal by illumination-constrained inpainting. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003. [Google Scholar]
- Akashi, Y.; Okatani, T. Separation of reflection components by sparse non-negative matrix factorization. Comput. Vis. Image Underst. 2016, 146, 77–85. [Google Scholar] [CrossRef]
- Arnold, M.; Ghosh, A.; Ameling, S.; Lacey, G. Automatic segmentation and inpainting of specular highlights for endoscopic imaging. EURASIP J. Image Video Process. 2010, 2010, 1–12. [Google Scholar] [CrossRef]
- Saint-Pierre, C.A.; Boisvert, J.; Grimard, G.; Cheriet, F. Detection and correction of specular reflections for automatic surgical tool segmentation in thoracoscopic images. Mach. Vis. Appl. 2011, 22, 171–180. [Google Scholar] [CrossRef]
- Meslouhi, O.; Kardouchi, M.; Allali, H.; Gadi, T.; Benkaddour, Y. Automatic detection and inpainting of specular reflections for colposcopic images. Open Comput. Sci. 2011, 1, 341–354. [Google Scholar] [CrossRef]
- Fedorov, V.; Facciolo, G.; Arias, P. Variational framework for non-local inpainting. Image Process. Line 2015, 5, 362–386. [Google Scholar] [CrossRef]
- Newson, A.; Almansa, A.; Gousseau, Y.; Pérez, P. Non-local patch-based image inpainting. Image Process. Line 2017, 7, 373–385. [Google Scholar] [CrossRef]
- Shih, T.K.; Chang, R.C. Digital inpainting-survey and multilayer image inpainting algorithms. In Proceedings of the Third International Conference on Information Technology and Applications (ICITA’05), Sydney, NSW, Australia, 4–7 July 2005. [Google Scholar]
- Kokaram, A.C. On missing data treatment for degraded video and film archives: A survey and a new Bayesian approach. IEEE Trans. Image Process. 2004, 13, 397–415. [Google Scholar] [CrossRef]
- Vogt, F.; Paulus, D.; Heigl, B.; Vogelgsang, C.; Niemann, H.; Greiner, G.; Schick, C. Making the invisible visible: Highlight substitution by color light fields. In Proceedings of the Conference on Colour in Graphics, Imaging, and Vision, Poitiers, France, 2–5 April 2002. [Google Scholar]
- Cao, Y.; Liu, D.; Tavanapong, W.; Wong, J.; Oh, J.; De Groen, P.C. Computer-aided detection of diagnostic and therapeutic operations in colonoscopy videos. IEEE Trans. Biomed. Eng. 2007, 54, 1268–1279. [Google Scholar] [CrossRef]
- Oh, J.; Hwang, S.; Lee, J.; Tavanapong, W.; Wong, J.; de Groen, P.C. Informative frame classification for endoscopy video. Med Image Anal. 2007, 11, 110–127. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, W.; Zheng, Y.; Cai, J.F.; Xu, W. Fast single image reflection suppression via convex optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Criminisi, A.; Pérez, P.; Toyama, K. Region filling and object removal by exemplar-based image inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal. Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Stokes, G.G. On the composition and resolution of streams of polarized light from different sources. Trans. Camb. Philos. Soc. 1851, 9, 399. [Google Scholar]
- Dowson, N.D.; Bowden, R. Simultaneous modeling and tracking (smat) of feature sets. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Chiu, S.Y.; Chiu, C.C.; Xu, S.S.D. A Background Subtraction Algorithm in Complex Environments Based on Category Entropy Analysis. Appl. Sci. 2018, 8, 885. [Google Scholar] [CrossRef]
- Somvanshi, S.S.; Kunwar, P.; Tomar, S.; Singh, M. Comparative statistical analysis of the quality of image enhancement techniques. Int. J. Image Data Fusion 2017, 9, 131–151. [Google Scholar] [CrossRef]








| Methods | Metrics | Object Index (Maximum SRD) | Overall Mean (SA) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O#1 | O#2 | O#3 | O#4 | O#5 | O#6 | O#7 | O#8 | O#9 | O#10 | O#11 | O#12 | O#13 | O#14 | O#15 | O#16 | O#17 | O#18 | |||
| Ak. [40] | Precision | 0.178 | 0.348 | 0.686 | 0.445 | 0.600 | 0.354 | 0.460 | 0.382 | 0.655 | 0.519 | 0.240 | 0.311 | 0.336 | 0.124 | 0.522 | 0.542 | 0.504 | 0.123 | 0.362 ± 0.24 |
| Recall | 0.628 | 0.629 | 0.662 | 0.427 | 0.514 | 0.345 | 0.426 | 0.417 | 0.771 | 0.536 | 0.598 | 0.866 | 0.658 | 0.622 | 0.466 | 0.727 | 0.328 | 0.747 | 0.512 ± 0.14 | |
| F1-Score | 0.277 | 0.448 | 0.673 | 0.436 | 0.554 | 0.350 | 0.443 | 0.398 | 0.708 | 0.528 | 0.342 | 0.457 | 0.445 | 0.207 | 0.493 | 0.621 | 0.398 | 0.211 | 0.377 ± 0.16 | |
| G-Mean | 0.769 | 0.781 | 0.810 | 0.644 | 0.710 | 0.578 | 0.644 | 0.634 | 0.874 | 0.722 | 0.749 | 0.917 | 0.795 | 0.754 | 0.676 | 0.835 | 0.567 | 0.834 | 0.689 ± 0.10 | |
| Accuracy | 0.935 | 0.962 | 0.981 | 0.943 | 0.957 | 0.939 | 0.946 | 0.939 | 0.986 | 0.948 | 0.928 | 0.970 | 0.951 | 0.910 | 0.960 | 0.944 | 0.940 | 0.929 | 0.926 ± 0.05 | |
| Sn. [35] | Precision | 0.220 | 0.610 | 0.759 | 0.509 | 0.613 | 0.437 | 0.527 | 0.477 | 0.602 | 0.579 | 0.462 | 0.447 | 0.574 | 0.388 | 0.590 | 0.642 | 0.622 | 0.505 | 0.655 ± 0.15 |
| Recall | 0.667 | 0.590 | 0.639 | 0.392 | 0.493 | 0.301 | 0.411 | 0.335 | 0.831 | 0.546 | 0.513 | 0.848 | 0.457 | 0.474 | 0.476 | 0.647 | 0.275 | 0.599 | 0.483 ± 0.15 | |
| F1-Score | 0.330 | 0.600 | 0.694 | 0.443 | 0.546 | 0.357 | 0.462 | 0.393 | 0.698 | 0.562 | 0.486 | 0.586 | 0.509 | 0.426 | 0.527 | 0.644 | 0.381 | 0.548 | 0.527 ± 0.13 | |
| G-Mean | 0.797 | 0.764 | 0.797 | 0.620 | 0.696 | 0.543 | 0.635 | 0.573 | 0.906 | 0.730 | 0.709 | 0.913 | 0.672 | 0.683 | 0.685 | 0.794 | 0.522 | 0.771 | 0.681 ± 0.11 | |
| Accuracy | 0.946 | 0.981 | 0.983 | 0.949 | 0.958 | 0.948 | 0.952 | 0.950 | 0.984 | 0.954 | 0.966 | 0.983 | 0.974 | 0.976 | 0.964 | 0.955 | 0.946 | 0.988 | 0.969 ± 0.01 | |
| Yn. [1] | Precision | 0.220 | 0.396 | 0.603 | 0.402 | 0.476 | 0.269 | 0.382 | 0.364 | 0.595 | 0.438 | 0.274 | 0.224 | 0.288 | 0.166 | 0.416 | 0.494 | 0.448 | 0.156 | 0.433 ± 0.19 |
| Recall | 0.817 | 0.638 | 0.673 | 0.457 | 0.562 | 0.430 | 0.442 | 0.475 | 0.831 | 0.571 | 0.630 | 0.884 | 0.671 | 0.652 | 0.484 | 0.758 | 0.383 | 0.754 | 0.529 ± 0.16 | |
| F1-Score | 0.346 | 0.488 | 0.636 | 0.428 | 0.515 | 0.331 | 0.410 | 0.413 | 0.694 | 0.496 | 0.382 | 0.358 | 0.403 | 0.265 | 0.447 | 0.598 | 0.413 | 0.258 | 0.446 ± 0.14 | |
| G-Mean | 0.877 | 0.789 | 0.815 | 0.664 | 0.737 | 0.636 | 0.652 | 0.675 | 0.906 | 0.739 | 0.772 | 0.919 | 0.798 | 0.782 | 0.686 | 0.848 | 0.609 | 0.845 | 0.707 ± 0.11 | |
| Accuracy | 0.939 | 0.968 | 0.977 | 0.937 | 0.946 | 0.917 | 0.936 | 0.935 | 0.984 | 0.937 | 0.936 | 0.954 | 0.941 | 0.931 | 0.950 | 0.936 | 0.934 | 0.945 | 0.953 ± 0.02 | |
| Ym. [37] | Precision | 0.199 | 0.409 | 0.657 | 0.435 | 0.531 | 0.282 | 0.302 | 0.357 | 0.631 | 0.406 | 0.243 | 0.222 | 0.296 | 0.122 | 0.403 | 0.364 | 0.513 | 0.143 | 0.307 ± 0.23 |
| Recall | 0.645 | 0.634 | 0.665 | 0.435 | 0.547 | 0.384 | 0.456 | 0.458 | 0.778 | 0.565 | 0.646 | 0.875 | 0.680 | 0.647 | 0.492 | 0.791 | 0.328 | 0.755 | 0.559 ± 0.15 | |
| F1-Score | 0.304 | 0.497 | 0.661 | 0.435 | 0.539 | 0.325 | 0.363 | 0.401 | 0.697 | 0.472 | 0.353 | 0.355 | 0.412 | 0.205 | 0.443 | 0.499 | 0.400 | 0.240 | 0.346 ± 0.17 | |
| G-Mean | 0.782 | 0.787 | 0.811 | 0.649 | 0.730 | 0.604 | 0.656 | 0.663 | 0.877 | 0.734 | 0.777 | 0.914 | 0.804 | 0.767 | 0.691 | 0.847 | 0.567 | 0.843 | 0.709 ± 0.10 | |
| Accuracy | 0.941 | 0.969 | 0.980 | 0.942 | 0.952 | 0.924 | 0.920 | 0.934 | 0.985 | 0.932 | 0.925 | 0.954 | 0.942 | 0.905 | 0.948 | 0.900 | 0.940 | 0.939 | 0.908 ± 0.06 | |
| Ar. [41] | Precision | 0.189 | 0.520 | 0.463 | 0.471 | 0.529 | 0.258 | 0.436 | 0.383 | 0.410 | 0.468 | 0.308 | 0.191 | 0.287 | 0.178 | 0.366 | 0.496 | 0.413 | 0.255 | 0.561 ± 0.12 |
| Recall | 0.594 | 0.587 | 0.668 | 0.394 | 0.391 | 0.351 | 0.422 | 0.449 | 0.763 | 0.526 | 0.609 | 0.877 | 0.353 | 0.281 | 0.467 | 0.727 | 0.371 | 0.447 | 0.434 ± 0.16 | |
| F1-Score | 0.287 | 0.552 | 0.547 | 0.429 | 0.450 | 0.298 | 0.428 | 0.414 | 0.534 | 0.495 | 0.409 | 0.314 | 0.317 | 0.218 | 0.410 | 0.590 | 0.391 | 0.325 | 0.466 ± 0.10 | |
| G-Mean | 0.750 | 0.761 | 0.808 | 0.620 | 0.619 | 0.577 | 0.640 | 0.658 | 0.863 | 0.713 | 0.763 | 0.910 | 0.586 | 0.524 | 0.671 | 0.831 | 0.598 | 0.663 | 0.644 ± 0.12 | |
| Accuracy | 0.941 | 0.977 | 0.967 | 0.946 | 0.951 | 0.921 | 0.943 | 0.939 | 0.971 | 0.942 | 0.945 | 0.944 | 0.955 | 0.962 | 0.944 | 0.936 | 0.930 | 0.976 | 0.966 ± 0.01 | |
| St. [42] | Precision | 0.461 | 0.679 | 0.680 | 0.597 | 0.692 | 0.344 | 0.609 | 0.392 | 0.586 | 0.616 | 0.340 | 0.237 | 0.491 | 0.360 | 0.421 | 0.631 | 0.487 | 0.193 | 0.702 ± 0.12 |
| Recall | 0.592 | 0.535 | 0.637 | 0.357 | 0.502 | 0.321 | 0.400 | 0.381 | 0.771 | 0.462 | 0.558 | 0.876 | 0.457 | 0.394 | 0.495 | 0.567 | 0.315 | 0.724 | 0.422 ± 0.15 | |
| F1-Score | 0.518 | 0.598 | 0.658 | 0.447 | 0.582 | 0.332 | 0.483 | 0.387 | 0.666 | 0.528 | 0.423 | 0.373 | 0.473 | 0.376 | 0.455 | 0.597 | 0.383 | 0.305 | 0.507 ± 0.11 | |
| G-Mean | 0.764 | 0.729 | 0.795 | 0.593 | 0.704 | 0.558 | 0.628 | 0.608 | 0.873 | 0.674 | 0.734 | 0.916 | 0.671 | 0.624 | 0.693 | 0.744 | 0.555 | 0.834 | 0.637 ± 0.12 | |
| Accuracy | 0.978 | 0.983 | 0.980 | 0.954 | 0.963 | 0.939 | 0.957 | 0.942 | 0.983 | 0.955 | 0.952 | 0.957 | 0.970 | 0.975 | 0.950 | 0.952 | 0.938 | 0.958 | 0.971 ± 0.01 | |
| Ms. [43] | Precision | 0.646 | 0.878 | 0.914 | 0.876 | 0.765 | 0.592 | 0.754 | 0.585 | 0.847 | 0.702 | 0.557 | 0.557 | 0.556 | 0.348 | 0.692 | 0.657 | 0.729 | 0.660 | 0.868 ± 0.09 |
| Recall | 0.580 | 0.367 | 0.502 | 0.248 | 0.485 | 0.212 | 0.393 | 0.307 | 0.568 | 0.445 | 0.507 | 0.831 | 0.489 | 0.572 | 0.366 | 0.627 | 0.240 | 0.338 | 0.283 ± 0.11 | |
| F1-Score | 0.611 | 0.518 | 0.648 | 0.387 | 0.593 | 0.312 | 0.517 | 0.403 | 0.680 | 0.545 | 0.530 | 0.667 | 0.520 | 0.433 | 0.479 | 0.642 | 0.361 | 0.447 | 0.412 ± 0.13 | |
| G-Mean | 0.759 | 0.606 | 0.708 | 0.498 | 0.694 | 0.459 | 0.625 | 0.551 | 0.753 | 0.664 | 0.707 | 0.907 | 0.695 | 0.748 | 0.603 | 0.783 | 0.489 | 0.581 | 0.520 ± 0.11 | |
| Accuracy | 0.985 | 0.983 | 0.984 | 0.959 | 0.966 | 0.956 | 0.963 | 0.956 | 0.988 | 0.960 | 0.972 | 0.988 | 0.973 | 0.971 | 0.967 | 0.956 | 0.949 | 0.989 | 0.971 ± 0.01 | |
| Proposed | Precision | 0.630 | 0.666 | 0.728 | 0.622 | 0.668 | 0.643 | 0.798 | 0.563 | 0.756 | 0.678 | 0.485 | 0.624 | 0.470 | 0.422 | 0.665 | 0.658 | 0.719 | 0.614 | 0.776 ± 0.10 |
| Recall | 0.630 | 0.585 | 0.737 | 0.798 | 0.946 | 0.281 | 0.767 | 0.452 | 0.808 | 0.613 | 0.526 | 0.720 | 0.554 | 0.718 | 0.553 | 0.784 | 0.320 | 0.578 | 0.444 ± 0.15 | |
| F1-Score | 0.630 | 0.623 | 0.732 | 0.699 | 0.783 | 0.391 | 0.782 | 0.501 | 0.781 | 0.644 | 0.504 | 0.668 | 0.509 | 0.531 | 0.604 | 0.715 | 0.442 | 0.596 | 0.546 ± 0.13 | |
| G-Mean | 0.791 | 0.762 | 0.855 | 0.881 | 0.960 | 0.528 | 0.871 | 0.666 | 0.896 | 0.777 | 0.718 | 0.846 | 0.737 | 0.839 | 0.739 | 0.873 | 0.563 | 0.759 | 0.654 ± 0.11 | |
| Accuracy | 0.985 | 0.983 | 0.984 | 0.965 | 0.973 | 0.958 | 0.978 | 0.957 | 0.990 | 0.963 | 0.967 | 0.990 | 0.968 | 0.976 | 0.970 | 0.961 | 0.951 | 0.990 | 0.974 ± 0.01 | |
| Methods | Metrics | Object Index (Maximum SRI) | Overall Mean (SA) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O#1 | O#2 | O#3 | O#4 | O#5 | O#6 | O#7 | O#8 | O#9 | O#10 | O#11 | O#12 | O#13 | O#14 | O#15 | O#16 | O#17 | O#18 | |||
| Ar. [41] | SSIM | 0.942 | 0.967 | 0.966 | 0.965 | 0.940 | 0.961 | 0.940 | 0.959 | 0.965 | 0.929 | 0.940 | 0.946 | 0.968 | 0.958 | 0.925 | 0.943 | 0.963 | 0.955 | 0.941 ± 0.02 |
| PSNR | 21.25 | 20.42 | 21.26 | 20.96 | 19.99 | 20.95 | 19.22 | 20.25 | 20.74 | 19.03 | 18.33 | 18.53 | 20.83 | 18.58 | 18.42 | 19.56 | 20.98 | 19.65 | 19.80 ± 0.99 | |
| IMMSE | 487.6 | 590.1 | 486.2 | 520.9 | 651.4 | 522.7 | 778.0 | 613.9 | 548.7 | 813.4 | 954.8 | 911.5 | 537.6 | 901.9 | 935.8 | 720.2 | 519.3 | 705.4 | 698.9 ± 162 | |
| MAD | 12.53 | 16.20 | 16.26 | 15.26 | 13.49 | 14.89 | 19.94 | 15.12 | 15.79 | 18.51 | 18.87 | 19.80 | 12.74 | 17.97 | 19.63 | 18.27 | 13.55 | 15.52 | 16.46 ± 2.36 | |
| Yg. [51] | SSIM | 0.887 | 0.956 | 0.943 | 0.951 | 0.926 | 0.951 | 0.910 | 0.952 | 0.954 | 0.922 | 0.944 | 0.943 | 0.960 | 0.948 | 0.911 | 0.915 | 0.958 | 0.957 | 0.926 ± 0.02 |
| PSNR | 18.31 | 19.74 | 20.16 | 21.42 | 18.44 | 20.53 | 19.29 | 20.12 | 20.43 | 18.72 | 18.95 | 19.06 | 21.36 | 18.98 | 17.68 | 18.78 | 22.01 | 20.45 | 19.53 ± 1.14 | |
| IMMSE | 958.6 | 690.6 | 626.5 | 468.5 | 931.3 | 574.9 | 766.7 | 632.8 | 589.2 | 872.9 | 828.4 | 807.7 | 475.5 | 822.3 | 1110 | 861.8 | 408.9 | 586.0 | 749.8 ± 190 | |
| MAD | 18.05 | 16.36 | 17.15 | 13.68 | 16.01 | 14.88 | 19.06 | 14.88 | 15.52 | 18.68 | 17.16 | 18.36 | 11.26 | 16.34 | 20.98 | 19.36 | 11.58 | 13.77 | 16.48 ± 2.58 | |
| Cr. [52] | SSIM | 0.956 | 0.968 | 0.964 | 0.948 | 0.924 | 0.963 | 0.922 | 0.961 | 0.965 | 0.927 | 0.944 | 0.947 | 0.962 | 0.956 | 0.925 | 0.940 | 0.962 | 0.955 | 0.935 ± 0.02 |
| PSNR | 22.50 | 20.60 | 21.40 | 20.48 | 19.52 | 21.31 | 19.06 | 20.64 | 20.84 | 19.16 | 18.68 | 18.90 | 20.97 | 18.63 | 18.60 | 19.65 | 21.23 | 19.74 | 19.89 ± 1.04 | |
| IMMSE | 365.8 | 566.9 | 471.8 | 582.8 | 726.3 | 480.6 | 807.4 | 561.7 | 536.1 | 789.5 | 881.6 | 838.4 | 519.9 | 891.1 | 897.0 | 704.5 | 489.6 | 690.5 | 685.5 ± 161 | |
| MAD | 11.41 | 15.90 | 16.09 | 16.04 | 14.36 | 14.31 | 20.33 | 14.56 | 15.69 | 18.23 | 18.12 | 19.08 | 12.45 | 17.78 | 19.25 | 18.03 | 13.24 | 15.34 | 16.27 ± 2.36 | |
| St. [42] | SSIM | 0.956 | 0.968 | 0.967 | 0.966 | 0.945 | 0.967 | 0.943 | 0.966 | 0.966 | 0.933 | 0.948 | 0.952 | 0.970 | 0.957 | 0.929 | 0.939 | 0.967 | 0.957 | 0.941 ± 0.02 |
| PSNR | 22.49 | 20.59 | 21.41 | 21.11 | 20.07 | 21.30 | 19.54 | 20.61 | 20.88 | 19.23 | 18.60 | 18.90 | 21.10 | 18.66 | 18.54 | 19.83 | 21.42 | 19.70 | 20.01 ± 1.05 | |
| IMMSE | 366.4 | 567.2 | 469.7 | 504.1 | 639.7 | 482.0 | 722.3 | 565.5 | 531.5 | 776.6 | 896.9 | 837.2 | 505.1 | 886.4 | 910.4 | 676.7 | 469.1 | 696.4 | 667.6 ± 162 | |
| MAD | 11.54 | 15.89 | 16.06 | 14.91 | 13.39 | 14.35 | 19.04 | 14.68 | 15.59 | 18.13 | 18.32 | 19.00 | 12.29 | 17.73 | 19.41 | 17.48 | 12.99 | 15.40 | 16.04 ± 2.31 | |
| Ak. [40] | SSIM | 0.918 | 0.979 | 0.938 | 0.941 | 0.913 | 0.928 | 0.900 | 0.929 | 0.943 | 0.899 | 0.907 | 0.912 | 0.942 | 0.933 | 0.889 | 0.914 | 0.931 | 0.928 | 0.899 ± 0.03 |
| PSNR | 19.36 | 24.30 | 18.49 | 18.93 | 17.00 | 17.89 | 16.82 | 17.17 | 18.41 | 16.27 | 15.49 | 16.00 | 17.80 | 16.09 | 15.84 | 16.48 | 17.89 | 17.29 | 17.08 ± 1.12 | |
| IMMSE | 753.7 | 241.5 | 921.2 | 831.6 | 1296 | 1057 | 1351 | 1248 | 936.8 | 1536 | 1838 | 1631 | 1080 | 1598 | 1694 | 1464 | 1057 | 1215 | 1315 ± 334 | |
| MAD | 16.45 | 6.36 | 21.45 | 18.77 | 19.43 | 21.19 | 25.70 | 21.51 | 19.96 | 25.54 | 26.17 | 26.52 | 17.80 | 23.90 | 26.31 | 25.87 | 19.20 | 20.28 | 22.23 ± 3.24 | |
| Sn. [35] | SSIM | 0.936 | 0.961 | 0.957 | 0.952 | 0.923 | 0.959 | 0.922 | 0.956 | 0.951 | 0.917 | 0.937 | 0.941 | 0.964 | 0.952 | 0.915 | 0.934 | 0.961 | 0.954 | 0.929 ± 0.02 |
| PSNR | 19.32 | 19.99 | 20.78 | 19.94 | 18.23 | 20.78 | 18.17 | 19.97 | 19.13 | 17.73 | 18.09 | 18.42 | 20.41 | 18.23 | 17.80 | 19.09 | 21.01 | 19.57 | 19.06 ± 1.05 | |
| IMMSE | 760.9 | 652.2 | 543.6 | 659.6 | 976.7 | 543.1 | 992.1 | 654.8 | 795.4 | 1101 | 1009 | 934.8 | 591.4 | 976.5 | 1079 | 802.5 | 515.3 | 717.4 | 830.7 ± 197 | |
| MAD | 14.60 | 16.80 | 16.93 | 16.37 | 15.95 | 15.05 | 21.35 | 15.56 | 17.49 | 20.55 | 19.31 | 20.04 | 13.20 | 18.55 | 20.66 | 18.99 | 13.48 | 15.61 | 17.43 ± 2.43 | |
| Ym. [37] | SSIM | 0.906 | 0.952 | 0.945 | 0.949 | 0.917 | 0.934 | 0.897 | 0.933 | 0.950 | 0.894 | 0.911 | 0.912 | 0.938 | 0.920 | 0.890 | 0.880 | 0.944 | 0.938 | 0.902 ± 0.03 |
| PSNR | 18.37 | 18.83 | 19.11 | 19.46 | 17.72 | 18.69 | 16.37 | 17.72 | 19.11 | 16.01 | 15.97 | 16.23 | 17.87 | 15.57 | 15.86 | 14.84 | 19.34 | 18.20 | 17.27 ± 1.44 | |
| IMMSE | 946.5 | 852.3 | 798.1 | 737.0 | 1100 | 879.5 | 1500 | 1098 | 797.6 | 1631 | 1643 | 1550 | 1061 | 1804 | 1686 | 2134 | 756.5 | 985.2 | 1289 ± 439 | |
| MAD | 17.89 | 18.57 | 19.20 | 17.36 | 17.35 | 18.92 | 25.95 | 19.38 | 17.99 | 25.54 | 23.94 | 25.24 | 16.79 | 24.04 | 25.59 | 29.90 | 15.81 | 18.03 | 21.27 ± 4.11 | |
| Proposed | SSIM | 0.992 | 0.990 | 0.989 | 0.972 | 0.941 | 0.984 | 0.961 | 0.973 | 0.991 | 0.947 | 0.964 | 0.977 | 0.978 | 0.982 | 0.950 | 0.953 | 0.983 | 0.983 | 0.956 ± 0.02 |
| PSNR | 33.43 | 26.16 | 29.24 | 22.79 | 22.26 | 29.85 | 25.60 | 25.06 | 29.27 | 23.84 | 22.76 | 24.62 | 26.52 | 24.91 | 21.76 | 22.37 | 27.64 | 25.36 | 24.51 ± 2.11 | |
| IMMSE | 29.54 | 157.4 | 77.50 | 341.9 | 386.7 | 67.34 | 179.2 | 202.9 | 76.95 | 268.6 | 344.8 | 224.2 | 145.1 | 209.9 | 433.9 | 376.7 | 112.1 | 189.2 | 257.6 ± 119 | |
| MAD | 1.172 | 7.903 | 5.205 | 7.680 | 8.536 | 4.529 | 8.723 | 8.277 | 4.959 | 10.07 | 11.07 | 8.888 | 5.257 | 7.880 | 13.26 | 12.97 | 5.545 | 7.665 | 8.427 ± 2.51 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.N.; Tahtali, M.; Pickering, M. Specular Reflection Detection and Inpainting in Transparent Object through MSPLFI. Remote Sens. 2021, 13, 455. https://doi.org/10.3390/rs13030455
Islam MN, Tahtali M, Pickering M. Specular Reflection Detection and Inpainting in Transparent Object through MSPLFI. Remote Sensing. 2021; 13(3):455. https://doi.org/10.3390/rs13030455
Chicago/Turabian StyleIslam, Md Nazrul, Murat Tahtali, and Mark Pickering. 2021. "Specular Reflection Detection and Inpainting in Transparent Object through MSPLFI" Remote Sensing 13, no. 3: 455. https://doi.org/10.3390/rs13030455
APA StyleIslam, M. N., Tahtali, M., & Pickering, M. (2021). Specular Reflection Detection and Inpainting in Transparent Object through MSPLFI. Remote Sensing, 13(3), 455. https://doi.org/10.3390/rs13030455