SMAP Salinity Retrievals near the Sea-Ice Edge Using Multi-Channel AMSR2 Brightness Temperatures
Abstract
:1. Introduction
- (1)
- The spatial resolution of the SMAP footprint (≈40 km) and the lowest frequency AMSR2 frequency channel at C-band (≈50 km) are close. When multi-day aggregates are considered, in which several footprints are averaged together, then both sensors, SMAP and AMSR2, see approximately the same Earth scenes. Observations at the higher AMSR2 frequencies can be spatially resampled to the coarser C-band resolution.
- (2)
- Compared to the SMAP L-band channels, the AMSR2 channels are insensitive or only very weakly sensitive to SSS. The AMSR2 ocean measurements are affected by sea-ice contamination but not by signals such as freshwater river plumes or melt run-off. This enables us to separate the spurious sea-ice signal from the real freshwater signals.
2. Materials and Methods
2.1. Study Data Sets
2.1.1. SMAP Brightness Temperatures
2.1.2. AMSR2 Brightness Temperatures
2.1.3. Expected Specular Surface Brightness Temperatures and Emissivities
2.1.4. External Ancillary Data
- (1)
- HYCOM SSS field [23] as the reference SSS. We are using the output from the operational ocean analysis that is run by the U.S. Navy [24]. In our study, this reference SSS is used in the computation of the SMAP TB0,exp, which serve as the basic metric for algorithm development and evaluation. The reference SSS field is not an input to the proposed sea-ice flagging or sea-ice correction algorithms or to the NASA/RSS SMAP SSS retrieval algorithm.
- (2)
- SST from the Canadian Meteorological Center (CMC) [25] as ancillary SST in the RTM computations for both SMAP and AMSR2.
- (3)
- Cross Calibrated Multi-Platform (CCMP) V2.0 wind speeds and directions [26,27,28] for the calculation of the wind induced rough surface emission for both SMAP and AMSR2. The CCMP winds are created by a variational analysis method that assimilates various microwave satellite wind measurements together with a background field from a numerical weather prediction model.
- (4)
- Atmospheric profiles for pressure, temperature, relative humidity, and cloud water density as well as total columnar water vapor and total columnar cloud water from the General Forecast System (GFS) of the National Centers for Environmental Prediction (NCEP) [29]. These fields are used for computing the atmospheric attenuation for both SMAP and AMSR2.
- (5)
- Precipitation rates from the Integrated Multi-satellitE Retrievals for the Global Precipitation Mission (IMERG) Version 6 [30] for rain-flagging of both SMAP and AMSR2 observations.
2.1.5. Training and Test Sets
2.1.6. A-Priori Sea-Ice Flagging
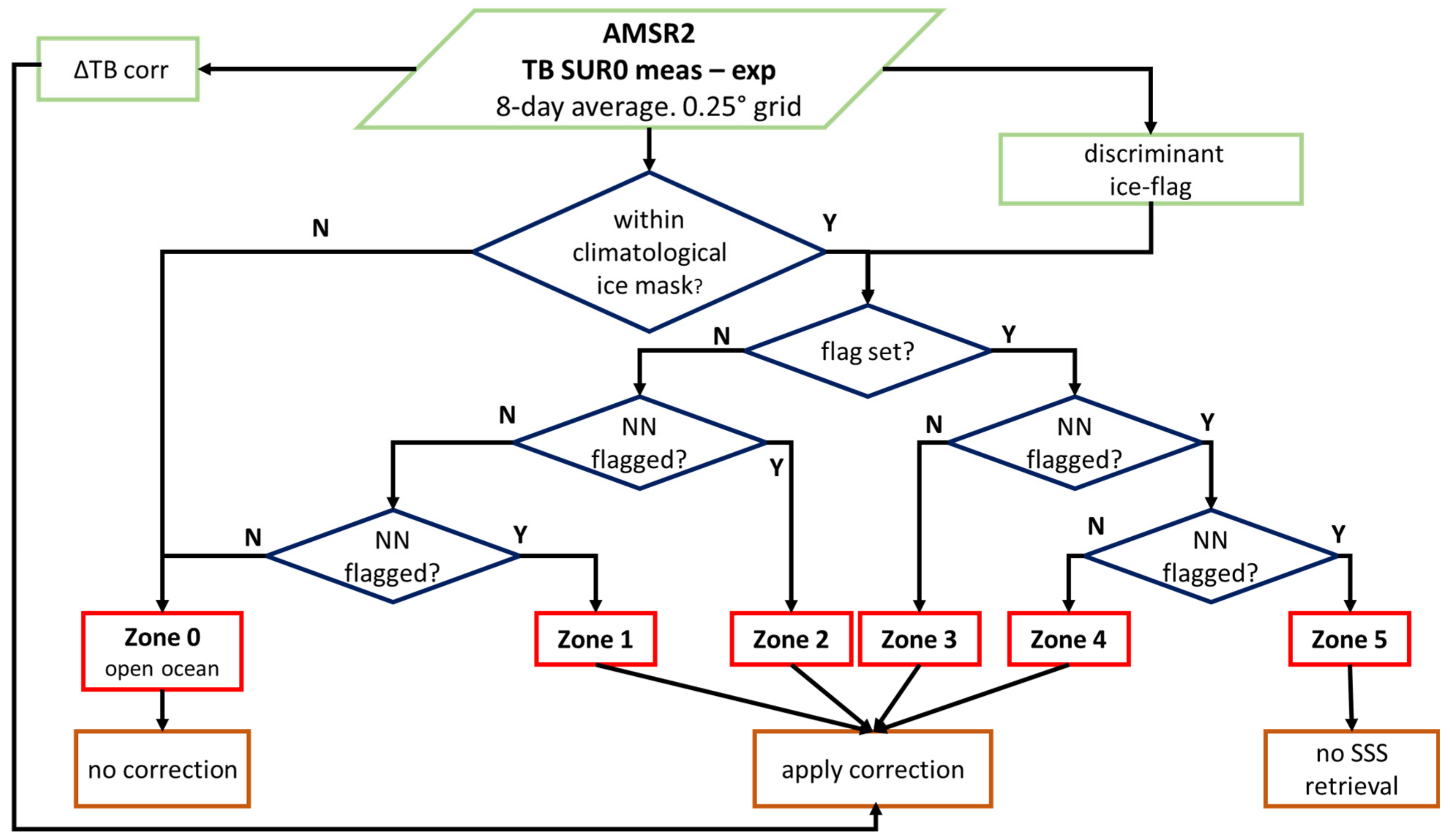
2.2. Sea-Ice Detection and Flagging
2.2.1. Discriminant Analysis
2.2.2. Nearest Neighbor Flagging
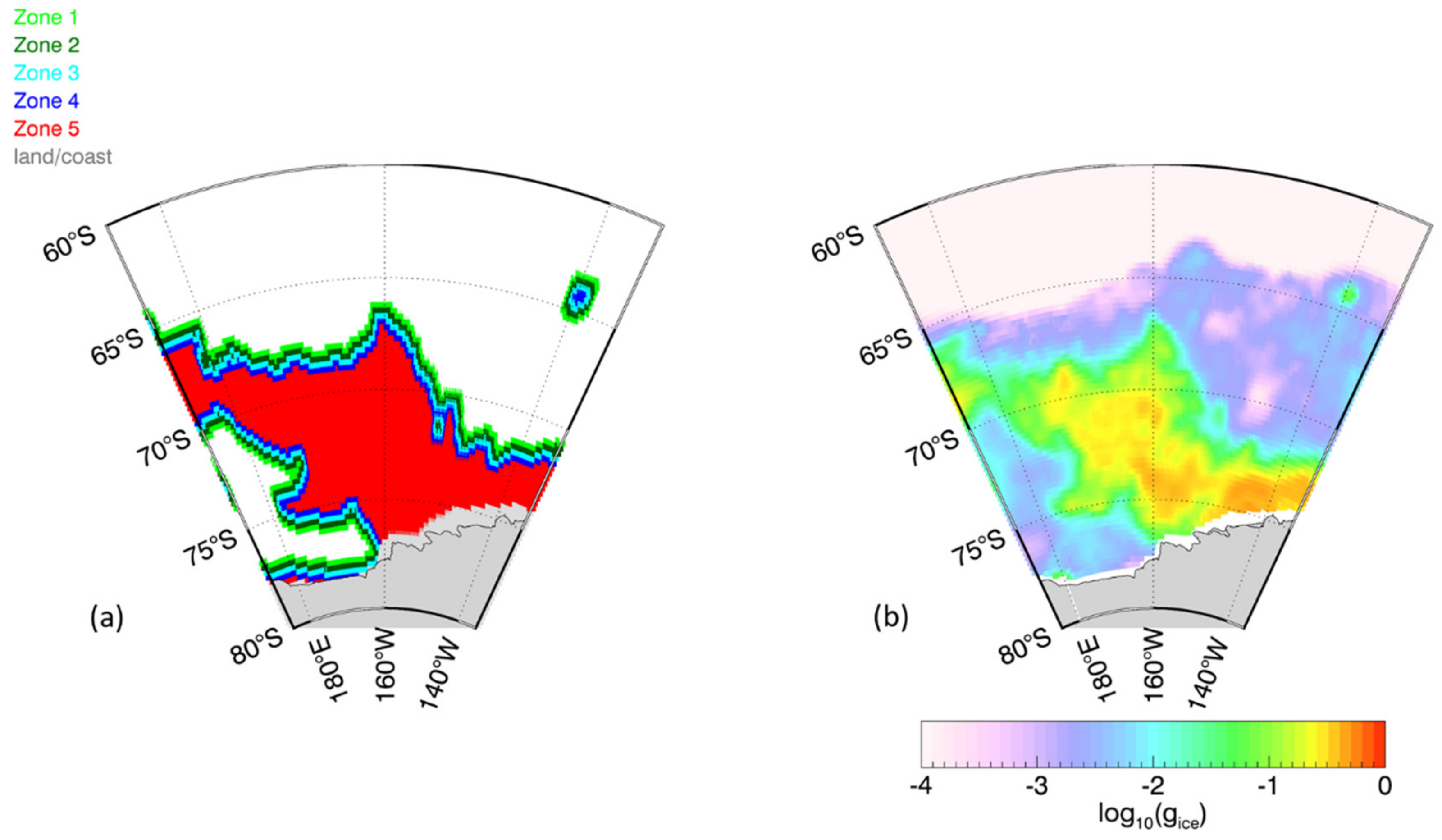
2.3. Sea-Ice Zones
2.4. Sea-Ice Correction
3. Results
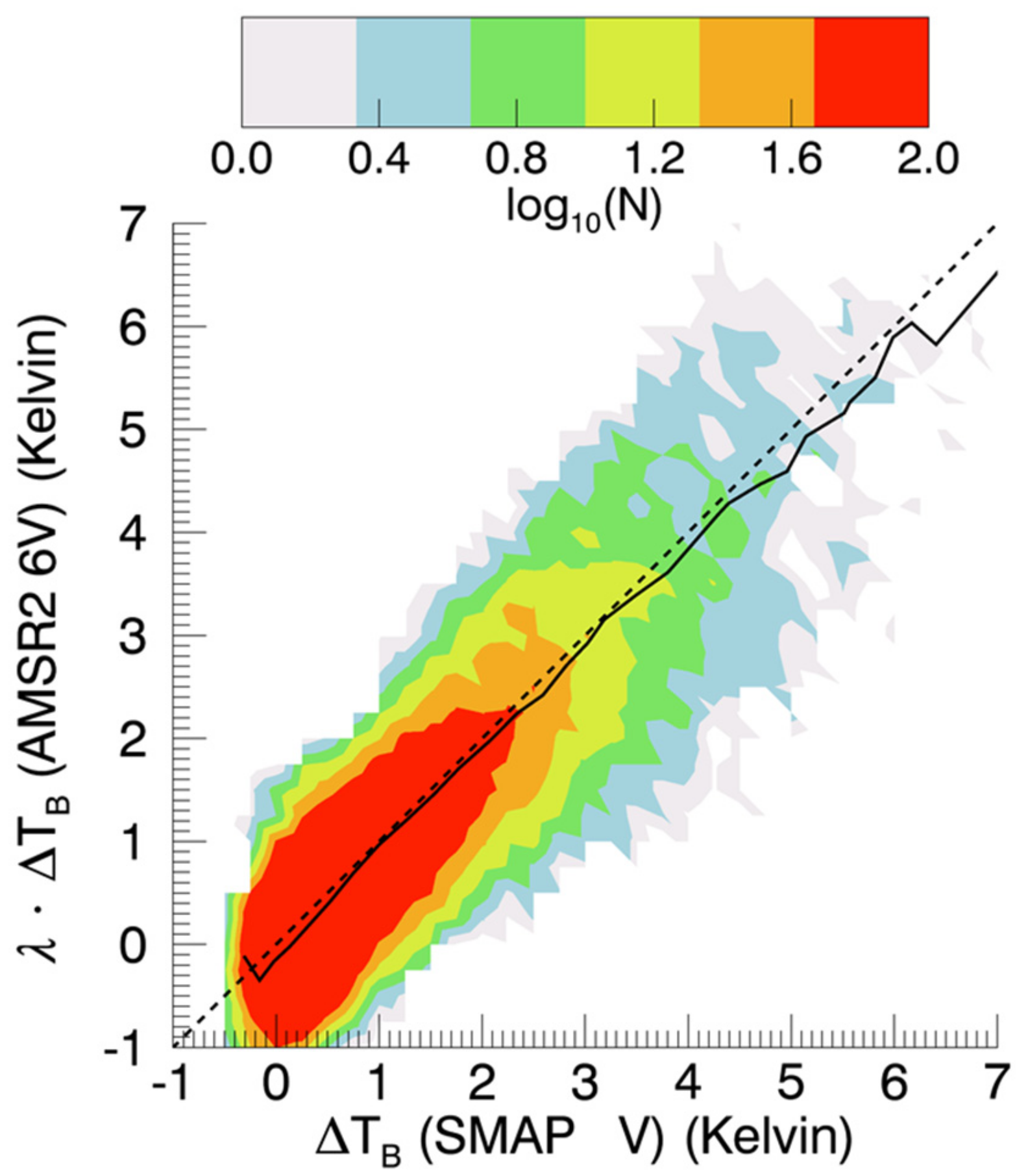
3.1. Correlation between SMAP and AMSR2 Brightness Temperatures
3.2. Performance Evaluation of the Sea-Ice Correction Algorithm
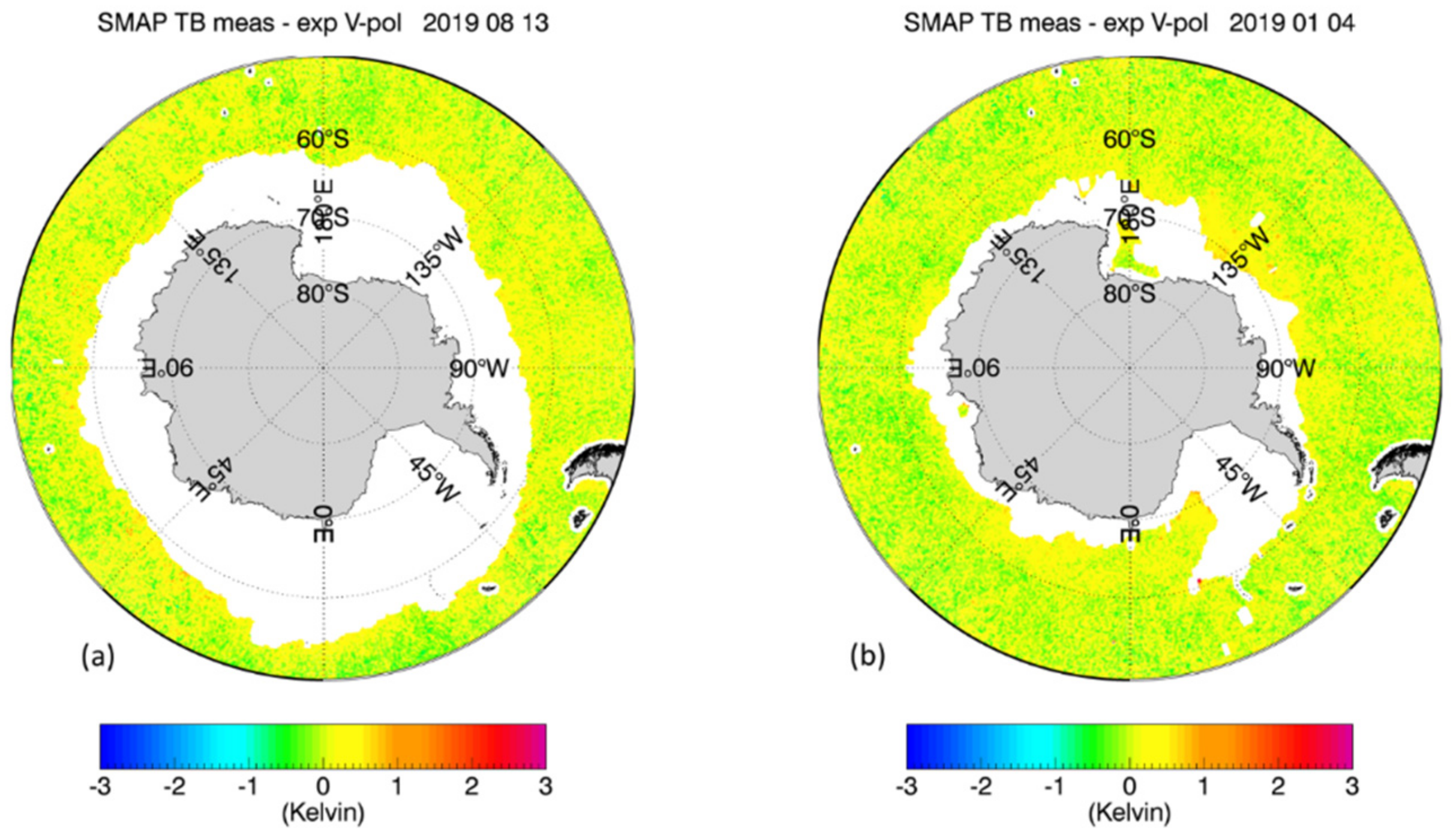
3.3. Antarctic Scene Examples
3.4. Arctic Scene Example
3.5. Icebergs
4. Discussion
- (1)
- Radiometer noise in the AMSR2 TB measurements is a source of error. However, the noise in the individual measurements is strongly reduced in the eight-day averages. Thus, the impact of AMSR2 radiometer noise on our detection and correction algorithms is small.
- (2)
- A larger uncertainty source are errors in the external ancillary fields, which might not get suppressed in the eight-day averaging. This impacts the algorithms from Case 2, which use the ancillary fields to remove atmospheric and wind roughness effects from the AMSR2 TOA TB. We expect the errors in the ancillary fields for SST, wind speed, and direction to increase with increasing sea-ice fraction gice and decreasing distance from the sea-ice edge. The ancillary data sets for these parameters are Level 4 products that rely on microwave satellite observations as input. When approaching the ice edge, the microwave satellite observations are flagged, and, thus, fewer satellite input data become available. This can result in lower accuracy of the ancillary Level 4 product [26].
- (3)
- One of the major assumptions when using the AMSR2 TB to flag and correct the sea-ice contaminated SMAP TB was that the spatial resolutions of the SMAP and the AMSR2 TB measurements are similar. When averaged over eight days, the different orientations of the antenna footprints at a certain location have less of an impact. This means that SMAP and AMSR2 see approximately the same Earth scene. That assumption is of course only approximately fulfilled, and in reality, there is some spatial mismatch between the SMAP and the AMSR2 observations. It is possible to reduce this uncertainty source by resampling the SMAP and all the AMSR2 channels to the same target location and the same spatial resolution by employing the Backus-Gilbert optimum interpolation technique [17]. This resampling would use a polar stereographic projection for selecting the target locations, which is better suited than a regular 0.25° grid in polar regions. This is a project that is currently being considered, but it will require considerable effort.
- (4)
- There are scenarios that can result in a degradation of the good correlation between the SMAP and the AMSR2 TB. The most important one is thin sea-ice, which impacts the higher AMSR2 frequencies more than the lower ones or the SMAP L-band. We note that, at L-band, the sea-ice penetration depth is approximately 0.5 m, and the penetration depth grows with the electromagnetic wavelength. Large areas of thin ice tend to form in the Arctic oceans during fall. In the S hemisphere, this problem is less prevalent. Further studies are necessary to examine if and how much this poses a problem for our flagging and correction method.
- (5)
- Undetected RFI in the AMSR2 TB also constitutes an error source.
- (6)
- A problematic case is sea-ice close to the coast, which can result in simultaneous land and sea-ice contamination of the SMAP antenna field of view. Our proposed sea-ice detection and correction algorithms were not designed to handle this case. Likewise, we expect that the sidelobe correction for land contamination that is currently applied in the NASA/RSS SMAP SSS retrievals [13,14] is not able to cope with this scenario either.
- (7)
- The flagging method is not able to detect observations of very small sea-ice fractions that are significantly lower than the detection threshold of the discriminant analysis (1.5%) and that are not NN or next to NN of an observation that has been flagged by the discriminant analysis.
- (8)
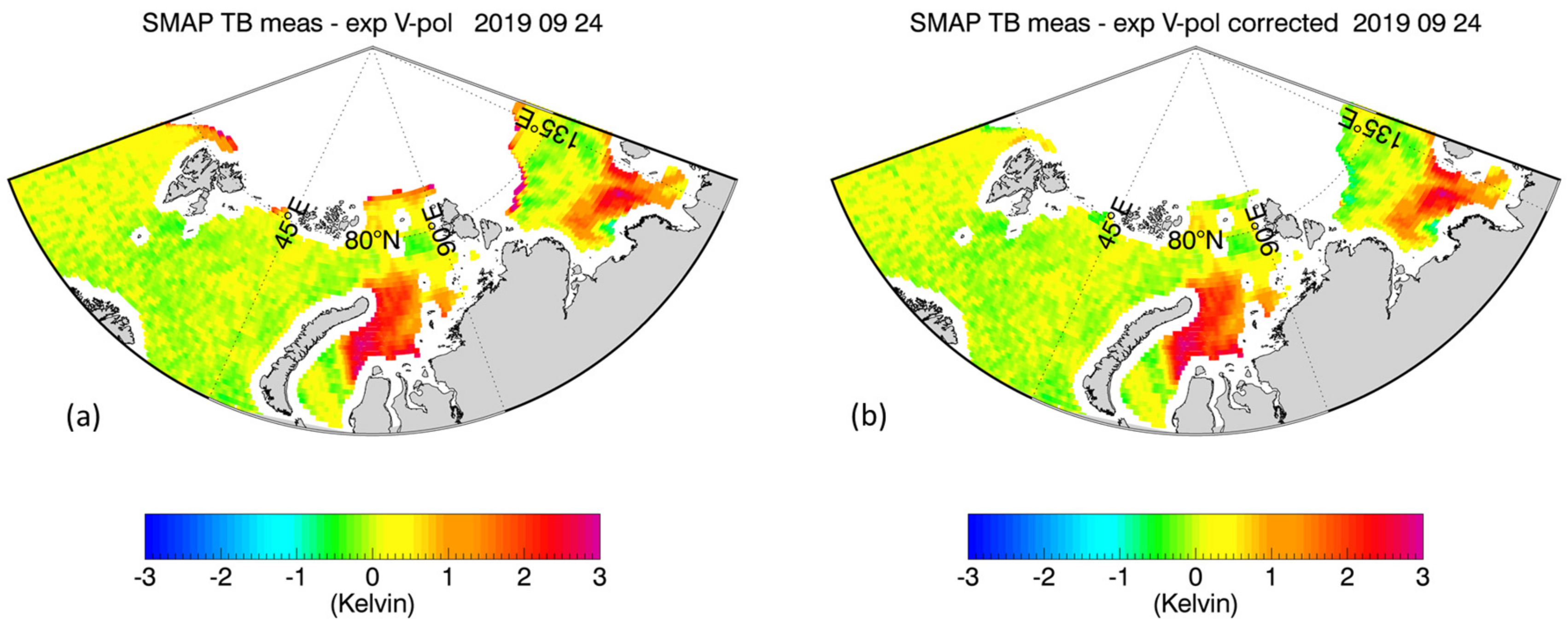
- The statistical linear regressions that are used in the sea-ice correction algorithm are designed to de-bias the ΔTB,0(SMAP) in each sea-ice zone, which they do (Table 5). The residual errors after applying the correction approximately add to zero when summing over all test scenes with standard deviation values listed in Table 5. However, we note that the spatial correlation scales of these residual errors can be quite large. For instance, in Figure 9a, Figure 10b, and Figure 11b green bands are visible in the corrected observations, which indicate larger areas where the algorithm slightly overcorrects. In Figure 9b, a few yellow–orange areas are visible, which indicate that the algorithm undercorrects in these locations. That means that we should not expect that this residual error can be significantly reduced by spatial smoothing. Consequently, we anticipate that the remaining errors in the 70-km NASA/RSS SMAP SSS product will have a similar magnitude than in the 40-km product near the sea-ice edge.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Fisher Linear Discriminant Analysis
References
- Reul, N.; Grodsky, S.A.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea surface salinity estimates from spaceborne L-band radiometers: An overview of the first decade of observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Kao, H.-Y.; Lagerloef, G.; Lee, T.; Melnichenko, O.; Meissner, T.; Hacker, P. Assessment of Aquarius Sea Surface Salinity. Remote Sens. 2018, 10, 1341. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Yueh, S.; Yang, D.; Fore, A.; Hayashi, A.; Lee, T.; Fournier, S.; Holt, B. The Potential and Challenges of Using Soil Moisture Active Passive (SMAP) Sea Surface Salinity to Monitor Arctic Ocean Freshwater Changes. Remote Sens. 2018, 10, 869. [Google Scholar] [CrossRef] [Green Version]
- Olmedo, E.; Gabarró, C.; González-Gambau, V.; Martínez, J.; Ballabrera-Poy, J.; Turiel, A.; Portabella, M.; Fournier, S.; Lee, T. Seven Years of SMOS Sea Surface Salinity at High Latitudes: Variability in Arctic and Sub-Arctic Regions. Remote Sens. 2018, 10, 1772. [Google Scholar] [CrossRef] [Green Version]
- Supply, A.; Boutin, J.; Vergely, J.-L.; Kolodziejczyk, N.; Reverdin, G.; Reul, N.; Tarasenko, A. New insights into SMOS sea surface salinity retrievals in the Arctic Ocean. Remote Sens. Environ. 2020, 249, 112027. [Google Scholar] [CrossRef]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Gordon, A.; et al. Satellite Salinity Observing System: Recent Discoveries and the Way Forward. Front. Mar. Sci. 2019, 6, 243. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J.; Le Vine, D.M. Aquarius Salinity Retrieval Algorithm Theoretical Basis Document (ATBD). End of Mission Version. RSS Technical Report 120117. 2017. Available online: images.remss.com/papers/tech_reports/2017/Meissner_AQ_ATBD_EOM_final.pdf (accessed on 30 October 2021).
- Heygster, G.; Huntemann, M.; Ivanova, N.; Saldo, R.; Pedersen, L.T. Response of passive microwave sea ice concentration algorithms to thin ice. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3618–3621. [Google Scholar]
- Meier, W.N.; Fetterer, F.; Savoie, M.; Mallory, S.; Duerr, R.; Stroeve, J. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 3. 2017. Available online: https://nsidc.org/data/g02202/versions/3 (accessed on 30 October 2021). [CrossRef]
- Danish Meteorological Institute Global Sea Ice Concentration (AMSR-2) | OSI SAF. Processed by the OSI-SAF Hybrid Dynamic Algorithm. Available online: https://osi-saf.eumetsat.int/products/osi-408 (accessed on 30 October 2021).
- Meissner, T.; Wentz, F.J.; Manaster, A.; Lindsley, R. NASA/RSS SMAP Level 2C Sea Surface Salinity V4.0 Validated Dataset. 2019. Available online: https://podaac.jpl.nasa.gov/dataset/SMAP_RSS_L2_SSS_V4 (accessed on 30 October 2021). [CrossRef]
- Fournier, S.; Lee, T.; Tang, W.; Steele, M.; Olmedo, E. Evaluation and Intercomparison of SMOS, Aquarius, and SMAP Sea Surface Salinity Products in the Arctic Ocean. Remote Sens. 2019, 11, 3043. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Wentz, F.J.; Manaster, A.; Lindsley, R. NASA/RSS SMAP Salinity: Version 4.0 Validated Release: Release Notes, Algorithm Theoretical Basis Document (ATBD), Validation, Data Format Specification. RSS Technical Report 082219. 2019. Available online: https://data.remss.com/smap/SSS/Release_V4.0.pdf (accessed on 30 October 2021).
- Meissner, T.; Wentz, F.J.; Vine, D.M.L. The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases. Remote Sens. 2018, 10, 1121. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Wentz, F.J.; Ricciardulli, L. The emission and scattering of L-band microwave radiation from rough ocean surfaces and wind speed measurements from the Aquarius sensor. J. Geophys. Res. Oceans 2014, 119, 6499–6522. [Google Scholar] [CrossRef]
- Ashcroft, P.; Wentz, F.J. AMSR Level 2A Algorithm Theoretical Basis Document (ATBD). RSS Technical Report 121599B-1. 2000. Available online: https://images.remss.com/papers/rsstech/2000_121599B-1_Wentz_AMSR_Level2A_Algorithm_ATBD.pdf (accessed on 30 October 2021).
- Poe, G.A. Optimum interpolation of imaging microwave radiometer data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 800–810. [Google Scholar] [CrossRef] [Green Version]
- Wentz, F.J. AMSR-2 Air-Sea Essential Climate Variables RSS Version 8.2. RSS Technical Report 05112021. 2021. Available online: https://images.remss.com/papers/tech_reports/2021/AMSR-2_Air-Sea_Essential_Climate_Variables_RSS_Version_8.2.pdf (accessed on 30 October 2021).
- Wentz, F.J.; Meissner, T. Atmospheric absorption model for dry air and water vapor at microwave frequencies below 100 GHz derived from spaceborne radiometer observations: Atmospheric Absorption Model. Radio Sci. 2016, 51, 381–391. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Wentz, F.J. The Emissivity of the Ocean Surface Between 6 and 90 GHz Over a Large Range of Wind Speeds and Earth Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Wentz, F.J.; Meissner, T. AMSR Ocean Algorithm Theoretical Basis Document (ATBD). RSS Technical Report 121599A-1. 2000. Available online: images.remss.com/papers/rsstech/2000_121599A-1_Wentz_AMSR_Ocean_Algorithm_ATBD_Version2.pdf (accessed on 30 October 2021).
- Meissner, T.; Wentz, F.J. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1836–1849. [Google Scholar] [CrossRef] [Green Version]
- Chassignet, E.; Hurlburt, H.; Metzger, E.J.; Smedstad, O.; Cummings, J.; Halliwell, G.; Bleck, R.; Baraille, R.; Wallcraft, A.; Lozano, C.; et al. US GODAE: Global Ocean Prediction with the HYbrid Coordinate Ocean Model (HYCOM). Oceanography 2009, 22, 64–75. [Google Scholar] [CrossRef]
- Global Ocean Forecasting System GOFS 3.1: 41-layer HYCOM + NCODA Global 1/12° Analysis. Available online: https://www.hycom.org/data/glby0pt08/expt-93pt0 (accessed on 20 October 2021).
- Canada Meteorological Center GHRSST Level 4 CMC0.1deg Global Foundation Sea Surface Temperature Analysis (GDS version 2). 2017. Available online: https://podaac.jpl.nasa.gov/dataset/CMC0.1deg-CMC-L4-GLOB-v3.0 (accessed on 20 October 2021). [CrossRef]
- Mears, C.A.; Scott, J.; Wentz, F.J.; Ricciardulli, L.; Leidner, S.M.; Hoffman, R.; Atlas, R. A Near-Real-Time Version of the Cross-Calibrated Multiplatform (CCMP) Ocean Surface Wind Velocity Data Set. J. Geophys. Res. Oceans 2019, 124, 6997–7010. [Google Scholar] [CrossRef]
- Wentz, F.J.; Scott, J.; Hoffman, R.; Leidner, M.; Atlas, R.; Ardizzone, J. Remote Sensing Systems Cross-Calibrated Multi-Platform (CCMP) 6-hourly ocean vector wind analysis product on 0.25 deg grid, Version 2.0. 2015. Available online: www.remss.com/measurements/ccmp (accessed on 30 October 2021).
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A Cross-calibrated, Multiplatform Ocean Surface Wind Velocity Product for Meteorological and Oceanographic Applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- National Centers for Environmental Prediction NCEP Data Products GFS and GDAS. Available online: https://www.nco.ncep.noaa.gov/pmb/products/gfs/ (accessed on 30 October 2021).
- Precipitation Processing System At NASA GSFC GPM IMERG Final Precipitation L3 Half Hourly 0.1 degree x 0.1 degree V06. 2019. Available online: https://disc.gsfc.nasa.gov/datacollection/GPM_3IMERGHH_06.html (accessed on 30 October 2021). [CrossRef]
- Meissner, T.; Wentz, F.J.; Scott, J.; Vazquez-Cuervo, J. Sensitivity of Ocean Surface Salinity Measurements From Spaceborne L-Band Radiometers to Ancillary Sea Surface Temperature. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7105–7111. [Google Scholar] [CrossRef]
- Andersen, S.; Tonboe, R.; Kern, S.; Schyberg, H. Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using numerical weather prediction model fields: An intercomparison of nine algorithms. Remote Sens. Environ. 2006, 104, 374–392. [Google Scholar] [CrossRef]
- Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef] [Green Version]
- Tian, T.; Tonboe, R.; Lavelle, J. The EUMETSAT OSI SAF AMSR-2 Sea Ice Concentration Algorithm Theoretical Basis Document (ATBD). Product OSI-408. Version 1.0. February 2015. Available online: https://osisaf-hl.met.no/sites/osisaf-hl.met.no/files/baseline_document/osisaf_cdop2_ss2_atbd_amsr2-sea-ice-conc_v1p1.pdf (accessed on 8 December 2021).
- U.S. National Ice Center Antarctic Iceberg Tracking. Available online: https://usicecenter.gov/Resources/AntarcticIcebergs (accessed on 30 October 2021).
- Vazquez-Cuervo, J.; Gentemann, C.; Tang, W.; Carroll, D.; Zhang, H.; Menemenlis, D.; Gomez-Valdes, J.; Bouali, M.; Steele, M. Using Saildrones to Validate Arctic Sea-Surface Salinity from the SMAP Satellite and from Ocean Models. Remote Sens. 2021, 13, 831. [Google Scholar] [CrossRef]
- Donlon, C. Copernicus Imaging Microwave Radiometer (CIMR) Mission Requirement Document. 2020. Available online: https://esamultimedia.esa.int/docs/EarthObservation/CIMR-MRD-v3.0-20190930_Issued.pdf (accessed on 30 October 2021).
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001; ISBN 9780471056690. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006; ISBN 9780387310732. [Google Scholar]
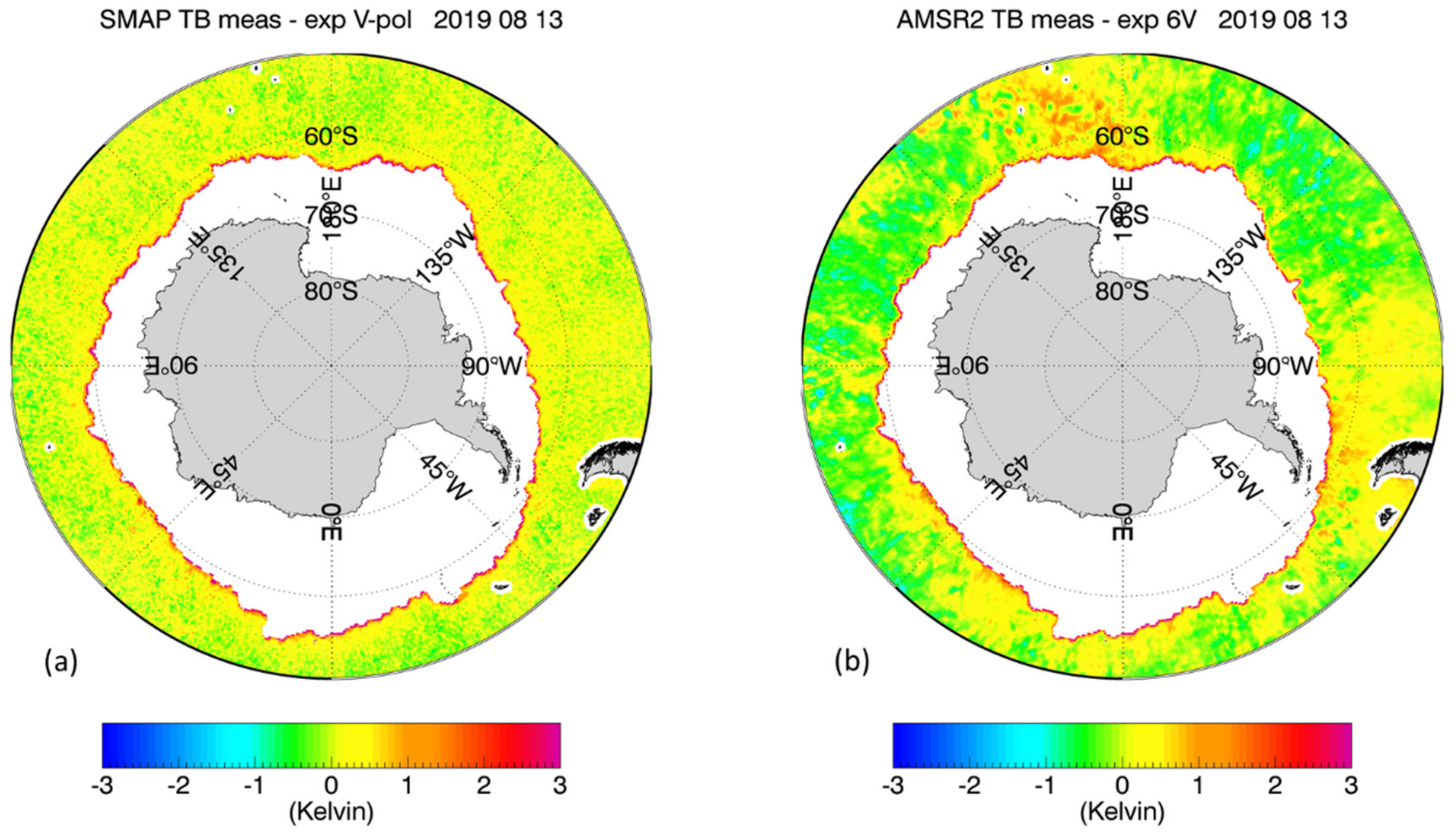
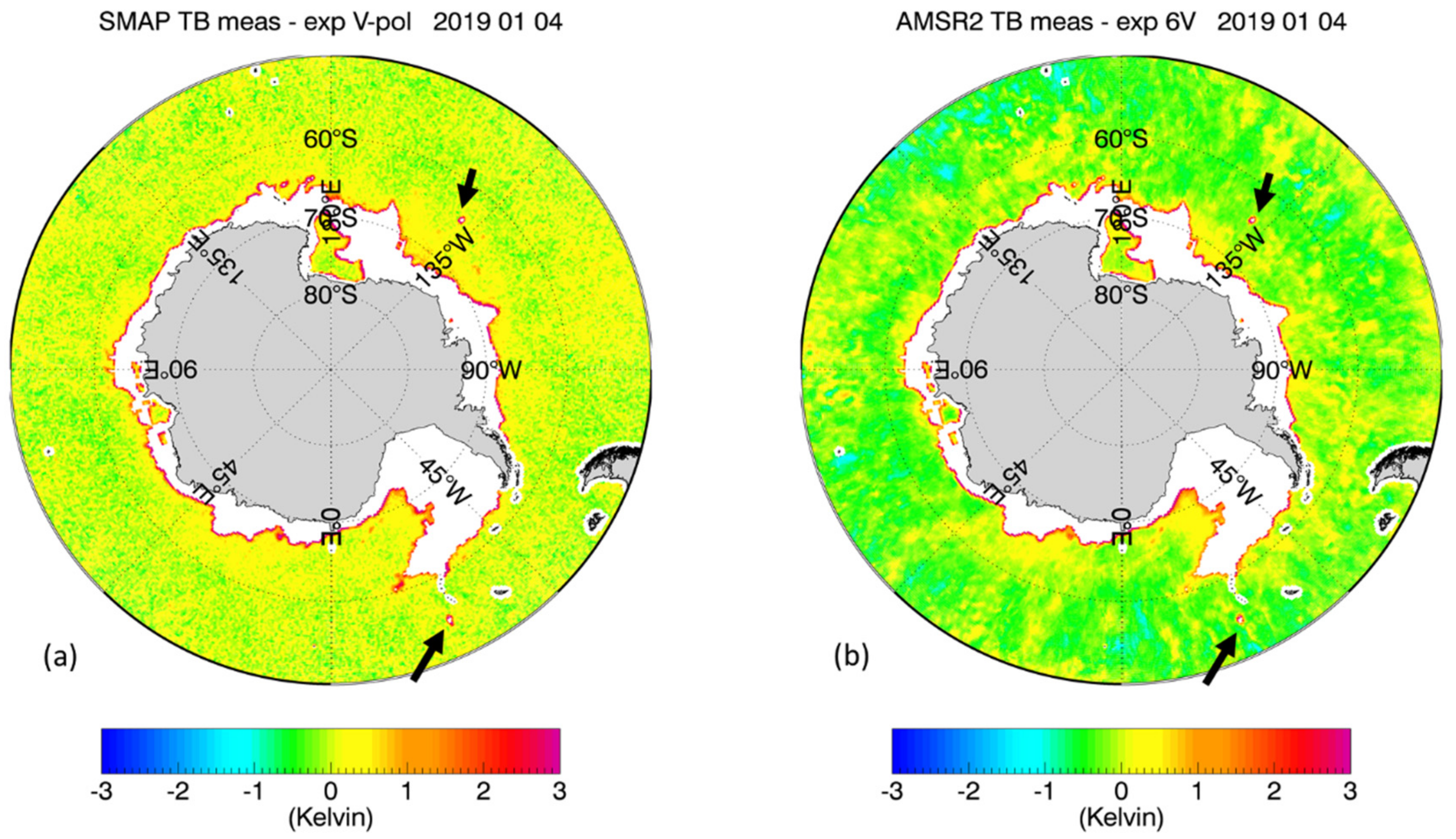
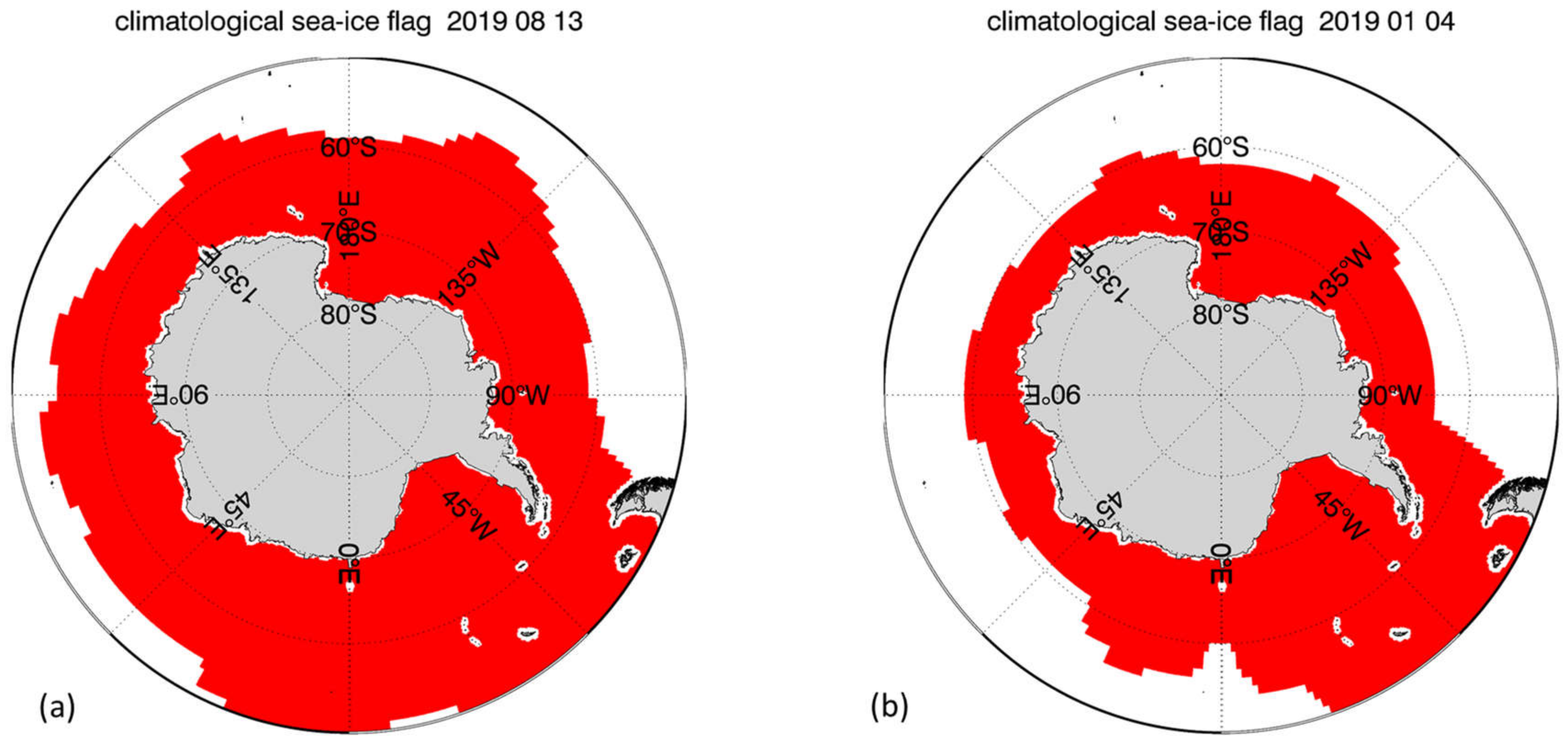
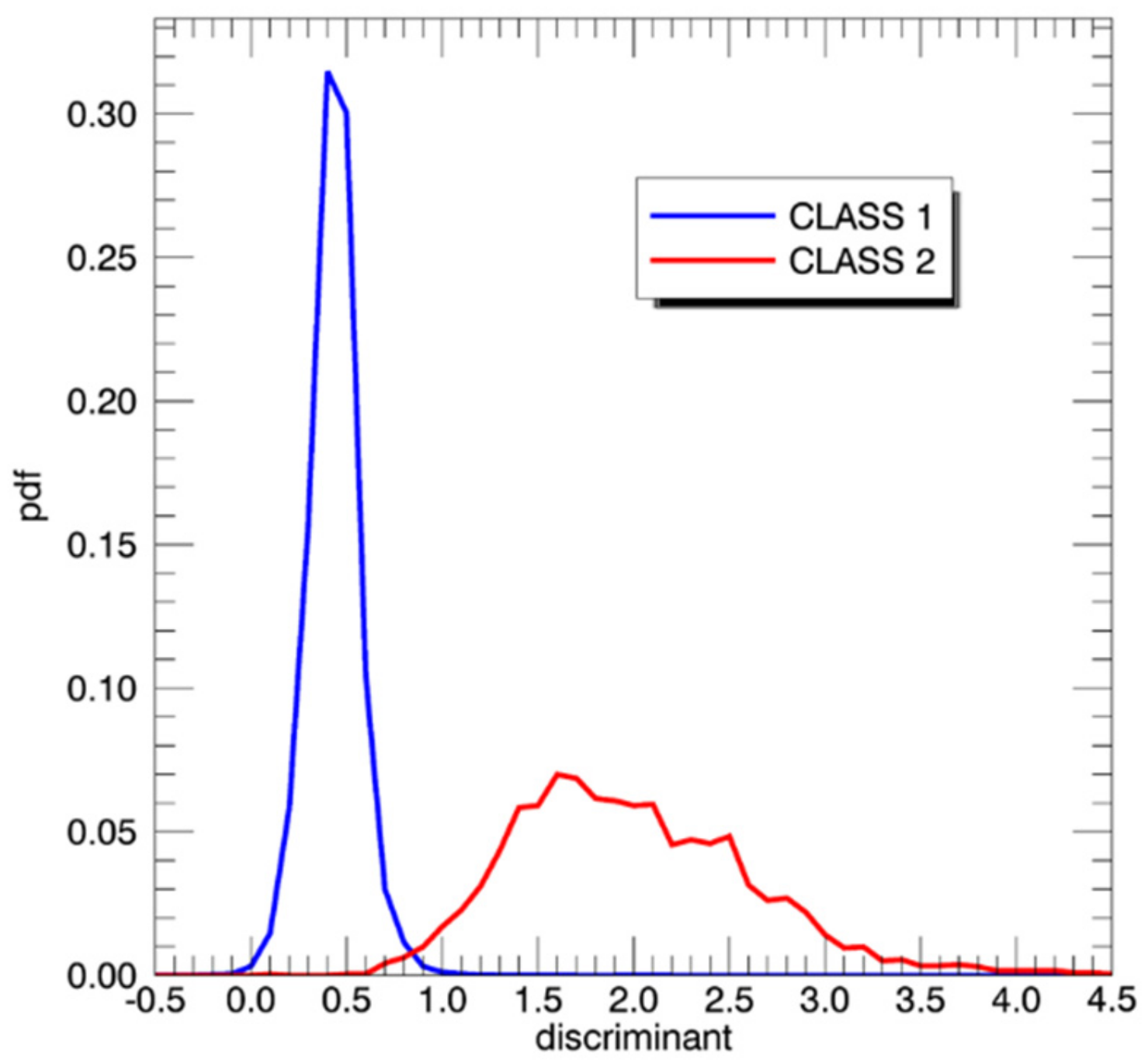


| Set | Date Range | SMAP Orbit Range | AMSR2 Orbit Range | Pole | Used for |
|---|---|---|---|---|---|
| 1 | 21–28 January 2018 | 15,875–15,991 | 30,209–30,325 | N | training discriminant flagging |
| S | training regressions for sea-ice correction | ||||
| 2 | 14–21 April 2018 | 17,089–17,205 | 31,418–31,533 | N | training discriminant flagging |
| S | training regressions for sea-ice correction | ||||
| 3 | 16–23 July 2018 | 18,448–18,565 | 32,772–32,888 | N | training discriminant flagging |
| S | training regressions for sea-ice correction | ||||
| 4 | 09–16 October 2018 | 19,692–19,808 | 34,010–34,125 | N | training discriminant flagging |
| S | training regressions for sea-ice correction | ||||
| 5 | 01–08 January 2019 | 20,920–21,037 | 35,233–35,349 | S | testing discriminant flagging testing regressions for sea-ice correction |
| 6 | 24–31 March 2019 | 22,120–22,236 | 36,427–36,543 | S | |
| 7 | 10–17 August 2019 | 24,153–24,269 | 38,452–38,567 | S | |
| 8 | 21–28 September 2019 | 24,767–24,883 | 39,063–39,179 | S | |
| N | Arctic example (Section 3.4) | ||||
| 9 | 27 February–06 March 2021 | 32,445–32,561 | 46,708–46,824 | S | iceberg A-68 (Section 3.5) |
| Channel i | 6.93 V | 6.93 H | 10.65 V | 10.65 H | 18.7 V | 18.7 H | 23.8 V | 23.8 H | 36.5 V | 36.5 H | d |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wi (case 1) | 0.140082 | −0.46514 | 0.254423 | −0.08172 | −0.62169 | 0.486014 | 0.168304 | −0.12771 | −0.15391 | 0.03985 | 52.05 |
| Wi (case 2) | 0.01366 | −0.50493 | 0.43747 | −0.10526 | −0.70372 | 0.20662 | −0.00025 | 0.06365 | −0.00406 | 0.02058 | 0.85 |
| Case 1 | Case 2 | |
|---|---|---|
| missed detection rate | 0.15% | 0.12% |
| false alarm rate | 0.39% | 0.06% |
| Product | ΔTB,0 (6V) | ΔTB,corr1 | ΔTB,corr2 |
|---|---|---|---|
| correlation | 0.96 | 0.96 | 0.96 |
| No Correction | Case 1 Using AMSR2 TB TOA | Case 2 Using AMSR2 E0 Meas-Exp | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Zone | estimated gice | Bias | Std.Dev | RMS | Bias | Std.Dev | RMS | Bias | Std.Dev | RMS |
| 0 | <0.05% | 0.07 | 0.20 | 0.21 | ||||||
| 1 | 0.3% | 0.33 | 0.28 | 0.43 | −0.03 | 0.27 | 0.27 | 0.02 | 0.28 | 0.28 |
| 2 | 0.6% | 0.70 | 0.56 | 0.89 | 0.06 | 0.52 | 0.52 | 0.02 | 0.50 | 0.50 |
| 3 | 2.2% | 2.76 | 2.02 | 3.42 | 0.19 | 1.32 | 1.33 | −0.10 | 1.33 | 1.33 |
| 4 | 9.6% | 11.62 | 8.07 | 14.14 | −0.01 | 3.12 | 3.12 | −0.51 | 3.35 | 3.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meissner, T.; Manaster, A. SMAP Salinity Retrievals near the Sea-Ice Edge Using Multi-Channel AMSR2 Brightness Temperatures. Remote Sens. 2021, 13, 5120. https://doi.org/10.3390/rs13245120
Meissner T, Manaster A. SMAP Salinity Retrievals near the Sea-Ice Edge Using Multi-Channel AMSR2 Brightness Temperatures. Remote Sensing. 2021; 13(24):5120. https://doi.org/10.3390/rs13245120
Chicago/Turabian StyleMeissner, Thomas, and Andrew Manaster. 2021. "SMAP Salinity Retrievals near the Sea-Ice Edge Using Multi-Channel AMSR2 Brightness Temperatures" Remote Sensing 13, no. 24: 5120. https://doi.org/10.3390/rs13245120
APA StyleMeissner, T., & Manaster, A. (2021). SMAP Salinity Retrievals near the Sea-Ice Edge Using Multi-Channel AMSR2 Brightness Temperatures. Remote Sensing, 13(24), 5120. https://doi.org/10.3390/rs13245120






